Laboratory Investigation on Shear Modulus and Damping Properties of Port Soft Clay Improved by Dynamic Compaction

Abstract

Dynamic compaction has been widely applied to reinforce soft soils in port areas due to its high efficiency and cost-effectiveness. However, a comprehensive understanding of the deformation mechanisms and stiffness evolution of treated soils under static and dynamic loading remains limited. This study integrated one-dimensional consolidation tests, resonant column tests, and bender element tests to systematically investigate the mechanical behavior of soft clay before and after dynamic compaction under varying stress levels and loading frequencies. The results show that dynamic compaction significantly enhances the compression modulus and consolidation stability of soft clay while reducing the settlement rate during primary consolidation. The shear modulus exhibits nonlinear degradation with increasing strain, whereas the damping ratio increases rapidly before reaching a plateau, indicating typical strain-dependent behavior. A three-parameter model and a second-order polynomial model effectively characterize the degradation of the shear modulus and the evolution of the damping behavior, respectively. Moreover, the strong consistency between the resonant column and bender element test results enables continuous characterization of the shear stiffness across small- to intermediate-strain ranges. These findings provide theoretical insight and practical guidance for modeling the dynamic response of soft clay and evaluating the effectiveness of dynamic compaction as a ground improvement technique.

1. Introduction

Soft clay is widely distributed in the coastal and lacustrine regions of China and is characterized by a high natural moisture content, large void ratio, high compressibility, and low shear strength [1,2]. In port areas, its substantial settlement and limited load-bearing capacity pose persistent challenges to the operational stability and long-term serviceability of port infrastructure [3,4]. To improve the bearing capacity and deformation resistance of soft clay foundations, various ground improvement techniques have been adopted. Among them, dynamic compaction is recognized as an efficient and cost-effective method. This technique applies high-energy impact loading to dissipate excess pore water pressure and restructure the soil fabric, thereby increasing its density and shear strength. Laboratory investigations by Zhou et al. [5] confirmed that dynamic compaction can significantly enhance the undrained shear strength and structural integrity of soft soils, demonstrating its suitability for port engineering applications. However, conventional assessments of dynamic compaction have primarily focused on static performance indicators, such as the bearing capacity, settlement magnitude, and compression modulus [6,7,8], with limited attention to the dynamic response under small-strain conditions. In particular, essential parameters such as the shear modulus and damping ratio remain insufficiently and systematically explored.

The one-dimensional consolidation test is a fundamental method for evaluating the compressibility and settlement behavior of soft soils. It enables quantitative assessment of the evolution of the compression modulus, initial settlement rate, and secondary consolidation under loading and is widely used to assess the effectiveness of ground improvement techniques in controlling deformation [9,10,11,12]. Peng et al. [13] demonstrated that factors such as temperature, the sample height, and bio-oxidation significantly influence the consolidation behavior of peat soils. Xia et al. [14] found that the combination of vacuum and surcharge preloading effectively accelerates the consolidation process and enhances pore pressure dissipation. Ren et al. [15] confirmed the advantages of a dual-vacuum preloading system for consolidating highly saturated soft soils through large-scale laboratory tests, which were further validated by numerical simulations. However, one-dimensional consolidation tests primarily capture the stress–strain response under static loading conditions and are insufficient for characterizing the stiffness response and energy dissipation behavior of soft soils subjected to dynamic disturbances such as seismic loading, wave action, or traffic-induced vibration.

The shear modulus and damping ratio of soft clay exhibit pronounced strain dependency within the small-strain range and are critical parameters for characterizing the dynamic shear stiffness and energy dissipation capacity. Resonant column tests (RCAs) enable the accurate determination of these parameters under controlled confining pressures by employing frequency sweeps and resonance response analysis across various soil types [16,17,18,19,20]. Similarly, bender element (BE) tests, as a non-destructive technique, measure the shear wave velocity at extremely small strains and allow for the calculation of the maximum shear modulus. Using both methods, Jurček et al. [21] demonstrated that the small-strain stiffness of soft soils is governed by the effective stress and plasticity index. Recent studies have systematically investigated the shear modulus and damping behavior of soft soils under varying disturbance levels, effective stress conditions, and loading paths [22,23,24]. Bao et al. [25] emphasized that frequency effects significantly influence damping ratios and should be considered in the calibration of dynamic constitutive models. Yan et al. [24] reported that elevated concentrations of heavy metal ions alter the soil microstructure and void ratio, leading to the degradation of dynamic properties and highlighting the regulatory influence of environmental factors. Abdelaal et al. [26] showed that particle size distribution strongly affects the small-strain stiffness and initial damping ratio, with the particle arrangement playing a dominant role in governing the nonlinear response behavior. These findings confirm the coupled effects of the stress state, strain amplitude, and excitation frequency on the dynamic response of soils and provide a robust parameter foundation for the development of dynamic constitutive models [17,27,28]. Lin et al. [29] quantitatively analyzed the variation in the shear modulus and damping ratio of representative soft clays in southern China using RCAs and cyclic triaxial tests under different stress paths and excitation frequencies. Similarly, Umut Umu [30] conducted a systematic investigation of the dynamic behavior of silty clay under multiple disturbance conditions.

To characterize the nonlinear variation in the shear modulus and damping ratio with the shear strain, various normalized predictive models have been proposed. Meng et al. [31] first introduced a hyperbolic normalization model for the shear modulus and damping ratio based on resonant column and torsional shear tests, laying the theoretical foundation for the small-strain stiffness and initial damping behavior. Yan et al. and Gobbi et al. [32,33] further developed normalized models for soils with varying plasticity indices, highlighting the dominant role of plasticity in dynamic nonlinearity. Subsequent studies, utilizing advanced testing systems with enhanced precision, extended these models to broader strain ranges and explored the coupled effects of confining the pressure, loading frequency, and strain amplitude [28,34,35,36]. Chen et al. [37] proposed a normalization model based on the equivalent modulus and damping ratio, revealing complex interactions among the steel slag content, curing time, and strain amplitude. Senetakis et al. [38] emphasized the importance of preserving sample integrity and controlling stress paths for the accurate characterization of dynamic parameters. Liu et al. [39] developed a normalization model for fill soils, demonstrating the coupled influence of the soil structure and stress history on the dynamic response. For marine soft soils commonly encountered in port and offshore engineering, high sensitivity to strain amplitude and excess pore pressure present additional challenges for model development [40,41]. Dai et al. [42] investigated the evolution of the shear modulus and damping ratio in Bohai silty clay and found that the loading frequency significantly influences the nonlinear behavior in the medium-strain range. Li et al. [43] examined the nonlinear control mechanisms of marine silty clay under varying disturbance levels and consolidation states. Liu et al. [44] developed a unified model for sand based on extensive cyclic loading tests, which is capable of capturing the evolution of the modulus and damping across small- to medium-strain ranges. Feng et al. [45] further introduced a deep neural network model, which significantly improved the fitting accuracy and generalization performance across a wide strain range. Nevertheless, most of the existing models do not account for the structural reorganization induced by dynamic compaction, and their applicability under such conditions remains to be validated.

Despite substantial research efforts, the static and dynamic responses of dynamically compacted soft clay remain insufficiently understood, hindering a comprehensive interpretation of its stress–strain behavior. To address this issue, the present study systematically investigated the deformation characteristics of soft clay before and after dynamic compaction through a series of laboratory experiments and model-fitting analyses. One-dimensional consolidation tests were conducted to examine the evolution of the settlement behavior under varying consolidation pressures and reinforcement conditions. Resonant column and bender element tests were jointly employed to obtain shear modulus and damping ratio curves as functions of the excitation frequency and shear strain, enabling an in-depth evaluation of the strain dependency and stiffness evolution. Furthermore, the predictive performances of the three-parameter model, the Modified Drucker model, and the Hardin–Drnevich model were assessed to determine their accuracy and applicability in capturing nonlinear dynamic behavior. The findings provide both technical support for and scientific insight into the dynamic characterization of reinforced soft clay and the optimization of ground improvement design.

2. Materials and Test Methods

2.1. Test Materials and Sample Preparation

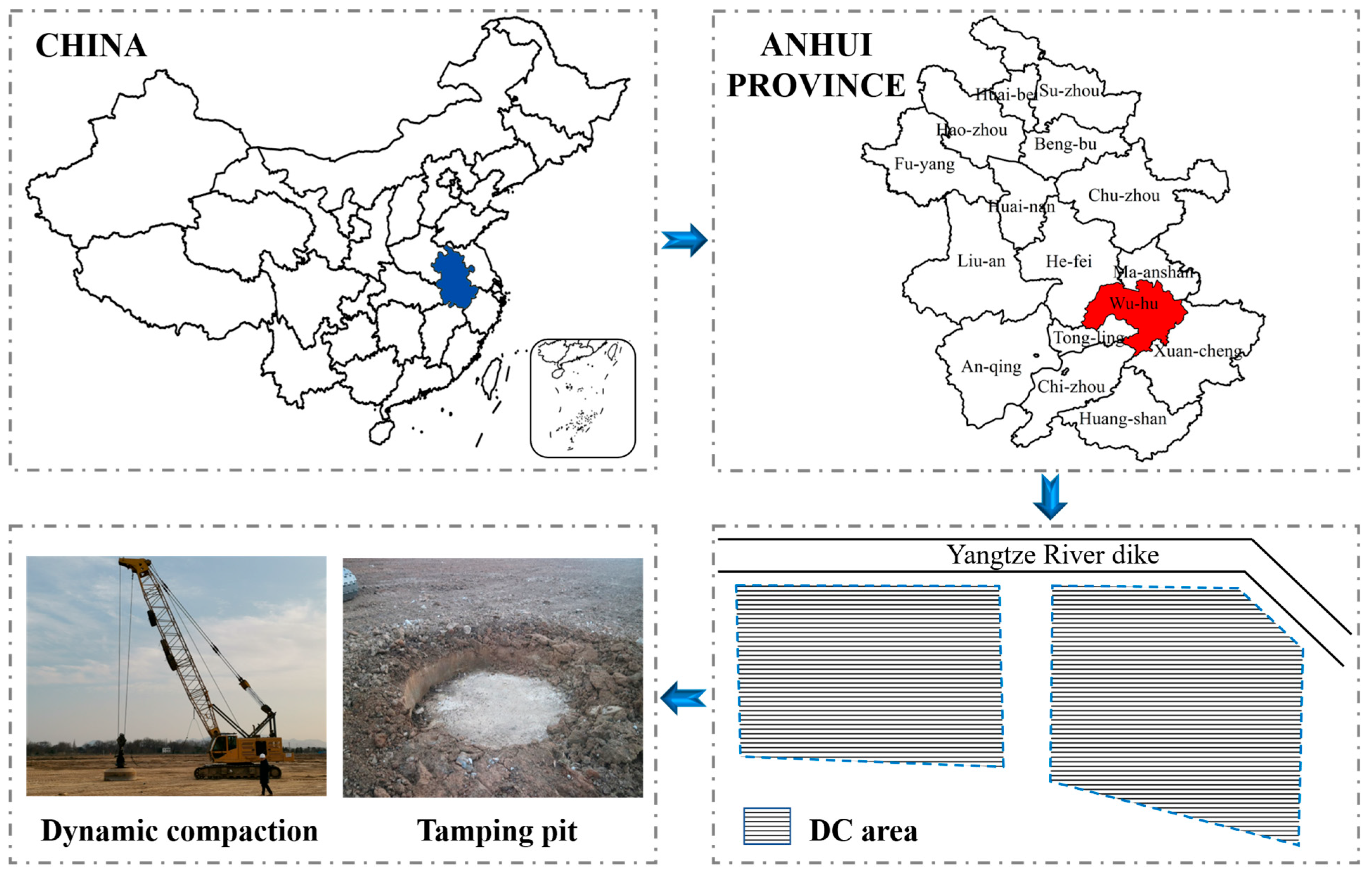
Soft soil samples for this study were collected from an LNG terminal construction site in Wuhu. The target stratum was a silty clay layer characterized by a high water content and low strength, a common critical foundation material in coastal engineering. Undisturbed specimens were obtained using thin-walled Shelby tubes (100 mm in diameter and 500 mm in height) to preserve their natural moisture and structure. Immediately after extraction, the tubes were sealed and transported under controlled conditions. Dynamic compaction was conducted using a 100 kN steel tamper dropped from a height of 10 m, delivering a single-blow energy of 1000 kN·m. Each tamping point received two blows in a staggered (plum-blossom) pattern with a 4 m spacing, resulting in approximately 25% overlap of the tamping footprints. Two full passes were carried out to ensure adequate soil densification and homogenization across the improvement zone (Figure 1). The adopted compaction protocol reflects commonly applied practices in large-scale ground improvement in soft clay foundations.

The tested soil, classified as silty clay with a mineralogical composition dominated by quartz and feldspar, was sampled from a representative stratum at depths of 2–4 m. Reinforced specimens were collected from the improved zone approximately 0.8–1.0 m from the center of each tamping crater, where the effects of dynamic compaction were most pronounced. In contrast, unreinforced specimens were obtained from adjacent untreated areas at comparable depths to ensure baseline consistency. At the microscopic scale, the soil displayed a loose skeletal framework interspersed with aggregated particles, characteristic of marine soft clay in eastern China. To preserve the in situ moisture and structural integrity, each specimen was immediately wrapped in sheet metal and sealed with paraffin after preparation. For each test condition, three parallel specimens were prepared, and the reported results represent average values to enhance the data reliability. Fundamental physical and mechanical properties were determined through conventional geotechnical testing and parameter conversion, as summarized in

Table 1. Basic physical and mechanical properties of soft soil in the port area.

Soil Type	Water Content (%)	Density (g/cm3)	Void Ratio	Plastic Limit (%)	Liquid Limit (%)	Plasticity Index	Liquidity Index
NC	38.8	1.84	1.067	21.2	38.7	17.5	1.01
DC	24.9	1.99	0.702	21.2	33.1	11.9	0.79

Note: NC refers to unreinforced (natural) soil samples, while DC refers to soil samples reinforced through dynamic compaction.

. The findings demonstrate that dynamic compaction markedly reduced the soil’s void ratio while increasing its density and shear stiffness, thereby providing a robust basis for subsequent analyses of its time-dependent and dynamic behavior.

2.2. One-Dimensional Consolidation Test Method

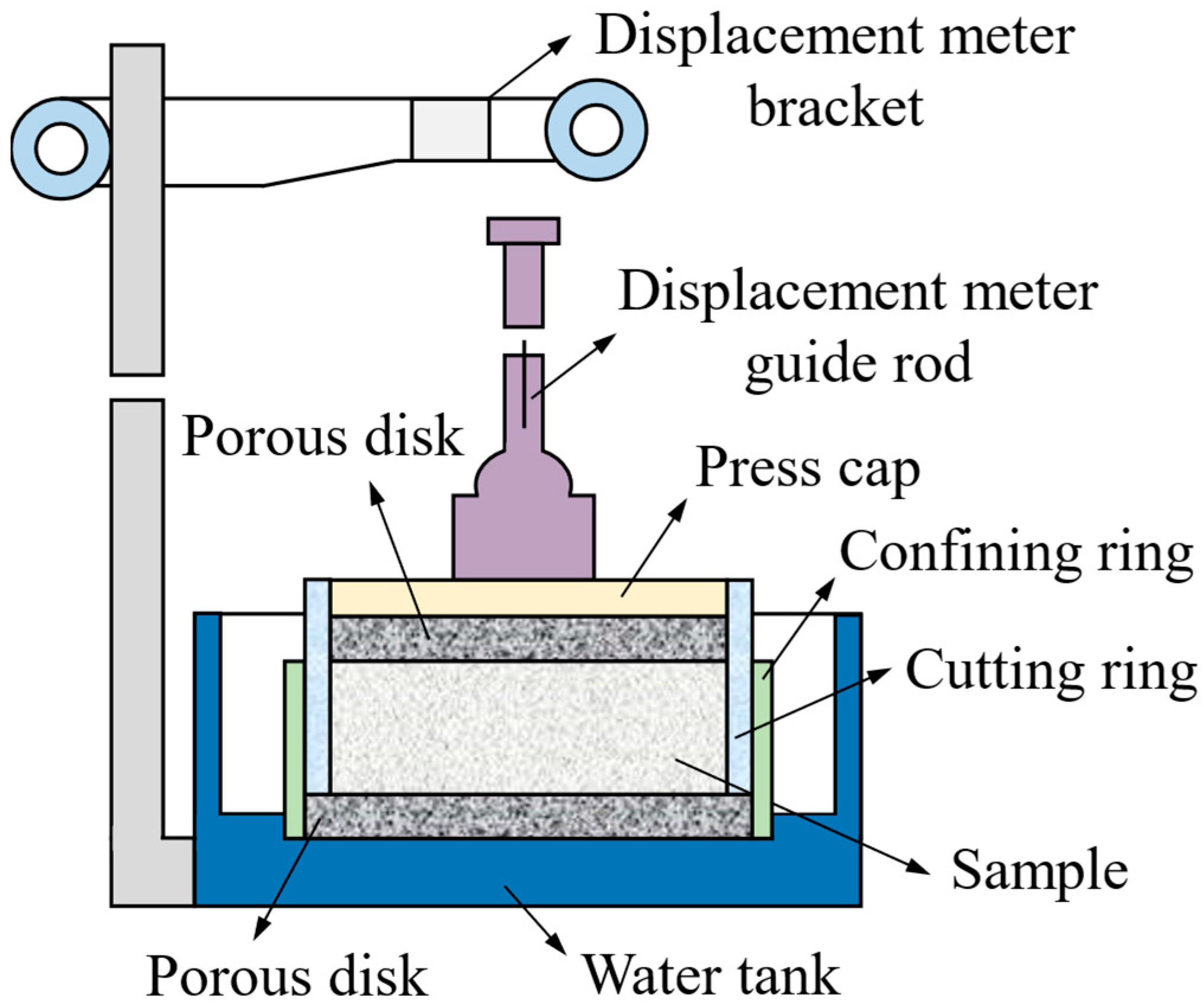
To systematically investigate the effects of dynamic compaction on the consolidation behavior and time-dependent response of soft marine clay, one-dimensional consolidation tests were performed using a single-lever consolidation apparatus, as illustrated in Figure 2. The apparatus consisted of a loading system composed of a lever arm and counterweights, enabling the application of constant pressure through multistage loading by adjusting the lever length and the mass of the weights. Soil specimens were placed within a consolidation ring, with porous stones and filter paper positioned at both the top and bottom to ensure uniform load transfer and prevent soil intrusion. To achieve single drainage during testing, the top boundary was sealed with a tight-fitting loading cap, and moistened cotton strips were embedded around it to minimize evaporation, while the bottom boundary remained free-draining. This setup ensured that water discharge occurred only in one direction during the consolidation process, thereby maintaining the intended drainage boundary condition.

The specimens were prepared using a standard cutting ring with a diameter of 61.8 mm and a height of 20 mm, and they were fully saturated prior to testing to ensure effective pore pressure transmission. After saturation, the specimens were placed into the consolidation ring, and the drainage system was assembled accordingly. A single-stage loading method was adopted with applied pressures of 50, 100, 150, and 200 kPa. Each loading stage was maintained under constant pressure, during which the settlement–time response was continuously recorded. The settlement data were automatically acquired using a high-precision displacement sensor. Based on the initial geometric parameters of the specimens, the corresponding compressive strain and strain rate at each stage were calculated to quantitatively assess the primary-consolidation behavior and the secondary-compression characteristics of the soft soils before and after dynamic compaction.

2.3. Resonant Column Test Method

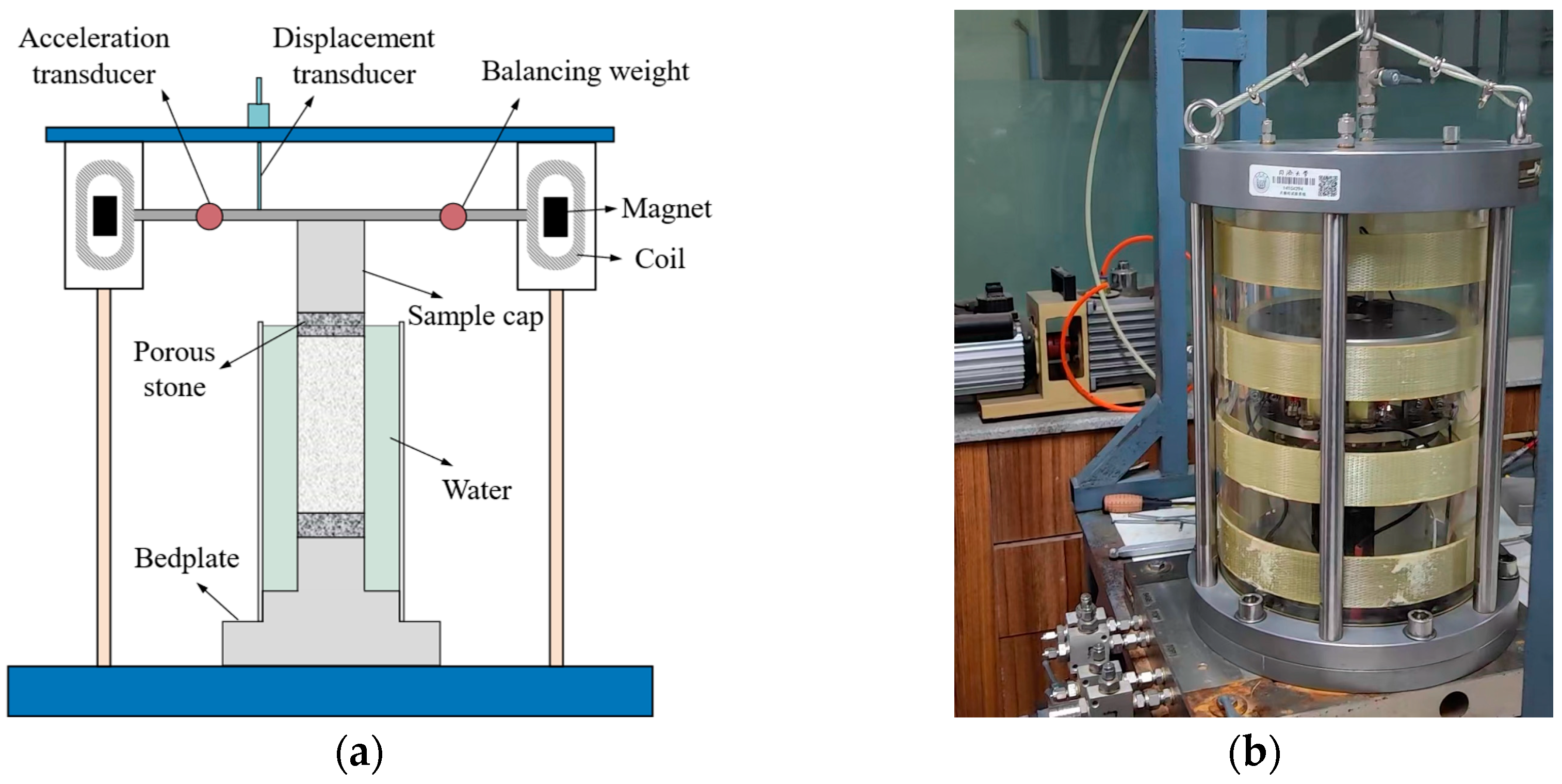
In this study, the small-strain dynamic properties of soft clay were investigated using a Stokoe-type fixed–free resonant column system developed by GDS Instruments (Hook, UK). The apparatus consists of a computer-controlled unit, a data acquisition module, confining and back pressure controllers, an RCA control box, an electromagnetic excitation device, and an array of high-precision sensors, as illustrated in Figure 3. Tests were conducted under fixed-base and free-top boundary conditions, where torsional excitation was applied to the top of the specimen via an electromagnetic driver to induce shear vibration around the vertical axis, enabling measurement of the resonant response.

In accordance with the requirements of the RCA, a standard cylindrical specimen measuring 50 mm in diameter and 100 mm in height was carefully trimmed from the undisturbed soil sample using a precision trimming device. The specimen was then enclosed in a rubber membrane and placed in the pressure chamber for testing. An isotropic static load was applied via the confining pressure system to simulate the in situ stress conditions of natural foundations. Prior to testing, the specimen was fully saturated, and the B-value was maintained above 0.95 using the back-pressure method to ensure effective pore pressure transmission. Confining pressures of 100, 140, and 180 kPa were applied to simulate the dynamic response of soft clay under varying stress conditions. The excitation voltage ranged from 0.002 to 0.512 V and was applied in increments increasing by a factor of two, corresponding to shear strain levels from 10⁻⁵ to 10⁻³. The frequency sweep was performed in two stages: a coarse sweep with 1.0 Hz increments to identify the approximate resonance frequency range, followed by a fine sweep with 0.1 Hz increments to accurately determine the resonance frequency and the corresponding maximum response voltage. The shear modulus was calculated based on the specimen geometry and resonance frequency, while the equivalent damping ratio was determined using the phase difference method.

2.4. Bender Element Test Method

The bender element testing system is integrated into the resonant column apparatus, enabling in situ wave velocity measurements to be conducted immediately after specimen consolidation. This configuration eliminates structural disturbances caused by handling, thereby improving the representativeness and reliability of the results. As illustrated in Figure 4, the transmitting and receiving bender elements are embedded along the central axes of the specimen’s top cap and bottom pedestal, respectively. These elements consist of piezoelectric ceramic plates measuring 11 mm in width and 1.2 mm in thickness, embedded to a depth of 2 mm. They are designed to minimize boundary effects and enhance the signal-to-noise ratio of the received waveforms.

The bender element test is based on the piezoelectric effect: when an excitation voltage is applied to the transmitting piezoceramic plate, a flexural shear wave is generated and propagates axially through the specimen to the receiving end, where it is detected by another piezoceramic plate and converted into an electrical signal. By measuring the travel distance and the arrival time of the wave’s first arrival, the shear wave velocity (V_s) can be accurately determined. Combined with the specimen’s wet density (ρ) under the current confining pressure, the small-strain shear modulus (G) is calculated using the equation G = ρV_s². To improve the accuracy of first-arrival identification, this study employed the Start–Start (S–S) method for wave velocity analysis, with a sampling frequency of no less than 1 MHz to ensure high-resolution waveform capture. During the test, both transmitted and received waveforms were synchronously recorded, and signal stacking and averaging techniques were applied to enhance the waveform stability. The confining pressures used were consistent with those in the resonant column tests, enabling a systematic analysis of the shear modulus variation and the effects of dynamic compaction under different stress levels.

3. Experimental Results

3.1. Consolidation Behavior Under Different Loading Levels

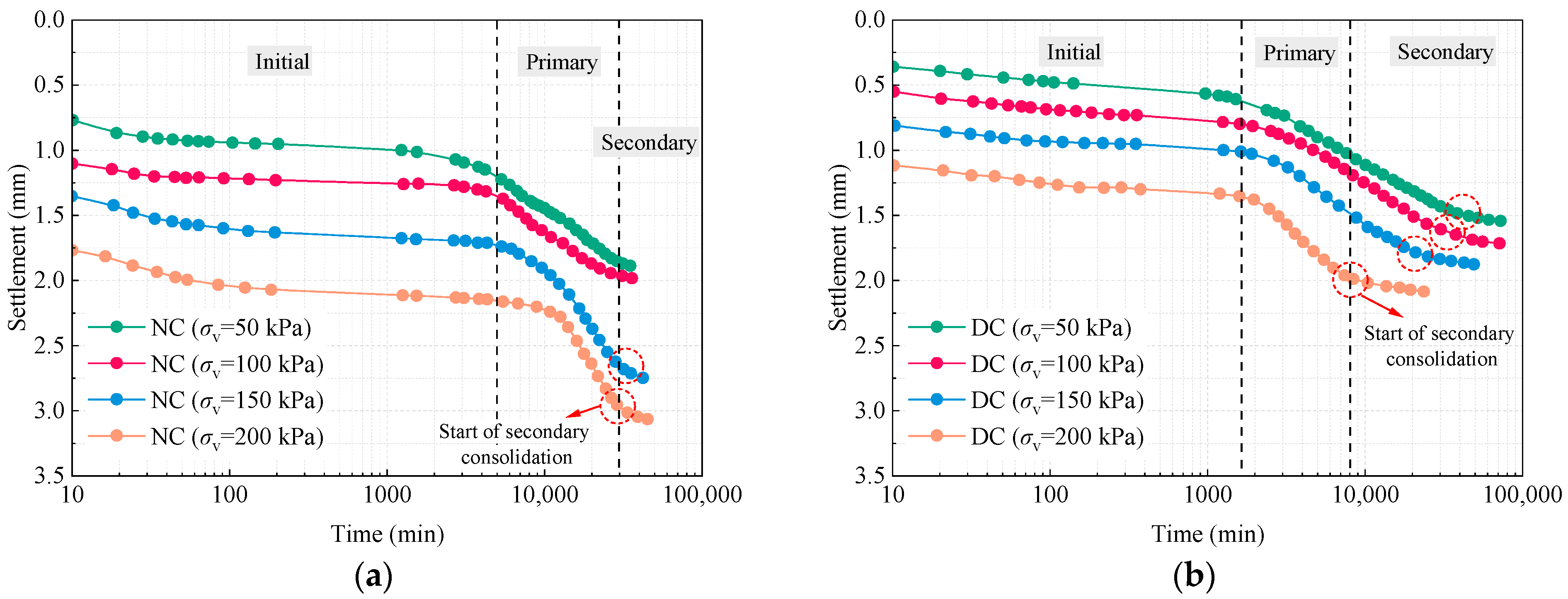
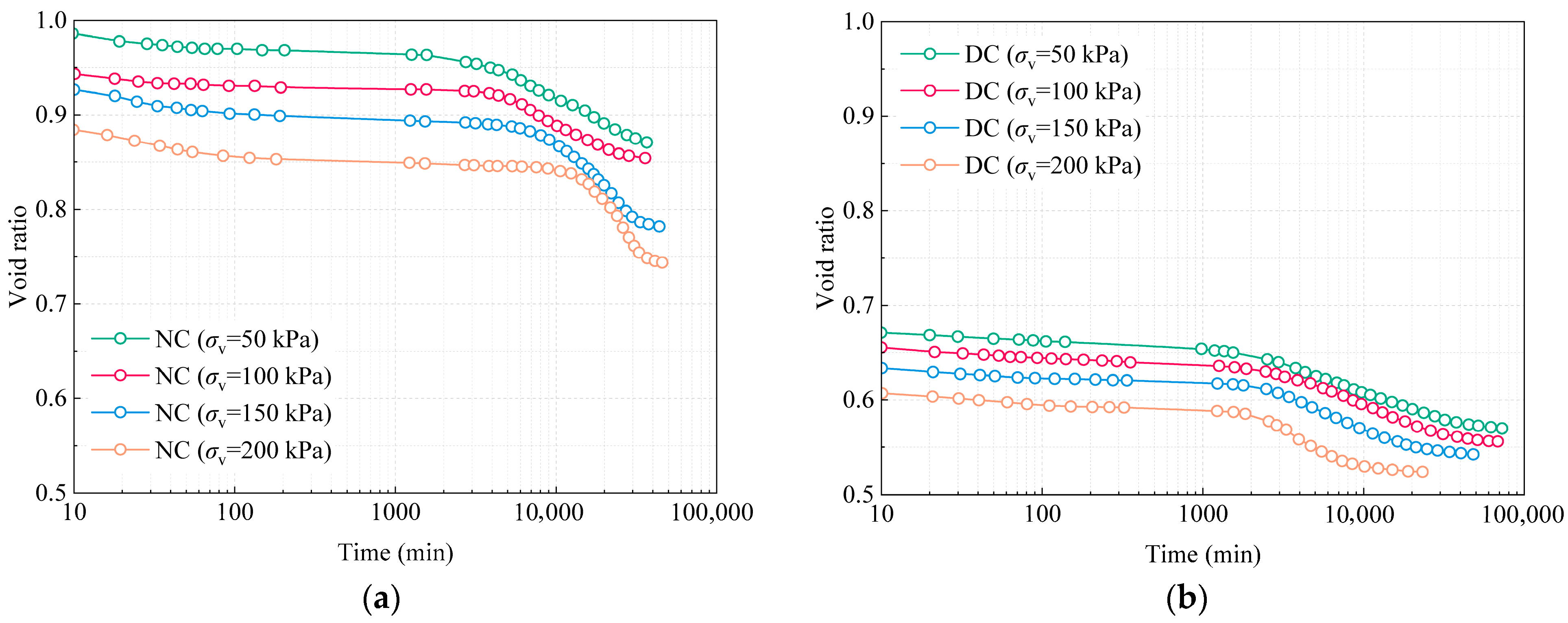
Figure 5 illustrates the settlement–logarithmic time curves of port soft clay under various vertical stress levels. The consolidation process can be delineated into three sequential stages: (i) initial consolidation, characterized by a rapid reduction in volume due to the expulsion of air from soil pores upon loading; (ii) primary consolidation, during which excess pore water pressure dissipates and effective stress is gradually transferred to the soil skeleton, resulting in substantial settlement; and (iii) secondary consolidation (or creep), representing the time-dependent deformation that occurs after pore pressure dissipation. The unreinforced specimens exhibited significantly steeper settlement–time curves, particularly under higher stress levels, indicating more pronounced delayed deformation and longer consolidation durations. This behavior reflects their loose structure, low shear strength, and high compressibility. In terms of final settlement, the unreinforced samples reached 1.89 mm, 1.98 mm, 2.75 mm, and 2.75 mm as the vertical stress increased. In contrast, the reinforced specimens exhibited markedly reduced ultimate settlements, with an average reduction of approximately 24.3%, confirming the improvement in deformation resistance due to reinforcement.

During the primary-consolidation stage, the reinforced soils exhibited a markedly reduced settlement rate, and the settlement curve became flatter during the secondary-consolidation phase. As the stress levels increased, the duration of primary consolidation was shortened, indicating an accelerated dissipation of excess pore water pressure. In contrast, the unreinforced soil displayed pronounced secondary-consolidation delays under high stress, reflecting its lower structural stability and a tendency for sustained structural rearrangement and time-dependent deformation. This behavior is attributed to the structural reorganization induced by dynamic compaction, which enhances the pore stability and interparticle contact stiffness, thereby substantially improving the soil’s resistance to creep deformation.

Figure 6 presents the evolution of the void ratio with the logarithmic time for soil specimens before and after reinforcement under varying vertical stress levels. Overall, the unreinforced specimens exhibited significantly higher initial void ratios across all loading stages and experienced greater reductions during consolidation, indicating a looser structure and higher compressibility. In contrast, specimens improved by dynamic compaction consistently showed lower initial void ratios and slower compaction rates, reflecting enhanced densification and greater compressive resistance. During primary consolidation, the unreinforced samples underwent a rapid decline in their void ratios, suggesting intensive pore water dissipation and substantial skeletal rearrangement. In comparison, the reinforced specimens exhibited a more gradual reduction, attributed to tighter particle packing and improved drainage. In the secondary-consolidation stage, the rate of void ratio reduction in reinforced specimens remained markedly lower than that in unreinforced ones, particularly under higher stress levels (150–200 kPa), where the reinforcement effect was more evident. These results demonstrate that dynamic compaction not only enhances the initial strength and compressibility of soft clay but also effectively mitigates time-dependent deformation, thereby improving the long-term stability of the foundation.

Figure 7 illustrates the isochronous stress–strain curves of soft clay specimens before and after reinforcement under various loading durations. As the loading time increases, the stress level at a given strain progressively rises, indicating compaction of the soil skeleton and enhanced resistance to deformation over time. The reinforced specimens consistently exhibit higher stress responses across all loading durations, with the improvement becoming more pronounced under long-term loading. This reflects a substantial enhancement in the shear stiffness and time-dependent mechanical stability resulting from dynamic compaction. From a microstructural perspective, this behavior is attributed to the densification of the particle arrangement and pore structure induced by the impact energy of dynamic compaction, which effectively suppresses the time-dependent plastic deformation typically observed in unreinforced soft clay.

3.2. Shear Modulus and Damping Ratio of Resonant Column Tests

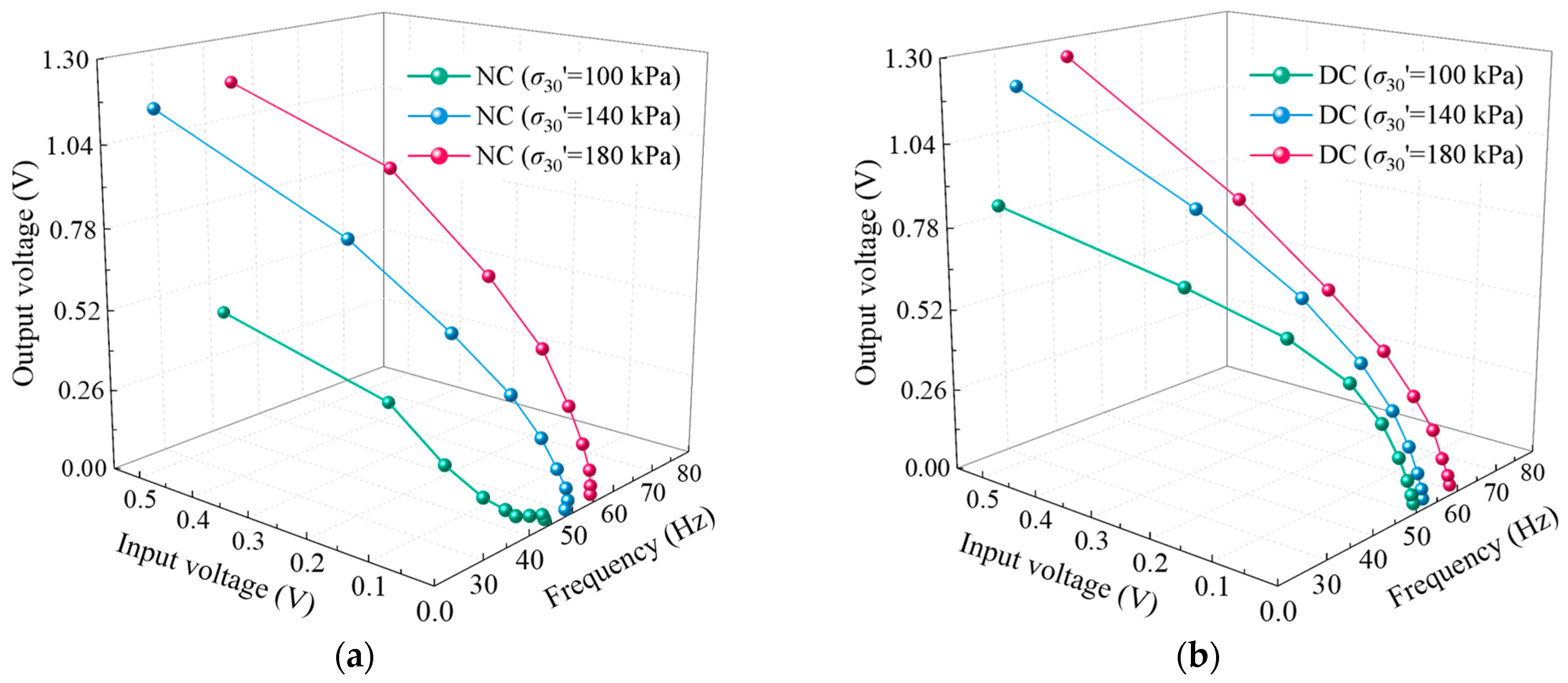
Figure 8 presents the response characteristics of soft clay specimens during the fine-frequency scanning phase, emphasizing the variations in the peak output voltage and resonant frequency with increasing excitation voltage. Generally, the peak output voltage increases monotonically with the excitation voltage, while the resonant frequency shows a decreasing trend. This behavior is primarily attributed to the increase in shear strain induced by higher excitation levels, which reduces the shear stiffness and subsequently lowers the resonant frequency. Distinct differences were observed among specimens subjected to different initial-consolidation pressures. Specimens with higher consolidation pressures displayed elevated initial resonant frequencies and peak output voltages, indicating reduced void ratios and increased shear moduli—features reflective of a denser structure and enhanced mechanical properties. Furthermore, under identical excitation voltage and consolidation conditions, reinforced specimens exhibited higher peak output voltages and smaller reductions in resonant frequency compared to unreinforced ones. These results demonstrate that dynamic compaction not only improves the initial stiffness of soft clay but also enhances its resistance to strain-induced stiffness degradation, thereby mitigating strain-dependent softening behavior.

Figure 9 further elucidates the shear strain response patterns of soft clay specimens before and after reinforcement under varying consolidation pressures. In general, the peak shear strain progressively decreased with increasing consolidation pressure, indicating that higher consolidation levels result in a denser soil fabric and significantly enhanced shear stiffness. However, the unreinforced specimens exhibited irregular and fluctuating shear strain responses near the peak under high excitation voltages. This phenomenon is likely attributed to the loose structure of unreinforced soils, which facilitates localized strain concentrations and nonlinear deformations, thereby reducing the reliability of shear strain measurements. Additionally, under large-strain conditions, the piezoelectric ceramic receiver may experience reverse-charging effects, leading to signal distortion, deformation of the resonant curve, and increased measurement errors. In contrast, reinforced specimens demonstrated a more stable and consistent attenuation trend during shear strain development, suggesting that dynamic compaction significantly improves the soil structural uniformity, enhances the signal transmission stability, and ensures the reliability of dynamic shear response measurements.

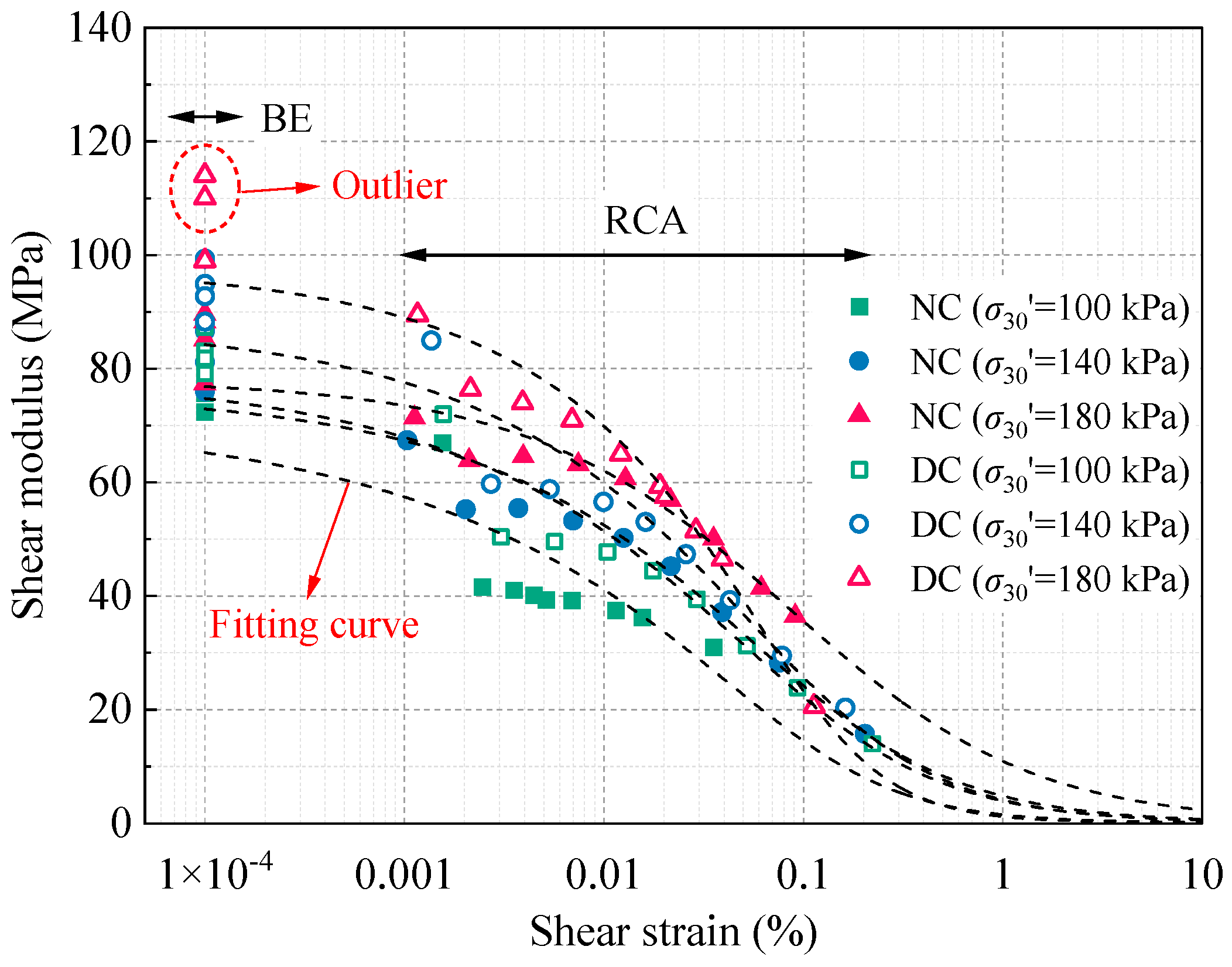
According to Figure 10, the evolution of the shear modulus with increasing shear strain exhibits distinct differences between reinforced and unreinforced soft clay under varying consolidation pressures, underscoring the combined effects of the reinforcement and consolidation state on the dynamic behavior of the soil. During torsional excitation in resonant column tests, variations in the induced shear strain were observed among specimens subjected to identical excitation voltages, primarily due to the natural heterogeneity of soft clay. 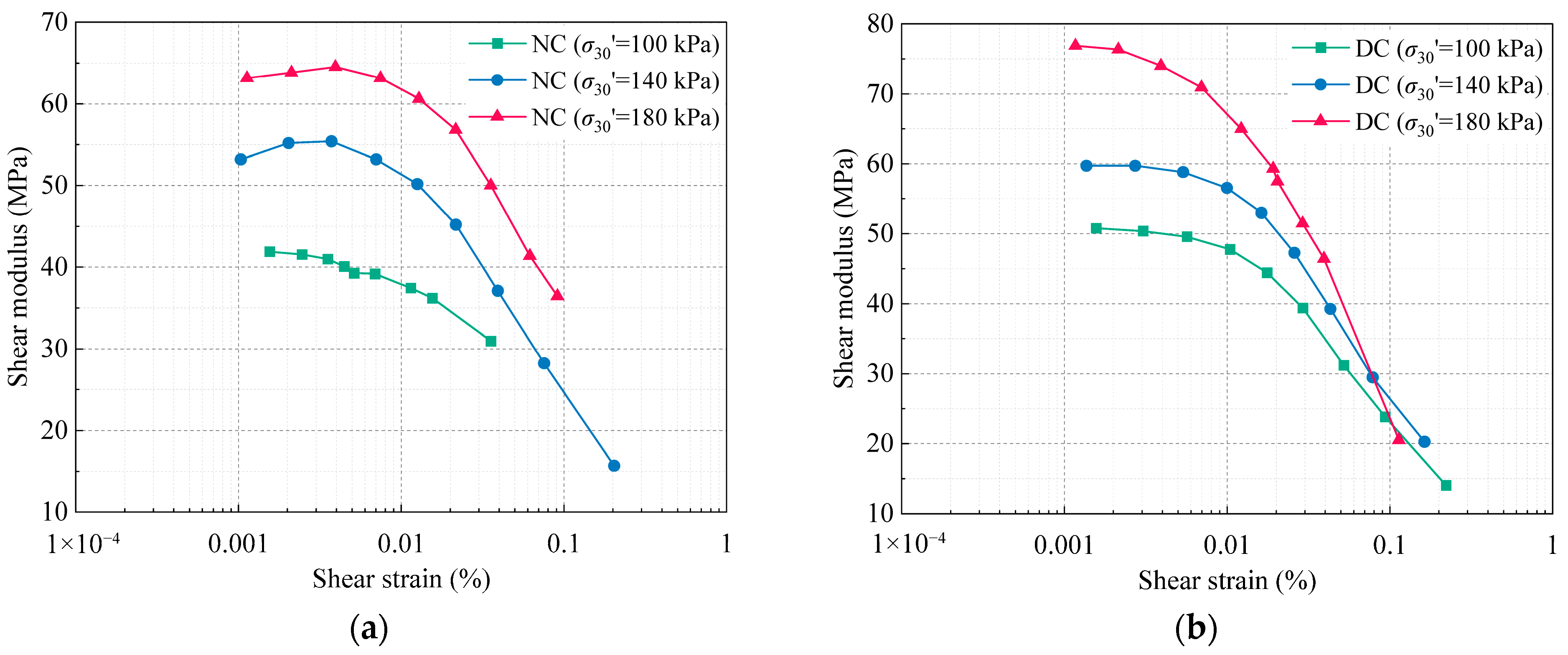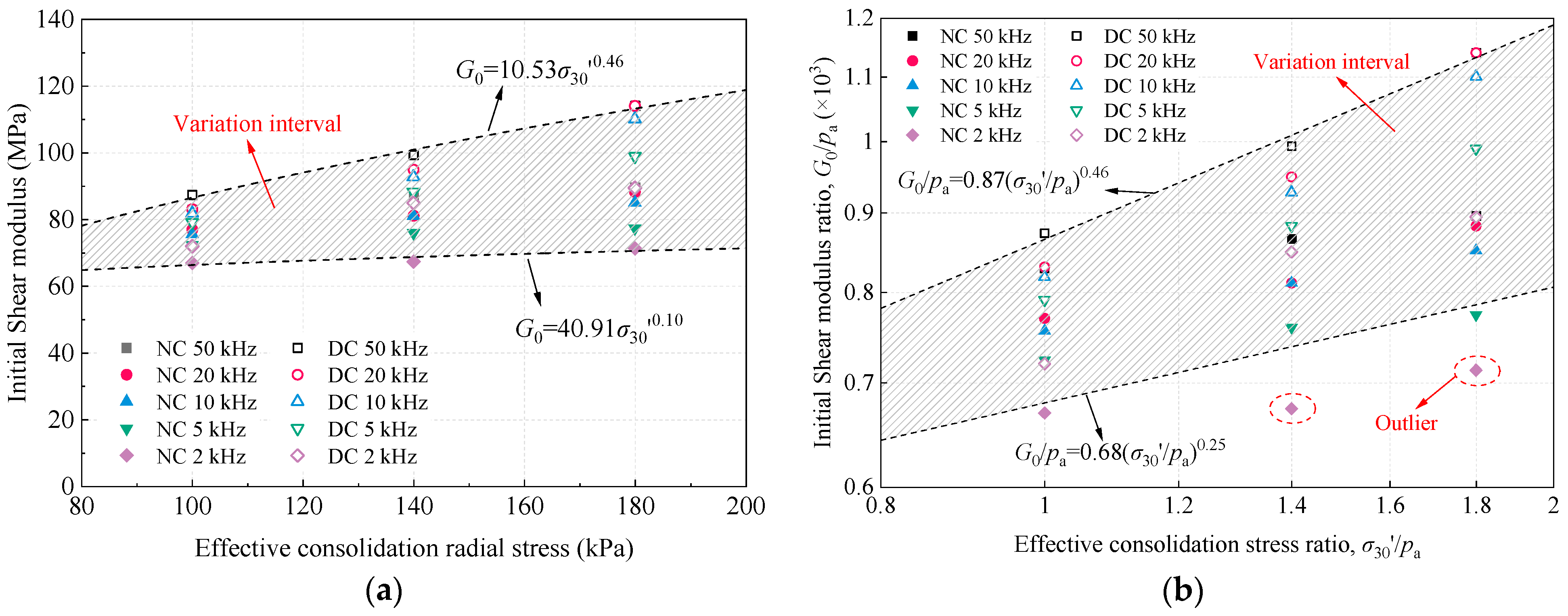The applied shear strain generally ranged from 1 × 10⁻⁵ to 3 × 10⁻³, covering the small- to medium-strain range. Within this interval, all specimens exhibited a monotonic reduction in their shear modulus with increasing shear strain, reflecting the nonlinear degradation of the soil stiffness. This trend is attributed to the progressive accumulation of microstructural damage, which disrupts the soil fabric and reduces stiffness. As the effective consolidation pressure increased, the initial shear modulus rose significantly, indicating a strong dependence on the initial stress state. For instance, in unreinforced specimens, the initial shear modulus was 41.8 MPa at an effective confining pressure of 100 kPa, increasing by factors of 1.27 and 1.51 at 140 kPa and 180 kPa, respectively. This trend suggests that higher consolidation pressures enhance interparticle contact and strengthen the soil skeleton, thereby improving the small-strain stiffness.

Dynamic compaction significantly improved the small-strain stiffness of soft clay, with reinforced specimens showing consistently higher initial shear moduli across all consolidation pressures. At an effective consolidation pressure of 180 kPa, the initial shear modulus increased by approximately 20% compared to unreinforced specimens, indicating a marked enhancement in the soil’s resistance to small-strain deformations. This improvement is particularly critical for port foundation systems, where cyclic loads from wave action, crane operations, and berthing impacts typically fall within the small-strain range. The increased modulus contributes directly to a higher shear wave velocity and stiffness-based bearing capacity while indirectly mitigating long-term consolidation settlement and lateral displacement risks. Combined with a 24.3% reduction in ultimate settlement observed in consolidation tests, dynamic compaction can effectively enhance the serviceability performance of marine soft clay, supporting compliance with the displacement control and differential settlement limits commonly specified in port design codes. Despite this improvement, anomalous behavior was noted at large shear strains under 180 kPa. When the strain exceeded 0.08%, the modulus of the reinforced specimen declined sharply, falling below that at 140 kPa and showing irregular fluctuations. This likely resulted from sample heterogeneity and strain-induced instability. Localized over-compaction or particle crushing may create microstructural defects or weak bonding, which are activated at high strains, causing stiffness loss and inconsistent response. Additionally, resonant column tests at large strains are more susceptible to uncertainties due to increased damping, lower signal-to-noise ratios, and possible mode switching. These factors reduce the reliability of amplitude detection and frequency identification, especially under higher confinement where nonlinearities are more pronounced.

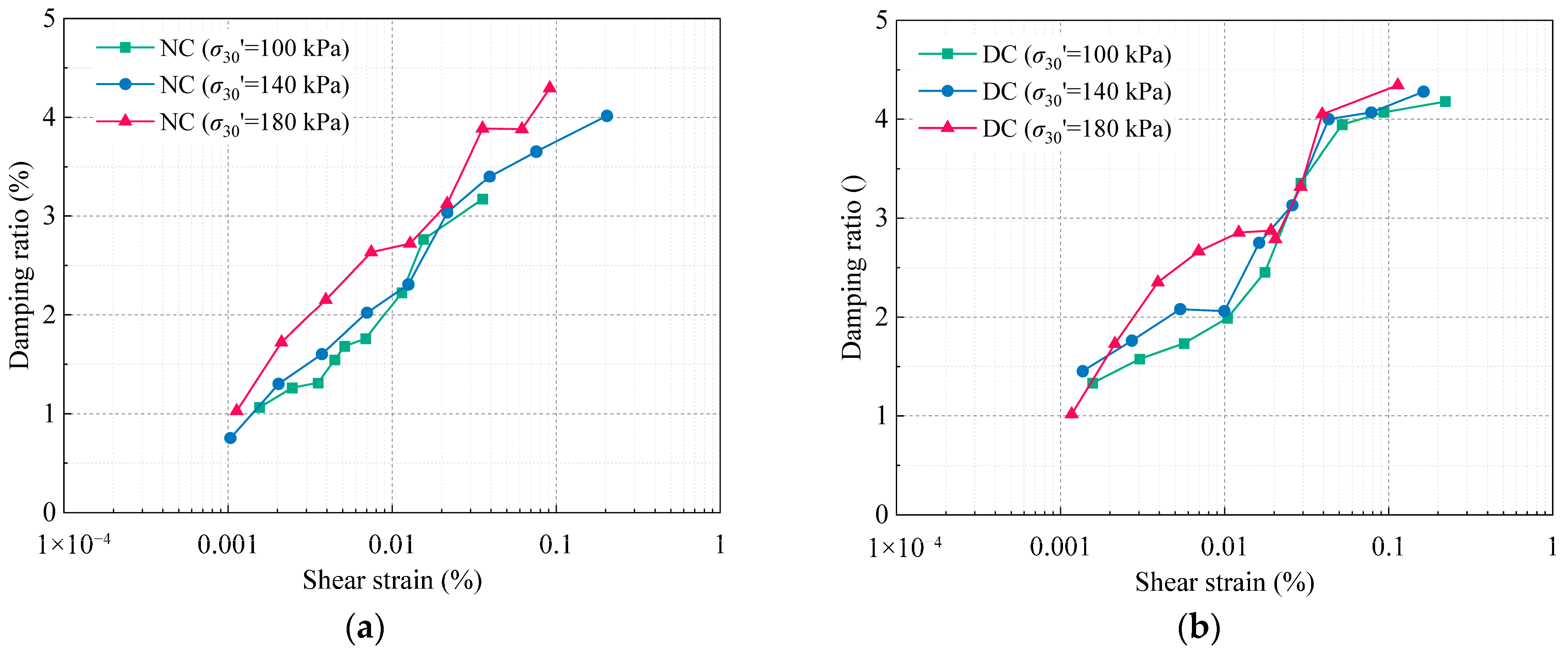
Figure 11 illustrates the relationship between the damping ratio and shear strain for soft clay specimens, both before and after reinforcement, under varying consolidation pressures. Overall, all groups exhibited a nearly linear increase in the damping ratio with increasing shear strain. Additionally, both reinforced and unreinforced samples showed a slight rise in the damping ratio with higher consolidation pressures. Although this trend may appear counterintuitive, as denser soil structures formed under higher consolidation typically exhibit lower energy dissipation and, hence, reduced damping, similar observations have been reported in previous studies. Hardenberg and Vrettos [28] found that for compacted clay (GGM97d), the minimum damping ratio increased from 4.1% to 4.7% as the consolidation pressure rose from 50 kPa to 200 kPa. Likewise, Zhang [46] observed that damping ratios at 0.1% shear strain increased from 5.3% to 6.9% under consolidation pressures of 100 kPa and 300 kPa, respectively, in resonant column tests on soft clay. Consistent with these findings, the damping ratios in our study at 0.1% shear strain were 4.07% and 4.31% for reinforced specimens under 100 kPa and 180 kPa, respectively. This phenomenon can be attributed to the frequency-dependent behavior of damping in cohesive soils. According to Karl et al. [47], when the resonant frequency exceeds 10 Hz, the influence of linear viscous damping becomes more significant, resulting in higher damping ratios. In our tests, specimens subjected to greater consolidation consistently exhibited resonant frequencies above 10 Hz, which supports this explanation. Furthermore, reinforced specimens exhibited smoother and more stable damping ratio curves at medium to high shear strains, indicating improved hysteretic behavior and enhanced energy dissipation capacity.

3.3. Results Analysis of Bender Element Tests

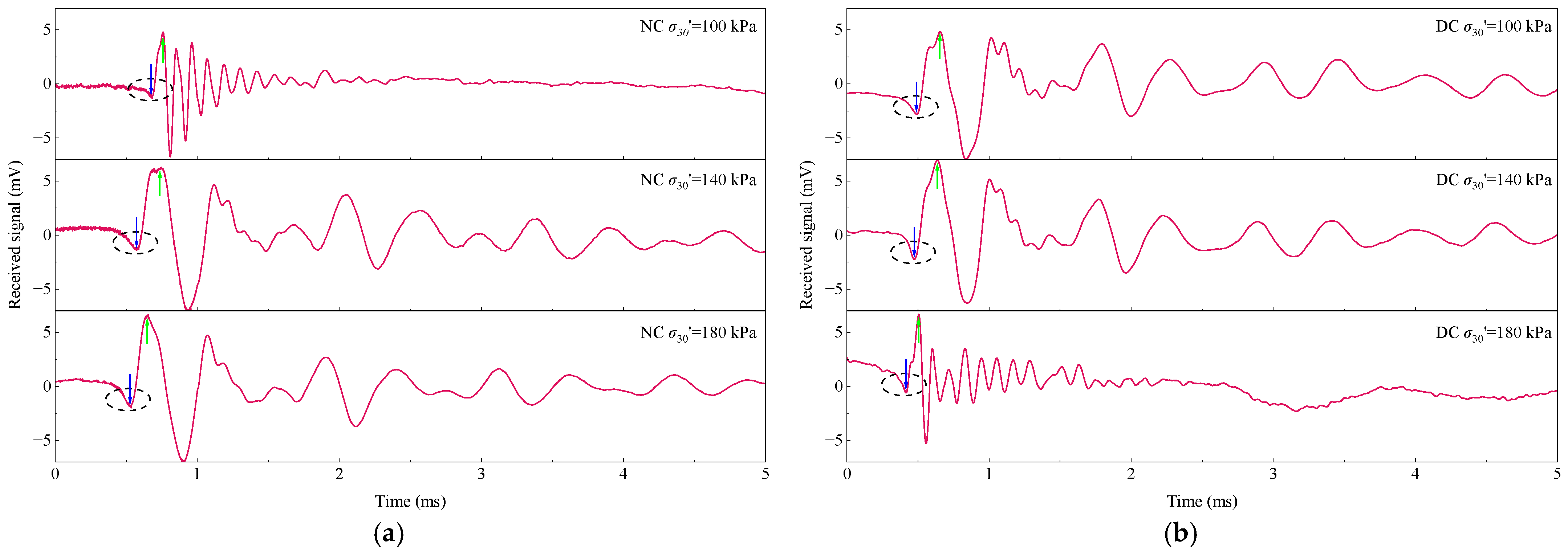
Figure 12 illustrates the time-domain response curves of received signals from bender element tests conducted on soft clay specimens before and after reinforcement under varying consolidation pressures. In these tests, shear waves propagate along the specimen’s axial direction, making precise determination of the travel time critical for calculating the shear wave velocity. Traditional approaches identify the travel time based on characteristic waveform features: the Start–Start (S–S) method uses the first zero-crossing after the near-field effect, while the Peak–Peak (P–P) method relies on the first prominent crest [48]. In the figure, the blue and green arrows indicate the reference points selected by the S–S and P–P methods, respectively. The signal initially remains near zero, then rises sharply to a distinct peak, marking the arrival of the shear wave. Subsequent attenuation and irregular oscillations were likely caused by multiple internal reflections within the specimen. A consistent near-field effect appears in all waveforms, characterized by a downward deflection preceding the main crest, indicating localized distortion before the arrival of the far-field wave. With increasing consolidation pressure, the waveform peak shifts leftward, signifying shorter travel times and thus higher shear wave velocities and initial shear moduli. These results highlight the critical role of the consolidation state in influencing wave propagation and confirm the strong dependence of the shear stiffness on the effective confining pressure in soft clay.

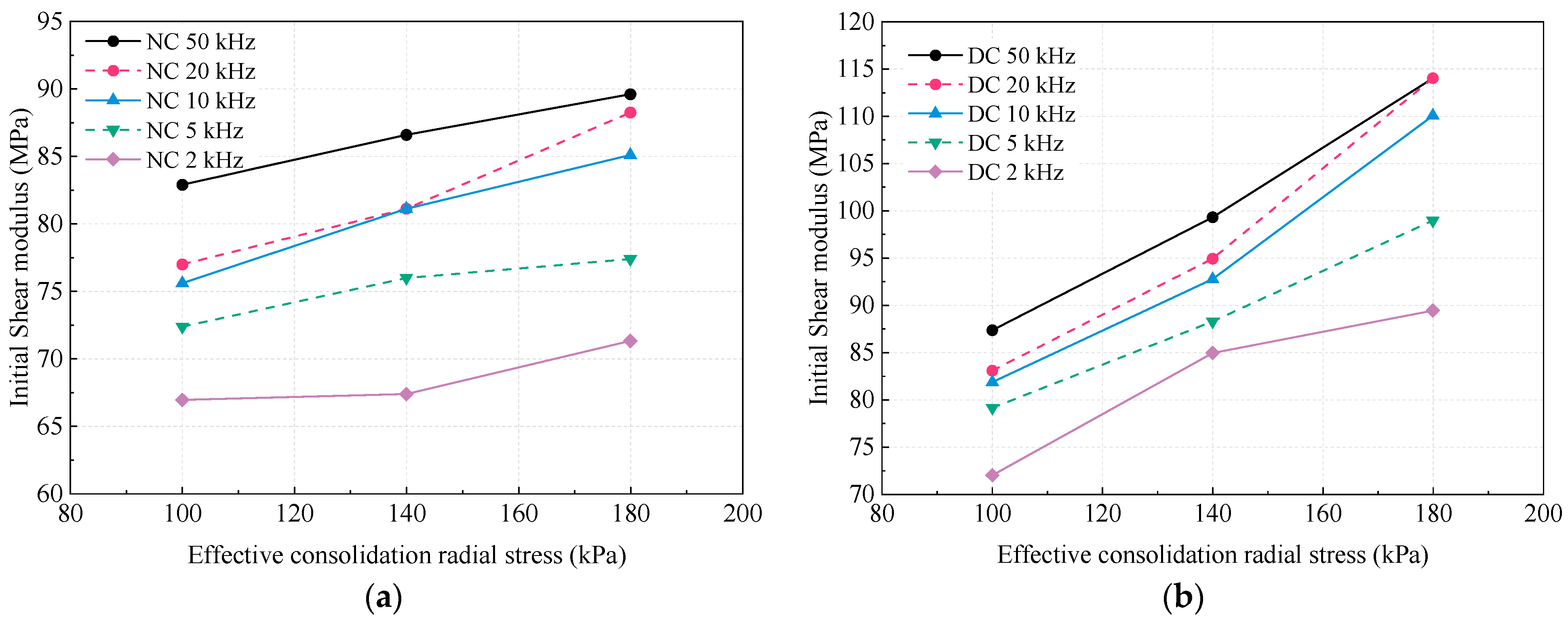
Figure 13 illustrates the variation in the shear modulus with the effective consolidation pressure under different excitation frequencies. Overall, regardless of reinforcement, the shear modulus increased with rising consolidation pressure, indicating a strong dependence of the shear stiffness on the effective stress. This trend is mainly attributed to soil matrix densification under higher stress levels, which enhances the shear wave velocity and thus increases the shear modulus. At identical excitation frequencies and consolidation pressures, reinforced specimens consistently exhibited higher shear moduli than those of unreinforced ones, with the disparity becoming more pronounced at medium to high frequencies. This demonstrates the effectiveness of dynamic compaction in improving soft clay stiffness. A positive correlation was also observed between the excitation frequency and shear modulus. For unreinforced specimens, the shear modulus at 50 kHz was significantly higher than that at 2 kHz, and this frequency-dependent increase was even more pronounced in reinforced specimens. Moreover, the rate of modulus growth accelerated with the frequency. For example, under 5 kHz excitation, unreinforced specimens reached shear moduli of 72.37, 75.98, and 77.39 MPa at consolidation pressures of 100, 140, and 180 kPa, respectively, while reinforced specimens attained 79.12, 88.26, and 98.96 MPa under the same conditions. The magnitude of improvement grew with the consolidation pressure, suggesting a synergistic effect between dynamic compaction and overburden stress. Additionally, the shear modulus exhibited greater sensitivity to consolidation pressure at higher excitation frequencies (20 kHz and 50 kHz), as reflected by the steeper growth trends compared to lower frequencies (2 kHz and 5 kHz). This behavior may be attributed to amplified strain-rate effects and enhanced viscous damping during high-frequency shear wave propagation.

3.4. Discussion of Experimental Findings

Table 2. Comparison of dynamic properties of soft clay reinforced by different methods.

Study	Method	G0 (MPa)	Dmin (%)	Test Conditions
This study	Dynamic compaction	41.86/50.77	1.06/1.33	$\mathrm{Clay},{\sigma }_0\prime =100\mathrm{kPa}$ Dynamic compaction
Hardenberg and Vrettos [28]	Laboratory compacted	64.30/89.30	2.80/3.20	$\mathrm{clay},{\sigma }_0\prime =100 \mathrm{kPa}$ Proctor density (97~100%)
Umut Umu [30]	Expanded glass granules	64.23/175.40	1.00/1.22	$\mathrm{clay},{\sigma }_0\prime =100 \mathrm{kPa}$ Reinforced with expanded glass granules

presents a comparative analysis of the dynamic properties of soft clay reinforced by different methods, including dynamic compaction (this study), laboratory compaction under varying consistencies [28], and reinforcement with expanded glass granules [30]. The results offer a quantitative benchmark for evaluating the stiffness enhancement and damping behavior across reinforcement strategies.

Specifically, the initial shear modulus (G₀) of dynamically compacted clay in this study increased from 41.86 to 50.77 MPa under an effective confining pressure of 100 kPa, representing a 21.3% improvement. This value is notably lower than that reported by Hardenberg and Vrettos [28], where laboratory-compacted clays exhibited an increase in the G₀ from 64.30 to 89.30 MPa at Proctor densities of 97% and 100%. The higher stiffness in that study is attributed to the controlled laboratory compaction under optimal moisture conditions, which produced a denser and more homogeneous soil structure. Similarly, Umut Umu [30] investigated clay reinforced with 2% expanded glass granules, resulting in a substantial increase in the G₀ from 64.23 to 175.40 MPa, corresponding to a 173.2% improvement. It is also noteworthy that the minimum damping ratio (D_min) increased slightly after reinforcement in all three studies. This phenomenon can be explained by the restructured internal fabric of the treated soils, where reinforcement introduced additional interparticle contacts and frictional interfaces that enhanced the energy dissipation under cyclic loading. From a mechanistic perspective, the effectiveness of dynamic compaction lies in its ability to densify the soil mass and improve interparticle contact without altering the mineral composition, making it particularly suitable for large-scale, site-wide applications. Although the stiffness improvement is less pronounced than that with other methods, the controlled enhancement in the damping ratio and the field feasibility of dynamic compaction provide distinct practical advantages.

Based on the above results, the applicability of dynamic compaction in port engineering was further evaluated. This technique effectively enhanced the small-strain stiffness and reduced consolidation-induced settlement, making it suitable for infrastructures subjected to moderate operational or cyclic loads, such as container yards and pavements. For projects with more severe dynamic demands, including seismic liquefaction mitigation or deep foundations under repeated lateral loading, supplementary reinforcement measures may be necessary, such as staged compaction control, preloading, or hybrid ground improvement methods. Moreover, the nonlinear energy dissipation observed in dynamic tests highlights the importance of incorporating realistic damping behavior into geotechnical models, which is critical for accurately simulating soil–structure interactions under cyclic or seismic loading.

Furthermore, the practical boundaries of dynamic compaction must be acknowledged. In this study, a single-blow energy of 1000 kN·m effectively improved fine-grained soils to depths of approximately 2.0–4.0 m, making the method suitable for ground improvement projects requiring enhanced small-strain stiffness and moderate settlement control. However, its effectiveness is limited in deep soft clay layers or in highly saturated, low-permeability soils, where energy attenuation may result in insufficient densification at depth and a reduced bearing performance. The technique may also cause destructuration in structured or sensitive clays, leading to post-treatment strength loss. Additional constraints, including proximity to sensitive structures, vibration restrictions, and shallow groundwater conditions, further limit its application. To ensure a reliable performance, dynamic compaction should be carried out with carefully controlled energy and supported by comprehensive site investigations. Integrating laboratory findings with engineering design is essential to define its operational boundaries and ensure safe and effective application under diverse geotechnical conditions.

4. Nonlinear Fitting Models for the Shear Modulus and Damping Ratio of Soft Clay

4.1. Nonlinear Fitting of Shear Modulus and Damping Ratio Based on RCA

To support the prediction of soil strength and deformation under dynamic loading conditions, this chapter presents a fitting analysis of the shear modulus degradation behavior of soft clay based on resonant column test results. Three representative nonlinear models are employed: the Hardin–Drnevich model [49], the Modified Drucker model [50], and the three-parameter model proposed by Zhang [46]. The H–D model assumes a hyperbolic relationship between the shear modulus and increasing shear strain. Its basic formulation is given as follows:

$${\displaystyle \frac{G}{G_0}}={\displaystyle \frac{1}{1+\gamma /{\gamma }_{\mathrm{r}}}}$$

(1)

where G₀ is the initial shear modulus, defined as the initial value obtained from the RCA; and γ_r represents the reference shear strain.

The M–D model is an extension of the H–D model, developed to improve the characterization of shear modulus degradation within the medium-strain range. Its mathematical formulation is expressed as follows:

$${\displaystyle \frac{G}{G_0}}=1-{\left({\displaystyle \frac{{\left(\gamma /{\gamma }_{\mathrm{r}}\right)}^{2B}}{1+{\left(\gamma /{\gamma }_{\mathrm{r}}\right)}^{2B}}}\right)}^A$$

(2)

where A and B are fitting parameters. When A = 1 and B = 0.5, the M–D model simplifies to the H–D model. However, the M–D model possesses a more complex mathematical structure.

Building upon the H–D hyperbolic model and the M–D model, Zhang [46] proposed a three-parameter model to describe the evolution of the shear modulus with increasing shear strain:

$${\displaystyle \frac{G}{G_0}}={\displaystyle \frac{1}{1+A{\gamma }^B/{\gamma }_{\mathrm{r}}}}$$

(3)

where A and B are fitting parameters. According to Hardin and Drnevich [51], the reference shear strain (γ_r) can be calculated as the ratio of the ultimate shear stress to the initial shear modulus of the soil:

$${\gamma }_{\mathrm{r}}={\displaystyle \frac{{\tau }_{\mathrm{ult}}}{G_0}}$$

(4)

where τ_ult is the ultimate shear stress corresponding to the reference shear strain, and it is calculated using the following equation:

$${\tau }_{\mathrm{ult}}={\left\{{\left[{\displaystyle \frac{1+K_0}{2}}{\sigma }_{\mathrm{v}}\prime \sin {\phi }^{\prime }+c^{\prime }\cos {\phi }^{\prime }\right]}^2-{\left[{\displaystyle \frac{1-K_0}{2}}{\sigma }_{\mathrm{v}}\prime \right]}^2\right\}}^{1/2}$$

(5)

where φ′ and c′ represent the effective internal friction angle and effective cohesion of the soil, respectively; K₀ is the coefficient of the earth pressure at rest; and σ_v′ denotes the effective vertical stress.

Figure 14 shows the variation in the normalized shear modulus with shear strain for soft clay specimens before and after reinforcement under different consolidation pressures. Taking the reinforced sample at an effective consolidation pressure of 100 kPa as an example, the experimental data were fitted using the H–D, M–D, and T–P models to evaluate their accuracy in capturing the nonlinear degradation of the shear modulus. The corresponding model parameters are listed in

Table 3. Parameters for different nonlinear models used in normalized shear modulus fitting.

Model	A	B	R2
H-D	-	-	0.92
M-D	0.62	1.23	0.93
T-P	2.13	1.16	0.93

. Overall, the normalized shear modulus decreases monotonically with increasing shear strain, indicating typical stiffness degradation and reflecting the nonlinear dynamic behavior of soft clay. When the shear strain exceeds 10⁻², the degradation rate increases sharply, signifying a transition into a strongly nonlinear regime. Among the three models, the H–D model underestimates the modulus in the small-strain range and fails to capture the residual stiffness, limiting its effectiveness at representing the full degradation process. The M–D model, which includes an exponential decay term, provides improved accuracy at medium to large strains and better agreement with experimental results. The T–P model achieves a comparable accuracy to that of the M–D model but with a simpler mathematical form, facilitating parameter identification and enhancing general applicability. Under the testing conditions of this study, the T–P model offers an optimal balance between predictive accuracy and practical usability and is therefore recommended for modeling the nonlinear shear modulus degradation behavior of soft clay.

To characterize the energy dissipation behavior of soft clay under dynamic shearing, a hyperbolic model was first employed to fit the relationship between the damping ratio and shear strain. The model is expressed as follows:

$$\lambda ={\displaystyle \frac{A\gamma }{B+\gamma }}$$

(6)

where λ is the damping ratio (%); γ is the shear strain; and A and B are fitting parameters. This model features a simple mathematical structure and a clear physical interpretation, effectively capturing the gradual increase in the damping ratio with strain as soft clay transitions from elastic to nonlinear behavior.

To elucidate the energy dissipation mechanisms induced by structural disturbance in soft clay, this study adopts the normalized shear modulus as the independent variable to establish a coupled model describing the relationship between the damping ratio and shear stiffness degradation. Given the nonlinear dependency between the shear modulus and damping ratio, a second-order polynomial function of the shear modulus is further introduced for fitting, expressed as follows:

$$\lambda =A{\left(G/G_0\right)}^2+B\left(G/G_0\right)+C$$

(7)

where A, B, and C are fitting coefficients; and the normalized shear modulus (G/G₀) used in this model is derived from Equation (3).

Using the RCA results of the NC specimen under a consolidation pressure of 140 kPa as an example, Figure 15 presents the evolution of the measured damping ratio with increasing shear strain and the corresponding model fitting performance. Within the small-strain range, the damping ratio increases gradually, indicating a near-linear response of the soil. As the shear strain increases, the damping ratio rises sharply, reflecting intensified structural disturbance and enhanced energy dissipation. At large strains, the damping ratio approaches a plateau, signifying substantial degradation of the shear stiffness and the onset of energy dissipation saturation. Compared with the conventional hyperbolic model, the adopted second-order polynomial function, formulated based on physically meaningful variables, provides a unified representation of the coupled evolution of the shear modulus degradation and damping behavior. The fitting results demonstrate that the proposed model maintains strong consistency and convergence across the entire strain range, accurately capturing the nonlinear growth trend of the damping ratio. These results confirm the model’s effectiveness and applicability in characterizing the dynamic behavior of soft soils.

In summary, the T–P model offers a well-balanced performance between fitting ac-curacy (R² = 0.93) and mathematical simplicity in representing the nonlinear behavior of the shear modulus. Its concise formulation and straightforward parameter identification ren-der it particularly suitable for capturing the degradation of the soft clay shear stiffness across the full strain range without compromising predictive reliability. Accordingly, the T–P model is recommended as a practical tool for estimating the nonlinear shear stiffness of soft soils in dynamic design and numerical simulations. For damping ratio modeling, the second-order polynomial model based on the normalized shear modulus and the conventional hyperbolic model achieved R² values of 0.94 and 0.91, respectively. The polynomial model demonstrated superior convergence and stability across the strain spectrum, making it appropriate for establishing a unified framework to evaluate energy dissipation characteristics. Collectively, these models enhance the representation of soft soil dynamic behavior and provide a robust foundation for constitutive modeling and site-specific seismic response analysis.

4.2. Nonlinear Fitting of Shear Modulus Based on BE

To analyze the variation in the initial shear modulus with the effective consolidation pressure under different excitation frequencies in bender element tests, both power function and logarithmic-linear models can be employed for fitting. According to Karl et al. [47], the initial shear modulus of soils typically follows a power law relationship with the effective consolidation pressure, which can be expressed as follows:

$$G_0=A{{\sigma }_{30}}^{\prime \Lambda }$$

(8)

where A and Λ are fitting parameters; and σ₃₀′ is the effective consolidation pressure.

In contrast, Rampello et al. [52] observed that the relationship between the initial shear modulus and consolidation pressure appears linear in a log–log coordinate system and can be expressed as follows:

$${\displaystyle \frac{G_0}{p_{\mathrm{atm}}}}=K{\left({\displaystyle \frac{{\sigma }_{30}\prime }{p_{\mathrm{atm}}}}\right)}^n$$

(9)

where K is the initial shear modulus when σ₃₀′/p_atm = 1; p_atm is the reference pressure, taken as 100 kPa; and n is the slope of the straight line.

Under varying excitation frequencies, the initial shear modulus of the specimens consistently exhibited a stable, monotonic increase with the effective consolidation pressure. As shown in Figure 16, the data points form an approximately linear trend in the log–log coordinate system, indicating that the power law model effectively captures this nonlinear relationship and offers strong fitting adaptability. A comparison of fitted slopes across different frequencies further reveals that the shear modulus increases with rising excitation frequency, reflecting enhanced material stiffness under higher-frequency loading. Notably, under the 2 kHz condition, several samples (highlighted with red circles in the figure) deviate from the primary fitting trend, likely due to localized disturbances, instability in the shear path, or insufficient excitation energy. This suggests that soft clay may be more vulnerable to localized relaxation or mechanical instability under low-frequency excitation. In summary, the power law model provides an accurate and robust representation of the coupled effects of the consolidation pressure and excitation frequency on the shear stiffness of soft clay.

To systematically evaluate the evolution of the shear stiffness in soft clay over a broad shear strain range, this study presents a comparative analysis of the shear modulus results obtained from combined resonant column and bender element tests, as shown in Figure 17. The dashed line in the figure denotes the fitted normalized shear modulus curve based on Equation (3). In resonant column tests, the initial shear modulus typically corresponds to a shear strain of approximately 1 × 10⁻³%, while in bender element tests—based on wave velocity measurements—it corresponds to about 1 × 10⁻⁴%. Due to excitation mode and modal limitations, resonant column tests may slightly underestimate the soil’s true initial stiffness. In contrast, bender element tests, conducted at significantly lower excitation strains, yield modulus values that more closely represent the intrinsic stiffness of undisturbed soil. Despite differences in the loading mechanisms, strain distributions, and testing configurations, Figure 17 demonstrates the strong numerical consistency and smooth continuity of results within a unified coordinate system, forming a continuous stiffness degradation curve spanning five orders of magnitude in strain. These results underscore the complementarity and integration potential of resonant column and bender element tests in characterizing the dynamic response of soft soils, offering a robust basis for constitutive model development and dynamic parameter identification across the full strain spectrum.

5. Conclusions

Based on a series of laboratory static and dynamic tests on dynamically compacted soft clay specimens, this study systematically evaluated the effects of dynamic compaction on the consolidation behavior and shear dynamic properties of soft clay. Model fitting and mechanistic analyses were further conducted to characterize the nonlinear evolution of the shear modulus and damping ratio. The main conclusions are as follows:

(1)

Dynamic compaction markedly improves the consolidation behavior of soft clay, as evidenced by a reduced settlement rate during primary consolidation and progressive stabilization during the secondary-consolidation stage. With increasing stress levels, the time to complete primary consolidation is significantly reduced, indicating that higher stresses densify the soil structure, enhance the interparticle contact stiffness, and improve both the drainage efficiency and compressive resistance.

(2)

The shear modulus increases with the effective consolidation pressure and excitation frequency, as observed in both resonant column and bender element tests. Reinforced specimens exhibit greater shear stiffness and more stable damping behavior, particularly in the medium- to high-frequency range. These findings confirm that dynamic compaction enhances structural uniformity, deformation resistance, and signal stability.

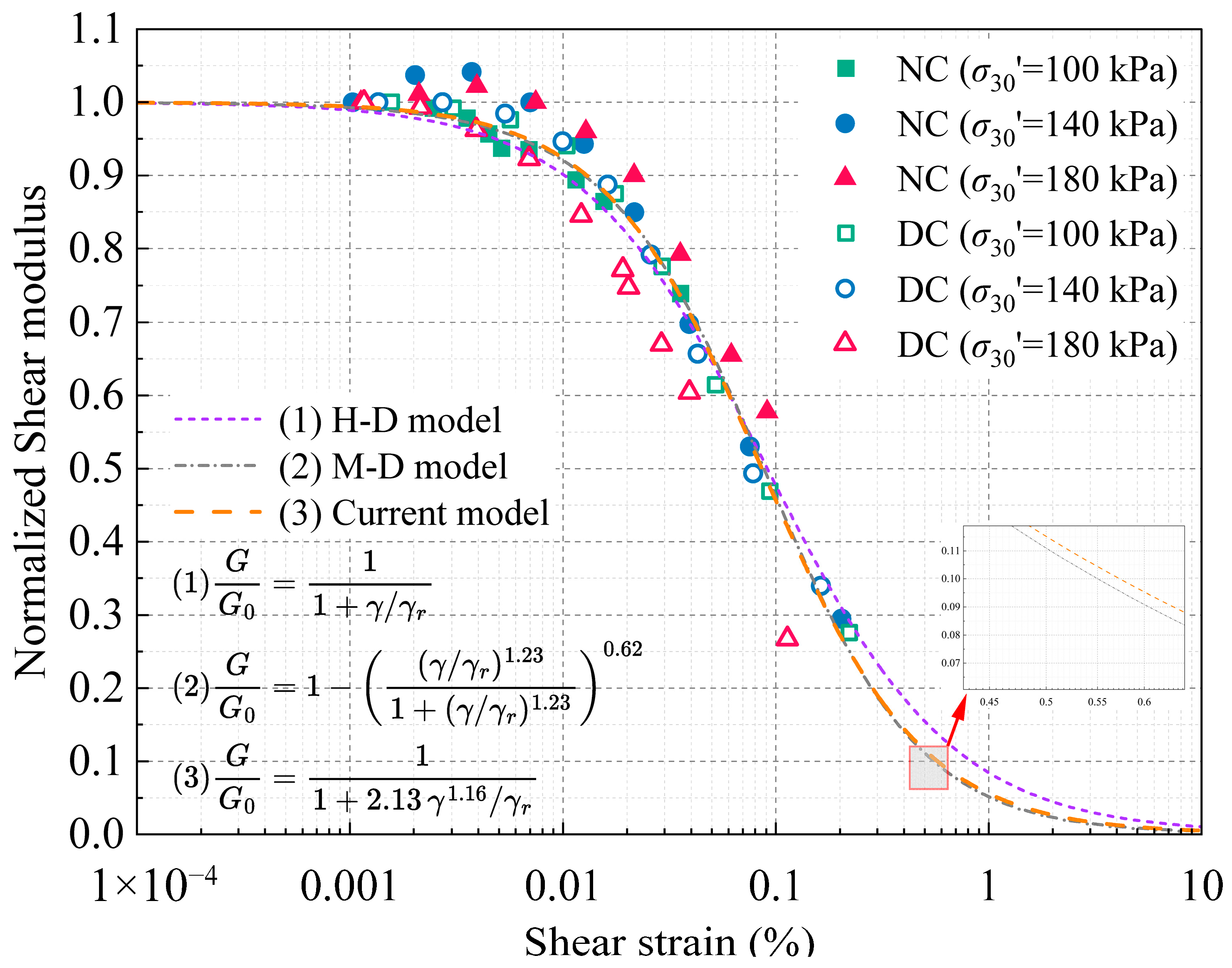
(3)

The T–P model achieves high fitting accuracy in representing the shear modulus degradation over the full strain range while maintaining a simple parameter structure. The second-order polynomial model effectively captures the nonlinear increase in the damping ratio. The combined use of these models provides a theoretical basis for constitutive modeling and enables quantitative evaluation of the dynamic compaction effect.

(4)

Results from the resonant column and bender element tests show strong consistency in the strain distribution and shear modulus evolution, enabling continuous characterization of the shear stiffness from small- to medium-strain levels. This demonstrates the complementary nature of the two methods in capturing the dynamic response characteristics of soft clay.

Although this study systematically examined the consolidation and dynamic response characteristics of dynamically compacted soft clay, several limitations remain concerning the excitation-loading methods, parameter selection ranges, and underlying model assumptions. The experiments primarily focused on regular loading paths and specific consolidation stress levels, which do not fully reflect the nonlinear evolution of soft clay under complex stress histories and multiaxial loading conditions. In addition, the soil samples were collected from a single site, potentially limiting the generalizability of the findings to other soft clay deposits with different mineralogical compositions or depositional environments. Future research should integrate in situ field tests and advanced constitutive models to expand the applicability of various loading paths and stress states. Moreover, sampling across multiple sites, increasing the number of test replicates, and employing rigorous statistical evaluations will be essential to improve the representative-ness and generalizability of conclusions regarding the engineering behavior of dynamically compacted soft clay.