Abstract
When the number of available training views is limited, the small quantity of images results in insufficient generation of Gaussian ellipsoids, leading to an empty Gaussian model. This constraint limits the generation of Gaussian ellipsoids within 3DGS. If the number of Gaussian ellipsoids is too low, the model is prone to overfitting and may learn incorrect scene geometry. To address this challenge, we propose 3DGS based on Gaussian probabilistic modeling and feature regularization (GPRGS). Our method employs Gaussian probabilistic modeling based on Gaussian distribution features, where we capture feature information from images and establish a Gaussian distribution to model the feature probability map. Additionally, feature regularization is introduced to enhance image features and prevent overfitting. Moreover, we introduce scale and densification thresholds and update the multi-scale densification and pruning strategy to avoid filtering out all low-opacity Gaussian points during the pruning process. We conducted evaluations for new view synthesis with both full and sparse inputs on real and synthetic datasets. The results demonstrate that GPRGS is on par with other models. In sparse environments, we achieve a slight advantage, specifically showing an approximately 4% improvement in the PSNR metric across multiple evaluation metrics.
1. Introduction
New View Synthesis (NVS) is an important field in computer graphics, aiming to capture and render realistic 3D representations of physical scenes [1,2]. NVS focuses on generating new 2D views of a scene from 3D models, allowing for the creation of realistic images of the scene from any desired viewpoint, even if the original image was not taken from that angle [3]. Three-Dimensional Gaussian Splatting (3DGS) [4] has gained significant popularity since its introduction. This technique involves iteratively refining multiple Gaussians. While 3DGS does not directly recover the entire 3D scene geometry, it stores information in a volumetric point cloud, where each point represents a Gaussian with parameters such as color, diffusion, and position, thus generating a volumetric representation that provides color and density for each point in the relevant 3D space. NeRF [5], similar to 3DGS, focuses on implicit representations [6,7,8], whereas 3DGS leans toward explicit representations. Both methods require a large number of scene images as datasets. When the number of images is small, or in sparse scenes, overfitting occurs, leading to incorrect scene geometry and poor rendering results. The main challenge with 3DGS in sparse environments arises because, in such settings, when cameras are placed close to each other rather than surrounding the scene, a small “scene radius” is obtained. Specifically, if there is only one camera position, only a single Gaussian ellipsoid is generated, which results in insufficient generation of Gaussians and low opacity of the Gaussians, causing all points to be filtered out during pruning and leaving the Gaussian model empty, leading to modeling failure. In other words, this issue stems from two main factors. The first is the lack of sufficient features in sparse scenes to support model completion, resulting in a reduced number of generated cameras. Second, during Gaussian optimization, already sparse Gaussian points are deleted due to low opacity during pruning, which may lead to errors in the training gradient calculations and ultimately cause modeling failure. To address these issues, various methods have emerged. In previous work on sparse inputs [9,10,11], introducing new frameworks and utilizing depth information to guide training has proven effective. Some NeRF methods [12,13] have also attempted to introduce new position encoding strategies or fusion networks to solve this problem. In this paper, we introduce a new probabilistic mapping framework and propose a sparse viewpoint real-time view synthesis method, GPRGS, based on feature regularization and Gaussian distribution probabilistic mapping.
First, during the training process, we use the image features as input, leveraging the existing Gaussian point information from 3DGS. For each feature tensor, we compute its Gaussian probability, assuming that the data points follow a normal distribution and use the mean and standard deviation to calculate the probability of the data points to assist in modeling. Building upon this, we introduce the elastic net regularization method, where the combination of L1 and L2 regularization allows the model to maintain sparsity and resistance to overfitting while also appropriately penalizing correlations between features. Finally, we compute the mean of the resulting Gaussian probabilities and incorporate this into the loss function. Additionally, we improve the densification and pruning strategies by introducing densification and pruning thresholds to prevent the issue of Gaussian counts being pruned to zero due to excessively low opacity under sparse conditions. These three improvements effectively enhance the accuracy of modeling, particularly when handling sparse data. By performing probabilistic mapping on the input feature tensors, this probabilistic-based modeling approach not only helps capture the underlying patterns in the data but also quantifies uncertainty.
Experiments conducted on the NeRF-Synthetic [5], LLFF [14], and Tanks and Temples datasets [15] demonstrate that GPRGS achieves superior rendering quality while maintaining high rendering speeds.
The main contributions of this paper are as follows:
- We analyzed the reasons for modeling failure and overfitting in 3DGS under sparse viewpoints. Based on this, we proposed an elastic net regularization method to constrain and enhance features, improving the modeling performance in environments with insufficient information.
- We introduced a Gaussian distribution-based probabilistic mapping to assist in modeling. By leveraging the mathematical properties of Gaussian distributions, this probabilistic modeling approach aids in capturing the underlying patterns of the data. It has demonstrated superior performance and efficiency in new view synthesis across multiple datasets, outperforming existing methods.
- We further improved the densification and pruning strategies by introducing densification and pruning thresholds, addressing the issue of low opacity in Gaussian points caused by insufficient image data, which could otherwise lead to modeling failure.
The main framework of this paper is shown in Figure 1.
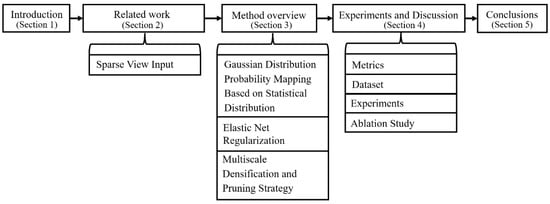
Section 2 reviews related work on sparse viewpoint inputs, including the advancements in NeRF and 3DGS for improving performance under sparse viewpoints. Section 3 provides a detailed description of our proposed elastic net regularization method, Gaussian distribution probabilistic mapping, and multi-scale densification and pruning strategies. Section 4 analyzes the quantitative results of the experiments as well as the ablation studies. Finally, Section 5 summarizes the contents of the paper.
2. Related Work
Here, we focus on discussing 3DGS and other methods related to new view generation under sparse viewpoints. A common limitation of the 3DGS rendering method is that, when observational data are insufficient, training often overfits, leading to inaccurate reconstructions, as illustrated in Figure 2.

Figure 2.
The specific issues associated with sparse viewpoints. In cases of insufficient images, we often encounter problems such as blurring, camera distortion, and aliasing, which degrade the image quality. However, when the number of images is severely limited, issues such as missing details and significant blurring arise, making it impossible to generate accurate images.
In sparse viewpoint scenarios, overfitting occurs when the number of images is limited, as shown in Figure 2. The figure illustrates renderings of the Lego dataset with only 20 images, where issues such as missing details, distortion, blurring, and incomplete generation arise, leading to severe blurring and aliasing. The primary cause of these problems is overfitting in the model under sparse conditions. Many approaches have been proposed to address the sparse viewpoint problem. Fei, Teng et al. [16] proposed combining multi-view stereo techniques with Gaussian splatting and improving the sampling strategy to address the issue of non-robust radiance field reconstruction typically caused by relying solely on sparse point inputs and simple optimization criteria. Their method enhances the explicit geometric radiance field using multi-view stereo techniques to bridge gaps in scene representation, replacing Structure from Motion (SfM) points with multi-view stereo points. They also introduced a pixel gradient-based discriminative strategy to prevent unnecessary splitting operations in well-rendered areas by calculating the relationship between pixel gradients and the scale of Gaussian ellipsoids. Y. Jiang et al. [11] proposed a method for high-quality multi-person mesh reconstruction in large-scale motion scenes using a camera array with a wide baseline. This method combines silhouette shapes, introduces a body shape prior, and implements a high-density scene resampling strategy based on spherical sampling of body bounding boxes using 3D Gaussian splatting to render new views and create precise and dense multi-view body contours. The 2D signed distance function of the body is integrated into the implicit surface field computation to produce smoother and more accurate surfaces. Z. Lu et al. [17] proposed 3DGS-CD, the first method based on 3DGS for detecting physical object rearrangement in 3D scenes. This method uses novel view rendering from 3DGS and the zero-shot segmentation capability of EfficientSAM to detect 2D object-level changes and then associates and merges views to estimate 3D change masks and object transformations. Z. Liu et al. [18] proposed GeoRGS, a geometry-regularized 3DGS method independent of priors for improving new view synthesis from sparse inputs. This method includes two geometry regularization approaches that do not require prior information: one based on selecting seed blocks of 3D Gaussians from the scene to guide the growth of correct scene geometry, and another focusing on the depth similarity between object surfaces and edges.
In the field of radiance field-based new view synthesis, similar overfitting issues arise when observational data are insufficient, leading to inaccurate reconstructions, as seen in NeRF [8]. S. Guo et al. [12] proposed a depth-guided robust point cloud fusion NeRF for sparse input synthesis. Using an additional lightweight scene fusion network, they merged point clouds from each input view to construct a complete scene point cloud. Xu, Kuo et al. [19] proposed a generalization method for SG NeRF (sparse input generalized NeRF). They developed an improved multi-view stereo structure based on convolutional attention and multi-level fusion mechanisms to extract scene geometry and appearance features from sparse input images and aggregated these features into the input of a neural radiance field using multi-head attention. Gao, Changbo et al. [9] proposed the MBS NeRF framework, which integrates depth information as a constraint to address the problem of insufficient view information. They also introduced a motion blur simulation module (MBSM) to simulate the physical process of motion blur formation. Lai, Song et al. [20] integrated NeRF with Shape from Silhouette, proposing a new explicit-implicit radiance field representation composed of voxel grids and multilayer perceptron networks with confidence and geometric feature embeddings to decode view-dependent color emission for appearance. W. Hu et al. [21] introduced a new type of neural radiance field based on transfer learning and diffusion modulation (TD-NeRFs). This method applies transfer learning to handle a limited set of images and their corresponding sparse depth information, obtaining complete depth and standard deviation (std) images for network supervision. They use a diffusion sampling module (DSM) to standardize the sampling process and employ a diffusion frequency module (DFM) during the initial training phase to suppress high-frequency signals, ensuring accurate low-frequency learning and preventing artifacts.
The introduction of prior-driven improvements to NeRF enables it to address certain issues in sparse scenes. This direction has also been widely discussed in the literature. Jin, Tianxing et al. [22] proposed a prior-driven NeRF model that accepts sparse views as input data and reduces the number of non-functional sampling points to improve training and prediction efficiency, enabling fast, high-quality rendering. Li, Yaokun et al. [23] introduced a new indirect diffusion-guided NeRF framework called ID-NeRF, which abandons the direct supervision commonly used in previous 3D generation models and adopts a new indirect prior injection strategy using score-based distillation to extract pre-trained knowledge into an imaginative latent space. They also proposed an attention-based refinement module to improve re-projected features extracted from sparse inputs using embedded priors. Qiu, Jiaxiong et al. [24] proposed a learning-based method called relative depth-guided NeRF (RDNeRF), which jointly renders RGB images in dense free views and recovers scene geometry by directly learning relative depth through implicit functions and converting it into geometric boundaries for NeRF’s geometry-aware sampling and integration. Fu, Tao et al. [25] introduced a new method for high-quality 3D reconstruction of spatial targets. They first used a NeRF model for preliminary 3D reconstruction, guided by optical images of the observed spatial targets and depth priors extracted from a customized monocular depth estimation network (MDE). Then, NeRF is used to synthesize optical images from unseen viewpoints, and the corresponding depth information for these viewpoints, derived from the same depth estimation network, is integrated as a supervisory signal to iteratively improve the 3D reconstruction. A. Carlson et al. [26] proposed constructing differentiable 3D occupancy grid maps in conjunction with the NeRF model and leverage these occupancy grids to enhance the point sampling along rays for volumetric rendering in the metric space. Y. J. Yuan et al. [27] proposed a novel framework, which first reconstructs the scene from the captured RGB-D images and then utilizes the rendered images of the reconstructed scene along with precise camera parameters to pre-train a network. Subsequently, the network is fine-tuned using a small set of real captured images. Barron, Jonathan T. [28] proposed Zip-NeRF, improving upon existing methods by combining mesh and multi-sampling techniques, effectively mitigating the aliasing distortions inherent in those approaches. Our approach differs from the aforementioned Zip-NeRF, which improves the grid method. We do not make modifications to the grid and sampling techniques; instead, we focus on enhancing the existing information through data augmentation.
Additionally, there has been limited work on sparse viewpoint improvements regarding opacity. For example, Xiaoyang Lyu et al. [29] proposed an implicit surface reconstruction method with 3DGS, where implicit signed distance fields (SDFs) are introduced into the 3D Gaussian model for surface modeling. They designed a coupling strategy to align and associate the SDF with the 3D Gaussians, integrating volumetric rendering and aligning the rendered geometric properties (depth, normals) with the attributes derived from 3DGS. This approach achieves the alignment and joint optimization of the SDF and the 3D Gaussian model.
In general, a common limitation of radiance field rendering methods and 3DGS rendering methods is the tendency for training to overfit when observational data are insufficient, leading to inaccurate reconstructions. As evidenced by the aforementioned literature and Table 1, two primary strategies are employed to address this issue: regularization-based methods and model-based methods. Regularization-based methods can be further divided into two categories: those that introduce priors and those that do not. Model-based methods, on the other hand, focus on improving the design of feature learning networks to enhance the performance of novel view synthesis. Furthermore, in terms of improvements related to densification and pruning strategies in 3DGS, most methods enhance the decision-making capacity of densification and pruning by introducing thresholds. However, progress in improving opacity remains limited.

Table 1.
The methods from the aforementioned literature have been categorized. Only some representative references are listed in the table, and our method falls under the category of regularization-based methods that do not introduce priors.
Model-based methods primarily focus on improving the overall framework. In contrast, regularization-based methods involve modifications to the training process, with regularization typically applied during the algorithm’s computation process. Our method introduces a Gaussian distribution-based probabilistic mapping to assist in modeling, and proposes a novel elastic network regularization method to constrain and enhance features, which belongs to the category of regularization-based methods that do not introduce priors. Additionally, we have further improved the densification and pruning strategies to address the issue of excessively low Gaussian point opacity due to insufficient image data. In other words, we have also made advancements in improving opacity.
3. Method
3.1. Gaussian Distribution Probabilistic Mapping
Probabilistic mapping refers to the process of mapping input data to a probability distribution using a certain mathematical model, thereby deriving the probability value for each data point. These probability values represent the relative likelihood of data points within a specific distribution and are typically used for data modeling, inference, and decision making. Probabilistic mapping is applied in various fields such as diffusion models and uncertainty quantification. Yalavarthi, Vijaya Krishna [30] proposed a model for probabilistic prediction of irregularly sampled time series using conditional normalizing flows. This model can learn the joint distribution of future values based on past observations and queries, without assuming a fixed shape for the underlying distribution. Yan, Tijin [31] introduced a decomposable denoising diffusion model, and based on this new framework, we proposed some simple yet efficient probabilistic mapping paths that offer higher generation speeds. Xu, Chen [32] developed a sequential conformal prediction method to construct prediction regions for multivariate responses and estimated finite sample high-probability bounds for the conditional coverage gap. Uncertainty is typically described by introducing noise (ϵ) and probability distributions. This uncertainty is quantified through the mean and standard deviation, which help us understand the relative position and dispersion of data points.
The core idea of 3DGS is to represent points or voxels in three-dimensional space using Gaussian distributions, where each Gaussian distribution is defined by parameters such as position, covariance matrix, color, and opacity. Specifically, in 3DGS, the color value C is gradually accumulated through weighted blending along the sampled rays.
The point-based blending imaging principle employed here is conceptually similar to the ray marching method in NeRF. In this approach, and represent the color and opacity of each point, denotes the volumetric density, and represents the sampling frequency. Here, 3DGS converts the input point cloud into a 3D Gaussian distribution, which is defined by a 3D covariance matrix used to represent the 3D scene. This distribution is then projected into the 2D image space using a transformation matrix .
Here, represents the observation transformation, and denotes the Jacobian matrix. Each 3D Gaussian includes its center position , opacity ∈ [0, 1], covariance matrix , and spherical harmonics that represent the color.
This paper primarily employs probabilistic mapping based on statistical distributions, utilizing the Gaussian point information from the existing 3DGS and assuming that data points follow a normal distribution. The probability of each data point is calculated using the mean and standard deviation to assist in modeling. We apply the probabilistic mapping to the modeling process, as shown in Figure 3.
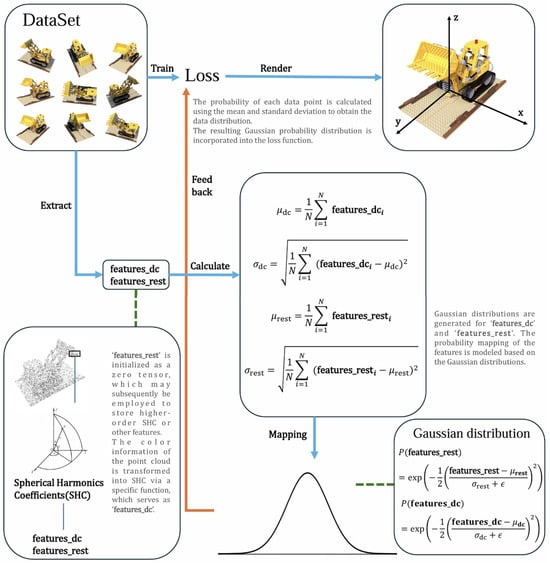
Figure 3.
Workflow of the Gaussian distribution probabilistic mapping method. The features extracted from the images in the dataset are computed and transformed into Gaussian distribution statistics. These distribution data are then fed back into the loss function to assist in the model’s inference.
Here, we assume that features_dc and features_rest are the input feature tensors; and are the means of the feature tensors; and are the standard deviations of the feature tensors; ϵ represents the noise level; and ϵ is introduced as noise to prevent the standard deviation from becoming too small or zero, thereby enhancing the stability of the computation.
Then, for each feature tensor, its Gaussian probability is calculated as follows:
By calculating the Gaussian probability of each feature tensor, we quantify the likelihood of the data point relative to the distribution. Here, and provide insights into the central tendency and dispersion of the data points, while ϵ helps mitigate potential instability in the calculations.
We compute the mean of the obtained Gaussian probabilities and then incorporate it into the loss function. While 3DGS leverages the mathematical properties of Gaussian distributions to describe scenes, primarily for 3D scene modeling and rendering, it primarily uses Gaussian distributions as a tool for scene representation. In contrast, we employ Gaussian distributions as a probabilistic mapping based on statistical distributions to assist in modeling, thereby enhancing the accuracy of modeling under sparse conditions.
3.2. Elastic Net Regularization
When 3D Gaussians are insufficient to represent the scene, the 3D Gaussian model activates an adaptive density control mechanism for densification. However, due to the lack of constraints, the newly generated 3D Gaussian functions are prone to overfitting the training views, leading to continuous development toward overfitting. Perceptual loss compares differences in the feature space rather than in the pixel space, which can lead to the loss of pixel-level details in the generated image. Additionally, perceptual loss typically relies on pre-trained convolutional neural networks, meaning the method is highly dependent on the dataset. This becomes a critical issue when applied to sparse scene datasets. On the other hand, adversarial loss enhances the model’s generative capability through generative adversarial networks. However, it often leads to excessive texturing, making the generated images appear unnatural, and can introduce artifacts. This approach is particularly unsuitable for sparse datasets. This is because the limited data can cause the overall structure to be inconsistent even if the details appear realistic. While each of these strategies has its merits, their drawbacks are amplified in sparse scenes. In contrast, elastic net regularization presents a lower risk of overfitting in sparse data modeling. It effectively controls the correlation between features, maintains model sparsity, and reduces noise in the training data. Therefore, we employed elastic net regularization for feature constraints, combining L1 and L2 regularization terms. L1 regularization serves the following function:
Here, and represent the sizes of the feature vectors of and , respectively. L2 regularization is defined as follows:
Finally, by combining L1 and L2 regularization, we obtain the elastic net regularization loss as follows:
and are regularization parameters that control the weight of the regularization. The pseudocode Algorithm 1. for elastic net regularization is as follows:
| Algorithm 1. Elastic Net Regularization Training Method | |
| 1. | FUNCTION Inference_Pipeline(feature_tensor, lambda_1, lambda_2, optimizer, num_iterations, batch_size, epsilon) |
| IN: feature_tensor: Input feature tensor to be processed. | |
| IN: lambda_1: Regularization parameter for L1 regularization. | |
| IN: lambda_2: Regularization parameter for L2 regularization. | |
| IN: optimizer: Optimizer for model parameters. | |
| IN: num_iterations: Number of iterations for optimization. | |
| IN: batch_size: Number of samples per batch. | |
| IN: epsilon: Small value to stabilize the calculation of Gaussian probability. | |
| ⊲ Initialization Phase. | |
| 2. | FOR initialize models DO |
| 3. | model = initialize_model() |
| 4. | END FOR |
| ⊲ Training Phase. | |
| FOR iteration ∈ {1, …, num_iterations} DO | |
| ⊲ Retrieve training batch. | |
| 5. | batch_features = sample_batch(feature_tensor, batch_size) |
| ⊲ Compute feature-based regularization (L1 and L2 regularization). | |
| 6. | L1_loss = sum(abs(batch_features)) |
| 7. | L2_loss = sqrt(sum(batch_features2)) |
| ⊲ Compute the total regularization loss. | |
| 8. | total_regularization_loss = lambda_1 * L1_loss + lambda_2 * L2_loss |
| ⊲ Compute Gaussian probability for feature tensors. | |
| 9. | gaussian_prob = exp(−1/2 * (batch_features/(sigma + epsilon))2) |
| ⊲ Compute the total loss. | |
| 10. | total_loss = total_regularization_loss + probability_mapping_loss |
| ⊲ Backpropagation and optimization. | |
| 11. | optimizer.zero_grad() |
| 12. | total_loss.backward() |
| 13. | optimizer.step() |
| 14. | END FOR |
| 15. | RETURN model, total_loss |
| 16. | END FUNCTION |
As shown in Pseudocode 1, we first input the regularization parameters, the processed feature tensors, and other model parameters. Next, we initialize the feature regularization model. During the training phase, we begin by computing the L1 and L2 regularization losses, which help control model complexity and prevent overfitting. Then, Gaussian distributions are used to compute the probability values for each feature, simulating the uncertainty in the data. Finally, the regularization losses and Gaussian probability losses are combined to form the final total loss. Afterward, the optimization process begins, where the model parameters are updated through backpropagation and optimization steps to minimize the total loss.
By utilizing feature-based probabilistic mapping and regularization, combined with the mathematical properties of Gaussian distributions and elastic net regularization, we effectively improve the accuracy of modeling, particularly when dealing with sparse data. The probabilistic mapping of input feature tensors not only helps capture the underlying patterns in the data but also quantifies uncertainty, thereby providing support for further inference and decision-making. L1 regularization aids in model sparsity but may overlook the correlation between features. In contrast, L2 regularization smooths the weights by reducing the sum of squared features, though it is less effective in preventing overfitting. With the combination of L1 and L2 regularization, the introduction of elastic net regularization further enhances the model’s generalization ability. The model is able to maintain sparsity and resistance to overfitting while appropriately penalizing correlations between features. This regularization strategy enables us to avoid excessive complexity in the model when handling high-dimensional feature spaces, thus improving its predictive performance. Therefore, the probabilistic mapping and regularization-based modeling framework provides an effective tool that allows for flexible modeling and optimization of different levels of features when faced with complex data. This method not only demonstrates advantages in 3D scene modeling but also shows good scalability and application potential in other fields requiring probabilistic inference and model refinement.
3.3. Multi-Scale Densification and Pruning Strategy
When using dense inputs, the number of 3D Gaussians and rendering performance steadily improve. One reason for this is that the density control strategy increases the number of 3D Gaussians to meet the rendering requirements of the training views. However, when sparse inputs are used, the limited information often leads to overfitting from a training perspective. This overfitting pattern results in a large number of floating points and incorrect geometries, preventing further optimization of the training view information and ultimately causing the failure of new view rendering. To address this issue, we have improved the multi-scale densification and pruning strategy to enable effective operation across multiple scales. The core idea of multi-scale densification is to improve the model’s density by operating at different resolutions or scales, while pruning operations determine, at the appropriate scale, which points should be removed. This is shown in Figure 4.
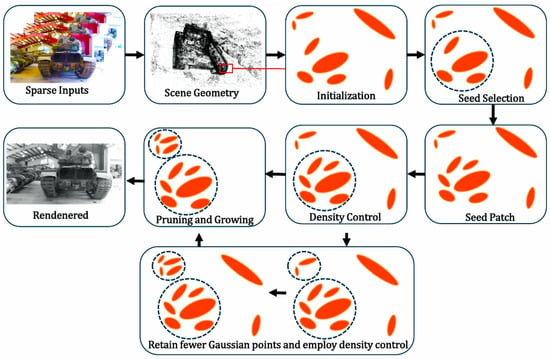
Figure 4.
The workflow of the multi-scale densification and pruning strategy. In the sparse point cloud of images, we initialize and extract Gaussian points based on the sparsity of the point cloud. Subsequently, seed selection and seed patch processes are performed. The purpose of these steps is to identify suitable Gaussian ellipsoids and densify them. Density control is an extension of these two steps, followed by pruning and growing to remove unnecessary Gaussian points and expand the confirmed Gaussian ellipsoids. Generally, when there are sufficient Gaussian points, pruning and growing are performed directly. However, when the Gaussian points are insufficient to generate model images, we further retain fewer Gaussian points and employ density control to fill the Gaussian ellipsoids and their corresponding Gaussian points to ensure image generation.
In Figure 4, it is important to note that if the number of seeds is too small, it can result in insufficient opacity of the generated Gaussians, leading to their removal during adaptive densification. Therefore, we introduced multiple thresholds into the regular process to control density and prevent the number of Gaussian spheres from being too low. In other words, in the current implementation, we dynamically adjust the density and accuracy of the point cloud through multi-scale densification and pruning operations. These operations are performed for each training iteration, with densification and pruning carried out based on different scales and gradients to improve training efficiency and control the complexity of the model. First, we introduced new densification threshold densify_threshold, gradient threshold grad_threshold, and scaling threshold scaling_threshold. Then, we use the following formulas:
represents the gradient magnitude of the point, and the is used to determine which points have larger gradients and require more points for densification. represents the scale of the point, and the is used to identify points that lie within a larger scale range and may require more points. For each point, we check whether its gradient exceeds the threshold and whether its scale meets the requirements. If both conditions are satisfied, the point is densified; otherwise, it is not. Specifically, we introduce an increasing densification threshold densify_threshold, and depending on the specific scale and gradient conditions of the point cloud, densification is performed when the threshold conditions are met. Sampling is then applied to the selected points, increasing the density of the point cloud to more finely represent the details of the model. Finally, different densification strategies are applied to each scale, which can be customized to adjust the granularity of densification. In addition, we introduce a progressively increasing prune_thresholds, where the opacity of a point serves as the decision criterion. Specifically, when the opacity of a point falls below the threshold, it is considered insignificant and can be pruned. Alternatively, pruning can also be determined by examining the maximum scale of the point. If a point has a very small scale, pruning may be considered.
In summary, compared to the original method, our approach introduces two key variables, the densification threshold and pruning threshold, for further multi-scale densification and multi-scale pruning data processing operations. Multi-scale densification refers to selecting which points should be densified based on the threshold for each scale and the current gradient values. Different densification thresholds are applied at each training step, allowing densification at various resolutions. This ensures that high-precision regions are densified while avoiding unnecessary densification in low-resolution areas. Multi-scale pruning refers to determining which points should be removed based on the threshold for each scale and the opacity of the points. Points that are no longer needed can be removed according to the criteria for different scales, thereby reducing model complexity and improving computational efficiency. This ensures that unimportant points are effectively pruned at each scale during training. In the original code, densification was based on a single threshold, and all points were sampled and densified according to a fixed condition. In contrast, our method introduces densification thresholds, where each scale now has its own densification threshold. This allows the selection of points to be densified based on different resolutions or scales, thus better controlling the density of the point cloud and avoiding the addition of excessive redundant points. Pruning in the original code was based on a single opacity or radius threshold, with uniform pruning operations applied to all points. In the new code, by using pruning thresholds, we introduce scale-specific pruning, where each scale has different pruning criteria. The purpose of this is to allow the model to flexibly remove unimportant points based on scale information. Additionally, to prevent gradient explosion and ensure training stability, the new code incorporates gradient clipping during the training process. This operation is performed before each optimization step, ensuring that the gradient magnitude does not exceed a certain limit, thereby avoiding instability during training. These operations collectively enhance training stability, accelerate the training process, and improve model performance.
4. Experiment
4.1. Metrics
In our experiment, the experimental parameters are presented in Table 2. A total of 30,000 training iterations were performed, with testing conducted at the 7000th and 30,000th iterations. Additionally, the default initial learning rate is set to 0.00016, with a learning rate delay multiplier of 0.01. The feature learning rate is 0.0025, the opacity learning rate is 0.025, the scaling learning rate is 0.005, and the rotation learning rate is 0.001. The density percentage is set to 0.01, the SSIM loss coefficient is 0.2, and the densification interval is 100. The opacity reset interval is 3000 iterations. Density optimization begins at the 500th iteration, with a density optimization gradient threshold of 0.0002. The default optimizer type is “adam.”

Table 2.
The experimental parameters.
For datasets that include both real data and reconstructed meshes, we compare the generated meshes with the ground truth meshes or point clouds. To assess the quality of the rendered RGB images, we utilize several evaluation metrics: Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index (SSIM) [33], and Learned Perceptual Image Patch Similarity (LPIPS) [34]. These metrics help quantify the visual fidelity and structural similarity between the rendered and ground truth images.
All experiments were performed on a single NVIDIA GeForce RTX 4070D Ti GPU.
4.2. Dataset
We evaluated the performance of our method on the NeRF-Synthetic, LLFF, and Tanks and Temples datasets, comparing it with the current state-of-the-art (SOTA) models.
4.3. Quantitative Results
The model employed in this study, compared to 3DGS, incorporates the generation of probability maps using Gaussian distributions and introduces a multi-scale densification strategy. The loss associated with the probability maps is added to the loss function. Additionally, in terms of sampling, this method places greater emphasis on the transparency of the images and subsequently considers densification and pruning based on the transparency.
Quantitative training was conducted on the NeRF-Synthetic, LLFF, and Tanks and Temples datasets. The results of the quantitative experiments we performed are shown in Table 3. Due to the variability in results based on the selected metrics and datasets, it is difficult to assess which method is superior. Therefore, we compute a comprehensive score. Since the training was conducted on three datasets, we sum the same metric across the datasets and then divide by three. However, for LPIPS, the values become very small and difficult to estimate, so we sum the LPIPS values without dividing by three. Higher values of PSNR and SSIM are preferred, while a lower LPIPS value is better. The calculation of the comprehensive score follows these steps: first, the scores for PSNR and SSIM are ranked, followed by the ranking of LPIPS. Subsequently, the rankings for these three metrics are summed, and the method with the lowest total rank is considered the best overall performer. It is important to note that when the total ranks for the three metrics are identical, priority is given to the ranking of PSNR, followed by SSIM. The results in Table 3 indicate that, based on the comprehensive score and ranking, our method outperforms existing methods, surpassing all others.

Table 3.
The quantitative results of various SOTA methods and our method on the NeRF-Synthetic, Tanks and Temples, and LLFF datasets. The best-performing metrics, except for the Rank, are highlighted in bold.
In Table 3, when comparing our method with current state-of-the-art models, based on the comprehensive scoring design, our approach outperforms the majority of other methods, surpassing 3DGS and achieving the top rank. However, specifically, on the NeRF-Synthetic and Tanks and Temples datasets, our method performs relatively moderately, while on the LLFF dataset, our method demonstrates slight improvements in both PSNR and SSIM metrics. On the other hand, our depth similarity regularization term produces smooth depth results on object surfaces while preserving significant depth differences at the edges. This results in clearer rendering in areas with thin objects, reducing blurring. The rendering results are shown in Figure 5 for comparison.

Figure 5.
Comparison of the rendering results on NeRF-Synthetic for various SOTA methods and our approach. It can be observed that our method achieves a relatively higher PSNR metric. However, in terms of detailed images, except for the images from NeRF and SparseNeRF, which are relatively blurred, the differences in other metrics are minimal. This demonstrates the superiority of our method in terms of the evaluation metrics.
As shown in Figure 5, our method performs well in the PSNR metric, exhibiting comparable performance to other state-of-the-art algorithms. Subsequently, we significantly reduced the number of images from different viewpoints in the NeRF-Synthetic dataset, particularly for the plant, chair, and hot dog image datasets. The original number of images was reduced to one-fifth of its size, and eight viewpoints were selected for experimentation. It is worth noting that this number strikes a balance between maintaining image quantity and avoiding modeling failures. Further reduction of the dataset could lead to modeling failures in some methods. We then conducted further quantitative testing, and similarly, we applied the same comprehensive scoring criteria as in Table 3. The test results are presented in Table 4.

Table 4.
The quantitative results for various SOTA methods and our approach on the NeRF-Synthetic, Tanks and Temples, and LLFF datasets after reducing the number of images and forming eight viewpoints. The best-performing metrics, except for the Rank, are highlighted in bold.
As shown in Table 4, we have compared our method only with relevant state-of-the-art models that focus on sparse viewpoint improvements. The results indicate that our method outperforms others, with our comprehensive score ranking first. Specifically, in the PSNR metric, our method achieves approximately an 11% improvement over 3DGS on the dataset, and a 4% improvement over FSGS, the second-best method in Table 4. In terms of SSIM and LPIPS metrics, our method slightly outperforms the others in most cases.
Overall, it can be observed from the ranking of the comprehensive score that our method outperforms other methods, particularly with a significant improvement in PSNR, and generally exhibits slight advantages in other metrics. Specifically, our method achieves approximately a 4% improvement in PSNR compared to current SOTA methods. This advantage arises from the fact that, in sparse scenes, effective information is limited. Particularly for 3DGS, some Gaussian ellipsoids are discarded during modeling due to their covariance matrices, preventing them from forming valid ellipsoids. Additionally, areas with subtle color variations, such as the mesh of a microphone, are prone to aliasing and blurred distortion. Our method obtains more accurate geometric structures through geometric constraints, thereby improving rendering quality. We rendered the training results from the NeRF-Synthetic dataset, particularly for the grass and chair categories, after reducing the number of images, as shown in Figure 6.
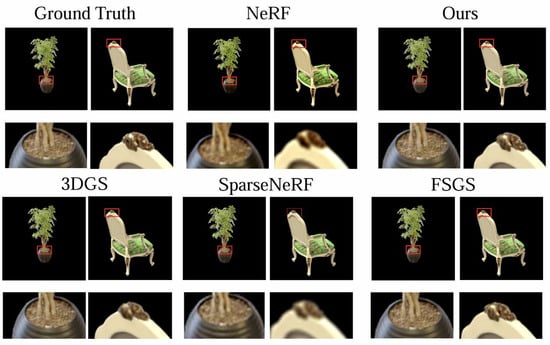
Figure 6.
Comparison of the rendering results on NeRF-Synthetic for various SOTA methods and our approach after reducing the number of images. It can be observed that in the detailed images, the images from NeRF and SparseNeRF are relatively blurred.
Figure 6 shows the corresponding training results from Table 4. As seen in the figure, the image quality generated by our method is nearly indistinguishable from that of other SOTA generative models.
Overall, we first conducted quantitative experiments using a widely used dataset, obtaining evaluation metrics for each method and designing a comprehensive scoring rule to compare these methods. From these metrics, it can be observed that our method achieved the top rank in the comprehensive score, performing comparably to other state-of-the-art methods in terms of the evaluation criteria. Additionally, we compared the evaluation metrics of the training results for the frog, drone, and hot dog categories in the NeRF-Synthetic dataset after reducing the number of images. The results also demonstrate that our method ranks first under sparse viewpoints, indicating that our approach surpasses others.
4.4. Ablation Study
We primarily improved three aspects. The first aspect is the overall improvement of the Gaussian model’s probabilistic mapping, where we model based on the Gaussian distribution by fully utilizing the feature information of the model. The second aspect is the regularization constraint on the features, which is aimed at ensuring our method can obtain more accurate geometric structures through geometric constraints, resulting in higher rendering quality. The third aspect is the multi-scale densification and pruning strategy, which primarily addresses opacity improvements. In sparse viewpoints, due to fewer image features, the overall opacity tends to be lower, leading to the loss of Gaussian ellipsoid opacity and ultimately causing modeling failure. We did not modify the original opacity algorithm, but instead approached the problem from another perspective by implementing multi-scale strategy improvements. When the number of images is low, we set a minimum threshold for opacity to ensure that the minimum opacity for generating Gaussian ellipsoids is maintained. As the number of images approaches the normal amount, the threshold weight gradually decreases, allowing the opacity of the original images to be properly represented. Based on these three aspects, we significantly reduced the number of images from different viewpoints in the NeRF-Synthetic dataset for the frog, drone, and hot dog categories. The number of images was reduced to one-fifth of the original size, and eight viewpoints were used for the ablation study. In other words, we performed an ablation study using the reduced image datasets of frog, drone, and hot dog from the NeRF-Synthetic dataset, and we used the original datasets for frog, drone, and hot dog as a baseline method to verify the effectiveness of our approach. In the table, we abbreviate Gaussian Probability as G, Regularization as R, and Multi-scale Densification and Pruning strategy as M(D&P). For these ablation experiments, we also conducted a consistent comprehensive score evaluation and ranking. The training results on the sparse dataset are shown in Table 5.

Table 5.
The ablation study results of our method on the frog, drone, and hot dog datasets, with eight viewpoints formed after reducing the number of images. In the table, Gaussian Probability is abbreviated as G, Regularization as R, and Multi-scale Densification and Pruning strategy as M(D&P). The best-performing metrics, except for the Rank, are highlighted in bold.
As shown in Table 5, it can be observed that the inclusion of the Gaussian model probabilistic mapping or regularization constraint modules results in a significant improvement in the PSNR metric. The multi-scale densification and pruning strategy, on the other hand, leads to a slight decrease in various metrics. However, as indicated in the table, even when all three components are included, they do not necessarily result in the best performance across all metrics, but instead demonstrate highly competitive results. This is evident in the ranking of our comprehensive score. Therefore, we observe that the most competitive metrics are achieved with the Gaussian model probabilistic mapping and regularization constraint modules, with the Gaussian model probabilistic mapping component contributing more significantly to the improvement. These two components are key to enhancing the metrics. While the multi-scale densification and pruning strategy does not show a clear impact on improving the metrics in the charts, it plays a crucial role in improving the environment, particularly in sparse scenarios, during the execution process. on the other hand, is a variable that may fluctuate significantly, mainly due to its dependency on the quality of the dataset images. When the image quality is insufficient or the number of images is too small, meaning there are not enough features to provide constraints, the effectiveness of this method is relatively low. Additionally, compared to Gaussian probabilistic mapping, the multi-scale densification strategy and feature constraint regularization take more time, but the corresponding performance improvements are not as significant. Overall, the Gaussian probabilistic mapping module in our improved method performs the best. Regularization is more suitable for scenarios with rich image features, while the multi-scale densification strategy is more applicable to sparse image scenarios. This method can improve situations where models fail to generate due to low opacity, enabling successful modeling in such cases. The training results with only R, all components included, and only G values are shown after rendering in Figure 7.
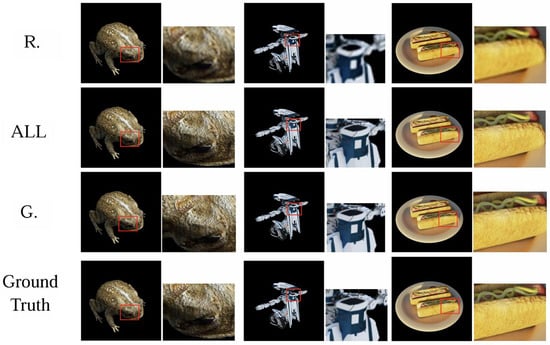
Figure 7.
The ablation study of our method on the sparse datasets of frog, drone, and hot dog. We abbreviate Gaussian Probability as G and Regularization as R. It can be seen that the effect of R on the sparse dataset is not significant, as the rendered images still exhibit considerable blurring. In contrast, the other methods are relatively clearer.
It can be observed that the effect of G in our method is significant, as it successfully improves the clarity of the images. In contrast, the effect of R is not as pronounced as that of G. The training results on the standard dataset are shown in Table 6.

Table 6.
Presents the ablation study results of our method on the original frog, drone, and hot dog datasets. In the table, Gaussian Probability is abbreviated as G, Regularization as R, and Multi-scale Densification and Pruning strategy as M(D&P). The best-performing metrics, except for the Rank, are highlighted in bold.
As shown in Table 6, the ranking of the comprehensive score indicates that even without the introduction of the Gaussian probabilistic module under specific conditions, our method still outperforms other methods that do not incorporate this module. Furthermore, the multi-scale densification and pruning strategy did not show significant effects on the standard datasets. The main reason for this is that the feature and opacity information provided by the image quantity in these datasets is already sufficient to construct the model, thus not requiring the assistance of multi-scale densification and pruning strategies. When sufficient information is available, feature constraints provide only a slight improvement in the model’s performance. Based on the comprehensive score ranking, it is evident that our Gaussian probabilistic module demonstrates superior performance. The additional time required for feature constraints and Gaussian probabilities is minimal, as the amount of feature computation remains fixed during each cycle. However, the time consumed by the added multi-scale densification and pruning strategy significantly increases. We present the time consumption for each module on the frog, drone, and their sparse datasets, as shown in Table 7. It can be observed that our method increases the time consumption. The Gaussian probabilistic module and regularization constraint consume a similar amount of time to 3DGS, whereas the method incorporating the multi-scale densification and pruning strategy shows a significant increase in time consumption.

Table 7.
The ablation study results of our method on the frog, drone, and their sparse datasets, with eight viewpoints formed after reducing the number of images. In the table, Gaussian Probability is abbreviated as G, Regularization as R, and Multi-scale Densification and Pruning strategy as M(D&P).
As shown in Table 7, the additional time required for feature constraints and Gaussian probabilities is relatively minimal. However, the incorporation of the multi-scale densification and pruning strategy significantly increases the time consumption. When all three modules are combined, the added time increases proportionally. As observed in the table, the time consumption of our method is approximately 50% higher than that of traditional methods, indicating that our approach is relatively less efficient. Consequently, it can be concluded that our method is not suitable for large datasets.
Overall, we did not introduce many additional parameters. The three aspects of our improvement are all based on the additional utilization of the information from the original code. One aspect focuses on the multi-scale densification and pruning strategy for sparse viewpoint datasets, while the other two aspects primarily utilize the inherent characteristics of the original code, such as the properties of Gaussian distributions and image feature extraction. We introduced new threshold parameters to make more effective use of the Gaussian distribution and feature information, enabling Gaussian probabilities and feature constraints to assist modeling according to the newly added parameters. Our ablation study also confirms the effectiveness of our approach. Furthermore, our method is time-intensive and often requires more time to generate better models.
5. Conclusions
This paper presents a novel optimization method, GPRGS, for optimizing 3DGS under both sparse views and standard input conditions. We observed at the beginning of training that in sparse scenes, insufficient generation of Gaussian ellipsoids leads to overfitting and even modeling failure. To address this issue, we propose a 3DGS method based on Gaussian probabilistic distribution and feature regularization (GPRGS). This method introduces Gaussian probabilistic modeling based on Gaussian distribution features, where feature information from images is used to establish Gaussian distributions and model the probability mapping of features, thereby achieving the correct representation of the scene. Furthermore, we introduce scale and densification thresholds, updating the multi-scale densification and pruning strategy to enhance sparse data. Compared to previous works, our approach does not rely on prior knowledge nor focus on designing better prior learning methods. Instead, we analyze and improve the sparse input 3DGS problem from an optimization perspective, and our method outperforms traditional 3DGS in regular scenes. We evaluated the performance of our method on the NeRF-Synthetic, LLFF, and Tanks and Temples datasets and compared it with current SOTA models. The results indicate that our method ranks first in the comprehensive score, demonstrating that its performance is comparable to, or even surpasses, existing state-of-the-art methods. Furthermore, a limitation of our method is its higher time consumption, and it is not suitable for large datasets. It is hoped that the findings of this study will encourage researchers to explore new view synthesis tasks under sparse inputs from an optimization perspective, thereby advancing the field of 3D geometric modeling.
Author Contributions
Conceptualization, Y.Q. and G.L.; Methodology, Y.Q.; Software, Y.Q.; Validation, G.L.; Formal analysis, Y.Q.; Investigation, Y.Q.; Resources, G.L. and J.W.; Data curation, J.W. and G.L.; Writing—original draft, Y.Q.; Writing—review and editing, Y.Q.; Visualization, J.W. and G.L.; Supervision, J.W. and G.L.; Project administration, J.W. and G.L.; Funding acquisition, J.W. and G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by R&D Program of Beijing Municipal Education Commission (KM202410016007) and the National Natural Science Foundation of China (42404035).
Data Availability Statement
The data presented are available on request from the corresponding author. The data are not publicly available due to privacy restrictions.
Acknowledgments
We acknowledge Yang Cui’s contributions in the areas of investigation, resource management, review and editing, supervision, and funding for this article. We used generative AI to improve the logical flow between the language in the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liang, H.; Wu, T.; Hanji, P.; Banterle, F.; Gao, H.; Mantiuk, R.; Öztireli, C. Perceptual Quality Assessment of NeRF and Neural View Synthesis Methods for Front-Facing Views. Comput. Graph. Forum 2024, 43, e15036. [Google Scholar] [CrossRef]
- Lv, J.; Guo, J.; Zhang, Y.; Zhao, X.; Lei, B. Neural Radiance Fields for High-Resolution Remote Sensing Novel View Synthesis. Remote Sens. 2023, 15, 3920. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Y.; Wang, Z.; Zhang, Z.; Jiang, Z.; Yu, Y.; Li, L.; Zhang, L. Shadow-Aware Point-Based Neural Radiance Fields for High-Resolution Remote Sensing Novel View Synthesis. Remote Sens. 2024, 16, 1341. [Google Scholar] [CrossRef]
- Kerbl, B.; Kopanas, G.; Leimkühler, T.; Drettakis, G. 3D gaussian splatting for real-time radiance field rendering. ACM Trans. Graph. 2023, 42, 139. [Google Scholar] [CrossRef]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. NeRF: Representing scenes as neural radiance fields for view synthesis. Commun. ACM 2020, 65, 99–106. [Google Scholar] [CrossRef]
- Martin, P.; Rodrigues, A.; Ascenso, J.; Queluz, M.P. NeRF View Synthesis: Subjective Quality Assessment and Objective Metrics Evaluation. IEEE Access 2025, 13, 26–41. [Google Scholar] [CrossRef]
- Qu, Q.; Liang, H.; Chen, X.; Chung, Y.Y.; Shen, Y. NeRF-NQA: No-Reference Quality Assessment for Scenes Generated by NeRF and Neural View Synthesis Methods. IEEE Trans. Vis. Comput. Graph. 2024, 30, 2129–2139. [Google Scholar] [CrossRef] [PubMed]
- Boss, M.; Jampani, V.; Braun, R.; Liu, C.; Barron, J.T.; Lensch, H.P.A. Neural-PIL: Neural Pre-Integrated Lighting for Reflectance Decomposition. In Proceedings of the Neural Information Processing Systems, Online, 6–14 December 2021. [Google Scholar]
- Gao, C.; Sun, Q.; Zhu, J.; Chen, J. MBS-NeRF: Reconstruction of sharp neural radiance fields from motion-blurred sparse images. Sci. Rep. 2025, 15, 5275. [Google Scholar] [CrossRef]
- Qin, Y.; Li, X.; Zu, L.; Jin, M.L. Novel View Synthesis with Depth Priors Using Neural Radiance Fields and CycleGAN with Attention Transformer. Symmetry 2025, 17, 59. [Google Scholar] [CrossRef]
- Jiang, Y.; Qin, H.; Dai, Y.; Liu, J.; Zhang, G.; Zhang, C.; Yang, T. GS-SFS: Joint Gaussian Splatting and Shape-From-Silhouette for Multiple Human Reconstruction in Large-Scale Sports Scenes. IEEE Trans. Multimed. 2024, 26, 11095–11110. [Google Scholar] [CrossRef]
- Guo, S.; Wang, Q.; Gao, Y.; Xie, R.; Li, L.; Zhu, F.; Song, L. Depth-Guided Robust Point Cloud Fusion NeRF for Sparse Input Views. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 8093–8106. [Google Scholar] [CrossRef]
- Wang, W.; An, L.; Zhou, M.Q.; Han, G.Y. Neighborhood transformer for sparse-view X-ray 3D foot reconstruction. Biomed. Signal Process. Control 2025, 100, 107082. [Google Scholar] [CrossRef]
- Knapitsch, A.; Park, J.; Zhou, Q.Y.; Koltun, V. Tanks and Temples: Benchmarking Large-Scale Scene Reconstruction. ACM Trans. Graph. 2017, 36, 78. [Google Scholar] [CrossRef]
- Mildenhall, B.; Srinivasan, P.P.; ORTIZ-Cayon, R.; Kalantari, N.K.; Ramamoorthi, R.; Ng, R.; Kar, A. Local Light Field Fusion: Practical View Synthesis with Prescriptive Sampling Guidelines. ACM Trans. Graph. 2019, 38, 29. [Google Scholar] [CrossRef]
- Fei, T.; Bi, L.; Gao, J.; Chen, S.; Zhang, G. MVSGS: Gaussian splatting radiation field enhancement using multi-view stereo. Complex Intell. Syst. 2024, 11, 80. [Google Scholar] [CrossRef]
- Lu, Z.; Ye, J.; Leonard, J. 3DGS-CD: 3D Gaussian Splatting-Based Change Detection for Physical Object Rearrangement. IEEE Robot. Autom. Lett. 2025, 10, 2662–2669. [Google Scholar] [CrossRef]
- Liu, Z.; Su, J.; Cai, G.; Chen, Y.; Zeng, B.; Wang, Z. GeoRGS: Geometric Regularization for Real-Time Novel View Synthesis from Sparse Inputs. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 13113–13126. [Google Scholar] [CrossRef]
- Xu, K.; Li, J.; Li, Z.-Q.; Cao, Y.-J. SG-NeRF: Sparse-Input Generalized Neural Radiance Fields for Novel View Synthesis. J. Comput. Sci. Technol. 2024, 39, 785–797. [Google Scholar] [CrossRef]
- Lai, S.; Cui, L.; Yin, J. Fast radiance field reconstruction from sparse inputs. Pattern Recognit. 2025, 157, 110863. [Google Scholar] [CrossRef]
- Hu, W.; Tian, C.; Wen, L.; Ding, H. TD-NeRF: Transfer Learning and Diffusion Regulation-Based NeRF for Scene Perception. IEEE Trans. Instrum. Meas. 2025, 74, 5004512. [Google Scholar] [CrossRef]
- Jin, T.; Zhuang, J.; Xiao, J.; Ge, J.; Ye, S.; Zhang, X.; Wang, J. Prior-Driven NeRF: Prior Guided Rendering. Electronics 2023, 12, 1014. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Tan, G. ID-NeRF: Indirect diffusion-guided neural radiance fields for generalizable view synthesis. Expert Syst. Appl. 2025, 266, 126068. [Google Scholar] [CrossRef]
- Qiu, J.; Zhu, Y.; Jiang, P.-T.; Cheng, M.-M.; Ren, B. RDNeRF: Relative depth guided NeRF for dense free view synthesis. Vis. Comput. 2024, 40, 1485–1497. [Google Scholar] [CrossRef]
- Fu, T.; Zhou, Y.; Wang, Y.; Liu, J.; Zhang, Y.; Kong, Q.; Chen, B. Neural Field-Based Space Target 3D Reconstruction with Predicted Depth Priors. Aerospace 2024, 11, 997. [Google Scholar] [CrossRef]
- Carlson, A.; Ramanagopal, M.S.; Tseng, N.; Johnson-Roberson, M.; Vasudevan, R.; Skinner, K.A. CLONeR: Camera-Lidar Fusion for Occupancy Grid-Aided Neural Representations. IEEE Robot. Autom. Lett. 2023, 8, 2812–2819. [Google Scholar] [CrossRef]
- Yuan, Y.-J.; Lai, Y.-K.; Huang, Y.-H.; Kobbelt, L.; Gao, L. Neural Radiance Fields from Sparse RGB-D Images for High-Quality View Synthesis. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 8713–8728. [Google Scholar] [CrossRef]
- Barron, J.T.; Mildenhall, B.; Verbin, D.; Srinivasan, P.P.; Hedman, P. Zip-NeRF: Anti-Aliased Grid-Based Neural Radiance Fields. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 2–6 October 2023; pp. 19640–19648. [Google Scholar]
- Lyu, X.; Sun, Y.-T.; Huang, Y.-H.; Wu, X.; Yang, Z.; Chen, Y.; Pang, J.; Qi, X. 3DGSR: Implicit Surface Reconstruction with 3D Gaussian Splatting. ACM Trans. Graph. 2024, 43, 198. [Google Scholar] [CrossRef]
- Yalavarthi, V.K.; Scholz, R.; Born, S.; Schmidt-Thieme, R. Probabilistic Forecasting of Irregular Time Series via Conditional Flows. arXiv 2024, arXiv:2402.06293. [Google Scholar] [CrossRef]
- Yan, T.J.; Gong, H.H.; He, Y.P.; Zhan, Y.F.; Xia, Y.Q. Probabilistic time series modeling with decomposable denoising diffusion model. In Proceedings of the Forty-First International Conference on Machine Learning, Vienna, Austria, 21 July 2024. [Google Scholar]
- Xu, C.; Jiang, H.; Xie, Y. Conformal prediction for multi-dimensional time series by ellipsoidal sets. arXiv 2024, arXiv:2403.03850. [Google Scholar] [CrossRef]
- Zhou, W.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The Unreasonable Effectiveness of Deep Features as a Perceptual Metric. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition 2018, Salt Lake City, UT, USA, 18–23 June 2018; pp. 586–595. [Google Scholar]
- Müller, T.; Evans, A.; Schied, C.; Keller, A. Instant neural graphics primitives with a multiresolution hash encoding. ACM Trans. Graph. TOG 2022, 41, 102. [Google Scholar] [CrossRef]
- Reiser, C.; Peng, S.; Liao, Y.; Geiger, A. KiloNeRF: Speeding Up Neural Radiance Fields with Thousands of Tiny MLPs. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021. [Google Scholar]
- Zhu, Z.; Fan, Z.; Jiang, Y.; Wang, Z.Y. FSGS: Real-Time Few-shot View Synthesis using Gaussian Splatting. In Proceedings of the European Conference on Computer Vision, Paris, France, 1–6 October 2023. [Google Scholar]
- Wang, G.; Chen, Z.; Loy, C.C.; Liu, Z. SparseNeRF: Distilling Depth Ranking for Few-shot Novel View Synthesis. In Proceedings of the 2023 International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 9031–9042. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).