Three-Way Decision-Driven Adaptive Graph Convolution for Deep Clustering
Abstract
1. Introduction
- We propose a k-order graph convolution paradigm and an adaptive framework, 3WDAGC, to automatically determine the optimal convolution order k to suit the characteristics of different graphs.
- We innovatively introduce the principles of three-way decisions to design an efficient adaptive search algorithm, significantly reducing the computational cost of finding the optimal k.
- Extensive experiments on multiple benchmark datasets demonstrate that our proposed 3WDAGC surpasses various state-of-the-art graph clustering methods in terms of clustering performance and showcases its superiority in handling network diversity.
2. Related Work
3. Preliminaries
3.1. Graph Smoothness and the Laplacian Operator
3.2. Spectral Decomposition and Graph Frequencies
3.3. Graph Filtering as Spectral Re-Weighting
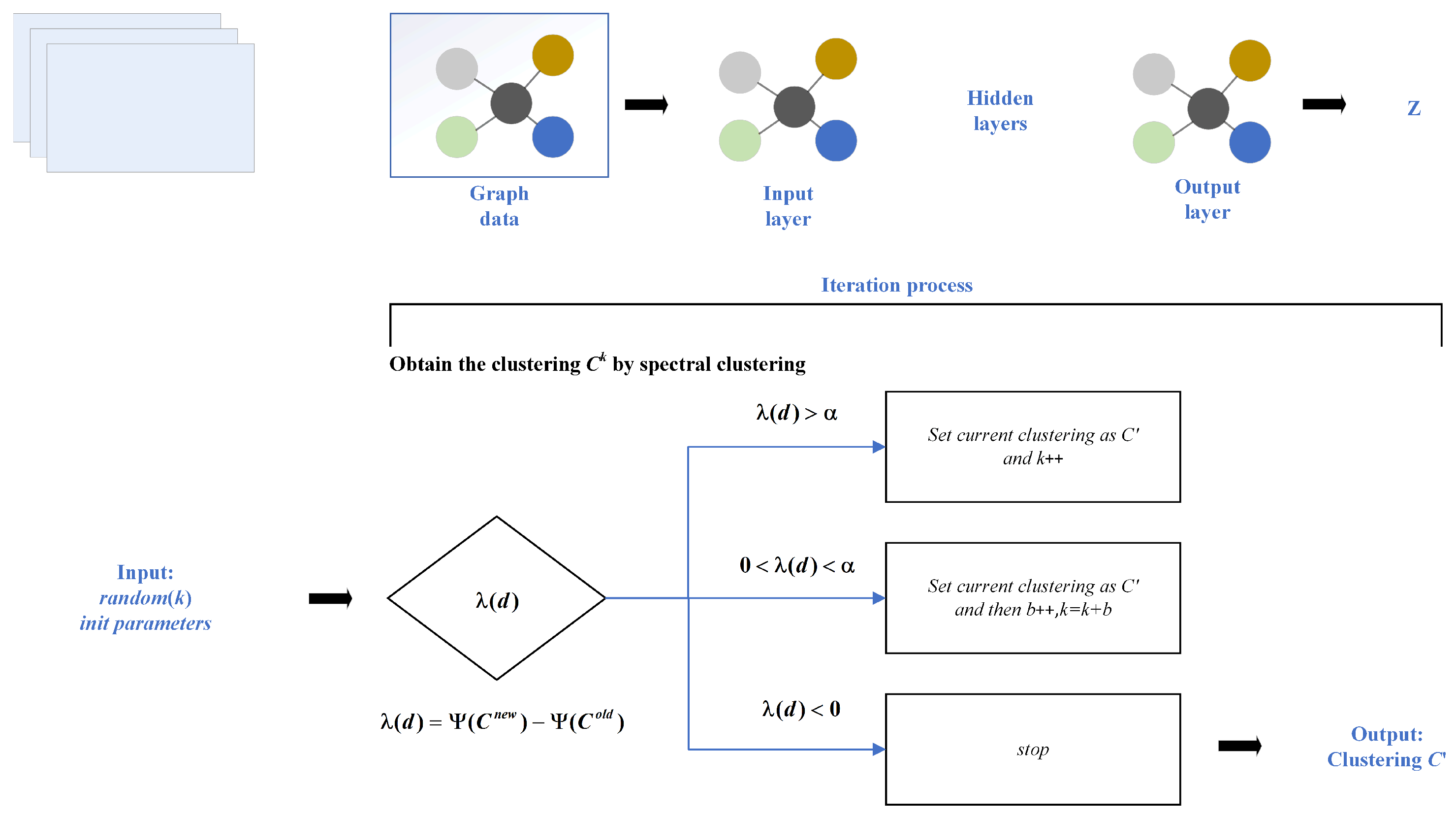
4. The Proposed Method: 3WDAGC
4.1. K-Order Feature Smoothing via Graph Filtering
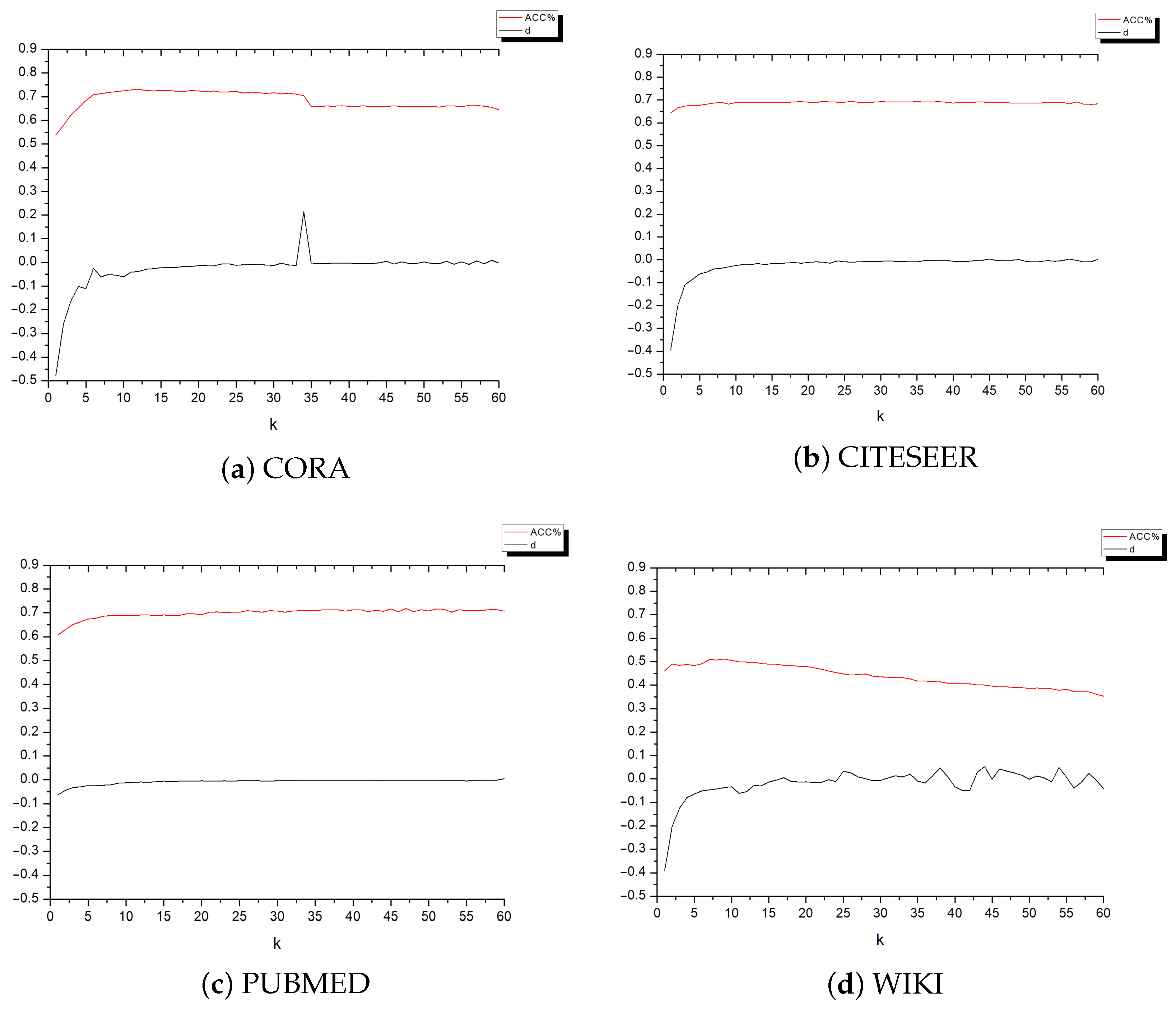
4.2. Adaptive Search for Optimal Order k
4.2.1. Objective Function: Clustering Compactness
4.2.2. Search Strategy Inspired by Three-Way Decisions
- Positive Region (Accept and Stop): If .
- –
- Decision: The compactness has significantly increased, indicating that the search has likely passed a local minimum.
- –
- Action: The search process terminates. The order from the previous step, , is selected as the optimal one.
- Boundary Region (Refine and Slow Down): If .
- –
- Decision: The compactness is still improving, but the rate of improvement has slowed, or minor fluctuations are occurring. This suggests the search is in the vicinity of the optimal solution.
- –
- Action: To avoid overshooting the optimum, the search switches to a fine-grained mode. The step size is reset to , and the search continues.
- Negative Region (Explore and Accelerate): If .
- –
- Decision: The compactness is decreasing consistently and effectively, indicating the search is likely still far from the optimal point.
- –
- Action: To improve search efficiency, the process is accelerated. The step size is increased (), and a larger step is taken ().
| Algorithm 1 3WDAGC Algorithm |
|
5. Experiments and Analysis
5.1. Datasets and Baseline Method
- Methods that only use node features: k-means and spectral clustering that constructs a similarity matrix with the node features by linear kernel.
5.2. Implementation Details
5.2.1. Experimental Environment
5.2.2. Scalability and Performance
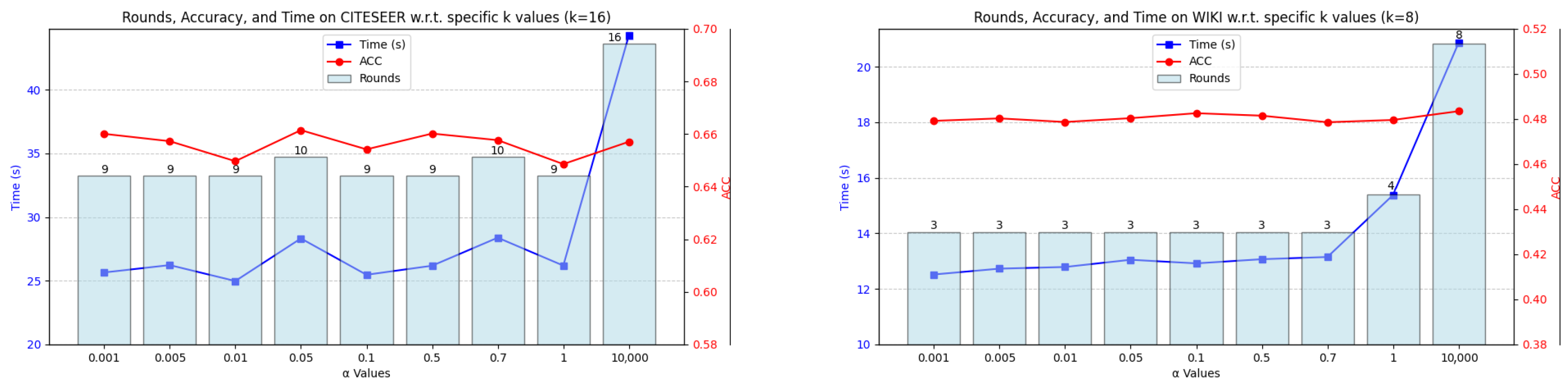
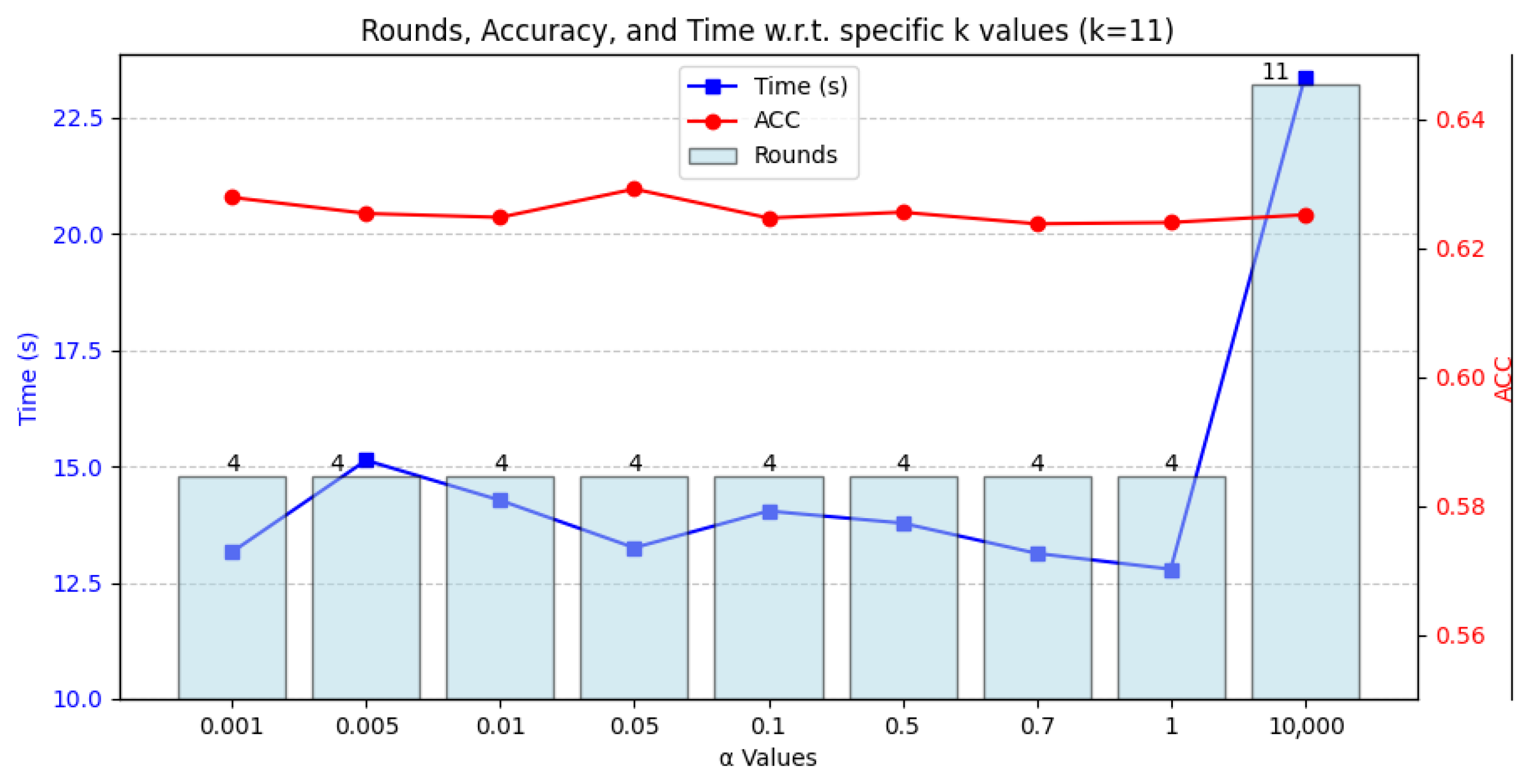
5.2.3. Parameter Settings
5.3. Evaluation Metrics
5.3.1. Clustering Accuracy (ACC)
5.3.2. F-Measure (FM)
- True Positives (TP): The number of pairs of points that are in the same cluster in both the ground truth and the predicted clustering.
- False Positives (FP): The number of pairs of points that are in the same cluster in the prediction but in different clusters in the ground truth.
- False Negatives (FN): The number of pairs of points that are in different clusters in the prediction but in the same cluster in the ground truth.
5.3.3. Normalized Mutual Information (NMI)
5.4. Experimental Analysis
5.5. In-Depth Analysis of 3WDAGC
5.5.1. Parameter Sensitivity Analysis
5.5.2. Ablation Study on the Search Strategy
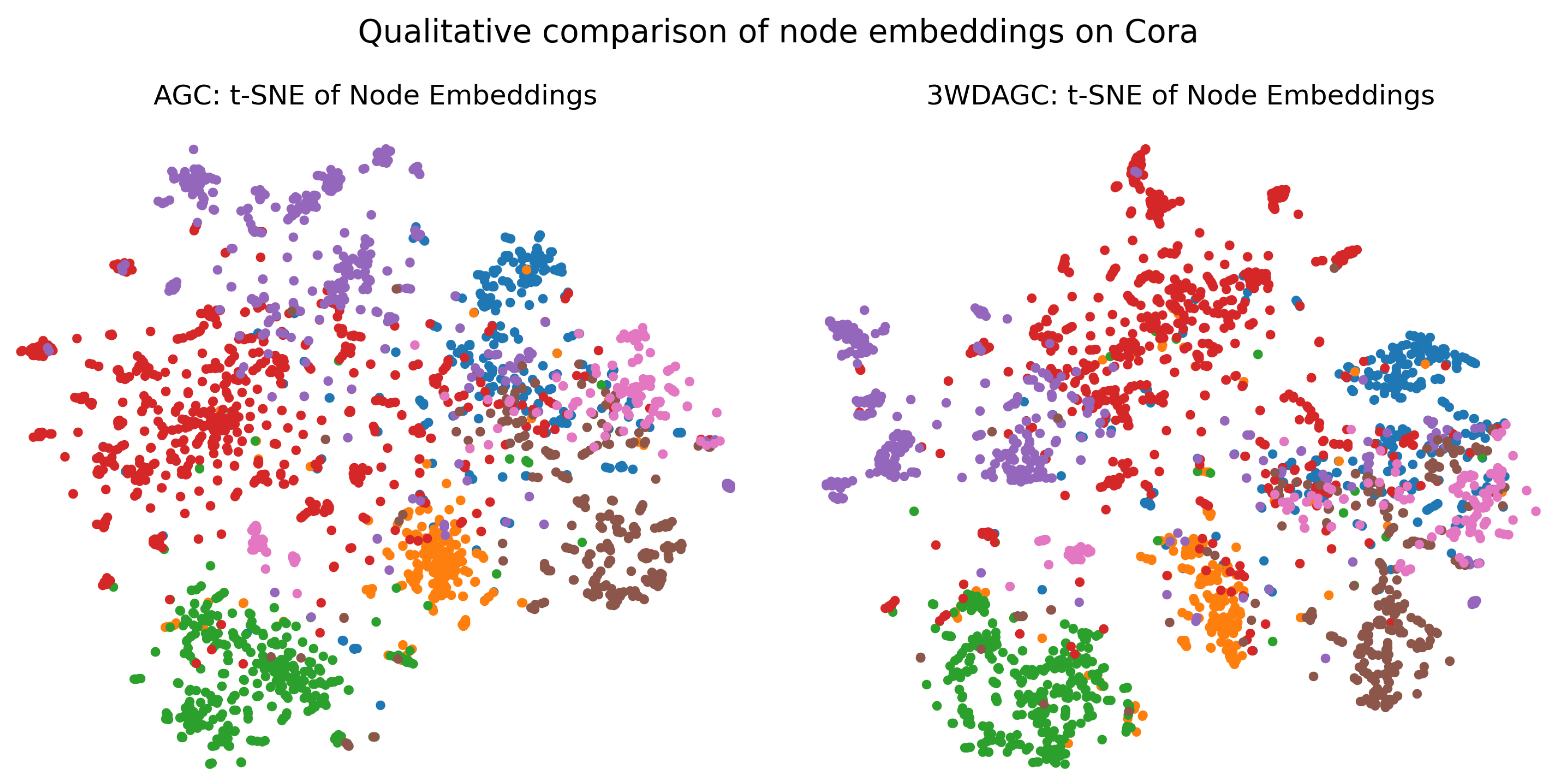
5.5.3. Qualitative Analysis and Case Studies
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Parameter Configuration
| Parameter | Value | Description |
|---|---|---|
| 0.02 | The upper threshold in the three-way decision strategy, controlling the switch from accelerated to fine-grained search. | |
| 0 | The lower threshold, fixed at zero for all experiments. | |
| Initial k | RandomInt(1, 10) | The initial convolution order k is randomly selected from the integer range [1, 10]. |
| Initial b | 1 | The initial step size for the search algorithm. |
| Random Seed | 42 | A fixed random seed was used for all experiments to ensure reproducibility. |
Appendix B. Additional Sensitivity Analysis
References
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. In Proceedings of the 5th International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Aljalbout, E.; Golkov, V.; Siddiqui, Y.; Strobel, M.; Cremers, D. Clustering with Deep Learning: Taxonomy and New Methods. arXiv 2018, arXiv:1801.07648. [Google Scholar] [CrossRef]
- Zhou, S.; Xu, H.; Zheng, Z.; Chen, J.; Zhao, L.; Bu, J.; Wu, J.; Wang, X.; Zhu, W.; Martin, E. A Comprehensive Survey on Deep Clustering: Taxonomy, Challenges, and Future Directions. arXiv 2022, arXiv:2206.06539. [Google Scholar] [CrossRef]
- Wang, C.; Pan, S.; Long, G.; Zhu, X.; Jiang, J. Mgae: Marginalized graph autoencoder for graph clustering. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, Singapore, 6–10 November 2017; pp. 889–898. [Google Scholar]
- Zhang, X.; Liu, H.; Li, Q.; Wu, X.M.; Zhang, X. Adaptive graph convolution methods for attributed graph clustering. IEEE Trans. Knowl. Data Eng. 2023, 35, 12384–12399. [Google Scholar] [CrossRef]
- Min, E.; Guo, X.; Liu, Q.; Zhang, G.; Cui, J.; Long, J. A survey of clustering with deep learning: From the perspective of network architecture. IEEE Access 2018, 6, 39501–39514. [Google Scholar] [CrossRef]
- Nasraoui, O.; Ben N’Cir, C.E. An Introduction to Deep Clustering. In Clustering Methods for Big Data Analytics; Springer International Publishing: Cham, Switzerland, 2018; pp. 73–89. [Google Scholar]
- Liang, W.; Zhang, Y.; Xu, J.; Lin, D. Optimization of basic clustering for ensemble clustering: An information-theoretic perspective. IEEE Access 2019, 7, 179048–179062. [Google Scholar] [CrossRef]
- Newman, M.E.J. Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. E 2006, 74, 036104. [Google Scholar] [CrossRef] [PubMed]
- Cao, S.; Lu, W.; Xu, Q. Grarep: Learning graph representations with global structural information. In Proceedings of the 24th ACM International on Conference on Information and Knowledge Management, Melbourne, Australia, 19–23 October 2015; pp. 891–900. [Google Scholar]
- Nikolentzos, G.; Meladianos, P.; Vazirgiannis, M. Matching node embeddings for graph similarity. In Proceedings of the 31st AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 2429–2435. [Google Scholar]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Grover, A.; Leskovec, J. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar]
- Yang, C.; Liu, Z.; Zhao, D.; Sun, M.; Chang, E.Y. Network representation learning with rich text information. In Proceedings of the 24th International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015; pp. 2111–2117. [Google Scholar]
- Wang, X.; Jin, D.; Cao, X.; Yang, L.; Zhang, W. Semantic community identification in large attribute networks. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining (ICDM), Barcelona, Spain, 12–15 December 2016; pp. 265–271. [Google Scholar]
- Cao, S.; Lu, W.; Xu, G. Deep neural networks for learning graph representations. In Proceedings of the 30th AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; pp. 1145–1152. [Google Scholar]
- Ye, F.; Chen, C.; Zheng, Z. Deep autoencoder-like nonnegative matrix factorization for community detection. In Proceedings of the 27th ACM International Conference on Information and Knowledge Management, Turin, Italy, 22–26 October 2018; pp. 1393–1402. [Google Scholar]
- Chang, J.; Blei, D.M. Relational topic models for document networks. In Proceedings of the 12th International Conference on Artificial Intelligence and Statistics, Clearwater Beach, FL, USA, 16–18 April 2009; pp. 81–88. [Google Scholar]
- Bojchevski, A.; Günnemann, S. Bayesian robust attributed graph clustering: Joint learning of partial anomalies and group structure. In Proceedings of the 32nd AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 2738–2745. [Google Scholar]
- Xia, R.; Pan, Y.; Du, L.; Yin, J. Robust multi-view spectral clustering via low-rank and sparse decomposition. In Proceedings of the 28th AAAI Conference on Artificial Intelligence, Québec City, QC, Canada, 27–31 July 2014; pp. 2149–2155. [Google Scholar]
- Wibisono, S.; Anwar, M.T.; Supriyanto, A.; Amin, I.H.A. Multivariate weather anomaly detection using dbscan clustering algorithm. J. Phys. Conf. Ser. 2021, 1869, 012077. [Google Scholar] [CrossRef]
- Liu, F.; Xue, S.; Wu, J.; Zhou, C.; Hu, W.; Paris, C.; Nepal, S.; Yang, J.; Yu, P.S. Deep learning for community detection: Progress, challenges and opportunities. In Proceedings of the 29th International Joint Conference on Artificial Intelligence, Yokohama, Japan, 7–15 January 2021; pp. 4981–4987. [Google Scholar]
- Tang, H.; Chen, K.; Jia, K. Unsupervised domain adaptation via structurally regularized deep clustering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 8722–8732. [Google Scholar]
- Meng, Y.; Zhang, Y.; Huang, J.; Zheng, Y.; Zhang, C.; Han, J. Hierarchical topic mining via joint spherical tree and text embedding. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, 6–10 July 2020; pp. 1908–1917. [Google Scholar]
- Yang, J.; Parikh, D.; Batra, D. Joint unsupervised learning of deep representations and image clusters. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5147–5156. [Google Scholar]
- Wang, X.; Shi, C.; Wang, Z.; Li, C.; Cheng, B. SIMPLE-GNN: A Simple and Efficient GNN for Large-scale Graph Learning. In Proceedings of the ACM Web Conference 2024 (WWW ’24), Singapore, 13–17 May 2024; pp. 2024–2035. [Google Scholar]
- Kipf, T.N.; Welling, M. Variational graph auto-encoders. arXiv 2016, arXiv:1611.07308. [Google Scholar] [CrossRef]
- Pan, S.; Hu, R.; Long, G.; Jiang, J.; Yao, L.; Zhang, C. Adversarially regularized graph autoencoder for graph embedding. In Proceedings of the 27th International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 2609–2615. [Google Scholar]
- Emadi, H.S.; Mazinani, S.M. A novel anomaly detection algorithm using dbscan and svm in wireless sensor networks. Wirel. Pers. Commun. 2018, 98, 2025–2035. [Google Scholar] [CrossRef]
- Su, X.; Xue, S.; Liu, F.; Wu, J.; Yang, J.; Zhou, C.; Hu, W.; Paris, C.; Nepal, S.; Jin, D.; et al. A comprehensive survey on community detection with deep learning. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 3333–3353. [Google Scholar] [CrossRef] [PubMed]
- Hou, Z.; Liu, Y.; Wang, X.; Wei, Y.; Wang, P.; Dong, Y.; Tang, J. GraphMAE2: A Decoding-Enhanced Masked Autoencoder for Self-Supervised Graph Learners. In Proceedings of the 41st International Conference on Machine Learning (ICML), Vienna, Austria, 21–27 July 2024; pp. 19253–19275. [Google Scholar]
- Zhou, Q.; Zhou, W.; Wang, S. Cluster adaptation networks for unsupervised domain adaptation. Image Vis. Comput. 2021, 108, 104137. [Google Scholar] [CrossRef]
- Cai, X.; Huang, X.; Liang, H.; Wang, X. LightGCL: Simple and Effective Graph Contrastive Learning for Recommendation. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD), Barcelona, Spain, 25–29 August 2024; pp. 187–197. [Google Scholar]
- Tixier, A.J.; Nikolentzos, G.; Meladianos, P.; Vazirgiannis, M. Graph classification with 2d convolutional neural networks. arXiv 2019, arXiv:1904.06132. [Google Scholar] [CrossRef]
- Lin, Z.; Kang, Z. Graph filter-based multi-view attributed graph clustering. In Proceedings of the 30th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 21–26 August 2021; pp. 2723–2729. [Google Scholar]
- Li, H.J.; Wang, Z.; Cao, J.; Pei, J.; Shi, Y. Optimal estimation of low-rank factors via feature level data fusion of multiplex signal systems. IEEE Trans. Knowl. Data Eng. 2022, 34, 2860–2871. [Google Scholar] [CrossRef]
- Bo, D.; Wang, X.; Shi, C.; Zhu, M.; Lu, E.; Cui, P. Structural deep clustering network. In Proceedings of the Web Conference 2020, Taipei, Taiwan, 20–24 April 2020; pp. 1400–1410. [Google Scholar]
- Wang, M.; Liang, D.; Li, D. A two-stage method for improving the decision quality of consensus-driven three-way group decision-making. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 2770–2780. [Google Scholar] [CrossRef]
- Zhu, J.; Ma, X.; Martinez, L.; Zhan, J. A probabilistic linguistic three-way decision method with regret theory via fuzzy c-means clustering algorithm. IEEE Trans. Fuzzy Syst. 2023, 31, 2821–2835. [Google Scholar] [CrossRef]
- Guo, L.; Zhan, J.; Zhang, C.; Xu, Z. A large-scale group decision-making method fusing three-way clustering and regret theory under fuzzy preference relations. IEEE Trans. Fuzzy Syst. 2023, 31, 4846–4860. [Google Scholar] [CrossRef]
- Li, Q.; Wu, X.M.; Liu, H.; Zhang, X.; Guan, Z. Label efficient semi-supervised learning via graph filtering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9574–9583. [Google Scholar]
- Van Der Maaten, L.; Hinton, G. Visualizing data using t-sne. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Fettal, C.; Labiod, L.; Nadif, M. Efficient graph convolution for joint node representation learning and clustering. In Proceedings of the 2022 International Joint Conference on Neural Networks (IJCNN), Padua, Italy, 18–23 July 2022; pp. 1–8. [Google Scholar]
- Fu, Y.; Yuan, J.; Song, G.; Wang, X.; Pan, S. Towards a Deeper Understanding of the Hub-induced Dilemma in Graph Neural Networks. In Proceedings of the Twelfth International Conference on Learning Representations (ICLR), Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Behrouz, A.; Al-Tahan, M. Graph Mamba: Towards Learning on Graphs with State Space Models. In Proceedings of the Thirteenth International Conference on Learning Representations (ICLR), Vienna, Austria, 5–9 May 2025. [Google Scholar]
- Feng, Y.; Chen, K.; Zhang, Y.; Guo, J.; Tang, S.; Wang, Y.; Hooi, B. Large Language Models are Not Yet Effective Abstract Reasoners on Graphs. In Proceedings of the 2024 Conference on Empirical Methods in Natural Language Processing (EMNLP), Miami, FL, USA, 12–16 November 2024; pp. 15888–15902. [Google Scholar]

| Dataset | Nodes | Edges | Features | Classes |
|---|---|---|---|---|
| CORA | 2708 | 5429 | 1433 | 7 |
| CITESEER | 3327 | 4732 | 3703 | 6 |
| PUBMED | 19,717 | 44,338 | 500 | 3 |
| WIKI | 2405 | 17,981 | 4973 | 17 |
| Method | CORA | CITESEER | ||||
|---|---|---|---|---|---|---|
| Acc | NMI | FM | Acc | NMI | FM | |
| k-means | 34.65 | 16.73 | 25.42 | 38.49 | 17.02 | 30.47 |
| Spectral-f | 36.26 | 15.09 | 25.64 | 46.23 | 21.19 | 33.70 |
| DeepWalk | 46.74 | 31.75 | 38.06 | 36.15 | 9.66 | 26.70 |
| DNGR | 49.24 | 37.29 | 37.29 | 32.59 | 18.02 | 44.19 |
| GAE | 57.31 | 40.69 | 41.97 | 41.26 | 18.34 | 29.13 |
| VGAE | 61.32 | 38.45 | 41.50 | 44.38 | 22.71 | 31.88 |
| MGAE | 63.43 | 45.57 | 38.01 | 63.56 | 39.75 | 39.49 |
| ARGE | 66.64 | 44.90 | 61.90 | 57.30 | 35.00 | 54.60 |
| ARVGE | 62.38 | 45.00 | 62.70 | 54.40 | 26.10 | 52.90 |
| SDCN | 65.45 | 47.10 | 57.32 | 65.74 | 38.51 | 62.07 |
| GCC | 62.71 | 49.89 | 53.89 | 67.36 | 43.15 | 65.46 |
| AGC (k-means) | 66.43 ± 0.51 | 52.79 ± 0.48 | 65.41 ± 0.55 | 54.41 ± 0.88 | 32.23 ± 0.91 | 52.04 ± 0.82 |
| AGC (spectral) | 68.92 ± 0.43 | 53.68 ± 0.41 | 65.61 ± 0.49 | 67.00 ± 0.45 | 41.13 ± 0.52 | 62.48 ± 0.48 |
| 3WDAGC (k-means) | 67.81 ± 0.48 | 54.15 ± 0.40 | 64.93 ± 0.51 | 66.20 ± 0.51 | 42.71 ± 0.45 | 59.13 ± 0.58 |
| 3WDAGC (spectral) | 69.01 ± 0.41 | 54.27 ± 0.39 | 65.87 ± 0.45 | 67.20 ± 0.42 | 41.17 ± 0.50 | 62.53 ± 0.46 |
| Method | PUBMED | WIKI | ||||
| Acc | NMI | FM | Acc | NMI | FM | |
| k-means | 57.32 | 29.12 | 57.35 | 33.37 | 30.20 | 24.51 |
| Spectral-f | 59.91 | 32.55 | 58.61 | 41.28 | 43.99 | 25.20 |
| DeepWalk | 61.86 | 16.71 | 47.06 | 38.46 | 32.38 | 25.74 |
| DNGR | 45.35 | 15.38 | 17.90 | 37.58 | 35.85 | 25.38 |
| GAE | 64.08 | 22.97 | 49.26 | 17.33 | 11.93 | 15.35 |
| VGAE | 65.48 | 25.09 | 50.95 | 28.67 | 30.28 | 20.49 |
| MGAE | 43.88 | 8.16 | 41.98 | 50.14 | 47.97 | 39.20 |
| ARGE | 59.12 | 23.17 | 58.41 | 41.40 | 39.50 | 38.27 |
| ARVGE | 58.22 | 20.62 | 23.04 | 41.55 | 40.01 | 37.80 |
| SDCN | 64.82 | 29.23 | 63.78 | 41.47 | 37.92 | 35.17 |
| GCC | 69.72 | 30.87 | 68.76 | 54.42 | 51.15 | 44.57 |
| AGC (k-means) | 68.71 ± 0.34 | 30.12 ± 0.41 | 68.06 ± 0.39 | 47.84 ± 1.12 | 43.64 ± 1.03 | 39.86 ± 1.21 |
| AGC (spectral) | 69.78 ± 0.29 | 31.59 ± 0.33 | 68.72 ± 0.31 | 47.65 ± 1.08 | 45.28 ± 1.15 | 40.36 ± 1.17 |
| 3WDAGC (k-means) | 69.85 ± 0.25 | 30.37 ± 0.39 | 69.37 ± 0.28 | 48.35 ± 1.01 | 46.14 ± 0.98 | 41.69 ± 1.05 |
| 3WDAGC (spectral) | 69.62 ± 0.28 | 31.73 ± 0.31 | 69.17 ± 0.29 | 47.96 ± 1.05 | 45.82 ± 1.11 | 40.87 ± 1.14 |
| Method | CORA | CITESEER | PUBMED | WIKI | ||||
|---|---|---|---|---|---|---|---|---|
|
Time (Total) |
Step (avg.) |
Time (total) |
Step (avg.) |
Time (Total) |
Step (avg.) |
Time (Total) |
Step (avg.) | |
| AGC | 153.5 | 12 | 547.8 | 16 | 622.6 | 15 | 106.3 | 8 |
| 3WDAGC | 47.1 | 4 | 147.9 | 9.2 | 153.7 | 6.4 | 57.2 | 3.2 |
| Method | ACC | NMI | FM | Time (s) |
|---|---|---|---|---|
| 3WDAGC-Linear | 0.6613 | 0.5274 | 0.6513 | 69.3 |
| 3WDAGC (Ours) | 0.6707 | 0.5419 | 0.6542 | 27.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, W.; Li, D.; Wang, C.; Chen, K.; Song, S. Three-Way Decision-Driven Adaptive Graph Convolution for Deep Clustering. Appl. Sci. 2025, 15, 9391. https://doi.org/10.3390/app15179391
Liang W, Li D, Wang C, Chen K, Song S. Three-Way Decision-Driven Adaptive Graph Convolution for Deep Clustering. Applied Sciences. 2025; 15(17):9391. https://doi.org/10.3390/app15179391
Chicago/Turabian StyleLiang, Wei, Dong Li, Chuanpeng Wang, Kai Chen, and Suijie Song. 2025. "Three-Way Decision-Driven Adaptive Graph Convolution for Deep Clustering" Applied Sciences 15, no. 17: 9391. https://doi.org/10.3390/app15179391
APA StyleLiang, W., Li, D., Wang, C., Chen, K., & Song, S. (2025). Three-Way Decision-Driven Adaptive Graph Convolution for Deep Clustering. Applied Sciences, 15(17), 9391. https://doi.org/10.3390/app15179391





