Numerical Mathematical Model for the Analysis of the Transient Regime Caused by a Phase-to-Earth Fault
Abstract
1. Introduction
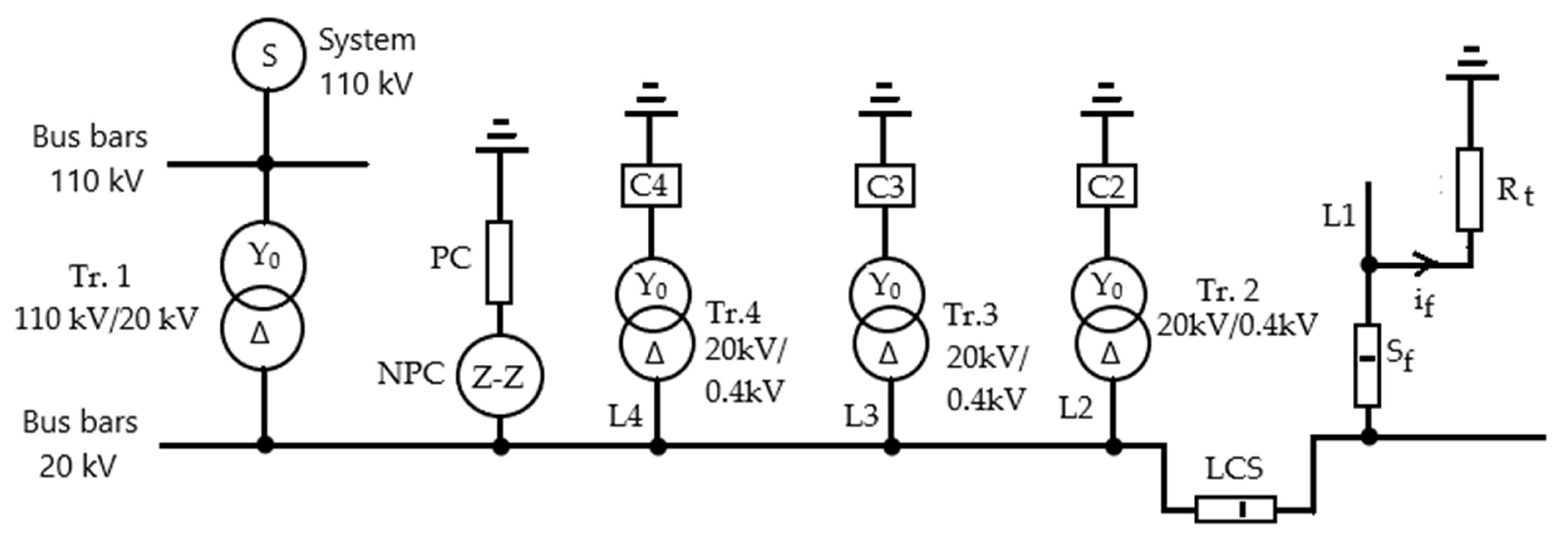
2. Objectives and the Studied Case
- (1)
- Establishing numerical mathematical models for calculating zero-sequence voltages and currents at the fault location during the transient regime caused by phase-to-earth faults.
- (2)
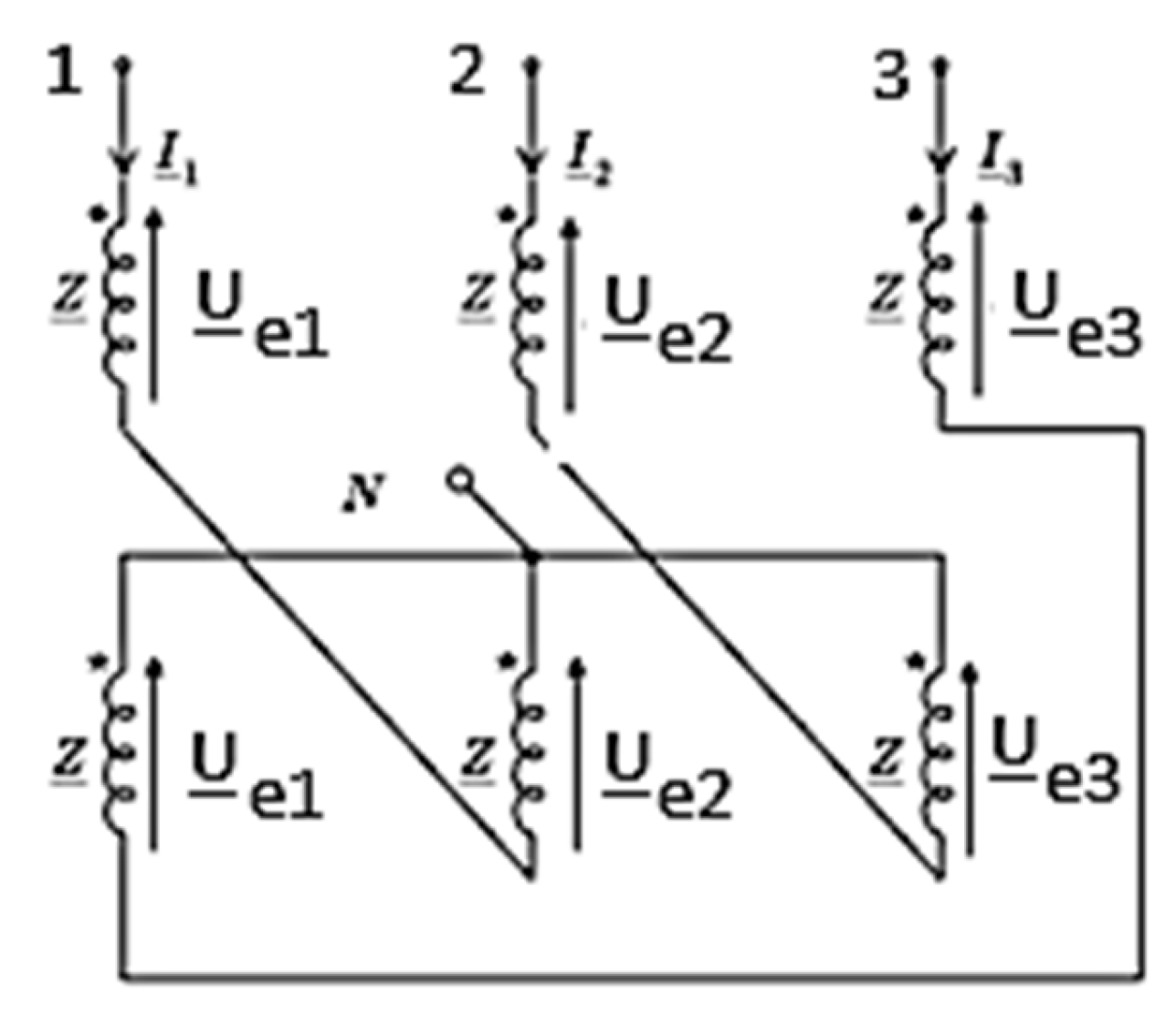
- Realization of the block dedicated to the modeling of the three-phase coil with a zig-zag connection (noted as NPC in Figure 1) and its implementation in MATLAB/Simulink.
- (3)
- Implementing the numerical mathematical model of the analyzed three-phase installation (Figure 1) in the MATLAB/Simulink programming environment.
- (4)
- Analysis of how the zero-sequence voltage and fault current are influenced by the conditions under which the phase-to-earth fault occurs (initial phase of the voltage at the fault location; insulation state of the 20 kV network (insulation resistance value); operating mode of the 20 kV network (resonance, over-compensated 6.1%, under-compensated 4.5%, under-compensated 36.9%); and contact resistance at the fault location (Rt)).
- (5)
- Validation of the numerical model of the analyzed three-phase installation implemented in the MATLAB/Simulink programming environment by comparing the results obtained using the model with those determined experimentally.
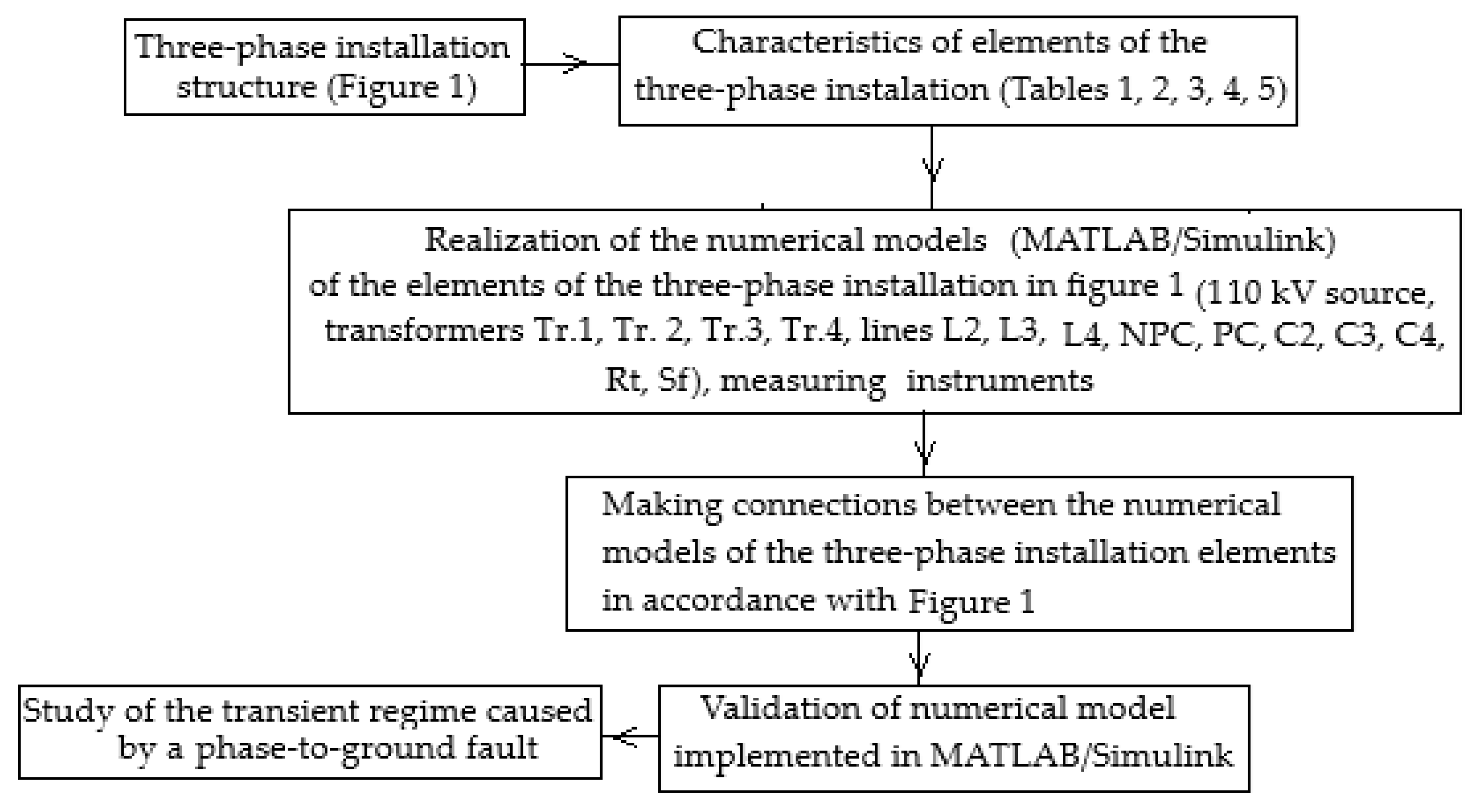
3. Materials and Methods
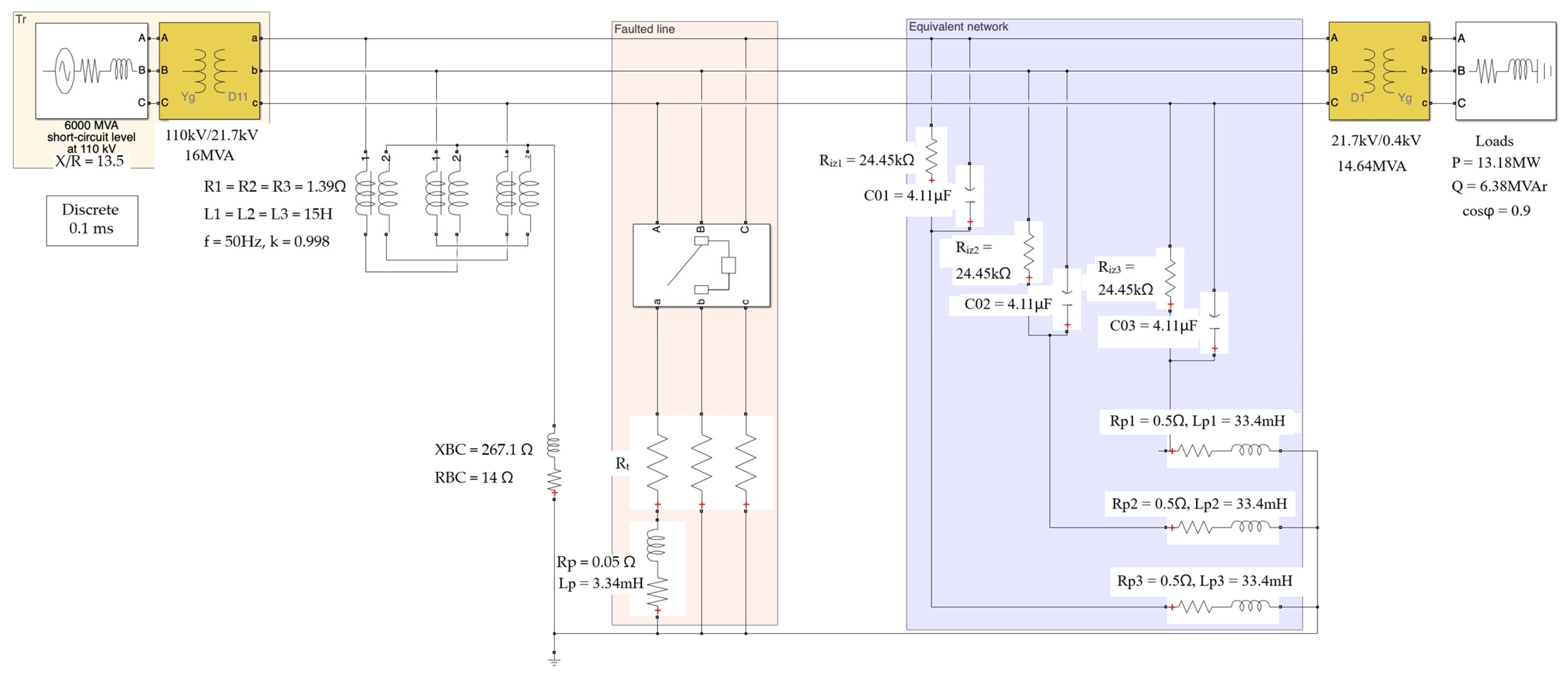
3.1. Numerical Model of the Electrical Network
3.2. Limitations of the Numerical Model
4. Validation of the Numerical Model
4.1. Experimental Measurements
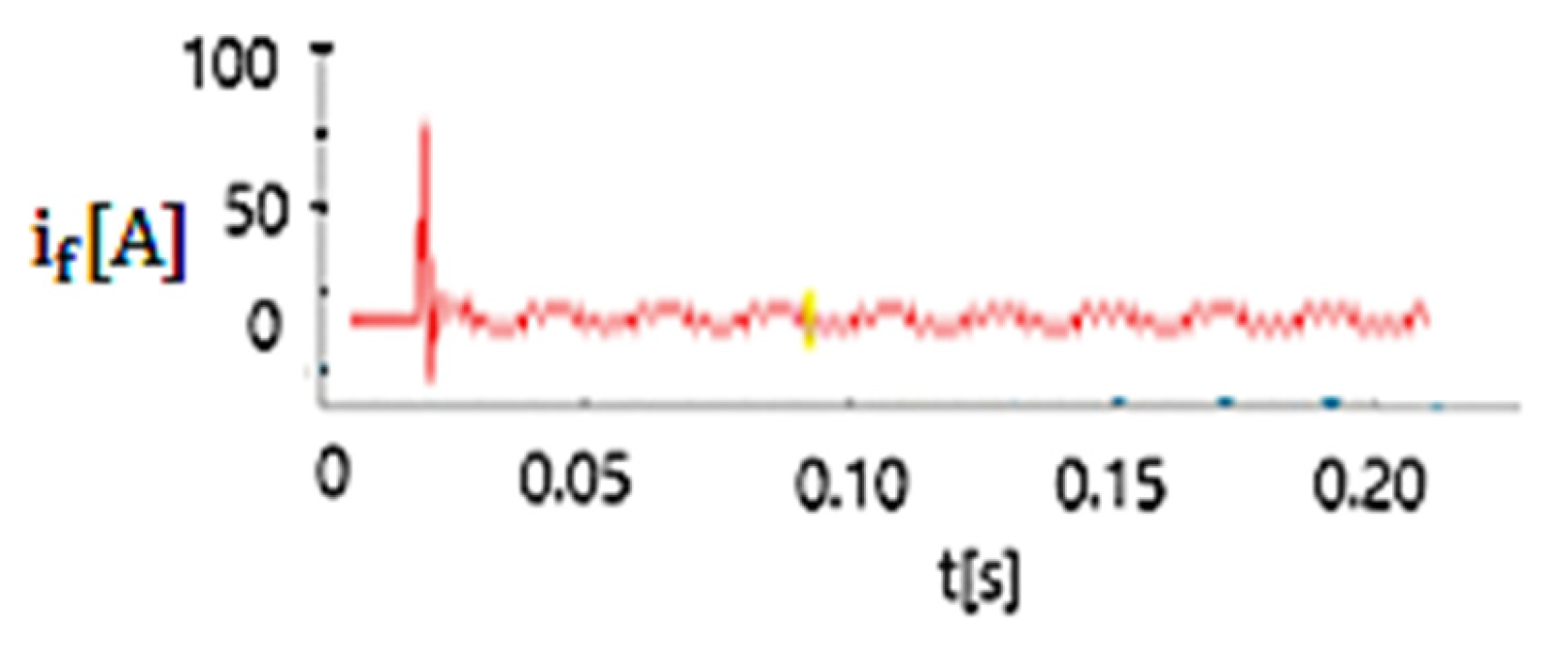
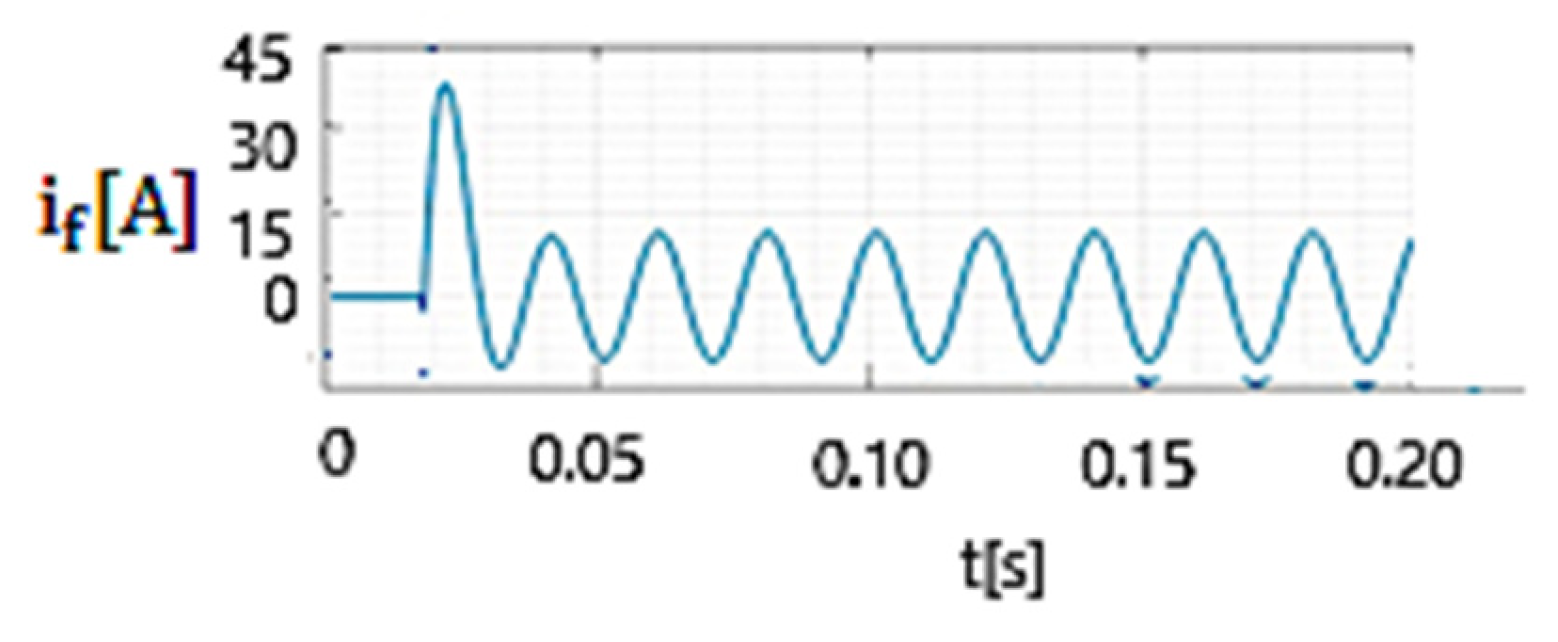
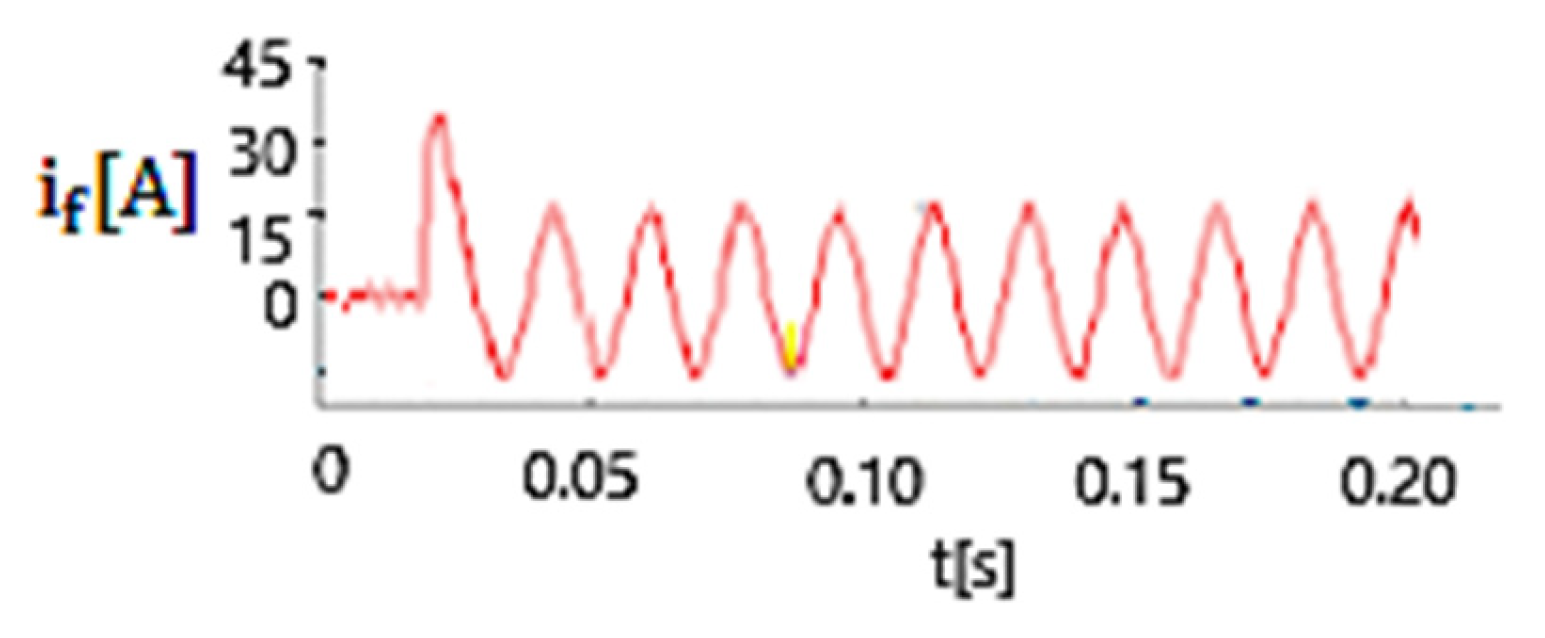
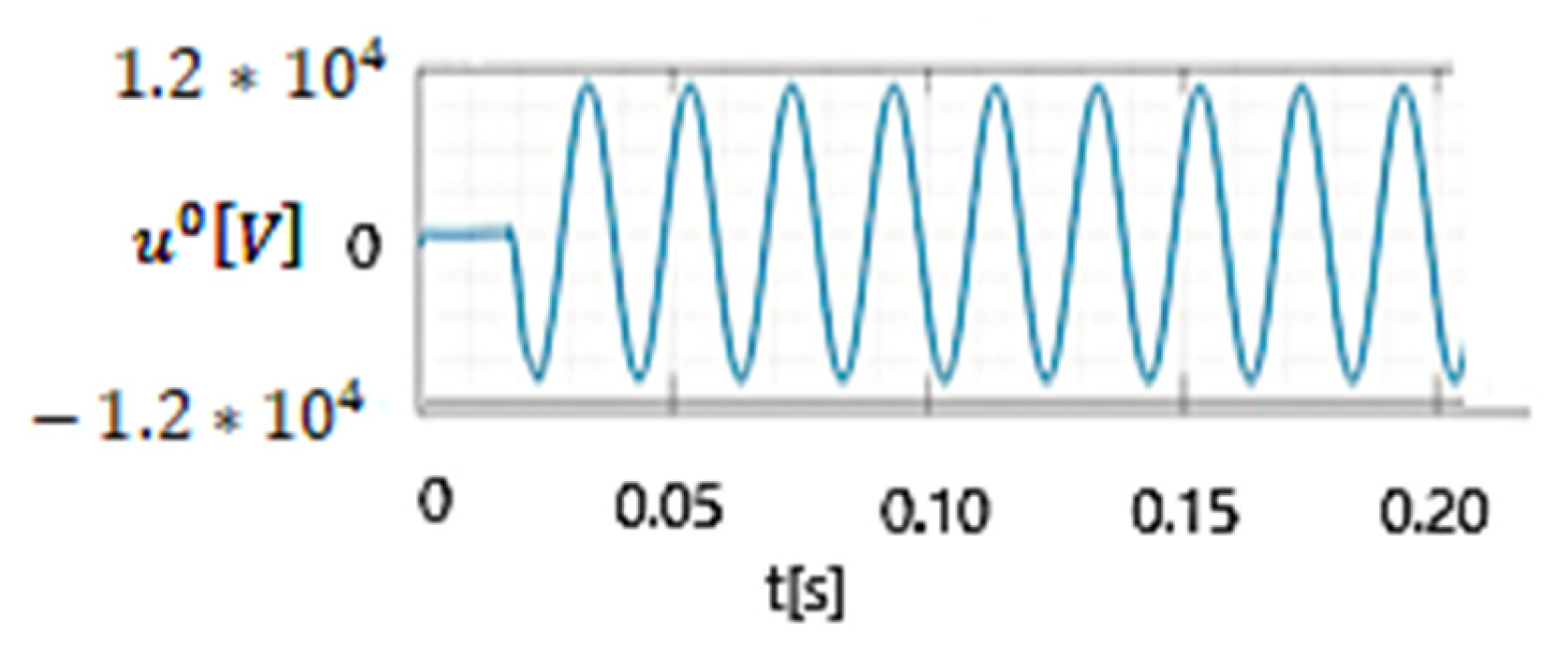
4.2. Comparison Between Experimental and Simulation Results
5. Analysis of the Transient Regime Caused by Phase-to-Ground Faults—Numerical Results
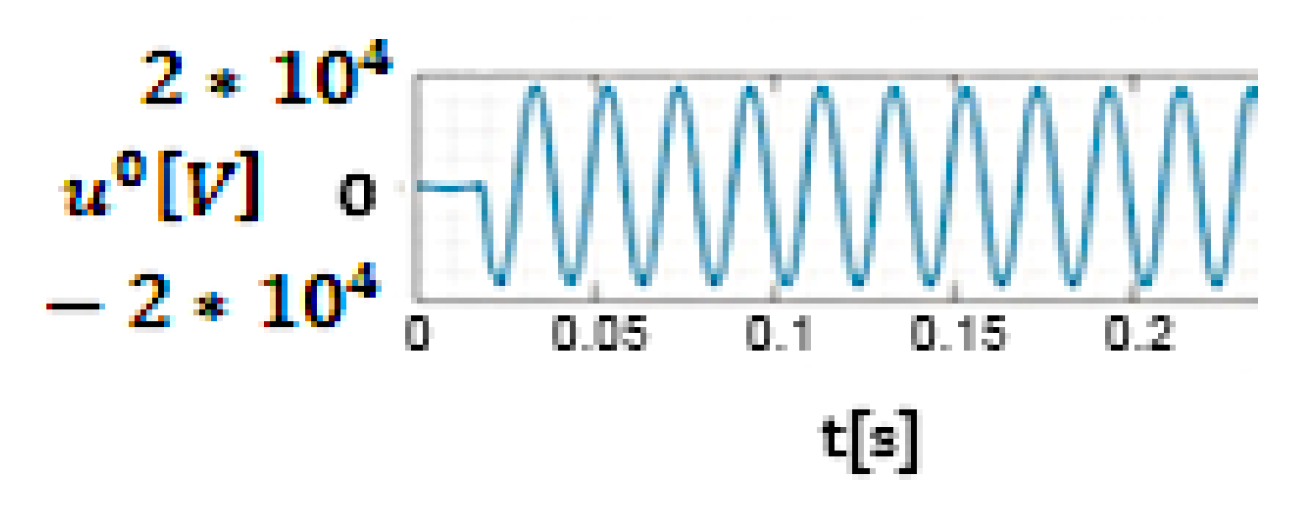
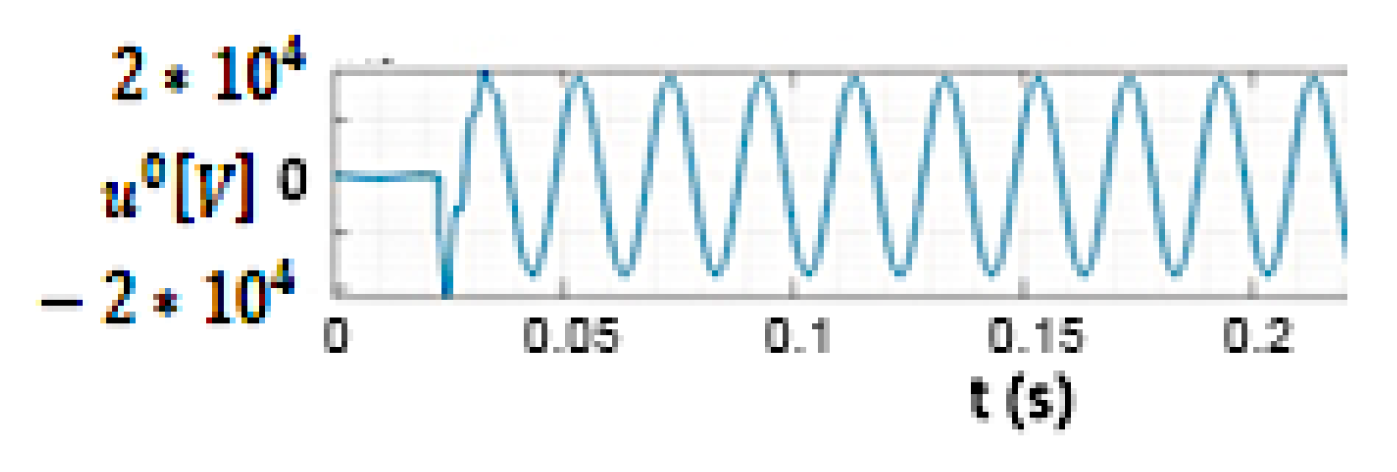
5.1. Influence of the Initial Phase of the Voltage at the Fault Location
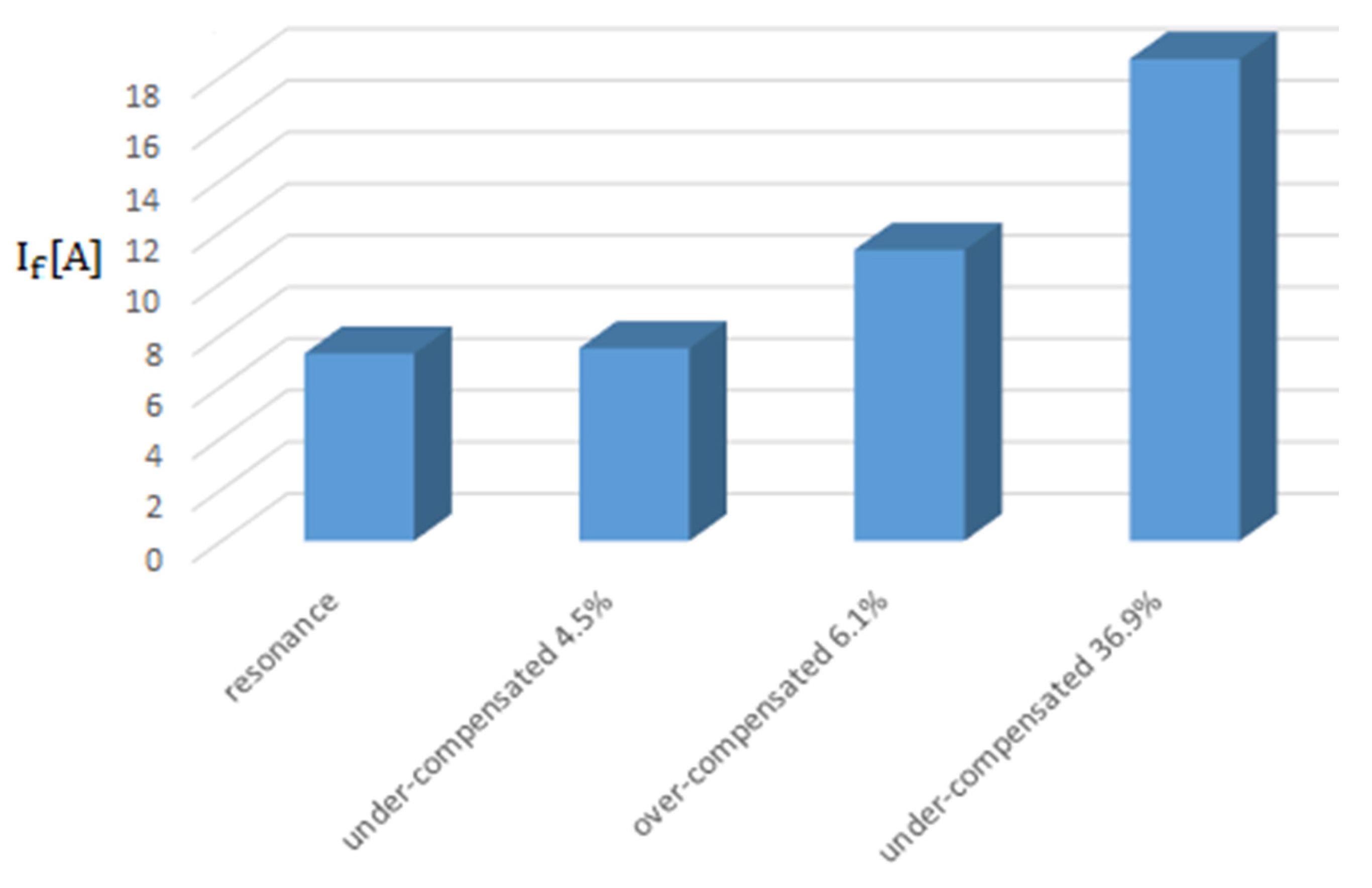
5.2. Influence of the Operating Mode of the Electrical Network
5.3. The Influence of the Insulation Resistance of the Electrical Network
5.4. Influence of the Contact Resistance at the Fault Location
5.5. Influence of Phase-to-Earth Capacitance on Fault Current
6. Discussions
7. Conclusions
- (a)
- From Table 3 it can be seen that the insulation of the 20 kV network is not ideal; Riz = 24.45 k does not have the value ∞. From Table 4, it can be seen that both the value of the Petersen coil inductance and its resistance depend on the regime in which the 20 kV network operates. Also, the resistance of the Petersen coil is different from zero, so this coil cannot be considered ideal. From Table 5, it can be seen that the three-phase coil with zig-zag connection used to create the artificial neutral of the 20 kV network is not ideal; its resistance and dispersion inductance are not zero. As a result, in creating the MATLAB/Simulink numerical model for the 20 kV network, real parameters must be used for these elements. Considering these elements as ideal can lead to unacceptable errors. In the case of a phase-to-ground fault, considering the Petersen coil and the network insulation as ideal, the calculation error of the fault current (in a stabilized mode) can exceed 30% [34,35].
- (b)
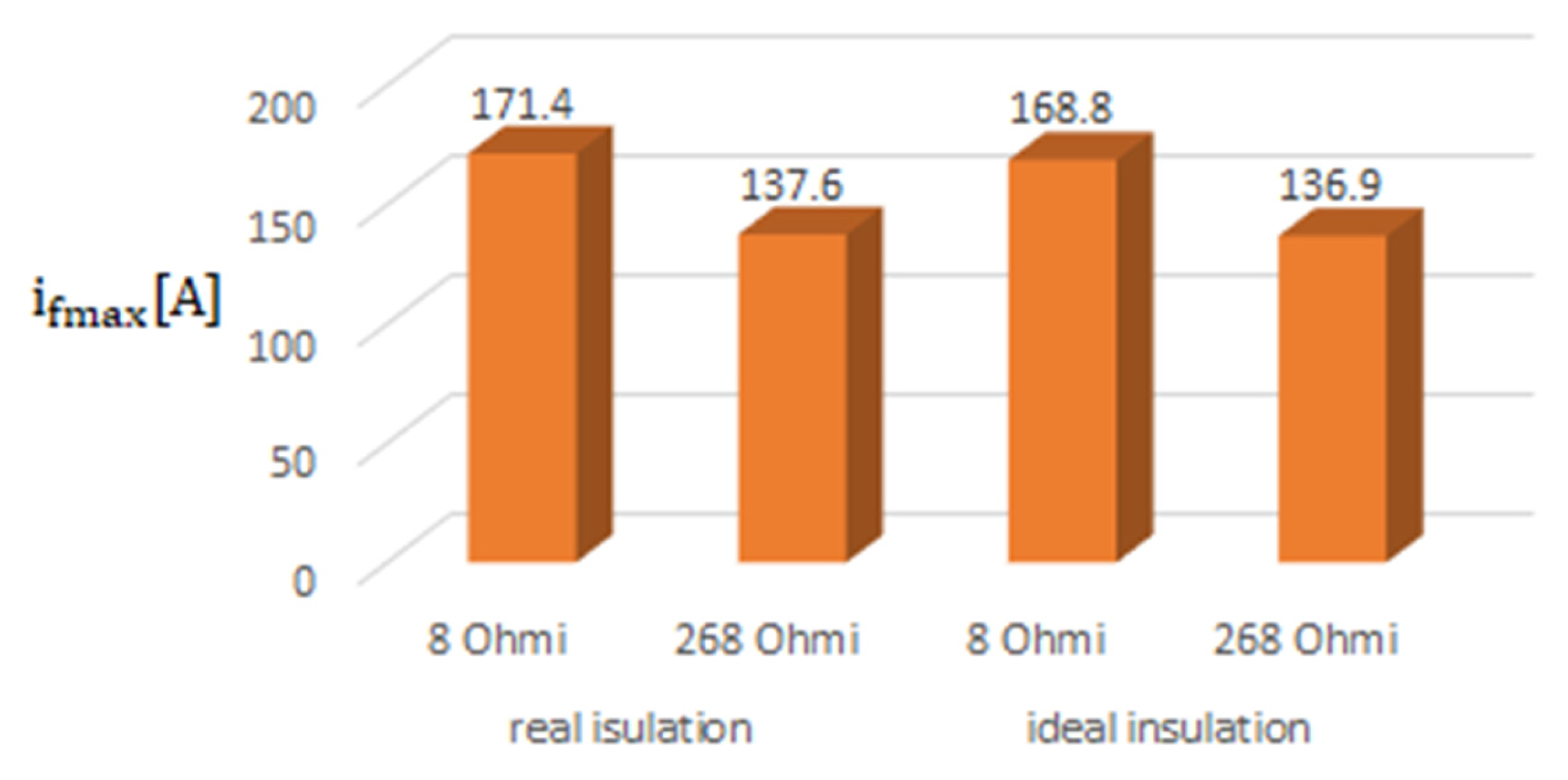
- The MATLAB/Simulik numerical model made using experimentally determined values for the three-phase coil with zig-zag connection, the Petersen coil, the insulation, and the phase-to-earth electrical capacitance of the 20 kV network led to differences between the fault current values obtained using the model and those determined experimentally of 6.67% if Rt = 8 Ω and 3.21% if Rt = 268 Ω. The differences between the zero-sequence voltage values for the 20 kV bus bars in the transformer station obtained using the MATLAB/Simulink model, determined experimentally, are 3.21% if Rt = 8 Ω and 6.19% if Rt = 268 Ω. These differences were obtained when the 20 kV network operated in a 4.5% under-compensation regime.
- (c)
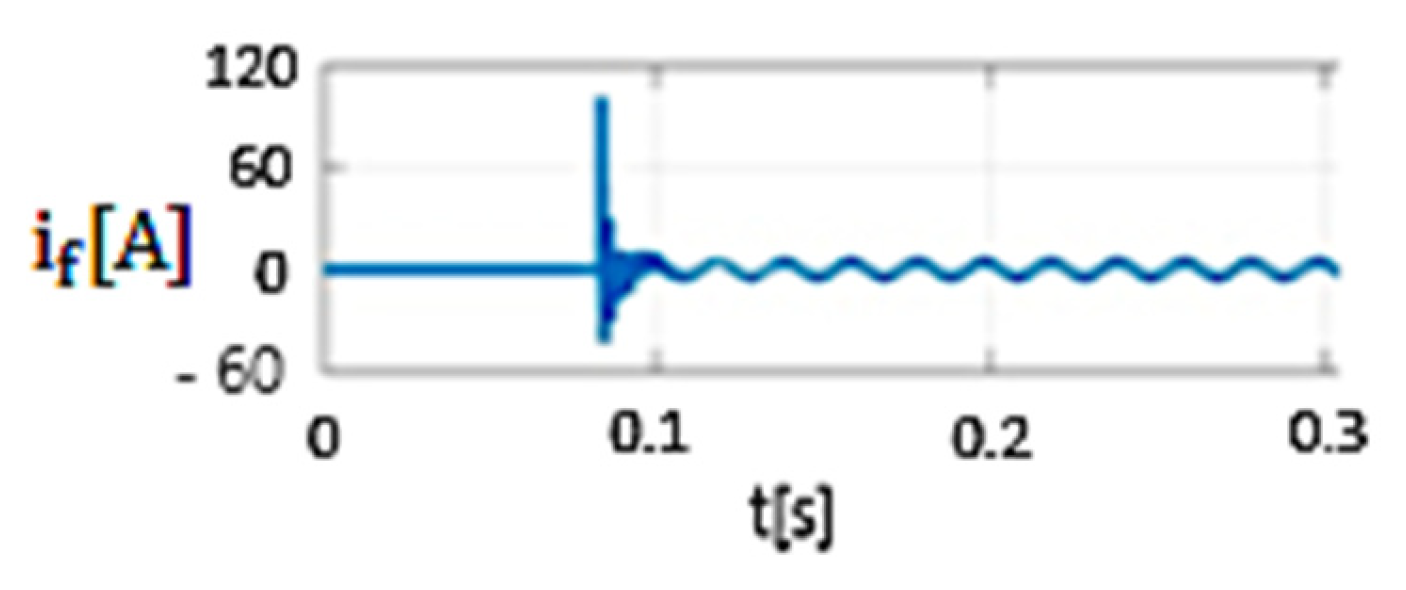
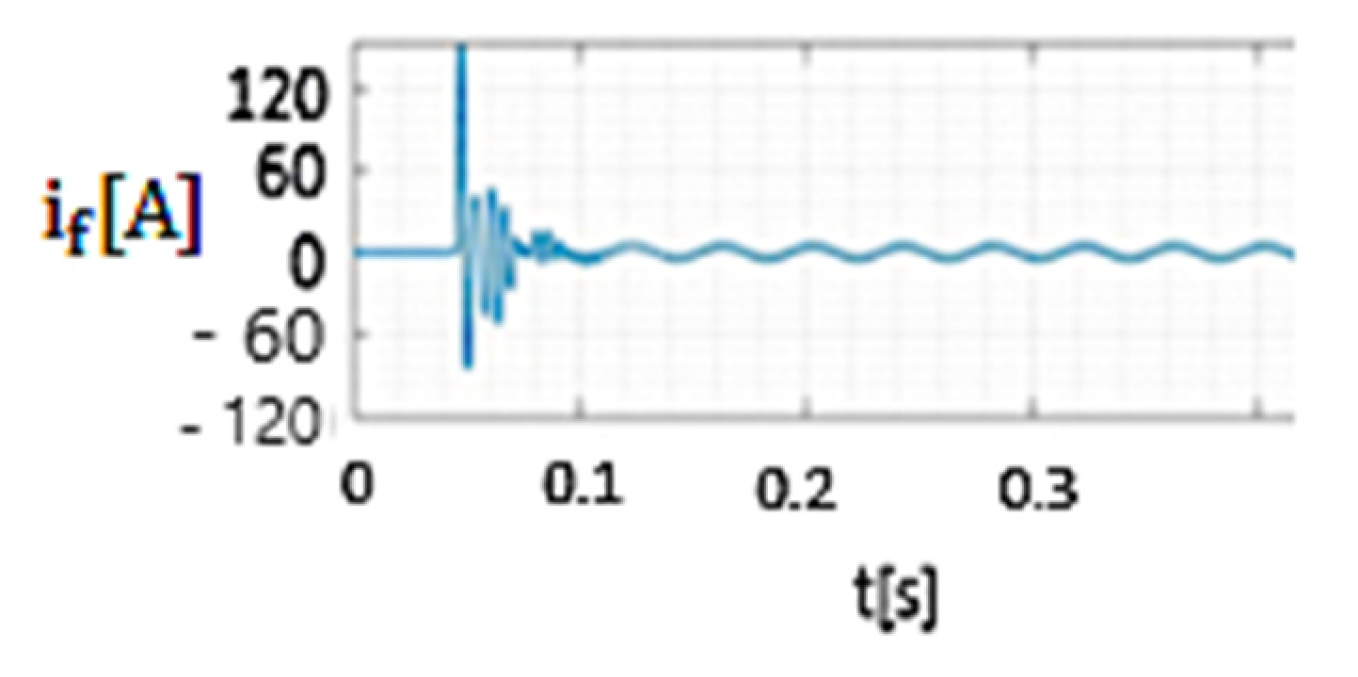
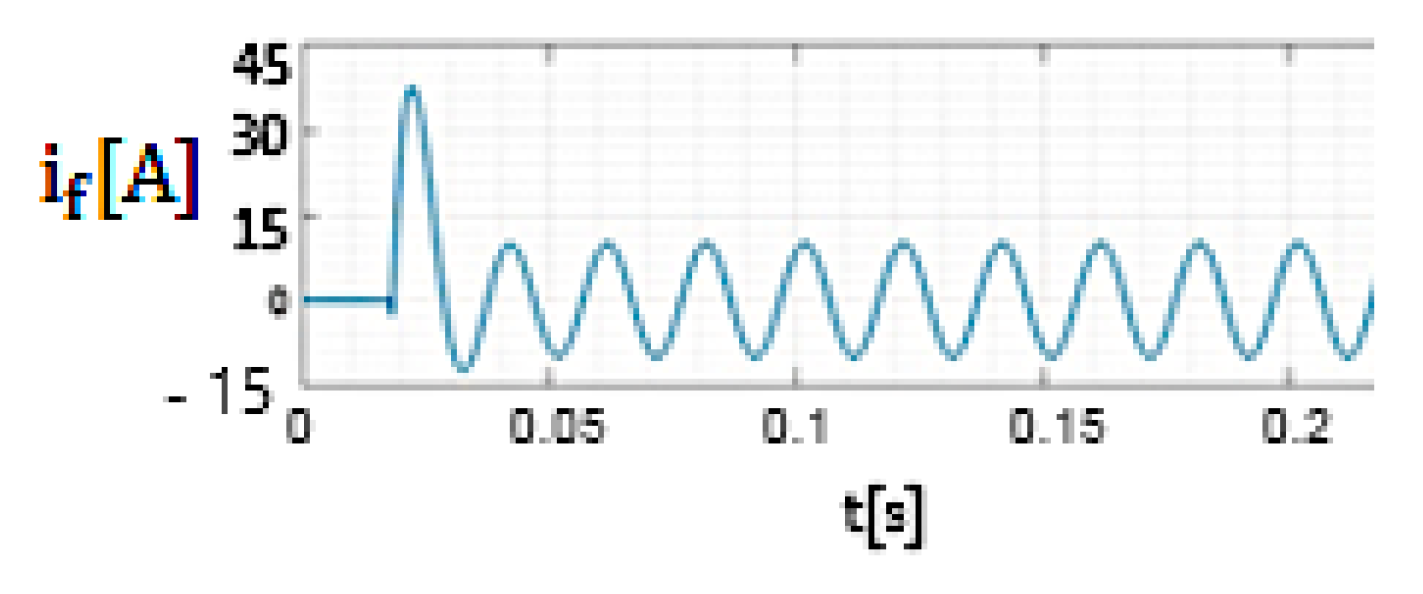
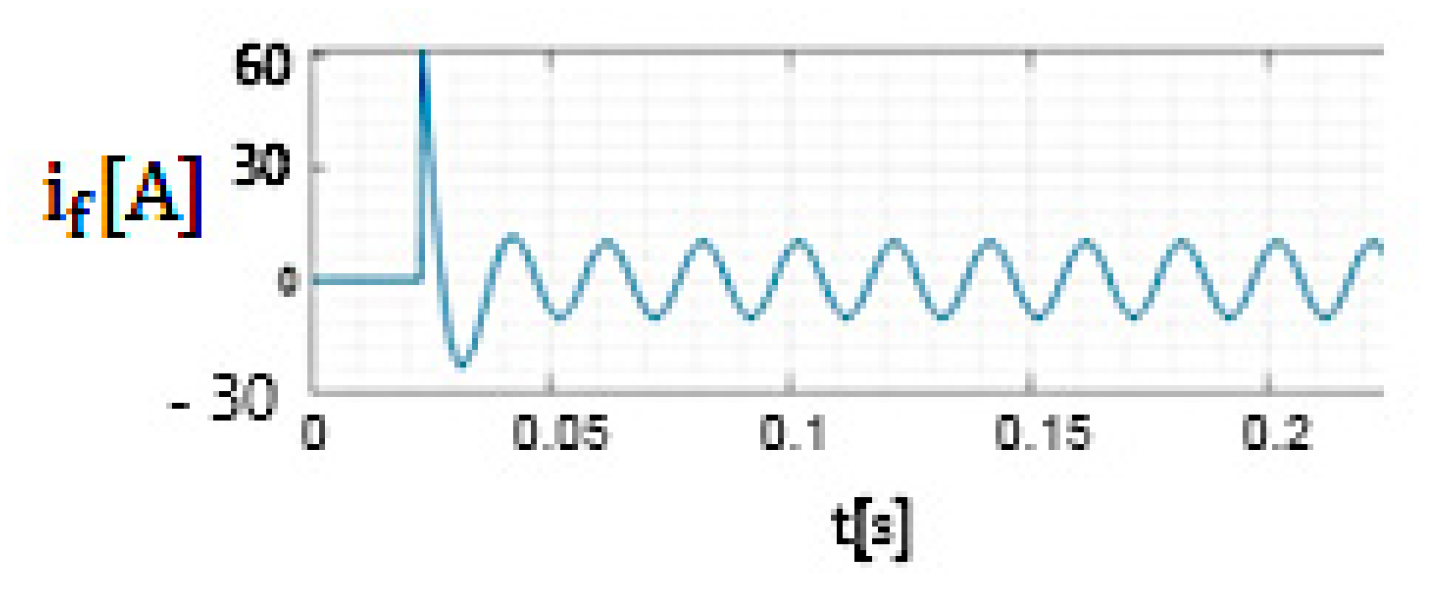
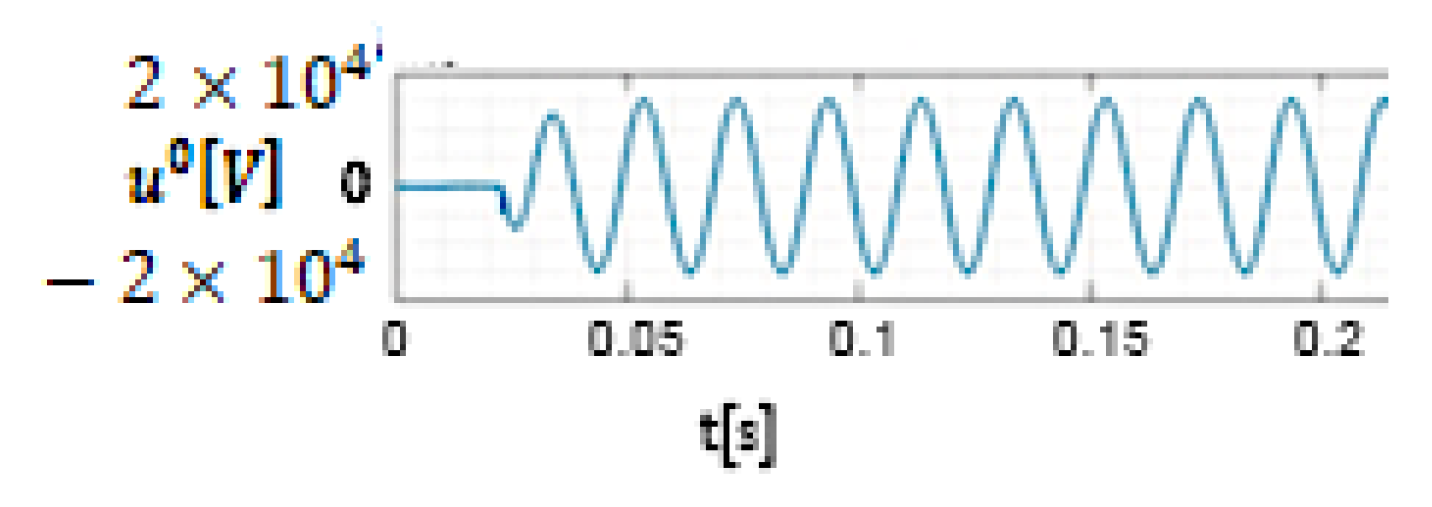
- The ratio between the maximum value of the fault current during the transient regime (which is obtained when the 20 kV network operates in resonance mode if the initial phase of the voltage at the fault location is 88°) and the amplitude of the fault current in the permanent regime is 15.5 if Rt = 8 Ω (Figure 17) and 10.2 if Rt = 268 Ω (Figure 22). As a result, in setting the protections that detect phase-to-ground faults, the transient component of the fault current cannot be ignored.
- (d)
- If the 20 kV network operates in resonance regime, the ratio between the maximum and minimum fault current values as a function of the initial phase of the voltage at the fault location (α) is 2.34, and if the network operates in 6.1% overcompensated regime the same ratio becomes 1.79 (Figure 24). The further the operating regime of the 20 kV network is from the resonance one, the lower the ratio of the maximum and minimum fault current value depending on the initial phase of the voltage at the fault location (α).
- (e)
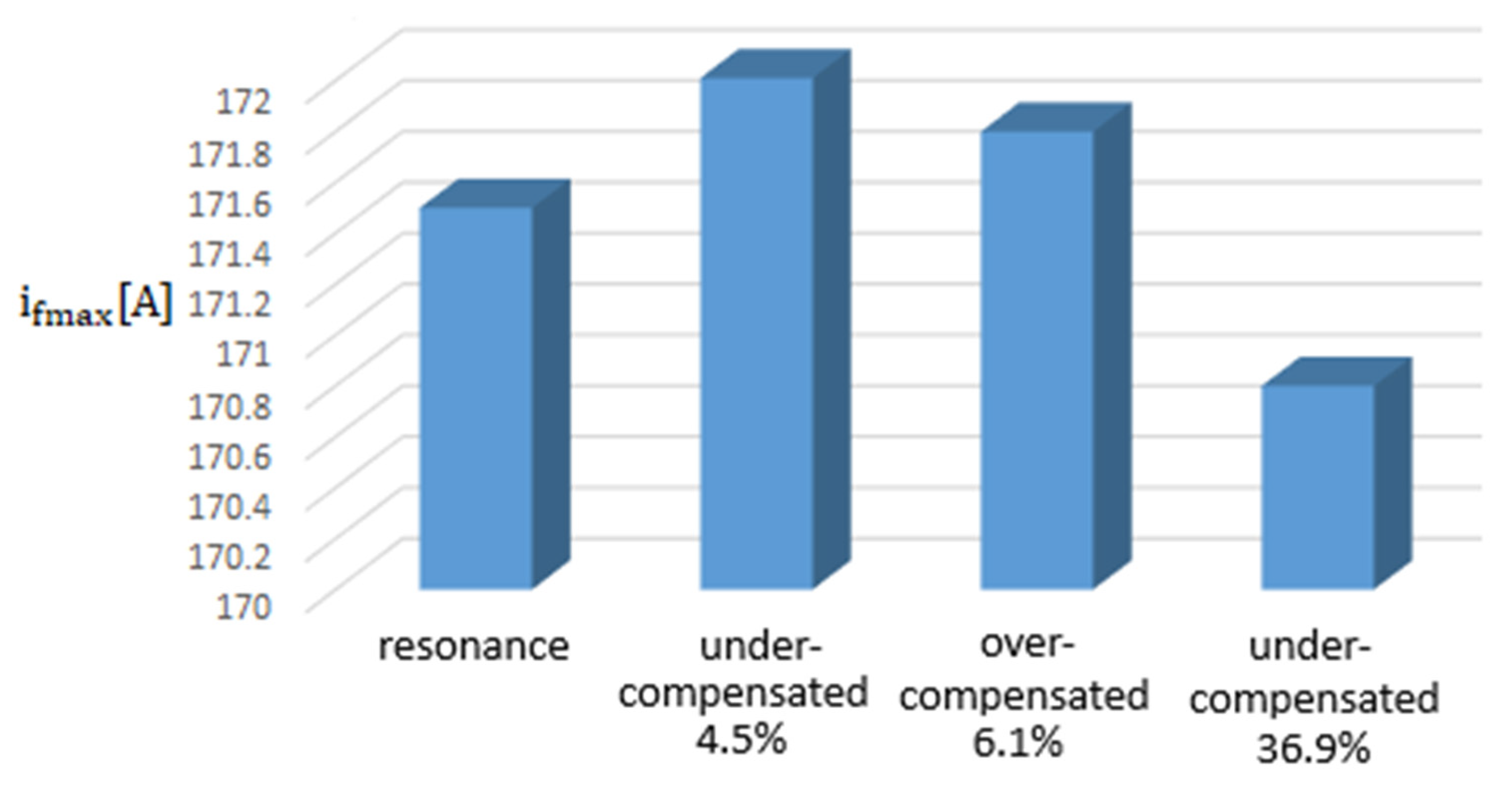
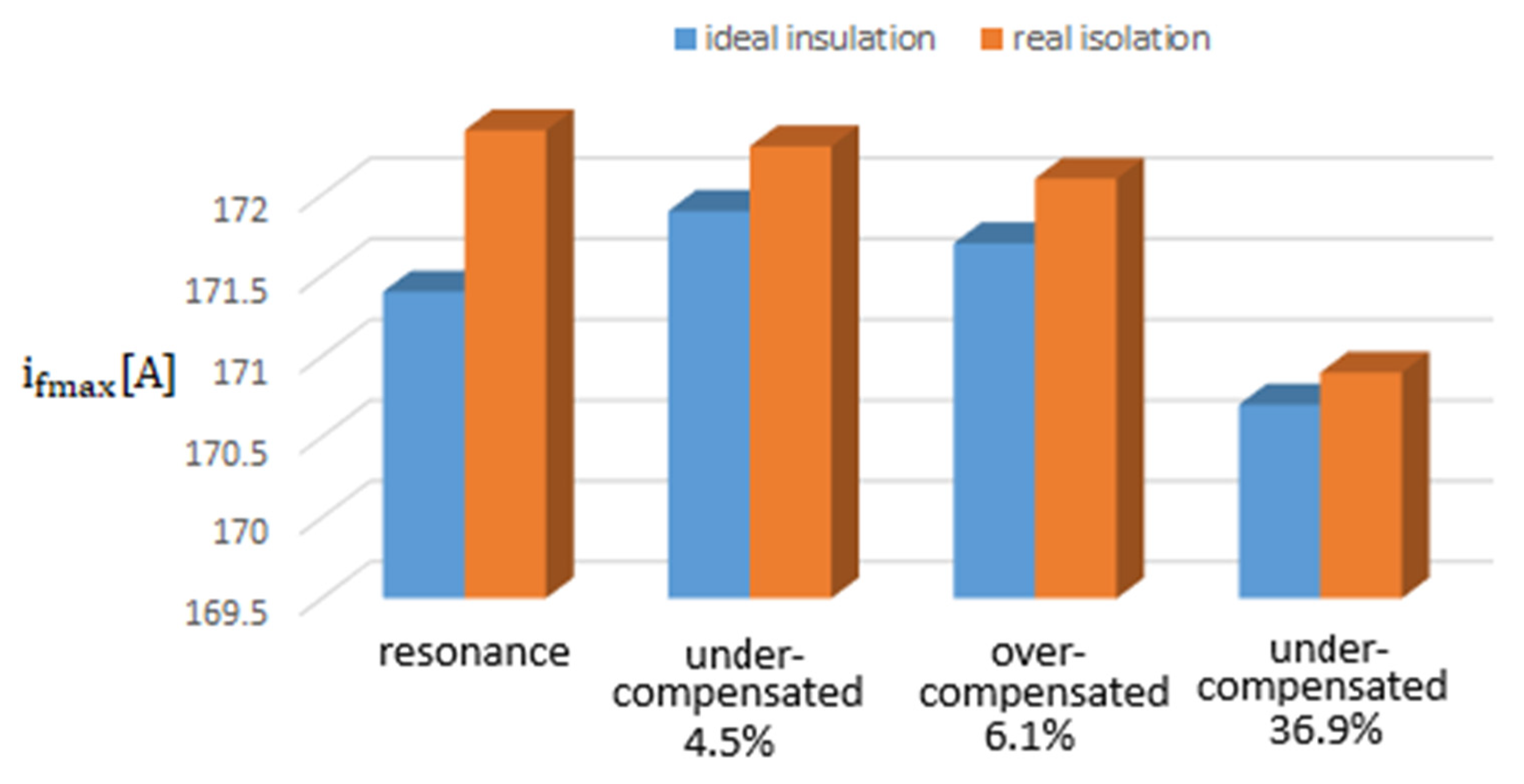
- The maximum value of the fault current during the transient regime caused by the phase-to-ground fault is the highest if the 20 kV network operates in resonance regime, and the lowest if the 20 kV network operates under-compensated by 36.9% (Figure 26). The difference between the two values is 0.29%, so the operating regime of the 20 kV network does not significantly influence the maximum value of the fault current.
- (f)
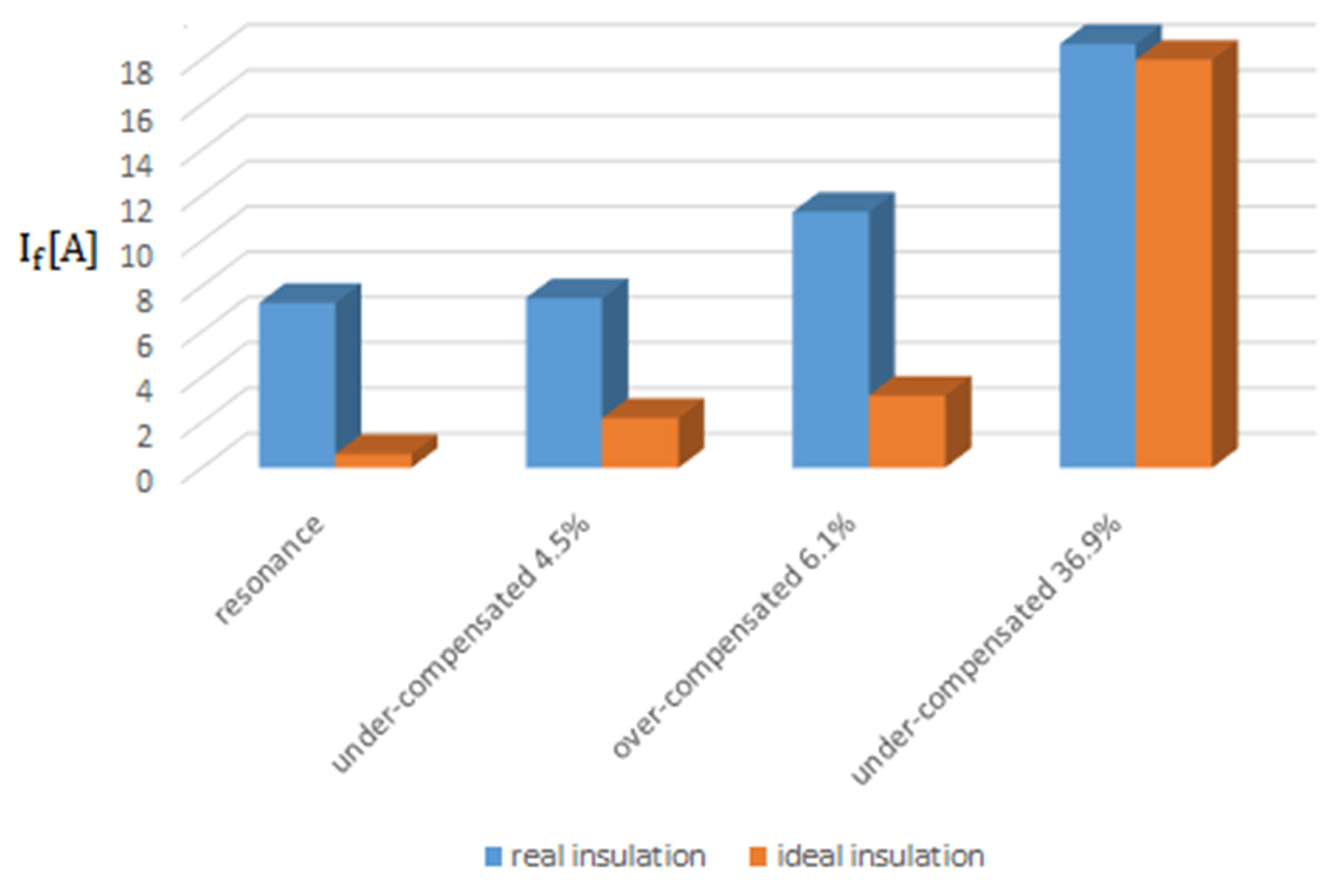
- The insulation condition of the 20 kV network does not significantly influence the maximum value of the fault current in the transient regime caused by the phase-to-ground fault (Figure 27); 1.52% if Rt = 8 Ω and 0.51% if Rt = 268 Ω. In the stabilized regime (after damping of the transient components), the influence of the insulation condition is much more pronounced [34,35].
- (g)
- Using the MATLAB/Simulink numerical model for calculating the fault current, it was found that the value of the phase-to-earth capacitance greatly influences the value of the fault current. If the phase-to-earth capacitance increases by 1%, the calculation error of the fault current increases by 3.31%, and if its value decreases by 1% the calculation error of the fault current decreases by 2.51% (Table 9). For this reason, it is recommended that the experimentally determined phase-to-earth capacitance value of the 20 kV network be used in the MATLAB/Simulink numerical model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, S.; Jiao, Y.; Chen, Q.; Li, H.; Zhou, L.; Zhu, H. A Single-Phase to Ground Fault Identification Method Based on Extremely Low Frequency Current Detection in Distribution Grids. IEEE Trans. Power Deliv. 2022, 37, 5214–5223. [Google Scholar] [CrossRef]
- Lin, J.; Guo, M.; Zheng, Z. Active Location Method for Single-Line-to-Ground Fault of Flexible Grounding Distribution Networks. IEEE Trans. Instrum. Meas. 2023, 72, 3524712. [Google Scholar] [CrossRef]
- He, L.; Li, Y.; Chu, X.; Shuai, Z.; Peng, Y.; Shen, J.Z. Single-Phase to Ground Fault Line Identification for Medium Voltage Islanded Microgrids With Neutral Ineffectively Grounded Modes. IEEE Trans. Smart Grid 2022, 13, 4312–4326. [Google Scholar] [CrossRef]
- Mukherjee, A.; Kundu, P.K.; Das, A. A supervised principal component analysis-based approach of fault localization in transmission lines for single line to ground faults. Electr. Eng. 2021, 103, 2113–2126. [Google Scholar] [CrossRef]
- Toader, D.; Blaj, C.; Ruset, P.; Hategan, I.D.; Pinte, N.; Arvinti, B. Device for Automatic Control of the Petersen Coil. In Soft Computing Applications. Advances in Intelligent Systems and Computing; Balas, V., Jain, L., Kovačević, B., Eds.; Springer: Cham, Switzerland, 2016; Volume 357. [Google Scholar] [CrossRef]
- Mehmed-Hamza, M.E.; Filipov, A.B.; Ivanova, M.D. Research and Analysis of Faults in Medium Voltage Distribution Grids. In Proceedings of the 56th International Scientific Conference on Information, Communication and Energy Systems and Technologies (ICEST), Sozopol, Bulgaria, 16–18 June 2021. [Google Scholar]
- Paulucci, M. Investigating the impact of short-circuit faults in different neutral configurations: A real case study. In Proceedings of the AEIT International Annual Conference (AEIT), Rome, Italy, 5–7 October 2023. [Google Scholar]
- Toader, D.; Vintan, M.; Solea, C.; Vesa, D.; Greconici, M. Analysis of the Possibilities of Selective Detection of a Single Line-to-Ground Fault in a Medium Voltage Network with Isolated Neutral. Energies 2021, 14, 7019. [Google Scholar] [CrossRef]
- Penaloza, J.D.R.; Borghetti, A.; Napolitano, F.; Tossani, F.; Nucci, C.A. A New Transient-Based Earth Fault Protection System for Unearthed Meshed Distribution Networks. IEEE Trans. Power Deliv. 2021, 36, 2585–2594. [Google Scholar] [CrossRef]
- Guo, A.; Zhang, X.; He, Y.; Xie, S.; Li, W.; Sun, H. A faulty feeder selection method based on the slope of zero sequence current fitting curve for the non-effectively grounded system. Electr. Power Syst. Res. 2023, 217, 109170. [Google Scholar] [CrossRef]
- Kuliński, K.; Heyduk, A. Ground Fault in Medium-Voltage Power Networks with an Isolated Neutral Point: Spectral and Wavelet Analysis of Selected Cases in an Example Industrial Network Modeled in the ATP-EMTP Package. Energies 2024, 17, 1532. [Google Scholar] [CrossRef]
- Bindi, M.; Piccirilli, M.C.; Luchetta, A.; Grasso, F. A Comprehensive Review of Fault Diagnosis and Prognosis Techniques in High Voltage and Medium Voltage Electrical Power Lines. Energies 2023, 16, 7317. [Google Scholar] [CrossRef]
- Atsever, M.B.; Hocaoglu, M.H. A faulty feeder selection method for distribution network with unintentional resonance in zero sequence circuit. Electr. Power Syst. Res. 2023, 223, 109587. [Google Scholar] [CrossRef]
- Gukovskiy, Y.L.; Sychev, Y.A.; Pelenev, D.N. The Automatic Correction of Selective Action of Relay Protection System against Single Phase Earth Faults In Electrical Networks of Mining Enterprises. Int. J. Appl. Eng. Res. 2017, 12, 833–838. [Google Scholar]
- Čučuković, J.; Hidić, F. Fault Identification in Electrical Power Distribution System–Case Study of the Middle Bosnia Medium Voltage Grid. In Advanced Technologies, Systems, and Applications III. IAT 2018; Avdaković, S., Ed.; Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2019; Volume 59. [Google Scholar] [CrossRef]
- Tang, Y.; Chang, Y.; Tang, J.; Xu, B.; Ye, M.; Yang, H. A Novel Faulty Phase Selection Method for Single-Phase-to-Ground Fault in Distribution System Based on Transient Current Similarity Measurement. Energies 2021, 14, 4695. [Google Scholar] [CrossRef]
- Chang, Y. A Novel Single-Phase-to-Ground Fault Location Method Based on Phase Current Differences in Power Distribution Systems. In Proceedings of the 4th International Conference on Smart Power & Internet Energy Systems (SPIES), Beijing, China, 9–12 December 2022. [Google Scholar] [CrossRef]
- Sun, G.; Ma, W.; Wei, S.; Cai, D.; Wang, W.; Xu, C.; Zhang, K.; Wang, Y. A Fault Location Method for Medium Voltage Distribution Network Based on Ground Fault Transfer Device. Electronics 2023, 12, 4790. [Google Scholar] [CrossRef]
- Lebedev, V.; Filatova, G. Study of Ground Faults Methods for Branched Overhead Power Lines. In Proceedings of the International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Sochi, Russian, 16–20 May 2022. [Google Scholar]
- Butoarca, E.; Ursu, D.; Mircea, P.-M.; Marin, I.; Ciurescu-Tibrian, M.; Buzatu, G.-C. Issues of selective detection and elimination of earth faults in MV networks with the neutral treated by Petersen coil. In Proceedings of the International Conference on Optimization of Electrical and Electronic Equipment (OPTIM) & Intl Aegean Conference on Electrical Machines and Power Electronics (ACEMP), Brasov, Romania, 25–27 May 2017. [Google Scholar]
- Toader, D.; Greconici, M.; Vesa, D.; Vintan, M.; Solea, C.; Maghet, A.; Tatai, I. The Influence of the Characteristics of the Medium Voltage Network on the Single Line-to-Ground Fault Current in the Resistor Grounded Neutral Networks. Designs 2021, 5, 53. [Google Scholar] [CrossRef]
- Lowczowski, K.; Olejnik, B. Monitoring, Detection and Locating of Transient Earth Fault Using Zero-Sequence Current and Cable Screen Earthing Current in Medium Voltage Cable and Mixed Feeders. Energies 2022, 15, 1066. [Google Scholar] [CrossRef]
- Liu, Y.; Cui, Q.; Luo, J.; Guo, H.; Shi, L. A Fault Location Algorithm for Distribution Network Based on Transient Feature Extraction. In Proceedings of the IEEE Sustainable Power and Energy Conference (iSPEC), Chongqing, China, 28–30 November 2023. [Google Scholar] [CrossRef]
- Mondal, S.; Pradhan, R. A Critical Analysis on Different High Impedance Fault Detection Schemes. Electr. Power Compon. Syst. 2023, 1–28. [Google Scholar] [CrossRef]
- Toader, D.; Vintan, M. Mathematical Models of the Phase Voltages of High-, Medium- and Low-Voltage Busbars in a Substation during a Phase-to-Ground Fault on High-Voltage Busbars. Mathematics 2023, 11, 3032. [Google Scholar] [CrossRef]
- Kustov, A.; Zatsepin, E.; Zatsepina, V. Analysis of Transient Regimes for Single-Phase Short Circuits in Electrical Lines with Isolated and Compensated Neutral. In Proceedings of the 2nd International Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency (SUMMA), Lipetsk, Russia, 11–13 November 2020. [Google Scholar]
- Dinavahi; Lin, N. Real-Time Electromagnetic Transient Simulation of AC-DC Networks; 1 online resource vol. în IEEE Press series on power and energy systems; John Wiley: Hoboken, NJ, USA; IEEE Press: Hoboken, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Arrillaga, N.R.W.Ș.J. Power Systems Electromagnetic Tranzients Simulation, 2nd ed.; 1 online resource (xxxii, 493 pages): Illustrations (black and white) vol.; The Institution of Engineering and Technology Stevenage: Stevenage, UK, 2018; Available online: https://books.google.ro/books?hl=ro&lr=&id=b4TYkhpCb80C&oi=fnd&pg=PR23&dq=Power+Systems+Electromagnetic+Tranzients+Simulation&ots=CZsAwl6HGb&sig=LiUfOrSu2VpUfOmDR9yoPyK3hOY&redir_esc=y#v=onepage&q=Power%20Systems%20Electromagnetic%20Tranzients%20Simulation&f=false (accessed on 20 March 2022).
- Akihiro Ametani Electromagnetic Transients Program: History and Future, First Published: 04 August 2020. Available online: https://onlinelibrary.wiley.com/doi/full/10.1002/tee.23192 (accessed on 15 February 2022).
- Manitoba Hydro International Ltd. PSCAD User’s Guide. May 2018. [Online]. Available online: https://www.pscad.com/knowledge-base/article/160 (accessed on 16 February 2022).
- Ametani, A. Electromagnetic Transients Program: History and Future. IEEJ Trans. Electr. Electron. Eng. 2021, 16, 1150–1158. [Google Scholar] [CrossRef]
- Vladimirescu, A. “Spice”, in Studio e Professione; McGraw-Hill Italia: Milano, Italy, 1995. [Google Scholar]
- Rashid, M.H. SPICE for Power Electronics and Electric Power; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar] [CrossRef]
- Toader, D.; Blaj, C.; Vesa, D.; Tatai, I.; Arvinti, B. Numeric Simulator for the Analysis of Transients due to Fault in Electric Networks. In Proceedings of the of 8th International Conference on Modern Power Systems (MPS), Cluj-Napoca, Romania, 21–23 May 2019. [Google Scholar]
- Toader, D.; Haragus, S.; Blaj, C. Numeric Simulation of Faults in Electrical Networks”, FS’09. In Proceedings of the 10th WSEAS International Conference on Fuzzy Systems, Prague, Czech Republic, 23–25 March 2009; pp. 128–135. [Google Scholar]
- The Math Works, Inc. Sim-Scape Electrical R2023b User’s Guide (Specialized Power Systems). 12 May 2024. [Online]. Available online: https://www.mathworks.com/help/pdf_doc/sps/%20powersys_ug.pdf (accessed on 18 April 2023).
- The Math Works, Inc. “Simulink® R2023b User’s Guide”. September 2023. [Online]. Available online: https://www.mathworks.com/help/pdf_doc/simulink/simulink_ug.pdf (accessed on 23 April 2023).
- “MATLAB Fundamentals”. [Online]. Available online: https://www.mathworks.com/learn/training/matlab-fundamentals.html (accessed on 5 July 2023).
- “Simulink Fundamentals”. [Online]. Available online: https://www.mathworks.com/learn/training/simulink-fundamentals.html (accessed on 5 July 2023).
- “MATLAB App Designer”. [Online]. Available online: https://www.mathworks.com/products/matlab/app-designer.html (accessed on 6 July 2023).
- “Simscape Electrical”. [Online]. Available online: https://www.mathworks.com/products/simscape-electrical.html (accessed on 12 July 2023).
- Solea, C. A MATLAB/Simulink Distribution Network Model for the Analysis of the Transient Regime Caused by a Phase-to-Earth Fault. (20 August 2025). [Online]. Available online: https://github.com/claudiusolea/medium_voltage_test-feeder_for_transients (accessed on 21 August 2023).
- Shen, M.; Ingratta, L.; Roberts, Ș.G. Grounding transformer application, modeling, and simulation. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–8. [Google Scholar] [CrossRef]
- Hu, C.; Zeng, X.; Tao, J.; Wang, Y. Fault analysis of a grounding transformer. In Proceedings of the 2010 International Conference on Modelling, Identification and Control, Okayama, Japan, 17–19 July 2010; pp. 579–584. [Google Scholar]
- “MATLAB Live Editor”. [Online]. Available online: https://www.mathworks.com/products/matlab/live-editor.html (accessed on 15 June 2023).
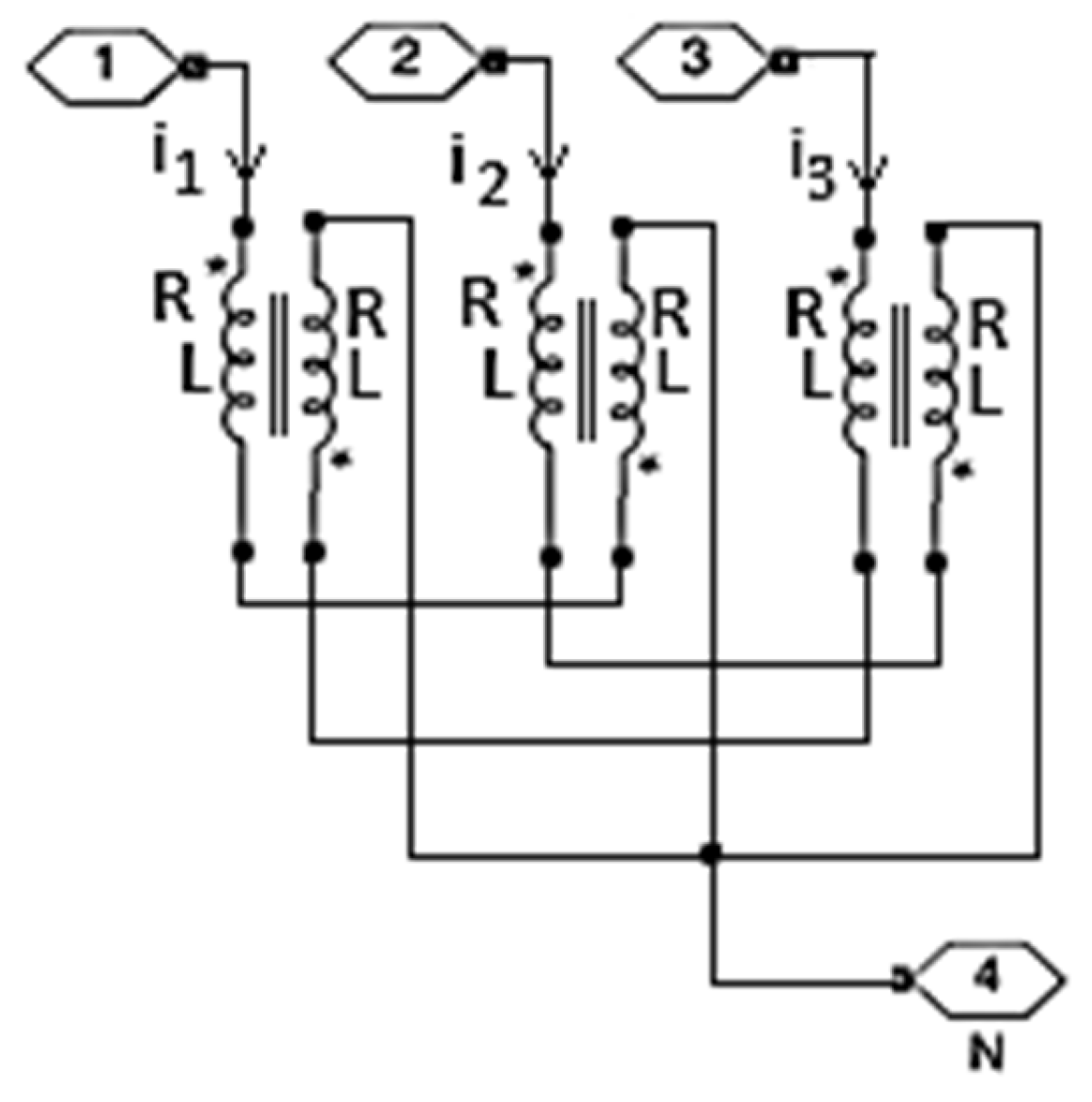

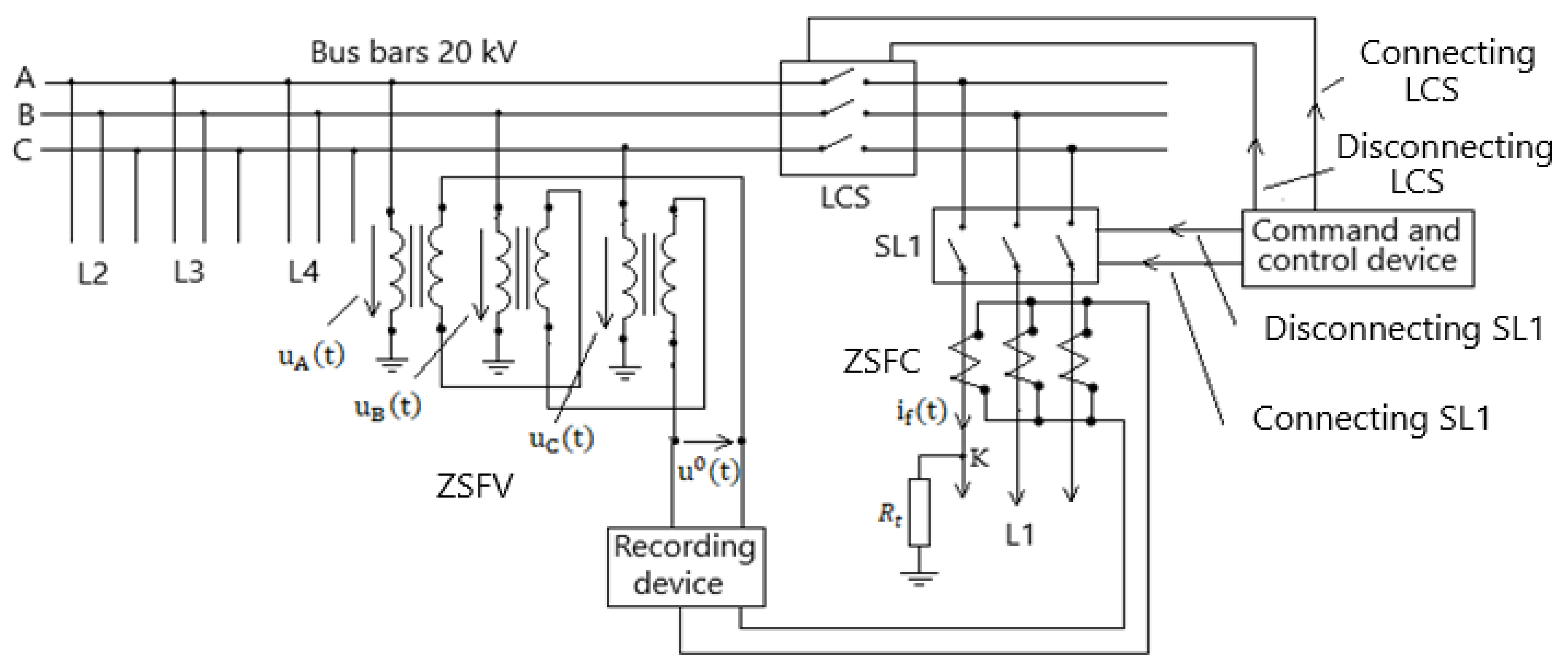
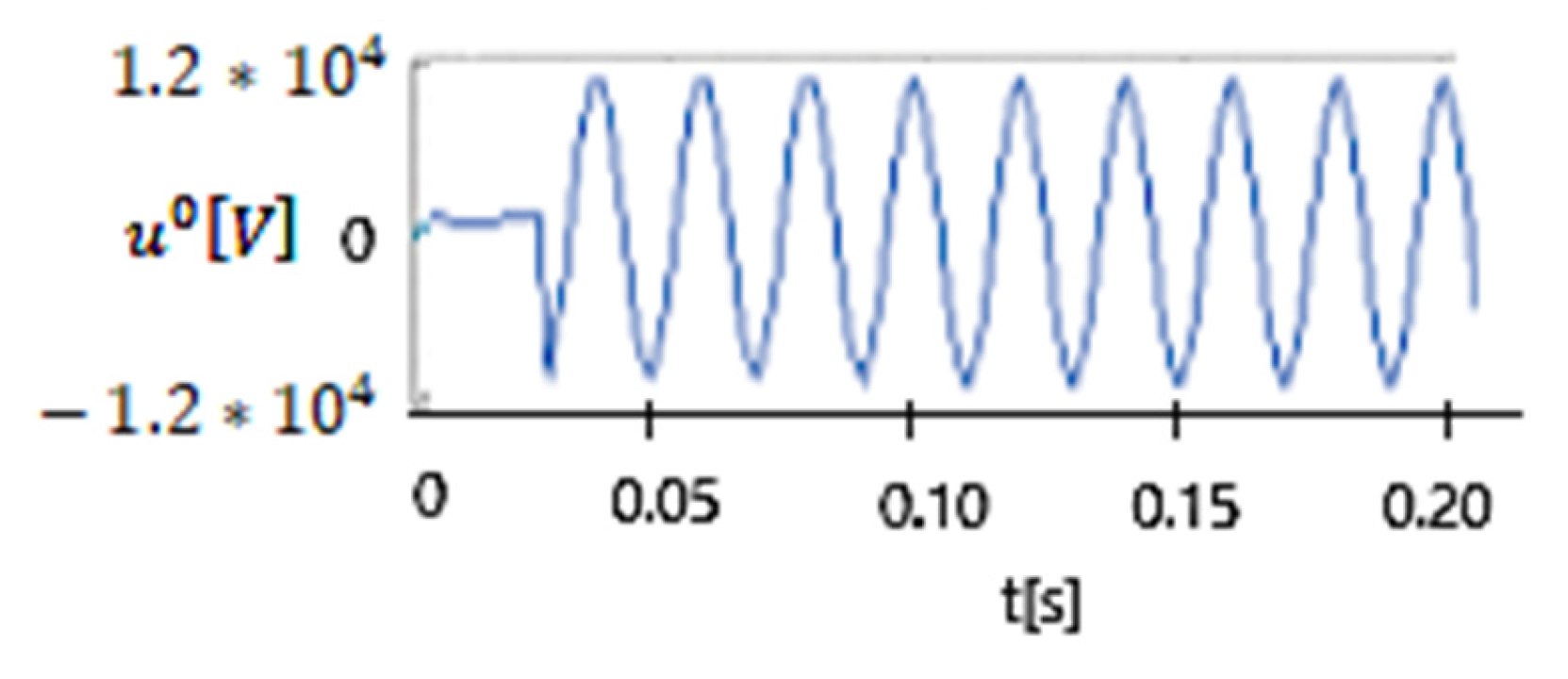
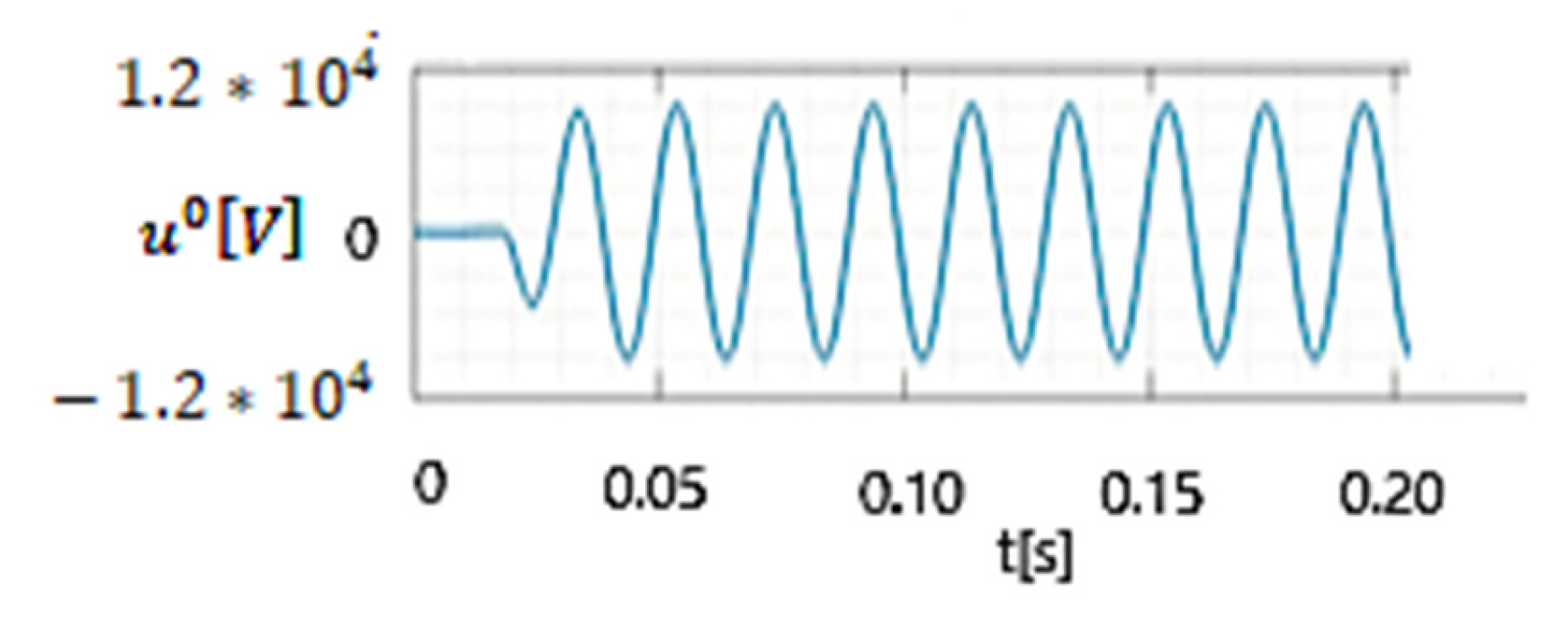
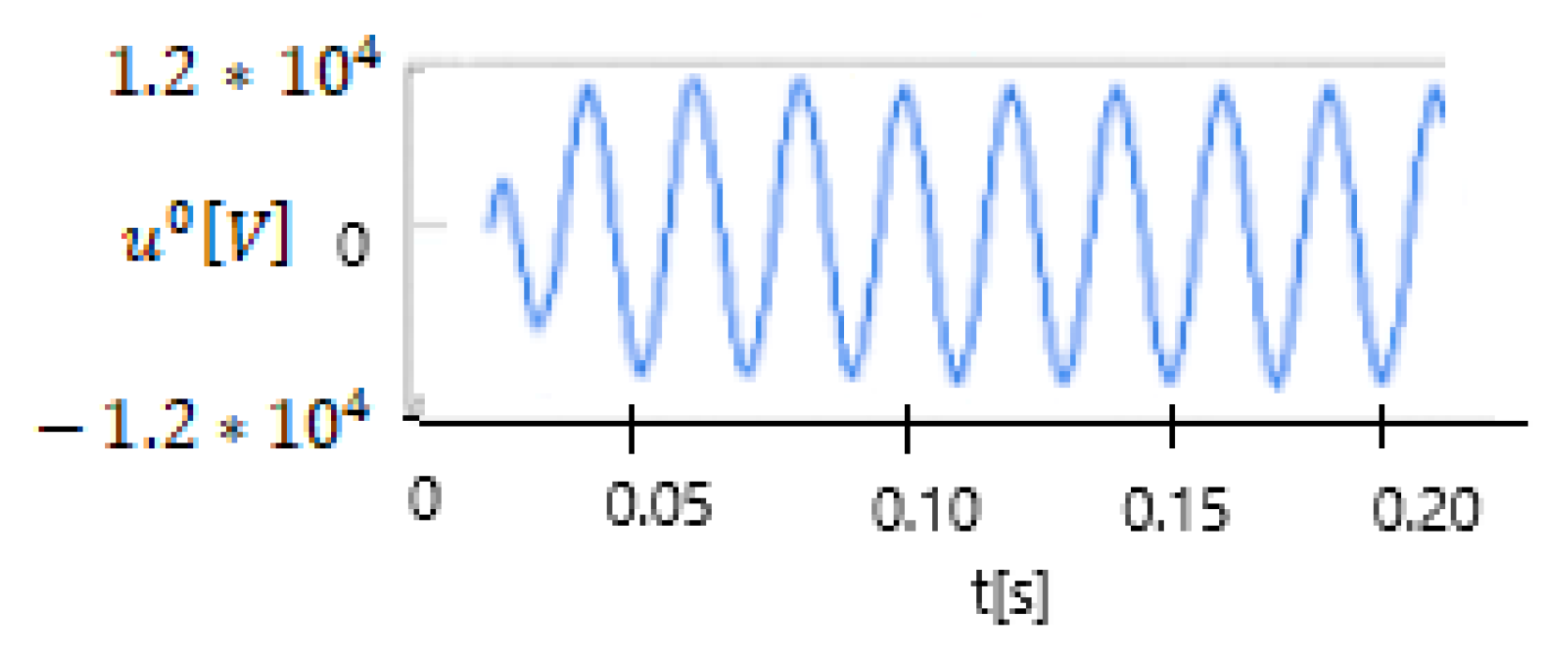
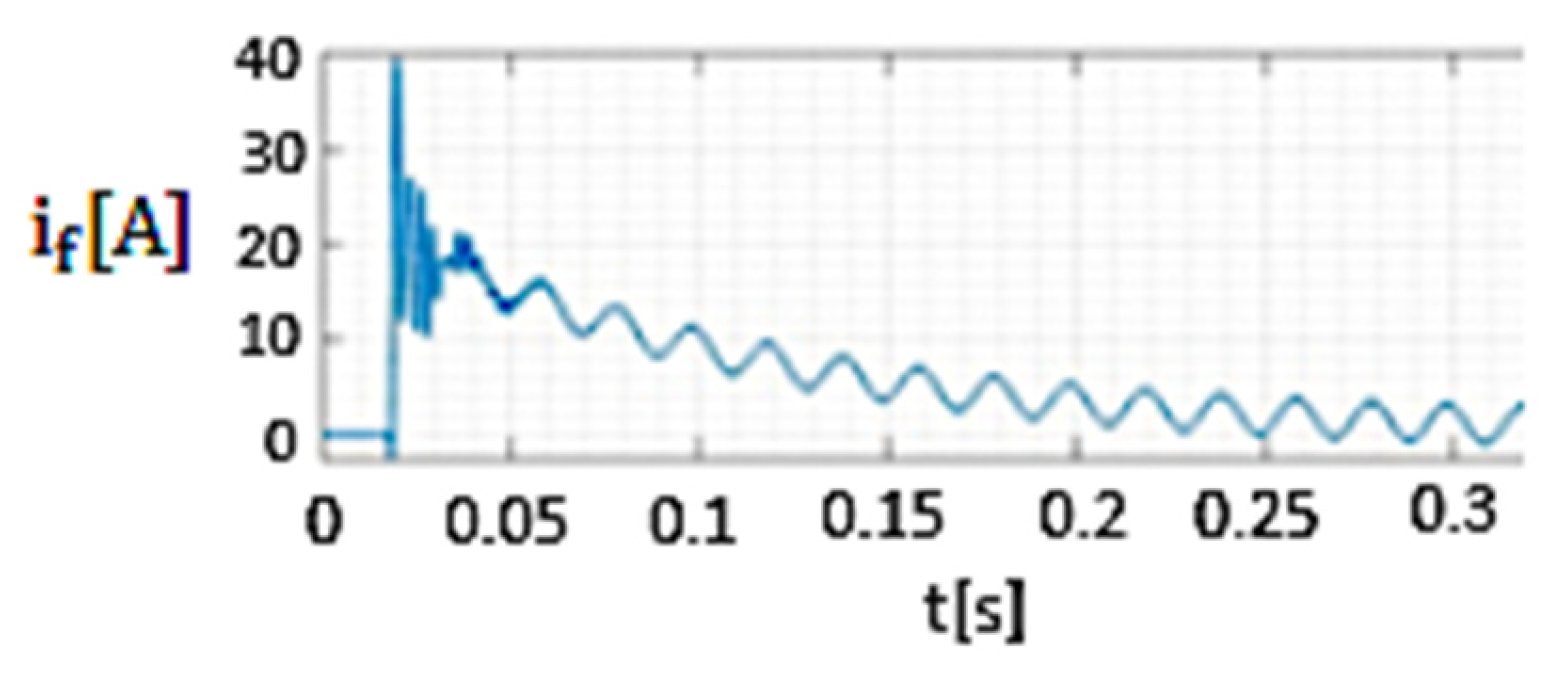


| Sn [MVA] | Transformer Connections | U1n [kV] | U2n [kV] | usc [%] | i0 [%] | Psc [kW] | P0 [kW] | |
|---|---|---|---|---|---|---|---|---|
| Tr.1 | 16 | Y0/Δ | 110 | 20 | 11 | 1 | 130 | 30 |
| Tr.2 | 4 | Δ/Y0 | 20 | 0.4 | 6 | 1.8 | 62 | 15 |
| Tr.3 | 6.3 | Δ/Y0 | 20 | 0.4 | 7 | 1.6 | 82 | 20 |
| Tr.4 | 10 | Δ/Y0 | 20 | 0.4 | 7 | 1.2 | 110 | 25 |
| Consumers Supplied Through Fault-Free Lines | Sn [MVA] | Equivalent Resistance of Consumers [Ω] | Equivalent Inductance of Consumers [H] |
|---|---|---|---|
| L2 | 1.35 | 275.6 | 0.347 |
| L3 | 4.53 | 82.12 | 0.103 |
| L4 | 8.76 | 42.47 | 0.0196 |
| Total | 14.64 | 25.41 | 0.0109 |
| 20 kV Lines | L2 | L3 | L4 | Total Network |
|---|---|---|---|---|
| Phase-to-earth capacitance [μF] | 0.596 | 1.755 | 1.757 | 4.108 |
| Insulation resistance values [Ω] | 19,891 | 51,915 | 19,769 | 8151.4 |
| Operating Modes | Resonance | Over- Compensated 6.1% | Under- Compensated 4.5% | Under- Compensated 36.9% |
|---|---|---|---|---|
| Resistance PC [Ω] | 13.36 | 29.2 | 14.1 | 7.1 |
| Inductance PC [H] | 0.811 | 0.757 | 0.851 | 1.294 |
| Resistance R [Ω] | Self-Inductance L [H] | Coupling Inductance Lm [H] |
|---|---|---|
| 1.39 | 15 | 14.987 |
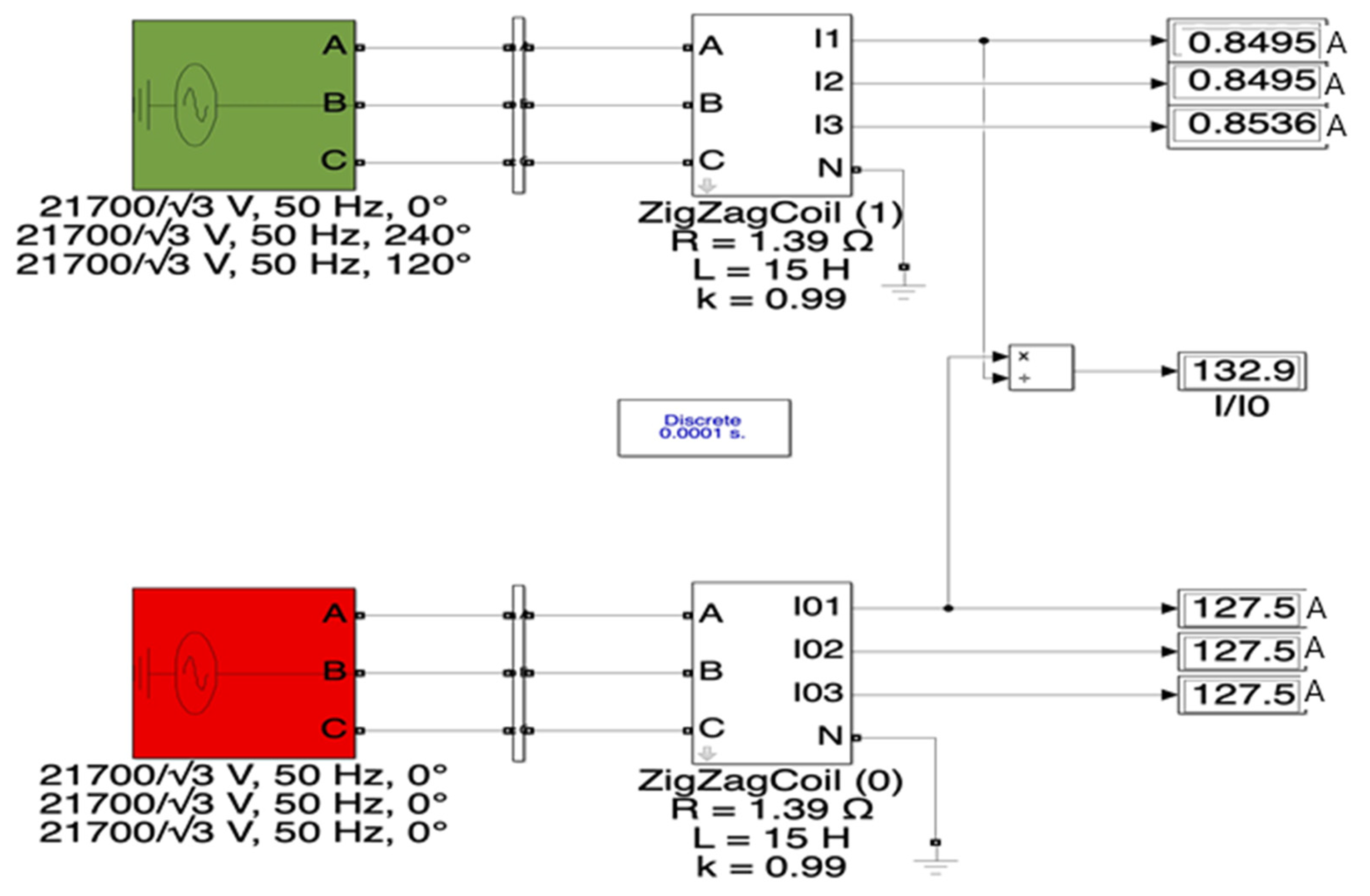
| Sequence Type | I1 [A] | I2 [A] | I3 [A] | In [A] | Zf [Ω] |
|---|---|---|---|---|---|
| Plus | 0.8495 | 0.8495 | 0.8495 | 0 | 14,715 |
| Zero | 127.5 | 127.5 | 127.5 | 382.5 | 98.1 |
| Rt (Ω)/Operating Regime | 8 | 100 | 268 | 575 | 1100 |
|---|---|---|---|---|---|
| Under-compensated at 4.5% | 171.9 | 169.1 | 140.5 | 98.1 | 34.6 |
| Over-compensated at 6.1% | 171.7 | 168.9 | 136.1 | 54.1 | 31.1 |
| Under-compensated at 36.9% | 170.7 | 168.7 | 145.6 | 73.6 | 45.5 |
| Resonance | 171.4 | 168.3 | 137.6 | 56.8 | 32.4 |
| Rt (Ω)/Operating Regime | 8 | 100 | 268 | 575 | 1100 |
|---|---|---|---|---|---|
| Under-compensated at 4.5% | 7.48 | 6.72 | 5.95 | 5.42 | 4.26 |
| Over-compensated at 6.1% | 11.29 | 9.69 | 8.94 | 8.18 | 6.43 |
| Under-compensated at 36.9% | 18.65 | 16.76 | 14.84 | 13.51 | 10.62 |
| Resonance | 7.23 | 6.49 | 5.75 | 5.24 | 4.12 |
| Change in Phase-Ground Capacity Values of the 20 kV Network [%] | +4 | +3 | +2 | +1 | 0 | −1 | −2 | −3 | −4 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Rt = 8 Ω | 17.5 | 13.9 | 10.1 | 6.38 | 3.07 | 0.58 | −1.91 | −3.98 | −5.28 | |
| Rt = 268 Ω | 23.97 | 19.85 | 16.01 | 12.53 | 9.35 | 6.61 | 4.23 | 2.29 | 0.85 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toader, D.; Solea, C.; Greconici, M.; Vintan, M.; Tatai, I.; Vesa, D. Numerical Mathematical Model for the Analysis of the Transient Regime Caused by a Phase-to-Earth Fault. Appl. Sci. 2025, 15, 9389. https://doi.org/10.3390/app15179389
Toader D, Solea C, Greconici M, Vintan M, Tatai I, Vesa D. Numerical Mathematical Model for the Analysis of the Transient Regime Caused by a Phase-to-Earth Fault. Applied Sciences. 2025; 15(17):9389. https://doi.org/10.3390/app15179389
Chicago/Turabian StyleToader, Dumitru, Claudiu Solea, Marian Greconici, Maria Vintan, Ildiko Tatai, and Daniela Vesa. 2025. "Numerical Mathematical Model for the Analysis of the Transient Regime Caused by a Phase-to-Earth Fault" Applied Sciences 15, no. 17: 9389. https://doi.org/10.3390/app15179389
APA StyleToader, D., Solea, C., Greconici, M., Vintan, M., Tatai, I., & Vesa, D. (2025). Numerical Mathematical Model for the Analysis of the Transient Regime Caused by a Phase-to-Earth Fault. Applied Sciences, 15(17), 9389. https://doi.org/10.3390/app15179389






