Intrinsic Temperature and Pressure Compensation of Thin-Film Acoustic Resonators
Abstract
1. Introduction
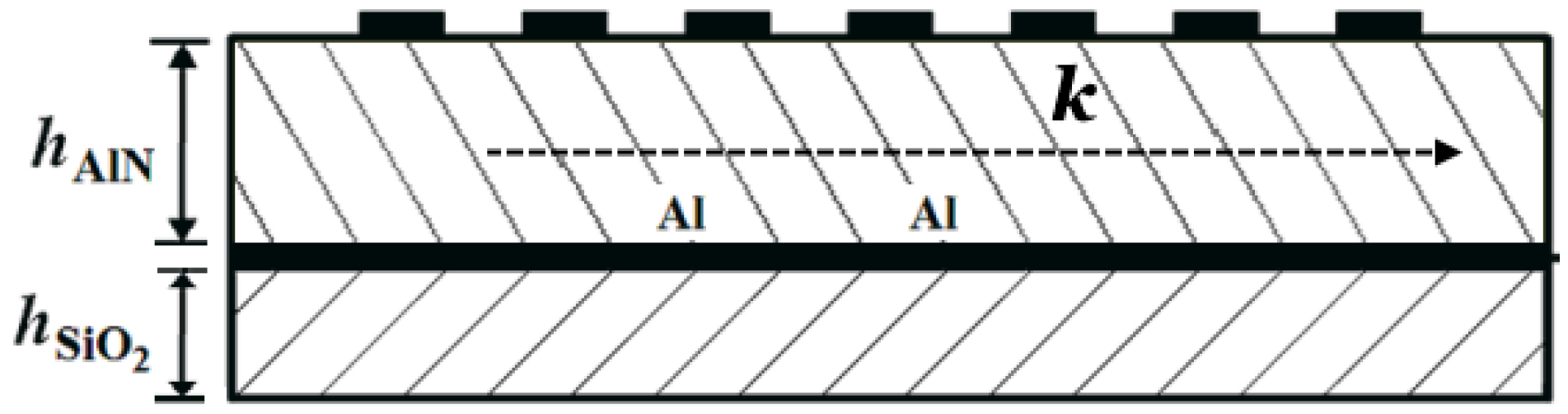
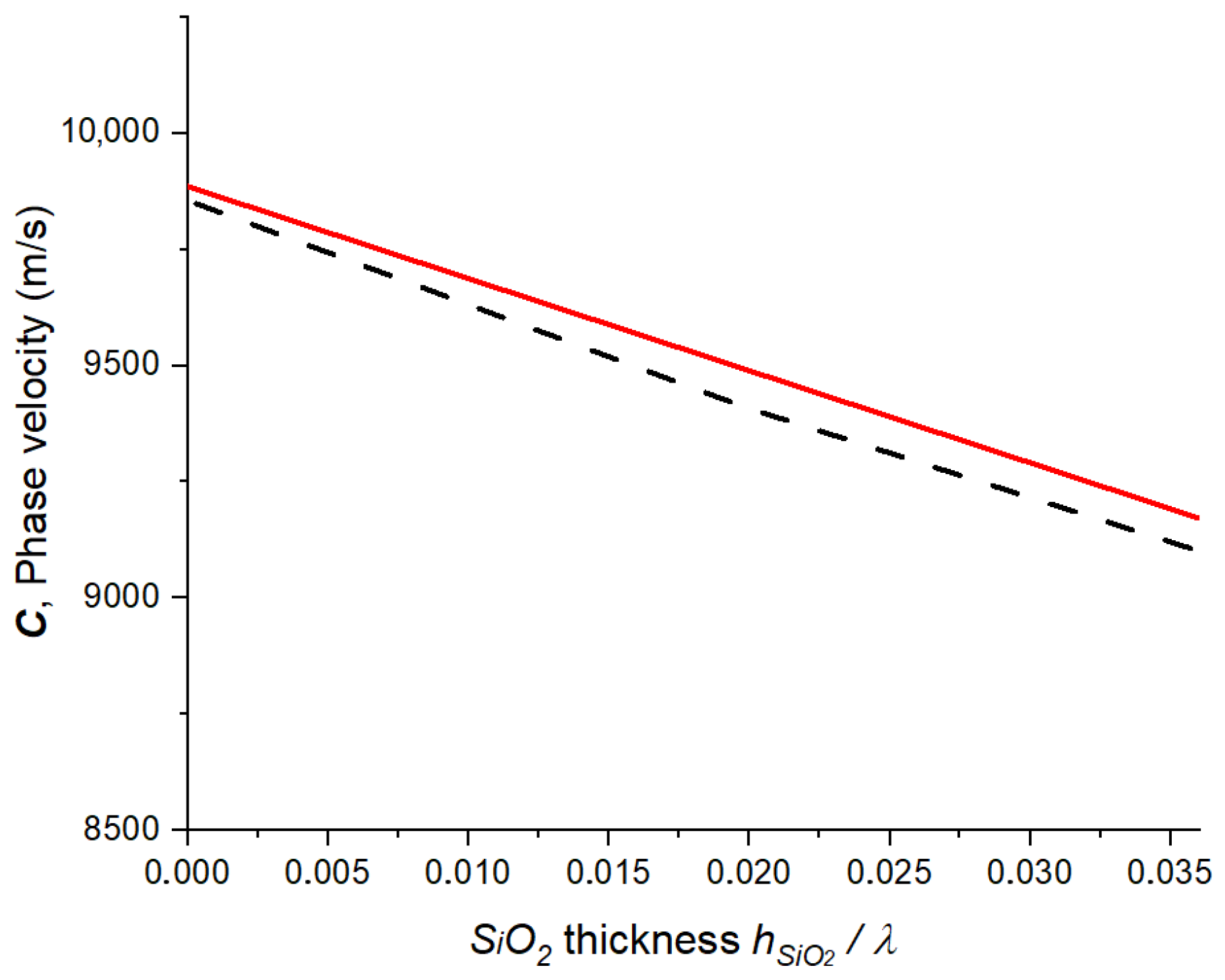
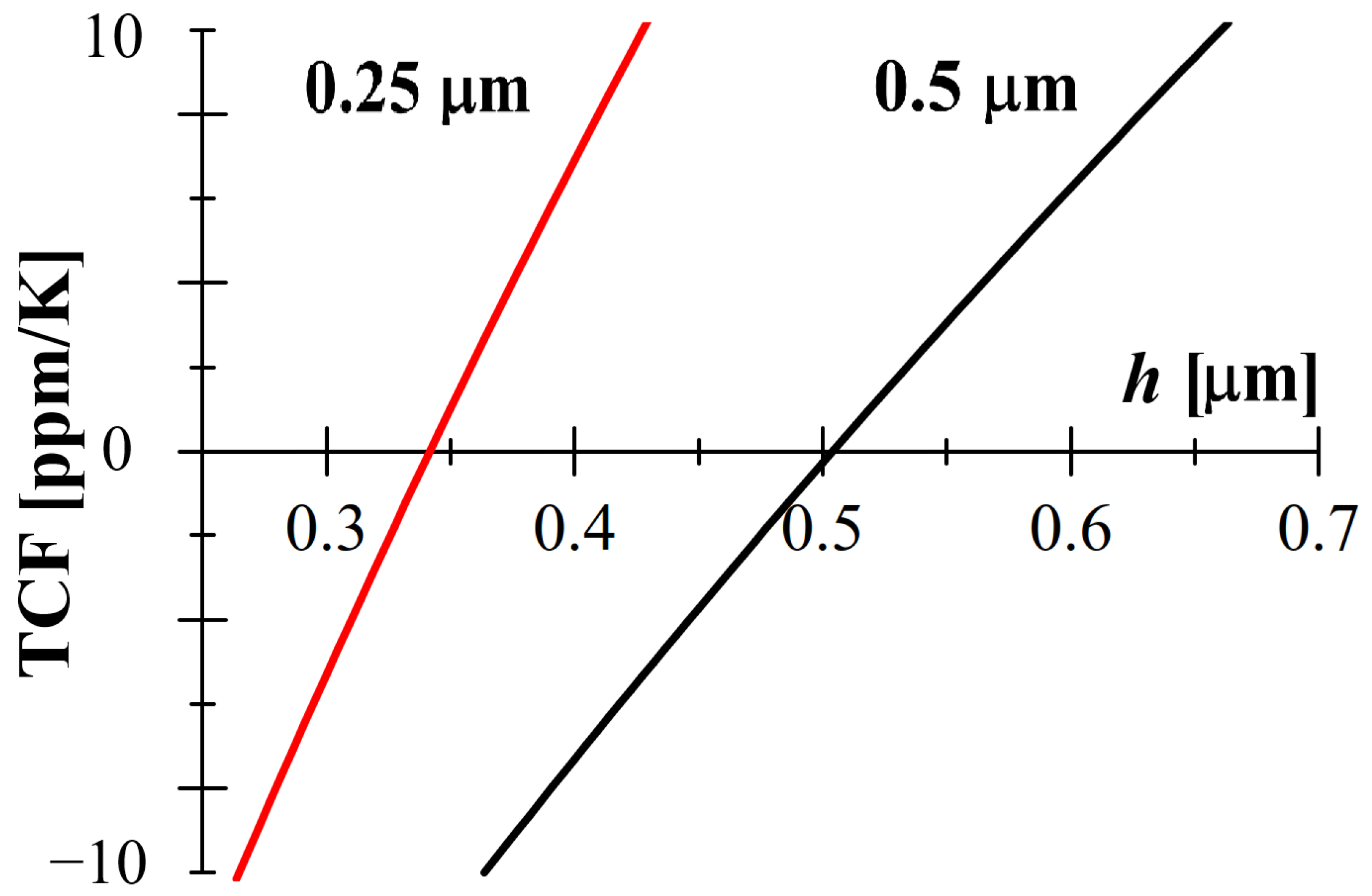
2. Temperature- and Pressure-Compensated Structure
3. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TCF and TCV | Temperature coefficients of frequency and velocity, respectively |
| PCF and PCV | Pressure coefficients of frequency and velocity, respectively |
| MCF | Mass coefficient of frequency |
| LW and SAW | Lamb and surface acoustic wave, respectively |
| MEMS | Microelectromechanical systems |
| , | Material index and phase velocity of the mode in a free plate , respectively |
| C | Phase velocity of the mode of a composite structure |
| and | Temperature and pressure partial response functions, respectively |
| , , and | Density, mass, and thickness of the layer, respectively |
| Poisson’s ratio | |
| and | Coefficient of linear thermal expansion and compressibility, respectively |
| and | Shear and longitudinal velocities, respectively |
| and | Shear modulus and Young’s modulus, respectively |
| T and P | Temperature and pressure, respectively |
Appendix A
References
- Lee, B.C.; Manson, G.; Staszewski, W.J. Environmental Effects on Lamb Wave Responses from Piezoceramic Sensors. Mater. Sci. Forum 2003, 440–441, 195–202. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, Q.; Zhang, L.; Zhang, W.; Xiong, J. A Novel SAW Temperature-Humidity-Pressure (THP) Sensor Based on LiNbO3 for Environment Monitoring. J. Phys. D Appl. Phys. 2020, 53, 375401. [Google Scholar] [CrossRef]
- Available online: https://www.jauch.com/blog/en/tcxo-design-and-functionality/ (accessed on 22 August 2025).
- McSkimin, H.J. Measurement of Elastic Constants at Low Temperatures by Means of Ultrasonic Waves–Data for Silicon and Germanium Single Crystals, and for Fused Silica. J. Appl. Phys. 1953, 24, 988–997. [Google Scholar] [CrossRef]
- Rouxel, T. Elastic Properties and Short-to Medium-Range Order in Glasses. J. Am. Ceram. Soc. 2007, 90, 3019–3039. [Google Scholar] [CrossRef]
- Le Parc, R.; Levelut, C.; Pelous, J.; Martinez, V.; Champagnon, B. Influence of Fictive Temperature and Composition of Silica Glass on Anomalous Elastic Behaviour. J. Phys. Condens. Matter 2006, 18, 7507. [Google Scholar] [CrossRef] [PubMed]
- Nicoloiu, A.; Boldeiu, G.; Nastase, C.; Nedelcu, M.; Ciornei, C.; Zdru, I.; Stavrinidis, G.; Vasilache, D.; Stavrinidis, A.; Dinescu, A.; et al. Temperature Behaviour of Rayleigh, Sezawa and Lamb Mode Resonance Frequencies of 30 % ScAlN/Si Saw Devices. In Proceedings of the 22nd International Conference on Solid-State Sensors, Actuators and Microsystems (Transducers), Kyoto, Japan, 25–29 June 2023; pp. 1608–1611. [Google Scholar]
- Pan, S.; Memon, M.M.; Wan, J.; Wang, T.; Zhang, W. The Influence of Pressure on the TCF of AlN-Based SAW Pressure Sensor. IEEE Sens. J. 2022, 22, 3097–3104. [Google Scholar] [CrossRef]
- Zagorac, D.; Zagorac, J.; Djukic, M.B.; Jordanov, D.; Matović, B. Theoretical Study of AlN Mechanical Behaviour under High Pressure Regime. Theor. Appl. Fract. Mech. 2019, 103, 102289. [Google Scholar] [CrossRef]
- Yu, Z.; Yue, Y.; Liang, Z.; Zhao, X.; Li, F.; Peng, W.; Zhu, Q.; He, Y. Physical Sensors Based on Lamb Wave Resonators. Micromachines 2024, 15, 1243. [Google Scholar] [CrossRef]
- Yantchev, V.; Katardjiev, I. Thin Film Lamb Wave Resonators in Frequency Control and Sensing Applications: A Review. J. Micromech. Microeng. 2013, 23, 043001. [Google Scholar] [CrossRef]
- Kuypers, J.H.; Lin, C.-M.; Vigevani, G.; Pisano, A.P. Intrinsic Temperature Compensation o f Aluminum Nitride Lamb Wave Resonators for Multiple-Frequency References. In Proceedings of the 2008 IEEE International Frequency Control Symposium, Honolulu, HI, USA, 19–21 May 2008; pp. 240–249. [Google Scholar]
- Lin, C.-M.; Yen, T.-T.; Lai, Y.-J.; Felmetsger, V.V.; Hopcroft, M.A.; Kuypers, J.H.; Pisano, A.P. Experimental Study of Temperature-Compensated Aluminum Nitride Lamb Wave Resonators. In Proceedings of the 2009 IEEE International Frequency Control Symposium Joint with the 22nd European Frequency and Time Forum, Besancon, France, 20–24 April 2009; pp. 5–9. [Google Scholar]
- Lin, C.-M.; Yen, T.-T.; Felmetsger, V.V.; Hopcroft, M.A.; Kuypers, J.H.; Pisano, A.P. Thermally Compensated Aluminum Nitride Lamb Wave Resonators for High Temperature Applications. Appl. Phys. Lett. 2010, 97, 083501. [Google Scholar] [CrossRef]
- Lu, X.; Ren, H. Micromachined Piezoelectric Lamb Wave Resonators: A Review. J. Micromech. Microeng. 2023, 33, 113001. [Google Scholar] [CrossRef]
- Zou, J.; Pisano, A.P. Temperature Compensation of the AlN Lamb Wave Resonators Utilizing the S1 Mode. In Proceedings of the 2015 IEEE International Ultrasonics Symposium (IUS), Taipei, Taiwan, 21–24 October 2015; pp. 1–4. [Google Scholar]
- Zou, J.; Lin, C.-M.; Senesky, D.G.; Pisano, A.P. Thermally Stable SiO2/AlN/SiO2 Lamb Wave Resonators Utilizing the Lowest-Order Symmetric Mode at High Temperatures. In Proceedings of the 2013 IEEE International Ultrasonics Symposium (IUS), Prague, Czech Republic, 21–25 July 2013; pp. 1077–1080. [Google Scholar]
- Caliendo, C.; D’Amico, A.; Lo Castro, F. Lamb Waves Propagation along 3C-SiC/AlN Membranes for Application in Temperature-Compensated, High-Sensitivity Gravimetric Sensors. Sensors 2013, 13, 550–564. [Google Scholar] [CrossRef]
- Rose, J.L. Ultrasonic Guided Waves in Solid Media; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Fainozzi, D.; Caporaletti, F.; Capotondi, F.; De Angelis, D.; Duncan, R.A.; Foglia, L.; Martinelli, A.; Mincigrucci, R.; Nelson, K.A.; Pedersoli, E.; et al. Temperature Effects on the Nanoscale Thermoelastic Response of a SiO2 Membrane. APL Mater. 2024, 12, 051122. [Google Scholar] [CrossRef]
- Li, H.; Zhou, J.; Xu, Q.; Liu, Z.; Ren, Y.; Liu, Y.; Guo, S.; Cai, Y.; Sun, C. Low Temperature Coefficient of Frequency AlN Lamb Wave Resonator Using Groove Structure between Interdigital Transducers. J. Appl. Phys. 2024, 136, 025702. [Google Scholar] [CrossRef]
- Zha, C.; Hemley, R.J.; Mao, H.; Duffy, T.S.; Meade, C. Acoustic Velocities and Refractive Index of SiO2 Glass to 57.5 GPa by Brillouin Scattering. Phys. Rev. B 1994, 50, 13105–13112. [Google Scholar] [CrossRef] [PubMed]
- Manghnani, M.H.; Williams, Q.; Matsui, T.; Schultz, P.C.; Kurkjian, C.R. Effects of Composition, Pressure, and Temperature on the Elastic Properties of SiO2–TiO2 Glasses: An Integrated Ultrasonic and Brillouin Study. Minerals 2020, 10, 481. [Google Scholar] [CrossRef]
- Deschamps, T.; Margueritat, J.; Martinet, C.; Mermet, A.; Champagnon, B. Elastic Moduli of Permanently Densified Silica Glasses. Sci. Rep. 2014, 4, 7193. [Google Scholar] [CrossRef]
- Guerette, M.; Ackerson, M.R.; Thomas, J.; Yuan, F.; Bruce Watson, E.; Walker, D.; Huang, L. Structure and Properties of Silica Glass Densified in Cold Compression and Hot Compression. Sci. Rep. 2015, 5, 15343. [Google Scholar] [CrossRef]
- Courtois, M.; Berthelot, A.; Cornet, A.; Le Floch, S.; Martinet, C.; Deschamps, T. Pressure-Induced Amorphous-Amorphous Transition in Pre-Densified Silica Glass: An Experimental Exploration of the Potential Energy Landscape. Sci. Rep. 2025, 15, 6719. [Google Scholar] [CrossRef]
- Takahashi, N.; Sakamaki, T.; Ikeda, O.; Kakizawa, S.; Higo, Y.; Suzuki, A. Elastic Wave Velocity Measurements of Sodium Aluminosilicate Glass and Melt at High Pressure and Temperature. Phys. Earth Planet. Inter. 2024, 350, 107167. [Google Scholar] [CrossRef]
- Sonneville, C.; De Ligny, D.; Mermet, A.; Champagnon, B.; Martinet, C.; Henderson, G.H.; Deschamps, T.; Margueritat, J.; Barthel, E. In Situ Brillouin Study of Sodium Alumino Silicate Glasses under Pressure. J. Chem. Phys. 2013, 139, 074501. [Google Scholar] [CrossRef]
- Sonneville, C.; Degioanni, S.; Martinet, C.; de Ligny, D.; Martinez, V.; Jurdyc, A.-M.; Braunn, A.; Raffaelly, L.; Champagnon, B.; Vouagner, D. Pressure-Independent Brillouin Fiber Optic Sensors for Temperature Measurements. J.-Non Solids 2014, 401, 36–39. [Google Scholar] [CrossRef]
- Kiefer, D.A.; Ponschab, M.; Rupitsch, S.J.; Mayle, M. Calculating the Full Leaky Lamb Wave Spectrum with Exact Fluid Interaction. J. Acoust. Soc. Am. 2019, 145, 3341–3350. [Google Scholar] [CrossRef]
- Cojocaru, S. Non-Monotonic Variation of Acoustic Spectrum with the Mass or Thickness of a Layered Structure. Acoustics 2024, 6, 805–817. [Google Scholar] [CrossRef]
- Cojocaru, S.; Anghel, D.V. Low-Temperature Electron-Phonon Heat Transfer in Metal Films. Phys. Rev. B 2016, 93, 115405. [Google Scholar] [CrossRef]
- Simmons, G.; Wang, H. Single Crystal Elastic Constants and Calculated Aggregate Properties: A Handbook; MIT Press: Cambridge, MA, USA, 1971. [Google Scholar]
- Augereau, F.; Laux, D.; Allais, L.; Mottot, M.; Caes, C. Ultrasonic Measurement of Anisotropy and Temperature Dependence of Elastic Parameters by a Dry Coupling Method Applied to a 6061-T6 Alloy. Ultrasonics 2007, 46, 34–41. [Google Scholar] [CrossRef]
- Dodson, J.C.; Inman, D.J. Thermal Sensitivity of Lamb Waves for Structural Health Monitoring Applications. Ultrasonics 2013, 53, 677–685. [Google Scholar] [CrossRef]
- Gerlich, D.; Slack, G.A. Pressure Dependence of the Thermal Conductivity of Glasses. J. Phys. Chem. Solids 1985, 46, 433–436. [Google Scholar] [CrossRef]
- Sun, N.; Mao, Z.; Zhang, X.; Tkachev, S.N.; Lin, J.-F. Hot Dense Silica Glass with Ultrahigh Elastic Moduli. Sci. Rep. 2022, 12, 13946. [Google Scholar] [CrossRef] [PubMed]
- Gerlich, D.; Dole, S.L.; Slack, G.A. Elastic Properties of Aluminum Nitride. J. Phys. Chem. Solids 1986, 47, 437–441. [Google Scholar] [CrossRef]
- Dandekar, D.P.; Abbate, A.; Frankel, J. Equation of State of Aluminum Nitride and Its Shock Response. J. Appl. Phys. 1994, 76, 4077–4085. [Google Scholar] [CrossRef]
- Available online: https://www.ioffe.ru/SVA/NSM/Semicond/AlN/mechanic.html (accessed on 22 August 2025).
- Song, W.; Tang, Q.; Su, C.; Chen, X.; Liu, Y. Ultrasonic Experimental Study on the Elasticity of Aluminum to 4.1 GPa in Multi-Anvil Apparatus. Phys. B 2021, 609, 412891. [Google Scholar] [CrossRef]

| Quantity | |||
|---|---|---|---|
| 3260 | 2210 | 2702 | |
| /K] | 18 | ||
| /GPa] | 27 | ||
| [m/s] | 6330 | 3757 | 3131 |
| [m/s] | 10,127 | 5954 | 6518 |
| [GPa] | 31 | ||
| [GPa] | 308 | 72 | 69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cojocaru, S. Intrinsic Temperature and Pressure Compensation of Thin-Film Acoustic Resonators. Appl. Sci. 2025, 15, 9349. https://doi.org/10.3390/app15179349
Cojocaru S. Intrinsic Temperature and Pressure Compensation of Thin-Film Acoustic Resonators. Applied Sciences. 2025; 15(17):9349. https://doi.org/10.3390/app15179349
Chicago/Turabian StyleCojocaru, Sergiu. 2025. "Intrinsic Temperature and Pressure Compensation of Thin-Film Acoustic Resonators" Applied Sciences 15, no. 17: 9349. https://doi.org/10.3390/app15179349
APA StyleCojocaru, S. (2025). Intrinsic Temperature and Pressure Compensation of Thin-Film Acoustic Resonators. Applied Sciences, 15(17), 9349. https://doi.org/10.3390/app15179349






