An Efficient Uncertainty Quantification Approach for Robust Design of Tuned Mass Dampers in Linear Structural Dynamics
Abstract
1. Introduction
2. Materials and Methods
2.1. Single-Degree-of-Freedom System
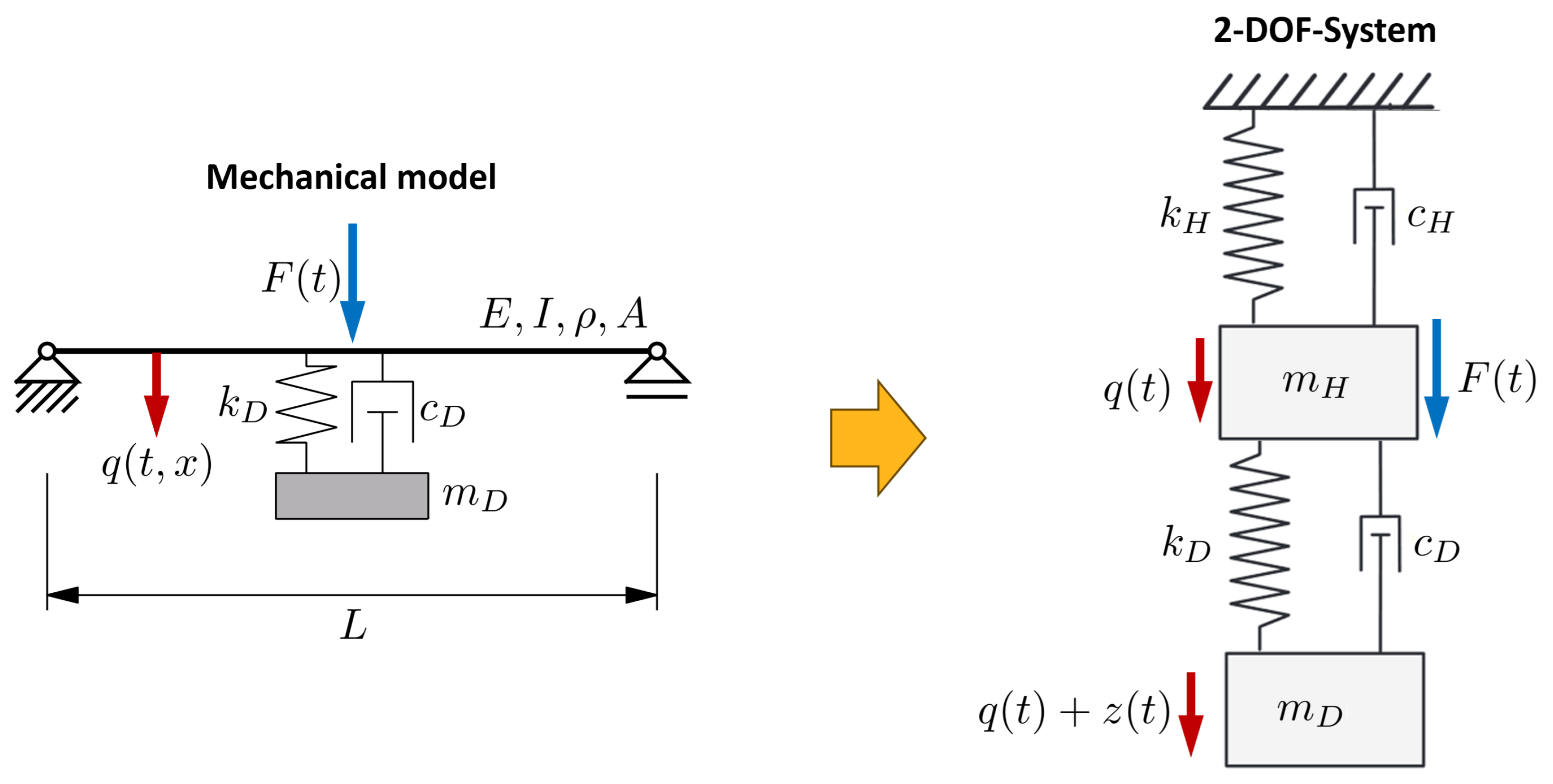
2.1.1. Mechanical Model
2.1.2. Optimal Tuning of the TMD Parameters
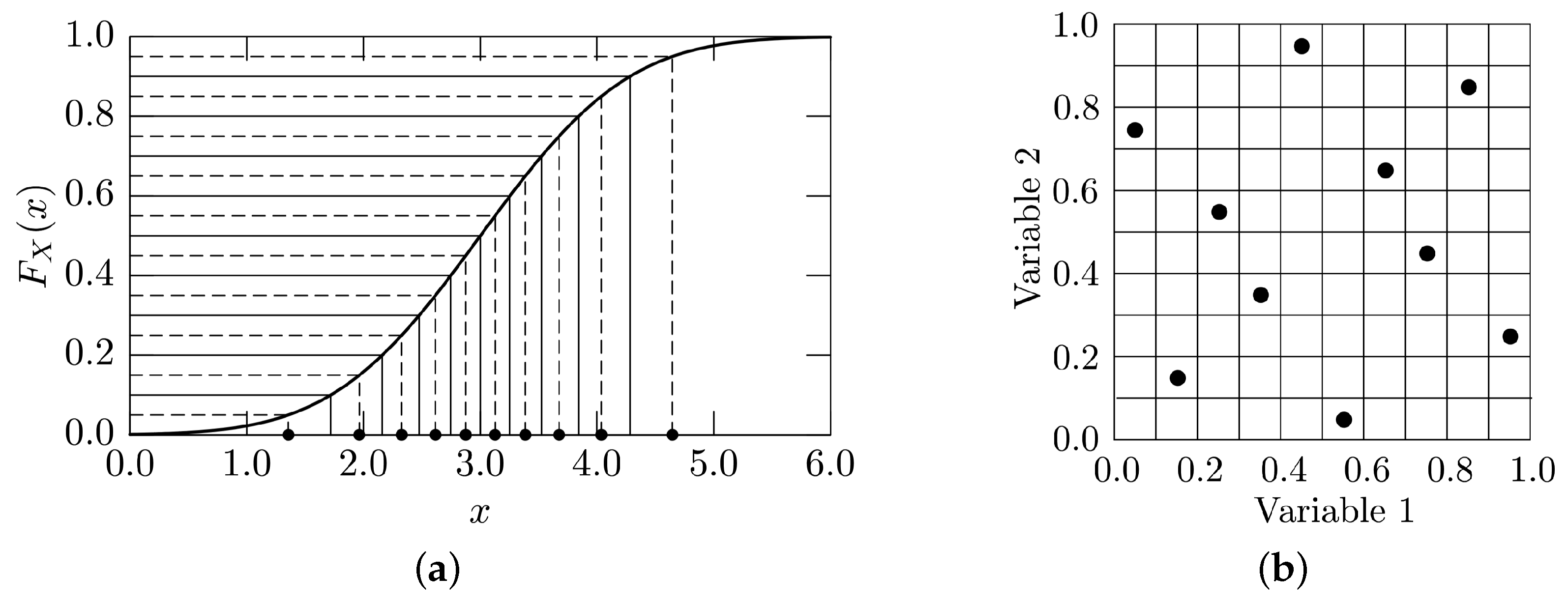
2.1.3. Uncertainty Propagation and Quantification
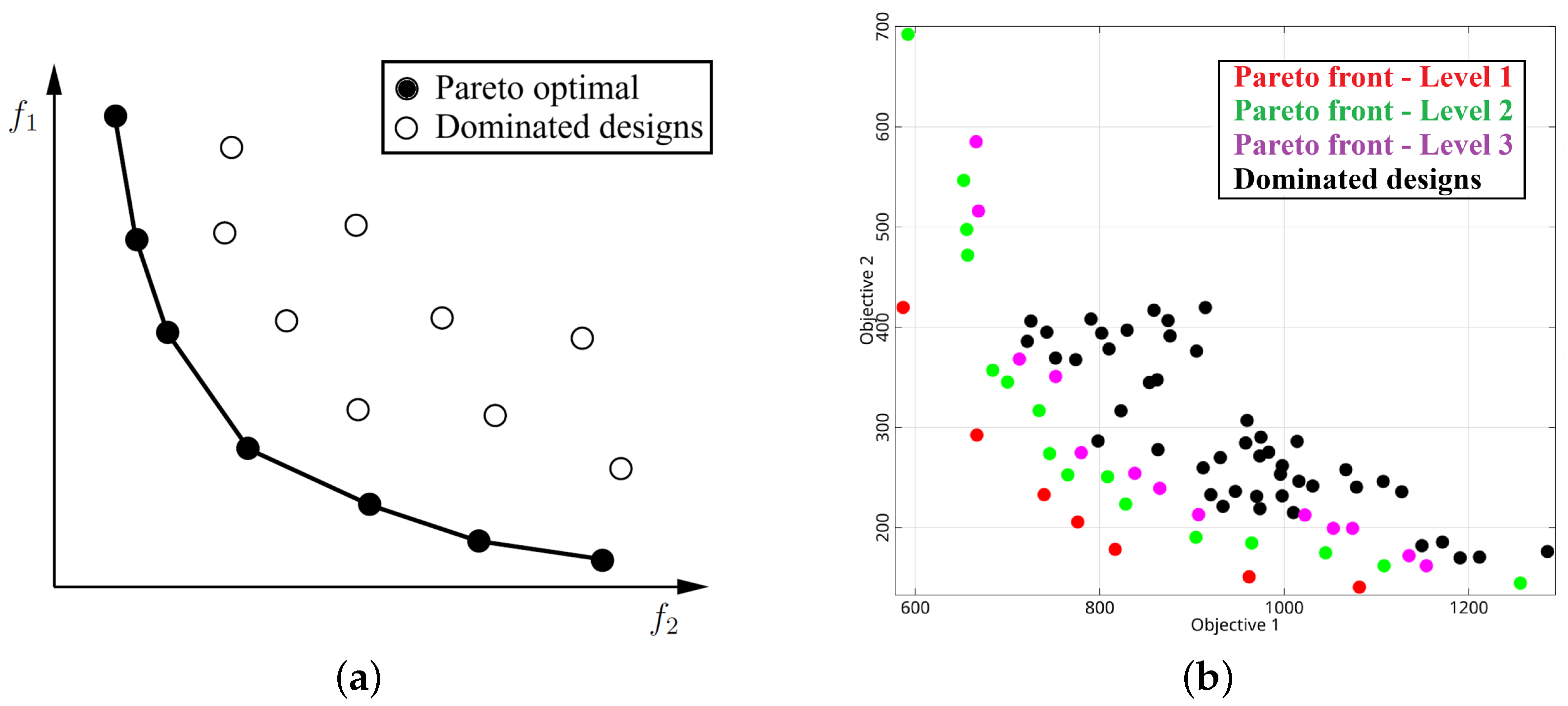
2.1.4. Optimization Under Uncertainty
2.2. Extension for Multi-Degree-of-Freedom Systems
2.2.1. Mechanical Model
2.2.2. Approximated Decoupled Stationary Solution
2.2.3. Uncertainty Quantification
2.2.4. Optimization Under Uncertainty
3. Results
3.1. Single-Degree-of-Freedom Example
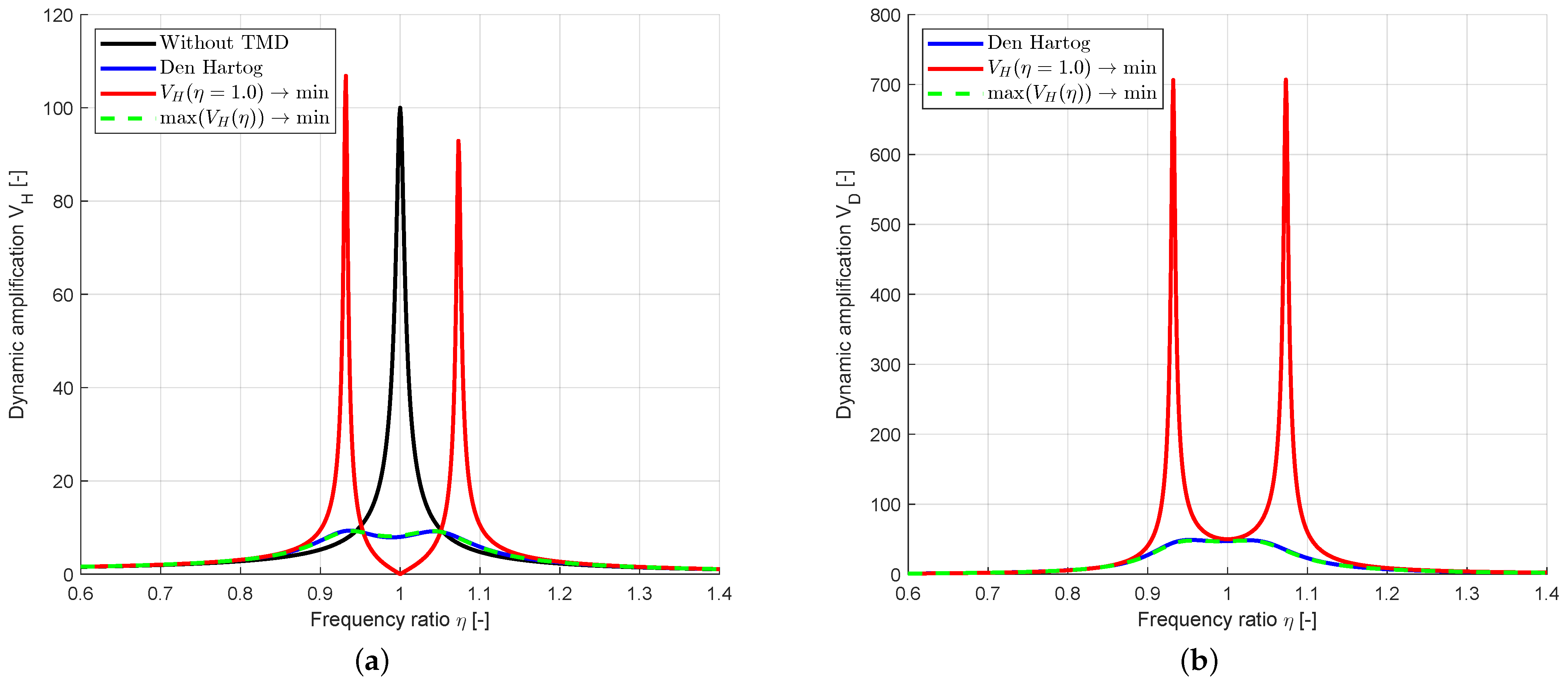
3.1.1. Deterministic Optimization
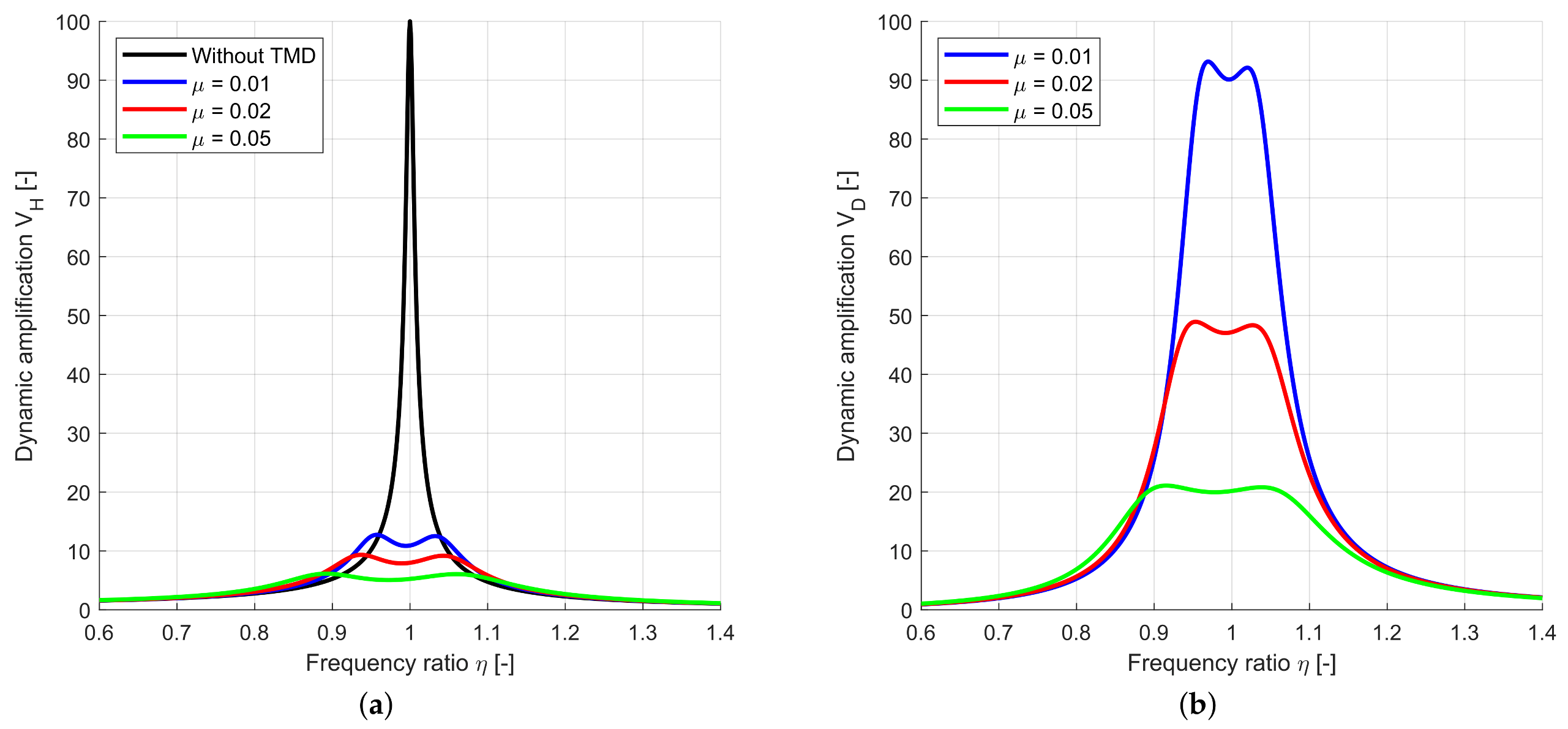
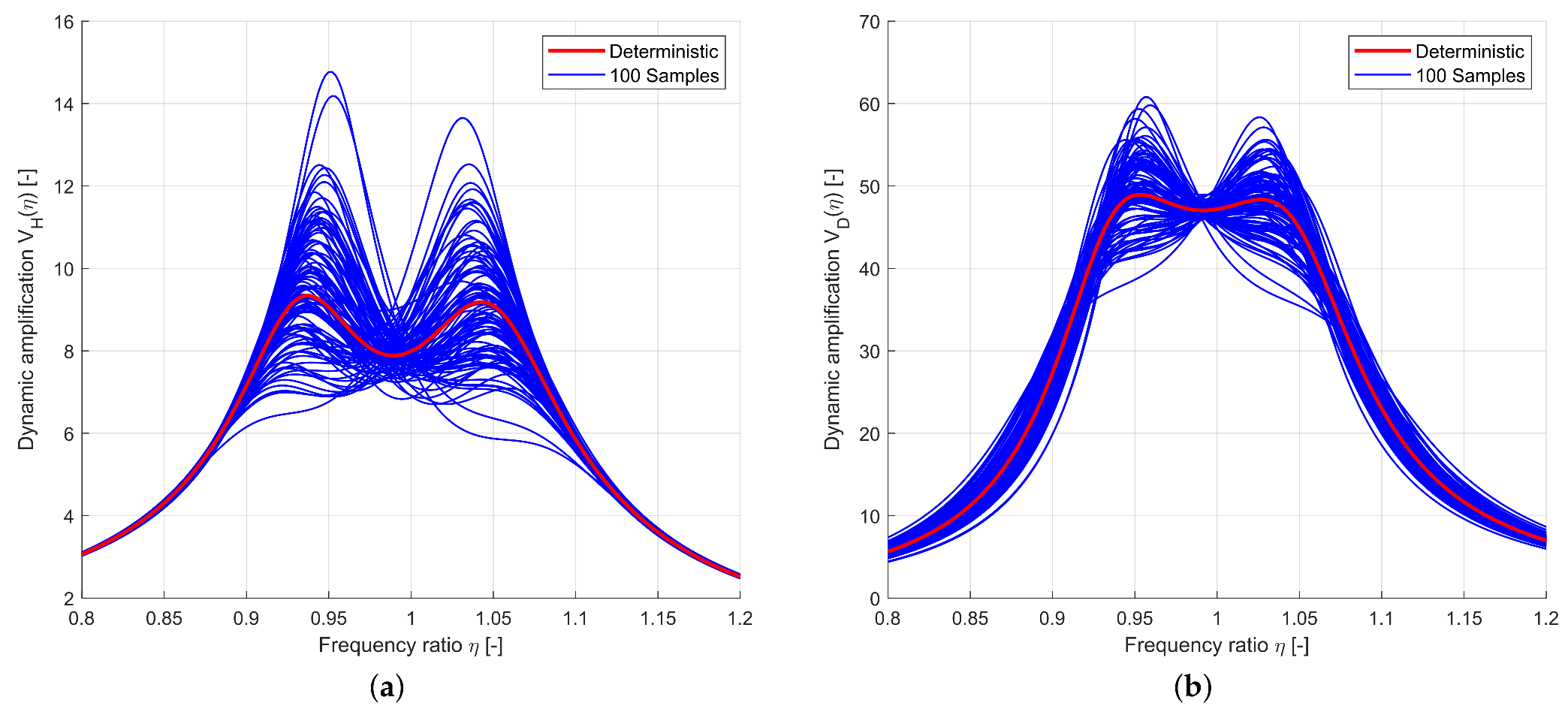
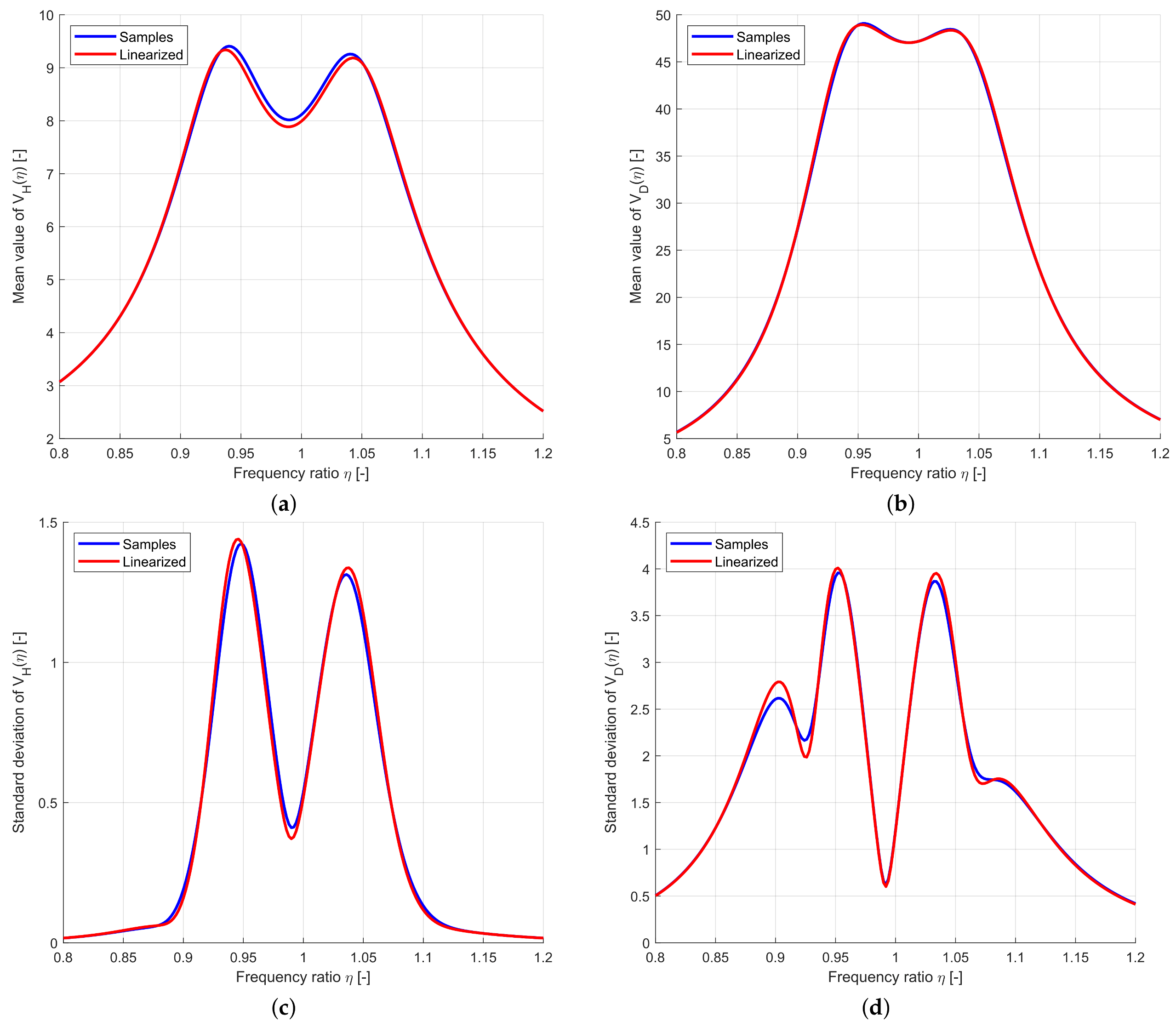
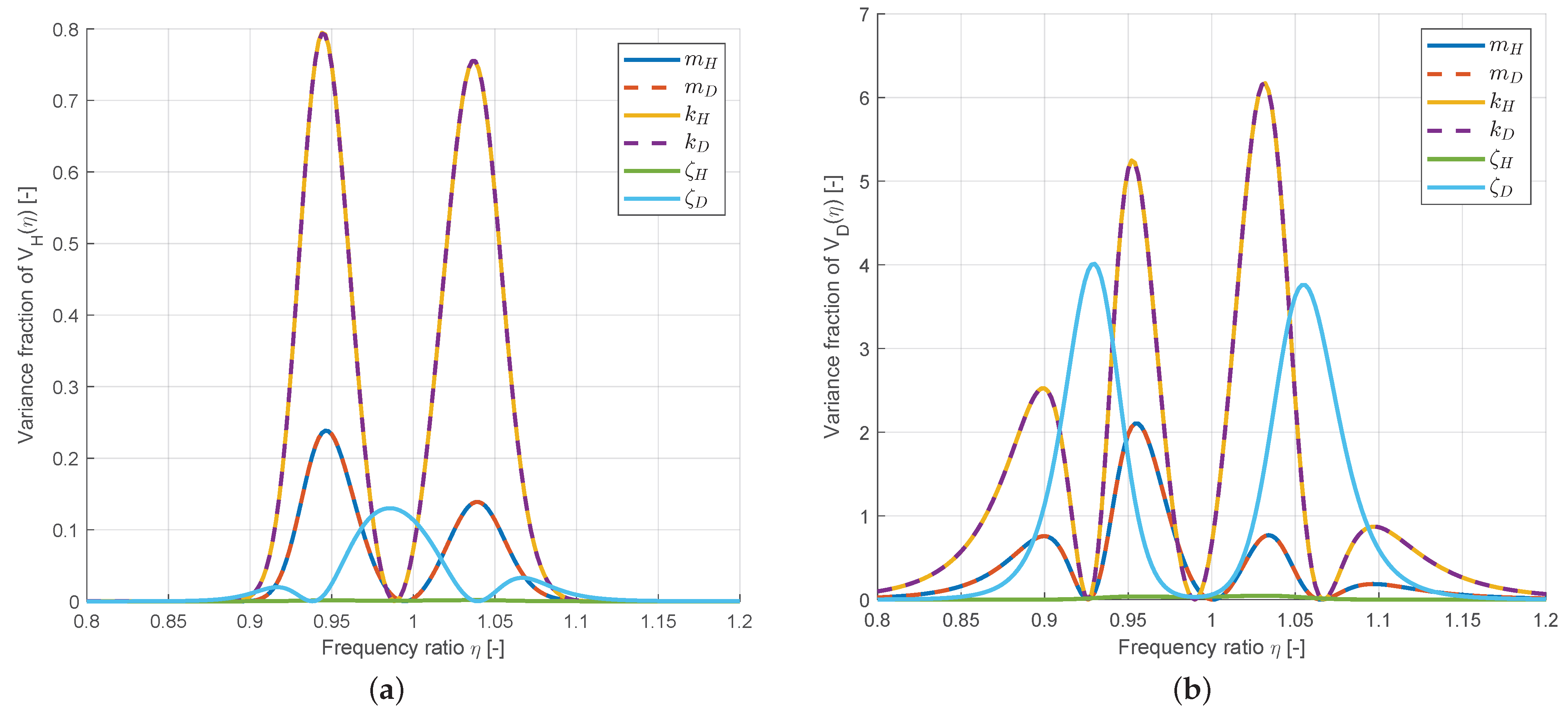
3.1.2. Uncertainty Quantification
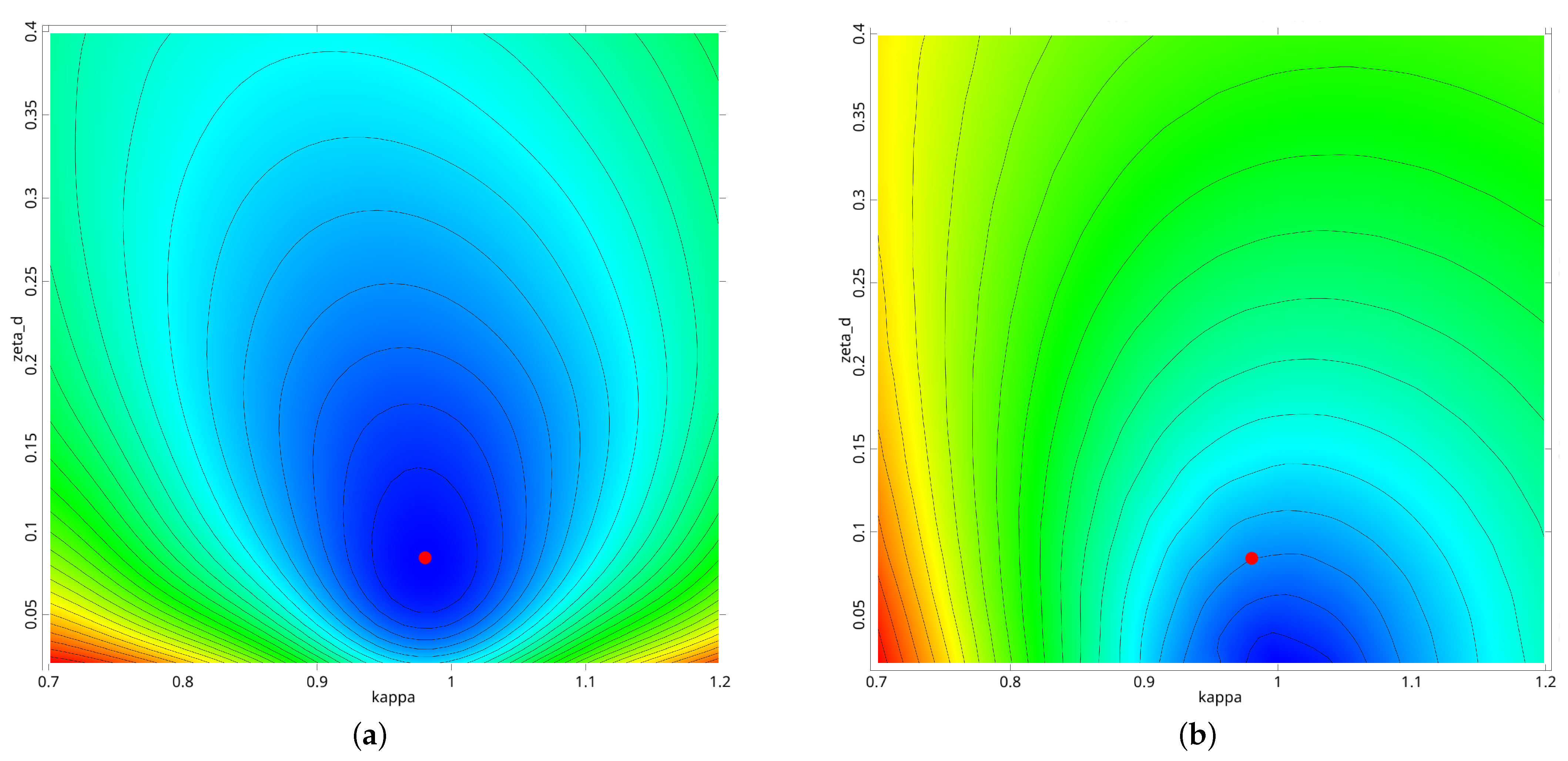
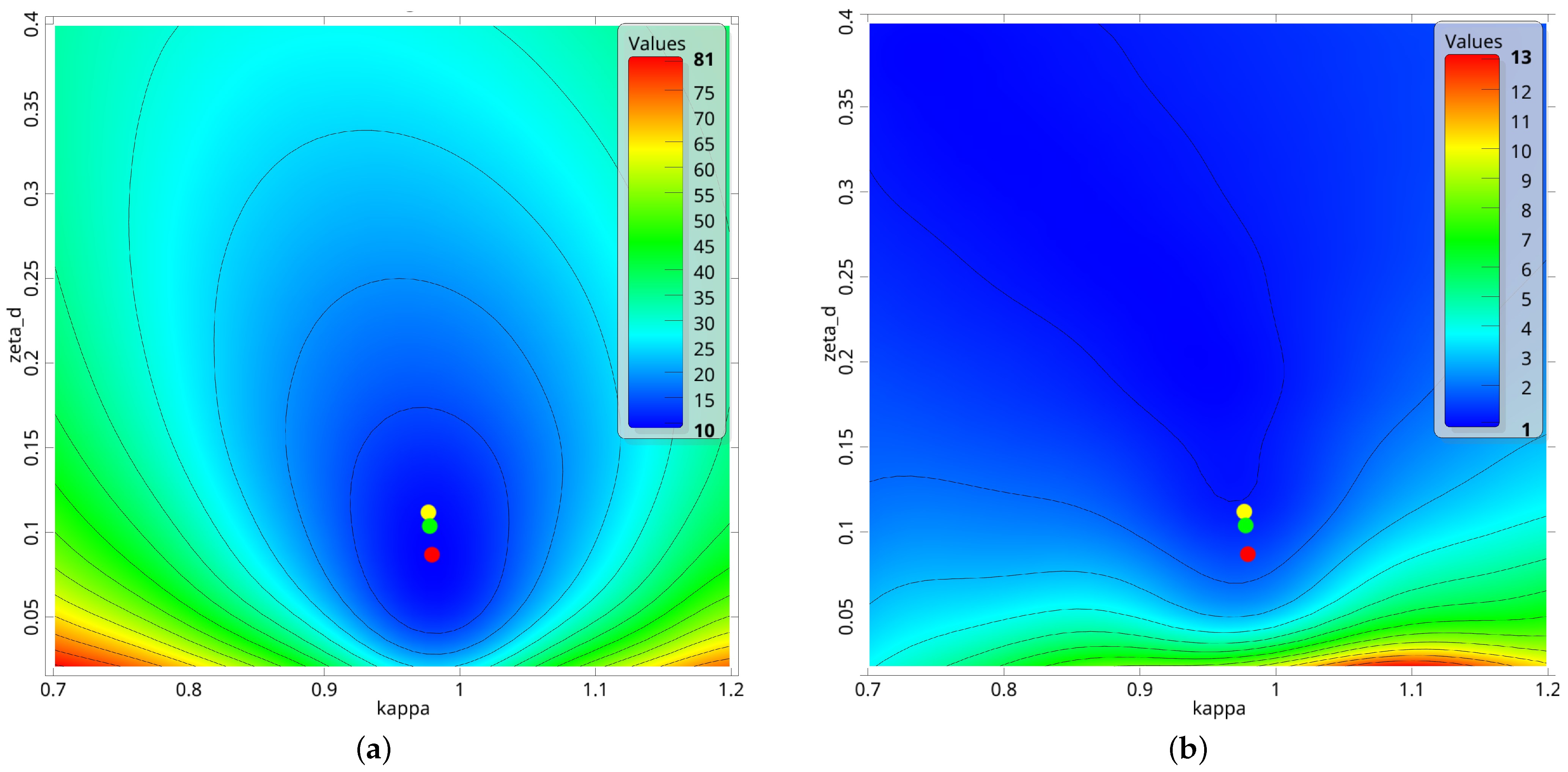
3.1.3. Optimization Under Uncertainty
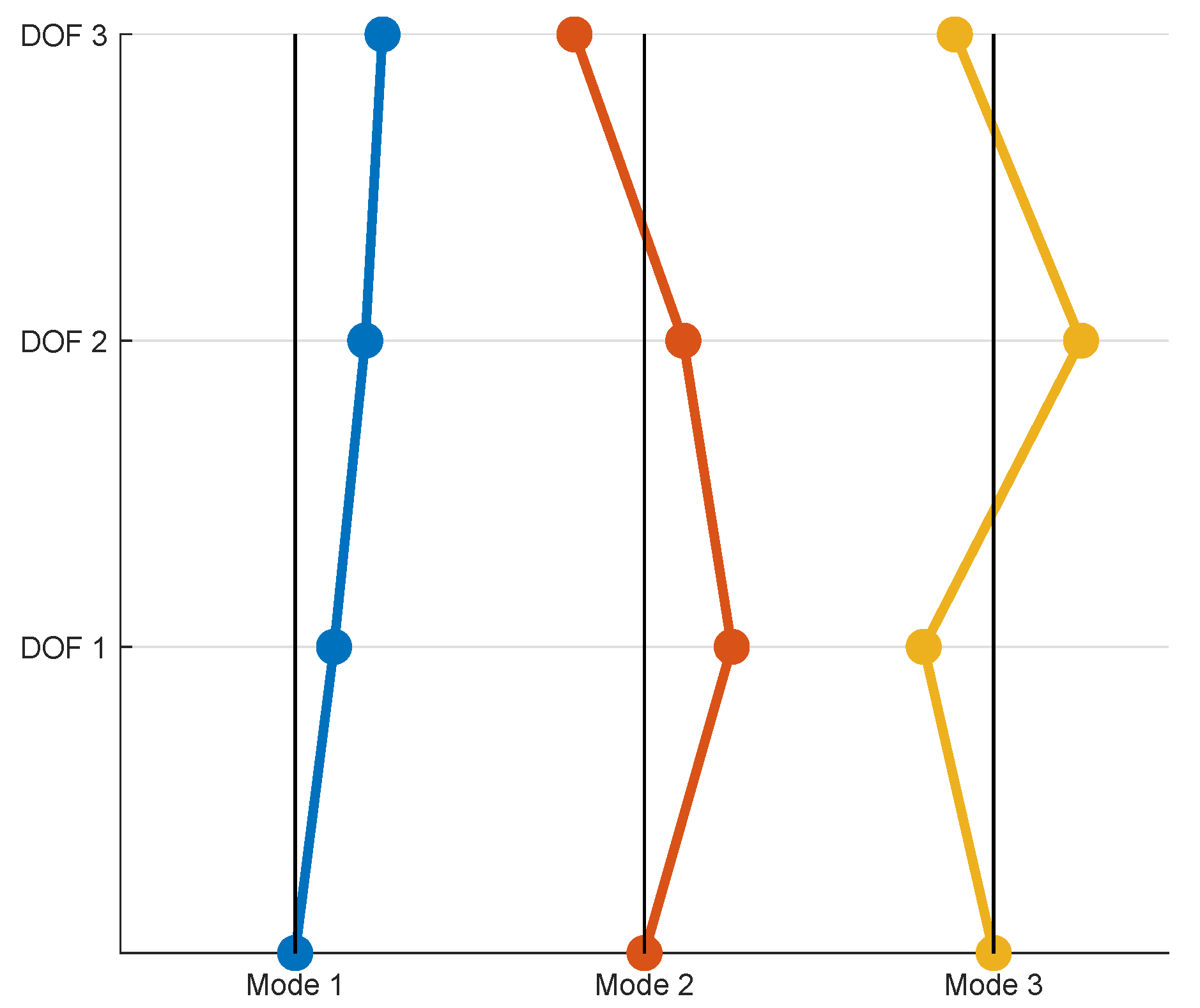
3.2. Multi-Degree-of-Freedom Example with Multiple Tuned Mass Dampers
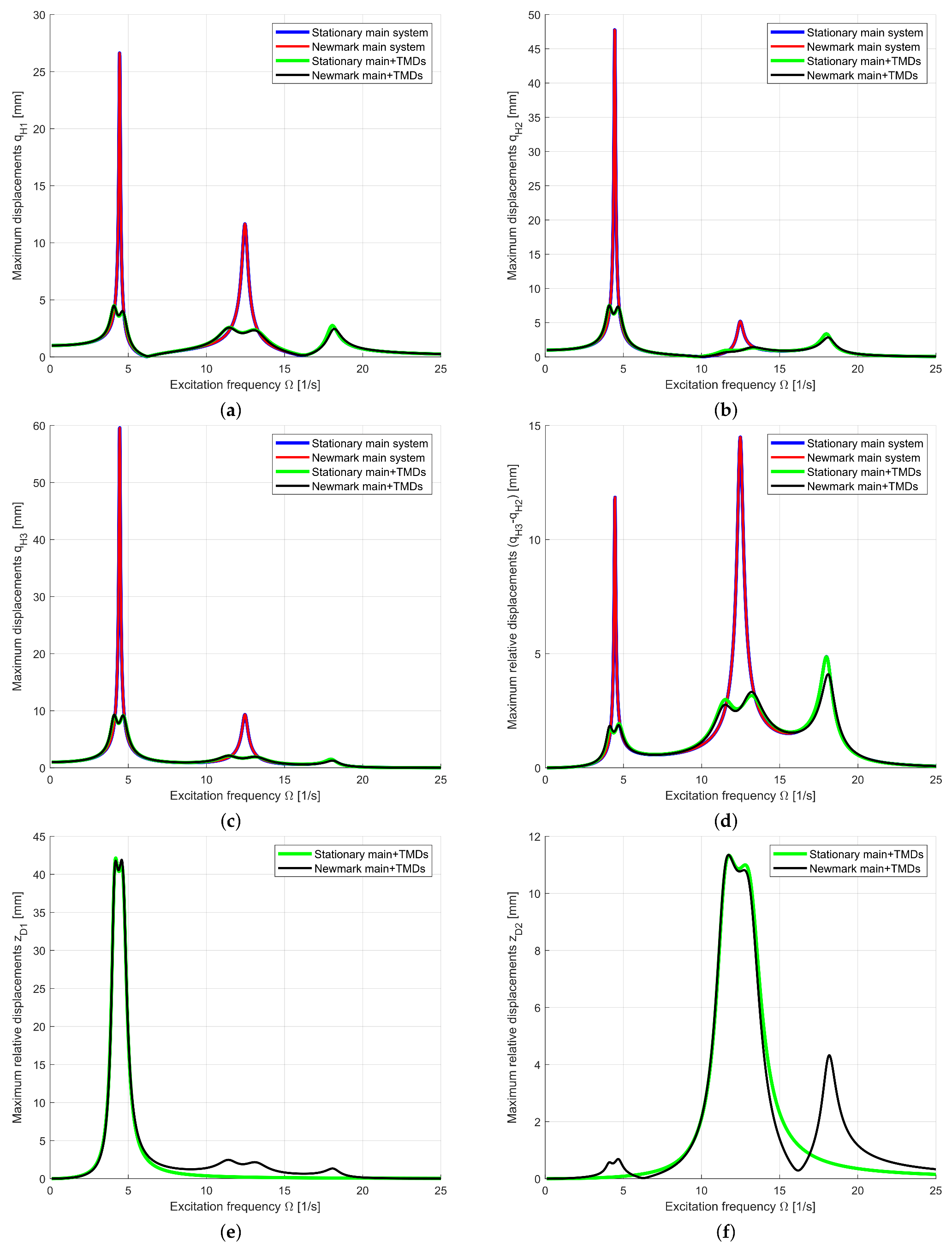
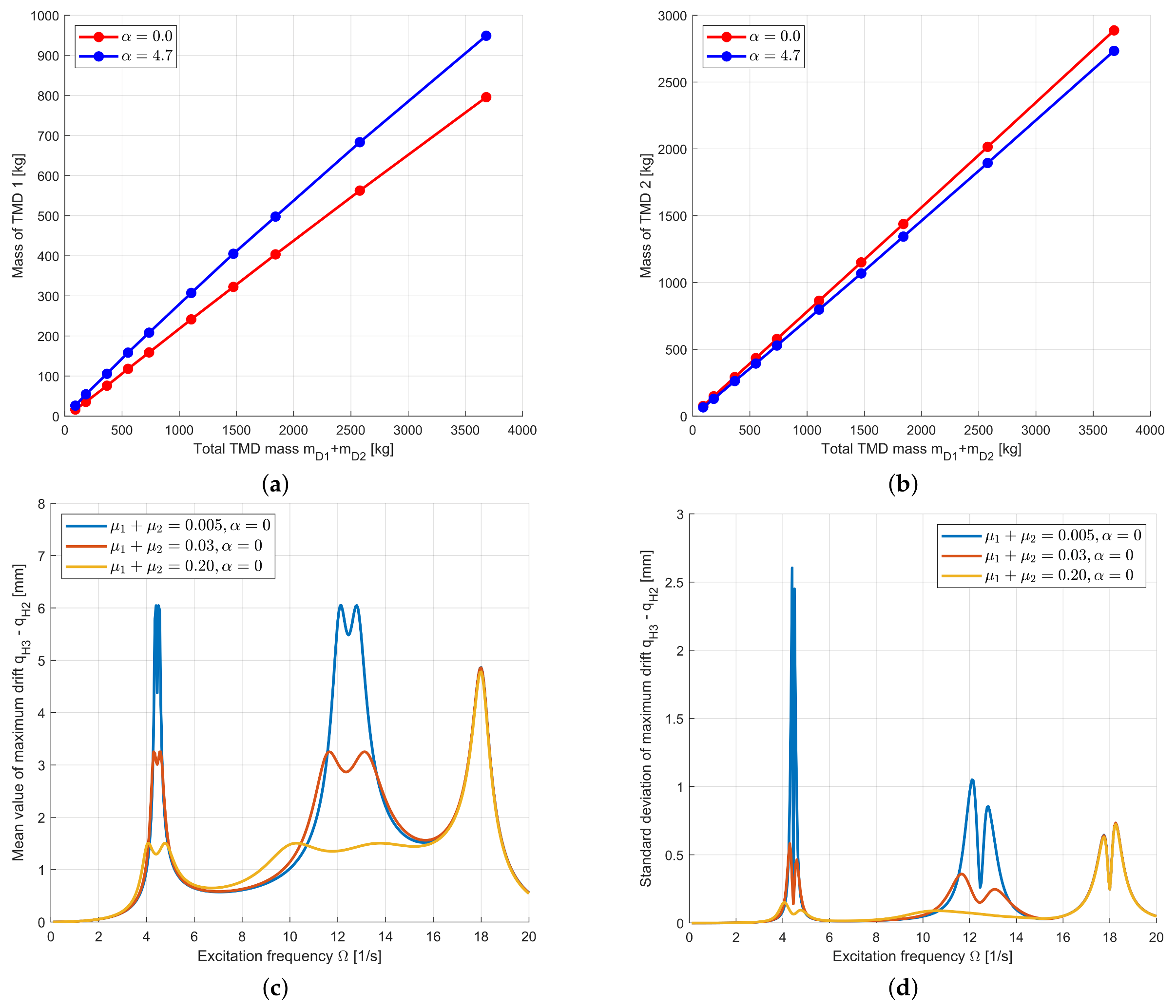
3.2.1. Deterministic Analysis
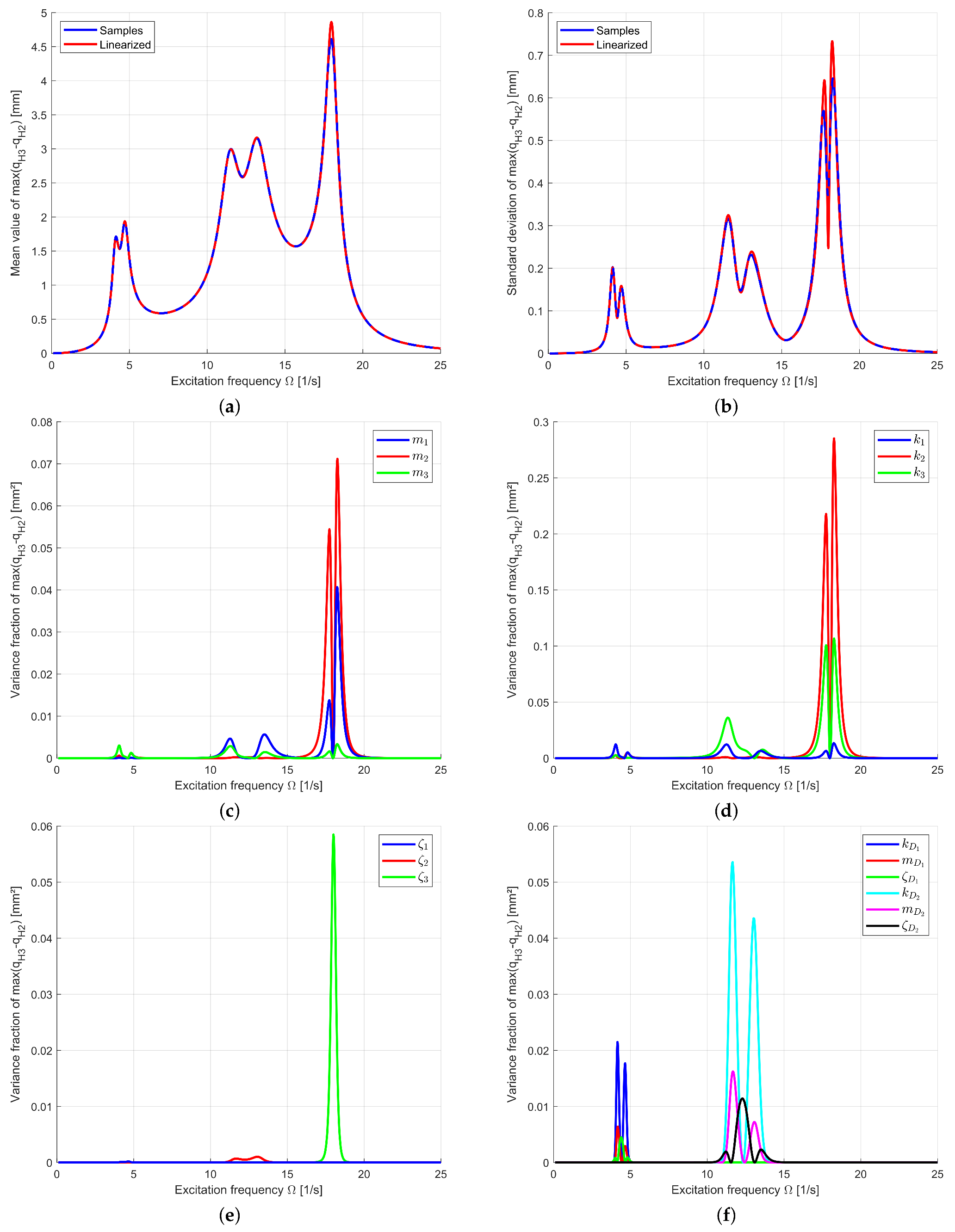
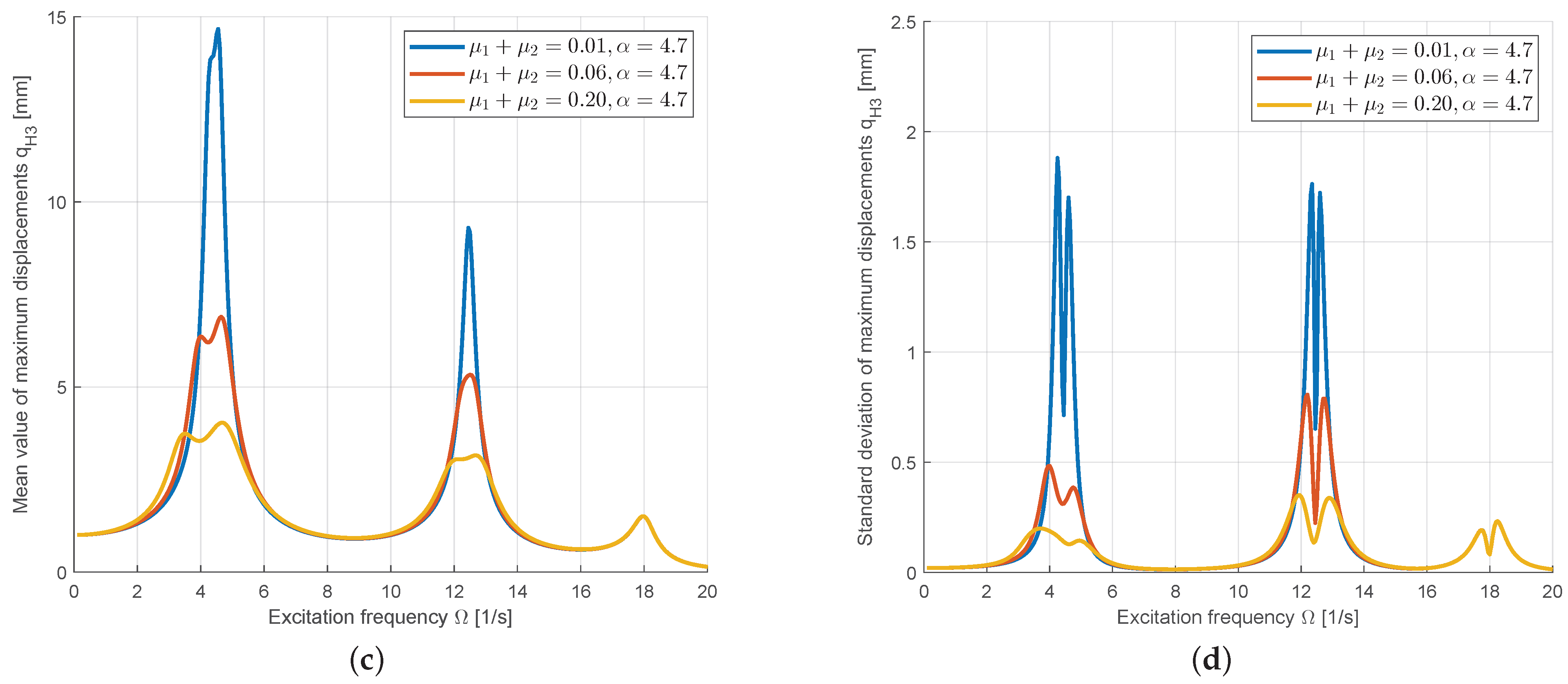
3.2.2. Uncertainty Quantification
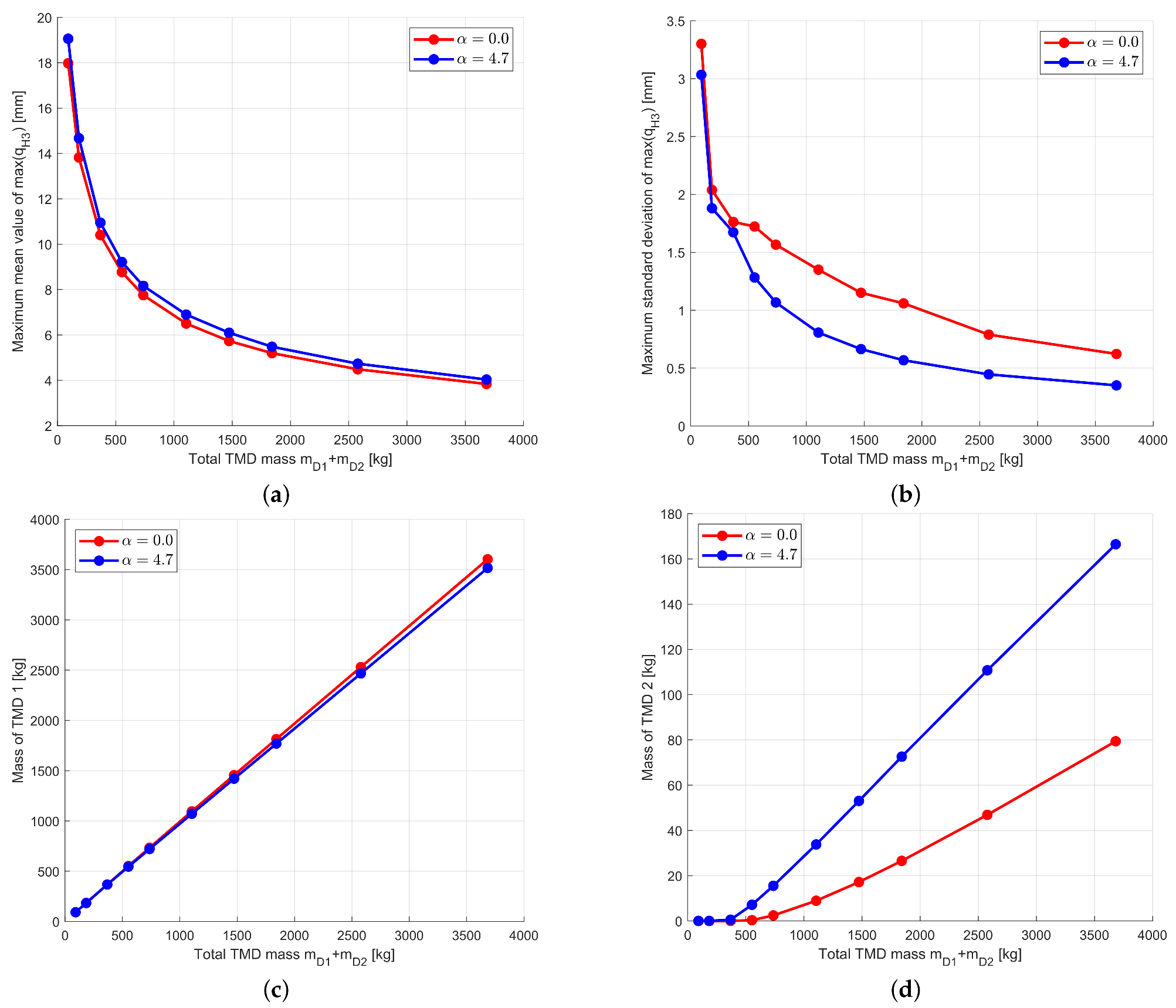
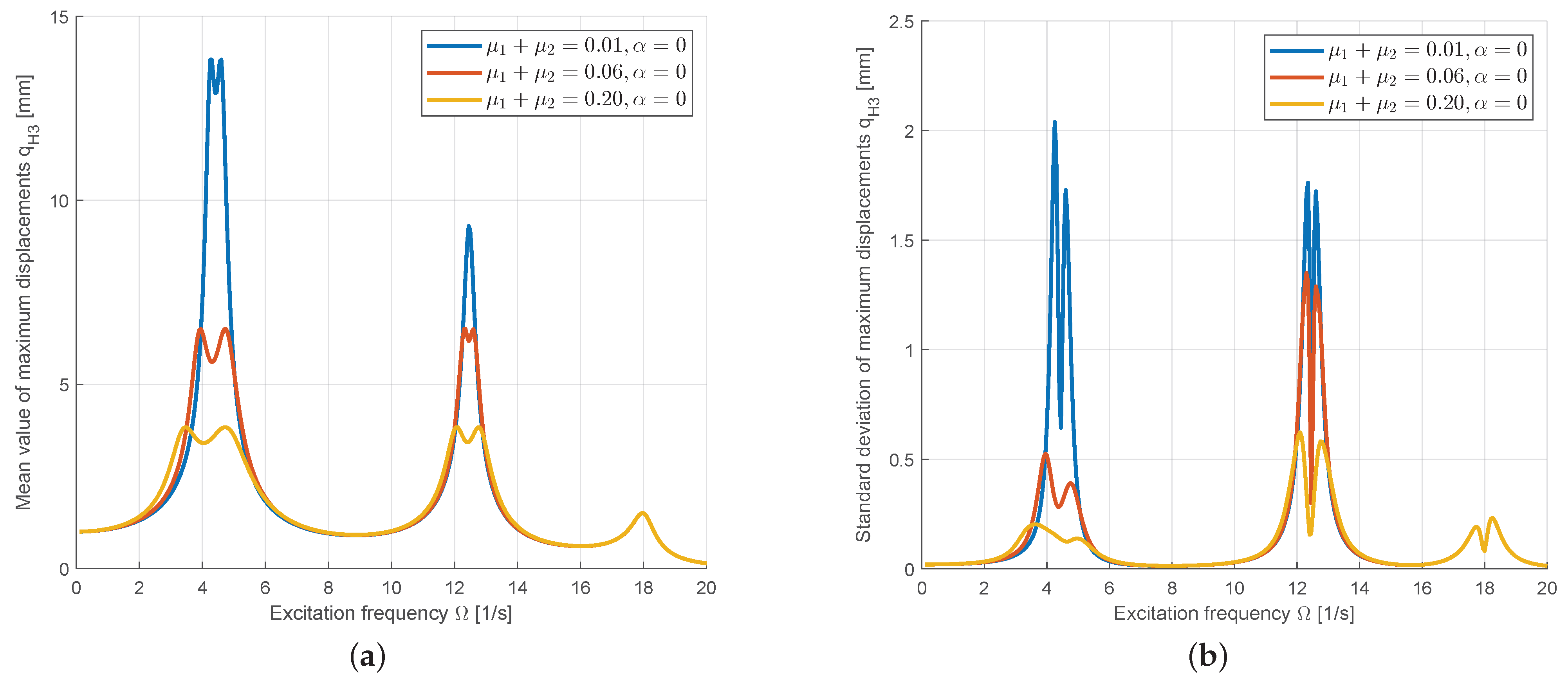
3.2.3. Optimization Under Uncertainty
4. Discussion
4.1. Single-Degree-of-Freedom Systems
4.2. Multi-Degree-of-Freedom Systems
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CoV | Coefficient of Variation |
| DOF | Degree of Freedom |
| LHS | Latin Hypercube Sampling |
| MDOF | Multi-Degree of Freedom |
| NSGA II | Non-dominated Sort Genetic Algorithm |
| RDO | Robust Design Optimization |
| SDOF | Single Degree of Freedom |
| TMD | Tuned Mass Damper |
References
- Ormondroyd, J.; Den Hartog, J. The theory of the dynamic vibration absorber. J. Fluids Eng. 1928, 49, 021007. [Google Scholar] [CrossRef]
- Gutierrez Soto, M.; Adeli, H. Tuned mass dampers. Arch. Comput. Methods Eng. 2013, 20, 419–431. [Google Scholar] [CrossRef]
- Xu, Y.; Kwok, K.; Samali, B. Control of wind-induced tall building vibration by tuned mass dampers. J. Wind. Eng. Ind. Aerodyn. 1992, 40, 1–32. [Google Scholar] [CrossRef]
- Kwok, K.; Samali, B. Performance of tuned mass dampers under wind loads. Eng. Struct. 1995, 17, 655–667. [Google Scholar] [CrossRef]
- Clark, A. Multiple passive tuned mass dampers for reducing earthquake induced building motion. In Proceedings of the 9th World Conference on Earthquake Engineering, Tokyo, Japan, 2–9 August 1988; Volume 5, pp. 779–784. [Google Scholar]
- Sadek, F.; Mohraz, B.; Taylor, A.; Chung, R. A method of estimating the parameters of tuned mass dampers for seismic applications. Earthq. Eng. Struct. Dyn. 1997, 26, 617–635. [Google Scholar] [CrossRef]
- Petersen, C.; Werkle, H. Dynamik der Baukonstruktionen, 2nd ed.; Springer Viehweg: Wiesbaden, Germany, 2017. [Google Scholar]
- Warburton, G.B. Optimum absorber parameters for various combinations of response and excitation parameters. Earthq. Eng. Struct. Dyn. 1982, 10, 381–401. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, S. The optimal design of dynamic absorber in the time domain and the frequency domain. Appl. Acoust. 1989, 28, 67–78. [Google Scholar] [CrossRef]
- Rana, R.; Soong, T. Parametric study and simplified design of tuned mass dampers. Eng. Struct. 1998, 20, 193–204. [Google Scholar] [CrossRef]
- De Fazio, N.; Placidi, L.; Tomassi, A.; Fraddosio, A.; Castellano, A.; Paparella, F. Different mechanical models for the study of ultrasonic wave dispersion for mechanical characterization of construction materials. Int. J. Solids Struct. 2025, 315, 113352. [Google Scholar] [CrossRef]
- Lee, C.L.; Chen, Y.T.; Chung, L.L.; Wang, Y.P. Optimal design theories and applications of tuned mass dampers. Eng. Struct. 2006, 28, 43–53. [Google Scholar] [CrossRef]
- Hadi, M.; Arfiadi, Y. Optimum design of absorber for MDOF structures. J. Struct. Eng. 1998, 124, 1272–1280. [Google Scholar] [CrossRef]
- Hoang, N.; Warnitchai, P. Design of multiple tuned mass dampers by using a numerical optimizer. Earthq. Eng. Struct. Dyn. 2005, 34, 125–144. [Google Scholar] [CrossRef]
- Zuo, L.; Nayfeh, S. Optimization of the individual stiffness and damping parameters in multiple-tuned-mass-damper systems. J. Vib. Acoust. 2005, 127, 77–83. [Google Scholar] [CrossRef]
- Leung, A.; Zhang, H. Particle swarm optimization of tuned mass dampers. Eng. Struct. 2009, 31, 715–728. [Google Scholar] [CrossRef]
- Arfiadi, Y. Optimum placement and properties of tuned mass dampers using hybrid genetic algorithms. Int. J. Optim. Civ. Eng. 2011, 1, 167. [Google Scholar]
- Radmard, R.; Könke, C. Seismic control of tall buildings using distributed multiple tuned mass dampers. Adv. Civ. Eng. 2019, 2019, 6480384. [Google Scholar] [CrossRef]
- Yucel, M.; Bekdaş, G.; Nigdeli, S.; Sevgen, S. Estimation of optimum tuned mass damper parameters via machine learning. J. Build. Eng. 2019, 26, 100847. [Google Scholar] [CrossRef]
- Yucel, M.; Bekdaş, G.; Nigdeli, S. Machine learning-based model for prediction of optimum TMD parameters in time-domain history. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 192. [Google Scholar] [CrossRef]
- Hu, W. Design Optimization Under Uncertainty; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Papadimitriou, C.; Katafygiotis, L.; Au, S.K. Effects of structural uncertainties on TMD design: A reliability-based approach. J. Struct. Control 1997, 4, 65–88. [Google Scholar] [CrossRef]
- Schmelzer, B.; Oberguggenberger, M.; Adam, C. Efficiency of tuned mass dampers with uncertain parameters on the performance of structures under stochastic excitation. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2010, 224, 297–308. [Google Scholar] [CrossRef]
- Moreno, C.; Thomson, P. Design of an optimal tuned mass damper for a system with parametric uncertainty. Ann. Oper. Res. 2010, 181, 783–793. [Google Scholar] [CrossRef]
- Pellizzari, F.; Marano, G.; Palmeri, A.; Greco, R.; Domaneschi, M. Robust optimization of MTMD systems for the control of vibrations. Probabilistic Eng. Mech. 2022, 70, 103347. [Google Scholar] [CrossRef]
- Shamsaddinlou, A.; Shirgir, S.; Hadidi, A.; Azar, B. An efficient reliability-based design of TMD & MTMD in nonlinear structures under uncertainty. Structures 2023, 51, 258–274. [Google Scholar] [CrossRef]
- Li, D.; Tang, H.; Xue, S. Robust design of tuned mass damper with hybrid uncertainty. Struct. Control Health Monit. 2021, 28, e2803. [Google Scholar] [CrossRef]
- Sreeman, D.; Roy, B. Robust design optimization of the friction pendulum system isolated building considering system parameter uncertainties under seismic excitations. J. Build. Eng. 2024, 82, 108320. [Google Scholar] [CrossRef]
- Huntington, D.; Lyrintzis, C. Improvements to and limitations of Latin hypercube sampling. Probabilistic Eng. Mech. 1998, 13, 245–253. [Google Scholar] [CrossRef]
- The MathWorks Inc. MATLAB, version R2024b; MATLAB User Documentation; The MathWorks Inc.: Natick, MA, USA, 2024; Available online: https://www.mathworks.com (accessed on 18 June 2025).
- Luersen, M.A.; Le Riche, R.; Guyon, F. A constrained, globalized, and bounded Nelder–Mead method for engineering optimization. Struct. Multidiscip. Optim. 2004, 27, 43–54. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Ansys Germany GmbH. Ansys optiSLang, version 2025R1; Ansys optiSLang User Documentation; Ansys Germany GmbH: Weimar, Germany, 2025; Available online: https://www.ansys.com/de-de/products/connect/ansys-optislang (accessed on 18 June 2025).
- Eibl, J.; Häussler-Combe, U. Baudynamik. In Betonkalender 1997; Ernst & Sohn: Berlin, Germany, 1997; pp. 755–863. [Google Scholar]
- Haftka, R.; Gürdal, Z. Elements of Structural Optimization; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1992. [Google Scholar]
- Nataf, A. Détermination des distributions de probabilités dont les marges sont données. Comptes Rendus L’academie Des Sci. 1962, 225, 42–43. [Google Scholar]
- Bucher, C. Computational Analysis of Randomness in Structural Mechanics; CRC Press, Taylor & Francis Group: London, UK, 2009. [Google Scholar]
- Rubinstein, R.Y. Simulation and the Monte Carlo Method; John Wiley & Sons: New York, NY, USA, 1981. [Google Scholar]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis. The Primer; John Wiley & Sons, Ltd: Chichester, UK, 2008. [Google Scholar]
- Koch, P.; Yang, R.J.; Gu, L. Design for six sigma through robust optimization. Struct. Multidiscip. Optim. 2004, 26, 235–248. [Google Scholar] [CrossRef]
- Most, T.; Will, J. Robust Design Optimization in industrial virtual product development. In Proceedings of the 5th International Conference on Reliable Engineering Computing (REC), Brno, Czech Republic, 13–15 June 2012; pp. 353–366. [Google Scholar]
- EN 1990:2021-10; Eurocode—Basis of Structural Design, Regulation 305/2011. The European Union: Brussels, Belgium, 2021.
- Chopra, A. Dynamics of Structures, 5th ed.; Pearson Education, Inc.: Uttar Pradesh, India, 2017. [Google Scholar]
- Khadka, A. Optimization of Tuned Mass Dampers in Multi-Degree-of-Freedom Systems. Master’s Thesis, Bauhaus-Universität Weimar, Weimar, Germany, 2025. [Google Scholar]








| Parameter | Unit | Reference | Den Hartog | Single-Objective | Multi-Objective | |
|---|---|---|---|---|---|---|
| Bounds | Optimum | |||||
| kg | ||||||
| kN/m | ||||||
| - | ||||||
| - | - | 0.00–0.20 | ||||
| - | - | 0.70–1.20 | 0.70–1.20 | |||
| - | - | 0.00–0.40 | 0.00–0.40 | |||
| Parameter | Unit | Mean Value | Coefficient of Variation | Distribution Type |
|---|---|---|---|---|
| kg | Normal | |||
| kN/m | Normal | |||
| - | Normal | |||
| kg | Normal | |||
| kN/m | Normal | |||
| - | Normal |
| Parameter | Unit | Mean Value | Coefficient of Variation | Distribution Type |
|---|---|---|---|---|
| ,, | kg | Normal | ||
| ,, | kN/m | Normal | ||
| - | Normal | |||
| - | Normal | |||
| - | Normal | |||
| kg | Normal | |||
| kg | Normal | |||
| kN/m | Normal | |||
| kN/m | Normal | |||
| - | Normal | |||
| - | Normal |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Most, T.; Zabel, V.; Das, R.R.; Khadka, A. An Efficient Uncertainty Quantification Approach for Robust Design of Tuned Mass Dampers in Linear Structural Dynamics. Appl. Sci. 2025, 15, 9329. https://doi.org/10.3390/app15179329
Most T, Zabel V, Das RR, Khadka A. An Efficient Uncertainty Quantification Approach for Robust Design of Tuned Mass Dampers in Linear Structural Dynamics. Applied Sciences. 2025; 15(17):9329. https://doi.org/10.3390/app15179329
Chicago/Turabian StyleMost, Thomas, Volkmar Zabel, Rohan Raj Das, and Abridhi Khadka. 2025. "An Efficient Uncertainty Quantification Approach for Robust Design of Tuned Mass Dampers in Linear Structural Dynamics" Applied Sciences 15, no. 17: 9329. https://doi.org/10.3390/app15179329
APA StyleMost, T., Zabel, V., Das, R. R., & Khadka, A. (2025). An Efficient Uncertainty Quantification Approach for Robust Design of Tuned Mass Dampers in Linear Structural Dynamics. Applied Sciences, 15(17), 9329. https://doi.org/10.3390/app15179329








