A Freight Train Optimized Scheduling Scheme Based on an Improved GJO Algorithm
Abstract
1. Introduction
- (1)
- We develop a freight train operation planning model with multiple objectives: maximizing enterprise operational efficiency, optimizing the number of services, minimizing intermediate stops, and accounting for train operational costs.
- (2)
- We propose a novel Improved Golden Jackal Optimizer-based Genetic Algorithm (IGJOGA) to solve the freight train operation planning model.
- (3)
- We verify the feasibility and effectiveness of the improved strategy through CEC2022 benchmark function tests and operational simulations. The experimental results demonstrate that the proposed algorithm effectively overcomes the limitations of the traditional GA, enabling freight trains to operate with maximum efficiency.
2. Description of the Problem
3. Freight Train Departure Scheme Model
3.1. Basic Assumption
- (1)
- The freight train path is defined as the shortest route from origin (O) to destination (D). We assume that cost parameters, timetable punctuality, and the O–D pairs remain fixed.
- (2)
- Trains carry only general cargo; commodities prohibited on high-speed lines (e.g., hazardous or restricted goods) are excluded.
- (3)
- Freight demands at nodes along the route are known and time-invariant.
- (4)
- Section headways and node handling capacities are computed under nominal conditions, without accounting for dynamic dispatching, maintenance windows, or other operational adjustments.
- (5)
- Trains adopt a passenger-style fixed-consist operating mode with high priority; exact departure/arrival timing is not modeled, and overtakes between passenger and freight trains are not considered.
- (6)
- All nodes traversed by the freight trains are freight-only facilities; passenger services and other functions are not modeled.
3.2. Description of Symbols in the Model
3.2.1. Set Definition
- (1)
- is denoted as the set of stations in the freight train network, .
- (2)
- denotes the originating city of the freight train, .
- (3)
- denotes the arrival city of the freight train, ; , .
- (4)
- denotes the set of segments in the railroad network, .
- (5)
- denotes the set of freight demand between nodes in the railroad network, .
- (6)
- denotes the number of trains a train can run per day, .
3.2.2. Parameter Definition
- (1)
- denotes the freight train running on the section .
- (2)
- denotes the number of cars loaded by freight train k from platform to platform .
- (3)
- denotes the predicted value of the cargo flow of a freight train from platform to platform .
- (4)
- denotes the distance between the freight train at the platform to the platform .
- (5)
- is the average operating revenue per ton-kilometer for freight trains.
- (6)
- is the operating cost of the train per kilometer, including line usage and locomotive traction costs.
- (7)
- is the cost required for technical operations at stations.
- (8)
- denotes the average number of tons loaded in each car of a freight train from platform to platform .
3.2.3. Decision Variables
3.3. Objective Function
3.4. Constraints
- (1)
- Freight demand constraint
- (2)
- Freight train stop constraints
- (3)
- Loading constraint
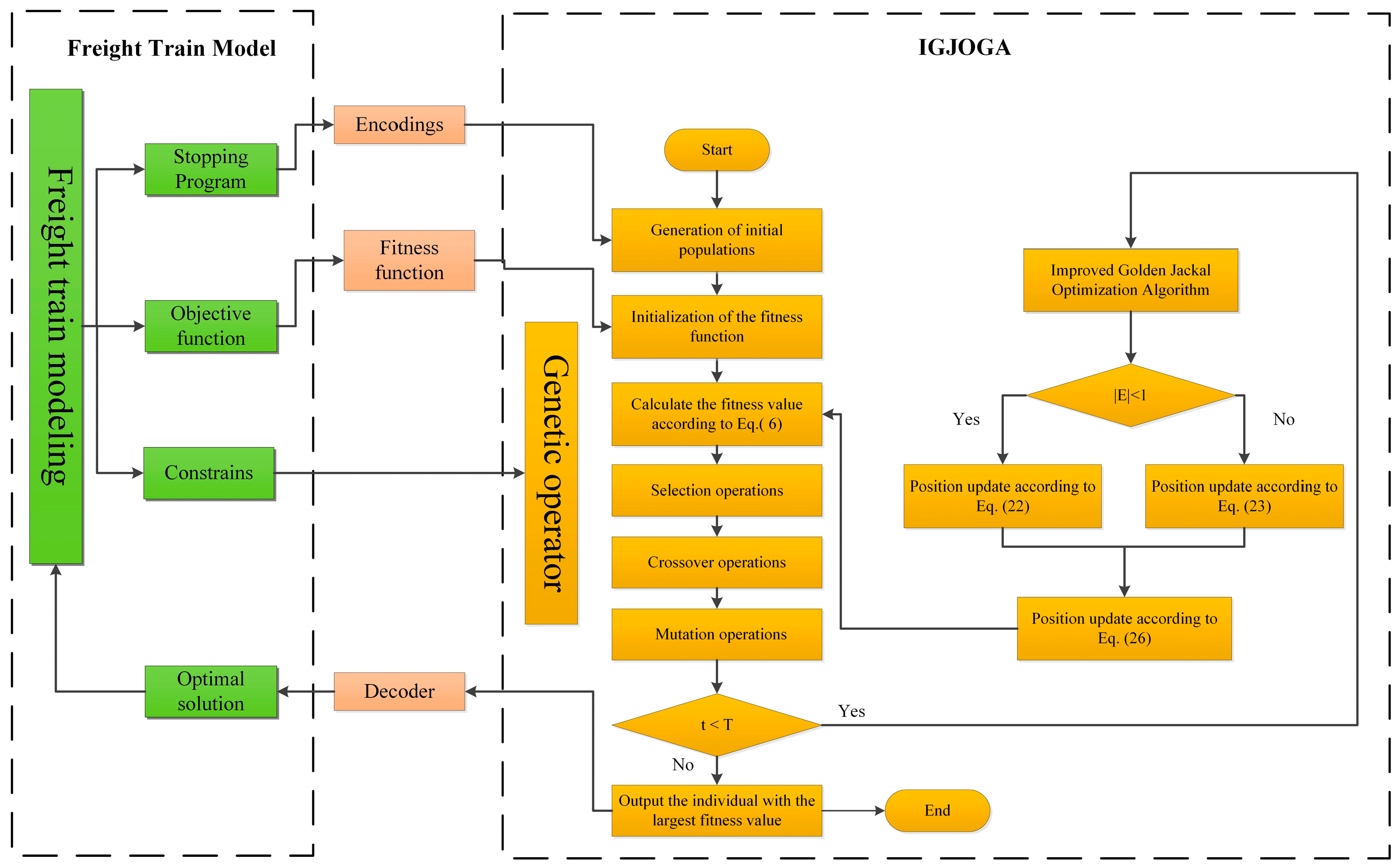
4. Algorithm Design
4.1. Coding Approach
4.2. Fitness Function
4.3. Selection
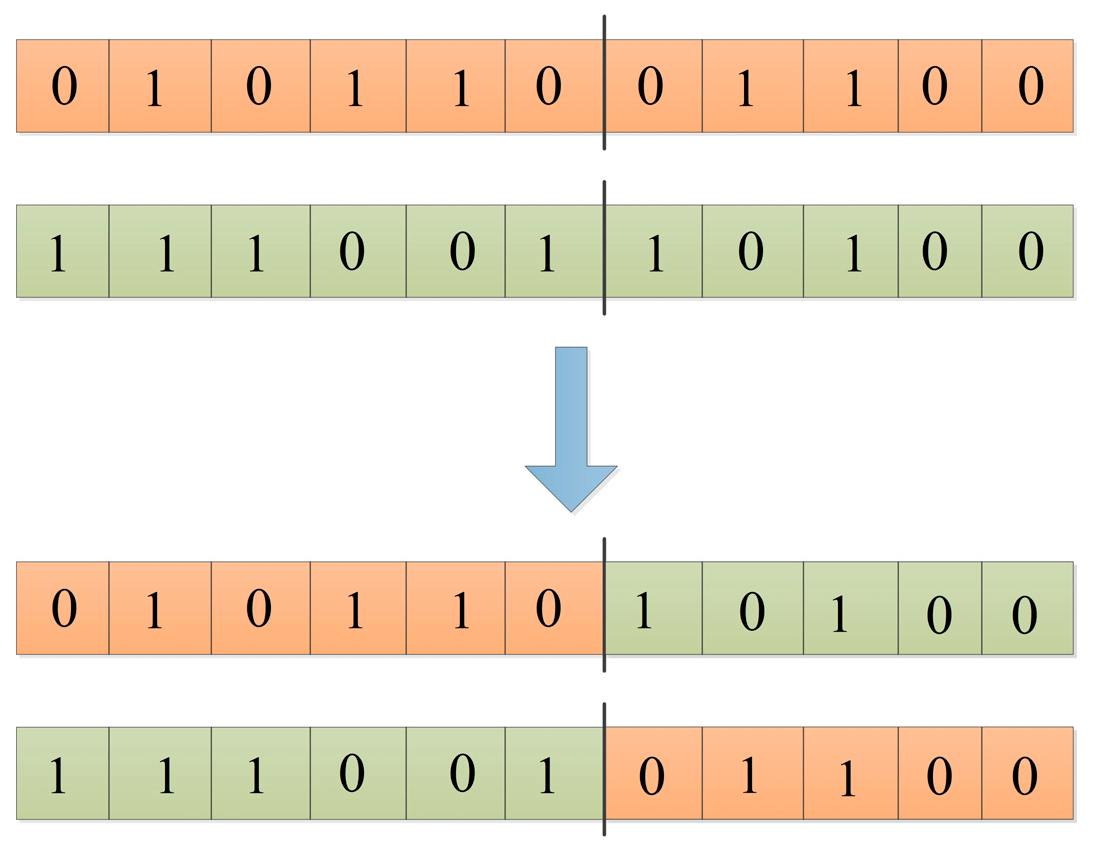
4.4. Cross-Over Operation
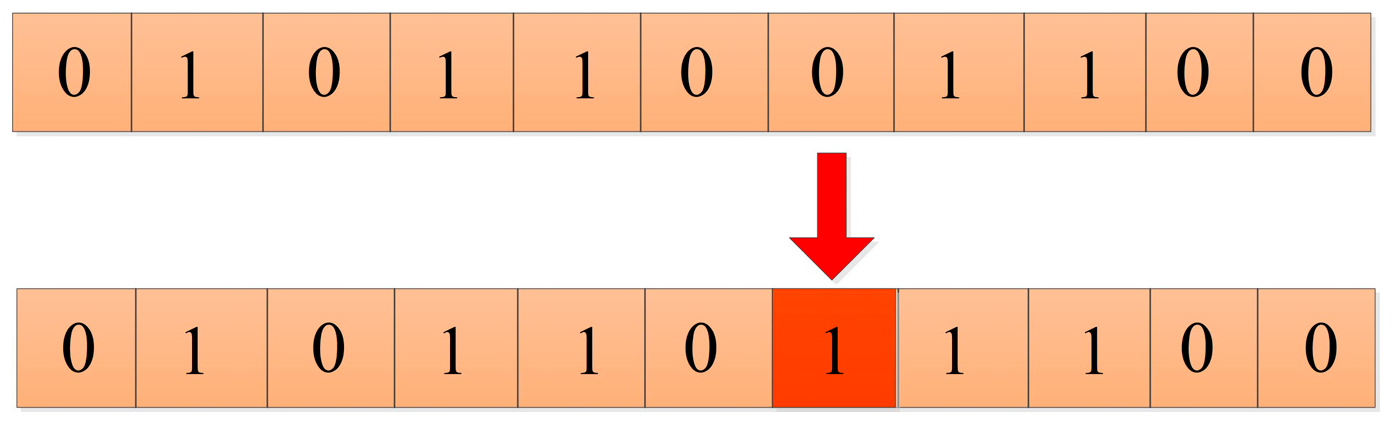
4.5. Mutation Operation
4.6. Improved Golden Jackal Optimizer-Based Genetic Algorithm
4.6.1. Golden Jackal Optimization Algorithm
4.6.2. Improved the Golden Jackal Optimization Algorithm
- (1)
- Adaptive weighting strategy
- (2)
- t-distribution mutation strategy
5. Simulation Experiment and Result Analysis
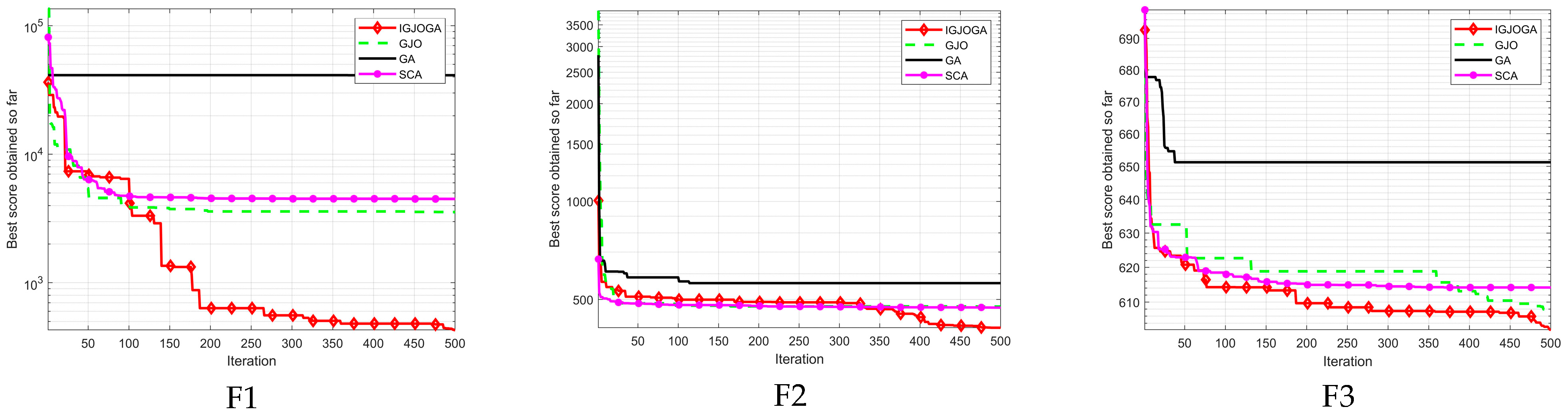
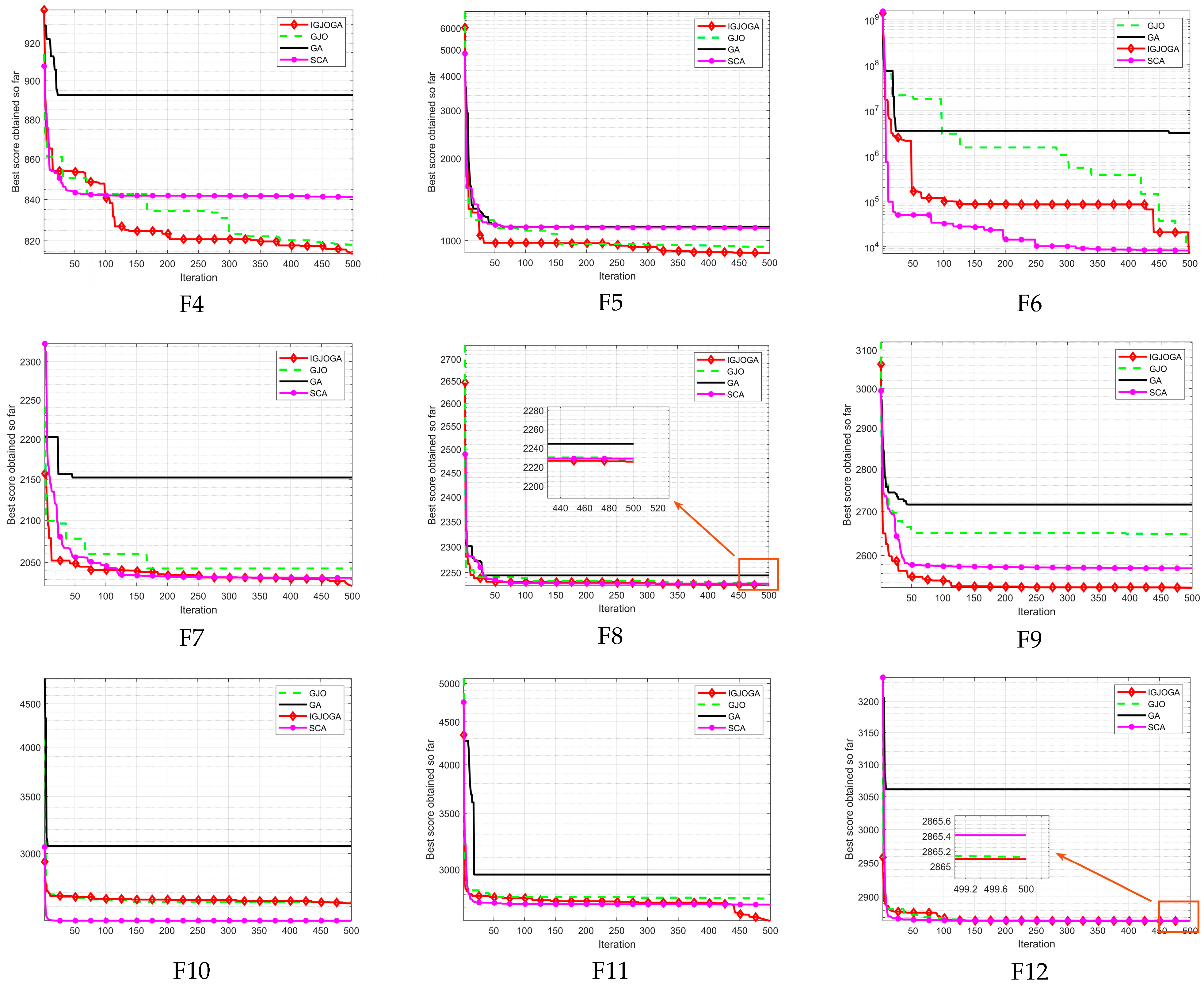
5.1. CEC2022 Test Function
5.2. Wilcoxon Rank Sum Test
5.3. Time Complexity Analysis
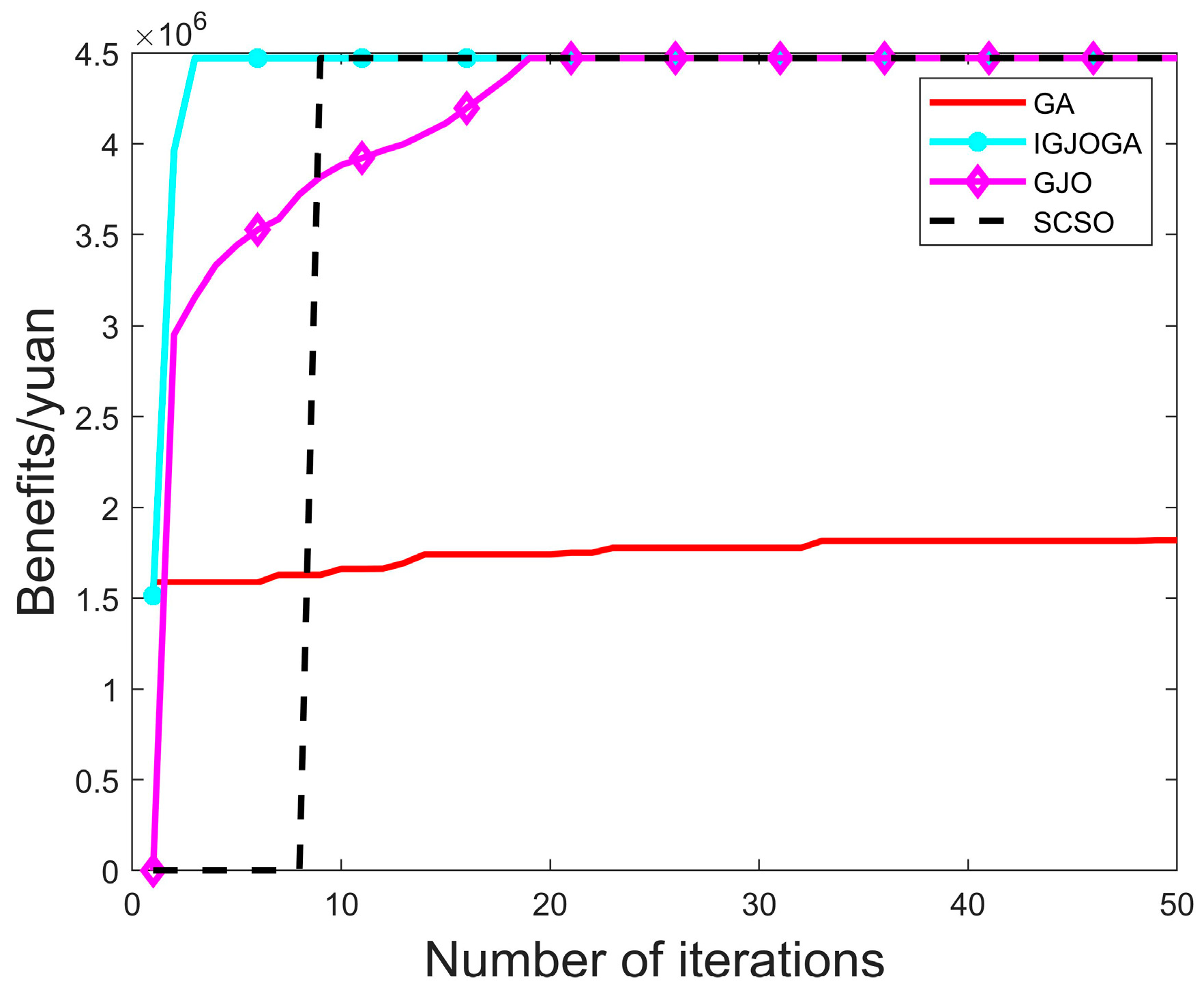
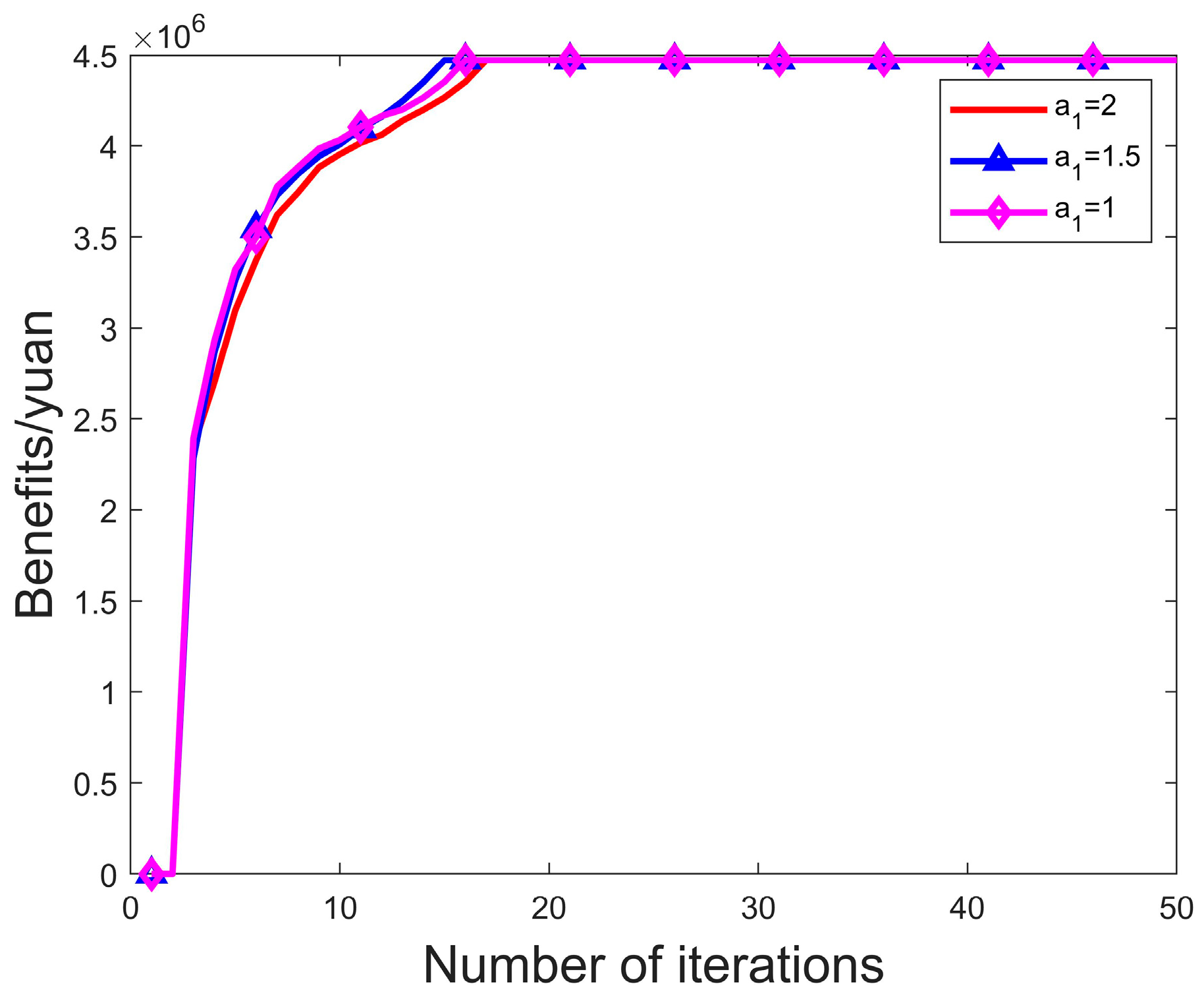
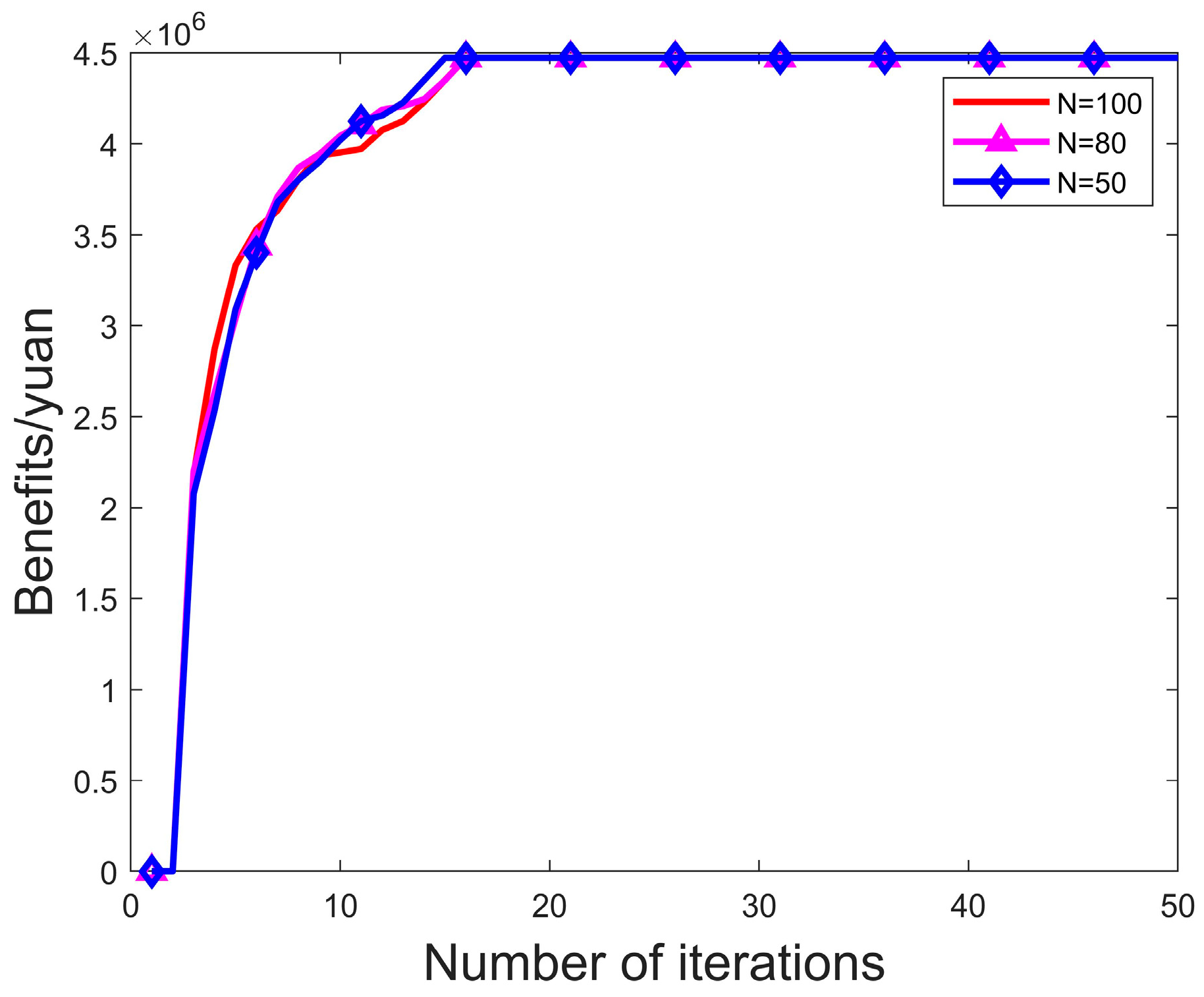
5.4. Example Simulation
6. Conclusions
- (1)
- We formulate a multi-objective freight train operation planning model that maximizes enterprise operational efficiency and the number of runs, minimizes intermediate stops, and explicitly accounts for train operating costs.
- (2)
- To solve the model, we propose an Improved Golden Jackal Optimizer–based Genetic Algorithm (IGJOGA), which effectively addresses the premature convergence and low efficiency of standard GA, thereby improving solution quality and convergence speed for this problem.
- (3)
- We study freight rail segments among five major Chinese cities, compile node-level data, and apply IGJOGA to the proposed model. Experimental results show that the algorithm identifies a maximum freight train benefit of 4,471,294 yuan, and the accommodated train demand increases by 50.27% compared with the GA baseline.
- (4)
- Compared with other state-of-the-art optimization algorithms, the proposed method is better suited to freight train operation planning and solves the model more efficiently.
- (1)
- It is necessary to further analyze the operation organization of freight train services, considering not only individual train conditions but also comprehensive passenger and freight scenarios;
- (2)
- The model assumes a constant operating speed and does not examine train performance under varying speeds or alternative speed profiles;
- (3)
- The study relies solely on numerical simulations and has not yet been validated in real-world operational settings.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| O | D | Number of Train Trips | i-j | Frequency | ||
|---|---|---|---|---|---|---|
| b | a | 1 | 7 | |||
| a | b | 1 | 7 | |||
| c | a | 1 | 7 | |||
| a | c | 1 | 7 | |||
| d | a | 1 | 7 | |||
| a | d | 1 | 7 | |||
| e | a | 1 | 7 | |||
| a | e | 1 | 7 | |||
| b | c | 1 | 7 | |||
| c | b | 1 | 7 | |||
| d | b | 1 | 7 | |||
| b | d | 1 | 7 | |||
| e | b | 1 | 7 | |||
| b | e | 1 | 7 | |||
| d | c | 1 | 7 | |||
| c | d | 1 | 7 | |||
| e | c | 1 | 7 | |||
| c | e | 1 | 7 | |||
| e | d | 1 | 7 | |||
| d | e | 1 | 7 | |||
| c | a | 1 | b | 7 | ||
| a | c | 1 | b | 7 | ||
| d | a | 1 | b | 7 | ||
| a | d | 1 | b | 7 | ||
| e | a | 1 | b | 7 | ||
| a | e | 1 | b | 7 | ||
| d | a | 1 | c | 7 | ||
| a | d | 1 | c | 7 | ||
| e | a | 1 | c | 7 | ||
| a | e | 1 | c | 7 | ||
| e | a | 1 | d | 7 | ||
| a | e | 1 | d | 7 | ||
| d | b | 1 | c | 7 | ||
| b | d | 1 | c | 7 | ||
| e | b | 1 | c | 7 | ||
| b | e | 1 | c | 7 | ||
| e | b | 1 | d | 7 | ||
| b | e | 1 | d | 7 | ||
| e | c | 1 | d | 7 | ||
| c | e | 1 | d | 7 | ||
| d | a | 1 | c | b | 7 | |
| a | d | 1 | b | c | 7 | |
| e | a | 1 | c | b | 7 | |
| a | e | 1 | b | c | 7 | |
| e | a | 1 | d | b | 7 | |
| a | e | 1 | b | d | 7 | |
| e | a | 1 | d | c | 7 | |
| a | e | 1 | c | d | 7 | |
| e | b | 1 | d | c | 7 | |
| b | e | 1 | c | d | 7 | |
| e | a | 1 | d | c | b | 7 |
| a | e | 1 | b | c | d | 7 |
| O | D | Number of Train Trips | i-j | Frequency | ||
|---|---|---|---|---|---|---|
| a | b | 1 | 5 | |||
| c | a | 1 | 6 | |||
| a | c | 1 | 6 | |||
| d | a | 1 | 7 | |||
| a | d | 1 | 6 | |||
| e | a | 1 | 7 | |||
| a | e | 1 | 4 | |||
| b | c | 1 | 1 | |||
| d | b | 1 | 3 | |||
| e | b | 1 | 3 | |||
| b | e | 1 | 1 | |||
| d | c | 1 | 4 | |||
| c | e | 1 | 1 | |||
| c | a | 1 | b | 5 | ||
| d | a | 1 | b | 4 | ||
| a | d | 1 | b | 7 | ||
| e | a | 1 | b | 3 | ||
| a | e | 1 | b | 4 | ||
| d | a | 1 | c | 5 | ||
| a | d | 1 | c | 4 | ||
| e | a | 1 | c | 1 | ||
| a | e | 1 | c | 1 | ||
| e | a | 1 | d | 6 | ||
| a | e | 1 | d | 7 | ||
| b | d | 1 | c | 7 | ||
| e | b | 1 | c | 7 | ||
| b | e | 1 | c | 7 | ||
| e | b | 1 | d | 3 | ||
| b | e | 1 | d | 6 | ||
| e | c | 1 | d | 6 | ||
| a | d | 1 | b | c | 4 | |
| e | a | 1 | c | b | 7 | |
| a | e | 1 | b | c | 7 | |
| e | a | 1 | d | b | 7 | |
| e | a | 1 | d | c | 5 | |
| a | e | 1 | c | d | 7 | |
| b | e | 1 | c | d | 6 | |
| e | a | 1 | d | c | b | 1 |
| Transportation Revenue/Yuan | Direct Cost/Yuan | Indirect Cost/Yuan | Enterprise Efficiency/Yuan |
|---|---|---|---|
| 4,536,894 | 19,600 | 46,000 | 4,471,294 |
References
- Wang, B.; He, S. Resource planning optimization model and algorithm for multi-modal express shipment network. Tiedao Xuebao/J. China Railw. Soc. 2017, 39, 10–16. [Google Scholar]
- Chang, Y.; Lei, S.; Teng, J.; Zhang, J.; Zhang, L.; Xu, X. The energy use and environmental emissions of high-speed rail transportation in China: A bottom-up modeling. Energy 2019, 182, 1193–1201. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, L.; Huo, M.; Yu, X. Research on High-Speed Railway Freight Train Organization Method considering Different Transportation Product Demands. Math. Probl. Eng. 2021, 2021, 5520867. [Google Scholar] [CrossRef]
- Xiao, H.; Huang, S.; Hang, B.; Zhang, Q. Optimization of operation scheme for express freight railway. Kuwait J. Sci. 2021, 48, 50–58. [Google Scholar] [CrossRef]
- Archetti, C.; Peirano, L.; Speranza, M.G. Optimization in multimodal freight transportation problems: A survey. Eur. J. Oper. Res. 2022, 299, 1–20. [Google Scholar] [CrossRef]
- Hosseini, S.; Al Khaled, A. Freight flow optimization to evaluate the criticality of intermodal surface transportation system infrastructures. Comput. Ind. Eng. 2021, 159, 107522. [Google Scholar] [CrossRef]
- Smolyanivov, A.; Yushkova, S.; Sirina, N. Transport infrastructure condition for organizing piggyback traffic. IOP Conf. Ser. Earth Environ. Sci. 2019, 403, 012200. [Google Scholar] [CrossRef]
- Taslimi, B.; Sarijaloo, F.B.; Liu, H.; Pardalos, P.M. A novel mixed integer programming model for freight train travel time estimation. Eur. J. Oper. Res. 2022, 300, 676–688. [Google Scholar] [CrossRef]
- Pineda-Jaramillo, J.; Viti, F. Identifying the rail operating features associated to intermodal freight rail operation delays. Transp. Res. Part C Emerg. Technol. 2023, 147, 103993. [Google Scholar] [CrossRef]
- Li, S.; Lv, H.; Xu, C.; Chen, T.; Zou, C. Optimized train path selection method for daily freight train scheduling. IEEE Access 2020, 8, 40777–40790. [Google Scholar] [CrossRef]
- Wang, Z.; Ceder, A. Efficient design of freight train operation with double-hump yards. J. Oper. Res. Soc. 2017, 68, 1600–1619. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Sohail, A. Genetic algorithms in the fields of artificial intelligence and data sciences. Ann. Data Sci. 2023, 10, 1007–1018. [Google Scholar] [CrossRef]
- Pehlivanoglu, Y.V.; Pehlivanoglu, P. An enhanced genetic algorithm for path planning of autonomous UAV in target coverage problems. Appl. Soft Comput. 2021, 112, 107796. [Google Scholar] [CrossRef]
- Zhu, Z.; Liu, Y.; He, Y.; Wu, W.; Wang, H.; Huang, C.; Ye, B. Fuzzy PID control of the three-degree-of-freedom parallel mechanism based on genetic algorithm. Appl. Sci. 2022, 12, 11128. [Google Scholar] [CrossRef]
- Jia, X.; He, R.; Chai, H. Optimizing the number of express freight trains on a high-speed railway corridor by the departure period. IEEE Access 2020, 8, 100058–100072. [Google Scholar] [CrossRef]
- Li, S.; Lang, M.; Li, S.; Chen, X.; Yu, X.; Geng, Y. Optimization of high-speed railway line planning with passenger and freight transport coordination. IEEE Access 2022, 10, 110217–110247. [Google Scholar] [CrossRef]
- Li, H.; Tian, C.; Zhang, S.; Jiang, Y. Calculation method for carrying capacity of mixed passenger and freight railway based on improved rotor model. China Railw. Sci. 2021, 42, 144–155. [Google Scholar]
- Hu, W.; Dong, J.; Hwang, B.G.; Ren, R.; Chen, Z. Is mass rapid transit applicable for deep integration of freight-passenger transport? A multi-perspective analysis from urban China. Transp. Res. Part A Policy Pract. 2022, 165, 490–510. [Google Scholar] [CrossRef]
- Milenković, M.; Bojović, N.; Abramin, D. Railway freight wagon fleet size optimization: A real-world application. J. Rail Transp. Plan. Manag. 2023, 26, 100373. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Chopra, N.; Ansari, M.M. Golden jackal optimization: A novel nature-inspired optimizer for engineering applications. Expert Syst. Appl. 2022, 198, 116924. [Google Scholar] [CrossRef]
- Lou, T.s.; Yue, Z.P.; Jiao, Y.Z.; He, Z.D. A hybrid strategy-based gjo algorithm for robot path planning. Expert Syst. Appl. 2024, 238, 121975. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2023, 39, 2627–2651. [Google Scholar] [CrossRef]
- Yazdani, D.; Branke, J.; Omidvar, M.N.; Li, X.; Li, C.; Mavrovouniotis, M.; Nguyen, T.T.; Yang, S.; Yao, X. IEEE CEC 2022 competition on dynamic optimization problems generated by generalized moving peaks benchmark. arXiv 2021, arXiv:2106.06174. [Google Scholar]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of non-parametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
| Algorithm | Parameters Value |
|---|---|
| IGJOGA | ω1 = 0.9 ω2 = 0.2 α = 1.5 Mutation probability pm = 0.001 Cross-over probability pc = 0.6 E1 linearly decreases from 1.5 to 0 |
| GJO GA | E1 linearly decreases from 1.5 to 0 |
| Mutation probability pm = 0.001 Cross-over probability pc = 0.6 |
| Name | No. | Function | Fmin |
|---|---|---|---|
| Unimodal Function | F1 | Shifted and full Rotated Zakharov Function | 300 |
| Basic Functions | F2 | Shifted and full Rotated Rosenbrock’s Function | 400 |
| F3 | Shifted and full Rotated Expanded Schaffer’s f6 Function | 600 | |
| F4 | Shifted and full Rotated Non-Continuous Rastrigin’s Function | 800 | |
| F5 | Shifted and full Rotated Lévy Function | 900 | |
| Hybrid Functions | F6 | Hybrid Function 1 (N = 3) | 1800 |
| F7 | Hybrid Function 2 (N = 6) | 2000 | |
| F8 | Hybrid Function 3 (N = 5) | 2200 | |
| Composition Functions | F9 | Composition Function 1 (N = 5) | 2300 |
| F10 | Composition Function 2 (N = 4) | 2400 | |
| F11 | Composition Function 3 (N = 5) | 2600 | |
| F12 | Composition Function 4 (N = 6) | 2700 | |
| Search Range: [−100, 100]Dim |
| Function | Indicators | IGJOGA | GJO | GA | SCSO |
|---|---|---|---|---|---|
| F1 | Best | 3.11 × 102 | 3.99 × 102 | 7.98 × 103 | 3.27 × 102 |
| Mean | 4.60 × 102 | 2.82 × 103 | 3.29 × 104 | 2.00 × 103 | |
| Std | 2.00 × 102 | 2.34 × 103 | 1.38 × 104 | 1.67 × 103 | |
| Worst | 1.46 × 103 | 1.02 × 104 | 6.19 × 104 | 7.42 × 103 | |
| Time | 6.9227 | 0.26377 | 0.21138 | 0.70663 | |
| F2 | Best | 4.00 × 102 | 4.08 × 102 | 4.42 × 102 | 4.00 × 102 |
| Mean | 4.23 × 102 | 4.41 × 102 | 5.07 × 102 | 4.37 × 102 | |
| Std | 2.73 × 101 | 2.88 × 101 | 4.56 × 101 | 2.98 × 101 | |
| Worst | 4.94 × 102 | 5.23 × 102 | 6.56 × 102 | 4.87 × 102 | |
| Time | 8.0709 | 0.29507 | 0.2277 | 0.75643 | |
| F3 | Best | 6.00 × 102 | 6.00 × 102 | 6.26 × 102 | 6.01 × 102 |
| Mean | 6.03 × 102 | 6.07 × 102 | 6.51 × 102 | 6.15 × 102 | |
| Std | 3.10 × 100 | 5.19 × 100 | 1.18 × 101 | 9.15 × 100 | |
| Worst | 6.13 × 102 | 6.18 × 102 | 6.75 × 102 | 6.45 × 102 | |
| Time | 7.4148 | 0.36261 | 0.36567 | 0.80324 | |
| F4 | Best | 8.08 × 102 | 8.08 × 102 | 8.32 × 102 | 8.14 × 102 |
| Mean | 8.19 × 102 | 8.26 × 102 | 8.55 × 102 | 8.30 × 102 | |
| Std | 7.88 × 100 | 1.04 × 101 | 1.18 × 101 | 6.74 × 100 | |
| Worst | 8.38 × 102 | 8.48 × 102 | 8.76 × 102 | 8.44 × 102 | |
| Time | 7.8114 | 0.29037 | 0.23989 | 0.75898 | |
| F5 | Best | 9.00 × 102 | 9.01 × 102 | 9.15 × 102 | 9.04 × 102 |
| Mean | 9.51 × 102 | 9.90 × 102 | 1.03 × 103 | 1.05 × 103 | |
| Std | 7.65 × 101 | 8.09 × 101 | 1.42 × 102 | 1.44 × 102 | |
| Worst | 1.26 × 103 | 1.19 × 103 | 1.47 × 103 | 1.49 × 103 | |
| Time | 7.4665 | 0.3068 | 0.25344 | 0.75544 | |
| F6 | Best | 3.00 × 103 | 3.75 × 103 | 1.91 × 103 | 1.92 × 103 |
| Mean | 8.14 × 103 | 9.56 × 103 | 8.70 × 103 | 3.94 × 103 | |
| Std | 2.51 × 103 | 2.66 × 103 | 2.02 × 104 | 2.04 × 103 | |
| Worst | 1.32 × 104 | 1.82 × 104 | 1.14 × 105 | 8.09 × 103 | |
| Time | 7.3499 | 0.28767 | 0.22811 | 0.74148 | |
| F7 | Best | 2.01 × 103 | 2.02 × 103 | 2.05 × 103 | 2.02 × 103 |
| Mean | 2.03 × 103 | 2.05 × 103 | 2.09 × 103 | 2.05 × 103 | |
| Std | 7.71 × 100 | 2.10 × 101 | 3.52 × 101 | 2.59 × 101 | |
| Worst | 2.04 × 103 | 2.10 × 103 | 2.20 × 103 | 2.12 × 103 | |
| Time | 7.4944 | 0.43297 | 0.32541 | 0.80438 | |
| F8 | Best | 2.20 × 103 | 2.20 × 103 | 2.23 × 103 | 2.22 × 103 |
| Mean | 2.22 × 103 | 2.23 × 103 | 2.26 × 103 | 2.23 × 103 | |
| Std | 5.52 × 100 | 5.55 × 100 | 4.43 × 101 | 4.04 × 100 | |
| Worst | 2.23 × 103 | 2.24 × 103 | 2.37 × 103 | 2.24 × 103 | |
| Time | 7.6649 | 0.3992 | 0.34441 | 0.83762 | |
| F9 | Best | 2.53 × 103 | 2.53 × 103 | 2.63 × 103 | 2.53 × 103 |
| Mean | 2.54 × 103 | 2.58 × 103 | 2.70 × 103 | 2.57 × 103 | |
| Std | 1.98 × 101 | 3.97 × 101 | 4.82 × 101 | 3.78 × 101 | |
| Worst | 2.59 × 103 | 2.68 × 103 | 2.81 × 103 | 2.68 × 103 | |
| Time | 7.6124 | 0.36173 | 0.30012 | 0.82552 | |
| F10 | Best | 2.50 × 103 | 2.50 × 103 | 2.50 × 103 | 2.50 × 103 |
| Mean | 2.56 × 103 | 2.56 × 103 | 2.64 × 103 | 2.54 × 103 | |
| Std | 5.87 × 101 | 6.23 × 101 | 2.80 × 102 | 5.98 × 101 | |
| Worst | 2.63 × 103 | 2.64 × 103 | 4.07 × 103 | 2.65 × 103 | |
| Time | 7.4346 | 0.33992 | 0.28829 | 0.79674 | |
| F11 | Best | 2.60 × 103 | 2.61 × 103 | 2.77 × 103 | 2.60 × 103 |
| Mean | 2.75 × 103 | 2.87 × 103 | 3.14 × 103 | 2.78 × 103 | |
| Std | 2.11 × 102 | 2.04 × 102 | 3.34 × 102 | 1.80 × 102 | |
| Worst | 3.23 × 103 | 3.25 × 103 | 3.96 × 103 | 3.24 × 103 | |
| Time | 7.5589 | 0.38665 | 0.3308 | 0.83284 | |
| F12 | Best | 2.86 × 103 | 2.86 × 103 | 2.92 × 103 | 2.86 × 103 |
| Mean | 2.86 × 103 | 2.87 × 103 | 3.01 × 103 | 2.87 × 103 | |
| Std | 2.58 × 100 | 1.50 × 101 | 4.25 × 101 | 1.56 × 101 | |
| Worst | 2.87 × 103 | 2.93 × 103 | 3.09 × 103 | 2.95 × 103 | |
| Time | 8.257 | 0.39103 | 0.3312 | 0.84761 |
| Function | Dim | IGJOGA vs. GJO | IGJOGA vs. GA | IGJOGA vs. SCSO |
|---|---|---|---|---|
| F1 | 10 | 7.39 × 10−11 | 3.02 × 10−11 | 7.60 × 10−7 |
| F2 | 10 | 3.34 × 10−3 | 5.53 × 10−8 | 9.07 × 10−3 |
| F3 | 10 | 2.88 × 10−6 | 3.02 × 10−11 | 1.01 × 10−8 |
| F4 | 10 | 9.07 × 10−3 | 4.50 × 10−11 | 2.77 × 10−5 |
| F5 | 10 | 9.88 × 10−3 | 1.37 × 10−3 | 2.39 × 10−8 |
| F6 | 10 | 1.49 × 10−4 | 3.77 × 10−4 | 2.03 × 10−7 |
| F7 | 10 | 1.03 × 10−6 | 3.02 × 10−11 | 2.77 × 10−5 |
| F8 | 10 | 3.37 × 10−5 | 4.08 × 10−11 | 5.56 × 10−4 |
| F9 | 10 | 3.47 × 10−10 | 3.02 × 10−11 | 9.88 × 10−3 |
| F10 | 10 | 5.83 × 10−3 | 6.53 × 10−8 | 7.96 × 10−1 |
| F11 | 10 | 1.64 × 10−5 | 1.07 × 10−9 | 1.54 × 10−1 |
| F12 | 10 | 1.60 × 10−3 | 3.02 × 10−11 | 3.64 × 10−2 |
| Place Name | Chengdu | Guiyang | Chongqing | Xi’an | Kunming |
|---|---|---|---|---|---|
| symbol | a | b | c | d | e |
| Upward Direction | Downward Directions | |||
|---|---|---|---|---|
| NO. | O | D | O | D |
| 1 | a | b | b | a |
| 2 | a | c | c | a |
| 3 | a | d | d | a |
| 4 | a | e | e | a |
| 5 | b | c | c | b |
| 6 | b | d | d | b |
| 7 | b | e | e | b |
| 8 | c | d | d | c |
| 9 | c | e | e | c |
| 10 | d | e | e | d |
| Midway Station 1 | Midway Station 2 | Midway Station 3 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 1 | 1 | 1 |
| O | a | b | c | d | e | |
| D | ||||||
| a | 0 | 157 | 533 | 688 | 996 | |
| b | 157 | 0 | 376 | 531 | 839 | |
| c | 533 | 376 | 0 | 155 | 463 | |
| d | 688 | 531 | 155 | 0 | 308 | |
| e | 996 | 839 | 463 | 308 | 0 | |
| O | a | b | c | d | e | |
| D | ||||||
| a | 0 | 59.14259 | 106.1204 | 85.54695 | 80.18532 | |
| b | 142.2271 | 0 | 85.63306 | 69.03144 | 64.70492 | |
| c | 133.4563 | 44.78157 | 0 | 64.77442 | 60.7147 | |
| d | 196.5877 | 65.9655 | 118.3629 | 0 | 89.4358 | |
| e | 188.3437 | 63.19919 | 113.3993 | 91.41463 | 0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Y.; Yue, Z.; Jing, Y.; Zhang, J. A Freight Train Optimized Scheduling Scheme Based on an Improved GJO Algorithm. Appl. Sci. 2025, 15, 9326. https://doi.org/10.3390/app15179326
Yao Y, Yue Z, Jing Y, Zhang J. A Freight Train Optimized Scheduling Scheme Based on an Improved GJO Algorithm. Applied Sciences. 2025; 15(17):9326. https://doi.org/10.3390/app15179326
Chicago/Turabian StyleYao, Yufeng, Zhepeng Yue, Yun Jing, and Jinchuan Zhang. 2025. "A Freight Train Optimized Scheduling Scheme Based on an Improved GJO Algorithm" Applied Sciences 15, no. 17: 9326. https://doi.org/10.3390/app15179326
APA StyleYao, Y., Yue, Z., Jing, Y., & Zhang, J. (2025). A Freight Train Optimized Scheduling Scheme Based on an Improved GJO Algorithm. Applied Sciences, 15(17), 9326. https://doi.org/10.3390/app15179326




