CFRCTop: An Efficient MATLAB Implementation for Topology Optimization of Continuous Fiber-Reinforced Composite Structures
Abstract
1. Introduction
2. Theory Fundamentals for Topology Optimization of Continuous Fiber-Reinforced Composite Structures
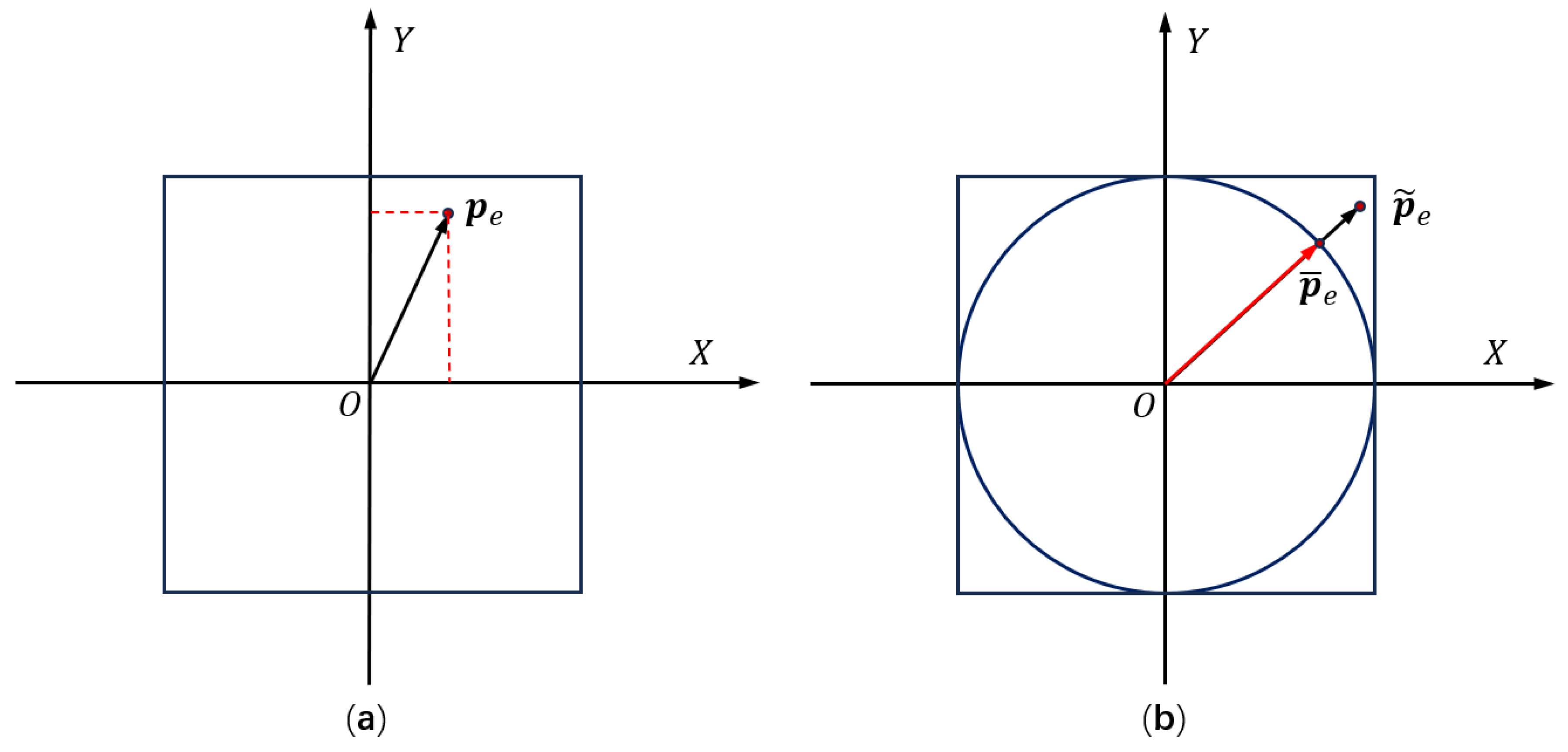
2.1. Design Variables
2.2. Material Interpolation Scheme
2.3. Minimum Compliance Design Problem Formulation
2.4. Efficient Solution Method
2.4.1. Finite Element Analysis
2.4.2. Sensitivity Analysis
2.4.3. Design Variable Update
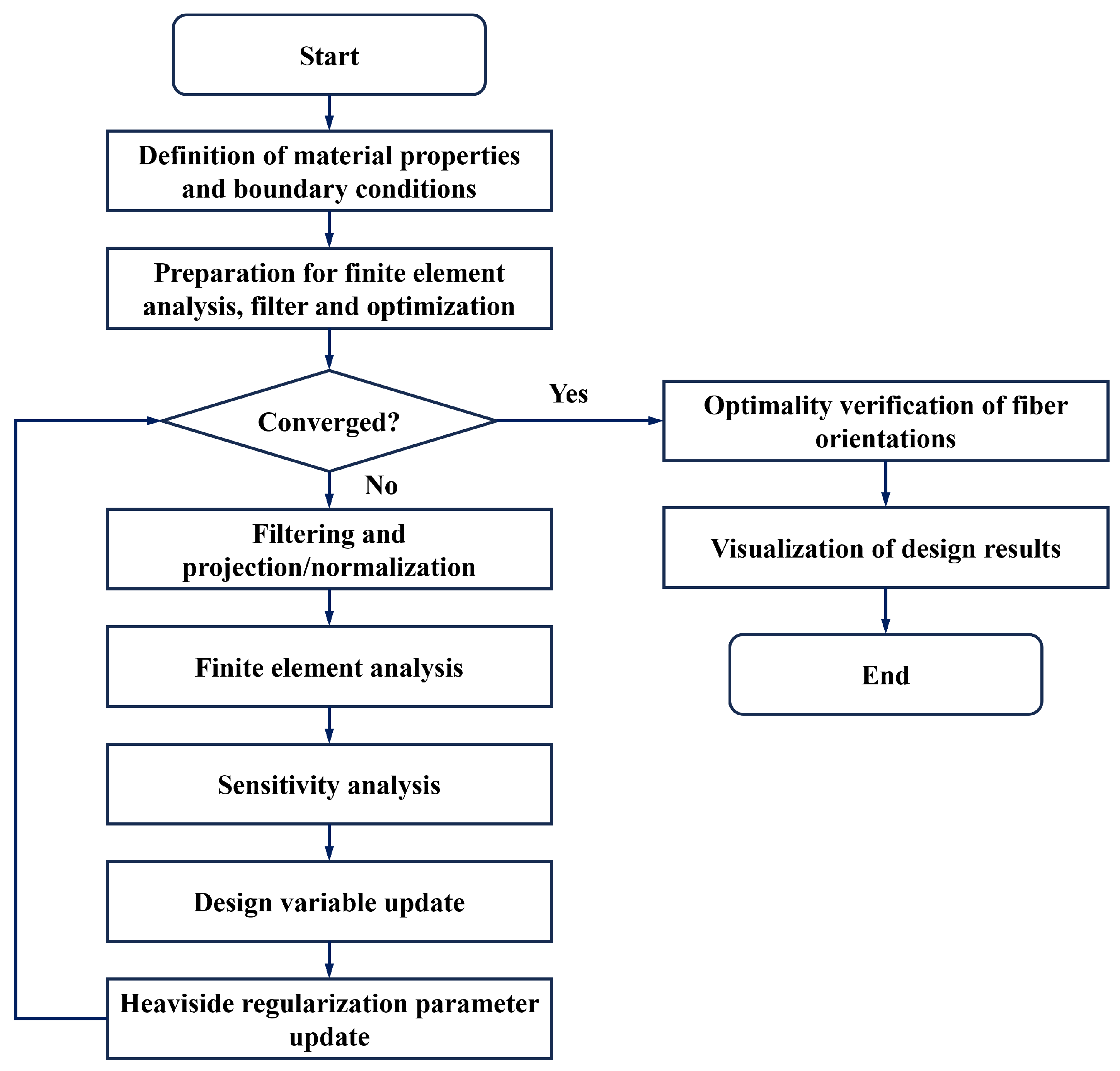
3. MATLAB Implementation
3.1. Architecture
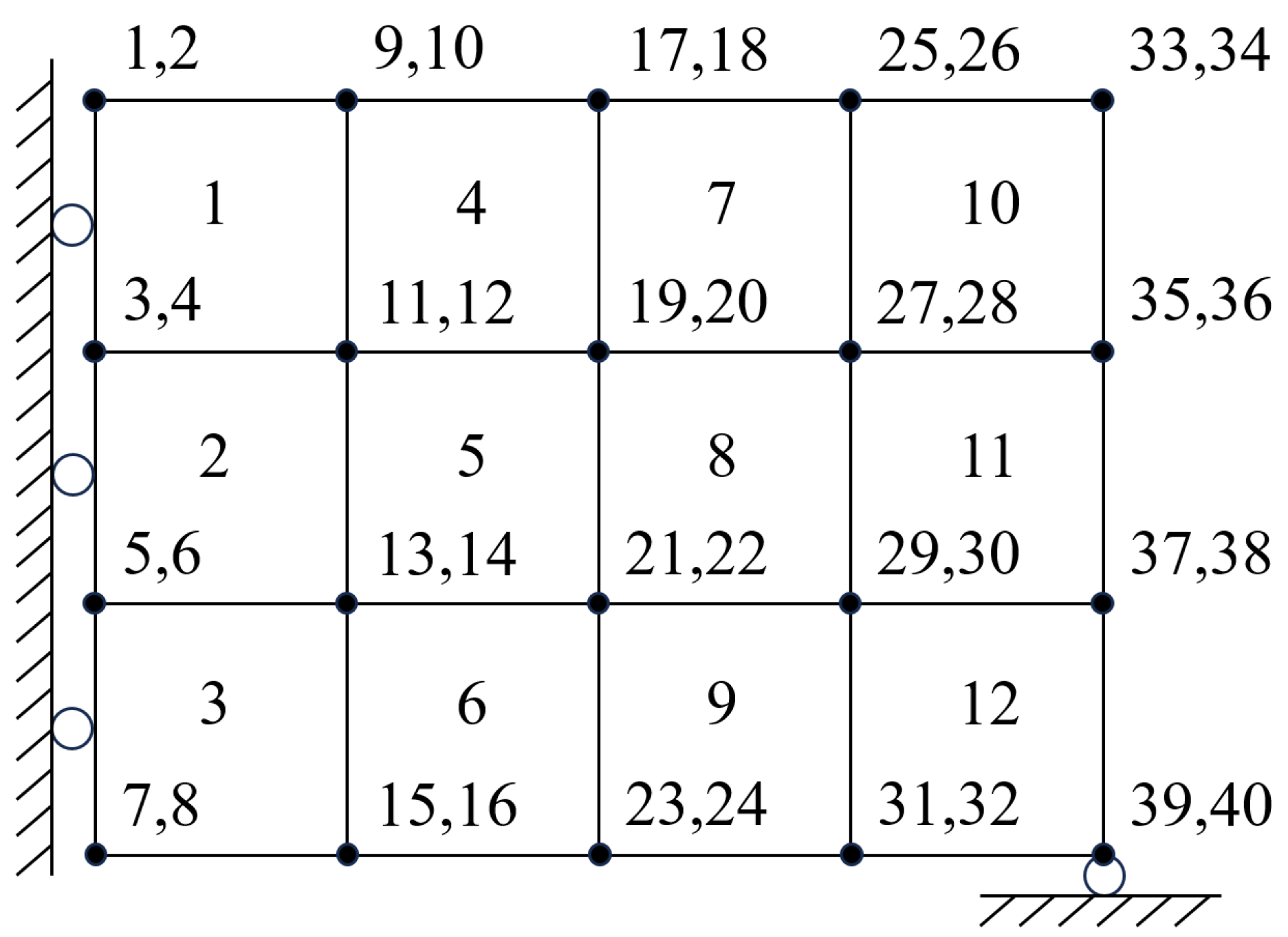
3.2. Finite Element Analysis
3.3. Filtering and Projection/Normalization
3.4. Sensitivity Analysis
3.5. Design Variable Update
3.6. Postprocessing
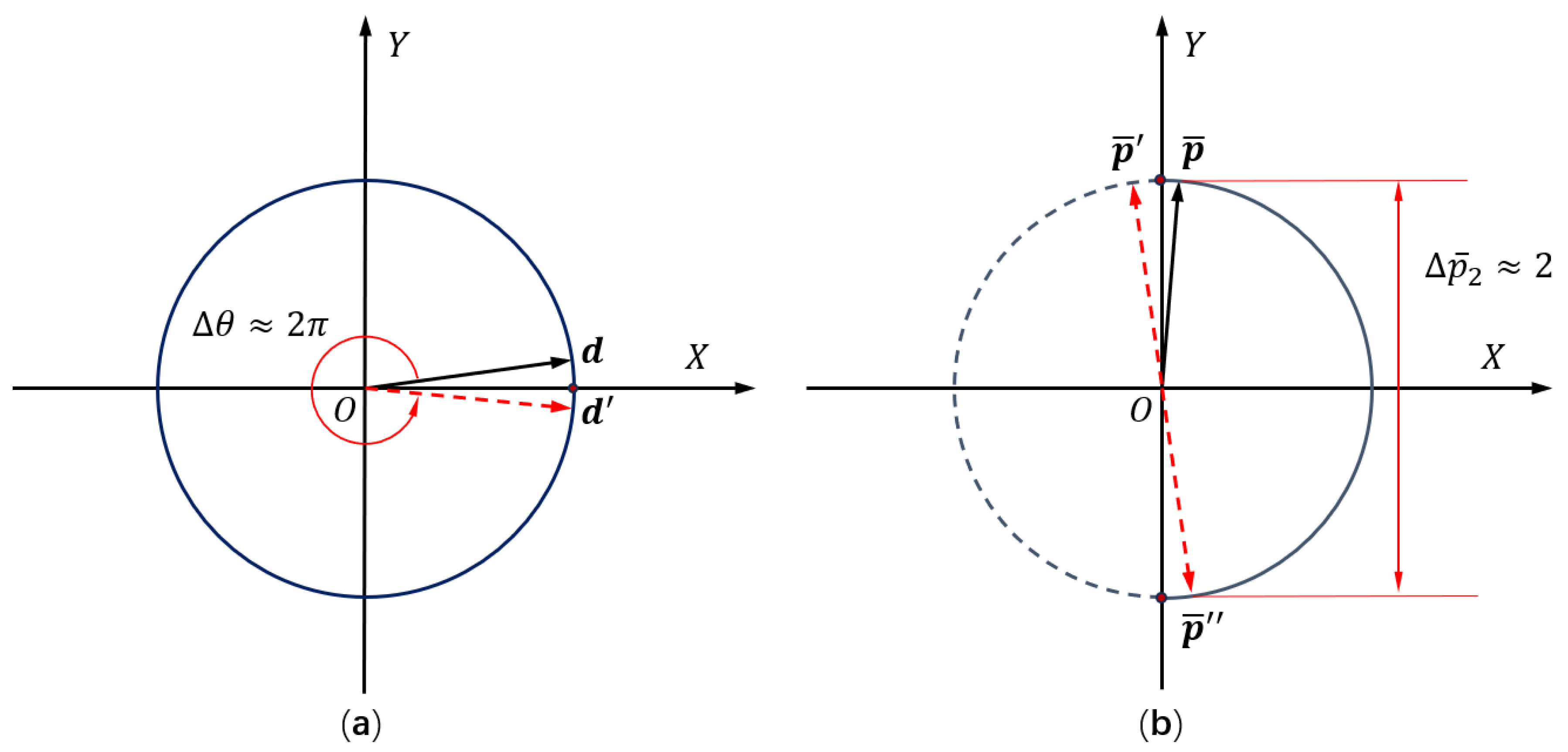
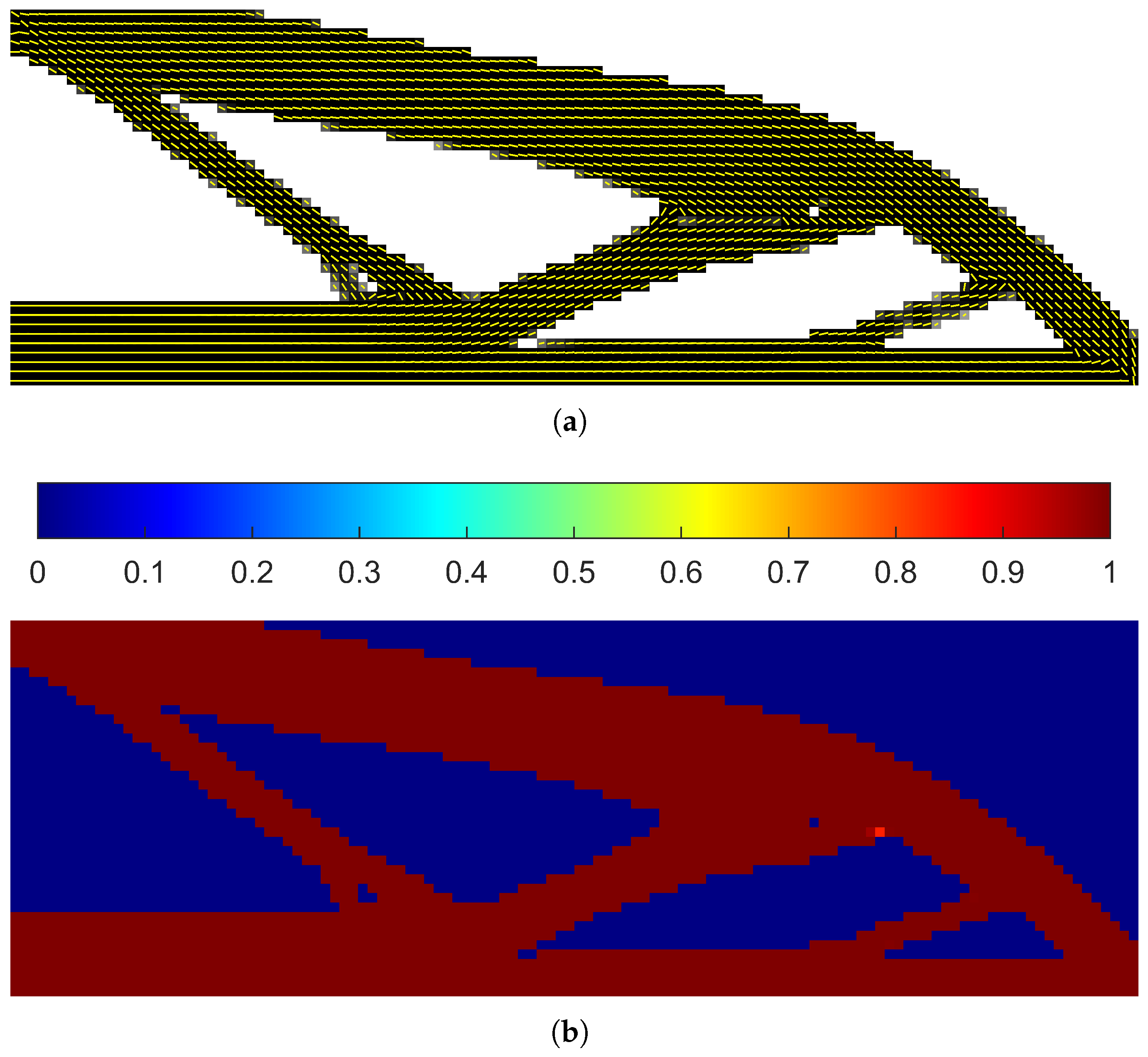
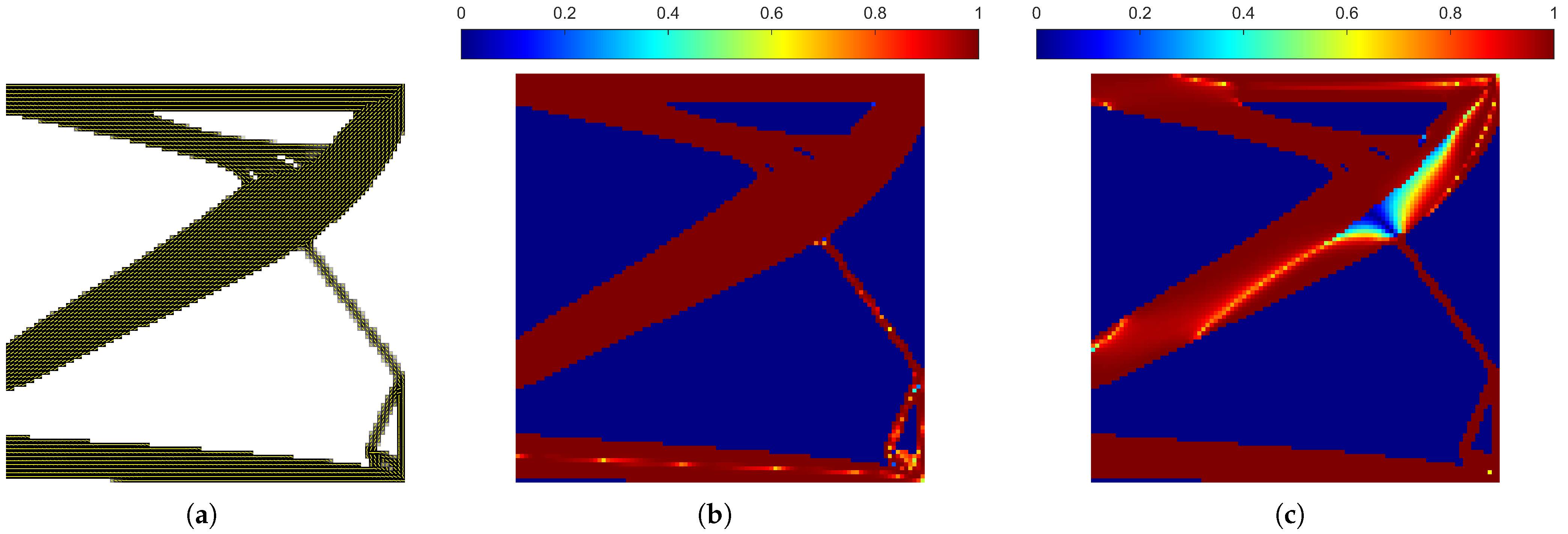
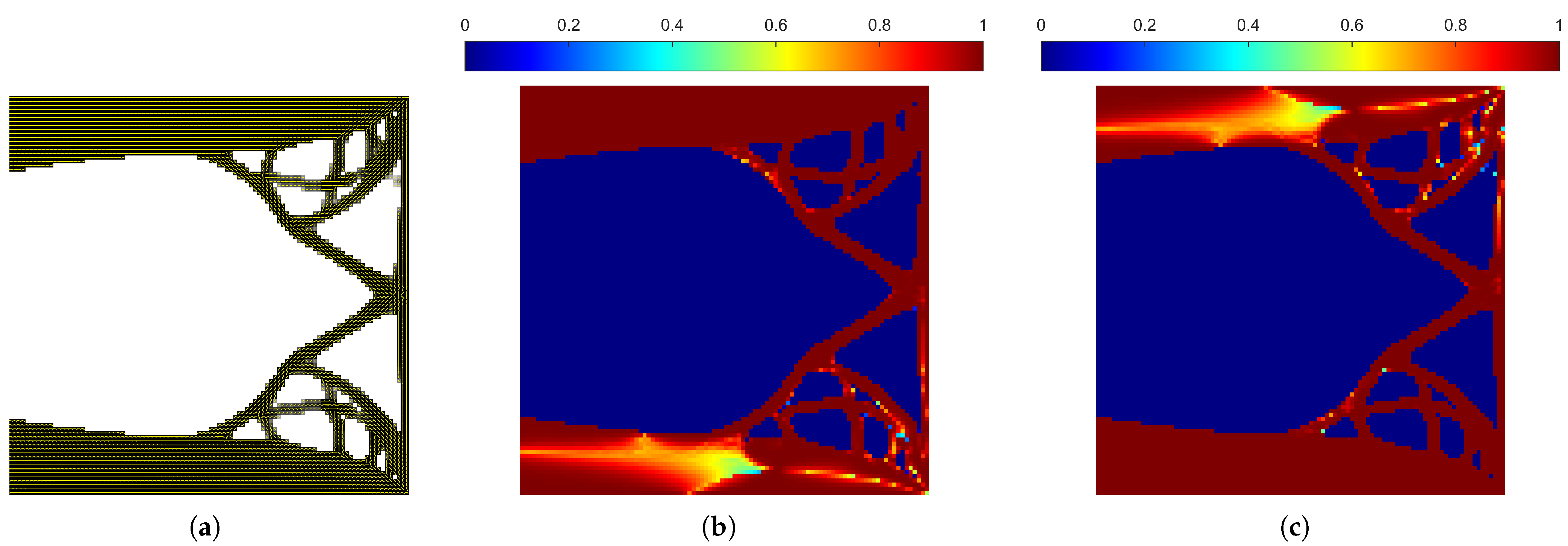
3.7. Optimality Verification of Fiber Orientations
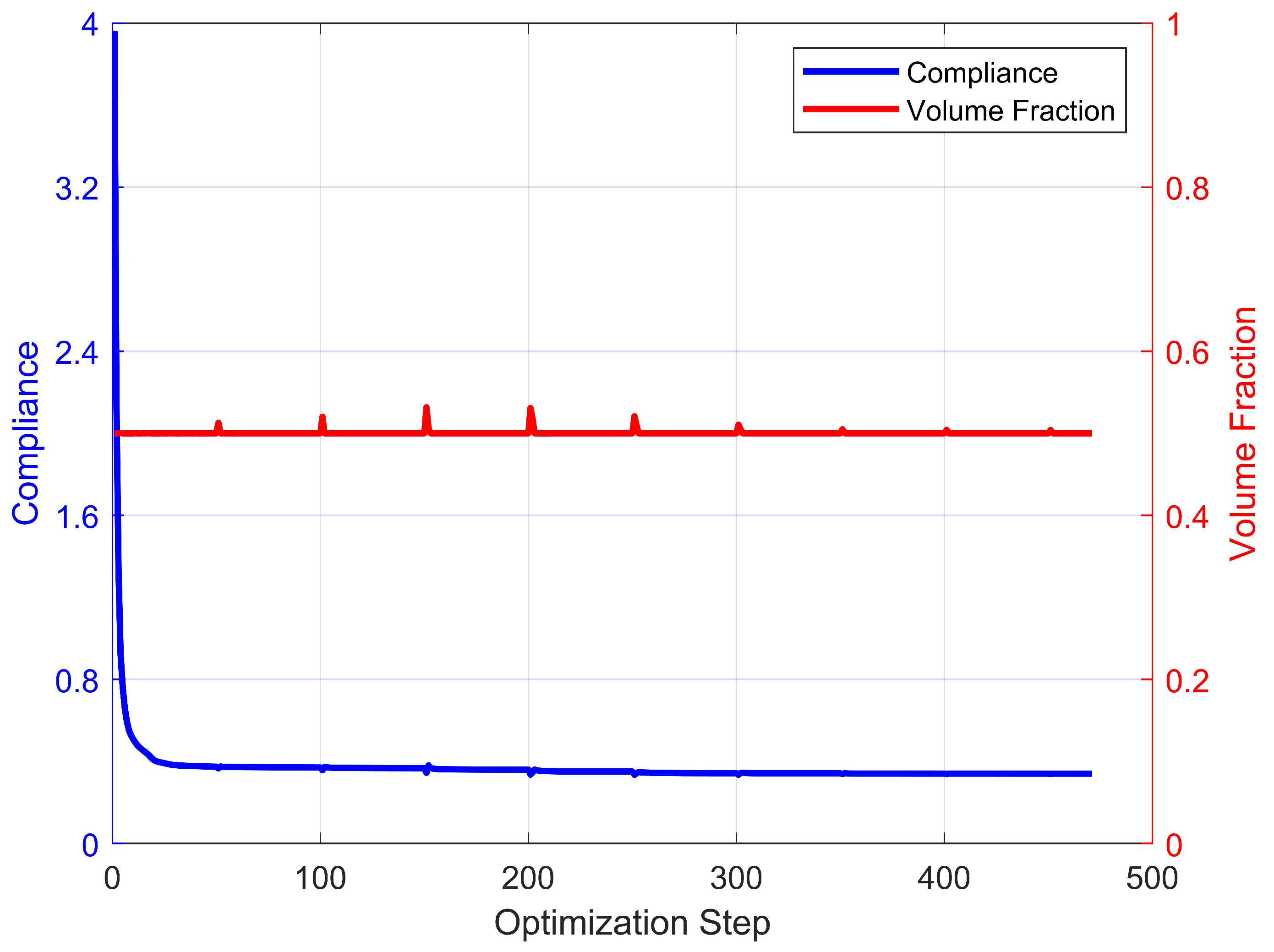
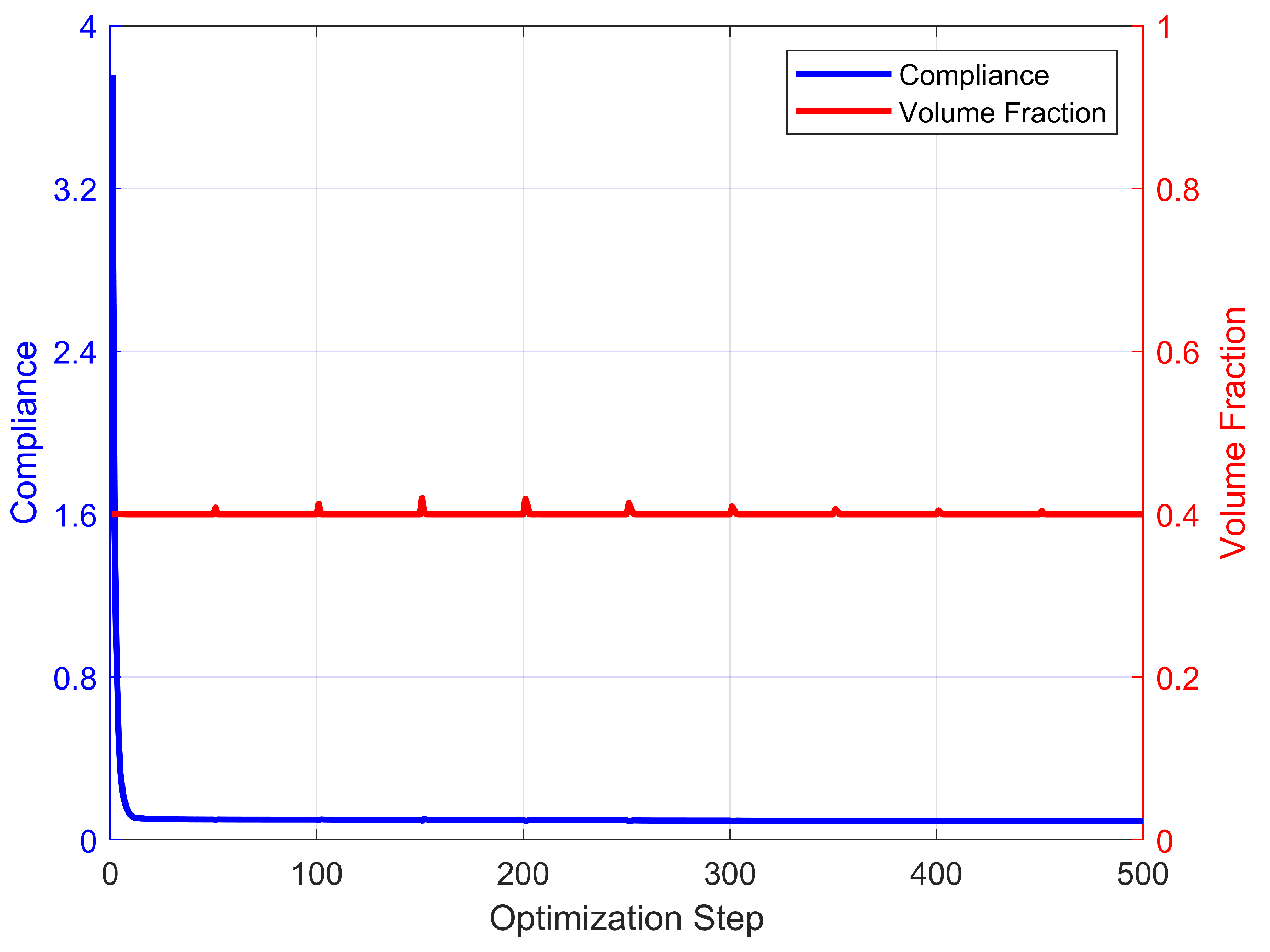
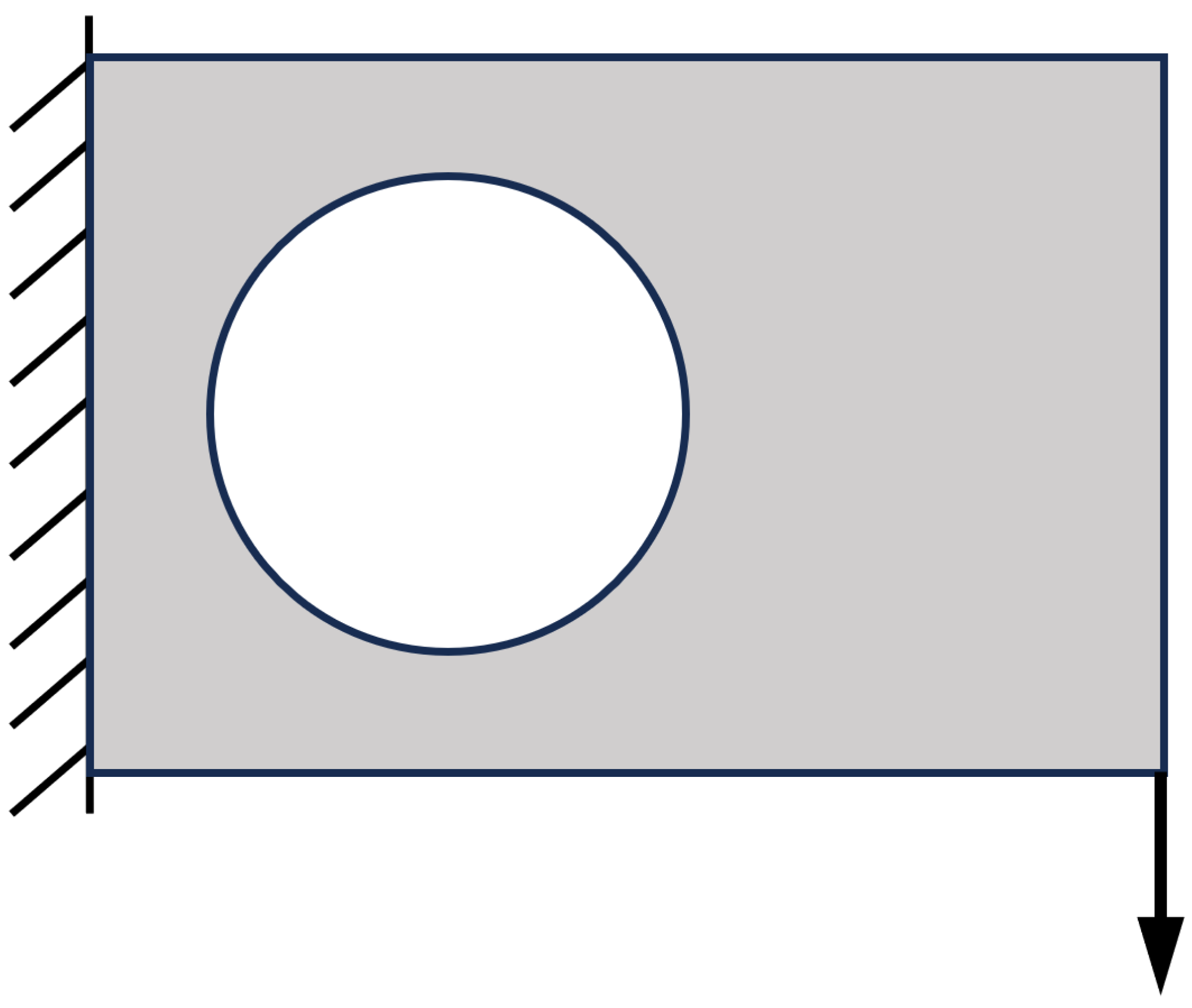
3.8. Results
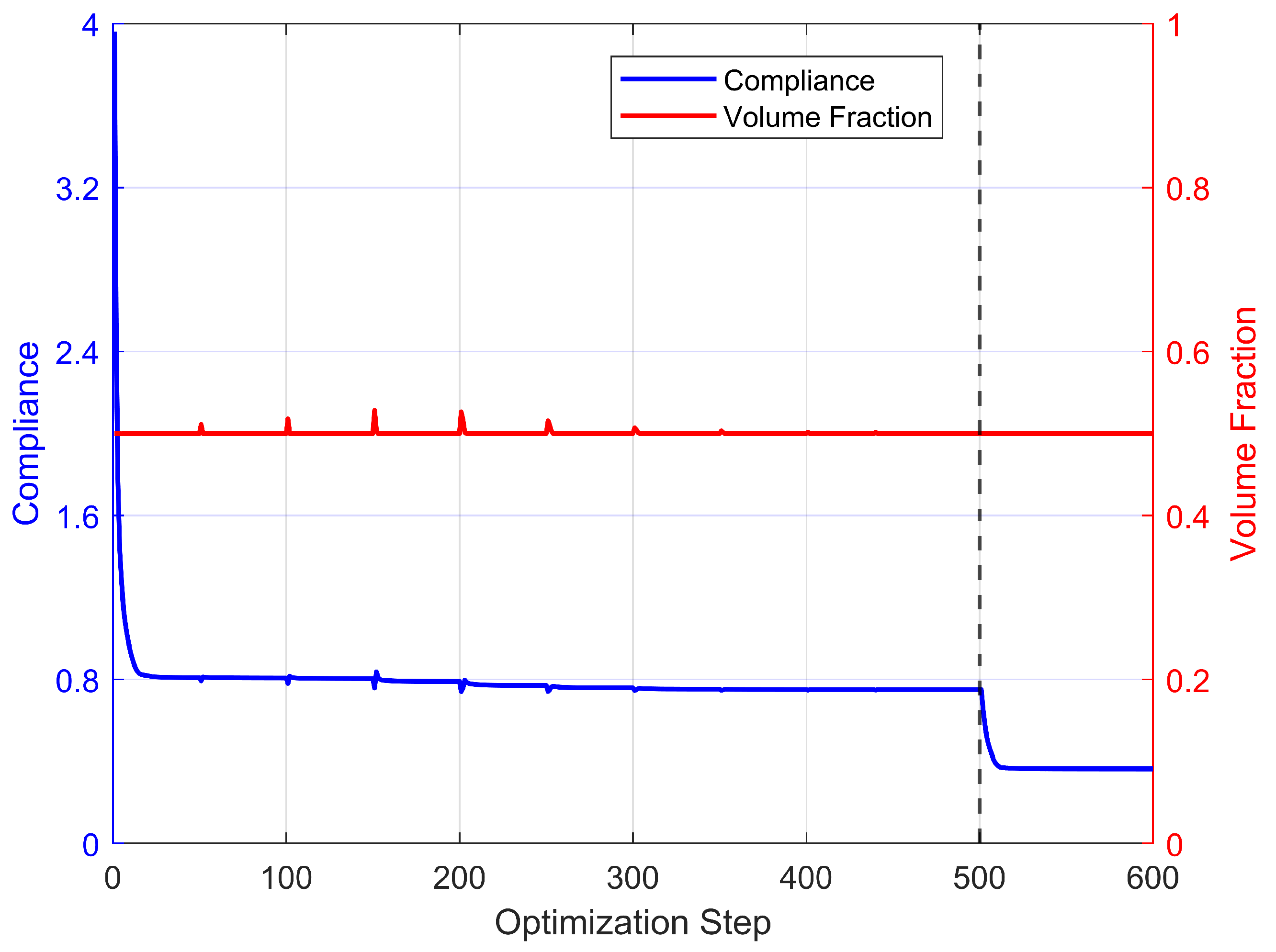
4. Extensions
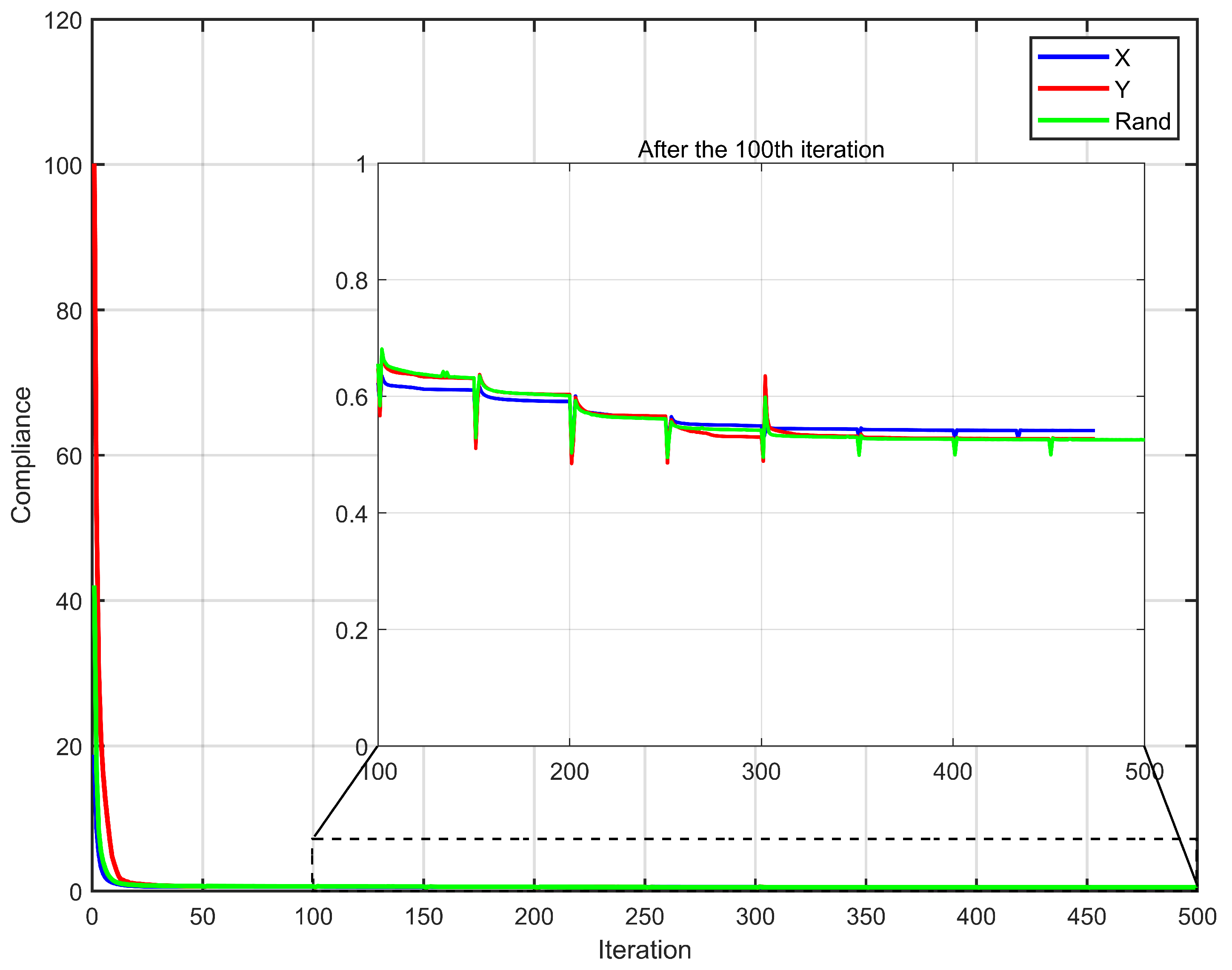
4.1. Different Initialization of the Fiber Orientations
 For the case of random initialization, just make the following change:
For the case of random initialization, just make the following change:
4.2. Other Boundary Conditions
 At the same time, line 11 must be changed as follows:
At the same time, line 11 must be changed as follows:
4.3. Multiple Load Cases





4.4. Passive Elements


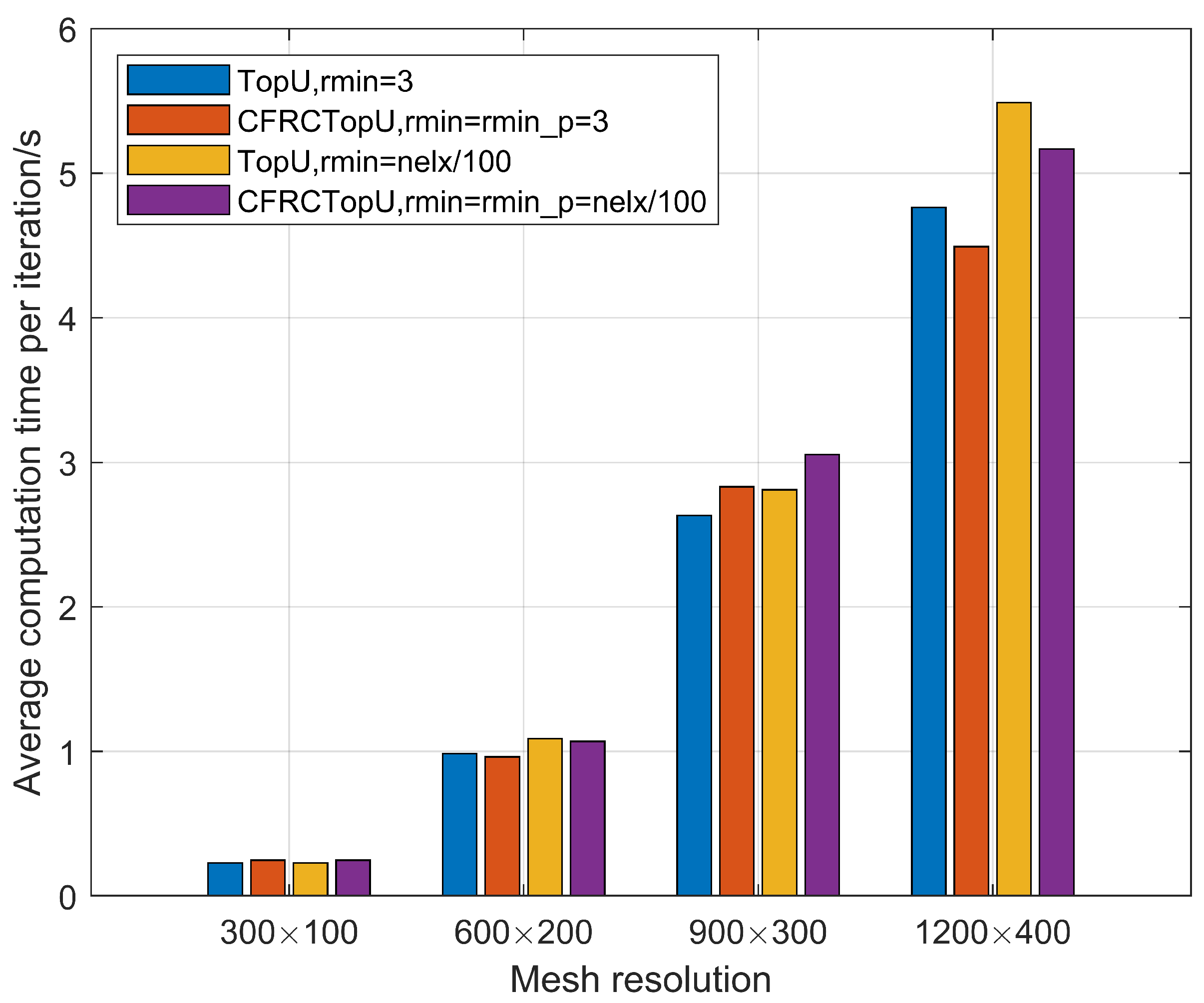
5. Computational Performance and Scalability
6. Limitations and Future Directions
7. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tian, X.; Todoroki, A.; Liu, T.; Wu, L.; Hou, Z.; Ueda, M.; Hirano, Y.; Matsuzaki, R.; Mizukami, K.; Iizuka, K.; et al. 3D printing of continuous fiber reinforced polymer composites: Development, application, and prospective. Chin. J. Mech. Eng. Addit. Manuf. Front. 2022, 1, 100016. [Google Scholar] [CrossRef]
- Cheng, P.; Peng, Y.; Li, S.; Rao, Y.; Le Duigou, A.; Wang, K.; Ahzi, S. 3D printed continuous fiber reinforced composite lightweight structures: A review and outlook. Compos. Part B Eng. 2022, 250, 110450. [Google Scholar] [CrossRef]
- Liu, G.; Xiong, Y.; Zhou, L. Additive manufacturing of continuous fiber reinforced polymer composites: Design opportunities and novel applications. Compos. Commun. 2021, 27, 100907. [Google Scholar] [CrossRef]
- Jiang, D.; Hoglund, R.; Smith, D.E. Continuous fiber angle topology optimization for polymer composite deposition additive manufacturing applications. Fibers 2019, 7, 14. [Google Scholar] [CrossRef]
- Safonov, A.A. 3D topology optimization of continuous fiber-reinforced structures via natural evolution method. Compos. Struct. 2019, 215, 289–297. [Google Scholar] [CrossRef]
- Chen, Y.; Ye, L. Topological design for 3D-printing of carbon fibre reinforced composite structural parts. Compos. Sci. Technol. 2021, 204, 108644. [Google Scholar] [CrossRef]
- Zhou, Y.; Nomura, T.; Zhao, E.; Saitou, K. Large-scale three-dimensional anisotropic topology optimization of variable-axial lightweight composite structures. J. Mech. Des. 2022, 144, 011702. [Google Scholar] [CrossRef]
- Qiu, Z.; Li, Q.; Luo, Y.; Liu, S. Concurrent topology and fiber orientation optimization method for fiber-reinforced composites based on composite additive manufacturing. Comput. Methods Appl. Mech. Eng. 2022, 395, 114962. [Google Scholar] [CrossRef]
- Habashneh, M.; Rad, M.M. Optimizing structural topology design through consideration of fatigue crack propagation. Comput. Methods Appl. Mech. Eng. 2024, 419, 116629. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods and Applications; Springer: Cham, Switzerland, 2003. [Google Scholar]
- Gandhi, Y.; Minak, G. A review on topology optimization strategies for additively manufactured continuous fiber-reinforced composite structures. Appl. Sci. 2022, 12, 11211. [Google Scholar] [CrossRef]
- Jiang, S.; Shang, C.; Li, J.; Yi, B.; Peng, X. Topology optimization of anisotropic materials with smooth fiber orientation. Appl. Sci. 2024, 14, 5947. [Google Scholar] [CrossRef]
- Sigmund, O. A 99 line topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2001, 21, 120–127. [Google Scholar] [CrossRef]
- Andreassen, E.; Clausen, A.; Schevenels, M.; Lazarov, B.S.; Sigmund, O. Efficient topology optimization in MATLAB using 88 lines of code. Struct. Multidiscip. Optim. 2011, 43, 1–16. [Google Scholar] [CrossRef]
- Liu, K.; Tovar, A. An efficient 3D topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2014, 50, 1175–1196. [Google Scholar] [CrossRef]
- Ferrari, F.; Sigmund, O. A new generation 99 line Matlab code for compliance topology optimization and its extension to 3D. Struct. Multidiscip. Optim. 2020, 62, 2211–2228. [Google Scholar] [CrossRef]
- Talischi, C.; Paulino, G.H.; Pereira, A.; Menezes, I.F. PolyTop: A Matlab implementation of a general topology optimization framework using unstructured polygonal finite element meshes. Struct. Multidiscip. Optim. 2012, 45, 329–357. [Google Scholar] [CrossRef]
- Giraldo-Londoño, O.; Paulino, G.H. PolyStress: A Matlab implementation for local stress-constrained topology optimization using the augmented Lagrangian method. Struct. Multidiscip. Optim. 2021, 63, 2065–2097. [Google Scholar] [CrossRef]
- Wei, P.; Li, Z.; Li, X.; Wang, M.Y. An 88-line MATLAB code for the parameterized level set method based topology optimization using radial basis functions. Struct. Multidiscip. Optim. 2018, 58, 831–849. [Google Scholar] [CrossRef]
- Sanders, E.D.; Pereira, A.; Aguiló, M.A.; Paulino, G.H. PolyMat: An efficient Matlab code for multi-material topology optimization. Struct. Multidiscip. Optim. 2018, 58, 2727–2759. [Google Scholar] [CrossRef]
- Gao, J.; Wang, L.; Luo, Z.; Gao, L. IgaTop: An implementation of topology optimization for structures using IGA in MATLAB. Struct. Multidiscip. Optim. 2021, 64, 1669–1700. [Google Scholar] [CrossRef]
- Du, Z.; Cui, T.; Liu, C.; Zhang, W.; Guo, Y.; Guo, X. An efficient and easy-to-extend Matlab code of the Moving Morphable Component (MMC) method for three-dimensional topology optimization. Struct. Multidiscip. Optim. 2022, 65, 158. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, Z.; Zhou, M.; Sigmund, O.; Zhang, X.S. A comprehensive review of educational articles on structural and multidisciplinary optimization. Struct. Multidiscip. Optim. 2021, 64, 2827–2880. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Long, K.; Wei, P. Open-source codes of topology optimization: A summary for beginners to start their research. Comput. Model. Eng. Sci. 2023, 137, 1–34. [Google Scholar] [CrossRef]
- Zheng, R.; Yi, B.; Peng, X.; Yoon, G.H. An efficient code for the multi-material topology optimization of 2D/3D continuum structures written in MATLAB. Appl. Sci. 2024, 14, 657. [Google Scholar] [CrossRef]
- Bendsøe, M.P. Optimal shape design as a material distribution problem. Struct. Optim. 1989, 1, 193–202. [Google Scholar] [CrossRef]
- Zhou, M.; Rozvany, G. The COC algorithm, Part II: Topological, geometrical and generalized shape optimization. Comput. Methods Appl. Mech. Eng. 1991, 89, 309–336. [Google Scholar] [CrossRef]
- Nomura, T.; Dede, E.M.; Lee, J.; Yamasaki, S.; Matsumori, T.; Kawamoto, A.; Kikuchi, N. General topology optimization method with continuous and discrete orientation design using isoparametric projection. Int. J. Numer. Methods Eng. 2015, 101, 571–605. [Google Scholar] [CrossRef]
- Luo, C.; Ferrari, F.; Guest, J.K. Design optimization of advanced tow-steered composites with manufacturing constraints. Compos. Part B Eng. 2024, 284, 111739. [Google Scholar] [CrossRef]
- Zhao, J.; Qi, T.; Wang, C. Topology optimization of 3D continuous fiber-reinforced composites using Cartesian parametrization of fiber orientations. Struct. Multidiscip. Optim. 2024, 67, 153. [Google Scholar] [CrossRef]
- Kumar, T.; Suresh, K. A density-and-strain-based K-clustering approach to microstructural topology optimization. Struct. Multidiscip. Optim. 2020, 61, 1399–1415. [Google Scholar] [CrossRef]
- Chandrasekhar, A.; Mirzendehdel, A.; Behandish, M.; Suresh, K. Frc-tounn: Topology optimization of continuous fiber reinforced composites using neural network. Comput. Aided Des. 2023, 156, 103449. [Google Scholar] [CrossRef]
- Zhao, J.; Qi, T.; Wang, C. Efficient GPU accelerated topology optimization of composite structures with spatially varying fiber orientations. Comput. Methods Appl. Mech. Eng. 2024, 421, 116809. [Google Scholar] [CrossRef]
- Gea, H.; Luo, J. On the stress-based and strain-based methods for predicting optimal orientation of orthotropic materials. Struct. Multidiscip. Optim. 2004, 26, 229–234. [Google Scholar] [CrossRef]
- Bourdin, B. Filters in topology optimization. Int. J. Numer. Methods Eng. 2001, 50, 2143–2158. [Google Scholar] [CrossRef]
- Nomura, T.; Kawamoto, A.; Kondoh, T.; Dede, E.M.; Lee, J.; Song, Y.; Kikuchi, N. Inverse design of structure and fiber orientation by means of topology optimization with tensor field variables. Compos. Part B Eng. 2019, 176, 107187. [Google Scholar] [CrossRef]
- Lee, J.; Kim, D.; Nomura, T.; Dede, E.M.; Jeonghoon, Y. Topology optimization for continuous and discrete orientation design of functionally graded fiber-reinforced composite structures. Compos. Struct. 2018, 201, 217–233. [Google Scholar] [CrossRef]
- Wong, J.; Sanders, E.D.; Rosen, D.W. Topology optimization of additively manufactured continuous fiber-reinforced structures with constraints on fiber path geometry. Struct. Multidiscip. Optim. 2025, 68, 87. [Google Scholar] [CrossRef]
- Kubalak, J.R.; Wicks, A.L.; Williams, C.B. Investigation of parameter spaces for topology optimization with three-dimensional orientation fields for multi-axis additive manufacturing. J. Mech. Des. 2021, 143, 051701. [Google Scholar] [CrossRef]
- Svanberg, K. The method of moving asymptotes¡ªa new method for structural optimization. Int. J. Numer. Methods Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
- Zhang, X.S.; Chi, H.; Zhao, Z. Topology optimization of hyperelastic structures with anisotropic fiber reinforcement under large deformations. Comput. Methods Appl. Mech. Eng. 2021, 378, 113496. [Google Scholar] [CrossRef]
- Aage, N.; Lazarov, B.S. Parallel framework for topology optimization using the method of moving asymptotes. Struct. Multidiscip. Optim. 2013, 47, 493–505. [Google Scholar] [CrossRef]
- Giraldo-Londono, O.; Paulino, G.H. PolyDyna: A Matlab implementation for topology optimization of structures subjected to dynamic loads. Struct. Multidiscip. Optim. 2021, 64, 957–990. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, S.; Zhang, K.; Wu, J.; Li, A.; Liu, J.; Yang, D. 3D printing of continuous carbon fibre reinforced polymer composites with optimised structural topology and fibre orientation. Compos. Struct. 2023, 313, 116914. [Google Scholar] [CrossRef]
- Fang, G.; Zhang, T.; Huang, Y.; Zhang, Z.; Masania, K.; Wang, C.C. Exceptional mechanical performance by spatial printing with continuous fiber: Curved slicing, toolpath generation and physical verification. Addit. Manuf. 2024, 82, 104048. [Google Scholar] [CrossRef]
- Schmidt, M.P.; Couret, L.; Gout, C.; Pedersen, C.B. Structural topology optimization with smoothly varying fiber orientations. Struct. Multidiscip. Optim. 2020, 62, 3105–3126. [Google Scholar] [CrossRef]
- Amir, O.; Aage, N.; Lazarov, B.S. On multigrid-CG for efficient topology optimization. Struct. Multidiscip. Optim. 2014, 49, 815–829. [Google Scholar] [CrossRef]
- Setoodeh, S.; Abdalla, M.M.; Gürdal, Z. Design of variable–stiffness laminates using lamination parameters. Compos. Part B Eng. 2006, 37, 301–309. [Google Scholar] [CrossRef]
- Izzi, M.I.; Catapano, A.; Montemurro, M. Strength and mass optimisation of variable-stiffness composites in the polar parameters space. Struct. Multidiscip. Optim. 2021, 64, 2045–2073. [Google Scholar] [CrossRef]
- Yan, X.; Lai, M.; Huang, D.; Zhang, Y.; Huang, X. Manufacturing-oriented topological design of CFRC structures with variable fiber volume and orientation. Compos. Struct. 2023, 310, 116779. [Google Scholar] [CrossRef]
- Huang, Y.; Tian, X.; Wu, L.; Zia, A.A.; Liu, T.; Li, D. Progressive concurrent topological optimization with variable fiber orientation and content for 3D printed continuous fiber reinforced polymer composites. Compos. Part B Eng. 2023, 255, 110602. [Google Scholar] [CrossRef]







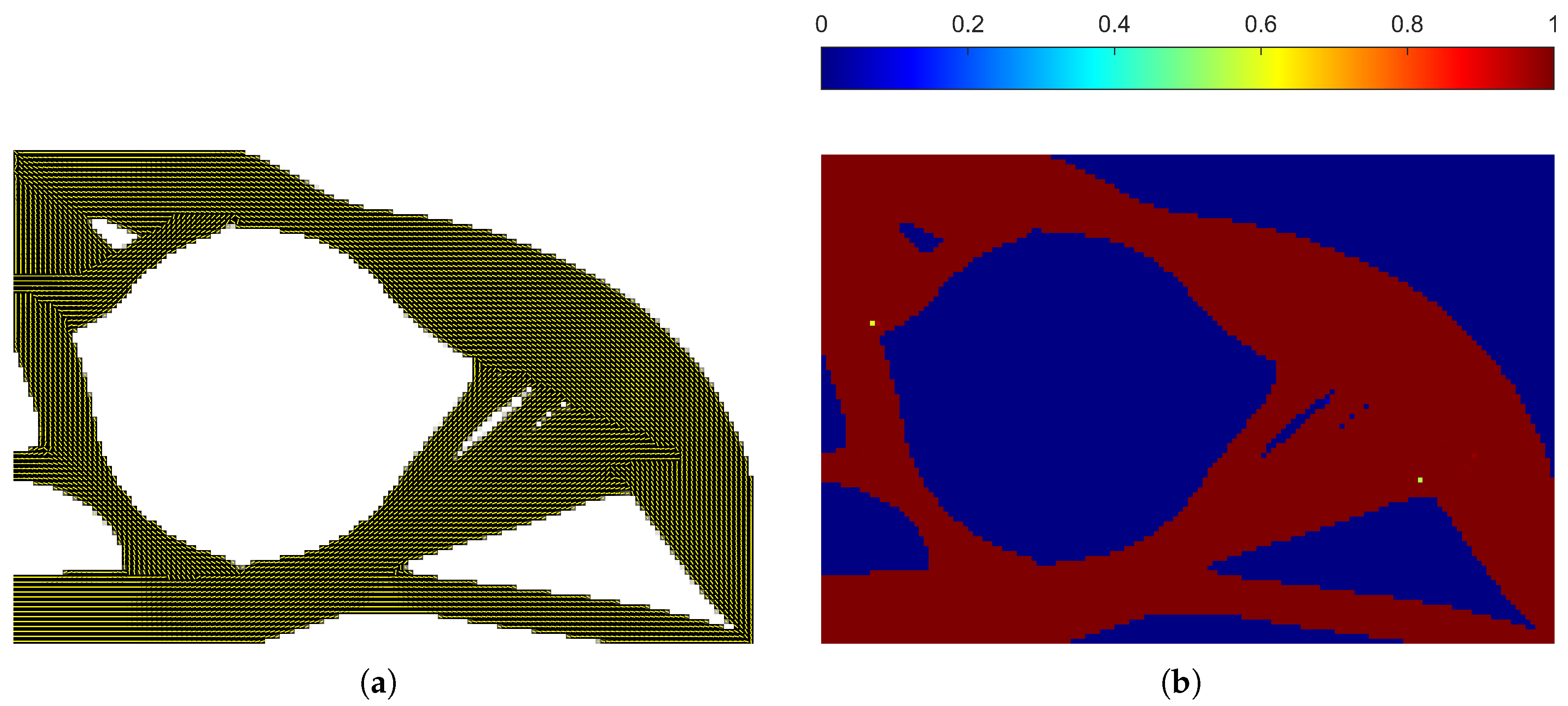

| Top | CFRCTop | Top | CFRCTop | Top | CFRCTop | Top | CFRCTop | |
|---|---|---|---|---|---|---|---|---|
| 0.0008 | 0.0023 | 0.0030 | 0.0087 | 0.0079 | 0.0260 | 0.0130 | 0.0412 | |
| 0.0363 | 0.0663 | 0.2098 | 0.3046 | 0.5056 | 0.7123 | 0.8528 | 1.2492 | |
| 0.1539 | 0.1319 | 0.7081 | 0.5601 | 1.8277 | 1.6832 | 3.4685 | 2.5831 | |
| 0.0041 | 0.0136 | 0.0130 | 0.0426 | 0.0329 | 0.1002 | 0.0503 | 0.1559 | |
| 0.0441 | 0.0486 | 0.1664 | 0.1938 | 0.6631 | 0.6978 | 0.9514 | 1.0766 | |
| Top | CFRCTop | Top | CFRCTop | Top | CFRCTop | Top | CFRCTop | |
|---|---|---|---|---|---|---|---|---|
| 0.0008 | 0.0023 | 0.0120 | 0.0328 | 0.0537 | 0.1631 | 0.1599 | 0.4570 | |
| 0.0363 | 0.0663 | 0.2304 | 0.3216 | 0.4963 | 0.7146 | 0.8777 | 1.2334 | |
| 0.1539 | 0.1319 | 0.7262 | 0.5803 | 1.8249 | 1.7011 | 3.5127 | 2.6115 | |
| 0.0041 | 0.0136 | 0.0324 | 0.0626 | 0.1251 | 0.1969 | 0.3431 | 0.4488 | |
| 0.0441 | 0.0486 | 0.6412 | 0.6757 | 3.3095 | 3.7538 | 9.7032 | 9.9716 | |
| TopU | CFRCTopU | TopU | CFRCTopU | TopU | CFRCTopU | TopU | CFRCTopU | |
|---|---|---|---|---|---|---|---|---|
| 0.0004 | 0.0011 | 0.0007 | 0.0020 | 0.0015 | 0.0073 | 0.0023 | 0.0105 | |
| 0.0383 | 0.0684 | 0.2132 | 0.3031 | 0.4911 | 0.7098 | 0.8631 | 1.2767 | |
| 0.1625 | 0.1399 | 0.7163 | 0.5598 | 1.8412 | 1.7014 | 3.4578 | 2.6024 | |
| 0.0034 | 0.0129 | 0.0091 | 0.0383 | 0.0207 | 0.0906 | 0.0320 | 0.1422 | |
| 0.0234 | 0.0258 | 0.0463 | 0.0601 | 0.2785 | 0.3217 | 0.4065 | 0.4593 | |
| TopU | CFRCTopU | TopU | CFRCTopU | TopU | CFRCTopU | TopU | CFRCTopU | |
|---|---|---|---|---|---|---|---|---|
| 0.0004 | 0.0011 | 0.0018 | 0.0043 | 0.0058 | 0.0167 | 0.0139 | 0.0357 | |
| 0.0383 | 0.0684 | 0.2362 | 0.3254 | 0.4837 | 0.7150 | 0.8689 | 1.2606 | |
| 0.1625 | 0.1399 | 0.7303 | 0.5758 | 1.7940 | 1.6966 | 3.5174 | 2.6221 | |
| 0.0034 | 0.0129 | 0.0117 | 0.0426 | 0.0269 | 0.0940 | 0.0519 | 0.1562 | |
| 0.0234 | 0.0258 | 0.1083 | 0.1219 | 0.5011 | 0.5314 | 1.0357 | 1.0914 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J. CFRCTop: An Efficient MATLAB Implementation for Topology Optimization of Continuous Fiber-Reinforced Composite Structures. Appl. Sci. 2025, 15, 9242. https://doi.org/10.3390/app15179242
Zhao J. CFRCTop: An Efficient MATLAB Implementation for Topology Optimization of Continuous Fiber-Reinforced Composite Structures. Applied Sciences. 2025; 15(17):9242. https://doi.org/10.3390/app15179242
Chicago/Turabian StyleZhao, Junpeng. 2025. "CFRCTop: An Efficient MATLAB Implementation for Topology Optimization of Continuous Fiber-Reinforced Composite Structures" Applied Sciences 15, no. 17: 9242. https://doi.org/10.3390/app15179242
APA StyleZhao, J. (2025). CFRCTop: An Efficient MATLAB Implementation for Topology Optimization of Continuous Fiber-Reinforced Composite Structures. Applied Sciences, 15(17), 9242. https://doi.org/10.3390/app15179242






