Validation of Acoustic Emission Tomography Using Lagrange Interpolation in a Defective Concrete Specimen
Abstract
1. Introduction
2. Identification of the Velocity Distributions Based on AET
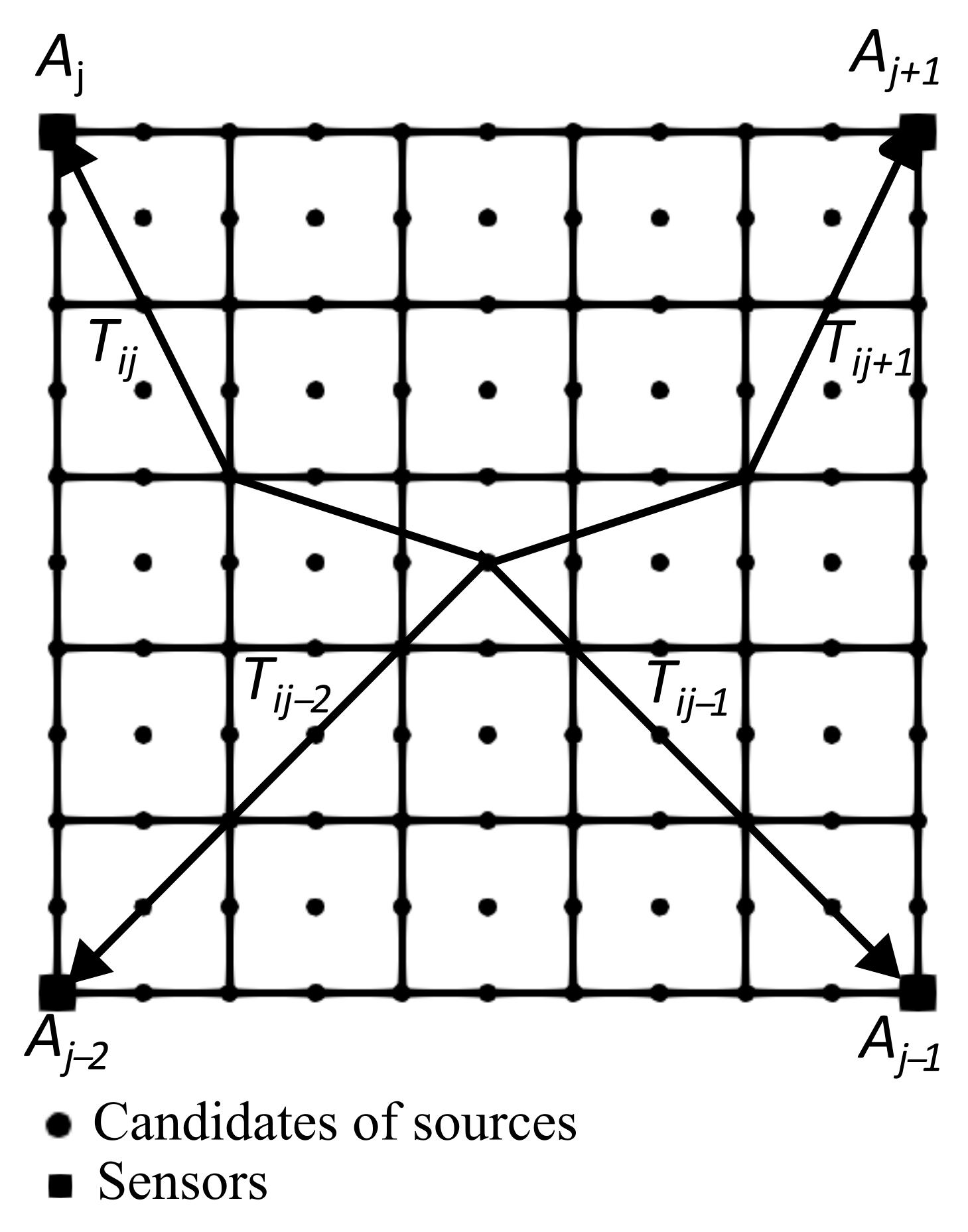
2.1. Conventional AET
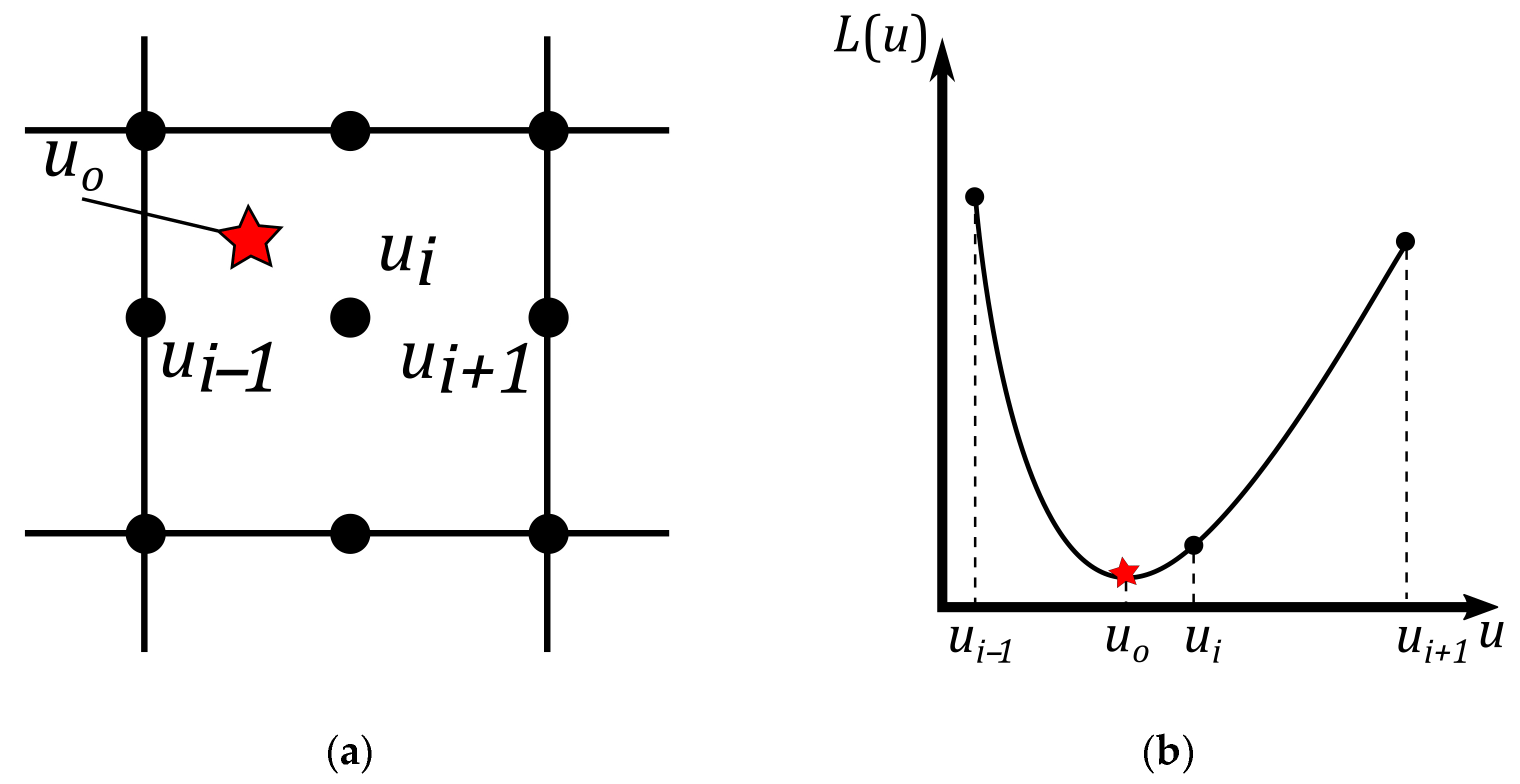
2.2. Application of Lagrange Interpolation
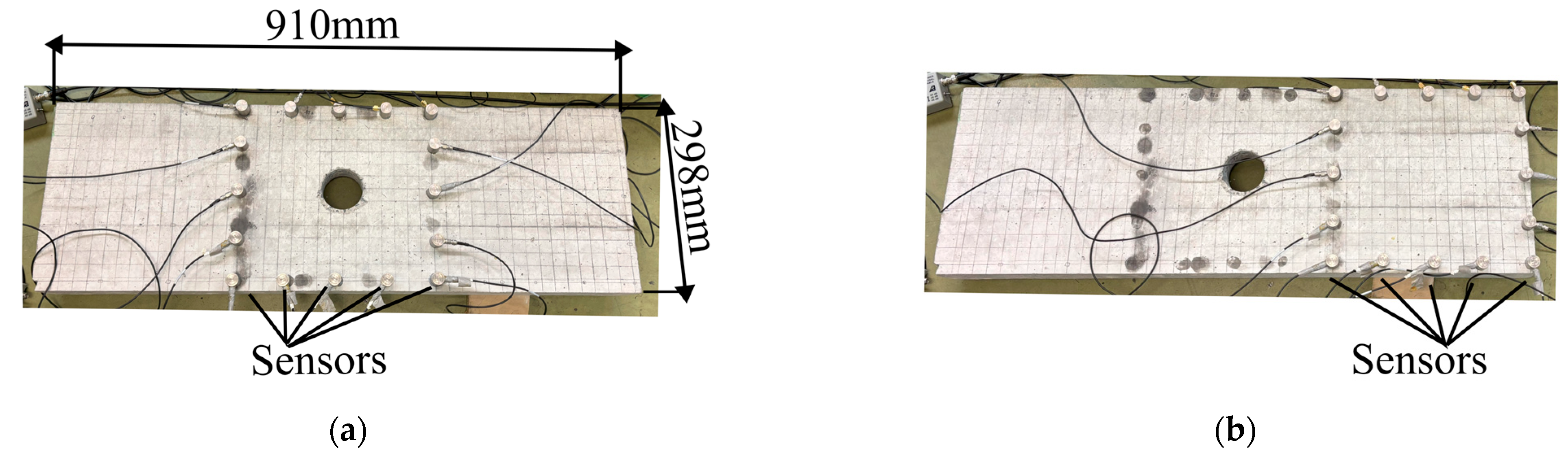
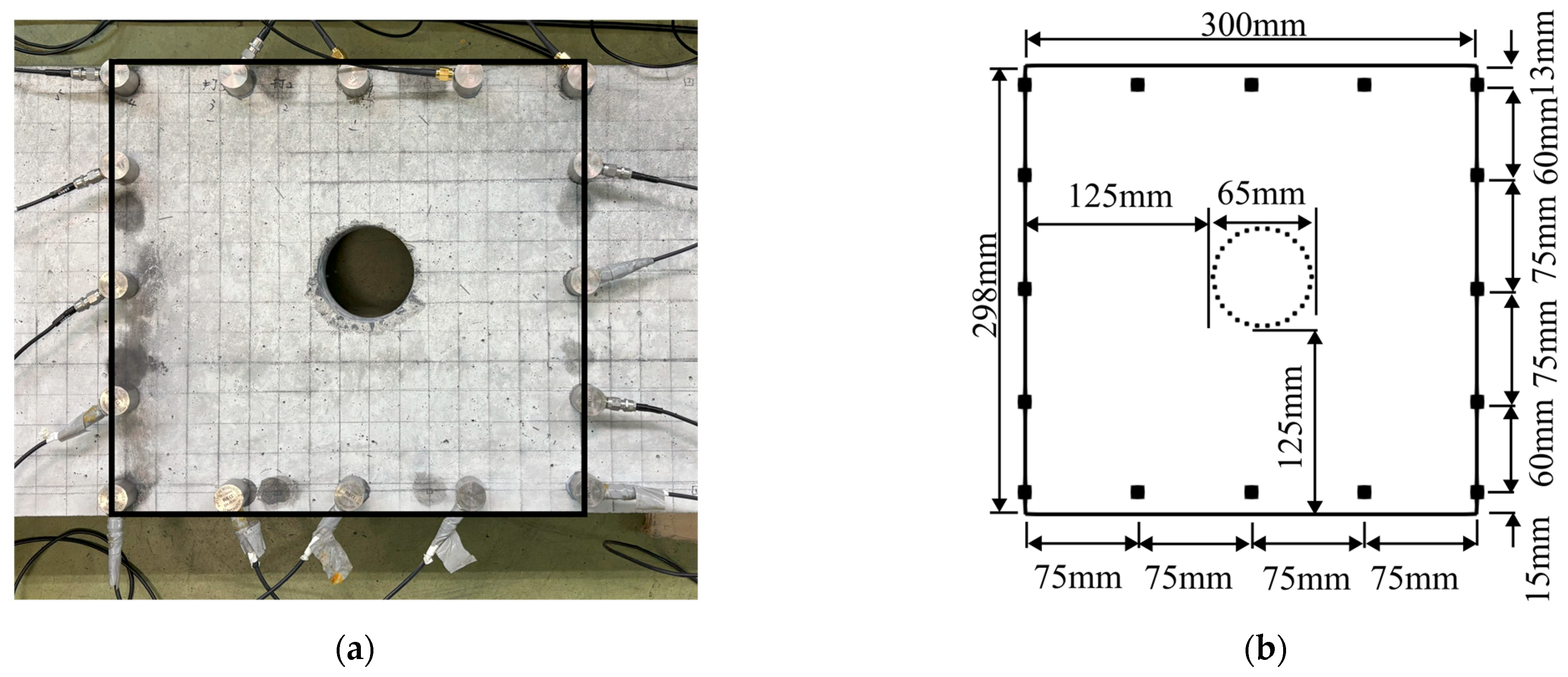
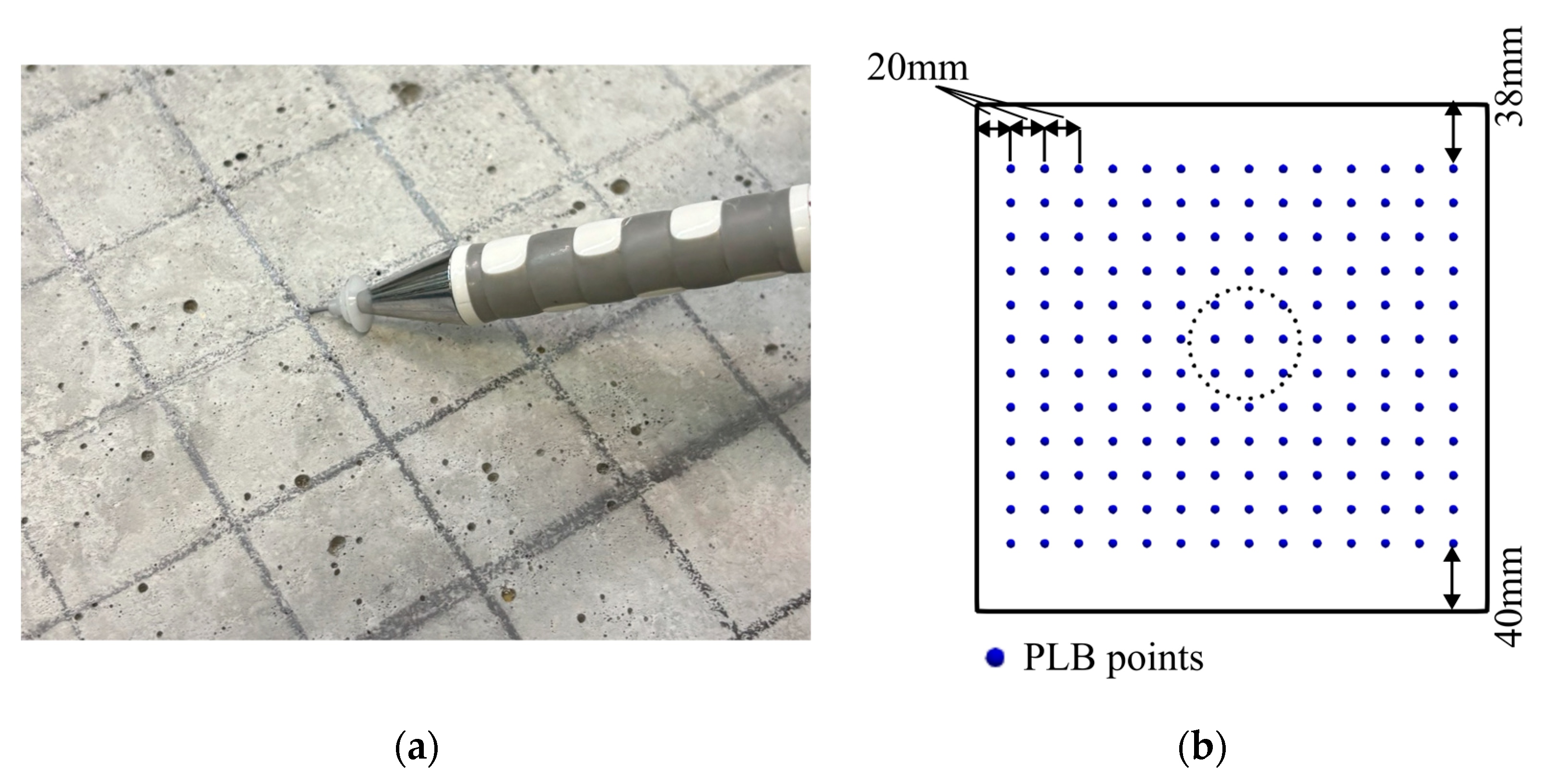
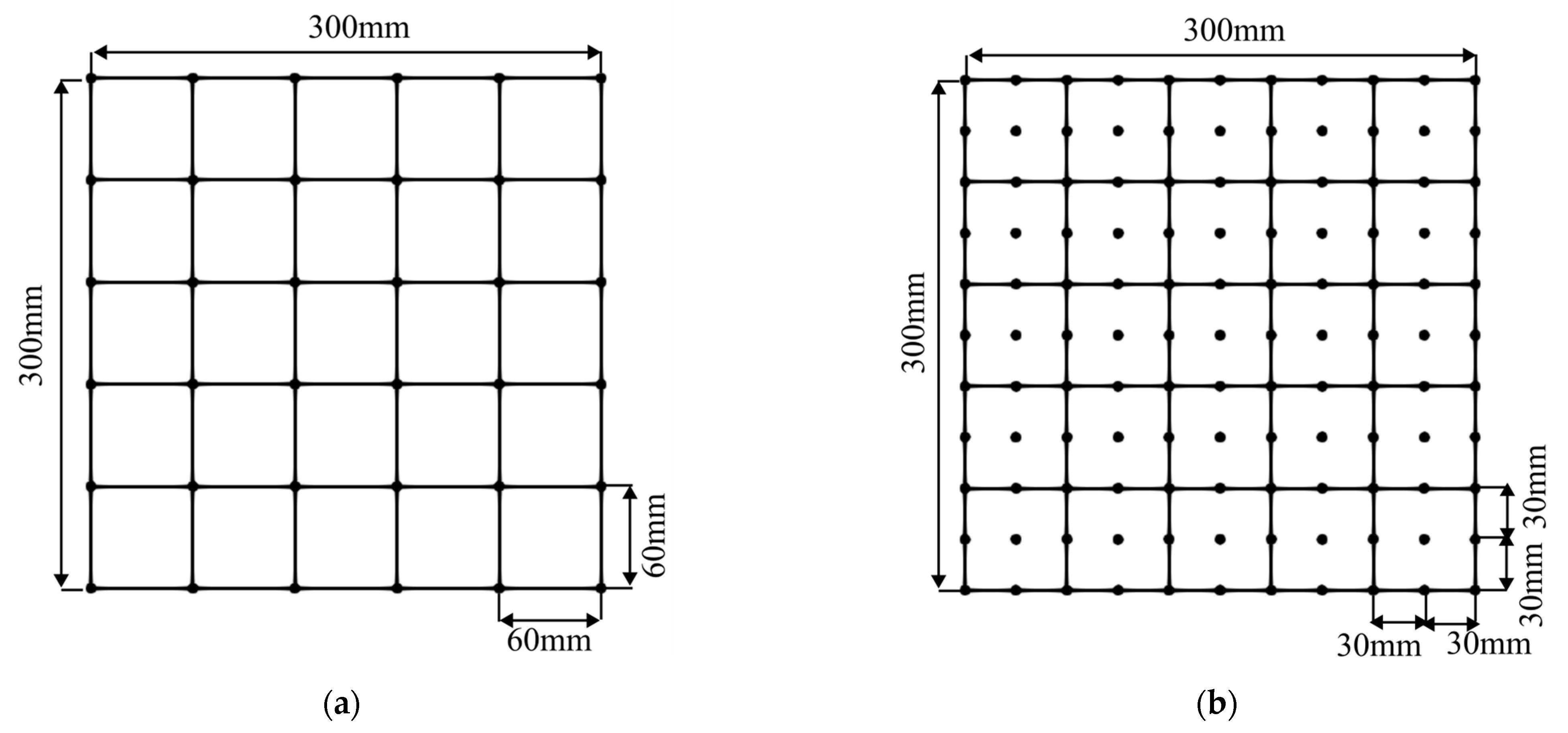
3. Experimental Setup
3.1. Elastic Wave Measurement Condition
3.2. Initial Condition of AET
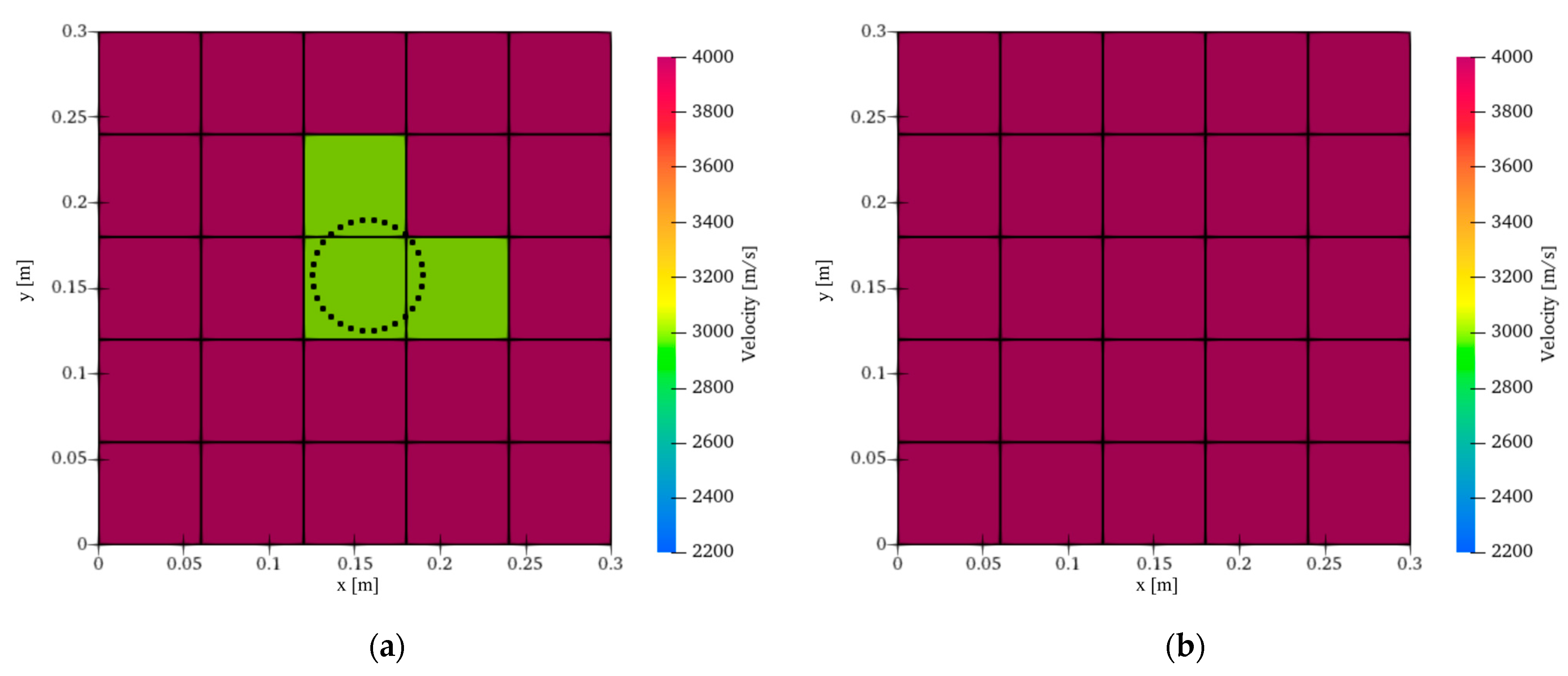
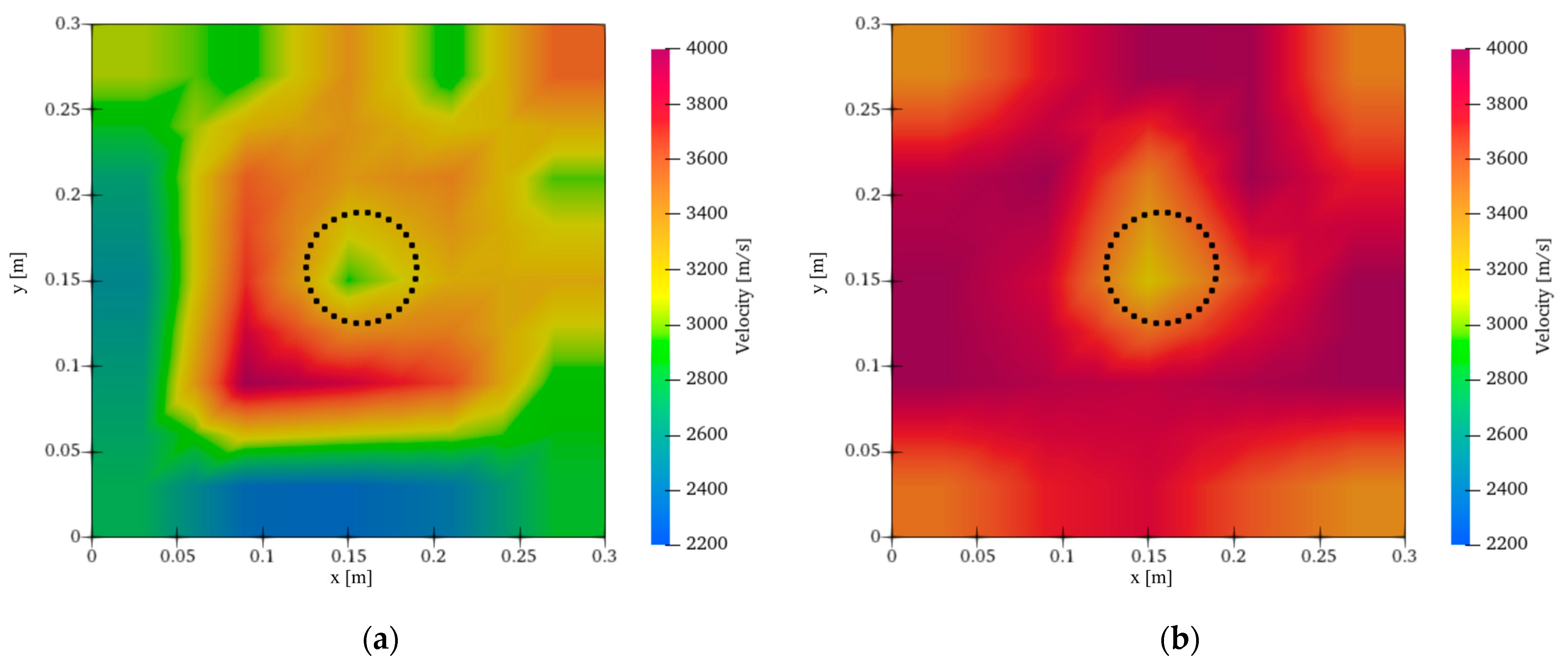
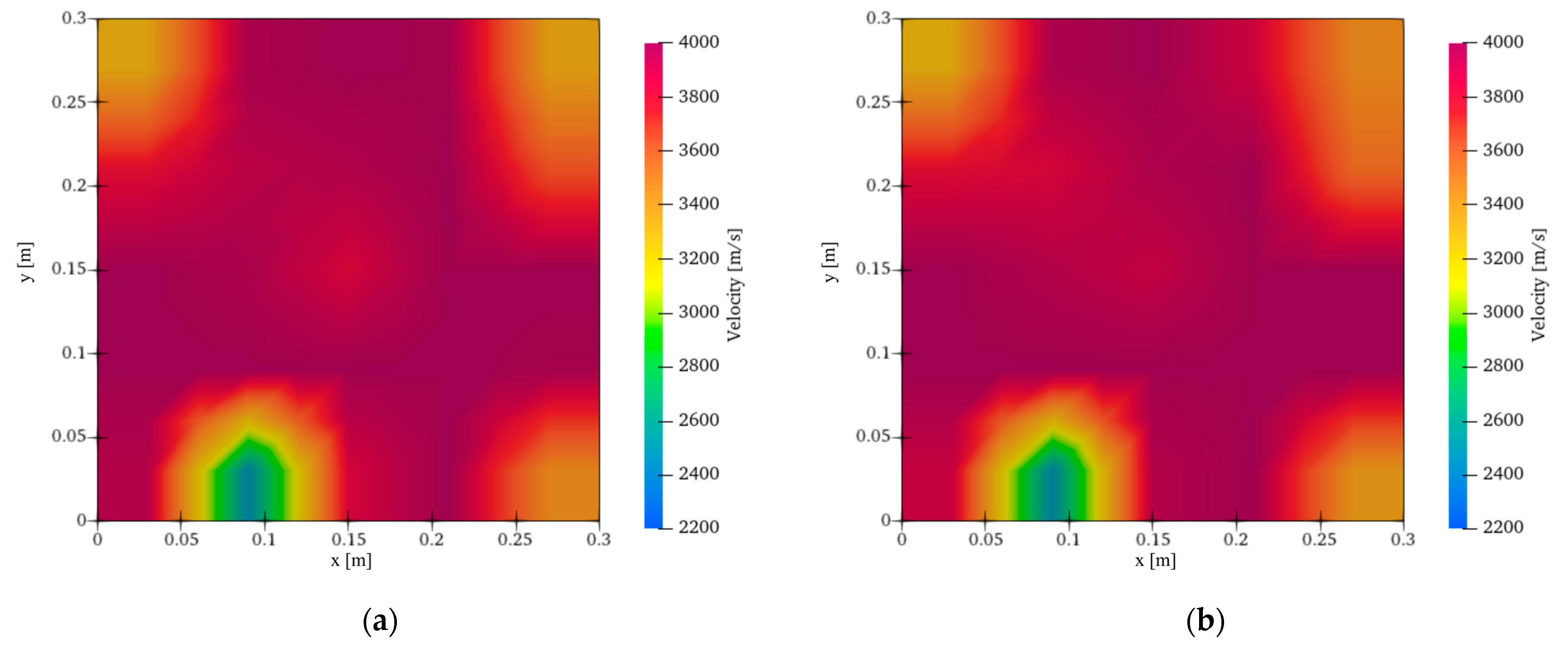
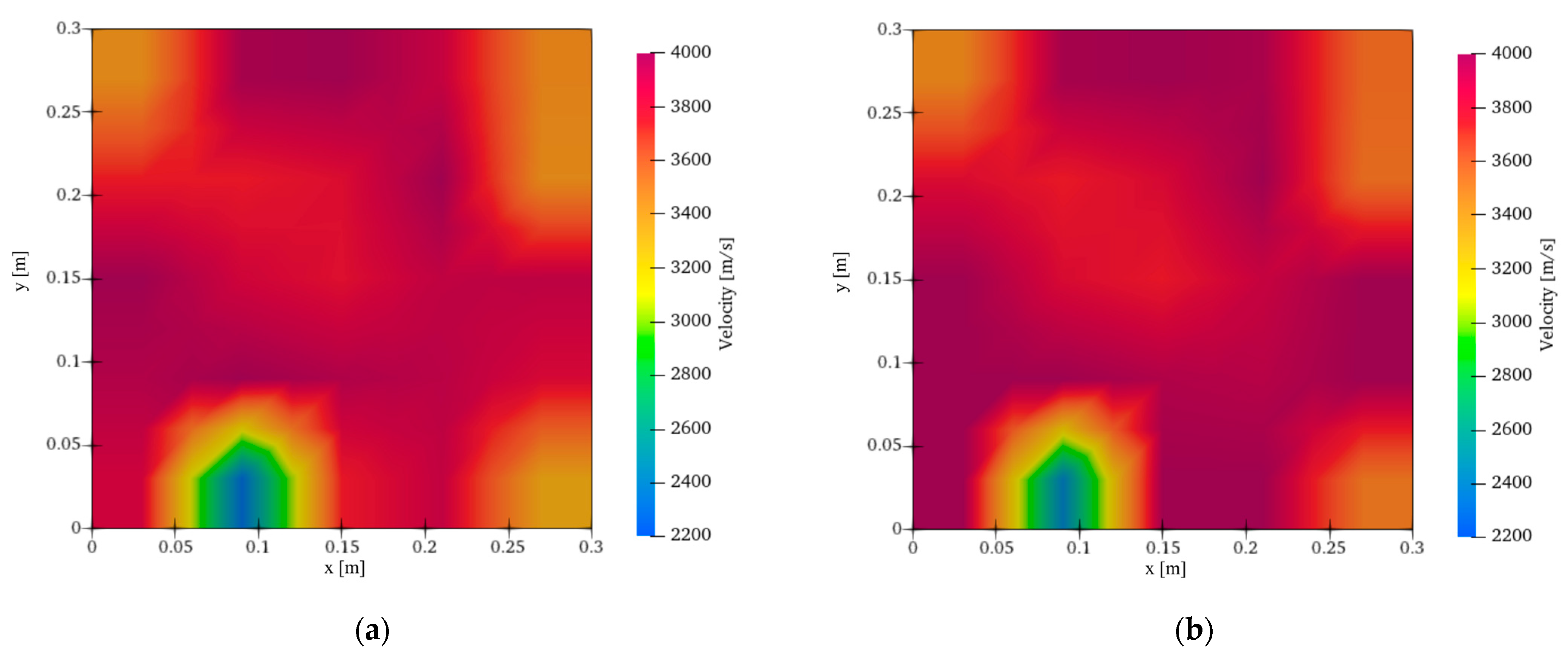
4. Results
4.1. Identification of the Defect Area
4.2. Identification of Undamaged Area
5. Discussion
6. Conclusions
- AET implementing Lagrange interpolation identified the defect and the undamaged area based on the identified velocity distribution. These results indicated that AET implementing Lagrange interpolation could be applied to the actual phenomenon.
- Although conventional AET requires 121 candidates to visualize the defect, AET implementing Lagrange interpolation requires 36 candidates to visualize it. Therefore, in this model test, it was noted that the application of Lagrange interpolation identified the practical velocity distribution using a number of candidates using only about 30% of the candidates required by the conventional AET analysis.
- If the candidate interval of 30 mm was used in the application of Lagrange interpolation, the identified velocity distribution is approximated as the result of conventional AET. These results confirmed that Lagrange interpolation may not contribute to improving the identified velocity distribution if the interval of 30 mm was used.
- In the results of AET obtained from the undamaged area, the low velocity errors were identified around the sensors. It is expected that the low velocity errors can be confirmed if additional AET analyses are conducted in a relocated analysis area or if accurate arrival times are applied.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shigeishi, M.; Colombo, S.; Broughton, K.J.; Rutledge, H.; Batchelor, A.J.; Forde, M.C. Acoustic emission to assess and monitor the integrity of bridges. Constr. Build. Mater. 2001, 15, 35–49. [Google Scholar] [CrossRef]
- Liu, R.; Li, S.; Zhang, G.; Jin, W. Depth detection of void defect in sandwich-structured immersed tunnel using elastic wave and decision tree. Constr. Build. Mater. 2021, 305, 124756. [Google Scholar] [CrossRef]
- Usui, T.; Ueda, Y.; Takamine, H.; Watabe, K.; Shiotani, T. Continuous Health Monitoring of Reinforced Concrete Bridge Deck based on Traffic Load-induced Acoustic Emission. In Proceedings of the 36th Conference of the European Working Group on Acoustic Emission, Potsdam, Germany, 18–20 September 2024; Volume 29. [Google Scholar] [CrossRef]
- Hashimoto, K.; Shiotani, T.; Nishida, T.; Miyagawa, T. Application of Elastic-Wave Tomography to Repair Inspection in Deteriorated Concrete Structures. J. Disaster Res. 2017, 12, 496–505. [Google Scholar] [CrossRef]
- Perlin, L.P.; de Andrade Pinto, R.C. Use of network theory to improve the ultrasonic tomography in concrete. Ultrasonics 2019, 96, 185–195. [Google Scholar] [CrossRef] [PubMed]
- Sassa, K. Suggested for seismic testing within and between boreholes. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1988, 25, 447–472. [Google Scholar] [CrossRef]
- Sanny, T.A.; Sassa, K. Detection of fault structure under a near-surface low velocity layer by seismic tomography: Synthetics studies. J. Appl. Geophys. 1996, 35, 117–131. [Google Scholar] [CrossRef]
- Schubert, F. Basic principles of acoustic emission tomography. J. Acoust. Emiss. 2024, 22, 147–158. [Google Scholar]
- Kobayashi, Y.; Shiotani, T. Computerized AE Tomography, Innovative AE and NDT Techniques for On-Site Measurement of Concrete and Masonry Structures: State-of-the-Art Report of the RILEM Technical Committee 239-MCM, 1st ed.; Ohtsu, M., Ed.; Springer: Dordrecht, The Netherlands, 2016; pp. 47–68. [Google Scholar]
- Kobayashi, Y.; Nakamura, K.; Oda, K. New algorithm of Acoustic Emission Tomography that considers change of emission times of AE events during identification of elastic wave velocity distribution. In Proceedings of the 11th International Conference on Bridge Maintenance, Safety and Management, Barcelona, Spain, 11–15 July 2022. [Google Scholar]
- Okude, N.; Shiotani, T.; Nishida, T.; Hashimoto, K.; Furuno, S. Evaluation of Crack Repair Effect for RC Slab Using AE Tomography. Proceedings 2018, 2, 433. [Google Scholar] [CrossRef]
- Cheng, Y.; Hagan, P.; Mitra, R.; Wang, S.; Yang, H.-W. Experimental Investigation of Progressive Failure Processes Using 3D Acoustic Emission Tomography. Front. Earth Sci. 2021, 9, 765030. [Google Scholar] [CrossRef]
- Kundu, T. Acoustic source localization. Ultrasonics 2014, 54, 25–38. [Google Scholar] [CrossRef]
- Manuello, A.; Gianni, N.; Carpinteri, A. AE monitoring of a concrete arch road tunnel: Damage evolution and localization. Eng. Fract. Mech. 2019, 210, 279–287. [Google Scholar] [CrossRef]
- Rodríguez, P.; Celestino, T.B. Assessment of damage distribution in brittle materials by application of an improved algorithm for three-dimensional localization of acoustic emission sources with P-wave velocity calculation. Constr. Build. Mater. 2020, 231, 117086. [Google Scholar] [CrossRef]
- Sagradyan, A.; Ogura, N.; Shiotani, T. Application of elastic wave tomography method for damage evaluation in a large-scale reinforced concrete structure. Dev. Built Environ. 2023, 14, 100127. [Google Scholar] [CrossRef]
- Xie, C.; Yuan, L.; Zhao, M.; Jia, Y. Study on failure mechanism of porous concrete based on acoustic emission and discrete element method. Constr. Build. Mater. 2020, 235, 117409. [Google Scholar] [CrossRef]
- Song, Z.; Li, S.; Cheng, L.; Yu, Q. Corrosion-induced deterioration and fracture mechanisms in ultra-high-performance fiber-reinforced concretet. Constr. Build. Mater. 2024, 423, 135886. [Google Scholar] [CrossRef]
- Nie, Q.; Liu, H.; Ma, T.; Cui, H. Experimental study on acoustic emission of steel fiber broken pebble recycled concrete. Constr. Build. Mater. 2024, 452, 138942. [Google Scholar] [CrossRef]
- Nakamura, K.; Furukawa, M.; Oda, K.; Shigemura, S.; Kobayashi, Y. Implementation of lagrange interpolation for optimization of computational resource used in ae tomography. In Proceedings of the 12th Annual Conference of Society for Structural Integrity and Life (DIVK12), Belgrade, Serbia, 17–19 November 2024. [Google Scholar]
- Sassa, K.; Ashida, Y.; Kozawa, T.; Yamada, M. Improvement in the accuracy of seismic tomography by use of an effective ray-tracing algorithm. In Proceedings of the MMIJ/IMM JOINT SYMPOSIUM, Today’s Technology for the Mining and Metallurgical Industries, Kyoto, Japan, 2–4 October 1989; pp. 129–136. [Google Scholar]
- JIS A 5372:2016; Precast Reinforced Concrete Products. Japanese Standards Association: Tokyo, Japan, 2016.
- Tian, H.; Qiang, P.; Xiandong, L.; Yingchun, S. AE beamforming method for damage inspection of aircraft structures. Procedia Eng. 2011, 17, 297–302. [Google Scholar] [CrossRef]
- Xiao, D.; He, T.; Pan, Q.; Liu, X.; Wang, J.; Shan, Y. A novel acoustic emission beamforming method with two uniform linear arrays on plate-like structures. Ultrasonics 2014, 54, 737–745. [Google Scholar] [CrossRef]
- Mirgal, P.; Pal, J.; Banerjee, S. Online acoustic emission source localization in concrete structures using iterative and evolutionary algorithms. Ultrasonics 2020, 108, 106211. [Google Scholar] [CrossRef]
- Physical Acoustics Corporation. AEwin Software User’s Manual, Express-8 AE System; Physical Acoustics Corporation: Princeton Junction, NJ, USA, 2014. [Google Scholar]
- Nakamura, K.; Kobayashi, Y.; Oda, K.; Shigemura, S. Application of Classified Elastic Waves for AE Source Localization Based on Self-Organizing Map. Appl. Sci. 2023, 13, 5745. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Takanami, T.; Kitagawa, G. A new efficient procedure for the estimation of onset times of seismic waves. J. Phys. Earth 1988, 36, 267–290. [Google Scholar] [CrossRef]
- Ohno, K.; Uji, K.; Ueno, A.; Ohtsu, M. Fracture process zone in notched concrete beam under three-point bending by acoustic emission. Constr. Build. Mater. 2014, 67, 139–145. [Google Scholar] [CrossRef]
- Jones, M.R.; Rogers, T.J.; Worden, K.; Cross, E.J. A Bayesian methodology for localising acoustic emission sources in complex structures. Mech. Syst. Signal Process. 2022, 15, 108143. [Google Scholar] [CrossRef]
- Tatsumi, E.; Nakata, Y.; Kawatani, S. Study on method for estimating compressive strength of concrete by impact elastic wave: Influence of variations of concrete materials and mix proportions on elastic wave velocity. J. Struct. Constr. Eng. 2005, 587, 15–21. (In Japanese) [Google Scholar] [CrossRef]
- Qixian, L.; Bungey, J.H. Using compression wave ultrasonic transducers to measure the velocity of surface waves and hence determine dynamic modulus of elasticity for concrete. Constr. Build. Mater. 1996, 10, 237–242. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Oda, K.; Nakamura, K. A Source Localization Technique Based on a Ray-Trace Technique with Optimized Resolution and Limited Computational Costs. Proceedings 2018, 2, 477. [Google Scholar] [CrossRef]
- Martin, J.; Hardy, M.S.A.; Usmani, A.S.; Forde, M.C. Accuracy of NDE in bridge assessment. Eng. Struct. 1998, 20, 979–984. [Google Scholar] [CrossRef]



| Analysis Area | Number of PLB Points | Number of Used Events |
|---|---|---|
| Defect area | 159 | 159 |
| Undamaged area | 168 | 159 |
| Case | Method | Interval of Candidates [mm] | Number of Candidates | Percentage Velocity Error [%] |
|---|---|---|---|---|
| C60D | Conventional AET | 60 | 36 | 25 |
| L60D | Application of Lagrange Interpolation | 60 | 36 | 8.4 |
| C30D | Conventional AET | 30 | 121 | 5.3 |
| L30D | Application of Lagrange Interpolation | 30 | 121 | 6.2 |
| Case | Method | Interval of Candidates [mm] | Number of Candidates | Percentage Velocity Error [%] |
|---|---|---|---|---|
| C60S | Conventional AET | 60 | 36 | 10 |
| L60S | Application of Lagrange Interpolation | 60 | 36 | 10 |
| C30S | Conventional AET | 30 | 121 | 11 |
| L30S | Application of Lagrange Interpolation | 30 | 121 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakamura, K.; Furukawa, M.; Oda, K.; Shigemura, S.; Kobayashi, Y. Validation of Acoustic Emission Tomography Using Lagrange Interpolation in a Defective Concrete Specimen. Appl. Sci. 2025, 15, 8965. https://doi.org/10.3390/app15168965
Nakamura K, Furukawa M, Oda K, Shigemura S, Kobayashi Y. Validation of Acoustic Emission Tomography Using Lagrange Interpolation in a Defective Concrete Specimen. Applied Sciences. 2025; 15(16):8965. https://doi.org/10.3390/app15168965
Chicago/Turabian StyleNakamura, Katsuya, Mikika Furukawa, Kenichi Oda, Satoshi Shigemura, and Yoshikazu Kobayashi. 2025. "Validation of Acoustic Emission Tomography Using Lagrange Interpolation in a Defective Concrete Specimen" Applied Sciences 15, no. 16: 8965. https://doi.org/10.3390/app15168965
APA StyleNakamura, K., Furukawa, M., Oda, K., Shigemura, S., & Kobayashi, Y. (2025). Validation of Acoustic Emission Tomography Using Lagrange Interpolation in a Defective Concrete Specimen. Applied Sciences, 15(16), 8965. https://doi.org/10.3390/app15168965







