Assessing Voided Reinforced Concrete by Numerical Modelling of Impact-Generated Rayleigh Waves
Abstract
Featured Application
Abstract
1. Introduction
2. Simulation Model
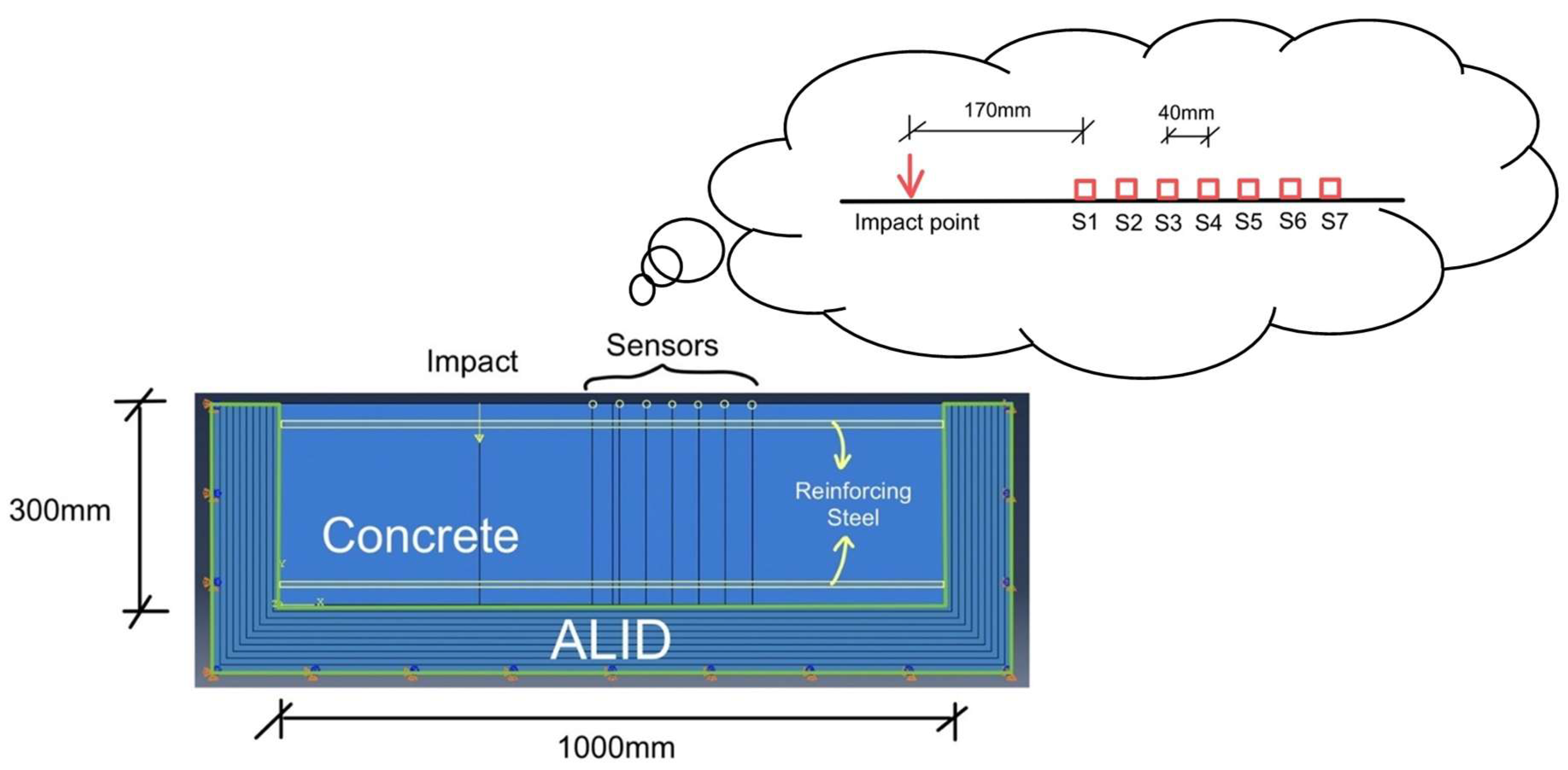
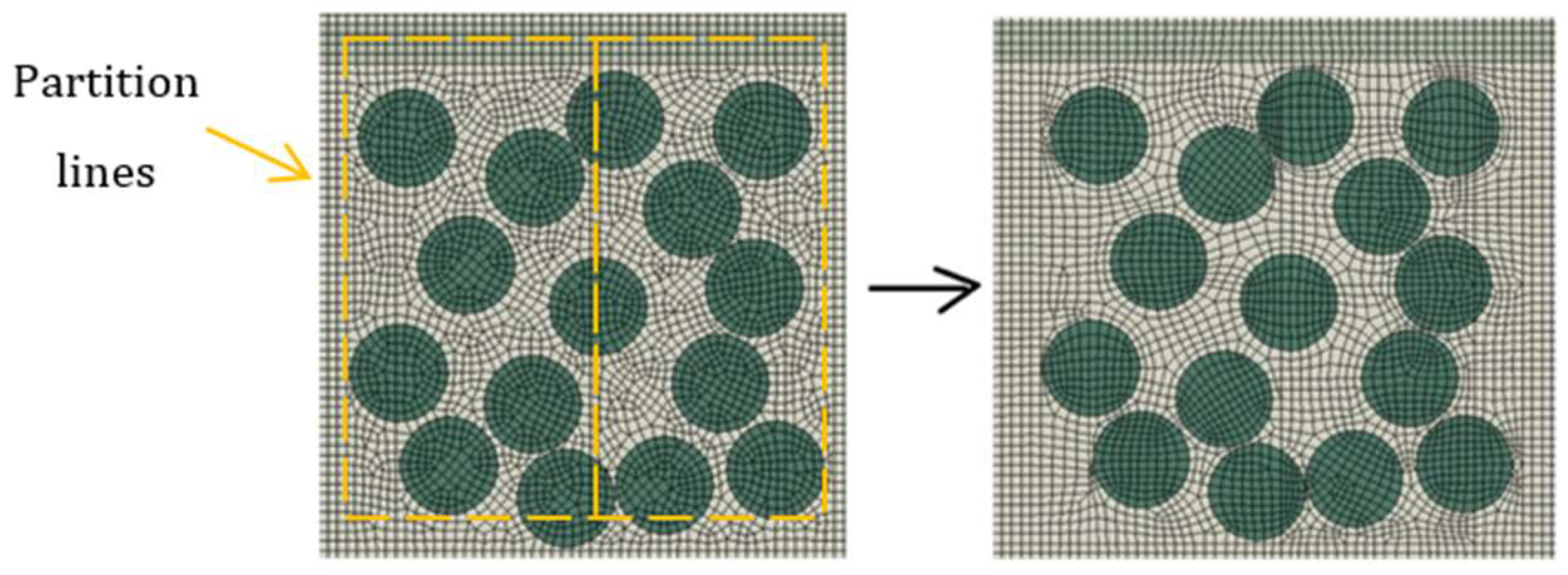
2.1. Reinforced Concrete Model
2.2. Element Type, Size and Wave Velocity
2.3. Explicit Simulation Time Control Parameters
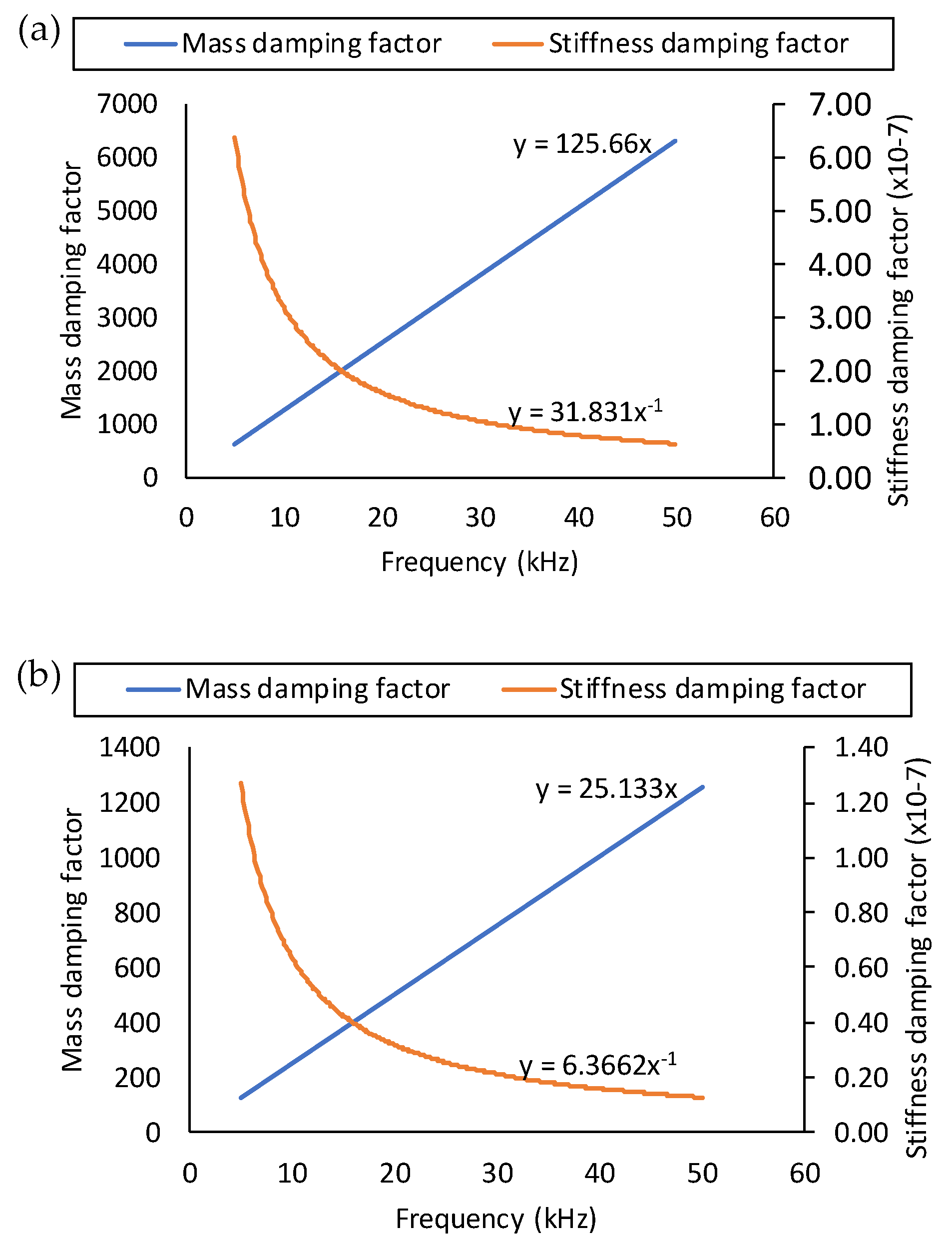
2.4. Material Properties and Damping Coefficients
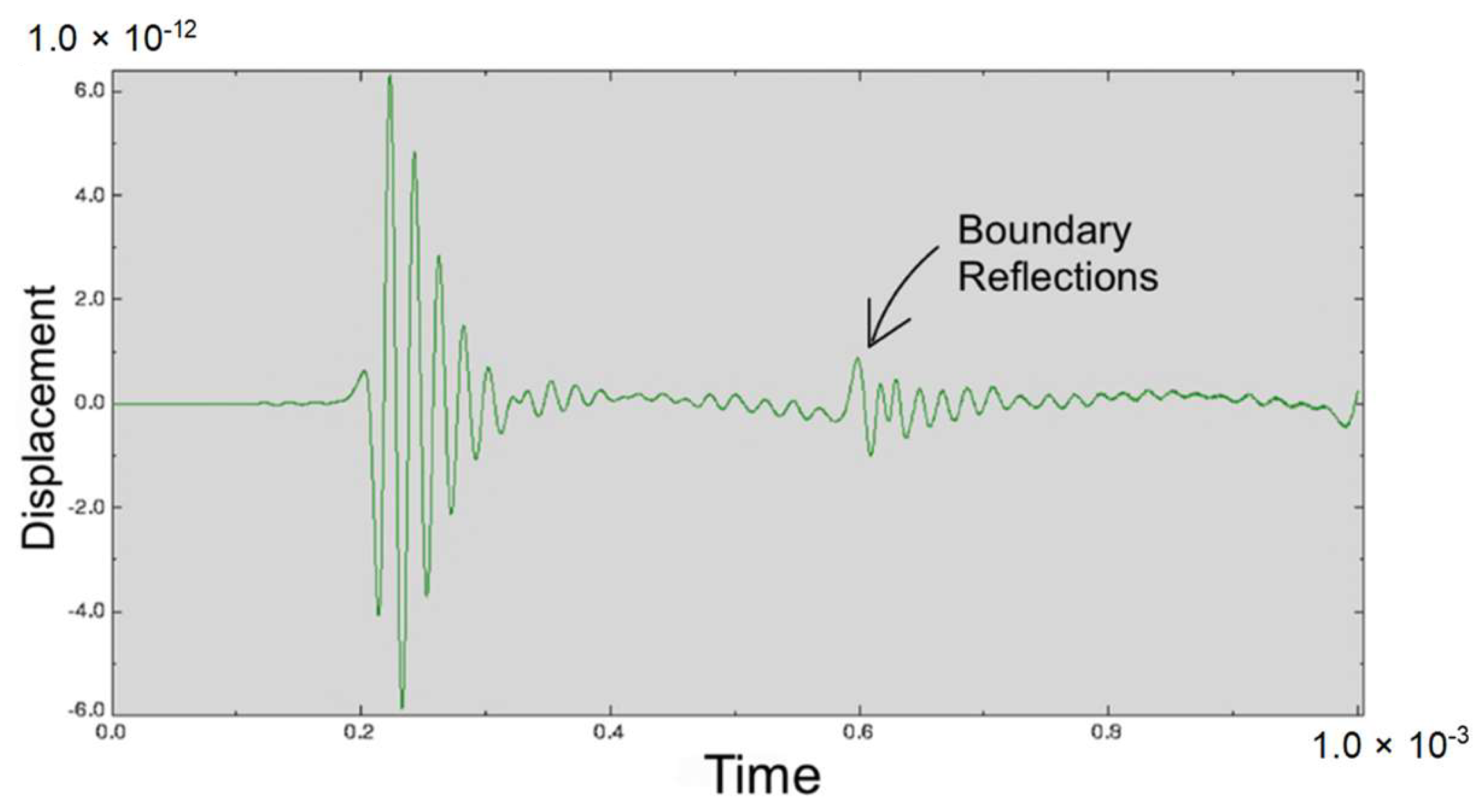
2.5. Model Boundary Conditions
3. Experimental Validation
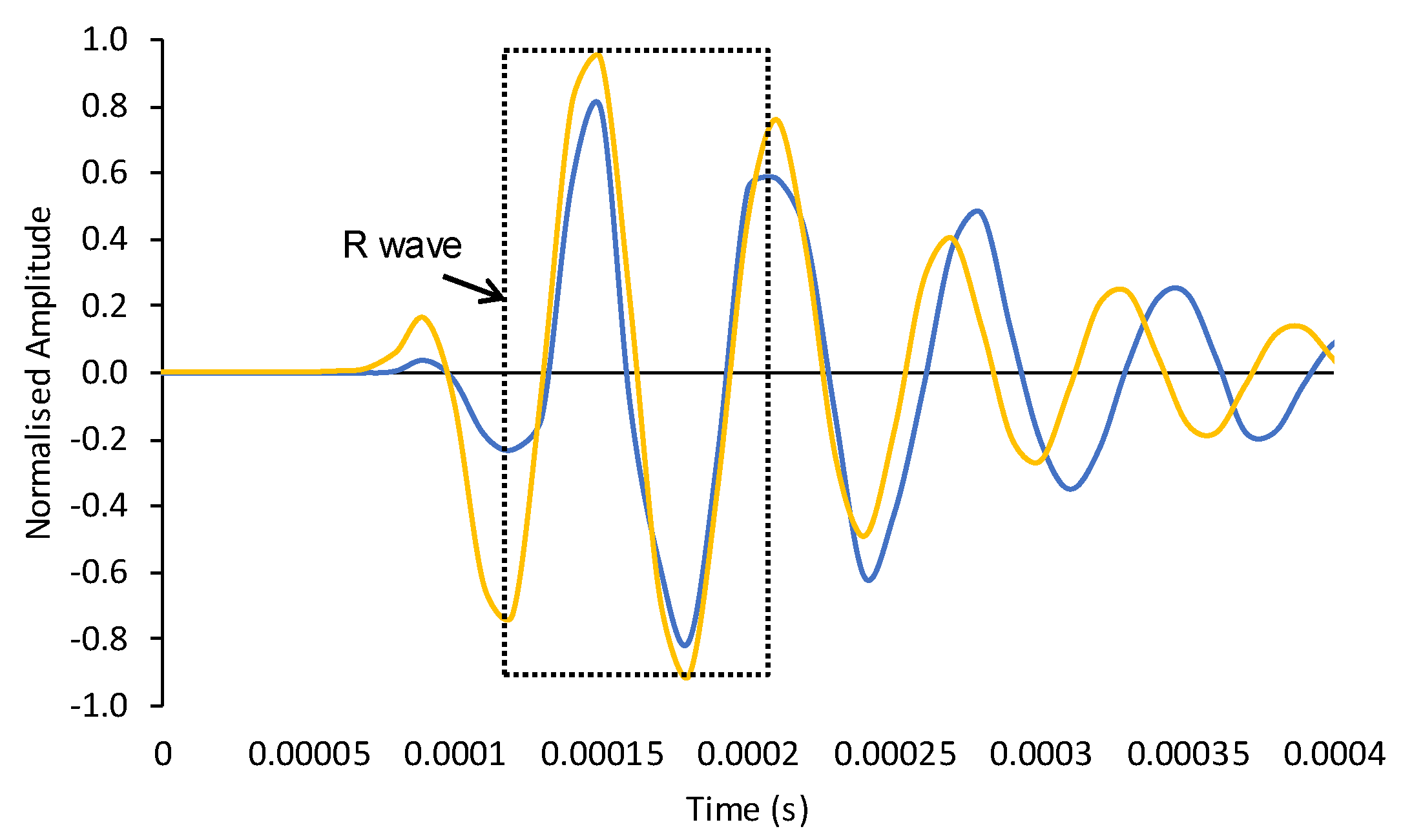
3.1. Waveform Calibration
3.2. Wave Velocity
4. Results of Simulations and Discussion
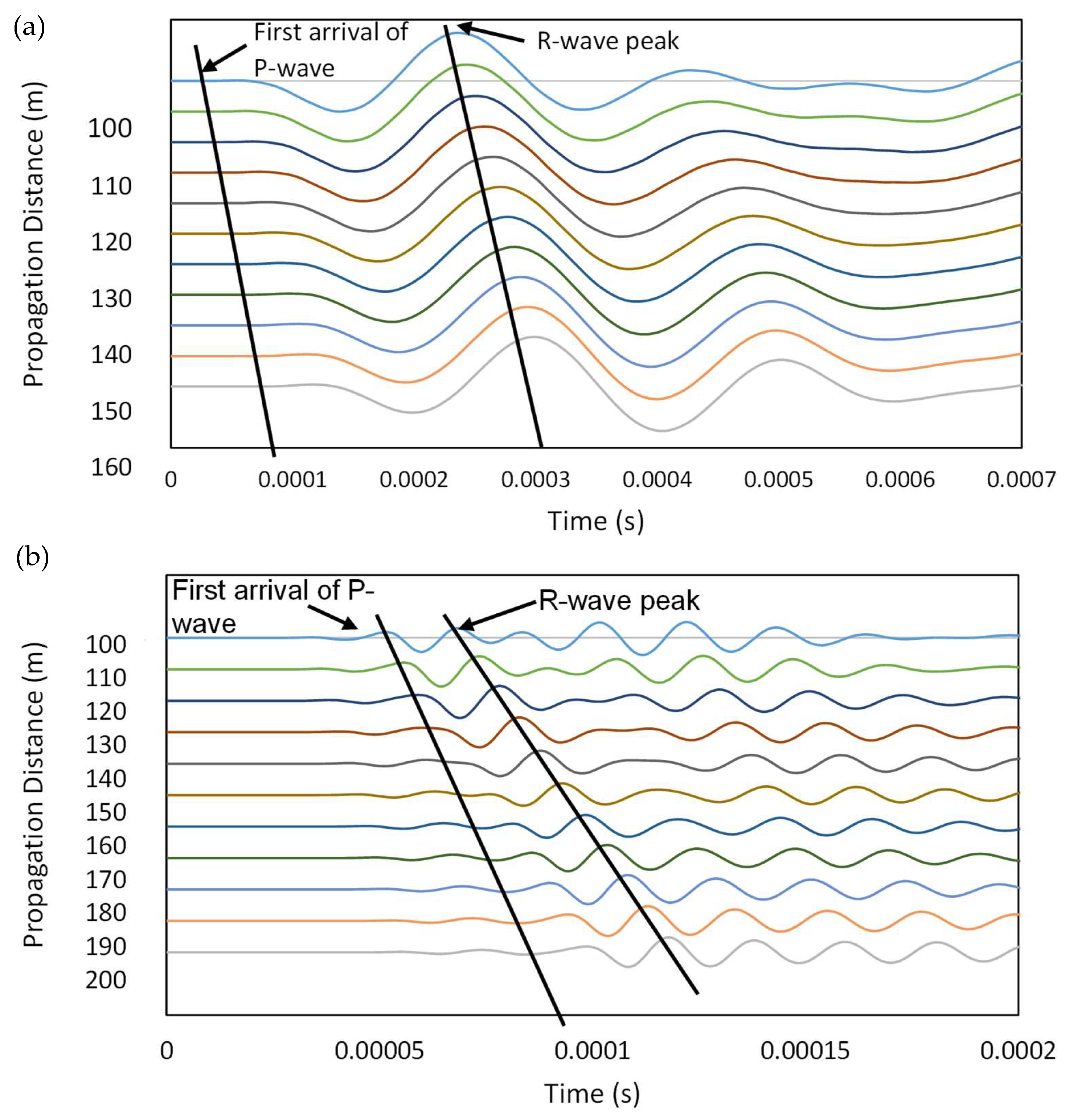
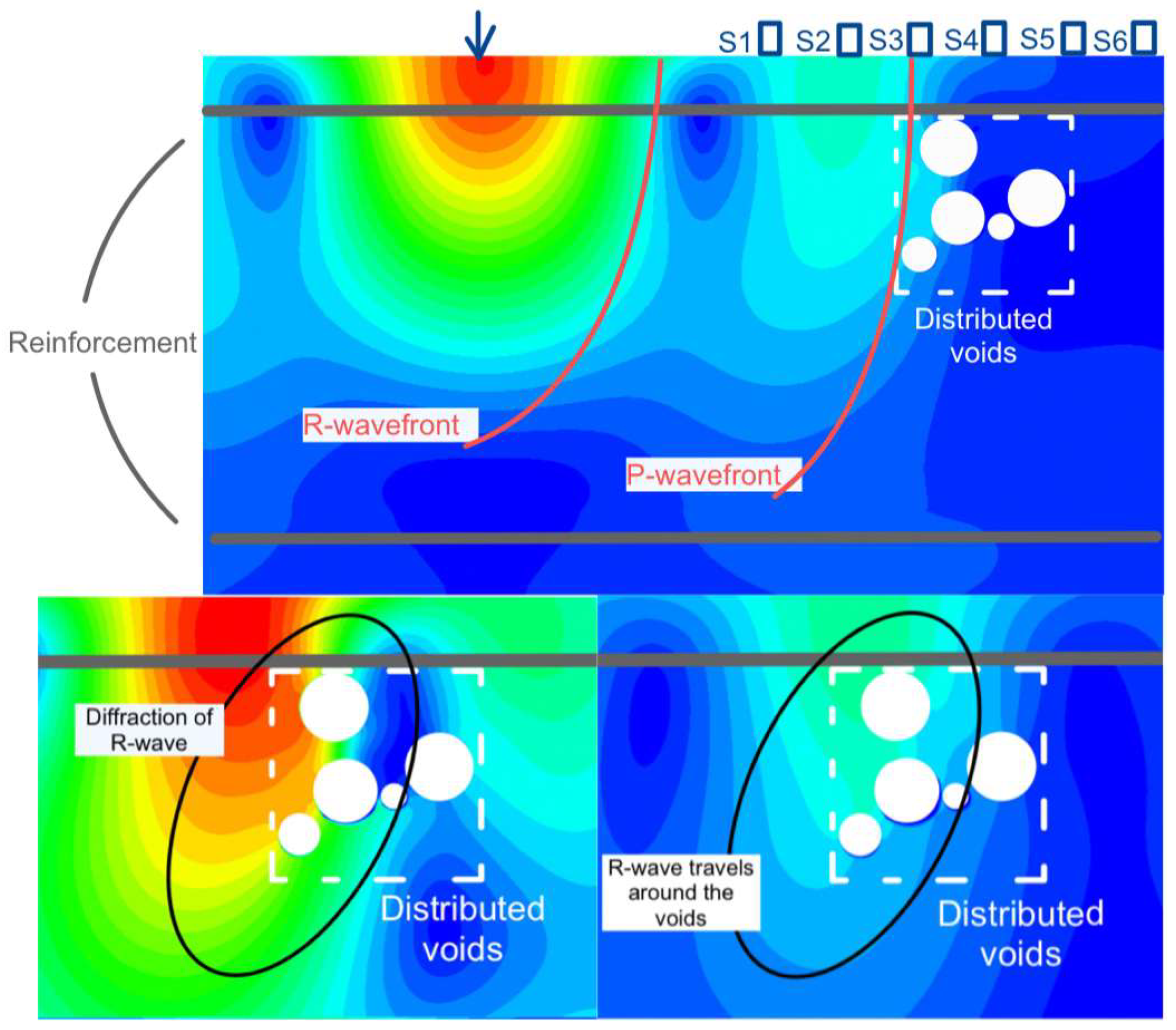
4.1. Near-Field Effect Study
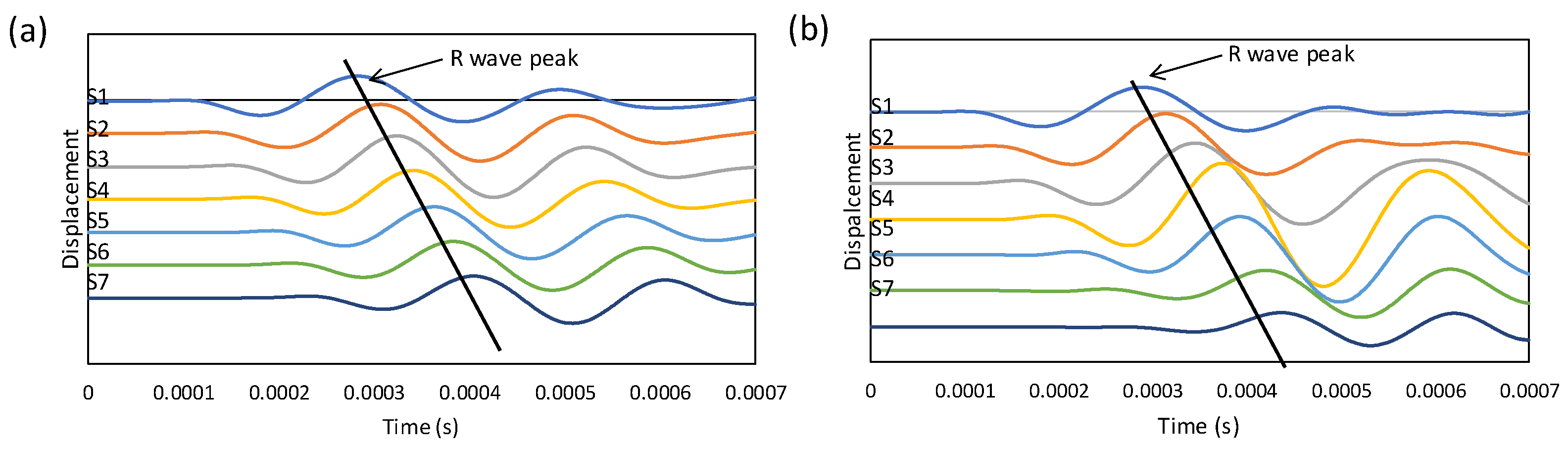
4.2. Time-Domain Data
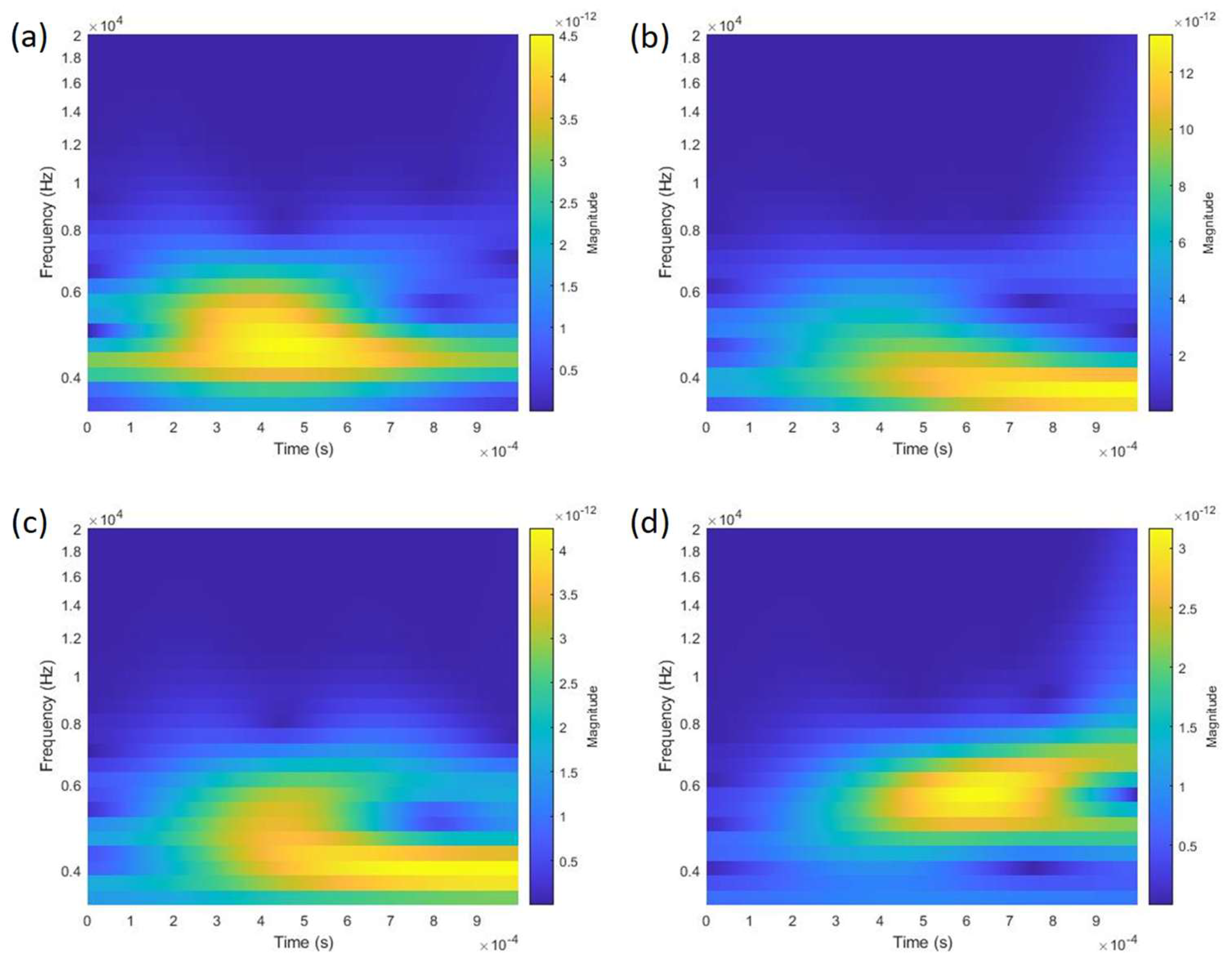
4.3. Frequency Domain Analysis
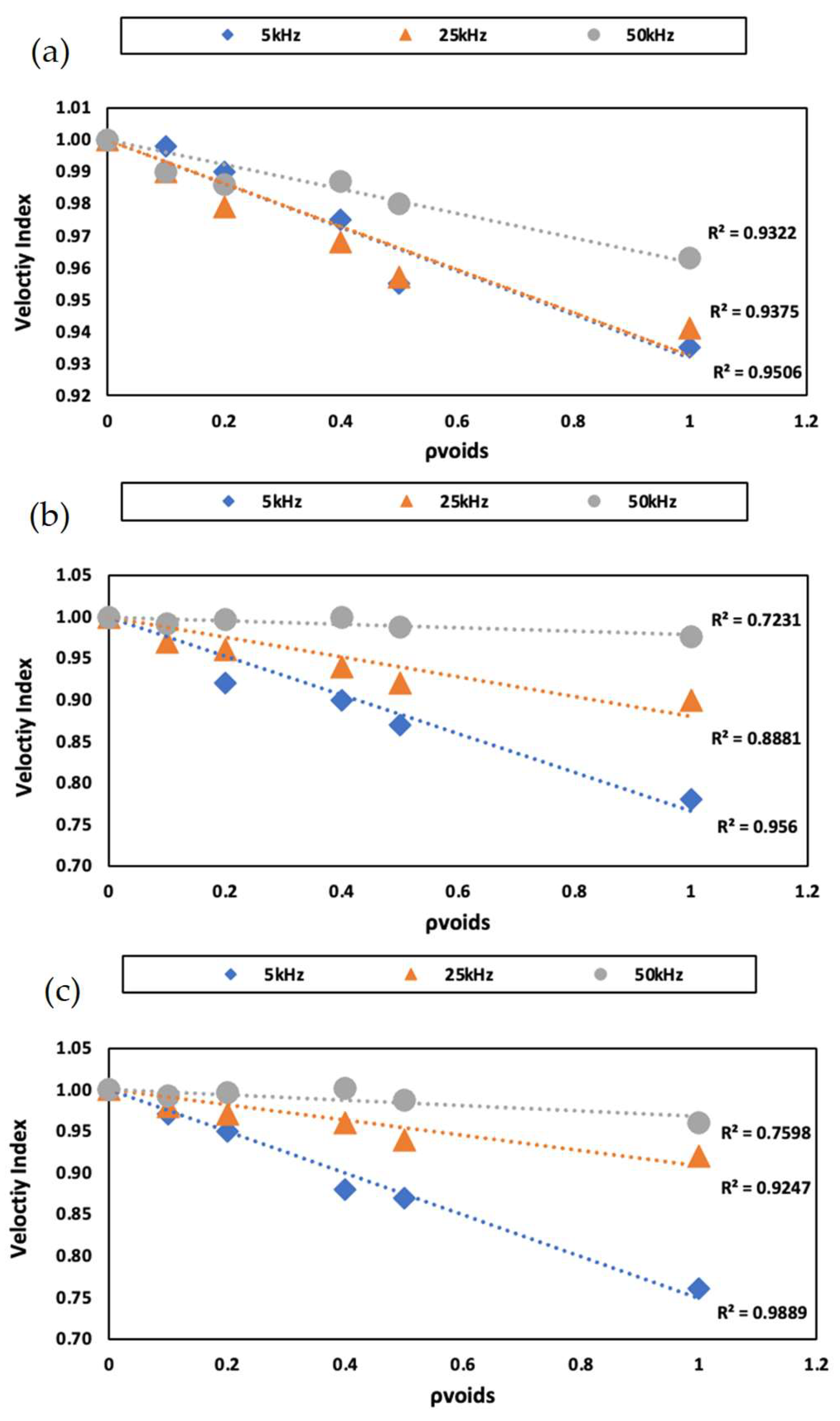
4.4. Correlation with Velocity Index
5. Feasibility of Modelling Framework
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 2D | Two-dimensional |
| NDT | Non-destructive test |
| R-wave | Rayleigh wave |
| RC | Reinforced concrete |
References
- Artola, I.; Rademaekers, K.; Williams, R.; Yearwood, J. Boosting Building Renovation: What Potential and Value for Europe; European Parliament: Brussels, Belgium, 2016. [Google Scholar]
- Lee, F.W.; Chai, H.K.; Tan, T.H. Feasibility Study on Evaluating Surface Opening Cracks in Concrete by Multi-Channel Instrumented Surface Rayleigh Wave Propagation. Adv. Struct. Eng. 2014, 17, 785–799. [Google Scholar]
- Dwivedi, S.K.; Vishwakarma, M.; Soni, A. Advances and researches on non destructive testing: A review. Mater. Today Proc. 2018, 5, 3690–3698. [Google Scholar] [CrossRef]
- Miller, G.F.; Pursey, H. On the partition of energy between elastic waves in a semi-infinite solid. Proceeding R. Soc. 1955, 233, 55–69. [Google Scholar]
- Hevin, G.; Abraham, O.; Pedersen, H.A.; Campillo, M. Characterisation of surface cracks with Rayleigh waves: A numerical model. NDT E Int. 1998, 31, 289–297. [Google Scholar]
- Carino, N.J.; Sansalone, M.; Hsu, N.N. A point source point receiver pulse-echo technique for flaw detection in concrete. ACI J. Proc. 1986, 83, 199–208. [Google Scholar]
- Carino, N.J.; Sansalone, M. Detection of voids in grouted ducts using the impact-echo method. ACI Mater. J. 1992, 89, 296–303. [Google Scholar]
- Lefever, G.; Snoeck, D.; De Belie, N.; Van Vlierberghe, S.; Van Hemelrijck, D.; Aggelis, D.G. The contribution of elastic wave NDT to the characterisation of modern cementitious media. Sensors 2020, 20, 2959. [Google Scholar] [CrossRef] [PubMed]
- Ivanchev, I. Experimental determination of concrete compressive strength by non-destructive ultrasonic pulse velocity method. Int. J. Res. Appl. Sci. Eng. Technol. 2018, 6, 2647–2651. [Google Scholar]
- Eraky, A.; Samir, R.; El-Deeb, W.S.; Salama, A. Determination of Surface and Sub-Surface Cracks Location in Beams Using Rayleigh-Waves. Prog. Electromagn. Res. C 2018, 80, 233–247. [Google Scholar]
- Chai, H.K.; Liu, K.F.; Behnia, A.; Yoshikazu, K.; Shiotani, T. Development of a tomography technique for assessment of the material condition of concrete using optimised elastic wave parameters. Materials 2016, 9, 291. [Google Scholar] [CrossRef] [PubMed]
- Zerwer, A.; Polak, M.A.; Santamarina, J.C. Rayleigh Wave Propagation for the Detection of Near Surface Discontinuities: Finite Element Modeling. J. Non-Destr. Eval. 2003, 22, 39–52. [Google Scholar]
- Lee, F.W.; Chai, H.K.; Lim, K.S. Characterising concrete surface notch using Rayleigh wave phase velocity and wavelet parametric analyses. Constr. Build. Mater. 2017, 136, 627–642. [Google Scholar]
- Semechko, A. Fill Area with Random Circles Having Different Diameters. 2018. Available online: https://uk.mathworks.com/matlabcentral/answers/405186-fill-area-with-random-circles-having-different-diameters (accessed on 14 April 2021).
- SIMULIA. Getting Started with Abaqus Intetactive Edition Version 6.8, s.l.; Dassault Systemes: Johnston, RI, USA, 2008. [Google Scholar]
- Petyt, M. Forced response, I. In Introduction to Finite Element Vibration Analysis; Cambridge University Press: New York, NY, USA, 1990; pp. 386–449. [Google Scholar]
- Bathe, K. Finite Element Procedures; Prentice Hall: Saddle River, NJ, USA, 1996. [Google Scholar]
- Bathe, K.J.; Wilson, E.L. Stability and accuracy analysis of direct integration methods. Earthq. Eng. Struct. Dyn. 1972, 1, 283–291. [Google Scholar]
- Swanson Analysis Systems. ANSYS User’s Manual for Revision 5.0; Swanson Analysis Systems: Houston, TX, USA, 1992. [Google Scholar]
- Oh, T. Numerical Models Are Helpful in Simulating a Large Number of Combination of Parameters, Such as Wave Frequency and Defect Properties, to Aid the Process of Investigating the Change of Rayleigh Wave Properties Against Different Defect Characteristics; University of Illinois: Champaign, IL, USA, 2007. [Google Scholar]
- Drozdz, M.B. Efficient Finite Element Modelling of Ultrasound Waves in Elastic Media; Imperial College London: London, UK, 2008. [Google Scholar]
- Courant RFriedrichs, K.; Lewy, H. Über die partiellen Differenzengleichungen der mathematischen Physik. Math. Ann. 1928, 100, 32–74. [Google Scholar] [CrossRef]
- Mahrenholtz, O.; Bachmann, H. Overall damping of a structure. In Vibration Problems in Structures Practical Guidelines Practical Guidelines; Birkäuser: Basel, Switzerland, 1995; pp. 166–168. [Google Scholar]
- Rajagopal, P.; Drozdz, M.; Skelton, E.A.; Lowe, M.J.; Craster, R.V. On the use of absorbing layers to simulate the propagation of elastic waves in unbounded isotropic media using commercially available Finite Element packages. NDT E Int. 2012, 51, 30–40. [Google Scholar] [CrossRef]
- Mohseni, H.; Ng, C.-T. Rayleigh wave propagation and scattering characteristics at debondings in fibre-reinforced polymer-retrofitted concrete structures. Struct. Health Monit. 2018, 18, 303–317. [Google Scholar]
- Sansalone, M.; Carino, N.J.; Hsu, N.N. A Finite Element Study Transient Wave Propagation in Plates. J. Res. Natl. Bur. Stand. 1987, 92, 267–278. [Google Scholar]
- Lee FW Lim, K.S.; Chai, H.K. Determination and extraction of Rayleigh-waves for concrete cracks characterisation based on matched filtering of center of energy. J. Sound Vib. 2016, 363, 303–315. [Google Scholar]
- Jones, R. Non-Destructive Testing of Concrete; Cambridge University Press: London, UK, 1962. [Google Scholar]
- Park, H.C. Development of a Microfluidic Mixer and Applications to Rapid Kinetic Studies of Calmodulin. Ph.D. Thesis, Korea Advanced Institute of Science and Technology, Daejeon, Republic of Kores, 2001. [Google Scholar]
- Sansalone, M.J.; Streett, W.B. Impact-Echo; Bullbrier Press: Ithaca, NY, USA, 1997. [Google Scholar]
- Leiber, C.-O.; Dobratz, B. Assessment of Safety and Risk with a Microscopic Model of Detonation; Elsevier: Amsterdam, The Netherlands, 2003; pp. 41–78. [Google Scholar]
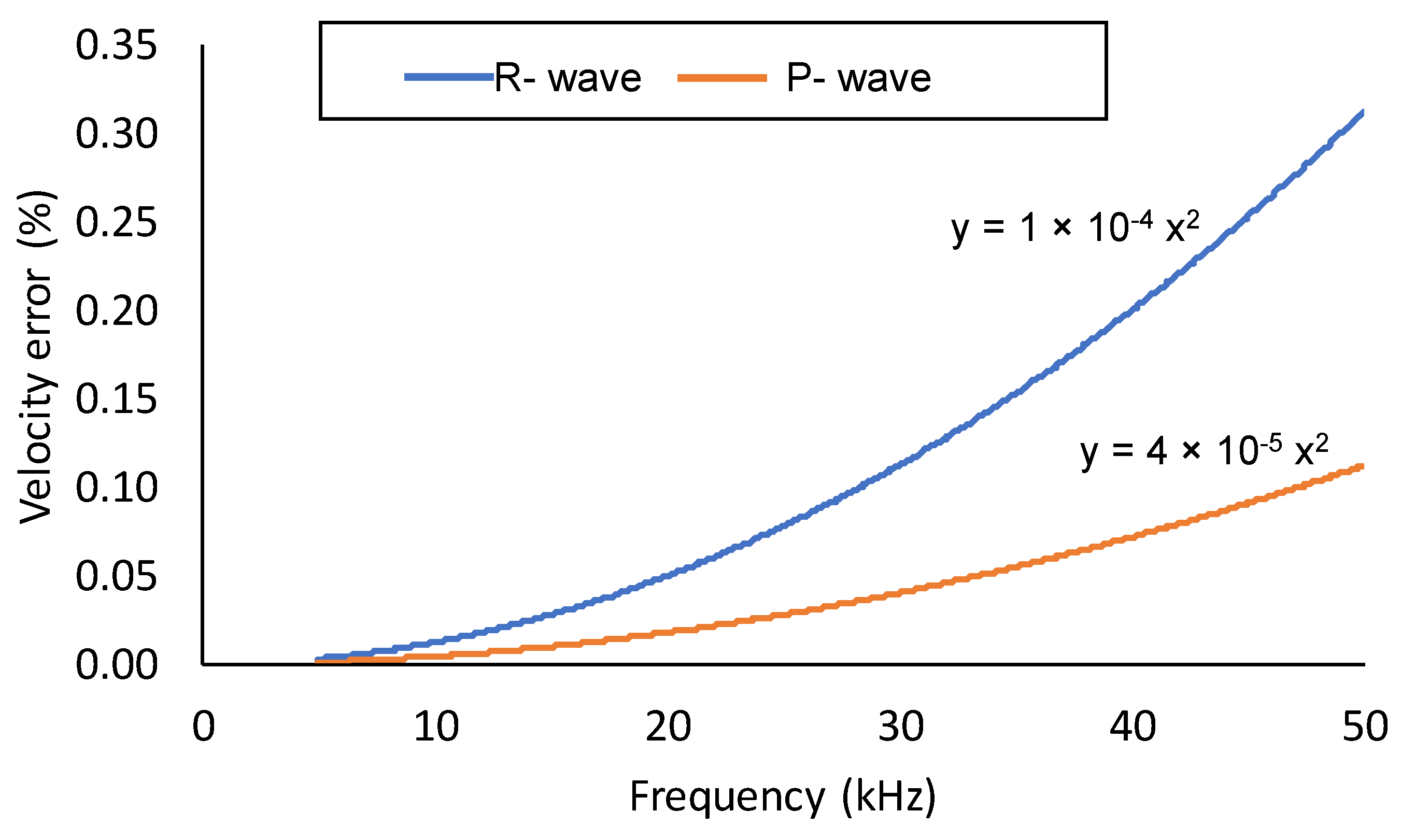
| fmax (kHz) | (m) | NR | (m) | NP |
|---|---|---|---|---|
| 50 | 0.048 | 24 | 0.080 | 40 |
| Concrete Properties | |
|---|---|
| Density (kg m−3) | 2313 |
| Young’s modulus (Pa) | 28 × 109 |
| Poisson’s ratio | 0.2 |
| Steel properties | |
| Density (kg m−3) | 7850 |
| Young’s modulus (Pa) | 200 × 109 |
| Poisson’s ratio | 0.3 |
| Air properties | |
| Density (kg m−3) | 1.225 |
| Bulk modulus (Pa) | 142,000 |
| Theoretical | Concrete | Reinforcing Steel |
|---|---|---|
| 3667 | 5856 | |
| (m/s) | 2047 | 2904 |
| Experimental | ||
| 4286 | 6099 | |
| 2308 | 3220 | |
| Numerical | ||
| 3940 | 5707 | |
| 2000 | 2778 |
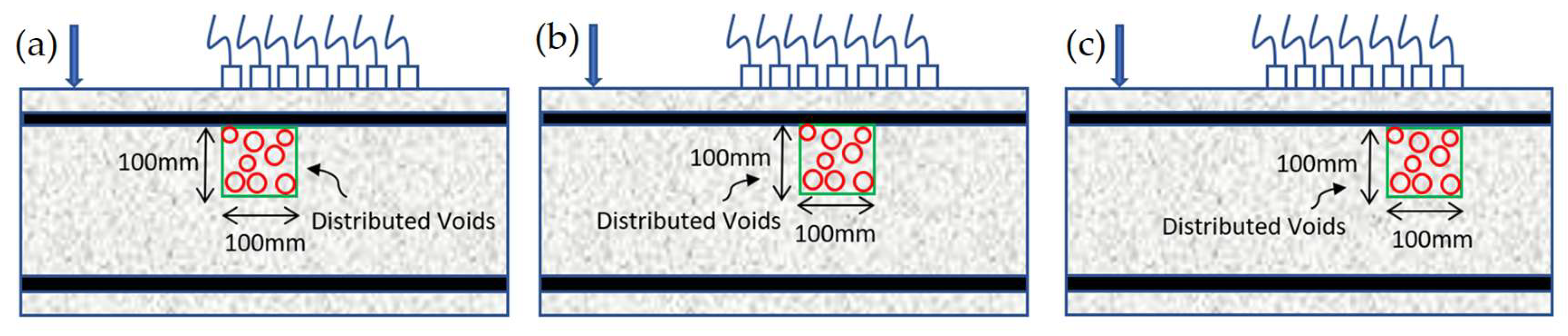
| Model | Defect Type | Wave Frequency (kHz) | Defective Area Density (% of Void) | Defect Depth from Surface (mm) | Defect Location |
|---|---|---|---|---|---|
| Sound RC | / | 5, 25 and 50 | / | / | / |
| Voided RC | Distributed Voids | 10, 20, 40, 50, 100% | 84 | Between S1 and S3; S3 and S5; S5 and S7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Y.; Chai, H.K.; Lee, F.W. Assessing Voided Reinforced Concrete by Numerical Modelling of Impact-Generated Rayleigh Waves. Appl. Sci. 2025, 15, 3635. https://doi.org/10.3390/app15073635
Ye Y, Chai HK, Lee FW. Assessing Voided Reinforced Concrete by Numerical Modelling of Impact-Generated Rayleigh Waves. Applied Sciences. 2025; 15(7):3635. https://doi.org/10.3390/app15073635
Chicago/Turabian StyleYe, Ying, Hwa Kian Chai, and Foo Wei Lee. 2025. "Assessing Voided Reinforced Concrete by Numerical Modelling of Impact-Generated Rayleigh Waves" Applied Sciences 15, no. 7: 3635. https://doi.org/10.3390/app15073635
APA StyleYe, Y., Chai, H. K., & Lee, F. W. (2025). Assessing Voided Reinforced Concrete by Numerical Modelling of Impact-Generated Rayleigh Waves. Applied Sciences, 15(7), 3635. https://doi.org/10.3390/app15073635







