Abstract
Controlling legged robots to run at high speeds or to traverse complex terrains remains challenging due to the difficulty of handling the interaction between the robot and the ground. Impedance control and model predictive control are widely used to account for ground reaction forces (GRFs) during dynamic locomotion. This paper introduces a model predictive impedance control (MPIC) method that combines the advantages of both strategies and applies it to a quadruped robot. The proposed approach reformulates MPIC within the single rigid body model (SRBM) framework and derives linear inequality constraints for the equivalent wrench, allowing explicit consideration of GRF limits while retaining compliant behavior against ground impacts and external disturbances. Furthermore, a novel optimized gait pattern based on a simplified dynamic model is introduced to minimize the effect of GRFs on the robot. The resulting gait improves stability compared to conventional gait patterns while maintaining a similar level of energy efficiency. The proposed method is validated through various simulations under diverse conditions. The results demonstrate that it enables the quadruped robot to run at a speed of 12 m/s while maintaining stability against repeated lateral disturbances.
1. Introduction
Quadrupedal locomotion is an attractive mode of mobility due to several distinct advantages over wheeled or tracked systems. Quadrupedal animals are capable of running effectively on complex terrains such as stairs, sand, and gravel, and can overcome obstacles like cliffs, crevices, and large barriers that conventional mobile robots cannot. Additionally, some animals can run at speeds comparable to wheeled robots.
Nevertheless, quadruped robots have not been widely adopted in practical applications because their stability is not guaranteed in complex environments where their advantages are evident, and their speed on flat terrain remains relatively low. To the best of our knowledge, the fastest running robot has achieved a speed of 6.4 m/s [1]. Even in simulation, the highest speed validated in our previous work was 7.5 m/s [2]. The primary difficulty in enabling robots to run at high speeds or navigate complex terrains is maintaining stability while accounting for interactions between the robot and the ground.
Impedance control is a widely adopted method for maintaining the stability of robots while accounting for interactions with the ground. In particular, it has been extensively studied since the early stages of bipedal robot research, primarily due to the inherent instability of bipedal locomotion. Representative early works on applying impedance control to bipedal robots include the use of virtual model control, a type of impedance control, to achieve compliant motion [3], and the application of impedance control to cope with ground reaction forces (GRFs) and sudden external disturbances during walking [4,5].
Impedance control has been broadly applied to quadruped robots as well. Studies implementing impedance control on the legs of quadruped robots to achieve compliant control considering external impacts [6,7,8] have demonstrated that robots can maintain stability while running or performing in-place jumps [9]. Similarly, simulation studies [10] and experiments with quadruped robots constrained to the sagittal plane [11] confirmed that the robots could maintain stability against large GRFs while running at speeds up to 6 m/s. The same research group also investigated the effects of impedance parameter values on walking stability and energy efficiency [12].
In addition, unexpected impacts on uneven surfaces such as slopes or stairs are one of the key reasons for applying impedance control to robots. Studies on variable impedance control, which adjusts impedance parameters according to the gait phase of the robot [13], have shown its effectiveness. Similarly, virtual model control approaches for posture control and swing leg tracking [14,15,16] demonstrate that impedance control enables maintenance of stability and overcoming uneven terrain despite unexpected impacts.
Additionally, research on real-time optimization of impedance parameters [17], quadratic programming optimization incorporating GRF constraints along with impedance control [18], task-priority whole-body impedance control based on null space projection [19], the combination of inverse dynamics and impedance control [20], and robust visual servoing of quadruped manipulators [21] are among the recent advances demonstrating the effective application of impedance control to quadruped robots.
Whereas impedance control provides active compliance to the robot, model predictive control (MPC) focuses on explicitly modeling the effects of GRFs to maintain stability. MPC approaches that utilize inverted pendulum models incorporate the concept of the zero moment point to explicitly account for unilateral interactions between the robot and the ground. These approaches enable stable gait transitions [22,23,24] and disturbance rejection [25,26] in quadruped robots. In contrast to simple pendulum models, more complex nonlinear MPC methods that consider the full-body dynamics of the robot along with explicit contact models have also been proposed [27]. A method that combines the advantages of the simple inverted pendulum model and the complex full-body model by integrating both has also been proposed [28], but the single rigid body model (SRBM) remains the most widely used approach.
The use of the SRBM in MPC as a substitute for complex full-body dynamics can be broadly categorized into two approaches. The first is a nonlinear MPC formulation that incorporates leg kinematics, enabling real-time generation of foot trajectories and GRFs to reject disturbances [29,30,31] and perform gap crossing [32,33]. In contrast, the second approach employs convex MPC with predefined leg trajectories, achieving highly dynamic motions such as high-speed galloping [34,35] and backflips [36,37,38], due to its superior computational speed.
Furthermore, an unconstrained MPC method utilizing a linearized SRBM based on variational techniques has been proposed, demonstrating dynamic behaviors such as two-legged balancing [39] and aerial rotations [40]. While MPC approaches employing predefined trajectories have yielded numerous results in dynamic motion generation, studies focusing on walking over uneven terrain [41,42] and on real-time adaptation of MPC parameters through reinforcement learning [43] have also been conducted.
Maintaining robot stability not only requires compliant behavior in response to external disturbances or determining appropriate magnitudes and directions of GRFs, but also necessitates considering the timing and sequence of these forces during the gait cycle. The effect of GRFs on the robot varies significantly not only with their magnitude and direction but also with the timing and sequence of their application. Nevertheless, the number of successful gait patterns employed by quadruped robots remains surprisingly limited.
Although most successful gait patterns are based on those observed in quadrupedal animals, many researchers have attempted to rationalize these patterns and explore improved alternatives. To emulate quadrupedal animal gait patterns, numerous studies have analyzed experimental data from various animals [44,45,46,47]. Although these results have often been directly applied to many robots, additional research has focused on their implications for stability and energy efficiency.
Studies analyzing gait stability have primarily focused on creeping gaits observed at low speeds [48,49,50]. Research focusing on energy efficiency has derived gait patterns through the use of genetic algorithms and other optimization techniques applied to simplified robot models in simulation [51,52,53]. Approaches employing central pattern generators have enabled natural gait transitions in robots by utilizing existing gait patterns [54] or by generating new gait patterns through feedback from leg loading [55,56]. Additionally, reinforcement learning methods have been employed to derive gait patterns that simultaneously optimize stability and energy efficiency [57,58,59].
This paper proposes a method to apply model predictive impedance control (MPIC) that integrates the advantages of two approaches considering GRFs to quadruped robots. Conventional impedance control provides compliance against large impacts or external forces from the ground but typically lacks explicit consideration of GRF constraints. On the other hand, SRBM-based MPC directly considers GRFs and their constraints but lacks sufficient consideration of compliance. The model predictive impedance control (MPIC) proposed in the field of robot manipulators [60,61] can simultaneously possess the advantages of both impedance control and MPC. However, the method originally proposed based on the dynamics of robot manipulators cannot be directly applied to quadruped robots.
To address this, MPIC is reformulated within the SRBM framework to accommodate the dynamics of quadruped locomotion. Linear inequality constraints are additionally derived for the equivalent wrench to reflect the physical limitations of contact forces. This formulation allows the integration of compliance and constraint handling in a manner suitable for quadruped robots. The proposed method is validated through high-speed locomotion scenarios involving repeated lateral disturbances.
Furthermore, a novel gait pattern is proposed that minimizes the effect of GRFs on the robot based on a simplified model. While many studies have considered energy efficiency and stability in gait patterns, research on the impact of GRFs on the robot at high speeds has been scarce. This paper formulates an optimization problem considering the influence of gait patterns on the robot, using a simplified quadruped robot model under several assumptions, and derives an optimal gait pattern that minimizes the effect of GRFs. Moreover, the energy efficiency and stability of this novel gait pattern are verified in comparison to conventional gait patterns. The effectiveness of the proposed gait pattern is established via application to a high-speed quadruped robot.
The contributions of this paper are summarized as follows:
- Introducing MPIC to quadruped robots by reformulating it based on the SRBM and deriving linear constraints for the resulting equivalent wrench.
- Proposing a novel gait pattern that minimizes the effect of GRFs on the robot at high speeds.
- Performing simulations of high-speed quadrupedal running up to 12 m/s based on these two methods and demonstrating stability against repeated disturbances.
The remainder of this paper is organized as follows. Section 2 presents a reformulation of MPIC for quadruped robots. Section 3 proposes an approach to optimize the gait patterns of quadruped robots. Section 4 describes the remaining components required to construct the overall control algorithm. Section 5 provides simulation results that evaluate the proposed methods, and Section 7 concludes the paper.
2. Model Predictive Impedance Control for Quadruped Robots
This section introduces a method to implement conventional impedance control on the robot body based on the SRBM and extends this to MPIC for quadruped robots. Additionally, a method to incorporate an extended form of the conventional friction cone constraint on GRFs into the MPIC framework is described.
2.1. Dynamics with Conventional Impedance Control for Single Rigid Body Model
The SRBM for a quadruped robot consists of a rigid body representing the torso and four legs, the latter of which have negligible masses, as shown in Figure 1. The SRBM is simpler than a full-body model and effectively captures the characteristics of quadruped robots, making it widely used in MPC.
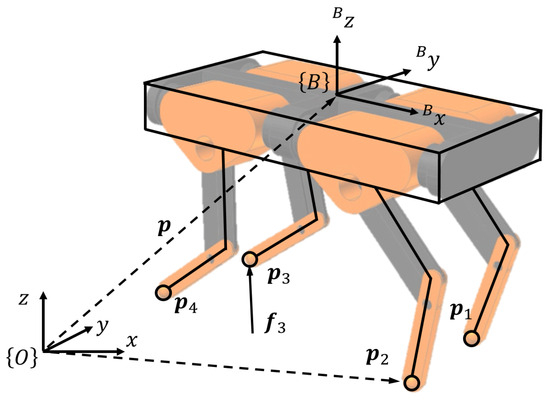
Figure 1.
Illustration of a quadruped robot and the single rigid body model (SRBM) that neglects the inertia of the legs. The frames and denote the world and body-fixed coordinate systems, respectively. The vector represents the position of the robot body, denotes the position of the i-th foot, and represents the ground reaction force acting on the i-th foot.
The dynamics of the SRBM can be expressed by
where m denotes the mass of the torso, is the position of the center of mass of the torso, i indexes the contact feet, , is the GRF at the i-th foot, is the gravity acceleration vector, is the inertia matrix of the torso, is the angular velocity of the torso, is the position of the i-th foot, the left superscript B indicates quantities expressed in the body-fixed coordinate system at the center of mass of the torso, and represents the torso orientation in the Z-Y-X Euler angles, where , , and correspond to roll, pitch, and yaw angles, respectively. denotes the rotation matrix.
After rearranging Equation (1) such that only the acceleration terms remain on the left-hand side, let the right-hand side be defined as the equivalent wrench
Thus, Equation (1) can be written as
By treating the equivalent wrench as a modified input to the quadruped robot system, suppose a body impedance control law is designed with
where , , , and represent the damping and stiffness matrices for translational and rotational motions, respectively. The subscript d indicates the desired value. The error terms are defined as , , , , and .
By substituting Equation (4) into Equation (3), the desired impedance model for the torso is obtained
Although the rotational model in Equation (5) is not strictly linear, it can be approximated as linear when is sufficiently small. Under this approximation, and when the wrench error remains bounded, the position and orientation errors stay bounded and exhibit stable behavior as governed by the impedance model. Thus, impedance control for the torso can be implemented through the control law in Equation (4). However, since the equivalent wrench is not the actual input to the robot, it is necessary to convert it into the input torque to the robot. This conversion process is detailed in Section 4.2.
2.2. Model Predictive Impedance Control
To implement the conventional impedance control derived in Section 2.1 for an MPC, it is necessary to transform the system model and control law into a state-space form. First, by converting Equation (3) into state-space form, the system can be represented as
where is the state vector, is the input vector, and E denotes the identity matrix. The system matrices are given by and .
Discretizing Equation (6) using the zero-order hold method yields
where k denotes the discrete time step and A and B are the discrete system matrices corresponding to and , respectively. Unlike conventional linearized SRBM dynamics in MPC for quadruped robots, which incorporate time-varying trajectories and, thus, become time-variant, Equation (7) has the advantage of being time-invariant.
Equation (4) can be expressed in state-space form
with and .
To predict the state over a prediction horizon of length , Equation (7) can be expressed as
where is the stacked state vector, is the stacked input vector, is the current state of the system, , and .
To realize the feedback law described in Equation (8), the optimal control problem for MPIC is formulated as the following unconstrained quadratic program.
where is a weight matrix and , , and denote the stacked versions of , L, and , respectively. This cost function can be simplified using and and expressed as
The optimal solution to the unconstrained problem yields , which is identical to the feedback law in Equation (8). This confirms that the unconstrained MPIC formulation is equivalent to the conventional impedance control described in Section 2.1. In this paper, to enable a fair comparison with conventional MPC under the same conditions, desired acceleration and force feedback are not considered, and therefore, is set to zero.
However, MPIC differs from conventional impedance control in that it can handle constraints. Fortunately, the friction cone constraint on GRFs, which is the most commonly applied constraint in conventional MPC for quadruped robots, is also applicable to MPIC. Yet, due to the difference between the equivalent wrench and the GRFs, directly applying the friction cone constraint is not appropriate. Instead, a suitable constraint for the equivalent wrench is derived as follows. First, the friction cone for the GRF is defined as
where , , and are the x, y, and z components of , respectively, and is the friction coefficient, which is assumed to be constant in all directions of the terrain. To apply the constraints in a linear MPC, Equation (12) is typically approximated [34,37] using linear constraints of the form
Since
where . Equation (13) yields the equivalent force constraints
Note that these constraints are necessary conditions of Equation (13). Some conditions are omitted in this reduction of the constraints on the four feet to the equivalent force constraints. Aggregating individual contact forces into a single equivalent force fails to capture the moment generated by each foot.
To compensate for this, additional moment constraints are introduced by defining the maximum moment arms in the , , , and radial directions, denoted by , , , and , respectively, based on the workspace of the robot. The values of these moment arms are conservatively chosen as upper bounds and can be precomputed from the geometry of the robot. First, the upper bound of the rolling moment can be approximated as
This expression is based on the assumption that gives the upper bound of the rolling moment induced by the vertical force component, while accounts for the lateral contribution. Given that from Equation (15), the upper bound can be rewritten as
The lower bound for the rolling moment is similarly bounded, yielding
where . Applying the same approach to the pitching moment results in
where . The upper bound of the yawing moment is expressed as the product of the radial direction maximum moment arm and the magnitude of the tangential force
To simplify this expression, the tangential force can be bounded using a friction constraint analogous to Equation (12), which leads to
Similarly, the lower bound is given by
where .
All the constraints derived so far are linear with respect to the equivalent wrench and can be expressed as the following linear inequality constraints over the prediction horizon
where and .
The optimal problem with the obtained linear inequality constraints can be formulated as follows
Unlike the previous unconstrained optimal problem of Equation (11), this problem does not have an analytical solution but can be solved numerically. In this paper, the numerical solution is obtained using MATLAB‘s quadprog function. The current time step value of this optimal solution is then applied to the system to implement MPIC for quadruped robots. As in Section 2.1, how to convert this optimal equivalent wrench into torque is explained in Section 4.2.
3. Gait Optimization
The sequence and timing of foot–ground contacts during walking or running significantly influence the stability of quadruped robots, comparable to the effects of GRF magnitude and direction. This is evident from the fact that, despite the large number of gait patterns possible in theory, only a small number lead to successful and stable locomotion. Most gait patterns inherently have instability, while only a few possess inherent stability. These gait patterns are defined by gait variables such as duty factor, relative phases, and step period. This section explains a method to optimize the duty factor and relative phases as a function of the robot speed.
3.1. Duty Factor Optimization
The duty factor , defined as the ratio of the stance phase duration to the gait period, exerts two competing effects on legged robots. As the duty factor increases, the stance phase duration becomes longer, which in turn induces relatively smaller GRFs. Conversely, when the duty factor decreases, the swing phase duration becomes longer, leading to a reduction in the speed of the swing leg. Since both effects can benefit the robot, a trade-off is necessary. This section aims to model these two effects to derive the optimal duty factor.
First, the kinetic energy of the swing leg, which is closely related to the swing leg speed, can be approximated as follows
where is the approximated mass of the leg and represents the average speed of the leg during the swing phase. On the other hand, the relative displacement of the swing foot during the swing phase must match the step stride of the quadruped, which leads to the following relationship
where v is the average speed of the robot, represents the duration of the swing phase, and is the step stride. Equation (26) can be rewritten in terms of the duty factor as follows
where denotes the duration of the stance phase. By rearranging Equation (26) to express , the average swing leg speed is given by
Substituting this into the expression for the kinetic energy of the swing leg yields
Next, the relationship between the stance phase duration and the GRF is considered. To maintain repetitive steady motion in each gait period, denoted as T, the impulse caused by gravity over one period must be balanced by the impulse from the vertical component of the GRF. This balance can be expressed using the average vertical GRF during the stance phase, denoted as , as follows
Expressing Equation (30) in terms of the duty factor yields
To capture the trade-off between the two opposing effects of the duty factor, the following optimization problem is formulated using Equations (29) and (31). This problem takes the form
where is the weighting parameter. The problem can be further simplified as
with defined as . Solving this optimization yields the optimal duty factor depending on the speed v. Due to the convexity of the objective function, the optimal duty factor can be found by solving
Raising both sides to the power of three and rearranging the terms gives the explicit solution
where equals . Although Equation (34) may theoretically admit other roots, the discriminant of the corresponding cubic equation is always negative. Thus, no additional real roots exist, and Equation (35) provides the unique optimal duty factor.
Figure 2 illustrates the optimal duty factor depending on speed for several values of . The results align with the common intuition that the duty factor decreases as speed increases and are also similar to duty factors measured in animal experiments [44,46,47]. This confirms that the optimal duty factor obtained through the proposed method is physically meaningful and consistent with empirical observations. In this paper, the value of is set to 1.5 for all simulations.
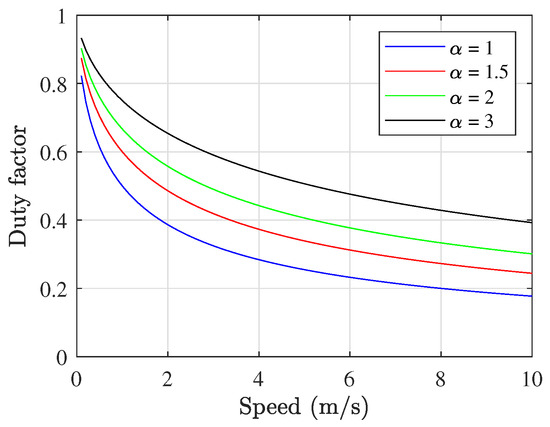
Figure 2.
Optimal duty factor as a function of speed for several values of .
3.2. Relative Phase Optimization
Among gait variables, the relative phase has the most significant influence on the gait pattern. As reviewed earlier, many studies have selected relative phases with a focus on stability or energy efficiency of quadruped robots. However, relatively few studies have addressed gait patterns that maintain stability at high speeds. This section presents a method to derive a simplified model of the GRF based on several assumptions used in a previous study [2], and introduces an approach to find the optimal relative phase that minimizes the impact of GRFs.
Assuming the robot is moving forward at a constant speed and maintaining steady motion, the analysis focuses on the effect of relative phase on GRFs under the following assumptions
where is the relative phase of the i-th leg, is the duration of the flight phase during one gait period, and is the number of contact legs. The bar notation is used to distinguish quantities for relative phase optimization from those introduced earlier. The vertical component of the GRF for each contact leg is assumed to be uniformly distributed. This assumption is based on the impulse balance in Equation (30), incorporating the flight phase duration . Applying this GRF assumption to the moment yields
where , , denote the x, y, z components of the moment, and , , represent the moment arm components for the i-th leg. Given that the robot is running forward at a constant speed, the x and y components of the moment arm are taken as
where and denote the positions of the first joint of the i-th leg in the x and y directions, respectively, to the center of mass of the robot. Accordingly, varies linearly by the step stride from front to back around , which is consistent with the assumption of forward running at constant speed.
The effects of the assumed GRFs and moments on the momentum of the robot are described by the following reduced-order dynamics
where is the vertical component of the linear momentum, and , are the x and y components of the angular momentum. The other components are constant and thus omitted. The above reduced-order dynamics can be represented in discrete state-space form as
where is the state vector, is the input vector, and are the system matrices, and represents the gravitational influence.
Using this model, the following optimization problem can be formulated to find the optimal relative phase that minimizes the effect of GRFs on the robot
where is the number of time steps per gait period, is discretized accordingly, and , are weight matrices. Although this optimization appears quadratic in form, the decision variable is , not , making it nonquadratic and unsolvable by standard quadratic program solvers. Thus, a brute-force method is employed.
Solving Equation (41) yields the optimal relative phase for a given duty factor. However, such optimization can lead to large discrepancies between adjacent duty factors, which may negatively impact gait transitions. To address this, an additional regularization term is introduced, modifying the optimization problem as follows
where and are the current and previous duty factors and represents the previously optimized relative phase. The additional term regulates the change in relative phase across duty factors, enabling smoother gait transitions. In this study, = diag([5, 5, 1, 1, 1, 1]), = diag([5, 1, 1]), and = 20 were used throughout the optimization process.
Due to the time complexity of per duty factor, this optimization problem is too computationally intensive for online solving. Therefore, optimal solutions for all duty factors are precomputed offline, and interpolation is used to obtain relative phases during online operation. Figure 3 shows the results of solving Equation (42) using brute-force search across uniformly discretized step periods, duty factors, and relative phases. For slow speeds with duty factors greater than 0.5, a trot pattern emerges, while faster speeds yield a gait pattern distinct from the traditional gallop. The effectiveness of these results is discussed in detail in Section 5.
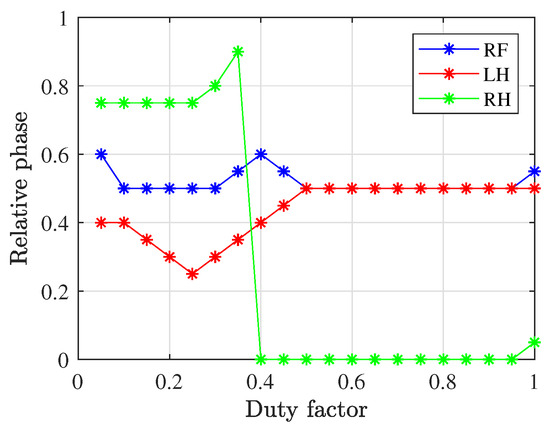
Figure 3.
Optimal relative phase along duty factor obtained from gait optimization based on the reduced-order model. RF, LH, and RH denote right front, left hind, and right hind legs, respectively. The relative phase for LF (left front) is always zero and thus omitted. Note that the apparent sudden drop in the relative phase of the RH leg near a duty factor of 0.4 is not a discontinuity. Since the relative phase is periodic and defined in the range [0, 1), values near 0 and 1 are equivalent. Thus, the phase transition from 0.9 to 0 reflects a smooth transition rather than an abrupt change.
4. Implementation Details
The overall control architecture for the quadruped robot proposed in this paper is illustrated in Figure 4. In addition to the constrained quadratic problem formulated for the proposed MPIC, the duty factor optimizer, and the relative phase planner, the control algorithm includes a reference trajectory generator, a wrench-to-torque conversion method for MPIC, and a joint-level PD controller, omitting the integral term to focus on transient tracking performance rather than steady-state accuracy. This section describes the design of the reference trajectory generation and the wrench-to-torque conversion process included in the control framework.
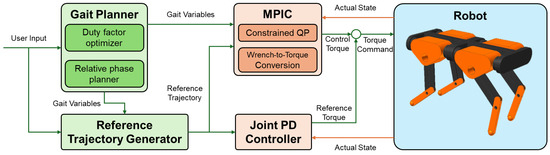
Figure 4.
Overall control architecture incorporating the proposed method. Blocks with green backgrounds represent feedforward components, responsible for planning the optimal gait variables and generating reference trajectories based on user input. Blocks with orange backgrounds indicate feedback components, which consist of two levels: a low-level PD controller for joint-level trajectory tracking and a high-level model predictive impedance controller that regulates overall robot posture.
4.1. Reference Trajectory Design
The reference trajectory generator shown in Figure 4 is adapted from our previous work on omni-directional motion planning [2]. Based on either user commands or a predefined target motion that specifies sagittal and lateral velocities along with yaw rotation, the x and y components of the desired leg trajectory velocity can be determined. Differentiating the kinematic chain of the robot yields the following relationship
where is the position vector from the center of mass of the body to the first joint of the i-th leg, and is the leg trajectory vector from the first joint to the foot of the i-th leg. Assuming no foot slip and sufficiently small roll and pitch angles, the x and y components of the leg trajectory velocity can be calculated as
where the subscript t denotes the target motion.
To complete the leg trajectory design, the stride length and gait period need to be defined. While stride is typically based on the forward speed of the robot, omni-directional motion makes the concept of a single forward speed ambiguous. To address this, our previous study [2] introduced a method based on the maximum leg trajectory velocity, defined as
Based on this, the step stride is defined as
where is a threshold speed and is the maximum allowable stride determined by the workspace of the robot. The step period is then given by
Using Equation (44) and the gait variables (i.e., duty factor , relative phases , and step period T), the stance phase leg trajectory can be expressed as
where the x and y components follow the same formulation as in [2], while the z component is newly designed as a quadratic polynomial to account for the flight phase of the robot. The coefficients of the polynomial are derived from the vertical GRF component in Equation (36) and the corresponding vertical acceleration .
4.2. Conversion of Equivalent Wrench to Torque
The equivalent wrench obtained from Equation (4) or (24) for impedance control or MPIC cannot be directly applied to the quadruped robot. To apply it to the robot, the equivalent wrench must be converted into joint torques. The relationship derived from the definition of the equivalent wrench in Equation (2) is expressed as
where , , and . In this expression, and are the equivalent wrench components determined from Equation (4) or (24). Moreover, defines the vector from the center of mass to the i-th foot (so that is its cross-product matrix) and denotes the contact index of the i-th foot (0 during swing, 1 during stance). Since is generally a singular matrix, the GRF is computed using the Moore–Penrose pseudoinverse as
where superscript † denotes the Moore–Penrose pseudoinverse.
In this paper, MPIC and PD control are used together in the control algorithm. Therefore, instead of directly converting the GRF in Equation (50) into torque, the influence of the PD controller must be considered. Although it is difficult to model the exact effect of the PD controller analytically, the GRF assumed in the trajectory generation is used to approximate its contribution during the stance phase as follows
Accordingly, the control torque for MPIC is computed as
where is the Jacobian matrix of the i-th leg.
5. Result
5.1. Simulation Setup
The effectiveness and performance of the proposed method were validated through several computer simulations using a quadruped robot simulator, illustrated in Figure 5. While the simulator was described in detail in our previous work [2], the key features of the robot are summarized here for clarity. As shown in Figure 6, the legs of the robot are designed with pantograph-type linkages. This structure concentrates the actuators in the upper body, resulting in lightweight limbs that are well-suited to the assumptions of the SRBM. The total mass of the robot is 24.78 kg, with each leg, except for the hip link, weighing only 1.18 kg, demonstrating the lightweight leg design. Both the thigh and shank links are 0.22 m long, resulting in an overall robot height of approximately 0.4 m. Detailed model parameters are provided in Table 1. To ensure realistic simulation conditions, the actuator torque is limited to a maximum of 100 Nm.
Figure 5.
Quadruped robot simulation environment used to validate the proposed method.
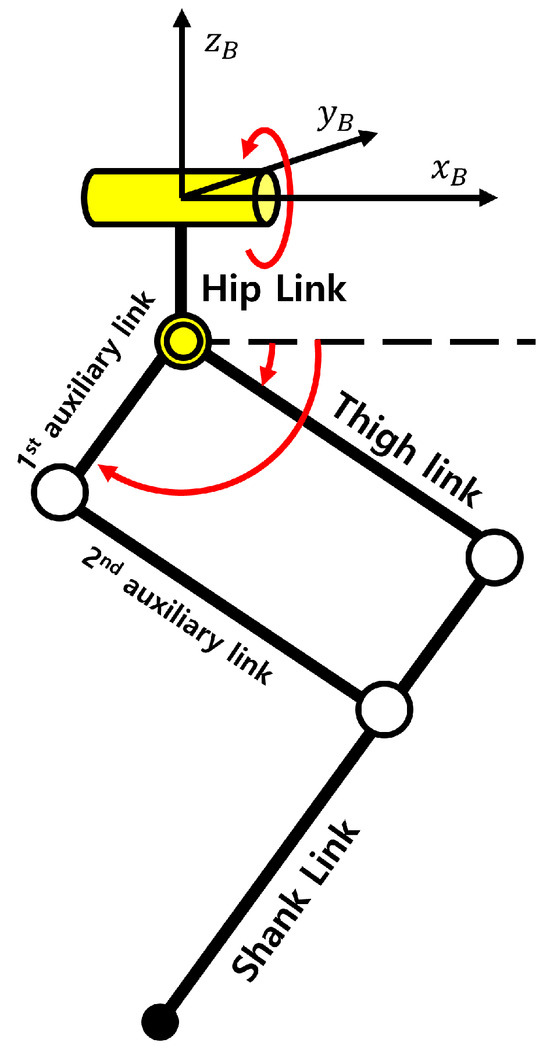
Figure 6.
Leg structure model used in the simulation. Yellow parts indicate actuated joints. The proximal joint is responsible for hip abduction and adduction. The double-circle joint represents two overlapping actuators: one drives the thigh link relative to the hip link and the other drives the first auxiliary link, also relative to the hip link. Together, these two actuators enable hip and knee flexion and extension. The unshaded circles represent passive joints.

Table 1.
Mass and geometric dimensions of each component in the quadruped robot.
The simulation environment was built using MATLAB R2019a (MathWorks, Natick, MA, USA) and RecurDyn V8R5, a commercial multibody dynamics simulator. To model the interaction between the robot and the ground, RecurDyn’s built-in contact model was used. The contact model and its parameters are provided in [2].
The following simulations were conducted to validate the proposed method:
- Comparison of optimal relative phase and reference gait patterns based on the reduced-order model described in Section 3.2;
- Evaluation of energy efficiency across different gait patterns;
- High-speed running simulation;
- High-speed running simulation under external disturbances.
Except for the first test, all simulations were conducted using the full-model simulator shown in Figure 5. Both the proposed controller (Equation (24)) and a conventional MPC used for comparison were first optimized using a real-coded genetic algorithm during the high-speed running simulation (Test 3), and subsequently fine-tuned. Additionally, the conventional impedance control (Equation (4)) used for comparison shares the same impedance parameters as MPIC (Equation (24)). These parameter values are listed in Table 2. In addition to the impedance parameters, the prediction horizon length for MPIC was set to = 10, corresponding to one step period of the robot. To align the MPIC formulation with the step duration, the discrete time interval was computed based on the step period and horizon length. Meanwhile, the simulation itself was executed with a fixed control timestep of 1 ms. Parameters related to the friction coefficient and workspace constraints used in the MPIC are summarized in Table 3.

Table 2.
Impedance parameters used in the proposed controller.

Table 3.
Parameters used in the constraint formulation of the proposed controller.
5.2. Gait Pattern Comparison
To evaluate the effectiveness of the optimal gait pattern derived using the method proposed in Section 3.2, the performance index defined in Equation (42) was computed and compared across various gait patterns. The index values were calculated based on the reduced-order model described in Equation (39). The gait patterns considered for comparison include trot, transverse gallop, pace, trot-to-gallop transition, and the gait pattern optimized by the proposed method. The corresponding relative phase values for each gait are summarized in Table 4.

Table 4.
Relative phase values for each gait pattern.
Figure 7a presents the performance index values for five different gait patterns across the full range of duty factors from 0 to 1, while Figure 7b provides a zoomed-in view focusing on the high-speed region corresponding to duty factors between 0.15 and 0.5. As expected, the optimal gait pattern consistently shows the lowest performance index across all duty factor values.
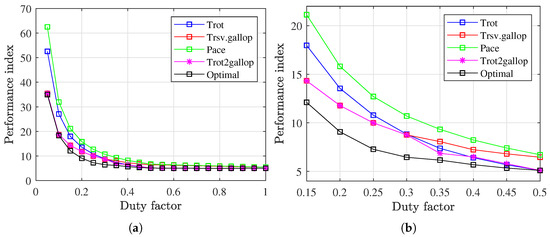
Figure 7.
Objective function values from Equation (42) for relative phase optimization across different gait patterns with respect to the duty factor. (a) Results over the full range of duty factors. (b) Zoomed-in results for the high-speed range corresponding to a duty factor between 0.15 and 0.5. “Trsv. gallop” denotes transverse gallop, and “trot2gallop” refers to the trot-to-gallop transition.
In the low-speed region (duty factor between 0.5 and 1), the trot, the trot-to-gallop transition, and the optimized gait pattern all exhibit relatively low index values, as they effectively share the same trot configuration. In contrast, gallop and pace exhibit higher index values in this region.
As the duty factor decreases (i.e., as speed increases), the index value for trot rises significantly, while that of gallop decreases, indicating a more efficient pattern at higher speeds. This trend aligns with general insights into quadruped gait dynamics, suggesting that the performance index reflects physically meaningful characteristics. Lastly, pace yields the highest index values across all duty factors because it tends to induce excessive roll motion.
In addition to comparing the performance index related to gait stability, energy efficiency, which was not explicitly considered during the optimization process, was also evaluated using the full-model simulation shown in Figure 5. Among the four gait patterns listed in Table 4 and the proposed optimal gait pattern, pace and transverse gallop were excluded from comparison because they could not maintain stable locomotion. Simulations were, thus, conducted for the remaining three gaits: trot, trot-to-gallop transition, and the optimized gait pattern.
To assess energy efficiency across different speeds, simulations were performed at target forward speeds of 2, 4, 6, 8, and 10 m/s. During the acceleration phase, as the robot increased its speed from rest to each target speed with a constant acceleration of 1 m/s2, the duty factor was determined based on Equation (35) according to the instantaneous speed. In this evaluation, only a joint-level PD controller was employed.
To quantify energy efficiency, the root mean square (RMS) value of power consumption was computed during the interval from 10 to 15 s. Two metrics were considered: the sum of RMS power across all joints and the maximum among the total RMS power values computed for each leg by summing the RMS power of all joints within that leg. The former reflects the overall energy efficiency of the robot, while the latter indicates load imbalance by identifying if any single leg is excessively burdened. This power-based metric is closely related to the cost of transport (COT), which, although often defined as work per unit distance, can equivalently be expressed as power divided by speed.
Figure 8 presents the maximum RMS sum of joint power in a single leg and the total RMS power across all joints of the robot for each gait pattern at different target speeds. As shown in Figure 8a, the maximum RMS power per leg increases with speed, but there is no significant difference between gait patterns. In contrast, Figure 8b shows that total RMS power not only increases with speed but also varies noticeably depending on the gait pattern.
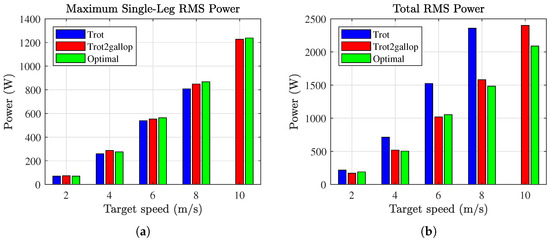
Figure 8.
For the three gait patterns, (a) shows the maximum root mean square (RMS) sum of joint power among all legs and (b) shows the total RMS power across all joints of the robot, both measured during the interval from 10 to 15 s at each speed. For the trot gait at 10 m/s, the robot failed to maintain its gait until 15 s and fell, so the RMS value was not calculated for that case. “Trot2gallop” indicates the transition from trot to gallop.
At a target speed of 2 m/s, all gaits exhibit similar power consumption since they closely resemble the trot pattern. However, as speed increases, the trot gait requires significantly more power than the others. The trot-to-gallop transition and the optimal gait pattern both show similar increases in power consumption as speed increases. At 10 m/s, the robot using the trot gait was unable to maintain stable locomotion and fell before reaching 15 s, so its power was not measured. Under the same condition, the optimal gait pattern required only about 87% of the power used by the trot-to-gallop transition.
These results demonstrate that the optimized gait pattern achieves good energy efficiency, even though energy consumption was not explicitly considered in the performance index (Equation (42)). Furthermore, the power distribution indicates that no excessive load is placed on any individual leg.
5.3. High-Speed Running
This section presents the results of a high-speed running simulation at 12 m/s using the proposed MPIC and gait optimization method. To evaluate the effectiveness of MPIC, simulations were performed under the following four control strategies:
- Using only a joint-level PD controller;
- Applying the proposed MPIC;
- Applying a conventional MPC;
- Applying a conventional impedance controller.
The robot was accelerated with a target acceleration of 2 m/s2 for 6 s to reach a forward speed of 12 m/s, which was then maintained. To determine the gait variables as a function of speed, the duty factor is computed according to Equation (35), and the relative phase is interpolated based on the pre-optimized results shown in Figure 3, following Equation (42).
Figure 9a shows the forward speed of the robot under each control strategy throughout the 20 s of simulation. In the first case, which applied only a joint-level PD controller, the robot accelerated close to 12 m/s but eventually lost stability and fell. In the second and fourth cases, where the proposed MPIC and the conventional impedance controller were applied, respectively, the robot reached speeds close to 12 m/s and maintained stable locomotion, although it accelerated more gradually compared to the target acceleration profile. In the third case, where the conventional MPC was applied, the robot also maintained stable locomotion for the entire simulation, but its speed converged to a value approximately 0.7 m/s below the target.
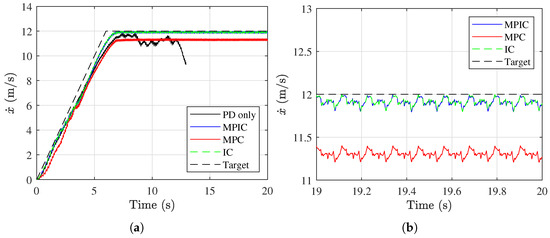
Figure 9.
Forward speed (x-direction) during the high-speed running simulation. (a) Forward speed over the entire simulation duration (0–20 s). (b) Zoomed-in view highlighting steady-state behavior (19–20 s).
Figure 9b shows a zoomed-in view of the forward speed between 19 and 20 s. With the PD-only case excluded due to failure, the remaining three cases exhibit clear periodic speed patterns. The MPIC and impedance control cases show stabilized speeds within a narrow range of 11.8 to 12 m/s, whereas the third case exhibits periodic fluctuations between 11.2 and 11.4 m/s.
Figure 10 presents the lateral speed and vertical position from 19 to 20 s. Similar to the forward motion results, all three successful cases exhibit clear periodic behavior. Additionally, the MPIC and impedance control cases show nearly identical responses, indicating that both control strategies maintain comparable stability in the motion of the robot.
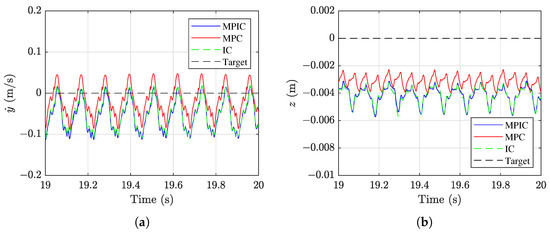
Figure 10.
(a) Lateral speed (y-direction) and (b) vertical motion (z-direction) of the robot from 19 to 20 s during the high-speed running simulation.
Figure 11 illustrates the phase plots for roll, pitch, and yaw motions from 15 to 20 s. All three stable cases exhibit clearly periodic orbits in each rotational axis, indicating stable control of body orientation. While the conventional MPC case shows a slightly different orbit shape, there is no meaningful difference in stability compared to the MPIC and impedance control cases.

Figure 11.
Phase plots of body orientation from 15 to 20 s during the high-speed running simulation: (a) roll, (b) pitch, and (c) yaw motion.
These results confirm that the proposed MPIC and gait optimization enable stable high-speed running at up to 12 m/s. However, since the MPIC and conventional impedance control cases demonstrate similar performance, and the conventional MPC case also maintains comparable stability except in terms of forward speed, the proposed method does not clearly demonstrate superior performance in this scenario. To more clearly evaluate the advantages of MPIC over other control strategies, additional simulations are presented in the following section.
5.4. Running Under Disturbance
Section 5.3 confirmed that not only the proposed MPIC but also the conventional impedance control and MPC maintained stability during high-speed running of the quadruped robot. Although MPIC achieved better forward speed tracking compared to MPC, the overall control performance differences were not substantial. This section aims to evaluate how the robot, controlled by MPIC, compliantly responds to lateral disturbances during high-speed running. The simulation scenarios are as follows: under the same high-speed conditions as in Section 5.3, disturbances were applied at 15 s, once the robot motion had sufficiently stabilized. Three types of disturbances were applied:
- An 80 N rightward disturbance lasting 0.1 s;
- An 80 N leftward disturbance lasting 0.1 s;
- Six rightward disturbances of 20 N, each lasting 1 s and applied every 3 s.
Disturbances were distributed across the front and hind hip joints. Rightward forces were applied to the left hip joints, and leftward forces to the right hip joints. The three control strategies compared were MPIC, conventional impedance control, and conventional MPC. The PD-only controller was excluded since it failed to maintain stability even without disturbances.
5.4.1. Running Under Single Disturbance
Simulation results for the first disturbance scenario are shown in Figure 12 and Figure 13. As seen in Figure 12, sudden changes in lateral speed and roll motion occur immediately after the disturbance is applied at 15 s. The forward speed also slightly decreases. After the disturbance that lasted 0.1 s ends, both the MPIC and impedance control cases initially respond similarly. However, around 15.6 s, the impedance control case loses stability and falls, whereas the MPIC case recovers and returns to its original state. This difference can be attributed to the constraint on equivalent wrench defined in Equation (23) in the MPIC formulation. Under regular conditions, the controllers show little difference in behavior. In contrast, under more extreme conditions, such as disturbances, the constraint is significantly more influential.
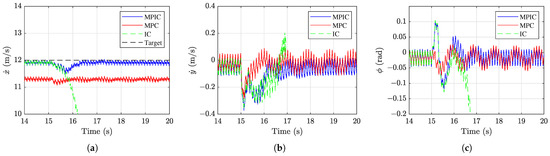
Figure 12.
Results from 14 to 20 s under a single rightward disturbance: (a) forward speed, (b) lateral speed, and (c) roll motion.
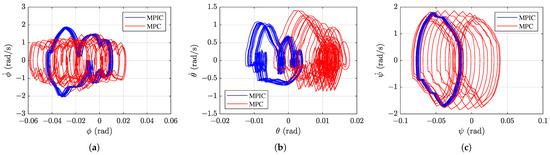
Figure 13.
Phase plots from 18 to 20 s under a single rightward disturbance: (a) roll, (b) pitch, and (c) yaw motion.
Comparing MPIC with MPC, the MPIC case shows larger initial deviations and slower recovery. However, the MPC case exhibits more significant residual oscillations, despite its smaller immediate response. This suggests that the inherent compliance of MPIC allows it to absorb and adapt to the disturbance more naturally, while the stiffer response of MPC leads to larger residual oscillations. Indeed, both the lateral speed and roll motion amplitudes in the MPIC and impedance control cases are larger than those in the MPC case. This clearly highlights the higher compliance of the MPIC and impedance control cases compared to the MPC case. Figure 13 presents the phase plots once the robot motion has returned to a steady state after the disturbance. In the MPIC case, oscillations return to the level observed before the disturbance was applied, whereas in the MPC case, noticeably larger oscillations remain.
Results for the leftward disturbance scenario are shown in Figure 14 and Figure 15. As in the previous case, the impedance control case loses stability shortly after the disturbance is applied. The MPC case shows a smaller immediate deviation and faster recovery compared to the other cases. In the phase plots of Figure 15, the MPIC case clearly returns to the motion before the disturbance, whereas the MPC case shows significant residual oscillations that remain.
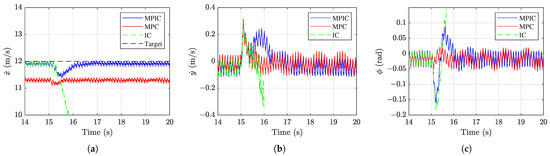
Figure 14.
Results from 14 to 20 s under a single leftward disturbance: (a) forward speed, (b) lateral speed, and (c) roll motion.
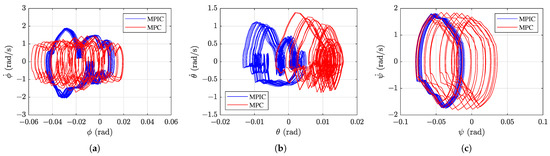
Figure 15.
Phase plots from 18 to 20 s under a single leftward disturbance: (a) roll, (b) pitch, and (c) yaw motion.
5.4.2. Running Under Repeated Disturbances
The previous section showed that MPC resulted in greater residual oscillations than MPIC under single disturbances. This section examines how both controllers respond to repeated disturbances. Figure 16 shows the forward and lateral speeds and roll motion. The robot experienced repeated rightward disturbances every 3 s, each lasting 1 s, for a total of six disturbances. With MPIC, the robot maintained stability throughout. Although the MPC case exhibits smaller motion changes after each disturbance, the residual oscillations gradually increase. The MPC case ultimately lost stability and fell after the third disturbance, around 23 s.
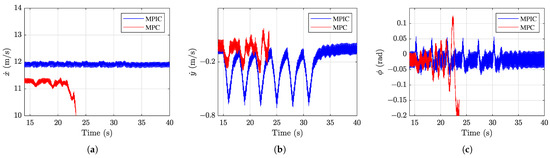
Figure 16.
Results from 14 to 40 s under repeated rightward disturbances: (a) forward speed, (b) lateral speed, and (c) roll motion. Disturbances were applied six times at 15, 18, 21, 24, 27, and 30 s, each lasting 1 s.
Figure 17 shows the phase plots after the final disturbance. In the MPIC case, the oscillation levels return to those seen before the disturbances. Although the yaw motion in Figure 17c shifts slightly in the negative direction, the overall orbit shape remains consistent. These results, like the previous scenarios, demonstrate that the compliance afforded by MPIC enables the robot to absorb and adapt to external disturbances effectively.
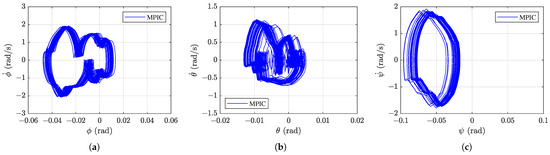
Figure 17.
Phase plots from 35 to 40 s under repeated rightward disturbances: (a) roll, (b) pitch, and (c) yaw motion.
6. Discussion
This study proposed an MPIC combined with gait optimization for high-speed quadrupedal locomotion, and its effectiveness was validated through various simulations. In this section, the limitations of the proposed method and potential directions for future research are discussed.
The proposed MPIC utilizes an SRBM to define an equivalent wrench, simplifying the robot dynamics by neglecting leg inertia. While this assumption is generally valid in quadruped robots, it may lead to inaccuracies when the inertia of the legs becomes significant. This limitation could be addressed by defining the equivalent wrench based on centroidal dynamics [62], which incorporates the full-body momentum equations, including leg dynamics.
Moreover, the body posture was represented using Euler angles and assuming small-angle deviations. Although this is generally sufficient for most locomotion tasks, it may introduce significant errors during large rotational motions, such as backflips. In such cases, alternative formulations such as variation-based linearization methods [37,38,40] could be considered to improve model accuracy.
The gait optimization was designed based solely on forward motion and thus does not account for lateral or rotational movement. Extending the gait pattern to support omni-directional motion would require additional modeling and optimization considerations.
In addition, the optimization process does not explicitly consider accelerations in the x and y directions. This simplification is consistent with the assumption of constant-speed trajectories. While MPIC compensates for this limitation to some extent, incorporating acceleration terms could improve performance in highly dynamic conditions.
While the proposed approach has been validated through simulations under various conditions, it has not been tested on hardware. Therefore, several practical considerations are worth discussing.
First, the simulation used a nonlinear spring-damper ground contact model for a realistic simulation. While this approach may be computationally more demanding than rigid contact formulations used in simulators such as MuJoCo [63], it more closely captures the compliant behavior of real-world terrain. However, more complex terrains, including deformable or uneven surfaces, were not considered and warrant further investigation.
Second, all simulations in this study were conducted on flat terrain. Real-world environments often contain obstacles and varying terrain geometries, which require online trajectory modification. Real-time trajectory planning based on onboard sensors such as cameras or LiDAR will be essential for deployment in such environments. The proposed MPIC framework is advantageous in this regard, as it does not rely on trajectory-based linearization, making it well-suited for integration with perception-driven control.
Furthermore, real actuators are subject to limitations in both torque and speed. Although actuator torque limits were considered in the simulations, motor speed constraints were not considered. This may pose challenges for achieving speeds up to 12 m/s in hardware. Nonetheless, demonstrating the feasibility of such high-speed locomotion in simulation is a significant contribution, particularly given that this speed has rarely been explored even in prior simulation-based studies.
Real-time control is a critical requirement for hardware implementation. In this study, solving the quadratic program for MPIC is the most computationally demanding task. However, compared to other MPC-based methods [34,35,36], the complexity of the proposed formulation remains moderate, suggesting that real-time execution is feasible with an appropriate quadratic program solver.
Lastly, real robots are subject to model uncertainties and sensor noise, which are not explicitly considered in these simulations. Nevertheless, the robot successfully maintained stable locomotion under repeated external disturbances, which may indicate the inherent robustness of MPIC to such uncertainties.
7. Conclusions
This paper introduces the method for applying MPIC, which combines the strengths of MPC and impedance control, to quadruped robots. Unlike conventional MPC, which requires linearization of the SRBM or solving nonlinear optimization problems, MPIC is derived from a linear time-invariant impedance model.
To make it applicable to legged locomotion, MPIC is reformulated within the SRBM framework, and linear inequality constraints are derived for the equivalent wrench to account for contact force limitations. This formulation enables both compliance and constraint handling in a unified manner. By inheriting the compliant properties of impedance control, MPIC improves the ability of the robot to maintain stability under repeated external disturbances. Moreover, following the MPC-style formulation, MPIC allows for the straightforward implementation of GRF constraints.
In addition, the method is proposed to optimize the gait pattern based on the simplified model, rather than relying on predefined animal-inspired sequences. The optimized gait pattern reduces the influence of GRFs on the robot, thereby enhancing locomotion stability. It also achieves energy efficiency comparable to that of conventional gait patterns.
The comparison between conventional gait patterns and the proposed optimal gait was conducted using both the simplified model employed during the gait optimization process and the full model of the robot. Simulations with the simplified model confirmed the superiority of the optimal gait pattern and validated the reliability of the model by producing consistent results across various gait types. The full-model simulation further demonstrates that the optimized gait pattern, designed with consideration of GRFs, achieved comparable energy efficiency.
In the high-speed running simulation, the proposed MPIC and optimal gait pattern enable stable locomotion at speeds up to 12 m/s, significantly faster than those achieved in prior studies. Comparative evaluations with conventional impedance control and MPC cases show that both yield similar performance, while the MPC case produces slightly slower forward speeds but otherwise comparable results.
Disturbance rejection simulations demonstrate the advantages of MPIC over other control strategies. While MPIC and conventional impedance control exhibited similar behavior under undisturbed conditions, their differences became apparent under lateral disturbances. The presence or absence of GRF constraints, an essential distinction between the two, becomes critical when external disturbances are applied. In comparison to MPC, the compliance offered by MPIC enables the robot to maintain stability even under repeated disturbances.
Overall, this paper demonstrates that the proposed MPIC and gait optimization method allows a quadruped robot to maintain high-speed locomotion and respond compliantly to repeated disturbances without losing stability. This method shows promise for high-speed running over complex terrains. Future work will focus on combining the proposed framework with online trajectory generation in complex environments to enable robust high-speed locomotion over complex terrains.
Author Contributions
Conceptualization, D.H.K.; methodology, D.H.K.; software, D.H.K.; validation, D.H.K.; formal analysis, D.H.K.; investigation, D.H.K.; resources, J.H.P.; data curation, D.H.K.; writing—original draft preparation, D.H.K.; writing—review and editing, J.C. and J.H.P.; visualization, D.H.K.; supervision, J.H.P.; project administration, J.H.P.; funding acquisition, J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Ministry of Trade, Industry and Energy (MOTIE) in the year 2022 Robot Industrial Technology Project “Development of companion robot technologies capable of emotional connection based on Human-Robot physical and cognitive interaction.” (No. 20018513).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The simulation results are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
List of Symbols
The following symbols are used in this paper: vectors are denoted in boldface, matrices in nonbold uppercase, and scalars in regular font. Variables with an overline (e.g., ) are used in the context of relative phase optimization.
| World coordinate system | |
| Body-fixed coordinate system | |
| m | Mass of the torso |
| Inertia matrix of the torso expressed in the body-fixed coordinate system | |
| Gravity acceleration vector | |
| Position of the center of mass of the torso | |
| Desired position of the center of mass of the torso | |
| Orientation of the torso expressed in the Euler angles | |
| Desired orientation of the torso expressed in the Euler angles | |
| Angular velocity of the torso expressed in the body-fixed coordinate system | |
| Desired angular velocity of the torso expressed in the body-fixed coordinate system | |
| Set of foot indices | |
| Position vector of the i-th foot | |
| Ground reaction force at the i-th foot | |
| R | Rotation matrix |
| Equivalent wrench defined as Equation (2) | |
| Desired equivalent wrench | |
| Error vector: | |
| Error vector: | |
| Error vector: | |
| Error vector: | |
| Error vector: | |
| Damping matrix for translational motion | |
| Damping matrix for rotational motion | |
| Stiffness matrix for translational motion | |
| Stiffness matrix for rotational motion | |
| State vector: | |
| Desired state vector | |
| State vector at discrete time step k | |
| Prediction horizon length for the model predictive impedance control | |
| Stacked state vector: | |
| Stacked desired state vector | |
| Input vector: | |
| Desired input vector: | |
| Input vector at discrete time step k | |
| Stacked input vector: | |
| Stacked desired input vector | |
| E | Identity matrix |
| System matrices for Equation (6) | |
| Discretized system matrices corresponding to | |
| Stacked system matrices corresponding to | |
| L | Impedance control gain matrix: |
| Stacked impedance control gain matrix | |
| W | Weight matrix for optimal problem in Equations (10) and (24) |
| Q | Matrix defined as for simplicity |
| Coefficient matrix for inequality in Equation (23) | |
| Vector defined as for simplicity | |
| Constant vector for inequality in Equation (23) | |
| Static friction coefficient | |
| Maximum moment arm in the x-direction | |
| Maximum moment arm in the y-direction | |
| Maximum moment arm in the z-direction | |
| Maximum moment arm in the radial direction | |
| Coefficient: for simplicity | |
| Coefficient: for simplicity | |
| Coefficient: for simplicity | |
| Duty factor defined as the ratio of the stance phase duration to the step period | |
| Optimal duty factor derived from Equation (35) | |
| Kinetic energy of the swing leg | |
| Approximated mass of the leg | |
| Average speed of the swing leg | |
| v | Average speed of the robot |
| T | Step period |
| Duration of the swing phase | |
| Duration of the stance phase | |
| Duration of the flight phase | |
| Step stride | |
| Average vertical ground reaction force during the stance phase | |
| Weighting parameter in Equation (32) | |
| Weighting parameter: for simplicity | |
| Weighting parameter: for simplicity | |
| x, y, and z components of the ground reaction force for the i-foot in the relative phase optimization, respectively | |
| Relative phase of the i-th foot | |
| Number of contact feet | |
| x, y, and z components of the moment in the relative relative phase optimization, respectively | |
| x, y, and z components of the moment arm for i-th foot in the relative phase optimization, respectively | |
| Position of the first joint of the i-th leg in the x and y directions, respectively | |
| Vertical component of the linear momentum in the relative phase optimization | |
| x and y components of the angular momentum in the relative phase optimization, respectively | |
| State vector: | |
| Input vector: | |
| System matrices for Equation (40) | |
| Gravitational vector for Equation (40) | |
| Number of discretized time steps for relative phase optimization in Equations (41) and (42) | |
| Weight matrices for relative phase optimization in Equations (41) and (42) | |
| Current and previous duty factors during optimization process in Equation (42) | |
| Previously optimized relatvie phase during optimization process in Equation (42) | |
| Position vector from the center of mass of the body to the first joint of the i-th leg | |
| Leg trajectory vector from the first joint to the foot for the i-th leg | |
| Position vector expressed in the body-fixed coordinate system | |
| Leg trajectory vector of the i-th leg expressed in the body-fixed coordinate system | |
| Target forward speed of the robot | |
| Target lateral speed of the robot | |
| Target yaw rate of the robot | |
| Maximum leg trajectory velocity | |
| Maximum allowable stride | |
| Threshold speed for | |
| Vector for ground reaction forces defined as | |
| Moment arm vector defined as | |
| Components of optimal equivalent wrench | |
| Matrix defined as for simplicity | |
| Vector defined as for simplicity | |
| Moore-Penrose pseudoinverse of | |
| Approximated PD control effect on ground reaction force at i-th foot | |
| Control torque of the i-th leg for model predictive impedance control | |
| Jacobian matrix of the i-th leg |
References
- Park, H.W.; Wensing, P.M.; Kim, S. High-speed bounding with the MIT Cheetah 2: Control design and experiments. Int. J. Robot. Res. 2017, 36, 167–192. [Google Scholar] [CrossRef]
- Kim, D.; Park, J.H. Reduced Model Predictive Control Toward Highly Dynamic Quadruped Locomotion. IEEE Access 2024, 12, 20003–20018. [Google Scholar] [CrossRef]
- Pratt, J.E.; Pratt, G.A. Virtual model control of a biped walking robot. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Albuquerque, NM, USA, 20–25 April 1997; IEEE: Piscataway, NJ, USA, 1997; pp. 193–198. [Google Scholar]
- Park, J.H. Impedance control for biped robot locomotion. IEEE Trans. Robot. Autom. 2001, 17, 870–882. [Google Scholar] [CrossRef]
- Lim, H.O.; Setiawan, S.A.; Takanishi, A. Balance and impedance control for biped humanoid robot locomotion. In Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems, Maui, HI, USA, 29 October–3 November 2001; IEEE: Piscataway, NJ, USA, 2001; Volume 1, pp. 494–499. [Google Scholar]
- Focchi, M.; Boaventura, T.; Semini, C.; Frigerio, M.; Buchli, J.; Caldwell, D.G. Torque-control based compliant actuation of a quadruped robot. In Proceedings of the 2012 12th IEEE International Workshop on Advanced Motion Control (AMC), Sarajevo, Bosnia and Herzegovina, 25–27 March 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–6. [Google Scholar]
- Boaventura, T.; Medrano-Cerda, G.A.; Semini, C.; Buchli, J.; Caldwell, D.G. Stability and performance of the compliance controller of the quadruped robot HyQ. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1458–1464. [Google Scholar]
- Boaventura, T.; Buchli, J.; Semini, C.; Caldwell, D.G. Model-based hydraulic impedance control for dynamic robots. IEEE Trans. Robot. 2015, 31, 1324–1336. [Google Scholar] [CrossRef]
- Semini, C.; Barasuol, V.; Boaventura, T.; Frigerio, M.; Focchi, M.; Caldwell, D.G.; Buchli, J. Towards versatile legged robots through active impedance control. Int. J. Robot. Res. 2015, 34, 1003–1020. [Google Scholar] [CrossRef]
- Hyun, D.J.; Seok, S.; Lee, J.; Kim, S. High speed trot-running: Implementation of a hierarchical controller using proprioceptive impedance control on the MIT Cheetah. Int. J. Robot. Res. 2014, 33, 1417–1445. [Google Scholar] [CrossRef]
- Lee, J.; Hyun, D.J.; Ahn, J.; Kim, S.; Hogan, N. On the dynamics of a quadruped robot model with impedance control: Self-stabilizing high speed trot-running and period-doubling bifurcations. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 4907–4913. [Google Scholar]
- Bosworth, W.; Kim, S.; Hogan, N. The effect of leg impedance on stability and efficiency in quadrupedal trotting. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 4895–4900. [Google Scholar]
- Park, J.; Park, J.H. Impedance control of quadruped robot and its impedance characteristic modulation for trotting on irregular terrain. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Algarve, Portugal, 7–12 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 175–180. [Google Scholar]
- Ajallooeian, M.; Pouya, S.; Spröwitz, A.; Ijspeert, A.J. Central pattern generators augmented with virtual model control for quadruped rough terrain locomotion. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 3321–3328. [Google Scholar]
- Zhang, G.; Rong, X.; Hui, C.; Li, Y.; Li, B. Torso motion control and toe trajectory generation of a trotting quadruped robot based on virtual model control. Adv. Robot. 2016, 30, 284–297. [Google Scholar] [CrossRef]
- Chen, G.; Guo, S.; Hou, B.; Wang, J. Virtual model control for quadruped robots. IEEE Access 2020, 8, 140750–140763. [Google Scholar] [CrossRef]
- Angelini, F.; Xin, G.; Wolfslag, W.J.; Tiseo, C.; Mistry, M.; Garabini, M.; Bicchi, A.; Vijayakumar, S. Online optimal impedance planning for legged robots. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 4–8 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 6028–6035. [Google Scholar]
- Xin, G.; Wolfslag, W.; Lin, H.C.; Tiseo, C.; Mistry, M. An Optimization-Based Locomotion Controller for Quadruped Robots Leveraging Cartesian Impedance Control. Front. Robot. AI 2020, 7, 48. [Google Scholar] [CrossRef]
- Li, Q.; Qian, L.; Wang, S.; Sun, P.; Luo, X. Towards Generation and Transition of Diverse Gaits for Quadrupedal Robots Based on Trajectory Optimization and Whole-Body Impedance Control. IEEE Robot. Autom. Lett. 2023, 8, 2389–2396. [Google Scholar] [CrossRef]
- Pedro, G.D.G.; Bermudez, G.; Medeiros, V.S.; Cruz Neto, H.J.d.; Barros, L.G.D.d.; Pessin, G.; Becker, M.; Freitas, G.M.; Boaventura, T. Quadruped Robot Control: An Approach Using Body Planar Motion Control, Legs Impedance Control and Bézier Curves. Sensors 2024, 24, 3825. [Google Scholar] [CrossRef]
- Parosi, R.; Risiglione, M.; Caldwell, D.G.; Semini, C.; Barasuol, V. Kinematically-Decoupled Impedance Control for Fast Object Visual Servoing and Grasping on Quadruped Manipulators. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 6411–6418. [Google Scholar]
- Bellicoso, C.D.; Jenelten, F.; Fankhauser, P.; Gehring, C.; Hwangbo, J.; Hutter, M. Dynamic Locomotion and Whole-Body Control for Quadrupedal Robots. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 3359–3365. [Google Scholar]
- Bellicoso, C.D.; Jenelten, F.; Gehring, C.; Hutter, M. Dynamic locomotion through online nonlinear motion optimization for quadrupedal robots. IEEE Robot. Autom. Lett. 2018, 3, 2261–2268. [Google Scholar] [CrossRef]
- Liu, X.; Ma, H.; Lang, L.; An, H. Online Foot Location Planning for Gait Transitioning Using Model Predictive Control. Appl. Sci. 2021, 11, 7866. [Google Scholar] [CrossRef]
- Xin, S.; Orsolino, R.; Tsagarakis, N. Online Relative Footstep Optimization for Legged Robots Dynamic Walking Using Discrete-Time Model Predictive Control. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 4–8 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 513–520. [Google Scholar]
- Dini, N.; Majd, V.J. An MPC-based two-dimensional push recovery of a quadruped robot in trotting gait using its reduced virtual model. Mech. Mach. Theory 2020, 146, 103737. [Google Scholar] [CrossRef]
- Neunert, M.; Stäuble, M.; Giftthaler, M.; Bellicoso, C.D.; Carius, J.; Gehring, C.; Hutter, M.; Buchli, J. Whole-body nonlinear model predictive control through contacts for quadrupeds. IEEE Robot. Autom. Lett. 2018, 3, 1458–1465. [Google Scholar] [CrossRef]
- Li, H.; Frei, R.J.; Wensing, P.M. Model hierarchy predictive control of robotic systems. IEEE Robot. Autom. Lett. 2021, 6, 3373–3380. [Google Scholar] [CrossRef]
- Bledt, G.; Wensing, P.M.; Kim, S. Policy-regularized model predictive control to stabilize diverse quadrupedal gaits for the MIT cheetah. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 4102–4109. [Google Scholar]
- Farshidian, F.; Jelavic, E.; Satapathy, A.; Giftthaler, M.; Buchli, J. Real-time motion planning of legged robots: A model predictive control approach. In Proceedings of the 2017 IEEE-RAS 17th International Conference on Humanoid Robotics (Humanoids), Birmingham, UK, 15–17 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 577–584. [Google Scholar]
- Bledt, G.; Kim, S. Extracting legged locomotion heuristics with regularized predictive control. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 406–412. [Google Scholar]
- Cebe, O.; Tiseo, C.; Xin, G.; Lin, H.c.; Smith, J.; Mistry, M. Online dynamic trajectory optimization and control for a quadruped robot. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 12773–12780. [Google Scholar]
- Farshidian, F.; Neunert, M.; Winkler, A.W.; Rey, G.; Buchli, J. An efficient optimal planning and control framework for quadrupedal locomotion. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 93–100. [Google Scholar]
- Bledt, G.; Kim, D.; Wensing, P.M.; Kim, S. Dynamic locomotion in the MIT cheetah 3 through convex model-predictive control. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–9. [Google Scholar]
- Kim, D.; Di Carlo, J.; Katz, B.; Bledt, G.; Kim, S. Highly dynamic quadruped locomotion via whole-body impulse control and model predictive control. arXiv 2019, arXiv:1909.06586. [Google Scholar] [CrossRef]
- Katz, B.; Di Carlo, J.; Kim, S. Mini cheetah: A platform for pushing the limits of dynamic quadruped control. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 6295–6301. [Google Scholar]
- Ding, Y.; Pandala, A.; Park, H.W. Real-time model predictive control for versatile dynamic motions in quadrupedal robots. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 8484–8490. [Google Scholar]
- Ding, Y.; Pandala, A.; Li, C.; Shin, Y.H.; Park, H.W. Representation-free model predictive control for dynamic motions in quadrupeds. IEEE Trans. Robot. 2021, 37, 1154–1172. [Google Scholar] [CrossRef]
- Chignoli, M.; Wensing, P.M. Variational-based optimal control of underactuated balancing for dynamic quadrupeds. IEEE Access 2020, 8, 49785–49798. [Google Scholar] [CrossRef]
- Chignoli, M.; Kim, S. Online trajectory optimization for dynamic aerial motions of a quadruped robot. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 7693–7699. [Google Scholar]
- Villarreal, O.; Barasuol, V.; Wensing, P.M.; Caldwell, D.G.; Semini, C. MPC-based controller with terrain insight for dynamic legged locomotion. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 2436–2442. [Google Scholar]
- Ding, C.; Zhou, L.; Li, Y.; Rong, X. A novel dynamic locomotion control method for quadruped robots running on rough terrains. IEEE Access 2020, 8, 150435–150446. [Google Scholar] [CrossRef]
- Zhang, Z.; Chang, X.; Ma, H.; An, H.; Lang, L. Model Predictive Control of Quadruped Robot Based on Reinforcement Learning. Appl. Sci. 2023, 13, 154. [Google Scholar] [CrossRef]
- Alexander, R.M. The gaits of bipedal and quadrupedal animals. Int. J. Robot. Res. 1984, 3, 49–59. [Google Scholar] [CrossRef]
- Alexander, R.M. Optimization and gaits in the locomotion of vertebrates. Physiol. Rev. 1989, 69, 1199–1227. [Google Scholar] [CrossRef]
- Maes, L.D.; Herbin, M.; Hackert, R.; Bels, V.L.; Abourachid, A. Steady locomotion in dogs: Temporal and associated spatial coordination patterns and the effect of speed. J. Exp. Biol. 2008, 211, 138–149. [Google Scholar] [CrossRef]
- Herbin, M.; Hommet, E.; Hanotin-Dossot, V.; Perret, M.; Hackert, R. Treadmill locomotion of the mouse lemur (Microcebus murinus); kinematic parameters during symmetrical and asymmetrical gaits. J. Comp. Physiol. A 2018, 204, 537–547. [Google Scholar] [CrossRef] [PubMed]
- McGhee, R.B.; Frank, A.A. On the stability properties of quadruped creeping gaits. Math. Biosci. 1968, 3, 331–351. [Google Scholar] [CrossRef]
- Lee, T.T.; Shih, C.L. A study of the gait control of a quadruped walking vehicle. IEEE J. Robot. Autom. 1986, 2, 61–69. [Google Scholar] [CrossRef][Green Version]
- Ju, Z.; Wei, K.; Jin, L.; Xu, Y. Investigating stability outcomes across diverse gait patterns in quadruped robots: A comparative analysis. IEEE Robot. Autom. Lett. 2024, 9, 795–802. [Google Scholar] [CrossRef]
- Kiguchi, K.; Kusumoto, Y.; Watanabe, K.; Izumi, K.; Fukuda, T. Energy-optimal gait analysis of quadruped robots. Artif. Life Robot. 2002, 6, 120–125. [Google Scholar] [CrossRef]
- Xi, W.; Yesilevskiy, Y.; Remy, C.D. Selecting gaits for economical locomotion of legged robots. Int. J. Robot. Res. 2016, 35, 1140–1154. [Google Scholar] [CrossRef]
- Pepe, G.; Laurenza, M.; Belfiore, N.P.; Carcaterra, A. Quadrupedal robots’ gaits identification via contact forces optimization. Appl. Sci. 2021, 11, 2102. [Google Scholar] [CrossRef]
- Tsujita, K.; Tsuchiya, K.; Onat, A. Adaptive gait pattern control of a quadruped locomotion robot. In Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Maui, HI, USA, 29 October–3 November 2001; IEEE: Piscataway, NJ, USA, 2001; pp. 2318–2323. [Google Scholar]
- Fukuoka, Y.; Habu, Y.; Fukui, T. A simple rule for quadrupedal gait generation determined by leg loading feedback: A modeling study. Sci. Rep. 2015, 5, 8169. [Google Scholar] [CrossRef]
- Owaki, D.; Ishiguro, A. A quadruped robot exhibiting spontaneous gait transitions from walking to trotting to galloping. Sci. Rep. 2017, 7, 277. [Google Scholar] [CrossRef]
- Shao, Y.; Jin, Y.; Liu, X.; He, W.; Wang, H.; Yang, W. Learning free gait transition for quadruped robots via phase-guided controller. IEEE Robot. Autom. Lett. 2022, 7, 1230–1237. [Google Scholar] [CrossRef]
- Bellegarda, G.; Shafiee, M.; Ijspeert, A. AllGaits: Learning all quadruped gaits and transitions. arXiv 2024, arXiv:2411.04787. [Google Scholar] [CrossRef]
- Sulpice, L.; Owaki, D.; Hayashibe, M. Footstep reward for energy-efficient quadruped gait generation and transition through deep reinforcement learning. Adv. Robot. 2025, 39, 71–78. [Google Scholar] [CrossRef]
- Bednarczyk, M.; Omran, H.; Bayle, B. Model predictive impedance control. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 470–476. [Google Scholar]
- Jin, Z.; Qin, D.; Liu, A.; Zhang, W.a.; Yu, L. Model predictive variable impedance control of manipulators for adaptive precision-compliance tradeoff. IEEE/ASME Trans. Mechatron. 2023, 28, 1174–1187. [Google Scholar] [CrossRef]
- Orin, D.E.; Goswami, A.; Lee, S.H. Centroidal dynamics of a humanoid robot. Auton. Robot. 2013, 35, 161–176. [Google Scholar] [CrossRef]
- Todorov, E.; Erez, T.; Tassa, Y. Mujoco: A physics engine for model-based control. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Algarve, Portugal, 7–12 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 5026–5033. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).