Stackade Ensemble Learning for Resilient Forecasting Against Missing Values, Adversarial Attacks, and Concept Drift
Abstract
Featured Application
Abstract
1. Introduction
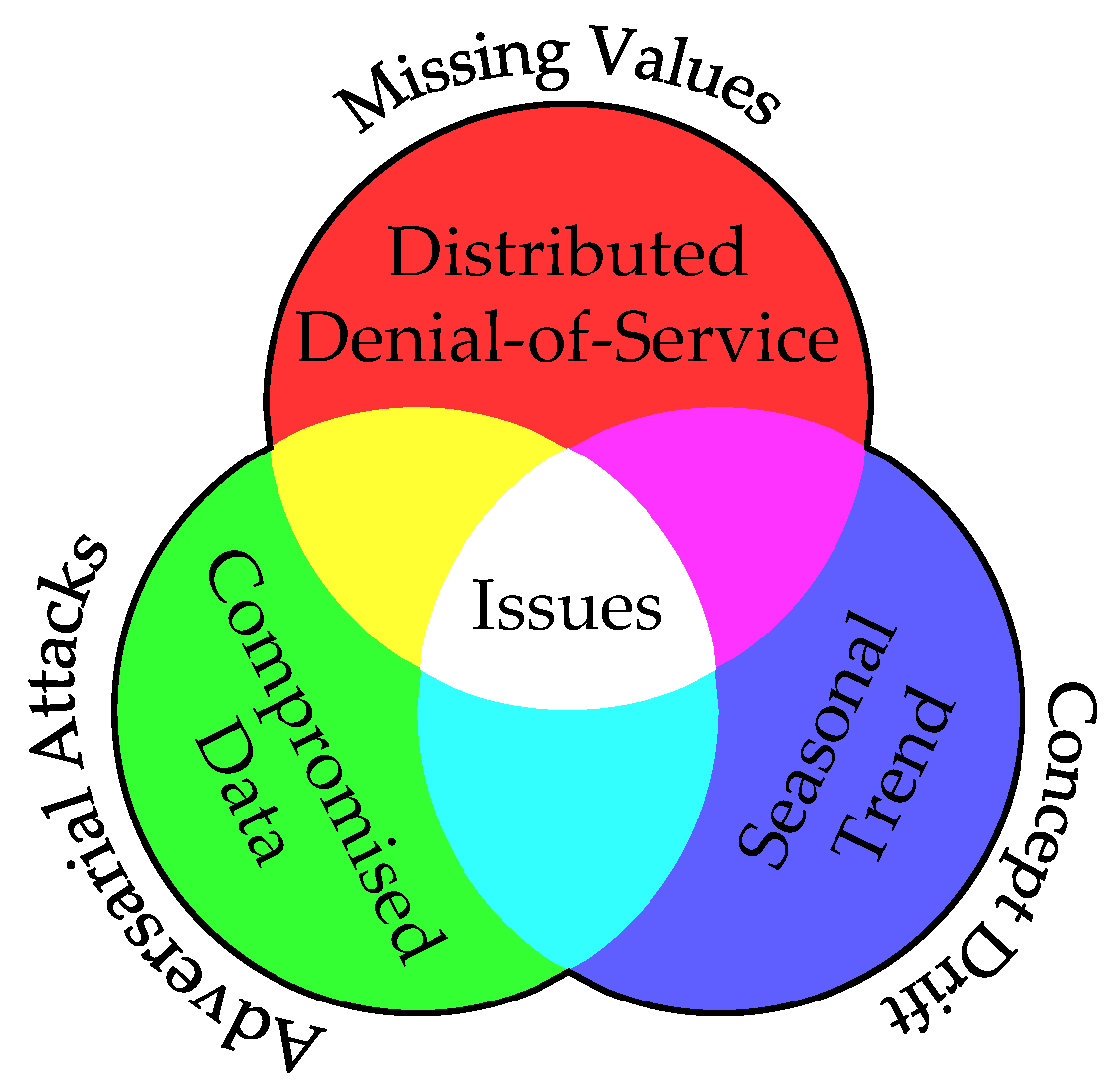
- Missing values (MV);
- Adversarial attacks (AA);
- Concept drift (CD).
- “Forecast” “Smart Grid” “Missing Values”—“Adversarial Attacks”—“Concept Drift”;
- “Forecast” “Smart Grid” “Adversarial Attacks”—“Concept Drift”—“Missing Values”;
- “Forecast” “Smart Grid” “Concept Drift”—“Missing Values”—“Adversarial Attacks”;
- “Forecast” “Smart Grid” “Concept Drift” “Missing Values” “Adversarial Attacks”.
2. Preliminary
2.1. Problems
2.1.1. Missing Values
| Algorithm 1 Missing values with varying percentages implementation |
| Input: Time series X, missing percentage , randomization seed |
| Output: Time series with missing values |
| 1: Function missing_values |
| 2: Apply randomization seed: |
| 3: Copy the sequence: |
| 4: Find the total element in X: |
| 5: Find total number of missing values: |
| 6: Generate index: |
| 7: Choose random indices: |
| 8: Replace value with null on chosen indices: |
| 9: return |
| 10: End Function |
2.1.2. Adversarial Attacks
| Algorithm 2 Projected gradient descent implementation |
| Input: Time series X, surrogate model , intensity , iteration |
| Output: Adversarial time series |
| 1: Function pgd_sample |
| 2: Get forecast using surrogate model: |
| 3: Create a copy of the array: copy |
| 4: Generate uniform noise: random.uniform(, , len(X)) |
| 5: Add noise to the copied array: |
| 6: Get minimum clipping: |
| 7: Get maximum clipping: |
| 8: Clip the added noise: clip(, , ) |
| 9: Calculate the alpha: |
| 10: for to do |
| 11: with GradientTape() as tape do |
| 12: Tape on : tape.watch() |
| 13: Get prediction: |
| 14: Compute loss: |
| 15: end with |
| 16: Compute gradient: |
| 17: Insert perturbation: |
| 18: Clip perturbations: clip(, , ) |
| 19: end for |
| 20: return |
| 21: End Function |
2.1.3. Concept Drift
2.1.4. Compounding Problem
2.2. Previous Studies
- Single-purpose solution;
- Multi-purpose solution.
2.2.1. Single-Purpose Solution
2.2.2. Multi-Purpose Solution
3. Implementation
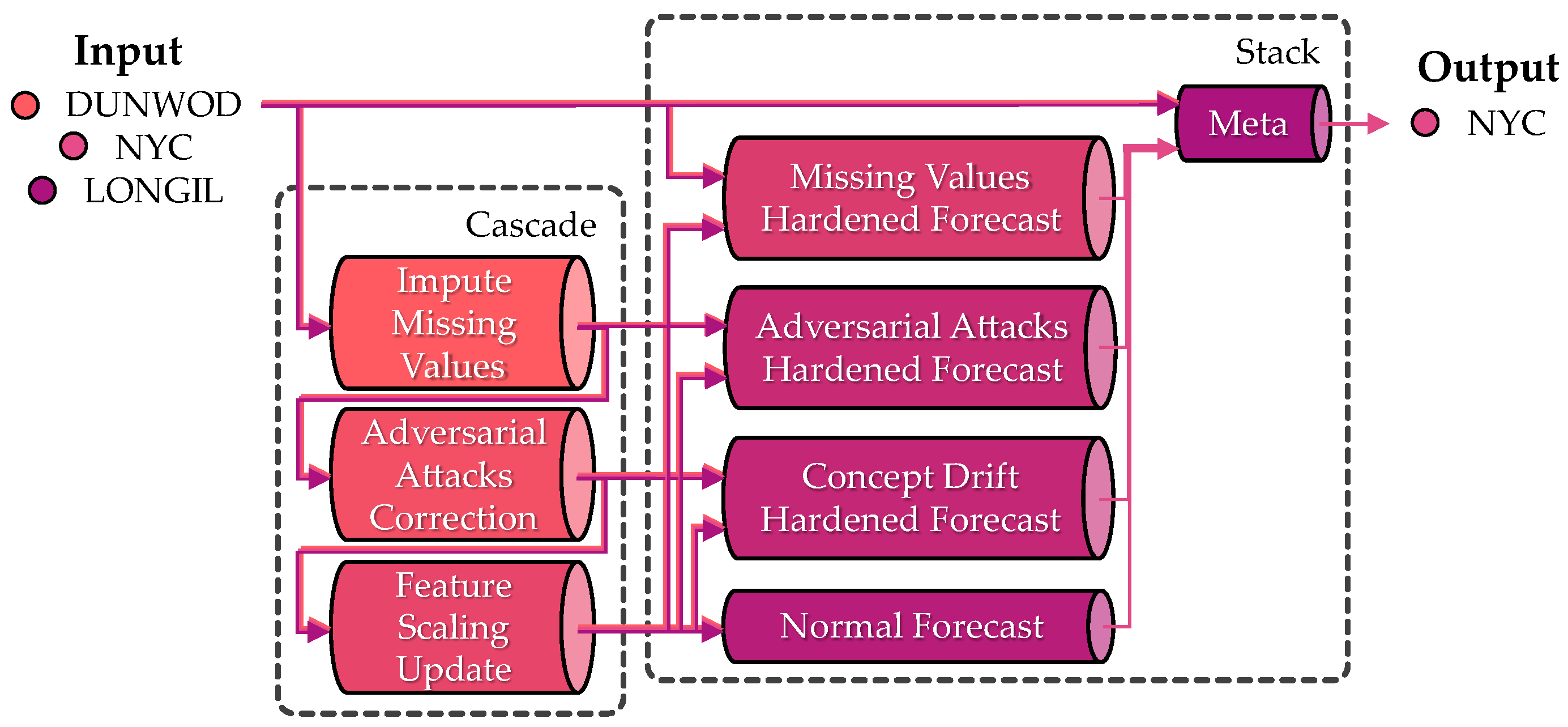
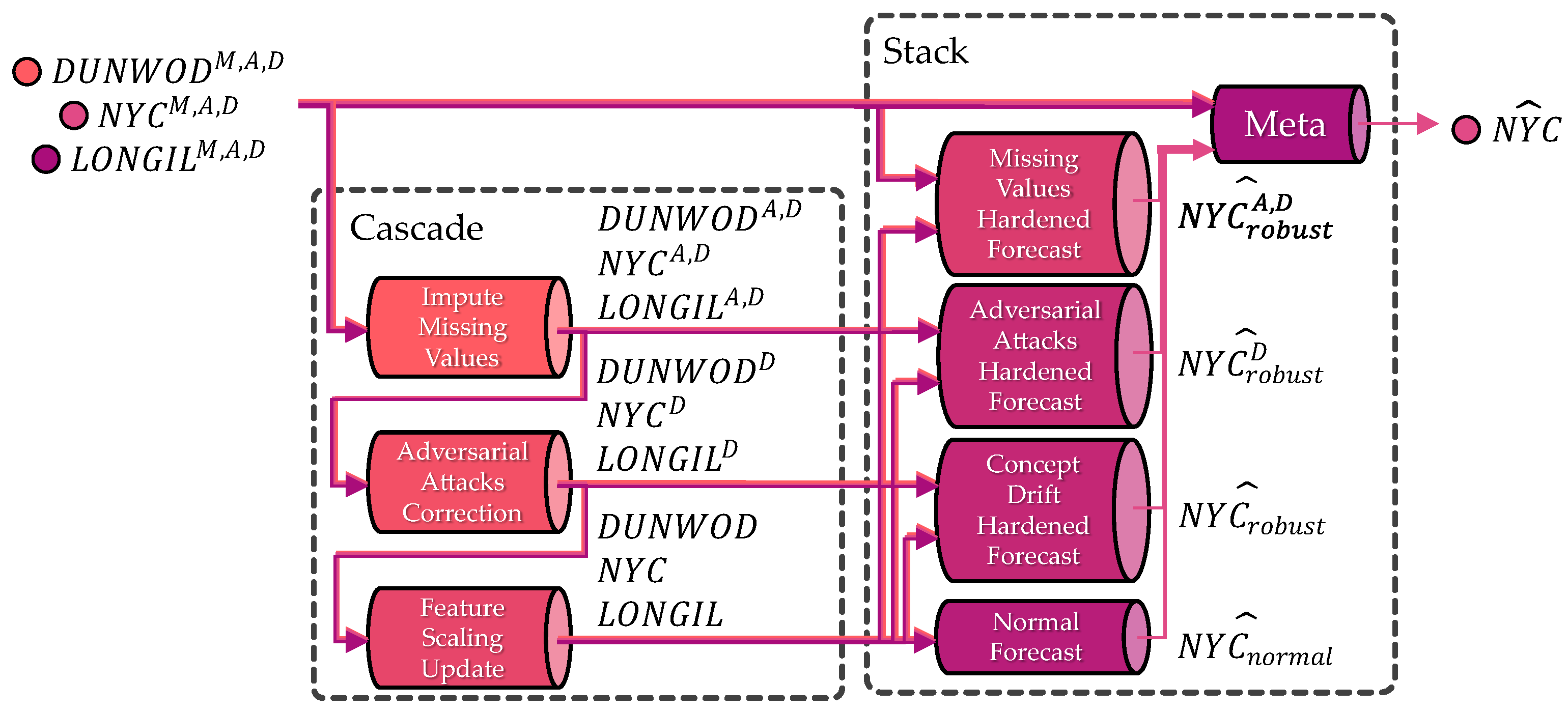
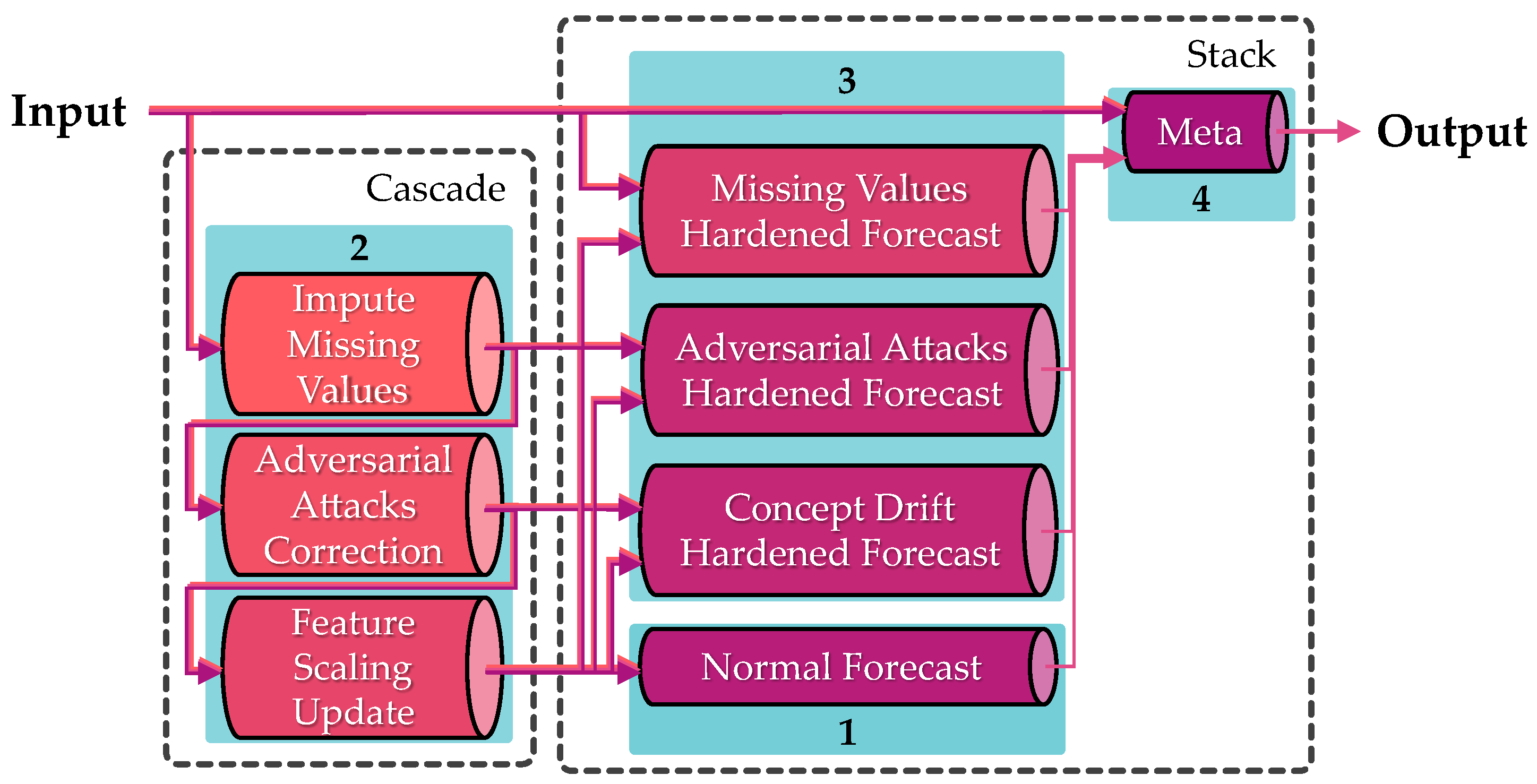
3.1. Stackade Ensemble Learning
3.1.1. Ensemble Strategy
3.1.2. Training Strategy
3.2. Implemented Solutions
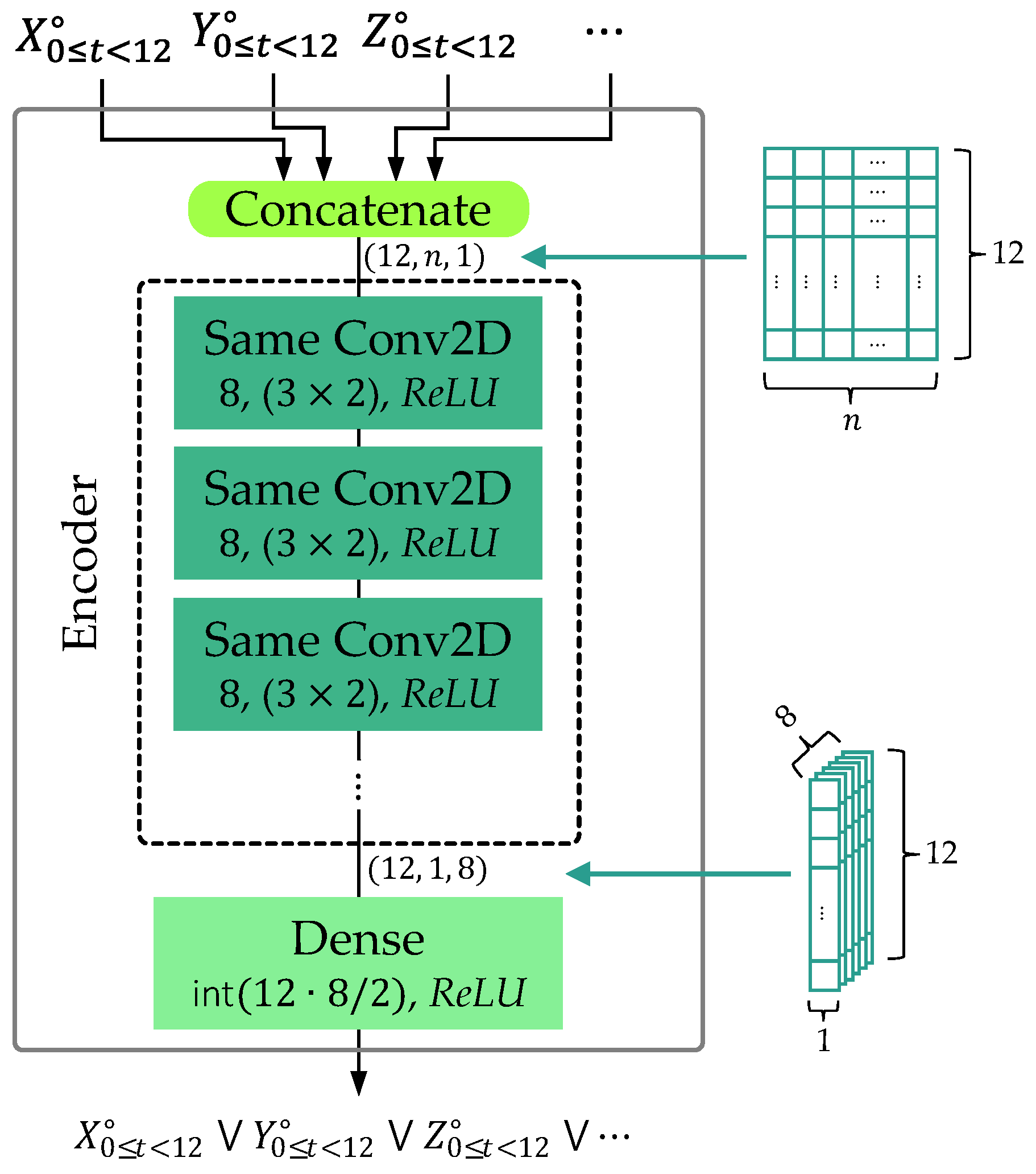
3.2.1. Cascade Modules
3.2.2. Stack Modules
4. Experiment
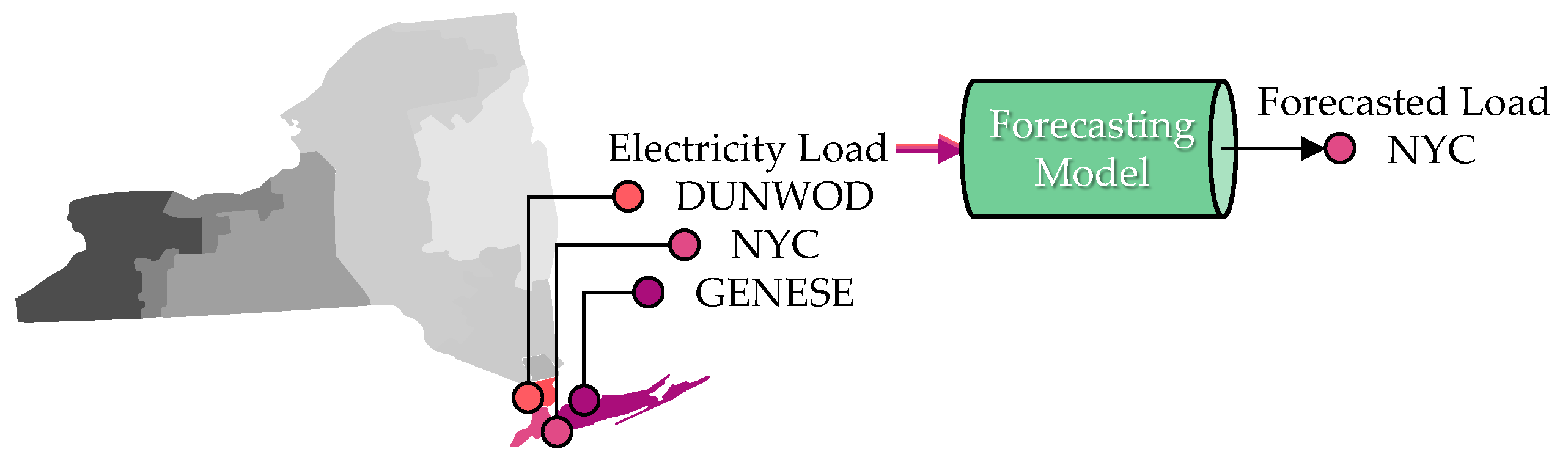
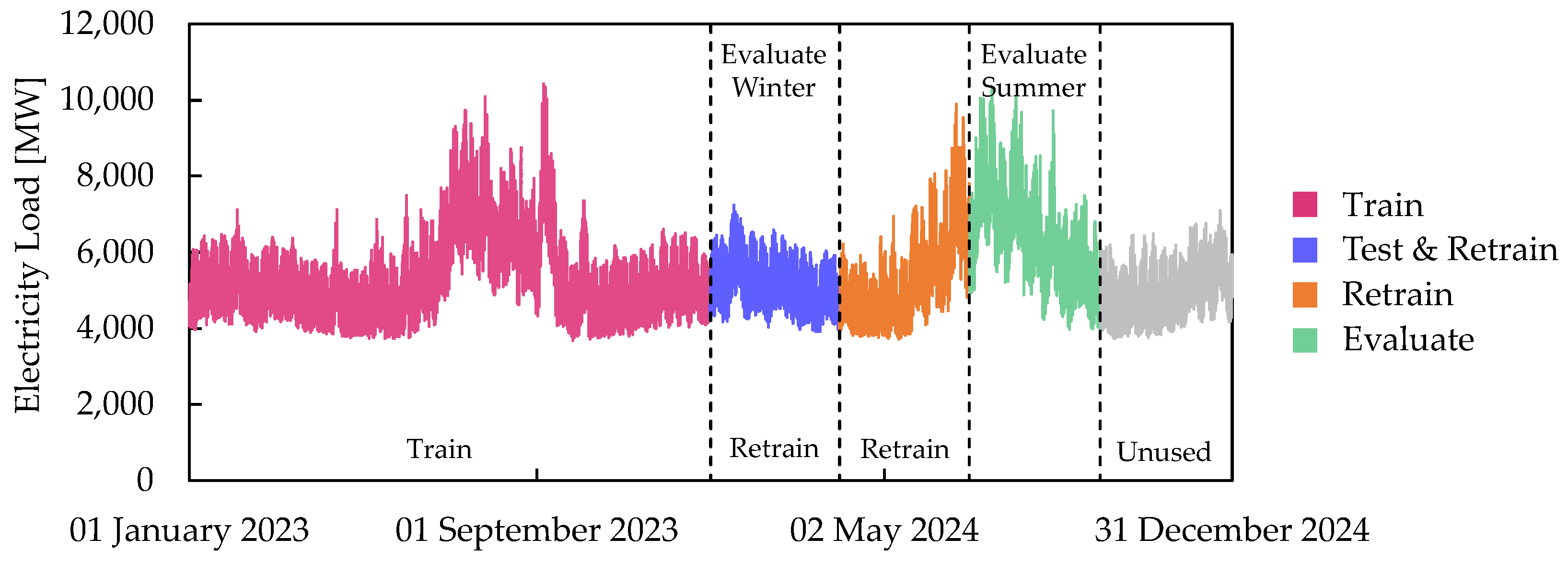
4.1. Real-World Dataset
4.2. Proposed Method Application
| Algorithm 3 Independent and dependent sequencer |
| Input: Electricity load data , sequence length l, step s |
| Output: Independent array , dependent array |
| 1: Function |
| 2: Initialize empty arrays: |
| 3: |
| 4: Append sliced sequence: |
| 5: Append sliced sequence: |
| 6: |
| 7: return |
| 8: End Function |
4.3. Baseline Methods Application
- Trivial solution;
- Federated solution.
| Algorithm 4 Federated learning implementation with fine-tuning |
| Input: Scaled dataset , untrained model classes |
| Output: Fine-tuned global models |
| 1: Function |
| 2: Create the list to store the weights: |
| 3: |
| 4: |
| 5: Get sequence: |
| 6: Train the local model: |
| 7: Save the weight: |
| 8: |
| 9: |
| 10: Average the saved weights: |
| 11: Replace weight with global: |
| 12: |
| 13: |
| 14: return |
| 15: End Function |
5. Result
5.1. Clean Data
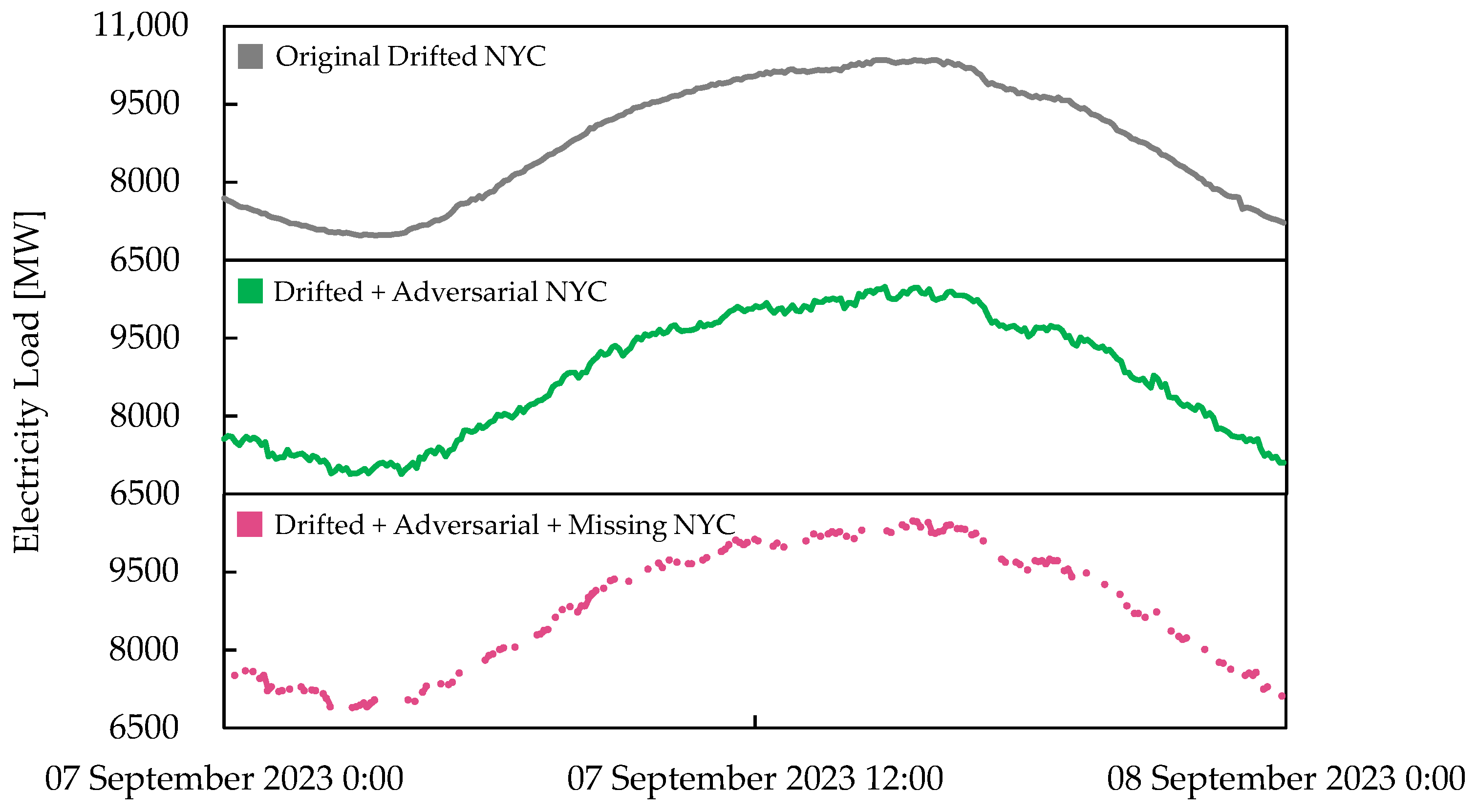
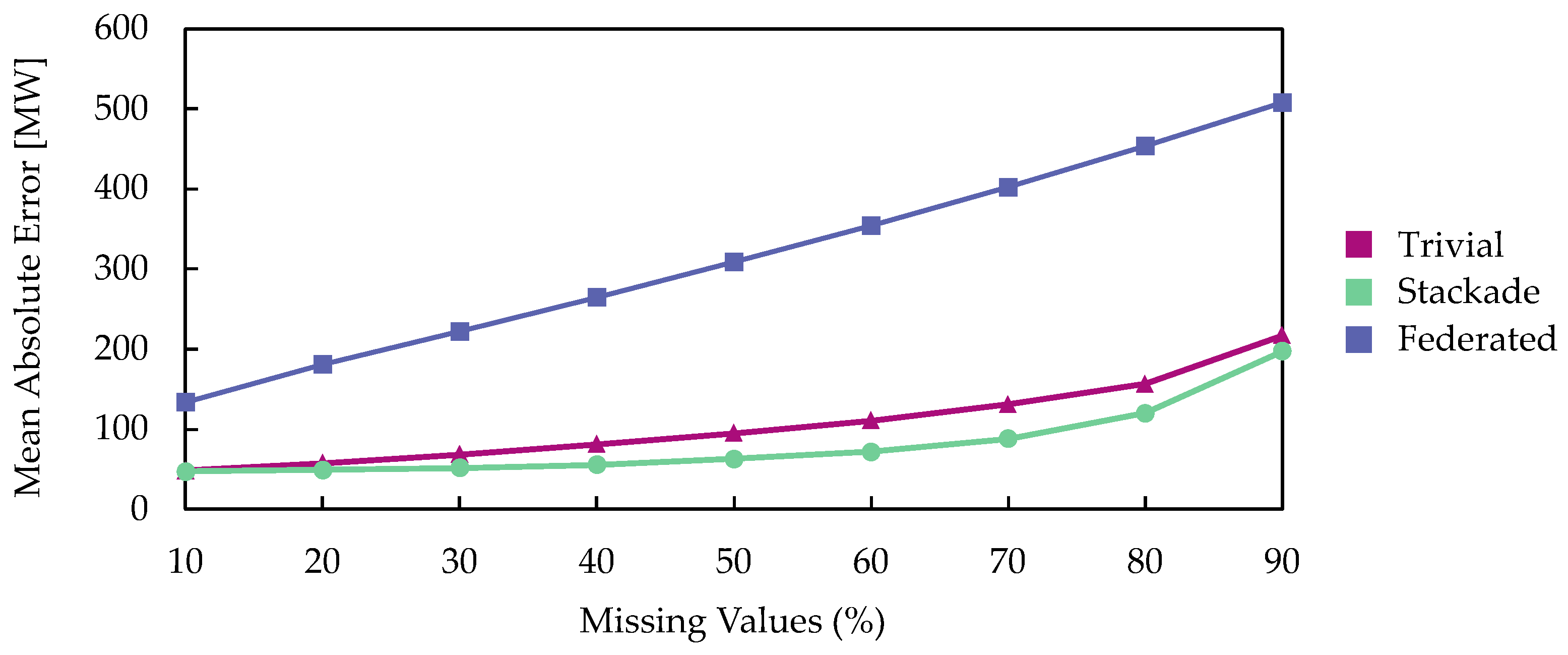
5.2. Missing Data
5.3. Adversarial Data
5.4. Drifted Data
5.5. Compounding Data
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ML | Machine learning |
| MV | Missing values |
| AA | Adversarial attacks |
| CD | Concept drift |
| DDoS | Distributed denial-of-service |
| AI | Artificial intelligence |
| IoT | Internet of Things |
| NYC | New York City |
| StEL | Stackade Ensemble Learning |
| CEL | Cascading Ensemble Learning |
| SEL | Stacking Ensemble Learning |
| PGD | Projected gradient descent |
| FGSM | Fast gradient sign method |
| BIM | Basic iterative method |
| LSTM | Long short-term memory |
| TanH | Hyperbolic tangent |
| MSE | Mean squared error |
| GAN | Generative adversarial network |
| DL | Deep learning |
| Conv2D | Convolutional 2D |
| ReLU | Rectified linear unit |
| Conv1D | Convolutional 1D |
| NYISO | New York Independent System Operator |
| seq2seq | Sequence-to-seqence |
| Coefficient of determination | |
| RMSE | Root mean squared error |
| MAE | Mean absolute error |
References
- Ruan, J.; Liu, G.; Qiu, J.; Liang, G.; Zhao, J.; He, B.; Wen, F. Time-Varying Price Elasticity of Demand Estimation for Demand-Side Smart Dynamic Pricing. Appl. Energy 2022, 322, 119520. [Google Scholar] [CrossRef]
- Torres, J.F.; Martínez-Álvarez, F.; Troncoso, A. A Deep LSTM Network for the Spanish Electricity Consumption Forecasting. Neural Comput. Appl. 2022, 34, 10533–10545. [Google Scholar] [CrossRef]
- Zheng, J.; Du, J.; Wang, B.; Klemeš, J.J.; Liao, Q.; Liang, Y. A Hybrid Framework for Forecasting Power Generation of Multiple Renewable Energy Sources. Renew. Sustain. Energy Rev. 2023, 172, 113046. [Google Scholar] [CrossRef]
- Rodrigues, F.; Cardeira, C.; Calado, J.M.F.; Melicio, R. Short-Term Load Forecasting of Electricity Demand for the Residential Sector Based on Modelling Techniques: A Systematic Review. Energies 2023, 16, 4098. [Google Scholar] [CrossRef]
- Mohammed, S.; Budach, L.; Feuerpfeil, M.; Ihde, N.; Nathansen, A.; Noack, N.; Patzlaff, H.; Naumann, F.; Harmouch, H. The Effects of Data Quality on Machine Learning Performance on Tabular Data. Inf. Syst. 2025, 132, 102549. [Google Scholar] [CrossRef]
- Ahalawat, A.; Babu, K.S.; Turuk, A.K.; Patel, S. A Low-Rate Ddos Detection and Mitigation for SDN Using Renyi Entropy with Packet Drop. J. Inf. Secur. Appl. 2022, 68, 103212. [Google Scholar] [CrossRef]
- Bin Kamilin, M.H.; Yamaguchi, S. Resilient Electricity Load Forecasting Network with Collective Intelligence Predictor for Smart Cities. Electronics 2024, 13, 718. [Google Scholar] [CrossRef]
- Couldflare. Record-Breaking 5.6 Tbps DDoS Attack and Global DDoS Trends for 2024 Q4. Available online: https://blog.cloudflare.com/ddos-threat-report-for-2024-q4/ (accessed on 16 May 2025).
- IBM X-Force. X-Force Threat Intelligence Index 2025. Available online: https://www.ibm.com/reports/threat-intelligence (accessed on 20 May 2025).
- Liang, H.; He, E.; Zhao, Y.; Jia, Z.; Li, H. Adversarial Attack and Defense: A Survey. Electronics 2022, 11, 1283. [Google Scholar] [CrossRef]
- Bin Kamilin, M.H.; Yamaguchi, S.; Bin Ahmadon, M.A. Leveraging Trusted Input Framework to Correct and Forecast the Electricity Load in Smart City Zones Against Adversarial Attacks. In Proceedings of the 2024 International Conference on Future Technologies for Smart Society (ICFTSS), Kuala Lumpur, Malaysia, 7–8 August 2024; pp. 177–182. [Google Scholar]
- Bayram, F.; Ahmed, B.S.; Kassler, A. From Concept Drift to Model Degradation: An Overview on Performance-Aware Drift Detectors. Knowl.-Based Syst. 2022, 245, 108632. [Google Scholar] [CrossRef]
- Bin Kamilin, M.H.; Yamaguchi, S.; Bin Ahmadon, M.A. Radian Scaling and Its Application to Enhance Electricity Load Forecasting in Smart Cities Against Concept Drift. Smart Cities 2024, 7, 3412–3436. [Google Scholar] [CrossRef]
- Perianes-Rodriguez, A.; Waltman, L.; van Eck, N.J. Constructing Bibliometric Networks: A Comparison Between Full and Fractional Counting. J. Inf. 2016, 10, 1178–1195. [Google Scholar] [CrossRef]
- Spodniak, P.; Ollikka, K.; Honkapuro, S. The Impact of Wind Power and Electricity Demand on the Relevance of Different Short-Term Electricity Markets: The Nordic Case. Appl. Energy 2021, 283, 116063. [Google Scholar] [CrossRef]
- Li, L.; Ju, Y.; Wang, Z. Quantifying the Impact of Building Load Forecasts on Optimizing Energy Storage Systems. Energy Build. 2024, 307, 113913. [Google Scholar] [CrossRef]
- Miller, D.; Kim, J.-M. Univariate and Multivariate Machine Learning Forecasting Models on the Price Returns of Cryptocurrencies. J. Risk Financ. Manag. 2021, 14, 486. [Google Scholar] [CrossRef]
- Song, L.-K.; Li, X.-Q.; Zhu, S.-P.; Choy, Y.-S. Cascade Ensemble Learning for Multi-Level Reliability Evaluation. Aerosp. Sci. Technol. 2024, 148, 109101. [Google Scholar] [CrossRef]
- Abdellatif, A.; Mubarak, H.; Ahmad, S.; Ahmed, T.; Shafiullah, G.M.; Hammoudeh, A.; Abdellatef, H.; Rahman, M.M.; Gheni, H.M. Forecasting Photovoltaic Power Generation with a Stacking Ensemble Model. Sustainability 2022, 14, 11083. [Google Scholar] [CrossRef]
- Djuitcheu, H.; Shah, T.; Tammen, M.; Schotten, H.D. DDoS Impact Assessment on 5G System Performance. In Proceedings of the 2023 IEEE Future Networks World Forum (FNWF), Baltimore, MD, USA, 13–15 November 2023; pp. 1–6. [Google Scholar]
- Eliyan, L.F.; Di Pietro, R. DoS and DDoS attacks in Software Defined Networks: A survey of existing solutions and research challenges. Future Gener. Comput. Syst. 2021, 122, 149–171. [Google Scholar] [CrossRef]
- Couldflare. DDoS Threat Report for 2025 Q1. Available online: https://radar.cloudflare.com/reports/ddos-2025-q1 (accessed on 4 June 2025).
- Chaddad, A.; Jiang, Y.; Daqqaq, T.S.; Kateb, R. EAMAPG: Explainable Adversarial Model Analysis via Projected Gradient Descent. Comput. Biol. Med. 2025, 188, 109788. [Google Scholar] [CrossRef]
- Değirmenci, E.; İ, Ö.; Yazıcı, A. Adversarial Attack Detection Approach for Intrusion Detection Systems. IEEE Access 2024, 12, 195996–196009. [Google Scholar] [CrossRef]
- Khan, Z.A.; Ullah, A.; Ul Haq, I.; Hamdy, M.; Maria Mauro, G.; Muhammad, K.; Hijji, M.; Baik, S.W. Efficient Short-Term Electricity Load Forecasting for Effective Energy Management. Sustain. Energy Technol. Assess. 2022, 53, 102337. [Google Scholar] [CrossRef]
- Hinder, F.; Vaquet, V.; Brinkrolf, J.; Hammer, B. Model-based Explanations of Concept Drift. Neurocomputing 2023, 555, 126640. [Google Scholar] [CrossRef]
- Meier, S.; Marcotullio, P.J.; Carney, P.; DesRoches, S.; Freedman, J.; Golan, M.; Gundlach, J.; Parisian, J.; Sheehan, P.; Slade, W.V.; et al. New York State Climate Impacts Assessment Chapter 06: Energy. Ann. N. Y. Acad. Sci. 2024, 1542, 341–384. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- NumPy. numpy.histogram. Available online: https://numpy.org/doc/stable/reference/generated/numpy.histogram.html (accessed on 13 June 2025).
- Hou, Z.; Liu, J. Enhancing Smart Grid Sustainability: Using Advanced Hybrid Machine Learning Techniques While Considering Multiple Influencing Factors for Imputing Missing Electric Load Data. Sustainability 2024, 16, 8092. [Google Scholar] [CrossRef]
- Hwang, J.; Suh, D. CC-GAIN: Clustering and Classification-Based Generative Adversarial Imputation Network for Missing Electricity Consumption Data Imputation. Expert Syst. Appl. 2024, 255, 124507. [Google Scholar] [CrossRef]
- Li, D.; Yang, P.; Zou, Y. Optimizing Insulator Defect Detection with Improved DETR Models. Mathematics 2024, 12, 1507. [Google Scholar] [CrossRef]
- Zhou, Y.; Ding, Z.; Wen, Q.; Wang, Y. Robust Load Forecasting Towards Adversarial Attacks via Bayesian Learning. IEEE Trans. Power Syst. 2023, 38, 1445–1459. [Google Scholar] [CrossRef]
- Mahmoudnezhad, F.; Moradzadeh, A.; Mohammadi-Ivatloo, B.; Zare, K.; Ghorbani, R. Electric Load Forecasting Under False Data Injection Attacks via Denoising Deep Learning and Generative Adversarial Networks. IET Gener. Transm. Distrib. 2024, 18, 3247–3263. [Google Scholar] [CrossRef]
- Azeem, A.; Ismail, I.; Mohani, S.S.; Danyaro, K.U.; Hussain, U.; Shabbir, S.; Bin Jusoh, R.Z. Mitigating Concept Drift Challenges in Evolving Smart Grids: An Adaptive Ensemble LSTM for Enhanced Load Forecasting. Energy Rep. 2025, 13, 1369–1383. [Google Scholar] [CrossRef]
- Jagait, R.K.; Fekri, M.N.; Grolinger, K.; Mir, S. Load Forecasting Under Concept Drift: Online Ensemble Learning with Recurrent Neural Network and ARIMA. IEEE Access 2021, 9, 98992–99008. [Google Scholar] [CrossRef]
- Zhou, Y.; Ge, Y.; Jia, L. Double Robust Federated Digital Twin Modeling in Smart Grid. IEEE Internet Things J. 2024, 11, 39913–39931. [Google Scholar] [CrossRef]
- Dorji, K.; Jittanon, S.; Thanarak, P.; Mensin, P.; Termritthikun, C. Electricity Load Forecasting using Hybrid Datasets with Linear Interpolation and Synthetic Data. Eng. Technol. Appl. Sci. Res. 2024, 14, 17931–17938. [Google Scholar] [CrossRef]
- Milan Kummaya, A.; Joseph, A.; Rajamani, K.; Ghinea, G. Fed-Hetero: A Self-Evaluating Federated Learning Framework for Data Heterogeneity. Appl. Syst. Innov. 2025, 8, 28. [Google Scholar] [CrossRef]
- Alwateer, M.; Atlam, E.-S.; Abd El-Raouf, M.M.; Ghoneim, O.A.; Gad, I. Missing data imputation: A comprehensive review. J. Comput. Commun. 2024, 12, 53–75. [Google Scholar] [CrossRef]
- Stevens, A.; Smedt, J.D.; Peeperkorn, J.; Weerdt, J.D. Assessing the Robustness in Predictive Process Monitoring through Adversarial Attacks. In Proceedings of the 2022 4th International Conference on Process Mining (ICPM), Bolzano, Italy, 23–28 October 2022; pp. 56–63. [Google Scholar]
- Korycki, Ł.; Krawczyk, B. Adversarial Concept Drift Detection under Poisoning Attacks for Robust Data Stream Mining. Mach. Learn. 2023, 112, 4013–4048. [Google Scholar] [CrossRef]
- Alabadla, M.; Sidi, F.; Ishak, I.; Ibrahim, H.; Affendey, L.S.; Ani, Z.C.; Jabar, M.A.; Bukar, U.A.; Devaraj, N.K.; Muda, A.S.; et al. Systematic Review of Using Machine Learning in Imputing Missing Values. IEEE Access 2022, 10, 44483–44502. [Google Scholar] [CrossRef]
- Gupta, V.; Hewett, R. Adaptive Normalization in Streaming Data. In Proceedings of the 3rd International Conference on Big Data Research (ICBDR 2019), Cergy-Pontoise, France, 20–22 November 2019; pp. 12–17. [Google Scholar]
- Yang, L.; Shami, A. A Lightweight Concept Drift Detection and Adaptation Framework for IoT Data Streams. IEEE Internet Things Mag. 2021, 4, 96–101. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, X.; Wei, X. Mitigating Accuracy-Robustness Trade-Off via Balanced Multi-Teacher Adversarial Distillation. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 9338–9352. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Shen, W. A Review of Ensemble Learning Algorithms Used in Remote Sensing Applications. Appl. Sci. 2022, 12, 8654. [Google Scholar] [CrossRef]
- New York Independent System Operator. Load Data. Available online: https://www.nyiso.com/load-data/ (accessed on 2 May 2025).
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Annual Scientific Computing with Python Conference (SciPy 2010), Austin, TX, USA, 28 June–3 July 2010; pp. 56–61. [Google Scholar]
- The Pandas Development Team. pandas.Series.interpolate. Available online: https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.Series.interpolate.html (accessed on 3 June 2025).
- Seabold, S.; Perktold, J. Statsmodels: Econometric and Statistical Modeling with Python. In Proceedings of the 9th Annual Scientific Computing with Python Conference (SciPy 2010), Austin, TX, USA, 28 June–3 July 2010; pp. 92–96. [Google Scholar]
- Statsmodels. statsmodels.tsa.seasonal.seasonal_decompose. Available online: https://www.statsmodels.org/dev/generated/statsmodels.tsa.seasonal.seasonal_decompose.html (accessed on 3 June 2025).
- Lima, M.; Neto, M.; Silva Filho, T.; de A. Fagundes, R.A. Learning Under Concept Drift for Regression—A Systematic Literature Review. IEEE Access 2022, 10, 45410–45429. [Google Scholar] [CrossRef]
- van den Heuvel, E.; Zhan, Z. Myths About Linear and Monotonic Associations: Pearson’s r, Spearman’s ρ, and Kendall’s τ. Am. Stat. 2022, 76, 44–52. [Google Scholar] [CrossRef]
- Dehghani, A.; Sarbishei, O.; Glatard, T.; Shihab, E. A Quantitative Comparison of Overlapping and Non-Overlapping Sliding Windows for Human Activity Recognition Using Inertial Sensors. Sensors 2019, 19, 5026. [Google Scholar] [CrossRef]
- Wen, H.; Liu, X.; Lei, B.; Yang, M.; Cheng, X.; Chen, Z. A Privacy-Preserving Heterogeneous Federated Learning Framework with Class Imbalance Learning for Electricity Theft Detection. Appl. Energy 2025, 378, 124789. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, Y.; Liang, J.; Bai, K.; Yang, Q. Two sides of the same coin: White-Box and Black-Box Attacks for Transfer Learning. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, 6–10 July 2020; pp. 2989–2997. [Google Scholar]
- Maleki, S.; Pan, S.; Lakshminarayana, S.; Konstantinou, C. Survey of Load-Altering Attacks Against Power Grids: Attack Impact, Detection, and Mitigation. IEEE Open Access J. Power Energy 2025, 12, 220–234. [Google Scholar] [CrossRef]
- Gao, S.; Zou, Y.; Feng, L. A Lightweight Double-Deep Q-Network for Energy Efficiency Optimization of Industrial IoT Devices in Thermal Power Plants. Electronics 2025, 14, 2569. [Google Scholar] [CrossRef]
- Sarmas, E.; Dimitropoulos, N.; Marinakis, V.; Mylona, Z.; Doukas, H. Transfer learning strategies for solar power forecasting under data scarcity. Sci. Rep. 2022, 12, 14643. [Google Scholar] [CrossRef]


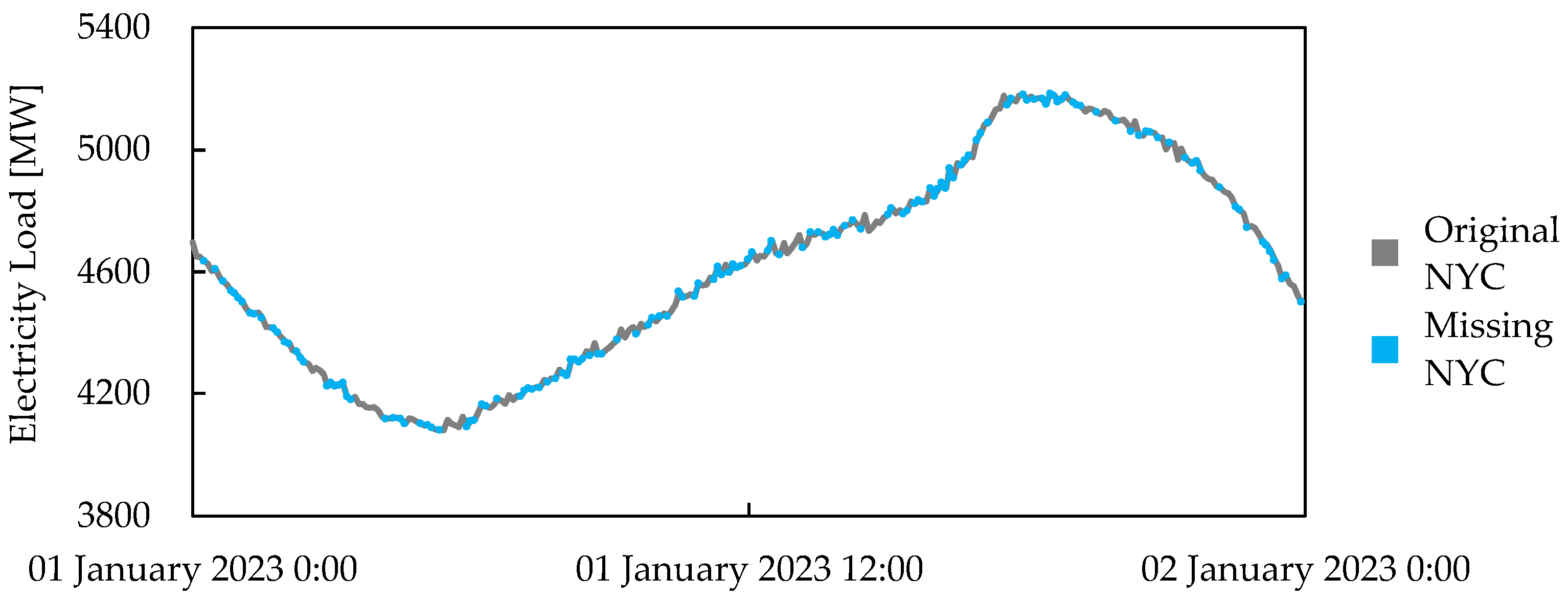

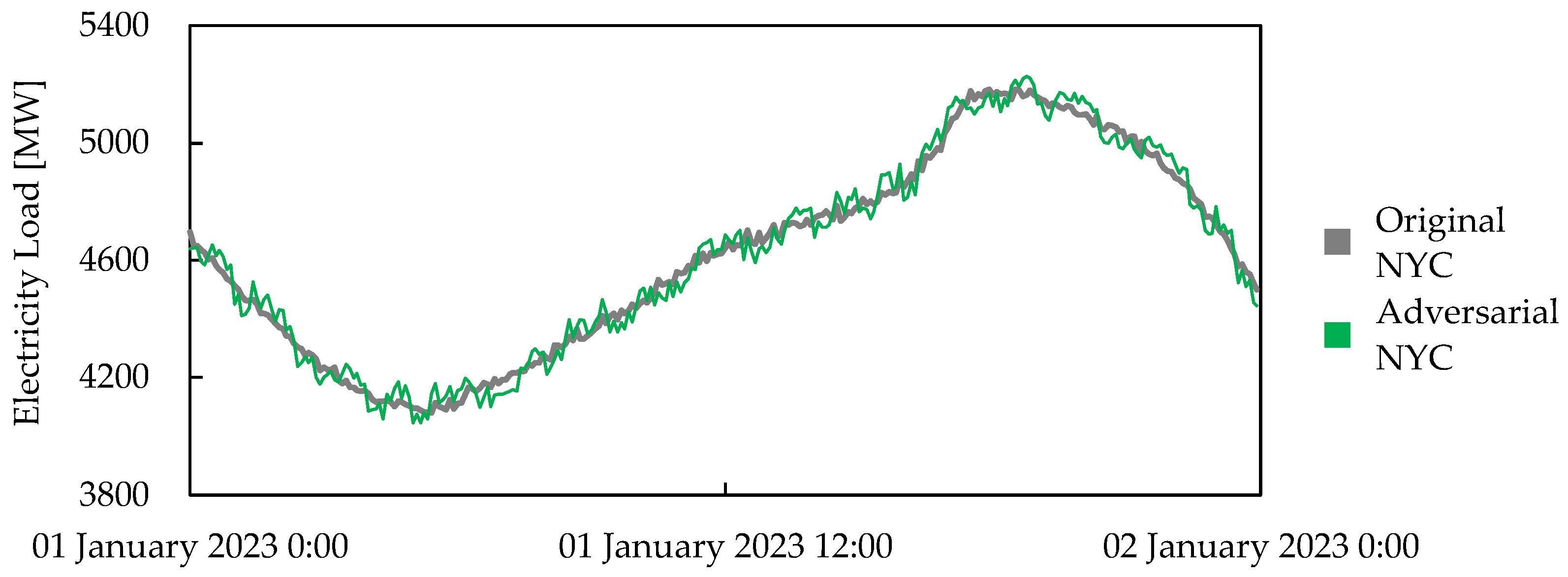
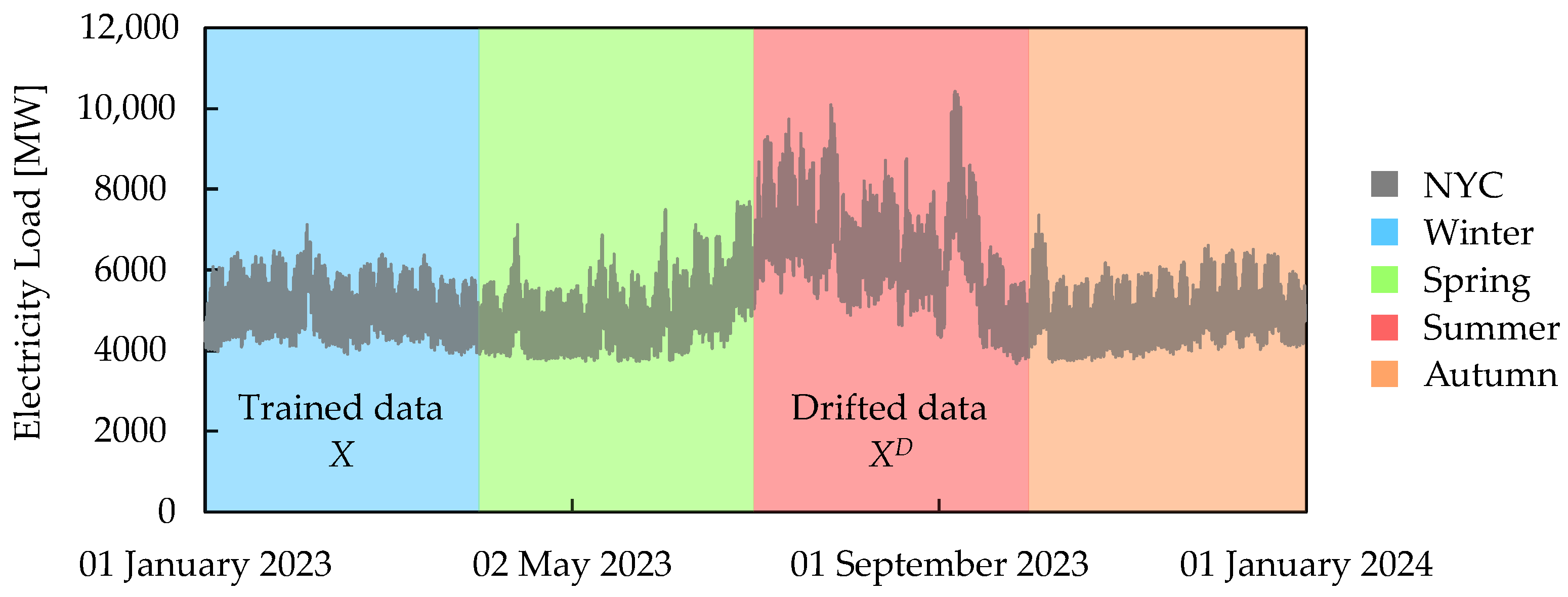
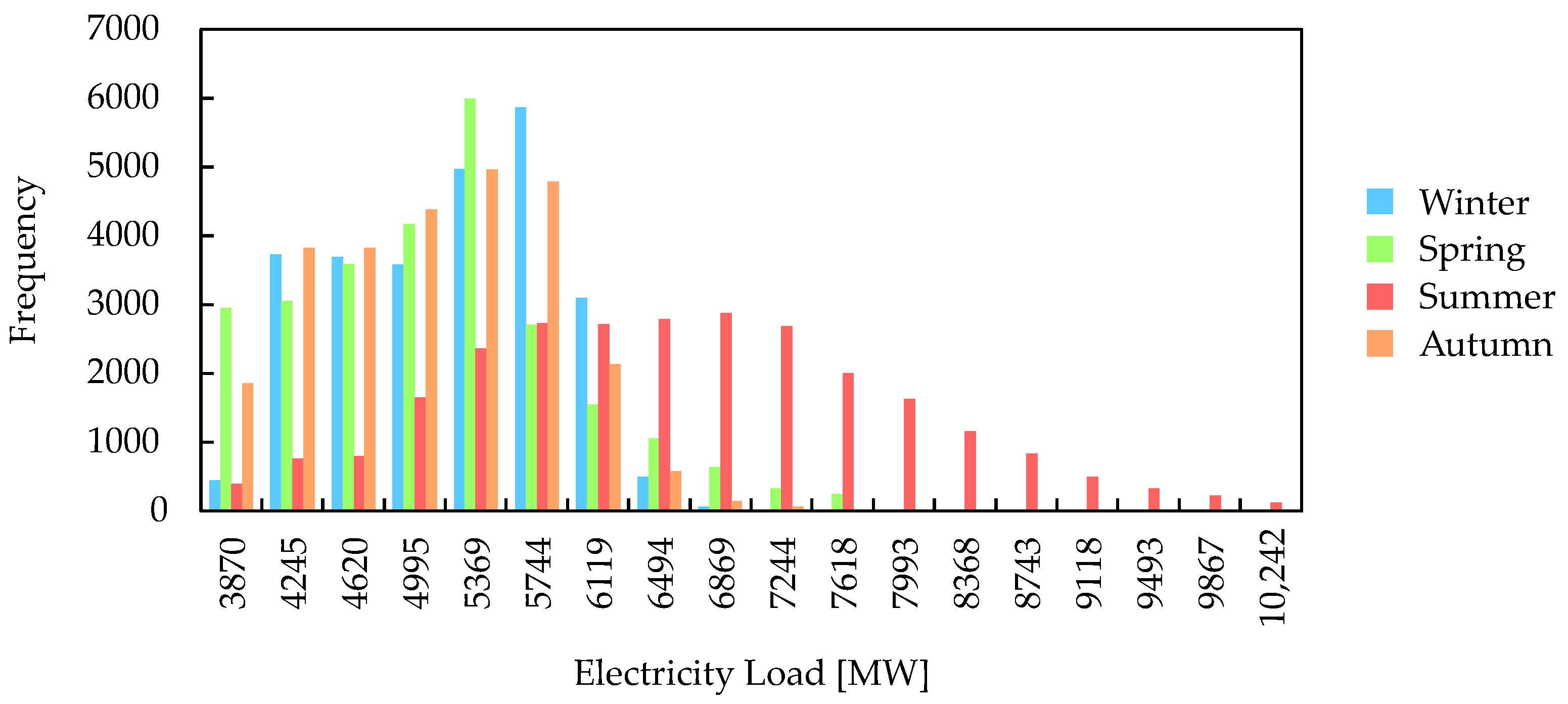
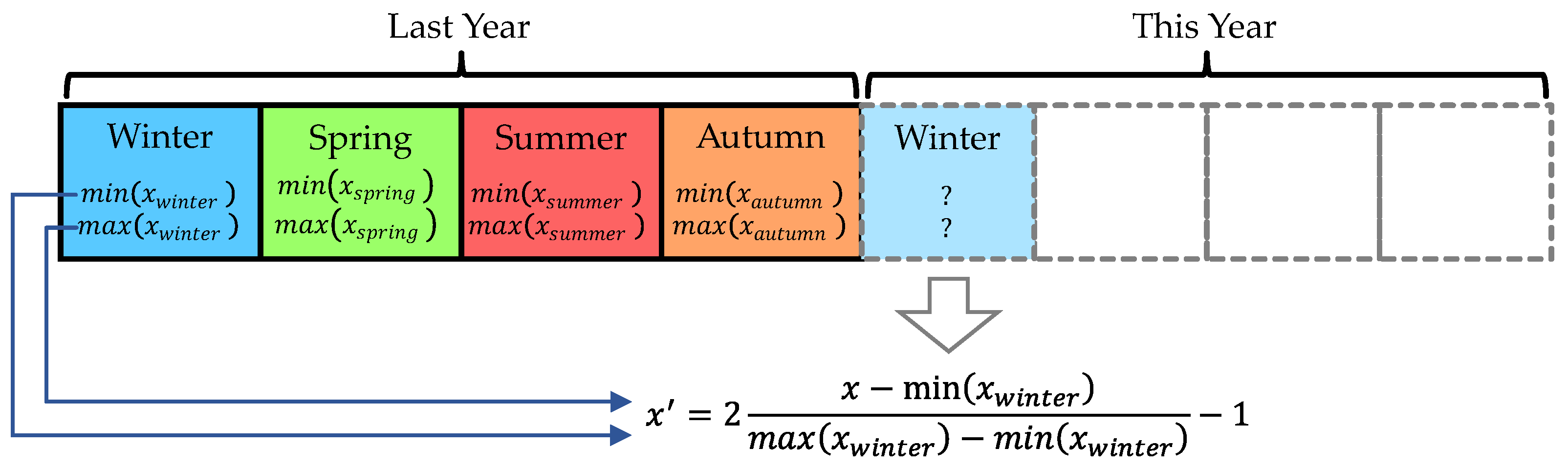
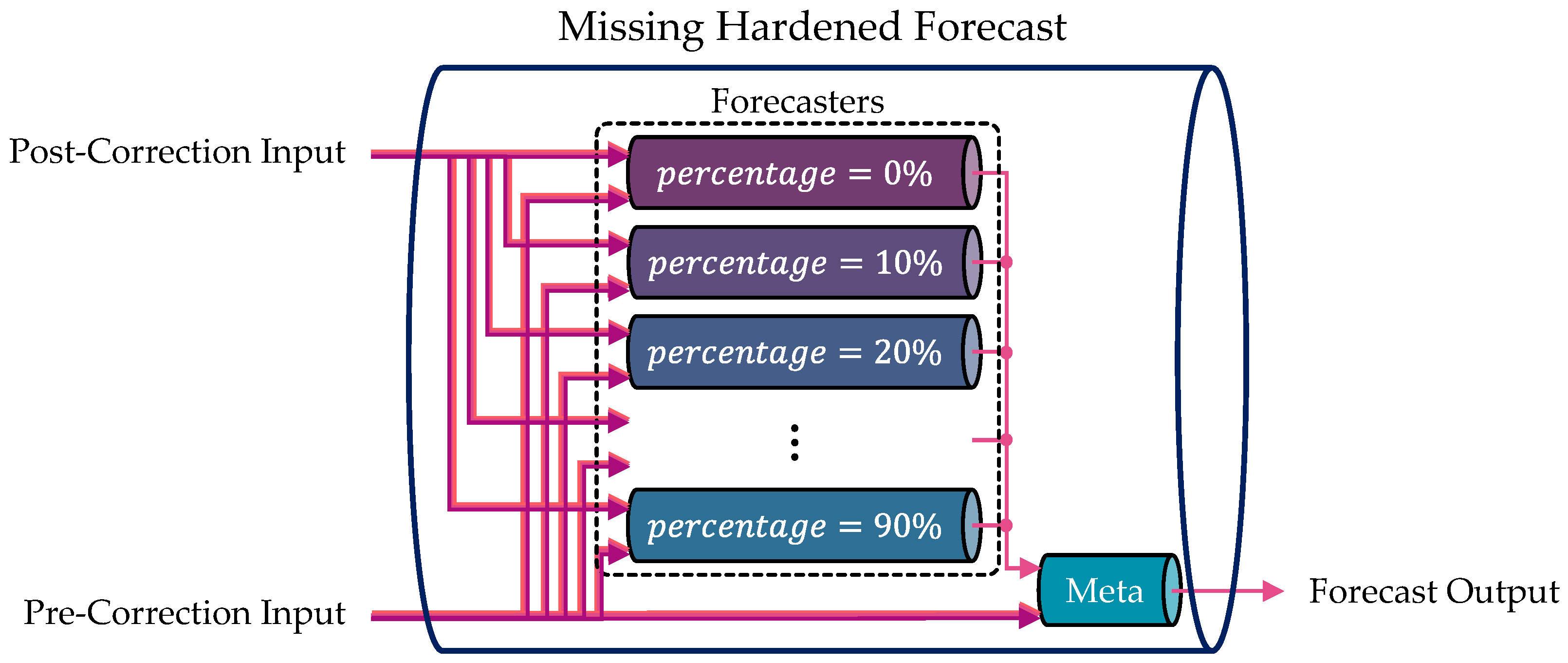



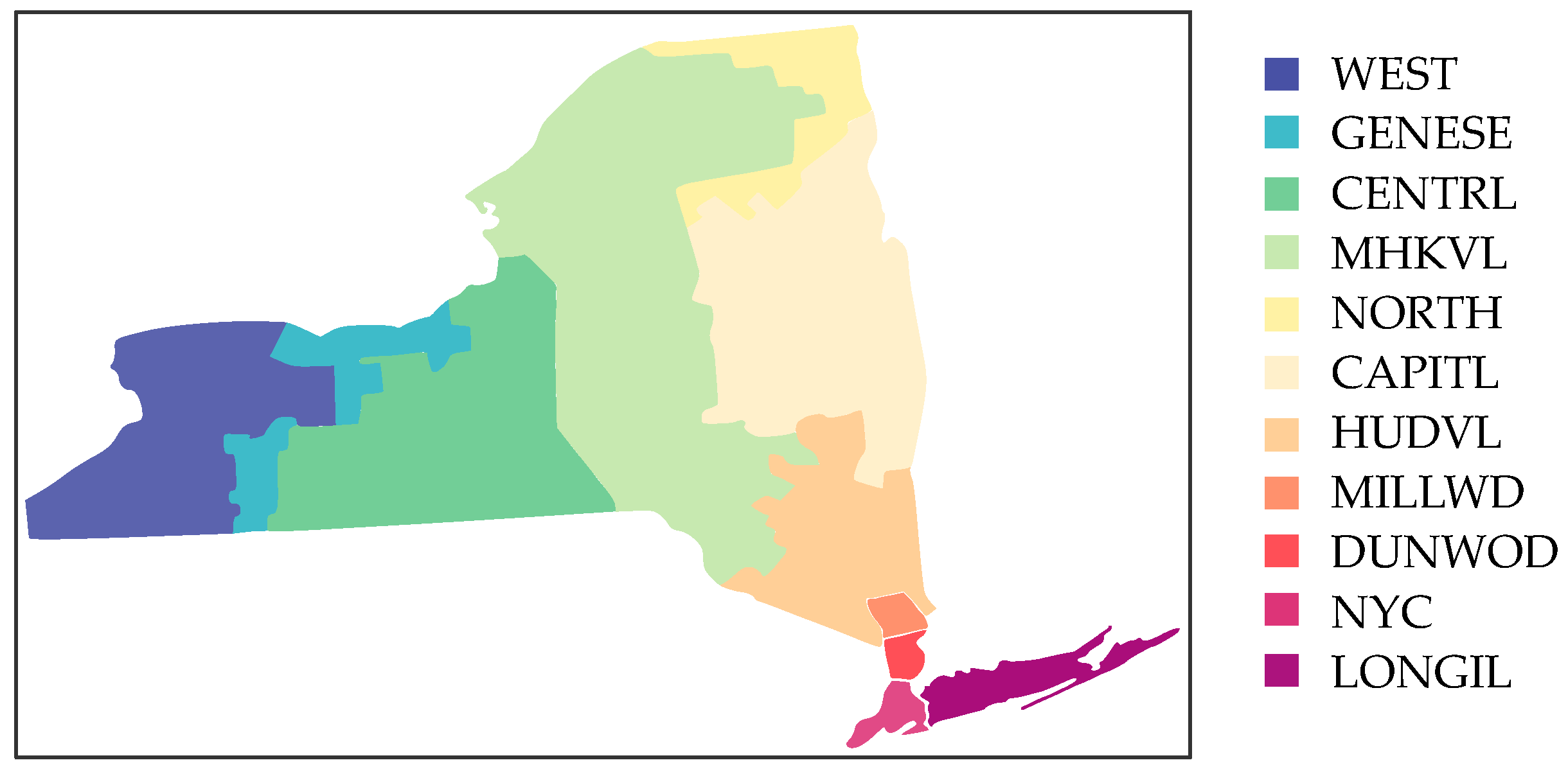
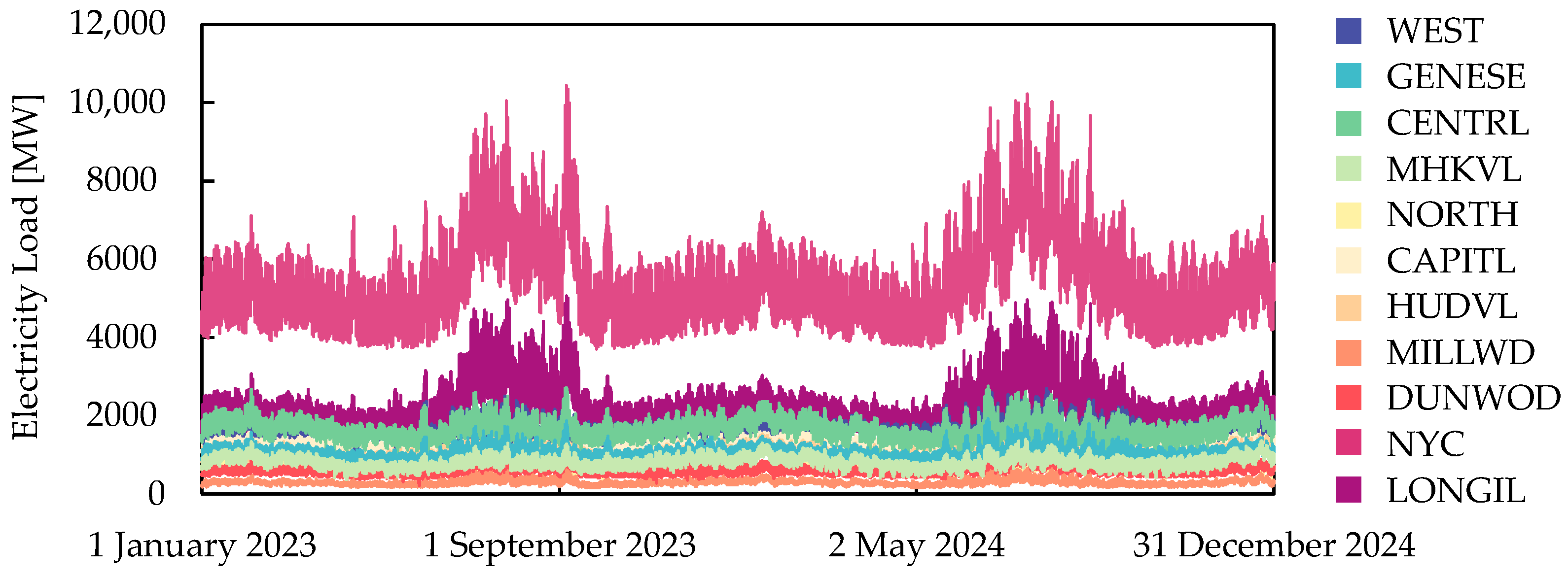





| Solution | Authors | Missing Values | Adversarial Attacks | Concept Drift |
|---|---|---|---|---|
| Single- Purpose | Hou et al. [30] | ✓ | ||
| Hwang et al. [31] | ✓ | |||
| Yihong Zhou et al. [33] | ✓ | |||
| Mahmoudnezhad et al. [34] | ✓ | |||
| Azeem et al. [35] | ✓ | |||
| Jagait et al. [36] | ✓ | |||
| Multi- Purpose | Yang Zhou et al. [37] | ✓ | ✓ * | ✓ * |
| Priority | Solution | Issues | ||
|---|---|---|---|---|
| Missing Values | Adversarial Attacks | Concept Drift | ||
| 1 | Impute | ✓ | ✗ | ✗ |
| 2 | Adversarial Correction | ✓ | ✗ | |
| 3 | Scaling Update | ✓ | ||
| Cascading Module | Training Data | |||
|---|---|---|---|---|
| Normal | Missing Values | Adversarial Attacks | Concept Drift | |
| Impute | ✓ | ✓ | ||
| Adversarial Correction | ✓ | ✓ | ||
| Scaling Update | ✓ | ✓ | ||
| Stacking Module | Training Data | |||
|---|---|---|---|---|
| Normal | Missing Values | Adversarial Attacks | Concept Drift | |
| Missing Hardened Forecast | ✓ | ✓ * | ||
| Adversarial Hardened Forecast | ✓ | ✓ * | ||
| Drift-Hardened Forecast | ✓ | ✓ * | ||
| Normal Forecaster | ✓ | |||
| Meta | ✓ | ✓ ** | ✓ ** | ✓ ** |
| Parameter | Value |
|---|---|
| Epoch | 300 |
| Optimizer | Adam |
| Batch Size | 1000 |
| Early Stop | 3, 0.001 |
| Learning Rate | 0.001 |
| Parameter | Value |
|---|---|
| Epoch | 300 |
| Optimizer | Adam |
| Batch Size | base = 1000, meta = 500 |
| Early Stop | 3, 0.0001 |
| Learning Rate | 0.001 |
| Zone | Spearman’s Rank Correlation Coefficient |
|---|---|
| DUNWOD | 0.9335 |
| LONGIL | 0.8787 |
| Solution | Average Metrics | ||
|---|---|---|---|
| Coefficient of Determination | Mean Absolute Error | Root Mean Squared Error | |
| Trivial | 0.9927 | 41.6954 | 58.3465 |
| Stackade | 0.9927 | 41.6954 | 58.3465 |
| Federated | 0.9808 | 70.7021 | 94.2437 |
| Solution | Average Metrics Difference Against Stackade | ||
|---|---|---|---|
| Coefficient of Determination (%) | Mean Absolute Error (%) | Root Mean Squared Error (%) | |
| Trivial | 0.0000 | 0.0000 | 0.0000 |
| Federated | −1.1974 | 69.5681 | 61.5242 |
| Missing Values (%) | Average Coefficient of Determination | ||
|---|---|---|---|
| Trivial | Stackade | Federated | |
| 10 | 0.9898 | 0.9912 | 0.9270 |
| 20 | 0.9856 | 0.9906 | 0.8674 |
| 30 | 0.9794 | 0.9895 | 0.8045 |
| 40 | 0.9720 | 0.9876 | 0.7297 |
| 50 | 0.9623 | 0.9835 | 0.6458 |
| 60 | 0.9490 | 0.9772 | 0.5600 |
| 70 | 0.9315 | 0.9643 | 0.4563 |
| 80 | 0.9052 | 0.9328 | 0.3453 |
| 90 | 0.8133 | 0.8323 | 0.2213 |
| Missing Values (%) | Average Mean Absolute Error | ||
|---|---|---|---|
| Trivial | Stackade | Federated | |
| 10 | 48.5296 | 47.2070 | 133.2267 |
| 20 | 57.4303 | 49.0083 | 180.9100 |
| 30 | 68.6636 | 51.9195 | 222.2344 |
| 40 | 81.2387 | 55.7631 | 264.6083 |
| 50 | 95.1206 | 62.9048 | 308.5070 |
| 60 | 110.9104 | 71.7296 | 353.5963 |
| 70 | 130.8465 | 88.2006 | 402.6867 |
| 80 | 156.2930 | 120.3464 | 453.6296 |
| 90 | 217.2589 | 197.4284 | 507.5620 |
| Missing Values (%) | Average Root Mean Squared Error | ||
|---|---|---|---|
| Trivial | Stackade | Federated | |
| 10 | 69.1110 | 64.0279 | 184.5113 |
| 20 | 81.9623 | 66.2038 | 248.5724 |
| 30 | 98.0435 | 69.9228 | 302.0623 |
| 40 | 114.3206 | 76.1218 | 355.3547 |
| 50 | 132.6067 | 87.7459 | 406.9709 |
| 60 | 154.3411 | 103.4197 | 453.7577 |
| 70 | 178.9805 | 129.3410 | 504.5537 |
| 80 | 210.6709 | 177.4555 | 553.7685 |
| 90 | 295.7594 | 280.3288 | 603.9647 |
| Missing Values (%) | Average Mean Absolute Error Difference Against Stackade MAE (%) | |
|---|---|---|
| Trivial | Federated | |
| 10 | 2.8017 | 182.2179 |
| 20 | 17.1848 | 269.1417 |
| 30 | 32.2501 | 328.0363 |
| 40 | 45.6854 | 374.5219 |
| 50 | 51.2136 | 390.4347 |
| 60 | 54.6229 | 392.9572 |
| 70 | 48.3510 | 356.5576 |
| 80 | 29.8692 | 276.9364 |
| 90 | 10.0444 | 157.0866 |
| Perturbation Intensity | Average Coefficient of Determination | ||
|---|---|---|---|
| Trivial | Stackade | Federated | |
| 0.01 | 0.9902 | 0.9926 | 0.9727 |
| 0.02 | 0.9886 | 0.9910 | 0.9491 |
| 0.03 | 0.9861 | 0.9885 | 0.9100 |
| 0.04 | 0.9827 | 0.9853 | 0.8554 |
| 0.05 | 0.9782 | 0.9810 | 0.7853 |
| 0.06 | 0.9726 | 0.9761 | 0.6996 |
| 0.07 | 0.9665 | 0.9702 | 0.5984 |
| 0.08 | 0.9601 | 0.9652 | 0.4817 |
| 0.09 | 0.9526 | 0.9588 | 0.3489 |
| Perturbation Intensity | Average Mean Absolute Error | ||
|---|---|---|---|
| Trivial | Stackade | Federated | |
| 0.01 | 49.3087 | 42.8570 | 85.7619 |
| 0.02 | 54.4565 | 47.8518 | 119.6913 |
| 0.03 | 61.4071 | 55.1187 | 160.4445 |
| 0.04 | 69.6942 | 62.9749 | 204.3047 |
| 0.05 | 79.0866 | 72.1098 | 249.7080 |
| 0.06 | 89.5034 | 81.1657 | 295.9888 |
| 0.07 | 99.1746 | 90.3727 | 342.7014 |
| 0.08 | 108.8970 | 98.0133 | 389.7609 |
| 0.09 | 118.8386 | 106.0729 | 437.2502 |
| Perturbation Intensity | Average Root Mean Squared Error | ||
|---|---|---|---|
| Trivial | Stackade | Federated | |
| 0.01 | 67.7410 | 59.0411 | 111.4676 |
| 0.02 | 72.8777 | 64.4952 | 149.4747 |
| 0.03 | 80.0535 | 72.5370 | 196.1288 |
| 0.04 | 88.7196 | 81.4213 | 246.6188 |
| 0.05 | 98.5214 | 91.6195 | 299.1346 |
| 0.06 | 109.9490 | 102.3596 | 352.9021 |
| 0.07 | 120.8568 | 113.7136 | 407.3712 |
| 0.08 | 130.9023 | 121.9266 | 462.2885 |
| 0.09 | 141.7989 | 131.6548 | 517.7465 |
| Perturbation Intensity | Average Mean Absolute Error Difference Against Stackade MAE (%) | |
|---|---|---|
| Trivial | Federated | |
| 0.01 | 15.0540 | 100.1118 |
| 0.02 | 13.8023 | 150.1288 |
| 0.03 | 11.4089 | 191.0891 |
| 0.04 | 10.6699 | 224.4225 |
| 0.05 | 9.6753 | 246.2887 |
| 0.06 | 10.2725 | 264.6723 |
| 0.07 | 9.7395 | 279.2088 |
| 0.08 | 11.1043 | 297.6613 |
| 0.09 | 12.0349 | 312.2168 |
| Solution | Average Metrics | ||
|---|---|---|---|
| Coefficient of Determination | Mean Absolute Error | Root Mean Squared Error | |
| Trivial | 0.9966 | 53.7347 | 76.7410 |
| Stackade | 0.9968 | 52.5382 | 73.6552 |
| Federated | 0.9808 | 70.7021 | 94.2437 |
| Solution | Average Metrics Difference Against Stackade | ||
|---|---|---|---|
| Coefficient of Determination (%) | Mean Absolute Error (%) | Root Mean Squared Error (%) | |
| Trivial | −0.0272 | 2.2774 | 4.1896 |
| Federated | −1.5786 | 34.5729 | 27.9525 |
| Solution | Average Metrics | ||
|---|---|---|---|
| Coefficient of Determination | Mean Absolute Error | Root Mean Squared Error | |
| Trivial | 0.9811 | 132.8607 | 180.2155 |
| Stackade | 0.9889 | 101.9040 | 137.9911 |
| Federated | 0.7701 | 456.9376 | 628.6633 |
| Solution | Average Metrics Difference Against Stackade | ||
|---|---|---|---|
| Coefficient of Determination (%) | Mean Absolute Error (%) | Root Mean Squared Error (%) | |
| Trivial | −0.7896 | 30.3783 | 30.5994 |
| Federated | −21.5088 | 348.4002 | 355.5826 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bin Kamilin, M.H.; Yamaguchi, S. Stackade Ensemble Learning for Resilient Forecasting Against Missing Values, Adversarial Attacks, and Concept Drift. Appl. Sci. 2025, 15, 8859. https://doi.org/10.3390/app15168859
Bin Kamilin MH, Yamaguchi S. Stackade Ensemble Learning for Resilient Forecasting Against Missing Values, Adversarial Attacks, and Concept Drift. Applied Sciences. 2025; 15(16):8859. https://doi.org/10.3390/app15168859
Chicago/Turabian StyleBin Kamilin, Mohd Hafizuddin, and Shingo Yamaguchi. 2025. "Stackade Ensemble Learning for Resilient Forecasting Against Missing Values, Adversarial Attacks, and Concept Drift" Applied Sciences 15, no. 16: 8859. https://doi.org/10.3390/app15168859
APA StyleBin Kamilin, M. H., & Yamaguchi, S. (2025). Stackade Ensemble Learning for Resilient Forecasting Against Missing Values, Adversarial Attacks, and Concept Drift. Applied Sciences, 15(16), 8859. https://doi.org/10.3390/app15168859







