Abstract
Images captured under complex lighting conditions often suffer from local under/ overexposure and detail loss. Existing methods typically process illumination and texture information in a mixed manner, making it difficult to simultaneously achieve precise exposure adjustment and preservation of detail. To address this challenge, we propose LapECNet, an enhanced Laplacian pyramid network architecture for image exposure correction and detail reconstruction. Specifically, it decomposes the input image into different frequency bands of a Laplacian pyramid, enabling separate handling of illumination adjustment and detail enhancement. The framework first decomposes the image into three feature levels. At each level, we introduce a feature enhancement module that adaptively processes image features across different frequency bands using spatial and channel attention mechanisms. After enhancing the features at each level, we further propose a dynamic aggregation module that learns adaptive weights to hierarchically fuse multi-scale features, achieving context-aware recombination of the enhanced features. Extensive experiments with public benchmarks on the MSEC dataset demonstrated that our method gave improvements of 15.4% in PSNR and 7.2% in SSIM over previous methods. On the LCDP dataset, our method demonstrated improvements of 7.2% in PSNR and 13.9% in SSIM over previous methods.
1. Introduction
In the field of computational photography, image quality degradation under complex lighting conditions has long posed challenges for practical applications and has become one of the key bottlenecks limiting the performance of computer vision systems. Since the dynamic range of real-world scenes far exceeds the perceptual capabilities of image sensors, captured images often suffer from local underexposure or overexposure. This not only leads to the loss of critical details and color distortion in key regions, but also triggers a range of issues such as nonlinear noise amplification and edge artifacts. These degradation effects severely impact the performance of subsequent high-level vision tasks. For example, in object detection tasks [1], saturated pixels in overexposed areas can significantly undermine the reliability of feature extraction; in semantic segmentation tasks [2], low-contrast boundaries caused by uneven lighting can greatly reduce the accuracy of pixel-level classification.
Existing exposure correction methods can be broadly categorized into two types: image decomposition methods based on deep Retinex models [3,4,5,6,7], and end-to-end enhancement methods based on deep learning [8,9,10,11,12]. The former aim to correct illumination through modeling the illumination–reflectance relationship, but tend to rely heavily on prior assumptions and struggle to adapt to complex scenes. The latter learn image enhancement mappings in a data-driven manner, offering strong representation capabilities. However, a more fundamental challenge lies in the difficulty of achieving a good balance between exposure correction accuracy and the preservation of image details. Global adjustment methods, while generally stable in maintaining overall brightness consistency, often introduce over-smoothing, which damages local texture coherence and blurs structural boundaries. On the other hand, local enhancement algorithms may improve brightness in dark regions but can easily introduce side effects such as halo artifacts, noise amplification, or even color shifts. Moreover, in complex scenes where multiple lighting types (e.g., strong light, backlight, and shadows) coexist, exposure imbalance often exhibits high spatial non-uniformity, placing greater demands on the regional adaptability of correction algorithms. Consequently, these issues limit the robustness and enhancement performance of existing methods.
To overcome the bottleneck in existing methods, where detail restoration and global exposure adjustment are difficult to balance simultaneously, this paper proposes an innovative exposure correction network based on Laplacian pyramid decomposition (LapECNet). LapECNet first utilizes a Laplacian pyramid to perform multi-scale decomposition of the input image, breaking it down into three frequency levels. The high-frequency and mid-frequency layers contain abundant texture detail information and are responsible for detail restoration and sharpening of the image; the low-frequency layer reflects the overall illumination distribution and governs global exposure balancing. This hierarchical decomposition effectively realizes the physical separation of illumination adjustment and detail enhancement.
A Feature Enhancement Module (FEM) for frequency-specific feature calibration, employs dual attention mechanisms (spatial and channel attention) to adaptively calibrate multi-frequency features, enabling precise enhancement of texture details, while suppressing noise. In addition, a Dynamic Aggregation Module (DAM) implements a learnable aggregation strategy, replacing heuristic fixed fusion rules with adaptive context-aware weights. By adopting a divide-and-conquer processing strategy, LapECNet achieves frequency-domain decomposition of the input image and differentiated optimization of hierarchical features, demonstrating that its systematic architectural design can achieve substantial performance improvements over existing approaches.
The contributions of this paper are summarized as follows:
- We present LapECNet, which integrates Laplacian pyramid decomposition into deep learning-based exposure correction, providing explicit frequency-domain separation to achieve independent optimization of illumination distribution and texture details.
- We design an FEM module that employs dual attention mechanisms to adaptively calibrate multi-frequency features. Moreover, we design a DAM module that implements learnable adaptive weights to replace fixed fusion rules.
- Our method achieved state-of-the-art results on multiple public datasets, while providing satisfactory visual quality and computational efficiency.
2. Related Work
2.1. Traditional Methods
Traditional exposure correction methods mainly rely on physical models or statistical characteristics of images. Common techniques include histogram equalization, curve adjustment, and the Retinex theory. Histogram equalization [13,14] enhances contrast by adjusting the brightness distribution of an image. Specifically, it stretches the grayscale range so that the pixel values are more evenly distributed across the available interval, thereby improving the overall contrast and visibility of detail. Building upon this, CLAHE (Contrast Limited Adaptive Histogram Equalization) [15] divides an image into smaller regions and limits the enhancement of local contrast. This effectively avoids unnatural halos and inconsistent contrast in areas with similar grayscale values or near texture boundaries.
Among curve adjustment methods, the most common is gamma correction. This technique is a nonlinear brightness transformation based on the human eye’s nonlinear perception of light intensity. It adjusts image brightness using a power-law function, making the image visually more in line with human perception. Beyond gamma correction, researchers have proposed various S-curve-based image enhancement methods. These approaches optimize brightness and contrast adjustment effects by designing different S-shaped mapping functions. To further improve enhancement performance, many studies have adopted hierarchical or zonal processing strategies. Bennett et al. [16] proposed a hierarchical processing method that first decomposes the input image into a low-frequency base layer and high-frequency detail layer, then uses optimal S-curve mapping functions for different hierarchical features, and finally obtains the enhanced image through layer recombination. Yuan et al. [17] proposed an improved region-based solution that uses superpixel segmentation technology to divide the input image into multiple sub-regions with similar characteristics, then adaptively designs specific S-curve mapping functions for each sub-region, to achieve a more precise region-aware exposure correction.
The Retinex model, from a physical perspective, decomposes an image into illumination and reflectance components, and processes them separately to enhance image quality. Common variants include Single-Scale Retinex [18] and Multi-Scale Retinex [19] methods, which estimate the illumination map and enhance its contrast, while preserving the details in the reflectance component. To mitigate noise issues, improved methods [20,21,22] such as LIME [23,24] generate an initial illumination map using an image’s maximum channel and optimize it using structure-aware smoothing priors to achieve more natural enhancement effects. The Robust Retinex model [25] further introduced a noise component to more effectively handle image noise and improve overall image quality.
Although the above traditional methods improved image quality to some extent through manually designing features and mathematical models to adjust the dynamic range, they still face many limitations. These include noise amplification, halo artifacts, and color distortions, and they often struggle to adapt to complex lighting conditions, making them less suitable for diverse real-world applications.
2.2. Deep-Learning-Based Methods
In recent years, with the rapid development of deep learning technology, deep-learning-based exposure correction methods have [26,27,28,29,30,31,32,33,34,35,36,37,38] have gradually emerged, becoming a research hotspot in the field of image enhancement. Compared with traditional methods relying on physical models or manually designed features, deep learning can learn the exposure patterns of images through large-scale data, achieving more intelligent and adaptive exposure correction.
Some methods primarily address underexposed images. Zero-DCE [39,40] proposed a lightweight DCE-Net trained with a no-reference loss function, achieving low-light enhancement without reference images by predicting pixel-level transformation curves. EnlightenGAN [41] effectively improves overall image quality and detail representation through the collaboration of a generator and two discriminators, global and local. DRBN [42,43] constructs a semi-supervised low-light image enhancement framework combining a supervised branch with frequency band feature learning and an unsupervised adversarial branch based on high-perceptual-quality images, significantly enhancing image detail restoration and visual quality.
Other approaches simultaneously address both underexposed and overexposed images. CLIP-LIT [44] utilizes the text–image contrast capability of the CLIP model to achieve efficient pixel-level image enhancement through unsupervised learning and ranking optimization. CoTF [45] combines 3D LUT global mapping with low-resolution local transformations and improves data quality through adaptive sampling, enabling real-time processing of high-resolution images. ENC [8] achieves alignment and fusion of different exposure features through exposure normalization and compensation modules, enhancing multi-exposure image enhancement effects by combining channel attention and parameter regularization. LACT [46] models the brightness ranking relationship between images, integrates semantic features, and completes color transformation and adjustment across multiple channel dimensions. DDNet [10] dynamically adjusts the network structure to perform finer processing of more challenging regions in images, improving local quality, while reducing computational costs. DAConv [47] introduced structurally decoupled aggregation convolution, separately handling contrast and details through addition and difference operations, supplemented by two types of perception unit, for effective image quality enhancement. Li et al. [48] designed two modules to identify and correct color deviations in exposure-abnormal regions, generating more natural images, while Li et al. [11] developed a lightweight multi-head attention mechanism that integrates window aggregation and partitioning strategies, balancing global context capture and local feature retention.
Among these methods, MSEC [49] and FECNet [9] represent two important paradigms. MSEC divides exposure adjustment into two stages: color enhancement and detail restoration, constructing a multi-scale network based on the Laplacian pyramid and training with multi-exposure datasets. While MSEC employs Laplacian pyramid decomposition, it requires multiple specialized sub-networks for different processing stages, resulting in increased computational overhead (18.45 G FLOPs) and architectural complexity. FECNet implements a dual-branch network based on Fourier frequency domain information, separately restoring luminance and structural features through frequency-domain processing. However, FECNet operates primarily in the global Fourier frequency domain, with separate branches for different feature types, leading to higher computational complexity (23.28 G FLOPs) and less direct control over specific frequency bands compared to localized pyramid-based approaches.
3. Methods
The proposed LapECNet is an exposure correction network based on Laplacian pyramid decomposition, whose core idea lies in the synergistic optimization of illumination adjustment and detail restoration through multi-scale feature decomposition and adaptive enhancement. Unlike existing methods that either rely on global frequency analysis or require multiple specialized sub-networks, our approach achieves both interpretable frequency separation and computational efficiency through a unified architectural design.
The synergistic combination of frequency–space separation and attention-based modules provides an interpretable processing pipeline, with clear separation between illumination and detail enhancement, computational efficiency through a unified architecture that reduces complexity compared to multi-stage approaches, and adaptive processing that enables scene-specific optimization through context-aware fusion. The details of LapECNet each module are elaborated in Figure 1.
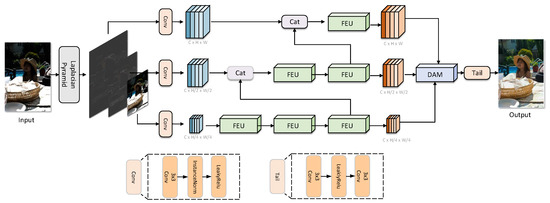
Figure 1.
The overall framework of LapECNet consists of three main modules: Laplacian Pyramid Decomposition, Feature Enhancement Module (FEM), and Dynamic Aggregation Module (DAM).
3.1. Laplacian Pyramid
The Laplacian Pyramid (LP) is a classic multi-scale image representation method that captures detail information across different frequency bands through differential computation of a Gaussian Pyramid (GP). Given an input image , we first construct its Gaussian Pyramid , where and represents the downsampled result of the l-th layer. Subsequently, the Laplacian Pyramid is computed as follows:
Here, , , and correspond to high/mid-frequency (texture details) and low-frequency (illumination distribution) components, respectively. This decomposition enables the network to independently process information from different frequency bands, avoiding detail loss caused by global adjustments.
3.2. Feature Enhancement Module (FEM)
To address the distinctive characteristics of different frequency bands, we have designed an efficient and adaptive Feature Enhancement Module (FEM). At its core lie the Spatial Attention (SA) and Channel Attention (CA) mechanisms, whose synergistic interaction enables precise feature modulation and enhancement, thereby improving the model’s perception and representation capabilities for multi-band information. The structure of the Feature Enhancement Module (FEM) is shown in Figure 2.
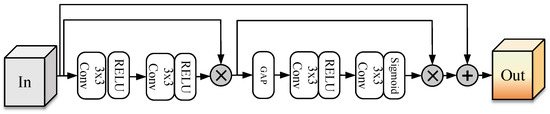
Figure 2.
The structure of the Feature Enhancement Module (FEM).
The FEM implements dual attention mechanisms that synergistically combine spatial and channel dependencies for adaptive feature calibration. The spatial attention mechanism employs a dynamic weight allocation strategy that effectively highlights critical regions, while suppressing irrelevant background information. Specifically, we perform both global average pooling and max pooling on the input feature map, aggregating dual-path information to capture rich spatial context. These pooled results are concatenated and processed through convolutional operations to generate spatial attention weights for each location.
The channel attention mechanism dynamically adjusts channel weights by modeling inter-channel dependencies, thereby emphasizing task-relevant feature channels, while suppressing redundant information. We apply global average pooling to compress spatial dimensions and obtain channel descriptor vectors, which then pass through two fully-connected layers with nonlinear activation functions to generate normalized channel weight vectors for channel-wise feature recalibration.
After obtaining spatially weighted and channel-wise attention-weighted features, we employ residual connections to fuse these enhanced features with the original input. In neural networks, the symbol ⊕ represents element-wise addition (residual connection), while the symbol ⊙ represents element-wise multiplication (Hadamard product). The complete FEM transformation can be expressed as follows:
This unified architecture effectively combines local feature extraction (, ) with global context modeling (GAP) through a bottleneck design (, ) that provides dimensionality reduction, while maintaining expressiveness. By organically integrating dual attention mechanisms in the spatial and channel dimensions, this feature enhancement module significantly improves the model’s adaptive calibration capability for multi-band features and substantially boosts the representational performance, while theoretically minimizing information loss through principled optimization.
From an information-theoretic perspective, the channel attention mechanism can be viewed as an optimal information compression and selection process that adheres to the Information Bottleneck principle. Let denote the input feature map, represent the attention-weighted output, and Y denote the target variable (ground truth). The channel attention mechanism seeks to find a compressed representation that preserves task-relevant information, while discarding redundant information:
where denotes mutual information, Z represents the attention weight vector, and is a trade-off parameter. This formulation ensures that the attention mechanism maximally preserves information relevant to the exposure correction task, while minimizing the complexity of the compressed representation. The global average pooling operation acts as a sufficient statistic that captures the most informative channel-wise features, thereby satisfying the data processing inequality . The bottleneck design with dimensionality reduction ensures computational efficiency, while the theoretical guarantee of information preservation provides the foundation for the superior feature representation capability observed in our experiments.
3.3. Dynamic Aggregation Module (DAM)
Traditional pyramid reconstruction methods typically employ fixed weights (e.g., direct summation) during multi-scale feature fusion, making it difficult to adapt to the exposure requirements of different image components in the Laplacian pyramid. This approach assumes equal importance across all frequency bands, which is theoretically suboptimal for exposure correction, where different regions require different frequency emphasis. To address this fundamental limitation, we propose a Dynamic Aggregation Module (DAM) that achieves context-aware fusion of multi-scale features by learning adaptive weights through principled optimization. The structure of the Dynamic Aggregation Module (DAM) is illustrated in Figure 3.
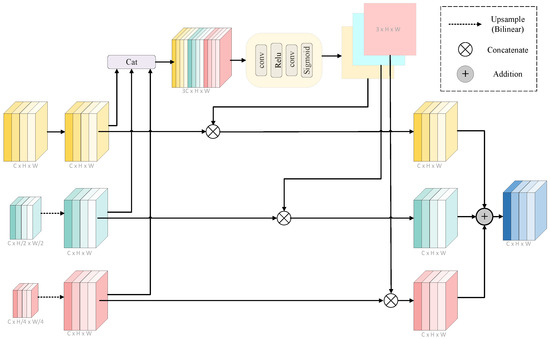
Figure 3.
The structure of the Dynamic Aggregation Module (DAM).
Specifically, the DAM module takes the enhanced multi-scale feature set from the FEM modules as input, where features exist at different spatial resolutions corresponding to the pyramid levels. The weight learning branch first upsamples all features to ensure spatial consistency, then concatenates them to form a comprehensive multi-scale representation. This concatenated feature undergoes channel compression and nonlinear transformation through two layers of convolutions with ReLU activation, followed by a Softmax operation to generate pixel-level adaptive weights , where each represents the adaptive weight map for the corresponding feature level.
The core dynamic aggregation process can be formulated as
where ⊙ denotes element-wise multiplication. This module dynamically adjusts the fusion strategy based on the exposure distribution of the input image, effectively enhancing high-frequency details in underexposed regions, while suppressing noise in overexposed areas, and thereby significantly improving the visual quality and detail recovery capability of the fused image. Experimental results demonstrated the superiority of the Dynamic Aggregation Module in multi-exposure image fusion tasks, endowing traditional pyramid reconstruction methods with enhanced adaptability and context-awareness.
3.4. Loss Function
To achieve a synergistic optimization of illumination enhancement and detail preservation, this paper implements a hybrid loss function that integrates pixel-level, semantic-level, and structural-level constraints. This function guides the model parameter updates end-to-end, from multiple complementary perspectives, significantly improving the quality and visual fidelity of image restoration. The detailed explanation of each loss term is as follows:
L1 Reconstruction Loss: The L1 reconstruction loss acts as a pixel-level fidelity constraint by directly measuring the absolute pixel-wise difference between the output image and the ground truth image , encouraging the model to generate images that are numerically consistent with the ground truth. It is defined as follows:
where C, H, and W denote the number of channels, height, and width of the image, respectively. Compared with L2 loss, L1 loss is more robust to outliers, converges faster, and better avoids over-smoothing, thus facilitating precise detail recovery.
Perceptual Loss: Pixel-wise errors alone are insufficient to ensure the semantic integrity and visual naturalness of the image. Therefore, this work employs a perceptual loss computed via a pre-trained VGG-19 network (using features from the ReLU3 layer) to extract deep semantic features and measure the discrepancy between the output and ground truth images in the semantic feature space:
where denotes the VGG network feature mapping, and N is the number of elements in that feature layer. This loss effectively captures high-level semantic information such as shape, texture, and edges, reducing the blurring and semantic distortion caused by relying solely on pixel alignment, thereby enhancing visual naturalness.
Structural Similarity (SSIM) Loss: To preserve the image’s structural information and texture consistency, the Structural Similarity Index (SSIM) is introduced as a loss constraint. SSIM loss computes local similarity in brightness, contrast, and structure via a sliding window, defined as follows:
where M is the number of sliding windows, denotes local means, denotes local variances or covariances, and are stabilization constants. This loss helps the model better restore natural textures and image structures, especially excelling in edge details.
Total Loss Function: By integrating the above multi-level constraints, the final hybrid loss function is formulated as a weighted sum:
where are the weights for each loss term. The selection of these hyperparameters reflects careful consideration of the relative importance and convergence properties of each loss component within the optimization framework.
4. Experiments
4.1. Datasets
We utilized two exposure correction datasets for model training and testing: the MSEC and LCDP datasets.
The MSEC dataset [49] comprises multiple images with varying exposure levels, where each scene consists of five images at different exposure values (EV) covering −1.5 EV, −1 EV, 0 EV, +1 EV, and +1.5 EV. The images in this dataset primarily exhibit either overexposure or underexposure issues individually, containing 17,675 training images, 750 validation images, and 5905 test images.
The LCDP dataset [50] contains only one input image per scene, characterized by the simultaneous presence of both overexposed and underexposed regions within a single image. This better simulates complex real-world lighting conditions and is particularly suitable for addressing mixed exposure correction problems. The dataset includes a total of 1733 images, specifically divided into 1415 training images, 100 validation images, and 218 test images.
The selection of these two datasets was motivated by their complementary characteristics and comprehensive coverage of exposure correction challenges. Both the MSEC and LCDP datasets contain comprehensive exposure scenarios that demonstrated our method’s adaptability across diverse illumination conditions. MSEC provided a controlled evaluation of our frequency decomposition strategy across different exposure intensities. LCDP presented challenging real-world scenarios, including backlight conditions, strong directional lighting, and mixed illumination environments.
4.2. Implementation Details
The proposed method was implemented based on the PyTorch(v1.8, CUDA 10.2) deep learning framework, with both training and testing conducted on a device equipped with an NVIDIA TITAN V GPU. Our training configuration reflected careful consideration of optimization theory and convergence requirements for multi-scale pyramid processing. The network model employed the Adam optimizer with parameters and set to 0.9 and 0.999, respectively, as the adaptive moment estimation mechanism provides robust convergence characteristics essential for processing different frequency bands within the pyramid structure. These momentum parameters ensured stable gradient accumulation across the diverse frequency components, while maintaining computational stability throughout the 200-epoch training process.
We used 384 × 384 as the input image size, with a batch size of 4, ensuring that each pyramid level contained sufficient meaningful frequency information and accommodated the GPU memory constraints. The learning rate schedule followed a cosine annealing strategy, with an initial rate , gradually reducing to , and implementing the function . This approach provided smooth convergence, while preventing oscillations that could have disrupted the delicate balance between illumination and detail optimization in the final training stages. We also used random cropping, flipping, and rotation as data augmentation techniques.
In the total loss function, the weights , , and were empirically set to 10, 1, and 0.1, respectively.
4.3. Comparison with Other Methods
In this section, we present a comprehensive quantitative and qualitative comparative analysis between the proposed method and state-of-the-art techniques on the MSEC and LCDP datasets. For quantitative evaluation, we employed two metrics: Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM), where PSNR measures the overall reconstruction quality of images, while SSIM focuses on assessing the fidelity of local structural features.
4.3.1. Quantitative Comparison
Table 1 presents the quantitative comparison results between our proposed method and various state-of-the-art approaches on the MSEC dataset. In the table, the symbol ↑ indicates that higher values represent better performance for the corresponding metric. To highlight the advantages of each method, the highest metric values are marked in red. As seen from the overall dataset performance, our method achieved the best results, with PSNR and SSIM reaching 23.18 dB and 0.8691, respectively, representing statistically significant improvements over the other comparative methods. In the exposure correction domain, PSNR improvements of 0.5 dB or greater are considered substantial and practically meaningful. Our method demonstrated significant improvements: 0.83 dB over ENC-DRBN, 1.10 dB over MSEC, and 1.88 dB over LCDPNet, all exceeding the practical significance threshold and representing quantitatively meaningful advances in exposure correction performance. Furthermore, we conducted specialized quantitative tests on underexposed and overexposed subsets. On the underexposed subset, our method achieved the highest PSNR and SSIM values, proving its exceptional capability for recovering image details under low-light conditions. Similarly, on the overexposed subset, our method also demonstrated strong robustness, effectively restoring detail information in highlight regions.

Table 1.
Quantitative comparison results on the MSEC dataset between our method and state-of-the-art methods. Red bold numbers indicate the best performance values.
To address deployment feasibility concerns, we conducted runtime evaluations across multiple platforms. All timing measurements were performed with images of size 512 × 512 pixels, with results averaged over 100 inference runs. As detailed in Table 2, our method achieved an inference time of 0.0536 s on an NVIDIA TITAN V GPU, demonstrating competitive efficiency compared to LCDPNet (0.0472 s), while delivering superior quality metrics. The slight increase in inference time (13.6% overhead) was justified by the substantial quality improvements: 0.88 dB PSNR gain and 0.0139 SSIM improvement over LCDPNet. The unified architecture design enabled efficient deployment across diverse hardware configurations, while maintaining consistent quality improvements, supporting the claimed suitability for edge deployment applications.

Table 2.
Quantitative comparison, computational complexity and runtime performance results between our method and state-of-the-art methods on the LCDP dataset. Red bold numbers indicate the best performance values.
Table 2 presents a comprehensive quantitative comparison including computational complexity and runtime performance results between our proposed method and other state-of-the-art approaches on the LCDP dataset. The experimental results demonstrate that our method achieved 23.65 dB PSNR and 0.8524 SSIM on the LCDP dataset, representing statistically meaningful improvements over the competing methods. Applying the same practical significance thresholds, our method showed substantial advantages: 0.41 dB over LCDPNet, 0.57 dB over ENC-DRBN, and 1.31 dB over FECNet. While the improvement over LCDPNet approached the significance threshold, the substantial gains over the other methods, combined with consistent SSIM improvements, quantitatively demonstrate measurable advantages in handling non-uniform exposure correction tasks.
Regarding runtime performance, our method achieved competitive inference efficiency, with 0.0536 s per image on an NVIDIA TITAN V GPU, representing only a 13.6% increase compared to the fastest comparable method LCDPNet (0.0472 s). This modest runtime overhead is well justified considering the substantial quality improvements achieved: 0.41 dB PSNR gain and 0.0104 SSIM improvement over LCDPNet. Compared to other high-performing methods, our approach demonstrated superior time-quality trade-offs, requiring significantly less inference time than ENC-DRBN (0.1869 s), while achieving comparable or better quality metrics. Notably, our method substantially outperformed computationally intensive approaches like URetinexNet (0.1877 s) and FECNet (0.1261 s) in both speed and quality metrics. The runtime analysis revealed that our unified architecture effectively balances computational efficiency with performance gains, positioning our method as highly suitable for real-time applications, where both quality and speed are critical requirements. Furthermore, the inference time demonstrates practical viability across diverse deployment scenarios, from edge devices requiring rapid processing, to cloud-based systems handling batch workloads.
Our method demonstrated significant computational advantages by achieving superior performance, while maintaining exceptional efficiency, requiring only 7.26 G FLOPs at 512 × 512 resolution with 0.17 M parameters. These efficiency improvements translate to practical benefits, including reduced power consumption and broader hardware compatibility. Our approach required 68.8% fewer FLOPs compared to FECNet and 60.6% fewer compared to MSEC, representing substantial reductions that directly translate to decreased memory requirements and execution time across diverse hardware platforms. The architectural design efficiency becomes evident through a detailed computational breakdown analysis: Laplacian Pyramid Decomposition operates as a lightweight process requiring approximately 0.8 G FLOPs, the Feature Enhancement Modules across three pyramid levels consume about 4.2 G FLOPs for comprehensive dual-attention processing, and the Dynamic Aggregation Module utilizes approximately 2.26 G FLOPs for learnable fusion weight computation. This distribution reflects the careful balance between processing capability and computational efficiency inherent in our architectural design, where consistent PSNR and SSIM improvements indicate the improved detail preservation essential for practical systems.
Although our current evaluation framework utilized NVIDIA TITAN V GPU hardware, comprehensive computational analysis provided substantial evidence supporting edge device deployment feasibility. The single-stage unified architecture fundamentally eliminates the computational overhead associated with multi-stage processing approaches, thereby providing inherent efficiency advantages, which is particularly beneficial for resource-constrained deployment environments.
The exceptional parameter efficiency of 0.17 M parameters facilitates deployment on devices with stringent memory constraints, while the overall computational profile positions our method as highly suitable for diverse deployment scenarios, including high-end smartphones equipped with dedicated neural processing units, edge devices requiring real-time processing capabilities, and cloud-based applications handling batch processing workloads. The unified single-stage design reduces the integration complexity for downstream applications, facilitating easier adoption in real-world systems compared to multi-stage processing approaches. These computational characteristics serve as reliable indicators for deployment feasibility assessment, given their direct correlation with hardware resource requirements and execution performance across different computing platforms.
This outstanding performance primarily stems from our method’s effective decoupling of luminance and detail components, along with the synergistic effects of the carefully designed feature enhancement module and dynamic aggregation module.
To address the critical concern of result variability and provide the statistical analysis required for a rigorous evaluation, we conducted a comprehensive assessment of the PSNR variance across different methods. Figure 4 presents the statistical distribution of PSNR values for representative methods on the LCDP dataset, revealing important insights into method stability and reliability.
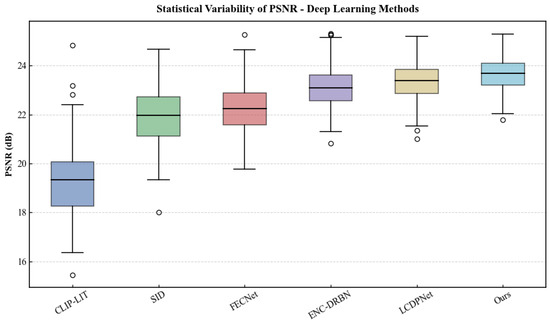
Figure 4.
Statistical variability analysis of PSNR across different methods. The boxplot demonstrates the distribution characteristics, including median, quartiles, and outliers for each method.
The statistical analysis revealed several critical findings that demonstrate the superiority and reliability of our proposed method compared to recent deep learning approaches. Our approach exhibited exceptional stability, with the smallest variance ( = 0.41) and tightest interquartile range among all recent methods tested, indicating remarkable consistency across diverse test images.
In contrast, recent methods showed varying degrees of stability, with CLIP-LIT demonstrating the largest variance ( = 2.10) and SID showing = 1.44, reflecting their limited adaptability to diverse exposure conditions. Even competitive methods like LCDPNet ( = 0.61) and ENC-DRBN ( = 0.72) exhibited a larger variance than our approach. Our method’s minimal spread in results, characterized by a standard deviation of = 0.64 dB compared to methods such as CLIP-LIT with = 1.45 dB and SID with = 1.2 dB, provides compelling statistical evidence of its superior robustness.
4.3.2. Qualitative Comparison
We further conducted visual comparison experiments to vividly demonstrate the performance differences between our proposed method and current state-of-the-art approaches. To highlight the comparative effectiveness, we selected the top-performing methods from the quantitative evaluations as benchmarks.
Figure 5 presents the visual comparison results on the MSEC dataset. Our enhanced visual validation included extensive comparative analysis with multiple methods: CLIP-LIT, ENC-DRBN, FECNet, LCDPNet, MSEC, alongside ground truth (GT) and input images. Figure 5 demonstrates the comparative advantages: Visual inspection reveals that texture details in vegetation areas show enhanced leaf structure definition, while water regions exhibit more natural brightness gradation, with reduced halo artifacts. Our method successfully recovered detailed features in the dark areas, strongly validating its unique advantages in addressing non-uniform exposure problems.

Figure 5.
Visual comparison results on the MSEC dataset between our method and state-of-the-art methods. Red bounding boxes highlight regions where our method showed particularly notable improvements.
Figure 6 displays the comparative experimental results on the LCDP dataset. For the severe dark areas present in the input images (particularly on house walls and windows), most existing methods struggled, leading to a substantial loss of detail information in these regions. Texture details in the building facade show enhanced window structure definition, with preserved architectural details, while sky regions exhibit a more natural brightness gradation, with reduced halo artifacts. The analysis reveals that existing methods generally suffered from inadequate exposure control, manifesting as localized overexposure or underexposure issues. Additionally, LCDPNet exhibited noticeable color distortion. In contrast, our method quantifiably enhanced the dynamic range performance, while preserving natural colors, achieving not only a more balanced global brightness distribution, but also an improved texture detail representation, resulting in markedly enhanced image clarity.

Figure 6.
Visual comparison results on the LCDP dataset between our method and state-of-the-art methods. Red bounding boxes highlight regions where our method showed particularly notable improvements.
To further demonstrate the robustness and generalizability of our approach, we conducted additional experiments on real-world images collected from publicly available sources. In Figure 7, the input image exhibits noticeable illumination and color distortions. Compared to the other methods, our method produced results that were closer to the ground truth in terms of detail restoration for a patch of aquatic plants, and better color consistency. This demonstrates that the proposed deep correction network based on Laplacian multi-frequency decomposition effectively captures multi-scale information and enhances reconstruction quality.

Figure 7.
Visual comparison results on the online image between our method and state-of-the-art methods. Red bounding boxes highlight regions where our method showed particularly notable improvements.
4.4. Ablation Studies
4.4.1. Impact of Laplacian Pyramid Levels
To validate the effectiveness of our frequency-domain decomposition strategy, we conducted systematic ablation experiments focusing on how the number of Laplacian pyramid decomposition layers affected model performance. The ablation analysis results are reported in Table 3. In the table, the symbol ↑ indicates that higher values represent better performance for the corresponding metric. While keeping the other network parameters constant, we comparatively analyzed pyramid decomposition levels set at 1, 2, 3, and 4 layers. Here, a single-layer decomposition indicates unseparated processing of luminance and detail information, maintaining a mixed processing approach. Through this experimental design, we demonstrated that our proposed 3-layer Laplacian pyramid decomposition achieved the optimal performance, with 23.65 dB PSNR and 0.8524 SSIM, confirming that proper frequency-domain separation is crucial for achieving a delicate balance between illumination adjustment and detail preservation. The results show a clear performance progression from 1-layer (22.84 dB) to 3-layer (23.65 dB), representing a substantial 0.81 dB improvement through effective architectural frequency separation. However, excessive decomposition layers (4-layer: 23.67 dB) yielded diminishing returns, while increasing computational complexity. These experimental results thoroughly validate the architectural contribution of our frequency-domain decomposition strategy.

Table 3.
Performance comparison with varying Laplacian pyramid decomposition layers. Bold numbers indicate the best performance values.
4.4.2. The Effectiveness of FEM and DAM
To validate the effectiveness of the proposed feature enhancement module and dynamic aggregation module, this study designed a series of ablation experiments by systematically removing or replacing these two modules, to evaluate their impact on the network performance. Table 4 shows the results of the ablation analysis for the module. In the table, the symbol ↑ indicates that higher values represent better performance for the corresponding metric. Specifically, the feature enhancement module was first replaced with a traditional residual module to verify its performance improvement effect; then, the dynamic aggregation module was replaced with basic operations of simple feature addition and feature concatenation, to assess the influence of different aggregation strategies on the information fusion capability. The experimental results demonstrated that compared with ordinary residual modules, the feature enhancement module significantly improved the feature representation capability; meanwhile, the dynamic aggregation module exhibited a superior adaptive multi-scale information fusion ability over traditional addition and concatenation operations. When both the feature enhancement module and dynamic aggregation module were employed, the model achieved the most substantial performance improvement, fully proving the effectiveness and complementary nature of these two modules.

Table 4.
Ablation study of the proposed FEM and DAM. Bold numbers indicate the best performance values.
4.4.3. Impact of Loss Function Weights
To evaluate the robustness and stability of our method with respect to parameter variations, we conducted a systematic analysis of the loss function weight parameters , , and . This ablation study addressed the critical question of parameter sensitivity and provided an insight into the optimization landscape of our hybrid loss function. Table 5 presents the quantitative results for different weight combinations on the LCDP dataset. In the table, the symbol ↑ indicates that higher values represent better performance for the corresponding metric.

Table 5.
Ablation study of loss function weight parameters. Bold numbers indicate the best performance values.
The experimental results provide valuable insights into the parameter stability characteristics of our proposed method. Our carefully selected configuration () achieved an optimal balance between pixel-level fidelity (PSNR) and structural preservation (SSIM), thereby confirming the theoretical soundness of our weight selection strategy. Notably, when examining the impact of varying values, we observed that increasing this parameter enhanced the structural similarity, at the expense of pixel-level accuracy, revealing an inherent trade-off between the different quality metrics. This behavior is consistent with theoretical expectations, as SSIM loss emphasizes perceptual quality, while potentially sacrificing numerical precision. Furthermore, our analysis of variations demonstrated that the perceptual loss component exhibited moderate sensitivity, where extreme values (0.1 or 10) led to suboptimal performance. This finding suggests that semantic feature alignment requires careful calibration to avoid under-regularization or over-smoothing effects. Additionally, the relatively small performance variations observed across the different parameter settings—with PSNR ranging within 0.27 dB and SSIM within 0.007—indicate that our method exhibited good stability with respect to hyperparameter changes, which is particularly crucial for practical deployment scenarios.
4.5. User Study
To provide a comprehensive evaluation beyond objective metrics and address the critical gap between computational measures and human perception, we conducted a systematic user study involving approximately 150 images selected from diverse exposure correction scenarios. The study was designed to evaluate perceptual quality through subjective human assessment, addressing the fundamental question of whether our technical improvements translated to meaningful visual enhancements in real-world scenarios.
The experimental design employed a comparative assessment framework, where evaluators examined image pairs processed by different deep learning methods. Participants were asked to evaluate three distinct aspects of image quality: details easy to perceive, which measured the clarity and preservation of fine textures and structural elements; proper exposure, which assessed the naturalness and balance of exposure correction, without artifacts; and overall rating, which captured the comprehensive aesthetic quality and realism of the processed images. Each aspect was rated using a 5-point Likert scale, ranging from poor to excellent. To ensure unbiased evaluation, images were presented in randomized order, without method identification, and participants were given sufficient time for careful examination of each image pair.
Figure 8 presents the comprehensive rating distributions across all evaluation criteria, revealing several statistically significant insights. Regarding detail preservation, our method received predominantly high ratings, with 80% of evaluations scoring it as very good or excellent, compared to 69% for the second-best method LCDPNet. This substantial difference validates our frequency-domain decomposition strategy’s effectiveness in preserving fine textures, while correcting exposure. Furthermore, illumination quality assessment demonstrated our method’s superior performance, achieving the highest satisfaction rates, with 85% of evaluations scoring 4 or above, indicating superior exposure correction, without introducing artifacts such as halos or color shifts. Recent deep learning methods showed more varied and generally lower responses, reflecting inconsistent illumination handling across different image scenarios. Additionally, the overall rating distribution shows our method received the most concentrated high scores, with a mean rating of 4.2 ( = 0.71), compared to 3.9 ( = 0.89) for competitive deep learning methods. The minimal variance in our ratings indicates consistent quality across diverse image contents and evaluation scenarios.
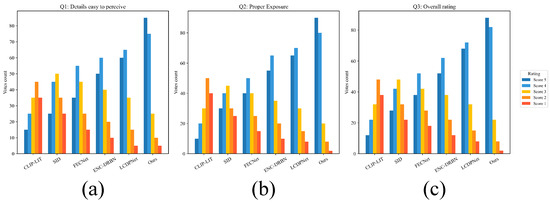
Figure 8.
User study results showing rating distributions for three evaluation criteria: (a) details easy to perceive, (b) proper exposure, and (c) overall rating.
This user study provided crucial validation and addressed fundamental concerns about the practical relevance of our technical contributions when compared against state-of-the-art deep learning methods, including CLIP-LIT, SID, FECNet, ENC-DRBN, and LCDPNet. The statistical evidence demonstrates that our architectural innovations in frequency-domain processing and dynamic aggregation translated directly to measurable improvements in human-perceived quality. The consistent preference for our method across all evaluation dimensions confirms that the theoretical advantages of Laplacian pyramid decomposition and attention-based feature enhancement manifested as genuine perceptual benefits. This human-centered validation complements our objective metrics and provides strong evidence for the real-world applicability of our approach in scenarios where visual quality assessment by human observers represents the ultimate criterion for success.
5. Conclusions
This paper presented LapECNet, an enhanced Laplacian pyramid network for image exposure correction that addresses the challenge of balancing global illumination adjustment with local detail preservation. Our method integrates Laplacian pyramid decomposition for frequency-domain separation of illumination and texture components, with Feature Enhancement Modules with dual-attention mechanisms for adaptive processing across different frequency bands, and a Dynamic Aggregation Module for context-aware multi-scale feature fusion. Experimental validation on the MSEC and LCDP datasets demonstrated significant performance improvements, achieving 23.18 dB PSNR and 0.8691 SSIM on MSEC, and 23.65 dB PSNR and 0.8524 SSIM on LCDP, while maintaining computational efficiency, with only 7.26 G FLOPs and 0.17 M parameters.
Despite these achievements, our work has limitations, including an incomplete evaluation on mobile devices and edge computing platforms; an exclusive focus on static images, without temporal consistency investigation for video applications; and a lack of formal user studies on perceptual quality. Future work will focus on exploring video sequence processing with temporal consistency; conducting real-world application integration studies, including mobile deployment; performing systematic user studies and out-of-distribution generalization analysis; and evaluating the method across a wider range of downstream tasks, to establish practical utility. Our frequency-domain foundation could potentially be enhanced by integrating perceptual learning modules to better model human visual preferences, semantic guidance to apply context-aware exposure correction, and adversarial training to improve visual realism.
Author Contributions
Conceptualization, J.J.; methodology, J.J. and Y.L.; software, Y.L.; validation, Y.L. and J.J.; formal analysis, Y.L.; investigation, Y.L.; resources, J.J.; data curation, Y.L.; writing—original draft preparation, Y.L.; writing—review and editing, J.J.; visualization, Y.L.; supervision, J.J.; project administration, J.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Horizontal General Project (Science and Technology Category) of Beijing Union University, titled “Development of Video-Based Extensometry Technology Using Digital Image Correlation (DIC)”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data were derived from public-domain resources. The LCDP dataset can be accessed at https://www.whyy.site/paper/lcdp (accessed on 6 August 2025), and the Exposure Correction dataset is available at https://github.com/mahmoudnafifi/Exposure_Correction (accessed on 6 August 2025).
Acknowledgments
The authors would like to thank all individuals who contributed to the creation and annotation of the datasets used in this research. We also acknowledge the Laboratory of Beijing Union University for providing experimental and technical support. The authors have reviewed and approved the final version of the manuscript and take full responsibility for its contents.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yang, W.; Yuan, Y.; Ren, W.; Liu, J.; Scheirer, W.J.; Wang, Z.; Zhang, T.; Zhong, Q.; Xie, D.; Pu, S.; et al. Advancing Image Understanding in Poor Visibility Environments: A Collective Benchmark Study. IEEE Trans. Image Process. 2020, 29, 5737–5752. [Google Scholar] [CrossRef] [PubMed]
- Strudel, R.; Garcia, R.; Laptev, I.; Schmid, C. Segmenter: Transformer for semantic segmentation. In Proceedings of the IEEE International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 7262–7272. [Google Scholar]
- Wei, C.; Wang, W.; Yang, W.; Liu, J. Deep Retinex decomposition for low-light enhancement. In Proceedings of the British Machine Vision Conference, Newcastle, UK, 3–6 September 2018; pp. 1–12. [Google Scholar]
- Yang, W.; Wang, W.; Huang, H.; Wang, S.; Liu, J. Sparse gradient regularized deep Retinex network for robust low-light image enhancement. IEEE Trans. Image Process. 2021, 30, 2072–2086. [Google Scholar] [CrossRef]
- Wu, W.; Weng, J.; Zhang, P.; Wang, X.; Yang, W.; Jiang, J. URetinex-net: Retinex-based deep unfolding network for low-light image enhancement. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5901–5910. [Google Scholar]
- Zhao, Z.; Xiong, B.; Wang, L.; Ou, Q.; Yu, L.; Kuang, F. RetinexDIP: A unified deep framework for low-light image enhancement. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 1076–1088. [Google Scholar] [CrossRef]
- Liu, R.; Ma, L.; Zhang, J.; Fan, X.; Luo, Z. Retinex-inspired unrolling with cooperative prior architecture search for low-light image enhancement. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 10556–10565. [Google Scholar] [CrossRef]
- Huang, J.; Liu, Y.; Fu, X.; Zhou, M.; Wang, Y.; Zhao, F.; Xiong, Z. Exposure normalization and compensation for multiple-exposure correction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 6043–6052. [Google Scholar]
- Huang, J.; Liu, Y.; Zhao, F.; Yan, K.; Zhang, J.; Huang, Y.; Zhou, M.; Xiong, Z. Deep fourier-based exposure correction network with spatial-frequency interaction. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 163–180. [Google Scholar]
- Li, Z.; Shao, Y.; Zhang, F.; Zhang, J.; Wang, Y.; Sang, N. Difficulty-aware dynamic network for lightweight exposure correction. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 5033–5048. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, J.; Wang, Y. Half aggregation transformer for exposure correction. In Proceedings of the Chinese Conference on Pattern Recognition and Computer Vision, Xiamen, China, 13–15 October 2023; pp. 469–481. [Google Scholar]
- Li, Z.; Wang, Y.; Zhang, J. Low-light image enhancement with knowledge distillation. Neurocomputing 2023, 518, 332–343. [Google Scholar] [CrossRef]
- Cheng, H.D.; Shi, X. A simple and effective histogram equalization approach to image enhancement. Digit. Signal Process. 2004, 14, 158–170. [Google Scholar] [CrossRef]
- Pizer, S.M.; Amburn, E.P.; Austin, J.D.; Cromartie, R.; Geselowitz, A.; Greer, T.; ter Haar Romeny, B.; Zimmerman, J.B.; Zuiderveld, K. Adaptive histogram equalization and its variations. Comput. Vision Graph. Image Process. 1987, 39, 355–368. [Google Scholar] [CrossRef]
- Pizer, S.; Johnston, R.; Ericksen, J.; Yankaskas, B.; Muller, K. Contrast-limited adaptive histogram equalization: Speed and effectiveness. In Proceedings of the International Conference on Visualization in Biomedical Computing, Atlanta, GA, USA, 22–25 May 1990; pp. 337–345. [Google Scholar]
- Bennett, E.P.; McMillan, L. Video enhancement using per-pixel virtual exposures. ACM Trans. Graph. 2005, 24, 845–852. [Google Scholar] [CrossRef]
- Yuan, L.; Sun, J. Automatic exposure correction of consumer photographs. In Proceedings of the European Conference on Computer Vision, Lorence, Italy, 7–13 October 2012; pp. 771–785. [Google Scholar]
- Jobson, D.; Rahman, Z.; Woodell, G. Properties and performance of a center/surround Retinex. IEEE Trans. Image Process. 1997, 6, 451–462. [Google Scholar] [CrossRef]
- Jobson, D.; Rahman, Z.; Woodell, G. A multiscale Retinex for bridging the gap between color images and the human observation of scenes. IEEE Trans. Image Process. 1997, 6, 965–976. [Google Scholar] [CrossRef]
- Fu, X.; Zeng, D.; Huang, Y.; Zhang, X.P.; Ding, X. A weighted variational model for simultaneous reflectance and illumination estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2782–2790. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, G.; Xiao, C.; Zhu, L.; Zheng, W.S. High-quality exposure correction of underexposed photos. In Proceedings of the ACM International Conference on Multimedia, Yokohama, Japan, 11–14 June 2018; pp. 582–590. [Google Scholar]
- Zhang, Q.; Nie, Y.; Zheng, W.S. Dual illumination estimation for robust exposure correction. Comput. Graph. Forum 2019, 38, 243–252. [Google Scholar] [CrossRef]
- Guo, X.; Li, Y.; Ling, H. LIME: Low-light image enhancement via illumination map estimation. IEEE Trans. Image Process. 2017, 26, 982–993. [Google Scholar] [CrossRef]
- Guo, X. LIME: A method for low-light image enhancement. In Proceedings of the ACM International Conference on Multimedia, New York, NY, USA, 6–9 June 2016; pp. 87–91. [Google Scholar]
- Li, M.; Liu, J.; Yang, W.; Sun, X.; Guo, Z. Structure-revealing low-light image enhancement via robust Retinex model. IEEE Trans. Image Process. 2018, 27, 2828–2841. [Google Scholar] [CrossRef]
- Qu, Z.; Xing, Y.; Song, Y. An image enhancement method based on non-subsampled shearlet transform and directional information measurement. Information 2018, 9, 308. [Google Scholar] [CrossRef]
- Yang, X.; Nie, L.; Zhang, Y.; Zhang, L. Image Generation and Super-Resolution Reconstruction of Synthetic Aperture Radar Images Based on an Improved Single-Image Generative Adversarial Network. Information 2025, 16, 370. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, F.; Li, J. Efcanet: Exposure fusion cross-attention network for low-light image enhancement. Appl. Sci. 2022, 13, 380. [Google Scholar] [CrossRef]
- Li, G.; Li, G.; Han, G. Enhancement of low contrast images based on effective space combined with pixel learning. Information 2017, 8, 135. [Google Scholar] [CrossRef]
- Li, Y.; Yang, M.; Bian, T.; Wu, H. MRI Super-Resolution Analysis via MRISR: Deep Learning for Low-Field Imaging. Information 2024, 15, 655. [Google Scholar] [CrossRef]
- Liu, X.; Tong, Z.; Wang, H.; Li, P. ZRRD-MBNet: Zero-Reference Retinex Decomposition-Based Multi-Branch Network for Low-Light Image Enhancement. Res. Sq. 2024. [Google Scholar] [CrossRef]
- Wang, C.; Gao, G.; Wang, J.; Lv, Y.; Li, Q.; Li, Z.; Wu, H. GCT-VAE-GAN: An Image Enhancement Network for Low-Light Cattle Farm Scenes by Integrating Fusion Gate Transformation Mechanism and Variational Autoencoder GAN. IEEE Access 2023, 11, 126650–126660. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, Y.; Zhang, R.; Lu, H.; Wang, W.; Zhang, Z. Low-Light Image Enhancement via Multistage Laplacian Feature Fusion. J. Electron. Imaging 2024, 33, 023020. [Google Scholar] [CrossRef]
- Xue, W.; Wang, Y.; Qin, Z. Multiscale Feature Attention Module Based Pyramid Network for Medical Digital Radiography Image Enhancement. IEEE Access 2024, 12, 53686–53697. [Google Scholar] [CrossRef]
- Lai, W.; Huang, J.; Ahuja, N.; Yang, M. Fast and Accurate Image Super-Resolution with Deep Laplacian Pyramid Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 2599–2613. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, D.; Zou, P.; Zhang, W.; Zhang, W. Retinex-Based Laplacian Pyramid Method for Image Defogging. IEEE Access 2019, 7, 122459–122472. [Google Scholar] [CrossRef]
- Mok, T.C.W.; Chung, A.C.S. Large Deformation Diffeomorphic Image Registration with Laplacian Pyramid Networks. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2020, Lima, Peru, 4–8 October 2020; pp. 211–221. [Google Scholar] [CrossRef]
- Hu, L.; Chen, H.; Allebach, J. Joint Multi-Scale Tone Mapping and Denoising for HDR Image Enhancement. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 729–738. [Google Scholar] [CrossRef]
- Guo, C.; Li, C.; Guo, J.; Loy, C.C.; Hou, J.; Kwong, S.; Cong, R. Zero-reference deep curve estimation for low-light image enhancement. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1777–1786. [Google Scholar] [CrossRef]
- Li, C.; Guo, C.; Loy, C.C. Learning to enhance low-light image via zero-reference deep curve estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 4225–4238. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Gong, X.; Liu, D.; Cheng, Y.; Fang, C.; Shen, X.; Yang, J.; Zhou, P.; Wang, Z. EnlightenGAN: Deep light enhancement without paired supervision. IEEE Trans. Image Process. 2021, 30, 2340–2349. [Google Scholar] [CrossRef]
- Yang, W.; Wang, S.; Fang, Y.; Wang, Y.; Liu, J. From fidelity to perceptual quality: A semi-supervised approach for low-light image enhancement. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 3060–3069. [Google Scholar] [CrossRef]
- Yang, W.; Wang, S.; Fang, Y.; Wang, Y.; Liu, J. Band representation-based semi-supervised low-light image enhancement: Bridging the gap between signal fidelity and perceptual quality. IEEE Trans. Image Process. 2021, 30, 3461–3473. [Google Scholar] [CrossRef] [PubMed]
- Liang, Z.; Li, C.; Zhou, S.; Feng, R.; Loy, C.C. Iterative prompt learning for unsupervised backlit image enhancement. In Proceedings of the IEEE International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 8094–8103. [Google Scholar]
- Li, Z.; Zhang, F.; Cao, M.; Zhang, J.; Shao, Y.; Wang, Y.; Sang, N. Real-time exposure correction via collaborative transformations and adaptive sampling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 2984–2994. [Google Scholar]
- Baek, J.H.; Kim, D.; Choi, S.M.; Lee, H.J.; Kim, H.; Koh, Y.J. Luminance-aware Color Transform for Multiple Exposure Correction. In Proceedings of the IEEE International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 6133–6142. [Google Scholar]
- Wang, Y.; Peng, L.; Li, L.; Cao, Y.; Zha, Z.J. Decoupling-and-aggregating for image exposure correction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 18115–18124. [Google Scholar]
- Li, Y.; Xu, K.; Hancke, G.P.; Lau, R.W. Color shift estimation-and-correction for image enhancement. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 25389–25398. [Google Scholar]
- Afifi, M.; Derpanis, K.G.; Ommer, B.; Brown, M.S. Learning multi-scale photo exposure correction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 9157–9167. [Google Scholar]
- Wang, H.; Xu, K.; Lau, R.W. Local color distributions prior for image enhancement. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 343–359. [Google Scholar]
- Ignatov, A.; Kobyshev, N.; Timofte, R.; Vanhoey, K.; Van Gool, L. Dslr-quality photos on mobile devices with deep convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3277–3285. [Google Scholar]
- Chen, C.; Chen, Q.; Xu, J.; Koltun, V. Learning to see in the dark. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3291–3300. [Google Scholar] [CrossRef]
- Ma, L.; Ma, T.; Liu, R.; Fan, X.; Luo, Z. Toward fast, flexible, and robust low-light image enhancement. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5637–5646. [Google Scholar]
- Fu, Z.; Yang, Y.; Tu, X.; Huang, Y.; Ding, X.; Ma, K.K. Learning a simple low-light image enhancer from paired low-light instances. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 22252–22261. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).