Crystallographic Effect of TiAl Alloy Under High-Speed Shock Deformation
Abstract
1. Introduction
2. Methodology
2.1. Simulation Details
2.2. Visualization and Parameter Calculation
3. Result and Discussion
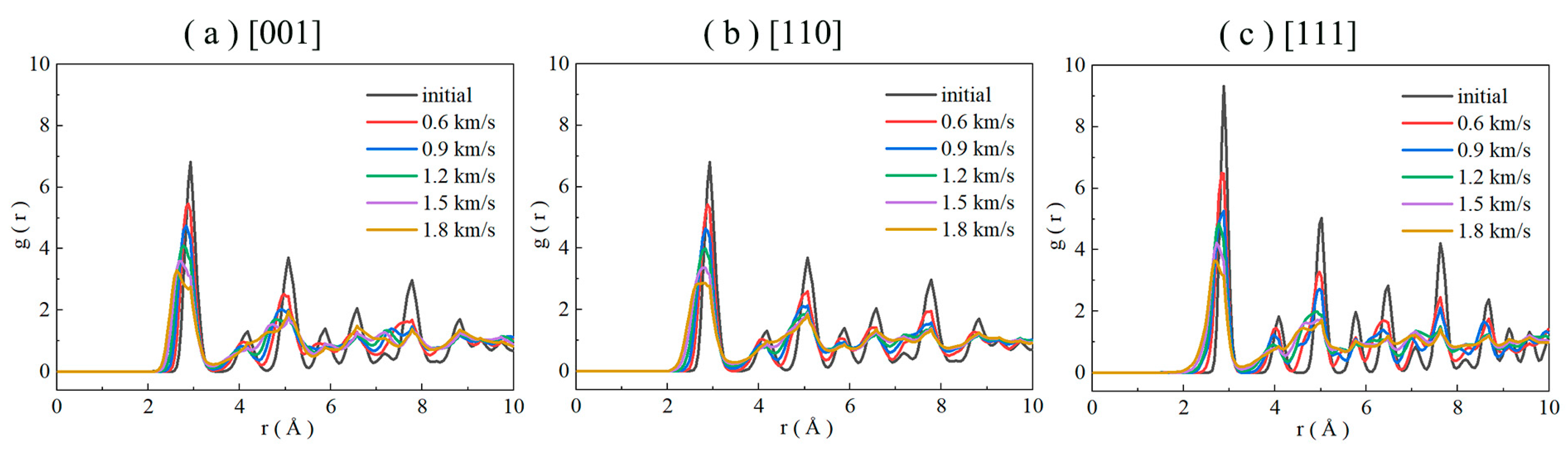
3.1. The Impact Response Characteristics of Different Downward Grain Velocities, Pressures, and Shear Stresses
3.2. Analysis of Shock Wave Structure and Plastic Behavior
3.3. Shock-Induced Phase Transition and Dislocation Evolution Mechanism
3.4. Distribution and Evolution of Defect Types Under Impact
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, S.; Yin, S.; Liang, X.; Cao, F.; Yu, Q.; Zhang, R.; Dai, L.; Ruestes, C.J.; Ritchie, R.O.; Minor, A.M. Deformation and failure of the CrCoNi medium-entropy alloy subjected to extreme shock loading. Sci. Adv. 2023, 9, eadf8602. [Google Scholar] [CrossRef]
- Mantha, L.S.; MacDonald, B.E.; Mu, X.; Mazilkin, A.; Ivanisenko, J.; Hahn, H.; Lavernia, E.J.; Katnagallu, S.; Kübel, C. Grain boundary segregation induced precipitation in a non equiatomic nanocrystalline CoCuFeMnNi compositionally complex alloy. Acta Mater. 2021, 220, 117281. [Google Scholar] [CrossRef]
- Yang, D.; Deng, Q.; Yuan, M.; Cui, G.; Fan, D.; Jia, B. Safety Evaluation of Perforated String by Simulation Modeling and Mechanics Analysis Under Shock Loading. Appl. Sci. 2025, 15, 7249. [Google Scholar] [CrossRef]
- Liu, J. Molecular dynamic study of temperature dependence of mechanical properties and plastic inception of CoCrCuFeNi high-entropy alloy. Phys. Lett. A 2020, 384, 126516. [Google Scholar] [CrossRef]
- Dragoni, M.; Santoro, D. A model for the atmospheric shock wave produced by a strong volcanic explosion. Geophys. J. Int. 2020, 222, 735–742. [Google Scholar] [CrossRef]
- Cummins, P.R.; Pranantyo, I.R.; Pownall, J.M.; Griffin, J.D.; Meilano, I.; Zhao, S. Earthquakes and tsunamis caused by low-angle normal faulting in the Banda Sea, Indonesia. Nat. Geosci. 2020, 13, 312–318. [Google Scholar] [CrossRef]
- Zhu, M.-H.; Morbidelli, A.; Neumann, W.; Yin, Q.-Z.; Day, J.M.D.; Rubie, D.C.; Archer, G.J.; Artemieva, N.; Becker, H.; Wünnemann, K. Common feedstocks of late accretion for the terrestrial planets. Nat. Astron. 2021, 5, 1286–1296. [Google Scholar] [CrossRef]
- Sims, M.; Briggs, R.; Volz, T.J.; Singh, S.; Hamel, S.; Coleman, A.L.; Coppari, F.; Erskine, D.J.; Gorman, M.G.; Sadigh, B.; et al. Experimental and theoretical examination of shock-compressed copper through the fcc to bcc to melt phase transitions. J. Appl. Phys. 2022, 132, 075902. [Google Scholar] [CrossRef]
- Basavaraj, K.; Ray, A. Phase transition lowering in shock compressed single-crystal aluminum: Atomistic insights. Phys. Rev. B 2024, 109, 104101. [Google Scholar] [CrossRef]
- Liu, T.; Chen, L.; Li, W.; Liu, Z.; Zhang, J.; Zhang, X.; Zhang, X.; Zhu, S.; Hou, X. Orientation-dependent phase transition pathways of single-crystal nickel over large shock range. Int. J. Mech. Sci. 2024, 261, 108689. [Google Scholar] [CrossRef]
- Liu, B.; Guo, L.; Chen, Y.; Li, X.; Wang, K.; Deng, H.; Hu, W.; Xiao, S.; Yuan, D. Role of micro-alloying element in dynamic deformation of Mg-Y alloys. Int. J. Mech. Sci. 2024, 269, 109057. [Google Scholar] [CrossRef]
- Sinha, S.; Nene, S.; Frank, M.; Liu, K.; Lebensohn, R.; Mishra, R. Deformation mechanisms and ductile fracture characteristics of a friction stir processed transformative high entropy alloy. Acta Mater. 2020, 184, 164–178. [Google Scholar] [CrossRef]
- Hua, D.; Zhou, Q.; Shi, Y.; Li, S.; Hua, K.; Wang, H.; Li, S.; Liu, W. Revealing the deformation mechanisms of <110> symmetric tilt grain boundaries in CoCrNi medium-entropy alloy. Int. J. Plast. 2023, 171, 103832. [Google Scholar]
- Chen, G.; Peng, Y.; Zheng, G.; Qi, Z.; Wang, M.; Yu, H.; Dong, C.; Liu, C.T. Polysynthetic twinned TiAl single crystals for high-temperature applications. Nat. Mater. 2016, 15, 876–881. [Google Scholar] [CrossRef]
- Schütze, M. Single-crystal performance boost. Nat. Mater. 2016, 15, 823–824. [Google Scholar] [CrossRef] [PubMed]
- Perepezko, J.H. The hotter the engine, the better. Science 2009, 326, 1068–1069. [Google Scholar] [CrossRef] [PubMed]
- Zheng, D.; Chen, R.; Wang, J.; Ma, T.; Ding, H.; Su, Y.; Guo, J.; Fu, H. Novel casting TiAl alloy with fine microstructure and excellent performance assisted by ultrasonic melt treatment. Mater. Lett. 2017, 200, 67–70. [Google Scholar] [CrossRef]
- Feng, R.; Song, W.; Li, H.; Qi, Y.; Qiao, H.; Li, L. Effects of annealing on the residual stress in γ-TiAl alloy by molecular dynamics simulation. Materials 2018, 11, 1025. [Google Scholar] [CrossRef]
- Li, L.; Zhang, W.; Li, G.; Wang, J.; Li, L.; Xie, M. Simulation Study of Thermal–Mechanical Coupling Fretting Wear of Ti-6Al-4V Alloy. Appl. Sci. 2022, 12, 7400. [Google Scholar] [CrossRef]
- Radu, P.; Schnakovszky, C.; Herghelegiu, E.; García-Martínez, E.; Miguel, V. Study on the current state of research in the field of titanium aluminides milling processes. Key Eng. Mater. 2023, 955, 3–13. [Google Scholar] [CrossRef]
- Jiang, B.; Wang, D.; Zhao, P.; Sang, H. Identification of Torsional Fatigue Properties of Titanium Alloy Turned Surfaces and Their Distribution Characteristics. Appl. Sci. 2025, 15, 6767. [Google Scholar] [CrossRef]
- Zhang, C.; Godbole, A.; Michal, G.; Lu, C. High shock resistance and self-healing ability of graphene/nanotwinned Cu nanolayered composites. J. Alloys Compd. 2021, 860, 158435. [Google Scholar] [CrossRef]
- Song, S.; Li, H.; Peng, X. Role of Fe/Mn elements tuning in the shock dynamics of CoCrNi-based alloy. Int. J. Mech. Sci. 2024, 281, 109585. [Google Scholar] [CrossRef]
- Xiong, Y.; Li, X.; Xiao, S.; Deng, H.; Huang, B.; Zhu, W.; Hu, W. Effect of particle packing and density on shock response in ordered arrays of Ni + Al nanoparticles. Phys. Chem. Chem. Phys. 2019, 21, 7272–7280. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, S.; Lu, J.; Ravichandran, G. Shock wave response of a zirconium-based bulk metallic glass and its composite. Appl. Phys. Lett. 2002, 80, 4522–4524. [Google Scholar] [CrossRef]
- Wang, X.X.; Zhou, T.T.; Sun, Z.Y.; Shi, X.F.; Sun, H.Q.; Zhang, F.G.; Yin, J.W.; He, A.M.; Wang, P. Micro-spall damage and subsequent re-compaction of release melted lead under shock loading. Comput. Mater. Sci. 2022, 203, 111178. [Google Scholar] [CrossRef]
- Song, W.; Yu, Y.; Guan, Y. Role of void shape on shock responses of nanoporous metallic glasses via molecular dynamics simulation. Int. J. Mech. Sci. 2022, 218, 107076. [Google Scholar] [CrossRef]
- Wu, C.; Zhigilei, L.V. Microscopic mechanisms of laser spallation and ablation of metal targets from large-scale molecular dynamics simulations. Appl. Phys. A 2014, 114, 11–32. [Google Scholar] [CrossRef]
- Galitskiy, S.; Ivanov, D.S.; Dongare, A.M. Dynamic evolution of microstructure during laser shock loading and spall failure of single crystal Al at the atomic scales. J. Appl. Phys. 2018, 124, 205901. [Google Scholar] [CrossRef]
- Galitskiy, S.; Dongare, A.M. Modeling the damage evolution and recompression behavior during laser shock loading of aluminum microstructures at the mesoscales. J. Mater. Sci. 2021, 56, 4446–4469. [Google Scholar] [CrossRef]
- Chen, P.; Wang, X.; Wang, P.; He, A.M. Shock response of pre-existing spall damage in copper. J. Appl. Phys. 2022, 131, 015903. [Google Scholar] [CrossRef]
- Wang, J.; Wu, F.; Wang, P.; He, A.; Wu, H. Double-shock-induced spall and recompression processes in copper. J. Appl. Phys. 2020, 127, 135903. [Google Scholar] [CrossRef]
- Rong, J.C.; Zhu, P.Z.; Xu, Y.M. Molecular dynamics simulation of mechanical response of Cu50Zr50 metallic glass under double shock loading. J. Appl. Phys. 2023, 133, 175104. [Google Scholar] [CrossRef]
- Tian, X.; Cui, J.; Yang, M.; Ma, K.; Xiang, M. Molecular dynamics simulations on shock response and spalling behaviors of semi-coherent {111} Cu-Al multilayers. Int. J. Mech. Sci. 2020, 172, 105414. [Google Scholar] [CrossRef]
- Zhu, Y.; Hu, J.; Huang, S.; Wang, J.; Luo, G.; Shen, Q. Molecular dynamics simulation on spallation of [111] Cu/Ni nano-multilayers: Voids evolution under different shock pulse duration. Comput. Mater. Sci. 2022, 202, 110923. [Google Scholar] [CrossRef]
- Liao, Y.; Hong, S.; Ge, L.; Chen, J.; Xiang, M. Shock wave characteristics and spalling behavior of non-coherent Cu/Nb multilayers. Mech. Mater. 2022, 173, 104439. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Zope, R.R.; Mishin, Y. Interatomic potentials for atomistic simulations of the Ti-Al system. Phys. Rev. B 2003, 68, 024102. [Google Scholar] [CrossRef]
- Xiang, H.; Guo, W. Synergistic effects of twin boundary and phase boundary for enhancing ultimate strength and ductility of lamellar TiAl single crystals. Int. J. Plast. 2022, 150, 103197. [Google Scholar] [CrossRef]
- Xiang, H.; Guo, W. Post-yielding dislocation retraction of nano-lamellar TiAl single crystals. Sci. China Phys. Mech. Astron. 2021, 64, 264611. [Google Scholar] [CrossRef]
- Neogi, A.; Janisch, R. Twin-boundary assisted crack tip plasticity and toughening in lamellar γ-TiAl. Acta Mater. 2021, 213, 116924. [Google Scholar] [CrossRef]
- Wang, J.; Wang, F.; Wu, X.; Xu, Z.; Yang, X. Orientation-induced anisotropy of plasticity and damage behavior in monocrystalline tantalum under shock compression. Vacuum 2023, 207, 111679. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Amadou, N.; De Resseguier, T.; Dragon, A.; Brambrink, E. Coupling between plasticity and phase transition in shock-and ramp-compressed single-crystal iron. Phys. Rev. B 2018, 98, 024104. [Google Scholar] [CrossRef]
- Xie, H.; Ma, Z.; Zhang, W.; Zhao, H.; Ren, L. Graphene enables equiatomic FeNiCrCoCu high-entropy alloy with improved TWIP and TRIP effects under shock compression. J. Mater. Sci. Technol. 2024, 170, 186–199. [Google Scholar] [CrossRef]
- Li, C.H.; Dedoncker, R.; Li, L.W.; Sedghgooya, F.; Zighem, F.; Ji, V.; Depla, D.; Djemia, P.; Faurie, D. Mechanical properties of CoCrCuFeNi multi-principal element alloy thin films on Kapton substrates. Surf. Coat. Technol. 2020, 402, 126474. [Google Scholar] [CrossRef]
- Li, J.; Dong, L.; Zang, X.; Zhang, X.; Zhao, W.; Wang, F. Study on micro-crack propagation behavior of single-crystal α-Ti under shear stress based on molecular dynamics. Mater. Today Commun. 2020, 25, 101622. [Google Scholar] [CrossRef]
- Tan, J.; Jian, Z.; Xiao, S.; Li, X.; Wang, K.; Wang, L.; Huang, B.; Deng, H.; Zhu, W.; Hu, W. The mechanism of plasticity and phase transition in iron single crystals under cylindrically divergent shock loading. Int. J. Mech. Sci. 2022, 217, 107032. [Google Scholar] [CrossRef]
- Huang, Y.; Xiong, Y.; Li, P.; Li, X.; Xiao, S.; Deng, H.; Zhu, W.; Hu, W. Atomistic studies of shock-induced plasticity and phase transition in iron-based single crystal with edge dislocation. Int. J. Plast. 2019, 114, 215–226. [Google Scholar] [CrossRef]
- Liu, B.; Jian, Z.; Guo, L.; Li, X.; Wang, K.; Deng, H.; Hu, W.; Xiao, S.; Yuan, D. Effect of crystallographic orientations on shock-induced plasticity for CoCrFeMnNi high-entropy alloy. Int. J. Mech. Sci. 2022, 226, 107373. [Google Scholar] [CrossRef]
- Li, L.; Li, H.; Li, S.; Xu, L.; Fan, X.; Shi, J. Plastic evolution and phase transition mechanisms in γ-TiAl nano polycrystal by a molecular dynamics simulation. J. Mater. Res. Technol. 2024, 33, 1504–1511. [Google Scholar] [CrossRef]






| Z-Axis Orientation | Lx (Å) | Ly (Å) | Lz (Å) | Number of Atoms |
|---|---|---|---|---|
| [001] | 141.75 | 141.75 | 1011.50 | 1,225,000 |
| [110] | 143.85 | 140.30 | 1010.92 | 1,228,440 |
| [111] | 143.85 | 140.33 | 1010.13 | 1,227,744 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Liu, H.; Zhang, Z. Crystallographic Effect of TiAl Alloy Under High-Speed Shock Deformation. Appl. Sci. 2025, 15, 8837. https://doi.org/10.3390/app15168837
Liu J, Liu H, Zhang Z. Crystallographic Effect of TiAl Alloy Under High-Speed Shock Deformation. Applied Sciences. 2025; 15(16):8837. https://doi.org/10.3390/app15168837
Chicago/Turabian StyleLiu, Jiayu, Huailin Liu, and Zhengping Zhang. 2025. "Crystallographic Effect of TiAl Alloy Under High-Speed Shock Deformation" Applied Sciences 15, no. 16: 8837. https://doi.org/10.3390/app15168837
APA StyleLiu, J., Liu, H., & Zhang, Z. (2025). Crystallographic Effect of TiAl Alloy Under High-Speed Shock Deformation. Applied Sciences, 15(16), 8837. https://doi.org/10.3390/app15168837




