Advances in Computational Fluid Dynamics of Mechanical Processes in Food Engineering: Mixing, Extrusion, Drying, and Process Optimization
Abstract
1. Introduction
1.1. Background and Motivation
- “CFD food engineering”
- “food processing simulation”
- “mixing modeling food”
- “extrusion simulation food”
- “drying CFD food”
- “food process optimization”
- “rheology food modeling”
- “multiphase food flow”
1.2. Importance of Mechanical Processes in Food Engineering
- Mixing and Homogenization: Ensuring uniform ingredient distribution, texture control, and product stability (e.g., emulsions, doughs) [6].
- Extrusion: Combining thermal and mechanical energy to create texturized products like cereals, snacks, pasta, and meat analogues through continuous processing, shaping, and even encapsulation [7].
- Size Reduction and Shaping: Operations like cutting, grinding, and forming that impact product uniformity and subsequent processing [8].
- Mechanical Drying Assistance: Systems (e.g., fluid-bed, vibratory) that use airflow and mechanical agitation to enhance mass and heat transfer, reduce drying times, and prevent agglomeration [9].
2. Overview of Mechanical Processes in the Food Industry
2.1. Classification of Mechanical Unit Operations
- (a)
- Size Reduction and Comminution
- (b)
- Mixing and Homogenization
- (c)
- Shaping and Forming
- (d)
- Mechanical Drying Assistance
- (e)
- Mechanical Separation
- (f)
- Transport and Conveyance
2.2. Relevance to Product Quality, Safety, and Process Efficiency
- (a)
- Product Quality and Functional Attributes
- Texture and mouthfeel—determined by the degree of mixing, shear history, or expansion during extrusion.
- Homogeneity and stability—influenced by mixing intensity and residence time; insufficient mixing can lead to ingredient separation, while overmixing may cause structural breakdown.
- Microstructure formation—such as air incorporation in whipped products or matrix development in extruded snacks and plant-based meat analogues.
- (b)
- Food Safety and Process Hygiene
- Reduction of microbial load—in some cases, such as extrusion, the combination of mechanical and thermal energy may reduce microbial populations.
- Prevention of contamination—through proper equipment design that avoids dead zones and facilitates cleaning.
- Uniform distribution of preservatives or critical ingredients, which supports consistent antimicrobial efficacy.
- (c)
- Process Efficiency and Resource Optimization
- Reduce energy and water usage by improving mixing or drying uniformity,
- Minimize material losses by preventing product buildup or segregation,
- Enhance throughput and equipment utilization through better flow dynamics and reduced downtime.
- (d)
- Process Scalability and Reproducibility
3. Fundamentals of CFD in the Context of Mechanical Processes
3.1. Governing Equations
3.2. Boundary Conditions, Mesh Generation, Solver Types
3.3. CFD Models for Non-Newtonian and Viscoelastic Food Materials
3.4. Coupling with Other Simulation Tools (DEM, FEM, etc.)
4. CFD Simulation of Mixing Processes
4.1. Types of Mixers and Their Working Principles
4.2. CFD Modeling of Laminar and Turbulent Mixing
| Mixer Type | Mixing Mechanism | Typical Food Systems | CFD Modeling Approach | References |
|---|---|---|---|---|
| Ribbon blender | Convective | Powders, spices | RANS, steady-state, single-phase | [60] |
| Paddle mixer | Convective + shear | Granules, fragile solids | RANS, Eulerian, DEM coupling (optional) | [61] |
| Spiral/planetary mixer | Shear-induced, viscoelastic deformation | Doughs, batters | Laminar CFD, non-Newtonian, viscoelastic | [62] |
| Rotor–stator mixer | High shear, turbulence | Emulsions, sauces | Transient RANS or LES, VOF (for multiphase) | [63] |
| Static mixer | Flow redirection, laminar or turbulent | Liquids, miscible additives | Laminar or turbulent CFD, passive scalar | [64] |
| V-blender/double-cone | Gravitational, diffusive | Nutraceutical powders | Not typically modeled (quasi-static) | [65] |
| Twin-screw extruder mixer | Shear, distributive and dispersive mixing | Meat analogues, cereal doughs | Transient, moving mesh, non-Newtonian CFD | [66] |
| Fluidized bed mixer | Pneumatic agitation, collisions | Powders, granules (during drying) | Euler–Euler or CFD–DEM | [67] |
4.3. RTD and Mixing Indices
5. CFD in Extrusion Processes
5.1. Extrusion Mechanisms in Food Processing
5.2. Multiphase and Thermal Aspects in CFD Models
5.3. Prediction of Pressure, Temperature, and Shear Profiles
5.4. Coupling CFD with Reaction Kinetics and Product Texture Modelling
6. CFD Analysis of Drying as a Mechanically Aided Process
6.1. Fluid-Bed Drying and Spray Drying as Coupled Heat-Mass Transfer and Mechanical Systems
6.2. CFD Modeling of Particle-Fluid Interactions
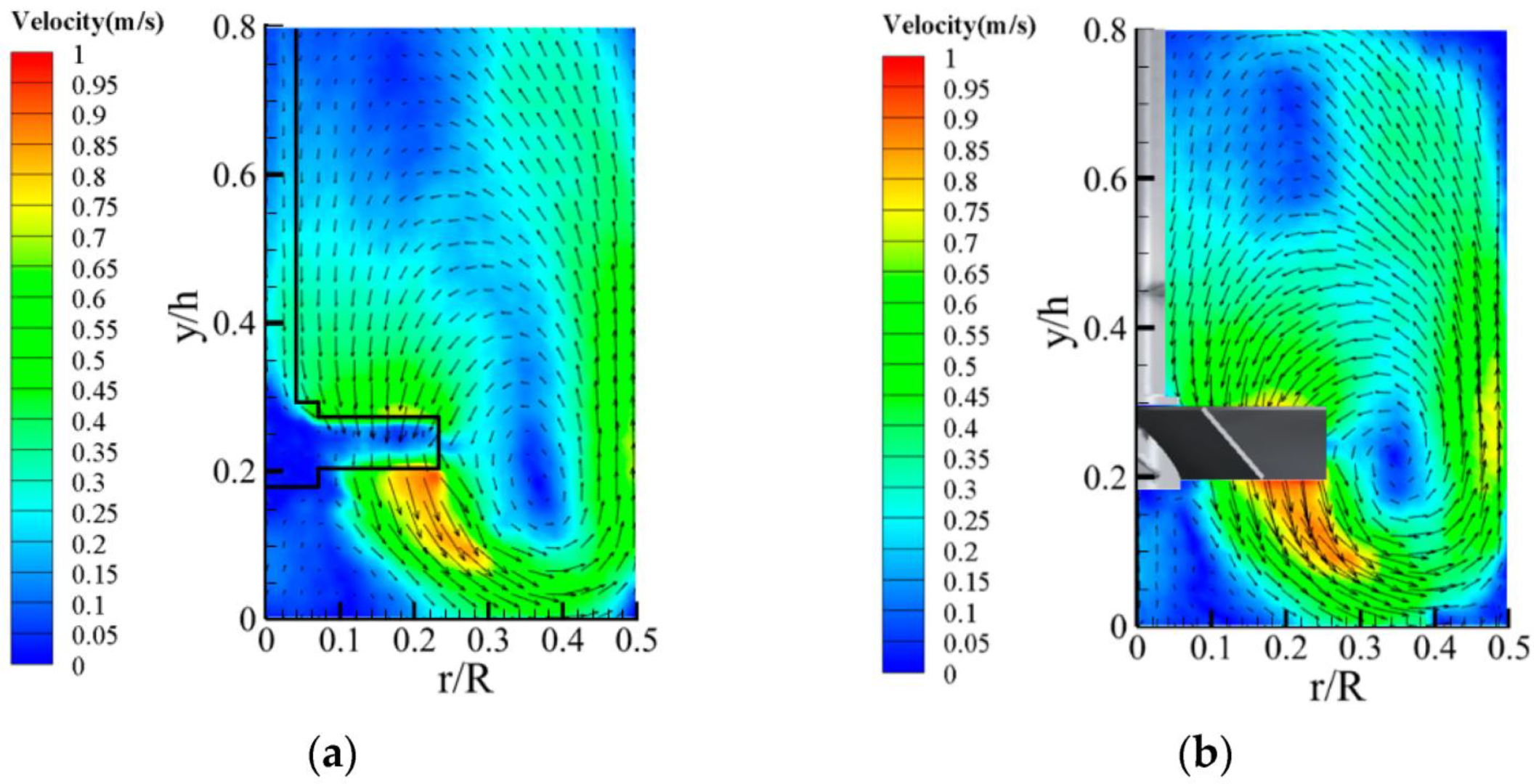
6.3. Optimization of Drying Chamber Geometry and Air Flow
- Role of Geometry in Drying Performance
- CFD-Based Analysis of Airflow Dynamics
- Optimization Strategies Using CFD
- Reducing recirculation and energy losses through smoother transitions and optimized chamber tapers,
- Improving dispersion by selecting appropriate inlet angles and nozzle sizes,
- Enhancing drying uniformity with balanced airflow from distributor plates,
- Minimizing powder loss or fouling through optimized exhaust duct design.
7. Process Optimization Through CFD Simulations
7.1. DoE and CFD
7.2. Sensitivity Analysis and Parameter Estimation
- SA: Scope and Methods
- Local SA, which evaluates small perturbations of individual parameters using partial derivatives or finite difference methods. It is best suited for smooth, deterministic models but is limited in nonlinear or interactive systems.
- Global SA, which assesses variability across the entire parameter space using statistical techniques such as:
- ○
- Morris screening (qualitative ranking),
- ○
- Sobol’ indices (variance-based decomposition),
- ○
- Fourier amplitude sensitivity testing (FAST),
- ○
- LHS with regression or surrogate modeling.
- Global SA is particularly useful in complex CFD scenarios such as extrusion, spray drying, or fluidized bed systems, where nonlinear interactions between inputs are common [136].
- PE in CFD Models
- Rheological laws (e.g., power-law, Herschel–Bulkley),
- Kinetic expressions (e.g., reaction rate constants, activation energy),
- Transport coefficients (e.g., diffusivity, evaporation rates),
- Boundary conditions (e.g., convective heat transfer coefficients).
- Integrated SA–PE Workflows
- Challenges and Best Practices
- High computational cost: Repeated simulations across parameter sets are resource-intensive; surrogate models (e.g., Kriging, neural networks) can help alleviate this burden.
- Identifiability issues: Multiple parameter combinations may yield similar outputs, requiring regularization and sensitivity-based filtering.
- Uncertain or noisy experimental data: In-process measurements (e.g., local temperature, velocity) are often difficult to obtain with sufficient accuracy.
- Future Directions
- Real-time PE using sensor data within digital twin environments,
- Integrated uncertainty quantification and risk-informed design,
- ML-assisted surrogate modeling for rapid SA/PE in large-scale CFD problems,
- Open-source workflows combining solvers (e.g., OpenFOAM) with libraries such as SALib or UQLab.
7.3. Limitations and Challenges in CFD of Food Processes
7.4. Coupling CFD with AI/ML for Optimization
7.5. Reduction of Energy Consumption and Improvement of Product Quality
8. Current Challenges and Future Perspectives
8.1. Model Validation and Scalability
8.2. Integration with Real-Time Process Control
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Full name |
| ANN | Artificial Neural Networks |
| CFD | Computational Fluid Dynamics |
| CIP | Clean-in-Place |
| CoV | Coefficient of Variation |
| DEM | Discrete Element Method |
| DES | Detached Eddy Simulation |
| DNS | Direct Numerical Simulation |
| DoE | Design of Experiments |
| EE | Euler–Euler (multiphase model) |
| EL | Euler–Lagrange (multiphase model) |
| FAST | Fourier amplitude sensitivity testing |
| FEM | Finite Element Method |
| FSI | Fluid–Structure Interactions |
| GPR | Gaussian Process Regression |
| HME | High-Moisture Extrusion |
| LES | Large Eddy Simulation |
| LHS | Latin Hypercube Sampling |
| MCMC | Markov Chain Monte Carlo |
| ML | Machine Learning |
| MRI | Magnetic Resonance Imaging |
| NIR | Near-Infrared Spectroscopy |
| PBM | Population Balance Model |
| PE | Parameter Estimation |
| PET | Positron Emission Tomography |
| PINN | Physics-Informed Neural Networks |
| PIV | Particle Image Velocimetry |
| PTV | Particle Tracking Velocimetry |
| RANS | Reynolds-Averaged Navier–Stokes |
| RSM | Reynolds Stress Model |
| RTD | Residence Time Distribution |
| SA | Sensitivity Analysis |
| SVM | Support Vector Machines |
| TKE | Turbulent Kinetic Energy |
| UDF | User Defined Function |
| VOF | Volume of Fluid |
References
- Arora, B.; Yoon, A.; Sriram, M.; Singha, P.; Rizvi, S.S.H. Reactive Extrusion: A Review of the Physicochemical Changes in Food Systems. Innov. Food Sci. Emerg. Technol. 2020, 64, 102429. [Google Scholar] [CrossRef]
- Mahfoud, F.; Frem, J.; Assaf, J.C.; Maache-Rezzoug, Z.; Rezzoug, S.A.; Elias, R.; Debs, E.; Louka, N. Evolution of Dried Food Texturization: A Critical Review of Technologies and Their Impact on Organoleptic and Nutritional Properties. Processes 2025, 13, 799. [Google Scholar] [CrossRef]
- Hassoun, A.; Jagtap, S.; Trollman, H.; Garcia-Garcia, G.; Abdullah, N.A.; Goksen, G.; Bader, F.; Ozogul, F.; Barba, F.J.; Cropotova, J.; et al. Food Processing 4.0: Current and Future Developments Spurred by the Fourth Industrial Revolution. Food Control 2023, 145, 109507. [Google Scholar] [CrossRef]
- Knoerzer, K.; Buckow, R.; Chapman, B.; Juliano, P.; Versteeg, C. Carrier Optimisation in a Pilot-Scale High Pressure Sterilisation Plant—An Iterative CFD Approach Employing an Integrated Temperature Distributor (ITD). J. Food Eng. 2010, 97, 199–207. [Google Scholar] [CrossRef]
- Cui, X.; Adebayo, D.; Zhang, H.; Howarth, M.; Anderson, A.; Olopade, T.; Salami, K.; Farooq, S. Simulation of Granular Flows and Machine Learning in Food Processing. Front. Food Sci. Technol. 2024, 4, 1491396. [Google Scholar] [CrossRef]
- Guo, C.; Zhang, M.; Devahastin, S. 3D Extrusion-Based Printability Evaluation of Selected Cereal Grains by Computational Fluid Dynamic Simulation. J. Food Eng. 2020, 286, 110113. [Google Scholar] [CrossRef]
- Ramachandran, R.P.; Akbarzadeh, M.; Paliwal, J.; Cenkowski, S. Computational Fluid Dynamics in Drying Process Modelling—A Technical Review. Food Bioprocess Technol. 2018, 11, 271–292. [Google Scholar] [CrossRef]
- Seok, W.; Kim, G.H.; Seo, J.; Rhee, S.H. Application of the Design of Experiments and Computational Fluid Dynamics to Bow Design Improvement. J. Mar. Sci. Eng. 2019, 7, 226. [Google Scholar] [CrossRef]
- Azmir, J.; Hou, Q.; Yu, A. CFD-DEM Simulation of Drying of Food Grains with Particle Shrinkage. Powder Technol. 2019, 343, 792–802. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Nithiarasu, P. The Finite Element Method for Fluid Dynamics; Elsevier Ltd.: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Shang, X.; Wan, M.P.; Ng, B.F.; Ding, S. A CFD-Sectional Algorithm for Population Balance Equation Coupled with Multi-Dimensional Flow Dynamics. Powder Technol. 2020, 362, 111–125. [Google Scholar] [CrossRef]
- Brosh, T.; Kalman, H.; Levy, A.; Peyron, I.; Ricard, F. DEM-CFD Simulation of Particle Comminution in Jet-Mill. Powder Technol. 2014, 257, 104–112. [Google Scholar] [CrossRef]
- Havlica, J.; Kozakovic, M.; Kramolis, D.; Travnickova, T.; Kohout, M. The Effect of Primary and Secondary Flows on the Homogenization Process in a Vertical Bladed Mixer. Powder Technol. 2021, 391, 253–266. [Google Scholar] [CrossRef]
- Blauth, S.; Stucke, D.; Ashour, M.A.; Schnebele, J.; Grützner, T.; Leithäuser, C. CFD-Based Shape Optimization of Structured Packings for Enhancing Separation Efficiency in Distillation. Chem. Eng. Sci. 2025, 302, 120803. [Google Scholar] [CrossRef]
- Aziz, H.; Ahsan, S.N.; De Simone, G.; Gao, Y.; Chaudhuri, B. Computational Modeling of Drying of Pharmaceutical Wet Granules in a Fluidized Bed Dryer Using Coupled CFD-DEM Approach. AAPS PharmSciTech 2022, 23, 59. [Google Scholar] [CrossRef]
- Charton, S.; Randriamanantena, T.; Verdin, N.; Nemri, M. Relevance of CFD in the Development of Separation Processes. Procedia Chem. 2016, 21, 441–445. [Google Scholar] [CrossRef]
- Kuang, S.; Zhou, M.; Yu, A. CFD-DEM Modelling and Simulation of Pneumatic Conveying: A Review. Powder Technol. 2020, 365, 186–207. [Google Scholar] [CrossRef]
- Singh, S.; Gamlath, S.; Wakeling, L. Nutritional Aspects of Food Extrusion: A Review. Int. J. Food Sci. Technol. 2007, 42, 916–929. [Google Scholar] [CrossRef]
- Osuna-Gallardo, E.I.; Cuevas-Rodríguez, E.O.; Sepúlveda-García, C.I.; Reyes-Moreno, C.; León-López, L.; Han, R.; Hernández-Álvarez, A.J. Impact of Cooking and Extrusion Processing on Nutritional, Antinutritional, and Techno-Functional Characteristics of Indigenous Bean (Phaseolus coccineus). ACS Food Sci. Technol. 2023, 3, 1835–1853. [Google Scholar] [CrossRef]
- Faliarizao, N.; Berrios, J.D.J.; Dolan, K.D. Value-Added Processing of Food Legumes Using Extrusion Technology: A Review. Legum. Sci. 2024, 6, e231. [Google Scholar] [CrossRef]
- Verma, T.; Wei, X.; Kiatlau, S.; Bianchini, A.; Eskridge, K.M.; Stratton, J.; Anderson, N.M.; Thippareddi, H.; Subbiah, J. Response Surface Methodology for Salmonella Inactivation during Extrusion Processing of Oat Flour. J. Food Prot. 2018, 81, 815–826. [Google Scholar] [CrossRef]
- Yang, X.; Xi, T.; Qin, Y.; Zhang, H.; Wang, Y. Computational Fluid Dynamics–Discrete Phase Method Simulations in Process Engineering: A Review of Recent Progress. Appl. Sci. 2024, 14, 3856. [Google Scholar] [CrossRef]
- Ogunsesan, O.A.; Hossain, M.; Droubi, M.G. Computational Fluid Dynamics Modelling of Multiphase Flows in Double Elbow Geometries. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 235, 1835–1846. [Google Scholar] [CrossRef]
- Roşca, R.; Ţenu, I.; Cârlescu, P. Food Chilling Methods and CFD Analysis of a Refrigeration Cabinet as a Case Study. In Refrigeration; IntechOpen: London, UK, 2017. [Google Scholar] [CrossRef]
- Soleymani Serami, M.; Ramezan, Y.; Khashehchi, M. CFD Simulation and Experimental Validation of In-Container Thermal Processing in Fesenjan Stew. Food Sci. Nutr. 2021, 9, 1079–1087. [Google Scholar] [CrossRef] [PubMed]
- Joshi, A.R.; Datta, A.K. Non-Newtonian Flow Modelling Based Design of Plate Heat Exchangers. Agric. Eng. Int. CIGR J. 2017, 19, 195–204. [Google Scholar]
- Fan, Y.; Zhang, L.; Zheng, C.; Wang, X.; Wang, K.; Zhu, J. Motion Behavior of Non-Newtonian Fluid-Solid Interaction Foods. J. Food Eng. 2023, 347, 111448. [Google Scholar] [CrossRef]
- Katz, A.; Sankaran, V. Mesh Quality Effects on the Accuracy of CFD Solutions on Unstructured Meshes. J. Comput. Phys. 2011, 230, 7670–7686. [Google Scholar] [CrossRef]
- Allahyari, M.; Esfahanian, V.; Yousefi, K. The Effects of Grid Accuracy on Flow Simulations: A Numerical Assessment. Fluids 2020, 5, 110. [Google Scholar] [CrossRef]
- Tucker, P.G. Mesh Generation. In Advanced Computational Fluid and Aerodynamics; Cambridge University Press: Cambridge, UK, 2020; pp. 67–147. ISBN 9781139872010. [Google Scholar]
- Mejia, O.D.L.; Mejia, O.E.; Escorcia, K.M.; Suarez, F.; Laín, S. Comparison of Sliding and Overset Mesh Techniques in the Simulation of a Vertical Axis Turbine for Hydrokinetic Applications. Processes 2021, 9, 1933. [Google Scholar] [CrossRef]
- Hicks, C.I.; See, H.; Fletcher, D.F.; Ekwebelam, C. The Shear Rheology of Bread Dough: Analysis of Local Flow Behaviour Using CFD. Food Bioprod. Process. 2012, 90, 361–369. [Google Scholar] [CrossRef]
- Martínez-Padilla, L.P. Rheology of Liquid Foods under Shear Flow Conditions: Recently Used Models. J. Texture Stud. 2024, 55, e12802. [Google Scholar] [CrossRef]
- Tagliavini, G.; Solari, F.; Montanari, R. CFD Simulation of a Co-Rotating Twin-Screw Extruder: Validation of a Rheological Model for a Starch-Based Dough for Snack Food. Int. J. Food Eng. 2018, 14, 32–38. [Google Scholar] [CrossRef]
- Mondal, A.; Buchanan, R.L.; Lo, Y.M. Computational Fluid Dynamics Approaches in Quality and Hygienic Production of Semisolid Low-Moisture Foods: A Review of Critical Factors. J. Food Sci. 2014, 79, R1861–R1870. [Google Scholar] [CrossRef]
- Turabi, E.; Sumnu, G.; Sahin, S. Rheological Properties and Quality of Rice Cakes Formulated with Different Gums and an Emulsifier Blend. Food Hydrocoll. 2008, 22, 305–312. [Google Scholar] [CrossRef]
- Castillo Sánchez, H.A.; Jovanović, M.R.; Kumar, S.; Morozov, A.; Shankar, V.; Subramanian, G.; Wilson, H.J. Understanding Viscoelastic Flow Instabilities: Oldroyd-B and Beyond. J. Nonnewton. Fluid Mech. 2022, 302, 104742. [Google Scholar] [CrossRef]
- Sahin, S.; Servet, G.Ş. Physical Properties of Foods, 1st ed.; Heldman, D.R., Ed.; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 9783642253874. [Google Scholar]
- Oyinloye, T.M.; Yoon, W.B. Application of Computational Fluid Dynamics (CFD) Simulation for the Effective Ddesign of Food 3D Printing (A Review). Processes 2021, 9, 1867. [Google Scholar] [CrossRef]
- Comminal, R.; Pimenta, F.; Hattel, J.H.; Alves, M.A.; Spangenberg, J. Numerical Simulation of the Planar Extrudate Swell of Pseudoplastic and Viscoelastic Fluids with the Streamfunction and the VOF Methods. J. Nonnewton. Fluid Mech. 2018, 252, 1–18. [Google Scholar] [CrossRef]
- Kieckhefen, P.; Pietsch, S.; Dosta, M.; Heinrich, S. Possibilities and Limits of Computational Fluid Dynamics-Discrete Element Method Simulations in Process Engineering: A Review of Recent Advancements and Future Trends. Annu. Rev. Chem. Biomol. Eng. 2020, 11, 397–422. [Google Scholar] [CrossRef]
- Song, Y.; Zhou, T.; Bai, R.; Zhang, M.; Yang, H. Review of CFD-DEM Modeling of Wet Fluidized Bed Granulation and Coating Processes. Processes 2023, 11, 382. [Google Scholar] [CrossRef]
- Guo, C.F.; Zhang, M.; Bhandari, B. A Comparative Study between Syringe-Based and Screw-Based 3D Food Printers by Computational Simulation. Comput. Electron. Agric. 2019, 162, 397–404. [Google Scholar] [CrossRef]
- Connelly, R.K.; Valenti-Jordan, J. Mixing Analysis of a Newtonian Fluid in a 3D Planetary Pin Mixer. Chem. Eng. Res. Des. 2008, 86, 1434–1440. [Google Scholar] [CrossRef]
- Wang, H.; Cao, Y.; Huang, Z.; Liu, Y.; Hu, P.; Luo, X.; Song, Z.; Zhao, W.; Liu, J.; Sun, J.; et al. Recent Advances on Machine Learning for Computational Fluid Dynamics: A Survey. arXiv 2024, arXiv:2408.12171. [Google Scholar] [CrossRef]
- Håkansson, A.; Fuchs, L.; Innings, F.; Revstedt, J.; Trägårdh, C.; Bergenståhl, B. Experimental Validation of K-ε RANS-CFD on a High-Pressure Homogenizer Valve. Chem. Eng. Sci. 2012, 71, 264–273. [Google Scholar] [CrossRef]
- Raza, W.; Hossain, S.; Kim, K.Y. A Review of Passive Micromixers with a Comparative Analysis. Micromachines 2020, 11, 455. [Google Scholar] [CrossRef] [PubMed]
- Vashisth, V.; Nigam, K.D.P.; Kumar, V. Design and Development of High Shear Mixers: Fundamentals, Applications and Recent Progress. Chem. Eng. Sci. 2021, 232, 116296. [Google Scholar] [CrossRef]
- Viktorov, V.; Mahmud, M.R.; Visconte, C. Comparative Analysis of Passive Micromixers at a Wide Range of Reynolds Numbers. Micromachines 2015, 6, 1166–1179. [Google Scholar] [CrossRef]
- Camarri, S.; Mariotti, A.; Galletti, C.; Brunazzi, E.; Mauri, R.; Salvetti, M.V. An Overview of Flow Features and Mixing in Micro T and Arrow Mixers. Ind. Eng. Chem. Res. 2020, 59, 3669–3686. [Google Scholar] [CrossRef]
- Reviol, T.; Kluck, S.; Böhle, M. A New Design Method for Propeller Mixers Agitating Non-Newtonian Fluid Flow. Chem. Eng. Sci. 2018, 190, 320–332. [Google Scholar] [CrossRef]
- Delvar, E.; Oliveira, I.; Brito, M.S.C.A.; Silva, C.G.; Santamaria-Echart, A.; Barreiro, M.F.; Santos, R.J. Literature Review on Single and Twin-Screw Extruders Design for Polymerization Using CFD Simulation. Fluids 2025, 10, 9. [Google Scholar] [CrossRef]
- Barros, P.L.; Ein-Mozaffari, F.; Lohi, A. Gas Dispersion in Non-Newtonian Fluids with Mechanically Agitated Systems: A Review. Processes 2022, 10, 275. [Google Scholar] [CrossRef]
- Vignali, G.; Vitale, G. Life Cycle Assessment of Food Packaging; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Ferrari, M.; Boccardo, G.; Buffo, A.; Vanni, M.; Marchisio, D.L. CFD Simulation of a High-Shear Mixer for Food Emulsion Production. J. Food Eng. 2023, 358, 111655. [Google Scholar] [CrossRef]
- Joshi, J.B.; Nere, N.K.; Rane, C.V.; Murthy, B.N.; Mathpati, C.S.; Patwardhan, A.W.; Ranade, V.V. CFD Simulation of Stirred Tanks: Comparison of Turbulence Models. Part I: Radial Flow Impellers. Can. J. Chem. Eng. 2011, 89, 23–82. [Google Scholar] [CrossRef]
- Norton, T.; Sun, D.W. Computational Fluid Dynamics (CFD)—An Effective and Efficient Design and Analysis Tool for the Food Industry: A Review. Trends Food Sci. Technol. 2006, 17, 600–620. [Google Scholar] [CrossRef]
- Luchian, M.I.; Stefanov, S.; Litovchenko, I.; Mihailov, I.; Hadjiiski, W. Simulation of the Mixing Bread Dough Process Using Computational Techniques. Bull. Transilv. Univ. Brasov. Ser. II For. Wood Ind. Agric. Food Eng. 2013, 6, 129–134. [Google Scholar]
- Zhou, S.; Yang, Q.; Lu, L.; Xia, D.; Zhang, W.; Yan, H. CFD Analysis of Sine Baffles on Flow Mixing and Power Consumption in Stirred Tank. Appl. Sci. 2022, 12, 5743. [Google Scholar] [CrossRef]
- Jin, X.; Wang, S.; Shen, Y. DEM Study of Mixing Behaviours of Cohesive Particles in a U-Shaped Ribbon Mixer. Powder Technol. 2022, 399, 117097. [Google Scholar] [CrossRef]
- Jadidi, B.; Ebrahimi, M.; Ein-Mozaffari, F.; Lohi, A. Investigation of Impacts of Particle Shape on Mixing in a Twin Paddle Blender Using GPU-Based DEM and Experiments. Powder Technol. 2023, 417, 118259. [Google Scholar] [CrossRef]
- Abu-Farah, L.; Goudoulas, T.B.; Hooshyar, S.; Germann, N. Numerical and Experimental Investigation of Dough Kneading in a Three-Dimensional Spiral Kneader. Phys. Fluids 2019, 31, 113104. [Google Scholar] [CrossRef]
- Barailler, F.; Heniche, M.; Tanguy, P.A. CFD Analysis of a Rotor-Stator Mixer with Viscous Fluids. Chem. Eng. Sci. 2006, 61, 2888–2894. [Google Scholar] [CrossRef]
- Lindenberg, C.; Schöll, J.; Vicum, L.; Mazzotti, M.; Brozio, J. Experimental Characterization and Multi-Scale Modeling of Mixing in Static Mixers. Chem. Eng. Sci. 2008, 63, 4135–4149. [Google Scholar] [CrossRef]
- Alizadeh, E.; Hajhashemi, H.; Bertrand, F.; Chaouki, J. Experimental Investigation of Solid Mixing and Segregation in a Tetrapodal Blender. Chem. Eng. Sci. 2013, 97, 354–365. [Google Scholar] [CrossRef]
- Oldemeier, J.P.; Schöppner, V. Analysis of the Dispersive and Distributive Mixing Effect of Screw Elements on the Co-Rotating Twin-Screw Extruder with Particle Tracking. Polymers 2024, 16, 2952. [Google Scholar] [CrossRef]
- Hamzehei, M. CFD Modeling and Simulation of Hydrodynamics in a Fluidized Bed Dryer with Experimental Validation. ISRN Mech. Eng. 2011, 2011, 131087. [Google Scholar] [CrossRef]
- Zand, M.K.; Saidi, M. Hydrodynamics and Particles Mixing in Rectangular Spouted Bed with Different Base Geometries Using CFD-DEM. Korean J. Chem. Eng. 2023, 40, 1297–1308. [Google Scholar] [CrossRef]
- Kumar, A.; Ganjyal, G.M.; Jones, D.D.; Hanna, M.A. Modeling Residence Time Distribution in a Twin-Screw Extruder as a Series of Ideal Steady-State Flow Reactors. J. Food Eng. 2008, 84, 441–448. [Google Scholar] [CrossRef]
- Miller, R.; Cardona Barber, I.; Lue, L.; Sefcik, J.; Nazemifard, N. Mixing Times of Miscible Liquid Systems in Agitated Vessels. Processes 2025, 13, 1083. [Google Scholar] [CrossRef]
- Ramírez-López, A. Analysis of Mixing Efficiency in a Stirred Reactor Using Computational Fluid Dynamics. Symmetry 2024, 16, 237. [Google Scholar] [CrossRef]
- Xiong, X.; Wang, S.; Liu, P.; Tao, C.; Wang, Y.; Liu, Z. Numerical Investigation on Intensified Mixing Performance with Modified Dual Impeller. Chem. Eng. Sci. 2023, 274, 118698. [Google Scholar] [CrossRef]
- Xia, B.; Sun, D.W. Applications of Computational Fluid Dynamics (CFD) in the Food Industry: A Review. Comput. Electron. Agric. 2002, 34, 5–24. [Google Scholar] [CrossRef]
- Chai, J.; Su, H.; Li, X.; Zhang, Y.; Xiao, D.; Kang, J.; Dong, A. Computational Fluid Dynamics (CFD) Modeling and Application for Cleaning of Food-Contact Surfaces: A Review. J. Food Process Eng. 2024, 47, e14605. [Google Scholar] [CrossRef]
- Mittal, G.; Issao Kikugawa, R. Computational Fluid Dynamics Simulation of a Stirred Tank Reactor. Mater. Today Proc. 2021, 46, 11015–11019. [Google Scholar] [CrossRef]
- Lysova, N.; Solari, F.; Suppini, C.; Bocelli, M.; Volpi, A.; Montanari, R. Mixing of Non-Newtonian Fluids: From CFD Simulations to Predictive Performance Metrics. In Proceedings of the 9th International Food Operations and Processing Simulation Workshop, Athens, Greece, 18–20 September 2023. [Google Scholar] [CrossRef]
- Emin, M.A.; Wittek, P.; Schwegler, Y. Numerical Analysis of Thermal and Mechanical Stress Profile during the Extrusion Processing of Plasticized Starch by Non-Isothermal Flow Simulation. J. Food Eng. 2021, 294, 110407. [Google Scholar] [CrossRef]
- Malekjani, N.; Jafari, S.M. Simulation of Food Drying Processes by Computational Fluid Dynamics (CFD); Recent Advances and Approaches; Recent Advances and Approaches. Trends Food Sci. Technol. 2018, 78, 206–223. [Google Scholar] [CrossRef]
- Ma, H.; Liu, Z.; Zhou, L.; Du, J.; Zhao, Y. Numerical Investigation of the Particle Flow Behaviors in a Fluidized-Bed Drum by CFD-DEM. Powder Technol. 2023, 429, 118891. [Google Scholar] [CrossRef]
- Michael, V.; Prosser, R.; Kowalski, A. CFD-PBM Simulation of Dense Emulsion Flows in a High-Shear Rotor–Stator Mixer. Chem. Eng. Res. Des. 2017, 125, 494–510. [Google Scholar] [CrossRef]
- Sattar, M.A.; Naser, J.; Brooks, G. Numerical Simulation of Creaming and Foam Formation in Aerated Liquid with Population Balance Modeling. Chem. Eng. Sci. 2013, 94, 69–78. [Google Scholar] [CrossRef]
- Deotale, S.; Dutta, S.; Moses, J.A.; Balasubramaniam, V.M.; Anandharamakrishnan, C. Foaming Characteristics of Beverages and Its Relevance to Food Processing. Food Eng. Rev. 2020, 12, 229–250. [Google Scholar] [CrossRef]
- Hussain, F.; Jaskulski, M.; Piatkowski, M.; Tsotsas, E. CFD Simulation of Agglomeration and Coalescence in Spray Dryer. Chem. Eng. Sci. 2022, 247, 117064. [Google Scholar] [CrossRef]
- Jaskulski, M.; Wawrzyniak, P.; Zbiciński, I. CFD Simulations of Droplet and Particle Agglomeration in an Industrial Counter-Current Spray Dryer. Adv. Powder Technol. 2018, 29, 1724–1733. [Google Scholar] [CrossRef]
- Ma, Z.; Tu, Q.; Liu, Z.; Xu, Y.; Ge, R.; Wang, H. CFD-DEM Investigation of the Gas-Solid Flow Characteristics in a Fluidized Bed Dryer. Chem. Eng. Res. Des. 2023, 196, 235–253. [Google Scholar] [CrossRef]
- Hu, X.; Ilgun, A.D.; Passalacqua, A.; Fox, R.O.; Bertola, F.; Milosevic, M.; Visscher, F. CFD Simulations of Stirred-Tank Reactors for Gasliquid and Gas-Liquid-Solid Systems Using OpenFOAM®. Int. J. Chem. React. Eng. 2021, 19, 193–207. [Google Scholar] [CrossRef]
- Ajani, C.K.; Zhu, Z.; Sun, D.W. Recent Advances in Multiscale CFD Modelling of Cooling Processes and Systems for the Agrifood Industry. Crit. Rev. Food Sci. Nutr. 2021, 61, 2455–2470. [Google Scholar] [CrossRef]
- Debaste, F.; Kegelaers, Y.; Liégeois, S.; Ben Amor, H.; Halloin, V. Contribution to the Modelling of Chocolate Tempering Process. J. Food Eng. 2008, 88, 568–575. [Google Scholar] [CrossRef]
- Kneidinger, C.; Schroecker, E.; Zitzenbacher, G.; Miethlinger, J. Melting Behavior of Heterogeneous Polymer Bulk Solids Related to Flood Fed Single Screw Extruders. Polymers 2020, 12, 2893. [Google Scholar] [CrossRef] [PubMed]
- Adekola, K.A. Influence of Food Extruder Die Dimensions on Extruded Products Expansion. Agric. Eng. Int. CIGR J. 2015, 17, 255–263. [Google Scholar]
- Mollah, T. Computational Fluid Dynamics Modelling and Experimental Analysis of Material Extrusion Additive Manufacturing, 1st ed.; Technical University of Denmark: Copenhagen, Denmark, 2023. [Google Scholar]
- Yacu, W. Extruder screw, barrel, and die assembly: General design principles and operation. In Extrusion Cooking; Ganjyal, G.M., Ed.; Elsevier Inc.: London, UK, 2020; pp. 73–117. ISBN 9780128153604. [Google Scholar]
- Bamidele, O.P.; Emmambux, M.N. Encapsulation of Bioactive Compounds by “Extrusion” Technologies: A Review. Crit. Rev. Food Sci. Nutr. 2021, 61, 3100–3118. [Google Scholar] [CrossRef]
- Villacís-Chiriboga, J.; Sharifi, E.; Elíasdóttir, H.G.; Huang, Z.; Jafarzadeh, S.; Abdollahi, M. Hybrid Plant-Based Meat Alternatives Structured via Co-Extrusion: A Review. Trends Food Sci. Technol. 2025, 160, 105013. [Google Scholar] [CrossRef]
- Luo, S.; Koksel, F. Real-Time Thermal Imaging of Expansion Dynamics during Extrusion of Protein-Fortified Snacks: Effects of Nitrogen Gas and Protein Concentration. Food Res. Int. 2025, 199, 115349. [Google Scholar] [CrossRef]
- Kudryashova, O.; Toropkov, N.; Lerner, M.; Promakhov, V.; Vorozhtsov, A.; Mironov, E. Mathematical Modeling of High-Energy Materials Rheological Behavior in 3D Printing Technology. Heliyon 2023, 9, e12026. [Google Scholar] [CrossRef]
- Hao, Y.; Guo, F.; Wu, G.; Hou, Z.; Li, N.; Liu, G.; Cui, X.; Meng, D.; Li, Y.; Li, X. Numerical Simulation and Experimental Research on Heat Transfer Characteristics Based on Internal Meshing Screw. Appl. Sci. 2024, 14, 220. [Google Scholar] [CrossRef]
- Jamaleddine, T.J.; Ray, M.B. Application of Computational Fluid Dynamics for Simulation of Drying Processes: A Review. Dry. Technol. 2010, 28, 120–154. [Google Scholar] [CrossRef]
- Oyinloye, T.M.; Yoon, W.B. Application of Computational Fluid Dynamics (CFD) in the Deposition Process and Printability Assessment of 3D Printing Using Rice Paste. Processes 2022, 10, 68. [Google Scholar] [CrossRef]
- Ramya, V. Rheological Properties of Food: A Review. Int. J. Gen. Eng. Technol. 2020, 9, 47–54. [Google Scholar]
- Cordioli, M.; Rinaldi, M.; Copelli, G.; Casoli, P.; Barbanti, D. Computational Fluid Dynamics (CFD) Modelling and Experimental Validation of Thermal Processing of Canned Fruit Salad in Glass Jar. J. Food Eng. 2015, 150, 62–69. [Google Scholar] [CrossRef]
- Norton, T.; Tiwari, B.; Sun, D.W. Computational Fluid Dynamics in the Design and Analysis of Thermal Processes: A Review of Recent Advances. Crit. Rev. Food Sci. Nutr. 2013, 53, 251–275. [Google Scholar] [CrossRef]
- Huang, X.; Liu, H.; Ma, Y.; Mai, S.; Li, C. Effects of Extrusion on Starch Molecular Degradation, Order–Disorder Structural Transition and Digestibility—A Review. Foods 2022, 11, 2538. [Google Scholar] [CrossRef]
- Zhou, Z.; Langrish, T. Modeling Maillard Reaction Kinetics in Spray Dryers Using Both Lumped- and Distributed-Parameter Modeling Approaches. J. Food Process Eng. 2024, 47, e14599. [Google Scholar] [CrossRef]
- Therdthai, N.; Zhou, W.; Adamczak, T. Simulation of Starch Gelatinisation during Baking in a Travelling-Tray Oven by Integrating a Three-Dimensional CFD Model with a Kinetic Model. J. Food Eng. 2004, 65, 543–550. [Google Scholar] [CrossRef]
- Jamil Ur Rahman, U.; Pozarlik, A.K. Numerical Study and Experimental Validation of Skim Milk Drying in a Process Intensified Counter Flow Spray Dryer. Energies 2021, 14, 4974. [Google Scholar] [CrossRef]
- Park, H.W.; Yoon, W.B. Computational Fluid Dynamics (CFD) Modelling and Application for Sterilization of Foods: A Review. Processes 2018, 6, 62. [Google Scholar] [CrossRef]
- Wittek, P.; Ellwanger, F.; Karbstein, H.P.; Emin, M.A. Morphology Development and Flow Characteristics during High Moisture Extrusion of a Plant-Based Meat Analogue. Foods 2021, 10, 1753. [Google Scholar] [CrossRef]
- Wittek, P.; Karbstein, H.P.; Emin, M.A. Blending Proteins in High Moisture Extrusion to Design Meat Analogues: Rheological Properties, Morphology Development and Product Properties. Foods 2021, 10, 1509. [Google Scholar] [CrossRef]
- Scott, G.; Richardson, P. The Application of Computational Fluid Dynamics in the Food Industry. Trends Food Sci. Technol. 1997, 8, 119–124. [Google Scholar] [CrossRef]
- Langrish, T.A.G.; Harrington, J.; Huang, X.; Zhong, C. Using CFD Simulations to Guide the Development of a New Spray Dryer Design. Processes 2020, 8, 932. [Google Scholar] [CrossRef]
- de Munck, M.J.A.; Peters, E.A.J.F.; Kuipers, J.A.M. CFD-DEM Modeling and Validation of Solids Drying in a Gas-Fluidized Bed. Chem. Eng. Sci. 2024, 291, 119922. [Google Scholar] [CrossRef]
- Longest, P.W.; Farkas, D.; Hassan, A.; Hindle, M. Computational Fluid Dynamics (CFD) Simulations of Spray Drying: Linking Drying Parameters with Experimental Aerosolization Performance. Pharm. Res. 2020, 37, 101. [Google Scholar] [CrossRef]
- Kumar, V.; Sharma, H.K.; Mishra, S. Simulation of Spray Drying of Tomato Juice Using Computational Fluid Dynamics (CFD). Cogent Food Agric. 2017, 3, 1310596. [Google Scholar] [CrossRef]
- Harish, S.; Kishorre Annanth, V.; Abinash, M.; Kannan, K.R.; Agarwal, S.; Mohana, N. A Study on Numerical Methodologies in Solving Fluid Flow and Heat Transfer Problems. IOP Conf. Ser. Earth Environ. Sci. 2021, 850, 012021. [Google Scholar] [CrossRef]
- Ranjbarzadeh, R.; Sappa, G. Numerical and Experimental Study of Fluid Flow and Heat Transfer in Porous Media: A Review Article. Energies 2025, 18, 976. [Google Scholar] [CrossRef]
- Imran, M.; Lau, K.K.; Ahmad, F.; Mohd Laziz, A. A Comprehensive Review of Computational Fluid Dynamics (CFD) Modelling of Membrane Gas Separation Process. Results Eng. 2025, 26, 105531. [Google Scholar] [CrossRef]
- Ranganathan, P.; Pandey, A.K.; Sirohi, R.; Tuan Hoang, A.; Kim, S.H. Recent Advances in Computational Fluid Dynamics (CFD) Modelling of Photobioreactors: Design and Applications. Bioresour. Technol. 2022, 350, 126920. [Google Scholar] [CrossRef]
- Ian Wilson, D.; John Chew, Y.M. Fluid Mechanics in Food Engineering. Curr. Opin. Food Sci. 2023, 51, 101038. [Google Scholar] [CrossRef]
- Abdurrahman, E.E.M.; Ferrari, G. Digital Twin Applications in the Food Industry: A Review. Front. Sustain. Food Syst. 2025, 9, 1538375. [Google Scholar] [CrossRef]
- Wang, Y. Applications of Artificial Intelligence in Food Industry: A Review. Agric. Sci. Food Process. 2025, 2, 68–88. [Google Scholar] [CrossRef]
- Akter, F.; Muhury, R.; Sultana, A.; Deb, U.K. A Comprehensive Review of Mathematical Modeling for Drying Processes of Fruits and Vegetables. Int. J. Food Sci. 2022, 2022, 6195257. [Google Scholar] [CrossRef]
- Gutiérrez Suárez, J.A.; Galeano Urueña, C.H.; Gómez Mejía, A. Parametric CFD Study of Spray Drying Chamber Geometry: Part I—Effects on Airflow Dynamics. ChemEngineering 2025, 9, 5. [Google Scholar] [CrossRef]
- Longest, W.; Hassan, A.; Farkas, D.; Hindle, M. Computational Fluid Dynamics (CFD) Guided Spray Drying Recommendations for Improved Aerosol Performance of a Small-Particle Antibiotic Formulation. Pharm. Res. 2022, 39, 295–316. [Google Scholar] [CrossRef]
- Handayani, S.U.; Wahyudi, H.; Agustina, S.; Yulianto, M.E.; Aryanto, H.D. CFD-DEM Study of Heat and Mass Transfer of Ellipsoidal Particles in Fluidized Bed Dryers. Powder Technol. 2023, 425, 118535. [Google Scholar] [CrossRef]
- Jaiswal, P. A Comprehensive Review on Computational Fluid Dynamics and Its Diverse Applications. J. Adv. Res. Appl. Mech. Comput. Fluid Dyn. 2023, 10, 1–5. [Google Scholar]
- Pragati, K.; Sharma, H. Concept of Computational Fluid Dynamics (CFD) and Its Applications in Food Processing Equipment Design. J. Food Process. Technol. 2011, 03, 1–7. [Google Scholar] [CrossRef]
- Choi, J.; Cho, H.; Choi, Y.; Lee, S. Combination of Computational Fluid Dynamics and Design of Experiments to Optimize Modules for Direct Contact Membrane Distillation. Desalination 2022, 524, 115460. [Google Scholar] [CrossRef]
- Zhao, Z.; Baumann, A.; Ryan, E.M. Using Machine-Learning-Aided Computational Fluid Dynamics to Facilitate Design of Experiments. Ind. Eng. Chem. Res. 2024, 63, 21444–21454. [Google Scholar] [CrossRef]
- Muktiarni, M.; Rahayu, N.I.; Zakariah, S.H. Computational Fluid Dynamics Approaches in Quality and Hygienic Production of Foods: A Review of Critical Factors. CFD Lett. 2025, 17, 216–226. [Google Scholar] [CrossRef]
- Cui, P.; Yu, Y.; Xue, Q.; Wu, Z.; Miao, K.; Liu, C.; Zhao, L.; Li, Z. Numerical Simulation and Optimization of Lonicerae Japonicae Flos Extract Spray Drying Process Based on Temperature Field Verification and Deep Reinforcement Learning. J. Food Eng. 2023, 345, 111425. [Google Scholar] [CrossRef]
- Solari, F.; Lysova, N.; Dalla Fiora, A.; Volpi, A.; Rizzi, A.; Montanari, R. Mitigating Design Errors in Standardized Food Processing Plants: Insights from CFD Simulation of a Tomato Concentration Process. In Proceedings of the 10th International Food & Operations Simulation Workshop, Tenerife, Spain, 18–20 September 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Runchal, A.K. Evolution of CFD as an Engineering Science. A Personal Perspective with Emphasis on the Finite Volume Method. Comptes Rendus Mec. 2022, 350, 233–258. [Google Scholar] [CrossRef]
- Zhang, L.; Boom, R.M.; Ma, Y. Machine Learning in Automated Food Processing: A Mini Review. Annu. Rev. Food Sci. Technol. 2025, 16, 25–37. [Google Scholar] [CrossRef]
- Muktiarni, M.; Rahayu, N.I.; Nurhayati, A.; Bachari, A.D.; Ismail, A. Concept of Computational Fluid Dynamics Design and Analysis Tool for Food Industry: A Bibliometric. CFD Lett. 2024, 16, 1–23. [Google Scholar] [CrossRef]
- Borgonovo, E.; Plischke, E. Sensitivity Analysis: A Review of Recent Advances. Eur. J. Oper. Res. 2016, 248, 869–887. [Google Scholar] [CrossRef]
- Reddy, R.S.; Arepally, D.; Datta, A.K. Inverse Problems in Food Engineering: A Review. J. Food Eng. 2022, 319, 110909. [Google Scholar] [CrossRef]
- Dolan, K.D.; Mishra, D.K. Parameter Estimation in Food Science. Annu. Rev. Food Sci. Technol. 2013, 4, 401–422. [Google Scholar] [CrossRef]
- Orona, J.D.; Zorrilla, S.E.; Peralta, J.M. Sensitivity Analysis Using a Model Based on Computational Fluid Dynamics, Discrete Element Method and Discrete Phase Model to Study a Food Hydrofluidization System. J. Food Eng. 2018, 237, 183–193. [Google Scholar] [CrossRef]
- Lobatón-García, H.F.; López-Mejía, N.; Cruz-Guayacundo, W. CFD Acoplada a La Metodología de Superficie de Respuesta Para Optimizar La Conductividad Térmica Efectiva y La Homogeneidad En Un Secador de Bandejas CFD-Response Surface Methodology to Optimize the Effective Thermal Conductivity and Homogeneity in Tray D. Sci. Artic. 2023, 26, 1–11. [Google Scholar]
- Of, A.; Fluid, C.; In, D.; Food, T.H.E. Applications of Computational Fluid Dynamics. In Flow-Induced Vibration; CRC Press: Boca Raton, FL, USA, 2020; Chapter 3; pp. 255–340. [Google Scholar] [CrossRef]
- Ramirez-Asis, E.; Vilchez-Carcamo, J.; Thakar, C.M.; Phasinam, K.; Kassanuk, T.; Naved, M. A Review on Role of Artificial Intelligence in Food Processing and Manufacturing Industry. Mater. Today Proc. 2022, 51, 2462–2465. [Google Scholar] [CrossRef]
- Carson, J.K. Thermal Conductivity Measurement and Prediction of Particulate Foods. Int. J. Food Prop. 2015, 18, 2840–2849. [Google Scholar] [CrossRef]
- Srikiatden, J.; Roberts, J.S. Moisture Transfer in Solid Food Materials: A Review of Mechanisms, Models, and Measurements. Int. J. Food Prop. 2007, 10, 739–777. [Google Scholar] [CrossRef]
- Takhar, P.S. Role of Glass-Transition on Fluid Transport in Porous Food Materials. Int. J. Food Eng. 2008, 4, 1–15. [Google Scholar] [CrossRef]
- Renzetti, S.; Voogt, J.A.; Oliver, L.; Meinders, M.B.J. Water Migration Mechanisms in Amorphous Powder Material and Related Agglomeration Propensity. J. Food Eng. 2012, 110, 160–168. [Google Scholar] [CrossRef]
- Joardder, M.U.H.; Kumar, C.; Karim, M.A. Prediction of Porosity of Food Materials during Drying: Current Challenges and Directions. Crit. Rev. Food Sci. Nutr. 2018, 58, 2896–2907. [Google Scholar] [CrossRef]
- Pereira, T.; Barroso, S.; Gil, M.M. Food Texture Design by 3d Printing: A Review. Foods 2021, 10, 320. [Google Scholar] [CrossRef]
- Voong, K.Y.; Norton-Welch, A.; Mills, T.B.; Norton, I.T. Understanding and Predicting Sensory Crispness of Deep-Fried Battered and Breaded Coatings. J. Texture Stud. 2019, 50, 456–464. [Google Scholar] [CrossRef]
- Chanvrier, H.; Jakubczyk, E.; Gondek, E.; Gumy, J.C. Insights into the Texture of Extruded Cereals: Structure and Acoustic Properties. Innov. Food Sci. Emerg. Technol. 2014, 24, 61–68. [Google Scholar] [CrossRef]
- Addanki, M.; Patra, P.; Kandra, P. Recent Advances and Applications of Artificial Intelligence and Related Technologies in the Food Industry. Appl. Food Res. 2022, 2, 100126. [Google Scholar] [CrossRef]
- Ghosh, D.; Datta, A. Deep Learning Enabled Surrogate Model of Complex Food Processes for Rapid Prediction. Chem. Eng. Sci. 2023, 270, 118515. [Google Scholar] [CrossRef]
- Yang, H.; Jiao, W.; Zouyi, L.; Diao, H.; Xia, S. Artificial Intelligence in the Food Industry: Innovations and Applications; Springer International Publishing: Berlin/Heidelberg, Germany, 2025; Volume 5, ISBN 4416302500296. [Google Scholar]
- Nath, P.C.; Mishra, A.K.; Sharma, R.; Bhunia, B.; Mishra, B.; Tiwari, A.; Nayak, P.K.; Sharma, M.; Bhuyan, T.; Kaushal, S.; et al. Recent Advances in Artificial Intelligence towards the Sustainable Future of Agri-Food Industry. Food Chem. 2024, 447, 138945. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, S.; Zhang, Y.; Feng, Y.; Liu, J.; Zhu, H. Artificial Intelligence in Food Safety: A Decade Review and Bibliometric Analysis. Foods 2023, 12, 1242. [Google Scholar] [CrossRef] [PubMed]
- Song, X.; Zhang, X.; Dong, G.; Ding, H.; Cui, X.; Han, Y.; Huang, H.; Wang, L. AI in Food Industry Automation: Applications and Challenges. Front. Sustain. Food Syst. 2025, 9, 1–9. [Google Scholar] [CrossRef]
- Puri, N.R.; Qomariyah, L.; Winardi, S.; Kharisma, A.D.; Altway, S.; Alawiyah, L.; Firmansyah, F.; Putra, N.R.; Sabar, S. Using Computational Fluid Dynamic (CFD) Simulation to Predict the Silica Particle Size in Spray Dryer under the Influence of Colloidal Properties. CFD Lett. 2025, 17, 30–44. [Google Scholar] [CrossRef]
- Rauh, C.; Delgado, A. Different Modelling and Simulation Approaches for Food Processing Operations; Elsevier Ltd.: Amsterdam, The Netherlands, 2015; ISBN 9781782422846. [Google Scholar]
- Verboven, P.; Defraeye, T.; Datta, A.K.; Nicolai, B. Digital Twins of Food Process Operations: The next Step for Food Process Models? Curr. Opin. Food Sci. 2020, 35, 79–87. [Google Scholar] [CrossRef]
- Krupitzer, C.; Noack, T.; Borsum, C. Digital Food Twins Combining Data Science and Food Science: System Model, Applications, and Challenges. Processes 2022, 10, 1781. [Google Scholar] [CrossRef]
- Monteiro, J.; Barata, J. Digital Twin-Enabled Regional Food Supply Chain: A Review and Research Agenda. J. Ind. Inf. Integr. 2025, 45, 100851. [Google Scholar] [CrossRef]
- Kannapinn, M.; Pham, M.K.; Schäfer, M. Physics-Based Digital Twins for Autonomous Thermal Food Processing: Efficient, Non-Intrusive Reduced-Order Modeling. Innov. Food Sci. Emerg. Technol. 2022, 81, 103143. [Google Scholar] [CrossRef]

| Process | Dominant Physical Phenomena | CFD Modeling Approaches | Example Industrial Applications | Applications in Food Industry | References |
|---|---|---|---|---|---|
| Mixing | Laminar or turbulent flow Rotational motion, shearing, recirculation Dispersing multiple phases | Navier–Stokes (RANS, LES) Turbulence models: k-ε, k-ω, RSM Non-Newtonian fluid models (Power-law, Herschel–Bulkley) RTD & mixing indices CFD–DEM coupling | Emulsion homogenization Dough or batter mixing Inline blending in beverage and dairy industries | Quality control in sauces, batters, emulsions; Uniform ingredient distribution; Viscosity optimization | [75,76] |
| Extrusion | Thermo-mechanical coupling Shear-induced structuring Phase transitions (e.g., vaporization, expansion) | Coupled thermal–fluid simulations Non-Newtonian models (Herschel–Bulkley, viscoelastic) VOF for expansion CFD + reaction kinetics CFD–FEM for deformation | Expanded snacks, breakfast cereals Plant-based meat extrusion Optimization of die and screw configuration | Texturization of meat analogs; Control of porosity and expansion; Nutrient delivery modulation | [34,77] |
| Mechanically Aided Drying | Gas–solid interactions Heat and mass transfer Fluidization, vibration | Multiphase CFD (EE or EL) Evaporation and moisture transport models Turbulence: k-ε, LES CFD–DEM for particle motion | Fluidized bed and vibratory drying Powder drying (milk, coffee, flavors) Granule/agglomerate stabilization | Moisture reduction in powders; Shelf-life extension; Prevention of caking or collapse | [78,79] |
| Homogenization & Emulsification | High shear, cavitation Droplet breakup and dispersion Two-phase mixing | Rotor–stator CFD geometries Shear rate and energy dissipation modeling EL (for droplets) VOF for immiscible interface tracking | Mayonnaise and sauce emulsification Dairy product homogenization Emulsion stabilization processes | Stable emulsion formation; Reduced fat content products; Improved mouthfeel and rheology | [55,80] |
| Foaming/Aeration | Gas incorporation Bubble formation and stabilization Surface tension effects | EL or VOF (for bubbles) Surface tension and bubble coalescence models Turbulence: LES, RANS | Aerated desserts and whipped toppings Foam-based dairy and confectionery products | Structure control in mousses and whipped products; Sensory texture improvement; Gas volume consistency | [81,82] |
| Coating/ Agglomeration | Droplet–particle interaction Growth, coalescence, consolidation Moisture and heat transfer | CFD–PBM EL (droplet tracking) DEM for particle interactions Adhesion and wetting models | Instantized powders Flavor/encapsulation coating Agglomerated granules | Controlled release (flavors, nutrients); Improved solubility and dispersibility; Functional food coatings | [83,84] |
| Mechanical Conveying | Multiphase flow (solid–gas) Pressure drop and friction Shear-induced degradation or segregation | CFD–DEM coupling (e.g., screw conveyors) RANS for air–solid interactions Wall shear and slip analysis | Pneumatic transport systems Screw and belt conveyors Optimizing feed uniformity and throughput | Bulk material handling; Reducing breakage and segregation; Consistent throughput | [85] |
| Mechanically Mixed Reactors | Solid–liquid or gas–liquid mixing Oxygen or substrate transport Heat and shear interactions affecting biochemical reactions | Newtonian/non-Newtonian CFD models Mass transfer and oxygen solubility modeling Optionally coupled with kinetic or enzymatic models | Yogurt, kefir, or enzyme reactors Bioreactor design and scale-up | Fermentation optimization; Enzyme reaction control; Flavor and texture consistency in cultured products | [86] |
| Mechanical Cooling | Forced convection Air or fluid flow around products Heat removal efficiency | CFD with conjugate heat transfer Airflow turbulence models (k-ε, k-ω) Thermal gradient visualization | Cooling of bars, baked goods, or chocolate Design of tunnel coolers and refrigerated conveyors | Post-baking cooling; Chocolate tempering; Crystallization control | [87,88] |
| High-Shear Inline Processing | Extreme velocity gradients Energy dissipation Short residence time with rapid mixing/shearing | CFD for shear rate, turbulence intensity Inline geometry modeling RTD analysis | Inline emulsification Functional ingredient dispersion Continuous thermal/mechanical treatment | Rapid emulsification of dairy/fat mixtures; Inline processing of functional drinks; Minimization of microbial growth time window | [80] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szpicer, A.; Bińkowska, W.; Stelmasiak, A.; Wojtasik-Kalinowska, I.; Czajkowska, A.; Mierzejewska, S.; Domiszewski, Z.; Rydzkowski, T.; Piepiórka-Stepuk, J.; Półtorak, A. Advances in Computational Fluid Dynamics of Mechanical Processes in Food Engineering: Mixing, Extrusion, Drying, and Process Optimization. Appl. Sci. 2025, 15, 8752. https://doi.org/10.3390/app15158752
Szpicer A, Bińkowska W, Stelmasiak A, Wojtasik-Kalinowska I, Czajkowska A, Mierzejewska S, Domiszewski Z, Rydzkowski T, Piepiórka-Stepuk J, Półtorak A. Advances in Computational Fluid Dynamics of Mechanical Processes in Food Engineering: Mixing, Extrusion, Drying, and Process Optimization. Applied Sciences. 2025; 15(15):8752. https://doi.org/10.3390/app15158752
Chicago/Turabian StyleSzpicer, Arkadiusz, Weronika Bińkowska, Adrian Stelmasiak, Iwona Wojtasik-Kalinowska, Anna Czajkowska, Sylwia Mierzejewska, Zdzisław Domiszewski, Tomasz Rydzkowski, Joanna Piepiórka-Stepuk, and Andrzej Półtorak. 2025. "Advances in Computational Fluid Dynamics of Mechanical Processes in Food Engineering: Mixing, Extrusion, Drying, and Process Optimization" Applied Sciences 15, no. 15: 8752. https://doi.org/10.3390/app15158752
APA StyleSzpicer, A., Bińkowska, W., Stelmasiak, A., Wojtasik-Kalinowska, I., Czajkowska, A., Mierzejewska, S., Domiszewski, Z., Rydzkowski, T., Piepiórka-Stepuk, J., & Półtorak, A. (2025). Advances in Computational Fluid Dynamics of Mechanical Processes in Food Engineering: Mixing, Extrusion, Drying, and Process Optimization. Applied Sciences, 15(15), 8752. https://doi.org/10.3390/app15158752














