Enhanced Cuckoo Search Optimization with Opposition-Based Learning for the Optimal Placement of Sensor Nodes and Enhanced Network Coverage in Wireless Sensor Networks

Featured Application

This work enables effective data collection and transmission in wireless sensor network applications such as industry automation, healthcare, environmental monitoring, and agriculture.

Abstract

Network connectivity and area coverage are the most important aspects in the applications of wireless sensor networks (WSNs). The resource and energy constraints of sensor nodes, operational conditions, and network size pose challenges to the optimal coverage of targets in the region of interest (ROI). The main idea is to achieve maximum area coverage and connectivity with strategic deployment and the minimal number of sensor nodes. This work addresses the problem of network area coverage in randomly distributed WSNs and provides an efficient deployment strategy using an enhanced version of cuckoo search optimization (ECSO). The “sequential update evaluation” mechanism is used to mitigate the dependency among dimensions and provide highly accurate solutions, particularly during the local search phase. During the preference random walk phase of conventional CSO, particle swarm optimization (PSO) with adaptive inertia weights is defined to accelerate the local search capabilities. The “opposition-based learning (OBL)” strategy is applied to ensure high-quality initial solutions that help to enhance the balance between exploration and exploitation. By considering the opposite of current solutions to expand the search space, we achieve higher convergence speed and population diversity. The performance of ECSO-OBL is evaluated using eight benchmark functions, and the results of three cases are compared with the existing methods. The proposed method enhances network coverage with a non-uniform distribution of sensor nodes and attempts to cover the whole ROI with a minimal number of sensor nodes. In a WSN with a 100 m² area, we achieved a maximum coverage rate of 98.45% and algorithm convergence in 143 iterations, and the execution time was limited to 2.85 s. The simulation results of various cases prove the higher efficiency of the ECSO-OBL method in terms of network coverage and connectivity in WSNs compared with existing state-of-the-art works.

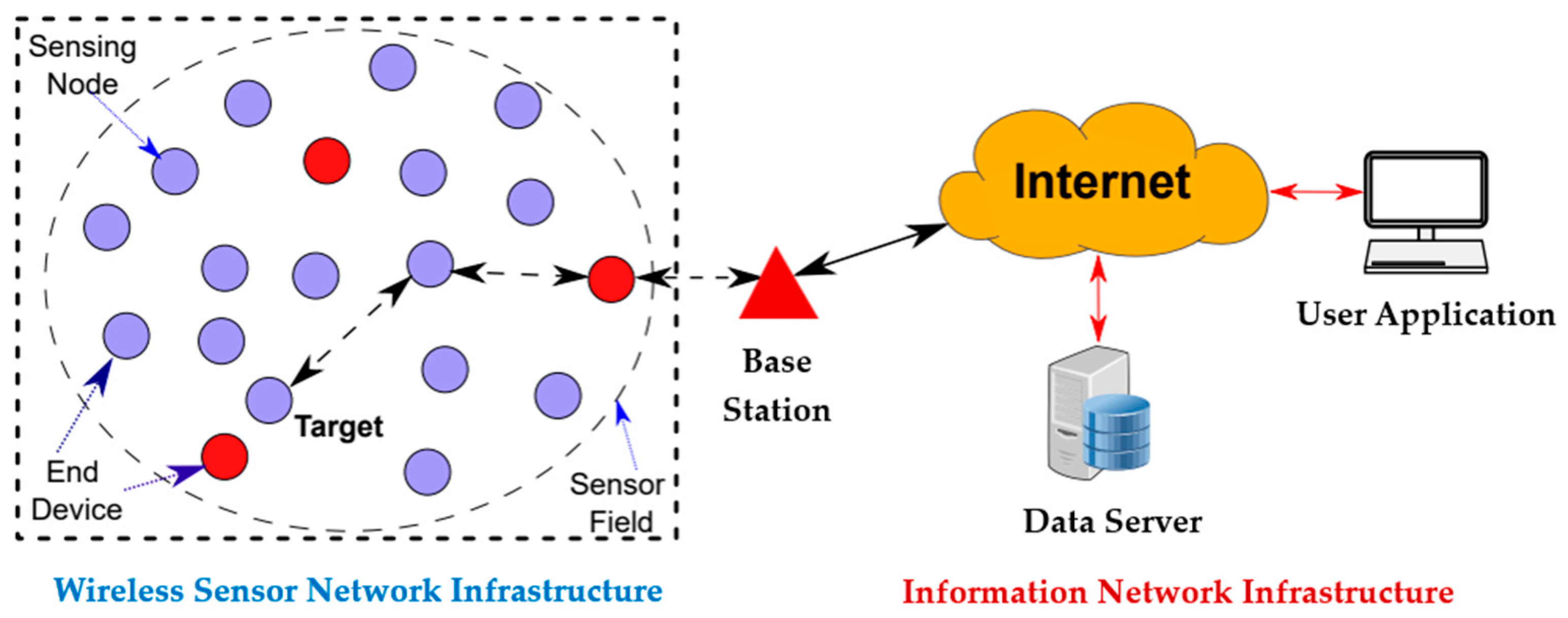
1. Introduction

A wireless sensor network (WSN) is composed of sensor nodes meant for a specific purpose and deployed in the given geographical area. The main operations involved at each sensor node are sensing, processing, and communication. Each sensor node in the network senses the physical environment, processes the sensed parameter values (such as ambient light, pressure, humidity, etc.), and sends these data to the base station (BS) through cluster heads. Further, the BS (which is the sink node) communicates the sensed data to the control station through the Internet, as shown in Figure 1. At later stages, the data can be viewed and interpreted by the user application, and deeper data analytics are performed on the stored data at servers. In industry automation applications [1], the role of WSNs becomes essential, as it does in all the advanced applications of the Internet of things (IoT) and the Industrial IoT in their perception layer.

In Figure 2, a sensor node’s hardware architecture is presented; it mainly consists of sensing modules, a processing unit, a communication unit, and a power unit. It has components including a sensor node, a power source, an analog-to-digital converter (ADC), a controller, a memory unit, and a transceiver. The sensor circuitry converts the physical sensed quantities into equivalent electrical signals. The ADC module converts the analog values or signals into their digital equivalents and feeds them to the controller. The controller processes the signals which can be feasible for transmission over the communication network, as well as for storage in the memory unit. The transceiver module is used to send and receive data simultaneously. Every sensor node can communicate with other sensor nodes, as well as with the BS, via direct links or through multi-hops. Though there exist two types of WSN architectures, namely, layer-based and cluster-based, most of the practical applications use cluster-based architectures. In cluster-based architectures, there exist cluster heads, which take responsibility for collecting sensed data from cluster members and perform data fusion before sending them to the BS. The data fusion process eliminates redundant data transmissions and improves network lifetime. The role of CH is changed among sensor nodes based on certain criteria to avoid energy depletion at the sensor nodes.

In WSNs, each sensor node identifies the occurrence of an event within its sensing range and transmits this information to its neighborhood present in its communication range. This information is finally sent to the sink node through multi-hop communication. The information should arrive at the sink node along the optimal path and should avoid travelling through uncovered regions of the network. Therefore, the strategic deployment of sensor nodes plays an important role in maintaining connectivity and coverage optimization. In the pre-determined or pre-planned deployment method, the sensor nodes are placed at pre-defined coordinates to achieve maximum connectivity and coverage. But such deployments are not suitable for the military and hard-to-reach applications. Therefore, the coverage and connectivity in randomly deployed WSNs draws the attention of researchers in nascent works.

In modern data-driven applications of WSNs, the best network coverage and connectivity are essential aspects for seamless data collection and transmission. WSN coverage can be measured in terms of area, point, or boundary. Area coverage aims to cover the whole region of interest (ROI) with fewer sensor nodes. Point coverage tries to focus on individual target nodes in the ROI. Boundary coverage prevents infiltration by covering certain paths in the ROI including the network boundaries. Point coverage in WSNs is used to monitor the target nodes in particular regions of the network and be observed by at least one anchor node. The optimal selection of anchor nodes leads to increased lifetime of the network. To optimize network coverage, the competitiveness of the metaheuristic algorithm [2] lies in its search accuracy, stability, and convergence speed. Existing coverage algorithms [3,4,5,6] have a larger number of coverage holes and also higher redundancy in the monitoring area. We propose an algorithm that provides a more uniform distribution of sensor nodes with minimal redundancy and enhances network area coverage and connectivity.

2. Contributions

2.1. Motivation

The conventional “Cuckoo search optimization” (CSO) is an iterative method that gives best possible solution during the global search with limited local search capabilities due to randomness of Lévy flights. However, this conventional algorithm suffers from weak local search capabilities. Also, it suffers from interference among the multiple dimensions in handling a multi-dimensional optimization problem. The proposed ECSO-OBL algorithm introduces an adaptive step size (the step size is proportional to the value of the fitness function) and controls the random walk of cuckoo search. The coverage optimization problem is described using an objective function. The main objective of this work is to cover the monitoring area of the network with a smaller number of sensor nodes and optimally define their deployment locations.

2.2. Main Contributions

This work mainly focused on identifying the best locations of sensor nodes (obtaining an optimal network layout) to support maximum network coverage and connectivity through the following steps:

(a)

The coverage model in the WSN is defined, and an objective function for the optimal coverage is established.

(b)

A “sequential update evaluation mechanism” is used, whereby each dimension is evaluated one by one, and this process mitigates the effect of dependency among dimensions and provides highly accurate solutions, particularly during the local search phase.

(c)

During the preference random walk phase of conventional CSO, PSO with adaptive inertia weights is integrated with the ECSO-OBL algorithm. This improves the local search capabilities.

(d)

The OBL strategy is applied to have high-quality initial solutions that help to balance the exploration and exploitation strategies. By considering the opposite of current solutions to expand the search space, we achieve higher convergence speed and population diversity.

The rest of the article is organized as follows: Section 3 presents the nascent techniques and methods related to network coverage and connectivity in WSNs, Section 4 introduces the proposed ECSO-OBL method and how it is applied to WSNs to enhance coverage, Section 5 discusses the simulation results, and Section 6 concludes our work along with possible future research directions.

3. Existing Works

This section presents nascent research on network coverage and deployment in WSNs, mainly based on CSO and its improved versions. We also discuss the hybrid versions of CSO along with other metaheuristic algorithms and their limitations. The deployment of sensor nodes with limited and uniform sensing radius can lead to optimal coverage in WSNs. The coverage area is classified into active coverage and blind spots. Active coverage is the sensing area covered by at least one sensor node and able to monitor events. The blind spots are the areas where no sensor nodes can monitor the events. The coverage accuracy will be high if the sensing area is covered by multiple sensor nodes. Most of the metaheuristic algorithms use the exploration and exploitation strategy to enhance network coverage through the optimal placement of sensor nodes. CSO has various applications in enhancing the performance of WSNs in terms of locating sensor nodes accurately, cost, energy consumption, and load distribution [7,8].

Table 1. Related works on self-localization and coverage techniques in WSNs using metaheuristic approaches.

Ref.	Authors	Objective	Methodology	Limitations
[9]	Yang and Xia (2024)	Design routing and coverage optimization in WSNs using improved CSO and non-uniform clustering.	Coverage optimization is addressed through Cauchy distribution. The average coverage is 96%.	The algorithm’s minimum run time is 1.47 min, with an energy loss rate of 0.84%.
[10]	Yang et al. (2023)	Maximize network coverage using a hybrid algorithm that combines CSO and PSO.	Convert the regional monitoring space into point monitoring space by using discretization methods.	Though the coverage rate of the proposed algorithm is enhanced by 18.36% compared with CSO, it enters an early stagnation state and is trapped in a local optimal solution. For all the network sizes, the accuracy and convergence speed are inferior.
[11]	Yang et al. (2024)	Increase network coverage by using a hybrid CSO-PSO algorithm and “opposition-based learning (OBL)”.	The OBL strategy broadens search space exploration to improve the diversity of the population.	The convergence time of the hybrid CSO-PSO algorithm is too high.
[12]	Bing and Youyou (2024)	Hybrid combination of LEACH and CSO to improve network lifetime and packet delivery ratios.	During clustering and cluster head selection, the LEACH protocol uses CSO. During the routing phase, fuzzy logic is used.	Performance is dependent on the distance between mobile and stationary sensors nodes.
[13]	Li and Cao (2021)	Improve the coverage rate in WSNs using discrete binary PSO.	For optimal deployment, an adaptive learning factor and inertia weights are introduced.	The coverage ratio decreases as the dimensions of the network increase.
[14]	Dao et al. (2022)	Use “Archimedes optimization” for optimal coverage in an unbalanced WSN distribution.	“Reverse learning” and “multidirectional” techniques are introduced. Coverage optimization is implemented through the evaluation of fitness per sub-area.	It falls into local minima and has a slow convergence rate.
[15]	Tushar et al. (2022)	Minimize the cost and energy consumption of relay nodes with uniform load distribution. Used for optimal placement and selection of relay nodes when using adaptive CSO in body area networks.	Optimal placement of relay nodes and routing are formulated as “a linear integer programming” model. CSO with an adaptive step size is defined. The fitness function is defined based on coverage, load, and energy consumption of the sensors nodes.	It is time-consuming due to the fixed relay nodes while starting and then increases to identify the optimal number. The search space is increased exponentially and causes higher execution time, and it further increases with network size.
[16]	Ramin and Seyed (2020)	The coverage problem is modeled to enhance the network lifetime.	Cooperative PSO and fuzzy logic are used to solve the node deployment problem. Fuzzy logic computes acceleration coefficients on a dynamic basis and enhances network lifetime.	The solution is limited to cover fixed target nodes, and the resolution of the coverage is poor.
[17]	Sajjad et al. (2022)	Node deployment problem is addressed using metaheuristic approach.	Mutant-GWO model ensures connectivity by generating topology graphs.	Power consumption is too high due to collisions.
[18]	Xu et al. (2023)	Coverage optimization problem in WSNs.	Whale optimization with Lévy flight and genetic algorithm is used.	Though the coverage rate is 90.33%, the complexity of this algorithm is too high.
[19]	Tian et al. (2021)	Regional coverage control in high-density WSNs is addressed.	Elite parallel CSO, which is randomized swarm optimization, is introduced.	It has a slow convergence rate and is not suitable for combinatorial optimization and discrete optimization problems.
[20]	Ajam et al. (2021)	Proposed to maximize network lifetime with variable ranges.	Hybrid combination of “Genetic Algorithm” and “Tabu Search” used to define cover sets with suitable sensing ranges.	This algorithm is not suitable for uniform WSNs.
[21]	Arivudainambi et al. (2020)	Optimize the sensing range by minimizing redundancy in WSNs.	Based on the sensing range, the CSO algorithm classifies the sensor nodes into non-disjoint subsets. At a given time, only one subset is activated to cover the network area. The activation of each subset is in cycles to enhance the network lifetime.	Convergence time is too high.
[22]	Chen et al. (2025)	Enhance and optimize coverage in 2D and 3D WSNs.	Multi-strategy dung beetle optimization algorithm that uses a random number to change the inertia factor.	The maximum coverage is limited to 77.7%.
[23]	Pavithra and Arivudainambi (2023)	Energy-efficient target coverage in WSNs.	Energy-efficient coverage is described as a set k-cover problem with independent sensor sets, and it is solved using graph theory.	The range of sensing is fixed, and it leads to lower energy efficiency.
[24]	Di Puglia et al. (2025)	Deploy minimum count of sensor nodes to fully cover the ROI and enhance connectivity.	The proposed method is described as a “connectivity problem” and a “covering problem”. It is solved using decomposition techniques based on the “Miller-Tucker-Zemlin” model.	It takes a greater number of iterations and execution time to achieve optimal results.

describes various network coverage and deployment techniques in WSNs based on CSO and integrated with other metaheuristic algorithms. Cauchy distribution-based CSO [9] enables improvement in the exploration ability and minimizes the risk of falling into local optima. It allows the algorithm to explore the entire solution space addresses. It provides better coverage and lifetime optimization in WSNs.

CSO [25] in combination with Lévy flights was introduced to solve structural engineering optimization problems. It has been used in WSN applications to enhance network performance in terms of energy consumption, CH selection, lifetime, coverage, and connectivity [26,27].

4. The Proposed ECSO-OBL Algorithm

This section presents the details of the proposed method to enhance coverage and connectivity in WSNs. First, we define the network coverage model as a multi-dimensional problem, and a uni-dimensional updating mechanism is proposed to mitigate the interdependencies among the dimensions. An “opposition-based learning” optimization strategy is introduced for cluster formation and CH selection, thereby enhancing convergence speed and population diversity.

4.1. WSN Node Coverage Model

Let “N” be number of sensor nodes deployed in a two-dimensional WSN with an area of $\left(W\times L\right)$ ${\mathrm{m}}^2$. The set of sensor nodes is represented as $S=\left\{s_1,s_2,s_3, \dots \dots \dots s_N, i=1,2,3,, \dots \dots \mathrm{N}\right\}$, and the location of each sensor node is $\left(x_i,y_i\right)$. Let “L” be the number of targets in the WSN represented as a set $T=\left\{T_1,T_2,T_3,\dots \dots T_L\right\}$, and their corresponding locations are represented as another set, $\{ (x_1,y_1), \left(x_2,y_2\right), \left(x_3,y_3\right) \dots \dots \dots \dots (x_L, y_L\}$. The target location is said to be covered by a sensor node when the Euclidean distance $E_d$ between the target location and the sensor node is less than or equal to the sensing radius of that sensor node, as given in Equation (1), i.e.,

$$E_d=\sqrt{{\left(x_i-x_j\right)}^2+{\left(y_i-y_j\right)}^2}\le R_s$$

(1)

where $\left(x_i,y_i\right)$ → location coordinates of the sensor node and $\left(x_j,y_j\right)$ → location coordinates of the target. The sensing model is described as the probability that a target is covered by a sensor node, and it is described using Equation (2).

$$p\left(S_i,T_j\right)=\left\{\begin{array}{c}1, E_d\le R_s\\ 0, E_d>R_s\end{array}\right.$$

(2)

where $p\left(S_i,T_j\right)$ → the probability that target $T_j$ is covered by sensor node $S_i$. If the target is covered by multiple sensor nodes simultaneously, then the probability of coverage is defined as per Equation (3).

$$p\left(S,T_j\right)=1-{\displaystyle {\prod }_{i=1}^N}\left[1-p\left(S_i,T_j\right)\right]$$

(3)

The following assumptions are made while modeling the WSN:

(a)

The sensing area of a sensor node is a circle with radius $R_s$, and the node is located at the center.

(b)

All sensor nodes have the same processing and communication features.

(c)

The communication radius $R_c$ of each senor node is at least twice the sensing radius, i.e., $R_c\ge 2R_s$.

(d)

When the sensor nodes are in motion, they update their location coordinates on a real-time basis.

4.2. Uni-Dimensional Update Mechanism

Since the proposed optimization method is multi-dimensional, simultaneously updating the existing solutions in all the dimensions causes interference and decreases the fitness of the solution. To overcome this problem, a sequential update evaluation mechanism whereby each dimension is evaluated one by one is used, and this mitigates the effect of dependency among dimensions. Particularly, during the local search phase, this sequential update mechanism efficiently uses the exceptional information from each dimension to tune the current solution, and it leads to highly accurate solutions.

The sequential update mechanism works as follows: Let a new solution be formed when there is an update in the $i^{th}$ dimension and be combined with the solution vectors of the remaining dimensions. If the newly formed solution is of higher quality, the update in the $i^{th}$ dimension is retained; otherwise, it is discarded, and the old value of the $i^{th}$ dimension is retained. Then, the evaluation procedure continues with the ${(i+1)}^{th}$, ${\left(i+2\right)}^{th}$, etc., dimensions.

The steps involved in the ECSO-OBL algorithm are summarized as follows:

• Step 1: Define and configure the initial parameters, such as search space dimensions, number of nests, maximum number of iterations, and optimization problem dimensions.
• Step 2: In the given N-dimensional search space, generate the initial population (“S” number of nests) using Equation (4), and evaluate their individual fitness values.

  $$P=X+rand\left(N\right)\times \left(Y-X\right)$$

  (4)

In Equation (4), $X$ and $Y$ are the lower and upper bounds of search space and $P$ is the set of nests, generated randomly. The function $rand\left(N\right)$ gives an $N$-dimensional random number, where each dimension value falls between 0 and 1.

• Step 3: Update the nest positions using Lévy flight, and retain the nests with higher fitness values as per Equation (5).

  $$p_i^{a+1}=p_i^a+\Delta \otimes Levy\left(\gamma \right),\hspace{1em}\hspace{1em}where i=1,2,3,\dots \dots S$$

  (5)

  where $p_i^a$ is the position of the $i^{th}$ nest for the $t^{th}$ generation and $p_i^{a+1}$ is the position of the $i^{th}$ nest for the ${\left(t+1\right)}^{th}$ generation. $\Delta$ is the step control volume; $Levy\left(\gamma \right)\sim \mu =a^{-\gamma }$, where $\gamma$ lies between 1 and 3, represents the random search; $\mu$ is the random step size following a normal distribution; and $\otimes$ is the pointwise multiplication operator.
• Step 4: Integrate the CSO with adaptive PSO to update the nest positions using the sequential update mechanism, as shown in Equations (6) and (7), and retain the nests with higher fitness values.

  $$v_i^{t+1}=\lambda v_i^t+l_1{r}_1\left(o_i^t-p_i^t\right)+l_2{r}_2\left(g^t-p_i^t\right)$$

  (6)

  $$p_i^{t+1}=p_i^t+v_i^{t+1}$$

  (7)

  where $l_1$ and $l_2$ → learning factors (they represent the social awareness and self-awareness of an individual nest); $\lambda$ → inertia weight; and $o_i^t$ → optimal value of the $i^{th}$ nest from the $1^{st}$ to the $t^{th}$ generations. $g^t$ → optimal value among all nests in the $t^{th}$ generation; $v_i^t$ and $v_i^{t+1}$ → velocities of the $i^{th}$ nest in the $t^{th}$ and ${\left(t+1\right)}^{th}$ generations. $p_i^t$ and $p_i^{t+1}$ → positions of the $i^{th}$ nest in the $t^{th}$ and ${\left(t+1\right)}^{th}$ generations. $r_1$ and $r_2$ → random numbers $\in$ [0, 1].

The “variance” of the population is updated adaptively, and it is decreased when the algorithm starts converging. Inertia weight ($\lambda$) gives how well the speed of the current generation influences the speed of the next generation. As the algorithm continues to execute, after sufficient iterations, the population distribution starts to concentrate, and the diversity reduces. In that case, the $\lambda$ value is increased to overcome premature convergence, and it is adaptively updated as per Equation (8).

$${\lambda }_t={\lambda }_{min}+\left({\lambda }_{max}-{\lambda }_{min}\right)\times F_t$$

(8)

where ${\lambda }_t$ → inertia weight in the $t^{th}$ generation, and ${\lambda }_{min}$ and ${\lambda }_{max}$ are the minimum and maximum values of the inertia weight ($\lambda$), respectively. $F_t$ is the population diversity function in Equation (9).

$$F_t=1-{\displaystyle \frac{1}{\left(\frac{\pi }{2}\right)}}ta{n}^{-1}\left(V\right)$$

(9)

$$V={\displaystyle \frac{1}{S}}{\displaystyle {\sum }_{i=1}^S}{[h\left(p_i\right)-{\displaystyle \frac{1}{S}}{\displaystyle {\sum }_{i=1}^S}h\left(p_i\right)]}^2$$

(10)

where $V$ → variance of the fitness values of an individual nest and $h\left(p_i\right)$ → adaption value of the current $i^{th}$ nest, as mentioned in Equation (10).

• Step 5: Apply “opposition-based learning” for the best 10% possible current solutions (whose fitness values are the highest), and generate their corresponding opposite solutions by using Equation (11). Accordingly, update the current nest positions, and retain the nests with the highest fitness values.

  $${\overline{S}}_{i,j}=\rho \left(min(B_{i,j})+max(B_{i,j})\right)-s_{i,j}$$

  (11)

  where $s_{i,j}$ → search space boundary in the $j^{th}$ dimension; $\rho$ → multiplication factor in the range [0, 1]; $S_i=\left\{s_{i,1},s_{i,2}, s_{i,3}, \dots s_{i,N}\right\}$ → set of the best current solutions; and ${\overline{S}}_i=\left({\overline{s}}_{i,1},{\overline{s}}_{i,2},{\overline{s}}_{i,3}, \dots \dots \dots {\overline{s}}_{i,N}\right)$→ set of the inverse solutions.
• Step 6: The algorithm stops executing once it meets the termination condition, and it gives best possible solution as output; otherwise, it moves to step 3.

4.3. Cluster Head Selection Using ECSO-OBL Algorithm

Opposition-based learning is an effective optimization strategy that provides initial solutions with high quality and accelerates the performance of global optimization algorithms. This allows for sufficient information sharing among Cuckoo search population and enhances the balance between exploration and exploitation. The strategy considers the opposite of current solutions to expand the search space, thereby enhancing convergence speed and population diversity. The sensor nodes’ locations are considered in defining clusters by using the ECSO-OBL algorithm. In the process of CH selection, the fitness values of the sensor nodes are defined based on the Euclidean distances between sensor nodes and the available energy at each sensor node. The following fitness function to balance coverage and available energy is defined:

$$F=\min \left[{\displaystyle \frac{{{\displaystyle \sum }}_i^S{C}_{ik}}{a}}\left({\displaystyle \frac{P_i}{E_i}}\right)\right], \forall k$$

(12)

where $C_{ik}$ = 1, if Equation (1) is satisfied; otherwise, $C_{ik}$ = 0. The second term in (12) represents the energy consumption of the sensor nodes. “a” is the coverage factor, $P_i$ = initial battery power, and $E_i$ = energy consumption rate.

The sensor nodes with higher fitness values are selected as CHs, and the rest of the sensor nodes select their CH based on the distance to reach the CH and the available energy at that node. “Lévy flight” is a random walk with random steps whose durations is as per the Lévy distribution. CH selection in the WSN is achieved through the ECSO-OBL algorithm as follows:

• Initial cluster vertices are produced randomly using Levi’s flight path.
• Initially, 10% of the total sensor nodes are selected as the best CHs, and the fitness function is used to assess their quality.
• Based on the fitness function, the solutions are revised if their quality is higher than the current solution.
• With the support of Levi’s flight, the worst nests are discarded and rebuilt in a new location.
• This procedure is continued until the termination condition is satisfied, and the algorithm execution is concluded.

The above steps are repeated in iterations as shown in Figure 3, and all the nests progressively approach the optimal solutions.

We consider coverage optimization in WSNs by using an improved CSO algorithm which is defined based on the brood parasitism of cuckoo species. The steps of the ECSO-OBL algorithm are shown in Algorithm 1, where the new solutions are generated by either the probability fraction “$P_m$” of the total host nests or Lévy flight (it is a random walk model with the Lévy distribution for step length). The best solution of global search in the CSO algorithm depends mainly on mutation probability and the step size control factor. Keeping constant values for these parameters minimizes the convergence rate and localization accuracy in WSNs. Therefore, we define dynamic values for mutation probability and Lévy flight using Equations (13) and (14) to achieve the global optimal solution with high localization accuracy.

Firstly, we define the mutation probability $P_m$ as per Equation (13), which is based on the fitness of solutions to overcome the problem of local convergence and enhance population diversity. If we choose $P_m$ as too small a value, localization accuracy is reduced, and the algorithm needs a greater number of iterations to achieve optimal performance. On the other hand, if $P_m$ is too large, convergence time is higher. Therefore, it is essential to have an optimal value of mutation probability that is proportional to the objective function value.

$$P_m\left(i\right)=\left\{\begin{array}{cc}\left(P_{m_{min}}+(P_{m_{max}}-P_{m_{min}}\right) \times & \left(fitness\left(i\right)-f_{min}\right) \mathrm{if} \left(fitness\left(i\right)-f_{min}\right)<1\\ {\displaystyle \frac{{\mathrm{P}}_{{\mathrm{m}}_{\max }}}{{\mathrm{N}}_{\mathrm{i}}}},& \mathrm{otherwise}, \mathrm{where} i=1, 2, 3, \dots \dots \dots .s\hfill \end{array}\right.$$

(13)

where $f_{min}$ is the current global optimal fitness value and $fitness\left(i\right)$ is the current fitness value of ith solution. $\left(fitness\left(i\right)-f_{min}\right)$ represents the quality of the ith solution. $P_{m_{min}}$ and $P_{m_{max}}$ are the minimum and maximum values of the mutation probabilities, respectively.

Algorithm 1. The proposed ECSO-OBL algorithm

Start

For i = 1 to N            /* N → Total number of target nodes (TN)

Select each TN;

Perform AN selection;      /* AN → anchor node

Compute distance between TN and each selected AN;

Assign weights to ANs;

Define the fitness function;

Define the range of $P_m$: set $P_{m_{min}} \& P_{m_{max}}$;

Generate initial set of solutions, $S_k$, k = 1, 2, 3, ……R;

Define the range of solutions: $S_{max} \& S_{min}$;

While $(N_i<N_T)$ do        /* $N_T$ → Maximum number of iterations

For each $S_k$ do

If $(S_k<S_{min})$ then

$S_k \leftarrow S_{min}$;      Else if $(S_k>S_{max})$ then

$S_{k }\to S_{max}$;

End if;

Set $f_{min}$ as current global optimal fitness value;

Calculate $P_m$ according to Equation (13);

Generate a fraction of $P_m$ as new solutions;

Compute the objective function;

Evaluate the fitness of the objective function;

End for;

End While;

End for;

Derive the new set of best or optimal solutions;

Arrange the solutions to find the best of them;

End

Secondly, the Lévy flight-based solution is the most efficient way of exploring the search space, and new solutions are generated as per Equation (14).

$$s_i^{\left(k+1\right)}=s_i^k+\Delta .Lévy\left(\gamma \right)$$

(14)

where $Lévy\left(\gamma \right)$ is the step size and it is defined as $Lévy\left(\gamma \right)={\displaystyle \frac{x}{{\left|y\right|}^{{\gamma }^{-1}}}}$. $\gamma$ is a constant that takes values as $1<\gamma \le 3$, and $\Delta$ is the step size control factor. x and y are the normal distributions where $x~N\left(0,{\sigma }_x^2\right), y~N\left(0,{\sigma }_y^2\right)$, and the corresponding variances are given in Equation (15).

$${\sigma }_x={\left[{\displaystyle \frac{\Gamma \left(1+\gamma \right)sin\left(\frac{\pi \gamma }{2}\right)}{\Gamma \left[\frac{1+\gamma }{2}\right]\gamma 2^{\left(\gamma -1\right)/2}}}\right]}^{{\gamma }^{-1}}, {\sigma }_y=1$$

(15)

When the step size control factor $\Delta$ is low, few of the newly generated solutions shown in Equation (14) walk around the existing best solution to speed up the local search. On the other hand, when $\Delta$ is high, the new solutions walk away from the present best solution and cause the absence of global optimal solution. Therefore, it is essential to define the variable step size as shown in Equation (16).

$$\Delta ={\Delta }_{max}-{\displaystyle \frac{N_i}{N_T}} \left({\Delta }_{max}-{\Delta }_{min}\right)$$

(16)

where $N_T$ and $N_i$ are the total number of iterations and the present iteration number, respectively. ${\Delta }_{min}$ and ${\Delta }_{max}$ are the minimum and maximum step sizes, respectively. From Equation (16), the size of $\Delta$ decreases when the iteration numbers increase. During the initial iterations, the higher step sizes maximize the global search, and at a later stage, the lower step sizes intensify the local search. Overall, we can achieve global optimal solutions and a higher conversion rate with enough iterations. The time complexity of the ECSO-OBL algorithm in generating population is $O\left(N\right)$, where $N$ is the size of the population. It also requires $O\left(N\right)$ to calculate the fitness of the initially generated population. After generating the initial solutions, the computation of the fitness function and the updating of the population at each iteration need $O\left(2N\right)$. And the time complexity involved in sorting all the solutions and finding optimal solutions is $O(N^2)$. Therefore, the total time complexity of the ECSO-OBL algorithm is $O[2N+N^2+\max O(N^2)+O(2N)]$.

5. Results and Discussions

This section is dedicated to discussing the numerical results and analyzing the performance of the ECSO-OBL algorithm for sensor node deployment and their coverage. The proposed algorithm and its counterparts are implemented in MATLAB version 2024b 64-bit, and the computing device specifications are reported in

Table 2. Hardware specifications of the computer system used for conducting simulations.

Processor configuration	12th Gen Intel Core i7-12700, 2.1 GHz
Operating system	Windows 11 (Microsoft) Enterprise
System model	HP Pro Tower 400 G9 PCI
System type	x64-based PC
Physical RAM	16 GB

. The efficiency of the ECSO-OBL algorithm is validated through a performance comparison in terms of coverage rate, number of iterations, and computational time.

Table 3. Simulation parameters and values of the proposed algorithm.

Network Parameter	Values
	Case 1	Case 2	Case 3
Network terrain dimensions $\left(W\times L\right)$	50 m2	100 m2	200 m2
Network size (in terms of number of sensor nodes, N)	20	40	80
Sensing radius	6 m	8 m	10 m
Communication radius	12 m	16 m	20 m
Carrier frequency	39 GHz	39 GHz	39 GHz
Number of iterations	100	200	300
Parameters of the various algorithms and their initialization
CSO [23]	$P_a=0.25$$, {\alpha }_0=0.01$
CD-CSO [9]	$P_a=0.25$$, P_b=0.35$ ${\alpha }_0=0.01$
ACSO [15]	$P_{a MAX}=0.25$$, P_{a MIN}=0.15$ ${\alpha }_0=0.01$
PSO-CSO [10]	$P_{a MAX}=1$$, P_{a MIN}=0.3$ ${\alpha }_0=0.01$
ICS-PSO-OBL [11]	$P_{a }=0.25$$, V_{min}=-1, V_{max}=1,$${\alpha }_0=1.3$
ECSO-OBL [proposed]	$P_{a MAX}=0.25, P_{a MIN}=0.1 {\alpha }_0=0.01$

provides specific network parameters and values for the network coverage simulation experiments. The network size and dimensions are varied in various cases, as presented in Table 3, and the communication radius is set to least twice the sensing range. For the performance comparison, the initial parameters of the various algorithms and their values are also defined as shown in Table 3. Coverage area can be defined as the sum of the joint sensing probabilities of all sensor nodes in the WSN. Coverage rate is computed as the ratio of the coverage area to the total area of network terrain. The coverage ratio in the WSN is defined as the ratio of the total covered area in the ROI to the dimensions of the ROI, as given in the following equation. The maximum value of coverage ratio is defined as the objective function in the proposed algorithm, and it is given in Equation (17).

$$F_{Objective}=maxC={\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^{N}P\left(S,T_j\right)}{W\times L}}$$

(17)

where $W\times L$ is the area of the ROI and $P\left(S,T_j\right)$ → probability that the given target is covered by one or more sensor nodes.

The ECSO-OBL based optimization experiments were conducted on eight test functions, as shown in

Table 4. Benchmark functions for the current experiment.

Function	Definition	Interval
Beale	${\left(1.5-x_1+x_1{x}_2\right)}^2+{(2.25-x_1+x_1{x}_2^2)}^2+{\left(2.625-x_1+x_1{x}_2^3\right)}^2$	[−4.5 4.5]
Rosenbrock	${\displaystyle \sum _{i=1}^D}\left[100{\left(x_{i+1}-x_i^2\right)}^2+{\left(x_i-1\right)}^2\right]$	[−30 30]
Step	${\displaystyle \sum _{i=1}^D}{\left(x_i+0.5\right)}^2$	[−100 100]
Sphere	${\displaystyle \sum _{i=1}^D}{x_i}^2$	[−5.12 5.12]
Rastrigin	$10+{\displaystyle {\sum }_{i=1}^D}[{x_i}^2-10cos\left(2\pi x_i\right)]$	[−5.12 5.12]
Schwefel	${\displaystyle \sum _{i=1}^D}\left|x_i\right|+{\displaystyle \prod _{i=1}^D}\left|x_i\right|$	[−100 100]
Griewank	${\displaystyle \sum _{i=1}^D}{\displaystyle \frac{x_i^2}{4000}}-{\displaystyle \prod _{i=1}^D}cos\left({\displaystyle \frac{x_i}{\sqrt{i}}}\right)+1$	[−600 600]
Schaffer	$0.5+{\displaystyle \frac{si{n}^2\left(x_1^2-x_2^2\right)-0.5}{{\left[1+0.001\left(x_1^2+x_2^2\right)\right]}^2}}$	[−100 100]

, and it was proved that the proposed algorithm improves optimization in terms of dimensionality, stability, and convergence accuracy and speed. Figure 4 represents the sensor nodes’ random distribution before and after ECSO-OBL optimization. It is very clear that the coverage holes are eliminated to the maximum possible extent and that the redundancy in the coverage area is minimized compared with the other recent algorithms under the same test conditions.

To evaluate the feasibility of the ECSO-OBL algorithm, eight benchmark functions are selected, as shown in Table 4. Figure 5 represents the average convergence curve of the ECSO-OBL algorithm for the benchmark functions, independently optimized in 30-dimensional space, and the best function value is defined. It is observed that the convergence curve shows significant differences over the iterations and is quick at converging. The fitness function is horizontal at certain iterations, and overall, it has a ladder shape. In the existing coverage algorithms, the fitness function is not derivable under the boundary conditions, and it is difficult to find the global optimal solution. The stepwise decrease in the fitness function indicates that the ECSO-OBL algorithm fell into local optimal solution multiple times because each dimension has been updated one by one. However, the integration of the ECSO-OBL algorithm with PSO leads to the best optimal and stable results. It is observed that the adaptive mutation probability of ECSO-OBL balances its global and local search abilities. The solution space in the existing algorithms is highly complex at higher dimensions, and they take a greater number of iterations to achieve similar convergence accuracy, which indicates ineffective optimization. Therefore, the dimension-by-dimension updating mechanism in ECSO-OBL allows for the efficient updating of current optimal solution at each iteration. The integration of the ECSO-OBL algorithm with PSO significantly enhances the speed of convergence towards global optimal solutions. Also, the iterative tendency of the ECSO-OBL algorithm is better than the existing nascent coverage techniques and provides higher accuracy in the search for the global optimal solution.

Table 5. Performance comparison between the proposed ECSO-OBL algorithm and the other existing algorithms.

Metric	Algorithm	Network Dimensions
		50 m2	100 m2	200 m2
N		20	40	80
Iterations for convergence	ICS-PSO-OBL [11]	158	194	417
	CD-CSO [9]	147	181	436
	ACSO [15]	182	214	524
	PSO-CSO [10]	226	289	559
	ECSO-OBL [proposed]	112	143	314
Execution time (sec)	ICS-PSO-OBL [11]	4.14	8.25	11.3
	CD-CSO [9]	3.95	7.19	10.4
	ACSO [15]	4.15	8.49	9.48
	PSO-CSO [10]	3.83	6.41	9.16
	ECSO-OBL [proposed]	2.26	2.85	6.02
Maximum coverage rate (%)	ICS-PSO-OBL [11]	83.42	84.39	86.31
	CD-CSO [9]	84.46	91.34	92.38
	ACSO [15]	78.13	80.38	85.13
	PSO-CSO [10]	82.75	88.42	89.35
	ECSO-OBL [proposed]	96.42	98.45	96.21
Fitness values	ICS-PSO-OBL [11]	1.0109	1.0005	1.0318
	CD-CSO [9]	1.0125	1.0813	1.0159
	ACSO [15]	1.0064	1.0071	1.0048
	PSO-CSO [10]	1.0137	1.0022	1.0039
	ECSO-OBL [proposed]	2.42483	1.3989	2.57732

presents the performance results of the ECSO-OBL algorithm in comparison with the other nascent coverage algorithms in terms of iterations for convergence, coverage rate, and convergence speed. The simulations were conducted for different network sizes (in terms of number of sensor nodes) and dimensions (or for different network areas). For example, in a WSN of a size of 20 sensor nodes over an area of 50 m², shown in case 1, the coverage rate is improved by 15.58%, 14.16%, 23.41%, and 16.52% compared with the ICS-PSO-OBL, CD-CSO, ACSO, and PSO-CSO algorithms, respectively. Similarly, in case 2, we consider 40 sensor nodes over a 100 m² area, and the average and maximum coverage rates are presented in Figure 6 and Figure 7. From these results, it is proved that the coverage rate is enhanced by 16.66%, 7.78%, 22.48%, and 11.34% by the ECSO-OBL algorithm. Overall, the average coverage rate of ECSO-OBL is improved by 14.54%, 8.55%, 19.48%, 11.73% compared with the ICS-PSO-OBL, CD-CSO, ACSO, and PSO-CSO algorithms, respectively.

In a WSN given 40 sensor nodes and with the same network dimensions, Figure 8 presents the maximum time taken for the execution of various coverage algorithms compared with the proposed ECSO-OBL algorithm. It is proved that the time taken by the ECSO-OBL algorithm is improved by 65.45%, 60.36%, 66.43%, and 55.54%. The reason why ECSO-OBL has superior performance is that the algorithm converges stably in fewer iterations and achieves the global optimal solution. Figure 9 represents the total time consumption of various coverage algorithms, and they are compared with the proposed ECSO-OBL algorithm. In a network of 80 sensor nodes, the execution time of the ECSO-OBL algorithm is improved by 33.89%, 17.98%, 20.65%, and 29.12% compared with the ICS-PSO-OBL, CD-CSO, ACSO, and PSO-CSO algorithms, respectively. Similarly, with a network size of 100 nodes, the time consumption of the ECSO-OBL algorithm decreases by 58.29%, 48.78%, 51.77%, and 46.14% compared with the ICS-PSO-OBL, CD-CSO, ACSO, and PSO-CSO algorithms, respectively. This is due to the better optimal iterative tendency and search accuracy of the ECSO-OBL algorithm compared with the other CSO-based algorithms. Overall, the proposed ECSO-OBL algorithm proved that its convergence time is superior to existing nascent techniques.

6. Conclusions and Future Work

This work is mainly aimed at achieving maximum network area coverage and connectivity with strategic deployment and a minimal number of sensor nodes. An efficient node deployment strategy is introduced using the ECSO-OBL algorithm to solve the coverage optimization in WSNs. The OBL strategy is applied to have high-quality initial solutions that help to enhance the balance between exploration and exploitation. By considering the current solutions and the opposite ones to expand the search space, we achieve higher convergence speed and population diversity. A sequential update evaluation mechanism is used to mitigate the dependency among dimensions and provide highly accurate solutions, particularly during the local search phase. PSO with adaptive inertia weights is integrated with the ECSO-OBL algorithm to enhance the local search capabilities. The proposed method enhances network coverage with a non-uniform distribution of sensor nodes, has minimal redundancy in covering the network area, and attempts to cover the whole ROI with a minimal number of sensor nodes. The simulation results prove the higher efficiency of the ECSO-OBL algorithm in terms of network coverage and convergence speed in WSNs compared with the existing state-of-the-art works. The average coverage rate of the ECSO-OBL algorithm is improved by 14.54%, 8.55%, 19.48%, and 11.73% compared with the ICS-PSO-OBL, CD-CSO, ACSO, and PSO-CSO algorithms, respectively. And the execution speed of the ECSO-OBL algorithm is improved by 56.12%, 48.22%, 51.65%, and 48.98% compared with ICS-PSO-OBL, CD-CSO, ACSO, and PSO-CSO, respectively. This helps to minimize the required sensor nodes to cover the given network area and thus minimize the cost of network deployment. The proposed algorithm can be applied to integrate the node localization and optimal deployment of sensor nodes in WSNs, which will be our future work. As part of future work, the proposed algorithm will be validated through experimental tests for applications including target tracking, healthcare monitoring, and industry monitoring environments [28]. Though the current sensor node placement strategies are adaptive, there is lack of real-time self-learning capabilities. Deep learning techniques, along with neural networks [29], may address the issue of optimal coverage in WSNs. With appropriate training and test data sets, AI/ML techniques can further decrease the number of iterations necessary for achieving more accurate optimal coverage solutions on a real-time basis.