Extreme Wind Speed Prediction Based on a Typhoon Straight-Line Path Model and the Monte Carlo Simulation Method: A Case for Guangzhou

Abstract

The southeastern coastal region of China has long been affected by typhoon disasters, which pose significant threats to the safety of offshore structures. Therefore, predicting extreme wind speeds corresponding to various return periods on the basis of limited typhoon samples is particularly important for wind-resistant design. This study systematically predicts extreme typhoon wind speeds for various return periods and quantitatively assesses the sensitivity of key parameters by employing a Monte Carlo stochastic simulation framework integrated with a typhoon straight-line trajectory model and the Yan Meng wind field model. Focusing on Guangzhou (23.13° N, 113.28 °E), a representative coastal city in southeastern China, this research establishes a modular analytical framework that provides generalizable solutions for typhoon disaster assessment in coastal regions. The probabilistic wind load data generated by this framework significantly increases the cost-effectiveness and safety of wind-resistant structural design.

1. Introduction

Typhoons are highly destructive meteorological disasters whose powerful winds and complex, variable weather conditions pose severe threats to various offshore structures, including oil platforms and wind farms. In July 2023, a tower collapse accident occurred at an offshore wind farm in Fujian Province during the landfall of Super Typhoon “Doksuri”, resulting in four workers being trapped. In September 2024, multiple wind turbines at the Yulan Bay Wind Farm in Wenchang, Hainan Province, successively toppled when Typhoon Yagi passed through the area. These incidents highlight the severe challenges posed by typhoon disasters to offshore renewable energy infrastructure. Heavy rains from tropical cyclones (TCs) significantly impact coastal areas, causing severe urban flooding and transportation disruptions [1]. Extreme wind events, such as hurricanes, typhoons, pose threats to residential buildings, commercial structures, and public infrastructure, and the debris carried by the wind during these events can cause significant harm to the environment and individuals [2]. Extreme wind speed serves as a critical indicator for typhoon intensity assessment and constitutes a key environmental parameter in the design of marine structures. Estimating typhoon-induced extreme wind speeds for specific return periods on the basis of limited historical data has long been recognized as both a focal point and a persistent challenge in engineering and academic research.

The calculation results of extreme wind speeds are significantly influenced by the number of available typhoon samples. Owing to the scarcity of observation stations and frequent failures of wind measurement equipment caused by the destructive nature of typhoons, the number of valid typhoon samples remains relatively limited. To address this issue, researchers have developed parametric typhoon simulation statistical models based on the Monte Carlo method, which have been widely applied in the design of wind-resistant engineering structures. The stochastic typhoon simulation approach primarily integrates typhoon track models with typhoon wind field models. By combining specific typhoon track models with corresponding wind field models and employing random sampling techniques, this method can generate sufficient typhoon samples to obtain adequate wind speed data. Subsequently, extreme value statistical analysis is performed to determine typhoon-induced extreme wind speeds for different return periods.

Typhoon track models include mainly single-point straight-line track models and basin-wide full-track models. The single-point straight-line track model focuses on a specific target location and was initially proposed by Russell [3,4] to estimate extreme typhoon wind speeds in the Gulf of Mexico. Researchers have subsequently developed various parameterized typhoon wind field models and filling models, employing either the segmented coastline approach [4,5] or the simulated circle method [6,7,8] to estimate extreme wind speeds in different regions. Both the United States [9] and Australia [10] have adopted single-point straight-line track models for developing design wind speed maps. The basin-wide full-track model, introduced by Vickery et al. [11], can simulate the entire lifecycle of typhoons from genesis to dissipation. Current research focuses on improving aspects of the Vickery model, such as parameter selection [12,13], probability distributions [14,15], and grid partitioning [14,15]. Some scholars have also proposed new full-track models based on the Vickery framework, including the Markov chain method [16,17], statistical-deterministic approach [16], and statistical-dynamic method [18]. Additionally, Huang et al. [19] developed a simulation method based on random forest and track clustering analysis, which significantly improved the accuracy of typhoon track prediction. This method has successfully simulated design wind speeds for nine southeastern coastal cities in China and demonstrates higher computational efficiency than does the Vickery model.

Currently, commonly used parametric typhoon wind field models can be classified into two categories: gradient wind balance-based models (including the Batts wind field model [5] and the Yan Meng wind field model [20]) and momentum balance-based models (comprising the Shapiro wind field model [21] and the CE wind field model (the U.S. Army Corps of Engineers Wind Field Model) [22]) [23]. The Yan Meng wind field model features a complete analytical solution that enables direct calculation of wind speeds at specific locations. Compared with the Shapiro and CE wind field models, the proposed model has superior computational efficiency. Moreover, the Yan Meng model incorporates a more physically meaningful boundary layer model than the empirical reduction factor used in the Batts model does and has proven its reliability in computational accuracy.

This study utilizes the Northwest Pacific tropical cyclone best-track dataset from the China Meteorological Administration–Shanghai Typhoon Institute (CMA-STI) to obtain historical typhoon samples. First, the simulated circle method is applied to screen typhoon events with potential impacts on the target region, followed by probabilistic distribution fitting of key parameters (e.g., central pressure deficit, translation speed, and radius of maximum winds). Second, the Monte Carlo method is employed to generate synthetic typhoon events through random sampling of the fitted parameters, and a straight-line track model is adopted to simulate typhoon trajectories. For landfalling typhoons, an exponential decay model is introduced to characterize their postlandfall intensity evolution. The Yan Meng gradient wind model is subsequently implemented to calculate the maximum wind speed sequences induced by synthetic typhoons in the target area. Finally, the generalized extreme value distribution (GEV) is applied to fit the wind speed sequences, enabling the prediction of extreme wind speeds for specific return periods. These results are compared with code-specified design wind speeds to validate the methodology’s robustness. The overall idea of using the typhoon straight-line path model and Monte Carlo simulation method to obtain the typhoon extreme value sequence is shown in Figure 1.

Therefore, this study aims to address the lack of localized probabilistic models for typhoon-induced extreme wind speed estimation in coastal regions of China, especially under conditions of limited historical observations. Specifically, we develop a modular simulation framework that integrates a straight-line typhoon path model, a physically based wind field model, and a Monte Carlo stochastic simulation to predict extreme wind speeds corresponding to various return periods for a target location. Unlike previous studies that focused primarily on full-track models or used empirical adjustments, this research systematically analyses the sensitivity of key parameters and simulation assumptions (e.g., data selection domain and genesis point generation) to quantify their effects on wind speed prediction. By comparing the simulation results with national code-specified wind speeds, this study also investigates the conservatism of current design standards. These analyses collectively contribute to improving the reliability and applicability of typhoon hazard assessment models in data-scarce coastal regions.

2. Methodology

2.1. Data Sources and Processing

The primary data source for historical tropical cyclone records in this study is the China Meteorological Administration (CMA) Tropical Cyclone Best Track dataset (1949–2023) [24,25]. Originally published by the Chinese Central Meteorological Bureau (1983–1992), this authoritative dataset has been subsequently maintained and updated by the CMA. It provides detailed 6-hourly (with partial 3-hourly) observational records of cyclone positions and intensity parameters, including standardized storm nomenclature, intensity classification, geospatial coordinates (at 0.1° resolution), and minimum sea-level pressure (hPa) measurements at cyclone centers.

Prior to utilizing the CMA dataset, essential data rectification and processing were implemented: (1) historical wind speed records prior to 1970 were calibrated via the methodology established by Li et al. [26], which addresses systematic biases inherent in legacy anemometric instrumentation; (2) tropical cyclones classified as tropical depressions or below were systematically excluded through quantitative filtering on the basis of intensity categorical indices in the dataset.

For the virtual typhoon simulation employing the linear trajectory model, historical events impacting the target location were identified through spatial screening. While conventional approaches include the simulated circular domain method and coastal intersection technique, this study adopted the former. The procedure involves constructing a circular buffer with the target location as the centroid and a predefined radius (250 km in this investigation). All typhoon trajectories intersecting this domain were extracted as impact samples. The selection radius critically influences sample representativeness, as demonstrated through parametric experiments by Li and Hong [12,27] and Vickery et al. [28]. Following their empirical recommendations, a 250 km radius was implemented to optimize simulation fidelity.

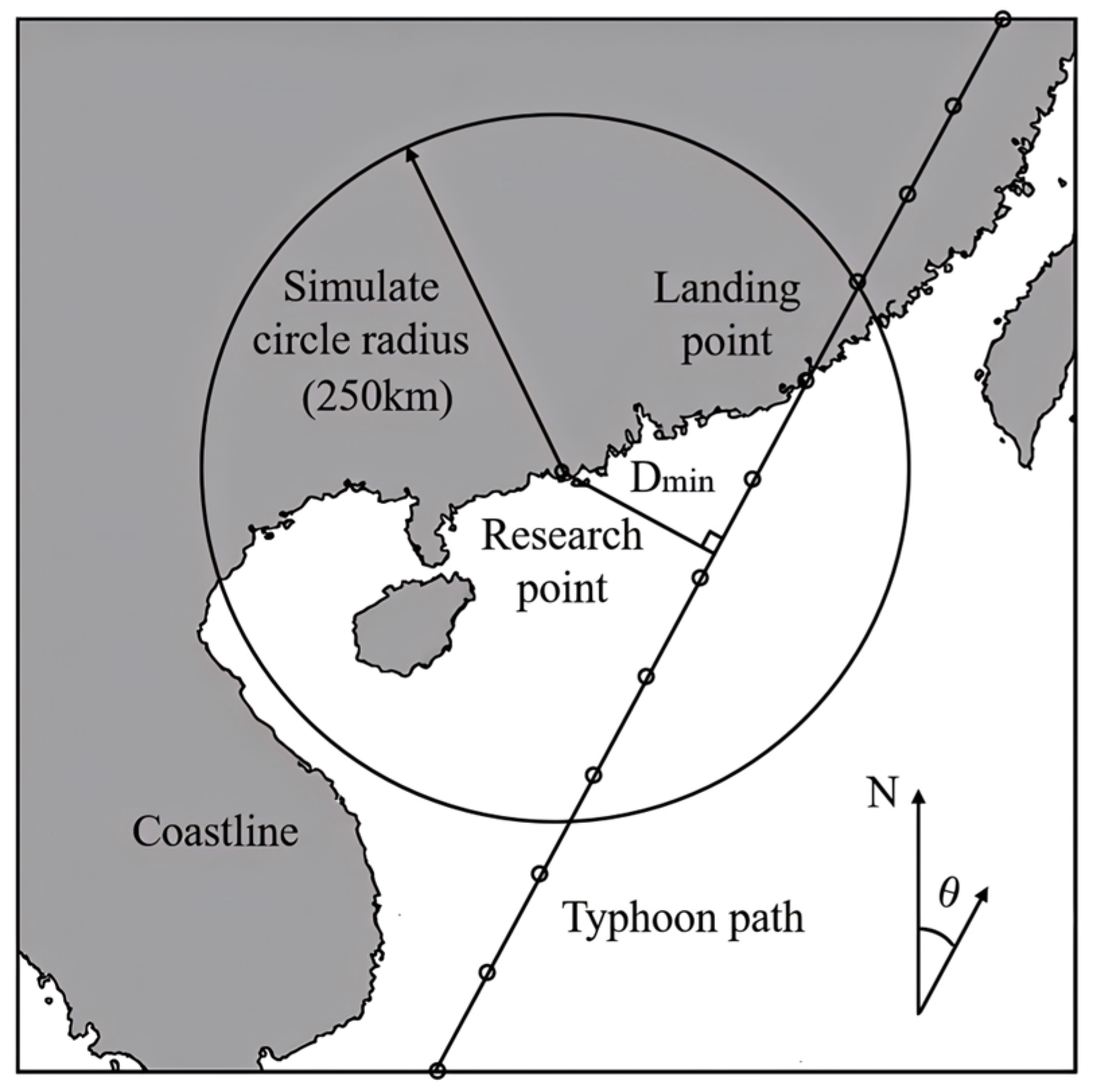
2.2. Key Parameters of Typhoons and Probability Distribution Models

When the linear trajectory model is employed for typhoon simulation, individual typhoon events are characterized by a set of key parameters: annual occurrence rate (λ), central pressure deficit (Δp), translational velocity (V_T), bearing angle (θ), and minimum approach distance (D_min). The optimal distribution for each parameter was determined through Kolmogorov–Smirnov (KS) goodness-of-fit tests at the 5% or 1% significance level. Parameters that failed statistical validation were modeled via empirical distributions.

The annual occurrence rate λ, defined as the annual frequency of typhoon impacts on the target location, is quantified by counting typhoon tracks intersecting the 250 km simulation circle. This parameter controls the annual typhoon count generated through Monte Carlo simulations. Common distributions include Poisson, binomial, and negative binomial distributions.

The central pressure deficit Δp represents the difference between the typhoon’s minimum central pressure and the ambient atmospheric pressure at the outermost closed isobar. Following the recommendations of Holland [29] for the Northwest Pacific region, the peripheral pressure is set to 1010.0 hPa. The candidate distributions include log-normal, gamma, and three-parameter Weibull distributions.

The translational velocity V_T is calculated as the ratio of the displacement distance to the time interval between consecutive records (6-hourly or 3-hourly) in the dataset. Potential distributions include log-normal, normal, and gamma distributions.

The movement direction θ, measured clockwise from true north (0°) within the range [−180°, 180°], is evaluated via normal, bimodal, and von Mises distributions.

The minimum distance D_min, defined as the perpendicular distance from the target location to the typhoon track (positive values indicate left-side passages relative to the movement direction), is modeled with uniform, trapezoidal, and linear distributions.

2.3. Monte Carlo Simulation

The Monte Carlo simulation method is a statistical computational technique that simulates probabilistic phenomena in practical problems by randomly generating system inputs, thereby enabling the estimation or prediction of expected outcomes [30]. When the Monte Carlo method is applied to simulate a specific process, the process must be decomposed into random variables describable by probability distributions. Statistical methods are then employed to estimate the numerical characteristics of the model, yielding numerical solutions to the practical problem. The procedure comprises three steps: (1) constructing or describing the probabilistic process, (2) sampling from known probability distributions, and (3) establishing estimators.

The law of large numbers and the central limit theorem in probability theory form the theoretical foundation of the Monte Carlo method. The law of large numbers describes the behavior of the sum (or average) of a large number of random variables, stating that the sample mean converges to the expected value of the function. The Central Limit Theorem asserts that, regardless of the distribution of individual random variables, the sum of a sufficiently large number of independent random variables will approximately follow a normal distribution. This theorem provides insight into the distribution of Monte Carlo estimators when the number of samples is large but finite.

On the basis of these two theorems, the fundamental principle of the Monte Carlo method can be described as follows: suppose that we are interested in a function $Y=f\left(X_1,X_2,\dots ,X_N\right)$, where the random variables $X_1,X_2,\dots ,X_N$ follow known probability distributions. The Monte Carlo method draws samples either directly or indirectly to generate values $x_{1i},x_{2i},\dots ,x_{ni}$ for each set of random variables and then computes the corresponding output $y_i=f\left(x_{1i},x_{2i},\dots ,x_{ni}\right)$. Repeating this sampling process independently for m iterations yields a set of sample outputs $y_1,y_2,\dots ,y_m$, which approximately follow a normal distribution. When the number of samples is sufficiently large, the resulting distribution of the function Y closely approximates its true probabilistic behavior.

To formalize this, one first constructs a probability space and defines a statistic g(x) that depends on the random variable x, with an expected value given by

$$E(g)={\displaystyle \int g(x)dF(x)}$$

(1)

where F(x) is the cumulative distribution function of x. Then, a simple random sample $x_1,x_2,\dots ,x_i,\dots ,x_n$ is generated from the distribution function. The arithmetic mean of the corresponding statistics $g(x_1),g(x_2),\dots ,g(x_n)$ is used to approximate the desired value G:

In general, the G_N serves as an unbiased estimator of E[g(x)].

$${\overline{G}}_N={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^{N}g\left(x_i\right)}$$

(2)

This study uses the Monte Carlo method to generate synthetic typhoons, with the workflow illustrated in Figure 2. On the basis of the prescreened typhoon sample set influencing the target study area, key parameters are extracted and fitted. The annual typhoon count is determined by sampling from the occurrence rate (λ), whereas other key parameters (e.g., θ = [−180°, 180°], D_min = [−250 km, 250 km]) are stochastically sampled, ensuring physical plausibility.

The linear trajectory model assumes uniform climatic conditions within the simulation circle. Nonlandfalling typhoons maintain constant intensity, with their initial generation points derived inversely from the movement direction (θ), minimum distance (D_min), and simulation circle radius. These initial points are predefined over the ocean. Typhoon paths are represented as straight lines discretized into sequential points along the directions θ and D_min. The typhoon intensity (central pressure deficit) remains constant during oceanic transit but decays postlandfall when a pressure deficit reduction model is used. Only data within the simulation circle are considered; typhoons exiting the circle radius are deemed dissipated. Quality control ensures that all typhoon generation points are located over the ocean.

2.4. Wind Field Model

2.4.1. Yan Meng Wind Field Model

This study employs the Yan Meng wind field model for typhoon wind field calculations. As a semiempirical numerical model, the Yan Meng wind field integrates Holland’s pressure profile with boundary layer friction-modified gradient wind balance equations, achieving computational efficiency while maintaining sufficient accuracy. It has been widely adopted in typhoon wind field simulations.

Prior to wind speed calculations, the pressure distribution model must be specified. The Yan Meng model uses the Holland pressure model [29] for atmospheric pressure distribution, which features a radial pressure profile defined in [20,31]:

$$P\left(\mathrm{r}\right)=P_c+\Delta p\exp \left(-{\left({\displaystyle \frac{R_{\max }}{r}}\right)}^B\right)$$

(3)

R_max, the radius of maximum winds, is estimated via an empirical formula derived from Vickery and Wadhera [32]:

$$\ln R_{\max }=3.859-7.700\times {10}^{-5}\Delta p^2$$

(4)

In this framework, P(r) denotes the atmospheric pressure at radial distance r from the typhoon center, P_c represents the central pressure, Δp represents the pressure difference between the typhoon center and peripheral environment (set at 1010.0 hPa in this study), R_max specifies the maximum wind radius, and B denotes the pressure profile parameter. All pressure values are measured in hPa, distances in kilometers, with B being dimensionless.

The Yan Meng model decomposes surface wind velocity vs. into vector components: gradient wind V_g induced by pressure gradients and frictional wind V_f caused by surface drag.

$$V_s=V_g+V_f$$

(5)

Gradient wind primarily manifests as a tangential component V_θg, whereas radial components are conventionally disregarded in gradient wind balance considerations.

$$V_{\theta g}={\displaystyle \frac{C_{\theta }-f_r}{2}}+{\left[{\left({\displaystyle \frac{C_{\theta }-f_r}{2}}\right)}^2+{\displaystyle \frac{r}{\rho }}{\displaystyle \frac{\partial P\left(r\right)}{\partial r}}\right]}^{{\displaystyle \frac{1}{2}}}$$

(6)

The tangential gradient wind formulation incorporates the typhoon translation speed C, angular parameters θ and β (defined in Figure 3 with counterclockwise orientation as positive), and the Coriolis parameter f, which is calculated from the Earth’s average angular velocity ω = 7.292 × 10⁻⁵ rad/s at latitude φ, and the air density ρ = 1.2 kg/m³. All velocity components are expressed in m/s with distances in meters.

Frictional wind components are determined through radial (V_rf) and tangential (V_θf) formulations that interact with surface wind velocities (V_rs, V_θs).

$$V_{\theta f}=\exp \left(-\mu z^{\prime }\right)\left[D_1\cos \left(\mu z^{\prime }\right)+D_2\sin \left(\mu z^{\prime }\right)\right]$$

(7)

$$V_{rf}=-\tau \exp \left(-\mu z^{\prime }\right)\left[D_2\cos \left(\mu z^{\prime }\right)-D_1\sin \left(\mu z^{\prime }\right)\right]$$

(8)

$$\tau ={\left({\displaystyle \frac{\alpha }{\beta }}\right)}^{{\displaystyle \frac{1}{2}}}$$

(9)

$$\mu ={\displaystyle \frac{{\left(\alpha \beta \right)}^{\frac{1}{4}}}{{\left(2K_m\right)}^{\frac{1}{2}}}}$$

(10)

$$\alpha ={\displaystyle \frac{\partial V_{\theta g}}{\partial r}}+{\displaystyle \frac{V_{\theta g}}{r}}+f$$

(11)

$$\beta ={\displaystyle \frac{2V_{\theta g}}{r}}+f$$

(12)

$$D_1=-{\displaystyle \frac{\gamma \left(\gamma +1\right)V_{\theta g}}{1+{\left(\gamma +1\right)}^2}}$$

(13)

$$D_2={\displaystyle \frac{\gamma V_{\theta g}}{1+{\left(\gamma +1\right)}^2}}$$

(14)

$$\gamma ={\displaystyle \frac{C_d\sqrt{{V_{\theta s}}^2+{V_{rs}}^2}}{K_m\mu }}$$

(15)

$$C_d={\displaystyle \frac{K^2}{\ln {\left(\frac{Z_{10}+h-d}{Z_0}\right)}^2}}$$

(16)

$$d=0.75h$$

(17)

$$h=11.4{Z_0}^{0.86}$$

(18)

The key parameters include the equivalent roughness height Z₀, roughness element height h, zero-plane displacement d, reference height Z₁₀ (10 m above the roughness elements), coordinate systems Z and Z’ (detailed in Figure 3 vertical profile), von Kármán constant K = 0.4, eddy viscosity K_m = 100 m²/s, and drag coefficient C_d. All height parameters are measured in meters.

Equation (16) reveals the interdependence between frictional wind velocity and surface wind velocity, necessitating iterative computation. As illustrated in Figure 4, the calculation process begins with the gradient wind velocity as the initial surface wind estimate, which progressively converges through successive iterations.

2.4.2. Filling Model

Typhoon intensity evolves temporally and is primarily sustained by energy derived from warm ocean surfaces. Postlandfall, the system experiences energy depletion due to severe thermal supply and surface friction effects, leading to progressive weakening characterized by central pressure recovery. To quantify this decay process, the Vickery and Twisdale [33] filling model is implemented:

$$\Delta p\left(t\right)=\Delta p_0\exp \left(-at\right)$$

(19)

$$a=a_0+a_1\Delta p_0+\epsilon$$

(20)

where the central pressure deficit Δp(t) at time t after landfall is expressed as a function of the initial deficit Δp₀, calibration coefficient a, and stochastic term ε conforming to a standard normal distribution with standard deviation σ_ε.

2.5. Numerical Simulation of Extreme Wind Speed

Extreme wind speed modeling follows established methodologies in typhoon engineering. Extreme wind speed sequences are typically modeled via extreme value distributions, primarily the Gumbel (Type I), Fréchet (Type II), and Weibull (Type III) distributions. Batts, Simiu and Russell [5] and Georgiou [34] employed the Weibull distribution to fit typhoon-induced extreme wind speed data. In contrast, Simiu and Filliben [35] and Simiu et al. [36] demonstrated a preference for the Gumbel distribution. Simiu and Miyata [37] further emphasized the applicability of empirical distributions when sufficient typhoon samples are available.

In this study, both Weibull and Gumbel distributions are applied to model extreme wind speeds. The Kolmogorov–Smirnov (KS) goodness-of-fit test is implemented at a 5% significance level to identify the optimal theoretical distribution on the basis of p values. If neither distribution satisfies the statistical criteria, empirical distributions are adopted for fitting.

The probability that a typhoon-induced maximum wind speed exceeds a predefined threshold v_i within a specified time interval t is defined as

$$P\left(V<v_i,t\right)={\displaystyle \sum _{n=0}^{\infty }P\left(V<v_i|n\right)p\left(n,t\right)}$$

(21)

$$P\left(V<v_i|n\right)=\left[F{\left(v_i\right)}^n\right],p\left(n,t\right)={\displaystyle \frac{{\left(\lambda t\right)}^n}{n!}}{e}^{-\lambda t}$$

(22)

where $P\left(V<v_i|n\right)$ is the probability that the maximum wind speed V exceeds threshold v_i given n typhoon events; F(v_i) is the nonexceedance probability of the wind speed v_i, modeled by an extreme value distribution; p(n,t) is the probability of experiencing n typhoons at the target location within t years; and λ is the parameter of the Poisson distribution governing typhoon frequency.

For t = 1 year, the annual nonexceedance probability is derived as

$$P\left(V<{\mathrm{v}}_i,1\right)=\exp \left[-\lambda \left(1-F_{vi}\right)\right]$$

(23)

where F(v_i) represents the cumulative distribution function of the validated extreme value model. The return period T for the wind speed v_i is then expressed as

$$1-{\displaystyle \frac{1}{T}}=P\left(V<v_i,1\right)=\exp \left[-\lambda \left(1-F_{vi}\right)\right]$$

(24)

Using the empirical distribution function (EDF) from simulated extreme wind speed sequences, the probability of any typhoon wind speed V being less than vi is quantified as

$$F_{vi}=\left({\displaystyle \frac{i}{N+1}}\right)$$

(25)

where N denotes the total sample size.

3. Results and Discussion

The southeastern coastal regions of China have been chronically affected by severe typhoon disasters. This study focuses on Guangzhou (latitude 23.13° N, longitude 113.28° E), a representative metropolis in the region, as the primary case study. Situated at the geographic nexus of the Pearl River Delta, Guangzhou exemplifies the vulnerability of coastal urban centers to typhoon-induced hazards.

3.1. Fitting and Testing of the Key Parameters

This study employs the Kolmogorov–Smirnov (KS) test to identify optimal probability distributions for key typhoon parameters. The hypothesis tests are conducted at the 5% or 1% significance level. If neither level yields statistical significance, empirical distributions are adopted, ultimately establishing optimal probabilistic models for typhoon parameters in Guangzhou. Since the negative binomial distribution is suitable for overdispersed data (variance > mean), it is not applicable to the historical typhoon data characteristics of Guangzhou; therefore, this distribution is not considered. The goodness-of-fit test results for Guangzhou’s typhoon parameters are summarized in

Table 1. Goodness-of-fit test for the typhoon key parameters and the optimal probability distributions at Guangzhou.

Key Parameters	Alternative Probability Distribution	p-Value	Test Statistic	Critical Value (5%)	Critical Value (1%)	Optimal Probability Distribution	Distribution Parameters
λ	Poisson	0.9516	0.0182	0.1568	0.1880	Poisson	λ = 2.52
	Binomial	0.9098	0.0251
Δp	Lognorm	~0	0.0459	0.0255	0.0306	Empirical	-
	Gamma	~0	0.0662
	Weibull	~0	0.0946
VT	Lognorm	~0	0.0530	0.0255	0.0306	Gamma	k = 3.988 θ = 4.477
	Gamma	0.1193	0.0194
	Normal	~0	0.0708
θ	Normal	~0	0.1623	0.0255	0.0306	Empirical	-
	von Mises	~0	0.0922
	BimodalVM	~0	0.0436
Dmin	Uniform	~0	0.0860	0.0255	0.0306	General linear	c = 2.527 d = 1.451
	Trapezoid	~0	0.0644
	General linear	0.1391	0.0187

, while statistical models comparing the simulated and observed key parameters are illustrated in Figure 5.

Parameter distribution selection follows rigorous statistical validation. The annual occurrence rate (λ) is estimated from 75 samples, whereas the other four key parameters are derived from 2834 samples. As shown in the table, the optimal distributions are identified as follows: the Poisson distribution for the annual occurrence rate, the gamma distribution for the translational velocity (V_T), and the generalized linear distribution for the minimum distance (D_min). The central pressure deficit (Δp) and movement direction (θ) were not statistically validated; thus, empirical distributions were employed for these parameters.

3.2. Filling Model Fitting and Verification

Using historical landfall typhoon observations, the filling model for Guangzhou typhoons was calibrated by excluding rapidly transiting and short-duration landfall events (typhoons with fewer than three valid observation points over land), resulting in 58 qualified typhoon samples. The normality test for the error term ε yielded a p value of 0.1283, indicating statistical validity. Representative typhoon samples were selected to plot their central pressure deficit (Δp) exponential decay curves, as shown in Figure 6, which demonstrated satisfactory goodness-of-fit for the exponential model. Figure 7 shows the linear regression between the decay constant (a) and initial central pressure deficit (Δp₀) at landfall, with the observed data points evenly distributed around the regression line, confirming the effectiveness of the regression analysis. The final coefficients of Guangzhou’s filling model are presented in

Table 2. Final coefficients of Guangzhou’s filling model.

City	a0	a1	σε
Guangzhou	0.008277	0.001085	0.022545

.

3.3. Estimation and Verification of Extreme Wind Speed

GB50009 [38] (Chinese National Standard: Load Code for Building Structures) specified design wind pressures for Guangzhou corresponding to different return periods, along with conversion formulae for reference wind pressures:

$$X_T=X_{10}+\left(X_{100}-X_{10}\right)\left({\displaystyle \frac{\ln T}{\ln 10}}-1\right)$$

(26)

where X_T is the reference wind pressure (kN/m²) for return period T (years) and X₁₀ is the reference wind pressure for the 10-year return period.

The basic wind speed v₀ (m/s) is derived from the reference wind pressure ω₀ (kN/m²) via

$$v_0=\sqrt{2{\omega }_0/\rho }$$

(27)

where the air density ρ (kg/m³) is calculated as $\rho =1.25e^{-0.001Z}$, with Z being Guangzhou’s altitude (m above sea level).

The designed wind pressures and corresponding wind speeds for Guangzhou under different return periods are summarized in

Table 3. The design wind pressures and speeds given by the code for Guangzhou.

Return Period (Year)	10	30	50	100	200
Basic wind pressure (kN/m2)	0.30	0.44	0.50	0.60	0.70
Basic wind speed (m/s)	21.94	26.62	28.37	31.08	33.40

.

There is currently no universally accepted formula for the determination of parameter B in China. When a fixed value for B is used, as long as the value is within a reasonable range, the simulated wind speeds can align well with the observed data. According to Xie [39], in the context of the Yan Meng wind field model, a fixed B value of approximately 0.9 yields wind speed simulations that closely match observations. Therefore, in this study, a constant B value is adopted following this recommendation.

The parameter Z₀ is assigned a fixed value on the basis of the terrain characteristics of the target location, representing its surface roughness. In general, Z₀ is smaller in flat and open areas and larger in densely built-up regions. According to previous studies [40,41], for urban areas with dense building clusters, a Z₀ value between 1.0 and 2.0 is recommended, whereas in cities with denser and taller buildings, a range of 2.0–4.0 is suggested. Considering that Guangzhou is a densely built-up city, Z₀ is set as a fixed value of 2.0 in this study.

The code specifies 10 min mean wind speeds at a height of 10 m. To enable comparative analysis with code specifications, this section calculates extreme wind speeds under identical conditions. As the Yan Meng model outputs hourly interval typhoon wind speeds, a conversion factor of 1.06 is applied to transform these values into equivalent 10 min averages [12,27,42].

During the generation of synthetic typhoons, the annual occurrence rate can be zero (i.e., no typhoon in a given year, approximately 10% of cases), and including these zeros directly in extreme-value fitting would severely bias the parameter estimates. Therefore, we fit the Weibull or Gumbel distribution only to the nonzero annual maximum wind speeds. When estimating return-level wind speeds, we then employ a dual strategy that combines a zero-inflated parametric approach with an empirical distribution method. On the one hand, if the probability corresponding to the target return period falls within the “no-typhoon” range, the return level is set to zero; otherwise, the remaining nonzero probability is rescaled and inverted through the fitted extreme-value distribution. On the other hand, we sort the full sample, including zeros, and directly select the ordered observation at the corresponding percentile as the empirical return level. This approach ensures that zero-occurrence years are properly accounted for while enabling cross-validation of the parametric model against the data-driven empirical estimates.

The extreme wind speeds for Guangzhou across different return periods, as predicted via empirical, Weibull, and Gumbel distributions, are summarized in

Table 4. Predicted average wind speeds as a function of the return period for Guangzhou.

Return Period (Year)	10	30	50	100	200
Weibull (m/s)	18.02	21.15	22.39	23.92	25.32
Gumbel (m/s)	17.32	21.50	23.40	25.96	28.52
Empirical (m/s)	18.28	22.30	23.62	26.57	27.95

. The Kolmogorov–Smirnov (KS) test results are presented in

Table 5. KS test results of extreme value distributions for Guangzhou.

Probability Distribution	p Value	Test Statistic	Critical Value (5%)	Critical Value (1%)
Weibull	0.0005	0.0676	0.0454	0.0544
Gumbel	0.0624	0.0437

and Figure 8. Only the Gumbel distribution was statistically validated through the Kolmogorov–Smirnov (KS) test, confirming its superior applicability for extreme wind speed modeling in Guangzhou. Notably, the wind speed estimates derived from all three distributions (empirical, Weibull, and Gumbel) across various return periods were consistently lower than the code-specified values, revealing the conservative nature of current regulatory standards in structural wind load design.

Notably, similar findings have been reported in other regions, suggesting that the conservative nature of design wind speeds may be a common feature in international standards. For example, postevent investigations by Ginger and Holmes [42] in Australia revealed that the maximum wind speeds observed during cyclones Yasi, Debbie, and Seroja were typically between 80% and 90% of the design wind speeds specified in AS/NZS 1170.2 [10]; however, structural damage was generally limited to construction deficiencies rather than wind speeds exceeding design levels. In India, Li and Suresh Kumar [43] reported that, for cities along the eastern coastline, estimated 50-year return period cyclone wind speeds were significantly lower than those prescribed by the national code. Similarly, in China, Huang, Wang, Li, Jing, Lin and Wang [17] reported that the wind speeds estimated for several southern coastal cities were lower than the current code recommendations, likely because of the influence of a mixed wind climate in the historical data used to define the design values.

These observations suggest that the conservatism embedded in wind design codes may reflect a deliberate safety margin rather than unnecessary overdesign. Given the inherent uncertainties associated with tropical cyclone modeling, data limitations, and potential future climate change, such conservatism can be viewed as a necessary measure to ensure structural safety under rare or extreme conditions not fully represented in historical records. Nonetheless, in certain cases, it may also lead to conservative design outcomes, with implications for construction costs. Therefore, while the model results indicate that current code-specific wind speeds are higher than simulation-based predictions are, this conservatism likely serves as a practical safety buffer to account for unquantified risks.

3.4. Sensitivity Analysis

3.4.1. Selection of Simulated Circular Data

Following the screening of historical typhoon samples impacting the target location via the simulated circular domain method, it is essential to extract and fit key parameters from the dataset. This process involves selective data inclusion from both inside and outside the simulated circular domain, requiring explicit consideration of their respective influences. While previous analyses utilized entire typhoon trajectory data, this section focuses exclusively on data within the simulated circular domain for comparative validation.

Furthermore, reduced sample sizes facilitated improved parametric distribution fitting for key typhoon parameters. Notably, parameters previously requiring empirical distributions (central pressure deficit and movement direction) achieved optimal representations through lognormal (lognormal) and bimodal von Mises (bimodalVM) distributions.

Table 6. Predicted average wind speeds as a function of the return period for Guangzhou (with simulated circle-only data).

Return Period (Year)	10	30	50	100	200
Weibull (m/s)	18.44	21.87	23.24	24.94	26.51
Gumbel (m/s)	17.03	20.98	22.78	25.21	27.62
Empirical(m/s)	18.25	22.30	23.94	25.05	29.76

presents extreme wind speed predictions for Guangzhou across various return periods via empirical, Weibull, and Gumbel distributions (with simulated circle-only data), and the corresponding Kolmogorov–Smirnov (KS) test results are summarized in

Table 7. KS test results of extreme value distributions for Guangzhou (with simulated circle-only data).

Probability Distribution	p Value	Test Statistic	Critical Value (5%)	Critical Value (1%)
Weibull	~0	0.1002	0.0444	0.0532
Gumbel	0.0665	0.0424

.

For Guangzhou, only the Gumbel distribution demonstrated statistical validation, confirming its superior applicability in this region. When exclusively considering simulated circle data, Gumbel-based return period wind speeds presented systematically lower estimates than did the full-trajectory results did, whereas the empirical and Weibull distributions yielded higher predictions.

The improvement in the statistical fitting of the central pressure deficit (Δp) and movement direction (θ) when only the simulated circle data are used can be attributed to two main factors. First, restricting the dataset to typhoon records within the simulation circle reduces sample heterogeneity. The retained samples are more directly relevant to the target location, excluding typhoon records from earlier or later stages of storm development, which often exhibit different characteristics. This reduction in data variability improves the internal consistency of the dataset and facilitates more reliable parameter fitting. Second, the restricted dataset naturally constrains the range of Δp and θ, as it excludes observations from distant segments of the typhoon trajectory. By focusing only on typhoons actively affecting the target area, extreme or atypical parameter values are filtered out, which helps improve the fit of standard probability distributions, such as lognormal and bimodal von Mises distributions. In summary, localized data filtering not only reduces heterogeneity but also limits parameter variability, collectively improving the statistical representation of key typhoon parameters. This result highlights that selective spatial data inclusion can be an effective strategy for enhancing parameter distribution fitting in typhoon hazard modeling.

3.4.2. Monte Carlo Sampling Starting Point Generation Logic

The genesis points of synthetic typhoons are primarily determined by movement direction (θ) and minimum distance (D_min), with their intersection with the simulation circle assumed to be the initial position, which must be located over the ocean. During Monte Carlo sampling of key parameters for typhoon generation, the independent sampling of θ and D_min—combined with the simulation circle radius constraint—may yield genesis points over land. The previous methodology discarded such cases through immediate resampling, but this approach risked permanently excluding typhoons with specific directional-distance combinations, contradicting observational reality. To address this, the genesis point generation logic is refined as follows: (1) Extend the simulation circle radius to 500 km; (2) check for viable oceanic genesis points along the extended trajectory; and (3) if no valid points exist within 500 km, trigger parameter resampling.

Table 8. Predicted average wind speeds as a function of the return period for Guangzhou (with the new starting point generation logic).

Return Period (Year)	10	30	50	100	200
Weibull (m/s)	17.66	20.92	22.23	23.84	25.32
Gumbel (m/s)	16.71	20.78	22.64	25.14	27.64
Empirical(m/s)	17.65	21.96	24.00	27.16	28.63

presents extreme wind speed predictions for Guangzhou across various return periods via empirical, Weibull, and Gumbel distributions (with the new starting point generation logic), and the corresponding Kolmogorov–Smirnov (KS) test results are summarized in

Table 9. KS test results of extreme value distributions for Guangzhou (with the new starting point generation logic).

Probability Distribution	p Value	Test Statistic	Critical Value (5%)	Critical Value (1%)
Weibull	~0	0.0843	0.0449	0.0538
Gumbel	0.0652	0.0430

.

Refinement of the genesis point generation logic addressed the unrealistic exclusion of certain typhoon scenarios in the original approach. Extending the permissible search radius for oceanic genesis points (up to 500 km) allowed for more diverse directional-distance combinations, improving the representativeness of synthetic typhoon origins without introducing spatial bias. While changes in return period wind speeds were not substantial, the method provides a physically more realistic mechanism for parameter sampling and genesis point determination, which contributes to the credibility of the simulation framework.

4. Conclusions

This study developed a Monte Carlo simulation framework that integrates a typhoon straight-line trajectory model and the Yan Meng wind field model to predict extreme wind speeds across various return periods, with Guangzhou as a representative case. Comprehensive sensitivity analyses were conducted on spatial data inclusion criteria (simulated circle interior vs. exterior) and genesis point determination protocols.

A probabilistic model for key typhoon parameters in Guangzhou was established, generating synthetic typhoon events spanning 1000 years. The results demonstrated the superior applicability of the Gumbel distribution for extreme wind speed modeling in this region while highlighting critical dependencies on spatial data selection and genesis logic. The proposed methodology forms a generalizable framework for typhoon hazard analysis in other coastal regions, providing substantial implications for typhoon disaster mitigation and enhancing structural safety assessments of typhoon hazards.

The developed framework can serve as a practical tool for local authorities, disaster management agencies, engineering firms, and infrastructure planners, supporting wind hazard assessment and resilient infrastructure design in typhoon-prone coastal regions. Specifically, the predicted extreme wind speeds corresponding to various return periods can assist in refining the design of wind load specifications for critical structures, including offshore wind farms, transmission towers, bridges, and coastal ports. In addition, the model’s modular structure allows for regional customization by adjusting input datasets and boundary conditions, offering a data-driven reference for local governments and standardization bodies seeking to update wind load codes on the basis of probabilistic hazard assessment.

Owing to the selected models and methodologies, this study has certain limitations.

(1) The straight-line typhoon path model employed in this research assumes climatic homogeneity within the simulation circle. As a result, it is only suitable for typhoon hazard analysis over relatively small regions. Its applicability becomes problematic when extended to larger spatial scales. Moreover, this model heavily relies on historical typhoon data, which are often sparse or unavailable in high-latitude areas, thereby limiting the reliability of analyses in those regions. (2) For the sake of computational simplification, the Monte Carlo simulations in this study generate each synthetic typhoon by sampling the key parameters only once. This approach differs from the actual evolution of real typhoons, in which key parameters may change continuously along the path.

In future work, we plan to incorporate the inherent stochasticity of the typhoon development process by statistically analyzing the temporal variation in each key parameter and embedding such dynamics into the simulation framework. Additionally, geographical features—such as topography—will also be integrated into the model, enabling a more comprehensive evaluation of their impact on typhoon behavior.

Moreover, uncertainty quantification was not performed in this study, as confidence intervals for the predicted extreme wind speeds were not provided. This limits the ability to assess the significance of differences between scenarios. In future research, uncertainty analysis methods, such as bootstrapping or Bayesian inference, will be incorporated to establish confidence intervals, improving the robustness of scenario comparisons.