The Influence of Hard Protection Structures on Shoreline Evolution in Riohacha, Colombia
Abstract
1. Introduction
2. Study Area and Geographical Data
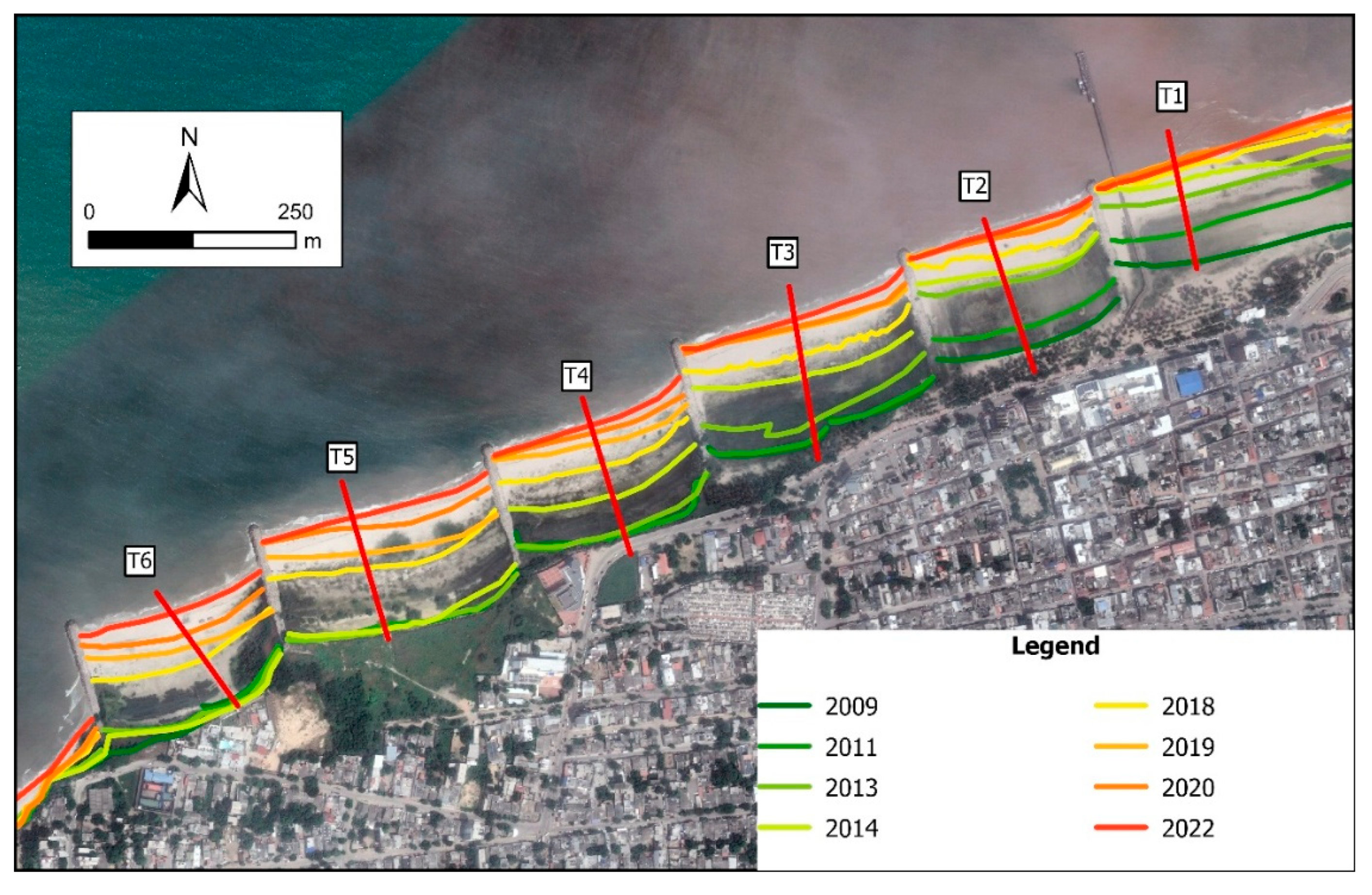
- Zone 1 (1450 m) extends from the river mouth to groin 6, encompassing the groin field and featuring well-developed beaches.
- Zone 2 (1900 m) stretches from groin 6 to the Nuevo Faro neighborhood. This section includes a small cliff (~6.5 m high) with narrow beaches at its base.
- Zone 3 (1600 m) runs from a coastal rocky outcrop to Las Delicias. Here, the cliffs are slightly higher (~9.1 m) with no beach at the base, except in the southern area.
3. Methodology
4. Results and Discussion
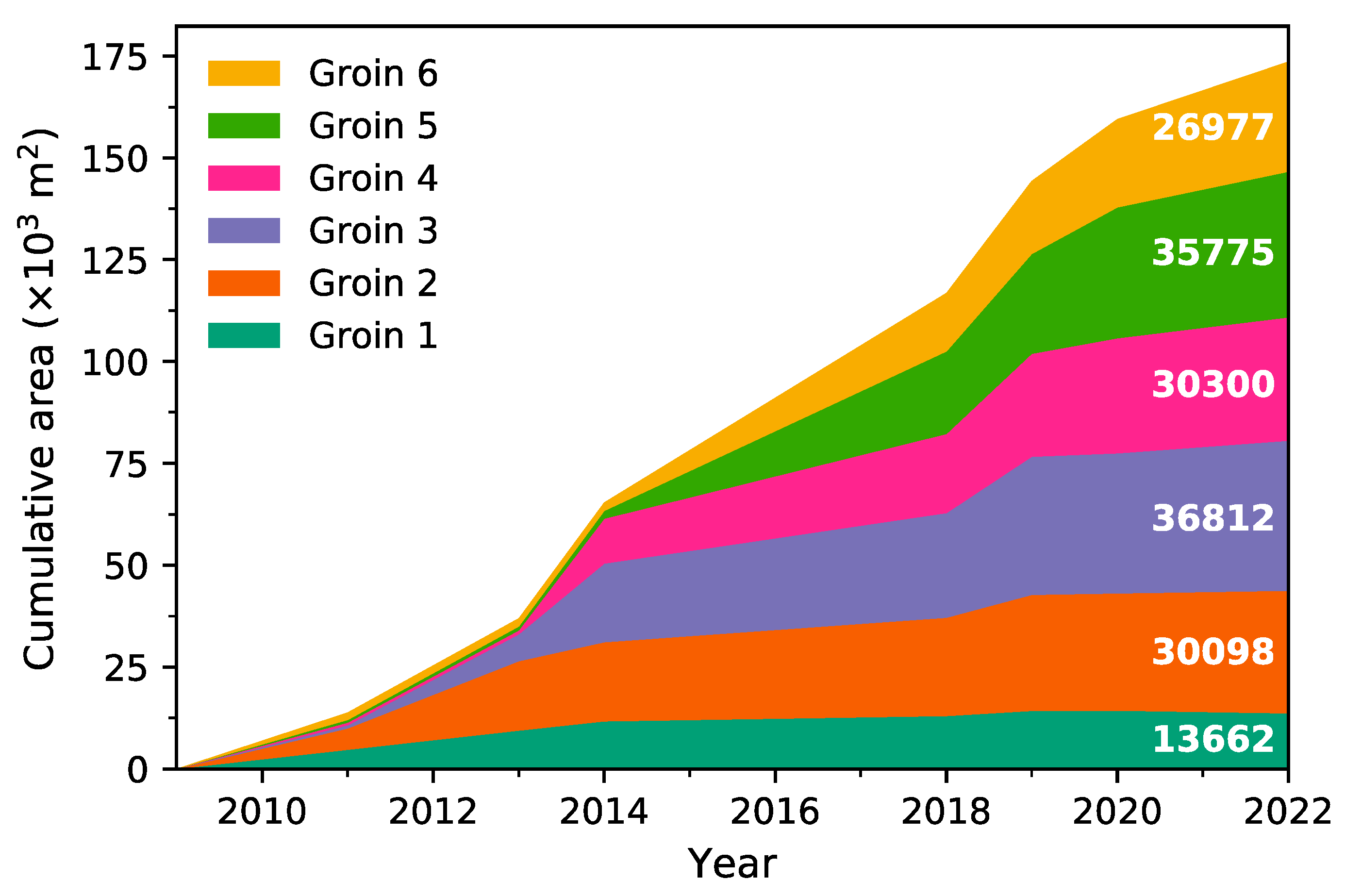
4.1. Zone 1: Effect of the Groins
4.2. Zone 2: Urban Cliff Area with Seawall
4.3. Zone 3: Cliff Area
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vallarino Castillo, R.; Negro Valdecantos, V.; del Campo, J.M. Understanding the Impact of Hydrodynamics on Coastal Erosion in Latin America: A Systematic Review. Front. Environ. Sci. 2023, 11, 1267402. [Google Scholar] [CrossRef]
- Velsamy, S.; Balasubramaniyan, G.; Swaminathan, B.; Kesavan, D. Multi-Decadal Shoreline Change Analysis in Coast of Thiruchendur Taluk, Thoothukudi District, Tamil Nadu, India, Using Remote Sensing and DSAS Techniques. Arab. J. Geosci. 2020, 13, 838. [Google Scholar] [CrossRef]
- Pagán, J.I.; Aragonés, L.; Tenza-Abril, A.J.; Pallarés, P. The Influence of Anthropic Actions on the Evolution of an Urban Beach: Case Study of Marineta Cassiana Beach, Spain. Sci. Total Environ. 2016, 559, 242–255. [Google Scholar] [CrossRef] [PubMed]
- Unguendoli, S.; Biolchi, L.G.; Aguzzi, M.; Pillai, U.P.A.; Alessandri, J.; Valentini, A. A Modeling Application of Integrated Nature Based Solutions (NBS) for Coastal Erosion and Flooding Mitigation in the Emilia-Romagna Coastline (Northeast Italy). Sci. Total Environ. 2023, 867, 161357. [Google Scholar] [CrossRef] [PubMed]
- Alves, B.; Angnuureng, D.B.; Morand, P.; Almar, R. A Review on Coastal Erosion and Flooding Risks and Best Management Practices in West Africa: What Has Been Done and Should Be Done. J. Coast. Conserv. 2020, 24, 38. [Google Scholar] [CrossRef]
- Arabadzhyan, A.; Figini, P.; García, C.; González, M.M.; Lam-González, Y.E.; León, C.J. Climate Change, Coastal Tourism, and Impact Chains–a Literature Review. Curr. Issues Tour. 2021, 24, 2233–2268. [Google Scholar] [CrossRef]
- Natarajan, L.; Sivagnanam, N.; Usha, T.; Chokkalingam, L.; Sundar, S.; Gowrappan, M.; Roy, P.D. Shoreline Changes over Last Five Decades and Predictions for 2030 and 2040: A Case Study from Cuddalore, Southeast Coast of India. Earth Sci. Inform. 2021, 14, 1315–1325. [Google Scholar] [CrossRef]
- Ayyam, V.; Palanivel, S.; Chandrakasan, S. Coastal Ecosystems of the Tropics-Adaptive Management; Springer: Singapore, 2019. [Google Scholar]
- Calil, J.; Reguero, B.G.; Zamora, A.R.; Losada, I.J.; Méndez, F.J. Comparative Coastal Risk Index (CCRI): A Multidisciplinary Risk Index for Latin America and the Caribbean. PLoS ONE 2017, 12, e0187011. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Jiménez, C.; Moreno, N.; Wang, P. Tsunami Characteristics and Source Estimation of the 2024 Yauca (Peru) Earthquake. Ocean. Eng. 2025, 331, 121325. [Google Scholar] [CrossRef]
- Silva, R.; Martínez, M.L.; Hesp, P.A.; Catalan, P.; Osorio, A.F.; Martell, R.; Fossati, M.; Da Silva, G.M.; Mariño-Tapia, I.; Pereira, P.; et al. Present and Future Challenges of Coastal Erosion in Latin America. J. Coast. Res. 2014, 11, 1–16. [Google Scholar] [CrossRef]
- Rangel-Buitrago, N.; Gracia, C.A. From the Closet to the Shore: Fashion Waste Pollution on Colombian Central Caribbean Beaches. Mar. Pollut. Bull. 2024, 199, 115976. [Google Scholar] [CrossRef] [PubMed]
- Salazar, F.J.; Ramirez, H.M. Evaluation of Coastal Erosion in the Jurisdiction of the Municipalities of Puerto Colombia and Tubara, Atlantico, Colombia in Google Earth Engine with Landsat and Sentinel 2 Images. Int. J. Geol. Environ. Eng. 2023, 17, 128–146. [Google Scholar]
- Botero, C.; Anfuso, G.; Rangel-Buitrago, N.; Correa, I.D. Coastal Erosion Monitoring in Colombia: Overview and Study Cases on Caribbean and Pacific Coasts; Universidad de Cádiz: Cádiz, Spain, 2013. [Google Scholar]
- Martínez-Pérez, E.J.; Arévalo-Quintero, J.S. Estudio y Plan de Control de La Erosión Costera Mediante Estructuras de Protección Costera En Una Playa de La Ciudad de Riohacha, La Guajira; Universidad Católica De Colombia: Bogota, Colombia, 2022. [Google Scholar]
- Rangel-Buitrago, N.G.; Anfuso, G.; Williams, A.T. Coastal Erosion along the Caribbean Coast of Colombia: Magnitudes, Causes and Management. Ocean. Coast. Manag. 2015, 114, 129–144. [Google Scholar] [CrossRef]
- Alvarez-Cuesta, M.; Toimil, A.; Losada, I.J. Modelling Long-Term Shoreline Evolution in Highly Anthropized Coastal Areas. Part 1: Model Description and Validation. Coast. Eng. 2021, 169, 103960. [Google Scholar] [CrossRef]
- Apostolopoulos, D.; Nikolakopoulos, K. A Review and Meta-Analysis of Remote Sensing Data, GIS Methods, Materials and Indices Used for Monitoring the Coastline Evolution over the Last Twenty Years. Eur. J. Remote Sens. 2021, 54, 240–265. [Google Scholar] [CrossRef]
- Crowell, M.; Leatherman, S.P.; Buckley, M.K. Shoreline Change Rate Analysis: Long Term Versus Short Term Data. Shore Beach 1993, 61, 13–20. [Google Scholar]
- Castedo, R.; de la Vega-Panizo, R.; Fernández-Hernández, M.; Paredes, C. Measurement of Historical Cliff-Top Changes and Estimation of Future Trends Using GIS Data between Bridlington and Hornsea–Holderness Coast (UK). Geomorphology 2015, 230, 146–160. [Google Scholar] [CrossRef]
- Ponte Lira, C.; Taborda, R.; Silva, A.N.; Andrade, C. Challenges and New Strategies in Assessing Multidecadal Shore Platform Sandy Beach Evolution from Aerial Imagery. Mar. Geol. 2021, 436, 106472. [Google Scholar] [CrossRef]
- Leisner, M.M.; de Paula, D.P.; Alves, D.C.L.; da Guia Albuquerque, M.; de Holanda Bastos, F.; Vasconcelos, Y.G. Long-Term and Short-Term Analysis of Shoreline Change and Cliff Retreat on Brazilian Equatorial Coast. Earth Surf. Process Landf. 2023, 48, 2987–3002. [Google Scholar] [CrossRef]
- Yadav, A.; Kuntoji, G.; Hiremath, C.G.; Narasimha, N.H.; Mutagi, S. Automatic Detection and Analysis of the Shoreline Change Rate at Maravanthe Coast, India. Mar. Geod. 2024, 47, 395–414. [Google Scholar] [CrossRef]
- Morales, J.A. Human Impacts on Coastal Systems; Springer: Cham, Switzerland, 2022; pp. 423–435. [Google Scholar]
- Villamizar, A.; Gutiérrez, M.E.; Nagy, G.J.; Caffera, R.M.; Leal Filho, W. Climate Adaptation in South America with Emphasis in Coastal Areas: The State-of-the-Art and Case Studies from Venezuela and Uruguay. Clim. Dev. 2017, 9, 364–382. [Google Scholar] [CrossRef]
- Winckler, P.; Martín, R.A.; Esparza, C.; Melo, O.; Sactic, M.I.; Martínez, C. Projections of Beach Erosion and Associated Costs in Chile. Sustainability 2023, 15, 5883. [Google Scholar] [CrossRef]
- Islam, M.S.; Crawford, T.W. Assessment of Spatio-Temporal Empirical Forecasting Performance of Future Shoreline Positions. Remote Sens. 2022, 14, 6364. [Google Scholar] [CrossRef]
- Palanisamy, P.; Sivakumar, V.; Velusamy, P.; Natarajan, L. Spatio-Temporal Analysis of Shoreline Changes and Future Forecast Using Remote Sensing, GIS and Kalman Filter Model: A Case Study of Rio de Janeiro, Brazil. J. S. Am. Earth Sci. 2024, 133, 104701. [Google Scholar] [CrossRef]
- Ülger, M.; Tanrıvermiş, Y. Prevention of the Effects of Coastal Structures on Shoreline Change Using Numerical Modeling. Ocean. Coast. Manag. 2023, 243, 106752. [Google Scholar] [CrossRef]
- Yu, H.; Weng, Z.; Chen, G.; Chen, X. Improved XBeach Model and Its Application in Coastal Beach Evolution under Wave Action. Coast. Eng. J. 2023, 65, 560–571. [Google Scholar] [CrossRef]
- Ciccaglione, M.C.; Buccino, M.; Calabrese, M. On the Evolution of Beaches of Finite Length. Cont. Shelf. Res. 2023, 259, 104990. [Google Scholar] [CrossRef]
- Stronkhorst, J.; Levering, A.; Hendriksen, G.; Rangel-Buitrago, N.; Appelquist, L.R. Regional Coastal Erosion Assessment Based on Global Open Access Data: A Case Study for Colombia. J. Coast. Conserv. 2018, 22, 787–798. [Google Scholar] [CrossRef]
- Martínez, J.; Yokoyama, Y.; Gomez, A.; Delgado, A.; Matsuzaki, H.; Rendon, E. Late Holocene Marine Terraces of the Cartagena Region, Southern Caribbean: The Product of Neotectonism or a Former High Stand in Sea-Level? J. S. Am. Earth Sci. 2010, 29, 214–224. [Google Scholar] [CrossRef]
- Rangel-Buitrago, N.; Williams, A.T.; Anfuso, G. Hard Protection Structures as a Principal Coastal Erosion Management Strategy along the Caribbean Coast of Colombia. A Chronicle of Pitfalls. Ocean. Coast. Manag. 2018, 156, 58–75. [Google Scholar] [CrossRef]
- IDEAM Boletín Condiciones Hidrometeorológicas. Available online: https://www.ideam.gov.co/sala-de-prensa/boletines (accessed on 14 February 2024).
- Andrade, C.A. Cambios Recientes Del Nivel Del Mar En Colombia. Deltas de Colombia: Morfodinámica y Vulnerabilidad Ante El Cambio Global; Fondo Editorial Universidad EAFIT: Medellín, Colombia, 2008; pp. 101–121. [Google Scholar]
- Corpoguajira. Invemar Atlas Marino Costero de La Guajira; Corpoguajira: Riohacha, Colombia, 2012; ISBN 9789588448459.
- Restrepo, J.C.; Otero, L.; Casas, A.C.; Henao, A.; Gutiérrez, J. Shoreline Changes between 1954 and 2007 in the Marine Protected Area of the Rosario Island Archipelago (Caribbean of Colombia). Ocean. Coast. Manag. 2012, 69, 133–142. [Google Scholar] [CrossRef]
- Restrepo, J.D.; López, S.A. Morphodynamics of the Pacific and Caribbean Deltas of Colombia, South America. J. S. Am. Earth Sci. 2008, 25, 1–21. [Google Scholar] [CrossRef]
- Restrepo-Ángel, J.D.; Mora-Páez, H.; Díaz, F.; Govorcin, M.; Wdowinski, S.; Giraldo-Londoño, L.; Tosic, M.; Fernández, I.; Paniagua-Arroyave, J.F.; Duque-Trujillo, J.F. Coastal Subsidence Increases Vulnerability to Sea Level Rise over Twenty First Century in Cartagena, Caribbean Colombia. Sci. Rep. 2021, 11, 18873. [Google Scholar] [CrossRef] [PubMed]
- Berrio, Y.; Rivillas-Ospina, G.; Ruiz-Martínez, G.; Arango-Manrique, A.; Ricaurte, C.; Mendoza, E.; Silva, R.; Casas, D.; Bolívar, M.; Díaz, K. Energy Conversion and Beach Protection: Numerical Assessment of a Dual-Purpose WEC Farm. Renew. Energy 2023, 219, 119555. [Google Scholar] [CrossRef]
- Rangel-Buitrago, N.; Melfi, G.A. Morfología, Morfodinámica y Evolución Reciente En La Península de La Guajira, Caribe Colombiano. Rev. Cienc. Ing. Día 2013, 8, 2357–5409. [Google Scholar]
- Ballén, S.; Barrios, J.D. Cuantificación de Las Transformaciones Territoriales Asociadas a Dinámicas de Producción Derivadas de Los Diferentes Sectores Productivos En La Cuenca Del Río Ranchería, La Guajira, Colombia; Universidad Santo Tomás: Antioquia, Colombia, 2019. [Google Scholar]
- Rodríguez, G.; Londoño, A.C. Mapa Geológico Del Departamento de La Guajira; Ministerio de Minas y Energía: Bogotá, Colombia, 2002.
- Mosquera, F.; Arango, J.; Carreño, J.; Aguilera, H. Exploración de Acuíferos de La Alta y Media Guajira. Capítulo I, Geología; Instituto Nacional de Investigaciones Geológico Mineras: Bogotá, Colombia, 1976. [Google Scholar]
- Granados, A. Resumen Del Estudio Hidrogeológico de La Media y Baja Guajira. Boletín Geológico 1988, 29, 45–83. [Google Scholar] [CrossRef]
- Molina, L.; Pérez, F.; Martínez, J.; Franco, V.; Marín, L.; González, J.; Carvajal, J. Geomorfología y Aspectos Erosivos Del Litoral Caribe Colombiano. INGEOMINAS 1998, 21, 1–73. [Google Scholar]
- Himmelstoss, E.A.; Henderson, R.E.; Kratzmann, M.G.; Farris, A.S. Shoreline Analysis System (DSAS). User Guide; U.S. Geological Survey: Reston, VA, USA, 2021; pp. 1–104.
- IGAC Web Page of the Instituto Geográfico Agustín Codazzi. Available online: https://www.igac.gov.co/ (accessed on 3 February 2024).
- Google Earth Pro Google Earth Pro. Available online: https://www.google.es/intl/es/earth/index.html (accessed on 9 January 2024).
- AgiSoft AgiSoft PhotoScan Professional. Available online: http://www.agisoft.com/downloads/installer/ (accessed on 2 February 2023).
- Tsiakos, C.A.D.; Chalkias, C. Use of Machine Learning and Remote Sensing Techniques for Shoreline Monitoring: A Review of Recent Literature. Appl. Sci. 2023, 13, 3268. [Google Scholar] [CrossRef]
- Ojeda Zújar, J.P.; Fernández Núñez, M.; Prieto Campos, A.; Pérez Alcántara, J.P.; Vallejo Villalta, I. Levantamiento de Líneas de Costa a Escalas de Detalle Para El Litoral de Andalucía: Criterios, Modelo de Datos y Explotación. In Proceedings of the Congreso Nacional de Tecnologías de la Información Geográfica, Sevilla, Spain, 13–17 September 2010; pp. 324–336. [Google Scholar]
- Fernández-Hernández, M.; Calvo, A.; Iglesias, L.; Castedo, R.; Ortega, J.J.; Diaz-Honrubia, A.J.; Mora, P.; Costamagna, E. Anthropic Action on Historical Shoreline Changes and Future Estimates Using GIS: Guardarmar Del Segura (Spain). Appl. Sci. 2023, 13, 9792. [Google Scholar] [CrossRef]
- Nithu Raj, R.; Rejin Nishkalank, A.; Chrisben Sam, S. Coastal Shoreline Changes in Chennai: Environment Impacts and Control Strategies of Southeast Coast. In Handbook of Environmental Materials Management; Springer: Cham, Switzerland, 2020; pp. 1–14. [Google Scholar]
- Environmental Systems Research Institute ESRI—Environmental Systems Research Institute 2024. Available online: https://www.esri.com/en-us/home (accessed on 9 January 2024).
- Davidson, M.A.; Lewis, R.P.; Turner, I.L. Forecasting Seasonal to Multi-Year Shoreline Change. Coast. Eng. 2010, 57, 620–629. [Google Scholar] [CrossRef]
- Hunt, E.; Davidson, M.; Steele, E.C.C.; Amies, J.D.; Scott, T.; Russell, P. Shoreline Modelling on Timescales of Days to Decades. In Cambridge Prisms: Coastal Futures; Cambridge University Press: Cambridge, UK, 2023; Volume 1. [Google Scholar] [CrossRef]
- Ciritci, D.; Türk, T. Assessment of the Kalman Filter-Based Future Shoreline Prediction Method. Int. J. Environ. Sci. Technol. 2020, 17, 3801–3816. [Google Scholar] [CrossRef]
- Leatherman, S.P. Modelling Shore Response to Sea-Level Rise on Sedimentary Coasts. Prog. Phys. Geogr. 1990, 14, 447–464. [Google Scholar] [CrossRef]
- Lee, E.M.; Clark, A.R. Investigation and Management of Soft Rock Cliffs; Thomas Telford: London, UK, 2002. [Google Scholar]
- Mishra, M.; Chand, P.; Beja, S.K.; Santos, C.A.G.; da Silva, R.M.; Ahmed, I.; Kamal, A.H.M. Quantitative Assessment of Present and the Future Potential Threat of Coastal Erosion along the Odisha Coast Using Geospatial Tools and Statistical Techniques. Sci. Total Environ. 2023, 875, 162488. [Google Scholar] [CrossRef] [PubMed]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Long, J.W.; Plant, N.G. Extended Kalman Filter Framework for Forecasting Shoreline Evolution. Geophys. Res. Lett. 2012, 39, 1–6. [Google Scholar] [CrossRef]
- Griggs, G.; Patsch, K.; Lester, C.; Anderson, R. Groins, Sand Retention, and the Future of Southern California’s Beaches. Shore Beach 2020, 88, 14–36. [Google Scholar] [CrossRef] [PubMed]
- U.S. Army Corps of Engineers. Corps of Engineers Coastal Groins and Nearshore Breakwaters Engineer Manual; Department of the Army, U.S. Army Corps of Engineers: Washington, DC, USA, 1992.
- Castedo, R.; Fernández, M.; Trenhaile, A.S.; Paredes, C. Modeling Cyclic Recession of Cohesive Clay Coasts: Effects of Wave Erosion and Bluff Stability. Mar. Geol. 2013, 335, 162–176. [Google Scholar] [CrossRef]
- Tierolf, L.; Haer, T.; Athanasiou, P.; Luijendijk, A.P.; Botzen, W.J.W.; Aerts, J.C.J.H. Coastal Adaptation and Migration Dynamics under Future Shoreline Changes. Sci. Total Environ. 2024, 917, 170239. [Google Scholar] [CrossRef] [PubMed]

| Image | Source | Date |
|---|---|---|
| IGAC1987 | Instituto Geográfico Agustín Codazzi | 14 September 1987 |
| IGAC1997 | Instituto Geográfico Agustín Codazzi | 12 January 1997 |
| GE2003-02 | Google Earth | February 2003 |
| GE2006-03 | Google Earth | March 2006 |
| GE2009-10 | Google Earth | October 2009 |
| GE2011-01 | Google Earth | January 2011 |
| GE2013-02 | Google Earth | February 2013 |
| GE2014-11 | Google Earth | November 2014 |
| GE2018-03 | Google Earth | March 2018 |
| GE2019-10 | Google Earth | October 2019 |
| GE2020-10 | Google Earth | October 2020 |
| GE2022-11 | Google Earth | November 2022 |
| Period | Transect | NSM (m) | LRR (m/yr) | LCI (m/yr) | LR2 |
|---|---|---|---|---|---|
| 1987–2006 | T1 | −2.1 | −0.3 | 4.4 | 0.43 |
| T2 | −3.3 | −0.4 | 3.3 | 0.72 | |
| T3 | −4.9 | −0.5 | 0.7 | 0.99 | |
| T4 | −4.3 | −0.5 | 2.7 | 0.85 | |
| T5 | −7.2 | −0.8 | 3.8 | 0.89 | |
| T6 | −4.0 | −0.5 | 5.7 | 0.58 | |
| 2009–2022 | T1 | 81.1 | 6.5 | 3.7 | 0.80 |
| T2 | 118.6 | 9.3 | 3.9 | 0.88 | |
| T3 | 146.6 | 13.2 | 3.6 | 0.95 | |
| T4 | 138.0 | 13.1 | 2.5 | 0.97 | |
| T5 | 134.9 | 13.6 | 4.9 | 0.91 | |
| T6 | 129.5 | 12.3 | 4.4 | 0.91 |
| Source | Sum of Squares | Degrees of Freedom | Mean Sum of Squares | F | p-Value |
|---|---|---|---|---|---|
| Period | 49,987.5 | 1 | 49,987.5 | 182.68 | 9.47 × 10−8 |
| Error | 2736.4 | 10 | 273.6 | ||
| Total | 52,723.9 | 11 |
| Transect | NSM (m) | LRR (m/yr) | LCI (m/yr) | LR2 |
|---|---|---|---|---|
| T7 | 67.7 | 6.2 | 2.9 | 0.90 |
| T8 | 65.1 | 5.9 | 2.7 | 0.90 |
| T9 | 87.6 | 8.6 | 2.3 | 0.98 |
| T10 | 90.9 | 10.0 | 4.7 | 0.94 |
| Transect | DSAS Years 2003–2022 | HTA | EHD | KFB | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NSM (m) | LRR (m/yr) | LCI (m/yr) | LR2 | Lower Bound | Upper Bound | Lower Bound | Upper Bound | Lower Bound | Upper Bound | |
| T11 | −1.5 | −0.1 | 0.2 | 0.26 * | N/A | N/A | N/A | N/A | N/A | N/A |
| T12 | −11.6 | −0.9 | 0.4 | 0.86 | −28.4 | −30.8 | −11.5 | −27.6 | −7.6 | −37.0 |
| T13 | −8.7 | −0.5 | 0.2 | 0.85 | −16.0 | −17.4 | −6.2 | −15.9 | 2.6 | −24.3 |
| T14 | −15.6 | −0.7 | 0.6 | 0.61 | −24.1 | −26.1 | −3.5 | −29.7 | 2.2 | −31.4 |
| T15 | −13.0 | −0.7 | 0.4 | 0.70 | −21.8 | −23.6 | −5.1 | −24.8 | 2.6 | −28.4 |
| T16 | 21.8 | 0.9 | 1.0 | 0.44 * | N/A | N/A | N/A | N/A | N/A | N/A |
| T17 | −4.2 | 0.2 | 0.6 | 0.10 * | N/A | N/A | N/A | N/A | N/A | N/A |
| T18 | −17.1 | −1.8 | 1.3 | 0.67 | −59.6 | −64.5 | −12.2 | −69.7 | −29.7 | −74.9 |
| T19 | −15.5 | −1.1 | 0.4 | 0.87 | −36.5 | −39.5 | −15.4 | −34.7 | −12.7 | −43.6 |
| T20 | −18.8 | −1.2 | 0.4 | 0.92 | −40.5 | −43.9 | −19.6 | −36.1 | −12.4 | −42.1 |
| Transect | DSAS Years 2003–2022 | HTA | EHD | KFB | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NSM (m) | LRR (m/yr) | LCI (m/yr) | LR2 | Lower Bound | Upper Bound | Lower Bound | Upper Bound | Lower Bound | Upper Bound | |
| T21 | −45.8 | −2.9 | 0.6 | 0.94 | −97.7 | −105.9 | −52.9 | −81.4 | −51.3 | −86.0 |
| T22 | −27.9 | −1.5 | 0.4 | 0.91 | −49.2 | −53.3 | −25.1 | −42.6 | −16.1 | −46.2 |
| T23 | −18.9 | −0.8 | 0.6 | 0.51 | −26.4 | −28.6 | −3.7 | −32.7 | 3.9 | −31.0 |
| T24 | −49.4 | −3.1 | 0.7 | 0.94 | −103.0 | −111.7 | −55.7 | −86.0 | −54.4 | −89.8 |
| T25 | −45.9 | −2.9 | 0.6 | 0.94 | −96.0 | −104.0 | −52.7 | −79.4 | −50.1 | −84.1 |
| T26 | −41.5 | −2.6 | 0.4 | 0.97 | −87.7 | −95.0 | −51.8 | −68.8 | −44.0 | −73.9 |
| T27 | −38.4 | −2.3 | 0.5 | 0.94 | −76.3 | −82.7 | −41.6 | −63.3 | −36.6 | −68.5 |
| T28 | −38.5 | −2.5 | 0.4 | 0.96 | −84.3 | −91.4 | −48.8 | −67.2 | −43.0 | −73.4 |
| T29 | −37.7 | −2.3 | 0.3 | 0.98 | −78.0 | −84.4 | −47.6 | −59.6 | −38.3 | −66.1 |
| T30 | −27.8 | −1.7 | 0.4 | 0.93 | −58.2 | −63.1 | −31.3 | −48.8 | −23.7 | −53.8 |
| T31 | −37.3 | −2.3 | 0.3 | 0.97 | −76.3 | −82.7 | −45.1 | −59.8 | −36.2 | −65.1 |
| T32 | −34.3 | −2.1 | 0.3 | 0.96 | −68.6 | −74.3 | −39.6 | −54.7 | −32.3 | −61.4 |
| Period | Years | Area Change (m2) | Rate of Area Change (m2/yr) |
|---|---|---|---|
| 2003–2006 | 3 | −7058 | −2353 |
| 2006–2009 | 3 | −13,115 | −4372 |
| 2009–2011 | 2 | −5635 | −2817 |
| 2011–2013 | 2 | −1733 | −867 |
| 2013–2014 | 1 | −5239 | −5239 |
| 2014–2018 | 4 | −13,446 | −3361 |
| 2018–2019 | 1 | −7758 | −7785 |
| 2019–2020 | 1 | −1356 | −1356 |
| 2020–2022 | 2 | −2715 | −1358 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández-Hernández, M.; Iglesias, L.; Escobar, J.; Ortega, J.J.; Pérez-Montiel, J.I.; Paredes, C.; Castedo, R. The Influence of Hard Protection Structures on Shoreline Evolution in Riohacha, Colombia. Appl. Sci. 2025, 15, 8119. https://doi.org/10.3390/app15148119
Fernández-Hernández M, Iglesias L, Escobar J, Ortega JJ, Pérez-Montiel JI, Paredes C, Castedo R. The Influence of Hard Protection Structures on Shoreline Evolution in Riohacha, Colombia. Applied Sciences. 2025; 15(14):8119. https://doi.org/10.3390/app15148119
Chicago/Turabian StyleFernández-Hernández, Marta, Luis Iglesias, Jairo Escobar, José Joaquín Ortega, Jhonny Isaac Pérez-Montiel, Carlos Paredes, and Ricardo Castedo. 2025. "The Influence of Hard Protection Structures on Shoreline Evolution in Riohacha, Colombia" Applied Sciences 15, no. 14: 8119. https://doi.org/10.3390/app15148119
APA StyleFernández-Hernández, M., Iglesias, L., Escobar, J., Ortega, J. J., Pérez-Montiel, J. I., Paredes, C., & Castedo, R. (2025). The Influence of Hard Protection Structures on Shoreline Evolution in Riohacha, Colombia. Applied Sciences, 15(14), 8119. https://doi.org/10.3390/app15148119








