Study on Air-Cooled Structure of Direct-Drive Outer-Rotor Permanent Magnet Synchronous Generator for Wind Power Generation
Abstract
1. Introduction
2. Establishment of the Fluid–Solid Coupling Structure for DD-PMSG
2.1. The Structure of the Wind Turbine Generator and Its Cooling System
2.2. Mathematical Modeling
- Conservation of mass:
- 2.
- Conservation of energy:
- 3.
- Conservation of momentum:
2.3. Assumptions and Boundary Condition Settings
- The fluid motion is complex, with a high Reynolds number (Re > 2300). Therefore, the flow field in the generator is calculated using a turbulent flow model (SST-k-omega model);
- Copper losses are uniformly distributed in the stator windings, while iron losses are uniformly distributed in the core;
- Since the air flow velocity is much lower than the speed of sound, air is considered as an incompressible fluid;
- The influence of gravity on fluid flow is neglected.
- Set the cooling air inlet as velocity inlet with an entrance velocity of 3 m/s, and the outlet as pressure outlet.
- Due to the circumferential symmetry of the model, the axial surfaces on both sides are set as periodic boundaries.
- The materials are specified as follows: the fluid is air, the stator is silicon steel, and the windings are copper.
3. Analysis of Fluid–Solid Coupled Heat Transfer on Different Radial Ventilation Ducts Structure
3.1. The Radial Ventilation Ducts Structure of the Stator Core
3.2. Simulation Analysis of Fluid Field in the Internal Cooling System of a Generator
3.2.1. Fluid Field Analysis of the Model
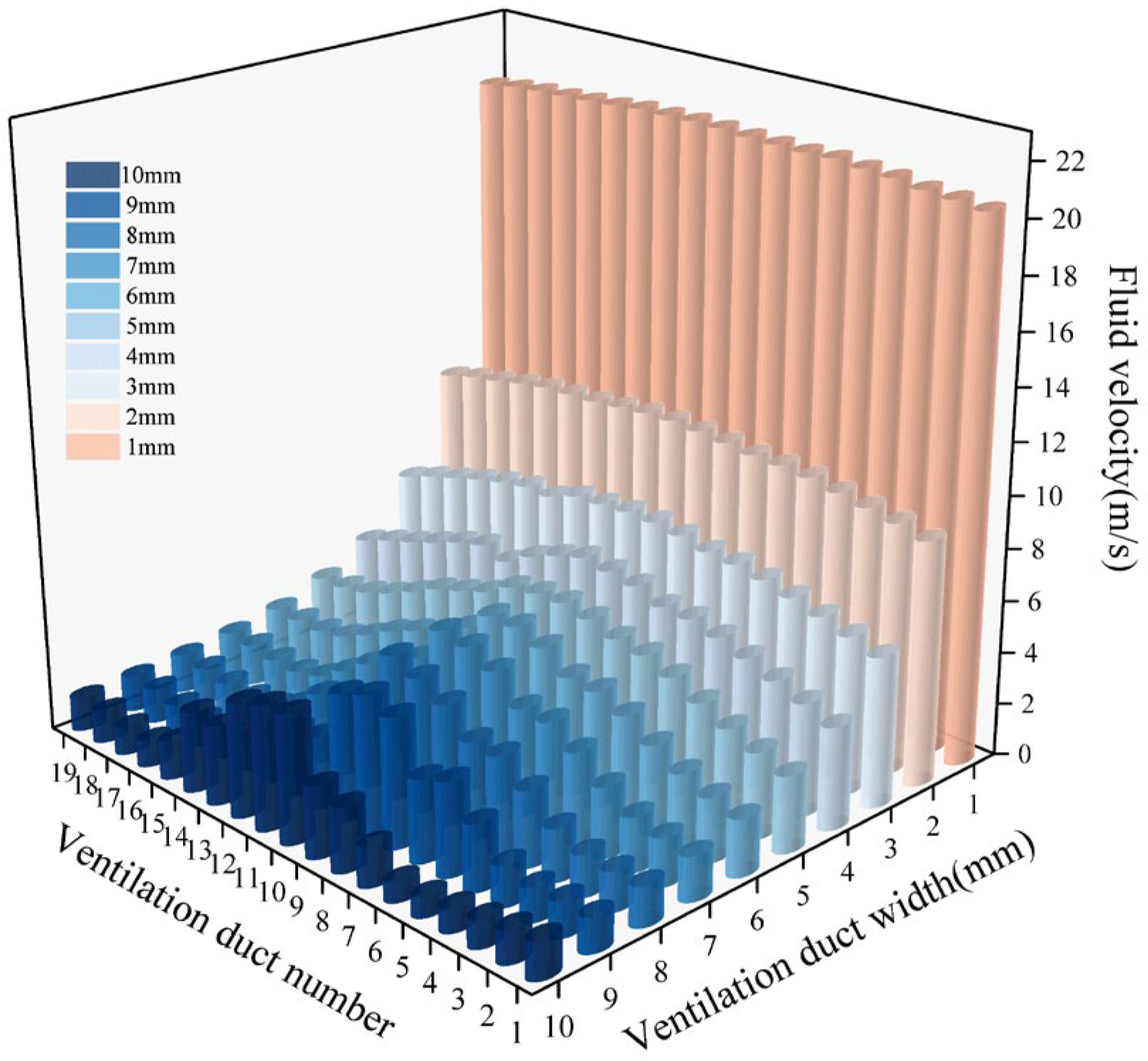
3.2.2. Numerical Study of the Fluid Field in Radial Ventilation Ducts with Different Widths
- (1)
- The velocity of the airflow within the radial ventilation ducts increases as the width of the ducts decreases, with more significant increases observed for narrower ducts.
- (2)
- When the ventilation ducts width is larger, the velocity and flow rate distribution along the axial direction of the 19 ducts generally show lower values on the sides and higher values in the middle.
- (3)
- Although the cross-sectional area of the radial ventilation ducts decreases with the reduction in ducts width, the overall flow rate does not decrease. Instead, the distribution of the flow rate becomes more uniform.
3.3. Simulation Analysis of the Temperature Field in the Internal Cooling System of a Generator
3.3.1. Temperature Field Analysis of the Model
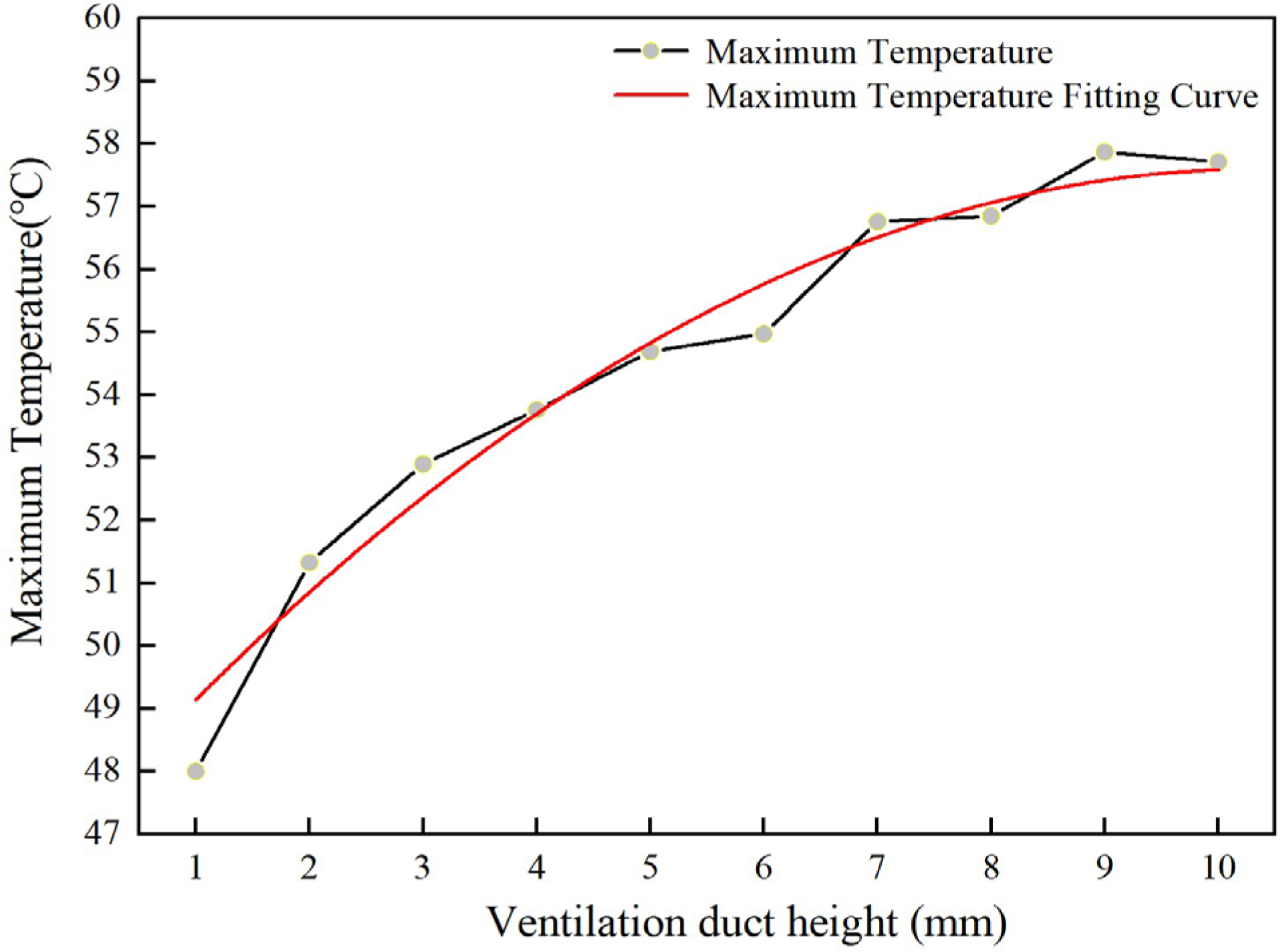
3.3.2. Numerical Influence of Temperature Field Under Different Widths of Radial Ventilation Ducts
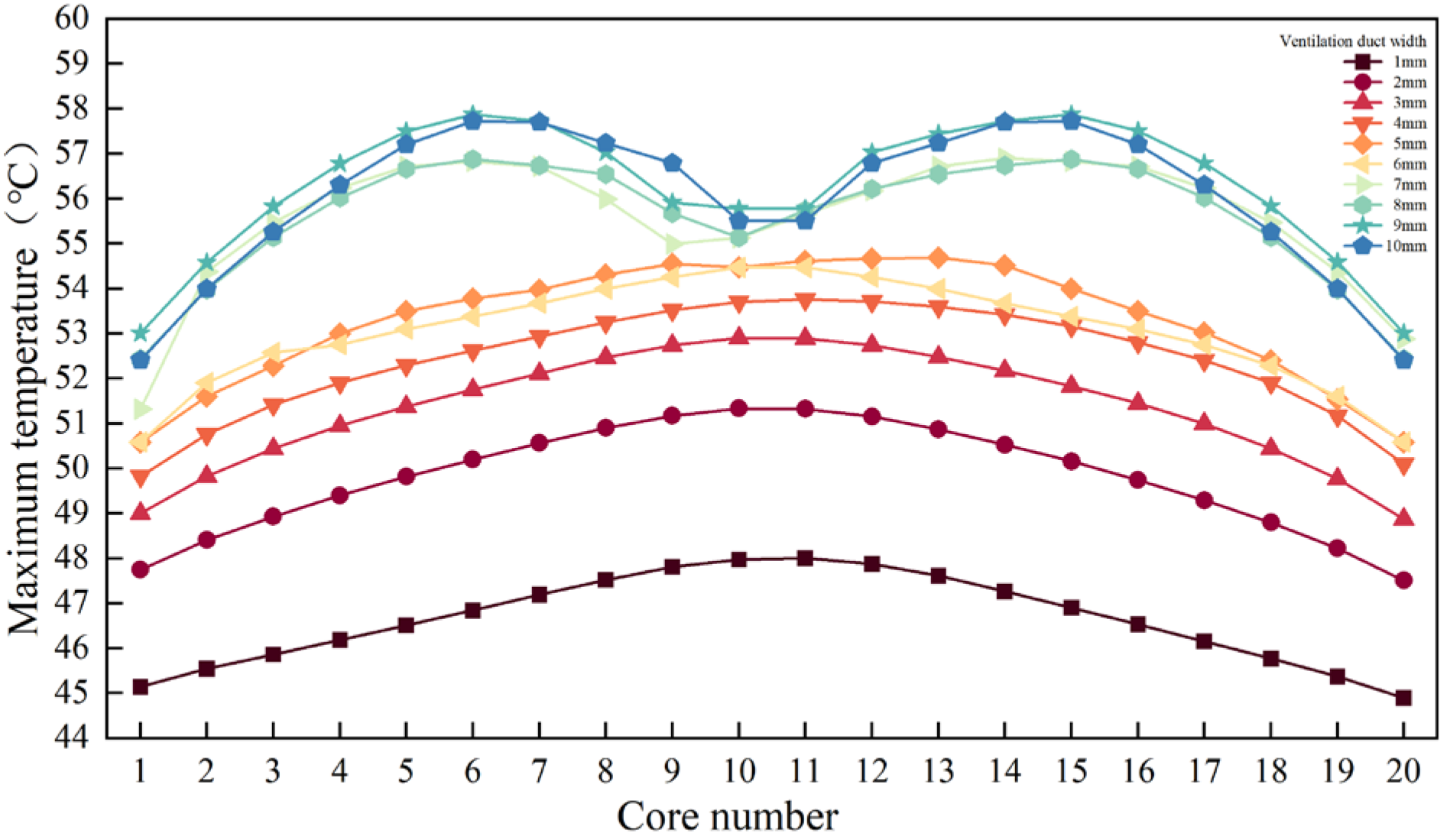
- (1)
- When the width of the ventilation ducts exceeds 6 mm, lower airflow and velocity appear in the center of the half section, which reduces the heat dissipation capacity of the ducts. Therefore, the maximum temperatures in the stator occur at these locations (Core Segments 6 and 15), with a “hump shaped” distribution.
- (2)
- Conversely, when the ventilation ducts width is within 6 mm (including 6 mm), the air flow and velocity are evenly distributed across all ducts. Here, the heat dissipation of the ventilation ducts mainly depends on the length of the heat dissipation path. At this point, the temperature distribution in the stator is higher in the middle and lower at the winding ends.
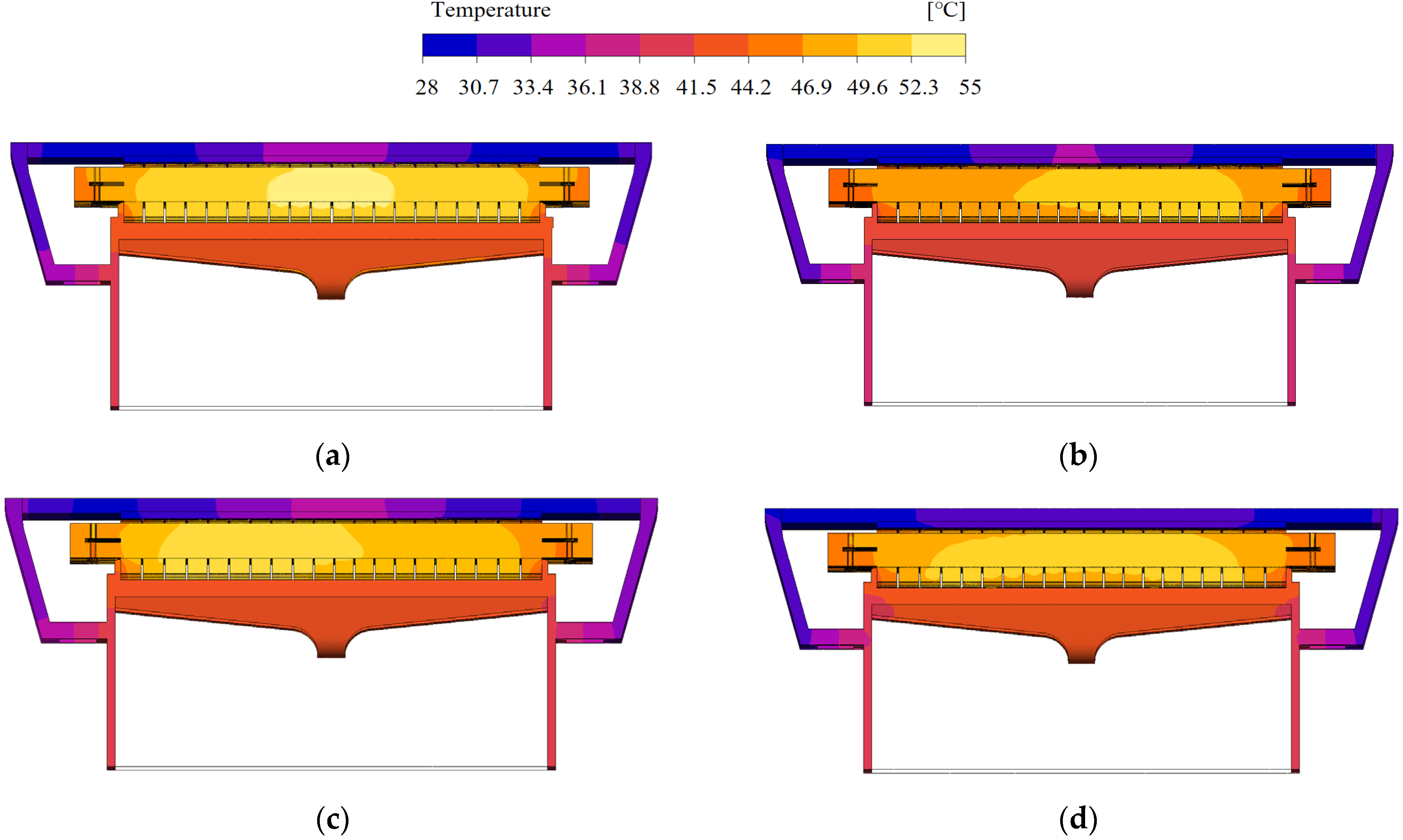
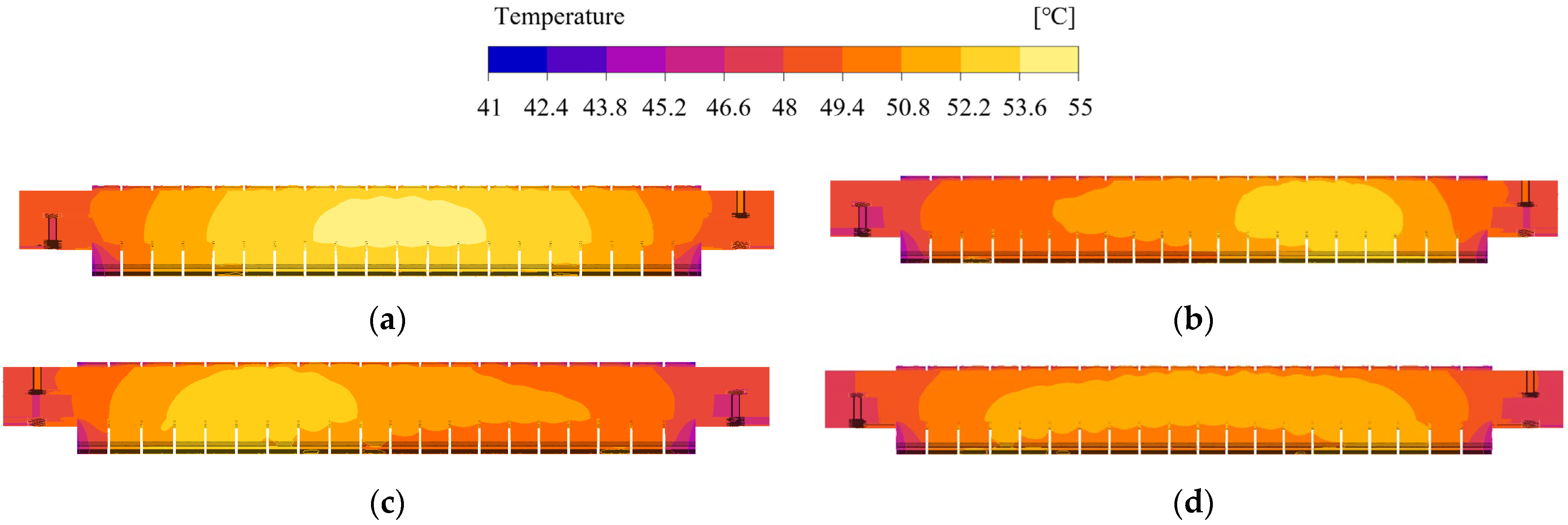
4. Ventilation Cooling Optimization Schemes with Non-Uniform Core Segments
4.1. Optimized Design of Non-Uniform Core Segments
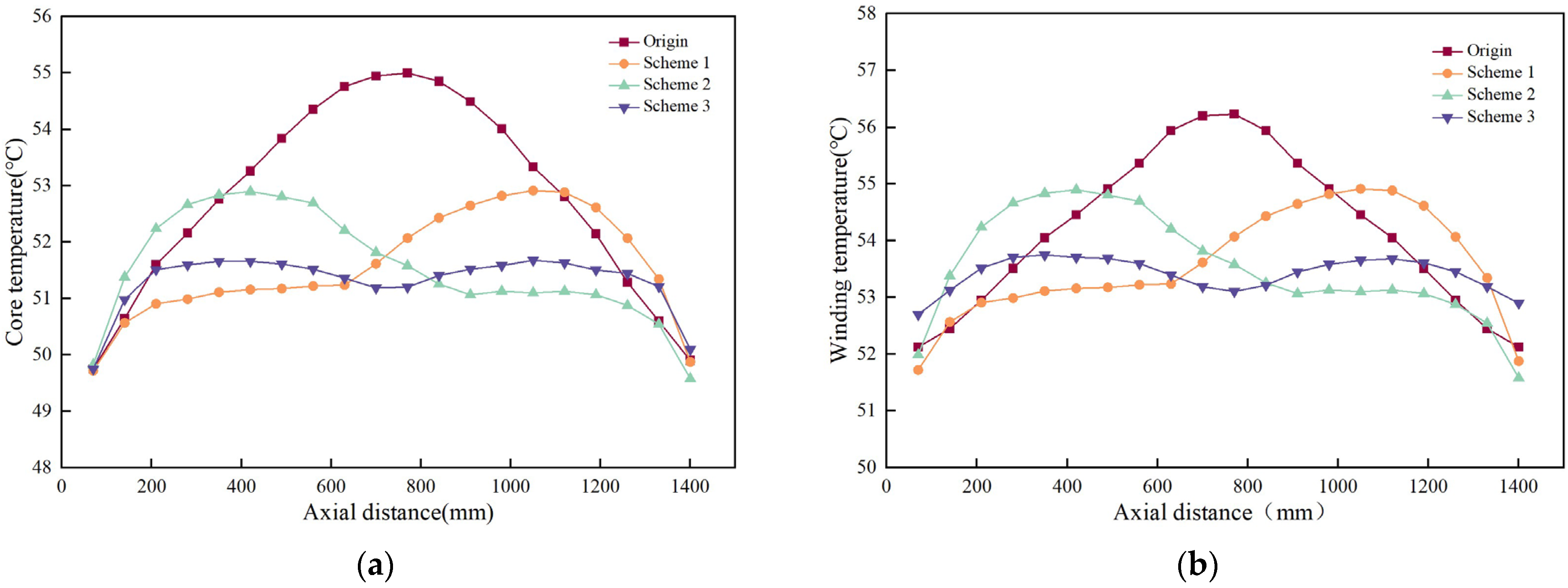
4.2. CFD Simulation Analysis
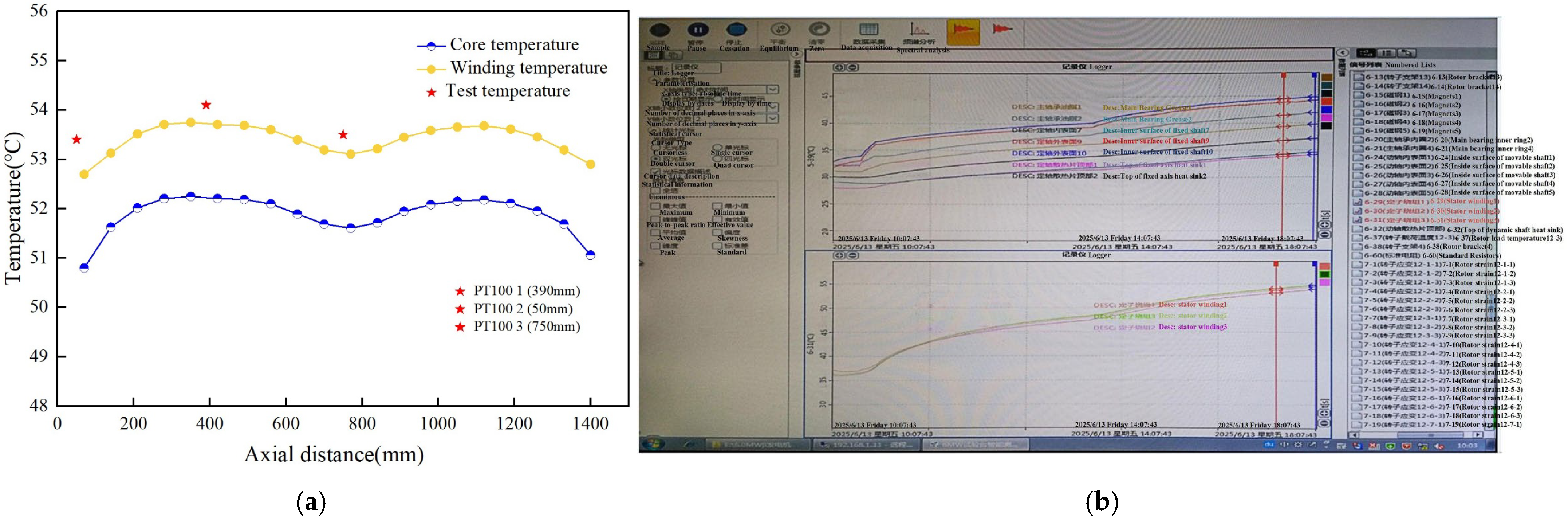
5. Experimental Verification
6. Conclusions
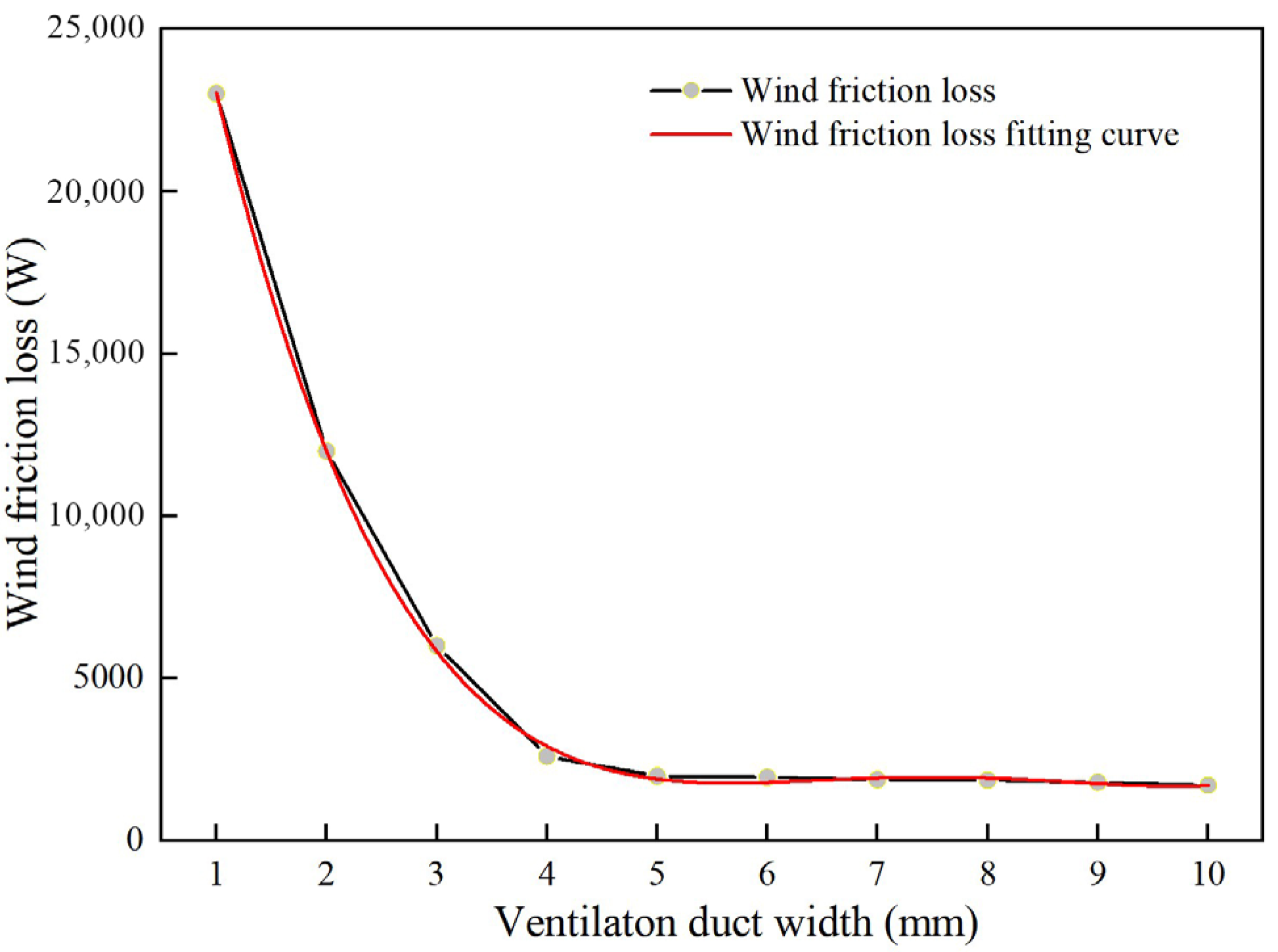
- With the stator core’s effective length constant, reducing the ventilation ducts width increases the fluid velocity inside the ducts and equalizes the flow distribution.
- Within the range of 1 mm to 10 mm, for every 1 mm reduction in the width of the ventilation ducts, the maximum temperature of the generator decreases by 3%, but it increases wind friction loss.
- This paper introduces a non-uniform stator core. Comparing three non-uniform cores with the original design, it was found that non-uniform cores effectively alter the motor’s internal temperature distribution and reduce the maximum temperature. The optimal scheme cuts the maximum temperature by 6.4% and reduces stator temperature differences.
- This study provides a quantitative relationship between ventilation width, temperature, and friction loss, demonstrates that non-uniform core design is superior to uniform structures in temperature control, and offers practical references for core ventilation design in large-scale wind turbines.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DD-PMSG | direct-drive permanent magnet synchronous generator |
| CFD | computational fluid dynamics |
| PMSWG | permanent magnet synchronous wind turbine generator |
References
- Wang, G.; Bai, L.; Chao, Y.; Chen, Z. How do solar photovoltaic and wind power promote the joint poverty alleviation and clean energy development: An evolutionary game theoretic study. Renew. Energy 2023, 218, 119296. [Google Scholar] [CrossRef]
- Liu, T.; Chen, Z.; Xu, J. Empirical evidence based effectiveness assessment of policy regimes for wind power development in China. Renew. Sustain. Energy Rev. 2022, 164, 112535. [Google Scholar] [CrossRef]
- Nomandela, S.; Mnguni, M.E.S.; Raji, A.K. A Case Study on the Validation of Renewable Energy Grid Code Compliance for a Large-Scale Wind Power Plant Grid-Connected Mode of Operation in Real-Time Simulation. Appl. Sci. 2025, 15, 5521. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Y.Z.; Zeng, T.; Wang, H.; Chan, S.; Ran, L. Wind turbine generator failure analysis and fault diagnosis: A review. IET Renew. Power Gener. 2024, 18, 3127–3148. [Google Scholar] [CrossRef]
- Singh, G.; Matuonto, M.; Sundaram, K. Impact of imbalanced wind turbine generator cooling on reliability. In Proceedings of the 2019 10th International Renewable Energy Congress (IREC), Sousse, Tunisia, 26–28 March 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Cen, Y.; Shen, H.; Wang, X.; Wu, Y.; Du, J. Multi-Objective Optimization Analysis of Electromagnetic Performance of Permanent Magnet Synchronous Motors Based on the PSO Algorithm. Energies 2024, 17, 4637. [Google Scholar] [CrossRef]
- Polikarpova, M.; Ponomarev, P.; Röyttä, P.; Semken, S.; Alexandrova, Y.; Pyrhönen, J. Direct liquid cooling for an outer-rotor direct-drive permanent-magnet synchronous generator for wind farm applications. IET Electr. Power Appl. 2015, 9, 523–532. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, Y.; Jin, S.; Xu, Z.; Zhang, F. Investigation of winding cooling enhancement and thermal modelling of large-power high-torque-density direct-drive PMSM. IET Electr. Power Appl. 2023, 17, 1401–1410. [Google Scholar] [CrossRef]
- Wu, Y.; Guo, Y. Study on the suppression effect of variable hydrogen parameters on the temperature rise of the turbo-generator rotor under deep peak regulation. IET Electr. Power Appl. 2023, 17, 1524–1534. [Google Scholar] [CrossRef]
- Shi, N.; Wei, M.; Zhang, L.; Hu, X.; Song, B. Design and research of cooling system for 2.5 MW permanent magnet wind turbine. Renew. Energy 2021, 168, 97–106. [Google Scholar] [CrossRef]
- Watson, B.; Venkiteswaran, V.K. Universal cooling of data centres: A cfd analysis. Energy Procedia 2017, 142, 2711–2720. [Google Scholar] [CrossRef]
- Calautit, J.K.; O’Connor, D.; Sofotasiou, P.; Hughes, B.R. CFD simulation and optimisation of a low energy ventilation and cooling system. Computation 2014, 3, 128–149. [Google Scholar] [CrossRef]
- Liu, W.; Chen, J.; Zhang, C.; Cui, Z.-Q.; Wang, X. Ventilation system design and rotor air friction loss of high-speed permanent magnet machines. In Proceedings of the 2017 IEEE International Conference on Cybernetics and Intelligent Systems (CIS) and IEEE Conference on Robotics, Automation and Mechatronics (RAM), Ningbo, China, 19–21 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 310–315. [Google Scholar]
- Li, W.; Li, D.; Li, J.; Zhang, X. Influence of rotor radial ventilation ducts number on temperature distribution of rotor excitation winding and fluid flow state between two poles of a fully air-cooled hydro-generator. IEEE Trans. Ind. Electron. 2017, 64, 3767–3775. [Google Scholar] [CrossRef]
- Zhou, G.H.; Han, L.; Fan, Z.N.; Zhang, H.-B.; Dong, X.-C.; Wang, J.; Sun, Z.; Zhang, B.-D. Ventilation cooling design for a novel 350-MW air-cooled turbo generator. IEEE Access 2018, 6, 62184–62192. [Google Scholar] [CrossRef]
- Xiao, X.; Baojun, G.; Dajun, T.; Jichao, H.; Likun, W. 3D temperature field of high-temperature gas cooled reactor cooling medium drive motor and ventilation structure improvement. IET Electr. Power Appl. 2018, 12, 1020–1026. [Google Scholar] [CrossRef]
- Ge, B.; Xu, X.; Tao, D.; Han, J.; Wang, L. Gas friction loss in stator ventilation ducts of the drive motor for the cooling medium in a high-temperature gas-cooled reactor. IEEE Trans. Ind. Electron. 2018, 66, 114–123. [Google Scholar] [CrossRef]
- Xu, X.; Ge, B.; Tao, D.; Han, J.; Wang, L. Effect of helium on temperature rise of helium blower drive motor in high-temperature gas-cooled reactor. Appl. Therm. Eng. 2019, 159, 113888. [Google Scholar] [CrossRef]
- Fan, X.; Qu, R.; Li, J.; Li, D.; Zhang, B.; Wang, C. Ventilation and thermal improvement of radial forced air-cooled FSCW permanent magnet synchronous wind generators. IEEE Trans. Ind. Appl. 2017, 53, 3447–3456. [Google Scholar] [CrossRef]
- Jamshidi, H.; Nilsson, H.; Chernoray, V. CFD-based design and analysis of the ventilation of an electric generator model, validated with experiments. Int. J. Fluid Mach. Syst. 2015, 8, 113–123. [Google Scholar] [CrossRef]
- Xie, Y.; Zhao, X.; Cai, W.; Qi, G.; Wang, Z.; Zhang, Y.; Yang, Y. Design and optimisation of oil injection pipe cooling structure for permanent magnet synchronous motors in hybrid electric vehicles. IET Electr. Power Appl. 2024, 18, 345–355. [Google Scholar] [CrossRef]
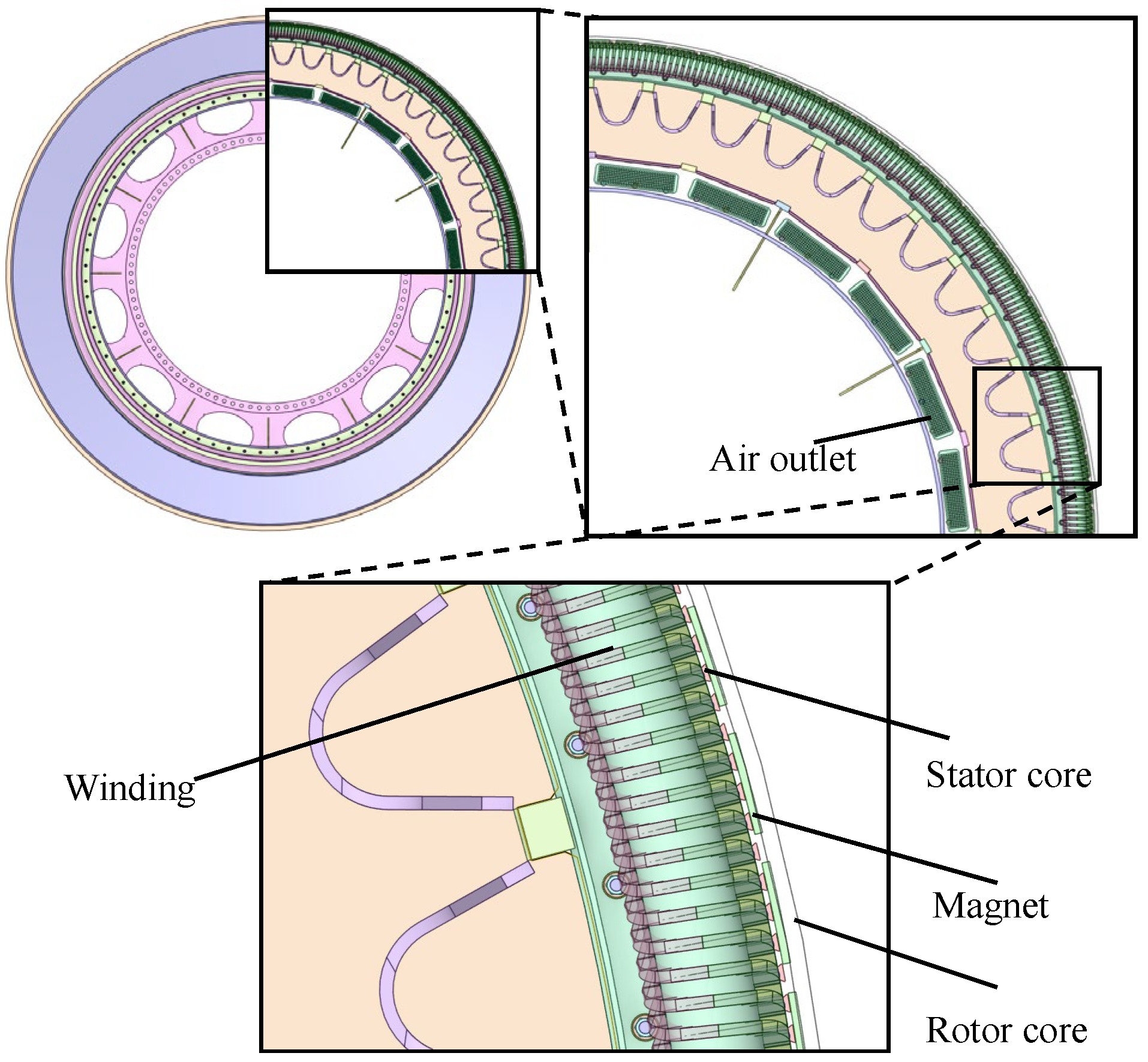

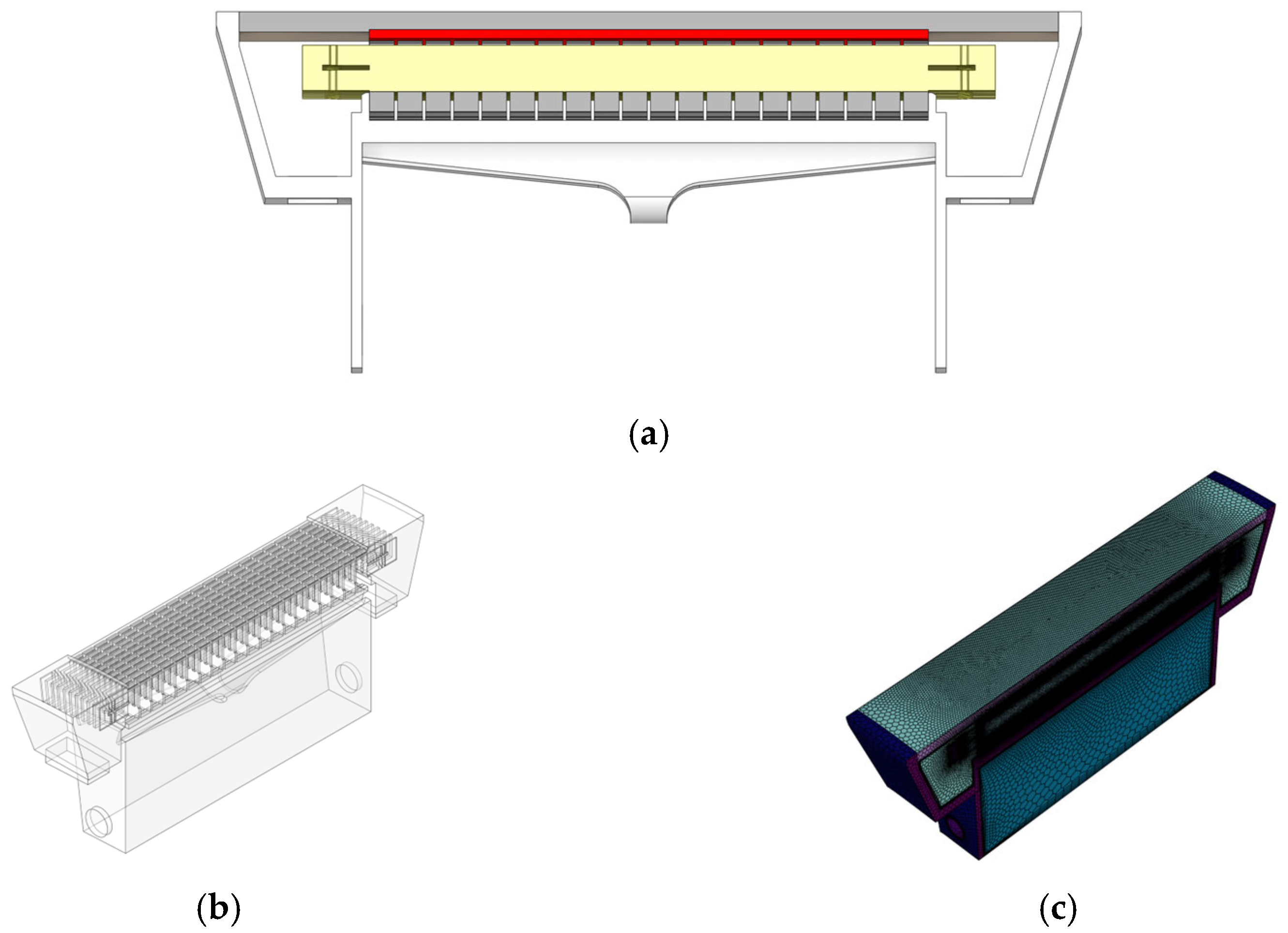
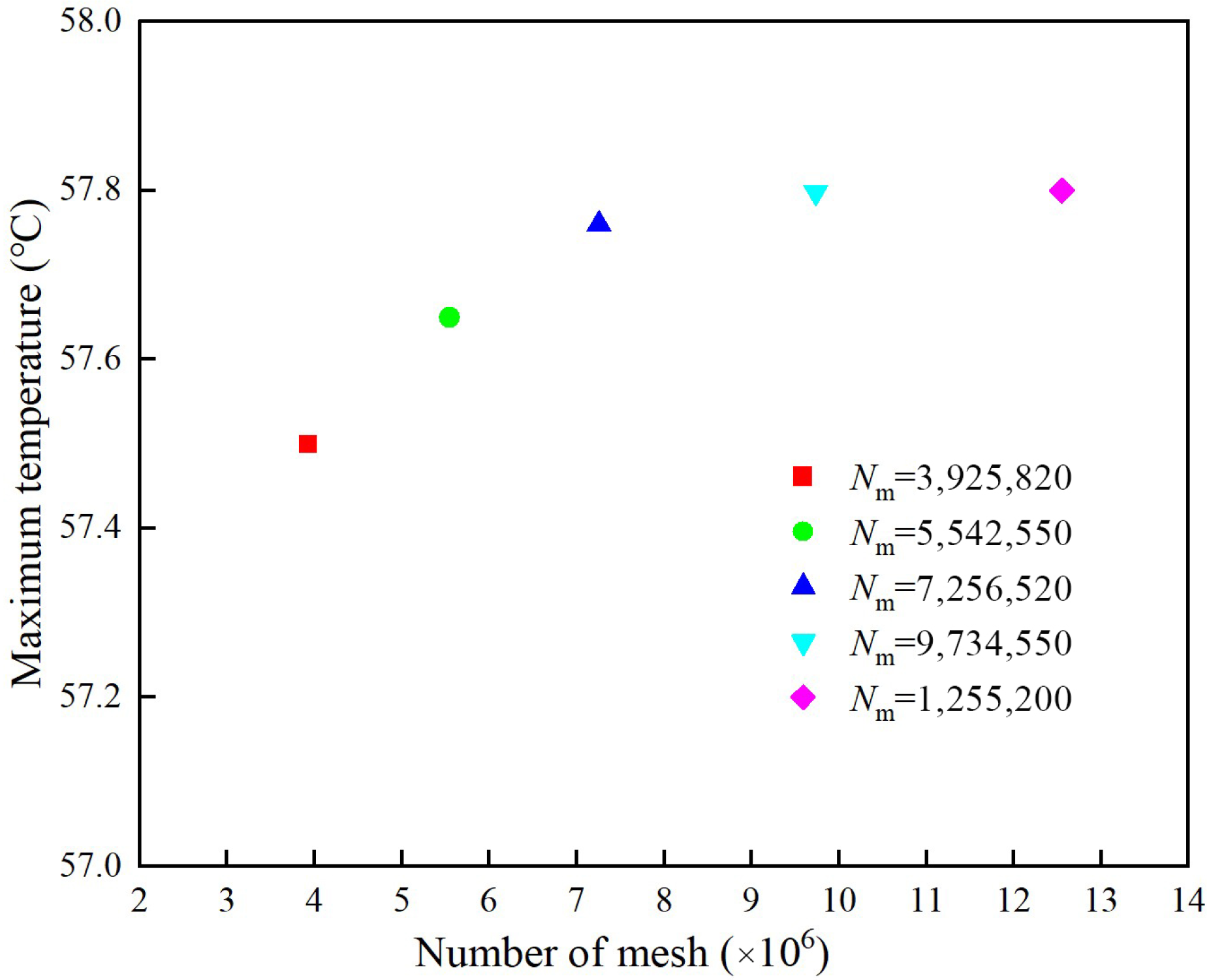

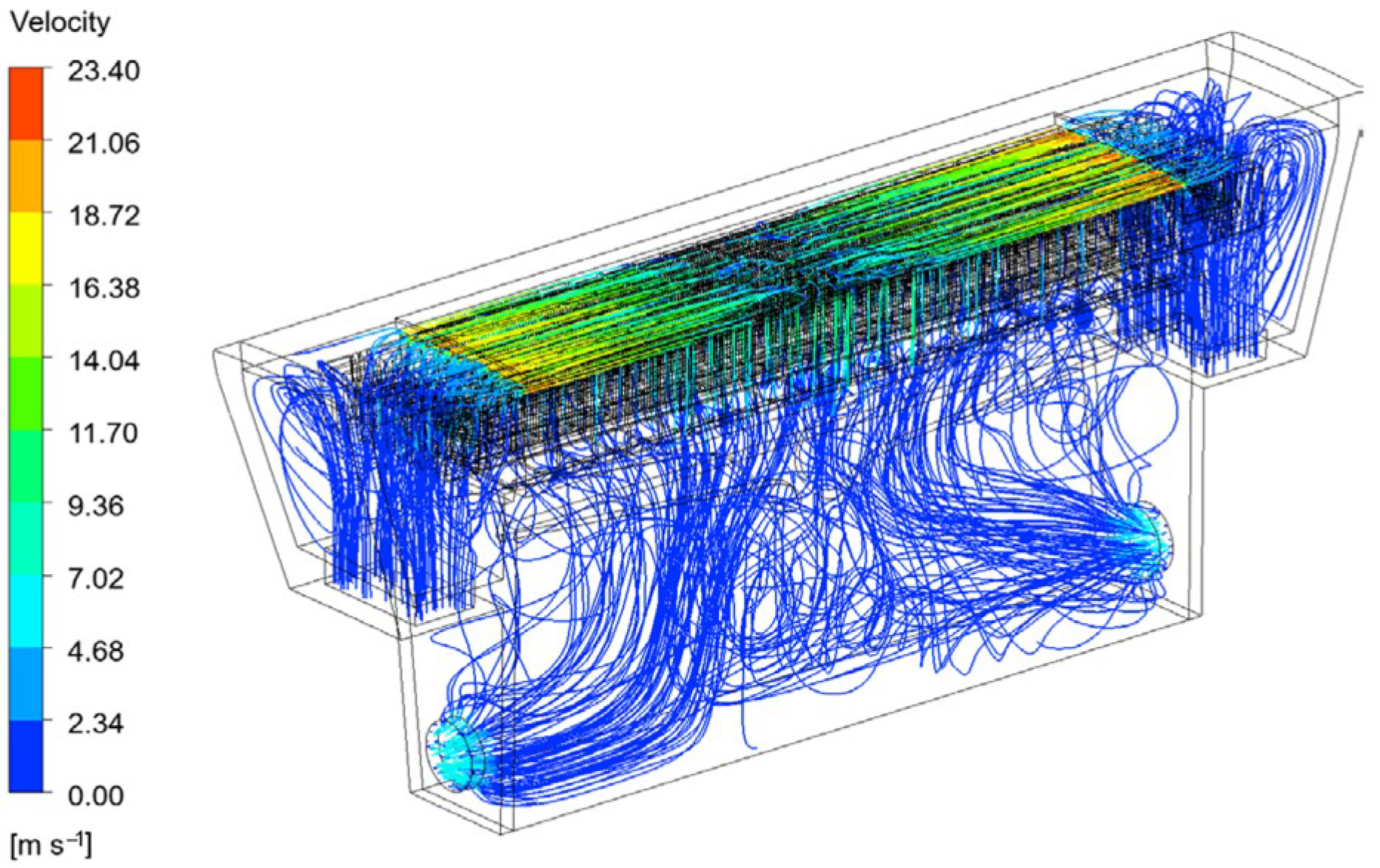




| Generator Parameters | Value | Unit | Generator Parameters | Value | Unit |
|---|---|---|---|---|---|
| Rated power/PN | 4500 | kW | Number of slots/Q | 480 | |
| Rotational speed/n | 9.5 | r·min−1 | Rotor outer diameter/D2 | 5498 | mm |
| Air-gap flux density/Bδ | 0.8 | T | Core length/L | 1382 | mm |
| Power factor/cosφ | 0.86 | Insulation class | F class | ||
| Number of pole-pairs/p | 56 | PM grade | N45H |
| Maximum Generator Temperature | Computational Error | Simulation Time Required | |
|---|---|---|---|
| Full-model | 57.31 °C | 0 | 160 h |
| Simplified 1/12 model | 56.85 °C | 0.80% | 60 h |
| Simplified 1/24 model | 56.62 °C | 1.3% | 25 h |
| Simplified 1/48 model | 56.51 °C | 1.40% | 10 h |
| Structural Scheme | Core Segment (Axial Length (mm) × Number) | Radial Ventilation Ducts (Axial Length (mm) × Number) |
|---|---|---|
| Origin | 63.4 × 20 | 6 × 19 |
| Scheme 1 | 67.4 × 3 + 60.4 × 8 + 63.4 × 6 + 67.4 × 3 | 6 × 19 |
| Scheme 2 | 67.4 × 3 + 63.4 × 6 + 60.4 × 8 + 67.4 × 3 | 6 × 19 |
| Scheme 3 | 67.4 × 3 + 63.4 × 3 + 60.4 × 8 + 63.4 × 3 + 67.4 × 3 | 6 × 19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Li, K.; Chen, Y.; Lv, H.; Du, J. Study on Air-Cooled Structure of Direct-Drive Outer-Rotor Permanent Magnet Synchronous Generator for Wind Power Generation. Appl. Sci. 2025, 15, 8008. https://doi.org/10.3390/app15148008
Yang X, Li K, Chen Y, Lv H, Du J. Study on Air-Cooled Structure of Direct-Drive Outer-Rotor Permanent Magnet Synchronous Generator for Wind Power Generation. Applied Sciences. 2025; 15(14):8008. https://doi.org/10.3390/app15148008
Chicago/Turabian StyleYang, Xudong, Ke Li, Yiguang Chen, Haiying Lv, and Jingjuan Du. 2025. "Study on Air-Cooled Structure of Direct-Drive Outer-Rotor Permanent Magnet Synchronous Generator for Wind Power Generation" Applied Sciences 15, no. 14: 8008. https://doi.org/10.3390/app15148008
APA StyleYang, X., Li, K., Chen, Y., Lv, H., & Du, J. (2025). Study on Air-Cooled Structure of Direct-Drive Outer-Rotor Permanent Magnet Synchronous Generator for Wind Power Generation. Applied Sciences, 15(14), 8008. https://doi.org/10.3390/app15148008







