Interpretable Ensemble Learning with Lévy Flight-Enhanced Heuristic Technique for Strength Prediction of MICP-Treated Sands
Abstract
1. Introduction
2. Research Methodology
2.1. Ensemble Learning Architecture
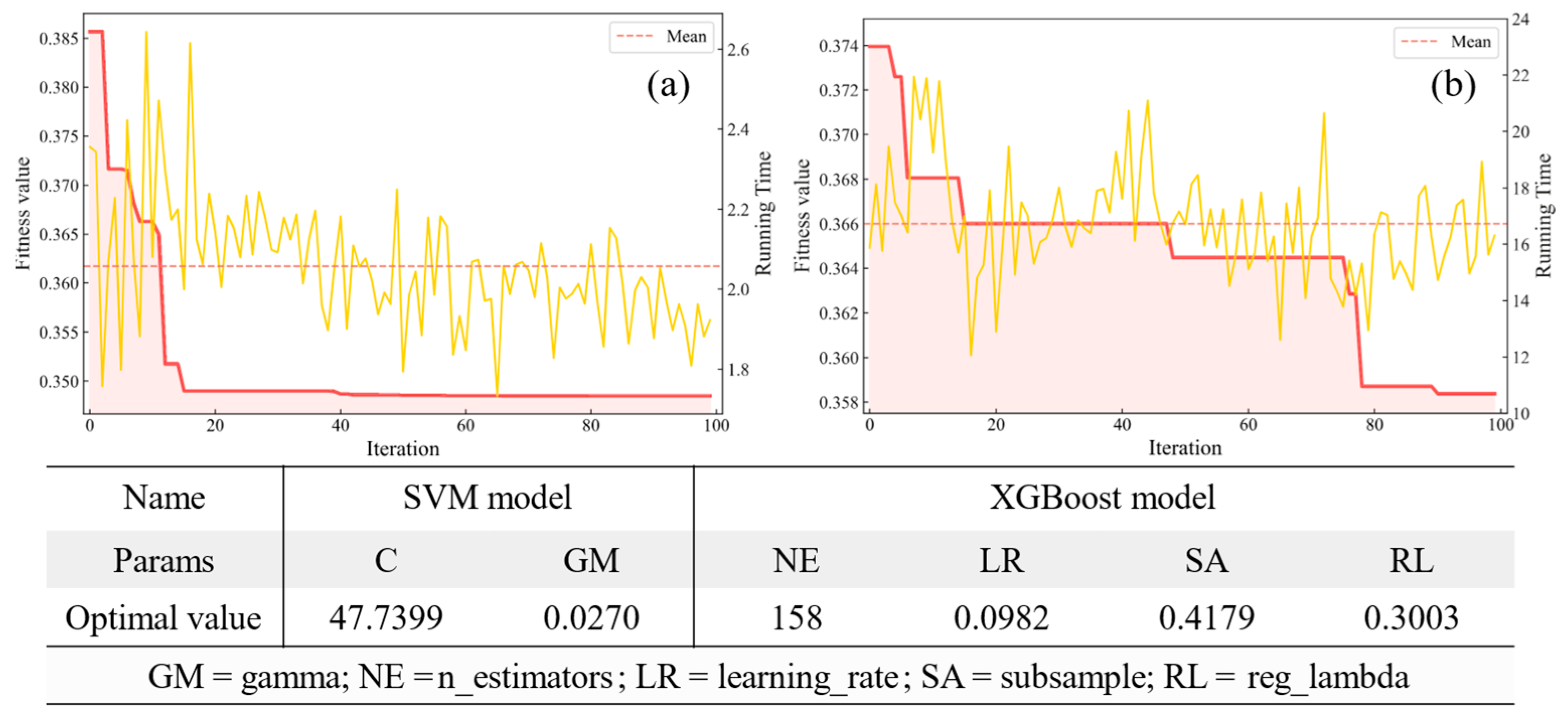
2.2. Improved Artificial Rabbits Optimisation Method
- (1)
- The Lévy flight method introduces dynamic characteristics to the ARO algorithm updates through heavy-tailed distribution random walk patterns, with step lengths following a Lévy distribution:where l represents step length, , , σv = 1, . During the random hiding phase, Lévy flight replaces the r4 random number (with parameter β typically set to 1.5 and α set to 0.1) to prevent the algorithm from falling into local optima:
- (2)
- Selective opposition (SO) learning enhances algorithm performance by modifying opposition-based learning states when rabbit colonies are distant from optimal solutions. This strategy influences rabbit colony deployment through linearly decreasing thresholds. When colonies are far from optimal positions, it calculates near and far rabbit positions and updates the corresponding difference distances. The SO core lies in determining search direction effectiveness through correlation analysis, triggering update strategies to help rabbits escape local optima when correlation is poor, calculated through the following formula:where ddi represents the difference distance between each rabbit and the optimal rabbit position across various dimensions, and Rsrc measures the correlation between current and optimal positions.
2.3. Model Evaluation Metrics
3. Database Construction
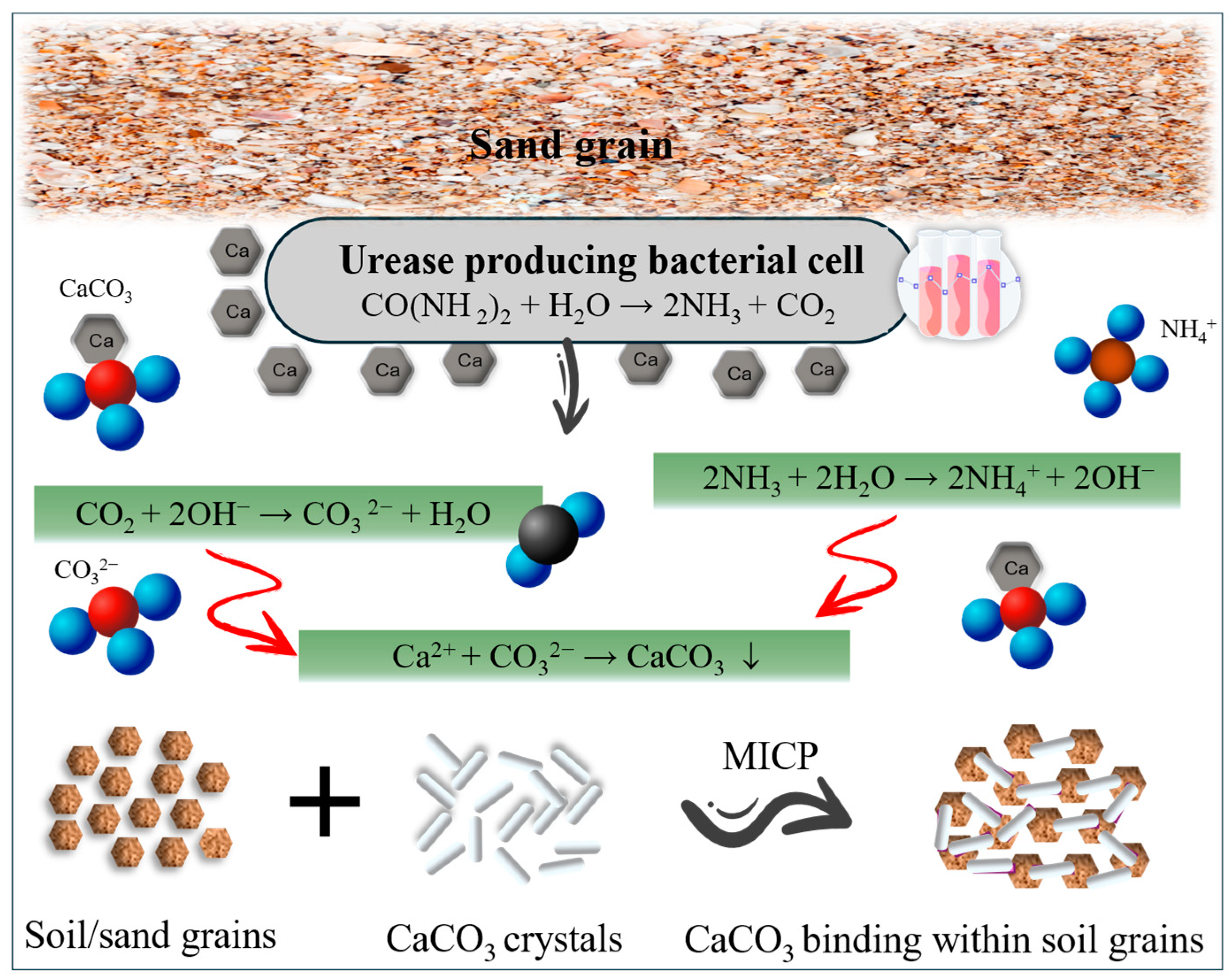
3.1. Microbially-Induced Calcite Precipitation
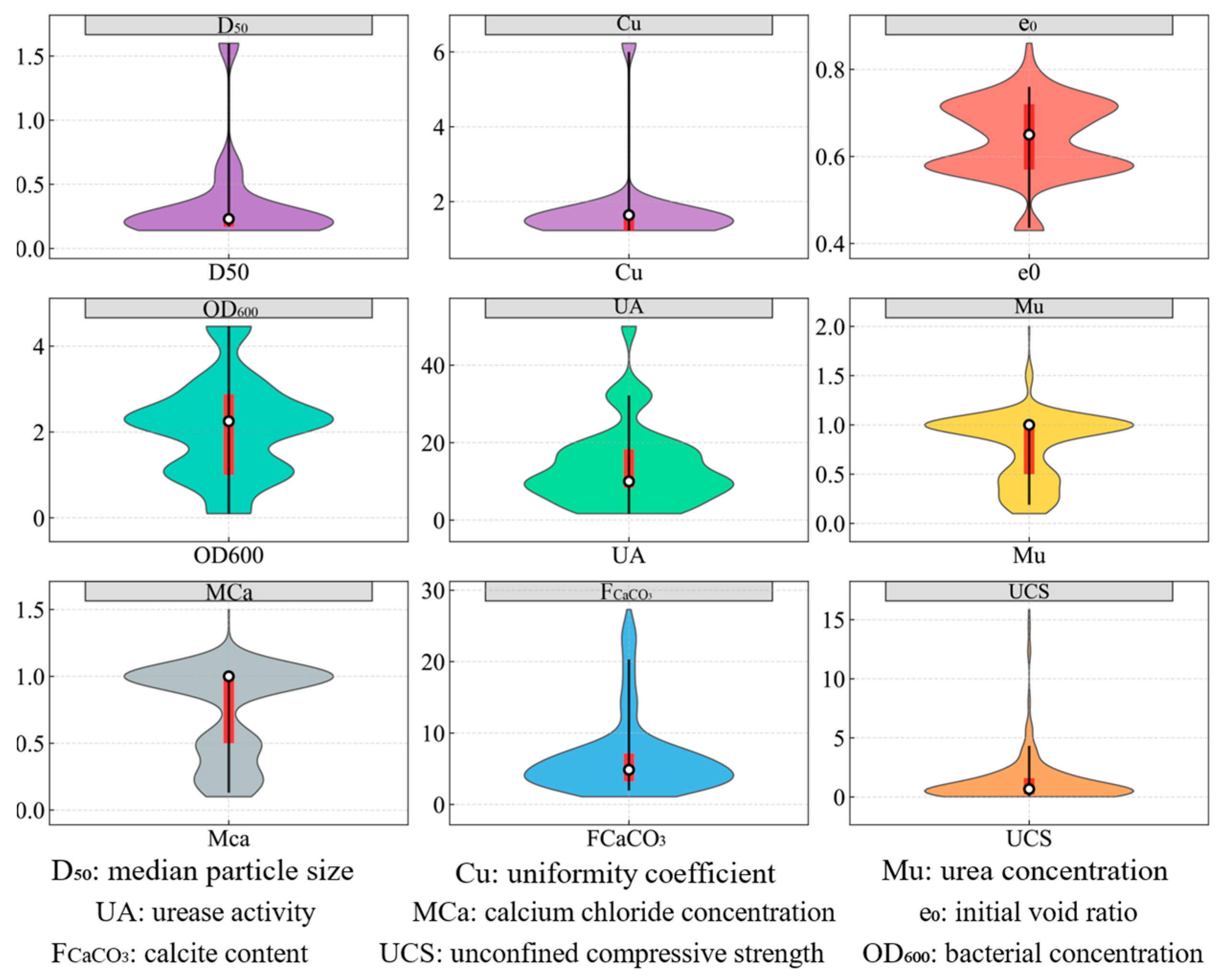
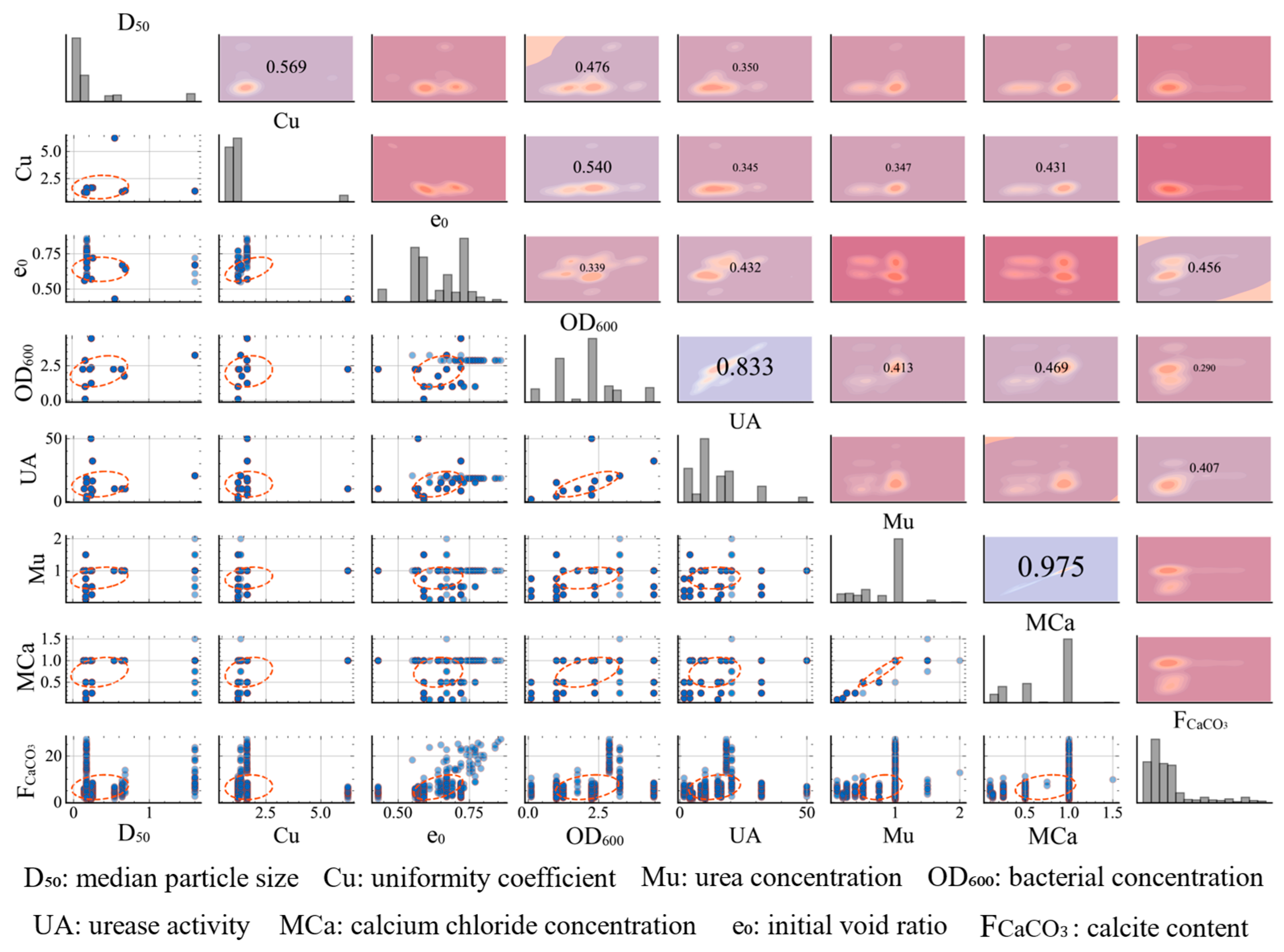
3.2. Data Statistical Analysis
4. Development of the Strength Model
4.1. Selection of the Base Model
4.2. Base Model Optimisation and Ensemble
5. Results and Discussion
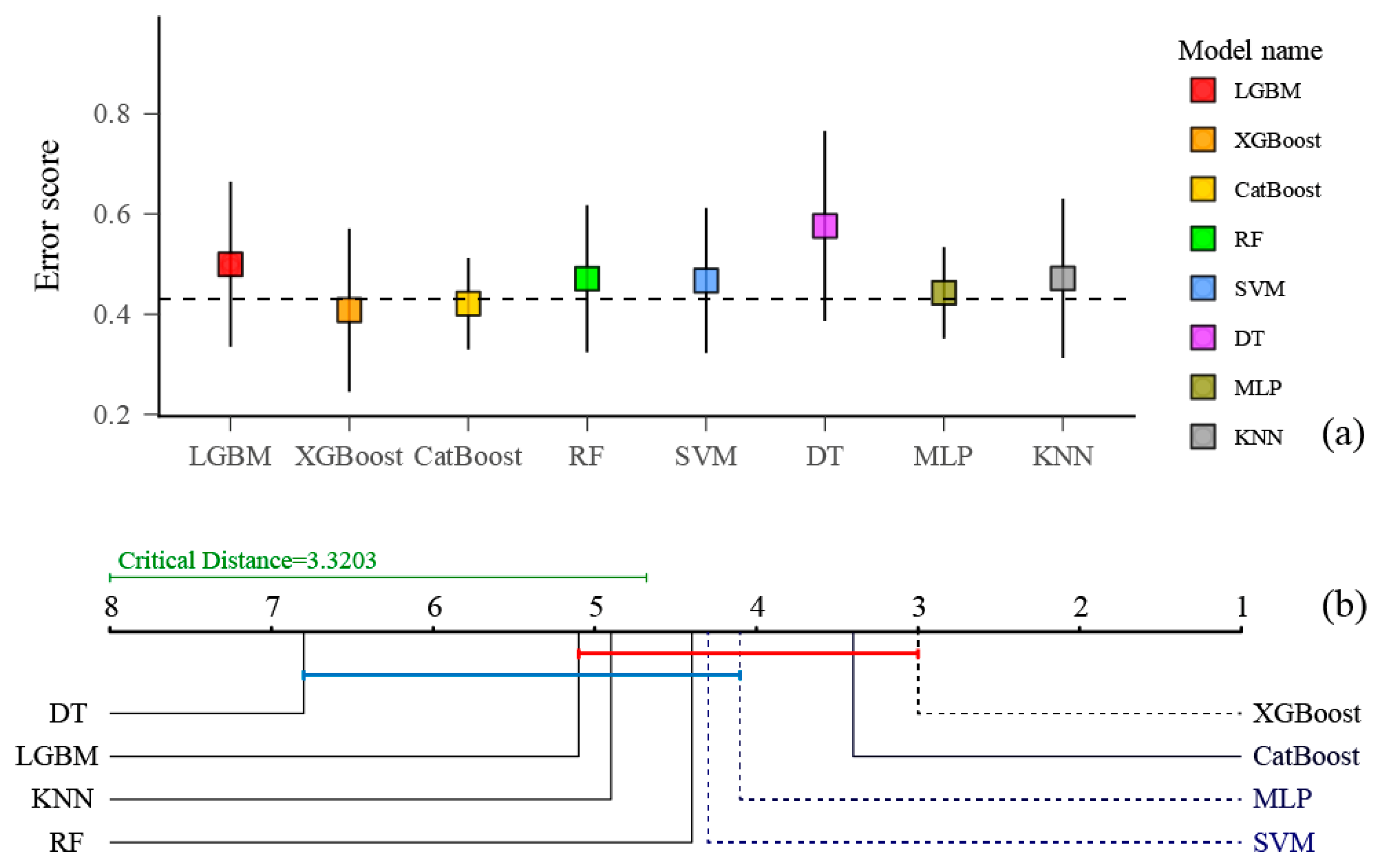
5.1. Performance Comparison
5.2. Sensitivity Analysis
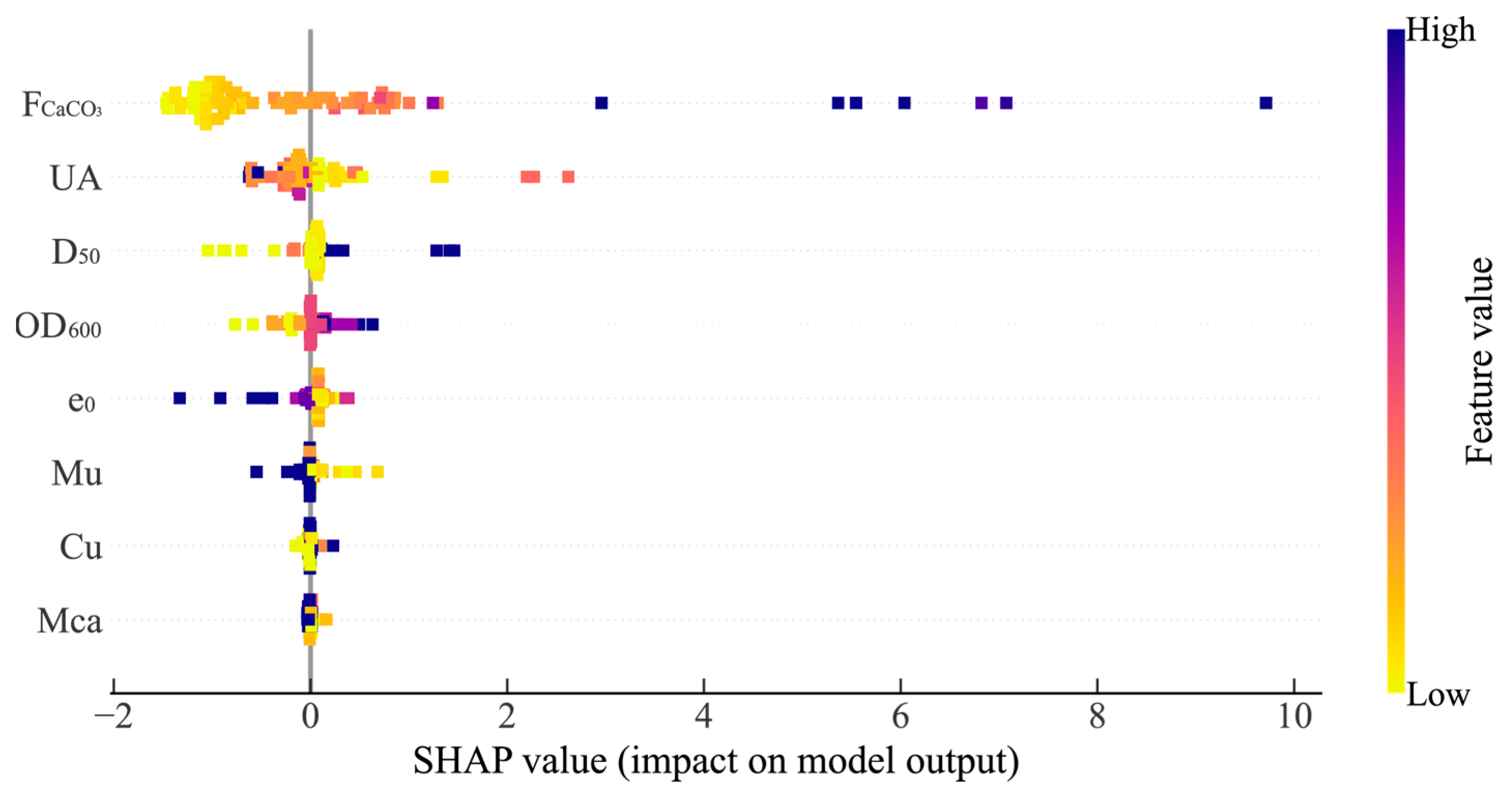
5.2.1. Overall Feature Analysis
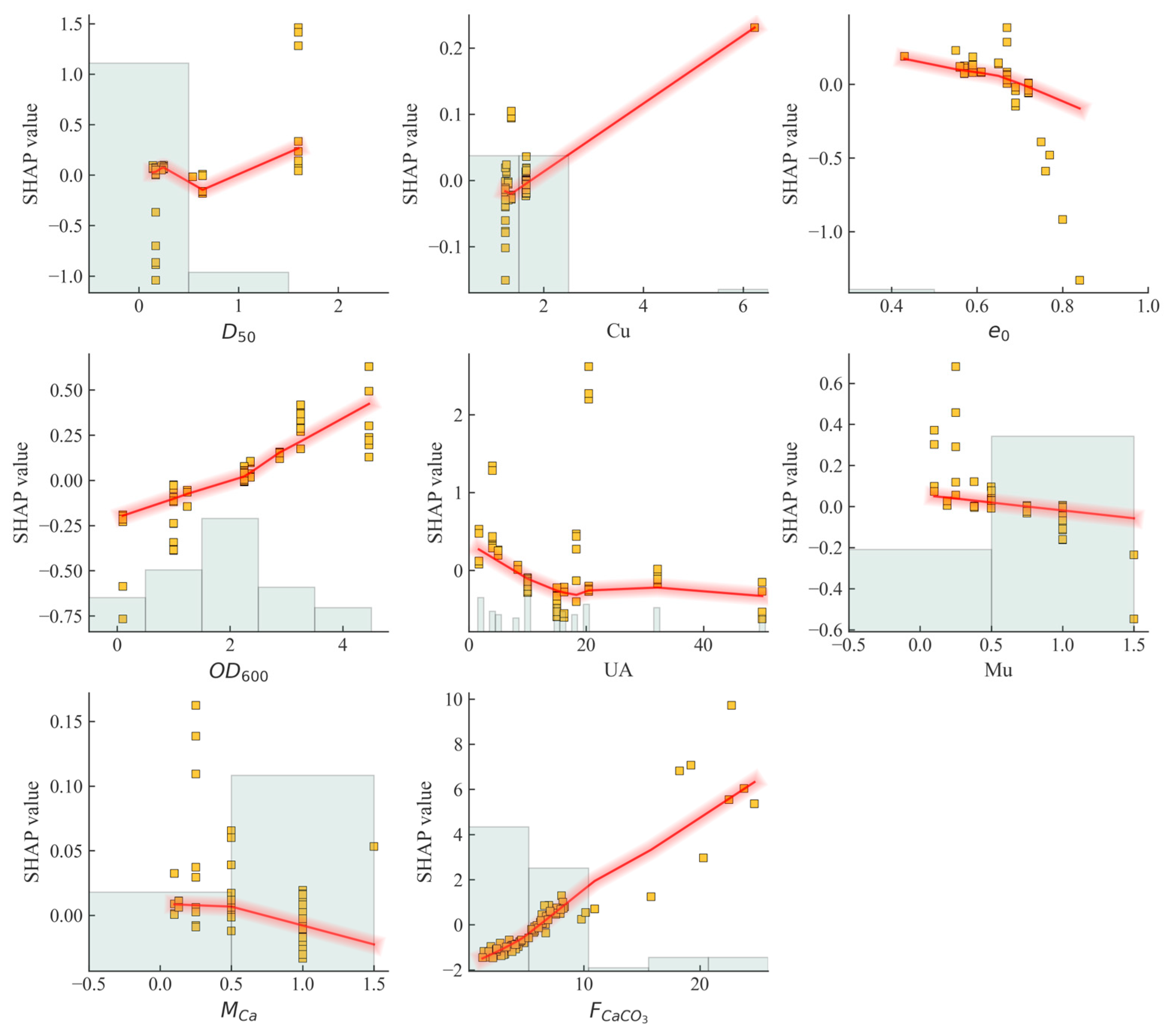
5.2.2. Feature Dependency Relationship Analysis
6. Conclusions
- (a)
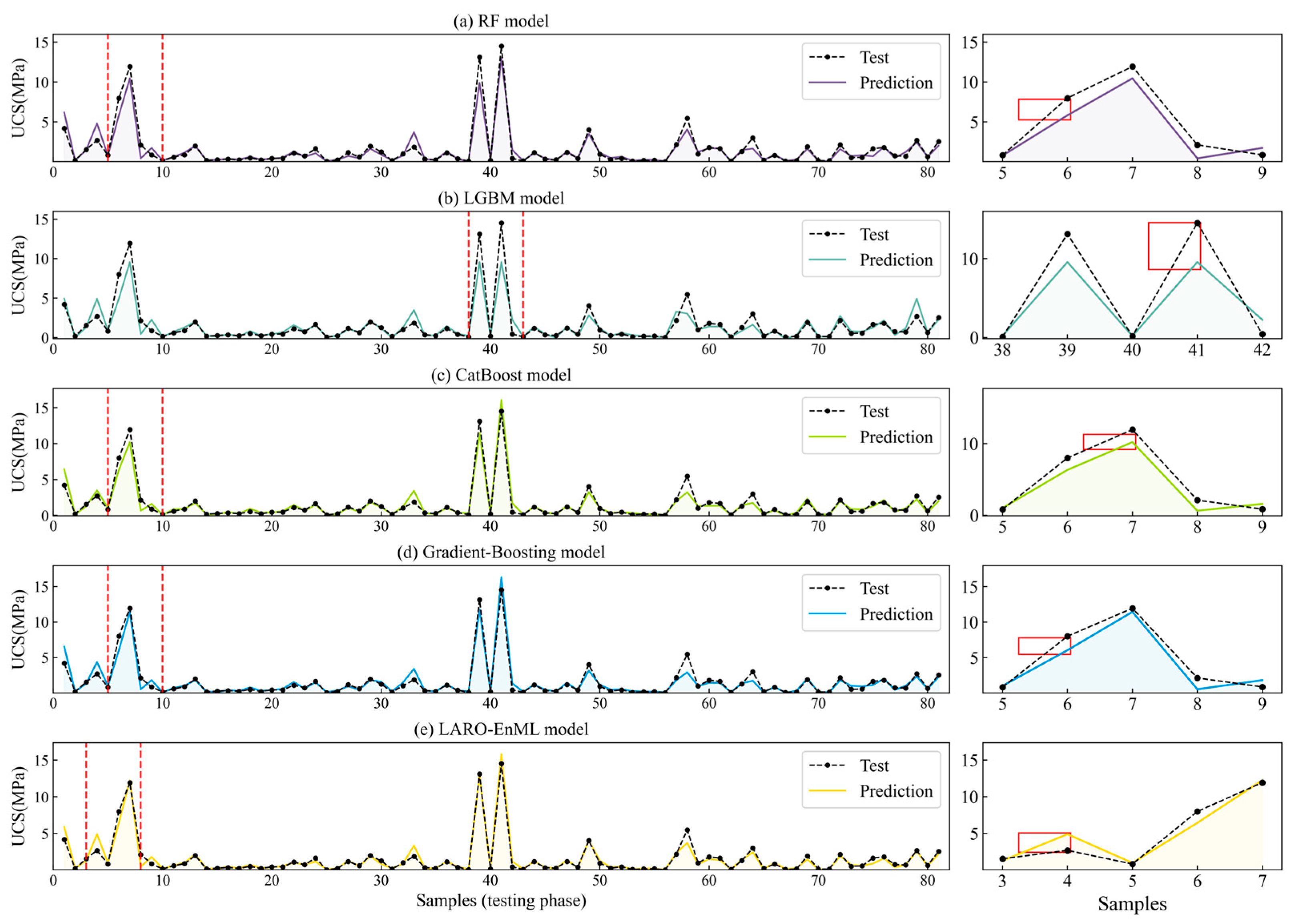
- The proposed LARO-EnML attained the best results (RMSE = 0.5449, MAE = 0.2853, R2 = 0.9570, OI = 0.9597) on the test data, compared to individual ML methods. The integration of LARO optimisation effectively enhanced base learner performance, while the hierarchical architecture successfully mitigated overfitting issues, resulting in superior generalisation capability and providing a robust prediction tool for complex bio-geotechnical systems.
- (b)
- SHAP interpretability analysis identified calcite content as the dominant factor governing MICP treatment effectiveness, exhibiting a strong positive correlation with strength enhancement. Urease activity demonstrated optimal effectiveness at lower concentrations with diminishing returns at higher levels, while median particle size revealed nonlinear dependency with distinct thresholds for bio-cementation efficiency. These findings establish fundamental parameter hierarchies and provide quantitative guidance for MICP process optimisation in engineering applications.
- (c)
- While bacterial optical density, initial void ratio, and nutrient solution parameters demonstrated relatively weaker individual contributions, their synergistic interactions with dominant factors proved essential for optimising MICP treatment outcomes. The analysis revealed that these secondary parameters influence bio-cementation efficiency through mechanisms affecting bacterial distribution, reaction kinetics, and precipitation uniformity, emphasising the necessity of holistic parameter optimisation strategies.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MICP | microbially induced calcite precipitation | UCS | unconfined compressive strength |
| SHAP | SHapley Additive exPlanations | LGBM | light gradient boosting machine |
| ML | machine learning | MAE | mean absolute error |
| MEP | multi-expression programming | RMSE | root mean square error |
| SVM | support vector machine | R2 | coefficient of determination |
| XGBoost | extreme gradient boosting | OI | overall index |
| MLP | multi-layer perceptron | ARO | artificial rabbits optimisation |
| OD600 | bacterial concentration | Mu | urea concentration |
| FCaCO3 | calcite content | D50 | median particle size |
| e0 | initial void ratio | MCa | calcium chloride concentration |
| UA | urease activity | Cu | uniformity coefficient |
| CaBoost | categorical boosting | RF | random forest |
| DT | decision tree | KNN | k-nearest neighbours |
| NE | number of estimators | RL | regularisation parameter |
| SA | subsample ratio | LR | learning rate |
| EC | efficiency coefficient | CD | critical difference |
References
- Jalili, M.; Ghasemi, M.R.; Pifloush, A.R. Stiffness and Strength of Granular Soils Improved by Biological Treatment Bacteria Microbial Cements. Emerg. Sci. J. 2018, 2, 219–227. [Google Scholar] [CrossRef]
- Naveed, M.; Duan, J.; Uddin, S.; Suleman, M.; Hui, Y.; Li, H. Application of microbially induced calcium carbonate precipitation with urea hydrolysis to improve the mechanical properties of soil. Ecol. Eng. 2020, 153, 105885. [Google Scholar] [CrossRef]
- Amini, O.; Ghasemi, M. Laboratory study of the effects of using magnesium slag on the geotechnical properties of cement stabilized soil. Constr. Build. Mater. 2019, 223, 409–420. [Google Scholar] [CrossRef]
- Tang, C.S.; Yin, L.; Jiang, N.; Zhu, C.; Zeng, H.; Li, H.; Shi, B. Factors affecting the performance of microbial-induced carbonate precipitation (MICP) treated soil: A review. Environ. Earth Sci. 2020, 79, 409–420. [Google Scholar] [CrossRef]
- Van Paassen, L.A.; Ghose, R.; van der Linden, T.J.; van der Star, W.R.; van Loosdrecht, M.C. Quantifying biomediated ground improvement by ureolysis: Large-scale biogrout experiment. J. Geotech. Geoenviron. Eng. 2010, 136, 1721–1728. [Google Scholar] [CrossRef]
- Wang, H.L.; Yin, Z.Y. Unconfined compressive strength of bio-cemented sand: State-of-the-art review and MEP-MC-based model development. J. Clean. Prod. 2021, 315, 128205. [Google Scholar] [CrossRef]
- Terzis, D.; Perego, C.; Cappa, M.; Pianta, E.; Mauri, F.; Principi, P. Biocementation beyond the Petri dish, scaling up to 900 L batches and a meter-scale column. Sci. Rep. 2025, 15, 3030. [Google Scholar] [CrossRef] [PubMed]
- De Jong, J.T.; Mortensen, B.M.; Martinez, B.C.; Nelson, D.C. Bio-mediated soil improvement. Ecol. Eng. 2010, 36, 197–210. [Google Scholar] [CrossRef]
- Ivanov, V.; Chu, J. Applications of microorganisms to geotechnical engineering for bioclogging and biocementation of soil in situ. Rev. Environ. Sci. Bio/Technol. 2008, 7, 139–153. [Google Scholar] [CrossRef]
- Chen, L.; Song, Y.; Fang, H.; Feng, Q.; Lai, C.; Song, X. Systematic optimization of a novel, cost-effective fermentation medium of Sporosarcina pasteurii for microbially induced calcite precipitation (MICP). Constr. Build. Mater. 2022, 348, 128632. [Google Scholar] [CrossRef]
- De Muynck, W.; De Belie, N.; Verstraete, W. Microbial carbonate precipitation in construction materials: A review. Ecol. Eng. 2010, 36, 118–136. [Google Scholar] [CrossRef]
- Ng, W.S.; Lee, M.L.; Hii, S.L. An overview of the factors affecting microbial-induced calcite precipitation and its potential application in soil improvement. In Proceedings of the World Academy of Science, Engineering and Technology; World Academy of Science, Engineering and Technology: New York, NY, USA, 2012; Volume 62, pp. 723–729. [Google Scholar]
- Mitchell, J.K.; Santamarina, J.C. Biological considerations in geotechnical engineering. J. Geotech. Geoenviron. Eng. 2005, 131, 1222–1233. [Google Scholar] [CrossRef]
- Chu, J.; Stabnikov, V.; Ivanov, V. Microbially induced calcium carbonate precipitation on surface or in the bulk of soil. Geomicrobiol. J. 2012, 29, 544–549. [Google Scholar] [CrossRef]
- Wani, K.M.N.S.; Mir, B.A. Microbial geo-technology in ground improvement techniques: A comprehensive review. Innov. Infrastruct. Solut. 2020, 5, 82. [Google Scholar] [CrossRef]
- Mujah, D.; Shahin, M.A.; Cheng, L. State-Of-The-Art Review Of Biocementation By Microbially Induced Calcite Precipitation (MICP) For Soil Stabilization. Geomicrobiol. J. 2016, 34, 524–537. [Google Scholar] [CrossRef]
- Chu, J.; Ivanov, V.; Naeimi, M.; Stabnikov, V.; Liu, H.-L. Optimization of calcium-based bioclogging and biocementation of sand. Acta Geotech. 2013, 9, 277–285. [Google Scholar] [CrossRef]
- Yang, P.; Yong, W.; Li, C.; Peng, K.; Wei, W.; Qiu, Y.; Zhou, J. Hybrid random forest-based models for earth pressure balance tunneling-induced ground settlement prediction. Appl. Sci. 2023, 13, 2574. [Google Scholar] [CrossRef]
- Sioutas, K.N.; Benardos, A. Boosting Model Interpretability for Transparent ML in TBM Tunneling. Appl. Sci. 2024, 14, 11394. [Google Scholar] [CrossRef]
- Navarro-Rodríguez, A.; Castro-Artola, O.A.; García-Guerrero, E.E.; Aguirre-Castro, O.A.; Tamayo-Pérez, U.J.; López-Mercado, C.A.; Inzunza-Gonzalez, E. Recent Advances in Early Earthquake Magnitude Estimation by Using Machine Learning Algorithms: A Systematic Review. Appl. Sci. 2025, 15, 3492. [Google Scholar] [CrossRef]
- Talamkhani, S. Machine Learning-Based Prediction of Unconfined Compressive Strength of Sands Treated by Microbially-Induced Calcite Precipitation (MICP): A Gradient Boosting Approach and Correlation Analysis. Adv. Civ. Eng. 2023, 2023, 3692090. [Google Scholar] [CrossRef]
- Cheng, C.; Xu, P.-F.; Cheng, H.; Ding, Y.; Zheng, J.; Ge, T.; Sun, D.; Xu, J. Ensemble learning approach based on stacking for unmanned surface vehicle’s dynamics. Ocean Eng. 2020, 207, 107388. [Google Scholar] [CrossRef]
- Shafieian, S.; Zulkernine, M. Multi-layer stacking ensemble learners for low footprint network intrusion detection. Complex Intell. Syst. 2022, 9, 3787–3799. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhou, J. Short-term rockburst damage assessment in burst-prone mines: An explainable xgboost hybrid model with scso algorithm. Rock Mech. Rock Eng. 2023, 56, 8745–8770. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Rokach, L. Ensemble-based classifiers. Artif. Intell. Rev. 2010, 33, 1–39. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhou, J. Short-term rockburst prediction in underground project: Insights from an explainable and interpretable ensemble learning model. Acta Geotech. 2023, 18, 6655–6685. [Google Scholar] [CrossRef]
- Wang, L.; Cao, Q.; Zhang, Z.; Mirjalili, S.; Zhao, W. Artificial rabbits optimization: A new bio-inspired meta-heuristic algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2022, 114, 105082. [Google Scholar] [CrossRef]
- Gülmez, B. Stock price prediction with optimized deep LSTM network with artificial rabbits optimization algorithm. Expert Syst. Appl. 2023, 227, 120346. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, L.; Zhong, J.; Hu, G. LARO: Opposition-Based Learning Boosted Artificial Rabbits-Inspired Optimization Algorithm with Lévy Flight. Symmetry 2022, 14, 2282. [Google Scholar] [CrossRef]
- Rezaeineshat, A.; Monjezi, M.; Mehrdanesh, A.; Khandelwal, M. Optimization of blasting design in open pit limestone mines with the aim of reducing ground vibration using robust techniques. Géoméch. Geophys. Geo-Energy Geo-Resour. 2020, 6, 1–14. [Google Scholar] [CrossRef]
- Zhang, Y.-L.; Qiu, Y.-G.; Armaghani, D.J.; Monjezi, M.; Zhou, J. Enhancing rock fragmentation prediction in mining operations: A Hybrid GWO-RF model with SHAP interpretability. J. Central South Univ. 2024, 31, 2916–2929. [Google Scholar] [CrossRef]
- Cheng, L.; Shahin, M.A. Microbially induced calcite precipitation (MICP) for soil stabilization. Ecol. Wisdom Inspired Restor. Eng. 2019, 47–68. [Google Scholar]
- Razbani, M.A.; Jettestuen, E.; Røyne, A. Direct Pore-Scale Numerical Simulation of Microbially Induced Calcium Carbonate Precipitation. Water Resour. Res. 2023, 59, e2022WR032988. [Google Scholar] [CrossRef]
- Jiang, L.; Xia, H.; Wang, W.; Zhang, Y.; Li, Z. Applications of microbially induced calcium carbonate precipitation in civil engineering practice: A state-of-the-art review. Constr. Build. Mater. 2023, 404, 133227. [Google Scholar] [CrossRef]
- Umar, M.; Kassim, K.A.; Chiet, K.T.P. Biological process of soil improvement in civil engineering: A review. J. Rock Mech. Geotech. Eng. 2016, 8, 767–774. [Google Scholar] [CrossRef]
- Huang, S.; Liu, K.; Li, Y.; Shi, X.; Fan, H.; Xu, M.; Jiang, Z.; Hu, F.; Ma, H.; Li, P. Electrolyte-rock interactions in salt cavern flow batteries. Energy 2025, 330, 136811. [Google Scholar] [CrossRef]
- Zehner, J.; Røyne, A.; Wentzel, A.; Sikorski, P. Microbial-induced calcium carbonate precipitation: An experimental toolbox for in situ and real time investigation of micro-scale pH evolution. RSC Adv. 2020, 10, 20485–20493. [Google Scholar] [CrossRef] [PubMed]
- Demšar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Zhou, J.; Li, X.; Mitri, H.S. Classification of rockburst in underground projects: Comparison of ten supervised learning methods. J. Comput. Civ. Eng. 2016, 30, 04016003. [Google Scholar] [CrossRef]
- Zhou, J.; Qiu, Y.; Khandelwal, M.; Zhu, S.; Zhang, X. Developing a hybrid model of Jaya algorithm-based extreme gradient boosting machine to estimate blast-induced ground vibrations. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2021, 145, 104856. [Google Scholar] [CrossRef]
- Cheng, L.; Shahin, M.A.; Mujah, D. Influence of key environmental conditions on microbially induced cementation for soil stabilization. J. Geotech. Geoenviron. Eng. 2017, 143, 04016083. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhou, J. Novel rockburst prediction criterion with enhanced explainability employing CatBoost and nature-inspired metaheuristic technique. Undergr. Space 2024, 19, 101–118. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, S.; Qiu, Y. Optimization of random forest through the use of MVO, GWO and MFO in evaluating the stability of underground entry-type excavations. Tunn. Undergr. Space Technol. 2022, 124, 104494. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhou, J. Methodology for Constructing Explicit Stability Formulas for Hard Rock Pillars: Integrating Data-Driven Approaches and Interpretability Techniques. Rock Mech. Rock Eng. 2025, 58, 5475–5502. [Google Scholar] [CrossRef]
- Mujah, D.; Cheng, L.; Shahin, M.A. Microstructural and geomechanical study on biocemented sand for optimization of MICP process. J. Mater. Civ. Eng. 2019, 31, 04019025. [Google Scholar] [CrossRef]
- Qabany, A.A.; Soga, K. Effect of chemical treatment used in MICP on engineering properties of cemented soils. In Bio-and Chemo-Mechanical Processes in Geotechnical Engineering: Géotechnique Symposium in Print 2013; ICE Publishing: London, UK, 2014; pp. 107–115. [Google Scholar] [CrossRef]
- Cheng, L.; Cord-Ruwisch, R.; Shahin, M.A. Cementation of sand soil by microbially induced calcite precipitation at various degrees of saturation. Can. Geotech. J. 2013, 50, 81–90. [Google Scholar] [CrossRef]
- Wang, Y.; Konstantinou, C.; Soga, K.; DeJong, J.T.; Biscontin, G.; Kabla, A.J. Enhancing strength of MICP-treated sandy soils: From micro to macro scale. arXiv 2020. [Google Scholar] [CrossRef]
- Mahawish, A.; Bouazza, A.; Gates, W.P. Factors affecting the bio-cementing process of coarse sand. Proc. Inst. Civ. Eng.-Ground Improv. 2019, 172, 25–36. [Google Scholar] [CrossRef]
- Mahawish, A.; Bouazza, A.; Gates, W.P. Unconfined compressive strength and visualization of the microstructure of coarse sand subjected to different biocementation levels. J. Geotech. Geoenvironmental Eng. 2019, 145, 04019033. [Google Scholar] [CrossRef]
| Model Name | Evaluation | |||
|---|---|---|---|---|
| RMSE | MAE | R2 | OI | |
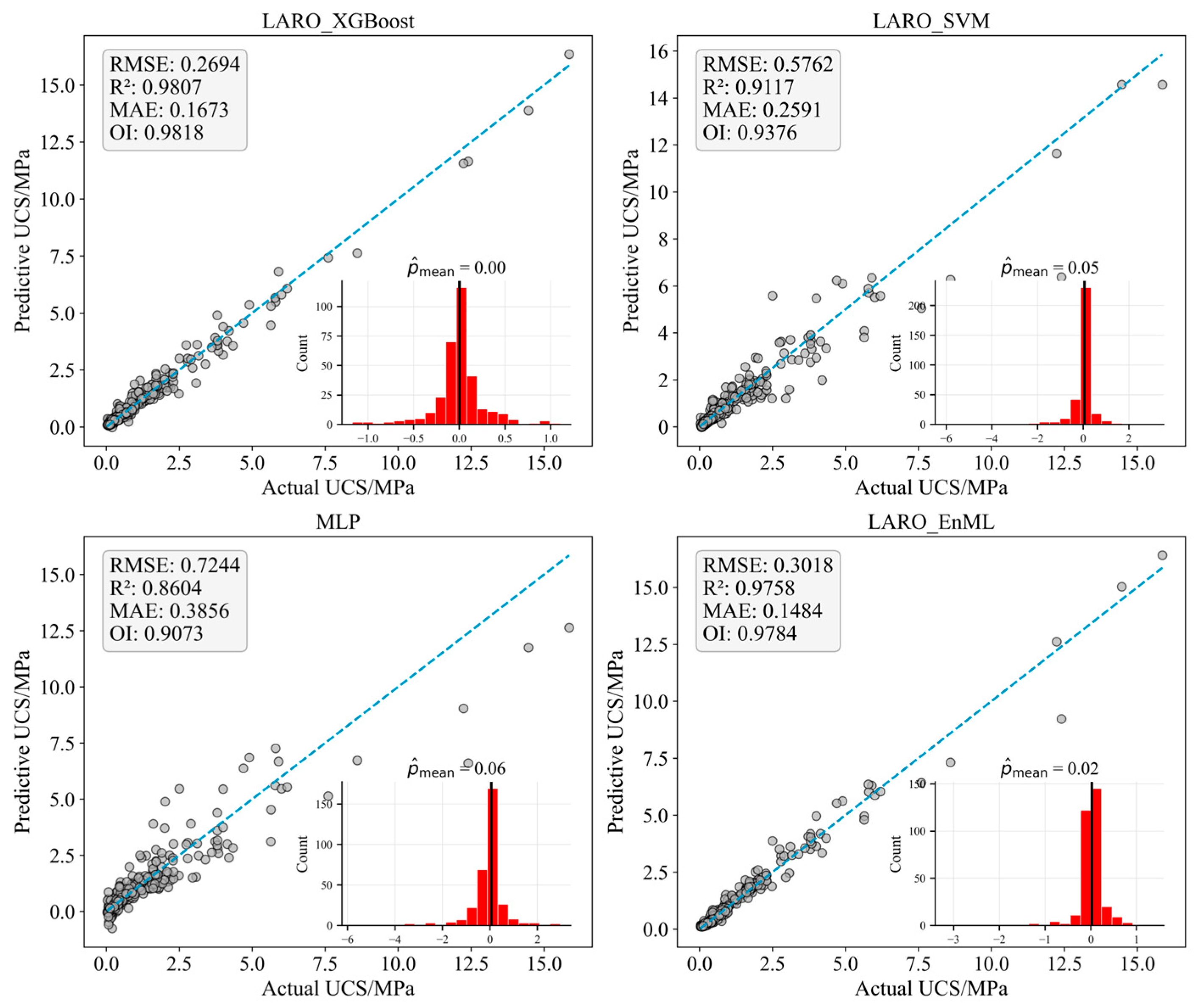
| XGBoost | 0.3262 | 0.2155 | 0.9717 | 0.9755 |
| LARO-XGBoost | 0.2694 | 0.1673 | 0.9807 | 0.9818 |
| SVM | 0.9323 | 0.4142 | 0.7688 | 0.8549 |
| LARO-SVM | 0.5762 | 0.2591 | 0.9117 | 0.9376 |
| MLP | 0.7244 | 0.3856 | 0.8604 | 0.9073 |
| LARO-EnML | 0.3018 | 0.1484 | 0.9758 | 0.9784 |
| Model Name | Evaluation | |||
|---|---|---|---|---|
| RMSE | MAE | R2 | OI | |
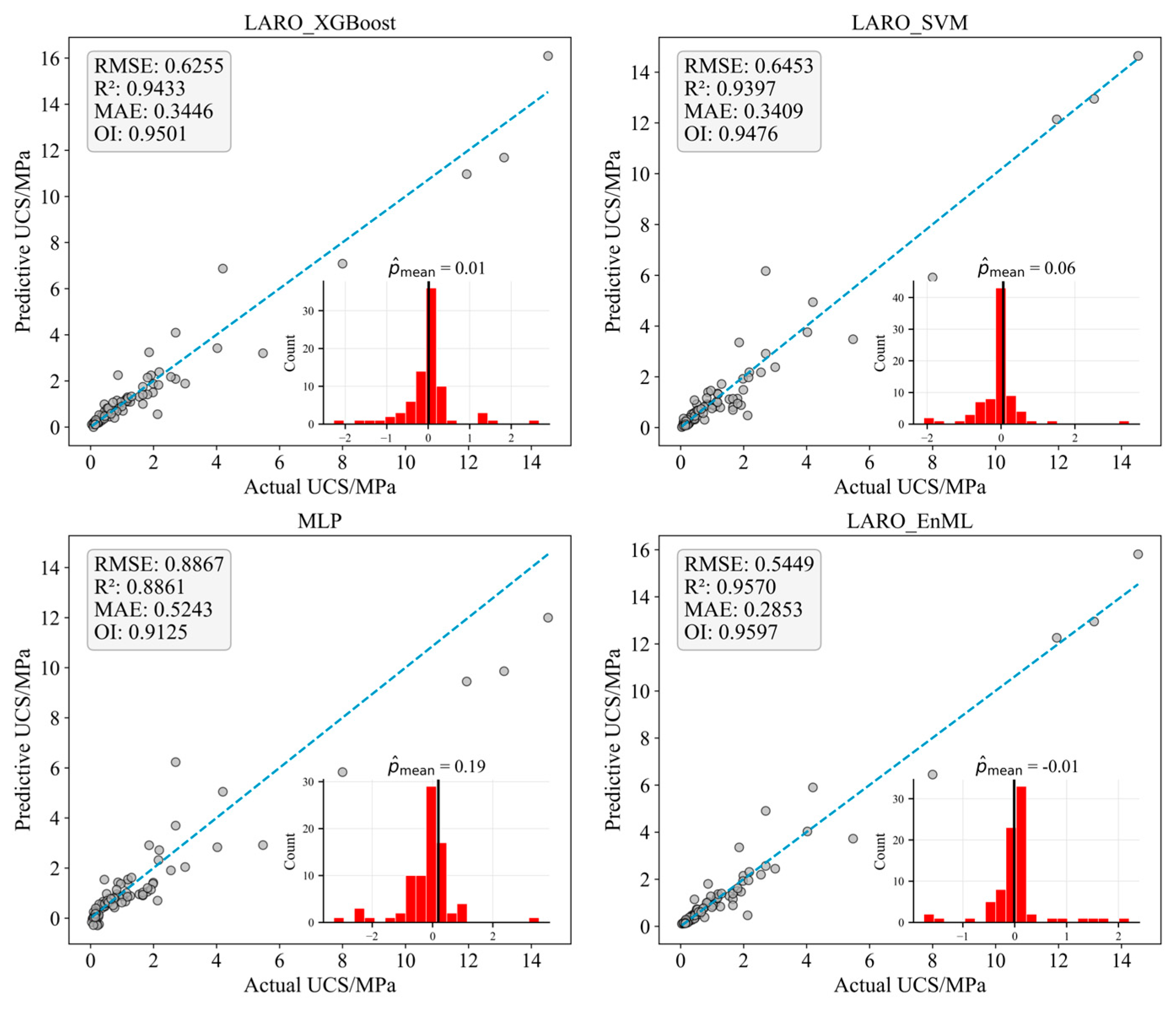
| XGBoost | 0.7043 | 0.4028 | 0.9282 | 0.9398 |
| LARO-XGBoost | 0.6255 | 0.3446 | 0.9433 | 0.9501 |
| SVM | 1.3681 | 0.6183 | 0.7290 | 0.8173 |
| LARO-SVM | 0.6453 | 0.3409 | 0.9397 | 0.9476 |
| MLP | 0.8867 | 0.5243 | 0.8861 | 0.9125 |
| LARO-EnML | 0.5449 | 0.2853 | 0.9570 | 0.9597 |
| Model Name | Evaluation | |||
|---|---|---|---|---|
| RMSE | MAE | R2 | OI | |
| LARO-EnML | 0.5449 | 0.2853 | 0.9570 | 0.9597 |
| CatBoost | 0.6425 | 0.3663 | 0.9402 | 0.9480 |
| RF | 0.7348 | 0.3838 | 0.9218 | 0.9356 |
| LGBM | 1.0382 | 0.5284 | 0.8439 | 0.8861 |
| Gradient Boosting | 0.6645 | 0.3684 | 0.9361 | 0.9451 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, Y.; Yao, S.; Qi, H.; Zhou, J.; Khandelwal, M. Interpretable Ensemble Learning with Lévy Flight-Enhanced Heuristic Technique for Strength Prediction of MICP-Treated Sands. Appl. Sci. 2025, 15, 7972. https://doi.org/10.3390/app15147972
Qiu Y, Yao S, Qi H, Zhou J, Khandelwal M. Interpretable Ensemble Learning with Lévy Flight-Enhanced Heuristic Technique for Strength Prediction of MICP-Treated Sands. Applied Sciences. 2025; 15(14):7972. https://doi.org/10.3390/app15147972
Chicago/Turabian StyleQiu, Yingui, Shibin Yao, Hongning Qi, Jian Zhou, and Manoj Khandelwal. 2025. "Interpretable Ensemble Learning with Lévy Flight-Enhanced Heuristic Technique for Strength Prediction of MICP-Treated Sands" Applied Sciences 15, no. 14: 7972. https://doi.org/10.3390/app15147972
APA StyleQiu, Y., Yao, S., Qi, H., Zhou, J., & Khandelwal, M. (2025). Interpretable Ensemble Learning with Lévy Flight-Enhanced Heuristic Technique for Strength Prediction of MICP-Treated Sands. Applied Sciences, 15(14), 7972. https://doi.org/10.3390/app15147972








