Abstract
Reliable rainfall thresholds are critical for effective early warning and mitigating the risks of rainfall-induced landslides. Traditional statistical models have limitations in multi-variable modeling, while machine learning models face interpretability challenges. Explainable machine learning methods can address these challenges, but they are rarely applied to rainfall threshold modeling. In this study, we compared the performance of an empirical statistical model and machine learning models for predicting rainfall-induced landslides in Italy. Based on the optimal model, we visualized refined rainfall thresholds at three probability levels and employed SHAP (Shapley Additive Explanations) to enhance model explainability by quantifying the contribution of each input variable to the predictions. The results demonstrated that the XGBoost model achieved a good performance (AUC = 0.917 ± 0.026) with well-balanced sensitivity (0.792 ± 0.075) and specificity (0.812 ± 0.033) in landslide susceptibility modeling. Hydrological factors, particularly total rainfall, were identified as the dominant triggering mechanisms, with SHAP analysis confirming their substantially greater contribution compared to environmental factors in rainfall threshold modeling. The developed visualized threshold maps revealed distinct spatial variations in landslide-triggering rainfall thresholds across Italy, characterized by lower thresholds in gentle slope areas with moderate annual precipitation and higher thresholds in steep slope and mid-to-low-elevation regions, while these regional differences decreased under high-probability scenarios. This study offered a modeling approach for regional rainfall threshold assessment by integrating multi-variable modeling with explainable methods, contributing to the development of landslide early warning systems.
1. Introduction
Rainfall-induced landslides are a significant geological hazard that poses severe threats to human lives and property [1]. Some countries have particularly high frequencies of such landslides due to their unique geographical locations, geological structure, and climatic conditions [2,3,4,5]. Therefore, diverse strategies for landslide prediction and prevention are being actively explored and implemented globally to answer the crucial question of “how much rainfall is required to trigger a landslide”.
To address this issue, previous studies have proposed empirical statistical models, primarily in the form of rainfall intensity–duration (I-D) curves [6] and cumulative rainfall–duration (E-D) curves [7]. These models establish regional rainfall threshold criteria by describing the statistical relationship between rainfall parameters and landslides, with the aim of determining the minimum rainfall required to trigger landslides in specific geological and climatic regions. Due to the ease of data acquisition and simple computation, these methods allow for the establishment of straightforward and practical early warning standards. Most empirical threshold models typically develop a single universal threshold for the entire study area, ignoring the comprehensive influence of factors such as soil type, vegetation cover, and topography [8,9,10]. Although some studies have successfully refined thresholds based on individual factors as division criteria [11,12], the comprehensive consideration of multiple geological and environmental conditions could further refine the thresholds and enhance their predictive performance. It has been demonstrated by numerous studies that landslide-triggering thresholds vary significantly depending on diverse regional geological and climatic conditions [13,14,15], suggesting that more accurate and regionally appropriate threshold models could be achieved through an approach that incorporates various environmental factors.
In recent years, machine learning techniques have shown remarkable potential in geohazard prediction accuracy by effectively integrating multiple influencing factors and significantly reducing the economic costs of prediction processes [16,17], while demonstrating superior performance in handling large-scale datasets to address complex geospatial modeling challenges [18]. Currently, their application is most prevalent in landslide susceptibility mapping. For instance, J.N. Goetz et al. incorporated 11 topographic factors (e.g., slope) in Lower Austria and systematically compared the performance of six models, including support vector machines (SVM) and random forests (RF) [19]. Liang Lv et al. proposed a heterogeneous ensemble learning (HEL) framework based on foundational models such as deep belief networks (DBN), convolutional neural networks (CNN), and residual networks (ResNet) to enhance modeling efficacy [20]. However, existing studies predominantly rely on static terrain features, neglecting dynamic triggers such as rainfall, which limits real-time early warning capabilities. To address this gap, researchers have begun integrating rainfall factors: Zhice Fang et al. used rainfall time series as the sole input variable with long short-term memory (LSTM) networks to predict landslide probability [21], while Te Xiao et al. developed a spatio-temporally coupled landslide prediction framework for rainstorm scenarios by comparing empirical and machine learning approaches [22]. With the increasing complexity of these machine learning models, “black box” problems have emerged as a significant concern, making it difficult to understand the model’s decision-making rationale [23]. Therefore, researchers have attempted to employ explainable techniques to enhance model transparency by quantifying the contribution of input variables [24,25].
Building upon the work of these previous studies, this study used machine learning to extend empirical rainfall threshold models by incorporating multiple environmental factors that potentially influence rainfall thresholds and employed explainable methods to ensure model transparency. In this way, an explainable landslide prediction model was developed that improved prediction accuracy and provides a reference for establishing regional rainfall thresholds. Specifically, our study includes the following contributions:
- We compared the predictive performance of empirical threshold models with four machine learning models on imbalanced datasets. The XGBoost model achieved optimal overall predictive performance and effectively balanced sensitivity and specificity;
- The SHAP methodology was employed to enhance the interpretability of the machine learning model, which helped clarify the model’s decision-making process. The results indicate that hydrological factors, particularly total rainfall, play a central role in the modeling process.
- Using the trained XGBoost model, we generated rainfall threshold maps for the Italian region under three different probability scenarios.
- This study established an intuitive and practical modeling framework for regional rainfall threshold development, offering reference for subsequent studies.
2. Study Area, Data, and Methodology
2.1. Study Area
This study focused on the entire territory of Italy, which is geographically defined by the Alps in the north and the Apennine Mountains running through the central and southern regions (Figure 1a). The study area is predominantly composed of sedimentary, metamorphic, and volcanic rocks, with cambisols, luvisols, and regosols as the primary soil types, collectively covering 63% of the total land area [26]. Italy experiences a typical Mediterranean climate, characterized by warm, dry summers and mild, humid winters. The northern Alpine region, in contrast, features an alpine climate with frequent snowfall during winter. Between 1981 and 2020, the mean annual precipitation across Italy ranged from 350 mm to 1895 mm (Figure 1b), exhibiting a highly uneven spatial distribution. The northern Alpine region received the highest precipitation, while a distinct high-rainfall belt extended along the Apennine Mountains. Conversely, lower precipitation levels were observed along the western coastal areas and the eastern Adriatic coast. Due to the combined effects of topography and climate, rainfall-induced landslides are highly frequent in Italy. Research conducted by Silvia Peruccacci et al. [27] identified 6312 temporally precise rainfall-triggered landslides between January 1996 and December 2021. Landslide activity peaked during autumn and winter, particularly in October and November, with November alone accounting for 17.3% of all recorded events. In contrast, the lowest landslide occurrences were observed in July and August, contributing only 3.8% and 3.9% of total events, respectively.
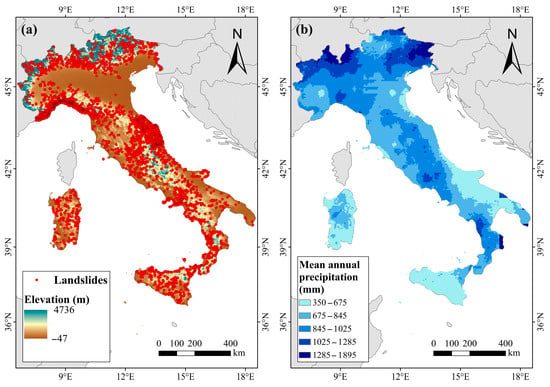
Figure 1.
Geographic and climatic characteristics of Italy: (a) topography and landslide distribution; (b) mean annual precipitation from 1981 to 2020.
2.2. Data
The landslide data used in this study were sourced from the Italian Rainfall-Triggered Landslide Inventory, compiled by Silvia Peruccacci et al. [27]. This catalog contains 6312 records of rainfall-induced landslides that occurred across Italy between January 1996 and December 2021. With relatively precise landslide locations and occurrence dates, this dataset provides a robust foundation for reconstructing rainfall-triggering events.
Based on previous studies [28,29,30], we incorporated key static environmental factors (Figure 2) that influence landslide initiation, including elevation, slope, lithology, soil type, land use, aspect, plan curvature, profile curvature, distance to the roads and distance to the rivers. The data sources and spatial resolutions of these factors are detailed in Table 1, and the code definitions for categorical factors with their corresponding full names are provided in Table 2. These static parameters play a crucial role in determining the rainfall thresholds required to trigger landslides. These spatial variables, which contribute to determining the rainfall thresholds required to trigger landslides [7,31,32,33], have been extensively validated for their effectiveness in enhancing the accuracy and reliability of landslide prediction models [34,35].
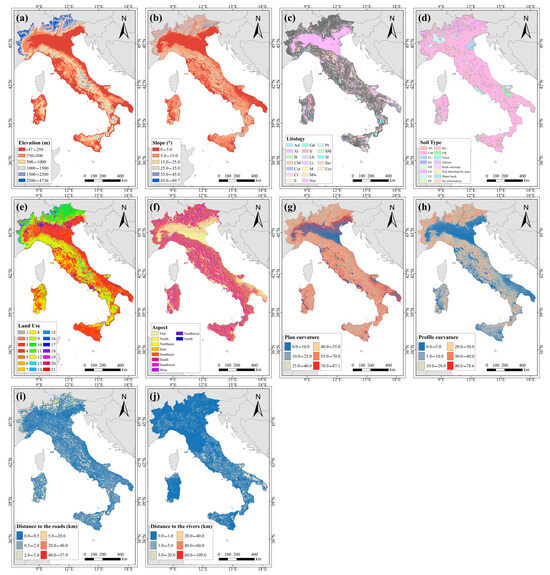
Figure 2.
Spatial distribution of static environmental factors used in this study: (a) elevation; (b) slope; (c) lithology; (d) soil type; (e) land use; (f) aspect; (g) plan curvature; (h) profile curvature; (i) distance to roads; (j) distance to rivers.

Table 1.
Data sources and spatial resolutions of static environmental factors used in this study.

Table 2.
Category factor codes and their corresponding full names.
This study employed the Climate Hazards Center InfraRed Precipitation with Station data (CHIRPS) [36] as the rainfall dataset. CHIRPS is a globally available raster data product with a spatial resolution of 0.05°, providing daily precipitation records from 1981 onward with continuous updates. Renowned for its high accuracy and reliability, CHIRPS is widely utilized in precipitation monitoring and the analysis of antecedent rainfall events in landslide studies.
As a key indicator of soil hydrological dynamics, soil moisture plays a crucial role in modulating the cumulative effects of rainfall events. It is essential for establishing precipitation thresholds that trigger landslides. Integrating soil moisture data enhances the predictive accuracy of landslide models and provides a robust foundation for defining rainfall thresholds [37,38]. In this study, we incorporated the European high-resolution soil moisture dataset (SoMo.ml-EU), developed by Sungmin O et al. [39]. This dataset provides daily soil moisture records spanning 2003 to 2020 at a spatial resolution of 0.1°, covering three soil layers (0–10 cm, 10–30 cm, and 30–50 cm).
To ensure consistency among all datasets, we resampled all spatial layers to a uniform resolution of 1 km using ArcGIS 10.8. Additionally, only landslide events and rainfall records from 2003 to 2020 were retained to match the temporal coverage of the SoMo.ml-EU soil moisture data, with events outside this period excluded.
2.3. Methods
The methodology of this study consists of six steps (Figure 3): (1) reconstruct rainfall events by segmenting continuous rainfall periods into independent events based on predefined criteria and extracting key hydrological variables, including total rainfall (mm), rainfall intensity (mm/day), and the seven-day antecedent average soil moisture at a depth of 30–50 cm (m3/m3); (2) prepare labeled input datasets containing both positive samples (landslide-triggering rainfall events, label = 1) and negative samples (non-triggering rainfall events, label = 0), along with corresponding hydrological and static environmental factors (elevation, slope, lithology, soil type, land use, aspect, plan curvature, profile curvature, distance to the roads and distance to the rivers); (3) use leave-one-region-out cross-validation for model training and validation on 80% of the dataset, where each macro-region is sequentially held out as the validation set, while the remaining macro-regions are used for training; (4) develop predictive models using cumulative rainfall–duration (E-D) curves, eXtreme Gradient Boosting (XGBoost), Random Forest (RF), Light Gradient Boosting Machine (LightGBM), and Logistic Regression (LR); (5) evaluate model performance; (6) analyze feature contributions using SHapley Additive exPlanations (SHAP) for the trained model on the remaining 20% of the dataset to gain insights into the influence of each variable on landslide prediction; and (7) apply the trained model to dynamically adjust rainfall parameters, analyze variations in prediction probabilities, and generate spatial distribution maps of rainfall thresholds under different probability scenarios.
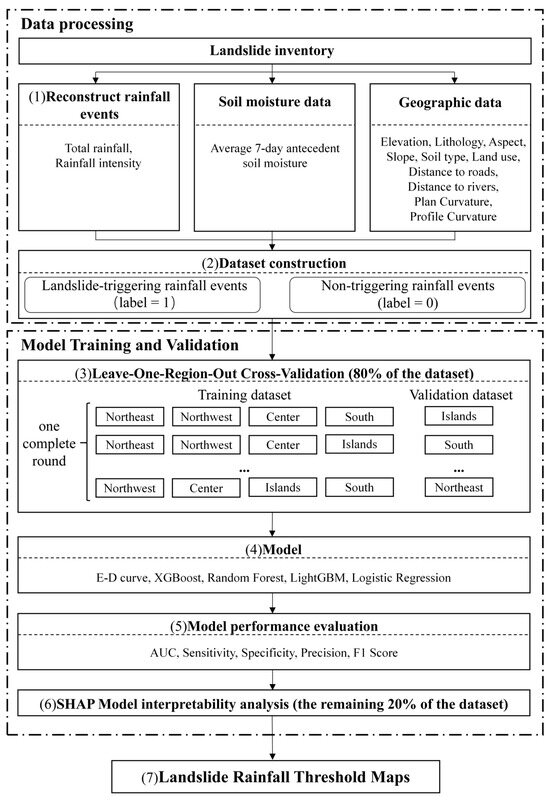
Figure 3.
Methodology flowchart of this study.
2.3.1. Rainfall Events
In this study, rainfall events were defined as continuous or temporally clustered precipitation periods separated by dry intervals of specific durations [12]. Specifically, dry intervals of 48 h (two days) and 96 h (four days) were used to delineate rainfall events during the dry season (June to September) and the wet season (October to May), respectively [40]. These different separation criteria were adopted to account for the distinct meteorological patterns of Mediterranean climate, as summer rainfall events were generally brief, while autumn and winter events tended to be more continuous [7,41]. For each landslide location, rainfall sequences spanning 365 days prior to the landslide occurrence were extracted and segmented into discrete rainfall events based on predefined criteria. The rainfall event closest to the landslide occurrence date was classified as a landslide-triggering event, while all others were designated as non-triggering events. However, this definition primarily considers direct rainfall impacts and does not account for additional influencing factors such as snowmelt, groundwater fluctuations, or potential inaccuracies in rainfall data, necessitating further refinement of triggering event identification [42]. Gariano et al. [43] excluded landslides with ambiguous or weak correlations to rainfall, particularly those associated with daily rainfall below the 25th percentile, while Smith et al. [44] empirically identified an approximate nine-day lag between rainfall peaks and subsequent landslide movements. Building on these findings, this study applied two exclusion criteria to refine the selection of landslide-triggering rainfall events: (1) events with cumulative rainfall within the lowest 10% of the dataset were excluded to remove low-rainfall occurrences unlikely to induce slope failure; (2) events where rainfall occurred more than 10 days before landslide initiation were omitted to reduce uncertainties associated with long-lag triggering mechanisms. This screening process enhanced the causal relevance of the selected rainfall events, improving the accuracy and reliability of the predictive model.
2.3.2. Rainfall Threshold Model
In this study, we adopted the empirical rainfall threshold model as the baseline for landslide prediction. Specifically, we used the power-law relationship between cumulative rainfall (E, in mm) and rainfall duration (D, in hours) proposed by Silvia et al. for Italy [12], which is expressed as follows:
This threshold reflects a 5% exceedance probability, meaning that only 5% of documented landslide-triggering rainfall events occur below this threshold, while the remaining 95% are above it. This empirical model was established as the baseline to provide a solid benchmark for assessing the effectiveness of the models evaluated in this research.
2.3.3. Machine Learning Models
This study employed four machine learning models: XGBoost, RF, LightGBM, and LR. XGBoost is an efficient gradient boosting algorithm based on decision tree ensembles [45], incrementally constructing multiple decision trees to correct residual errors with built-in regularization and parallel computing capabilities. RF constructs multiple independent decision trees using bootstrap sampling and random feature selection to enhance diversity, reduce overfitting, and provide robust aggregated predictions through majority voting or averaging [46]. LightGBM optimizes computational efficiency through histogram-based feature binning and leaf-wise tree growth, prioritizing high-gain splits and efficiently handling categorical features without encoding [47]. LR is a statistical binary classification model that converts linear combinations of predictors into probabilities via a logistic function; it is favored for its simplicity, interpretability, and computational efficiency [48].
The selected supervised learning algorithms span three core methodological categories: gradient boosting (XGBoost and LightGBM) for handling complex non-linear relationships, bagging-based ensemble (Random Forest) for robustness through bootstrap aggregation, and linear classification (Logistic Regression) as a statistical baseline. This diverse selection facilitates comprehensive performance comparison across distinct modeling approaches. Furthermore, hyperparameters for all machine learning models were optimized using GridSearchCV. The parameters and search spaces are detailed in Table 3.

Table 3.
Target hyperparameters and search spaces.
2.3.4. Imbalanced Sample Processing
Two critical challenges emerged from the dataset; namely, a regional distribution imbalance across geographic areas and a severe class imbalance with a positive to negative sample ratio of 1:10. These issues could compromise the model’s reliability and spatial generalizability, therefore requiring appropriate solutions.
The dataset was initially divided through stratified sampling [49], with 80% of samples from each macro-region allocated for training and validation, while the remaining 20% were reserved as a test set for subsequent analysis. For the training and validation portion, leave-one-region-out cross-validation (LORO-CV) was employed to ensure spatial generalizability, which is a region-based extension of k-fold cross-validation [50]. During LORO-CV, one macro-region served as the validation set while all remaining regions were used for training, with this process repeated until each region had been validated once. This approach guarantees model evaluation on geographically unseen areas, providing a robust assessment of spatial transferability.
Class imbalance was addressed using the Synthetic Minority Over-sampling Technique (SMOTE), applied exclusively to training data within each cross-validation fold [51]. This technique generates synthetic minority class samples by interpolating within the feature space, effectively balancing class distribution while mitigating overfitting risks and enhancing model sensitivity to the minority class. Validation sets remained unmodified to preserve their original class distributions and prevent data leakage, thereby ensuring objective evaluation and model generalizability. Table 4 presents the regional composition and sample distributions across macro-regions.

Table 4.
Distribution of positive and negative samples across macro-regions in Italy.
2.3.5. SHAP
Shapley Additive Explanations (SHAP) is a widely adopted technique for interpreting machine learning models, derived from Shapley values in game theory [52]. Shapley values quantify the contribution of each feature to model predictions by assessing its marginal impact across all possible subsets of features. SHAP provides a unified framework for measuring feature importance by calculating the weighted average of each feature’s marginal contributions to the model output across all feature subsets, thereby ensuring both consistency and fairness in model interpretation [53].
For a given model output , the SHAP value is calculated as follows:
where represents the shapley value of feature , is the model output for the feature subset , is a subset of the feature set, and is the size of subset . denotes the total number of features.
Using Formula (1), SHAP can accurately quantify the independent contribution of each feature to the model prediction, thereby ensuring both consistency and fairness in model interpretability.
In this study, SHAP was explicitly applied to the best-performing trained model to interpret the contribution of each predictor variable to landslide prediction. The SHAP analysis was implemented using the Python’s SHAP library and applied to the independent test set comprising 20% of the total dataset. This approach ensures unbiased interpretation by evaluating feature contributions on data that were not used during model training or validation.
2.3.6. Model Performance Evaluation
To comprehensively assess the performance of the developed models, this study utilized several widely adopted and practical evaluation metrics, including sensitivity, specificity, precision, and F1 score [54]. These metrics are derived from the four fundamental values in a confusion matrix: true positives (TP), false positives (FP), true negatives (TN), and false negatives (FN) [55]. Each metric evaluates the model’s classification performance from a different perspective, providing nuanced and holistic insights, especially when dealing with imbalanced datasets. The formulas for the evaluation metrics used in this study are defined as follows:
These metrics collectively evaluate model performance from complementary perspectives. Sensitivity measures the model’s ability to detect landslide-triggering events, thereby minimizing missed alarms. Specificity quantifies the accuracy in identifying non-triggering events, reducing false alarms. Precision reflects the reliability of positive predictions by assessing how many predicted landslides are actual events. The F1 score combines precision and sensitivity, offering a balanced measure, which is particularly crucial for imbalanced datasets.
Additionally, this study also utilized the Receiver Operating Characteristic (ROC) curve and the Area Under the Curve (AUC) as evaluation metrics [56,57]. The ROC curve visualizes the relationship between the True Positive Rate (TPR) and the False Positive Rate (FPR) across various classification thresholds, providing an intuitive assessment of model performance under different decision conditions. Meanwhile, the AUC quantifies the area under the ROC curve, where values closer to 1 indicate superior model performance in distinguishing between classes.
3. Results
3.1. Model Performance Comparison
The evaluation metrics in this study were reported as average values from 10 repetitions of the complete leave-one-region-out cross-validation procedure, involving 4412 positive samples and 44,120 negative samples in the training and validation process. The results included 95% confidence intervals, and McNemar’s test [58] was employed to analyze whether significant differences existed between model outputs. All analyses were conducted using Python 3.11.12 with relevant machine learning libraries (detailed information in Supplementary Material S1). On this imbalanced dataset, the four models (XGBoost, RF, LightGBM, and LR) exhibited distinct performance characteristics (Figure 4). Table 5 presents the detailed numerical values of these evaluation metrics and the optimal hyperparameter configurations for machine learning models.
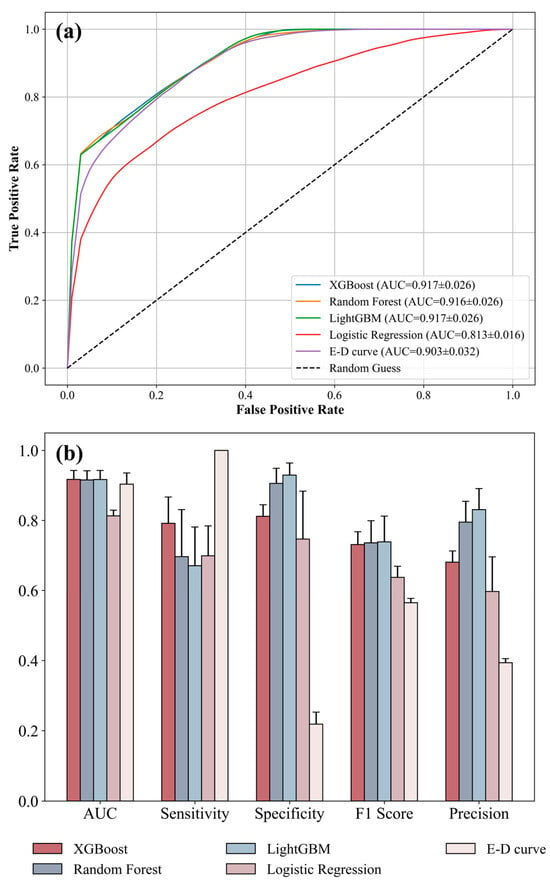
Figure 4.
(a) ROC curve comparison and (b) evaluation metric comparison.

Table 5.
Model performance and hyperparameter configurations of machine learning models.
The three tree-based methods (XGBoost, RF, and LightGBM) demonstrated consistently excellent predictive performance, achieving comparable AUC values of 0.917 ± 0.026, 0.916 ± 0.026, and 0.917 ± 0.026 respectively. In comparison, LR showed a relatively lower AUC of 0.813 ± 0.016, whereas the empirical E–D curve baseline reached 0.903 ± 0.032.
The sensitivity–specificity trade-off analysis presented varying behaviors across models. Random Forest and LightGBM exhibited high specificity (0.906 ± 0.043 and 0.930 ± 0.035) but compromised sensitivity (0.696 ± 0.134 and 0.670 ± 0.111), which reflected a bias toward the majority class typical of imbalanced datasets and may result in the omission of some landslides that were difficult to predict. By contrast, since the E–D curve prioritizes identifying all potential landslides, it achieved perfect sensitivity (1.000 ± 0.000) while greatly reducing specificity (0.219 ± 0.034), causing a high false positive rate.
Superior and well-balanced performance was observed for XGBoost across all key metrics, with sensitivity of 0.792 ± 0.075, specificity of 0.812 ± 0.033, an F1 score of 0.731 ± 0.037, and precision of 0.681 ± 0.032. This performance profile indicated that the XGBoost model effectively balances the trade-off between sensitivity and specificity, enabling enhanced landslide identification while simultaneously reducing false positive rates. We conducted McNemar’s test to compare XGBoost with other machine learning models and found highly significant differences across all comparisons (p < 0.001). When compared to Random Forest, LightGBM, and Logistic Regression, the test statistics were χ2 = 75.81 (p = 3.13 × 10−18), χ2 = 139.19 (p = 4.00 × 10−32), and χ2 = 478.66 (p = 4.18 × 10−106), respectively. Consequently, all subsequent experimental analyses were conducted based on the trained XGBoost model.
3.2. SHAP Value Analysis
SHAP analysis was applied to the trained XGBoost model on the test set to systematically investigate feature importance in landslide prediction, quantifying each variable’s contribution to the predictive process.
As shown in Figure 5a, total rainfall emerges as the primary driver of model predictions, with a mean SHAP value of approximately 5.0—far surpassing the contributions of other variables. Rainfall intensity ranked second (mean SHAP value ≈ 0.3), followed by soil moisture (mean SHAP value ≈ 0.15), highlighting the crucial role of hydrological factors in the predictive model. In comparison, topographic and environmental variables—including elevation, distance to river, plan curvature, soil type, profile curvature, distance to road, lithology, land use, slope, and aspect—all exhibited relatively low importance (mean SHAP values < 0.1), reflecting their limited contribution to rainfall threshold modeling within this modeling framework, though they still play a role to a certain extent in the modeling process.
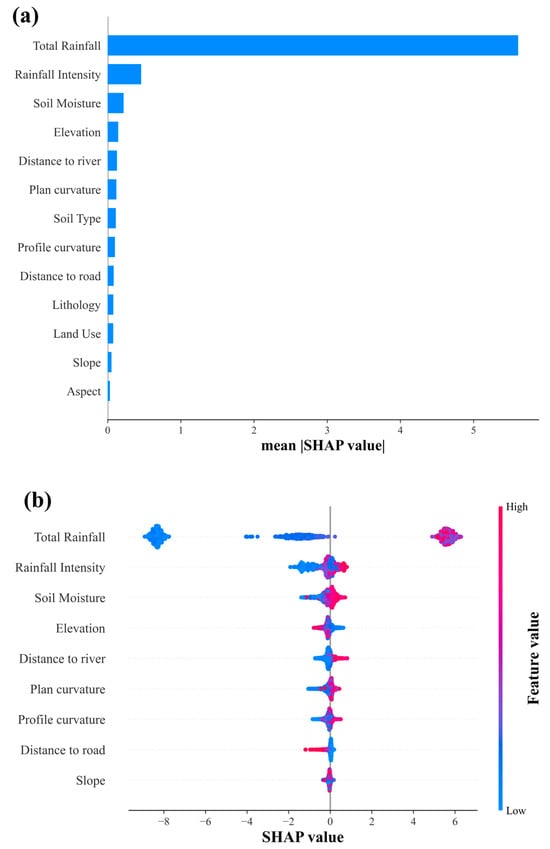
Figure 5.
(a) SHAP feature importance ranking and (b) SHAP summary plot for numerical features.
Figure 5b reveals complex relationships between feature values and landslide prediction, exhibiting distinct patterns in how different variables influence model outputs. Total rainfall exerted the strongest influence, with higher values (red points) consistently generating SHAP contributions ranging from 2 to 6, while lower values (blue points) yielded contributions around −8. This pattern indicated a clear threshold effect, where the amount of rainfall critically determines the landslide risk. Rainfall intensity and soil moisture followed similar trends, with elevated values increasing the landslide probability through enhanced SHAP contributions. Conversely, high elevation values correlated with reduced SHAP contributions, whereas the distance to river exhibits the reverse pattern. Topographic features such as slope presented more nuanced behavior, displaying both positive and negative SHAP values across different ranges, suggesting that terrain factors exert varying effects depending on specific environmental conditions. This analysis encompassed only numerical features, as categorical variables were excluded due to their encoded representations lacking meaningful interpretation within the SHAP analytical framework.
To further examine the nonlinear relationships identified in Figure 5b, partial dependence plots (Figure 6) were constructed to quantify the individual contribution patterns of the five most influential predictors. Total rainfall exhibited the pronounced threshold behavior previously observed, with SHAP values remaining near zero below 30 mm, escalating sharply within the 30–50 mm range, and reaching maximum contributions exceeding 6 beyond approximately 50 mm before stabilizing at higher precipitation levels. Rainfall intensity followed a comparable nonlinear trajectory, maintaining values between −1.5 and 0 below 21.5 mm/day and then increasing substantially beyond this critical threshold to peak around 1.0 for intensities exceeding 47.9 mm/day. Soil moisture displayed a consistent positive correlation, with SHAP values progressing from −0.5 to 0.5 as moisture content increased from 0.1 to 0.4 m3/m3. Elevation presented an inverse relationship, with values declining from 0.2 to −0.4 as elevation rose from 311.4 to 1549.0 m, remaining predominantly negative above 2000 m. Distance to river revealed proximity-dependent effects, with elevated SHAP values (approximately 0.2) within 1500 m of waterways, transitioning to negative values beyond 4500 m.
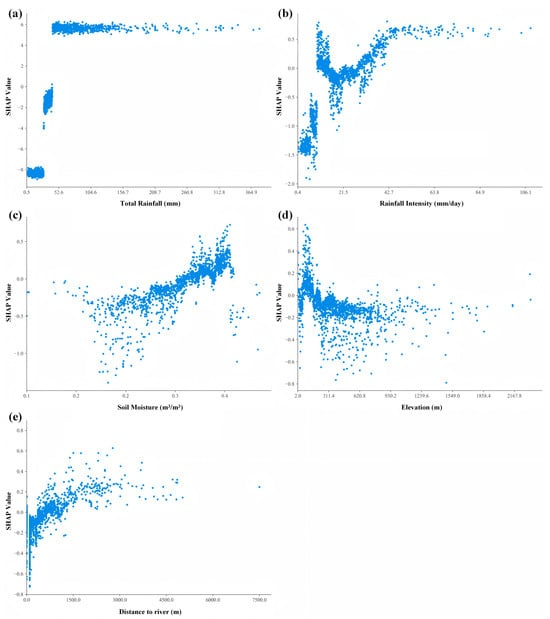
Figure 6.
SHAP partial dependence plots: (a) total rainfall, (b) rainfall intensity, (c) soil moisture, (d) elevation, (e) distance to river.
3.3. XGBoost Prediction Results
This study utilized the XGBoost model to predict landslide occurrence probabilities and compared the obtained probabilities with specific rainfall characteristics, including rainfall duration, total rainfall, and rainfall intensity, to visualize their distribution patterns. Rainfall duration was selected as the horizontal axis, while total rainfall and rainfall intensity were plotted on the vertical axis. A two-dimensional mapping approach was used to illustrate the relationships among these variables. The color gradient in the figures represents the probability of landslide occurrence, with deep red indicating high-probability areas and lighter shades representing lower-probability areas.
As shown in Figure 7a, the landslide probability increased as total rainfall rose. Notably, when total rainfall ranged between 10 mm and 100 mm, the probability exhibited a sharp upward trend, surging from approximately 0.2 to nearly 0.8. In cases of high total rainfall (≥100 mm), the landslide probability approached its maximum value.
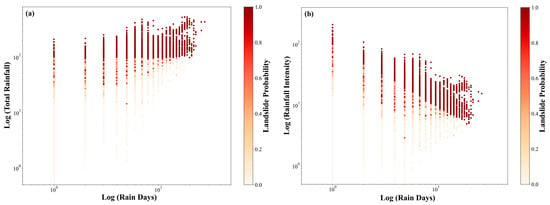
Figure 7.
Predicted landslide probability distribution by XGBoost model: (a) total rainfall—rain days and (b) rainfall intensity—rain days.
As shown in Figure 7b, when the rainfall duration was between 1 and 10 days, and rainfall intensity fell within the range of 10 mm/day to 100 mm/day, the landslide probability changed significantly, mostly rising from about 0.2 to its maximum. Moreover, when the rainfall duration exceeded 10 days, even with moderate rainfall intensity (5 mm/day to 10 mm/day), the probability of landslide occurrence remained high, typically ranging between 0.5 and 0.8.
3.4. Spatial Analysis of Rainfall Thresholds for Landslide Triggering
To analyze the spatial distribution characteristics of rainfall thresholds for landslide triggering in Italy, this study first refined the constructed dataset of landslide-triggering rainfall events. A statistical analysis of rainfall duration revealed that events lasting between 1 and 5 days account for 82% of the total dataset (Figure 8). Given this distribution pattern, the analysis focuses on 1–5-day rainfall events (a total of 4564 events) to ensure the representativeness of the sample.
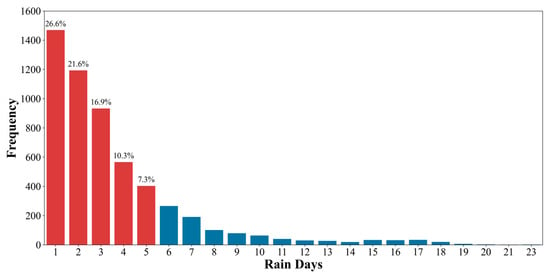
Figure 8.
Distribution of rainfall event durations.
Next, we loaded the pre-trained XGBoost model and reintroduced the filtered positive samples of 1–5-day rainfall events. Unlike previous analyses, during the adjustment process, we initially set both rainfall intensity and total rainfall to zero. Then, we gradually increased the total rainfall of each positive sample in increments of 0.1 mm until it reached 1.5 times its original value. Based on the relationship rainfall intensity = total rainfall/rain days, we simultaneously adjusted rainfall intensity while keeping all other features constant. The corresponding total rainfall values were recorded when the model’s predicted probability reached 50%, 70%, and 90%. This method aims to simulate potential rainfall scenarios for each possible feature combination within the study region.
As illustrated in Figure 9, we examined landslide-prone regions across Italy and randomly selected one representative site from each of four high-risk areas: Lombardy (LOM), Liguria (LIG), Marche (MAR), and Sicilia (SIC). All four cases demonstrated a gradual increase in landslide probability with rising total rainfall but exhibited variability in specific rainfall thresholds across regions.
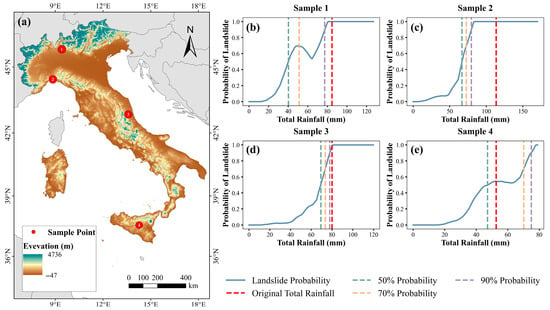
Figure 9.
Spatial distribution of sampling points and regional case studies: (a) Italy-wide sampling map, (b) Lombardy (LOM), (c) Liguria (LIG), (d) Marche (MAR), and (e) Sicily (SIC).
Based on the geographic coordinates and corresponding total rainfall data at 50%, 70%, and 90% probability levels for 1–5-day rainfall events, spatially interpolated minimum triggering rainfall threshold maps were generated using ordinary kriging in ArcGIS 10.8. The kriging interpolation utilized a spherical semivariogram model, with an output cell size set to 0.05 decimal degrees, a variable search radius approach, and 12 neighboring points for local estimation. The results revealed pronounced spatial heterogeneity in rainfall-triggered landslide thresholds across Italy. At the 50% and 70% probability levels (Figure 10a,b), regions requiring higher rainfall thresholds to trigger landslides were primarily concentrated along the Apennine Mountains, where annual precipitation was moderate, and the terrain was relatively gentle. In contrast, lower thresholds were prevalent in western and central Italy (e.g., Umbria, Liguria), the northern Alpine foothills, and southern regions (e.g., Calabria, Campania), where landslide susceptibility to rainfall was notably higher. At the 90% probability level (Figure 10c), rainfall thresholds increased substantially nationwide, with spatial variability diminishing as most regions converged toward uniformly high thresholds. This pattern underscored a key trend: threshold variability was most pronounced at 50% probability (exhibiting substantial inter-regional differences), moderately reduced at 70%, and nearly homogenized at 90%. These spatial distributions aligned with regional geophysical characteristics—lower thresholds in southern Italy corresponded to weathered soils and steep slopes, whereas higher thresholds in the Apennines reflected stable geological substrates and more gradual terrain.
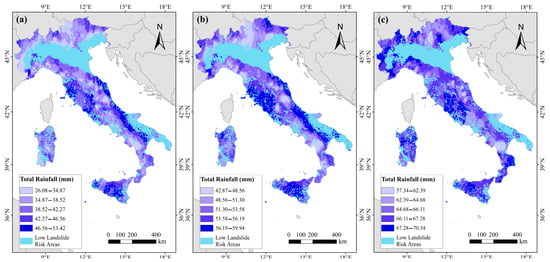
Figure 10.
Model-predicted rainfall threshold distribution maps for landslide triggering in Italy at (a) 50%, (b) 70%, and (c) 90% probability.
4. Discussion
4.1. Machine Learning Model Performance
Among all evaluated models, XGBoost delivered the best overall predictive performance, with an AUC of 0.917 ± 0.026, sensitivity of 0.792 ± 0.075, and specificity of 0.812 ± 0.033, aligning closely with findings reported by N. Dal Seno et al. [42]. The model’s ability to maintain a favorable balance between sensitivity and specificity stems from its integrated regularization mechanisms and capacity to capture complex nonlinear feature interactions, enabling effective discrimination between landslide-triggering and non-triggering events. Relative to other machine learning approaches, XGBoost exhibited superior identification of the minority (landslide) class while preserving overall accuracy.
Although Random Forest and LightGBM also demonstrated strong predictive abilities, as reflected in their high AUC values (0.916 ± 0.026 for Random Forest and 0.917 ± 0.026 for LightGBM), both exhibited a noticeable bias towards the majority (non-landslide) class. This tendency was evident in their high specificity but lower sensitivity, indicating reduced capabilities in detecting minority class events. Such outcomes are likely attributable to the inherent algorithmic characteristics and training mechanisms of these models, which tend to prioritize overall discrimination performance in the context of imbalanced datasets, often at the expense of minority class detection.
A relatively high AUC (0.903 ± 0.032) and perfect sensitivity (1.000 ± 0.000) were observed for the E–D curve threshold method, highlighting its exceptional ability to identify all potential landslide events. However, this came with a substantial reduction in specificity (0.219 ± 0.034) and the F1 score (0.565 ± 0.012). This trade-off is consistent with the primary aim of the E–D curve, which is to maximize the detection of possible landslides even at the risk of increasing false positives. The method’s high sensitivity underscores its value in early warning systems, especially in contexts where missing a potential landslide poses a greater risk than issuing unnecessary alerts.
Therefore, in practical landslide early warning applications, the balance between sensitivity and specificity should be carefully tailored to the specific context. For instance, prioritizing sensitivity in densely populated areas can help minimize missed detections and enhance public safety, whereas emphasizing specificity in low-risk regions may be preferable to reduce unnecessary false alarms. Ultimately, such context-specific optimization ensures that early warning systems are both effective and reliable in diverse real-world scenarios.
4.2. Landslide-Triggering Factors
This study used the XGBoost model with SHAP interpretation to identify which factors are most important for predicting rainfall-triggered landslides and understand how they work. Our results show that, in our temporal landslide prediction approach, dynamic weather and rainfall conditions are far more important than static environmental factors such as topography and geology. This pattern reflects the model’s effectiveness in capturing essential information to distinguish between landslide and non-landslide events.
Among all factors, total rainfall stands out as the most critical predictor, with SHAP values that are roughly ten times higher than other variables. Higher total rainfall consistently increases landslide probability, which matches our physical understanding of slope failure. When large amounts of rain fall over short periods, water infiltrates the soil, increases pore water pressure, and reduces the soil’s ability to resist sliding. This combination of effects directly destabilizes slopes and triggers landslides [1]. While rainfall intensity also contributes significantly to landslide prediction, it has much lower importance than total rainfall. This suggests that the cumulative amount of water entering the soil matters more than how fast it falls at any given moment. This makes physical sense because landslides typically occur when water reaches deeper soil layers and potential failure surfaces, rather than being triggered by surface conditions alone. The process depends more on sustained water infiltration than on peak rainfall rates [59,60].
The limited influence of static environmental factors can be understood from two perspectives. From a physical standpoint, while topographic and geological features determine long-term landslide susceptibility through gradual geological processes [61], they become less influential during actual rainfall events when dynamic hydrological processes directly control slope stability. The rapid changes in soil moisture and pore water pressure during storms override the influence of relatively uniform geological conditions. From a methodological perspective, our training data come from historical landslide locations where static environmental factors have already reached critical values over geological time scales. Since these sites are already predisposed to failure, the static factors show limited variation and thus provide little discriminatory power in distinguishing between triggering and non-triggering events.
This pattern also reflects a fundamental difference between our rainfall-event-based modeling approach and traditional landslide susceptibility mapping [62,63]. Susceptibility maps identify where landslides are likely to occur based on long-term geological predisposition, using spatial sampling to compare stable and unstable areas. In contrast, our models focus on when landslides will occur by distinguishing between rainfall events that trigger landslides and those that do not, using temporal sampling to capture the critical timing of landslide initiation.
4.3. Analysis of the Spatial Distribution of Rainfall Thresholds
To provide a flexible framework for landslide early warning applications with varying risk management requirements, this study generated threshold maps at three probability levels (50%, 70%, and 90%). These multiple probability thresholds are designed to accommodate different operational needs: the 50% threshold offers high sensitivity for areas requiring maximum protection such as densely populated regions or critical infrastructure, the 70% threshold provides a balanced approach for general warning purposes, while the 90% threshold serves as a conservative reference for regions prioritizing the reduction of false alarms.
Across the Italian territory, these multi-level thresholds exhibit significant spatial heterogeneity in rainfall requirements for landslide triggering. Under landslide occurrence probabilities of 50% and 70%, areas on both sides of the Apennine Mountains (e.g., Marche, Tuscany) required higher rainfall thresholds to trigger landslides. This phenomenon may be attributed to their relatively gentle terrain slopes (average slope gradients < 25°) and moderate annual rainfall (approximately 675–845 mm/yr). Gentle slopes likely prolong the time required for soil saturation by slowing surface runoff and promoting rainwater infiltration, necessitating stronger cumulative rainfall to destabilize slopes. In contrast, regions such as Liguria, Umbria, and southern Calabria exhibited lower thresholds, characterized by steeper terrain (average slope gradients > 35°) and frequent high-intensity rainfall events that rapidly reduce soil shear strength.
At the 90% probability threshold, a notable convergence emerged in regional precipitation thresholds, accompanied by a significant attenuation of spatial heterogeneity. This phenomenon can be primarily attributed to two synergistic mechanisms: (1) From a modeling paradigm perspective, machine learning algorithms demonstrate diminished sensitivity to regional covariates under high-probability regimes. This inherent model behavior prioritizes robust generalization capabilities over spatial specificity, adopting conservative estimations to mitigate overfitting risks while maintaining prediction reliability under stringent confidence requirements. (2) Physically, extreme precipitation events approaching the 90% probability level create hydrogeomorphic conditions that override typical regional discriminators. Under such intense rainfall scenarios, the critical thresholds for soil saturation and slope instability become predominantly governed by hydrological determinants rather than localized terrain or pedological properties. This homogenization effect arises from the nonlinear threshold behavior characteristic of geotechnical systems, where the overwhelming hydraulic forcing during extreme events effectively neutralizes baseline spatial variability in soil permeability and slope stability indices.
Previous studies [12,64,65] documented comparatively low precipitation thresholds in Sicily. In contrast, our study found that only the northern mountainous regions exhibited consistently lower thresholds across all probability quantiles, while the southern regions showed higher thresholds. This methodological divergence may arise from two principal considerations. First, despite their superior spatial continuity, the satellite-derived precipitation products adopted in this research exhibit less precise quantification of orographic precipitation than the rain gauge networks utilized in antecedent studies. Second, the machine-learning-driven predictive framework emphasizes the extraction of statistically significant patterns from global-scale multidimensional feature spaces, potentially inducing discrepant outcomes in localized geographical contexts (e.g., southern Sicily) relative to conventional regional modeling paradigms. Furthermore, it is plausible that the dataset for this region contains instances of extreme rainfall events within a relatively small spatial domain. When interpolated using ArcGIS 10.8, such localized extremes may be exaggerated, thereby inflating the derived precipitation thresholds for this area.
4.4. Limitations and Future Perspectives
This study presents a viable approach for determining regional rainfall thresholds but also faces several limitations that require further exploration. Although the model has proven effective in Italy, its transferability to other regions requires further validation due to data availability constraints. Future research directions should include expanding the training dataset to encompass multi-regional environments or implementing transfer learning methodologies to improve model adaptability across diverse geological and climatic settings. Utilizing satellite rainfall data facilitated model development through enhanced data accessibility and provided satisfactory results. Subsequent research could enhance accuracy by incorporating ground-based rain gauge measurements to reduce uncertainties, particularly in complex terrains. Additionally, soil moisture, a crucial variable for landslide prediction, was treated as a static initial environmental factor to characterize antecedent wetness conditions prior to landslide occurrence. This approach enabled the model to evaluate landslide probability under varying initial soil moisture conditions, thereby enhancing generalizability across diverse real-world scenarios. Nevertheless, this approach may constrain the model’s capacity to capture dynamic moisture changes during rainfall events, which significantly influence landslide initiation. Addressing this limitation in subsequent studies could involve integrating physically based hydrological models or sequential modeling techniques—such as time series analysis or advanced deep learning models (such as LSTM)—to better simulate and incorporate real-time soil moisture dynamics into landslide prediction frameworks.
5. Conclusions
This study comprehensively evaluated landslide prediction performance by comparing empirical rainfall threshold models with several machine learning algorithms. To enhance model transparency and interpretability, SHAP (Shapley Additive Explanations) analysis was employed to elucidate model decision-making processes. Building upon the optimal model, we developed visualized rainfall threshold maps for the Italian region under three probability scenarios. The key findings are as follows:
- (1)
- The XGBoost model achieved superior overall performance (AUC = 0.917 ± 0.026) with well-balanced sensitivity (0.792 ± 0.075) and specificity (0.812 ± 0.033), proving more suitable for modeling imbalanced datasets. The model significantly outperformed other machine learning approaches, thereby demonstrating its exceptional suitability for landslide modeling and early warning applications.
- (2)
- Total rainfall and rainfall intensity were the dominant triggering factors, far exceeding other factors in importance. SHAP analysis showed a pronounced increase in influence within the 30–50 mm range, with the maximum impact occurring beyond 50 mm. Rainfall intensity demonstrated critical thresholds above 21.5 mm/day, with peak influence beyond 47.9 mm/day. Among static environmental factors, elevation showed an inverse relationship with landslide probability, while proximity to rivers exhibited distance-dependent effects, with higher risk within 1500 m of waterways.
- (3)
- Regional differences in landslide-triggering rainfall thresholds were observed across Italy. Areas characterized by gentler terrain (slopes < 25°), such as Marche, Tuscany, and parts of Emilia-Romagna, along with moderate-rainfall regions including central Apennine areas and the Po Valley regions, demonstrated higher rainfall thresholds with values greater than 42 mm and 53 mm at 50% and 70% probability levels, respectively. In contrast, steeper slopes (>35°) found in regions such as Liguria, Umbria, and southern Calabria showed lower rainfall thresholds of less than 34 mm and 48 mm at the two probability levels, respectively. At the 90% probability level, thresholds universally increased, and regional disparities diminished.
Overall, this study provides a viable approach for rainfall-induced landslide prediction and offers a practical reference for regional early warning systems. Future research should focus on reducing intra-regional errors and enhancing the cross-regional transferability of the developed models.
Supplementary Materials
The Python environment and core Python libraries used in this study are detailed at: https://www.mdpi.com/article/10.3390/app15147937/s1.
Author Contributions
Conceptualization, X.S. (Xiangyu Shao) and W.Y.; methodology, X.S. (Xiangyu Shao) and C.Y.; software, X.S. (Xiangyu Shao) and J.Y.; validation, X.S. (Xiangyu Shao) and Y.W.; investigation, X.S. (Xiangyu Shao) and X.S. (Xia Shi); resources, X.S. (Xiangyu Shao) and H.D.; data curation, X.S. (Xiangyu Shao) and T.L.; visualization, X.S. (Xiangyu Shao) and P.Z.; supervision, Z.Z.; writing—original draft preparation, X.S. (Xiangyu Shao); writing—review and editing, W.Z. and J.J.; project administration, J.J.; funding acquisition, W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Science and Technology Projects of the Xizang Autonomous Region, China (No. XZ202402ZD0001), the Basic Research Program of Qinghai Province (2024-ZJ-904), and the Key Program of Gansu Joint Scientific Research Fund (Grant No. 25JRRA1106).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets generated and/or analyzed during this study are available from the first author (X.S.) upon reasonable request.
Acknowledgments
The authors acknowledge the use of ChatGPT-4 (OpenAI) and DeepSeek for their valuable assistance in refining the language and enhancing the clarity of this manuscript. These tools played a supplementary role in improving the overall readability and presentation of the study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sidle, R.C.; Bogaard, T.A. Dynamic earth system and ecological controls of rainfall-initiated landslides. Earth-Sci. Rev. 2016, 159, 275–291. [Google Scholar] [CrossRef]
- Jiang, Z.; Fan, X.; Siva Subramanian, S.; Yang, F.; Tang, R.; Xu, Q.; Huang, R. Probabilistic rainfall thresholds for debris flows occurred after the Wenchuan earthquake using a Bayesian technique. Eng. Geol. 2021, 280, 105965. [Google Scholar] [CrossRef]
- Saito, H.; Nakayama, D.; Matsuyama, H. Relationship between the initiation of a shallow landslide and rainfall intensity—Duration thresholds in Japan. Geomorphology 2010, 118, 167–175. [Google Scholar] [CrossRef]
- Guzzetti, F. Landslide fatalities and the evaluation of landslide risk in Italy. Eng. Geol. 2000, 58, 89–107. [Google Scholar] [CrossRef]
- Gariano, S.L.; Guzzetti, F. Landslides in a changing climate. Earth-Sci. Rev. 2016, 162, 227–252. [Google Scholar] [CrossRef]
- Caine, N. The rainfall intensity-duration control of shallow landslides and debris flows. Geogr. Ann. A Phys. Geogr. 1980, 62, 23–27. [Google Scholar]
- Peruccacci, S.; Brunetti, M.T.; Luciani, S.; Vennari, C.; Guzzetti, F. Lithological and seasonal control on rainfall thresholds for the possible initiation of landslides in central Italy. Geomorphology 2012, 139, 79–90. [Google Scholar] [CrossRef]
- Liu, S.; Du, J.; Yin, K.; Zhou, C.; Huang, C.; Jiang, J.; Yu, J. Regional early warning model for rainfall induced landslide based on slope unit in Chongqing, China. Eng. Geol. 2024, 333, 107464. [Google Scholar] [CrossRef]
- Yang, H.Q.; Zhang, L. Bayesian back analysis of unsaturated hydraulic parameters for rainfall-induced slope failure: A review. Earth-Sci. Rev. 2024, 251, 104714. [Google Scholar] [CrossRef]
- Segoni, S.; Piciullo, L.; Gariano, S.L. A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 2018, 15, 1483–1501. [Google Scholar] [CrossRef]
- Vessia, G.; Di Curzio, D.; Chiaudani, A.; Rusi, S. Regional rainfall threshold maps drawn through multivariate geostatistical techniques for shallow landslide hazard zonation. Sci. Total Environ. 2020, 705, 135815. [Google Scholar] [CrossRef] [PubMed]
- Peruccacci, S.; Brunetti, M.T.; Gariano, S.L.; Melillo, M.; Rossi, M.; Guzzetti, F. Rainfall thresholds for possible landslide occurrence in Italy. Geomorphology 2017, 290, 39–57. [Google Scholar] [CrossRef]
- Crosta, G. Regionalization of rainfall thresholds: An aid to landslide hazard evaluation. Environ. Geol. 1998, 35, 131–145. [Google Scholar] [CrossRef]
- Segoni, S.; Rosi, A.; Rossi, G.; Catani, F.; Casagli, N. Analysing the relationship between rainfalls and landslides to define a mosaic of triggering thresholds for regional-scale warning systems. Nat. Hazards Earth Syst. Sci. 2014, 14, 2637–2648. [Google Scholar] [CrossRef]
- Segoni, S.; Lagomarsino, D.; Fanti, R.; Moretti, S.; Cassagli, N. Integration of rainfall thresholds and susceptibility maps in the Emilia Romagna (Italy) regional-scale landslide warning system. Landslides 2015, 12, 773–785. [Google Scholar] [CrossRef]
- Liu, Z.; Gilbert, G.; Cepeda, J.M.; Lysdahl, A.O.K.; Piciullo, L.; Hefre, H.; Lacasse, S. Modelling of shallow landslides with machine learning algorithms. Geosci. Front. 2021, 12, 385–393. [Google Scholar] [CrossRef]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Bui, D.T.; Avtar, R.; Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth-Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Yang, B.; Liu, Z.Q.; Kwan, J.S.H.; Chen, L. Spatiotemporal modelling of rainfall-induced landslides using machine learning. Landslides 2021, 18, 2499–2514. [Google Scholar] [CrossRef]
- Goetz, J.N.; Brenning, A.; Petschko, H.; Leopold, P. Evaluating machine learning and statistical prediction techniques for landslide susceptibility modeling. Comput. Geosci. 2015, 81, 1–11. [Google Scholar] [CrossRef]
- Lv, L.; Chen, T.; Dou, J.; Plaza, A. A hybrid ensemble-based deep-learning framework for landslide susceptibility mapping. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102713. [Google Scholar] [CrossRef]
- Fang, Z.; Tanyas, H.; Gorum, T.; Dahal, A.; Wang, Y.; Lombardo, L. Speech-recognition in landslide predictive modelling: A case for a next generation early warning system. Environ. Model. Softw. 2023, 170, 105833. [Google Scholar] [CrossRef]
- Xiao, T.; Zhang, L.M. Data-driven landslide forecasting: Methods, data completeness, and real-time warning. Eng. Geol. 2023, 317, 107068. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, X.; Zhang, J.; Sun, D.; Zhou, X.; Mi, C.; Wen, H. Insights into geospatial heterogeneity of landslide susceptibility based on the SHAP-XGBoost model. J. Environ. Manag. 2023, 332, 117357. [Google Scholar] [CrossRef]
- Hu, W.; Yang, Z.; Yang, J.; Li, Q.; Deng, J.; Zhao, S.; Cui, Y. Scale effects in landslide susceptibility assessment: Integrating slope unit division and SHAP-based interpretability in a typical river basin. Water 2025, 17, 1877. [Google Scholar] [CrossRef]
- Zhou, X.; Wen, H.; Li, Z.; Zhang, H.; Zhang, W. An interpretable model for the susceptibility of rainfall-induced shallow landslides based on SHAP and XGBoost. Geocarto Int. 2022, 37, 13419–13450. [Google Scholar] [CrossRef]
- Fantappiè, M.; L’Abate, G.; Schillaci, C.; Costantini, E.A. Digital soil mapping of Italy to map derived soil profiles with neural networks. Geoderma Reg. 2023, 32, e00619. [Google Scholar] [CrossRef]
- Peruccacci, S.; Gariano, S.L.; Melillo, M.; Solimano, M.; Guzzetti, F.; Brunetti, M.T. The ITAlian rainfall-induced LandslIdes CAtalogue, an extensive and accurate spatio-temporal catalogue of rainfall-induced landslides in Italy. Earth Syst. Sci. Data 2023, 15, 2863–2877. [Google Scholar] [CrossRef]
- Di Napoli, M.; Carotenuto, F.; Cevasco, A.; Confuorto, P.; Di Martire, D.; Firpo, M.; Pepe, G.; Raso, E.; Calcaterra, D. Machine learning ensemble modelling as a tool to improve landslide susceptibility mapping reliability. Landslides 2020, 17, 1897–1914. [Google Scholar] [CrossRef]
- Meena, S.R.; Puliero, S.; Bhuyan, K.; Floris, M.; Catani, F. Assessing the importance of conditioning factor selection in landslide susceptibility for the province of Belluno (region of Veneto, northeastern Italy). Nat. Hazards Earth Syst. Sci. 2022, 22, 1395–1417. [Google Scholar] [CrossRef]
- Mehrabi, M. Landslide susceptibility zonation using statistical and machine learning approaches in Northern Lecco, Italy. Nat. Hazards 2021, 108, 1–37. [Google Scholar] [CrossRef]
- Panday, S.; Dong, J.J. Topographical features of rainfall-triggered landslides in Mon State, Myanmar, August 2019: Spatial distribution heterogeneity and uncommon large relative heights. Landslides 2021, 18, 3875–3889. [Google Scholar] [CrossRef]
- Marin, R.J. Physically based and distributed rainfall intensity and duration thresholds for shallow landslides. Landslides 2020, 17, 2907–2917. [Google Scholar] [CrossRef]
- Ávila, F.F.; Alvalá, R.C.; Mendes, R.M.; Amore, D.J. The influence of land use/land cover variability and rainfall intensity in triggering landslides: A back-analysis study via physically based models. Nat. Hazards 2021, 105, 1139–1161. [Google Scholar] [CrossRef]
- Guzzetti, F.; Melillo, M.; Mondini, A.C. Landslide predictions through combined rainfall threshold models. Landslides 2025, 22, 137–147. [Google Scholar] [CrossRef]
- Segoni, S.; Tofani, V.; Rosi, A.; Catani, F.; Casagli, N. Combination of rainfall thresholds and susceptibility maps for dynamic landslide hazard assessment at regional scale. Front. Earth Sci. 2018, 6, 85. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 1–21. [Google Scholar] [CrossRef]
- Wicki, A.; Lehmann, P.; Hauck, C.; Seneviratne, S.I.; Waldner, P.; Stähli, M. Assessing the potential of soil moisture measurements for regional landslide early warning. Landslides 2020, 17, 1881–1896. [Google Scholar] [CrossRef]
- Marino, P.; Peres, D.; Cancelliere, A.; Greco, R.; Bogaard, T. Soil moisture information can improve shallow landslide forecasting using the hydrometeorological threshold approach. Landslides 2020, 17, 2041–2054. [Google Scholar] [CrossRef]
- Orth, R.; Weber, U.; Park, S.K. High-resolution European daily soil moisture derived with machine learning (2003–2020). Sci. Data 2022, 9, 1–13. [Google Scholar] [CrossRef]
- Mondini, A.C.; Guzzetti, F.; Melillo, M. Deep learning forecast of rainfall-induced shallow landslides. Nat. Commun. 2023, 14, 2466. [Google Scholar] [CrossRef]
- Brunetti, M.T.; Peruccacci, S.; Rossi, M.; Luciani, S.; Valigi, D.; Guzzetti, F. Rainfall thresholds for the possible occur-rence of landslides in Italy. Nat. Hazards Earth Syst. Sci. 2010, 10, 447–458. [Google Scholar] [CrossRef]
- Dal Seno, N.; Evangelista, D.; Piccolomini, E.; Berti, M. Comparative analysis of conventional and machine learning techniques for rainfall threshold evaluation under complex geological conditions. Landslides 2024, 21, 2893–2911. [Google Scholar] [CrossRef]
- Gariano, S.L.; Sarkar, R.; Dikshit, A.; Dorji, K.; Brunetti, M.T.; Peruccacci, S.; Melillo, M. Automatic calculation of rainfall thresholds for landslide occurrence in Chukha Dzongkhag, Bhutan. Bull. Eng. Geol. Environ. 2019, 78, 4325–4332. [Google Scholar] [CrossRef]
- Lollino, G.; Arattano, M.; Allasia, P.; Giordan, D. Time response of a landslide to meteorological events. Nat. Hazards Earth Syst. Sci. 2006, 6, 179–184. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3147–3155. [Google Scholar]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Thompson, S.K. Sampling; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Stone, M. Cross-validatory choice and assessment of statistical predictions. J. R. Stat. Soc. B Stat. Methodol. 1974, 36, 111–133. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Kuhn, H.W. (Ed.) Classics in Game Theory; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4768–4777. [Google Scholar]
- He, H.; Garcia, E.A. Learning from imbalanced data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar] [CrossRef]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef]
- Kutlug Sahin, E.; Colkesen, I. Performance analysis of advanced decision tree-based ensemble learning algorithms for landslide susceptibility mapping. Geocarto Int. 2021, 36, 1253–1275. [Google Scholar] [CrossRef]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity–duration control of shallow landslides and debris flows: An update. Landslides 2008, 5, 3–17. [Google Scholar] [CrossRef]
- Guzzetti, F.; Carrara, A.; Cardinali, M.; Reichenbach, P. Landslide hazard evaluation: A review of current techniques and their application in a multi-scale study, Central Italy. Geomorphology 1999, 31, 181–216. [Google Scholar] [CrossRef]
- Azarafza, M.; Azarafza, M.; Akgün, H.; Atkinson, P.M.; Derakhshani, R. Deep learning-based landslide susceptibility mapping. Sci. Rep. 2021, 11, 24112. [Google Scholar] [CrossRef]
- Kumar, C.; Walton, G.; Santi, P.; Luza, C. An ensemble approach of feature selection and machine learning models for regional landslide susceptibility mapping in the arid mountainous terrain of Southern Peru. Remote Sens. 2023, 15, 1376. [Google Scholar] [CrossRef]
- Gariano, S.L.; Brunetti, M.; Iovine, G.; Melillo, M.; Peruccacci, S.; Terranova, O.; Vennari, C.; Huzzetti, F. Calibration and validation of rainfall thresholds for shallow landslide forecasting in Sicily, southern Italy. Geomorphology 2015, 228, 653–665. [Google Scholar] [CrossRef]
- Melillo, M.; Brunetti, M.T.; Peruccacci, S.; Gariano, S.L.; Guzzetti, F. Rainfall thresholds for the possible landslide occurrence in Sicily (Southern Italy) based on the automatic reconstruction of rainfall events. Landslides 2016, 13, 165–172. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).