Abstract
High-voltage unipolar square wave pulsed electric fields (PEFs) can cause cell membrane rupture and cell death during a process termed irreversible electroporation (IRE). PEF effects are influenced by pulse parameters like number of pulses (NP), voltage (PV), width (PW), and interval (PI). This study systematically evaluates their effects on the conductivity and relative conductivity changes between untreated and PEF-treated regions of potato tissue across a frequency range of 1 Hz to 5 MHz by means of electrochemical impedance spectroscopy (EIS), using a custom-made four-point EIS probe with RG58/U coaxial cables. Potatoes were chosen as a plant-based PEF model to reduce animal experiments and untreated tissue showed minimal conductivity variation across regions. Relative conductivity changes were maximal at 1000 Hz. At 1000 Hz, significant conductivity differences between untreated and PEF-treated regions were observed from PV = 200 V, NP = 10, PW = 10 µs, and PI = 50 ms onwards (most significant changes occurred for PV = 700 V; NP = 70; PW = 70 µs; PI = 250 ms and 500 ms). Our results may be beneficial for multiphysics modelling of IRE with specific electrical properties, conductivity mapping with optimal contrast—such as in electrical impedance tomography—and development of IRE procedures.
1. Introduction
High-voltage pulsed electric fields (PEFs) can induce the electrical breakdown and rupturing of cell membranes in biological tissues [1]. PEF treatment transiently increases the plasma membrane permeability by forming nanopores, thereby facilitating the transport of otherwise cell-impermeant molecules, which increases electrical conductivity. This phenomenon is referred to as electroporation or electro-permeabilization [2,3,4]. If the cell succeeds in restoring homeostasis by repairing its plasma membrane, the effect is transient and termed reversible electroporation (RE). However, when the PEF pulse parameters exceed certain thresholds, irreparable damage occurs in the plasma membrane, resulting in cell death. This effect is termed irreversible electroporation (IRE) [5].
A clinical application of RE and IRE is minimally invasive tumour treatment [6,7,8,9,10], with IRE being particularly effective for tumours near critical blood vessels in the liver, pancreas, and brain due to its non-thermal mechanism that preserves vascular structures [11].
Commonly, series of unipolar square wave pulses [12], characterized by parameters such as the number of pulses (NP), pulse voltage (PV), pulse width (PW), and pulse interval (PI) (see Figure 1d for parameter definitions), are locally applied to the treated tissue over a needle applicator [13]. The distance between the straight needle electrodes and the PV determines the maximum applied PEF field strength [14]. Numerous studies have explored the effects of PEF parameters across in vitro [15,16], in vivo [17,18], and in plant-based models [19,20]. Towards higher NP, the PV, PW, and smaller PI favour IRE over RE [5,21,22]. Eventually, if the PEFs start to cause Joule heating, thermal ablation will also contribute [14,23]. However, thresholds between the regimes may not only depend on the above-mentioned pulse parameters, but also on the tissue type [24] and shape of the needle applicator [21,25,26]. Understanding these influences is albeit crucial with respect to patient-specific individual treatment planning [27].
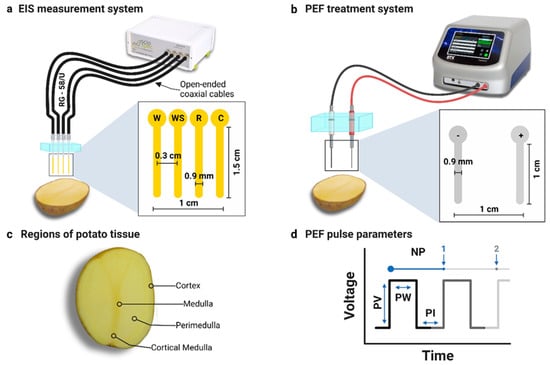
Figure 1.
(a) EIS measurement system featuring an open-ended coaxial four-point probe (abbreviations W, WS, R, and C correspond to working, working sense, reference, and counter electrodes, respectively). The excitation voltage was applied between electrodes W and C, while impedance spectra were acquired between WS and R. (b) Two-needle PEF treatment system. (c) Anatomical regions within potato tissue. (d) Definition of the unipolar pulse parameters (abbreviations NP, PV, PW, and PI correspond to number of pulses, pulse voltage, pulse width, and pulse interval, respectively).
A study in rabbit liver by Sel et al. found thresholds for RE and IRE at applied electric fields of 460 and 700 V/cm, respectively (NP = 8, PW = 100 μs, PI = 1 s) [28]. However, for RE treatment in humans, eight electric pulses with a PW of 100 μs are commonly delivered at an electric field of 1000 V/cm or higher [29]. An optimization study on clinical IRE treatments using a NanoKnife on swine liver found that increasing PW beyond 50 µs and NP beyond 50 did not significantly increase the ablation size due to IRE [30]. Furthermore, PW > 70 µs and NP > 70 caused white necrotic tissue next to the electrode because of thermal coagulation, similar to that seen in radiofrequency and microwave ablation [30]. It should be noted that plant tissues seem to require higher PW of around 100 µs–1000 µs for successful PEF treatment [31].
Importantly, pulse parameter experiments necessitate a substantial quantity of viable tissue, which can be either living animal or plant tissue. PEF effects, especially IRE and RE, were also explored at the single-cell level, but tissues present a more complex scenario due to the proximity of cells and the inherent tissue inhomogeneity [32]. In contrast to animal models, metabolic activity, including cellular respiration, persists in plant models even after harvesting [33]. Studying PEF in plant-based models aligns with the “Three Rs”—Replacement, Reduction, and Refinement—to minimize animal usage [34,35]. Also, the Biomedical Engineer’s Pledge 1.0 encourages minimizing animal experimentation [36]. Potatoes are widely used as a plant-based model for electroporation research, including device testing and the development of new measurement methods, due to their cost-effectiveness, availability, and lack of ethical concerns [37,38,39,40,41,42,43,44].
The effects of PEF in potatoes can be detected by dye staining [38], melanin browning [38,40,45], magnetic resonance imaging [39,46], fluorescence imaging [42,43,44], and electrochemical impedance spectroscopy (EIS) [47]. Compared to other techniques, EIS offers quantitative assessment of the electrical tissue properties, including conductivity and permittivity, which serve as indicators of pore formation and membrane permeabilization [48,49]. EIS perturbs an electrochemical system by applying a sinusoidal signal, typically an alternating voltage or current, across a range of frequencies. It then monitors the system’s response, either current or voltage, to study the frequency-dependant electrical impedance. The system is typically assumed to be linear and time-invariant, meaning its behaviour remains constant over time [50]. Even the slightest changes at the medium-electrode interface are detected by EIS, which finds extensive use in biosensing applications [51].
Accurate estimation of tissue-specific electrical conductivity and permittivity changes following electroporation, has multiple applications in optimizing and predicting PEF-induced ablations by allowing more precise numerical simulations [52,53].
Another application of tissue-specific electrical changes post-electroporation is the optimization of electrical impedance tomography (EIT), a low-cost, non-invasive imaging modality that maps tissue conductivity in real time [54]. EIT is sensitive to the passive electrical properties of tissues altered during electroporation, making it the only imaging modality that directly detects electroporation-mediated conductivity changes through its underlying impedance-based mechanism [55]. However, one must choose a frequency in advance that yields optimal contrast between electroporated and non-electroporated tissue, as tissue conductivity varies with frequency [54,56,57]. EIS with higher accuracy can further assist in identifying optimal frequencies with maximal conductivity changes.
Different electrode configurations can be used in EIS, i.e., two-, three- or four-electrode setups. The four-electrode method offers superior accuracy compared to the others [58]. In this setup, the outer electrodes inject current, while the inner electrodes measure frequency-dependent voltage signals, or vice versa [58]. The four-probe EIS method eliminates electrode polarization [59], which occurs at the tissue-electrode interface due to molecular charge organization forming ionic double layers [60]. Probes using open-ended coaxial cables have demonstrated the capability to rapidly evaluate highly accurate and precise dielectric properties in various materials after calibrating the probe by measuring its cell constant in a solution of known dielectric properties. Also, they only require a small sensing area as small probes can be constructed [61]. Gabriel et al. used an open-ended coaxial cable system to obtain the dielectric properties of biological tissues from EIS [62,63].
A recent systematic review of 18 preclinical studies in both animal and phantom models highlighted the need for research on the optimization of IRE treatment protocols to better predict the effect of specific pulse parameter combinations on treatment response [21]. Yet, to the best of the authors’ knowledge, comprehensive studies integrating PEF for a wide range of the above-mentioned pulse parameters and EIS measurements in plant tissues are so far absent in the literature. A previous study by Zhao et al. analysed impedance changes in potatoes using four 1.15 mm diameter electrodes in a square array, with one diagonal pair applying PEF and the alternating pairs measuring impedance changes from EIS (1 Hz to 1 MHz). It focused solely on impedance, without analysing conductivity and permittivity, and only varied PV and NP [64]. Another PEF study on potatoes by Genovese et al. employed four-point EIS with frequencies from 50 Hz to 1 MHz and copper needle electrodes. Their analysis showed a notable decrease in impedance above a threshold PEF field of 250 V/cm (NP = 8, PW = 100 μs, PI = 1 s). However, PEF parameters other than PV were not examined [47].
Additionally, open-ended coaxial four-point EIS probes have not been employed in the context of electroporation research on plant-based models.
Thus, the aim of this study was to comprehensively assess conductivity changes in response to PEF by EIS in potato samples as a model system. To that purpose, we varied diverse PEF parameters, i.e., PV, PV, PI, and NP, and performed EIS with a custom-designed four-point coaxial probe. We hypothesized that a specific frequency range would show high relative conductivity changes between PEF-treated and non-treated potato regions in EIS, which can be applied to EIT.
2. Materials and Methods
2.1. Fabrication of an Open-Ended Coaxial Four-Point Probe
A four-point EIS probe was custom-designed, as shown in Figure 1a and Supplementary Figure S1, with four open-ended RG58/U coaxial cables (Cnals, Jiangsu Elesun Cable Co., Ltd., Zhenjiang, Jiangsu, China) (45 cm long, copper core diameter of 0.9 mm, polyethylene insulation with an outer diameter of 2.95 mm, maximum capacitance of 101 pF/m, and impedance of 50 ± 2 Ω). BNC connectors were fitted to one end of each cable, while the opposite ends were modified to expose 4 cm of insulation and 1.5 cm of the copper core. These open ends were mounted in a polycarbonate block with evenly spaced holes to maintain a core-to-core distance of 0.3 cm between the exposed cores in a linear arrangement. Likewise, the setup minimized displacement and optimized contact during the measurements.
2.2. EIS Measurement System
EIS measurements were conducted using the ISX3 EIS analyser Version 4 (Sciospec Scientific Instruments GmbH, Bennewitz, Germany). The BNC ends of the four-point probe were connected in linear order to the W (work), WS (working sense), R (reference), and C (counter) connectors on the ISX3 EIS analyser, respectively, as shown in Figure 1a. The excitation voltage was applied between electrodes W and C, while EIS spectra were acquired between WS and R. A representative Nyquist plot of the sample EIS data is shown in Supplementary Figure S2. Prior to EIS measurements, the exposed cores of the four-point probe were inserted 1 cm deep into the samples.
To select an appropriate frequency range for our EIS measurements, we referred to the accuracy contour plot [ScioSpec ISX-3/ISX-3mini manual, version 87, 2021], which indicated an 0.01% error for 1 kΩ impedances from 1 Hz to 1 MHz and an 0.1% error for frequencies above 1 MHz. Also, coaxial cable capacitance, determined by shielding quality, sets an upper frequency limit, while cable inductance, influenced by length, defines a lower frequency limit for accurate impedance measurement [50]. All EIS scans, including calibration scans, were performed over a frequency range of 1 Hz to 5 MHz, using 2048 logarithmically spaced data points per sweep. An excitation voltage of 250.0 mV was applied. Mean and repeat count were set to 1.
The complex impedance () at each frequency point was determined based on the measured real () and imaginary () components of impedance, expressed as:
where is the imaginary unit. The equivalent circuit of the sample and electrode system was modelled as a resistor in parallel with a capacitor, assuming negligible contact resistance and inductance between the sample and the EIS probes [65,66]. For a parallel circuit, the admittance (), defined as the inverse of impedance, is given by:
Here, represents the conductance contributed by the resistor, while denotes the susceptance contributed by the capacitor with capacitance (), proportional to the relative permittivity of the sample (). The angular frequency is defined as , where is the frequency [47].
For the sample modelled as a parallel RC circuit, the conductance () and susceptance (B) were calculated from the measured impedance components as
The sample’s (real-valued) conductivity () and relative permittivity () were further derived using the following relations: and . Here, is the conductivity of the sample, is the permittivity of free space (8.85 × 10−12 Fm−1) and (in m−1) is the cell constant that depends on the geometry and properties of the electrode [67].
2.3. Calibration of the Four-Point Probe
The calibration of the four-point probe for EIS-based conductivity measurements, that is, determining the cell constant for transforming impedance spectra to conductivity, was performed using the HI70031 conductivity standard solution (Hanna Instruments Inc., Woonsocket, RI 02895, USA).
After each set of experiments, the cell constant was determined by performing a calibration EIS scan in 40 mL of the standard solution which had been allowed to equilibrate to room temperature before. The temperature was measured using a Brymen BM235 Multimeter (Brymen Technology Corporation, Taipei, Taiwan) paired with a K type temperature probe, which has an accuracy of ±1 °C. The conductivity of the HI70031 standard solution closest to the measured solution temperature, (), was read from the provided conductivity chart. At 21 and 22 °C, the provided conductivity values of the solution () are 0.1305 ± 0.0005 and 0.1332 ± 0.0005 S/m, respectively. The frequency-dependent cell constant () for the four-point probe was calculated according to
Here, “” designates the frequency. Subsequently, was utilized to calculate the conductivity of biological samples () [65] as
To compare the relative conductivity change () following PEF treatment with respect to an untreated control region with conductivity (), a relative conductivity change (in percent) was calculated as follows:
Similarly, the permittivity () and relative permittivity change () of biological samples were calculated as follows:
2.4. Heterogeneity Test of Untreated Potato Tissue
Potatoes (Solanum tuberosum var. Gala) were purchased as a single batch from a local supermarket.
As a pre-experiment, the heterogeneity of potato tissue was assessed. To that purpose, EIS spectra were acquired in different tissue locations, including three randomly selected regions within the perimedulla, and one region per medulla, cortex, and cortical medulla, respectively (c.f. Figure 1c). In total, N = 6 samples were investigated.
After a longitudinal bisection of the potatoes along their central axis, EIS spectra were obtained by inserting the above described four-point probe perpendicularly to the cut-plane into the respective regions. Frequency-dependent conductivity was derived using cell constants obtained from the standard conductivity solution (0.1332 ± 0.0005 S/m) at a solution temperature of 21.5 °C.
2.5. System Setup for PEF Treatment
The PEF treatment of potato samples was conducted using a BTX Gemini X2 Twin Wave Electroporation System (Harvard Apparatus, Holliston, MA, USA) and a dedicated, custom-designed two-needle electrode system (Figure 1b) [39,40]. The core-to-core distance between the parallel stainless steel needle electrodes, each with a 0.9 mm diameter, was 1 cm. The exposed length of the needles was 1 cm, and the remaining portions were insulated with heated PTFE Teflon tubing to prevent any additional contact with the surroundings. The electrodes were embedded into a transparent polycarbonate block to minimize inadvertent movements during needle insertion into the sample.
2.6. Assessment of PEF-Mediated Conductivity Changes
For PEF treatment, the potato samples were bisected along their longitudinal axis. The two-needle electrodes were inserted 1.3 cm deep into the perimedullar area, perpendicularly to the cut plane. A previously established set of IRE pulse parameters was utilized as a standard IRE protocol and starting point for our experiments, which included NP = 70 unipolar pulses with an applied voltage of PV = 1000 V (and, consequently, a maximum electric field strength of 1000 V/cm), a pulse duration of PW = 100 µs, and a pulse interval of PI = 100 ms.
In four sets of experiments, one parameter from the standard irreversible electroporation protocol, i.e., NP, PI, PW, or PV, was varied at a time, while the remaining parameters were kept at the standard values to assess PEF-mediated conductivity changes. Table 1 summarizes the four sets of experiments alongside with the temperature and conductivity of the standard solution. Each set of experiments was performed on six different potatoes (N = 6). Consequently, up to 10 different PEF treatments were conducted per sample, along with two untreated control measurements, on the available perimedullar area. The dimensions of the potatoes were measured using a digital caliper (Forum, E/D/E GmbH, Wuppertal, Germany) with a resolution of 0.01 mm.

Table 1.
Overview of the four sets of experiments, which varied the number of pulses, the pulse interval, the pulse width, and the pulse voltage while keeping other fixed pulse parameters constant in each set. Alongside, the temperature of the standard conductivity solution and corresponding conductivity as measured prior to calibrating the cell constant.
To verify that the PEF treatment did not cause any tissue heating, the temperature of the potato tissue close to one of the electroporation needle tips was measured after each PEF treatment by inserting a K-type temperature probe of the Multimeter into the needle hole, approximately 10 s after retracting the electroporation needle. Immediately afterwards, i.e., approximately 30 s after PEF treatment, the EIS spectrum was recorded. To that purpose, the four-point probe was positioned vertically about 1 cm deep in the potato tissue, in between the marks left by the electroporation needles.
2.7. Analysis of EIS Data
Per set of experiments and investigated PEF parameter, N = 6 individual conductivity and permittivity curves were calculated using Equations (3)–(5) and referenced to the ‘Ctrl’ regions according to Equation (6), yielding N = 6 relative conductivity () and relative permittivity () curves, respectively. Subsequently, a mean conductivity and permittivity curve and their standard deviation (SD) as well as the corresponding mean curves and their SDs were calculated. The maximum relative conductivity () and the corresponding frequency () were read from the relative conductivity curves. Based on , the optimal decade () for analyzing PEF-mediated conductivity changes was determined by rounding the logarithm of to the nearest integer and converting back to the linear scale. The same analysis was repeated for the permittivity data.
The relative standard deviation (RSD) in percent was used to assess the precision of replicate conductivity and permittivity measurements within each sample group. It was calculated as follows:
2.8. Statistical Analysis
Statistical analysis was performed using GraphPad Prism 10.1.1 (GraphPad Software, Inc., San Diego, CA, USA). One-way repeated-measures ANOVA was employed to compare the conductivity and permittivity of potato tissue before and after electroporation with varying pulse parameters. Per set of experiments, conductivity and permittivity were separately compared at six logarithmically spaced frequencies between 10 Hz and 1 MHz (i.e., 10; 100; 1000; 10,000; 100,000; 1,000,000 Hz), respectively. Tukey’s post hoc test was used to obtain multiplicity-adjusted p-values to address the multiple-comparison problem. The family-wise alpha threshold was set to 0.05.
3. Results
3.1. Study Samples Overview
In total, N = 30 potato samples (5 sets of experiments with N = 6 each) were measured in this study. Their average dimensions were 103 ± 10 mm in length, 76 ± 4 mm in width, and 68 ± 4 mm in height.
3.2. Heterogeneity Test
Conductivity in the untreated potato samples increased from approximately 1000 Hz onwards, while at 1 MHz the highest conductivity values were reached within the medulla region (Figure 2a–d). From 100 kHz onwards, a notable increase in standard deviation of conductivity could be observed.
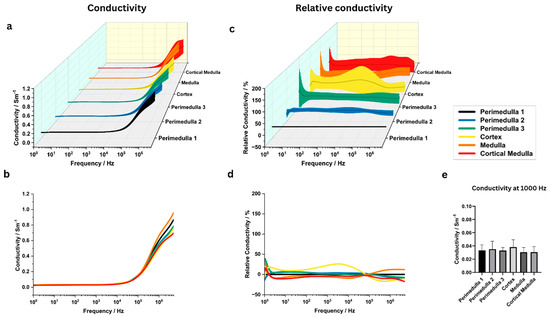
Figure 2.
Electrical conductivity analysis to test heterogeneity within and between distinct potato tissue regions (medulla, perimedulla, cortex, and cortical medulla). (a,b) Conductivity between 1 Hz and 5 MHz, averaged over N = 6 potato samples. The shaded area in (a) indicates the standard deviation. (c,d) Relative conductivity as compared to the perimedulla 1 region. Again, data points were averaged between samples and shaded areas indicate the standard deviation. (e) ANOVA results comparing mean conductivity at 1000 Hz. ANOVA results for other frequencies are stated in Supplementary Tables S1 and S2.
ANOVA at 1000 Hz revealed no significant conductivity differences between the investigated tissue regions (p > 0.9) (Figure 2e). Supplementary Figure S3 and Supplementary Tables S1 and S2 present the mean conductivity values and ANOVA results for the other investigated frequencies. The corresponding permittivity data can be found in Supplementary Figures S4 and S5 and Supplementary Tables S3 and S4. Additionally, ANOVA at 1000 Hz revealed no significant differences in permittivity between the investigated tissue regions (p > 0.9).
3.3. Effect of Different Pulse Voltages on Electrical Conductivity
The pulse voltage significantly influenced the measured conductivity values towards higher pulse voltages (Figure 3a–d). For 8 out of 10 investigated pulse voltages, the highest relative conductivity change was observed near 1000 Hz; the remaining two showed peaks near 10 Hz and 100,000 Hz (Table 2). At 1000 Hz, the relative conductivity increased from 230 ± 85% to 1644 ± 233% as the applied voltage was raised from 200 V to 1000 V.
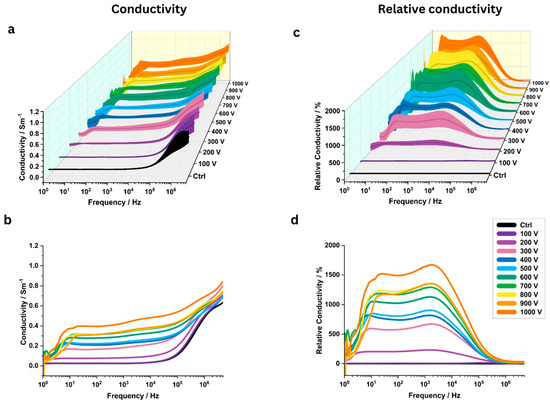
Figure 3.
The analysis of electrical conductivity of potato tissue at various pulse voltages (between 100 V and 1000 V across a frequency range of 1 Hz to 5 MHz (N = 6). (a) Three-dimensional conductivity map with standard deviation for different pulse voltages (N = 6). (b) Mean conductivity plots for different pulse voltages. (c) Three-dimensional plots of relative conductivity for different pulse voltages compared to a control group (“Ctrl”) with standard deviation. (d) Mean relative conductivity values.

Table 2.
Frequencies with highest relative conductivity changes. Per set of experiments and parameter investigated, the highest relative conductivity change observed (), the corresponding frequency at which was measured (), as well as the optimum decade for detecting PEF-induced conductivity changes () are listed.
At 1 kHz, the mean conductivity increased significantly from the control value of 0.025 ± 0.004 S/m to 0.08 ± 0.019 S/m for 200 V (p = 0.0099). At 400 V and above, very significant and extremely significant conductivity changes (p < 0.01) were observed (Figure 4a). The smallest p-value was observed at 700 V, with mean conductivity increasing from the control to 0.337 ± 0.060 S/m (p = 0.0007). The highest mean conductivity was measured at 1000 V, 0.428 ± 0.082 S/m (p = 0.0009).
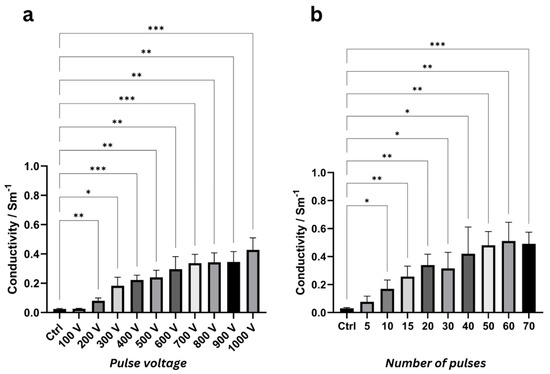
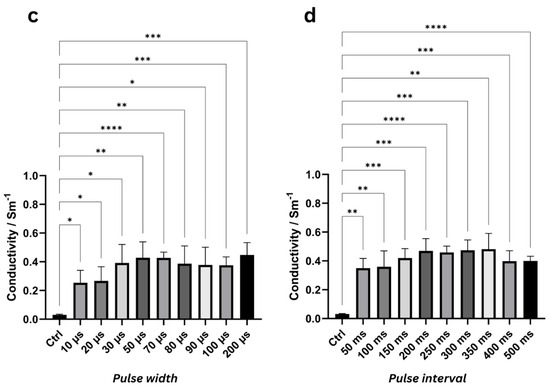
Figure 4.
ANOVA results at 1000 Hz highlighting significant differences in mean conductivity values with standard deviation (N = 6) for various pulse voltages (a), number of pulses (b), pulse widths (c), and pulse intervals (d) compared to the control group (“Ctrl”). Asterisks denote significance levels (* = p < 0.05, ** = p < 0.01, *** = p < 0.001, **** = p < 0.0001). ANOVA results for other frequencies with mean conductivity values are listed in Supplementary Tables S5–S12 and Supplementary Figures S6–S9, respectively.
Table 3 summarizes conductivity at 1 kHz; extended results (mean conductivity values and ANOVA results at other frequencies) are provided in Supplementary Tables S5 and S6.

Table 3.
Average conductivity values (N = 6) with standard deviation in S/m at 1000 Hz for different pulse parameters, including number of pulses, pulse voltage, pulse width, and pulse interval. p-value with respect to ‘Ctrl,’ from the one-way repeated-measures ANOVA. Abbreviations. N/A: not applicable, SD: standard deviation. Supplementary Tables S5, S7, S9 and S11 list the similar data for the other frequency decades.
3.4. Electrical Conductivity Analysis for Different Number of Pulses
In PEF-treated samples, the number of pulses had a significant impact on the measured conductivity (Figure 5a–d). Overall, the (relative) conductivity increased with the number of pulses. For 8/9 investigated NP, the most important relative conductivity changes were observed near 1000 Hz (Table 2). At 1000 Hz, relative conductivity increased from 470 ± 263% to 1535 ± 256% as the number of pulses increased from 10 to 70 (Figure 5c,d).
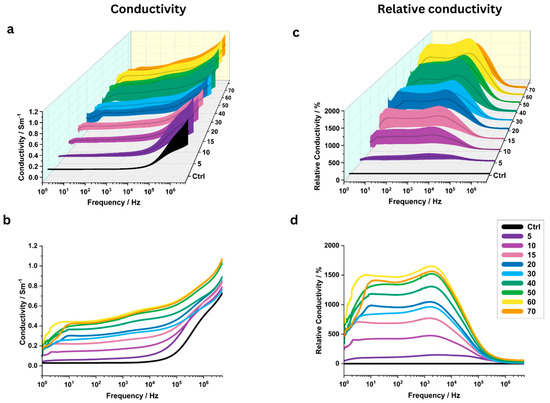
Figure 5.
Influence of the number of pulses on the electrical conductivity of potato tissue. All other IRE pulse parameters were held constant. (a,b) Conductivity between 1 Hz and 5 MHz, averaged over N = 6 potato samples. The shaded area in (a) indicates the standard deviation. (c,d) Relative conductivity as compared to the control (“Ctrl”) region. Again, data points were averaged between samples and shaded areas indicate the standard deviation.
At 1 kHz, mean conductivity increased significantly from the control value of 0.030 ± 0.006 S/m to 0.170 ± 0.063 S/m after 10 pulses (p = 0.033). Very significant changes (p < 0.01) were observed for 15, 20, 50, and 60 pulses (Figure 4b). The highest mean conductivity was measured for 60 pulses (0.511 ± 0.134 S/m, p = 0.004), while the most significant increase was observed at 70 pulses (0.491 ± 0.083 S/m, p = 0.0004).
Table 3 summarizes the conductivity values at 1 kHz; extended results are presented in Supplementary Tables S7 and S8.
3.5. Effect of Different Pulse Widths on Electrical Conductivity
Pulse width significantly influenced the measured conductivity values, with changes observed starting from the shortest pulse width of 10 µs (Figure 6a–d). For 7 out of 9 investigated pulse widths, the highest relative conductivity changes were observed near 1000 Hz; the remaining two showed peaks near 10 Hz (Table 2).
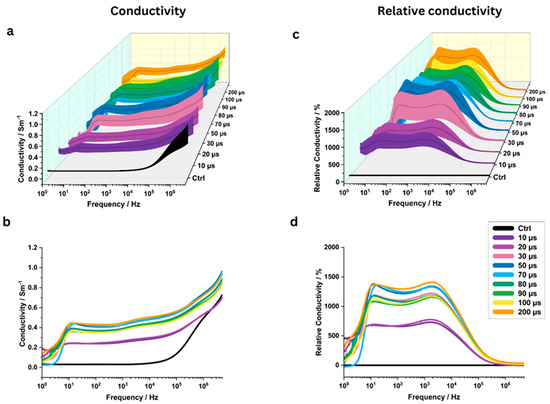
Figure 6.
The electrical conductivity of potato tissue analysis at various pulse widths (10, 20, 30, …, 200 microseconds) across a frequency range of 1 Hz to 5 MHz (N = 6). All other standard IRE pulse parameters were held constant. Three-dimensional conductivity map with standard deviation (a) and mean conductivity plots (b) for different pulse widths (N = 6). Three-dimensional plots of relative conductivity with standard deviation (c) and mean relative conductivity (d) compared to a control group (“Ctrl”) for different pulse widths.
At 1 kHz, conductivity for PW = 10 µs increased significantly from the control value of 0.031 ± 0.004 S/m to 0.254 ± 0.086 S/m (p = 0.0156), representing a relative increase of 722 ± 214%. Extremely significant conductivity changes were observed at 70 µs (0.427 ± 0.040 S/m, p < 0.0001) and 100 µs (0.376 ± 0.058 S/m, p = 0.0004) (Figure 4c). The highest conductivity was recorded at a pulse width of 200 µs, measuring 0.448 ± 0.085 S/m (p = 0.001), which corresponds to a relative increase of 1385 ± 314%.
Table 3 summarizes the conductivity values at 1 kHz; extended results are provided in Supplementary Tables S9 and S10.
3.6. Effect of Different Pulse Intervals on Electrical Conductivity
The pulse interval also significantly influenced the measured electrical conductivity across various pulse intervals (Figure 7a–d). For 8 out of 9 investigated pulse intervals, the highest relative conductivity changes were observed near 1000 Hz; one showed a peak near 10 Hz (Table 2).
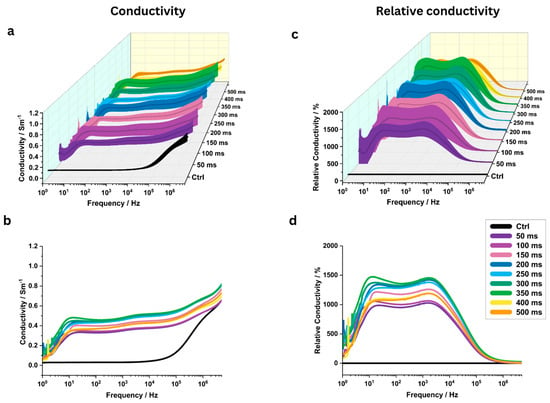
Figure 7.
Analysis of potato tissue electrical conductivity across 1 Hz to 5 MHz frequencies at pulse intervals from 50 to 500 ms (N = 6). Three-dimensional conductivity map with standard deviation (a) and mean conductivity plots (b) for different pulse intervals (N = 6). Three-dimensional plots of relative conductivity with standard deviation (c) and mean relative conductivity (d) compared to a control group (“Ctrl”) for different pulse intervals.
At 1 kHz, starting from the shortest investigated pulse interval of 50 ms, conductivity increased very significantly to 0.350 ± 0.070 S/m (p = 0.0011), representing a relative increase of 1019 ± 224% compared to the control (0.031 ± 0.003 S/m) (Figure 4d). Extremely significant conductivity changes (p < 0.0001) were observed at 250 ms and 500 ms, where conductivities reached 0.459 ± 0.044 S/m and 0.400 ± 0.032 S/m, corresponding to relative increases of 1367 ± 159% and 1177 ± 86%, respectively. The highest conductivity change of 0.482 ± 0.109 S/m (p = 0.002) was observed at a pulse interval of 350 ms, with a relative increase of 1437 ± 346%.
Table 3 summarizes the conductivity values at 1 kHz; extended results are presented in Supplementary Tables S11 and S12.
3.7. Effect of Different PEF Pulse Parameters on Permittivity and Tissue Temperature
The average permittivity values (F/m) and ANOVA results at different frequencies, evaluating the effects of PEF pulse parameters such as pulse voltage, number, width, and interval, are presented in the Supplementary Tables S13–S20 and Supplementary Figures S10–S17. Also, Supplementary Figure S18 and Supplementary Table S21 summarizes the temperatures measured within the samples directly after electroporation for all four sets of experiments.
3.8. Repeatability of Conductivity and Permittivity Measurements
Repeatability of conductivity and permittivity measurements, expressed as RSD (%) across frequencies for heterogeneity tests, is shown in the Supplementary Tables S22–S24. The assessment of repeatability for conductivity and permittivity measurements used to study the effects of PEF pulse parameters is presented in the Supplementary Tables S25 and S26, respectively.
4. Discussion
This study investigated the effects of PEF parameters on the electrical conductivity of potato tissue using open-ended four-probe coaxial cable EIS. We have shown that untreated potato tissue can be considered electrically homogeneous (p > 0.9). By covering a wide range of pulse parameters, our study gives indications for future studies in potato as a plant-based PEF model. Throughout four sets of PEF experiments that varied different treatment parameters, 1000 Hz was found to be the optimal frequency decade in most cases, as it yielded the maximal measured relative conductivity changes. However, in some experiments, 10 Hz resulted in the maximum conductivity changes (Table 2). At 1000 Hz, significant differences between an untreated control region and the PEF-treated regions were found from PV = 200 V, NP = 10, PW = 10 µs, and PI = 50 ms onwards, respectively, which comprised nearly all the investigated pulse parameter ranges. When varying the pulse voltage, the smallest p-value was found for PV = 700 V, corresponding to a mean conductivity increase from 0.025 ± 0.004 to 0.337 ± 0.060 S/m (p = 0.0007). When varying the number of pulses, the smallest p-value (at 1000 Hz) was found for NP = 70, resulting in a mean conductivity increase from 0.030 ± 0.006 S/m to 0.491 ± 0.083 S/m (p < 0.004). When varying the pulse width, the smallest p-value was found for PW = 70 µs, corresponding to a mean conductivity increase from 0.031 ± 0.004 to 0.427 ± 0.04 S/m (p < 0.0001). Lastly, when varying the pulse interval, the smallest p-values were found for PI = 250 ms and PI = 500 ms, corresponding to a mean conductivity increase from 0.031 ± 0.003 S/m to 0.459 ± 0.044 S/m (p < 0.0001) and to 0.400 ± 0.032 S/m (p < 0.0001), respectively.
In this study, we selected pulse parameters around the most reported ones for clinical IRE treatments, which are 100 µs pulse width and 1000 V/cm electric field strength [8,68]. While we intentionally employed “traditional” pulse protocols, recent studies have achieved nanopore formation by using nanosecond pulses with electric field strengths of 15–30 kV/cm (NP = 800, PW = 300 ns) [69]. Studies showed that a single pulse, even with supercritical amplitude, may not cause irreversible membrane rupture, indicating that the number of pulses (NP) is one of several parameters influencing membrane response [1]. This well-known behaviour was replicated with our setup: our results did not show any significant conductivity changes for the smallest number of pulses (NP = 5). In this study, we used high-voltage unipolar square wave pulses in line with other PEF studies [70].
This study focused on pulse intervals greater than 50 ms, although previous studies suggest that shorter intervals (<1 ms) may further enhance PEF treatment efficacy [71]. We observed significant conductivity changes at all pulse intervals up to 500 ms.
The stability of tissue temperature post-PEF treatment, as observed in Supplementary Figure S18, shows an advantage of irreversible electroporation (IRE) over thermal ablation methods such as radiofrequency ablation (RFA). Across varied PEF parameters, tissue temperatures remained close to room temperature, indicating minimal thermal effects. This supports the potential of IRE for applications where heat-induced damage is a concern.
Plant-based models were chosen for this study to accommodate the need for a larger number of samples in line with the 3R policy on animal research [34,35]. Moreover, potatoes were utilized in previous studies focusing on electrochemical EIS-based conductivity analysis [72]. From the non-significant conductivity changes within untreated potato tissue, we conclude that potato tissue is a suitable plant-based model for future EIS-based conductivity experiments to assess PEF effects. However, there may be overall conductivity differences between different potato variants.
The cell membrane behaves as a capacitor at low frequencies (around 1 kHz), preventing electric current flow in the intracellular medium. At higher frequencies (10 to 100 MHz), the membrane conducts electric current with similar impedance values for both intact and ruptured cells [73]. During PEF treatment, PEF exerts a force on ions, potentially disrupting membrane integrity and increasing conductivity. This is due to the formation of membrane nanopores, which enhance membrane permeability to Na+, K+, Cl− [74], and internal Ca2+ ions move to the extracellular matrix [22,75]. The higher standard deviation in electrical conductivity observed at lower frequencies in PEF-treated samples may be due to varying intracellular ionic concentrations and differing cellular responses among samples.
Electrical impedance tomography (EIT) is a recent technique that adds tomographic capacity to EIS. By a conventional EIT measurement, conductivity maps of (biological) samples at a single excitation frequency can be obtained [76]. Previously, researchers used a 5 kHz excitation signal to obtain in vivo EIT maps of irreversibly electroporated tissue [55]. This study rather recommends an excitation frequency closer to 1000 Hz to image PEF effects using EIT, at least for EIT on potato tissue. In the future, optimal frequencies derived from EIS could be employed for EIT to maximize conductivity differences between PEF-treated and untreated tissue, enabling high-contrast imaging.
Our study has limitations. First, we did not examine any time-dependent conductivity changes caused by PEF, but limited EIS analysis to approximately 30 s after treatment. The conductivity of PEF-treated samples is time-dependent. According to the literature, the resealing of pores caused by PEF occurs within 1–100 µs, if electroporation was reversible [77]. However, a study using EIS at 3 kHz to analyse the time-dependent changes of high-voltage PEF-treated potato tissue (PV = 4000 V, PW = 1000 µs) suggested that conductivity reached a plateau after 50 min [73]. Moreover, PEF treatments with smaller PV or PW may require more prolonged resealing times, ranging from seconds to days [77]. Summing up, 30 s after PEF treatment, tissue damage from IRE was likely to be complete, but conductivity changes may not have reached a plateau yet. Second, our study does not provide an external reference such as tissue staining to assess whether RE or IRE has happened, which is why we refrained from assigning the observed conductivity changes to one or the other regime. Third, EIS is inherently limited because it can only provide localized measurements. Future studies should investigate potential synergies between PEF parameters and explore different PEF treatment electrode configurations, as the current study focused on a single electrode setup and isolated parameter effects. Additionally, nuclear magnetic resonance (NMR) and Raman spectroscopy may be used to characterize extracellular chemical changes, alongside high-resolution confocal microscopy to reveal structural alterations.
5. Conclusions
Four-point open-ended coaxial probe EIS, after calibration to a standard reference solution, was identified as a highly suitable platform for estimating the dielectric properties of electroporated potato samples. Additionally, the non-significant conductivity changes between different regions within the potato indicate its suitability for EIS-based PEF pulse parameter optimization studies. The optimal measurement frequency for PEF-mediated changes in potato tissue was found to be 1000 Hz. At this frequency, EIS revealed significant increases in conductivity over a wide range of investigated PEF parameters, which has implications for conductivity mapping methods such as electrical impedance tomography that operate at a single frequency. Our findings indicate the influence of PEF parameters on conductivity changes measured by EIS, offering insights for multiphysics modelling of clinical IRE treatments with tissue-specific electrical properties and for optimizing excitation frequencies to enhance conductivity mapping contrast in applications such as electrical impedance tomography. These results and information may support future needle development and personalized clinical intervention protocols.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/app15147922/s1, Figure S1: Four-point open-ended coaxial probe for EIS; Figure S2: Representative Nyquist plot; Figure S3: Conductivity of potato tissue across frequencies; Figures S4 and S5: Permittivity of potato tissue across frequencies; Figure S6: Effect of pulse voltage on conductivity; Figure S7: Effect of number of pulses on conductivity; Figure S8: Effect of pulse width on conductivity; Figure S9: Effect of pulse interval on conductivity; Figures S10 and S11: Effect of pulse voltage on permittivity; Figures S12 and S13: Effect of number of pulses on permittivity; Figures S14 and S15: Effect of pulse width on permittivity; Figures S16 and S17: Effect of pulse interval on permittivity; Figure S18: Tissue temperature post-PEF treatment. Tables S1 and S2: Conductivity of potato tissue across frequencies; Tables S3 and S4: Permittivity of potato tissue across frequencies; Tables S5 and S6: Effect of pulse voltage on conductivity; Tables S7 and S8: Effect of number of pulses on conductivity; Tables S9 and S10: Effect of pulse width on conductivity; Tables S11 and S12: Effect of pulse interval on conductivity; Tables S13 and S14: Effect of pulse voltage on permittivity; Tables S15 and S16: Effect of number of pulses on permittivity; Tables S17 and S18: Effect of pulse width on permittivity; Tables S19 and S20: Effect of pulse interval on permittivity; Table S21: Tissue temperature post-PEF treatment; Tables S22–S26: Relative standard deviation (%) of conductivity and permittivity measurements.
Author Contributions
Conceptualization, methodology, instrumentation, validation, formal analysis, investigation, writing—original draft preparation, data curation, visualization: A.T. Review, supervision, formal analysis: T.L. and M.B. Instrumentation: J.-G.P. Review, supervision, project administration, funding acquisition: A.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received financial support from the ElectroPros project, funded by Marie Skłodowska-Curie Actions under H2020-EU.1.3.1 (grant No. 813192).
Institutional Review Board Statement
Ethical approval was not required for this research as it solely involved plant-based models.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available on request.
Acknowledgments
We, the authors, wish to express our gratitude to Sciospec Scientific Instruments GmbH for their support. Additionally, Figure 1 was created with BioRender.com.
Conflicts of Interest
Author Marco Baragona was employed by the company Philips Research. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ANOVA | analysis of variance |
| ATP | adenosine triphosphate |
| C | counter electrode |
| DNA | deoxyribonucleic acid |
| EIS | electrochemical impedance spectroscopy |
| EIT | electrical impedance tomography |
| IRE | irreversible electroporation |
| NP | numbers of pulses |
| NMR | nuclear magnetic resonance |
| PEF | pulsed electric fields |
| PI | pulse intervals |
| PTFE | polytetrafluoroethylene |
| PV | pulse voltage |
| PW | pulse width |
| R | reference electrode |
| RE | reversible electroporation |
| ROS | reactive oxygen species |
| RSD | relative standard deviation |
| SD | standard deviation |
| TMV | transmembrane voltage |
| VGICs | voltage-gated ion channels |
| W | working electrode |
| WS | working sense electrode |
References
- Angersbach, A.; Heinz, V.; Knorr, D. Effects of Pulsed Electric Fields on Cell Membranes in Real Food Systems. Innov. Food Sci. Emerg. Technol. 2000, 1, 135–149. [Google Scholar] [CrossRef]
- Weaver, J.C.; Chizmadzhev, Y.A. Theory of Electroporation: A Review. Bioelectrochem. Bioenerg. 1996, 41, 135–160. [Google Scholar] [CrossRef]
- Kotnik, T.; Rems, L.; Tarek, M.; Miklavcic, D. Membrane Electroporation and Electropermeabilization: Mechanisms and Models. Annu. Rev. Biophys. 2019, 48, 63–91. [Google Scholar] [CrossRef] [PubMed]
- Weaver, J.C.; Smith, K.C.; Esser, A.T.; Son, R.S.; Gowrishankar, T.R. A Brief Overview of Electroporation Pulse Strength–Duration Space: A Region Where Additional Intracellular Effects Are Expected. Bioelectrochemistry 2012, 87, 236–243. [Google Scholar] [CrossRef] [PubMed]
- Batista Napotnik, T.; Polajžer, T.; Miklavčič, D. Cell Death Due to Electroporation—A Review. Bioelectrochemistry 2021, 141, 107871. [Google Scholar] [CrossRef] [PubMed]
- Morozov, A.; Taratkin, M.; Barret, E.; Singla, N.; Bezrukov, E.; Chinenov, D.; Enikeev, M.; Gomez Rivas, J.; Shpikina, A.; Enikeev, D. A Systematic Review of Irreversible Electroporation in Localised Prostate Cancer Treatment. Andrologia 2020, 52, e13789. [Google Scholar] [CrossRef] [PubMed]
- Yeung, E.S.L.; Chung, M.W.Y.; Wong, K.; Wong, C.Y.K.; So, E.C.T.; Chan, A.C.Y. An Update on Irreversible Electroporation of Liver Tumours. Hong Kong Med. J. 2014, 20, 313–316. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Jourabchi, N.; Beroukhim, K.; Tafti, B.A.; Kee, S.T.; Lee, E.W. Irreversible Electroporation (NanoKnife) in Cancer Treatment. Gastrointest. Interv. 2014, 3, 8–18. [Google Scholar] [CrossRef]
- Valerio, M.; Dickinson, L.; Ali, A.; Ramachandran, N.; Donaldson, I.; Freeman, A.; Ahmed, H.U.; Emberton, M. A Prospective Development Study Investigating Focal Irreversible Electroporation in Men with Localised Prostate Cancer: Nanoknife Electroporation Ablation Trial (NEAT). Contemp. Clin. Trials 2014, 39, 57–65. [Google Scholar] [CrossRef] [PubMed]
- Yarmush, M.L.; Golberg, A.; Serša, G.; Kotnik, T.; Miklavčič, D. Electroporation-Based Technologies for Medicine: Principles, Applications, and Challenges. Annu. Rev. Biomed. Eng. 2014, 16, 295–320. [Google Scholar] [CrossRef] [PubMed]
- Kos, B.; Voigt, P.; Miklavcic, D.; Moche, M. Careful Treatment Planning Enables Safe Ablation of Liver Tumors Adjacent to Major Blood Vessels by Percutaneous Irreversible Electroporation (IRE). Radiol. Oncol. 2015, 49, 234–241. [Google Scholar] [CrossRef] [PubMed]
- Kotnik, T.; Pucihar, G.; Reberšek, M.; Miklavčič, D.; Mir, L.M. Role of Pulse Shape in Cell Membrane Electropermeabilization. Biochim. Biophys. Acta (BBA) Biomembr. 2003, 1614, 193–200. [Google Scholar] [CrossRef]
- Miklavčič, D.; Serša, G.; Brecelj, E.; Gehl, J.; Soden, D.; Bianchi, G.; Ruggieri, P.; Rossi, C.R.; Campana, L.G.; Jarm, T. Electrochemotherapy: Technological Advancements for Efficient Electroporation-Based Treatment of Internal Tumors. Med. Biol. Eng. Comput. 2012, 50, 1213–1225. [Google Scholar] [CrossRef] [PubMed]
- Jouni, A.; Baragona, M.; Pedersoli, F.; Ritter, A. Temperature Distribution on Classical Two Needles IRE Setup Versus a Single Needle Prototype. Technol. Cancer Res. Treat. 2024, 23, 15330338241288342. [Google Scholar] [CrossRef] [PubMed]
- Pasqualotto, E.; Ferrario, A.; Scaramuzza, M.; De Toni, A.; Maschietto, M. Monitoring Electropermeabilization of Adherent Mammalian Cells Through Electrochemical Impedance Spectroscopy. Procedia Chem. 2012, 6, 79–88. [Google Scholar] [CrossRef]
- Scuderi, M.; Dermol-Cern, J.; Scancar, J.; Markovic, S.; Rems, L.; Miklavcic, D. The Equivalence of Different Types of Electric Pulses for Electrochemotherapy with Cisplatin—An In Vitro Study. Radiol. Oncol. 2024, 58, 51–66. [Google Scholar] [CrossRef] [PubMed]
- Ivorra, A.; Al-Sakere, B.; Rubinsky, B.; Mir, L.M. In Vivo Electrical Conductivity Measurements during and after Tumor Electroporation: Conductivity Changes Reflect the Treatment Outcome. Phys. Med. Biol. 2009, 54, 5949. [Google Scholar] [CrossRef] [PubMed]
- Ivorra, A.; Rubinsky, B. In Vivo Electrical Impedance Measurements during and after Electroporation of Rat Liver. Bioelectrochemistry 2007, 70, 287–295. [Google Scholar] [CrossRef] [PubMed]
- Elez-Martínez, P.; Odriozola-Serrano, I.; Oms-Oliu, G.; Soliva-Fortuny, R.; Martín-Belloso, O. Effects of Pulsed Electric Fields Processing Strategies on Health-Related Compounds of Plant-Based Foods. Food Eng. Rev. 2017, 9, 213–225. [Google Scholar] [CrossRef]
- Leong, S.Y.; Oey, I. Pulsed Electric Fields Processing of Plant-Based Foods: An Overview. In Encyclopedia of Food Chemistry; Elsevier: Amsterdam, The Netherlands, 2019; pp. 245–254. [Google Scholar] [CrossRef]
- Hogenes, A.M.; Overduin, C.G.; Slump, C.H.; van Laarhoven, C.J.H.M.; Fütterer, J.J.; ten Broek, R.P.G.; Stommel, M.W.J. The Influence of Irreversible Electroporation Parameters on the Size of the Ablation Zone and Thermal Effects: A Systematic Review. Technol. Cancer Res. Treat. 2023, 22, 15330338221125003. [Google Scholar] [CrossRef] [PubMed]
- Pakhomova, O.N.; Gregory, B.W.; Khorokhorina, V.A.; Bowman, A.M.; Xiao, S.; Pakhomov, A.G. Electroporation-Induced Electrosensitization. PLoS ONE 2011, 6, e17100. [Google Scholar] [CrossRef] [PubMed]
- Davalos, R.V.; Bhonsle, S.; Neal, R.E. Implications and Considerations of Thermal Effects When Applying Irreversible Electroporation Tissue Ablation Therapy. Prostate 2015, 75, 1114–1118. [Google Scholar] [CrossRef] [PubMed]
- Beitel-White, N.; Lorenzo, M.F.; Zhao, Y.; Brock, R.M.; Coutermarsh-Ott, S.; Allen, I.C.; Manuchehrabadi, N.; Davalos, R.V. Multi-Tissue Analysis on the Impact of Electroporation on Electrical and Thermal Properties. IEEE Trans. Biomed. Eng. 2021, 68, 771–782. [Google Scholar] [CrossRef] [PubMed]
- Mathy, R.M.; Tinoush, P.; da Florencia, R.D.; Braun, A.; Ghamarnejad, O.; Radeleff, B.; Kauczor, H.U.; Chang, D.H. Impact of Needle Positioning on Ablation Success of Irreversible Electroporation: A Unicentric Retrospective Analysis. Sci. Rep. 2020, 10, 21902. [Google Scholar] [CrossRef] [PubMed]
- Ritter, A.; Bruners, P.; Isfort, P.; Barabasch, A.; Pfeffer, J.; Schmitz, J.; Pedersoli, F.; Baumann, M. Electroporation of the Liver: More Than 2 Concurrently Active, Curved Electrodes Allow New Concepts for Irreversible Electroporation and Electrochemotherapy. Technol. Cancer Res. Treat. 2018, 17, 153303381880999. [Google Scholar] [CrossRef] [PubMed]
- Lakshmi Narasimhan, P.; Tokoutsi, Z.; Baroli, D.; Baragona, M.; Veroy, K.; Maessen, R.; Ritter, A. Global Sensitivity Study for Irreversible Electroporation: Towards Treatment Planning under Uncertainty. Med. Phys. 2023, 50, 1290–1304. [Google Scholar] [CrossRef] [PubMed]
- Šel, D.; Cukjati, D.; Batiuskaite, D.; Slivnik, T.; Mir, L.M.; Miklavčič, D. Sequential Finite Element Model of Tissue Electropermeabilization. IEEE Trans. Biomed. Eng. 2005, 52, 816–827. [Google Scholar] [CrossRef] [PubMed]
- Rubinsky, B.; Onik, G.; Mikus, P. Irreversible Electroporation: A New Ablation Modality—Clinical Implications. Technol. Cancer Res. Treat. 2007, 6, 37–48. [Google Scholar] [CrossRef] [PubMed]
- Ben-David, E.; Appelbaum, L.; Sosna, J.; Nissenbaum, I.; Goldberg, S.N. Characterization of Irreversible Electroporation Ablation in In Vivo Porcine Liver. Am. J. Roentgenol. 2012, 198, W62–W68. [Google Scholar] [CrossRef] [PubMed]
- De Vito, F.; Ferrari, G.; Lebovka, N.I.; Shynkaryk, N.V.; Vorobiev, E. Pulse Duration and Efficiency of Soft Cellular Tissue Disintegration by Pulsed Electric Fields. Food Bioprocess Technol. 2008, 1, 307–313. [Google Scholar] [CrossRef]
- Kandušer, M.; Miklavčič, D. Electroporation in Biological Cell and Tissue: An Overview. In Food Engineering Series; Springer: New York, NY, USA, 2009; pp. 1–37. [Google Scholar] [CrossRef]
- Haider, M.W.; Nafees, M.; Iqbal, R.; Asad, H.U.; Azeem, F.; Ali, B.; Shaheen, G.; Iqbal, J.; Vyas, S.; Arslan, M.; et al. Postharvest Starch and Sugars Adjustment in Potato Tubers of Wide-Ranging Dormancy Genotypes Subjected to Various Sprout Forcing Techniques. Sci. Rep. 2023, 13, 14845. [Google Scholar] [CrossRef] [PubMed]
- Smith, A.J.; Lilley, E. The Role of the Three Rs in Improving the Planning and Reproducibility of Animal Experiments. Animals 2019, 9, 975. [Google Scholar] [CrossRef] [PubMed]
- Hubrecht, R.C.; Carter, E. The 3Rs and Humane Experimental Technique: Implementing Change. Animals 2019, 9, 754. [Google Scholar] [CrossRef] [PubMed]
- Ivorra, A.; Ausín, T.; Becerra-Fajardo, L.; del Ama, A.J.; Minguillón, J.; García-Moreno, A.; Aguiló, J.; Barroso, F.O.; Bijnens, B.; Camara, O.; et al. The Biomedical Engineer’s Pledge 1.0. Zenodo 2023. [Google Scholar] [CrossRef]
- Bhonsle, S.P.; Arena, C.B.; Sweeney, D.C.; Davalos, R. V Mitigation of Impedance Changes Due to Electroporation Therapy Using Bursts of High-Frequency Bipolar Pulses. Biomed. Eng. Online 2015, 14, S3. [Google Scholar] [CrossRef] [PubMed]
- Jeong, S.; Kim, H.; Park, J.; Kim, K.W.; Sim, S.B.; Chung, J.H. Evaluation of Electroporated Area Using 2,3,5-Triphenyltetrazolium Chloride in a Potato Model. Sci. Rep. 2021, 11, 20431. [Google Scholar] [CrossRef] [PubMed]
- Thomas, A.; Nolte, T.; Baragona, M.; Ritter, A. Finding an Effective MRI Sequence to Visualise the Electroporated Area in Plant-Based Models by Quantitative Mapping. Bioelectrochemistry 2023, 153, 108463. [Google Scholar] [CrossRef] [PubMed]
- Lindelauf, K.H.K.; Thomas, A.; Baragona, M.; Jouni, A.; Nolte, T.; Pedersoli, F.; Pfeffer, J.; Baumann, M.; Maessen, R.T.H.; Ritter, A. Plant-Based Model for the Visual Evaluation of Electroporated Area after Irreversible Electroporation and Its Comparison to in-Vivo Animal Data. Sci. Prog. 2023, 106, 00368504231156294. [Google Scholar] [CrossRef] [PubMed]
- Narkar, A.; Kaboudian, A.; Ardeshirpour, Y.; Casciola, M.; Feaster, T.; Blinova, K. In Vitro Assay Development to Study Pulse Field Ablation Outcome Using Solanum Tuberosum. Int. J. Mol. Sci. 2024, 25, 8967. [Google Scholar] [CrossRef] [PubMed]
- Galindo, F.G.; Vernier, P.T.; Dejmek, P.; Vicente, A.; Gundersen, M.A. Pulsed Electric Field Reduces the Permeability of Potato Cell Wall. Bioelectromagnetics 2008, 29, 296–301. [Google Scholar] [CrossRef] [PubMed]
- Janositz, A.; Noack, A.K.; Knorr, D. Pulsed Electric Fields and Their Impact on the Diffusion Characteristics of Potato Slices. LWT Food Sci. Technol. 2011, 44, 1939–1945. [Google Scholar] [CrossRef]
- Faridnia, F.; Burritt, D.J.; Bremer, P.J.; Oey, I. Innovative Approach to Determine the Effect of Pulsed Electric Fields on the Microstructure of Whole Potato Tubers: Use of Cell Viability, Microscopic Images and Ionic Leakage Measurements. Food Res. Int. 2015, 77, 556–564. [Google Scholar] [CrossRef]
- Castellví, Q.; Banús, J.; Ivorra, A. 3D Assessment of Irreversible Electroporation Treatments in Vegetal Models. IFMBE Proc. 2016, 53, 294–297. [Google Scholar] [CrossRef]
- Hjouj, M.; Rubinsky, B. Magnetic Resonance Imaging Characteristics of Nonthermal Irreversible Electroporation in Vegetable Tissue. J. Membr. Biol. 2010, 236, 137–146. [Google Scholar] [CrossRef] [PubMed]
- Genovese, J.; Kranjc, M.; Serša, I.; Petracci, M.; Rocculi, P.; Miklavčič, D.; Mahnič-Kalamiza, S. PEF-Treated Plant and Animal Tissues: Insights by Approaching with Different Electroporation Assessment Methods. Innov. Food Sci. Emerg. Technol. 2021, 74, 102872. [Google Scholar] [CrossRef]
- Chilcott, T.C.; Chan, M.; Gaedt, L.; Nantawisarakul, T.; Fane, A.G.; Coster, H.G.L. Electrical Impedance Spectroscopy Characterisation of Conducting Membranes: I. Theory. J. Memb. Sci. 2002, 195, 153–167. [Google Scholar] [CrossRef]
- Castellví, Q.; Mercadal, B.; Ivorra, A. Assessment of Electroporation by Electrical Impedance Methods. In Handbook of Electroporation; Springer International Publishing: Cham, Switzerland, 2017; Volume 1, pp. 671–690. [Google Scholar]
- Lazanas, A.C.; Prodromidis, M.I. Electrochemical Impedance Spectroscopy—A Tutorial. ACS Meas. Sci. Au 2023, 3, 162–193. [Google Scholar] [CrossRef] [PubMed]
- Bigdeli, I.K.; Yeganeh, M.; Shoushtari, M.T.; Zadeh, M.K. Electrochemical Impedance Spectroscopy (EIS) for Biosensing. In Nanosensors for Smart Manufacturing; Elsevier: Amsterdam, The Netherlands, 2021; pp. 533–554. [Google Scholar] [CrossRef]
- Guo, F.; Gou, X.; Sun, J.; Hong, J.; Zhang, Y. Modeling Methods in Overlapping Electroporation Treatments: Pulse Number Effects on Tissue Conductivity and Ablation Area. Electrochim. Acta 2024, 503, 144883. [Google Scholar] [CrossRef]
- Wardhana, G.; Raman, N.M.; Abayazid, M.; Fütterer, J.J. Investigating the Effect of Electrode Orientation on Irreversible Electroporation with Experiment and Simulation. Int. J. Comput. Assist. Radiol. Surg. 2022, 17, 1399–1407. [Google Scholar] [CrossRef] [PubMed]
- Mansouri, S.; Alharbi, Y.; Haddad, F.; Chabcoub, S.; Alshrouf, A.; Abd-Elghany, A.A. Electrical Impedance Tomography—Recent Applications and Developments. J. Electr. Bioimpedance 2021, 12, 50–62. [Google Scholar] [CrossRef] [PubMed]
- Granot, Y.; Ivorra, A.; Maor, E.; Rubinsky, B. In Vivo Imaging of Irreversible Electroporation by Means of Electrical Impedance Tomography. Phys. Med. Biol. 2009, 54, 4927. [Google Scholar] [CrossRef] [PubMed]
- Boone, K.; Barber, D.; Brown, B. Imaging with Electricity: Report of the European Concerted Action on Impedance Tomography. J. Med. Eng. Technol. 1997, 21, 201–232. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, N.; Fan, L.-F.; Zhao, P.-F.; Li, J.-H.; Huang, L.; Wang, Z.-Y. Robust Electrical Impedance Tomography for Biological Application: A Mini Review. Heliyon 2023, 9, e15195. [Google Scholar] [CrossRef] [PubMed]
- Fafilek, G. The Use of Voltage Probes in Impedance Spectroscopy. Solid. State Ion. 2005, 176, 2023–2029. [Google Scholar] [CrossRef]
- Schwan, H.P. Electrode polarization impedance and measurements in biological materials. Ann. N. Y. Acad. Sci. 1968, 148, 191–209. [Google Scholar] [CrossRef] [PubMed]
- Ishai, P.B.; Talary, M.S.; Caduff, A.; Levy, E.; Feldman, Y. Electrode Polarization in Dielectric Measurements: A Review. Meas. Sci. Technol. 2013, 24, 102001. [Google Scholar] [CrossRef]
- Raicu, V. A Simple Theoretical and Practical Approach to Measuring Dielectric Properties with an Open-Ended Coaxial Probe. Meas. Sci. Technol. 1995, 6, 410. [Google Scholar] [CrossRef]
- Gabriel, C.; Gabriel, S.; Corthout, E. The Dielectric Properties of Biological Tissues: I. Literature Survey. Phys. Med. Biol. 1996, 41, 2231–2249. [Google Scholar] [CrossRef] [PubMed]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The Dielectric Properties of Biological Tissues: III. Parametric Models for the Dielectric Spectrum of Tissues. Phys. Med. Biol. 1996, 41, 2271–2293. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Liu, H.; Bhonsle, S.P.; Wang, Y.; Davalos, R.V.; Yao, C. Ablation Outcome of Irreversible Electroporation on Potato Monitored by Impedance Spectrum under Multi-Electrode System. Biomed. Eng. Online 2018, 17, 126. [Google Scholar] [CrossRef] [PubMed]
- Oshin, E.A.; Guo, S.; Jiang, C. Determining Tissue Conductivity in Tissue Ablation by Nanosecond Pulsed Electric Fields. Bioelectrochemistry 2022, 143, 107949. [Google Scholar] [CrossRef] [PubMed]
- Miklavčič, D.; Pavšelj, N.; Hart, F.X. Electric Properties of Tissues. In Wiley Encyclopedia of Biomedical Engineering; Major Reference Works; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; ISBN 9780471740360. [Google Scholar]
- Laufer, S.; Ivorra, A.; Reuter, V.E.; Rubinsky, B.; Solomon, S.B. Electrical Impedance Characterization of Normal and Cancerous Human Hepatic Tissue. Physiol. Meas. 2010, 31, 995. [Google Scholar] [CrossRef] [PubMed]
- Cannon, R.; Ellis, S.; Hayes, D.; Narayanan, G.; Martin, R.C.G. Safety and Early Efficacy of Irreversible Electroporation for Hepatic Tumors in Proximity to Vital Structures. J. Surg. Oncol. 2013, 107, 544–549. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Xu, D.; Dong, G.; Ren, Z.; Zhang, W.; Aji, T.; Zhao, Q.; Chen, X.; Jiang, T. The Safety and Efficacy of Nanosecond Pulsed Electric Field in Patients With Hepatocellular Carcinoma: A Prospective Phase 1 Clinical Study Protocol. Front. Oncol. 2022, 12, 869316. [Google Scholar] [CrossRef] [PubMed]
- Raso, J.; Frey, W.; Ferrari, G.; Pataro, G.; Knorr, D.; Teissie, J.; Miklavčič, D. Recommendations Guidelines on the Key Information to Be Reported in Studies of Application of PEF Technology in Food and Biotechnological Processes. Innov. Food Sci. Emerg. Technol. 2016, 37, 312–321. [Google Scholar] [CrossRef]
- Lebar, A.M.; Troiano, G.C.; Tung, L.; Miklavčič, D. Inter-Pulse Interval between Rectangular Voltage Pulses Affects Electroporation Threshold of Artificial Lipid Bilayers. IEEE Trans. NanoBiosci. 2002, 1, 116–120. [Google Scholar] [CrossRef] [PubMed]
- Bonakdar, M.; Latouche, E.L.; Mahajan, R.L.; Davalos, R.V. The Feasibility of a Smart Surgical Probe for Verification of IRE Treatments Using Electrical Impedance Spectroscopy. IEEE Trans. Biomed. Eng. 2015, 62, 2674–2684. [Google Scholar] [CrossRef] [PubMed]
- Angersbach, A.; Heinz, V.; Knorr, D. Evaluation of Process-Induced Dimensional Changes in the Membrane Structure of Biological Cells Using Impedance Measurement. Biotechnol. Prog. 2002, 18, 597–603. [Google Scholar] [CrossRef] [PubMed]
- Romeo, S.; Wu, Y.H.; Levine, Z.A.; Gundersen, M.A.; Vernier, P.T. Water Influx and Cell Swelling after Nanosecond Electropermeabilization. Biochim. Biophys. Acta (BBA) Biomembr. 2013, 1828, 1715–1722. [Google Scholar] [CrossRef] [PubMed]
- Ruiz-Fernández, A.R.; Campos, L.; Gutierrez-Maldonado, S.E.; Núñez, G.; Villanelo, F.; Perez-Acle, T. Nanosecond Pulsed Electric Field (NsPEF): Opening the Biotechnological Pandora’s Box. Int. J. Mol. Sci. 2022, 23, 6158. [Google Scholar] [CrossRef] [PubMed]
- Moro, L.C.; Porto, R.W. Single Frequency Electrical Impedance Tomography System with Offline Reconstruction Algorithm. In Proceedings of the 2015 IEEE 6th Latin American Symposium on Circuits and Systems, LASCAS 2015—Conference Proceedings 2015, Montevideo, Uruguay, 24–27 February 2015. [Google Scholar] [CrossRef]
- Parniakov, O.; Lebovka, N.; Wiktor, A.; Alles, M.C.; Hill, K.; Toepfl, S. Applications of Pulsed Electric Fields for Processing Potatoes: Examples and Equipment Design. Res. Agric. Eng. 2022, 68, 47–62. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).