Deep Learning-Based Crack Detection on Cultural Heritage Surfaces
Abstract
1. Introduction
- A two-stage workflow is introduced, wherein image classification is first employed to identify images containing potential cracks, followed by semantic segmentation to delineate crack regions. This approach offers a lower computational cost compared to more complex instance segmentation models.
- By integrating segmentation outputs with a simple yet effective field-based tool (parallel lasers), the method facilitates accurate estimation of crack lengths.
- The proposed framework demonstrates strong adaptability to varying lighting conditions and background textures typical of heritage surfaces. Its lightweight design also enables potential deployment on portable platforms.
2. Materials and Methods
2.1. Image Collection
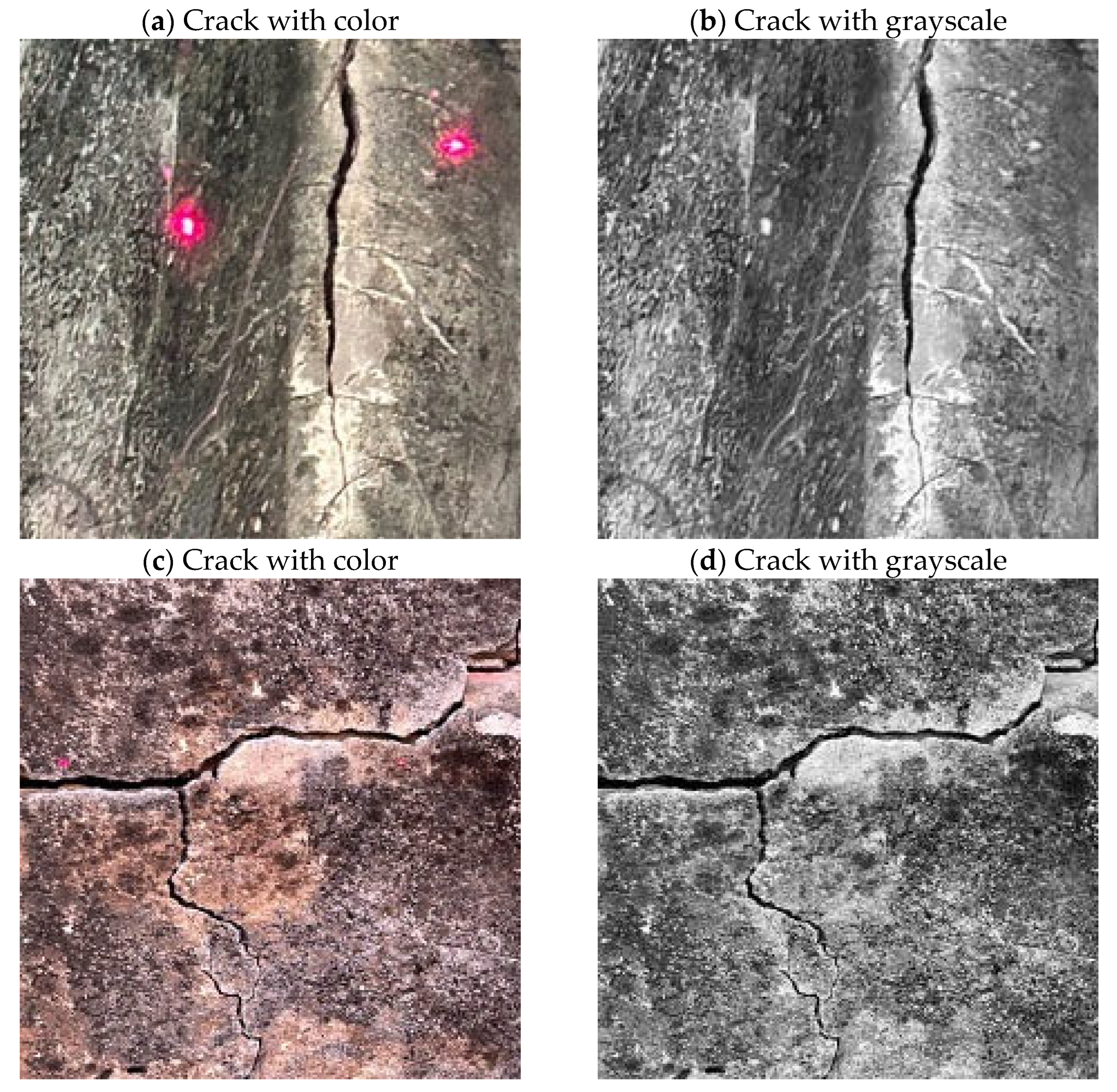
2.2. Image Preprocessing
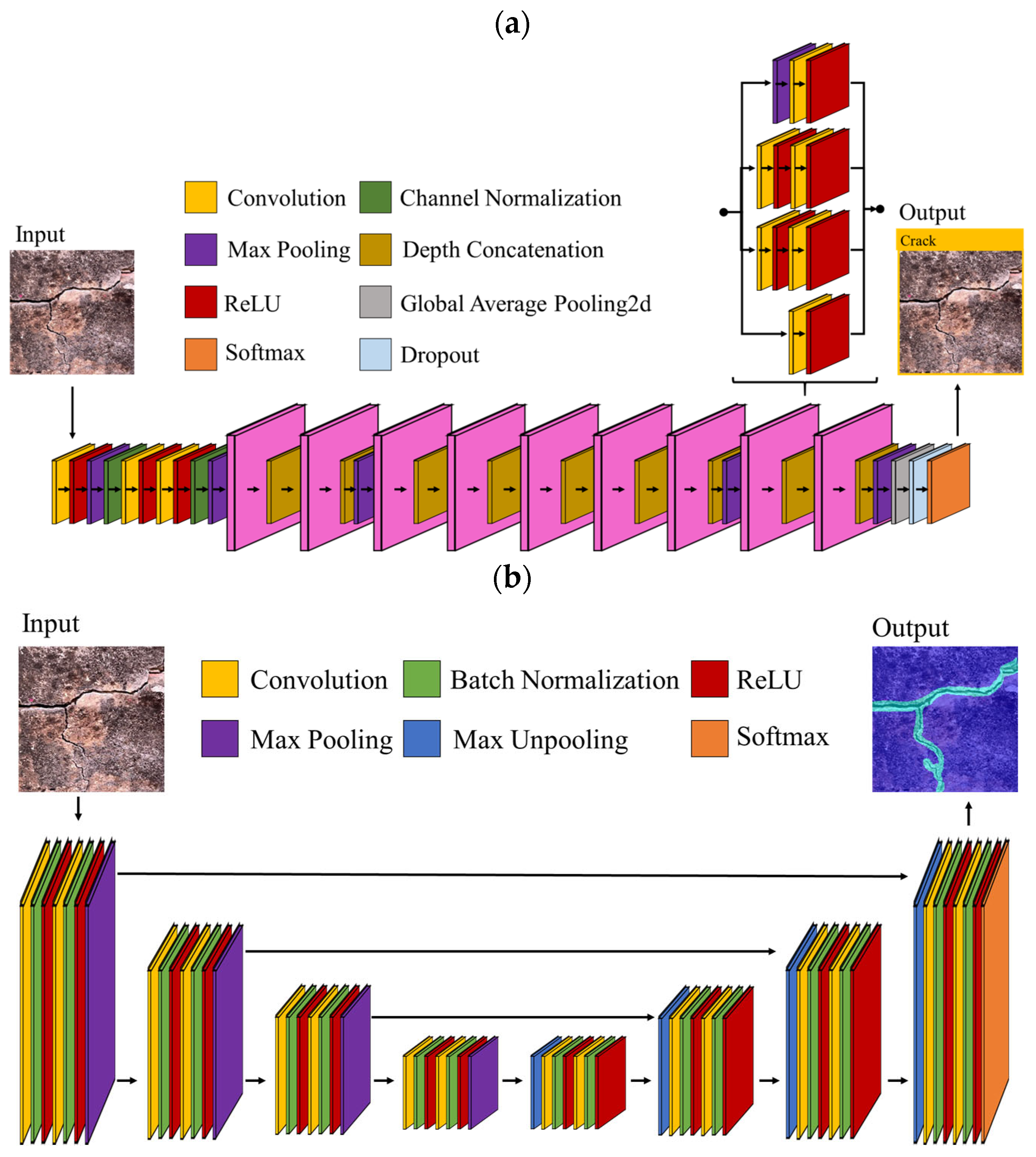
2.3. Deep Learning Models
2.3.1. GoogleNet Model
2.3.2. SegNet Model
2.4. Hardware and Software
2.5. Scale Conversion
2.6. Evaluation Indices
3. Results
3.1. Crack Identification Results
3.2. Pixel-Level Segmentation of Crack Regions
3.3. Crack Length Estimation Analysis
3.4. Crack Detection Limit Analysis
4. Discussion
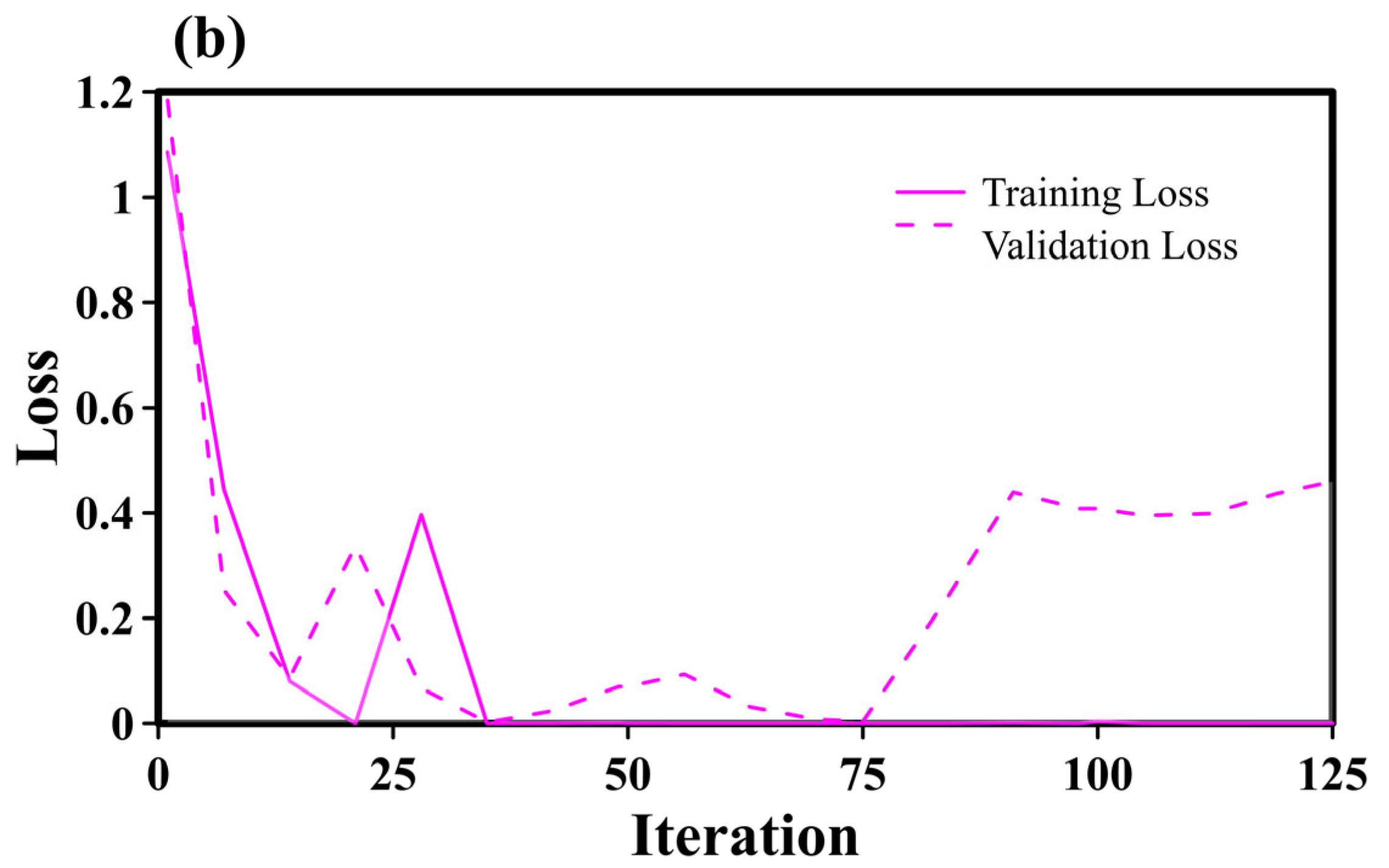
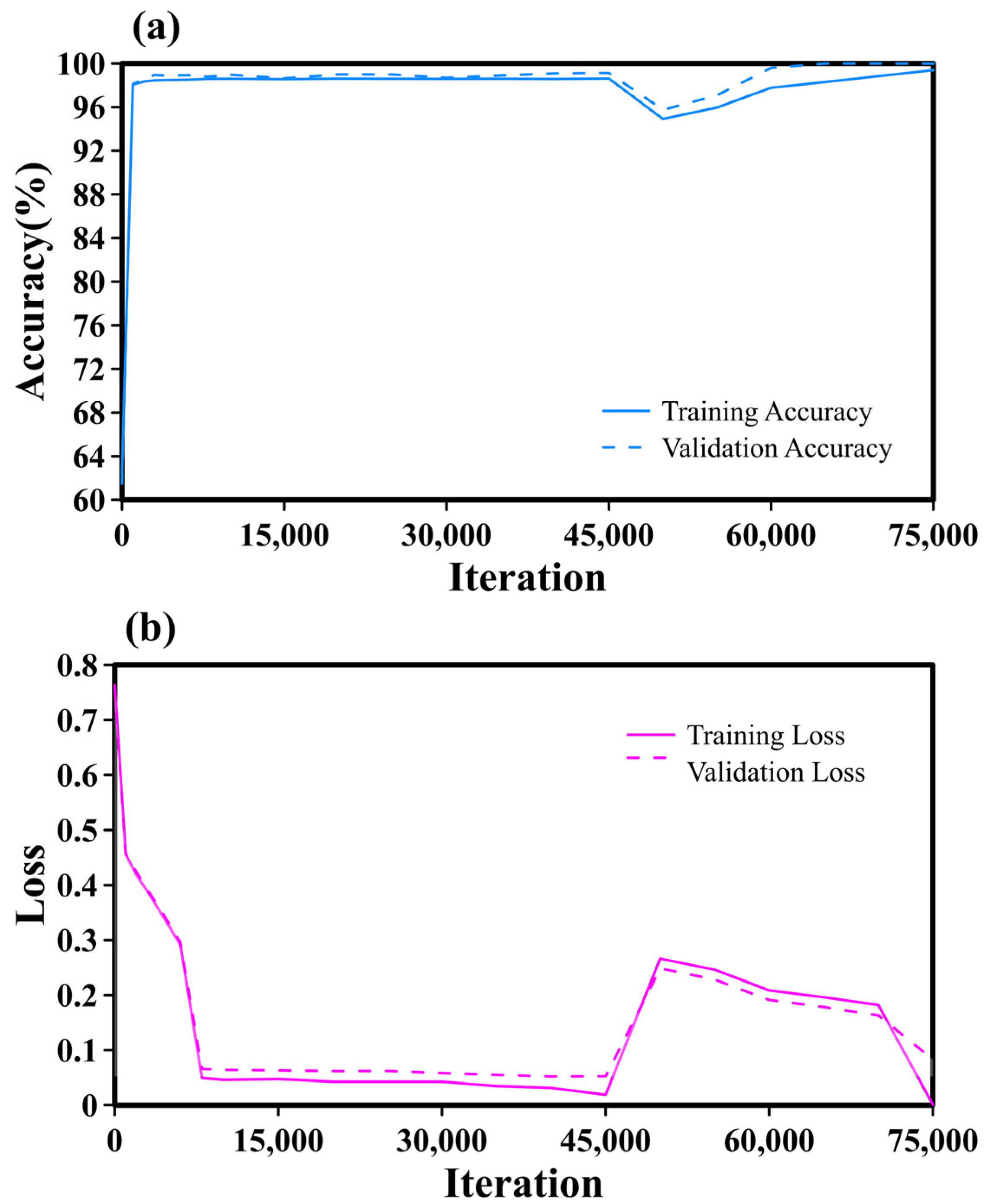
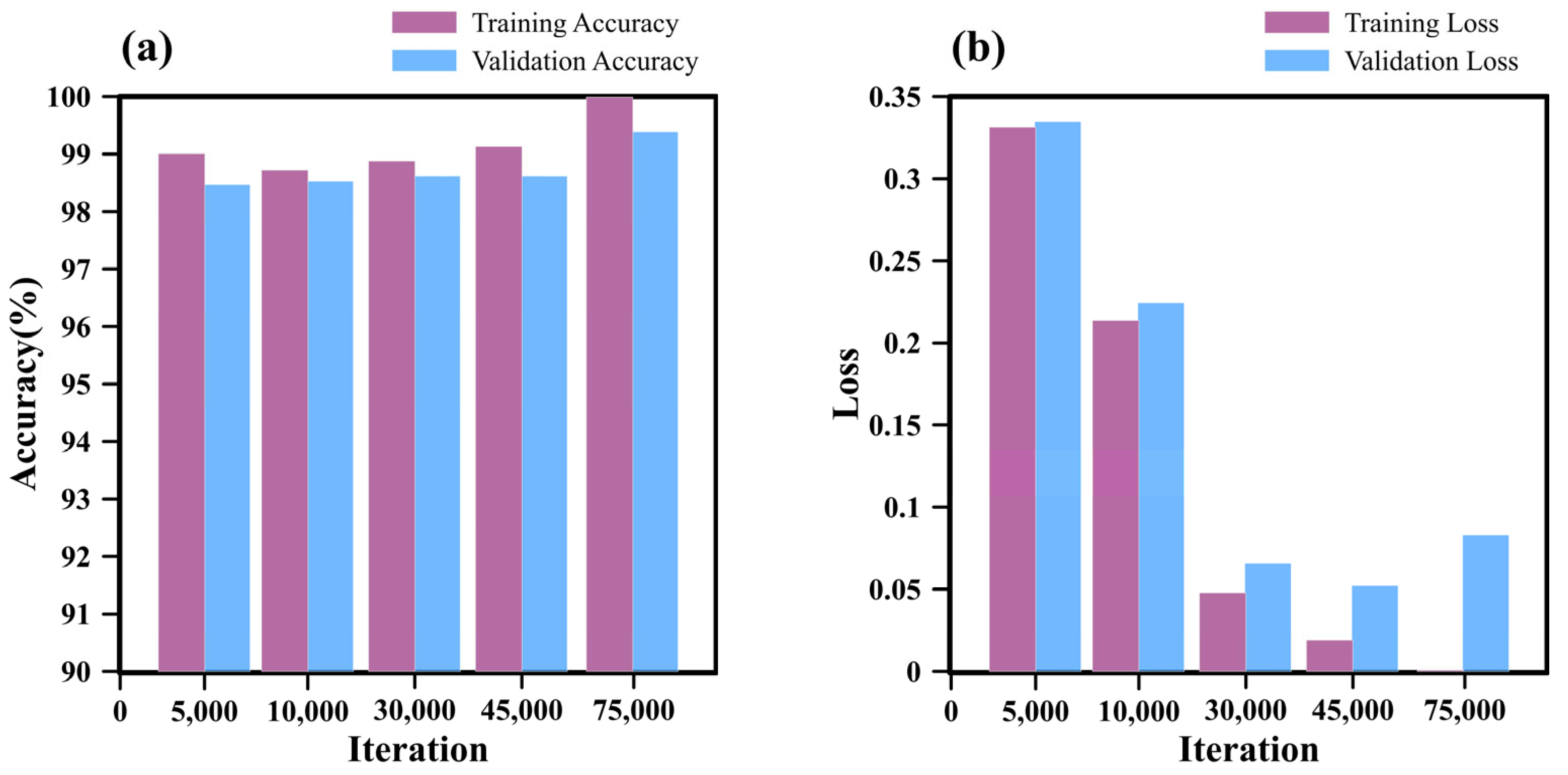
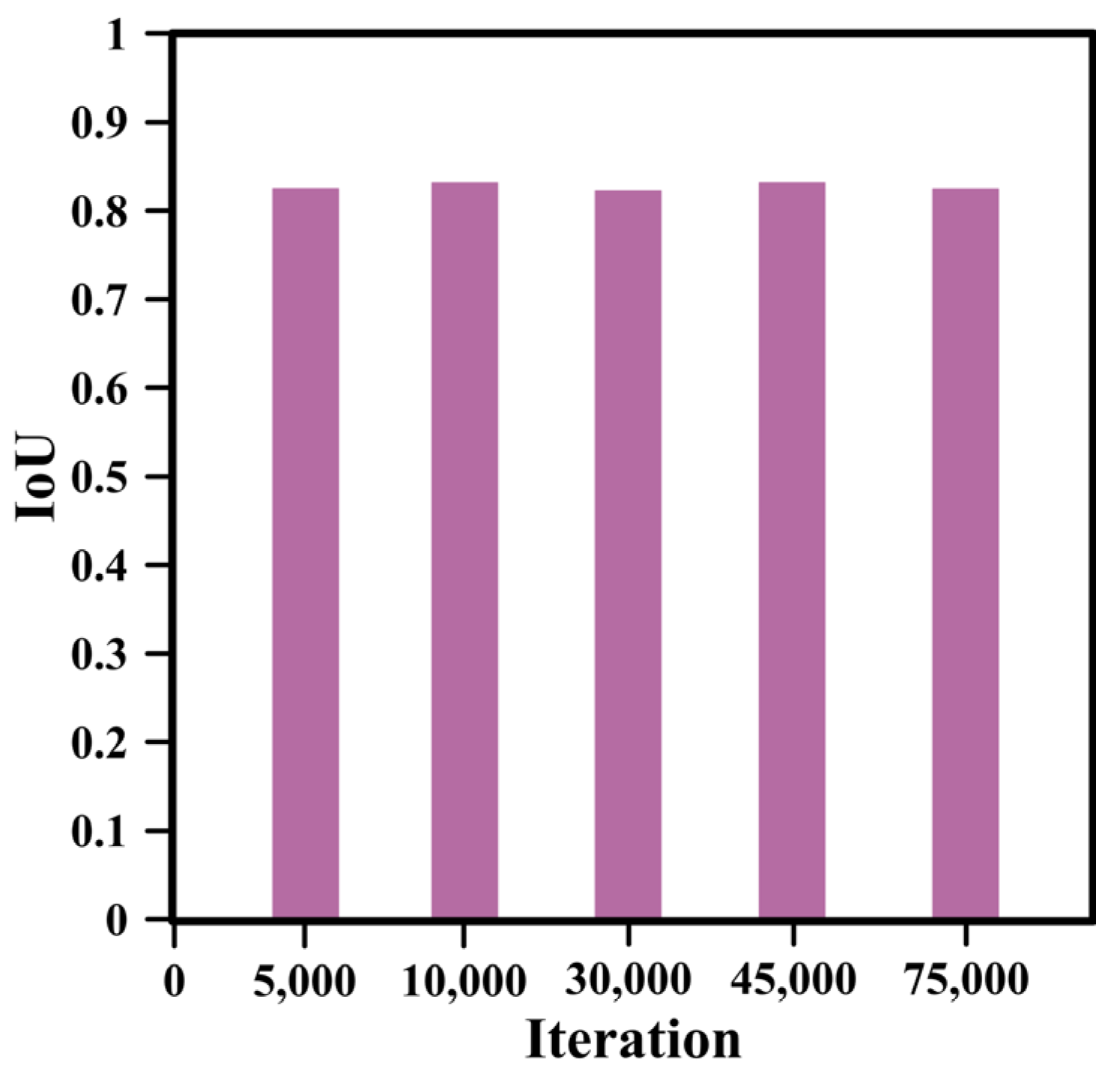
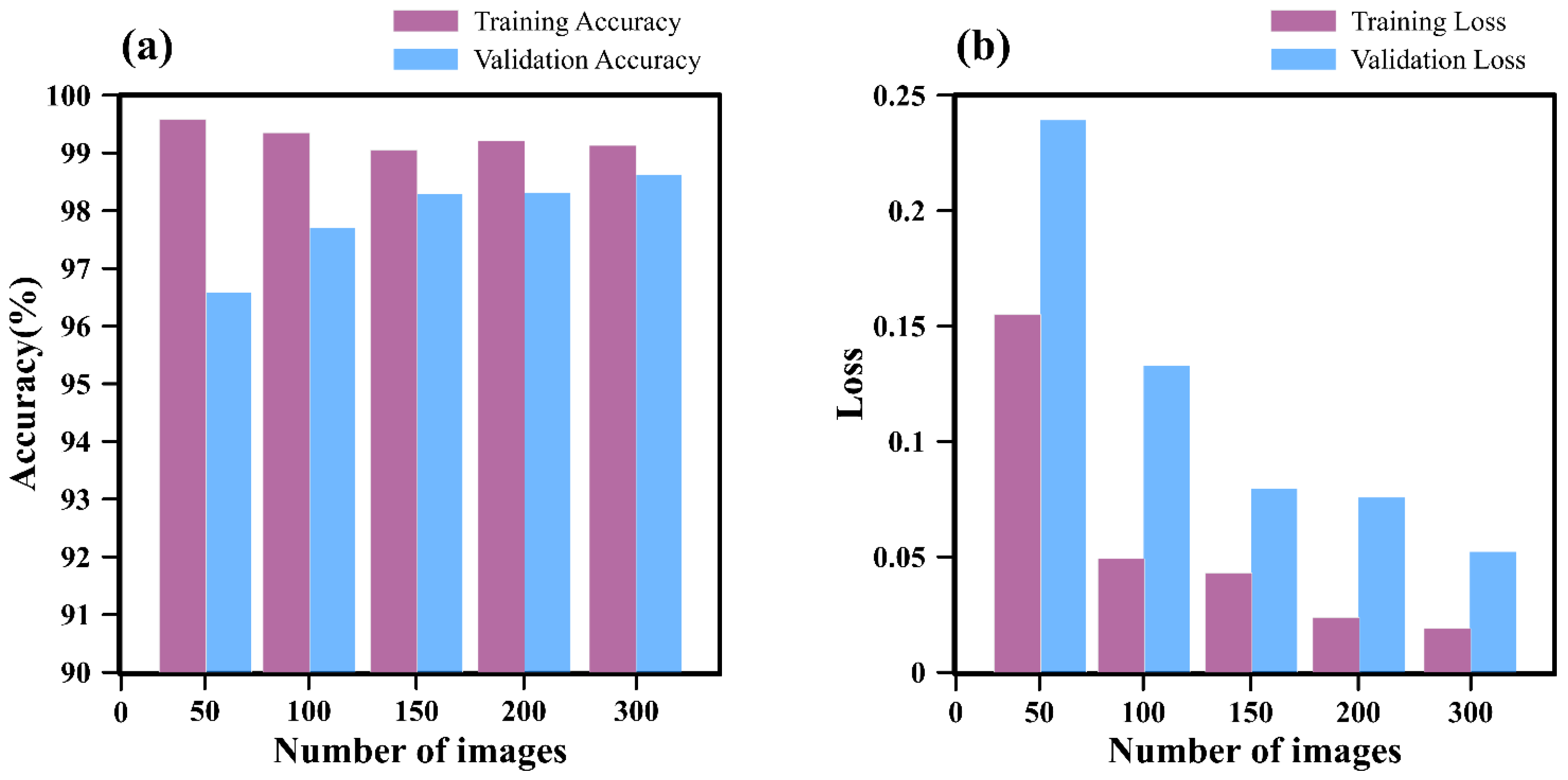
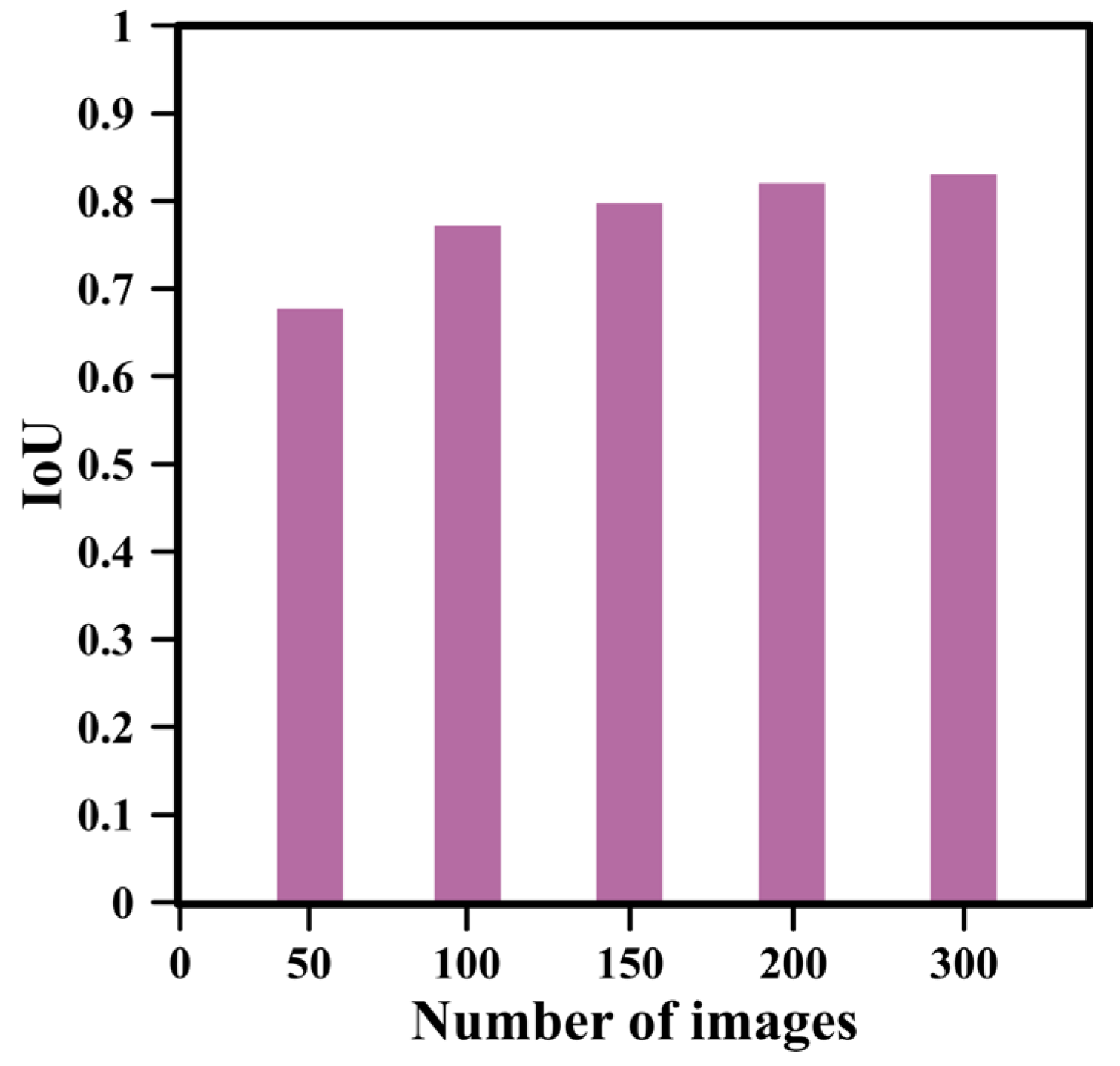
4.1. Number of Iterations
4.1.1. Impact of Iteration Count on GoogleNet
4.1.2. Impact of Iteration Count on SegNet
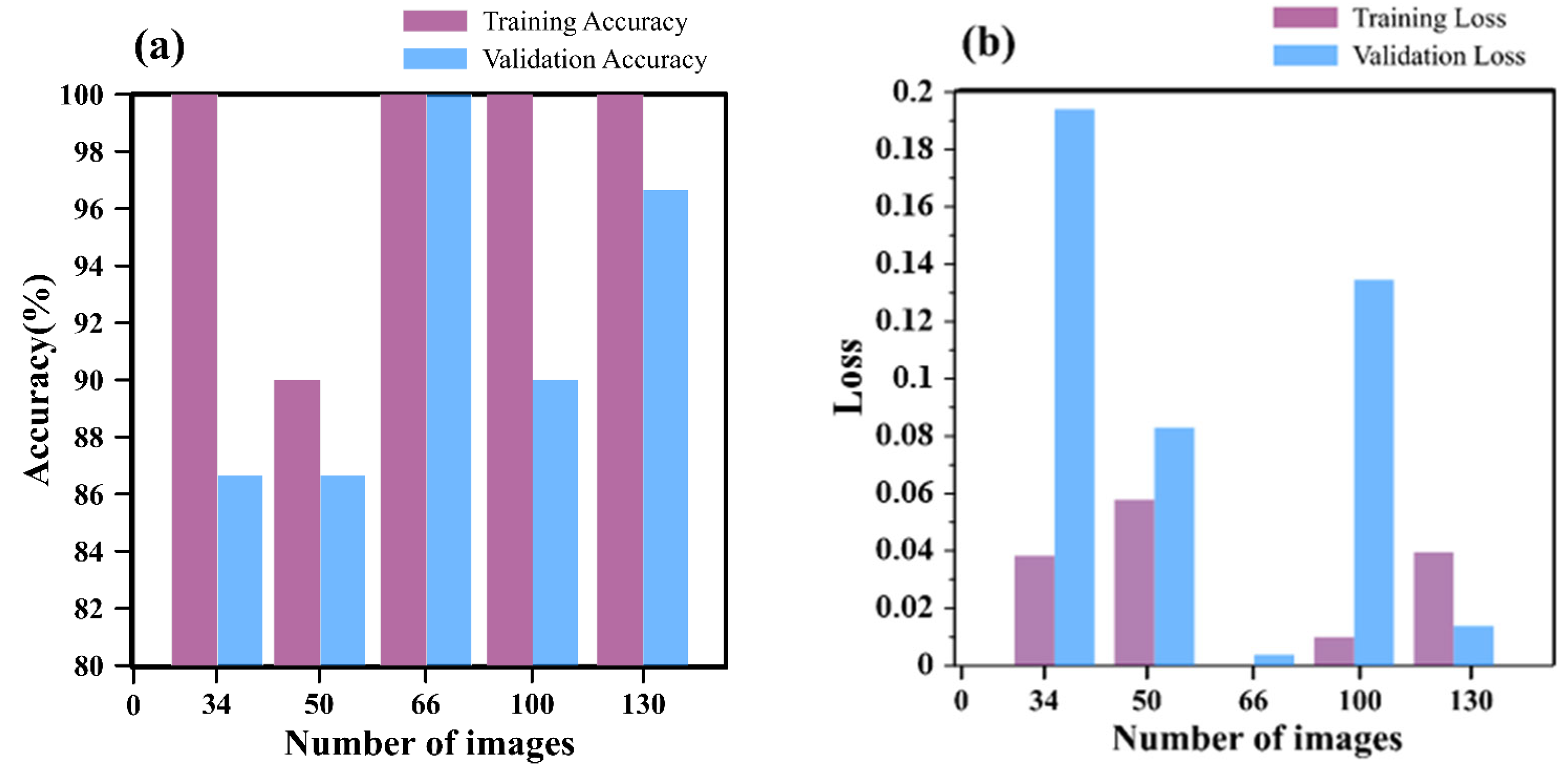
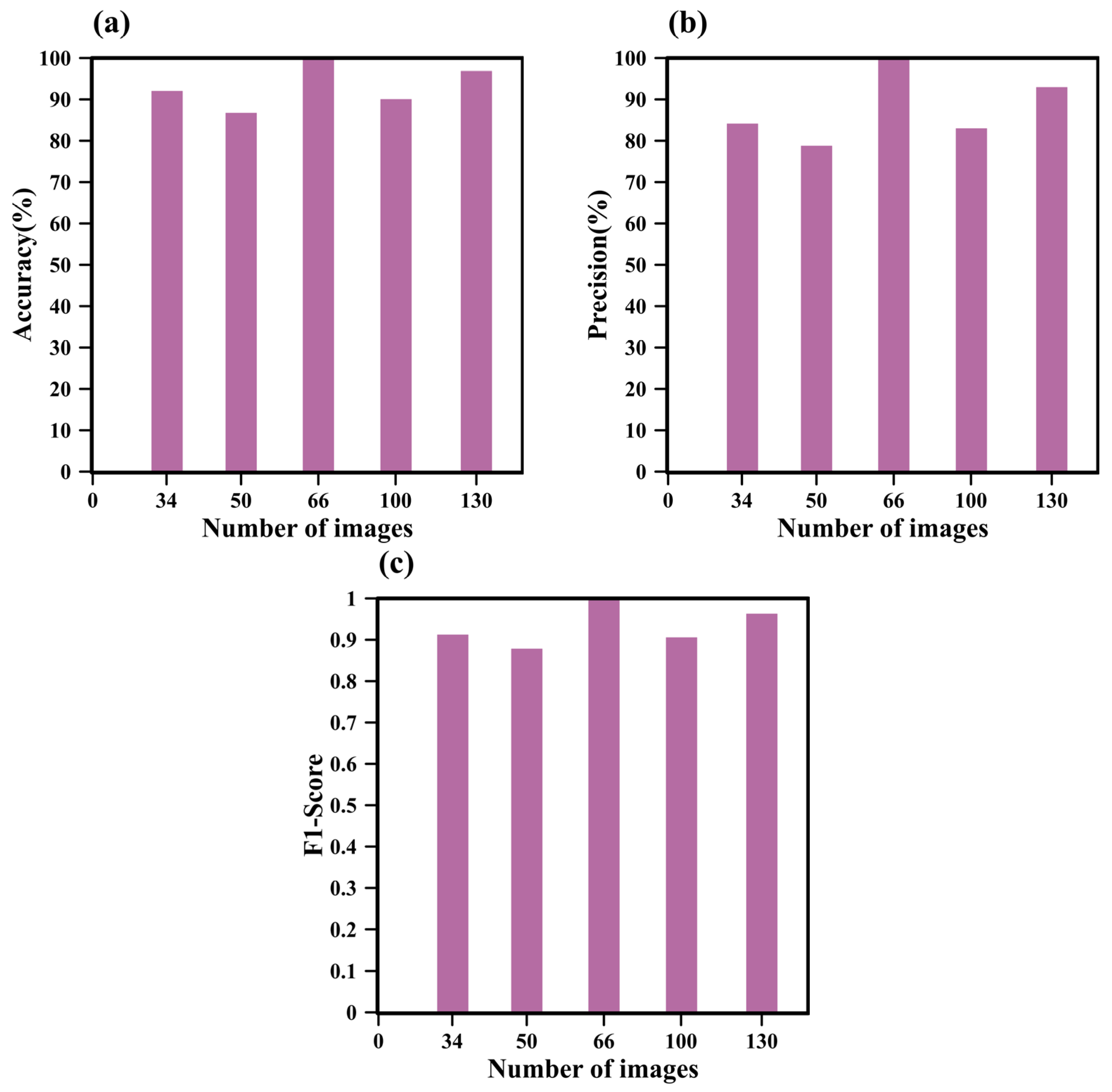
4.2. Number of Images
4.2.1. Impact of Image Quantity on GoogleNet
4.2.2. Impact of Image Quantity on SegNet
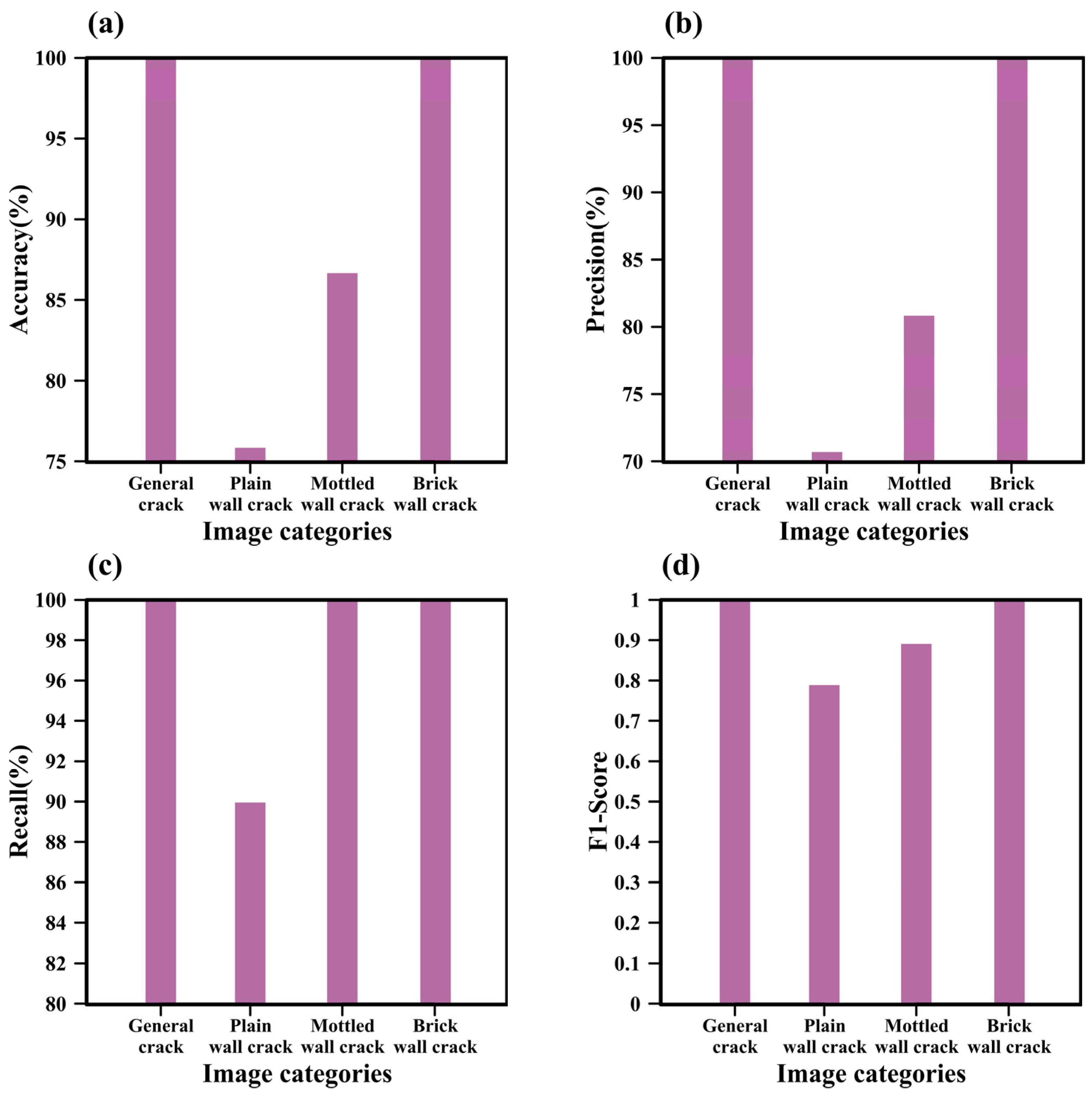
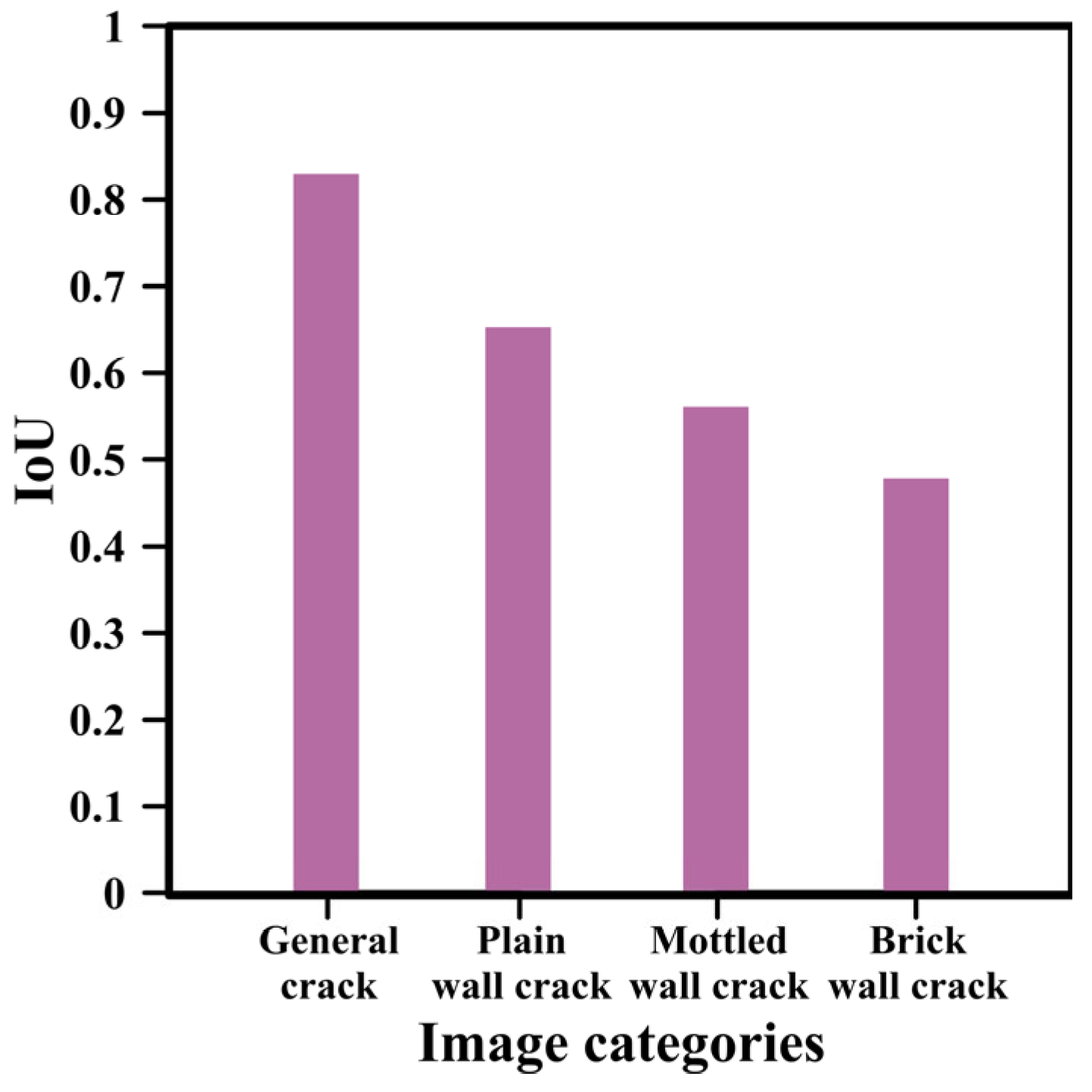
4.3. Image Categories
4.3.1. Impact of Image Categories on GoogleNet
4.3.2. Impact of Image Categories on SegNet
4.3.3. Texture Analysis
4.4. Comparison with Other Deep Learning Models
4.5. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CL | Crack Length |
| CLI | Crack Length in Image |
| CNNs | Convolutional Neural Networks |
| DA | Data Augmentation |
| DLP | Distance between Laser Points |
| DLPI | Distance between Laser Points in Image |
| FCNs | Fully Convolutional Networks |
| FN | False Negative |
| FP | False Positive |
| GLCM | Gray-Level Co-occurrence Matrix |
| ILSVRC | ImageNet Large Scale Visual Recognition Challenge |
| IoU | Intersection over Union |
| NiN | Network in Network |
| ReLU | Rectified Linear Unit |
| R-CNN | Region-based Convolutional Neural Networks |
| SGDM | Stochastic Gradient Descent with Momentum |
| TN | True Negative |
| TP | True Positive |
| UAVs | Unmanned Aerial Vehicles |
| YOLO | You Only Look Once |
References
- Świerczyńska, E.; Karsznia, K.; Książek, K.; Odziemczyk, W. Investigating diverse photogrammetric techniques in the hazard assessment of historical sites of the Museum of the Coal Basin Area in Będzin, Poland. Rep. Geod. Geoinformatics 2024, 118, 70–81. [Google Scholar] [CrossRef]
- Yigit, A.Y.; Uysal, M. Automatic crack detection and structural inspection of cultural heritage buildings using UAV photogrammetry and digital twin technology. J. Build. Eng. 2024, 94, 109952. [Google Scholar] [CrossRef]
- Li, L.; Tang, Y. Towards the contemporary conservation of cultural heritage: An overview of their conservation history. Heritage 2023, 7, 175–192. [Google Scholar] [CrossRef]
- Federal Highway Administration. Study of LTPP Distress Data Variability; FHWA-RD-99-074; U.S. Department of Transportation: Washington, DC, USA, 1999. [Google Scholar]
- Nyathi, M.A.; Bai, J.; Wilson, I.D. Deep learning for concrete crack detection and measurement. Metrology 2024, 4, 66–81. [Google Scholar] [CrossRef]
- Peta, K.; Stemp, W.J.; Stocking, T.; Chen, R.; Love, G.; Gleason, M.A.; Houk, B.A.; Brown, C.A. Multiscale geometric characterization and discrimination of dermatoglyphs (fingerprints) and hardened clay—A novel archaeological application of Gelsight Max. Materials 2025, 18, 2939. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Tan, J.; Liu, L.; Qiao, Q.; Wu, J.; Wang, Y.; Jie, L. Automatic crack inspection for concrete bridge bottom surfaces based on machine vision. In Proceedings of the Chinese Automation Congress Conference (CAC), Jinan, China, 20–22 October 2017. [Google Scholar]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Hatir, M.E.; Barstugan, M.; Ince, I. Deep learning-based weathering type recognition in historical stone monuments. J. Cult. Herit. 2020, 45, 193–203. [Google Scholar] [CrossRef]
- Luo, S.; Wang, H. Digital twin research on masonry-timber architectural heritage pathology cracks using 3D laser scanning and deep learning model. Buildings 2024, 14, 1129. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, H.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Proceedings of the Twenty-Sixth Annual Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–8 December 2012. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. arXiv 2014, arXiv:1409.4842v1. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. Adv. Neural Inf. Process. Syst. 2015, 1, 91–99. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar] [CrossRef]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single Shot MultiBox Detector. Comput. Vis. 2016, 9905, 21–37. [Google Scholar]
- Shelhamer, E.; Long, J.; Darrell, T. Fully convolutional networks for semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 640–651. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. Med. Image Comput. Comput. 2015, 9351, 234–241. [Google Scholar]
- Liu, W.C.; Huang, W.C. Evaluation of deep learning computer version for water level measurements in rivers. Helyion 2024, 10, e25989. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Gkioxari, G.; Dollar, P.; Girshick, R. Mask R-CNN. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Yang, G.; Feng, W.; Jin, J.; Lei, Q.; Li, X.; Gui, G.; Wang, W. Face mask recognition system with YOLOv5 based on image recognition. In Proceedings of the IEEE 6th International Conference on Computer and Communications, Chengdu, China, 11–14 December 2020; pp. 1398–1404. [Google Scholar]
- Bochkovskiy, A.; Wang, C.Y.; Liao, H.Y.M. YOLOv4: Optimal speed and accuracy of object detection. arXiv 2020, arXiv:2004.10934. [Google Scholar] [CrossRef]
- Mansuri, L.E.; Patel, D.A. Artificial intelligence-based automatic visual inspection system for built heritage. Smart Sustain. Built Environ. 2022, 11, 622–646. [Google Scholar] [CrossRef]
- Karimi, N.; Mishra, M.; Lourenco, P.B. Automated surface crack detection in historical constructions with various materials using deep learning-based YOLO network. Int. J. Archit. Herit. 2024, 19, 581–597. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, G.; Yang, P. CL-YOLOv8: Crack detection algorithm for fair-faced walls based on deep learning. Appl. Sci. 2024, 14, 9421. [Google Scholar] [CrossRef]
- Zhou, L.; Jia, H.; Jiang, S.; Xu, F.; Tang, H.; Xiang, C.; Wang, G.; Zheng, H.; Chen, L. Multi-Scale crack detection and quantification of concrete bridges based on aerial photography and improved object detection network. Buildings 2025, 15, 1117. [Google Scholar] [CrossRef]
- Zheng, X.; Zhang, S.; Li, X.; Li, G.; Li, X. Lightweight bridge crack detection method based on SegNet and bottleneck deep-separable convolution with residuals. IEEE Access 2021, 9, 161650–161668. [Google Scholar] [CrossRef]
- Yu, G.; Dong, J.; Wang, Y.; Zhou, X. RUC-Net: A residual-Unet-based convolutional neural network for pixel-level pavement crack segmentation. Sensor 2022, 23, 53. [Google Scholar] [CrossRef]
- Elhariri, E.; El-Bendary, N.; Taie, S.A. Automated pixel-level deep crack segmentation on historical surfaces using U-Net models. Algorithms 2022, 15, 281. [Google Scholar] [CrossRef]
- Tran, T.V.; Nguyen-Xuan, H.; Zhuang, X. Investigation of crack segmentation and fast evaluation of crack propagation, based on deep learning. Front. Struct. Civ. Eng. 2024, 18, 516–535. [Google Scholar] [CrossRef]
- Shi, X.; Song, W.; Sun, S. Multiscale feature fusion-based pavement crack detection using TransUNet. In Proceedings of the Third International Conference on Environmental Remote Sensing and Geographic Information Technology, Zhengzhou, China, 11–13 July 2025; Volume 13565. [Google Scholar]
- Attard, L.; Debono, C.J.; Valentino, G.; Castro, M.D.; Masi, A.; Scibile, L. Automatic crack detection using Mask R-CNN. In Proceedings of the 2019 11th International Symposium on Image and Signal Processing and Analysis, Dubrovnik, Croatia, 23–25 September 2019; pp. 152–157. [Google Scholar]
- Xu, X.; Zhao, M.; Shi, P.; Ren, R.; He, X.; Wei, X.; Yang, H. Crack detection and comparison study based on Faster R-CNN and Mask R-CNN. Sensors 2022, 22, 1215. [Google Scholar] [CrossRef]
- Choi, Y.; Bae, B.; Han, T.H.; Ahn, J. Application of Mask R-CNN and YOLOv8 algorithms for concrete crack detection. IEEE Access 2024, 12, 165314–165321. [Google Scholar] [CrossRef]
- Wu, L.; Lin, X.; Chen, Z.; Lin, P.; Cheng, S. Surface crack detection based on imagine stitching and transfer learning with pretrained convolution neural network. Struct. Control. Health Monit. 2021, 28, e2766. [Google Scholar] [CrossRef]
- Lin, H. GoogleNet transfer leaning with improved gorilla optimized kernel extreme learning machine for accurate detection of asphalt pavement cracks. Struct. Health Monit. 2024, 23, 2835–2868. [Google Scholar] [CrossRef]
- Loverdos, D.; Sarhosis, V. Automatic image-based brick segmentation and crack detection of masonry walls using machine learning. Autom. Constr. 2022, 140, 104389. [Google Scholar] [CrossRef]
- Golding, V.P.; Gharineiat, Z.; Munawar, H.S.; Ullah, F. Crack detection in concrete structures using deep learning. Sustainability 2022, 14, 8117. [Google Scholar] [CrossRef]
- Li, Y.; Shu, B.; Wu, C.; Liu, Z.; Deng, J.; Zeng, Z.; Jin, X.; Huang, Z. Deep learning-based multi-scale crack image segmentation and improved skeletonization measurement method. Mater. Today Commun. 2025, 46, 112727. [Google Scholar] [CrossRef]
- Kompanets, A.; Pai, G.; Duits, R.; Leonetti, D.; Snijder, B. Deep learning for segmentation of cracks in high-resolution images of steel bridges. Computer Vision and Pattern Recognition. arXiv 2024, arXiv:2403.17725. [Google Scholar]
- Li, Y.; Ma, R.; Liu, H.; Cheng, G. Real-time high-resolution neural network with semantic guidance for crack segmentation. Autom. Constr. 2023, 156, 105112. [Google Scholar] [CrossRef]
- Qiu, Q.; Lau, D. Real-time detection of cracks in tiled sidewalks using a YOLO-based method applied to unmanned aerial vehicle (UAV) images. Autom. Constr. 2023, 147, 104745. [Google Scholar] [CrossRef]
- Lin, M.; Chen, Q.; Yan, S. Network in network. In Proceedings of the International Conference on Learning Representations Conference (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the International Conference on Learning Representations Conference (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. arXiv 2013, arXiv:1311.2901. [Google Scholar] [CrossRef]
- Chen, K.; Reichard, G.; Xu, X.; Akanmu, A. Automated crack segmentation in close-range building façade inspection images using deep learning techniques. J. Build. Eng. 2021, 43, 102913. [Google Scholar] [CrossRef]
- Chen, D.; Yuqi, L.; Hsu, C.Y. Measurement invariance investigation for performance of deep learning architectures. IEEE Access 2022, 10, 78070–78087. [Google Scholar] [CrossRef]
- Nurfarahin, A.A.S.; Dziyauddin, R.A.; Norliza, M.N. Transfer learning with pre-trained CNNs for MRI brain tumor multi-classification: A comparative study of VGG, VGG19, and inception models. In Proceedings of the 2023 IEEE 2nd National Biomedical Engineering Conference (NBEC), Melaka, Malaysia, 5–7 September 2023. [Google Scholar]
- Gao, Q.; Zhao, Y.; Tong, T. Image super-Resolution using knowledge distillation. In Proceedings of the Asian Conference on Computer Vision, Perth, Australia, 2–6 December 2018. [Google Scholar]
- Yang, J.; Li, H.; Zou, J.; Jiang, S.; Li, R.; Liu, X. Concrete crack segmentation based on UAV-enabled edge computing. Neurocomputing 2022, 485, 233–241. [Google Scholar] [CrossRef]
- Wang, K.; Zhuang, J.; Li, G.; Fang, C.; Cheng, L.; Lin, L.; Zhou, F. De-biased teacher: Rethinking IoU matching for semi-supervised object detection. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 2573–2580. [Google Scholar]
- Özgenel, Ç.F.; Gönenç Sorguç, A. Performance comparison of pretrained convolutional neural networks on crack detection in buildings. In Proceedings of the ISARC 2018, Berlin, Germany, 20–25 July 2018. [Google Scholar]
- Liu, Y.; Yao, J.; Lu, X.; Xie, R.; Li, L. DeepCrack: A deep hierarchical feature learning architecture for crack segmentation. Neurocomputing 2019, 338, 139–153. [Google Scholar] [CrossRef]
- Parab, M.A.; Mehendale, N. Red blood cell classification using image processing and CNN. SN Comput. Sci. 2021, 2, 70. [Google Scholar] [CrossRef]
- Shon, I.H.; Reece, C.; Hennessy, T.; Horsfield, M.; McBride, B. Influence of X ray computed tomography (CT) exposure and reconstruction parameters on positron emission tomography (PET) quantitation. EJNMMI Phys. 2020, 7, 62. [Google Scholar] [CrossRef]
- Luca, A.R.; Ursuleanu, T.F.; Gheorghe, L.; Grigorovici, R.; Iancu, S.; Hlusneac, M.; Grigorovici, A. Impact of quality, type and volume of data used by deep learning models in the analysis of medical images. Inform. Med. Unlocked 2022, 29, 100911. [Google Scholar] [CrossRef]
- Zhang, J.; Cai, Y.-Y.; Tang, D.; Yuan, Y.; He, W.-Y.; Wang, Y.-J. MobileNetV3-BLS: A broad learning approach for automatic concrete surface crack detection. Constr. Build. Mater. 2023, 392, 131941. [Google Scholar] [CrossRef]
- Tanveer, M.; Kim, B.; Hong, J.; Sim, S.-H.; Cho, S. Comparative study of lightweight deep semantic segmentation models for concrete damage detection. Appl. Sci. 2022, 12, 12786. [Google Scholar] [CrossRef]
- Shojaei, D.; Jafary, P.; Zhang, Z. Mixed reality-based concrete crack detection and skeleton extraction using deep learning and image processing. Electronics 2024, 13, 4426. [Google Scholar] [CrossRef]
- Ashraf, A.; Sophian, A.; Shafie, A.A.; Gunawan, T.S.; Ismail, N.N.; Bawono, A.A. Efficient pavement crack detection and classification using custom YOLOv7 model. Indones. J. Electr. Eng. Inform. 2023, 11, 119–132. [Google Scholar] [CrossRef]
- Bai, Y.; Sezen, H.; Yilmaz, A. Detecting cracks and spalling automatically in extreme events by end-to-end deep learning frameworks. Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, 2, 161–168. [Google Scholar] [CrossRef]
- Chen, L.-C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. Comput. Vis. 2018, 2018, 833–851. [Google Scholar]
- Cha, Y.; Choi, W.; Büyüköztürk, O. Deep learning-based crack damage detection using convolutional neural networks. Comput. Aided Civ. Infrastruct. Eng. 2017, 32, 361–378. [Google Scholar] [CrossRef]
- Li, G.; Liu, Q.; Ren, W.; Qiao, W.; Ma, B.; Wan, J. Automatic recognition and analysis system of asphalt pavement cracks using interleaved low-rank group convolution hybrid deep network and SegNet fusing dense condition random field. Measurement 2021, 170, 108693. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, Y.; Yue, Q.; Liu, X. A deep learning framework for real-time multi-task recognition and measurement of concrete cracks. Adv. Eng. Inform. 2025, 65 Pt A, 103127. [Google Scholar] [CrossRef]
- Chen, T.; Cai, Z.; Zhao, X.; Chen, C.; Liang, X.; Zou, T.; Wang, P. Pavement crack detection and recognition using the architecture of segNet. J. Ind. Inf. Integr. 2020, 18, 100144. [Google Scholar] [CrossRef]













| K-Fold | Accuracy (%) | Precision (%) | Recall (%) | F1-Score |
|---|---|---|---|---|
| 1 | 95 | 91 | 100 | 95 |
| 2 | 100 | 100 | 100 | 100 |
| 3 | 95 | 100 | 90 | 95 |
| 4 | 100 | 100 | 100 | 100 |
| 5 | 100 | 100 | 100 | 100 |
| Average | 98 | 98 | 98 | 98 |
| Data Set | Number of Images | Accuracy (%) | Precision (%) | Recall (%) | F1-Score |
|---|---|---|---|---|---|
| 66 | 34 | 100 | 100 | 100 | 1.0 |
| 66 | 20,000 | 72 | 65 | 100 | 0.79 |
| 76 | 20,000 | 97 | 95 | 98 | 0.97 |
| Number of Images for Training and Validation | Images of Plain Wall Crack | Images of Mottled Wall Crack | Images of Brick Wall Crack | Images with Crack |
|---|---|---|---|---|
| 34 | 6 | 6 | 5 | 17 |
| 50 | 9 | 8 | 8 | 25 |
| 66 | 11 | 11 | 11 | 33 |
| 100 | 17 | 17 | 16 | 50 |
| 130 | 22 | 22 | 21 | 65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.-C.; Luo, Y.-S.; Liu, W.-C.; Liu, H.-M. Deep Learning-Based Crack Detection on Cultural Heritage Surfaces. Appl. Sci. 2025, 15, 7898. https://doi.org/10.3390/app15147898
Huang W-C, Luo Y-S, Liu W-C, Liu H-M. Deep Learning-Based Crack Detection on Cultural Heritage Surfaces. Applied Sciences. 2025; 15(14):7898. https://doi.org/10.3390/app15147898
Chicago/Turabian StyleHuang, Wei-Che, Yi-Shan Luo, Wen-Cheng Liu, and Hong-Ming Liu. 2025. "Deep Learning-Based Crack Detection on Cultural Heritage Surfaces" Applied Sciences 15, no. 14: 7898. https://doi.org/10.3390/app15147898
APA StyleHuang, W.-C., Luo, Y.-S., Liu, W.-C., & Liu, H.-M. (2025). Deep Learning-Based Crack Detection on Cultural Heritage Surfaces. Applied Sciences, 15(14), 7898. https://doi.org/10.3390/app15147898








