Ratcheting of Steel Samples Undergoing Asymmetric Loading Cycles at Elevated Operating Temperatures: Analytical and Numerical Assessments
Abstract
1. Introduction
2. Mathematical Formulation
2.1. Elements of Elasticity, Plasticity, and Visco-Plasticity
2.2. Hardening Framework
2.2.1. Isotropic Hardening Description
2.2.2. Ahmadzadeh–Varvani (A-V) Kinematic Hardening Rule
2.2.3. The Chaboche Kinematic Hardening Rule
3. Results and Discussion
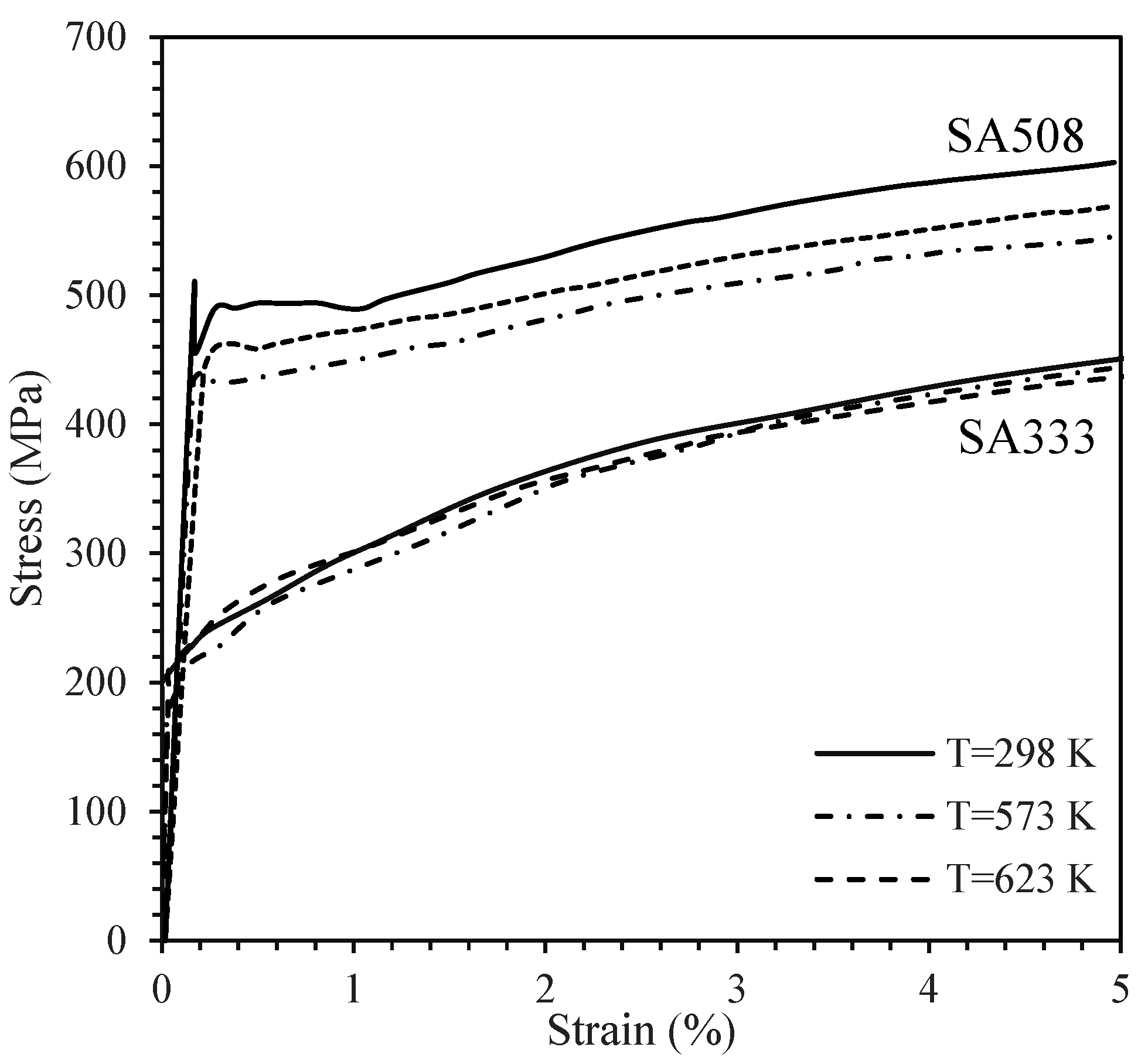
3.1. Tensile and Cyclic Test Data
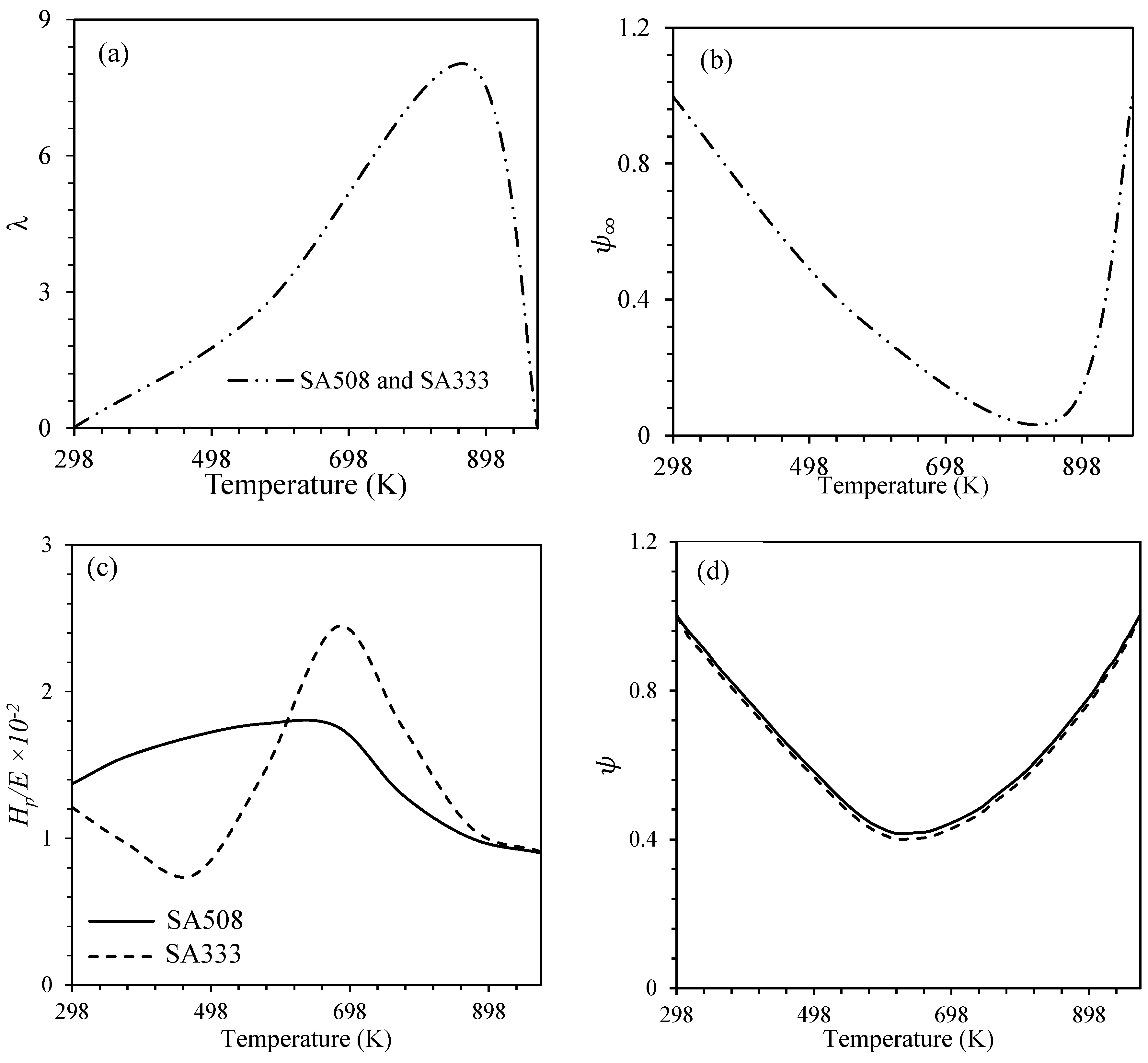
3.2. Dynamic Strain Aging (DSA) and Temperature Domain
3.3. A-V Kinematic Hardening Rule Coefficients
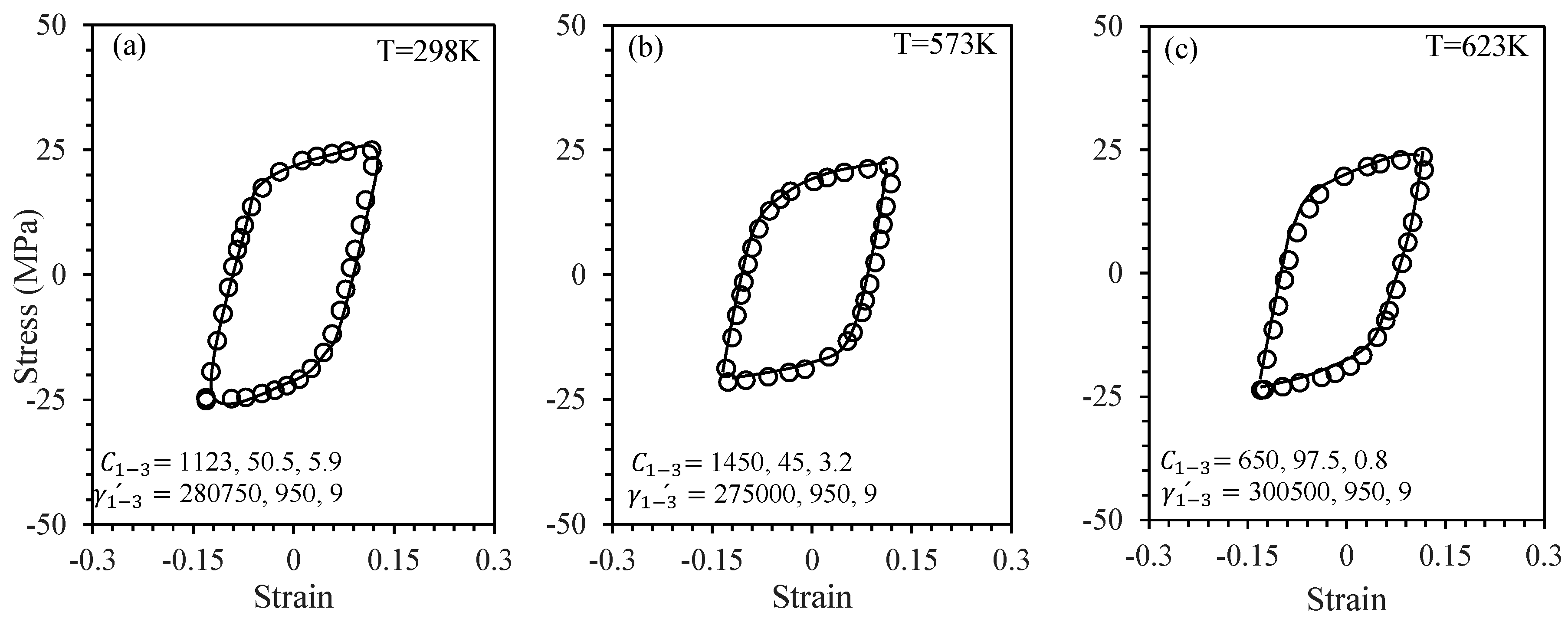
3.4. Chaboche’s Coefficients
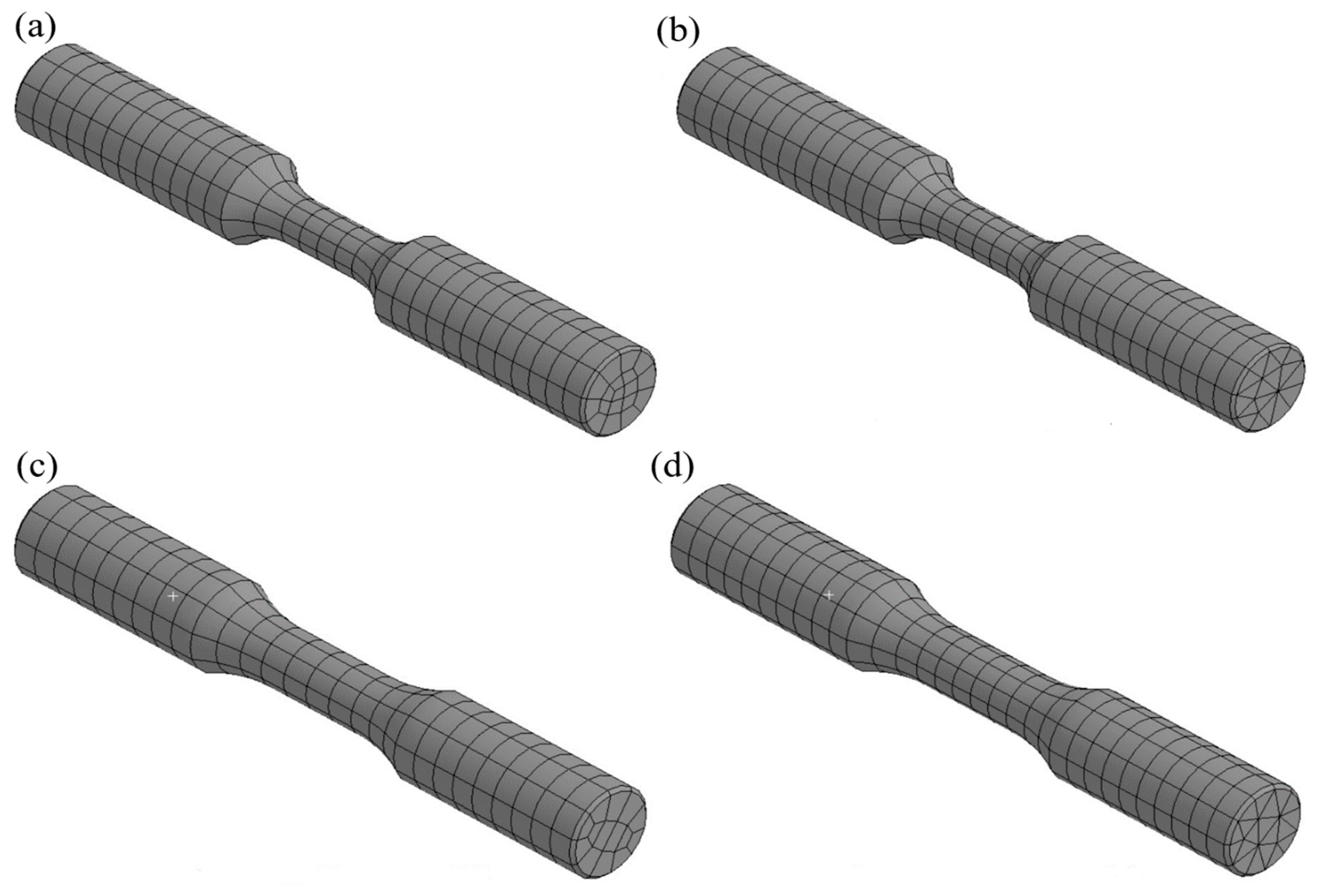
3.5. Finite Element Method
3.6. Backstress Increments
3.7. Ratcheting Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Varvani-Farahani, A.; Nayebi, A. Ratcheting in pressurized pipes and equipment: A review on affecting parameters, modelling, safety codes, and challenges. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 503–538. [Google Scholar] [CrossRef]
- Kaya, Ö.; Cavusoglu, O.; Güral, A. Investigation of mechanical property alterations in DP600 steel under cyclic static strain aging. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2025, 14644207241310410. [Google Scholar] [CrossRef]
- Rodriguez, P. Serrated plastic flow. Bull. Mater. Sci. 1984, 6, 653–663. [Google Scholar] [CrossRef]
- Hong, S.G.; Lee, S.B. The tensile and low-cycle fatigue behavior of cold worked 316L stainless steel: Influence of dynamic strain aging. Int. J. Fatigue 2004, 26, 899–910. [Google Scholar] [CrossRef]
- Huang, Z.Y.; Chaboche, J.L.; Wang, Q.Y.; Wagner, D.; Bathias, C. Effect of dynamic strain aging on isotropic hardening in low cycle fatigue for carbon manganese steel. Mater. Sci. Eng. A 2014, 589, 34–40. [Google Scholar] [CrossRef]
- Huang, Z.; Wagner, D.; Bathias, C. Some metallurgical aspects of Dynamic Strain Aging effect on the Low Cycle Fatigue behavior of C–Mn steels. Int. J. Fatigue 2015, 80, 113–120. [Google Scholar] [CrossRef]
- Avalos, M.; Alvarez-Armas, I.; Armas, A.F. Dynamic strain aging effects on low-cycle fatigue of AISI 430F. Mater. Sci. Eng. A 2009, 513, 1–7. [Google Scholar] [CrossRef]
- Caillard, D. Dynamic strain ageing in iron alloys: The shielding effect of carbon. Acta Mater. 2016, 112, 273–284. [Google Scholar] [CrossRef]
- Karimi, M.; Varvani-Farahani, A. Ratcheting prediction of stainless steel 304 and 316L samples undergoing asymmetric loading cycles at elevated temperatures incorporating dynamic strain aging phenomenon. Mater. Today Commun. 2024, 38, 107805. [Google Scholar] [CrossRef]
- Karimi, M.; Varvani-Farahani, A. Ratcheting Assessment of Rail Steel at Elevated Temperatures in the Presence of Dynamic Strain Aging. J. Mater. Eng. Perform. 2024, 34, 6817–6827. [Google Scholar] [CrossRef]
- Sun, X.; Xing, R.; Yu, W.; Chen, X. Uniaxial ratcheting deformation of 316LN stainless steel with dynamic strain aging: Experiments and simulation. Int. J. Solids Struct. 2020, 207, 196–205. [Google Scholar] [CrossRef]
- Ohno, N.; Wang, J.D. Kinematic hardening rules with critical state of dynamic recovery, part I: Formulation and basic features for ratchetting behavior. Int. J. Plast. 1993, 9, 375–390. [Google Scholar] [CrossRef]
- Nakkalil, R.; Hornaday, J.R., Jr.; Bassim, M.N. Characterization of the compression properties of rail steels at high temperatures and strain rates. Mater. Sci. Eng. A 1991, 141, 247–260. [Google Scholar] [CrossRef]
- Kumar, G.; Kumar, A.; Bar, H.N. Low Cycle Fatigue and Ratcheting Behavior of SA333 Gr-6 Steel at 300° C Temperature. SAE Int. J. Mater. Manuf. 2019, 12, 73–82. [Google Scholar] [CrossRef]
- Li, C.C.; Leslie, W.C. Effects of dynamic strain aging on the subsequent mechanical properties of carbon steels. Metall. Trans. A 1978, 9, 1765–1775. [Google Scholar] [CrossRef]
- Kumar, G.; Bar, H.N.; Kumar, A. Effect of dynamic strain aging on cyclic deformation in piping material SA333 Gr-6 steel. Int. J. Press. Vessels Pip. 2021, 194, 104529. [Google Scholar] [CrossRef]
- Kumar, G.; Bar, H.N.; Kumar, A. Influence of dynamic strain aging on ratcheting deformation behavior of SA333 Gr-6 steel. J. Mater. Eng. Perform. 2022, 31, 10332–10342. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Song, Y.; Rusinek, A. Constitutive model for metals with dynamic strain aging. Mech. Mater. 2019, 129, 352–360. [Google Scholar] [CrossRef]
- Servatan, M.; Hashemi, S.M.; Varvani-Farahani, A. Ratcheting Simulation of Additively Manufactured Aluminum 4043 Samples through Finite Element Analysis. Appl. Sci. 2023, 13, 11553. [Google Scholar] [CrossRef]
- Zhang, J.; Gu, Z.; Cao, G.; Jin, Y.; Liu, J. A modified continuum damage model considering cryogenic temperatures and its application in corrugated plates of the LNG membrane storage tank. Int. J. Press. Vessel. Pip. 2025, 214, 105412. [Google Scholar] [CrossRef]
- Shit, J.; Dhar, S.; Acharyya, S. Modeling and finite element simulation of low cycle fatigue behaviour of 316 SS. Procedia Eng. 2013, 55, 774–779. [Google Scholar] [CrossRef]
- Bosso, N.; Cantone, L.; Falcitelli, G.; Gjini, R.; Magelli, M.; Nigro, F.M.; Ossola, E.; Zampieri, N. Simulation of the thermo-mechanical behaviour of tread braked railway wheels by means of a 2D finite element model. Tribol. Int. 2022, 178, 108074. [Google Scholar] [CrossRef]
- Walia, M.S.; Esmaeili, A.; Vernersson, T.; Lundén, R. Thermomechanical capacity of wheel treads at stop braking: A parametric study. Int. J. Fatigue 2018, 113, 407–415. [Google Scholar] [CrossRef]
- Dong, Y.G.; Yi, S.; Huang, X.L.; Zheng, J.; Du, X.; Li, S. Prediction of fatigue crack initiation life of wheel tread during emergency braking of heavy haul train. China Railw. Sci. 2021, 42, 123–131. [Google Scholar]
- Li, L.; Chang, C. Thermal load analysis of wheel tread for heavy axle load freight car under braking conditions on the basis of thermal-mechanical coupling model. Railw. Locomot. Car 2014, 34, 25–30. [Google Scholar]
- Suresh Babu, A.; Siva Prasad, N. Coupled field finite element analysis of railway block brakes. Proc. Inst. Mech. Eng. Part F J. Rail. Rapid Transit. 2009, 223, 345–352. [Google Scholar] [CrossRef]
- Vernersson, T.; Lundén, R. Wear of brake blocks for in-service conditions—Influence of the level of modelling. Wear 2014, 314, 125–131. [Google Scholar] [CrossRef]
- Bari, S.; Hassan, T. An advancement in cyclic plasticity modeling for multiaxial ratcheting simulation. Int. J. Plast. 2002, 18, 873–894. [Google Scholar] [CrossRef]
- Ohno, N.; Wang, J.D. Kinematic hardening rules with critical state of dynamic recovery, part II: Application to experiments of ratchetting behavior. Int. J. Plast. 1993, 9, 391–403. [Google Scholar] [CrossRef]
- Abdel-Karim, M.; Ohno, N. Kinematic hardening model suitable for ratchetting with steady-state. Int. J. Plast. 2000, 16, 225–240. [Google Scholar] [CrossRef]
- Chen, X.; Jiao, R.; Kim, K.S. On the Ohno–Wang kinematic hardening rules for multiaxial ratcheting modeling of medium carbon steel. Int. J. Plast. 2005, 21, 161–184. [Google Scholar] [CrossRef]
- Chen, X.; Chen, X.; Yu, D.; Gao, B. Recent progresses in experimental investigation and finite element analysis of ratcheting in pressurized piping. Int. J. Press. Vessels Pip. 2013, 101, 113–142. [Google Scholar] [CrossRef]
- Halama, R.; Markopoulos, A.; Jančo, R.; Bartecký, M. Implementation of MAKOC cyclic plasticity model with memory. Adv. Eng. Softw. 2017, 113, 34–46. [Google Scholar] [CrossRef]
- Bonora, N.; Majzoobi, G.H.; Khademi, E. Numerical implementation of a new coupled cyclic plasticity and continuum damage model. Comput. Mater. Sci. 2014, 81, 538–547. [Google Scholar] [CrossRef]
- Koo, G.H.; Lee, J.H. Investigation of ratcheting characteristics of modified 9Cr–1Mo steel by using the Chaboche constitutive model. Int. J. Press. Vessels Pip. 2007, 84, 284–292. [Google Scholar] [CrossRef]
- Dalla Palma, M. Modelling of cyclic plasticity for austenitic stainless steels 304L, 316L, 316L (N)-IG. Fusion Eng. Des. 2016, 109, 20–25. [Google Scholar] [CrossRef]
- Agius, D.; Kajtaz, M.; Kourousis, I.; Wallbrink, C.; Wang, H.; Hu, W.; Silva, J. Sensitivity and optimisation of the Chaboche plasticity model parameters in strain-life fatigue predictions. Mater. Des. 2017, 118, 107–121. [Google Scholar] [CrossRef]
- Pate, S.B.; Dundulis, G.; Griskevicius, P. Modeling of LCF Behaviour on AISI316L Steel Applying the Armstrong–Frederick Kinematic Hardening Model. Materials 2024, 17, 3395. [Google Scholar] [CrossRef]
- Wu, L.; Wen, Z.; Li, W.; Jin, X. Thermo-elastic–plastic finite element analysis of wheel/rail sliding contact. Wear 2011, 271, 437–443. [Google Scholar] [CrossRef]
- Vo, K.D.; Tieu, A.K.; Zhu, H.T.; Kosasih, P.B. The influence of high temperature due to high adhesion condition on rail damage. Wear 2015, 330, 571–580. [Google Scholar] [CrossRef]
- Perzyna, P. The Constitutive Equation for Work-Hardening and Rate Sensitive Plastic Materials. Appl. Math. 1963, 20, 321–324. [Google Scholar]
- Lee, D.; Zavrel, F., Jr. A generalized strain rate dependent constitutive equation for anisotropic metals. Acta Metall. 1978, 26, 1771–1780. [Google Scholar] [CrossRef]
- Abed, F.H.; Voyiadjis, G.Z. Plastic deformation modeling of AL-6XN stainless steel at low and high strain rates and temperatures using a combination of bcc and fcc mechanisms of metals. Int. J. Plast. 2005, 21, 1618–1639. [Google Scholar] [CrossRef]
- Calhoun, R.B.; Dunand, D.C. Dislocations in metal matrix composites. In Comprehensive Composite Materials: Metal Matrix Composites; Kelly, A., Zweben, C., Eds.; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Ahmadzadeh, G.R.; Varvani-Farahani, A. Ratcheting assessment of materials based on the modified A–F hardening rule at various uniaxial stress levels. Fatigue Fract. Eng. Mater. Struct. 2013, 36, 1232–1245. [Google Scholar] [CrossRef]
- Karimi, M.; Varvani-Farahani, A. The concurrent ratcheting and stiffness degradation-based damage variable in SA508 steel samples undergoing stress cycles at room and elevated temperatures. J Mater. Res. Express, 2025; under reviewed. [Google Scholar]
- Karimi, M.; Varvani-Farahani, A. Ratcheting-fatigue interaction in SA508 and SA333 steels subjected to uniaxial asymmetric stress cycles at room and elevated temperatures. J. Fail. Anal. Prev. 2025, 1–17. [Google Scholar] [CrossRef]
- Gao, Q.; Kang, G.Z.; Yang, X.J. Uniaxial ratcheting of SS304 stainless steel at high temperatures: Visco-plastic constitutive model. Theor. Appl. Fract. Mech. 2003, 40, 105–111. [Google Scholar] [CrossRef]
- Chaboche, J.L. Constitutive equations for cyclic plasticity and cyclic viscoplasticity. Int. J. Plast. 1989, 5, 247–302. [Google Scholar] [CrossRef]
- Chaboche, J.L. On some modifications of kinematic hardening to improve the description of ratchetting effects. Int. J. Plast. 1991, 7, 661–678. [Google Scholar] [CrossRef]
- Tian, J.; Zhang, P.; Shao, J.; Du, J.; Kan, H. Ratcheting behavior of SA508-3 steel at elevated temperature: Experimental observation and simulation. Acta Metall. Sin. (Engl. Lett.) 2017, 30, 822–828. [Google Scholar] [CrossRef]
- Kumar, G.; Kumar, A.; Bar, H.N. Asymmetric cyclic deformation behavior of SA 333 steel at elevated temperatures. World J. Eng. 2020, 16, 78–86. [Google Scholar] [CrossRef]
- Dai, R.J.; Deng, K.K.; Wang, C.J.; Nie, K.B.; Zhang, G.W.; Liang, W. Effects of precipitates and solute atoms on the work hardening and softening behavior of Zn-rich aluminum alloy. Mater. Sci. Eng. A 2022, 848, 143388. [Google Scholar] [CrossRef]
- Samuel, K.G.; Ganesan, V.; Rao, K.B.S.; Mannan, S.L.; Kushwaha, H.S. Strain controlled LCF behaviour of SA-333 Gr 6 piping material in the range 298–673 K. Int. J. Press. Vessel. Pip. 2004, 81, 973–981. [Google Scholar] [CrossRef]
- Static Structural Analysis Guide, ANSYS® Workbench Release 22.1, Help System; ANSYS, Inc.: Canonsburg, PA, USA, 2022.



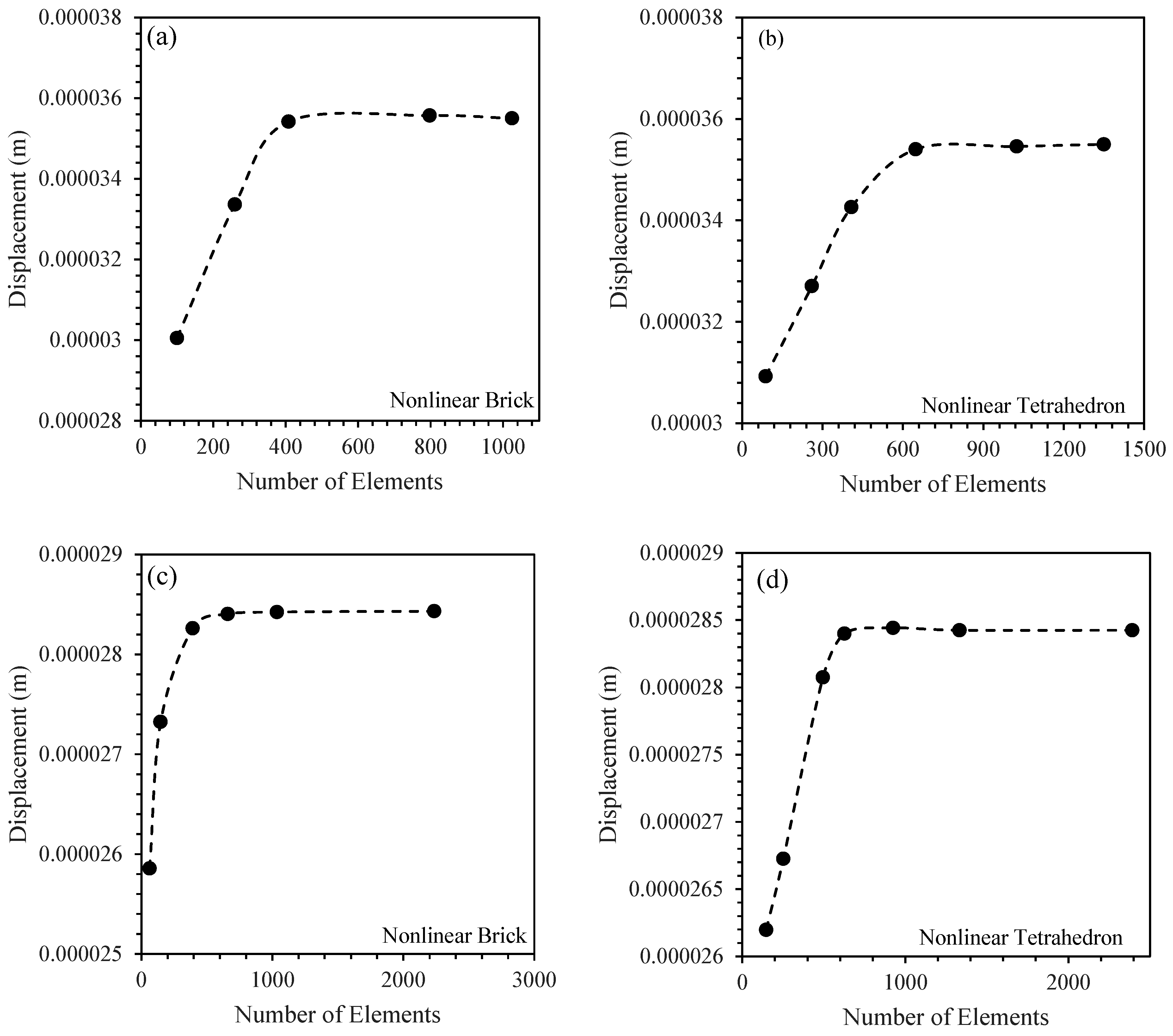

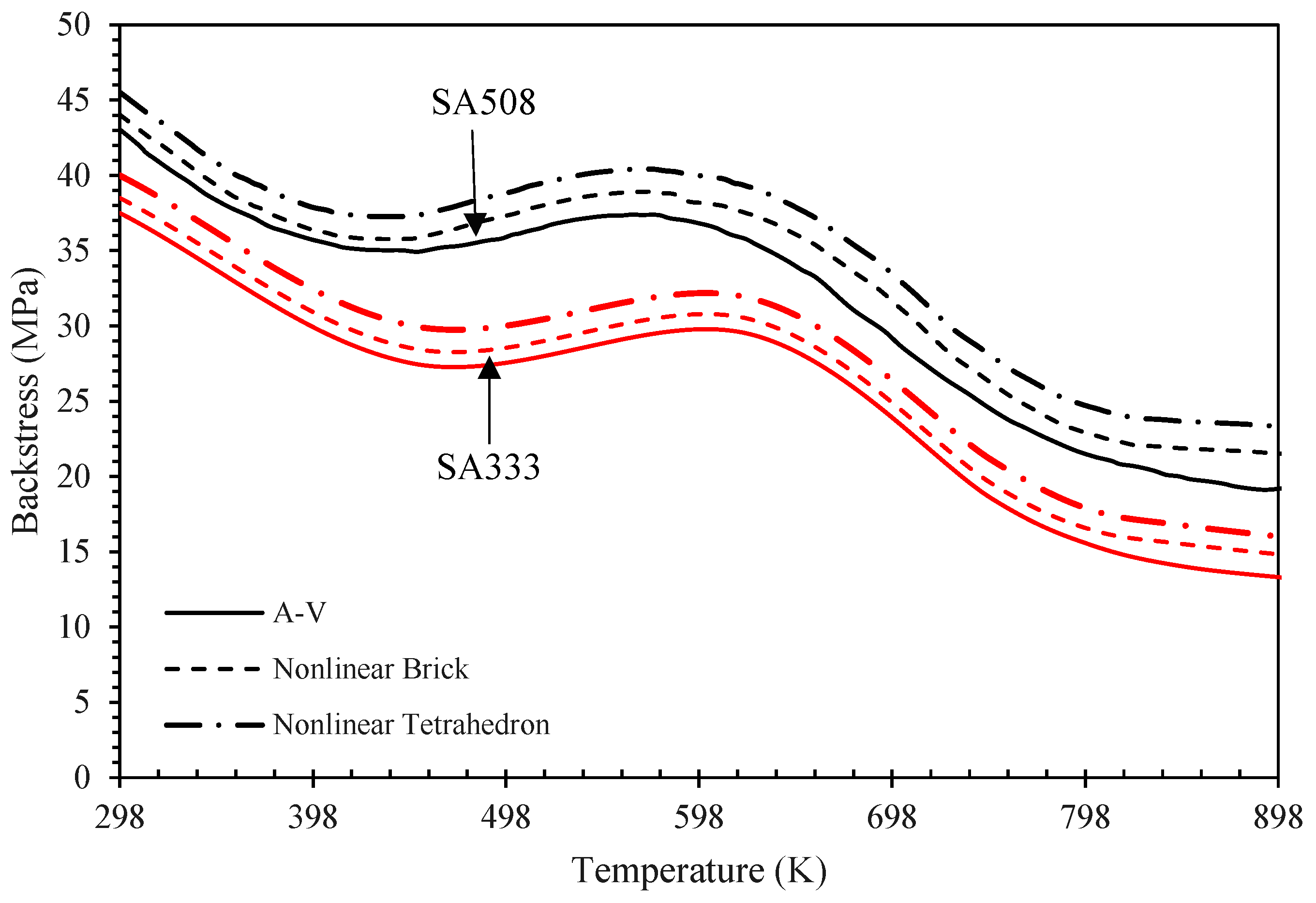
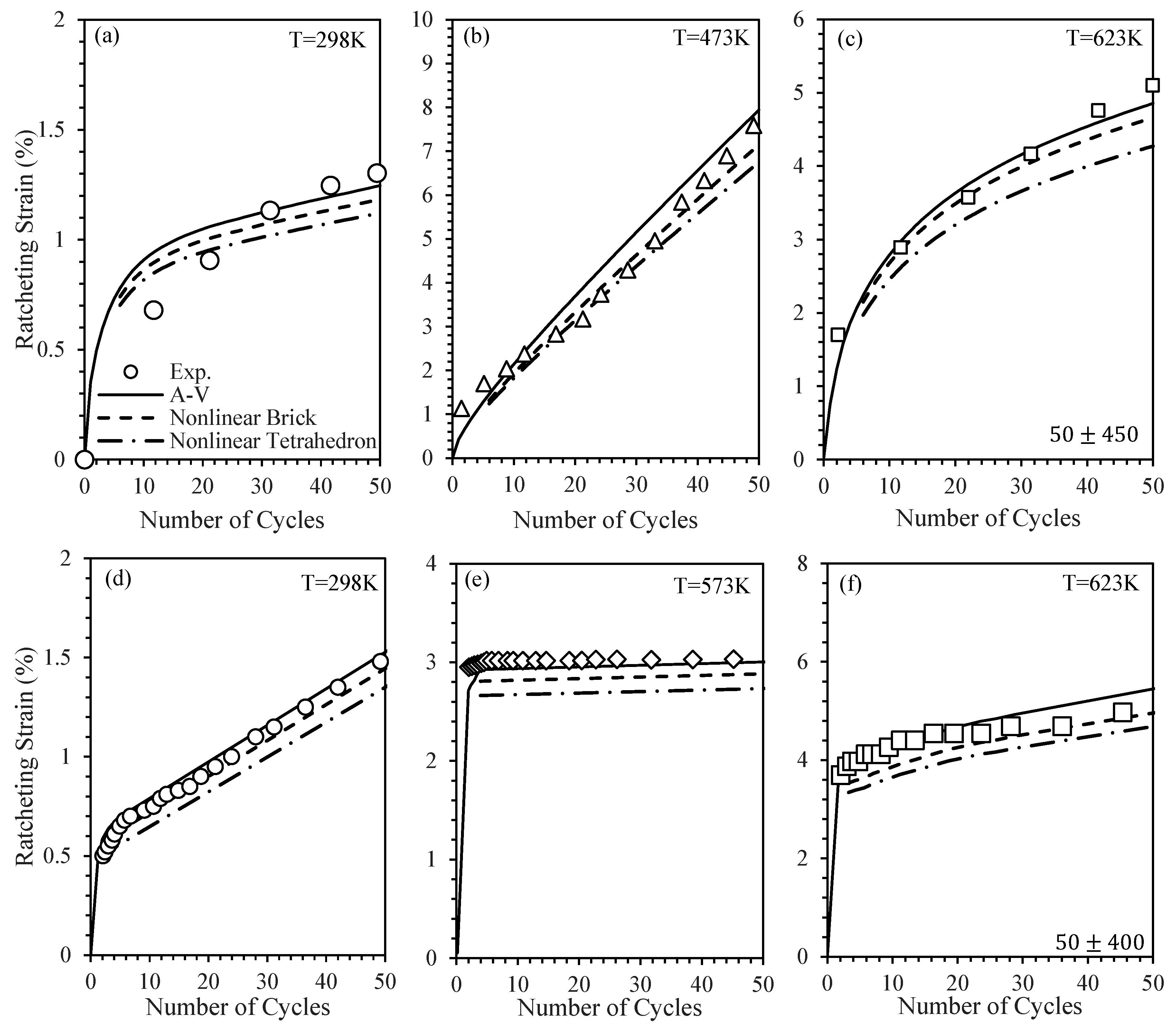
| Material | Temperature | Models | Parameters and Coefficients |
|---|---|---|---|
| SA508 | 298 K | Isotropic | |
| A-V | |||
| Chaboche | |||
| 473 K | Isotropic | ||
| A-V | |||
| Chaboche | |||
| 623 K | Isotropic | ||
| A-V | |||
| Chaboche | |||
| SA333 | 298 K | Isotropic | |
| A-V | |||
| Chaboche | |||
| 573 K | Isotropic | ||
| A-V | |||
| Chaboche | |||
| 623 K | Isotropic | ||
| A-V | |||
| Chaboche |
| Element Type | Pictorial | ANSYS Software Code | Integration Points |
|---|---|---|---|
| 20-Node Brick |  | SOLD186 | |
| 10-Node Tetrahedron |  | SOLID187 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karimi, M.; Varvani-Farahani, A. Ratcheting of Steel Samples Undergoing Asymmetric Loading Cycles at Elevated Operating Temperatures: Analytical and Numerical Assessments. Appl. Sci. 2025, 15, 7864. https://doi.org/10.3390/app15147864
Karimi M, Varvani-Farahani A. Ratcheting of Steel Samples Undergoing Asymmetric Loading Cycles at Elevated Operating Temperatures: Analytical and Numerical Assessments. Applied Sciences. 2025; 15(14):7864. https://doi.org/10.3390/app15147864
Chicago/Turabian StyleKarimi, M., and A. Varvani-Farahani. 2025. "Ratcheting of Steel Samples Undergoing Asymmetric Loading Cycles at Elevated Operating Temperatures: Analytical and Numerical Assessments" Applied Sciences 15, no. 14: 7864. https://doi.org/10.3390/app15147864
APA StyleKarimi, M., & Varvani-Farahani, A. (2025). Ratcheting of Steel Samples Undergoing Asymmetric Loading Cycles at Elevated Operating Temperatures: Analytical and Numerical Assessments. Applied Sciences, 15(14), 7864. https://doi.org/10.3390/app15147864







