Analysis and Application of Dual-Control Single-Exponential Water Inrush Prediction Mechanism for Excavation Roadways Based on Peridynamics
Abstract
Featured Application
Abstract
1. Introduction
2. Methodology
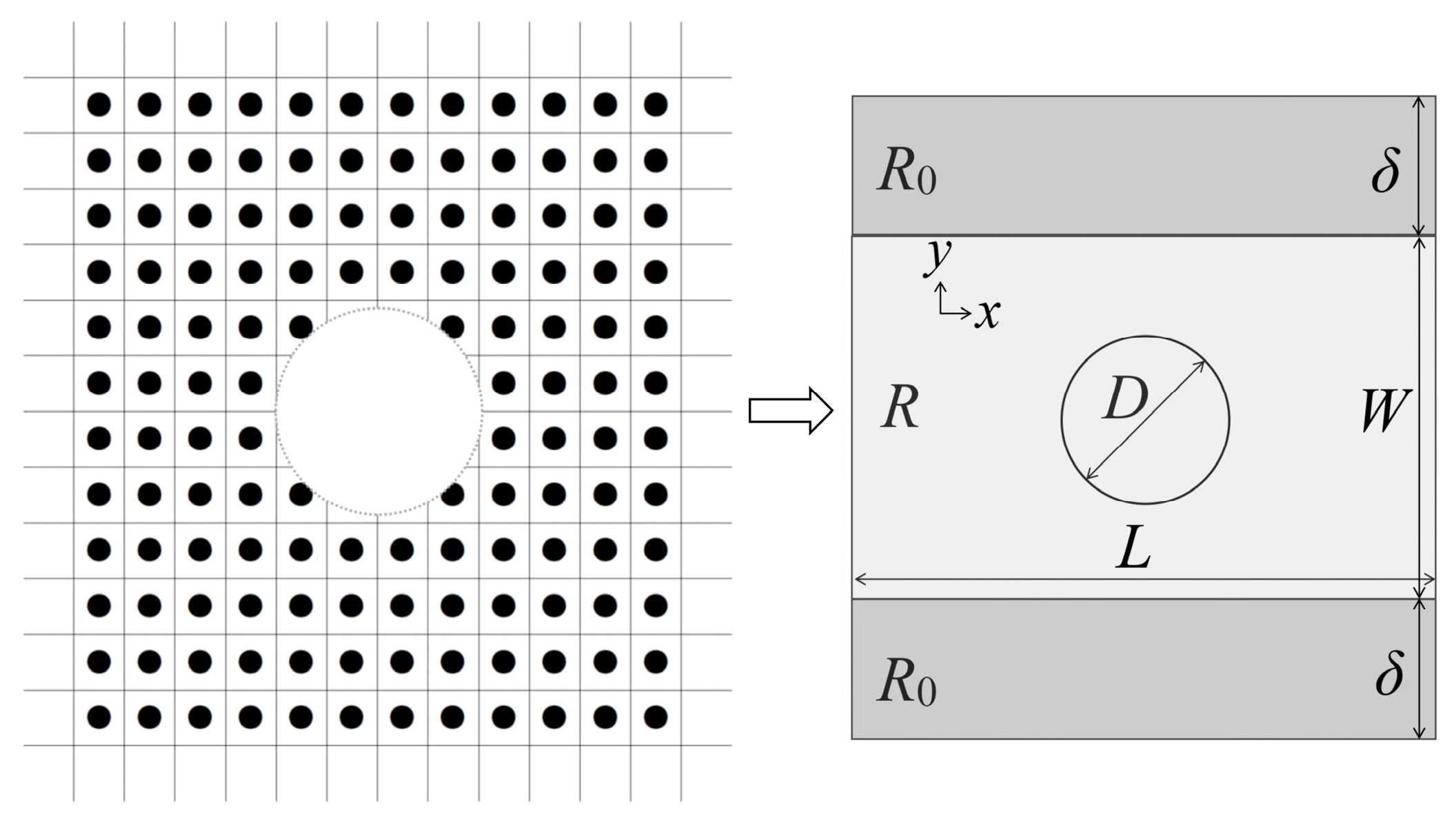
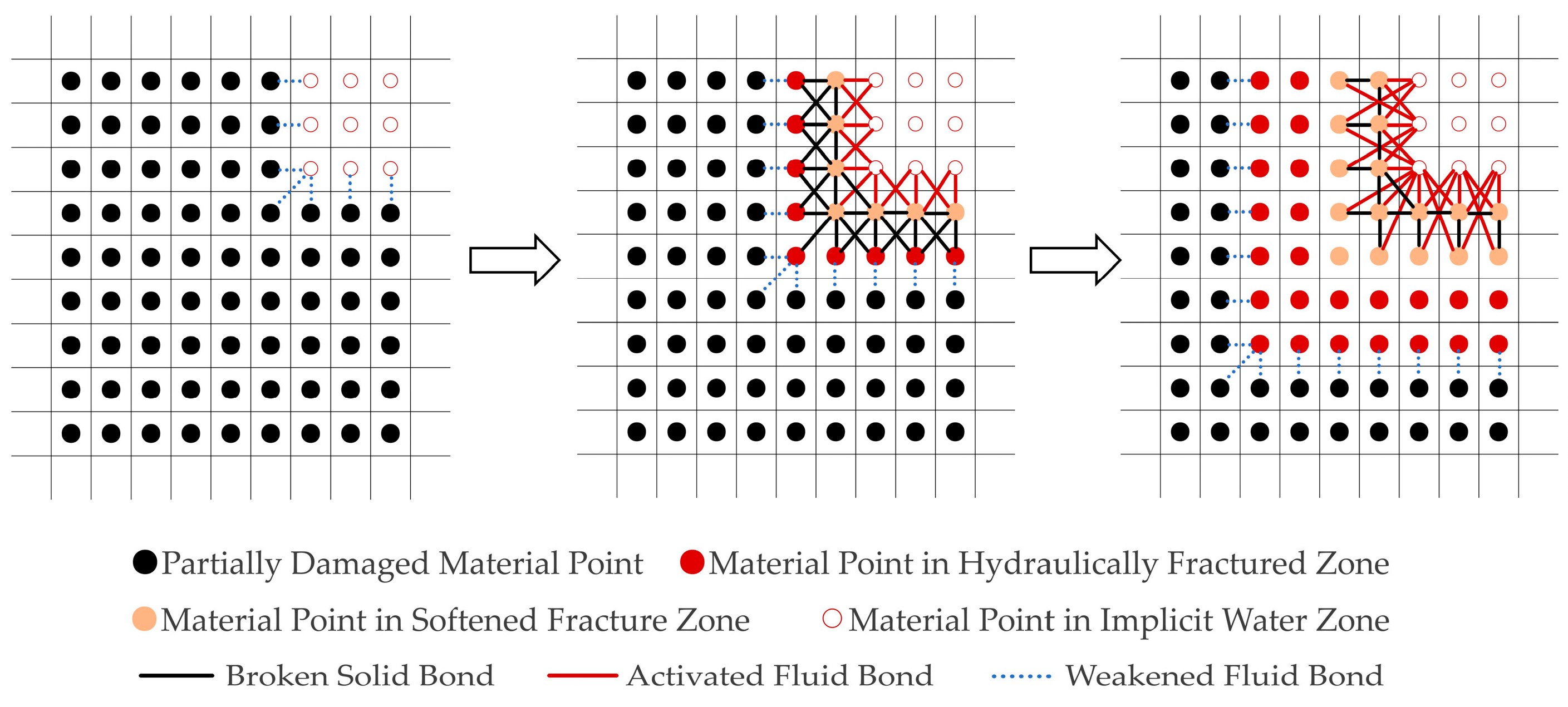
2.1. Peridynamics Damage Criterion of Coal–Rock Mass
2.2. Equivalent Continuous Porous Medium Model
- (1)
- Uniform type (ω = 1)
- (2)
- Linear model (ω = 1 − /δ)
- (3)
- Countdown type (ω = 1/)
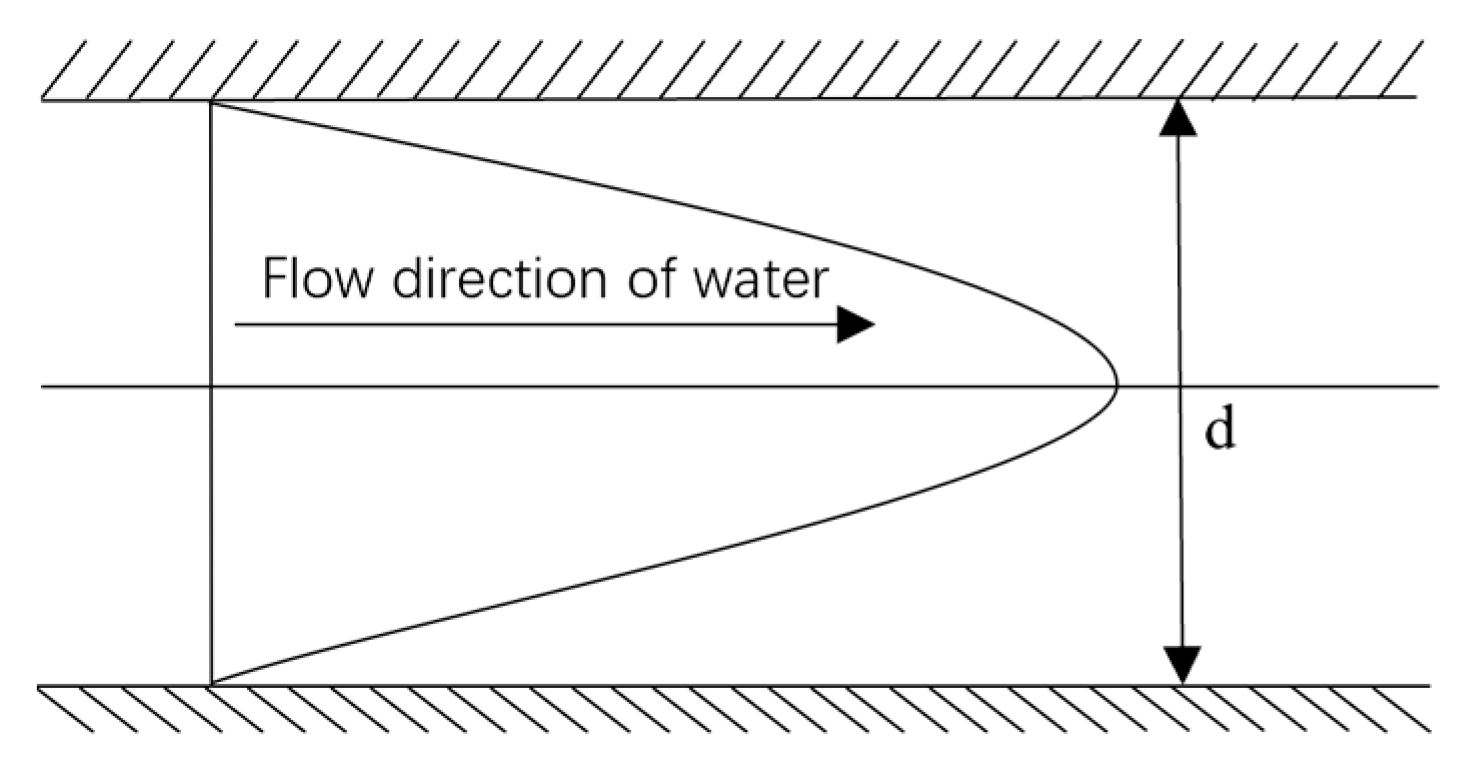
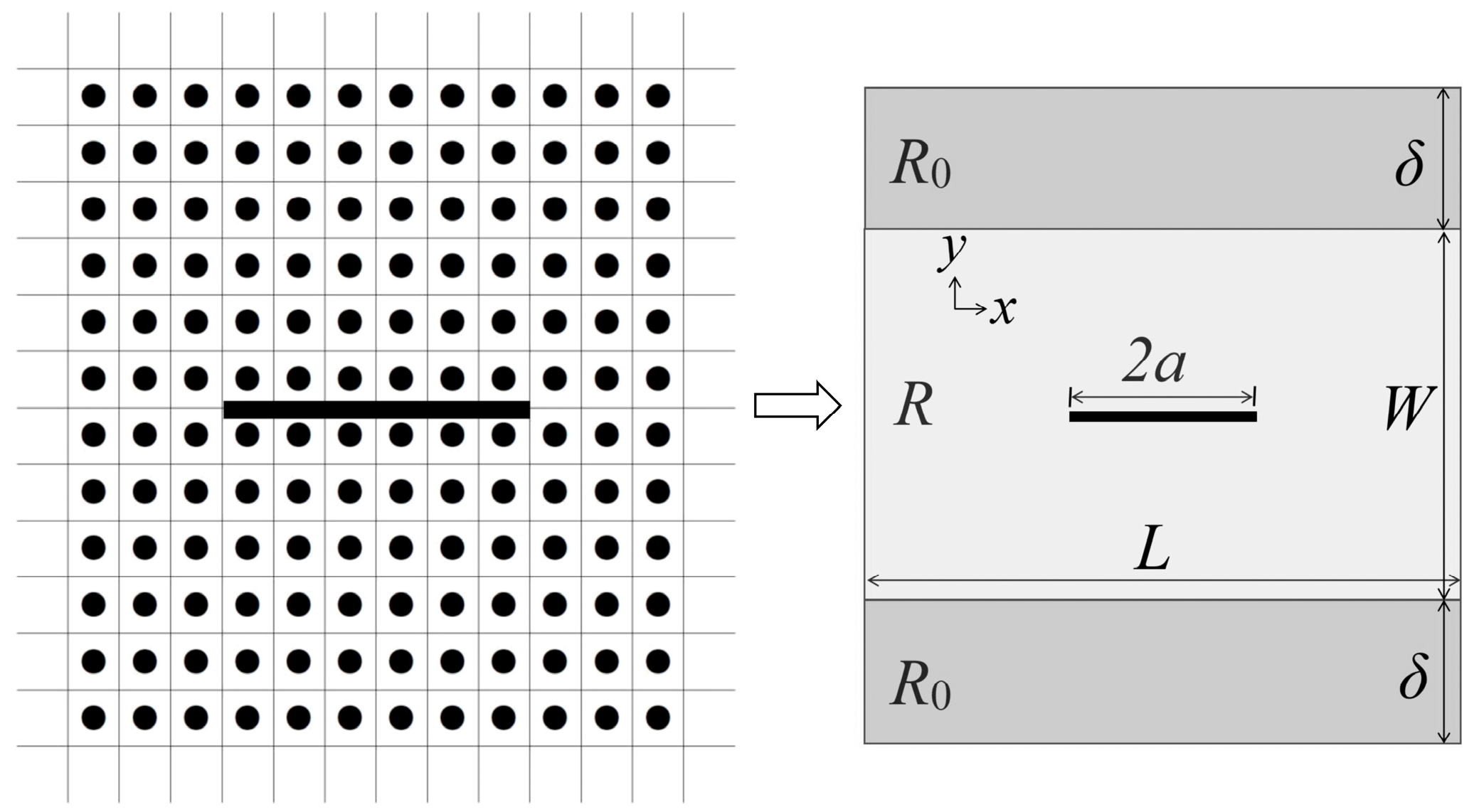
2.3. Discrete Fracture Network Model
- (1)
- Uniform type (ω = 1)
- (2)
- Linear model (ω = 1 − /δ)
- (3)
- Countdown type (ω = 1/)
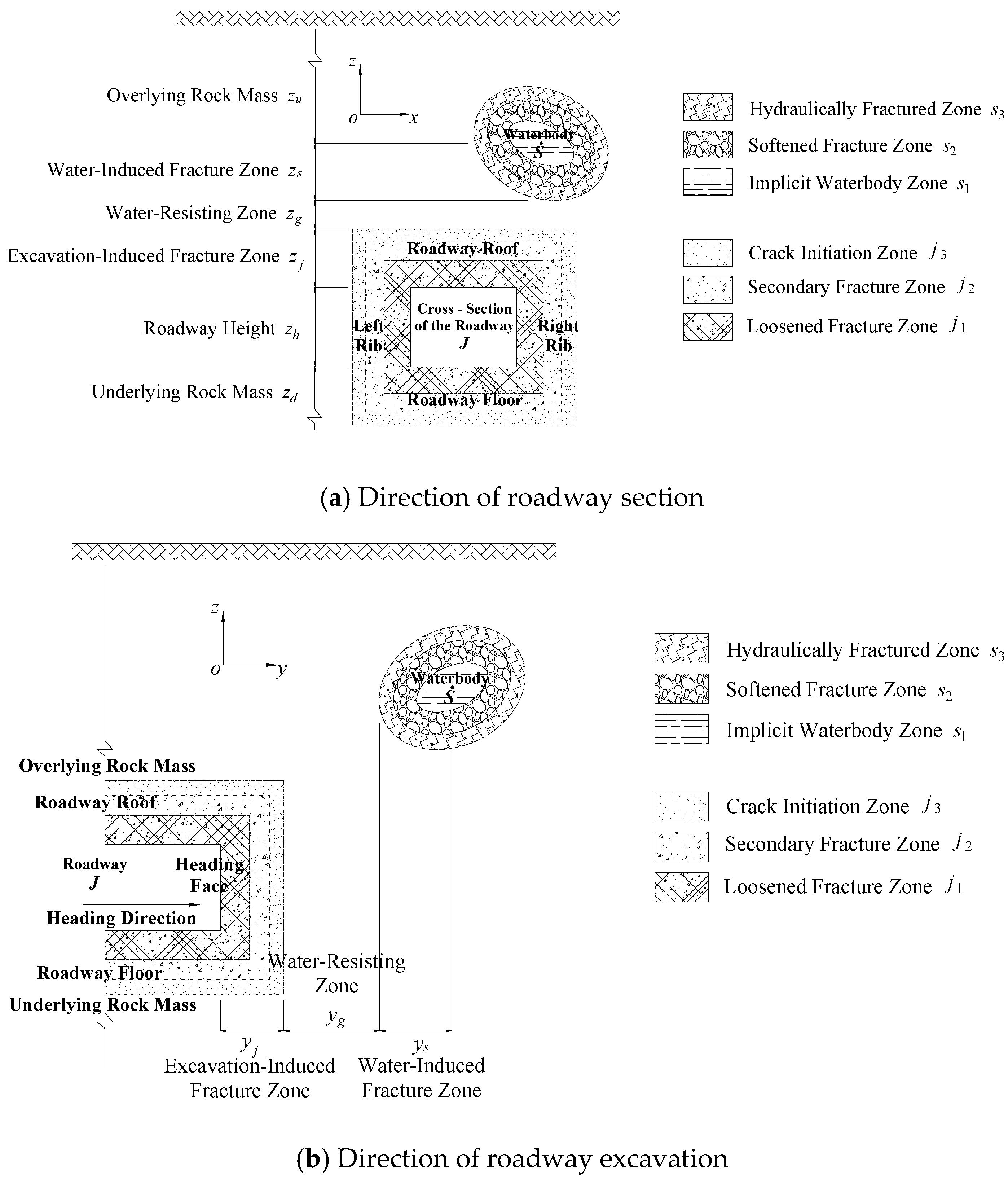
2.4. Geometric Damage Dual-Control Model
- (1)
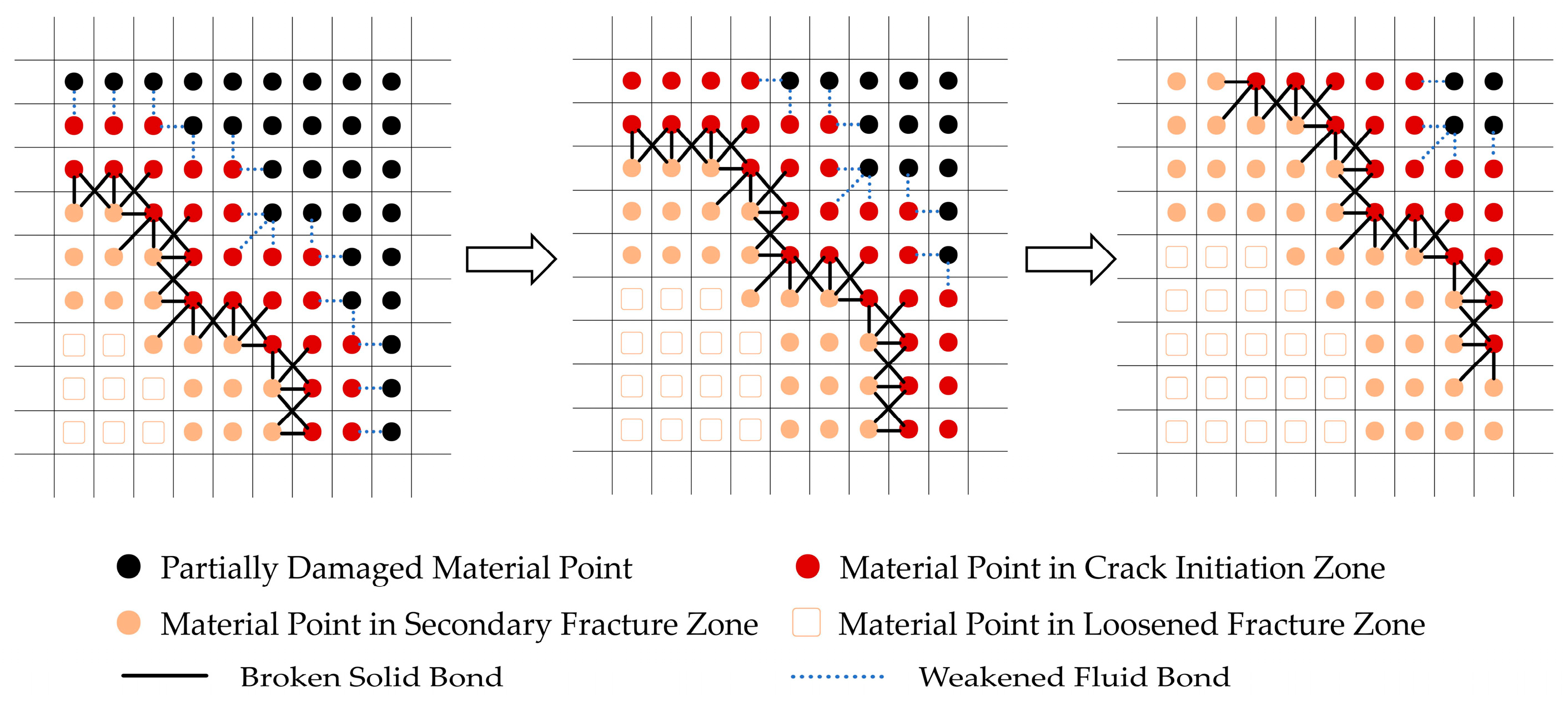
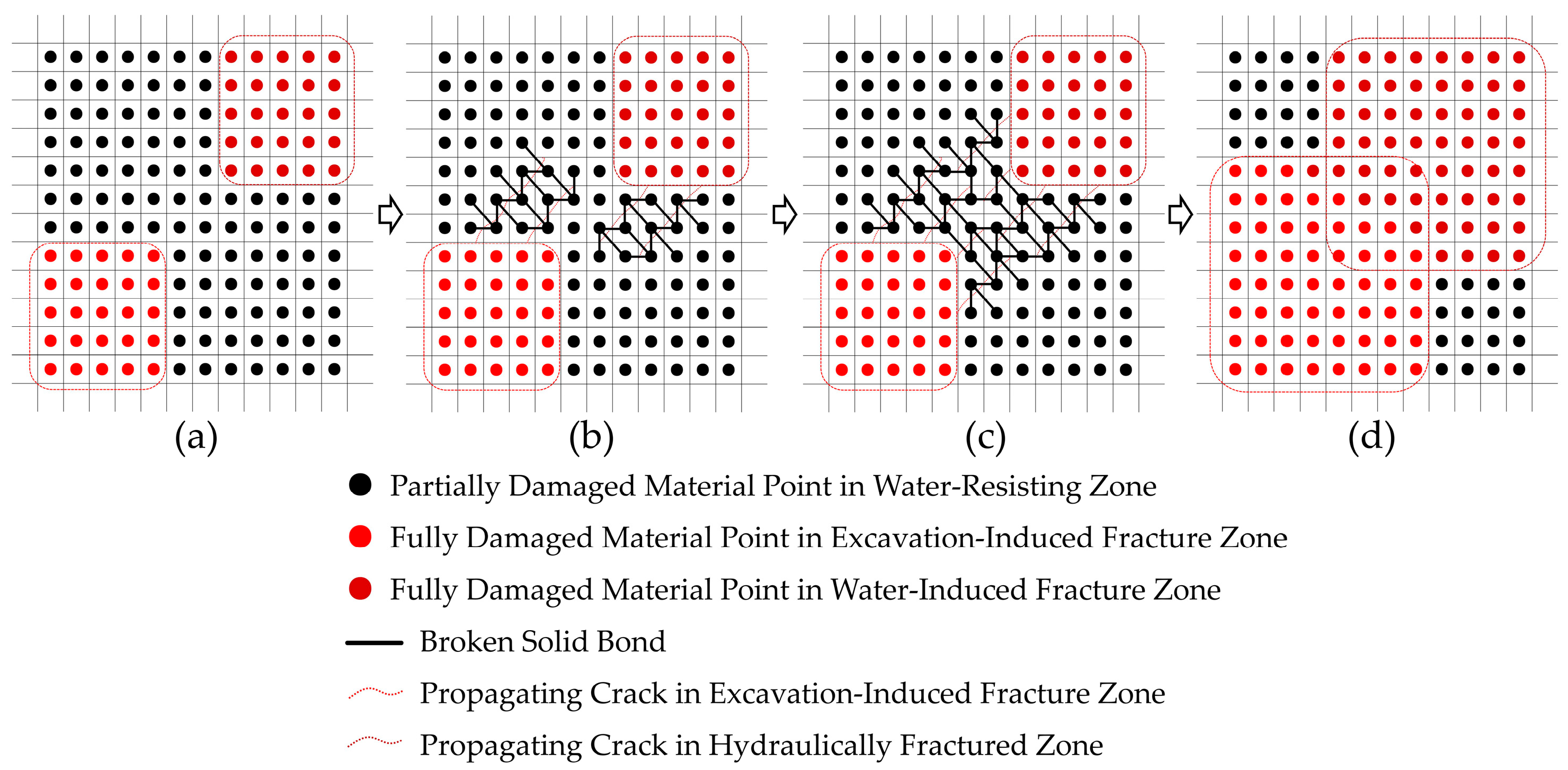
- The evolution process of water-induced fracture zone
- (2)
- The evolution process of the excavation-induced fracture zone
- (3)
- The destruction of the water-resisting zone and the effectiveness of the conduction
- (1)
- The water-resisting zone is completely undamaged (yg > 0 and zg > 0):
- (2)
- Part of the water-resisting zone is damaged (yg·zg ≤ 0):
- (3)
- The water-resisting zone was completely destroyed (yg < 0 and zg < 0):
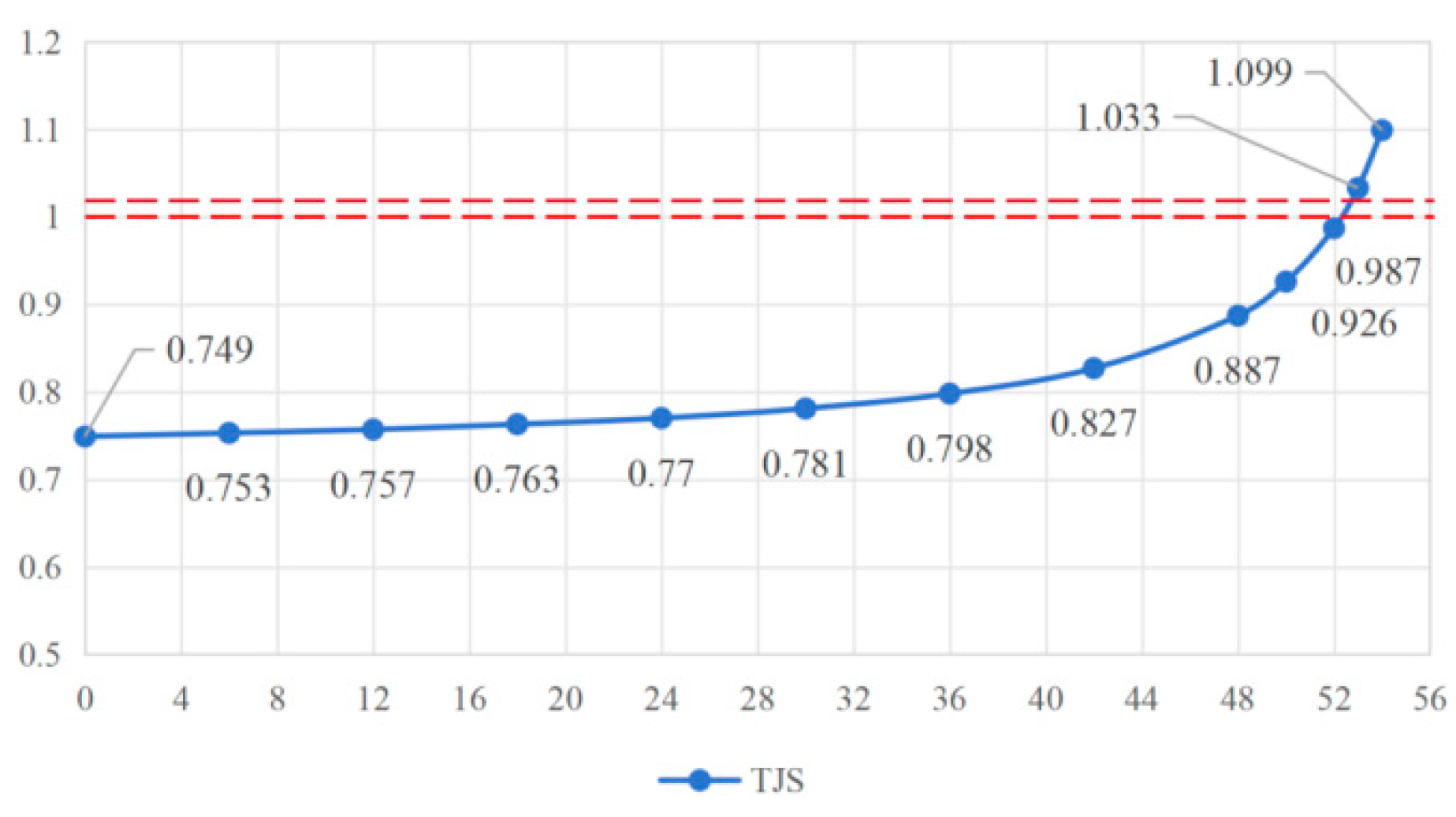
2.5. Unified Single-Exponential Discriminant Function (TJS)
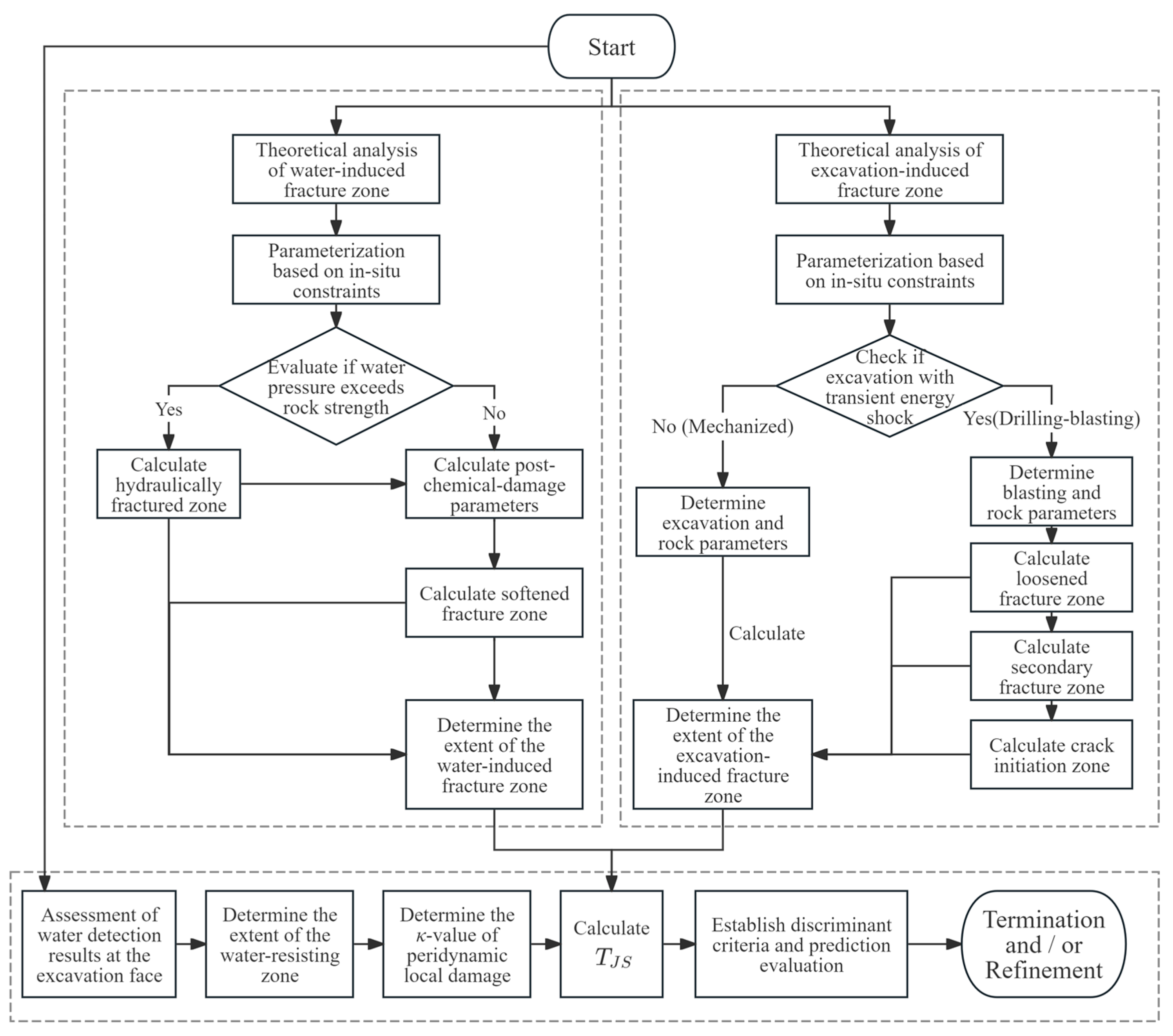
2.6. Coal Mine Roadway Water Inrush Prediction and Assessment Procedure
- (1)
- Water-induced fracture zone quantification
- (2)
- Excavation-induced fracture zone quantification
- (3)
- Prediction evaluation and refinement loop
3. Results
3.1. Cases 1: Prediction and Assessment of Water Inrush During Mechanized Excavation at Yishun Coalmine
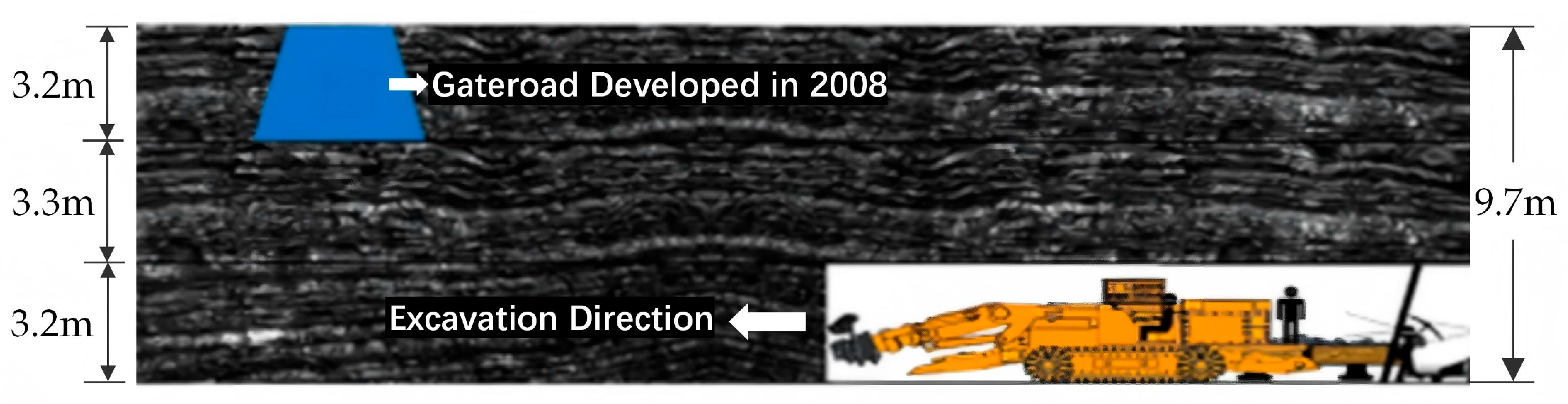
3.1.1. Case Overview
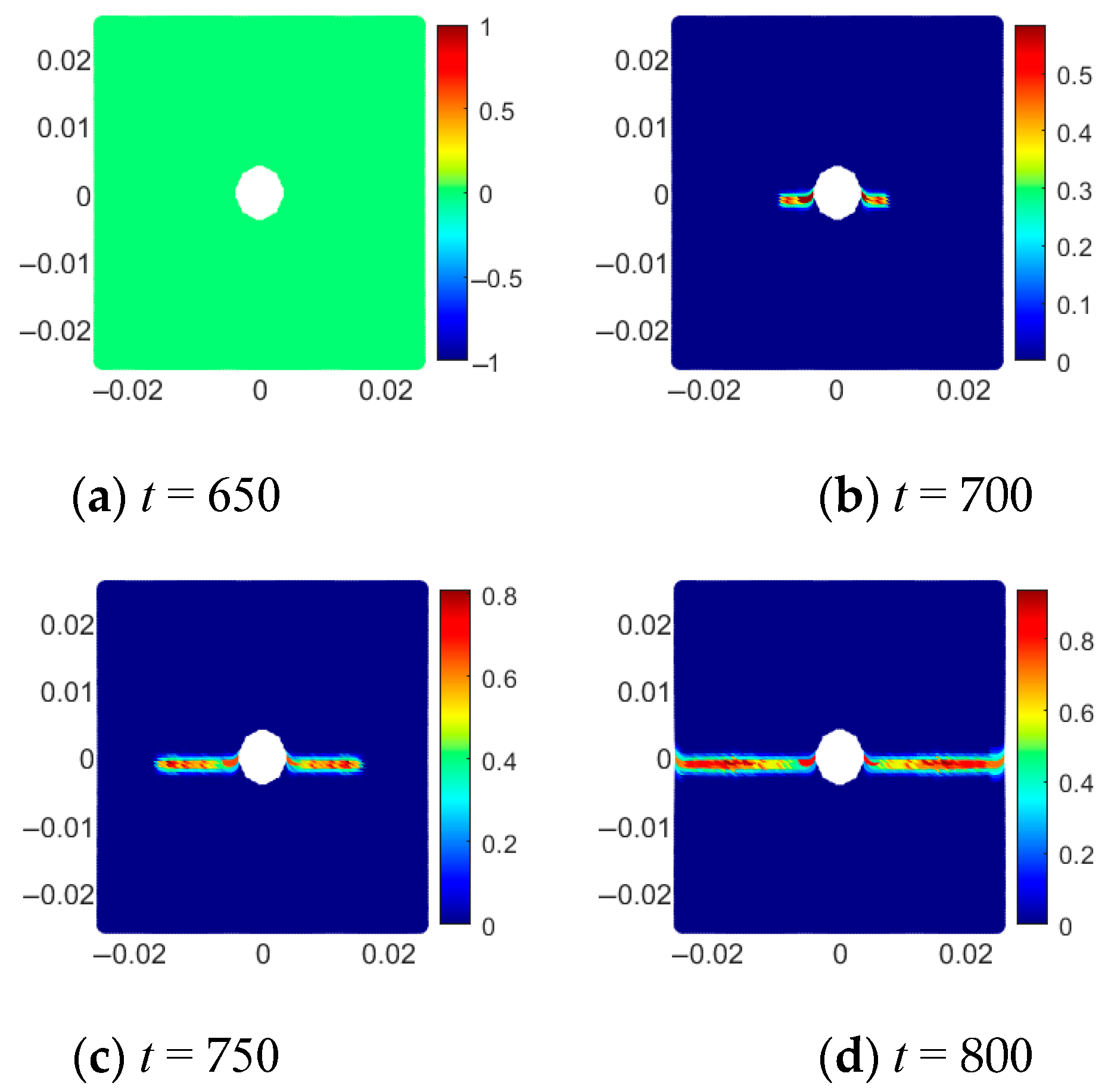
3.1.2. Quantification of Water-Induced Fracture Zone
3.1.3. Quantification of Excavation-Induced Fracture Zone
3.1.4. Prediction Evaluation of Single-Exponential TJS Index
3.2. Cases 2: Prediction and Assessment of Water Inrush During Drilling–Blasting Excavation with Transient Energy Shock at Zhongcun Coalmine
3.2.1. Cases Overview
3.2.2. Quantification of Water-Induced Fracture Zone
3.2.3. Quantification of Excavation-Induced Fracture Zone
3.2.4. Prediction Evaluation of Single-Exponential TJS Index
4. Discussion
4.1. Parameter Sensitivity Analysis
4.2. Comparative Study with Classical Methods
4.3. Limitations and Uncertainty
4.4. Practical Implications
5. Conclusions
5.1. Restated Objective
5.2. Key Findings
5.3. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, L.; Sun, S.; Wang, J.; Yang, W.; Song, S.; Fang, Z. Experimental study of the precursor information of the water inrush in shield tunnels due to the proximity of a water-filled cave. Int. J. Rock. Mech. Min. Sci. 2020, 130, 104320. [Google Scholar] [CrossRef]
- Li, Z.Q.; Nie, L.; Xue, Y.; Li, W.; Fan, K. Model Testing on the Processes, Characteristics, and Mechanism of Water Inrush Induced by Karst Caves Ahead and Alongside a Tunnel. Rock. Mech. Rock. Eng. 2025, 58, 5363–5380. [Google Scholar] [CrossRef]
- Cheng, W.; Yin, H.; Xie, D.; Dong, F.; Li, Y.; Zhu, T.; Wang, J. Prediction of dominant roof water inrush windows and analysis of control target area based on set pair variable weight—Forward correlation cloud model. J. Clean. Prod. 2024, 483, 144253. [Google Scholar] [CrossRef]
- Qlan, Z.; Sul, W.; Guan, Y. Mechanism and salvage of sand-water mixture inrush induced by roof fallingin deep coal roadway. J. China Univ. Min. Technol. 2024, 53, 915–924. [Google Scholar] [CrossRef]
- Wang, J.; Li, S.; Bai, J.; Zhang, Q. Probabilistic assessment of water inrush risk in coal mines through coupled Monte Carlo and peridynamics. Tunn. Undergr. Space Technol. 2023, 140, 105289. [Google Scholar] [CrossRef]
- Qiushuang, Z.; Changfeng, W.; Zhenhao, Z. Research on the prediction of mine water inrush disasters based on multi-factor spatial game reconstruction. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 41. [Google Scholar]
- Tang, S.; Fu, X.; Xie, B. Comprehensive Evaluation Method for the Grouting Management Effect of Mine Water Hazards Based on the Combined Assignment of the TOPSIS and RSR Methods. Appl. Sci. 2024, 14, 10228. [Google Scholar] [CrossRef]
- Liu, Z.L.; Chen, X.Y.; Cheng, W.D. A Novel Transitional Element-Based Approach for PD-FEM Coupling: Theoretical Development. Int. J. Simul. Model. 2025, 24, 321–332. [Google Scholar] [CrossRef]
- Qin, M.; Yang, D.; Jia, Y.; Zhou, Y. Peridynamics modeling of hydraulic fracture interaction with natural fractures in fractured rock mass. Eng. Fract. Mech. 2024, 307, 110299. [Google Scholar] [CrossRef]
- Qin, M.; Yang, D.; Chen, W. Numerical Investigation of Hydraulic Fracturing in a Heterogeneous Rock Mass Based on Peridynamics. Rock. Mech. Rock. Eng. 2023, 56, 4485–4505. [Google Scholar] [CrossRef]
- Li, M. Peridynamic Simulation Method and Application of Hydro-Mechanical Coupling in Fractured Rock Masses Under Dynamic Disturbance; Shandong University: Shangdong, China, 2023. [Google Scholar] [CrossRef]
- Ma, P.-F. Study on Damage-Seepage Characteristics of Fractured Rock Mass Using Peridynamics Method; Shandong University: Shangdong, China, 2022. [Google Scholar] [CrossRef]
- Shi, H.-T. Peridynamic Fluid-Solid Coupling Model For Hydraulic Fracturing Process in Rock Strata; Southeast University: Nanjing, China, 2022. [Google Scholar] [CrossRef]
- Zhang, G.-H.; Xie, Z.-Z.; Zhang, B.-W.; Jiao, Y.-Y.; Zou, J.-P.; Wu, J.-Q.; Xiong, F.; Tang, Z.-C. Sources of high-temperature water and gas inrush during tunnel excavation: A case of Bangfu tunnel in Southwest China. J. Rock. Mech. Geotech. Eng. 2024, 16, 5027–5049. [Google Scholar] [CrossRef]
- Dong, F.; Yin, H.; Cheng, W.; Zhang, C.; Zhang, D.; Ding, H.; Lu, C.; Wang, Y. Quantitative prediction model and prewarning system of water yield capacity (WYC) from coal seam roof based on deep learning and joint advanced detection. Energy 2004, 290, 130200. [Google Scholar] [CrossRef]
- Fan, K.; Li, W.; Wang, Q.; Liu, S.; Xue, S.; Xie, C.; Wang, Z. Formation mechanism and prediction method of water inrush from separated layers within coal seam mining: A case study in the Shilawusu mining area, China. Eng. Fail. Anal. 2019, 103, 158–172. [Google Scholar] [CrossRef]
- Sun, J.; Hu, Y.; Zhao, G. Relationship between water inrush from coal seam floors and main roof weighting. Int. J. Min. Sci. Technol. 2017, 27, 873–881. [Google Scholar] [CrossRef]
- Hou, E.; Yan, Y.; Wen, Q.; Che, X.; Miao, Y.; Li, H.; Lu, B. Study on prediction of water inrush hazard in roof of roadway driving. Coal Sci. Technol. 2022, 50, 110–120. [Google Scholar] [CrossRef]
- Yang, T.; Yan, Y.; Zhang, J.; Lin, H.; He, Y.; Zhang, Y.; Gao, S. Study on synergistic water-resisting stability of upper and lower soil layers and bedrock layer in shallow coal seam group. Coal Sci. Technol. 2023, 51, 234–242. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhu, H.; Wu, Q.; Guo, X.; Cui, F.; Pang, Z.; Liu, S.; Yang, W. Research status and prevention and control path of coal seam roof water disaster in China J. China Coal Soc. 2024, 49, 1539–1555. [Google Scholar] [CrossRef]
- Qiao, W.; Liu, M.; Li, L.; Guo, W.; Wang, Q.; Meng, X.; Li, X.; Duan, Z.; Chen, W.; Li, W. Disaster mechanism induced by structure evolution of ”water-inrus-hing separation zone” of mining rock mass and prediction method of water inrush from separation layer. J. China Coal Soc. 2023, 48, 818–832. [Google Scholar] [CrossRef]
- Ma, K.; Sun, X.; Tang, C.; Wang, S.-J.; Yuan, F.-Z.; Peng, Y.-L.; Liu, K. An early warning method for water inrush in Dongjiahe coal mine based on microseismic moment tensor. J. Cent. South. Univ. 2020, 27, 3133–3148. [Google Scholar] [CrossRef]
- Qiao, W.; Wang, Z.; Li, W.; Lu, Y.; Li, L.; Huang, Y.; He, J.; Li, X.; Zhao, S.; Liu, M. Formation mechanism, disaster-causing mechanism and prevention technology of roof bed separation water disaster in coal mines. J. China Coal Soc. 2021, 46, 507–522. [Google Scholar] [CrossRef]
- Gao, R.; Yan, H.; Ju, F.; Mei, X.; Wang, X. Influential factors and control of water inrush in a coal seam as the main aquifer. Int. J. Min. Sci. Technol. 2018, 28, 187–193. [Google Scholar] [CrossRef]
- Liu, T.; Xu, D.; Shi, L.; Qu, L.; Ji, K. Trapezoidal collapse model to calculate the height of the overburden collapse zone in coal seam mining: An example from Guo’Jiahe Coal Mine, Western China. Energy 2022, 256, 124609. [Google Scholar] [CrossRef]
- Liu, X. Deformation Failure Mechanism and Control Technology of Surrounding Rock in Loose Fractured Semi-Coal Rock Development Roadway; China University of Mining and Technology: Xuzhou, China, 2014. [Google Scholar]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Q.; Zhang, C.; Zhao, J. Uncertainty quantification of rock mass permeability using Monte Carlo and machine learning. Int. J. Rock Mech. Min. Sci. 2022, 152, 105137. [Google Scholar] [CrossRef]
- Lan, T.; Zhang, H.; Li, S.; Batugina, I.; Batugin, A. Application and Development of the Method of Geodynamic Zoning According to Geodynamic Hazard Forecasting at Coal Mines in China. IOP Conf. Ser. Earth Environ. Sci. 2019, 221, 012088. [Google Scholar] [CrossRef]
- Yang, J.; Peng, C.; Ye, Z.; Yao, C.; Zhang, X.; Ma, Y.; Zhou, C. Study on the efficiency of energy transfer in the blasting with different coupling mediums for deep rock mass excavation. Eng. Fract. Mech. 2025, 319, 111048. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, X.; Li, Z.; Gao, W.; Xu, Z.; Zhang, Y.; Zhou, J. Effects of In-Situ Stress on Damage and Fractal during Cutting Blasting Excavation. Fractal Fract. 2024, 8, 450. [Google Scholar] [CrossRef]
- Dai, J.; Gong, F.; He, Z.; Xu, L. Quantitative estimation of potential rockburst pit depths during blasting excavation in deep tunnels. Int. J. Rock. Mech. Min. Sci. 2024, 178, 105748. [Google Scholar] [CrossRef]
- Hong, Z.; Tao, M.; Wu, C.; Zhou, J.; Wang, D. The spatial distribution of excavation damaged zone around underground roadways during blasting excavation. Bull. Eng. Geol. Environ. 2023, 82, 155. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory, 2nd ed.; Taylor & Francis: London, UK, 1994. [Google Scholar]
- Oterkus, S.; Madenci, E.; Oterkus, E. Peridynamic modeling of anisotropic media. J. Elasticity 2023, 152, 1–24. [Google Scholar] [CrossRef]
- Zimmerman, R.W.; Al-Yaarubi, A. Non-linear regimes of fluid flow in rock fractures. Int. J. Rock. Mech. Min. Sci. 2004, 41, 163–169. [Google Scholar] [CrossRef]
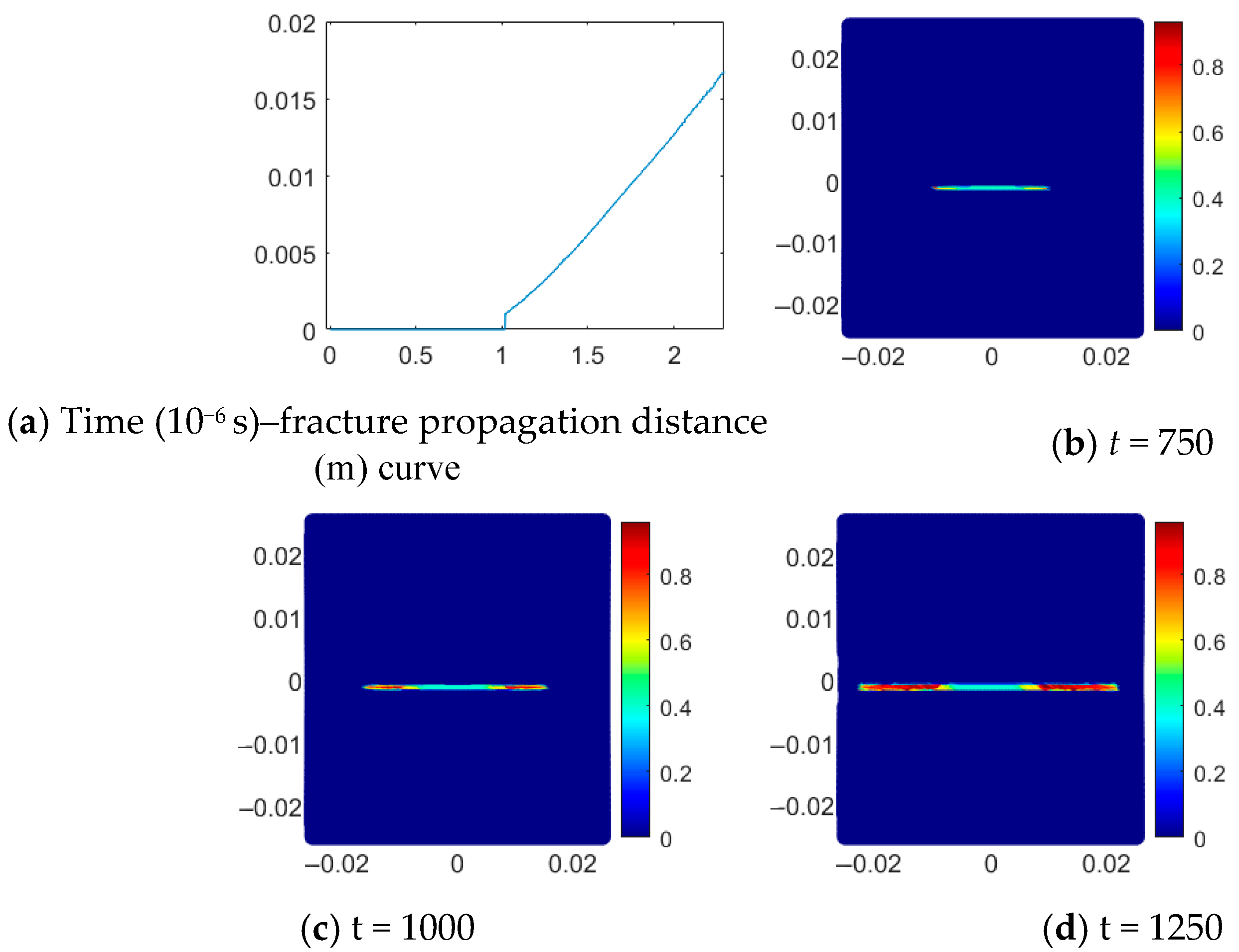
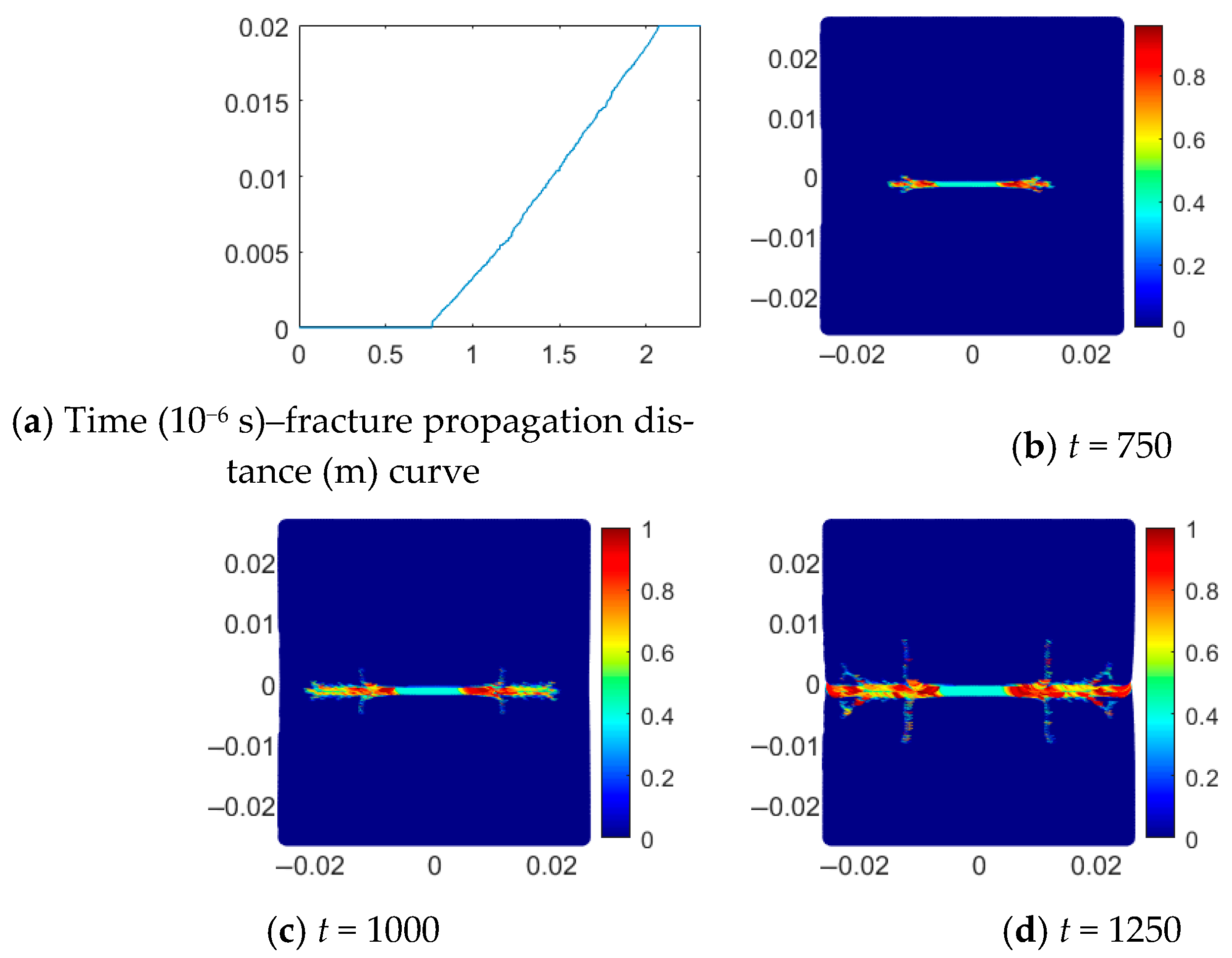

| Concrete Circumstances | Corresponding Conditions | Form of Effective Judgment Function of Water Diversion Channel | Principle of Effective Judgment of Water Conduction Channel |
|---|---|---|---|
| The water-resisting zone was completely undamaged | yg > 0 zg > 0 | TJS < 1. The closer TJS is to 0, the safer it is, and the water conduction channel is invalid, so it can be considered that there will be no sudden water inrush. | |
| Parts of the water-resisting zone were damaged | yg < 0 zg > 0 | TJS < 1: The closer TJS is to 0, the lower the effectiveness of the water conduction channel; it can be considered that the sudden water will not occur temporarily, but there is the possibility that lagging-type sudden water cannot be ruled out; the closer TJS is to 1, the higher the effectiveness of the water conduction channel. It can be considered that the lagging-type sudden water or instantaneous-type sudden water may occur. When TJS > 1, the water conduction channel is highly effective, and instantaneous water inrush may occur. When TJS > 1 + κ(yg·zg < 0) or 1 + (yg·zg = 0), the water conduction channel is effective, and instantaneous water inrush can be considered to occur. | |
| Yg < 0 zg = 0 | |||
| yg = 0 zg = 0 | |||
| yg = 0 zg < 0 | |||
| yg > 0 zg < 0 | |||
| The water-resisting zone was completely destroyed | yg < 0 zg < 0 | When TJS > 1, the larger the TJS, the more dangerous it is. The water conduction channel is effective, and instantaneous water inrush can be considered to occur. |
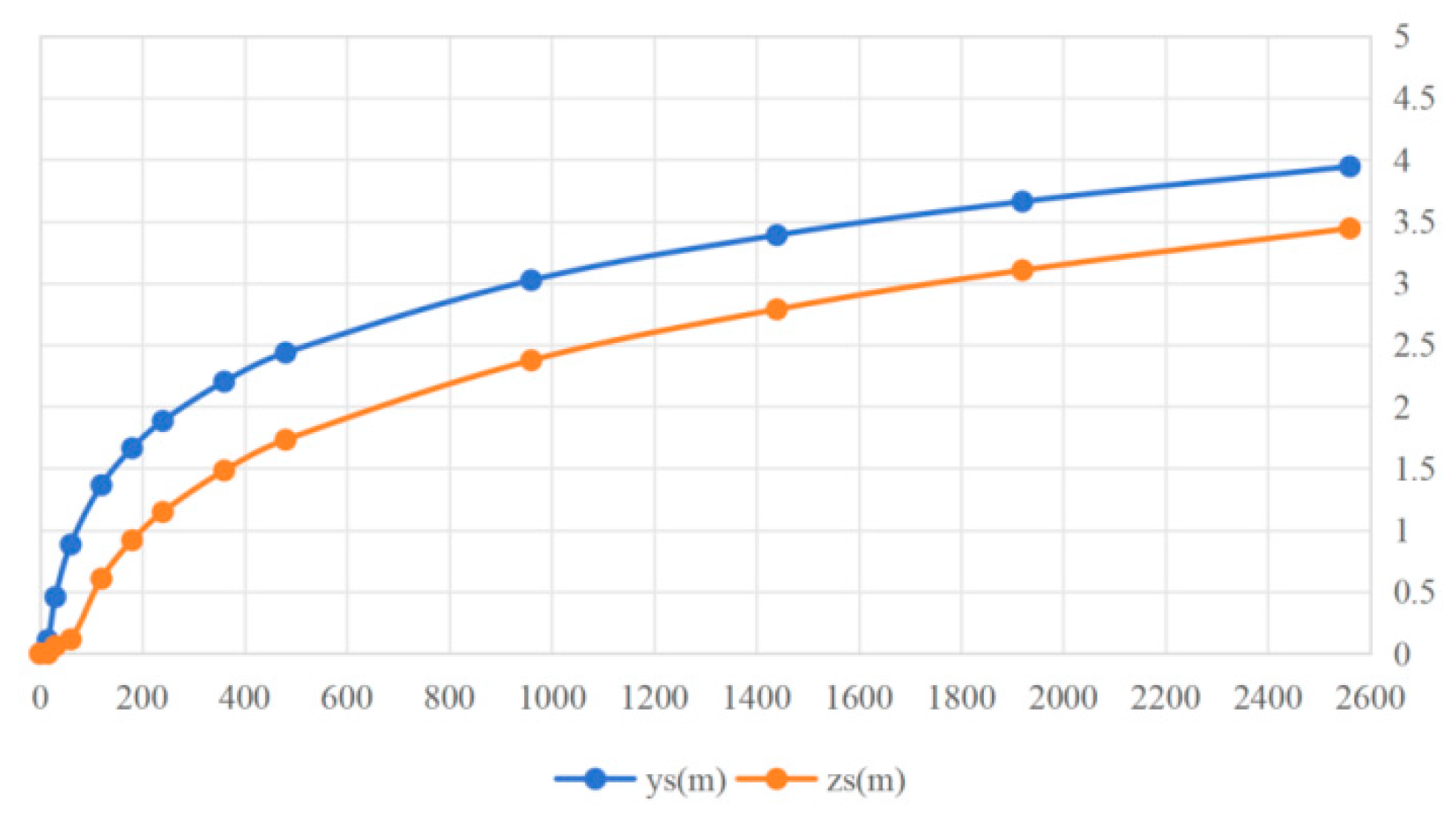
| Soak Period (d) | ys (m) | zs (m) | Soak Period (d) | ys (m) | zs (m) |
|---|---|---|---|---|---|
| 15 | 0.110 | 0 | 360 | 2.203 | 1.483 |
| 30 | 0.458 | 0.062 | 480 | 2.437 | 1.732 |
| 60 | 0.883 | 0.115 | 960 | 3.024 | 2.375 |
| 120 | 1.364 | 0.607 | 1440 | 3.389 | 2.788 |
| 180 | 1.664 | 0.918 | 1920 | 3.661 | 3.105 |
| 240 | 1.884 | 1.147 | 2560 | 3.945 | 3.444 |
| Decoupling Coefficients | Rj1 (m) | Rj2 (m) | Rj3 (m) | ∑Rji (m) |
|---|---|---|---|---|
| 1 | 3.819 | 2.919 | 195.334 | 1 |
| 1.1 | 2.694 | 2.059 | 37.484 | 1.1 |
| 1.2 | 1.958 | 1.497 | 8.242 | 1.2 |
| 1.3 | 1.463 | 1.119 | 2.063 | 1.3 |
| 1.4 | 1.116 | 0.853 | 0.567 | 1.4 |
| 1.5 | 0.867 | 0.663 | 0.170 | 1.5 |
| 1.6 | 0.685 | 0.524 | 0.055 | 1.6 |
| 1.7 | 0.549 | 0.420 | 0.019 | 1.7 |
| 1.8 | 0.445 | 0.340 | 0.007 | 1.8 |
| 1.9 | 0.365 | 0.279 | 0.003 | 1.9 |
| 2 | 0.303 | 0.232 | 0.001 | 2 |
| Model Type | Prediction Accuracy | Real-Time Applicability | Key Limitation |
|---|---|---|---|
| Empirical formulas [13,17] | 62.3 ± 8.7% | Low (requires manual measurement) | Ignores damage evolution |
| FEM simulations [19,22] | 74.1 ± 6.2% | Very low (hours per simulation) | Continuum assumption fails at fractures |
| PD dual-control (Ours) | 91.8 ± 3.5% | High (TJS updates in minutes) | Requires κ calibration |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Fang, X.; Liang, M.; Wu, G.; Chen, N.; Song, Y. Analysis and Application of Dual-Control Single-Exponential Water Inrush Prediction Mechanism for Excavation Roadways Based on Peridynamics. Appl. Sci. 2025, 15, 7621. https://doi.org/10.3390/app15137621
Liu X, Fang X, Liang M, Wu G, Chen N, Song Y. Analysis and Application of Dual-Control Single-Exponential Water Inrush Prediction Mechanism for Excavation Roadways Based on Peridynamics. Applied Sciences. 2025; 15(13):7621. https://doi.org/10.3390/app15137621
Chicago/Turabian StyleLiu, Xiaoning, Xinqiu Fang, Minfu Liang, Gang Wu, Ningning Chen, and Yang Song. 2025. "Analysis and Application of Dual-Control Single-Exponential Water Inrush Prediction Mechanism for Excavation Roadways Based on Peridynamics" Applied Sciences 15, no. 13: 7621. https://doi.org/10.3390/app15137621
APA StyleLiu, X., Fang, X., Liang, M., Wu, G., Chen, N., & Song, Y. (2025). Analysis and Application of Dual-Control Single-Exponential Water Inrush Prediction Mechanism for Excavation Roadways Based on Peridynamics. Applied Sciences, 15(13), 7621. https://doi.org/10.3390/app15137621







