RE-BPFT: An Improved PBFT Consensus Algorithm for Consortium Blockchain Based on Node Credibility and ID3-Based Classification
Abstract
1. Introduction
- What kind of node reputation evaluation and classification mechanism can effectively and dynamically manage node behaviors, thus boosting overall system performance and security?
- How can the primary node selection process be refined to mitigate risks of centralization and enhance resilience against Byzantine failures?
- What methods can practically reduce communication complexity and consensus latency when applying PBFT algorithms in large-scale networks?
- Development of a multi-faceted node reputation evaluation model enabling dynamic assessment and effective management of nodes.
- Application of an optimized ID3 decision tree algorithm for precise and automated node classification.
- Introduction of a novel weighted-random primary node election strategy to prevent centralization issues and enhance network robustness.
- Empirical validation through extensive experiments demonstrating RE-BPFT’s superior performance over traditional algorithms (PBFT, RBFT, and PPoR) in terms of reduced communication overhead, lower consensus latency, and increased throughput.
2. Related Work and Background
2.1. Consortium Blockchain Technology Overview
2.2. PBFT Algorithm and Its Improvements
2.3. ID3 Decision Tree Algorithm
3. Improved RE-BPFT Blockchain Consensus Algorithm
3.1. Node Credit Calculation
3.2. Node Classification
| Algorithm 1: ID3 Decision Tree-Based Consortium Blockchain Node Classification Algorithm |
| Output: Classified node sets: Excellent node set , Good node set , Normal node set , Malicious node set |
| 1. Initialize node attribute sets: Reputation score , Continuous consensus count , Downtime countDowntime , Communication error count , Node activity level |
| 2. Create decision tree training dataset |
| 3. for each node do |
| 4. Calculate node , continuous consensus count , downtime count , communication error count , activity level |
| 5. Extract node features and add to |
| 6. end for |
| 7. Calculate information entropy of each attribute based on dataset |
| 8. Calculate information gain of each attribute according to formula |
| 9. if maximum information gain then |
| 10. Partition dataset using attribute with maximum information gain to construct decision tree |
| 11. Predict the category of each node based on the decision tree model |
| 12. if the node category is ‘Excellent’ then |
| 13. add the node to |
| 14. else if the node category is ‘Good’ then |
| 15. add the node to |
| 16. else if the node category is ‘Average’ then |
| 17. add the node to |
| 18. else |
| 19. add the node to |
| 20. end if |
| 21. else |
| 22. Output warning: “Unable to effectively classify, insufficient information gain” |
| 23. end if |
| 24. Return the classified node set |
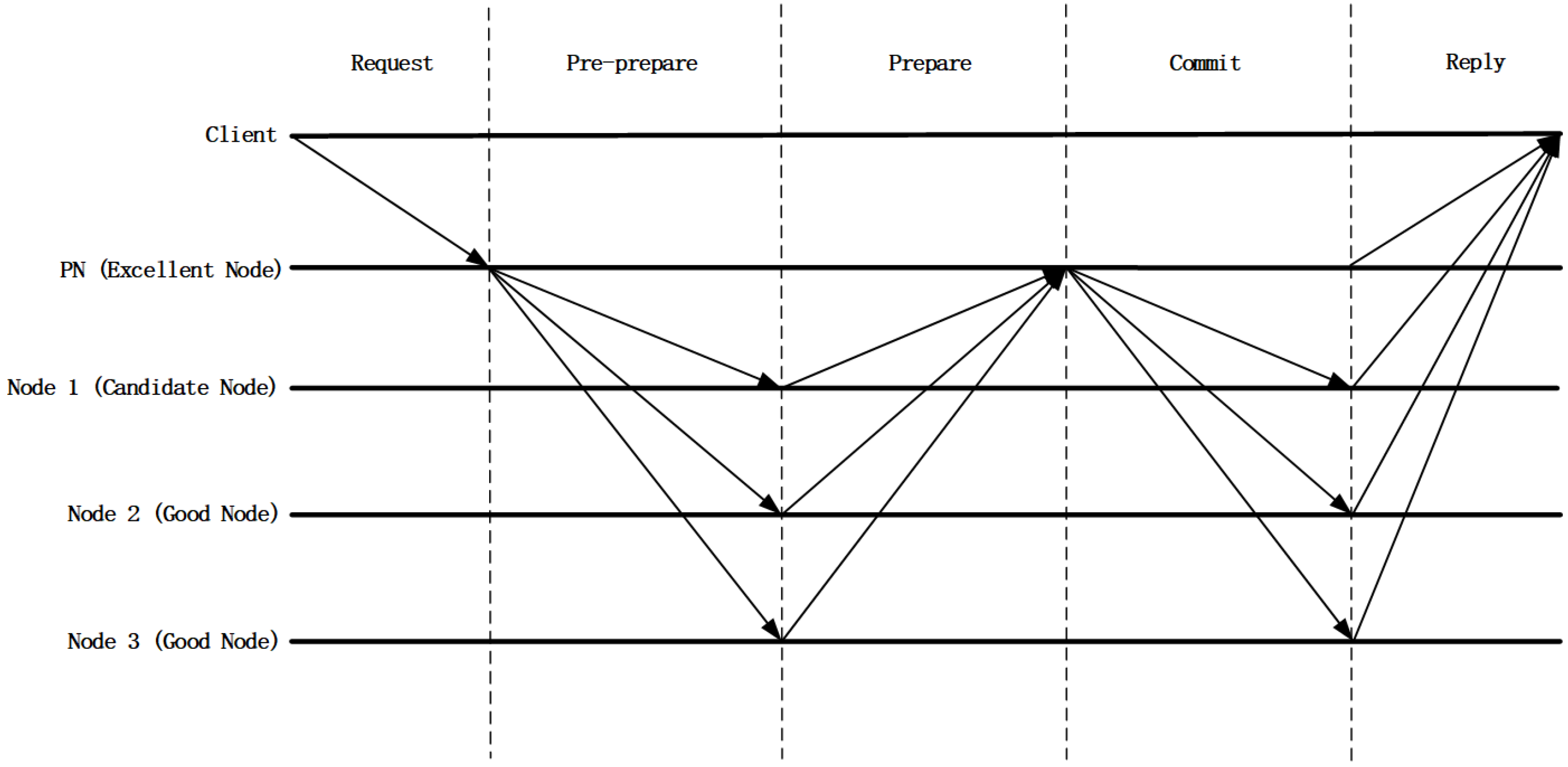
3.3. Consensus Protocol
- (1)
- All consensus nodes with inconsistencies will have their reputation scores deducted;
- (2)
- If the number of dissenting nodes the current primary node will also be demoted, and the consensus process will be restarted.
3.4. View Change Protocol
- (1)
- Fails to receive at least valid PREPARE messages within timeout period ;
- (2)
- Fails to successfully package and broadcast new block within maximum tolerance time .
| Algorithm 2: Consensus Protocol Algorithm |
| Input: Client request message
, view number , node set , system fault tolerance node count Output: Client response result, node ledger update |
| 1. The client sends a consensus request (containing operation, timestamp, client identifier) to the primary node //Client request phase |
| 2. The primary node assigns a number to and calculates the digest |
| 3. Calculate the primary node’s reputation value and generate the hash digest |
| 4. Construct the pre-prepare message |
| 5. broadcasts to all consensus nodes |
| 6. for each consensus node do//Consensus node preparation phase |
| 7. (validate , ) |
| 8. if verification passes then |
| 9. Calculate local reputation value |
| 10. to other consensus nodes |
| 11. end if |
| 12. end for |
| 13. Master node collects prepare messages |
| 14. If then |
| 15. contents are consistent then |
| 16. |
| 17. to consensus nodes |
| 18. else |
| 19. |
| 20. then |
| 21. is demoted; triggers view change |
| 22. end if |
| 23. end if |
| 24. else |
| 25. was demoted, triggering view change |
| 26. |
| 27. end if |
| 28. for do//Block commit phase |
| 29. then |
| 30. Commit new block to local ledger |
| 31. end if |
| 32. end for |
| 33. returns transaction processing result to client, ending consensus process//Client feedback phase |
4. Experimental Verification and Analysis
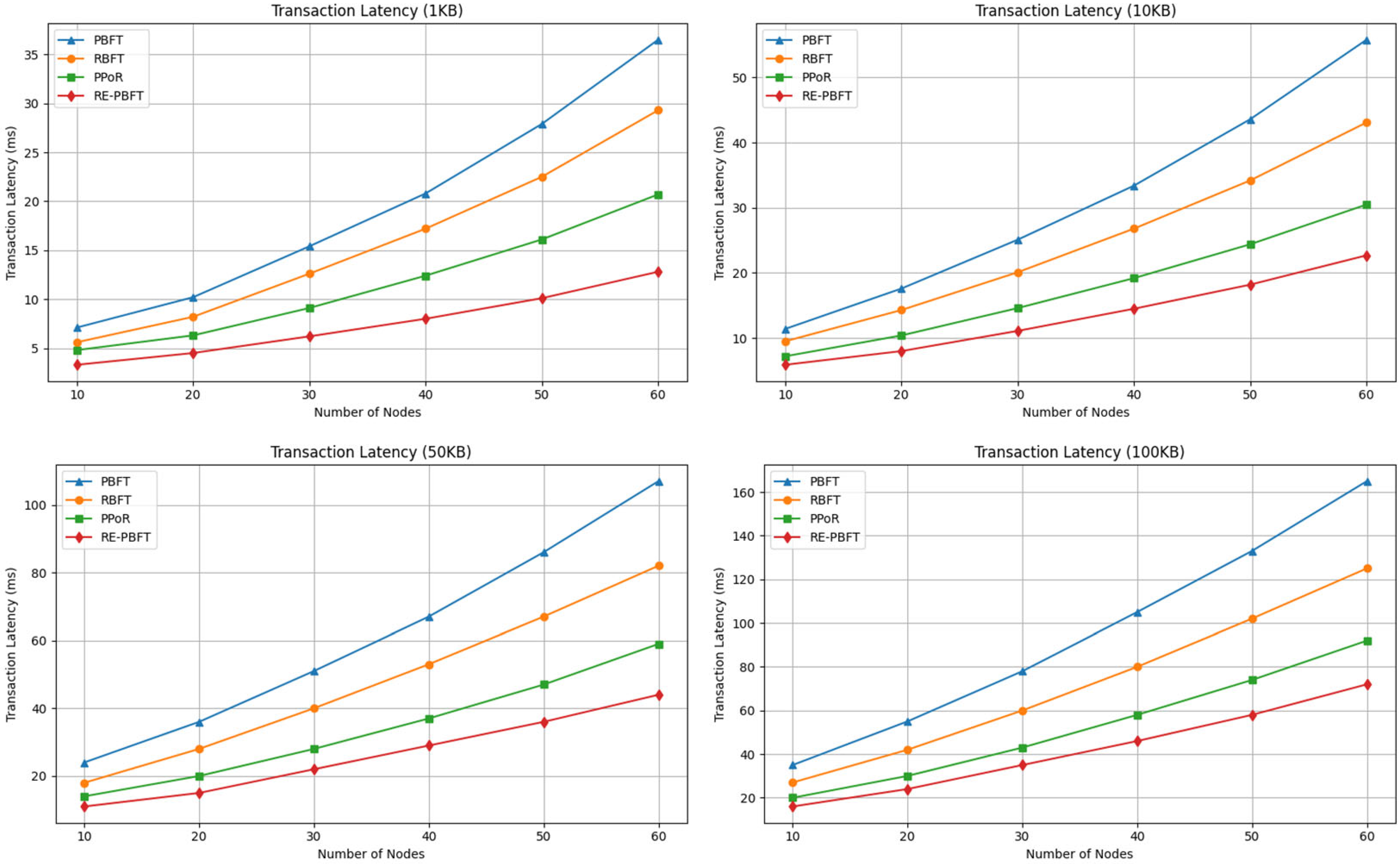
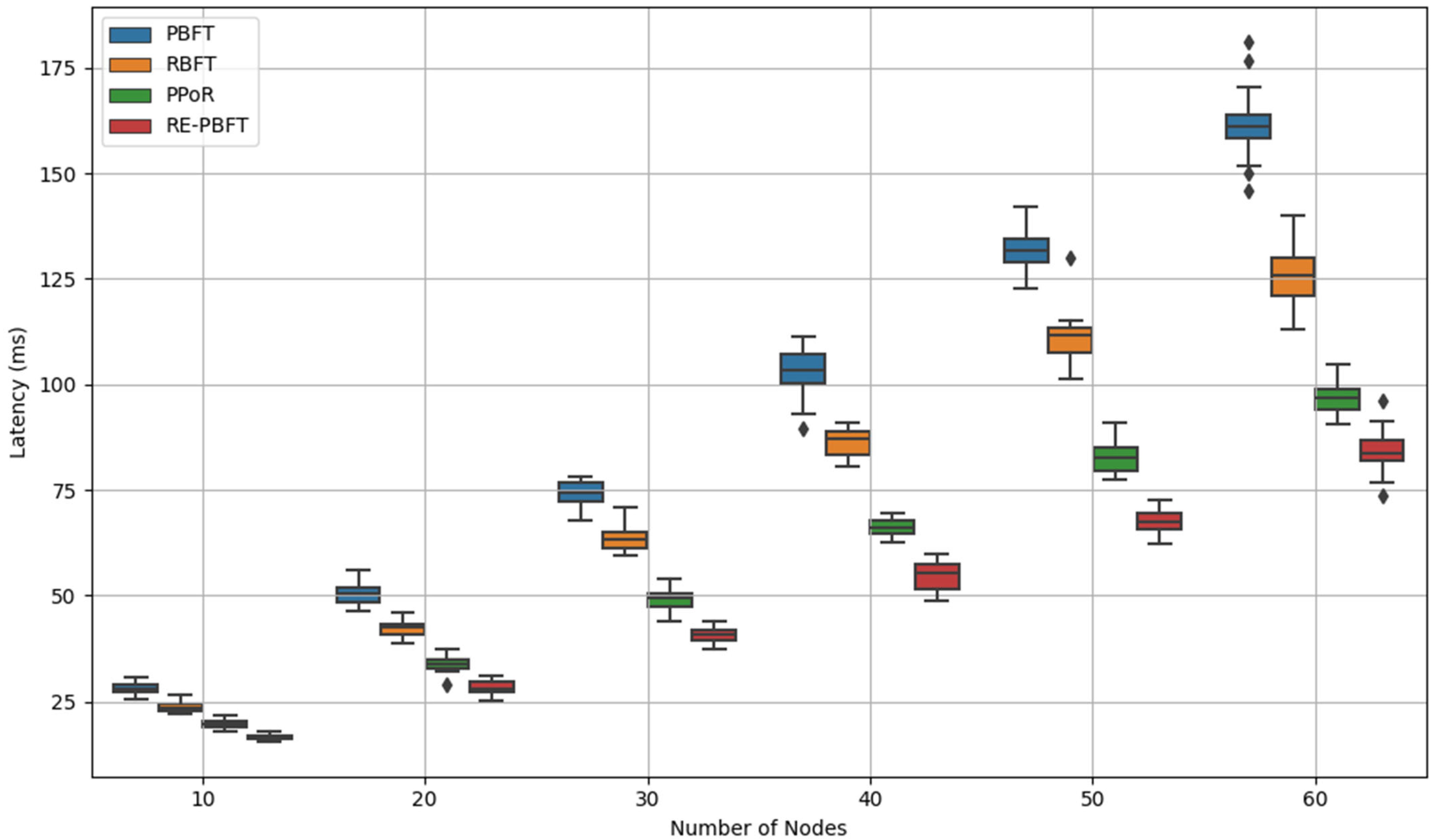
4.1. Consensus Latency
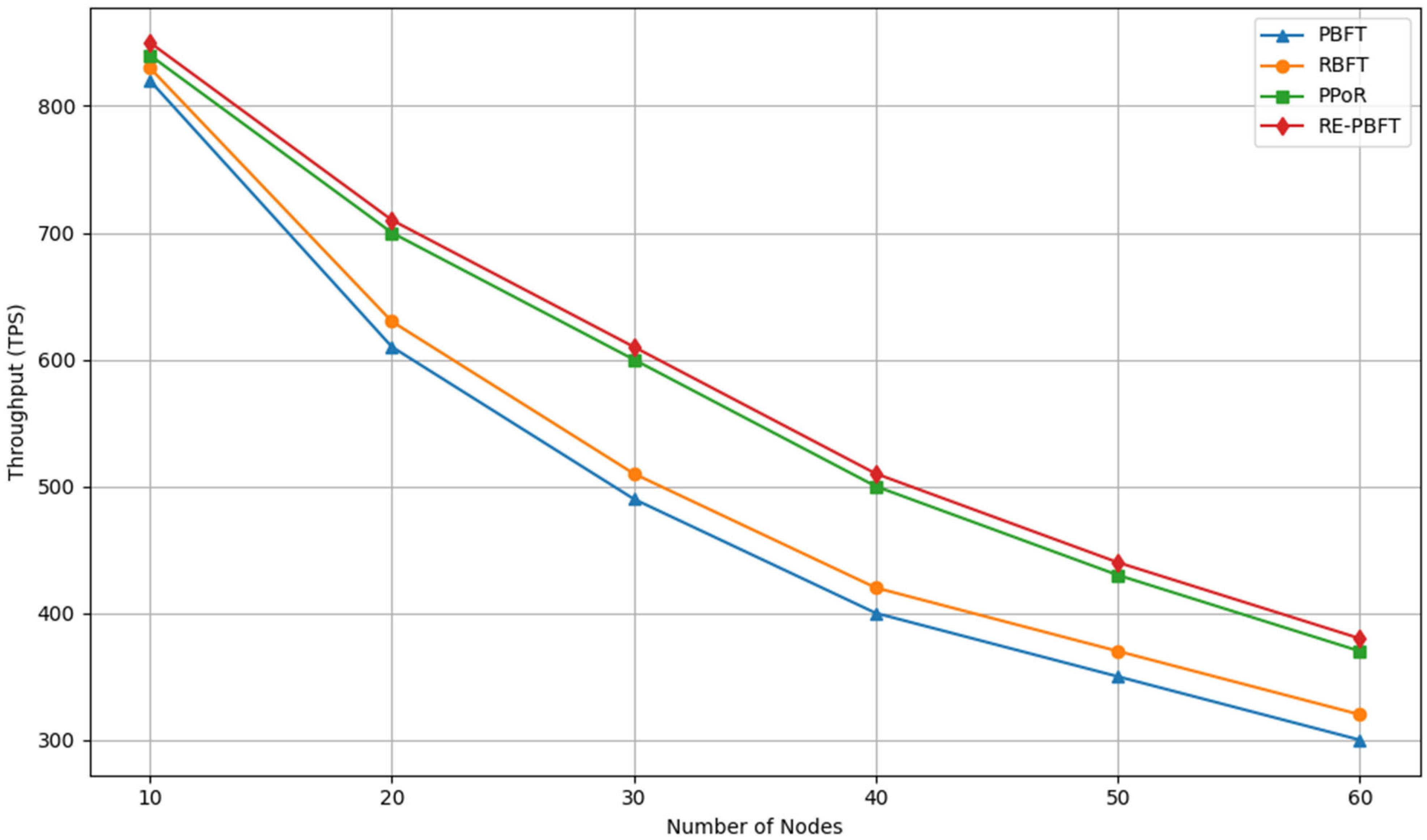
4.2. Throughput Testing
4.3. Communication Overhead Testing
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, X.; He, S.; Sun, L.; Zheng, Y.; Wu, C.Q. A Survey of Consortium Blockchain and Its Applications. Cryptography 2024, 8, 12. [Google Scholar] [CrossRef]
- World Food Programme. WFP Building Blocks | WFP Innovation. Available online: https://innovation.wfp.org/project/building-blocks (accessed on 14 June 2024).
- VAKT. VAKT: The Post-Trade Processing Platform for Physical Energy Commodities. Available online: https://www.vakt.com/ (accessed on 14 June 2024).
- Xu, G.; Bai, H.; Lu, W.; Xu, S. A Survey on Consensus Algorithms for Consortium Blockchain. Cybersecurity 2023, 6, 15. [Google Scholar]
- Yuan, F.; Huang, X.; Zheng, L.; Wang, L.; Wang, Y.; Yan, X.; Gu, S.; Peng, Y. The Evolution and Optimization Strategies of a PBFT Consensus Algorithm for Consortium Blockchains. Information 2025, 16, 268. [Google Scholar] [CrossRef]
- Khan, I.; Ali, Q.E.; Hadi, H.J.; Ahmad, N.; Ali, G.; Cao, Y.; Alshara, M.A. Securing Blockchain-Based Supply Chain Management: Textual Data Encryption and Access Control. Technologies 2024, 12, 110. [Google Scholar] [CrossRef]
- Castro, M.; Liskov, B. Practical Byzantine Fault Tolerance and Proactive Recovery. ACM Trans. Comput. Syst. 2002, 20, 398–461. [Google Scholar] [CrossRef]
- Wu, X.; Jiang, W.; Song, M.; Jia, Z.; Qin, J. An Efficient Sharding Consensus Algorithm for Consortium Chains. Sci. Rep. 2023, 13, 20. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, J. An Improved Practical Byzantine Fault Tolerance Algorithm for Aggregating Node Preferences. Sci. Rep. 2024, 14, 31200. [Google Scholar] [CrossRef]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. 2008. pp. 1–9. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 15 September 2022).
- Wu, H.; Yao, Q.; Liu, Z.; Huang, B.; Zhuang, Y.; Tang, H.; Liu, E. Blockchain for Finance: A Survey. IET Blockchain 2024, 4, 101–123. [Google Scholar] [CrossRef]
- Shakila, M.; Rama, A.; Christy, S.; Kanakala, A.; Lau, C.Y. Hyperledger Fabric and Beyond: A Comprehensive Review of Blockchain Innovations in Supply Chain. AIP Conf. Proc. 2024, 3161, 020306. [Google Scholar]
- Han, H.; Shiwakoti, R.K.; Chen, W. Unlocking Enterprise Blockchain Adoption: A R3 Corda Case Study. J. Gen. Manag. 2024, 50, 03063070241292701. [Google Scholar] [CrossRef]
- Androulaki, E.; Barger, A.; Bortnikov, V.; Cachin, C.; Christidis, K.; De Caro, A.; Enyeart, D.; Ferris, C.; Laventman, G.; Manevich, Y.; et al. Hyperledger Fabric: A Distributed Operating System for Permissioned Blockchains. Proc. EuroSys 2018, 30, 1–15. [Google Scholar]
- Le, D.-P.; Meng, H.; Su, L.; Yeo, S.L.; Thing, V. BIFF: A Blockchain-Based IoT Forensics Framework with Identity Privacy. In Proceedings of the TENCON 2018—IEEE Region 10 Conference, Jeju, Republic of Korea, 28–31 October 2018; pp. 2372–2377. [Google Scholar]
- Trofimov, S.; Voskov, L.; Komarov, M. Decentralized Public Transport Management System Based on Blockchain Technology. Appl. Sci. 2025, 15, 1348. [Google Scholar] [CrossRef]
- Castro, M.; Liskov, B. Practical Byzantine Fault Tolerance. In Proceedings of the Third Symposium on Operating Systems Design and Implementation, New Orleans, LA, USA, 22–25 February 1999. [Google Scholar]
- Ren, X.; Tong, X.; Zhang, W. Improved PBFT Consensus Algorithm Based on Node Role Division. J. Comput. Commun. 2023, 11, 20–38. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, R.; Liu, C.; Xu, C.; Wang, J. An Improved PBFT Consensus Algorithm Based on Grouping and Credit Grading. Sci. Rep. 2023, 13, 13030. [Google Scholar] [CrossRef]
- Hussain, M.; Mehmood, A.; Khan, M.A.; Lloret, J.; Maple, C. Performance Optimized Leader Selection Consensus Algorithm for Consortium Blockchain Using Trust Values of Nodes. In Proceedings of the International Conference on Cooperative Design, Visualization and Engineering, Hangzhou, China, 22–25 October 2023; pp. 253–264. [Google Scholar]
- Gao, S.; Yang, G.; Li, M.; Zhang, L. A Secure and Highly Efficient Blockchain PBFT Consensus Algorithm for Microgrid Electricity Transactions. PeerJ Comput. Sci. 2023, 9, e1100. [Google Scholar]
- Chen, Y.; Li, X.; Zhang, H. An Improved Algorithm for Practical Byzantine Fault Tolerance to Large-Scale Consortium Chain. Inf. Process. Manag. 2022, 59, 102884. [Google Scholar] [CrossRef]
- Hussain, F.; Abbas, S.G.; Fatima, A.; Masood, T.; Khan, M.A. Reputation-Based Leader Selection Consensus Algorithm with Voting Mechanism for Consortium Blockchain. Computers 2023, 12, 20. [Google Scholar]
- Xu, G.; Wang, Y.; Leng, J. Improved PBFT Algorithm Based on Vague Sets. Secur. Commun. Netw. 2022, 2022, 6144664. [Google Scholar] [CrossRef]
- Abishu, H.N.; Seid, A.M.; Yacob, Y.H.; Ayall, T.; Sun, G.; Liu, G. Consensus Mechanism for Blockchain-Enabled Vehicle-to-Vehicle Energy Trading in the Internet of Electric Vehicles. IEEE Trans. Veh. Technol. 2021, 71, 946–960. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of Decision Trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Yu, J.; Qiao, Z.; Tang, W.; Wang, D.; Cao, X. Blockchain-Based ID3 Decision Tree Classification in Distributed Networks. Intell. Autom. Soft Comput. 2021, 29, 713–728. [Google Scholar] [CrossRef]
- Lei, K.; Zhang, Q.; Xu, L.; Qi, Z. Reputation-based Byzantine Fault-Tolerance for Consortium Blockchain. In Proceedings of the 2018 IEEE 24th International Conference on Parallel and Distributed Systems (ICPADS), Singapore, 11–13 December 2018. [Google Scholar]
- Abishu, B.; The, N.B.; Shankar, S. PPoR: A pipelined proof-of-reputation consensus mechanism for enhanced scalability in blockchain. Ann. Telecommun. 2021, 76, 421–432. [Google Scholar]

| Reference | Algorithm Name | Main Improvement | Advantages | Disadvantages |
|---|---|---|---|---|
| Ren et al. [18] | Node Role Division PBFT | Division of nodes into specific roles | Clear role assignment and improved efficiency | Complex role management |
| Liu et al. [19] | Grouping and Credit PBFT | Node grouping and credit grading | Efficient consensus and reduced overhead | Difficulty in accurate initial grouping |
| Hussain et al. [20] | Trust-based Leader Selection PBFT | Leader selection based on node trust | Reduced leader centralization risk, enhanced fault tolerance | Dependence on trust evaluation accuracy |
| Gao et al. [21] | PBFT for Microgrid | Optimized PBFT consensus for electricity transactions | High efficiency, secure energy transactions | Limited to energy transaction scenarios |
| Chen et al. [22] | Large-Scale Consortium PBFT | Improved scalability for large-scale networks | Better scalability, reduced latency | Higher complexity in node management |
| Hussain et al. [23] | Reputation-Voting PBFT | Reputation-based leader selection with voting mechanism | Enhanced fairness and robustness | Complex reputation voting processes |
| Xu et al. [24] | Vague Sets PBFT | Integration of vague sets theory | Improved robustness under uncertainty | Increased computational complexity |
| Abishu et al. [25] | Proof of Power Reputation (PPoR) | Reputation and power-based node selection for V2V energy trading | Efficient consensus, reduced latency, fair node selection mechanism | Complexity in reputation evaluation |
| Node Type | Primary Indicator | Symbol | Weight | Secondary Indicator | Symbol | Weight | Description |
|---|---|---|---|---|---|---|---|
| Excellent Node, Good Node, Ordinary Node | Direct Credit Value | Consensus Credit | Measures a node’s ability to successfully complete consensus processes, reflecting its core contribution. | ||||
| Voting Credit | Evaluates a node’s active participation in voting processes, rewarding successful voting behavior. | ||||||
| Indirect Credit Value | Activity Credit | Assesses the node’s engagement by counting participations as master or consensus node, weighted by recent activity. | |||||
| Incentive Credit | Provides additional rewards based on node credit rankings to stimulate low-credit nodes to perform better. | ||||||
| Historical Credit Value | - | - | - | Reflects the node’s long-term behavioral stability by applying a moving average across T consensus rounds. | |||
| Malicious Node | Historical Credit Value | - | - | - | - | Reduces the historical credit score by half for nodes identified as malicious, penalizing improper behavior. |
| Secondary Indicator | Tertiary Indicator | Symbol | Weight | Description |
|---|---|---|---|---|
| Consensus Credit | Number of successful consensus rounds | - | Successful completion count; more completions enhance the node’s consensus credit | |
| Total number of consensus rounds | - | Total times participated in consensus rounds for normalization | ||
| Voting Credit | Number of successful voting rounds | - | Count of successful voting rounds completed by the node | |
| Total number of voting rounds | - | Total voting participations for normalization | ||
| Active Credit | Number of master node participation | Times the node acted as a master node, with higher weight | ||
| Number of consensus node participations | Times the node was a consensus node, with lower weight | |||
| Incentive Credit | Credit Ranking | - | Node’s current ranking position among all nodes | |
| Number of nodes | - | Total number of nodes participating in consensus |
| Experimental Setup | Configuration |
|---|---|
| Operating System | Windows 10 64-bit Professional Edition |
| Experimental Platform | Python 3.9 |
| Processor | Intel (R) Core (TM) i5-10400 |
| Memory | 16 GB RAM |
| Number of Nodes | 10–60 nodes |
| Network Model | Local area network simulating network latency |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, J.; Wu, X.; Tian, J.; Li, Y. RE-BPFT: An Improved PBFT Consensus Algorithm for Consortium Blockchain Based on Node Credibility and ID3-Based Classification. Appl. Sci. 2025, 15, 7591. https://doi.org/10.3390/app15137591
Ding J, Wu X, Tian J, Li Y. RE-BPFT: An Improved PBFT Consensus Algorithm for Consortium Blockchain Based on Node Credibility and ID3-Based Classification. Applied Sciences. 2025; 15(13):7591. https://doi.org/10.3390/app15137591
Chicago/Turabian StyleDing, Junwen, Xu Wu, Jie Tian, and Yuanpeng Li. 2025. "RE-BPFT: An Improved PBFT Consensus Algorithm for Consortium Blockchain Based on Node Credibility and ID3-Based Classification" Applied Sciences 15, no. 13: 7591. https://doi.org/10.3390/app15137591
APA StyleDing, J., Wu, X., Tian, J., & Li, Y. (2025). RE-BPFT: An Improved PBFT Consensus Algorithm for Consortium Blockchain Based on Node Credibility and ID3-Based Classification. Applied Sciences, 15(13), 7591. https://doi.org/10.3390/app15137591





