Characteristic Analysis of Bump Foil Gas Bearing Under Multi-Physical Field Coupling
Abstract
1. Introduction
2. Theoretical Modeling
2.1. Elastohydrodynamic Theoretical Model of Bump Foil Air Bearing
2.2. Theoretical Model of Temperature
3. Case Study
3.1. Static Characteristics Analysis
3.2. Thermal Characteristic Analysis
4. Conclusions
- (1)
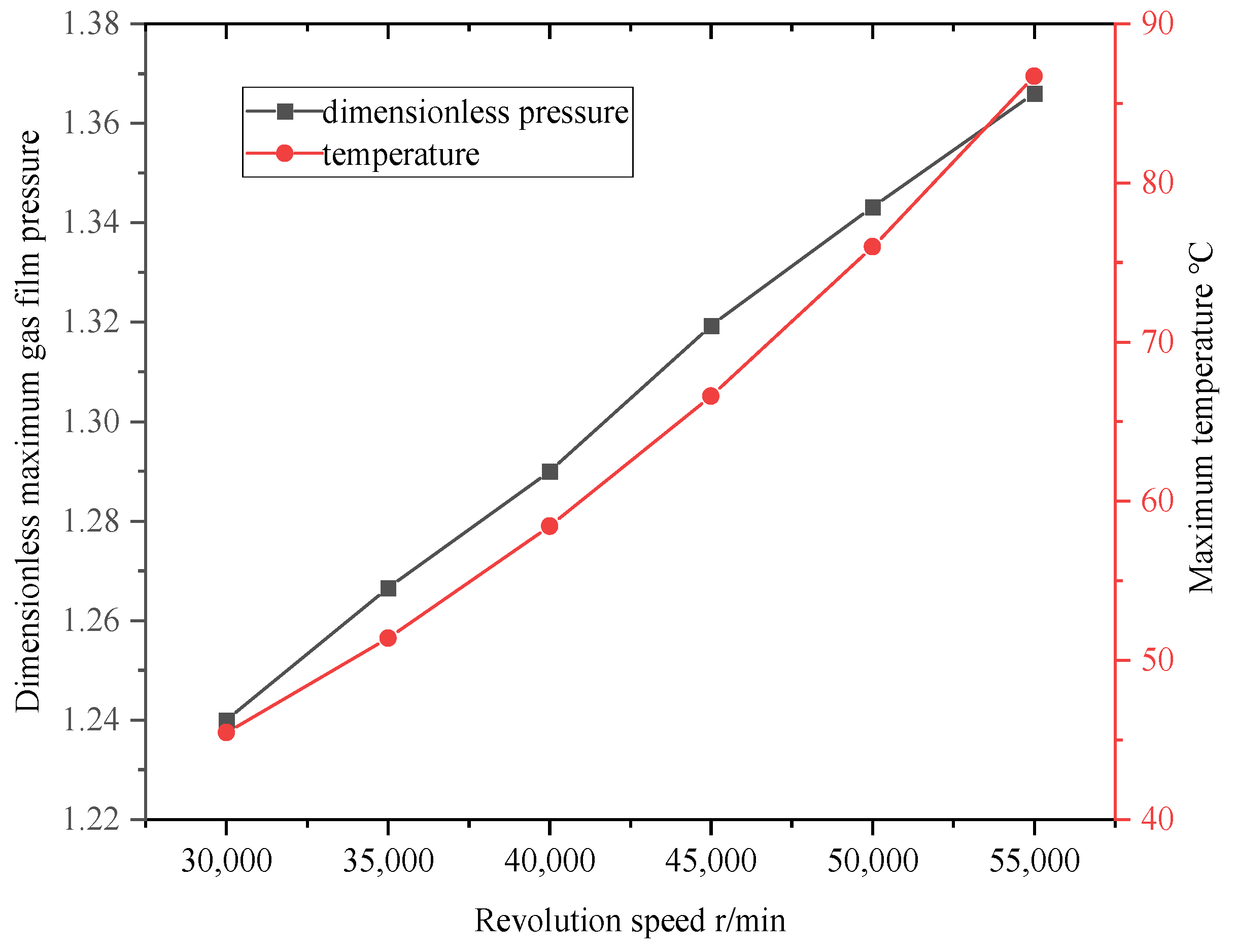
- The friction torque of the air bearing increases linearly with its rotational speed, and changes in eccentricity do not affect the increasing speed; within a certain range, the bearing load increases with the increase in wave foil thickness or the decrease in half-wave foil length. In a certain range, with the increase in journal radius clearance, the bearing load decreases. When under high-eccentricity conditions, the effect of journal radius clearance can be ignored; with increasing speed, the maximum temperature of the air film and the maximum pressure of the air film increase, considering the thermal deformation of the rotor, wave foil, flat foil, and other components caused by the increasing temperature, which restricts the speed of the rotor.
- (2)
- The temperature distribution in the gas film changes significantly along the circumference. In the section from the inlet to the maximum load of the gas film, the temperature of the gas film rises rapidly, after which the temperature decreases due to the decrease in air pressure, and finally, in the negative pressure region, the gas is absorbed, the pressure increases, and the gas reaches the inlet, where it mixes again with the ambient gas and re-enters the bearing. The high-temperature region is concentrated in the load region. Therefore, a cooling gas flow can be passed through the wave foil near the eccentricity angle to achieve a localized cooling effect. Changes in eccentricity lead to changes in the temperature concentration region, and the localized cooling region needs to be changed when the bearing is subjected to different load conditions.
- (3)
- The influence of whether or not the thermal field is considered on the bearing characteristics was investigated. Under the condition of considering the temperature field, the pressure of the air film and the load of the bearing will be somewhat higher than their values under the condition of not considering the temperature field, and the degree of this influence increases with the increase in eccentricity. When the bearing is at a low speed, the maximum temperature of the air film does not change much. Therefore, in the process of practical application, when the bearing is in a low-speed state, one should not consider the temperature conditions for the preliminary assessment of some bearing performance parameters.
- (4)
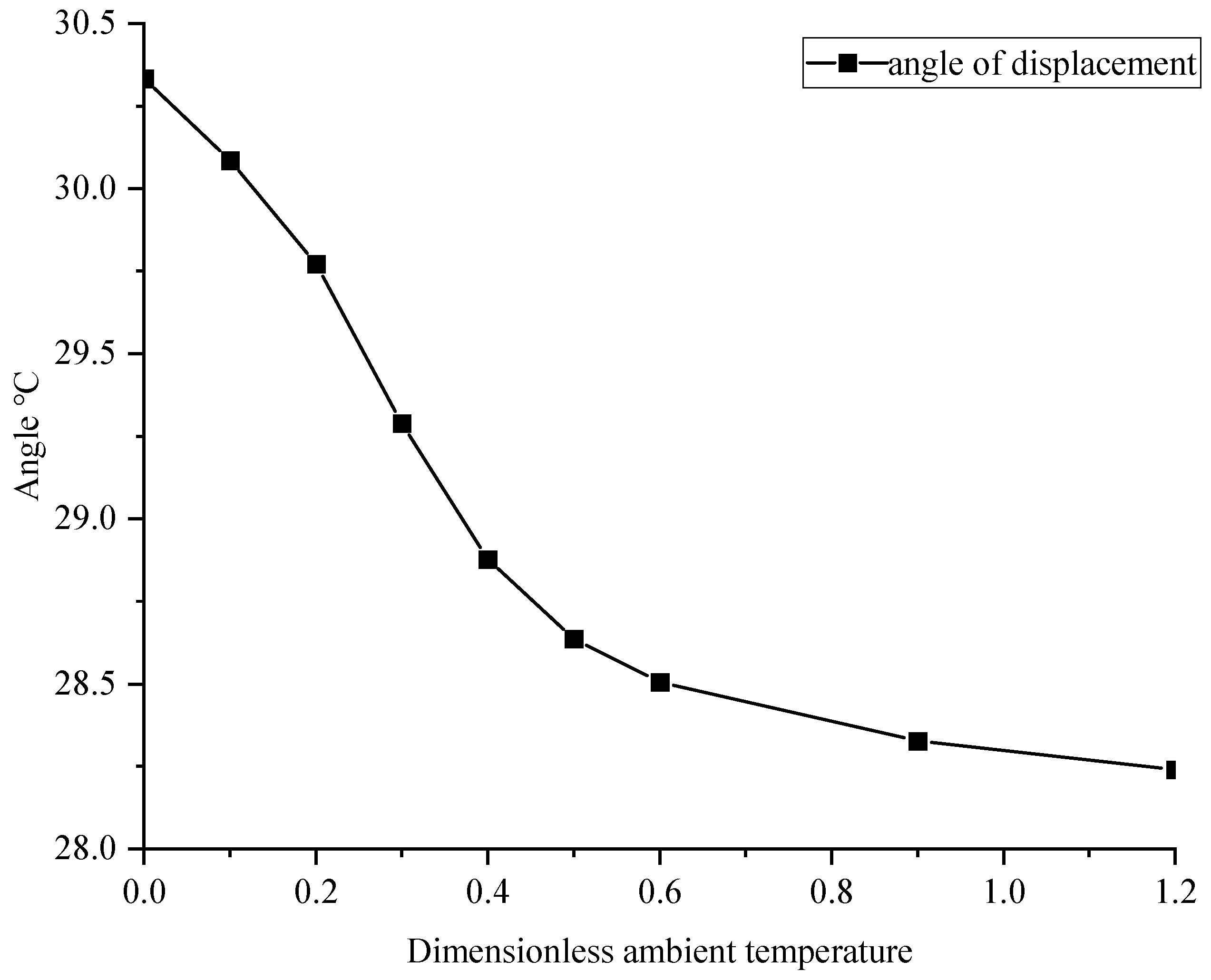
- Bearing load characteristics are affected by different ambient gas temperatures. Within a certain range, as the ambient temperature increases, the maximum gas temperature inside the bearing increases, but the degree of increase gradually decreases, and the degree of increase in load capacity also decreases. With an increase in ambient temperature, the stability of the bearing is improved to a certain extent. Therefore, the temperature difference between the inside and outside of the bearing working area should not be too large, which affects bearing capacity and stability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, W.; Kim, D. Rotordynamics of a rotor supported by foil bearings under various housing excitation. Tribol. Int. 2024, 199, 109956. [Google Scholar] [CrossRef]
- Shi, T.; Wang, H.; Yang, W.; Peng, X. Mathematical modeling and optimization of gas foil bearings-rotor system in hydrogen fuel cell vehicles. Energy 2024, 290, 130129. [Google Scholar] [CrossRef]
- Chakraborty, B.; Biswas, N.; Chakraborti, P. An Investigation to Find the Effects on Air Foil Bearing by the Variation of Foil’s Structural Parameters. J. Sci. Ind. Res. 2023, 82, 603–608. [Google Scholar] [CrossRef]
- Carpino, M.; Peng, J.P. Theoretical performance of a hydrostatic foil bearing. J. Tribol. 1994, 116, 83–89. [Google Scholar] [CrossRef]
- Peng, Z.C.; Khonsari, M.M. On the limiting load-carrying capacity of foil bearings. ASME J. Tribol. 2004, 126, 817–818. [Google Scholar] [CrossRef]
- San Andrés, L.; Kim, T.H. Analysis of gas foil bearings integrating FE top foil models. Tribol. Int. 2009, 42, 111–120. [Google Scholar] [CrossRef]
- Shi, T.; Huang, H.; Peng, X.; Feng, J.; Guo, Y. Experimental study on the static and dynamic performances of gas foil bearings for the centrifugal air compressor used in fuel cell vehicles. Int. J. Energy Res. 2022, 46, 4417–4433. [Google Scholar] [CrossRef]
- Li, W.; Wang, G.; Feng, K.; Zhang, Y.; Wang, P. CFD-based investigation and experimental study on the performances of novel back-flow channel aerostatic bearings. Tribol. Int. 2022, 165, 107319. [Google Scholar] [CrossRef]
- Shahdhaar, M.A.; Yadawad, S.S.; Khamari, D.S.; Behera, S.K. Numerical investigation of slip flow phenomenon on performance characteristics of gas foil journal bearing. SN Appl. Sci. 2020, 2, 1–18. [Google Scholar] [CrossRef]
- Samanta, P.; Murmu, N.C.; Khonsari, M.M. The evolution of foil bearing technology. Tribol. Int. 2019, 135, 305–323. [Google Scholar] [CrossRef]
- Salehi, M.; Swanson, E.; Heshmat, H. Thermal features of compliant foil bearings—Theory and experiments. J. Tribol. 2001, 123, 566–571. [Google Scholar] [CrossRef]
- Lee, D.; Kim, D. Thermohydrodynamic analyses of bump air foil bearings with detailed thermal model of foil structures and rotor. J. Tribol. 2010, 132, 021704. [Google Scholar] [CrossRef]
- Talmage, G.; Carpino, M. Thermal structural effects in a gas-lubricated foil journal bearing. Tribol. Trans. 2011, 5, 701–713. [Google Scholar] [CrossRef]
- Peng, Z.C.; Khonsari, M.M. A thermohydrodynamic analysis of foil journal bearings. J. Tribol. 2006, 128, 534–541. [Google Scholar] [CrossRef]
- San Andrés, L.; Kim, T.H. Thermohydrodynamic analysis of bump type gas foil bearings: A model anchored to test data. J. Eng. Gas Turbines Power 2010, 132, 042504. [Google Scholar] [CrossRef]
- Sim, K.; Kim, T.H. Thermohydrodynamic analysis of bump-type gas foil bearings using bump thermal contact and inlet flow mixing models. Tribol. Int. 2012, 48, 137–148. [Google Scholar] [CrossRef]
- Aksoy, S.; Aksit, M.F. A fully coupled 3D thermo-elastohydrodynamics model for a bump-type compliant foil journal bearing. Tribol. Int. 2015, 82, 110–122. [Google Scholar] [CrossRef]
- Gao, Q.H.; Sun, W.J.; Zhang, J.Z.; Li, J.Z.; Zhang, J.Y. Thermo-Elasto-Hydrodynamic Analysis of Gas Foil Bearing Considering Thermal Effects. Int. J. Mech. Sci. 2025, 288, 110008. [Google Scholar] [CrossRef]
- Jia, H.; Hu, N.; Yin, B.; Zhou, Z.; Xu, B. Research on foil thermal features of hydrodynamic air foil bearing with the Three-dimensional heat transfer model. Therm. Sci. Eng. Prog. 2023, 40, 101737. [Google Scholar] [CrossRef]
- Mahner, M.; Bauer, M.; Schweizer, B. Numerical analyzes and experimental investigations on the fully-coupled thermo-elasto-gasdynamic behavior of air foil journal bearings. Mech. Syst. Signal Process. 2021, 149, 107221. [Google Scholar] [CrossRef]
- Kim, D.; Ki, J.; Kim, Y.; Ahn, K. Extended three-dimensional thermo-hydrodynamic model of radial foil bearing: Case studies on thermal behaviors and dynamic characteristics in gas turbine simulator. Therm. Sci. Eng. Prog. 2012, 134, 052501. [Google Scholar] [CrossRef]
- Li, C.; Du, J.; Yao, Y. Study of load carrying mechanism of a novel three-pad gas foil bearing with multiple sliding beams. Mech. Syst. Signal Process. 2020, 135, 106372. [Google Scholar] [CrossRef]
- Gu, Y.; Lan, X.; Ren, G.; Zhou, M. An efficient three-dimensional foil structure model for bump-type gas foil bearings considering friction. Friction 2021, 9, 1450–1463. [Google Scholar] [CrossRef]
- Xu, Z.; Li, C.; Du, J. Modeling and static characteristics study of the double-layer bump gas foil bearing. Tribol. Int. 2021, 164, 107202. [Google Scholar] [CrossRef]
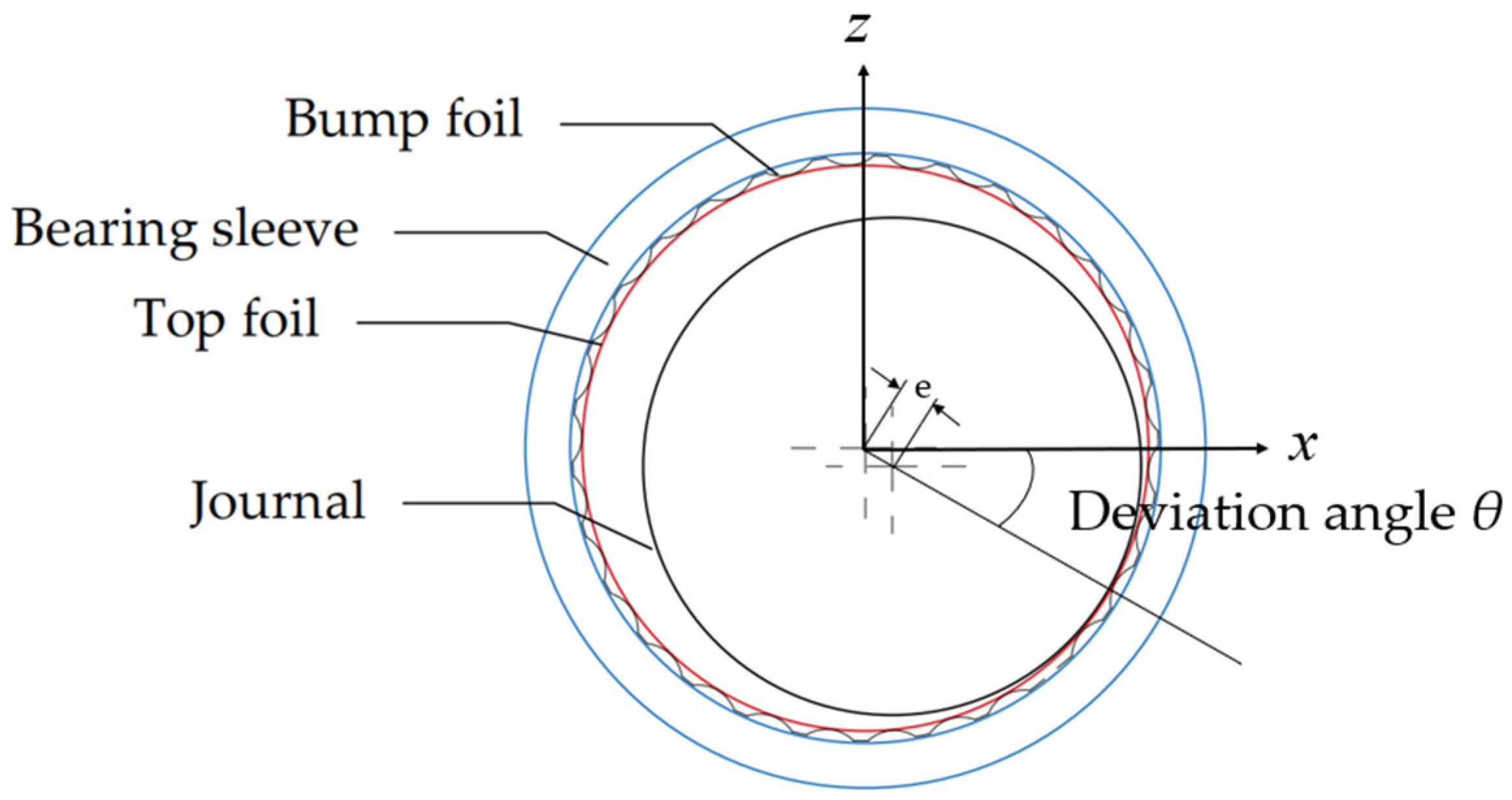

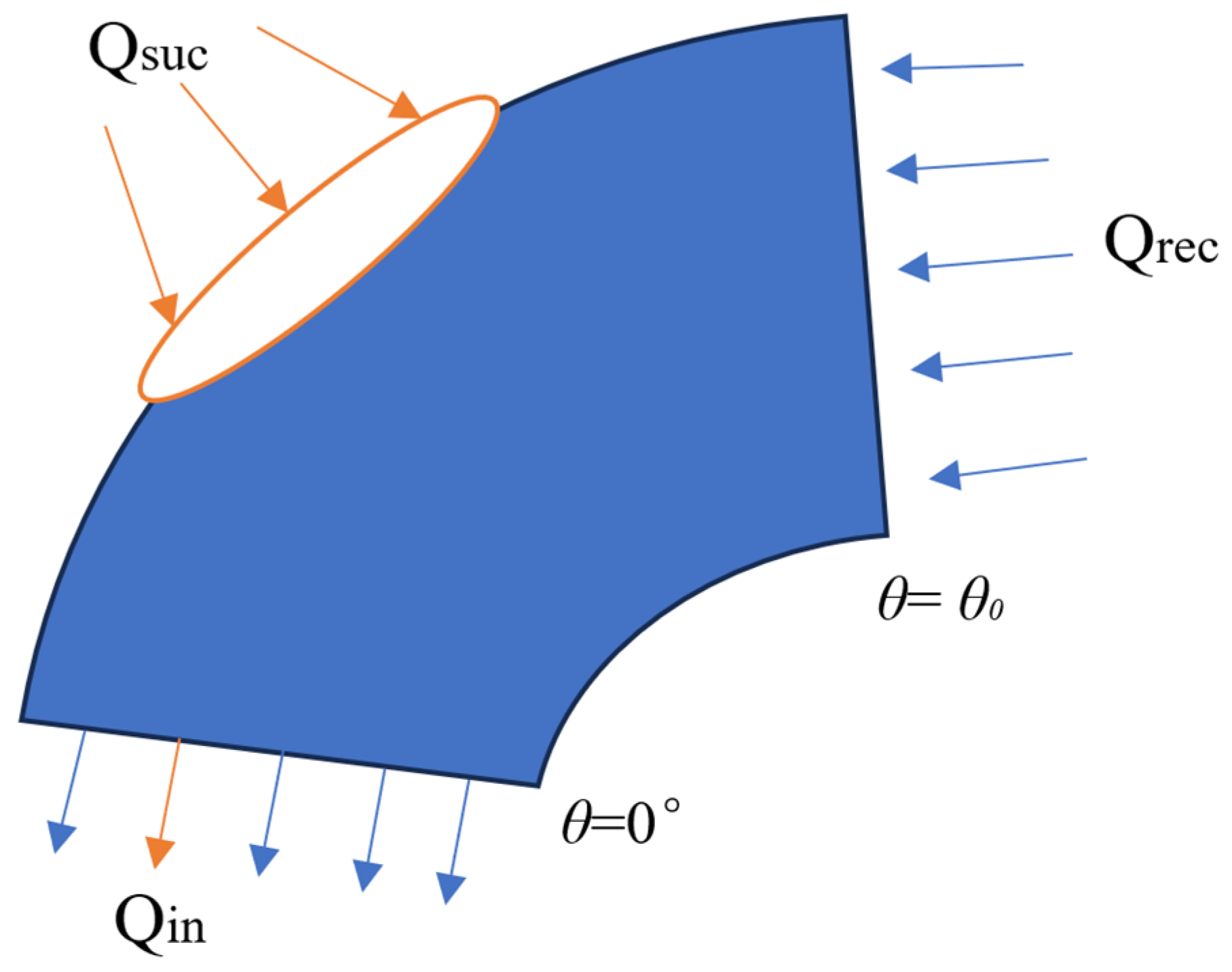





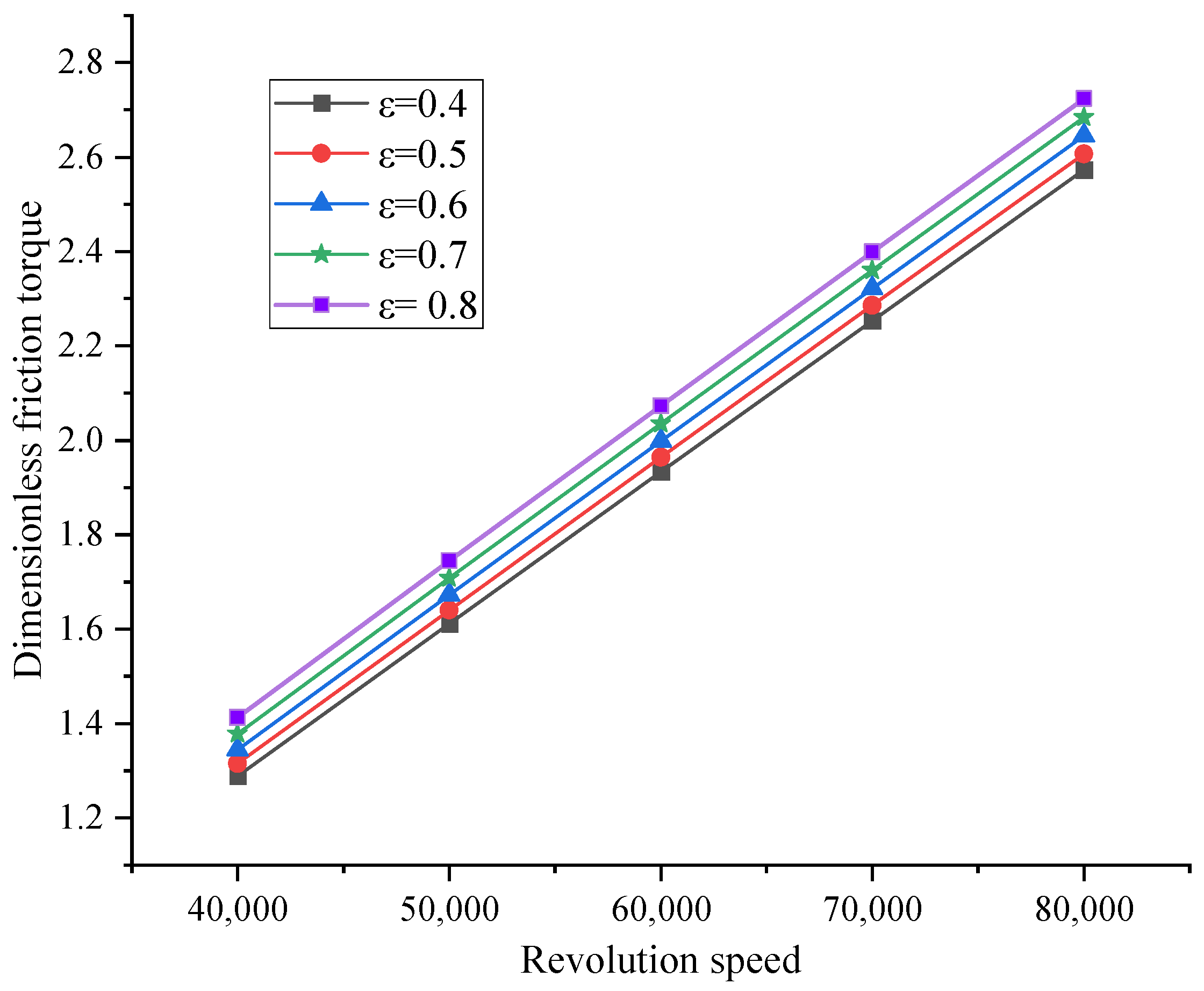

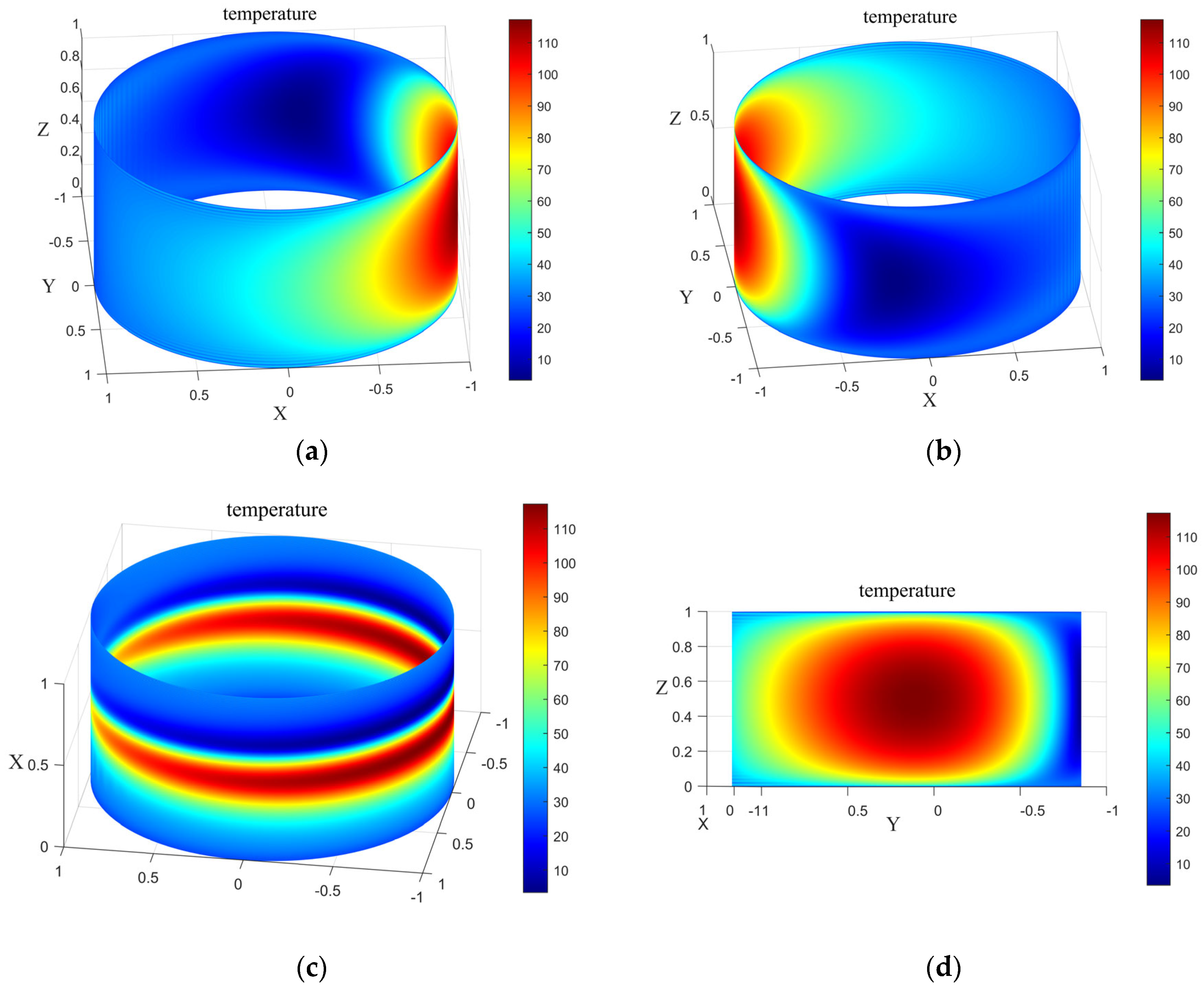




| Parameter | Value |
|---|---|
| R (m) | 5 × 10−2 |
| L (m) | 7.5 × 10−2 |
| C (m) | 1 × 10−4 |
| p0 (Pa) | 1.01325 × 105 |
| Eb (N/m2) | 2.14 × 1011 |
| ν | 0.3 |
| P (Pa) | 1.01325 × 105 |
| s (m) | 4.064 × 10−3 |
| l (m) | 1.717 × 10−3 |
| R0 (m) | 2.655 × 10−3 |
| tb (m) | 7.62 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, D.; Zhu, Z.; Lu, J. Characteristic Analysis of Bump Foil Gas Bearing Under Multi-Physical Field Coupling. Appl. Sci. 2025, 15, 7584. https://doi.org/10.3390/app15137584
Lu D, Zhu Z, Lu J. Characteristic Analysis of Bump Foil Gas Bearing Under Multi-Physical Field Coupling. Applied Sciences. 2025; 15(13):7584. https://doi.org/10.3390/app15137584
Chicago/Turabian StyleLu, Daixing, Zhengjun Zhu, and Junjie Lu. 2025. "Characteristic Analysis of Bump Foil Gas Bearing Under Multi-Physical Field Coupling" Applied Sciences 15, no. 13: 7584. https://doi.org/10.3390/app15137584
APA StyleLu, D., Zhu, Z., & Lu, J. (2025). Characteristic Analysis of Bump Foil Gas Bearing Under Multi-Physical Field Coupling. Applied Sciences, 15(13), 7584. https://doi.org/10.3390/app15137584






