Adaptive Motion Planning Leveraging Speed-Differentiated Prediction for Mobile Robots in Dynamic Environments
Abstract
1. Introduction
2. Related Work
2.1. Perception of Dynamic Obstacles
2.2. Robot Motion Planning in Dynamic Environments
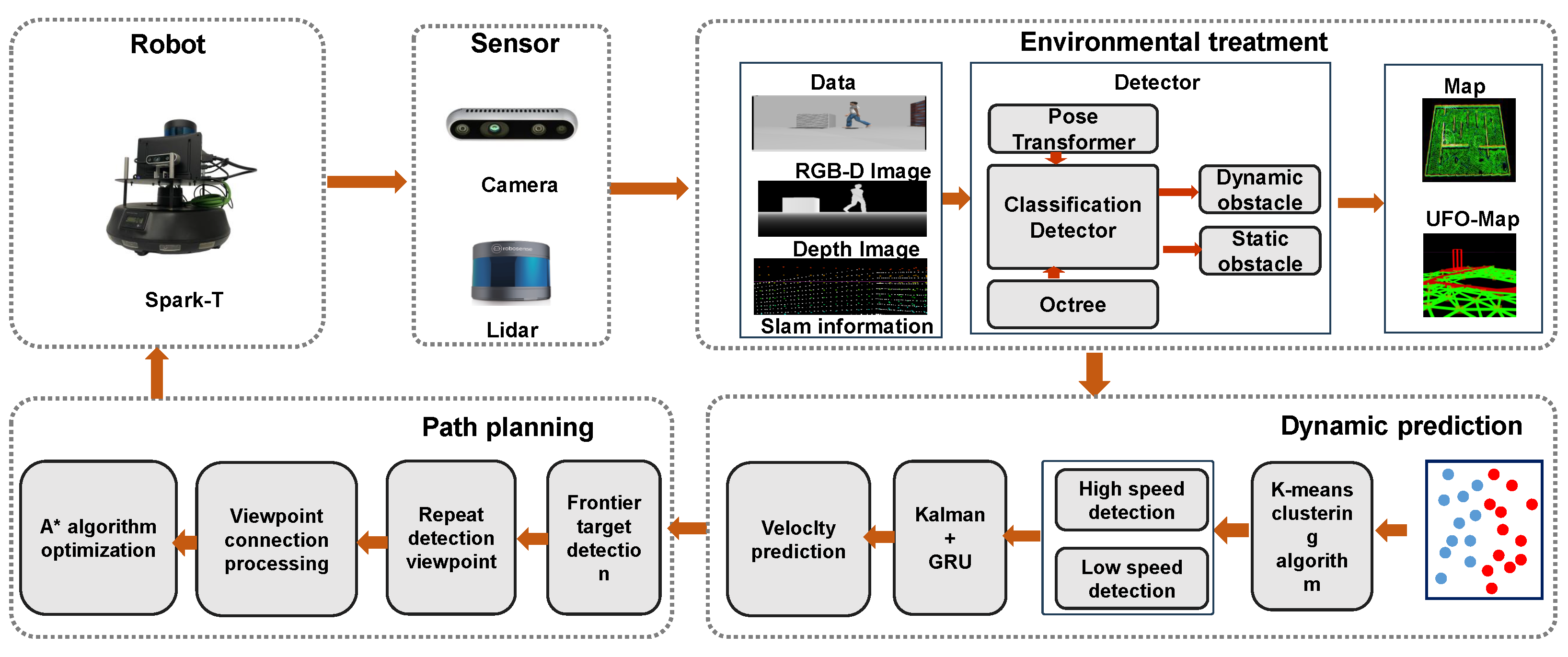
3. Methodology
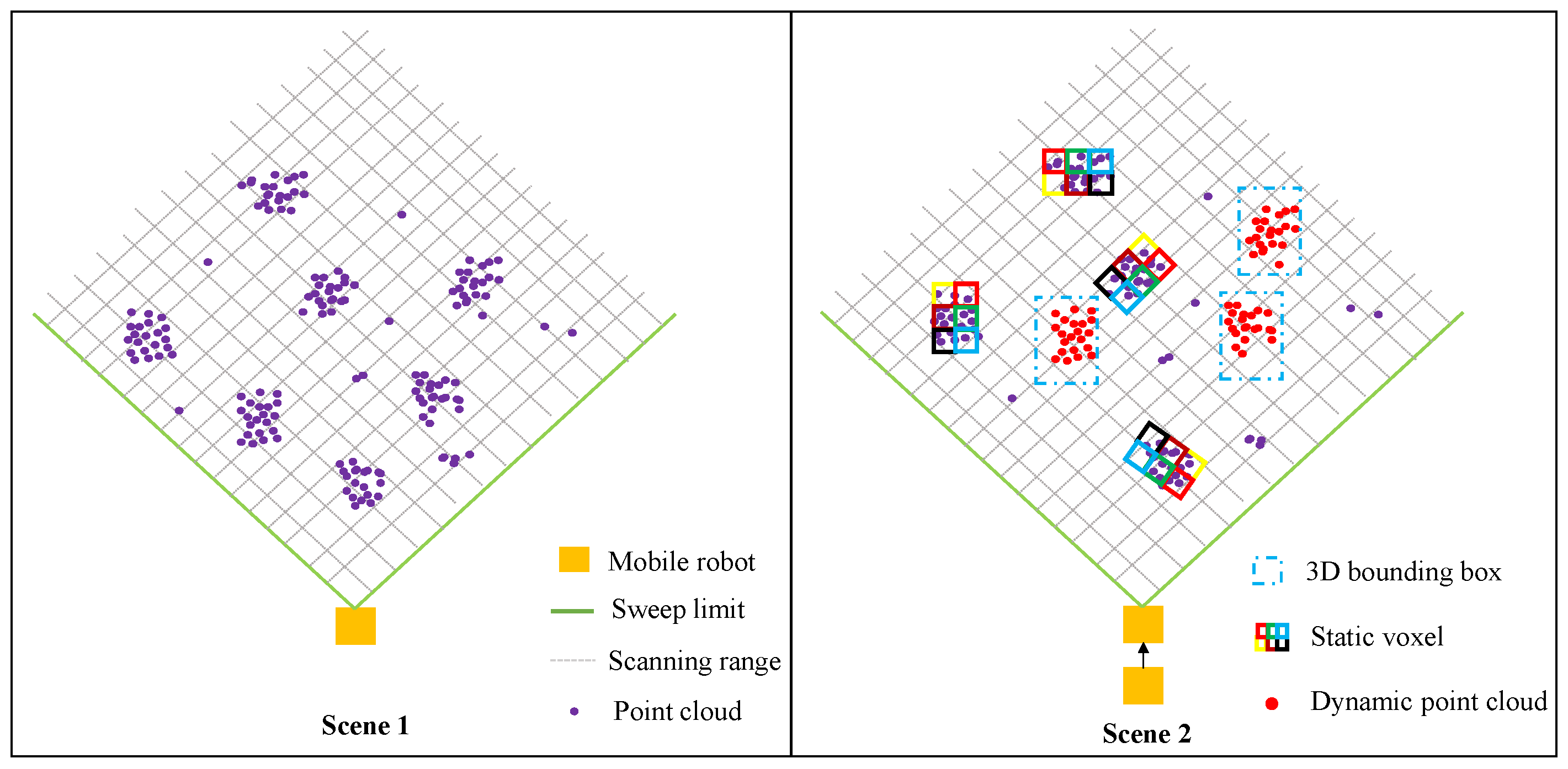
3.1. Environment Map Construction
3.2. Prediction of Obstacles
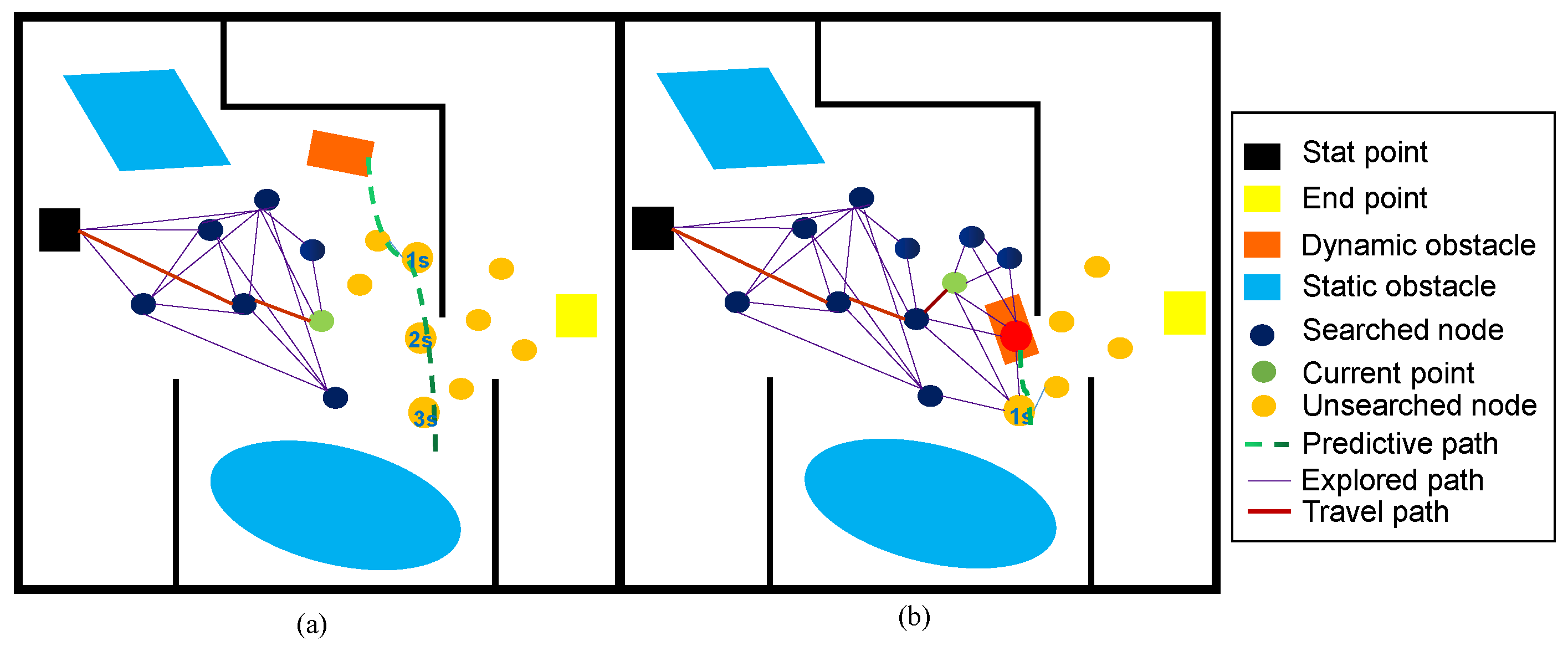
3.3. Motion Planning
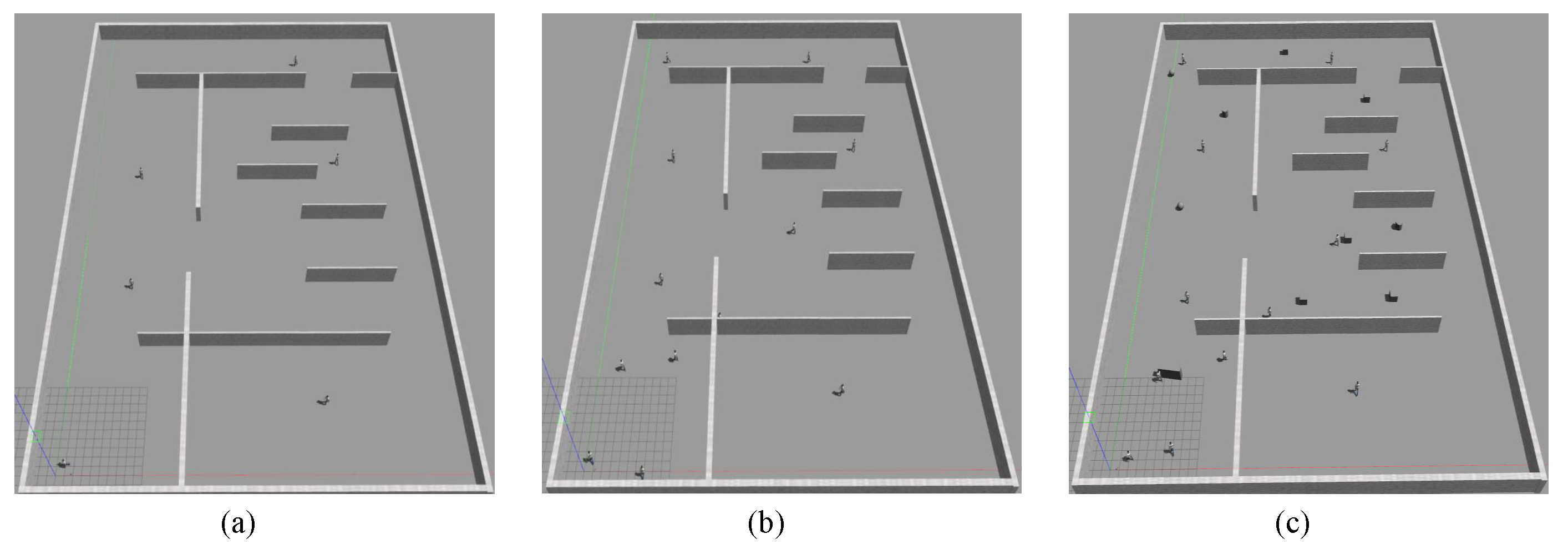
4. Experiments
4.1. Ablation Experiment
- Algorithm 1: This algorithm is derived from the TARE algorithm proposed in [13].
- Algorithm 2: This configuration excludes the prediction algorithm module from the system. The path optimization algorithm is incorporated on top of Algorithm 1 to improve performance.
- Ours: This refers to the algorithm proposed in this paper.
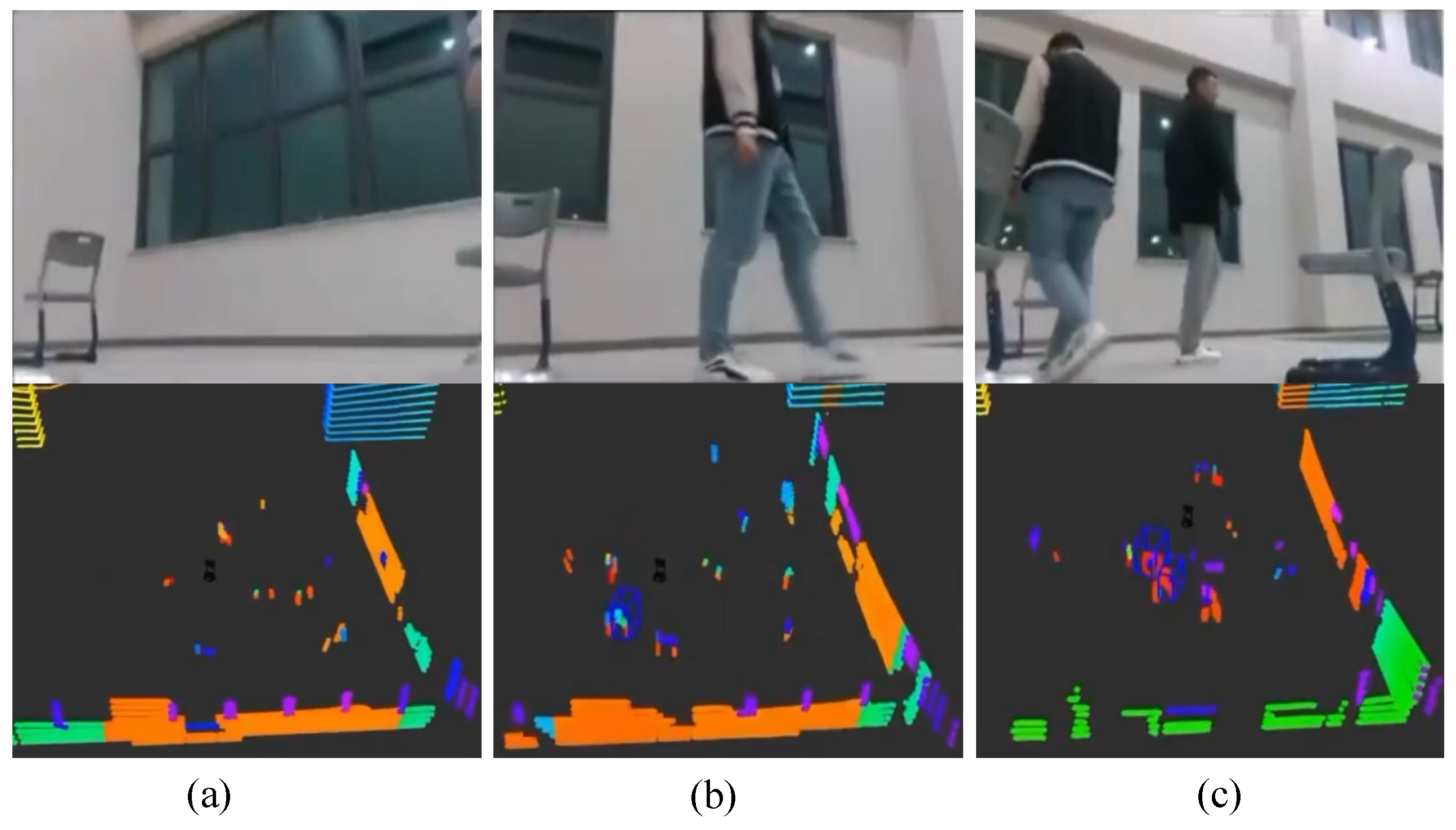
4.2. Experiments on Prediction
4.3. Experiments in the Real World
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roth-Tabak, Y.; Jain, R. Building an environment model using depth information. Computer 1989, 22, 85–90. [Google Scholar] [CrossRef]
- Hornung, A.; Wurm, K.M.; Bennewitz, M.; Stachniss, C.; Burgard, W. OctoMap: An efficient probabilistic 3D mapping framework based on octrees. Auton. Robot. 2013, 34, 189–206. [Google Scholar] [CrossRef]
- Duberg, D.; Jensfelt, P. UFOMap: An Efficient Probabilistic 3D Mapping Framework That Embraces the Unknown. IEEE Robot. Autom. Lett. 2020, 5, 6411–6418. [Google Scholar] [CrossRef]
- Cai, Y.; Kong, F.; Ren, Y.; Zhu, F.; Lin, J.; Zhang, F. Occupancy Grid Mapping Without Ray-Casting for High-Resolution LiDAR Sensors. IEEE Trans. Robot. 2024, 40, 172–192. [Google Scholar] [CrossRef]
- Lin, J.; Zhu, H.; Alonso-Mora, J. Robust Vision-based Obstacle Avoidance for Micro Aerial Vehicles in Dynamic Environments. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–4 June 2020. [Google Scholar]
- He, B.; Li, H.; Wu, S.; Wang, D.; Zhang, Z.; Dong, Q. FAST-Dynamic-Vision: Detection and Tracking Dynamic Objects with Event and Depth Sensing. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 25–29 October 2021; pp. 3071–3078. [Google Scholar] [CrossRef]
- He, J.; Sun, Z.; Cao, N.; Ming, D.; Cai, C. Target Attribute Perception Based UAV Real-Time Task Planning in Dynamic Environments. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023; pp. 888–895. [Google Scholar] [CrossRef]
- Newcombe, R.A.; Izadi, S.; Hilliges, O.; Molyneaux, D.; Kim, D.; Davison, A.J. KinectFusion: Real-time dense surface mapping and tracking. In Proceedings of the 10th IEEE International Symposium on Mixed and Augmented Reality, Basel, Switzerland, 26–29 October 2011; pp. 127–136. [Google Scholar] [CrossRef]
- Eppenberger, T.; Cesari, G.; Dymczyk, M.; Siegwart, R.; Dubé, R. Leveraging Stereo-Camera Data for Real-Time Dynamic Obstacle Detection and Tracking. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 12–16 October 2020; pp. 10528–10535. [Google Scholar] [CrossRef]
- Chen, G.; Dong, W.; Peng, P.; Alonso-Mora, J.; Zhu, X. Continuous Occupancy Mapping in Dynamic Environments Using Particles. IEEE Trans. Robot. 2023, 40, 64–84. [Google Scholar] [CrossRef]
- Yamauchi, B. A frontier-based approach for autonomous exploration. In Proceedings of the 1997 IEEE International Symposium on Computational Intelligence in Robotics and Automation CIRA ’97. “Towards New Computational Principles for Robotics and Automation”, Monterey, CA, USA, 28 July–1 August 1997; pp. 146–151. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, Y.; Chen, X.; Shen, S. FUEL: Fast UAV Exploration Using Incremental Frontier Structure and Hierarchical Planning. IEEE Robot. Autom. Lett. 2021, 6, 779–786. [Google Scholar] [CrossRef]
- Cao, C.; Zhu, H.; Choset, H.; Zhang, J. TARE: A hierarchical framework for efficiently exploring complex 3D environments. Front. Robot. AI Syst. 2021, 5. [Google Scholar] [CrossRef]
- LaValle, S. Rapidly-Exploring Random Trees: A New Tool for Path Planning; Research Report 9811; Department of Computer Science, Iowa State University: Ames, IA, USA, 1998. [Google Scholar]
- Fiorini, P.; Shiller, Z. Motion, planning in dynamic environments using velocity obstacles. Int. J. Robot. Res. 1998, 17, 760–772. [Google Scholar] [CrossRef]
- Malone, N.; Chiang, H.T.; Lesser, K.; Oishi, M.; Tapia, L. Hybrid dynamic moving obstacle avoidance using a stochastic reachable-set-based potential field. IEEE Trans. Robot. 2017, 33, 1121–1138. [Google Scholar] [CrossRef]
- Blackmore, I.; Ono, M.; Williams, B.C. Chance-Constrained Optimal Path Planning With Obstacles. IEEE Trans. Robot. 2011, 27, 1080–1094. [Google Scholar] [CrossRef]
- Wang, T.; Ji, J.; Wang, Q.; Xu, C.; Gao, F. Autonomous Flights in Dynamic Environments with Onboard Vision. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 25–29 October 2021; pp. 1966–1973. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter; University of North Carolina at Chapel Hill Chapel Hill: Chapel Hill, NC, USA, 2006. [Google Scholar]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Aryal, M. Object Detection, Classification, and Tracking for Autonomous Vehicle. Master’s Thesis, Grand Valley State University, Allendale, MI, USA, 2018. [Google Scholar]
- Karatzas, I.; Shreve, S.E. Brownian Motion. In Brownian Motion and Stochastic Calculus; Springer: New York, NY, USA, 1998; pp. 47–127. [Google Scholar]
- Ondruska, P.; Posner, I. Deep Tracking: Seeing Beyond Seeing Using Recurrent Neural Networks. Proc. AAAI Conf. Artif. Intell. 2016, 30, 1. [Google Scholar] [CrossRef]
- Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Fei-Fei, L.; Savarese, S. Social LSTM: Human Trajectory Prediction in Crowded Spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 961–971. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Djuric, P.M. Particle Filtering. IEEE Signal Process. Mag. 2003, 20, 19–38. [Google Scholar] [CrossRef]
- Wan, E.A.; Merwe, R.V.D. The unscented Kalman filter for nonlinear estimation. In Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium (Cat. No.00EX373), Lake Louise, AB, Canada, 10–13 September 2000; pp. 153–158. [Google Scholar]
| Environment | Algorithm | Time(s) | Success Rate (%) | ||
|---|---|---|---|---|---|
| min | avg | max | |||
| Algorithm 1 | 172.3 | 186.7 | 222.5 | 90 | |
| Scenario (a) | Algorithm 2 | 169.4 | 180.2 | 204.3 | 70 |
| Ours | 166.7 | 184.3 | 210.2 | 90 | |
| Algorithm 1 | 197.4 | 208.8 | 230.2 | 60 | |
| Scenario (b) | Algorithm 2 | 186.4 | 210.4 | 226.9 | 40 |
| Ours | 192.6 | 202.3 | 220.4 | 80 | |
| Algorithm 1 | 203.1 | 226.7 | 233.2 | 40 | |
| Scenario (c) | Algorithm 2 | 207.2 | 233.8 | 235.6 | 20 |
| Ours | 208.4 | 221.3 | 238.9 | 60 | |
| Environment | Algorithm | ADE | FDE |
|---|---|---|---|
| Scene1 | ours | 0.024 | 0.053 |
| LSTM [29] | 0.067 | 0.292 | |
| Kalman [19] | 1.250 | 2.033 | |
| Particle filter [30] | 1.250 | 2.033 | |
| UKF [31] | 2.281 | 4.360 | |
| Scene2 | ours | 0.021 | 0.020 |
| LSTM [29] | 0.096 | 0.108 | |
| Kalman [19] | 1.182 | 2.375 | |
| Particle filter [30] | 1.166 | 2.375 | |
| UKF [31] | 2.150 | 5.466 | |
| Scene3 | ours | 0.026 | 0.058 |
| LSTM [29] | 0.110 | 0.298 | |
| Kalman [19] | 1.278 | 2.033 | |
| Particle filter [30] | 1.277 | 2.033 | |
| UKF [31] | 2.208 | 5.784 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Wang, Z.; Hu, J.; Zeng, S.; Liu, X.; Zhang, T. Adaptive Motion Planning Leveraging Speed-Differentiated Prediction for Mobile Robots in Dynamic Environments. Appl. Sci. 2025, 15, 7551. https://doi.org/10.3390/app15137551
Liu T, Wang Z, Hu J, Zeng S, Liu X, Zhang T. Adaptive Motion Planning Leveraging Speed-Differentiated Prediction for Mobile Robots in Dynamic Environments. Applied Sciences. 2025; 15(13):7551. https://doi.org/10.3390/app15137551
Chicago/Turabian StyleLiu, Tengfei, Zihe Wang, Jiazheng Hu, Shuling Zeng, Xiaoxu Liu, and Tan Zhang. 2025. "Adaptive Motion Planning Leveraging Speed-Differentiated Prediction for Mobile Robots in Dynamic Environments" Applied Sciences 15, no. 13: 7551. https://doi.org/10.3390/app15137551
APA StyleLiu, T., Wang, Z., Hu, J., Zeng, S., Liu, X., & Zhang, T. (2025). Adaptive Motion Planning Leveraging Speed-Differentiated Prediction for Mobile Robots in Dynamic Environments. Applied Sciences, 15(13), 7551. https://doi.org/10.3390/app15137551





