Pre Hoc and Co Hoc Explainability: Frameworks for Integrating Interpretability into Machine Learning Training for Enhanced Transparency and Performance
Abstract
1. Introduction
- 1.
- We propose two complementary frameworks for integrating explainability into black-box model training: (i) pre hoc explainability, where a white-box model regularizes the black-box model, and (ii) co hoc explainability, where both models are jointly optimized. These frameworks ensure faithful explanations without post hoc computation overhead and maintain model accuracy.
- 2.
- We extend our frameworks to provide both global and local explanations by incorporating Jensen–Shannon divergence with neighborhood information. Our two-phase approach generates instance-specific explanations that are more stable and faithful than post hoc methods like LIME, while being 30× more computationally efficient at inference time.
- 3.
- We demonstrate through extensive experiments that our frameworks not only improve explainability but also enhance white-box model accuracy by up to 3% through co hoc learning. This finding is particularly valuable for regulated domains like healthcare and finance where interpretable models are mandatory.
2. Related Work
2.1. Explainability Approaches in Machine Learning
2.2. In-Training Explainability Techniques
2.3. Explanation Types and Evaluation
2.4. Factorization Machines
3. Methodology
3.1. Problem Formulation
Enforcing Fidelity
3.2. Pre Hoc Explainability Framework
- 1.
- Train the white-box explainer model on the training data to minimize the binary cross-entropy loss.
- 2.
- Fix the parameters of the explainer model.
- 3.
- Train the black-box predictor model to minimize the combined loss function .
3.3. Co Hoc Explainability Framework
- 1.
- Initialize the parameters of the predictor model and of the explainer model.
- 2.
- For each mini-batch of training data:
- (a)
- Compute the predictions of both models: and .
- (b)
- Calculate the combined loss function .
- (c)
- Update both sets of parameters and using gradient descent.
Comparison of Pre Hoc and Co Hoc Frameworks
3.4. Ensuring Explainer Quality
3.5. Extending to Local Explainability
3.5.1. Local Explainability with Neighborhood Information
3.5.2. Two-Phase Approach for Local Explainability
| Algorithm 1 Testing PHASE 2: Computing Local Explanations | |
| Require: White-box model , input training instances with their true labels y, nearest neighborhood function , number of neighborhood instances k, testing instance | |
▷ Get k-NN to training instance from training set | |
Compute | ▷ Predictions from explainer model |
for All do | ▷ Get predictor outputs for the local training neighbors |
end for | |
▷ initialize local model to the global model | |
for t = 1 to do | |
for All do | |
▷ Get local explainer outputs for the local training neighbors | |
end for | |
Update Local Explainer Loss using Equation (20) | |
▷ Update using gradient descent | |
end for | |
Extract feature importances feature_importances from using Equation (21) and the set of features in the data | |
return feature_importances | |
3.6. Generating Explanations
3.7. Experimental Setup
3.7.1. Datasets
3.7.2. Evaluation Metrics
3.7.3. Implementation Details
4. Results
4.1. Global Explainability Results
4.1.1. Accuracy and Fidelity Trade-Off
4.1.2. Effect of Regularization Parameter
4.2. Local Explainability Results
Comparison with LIME
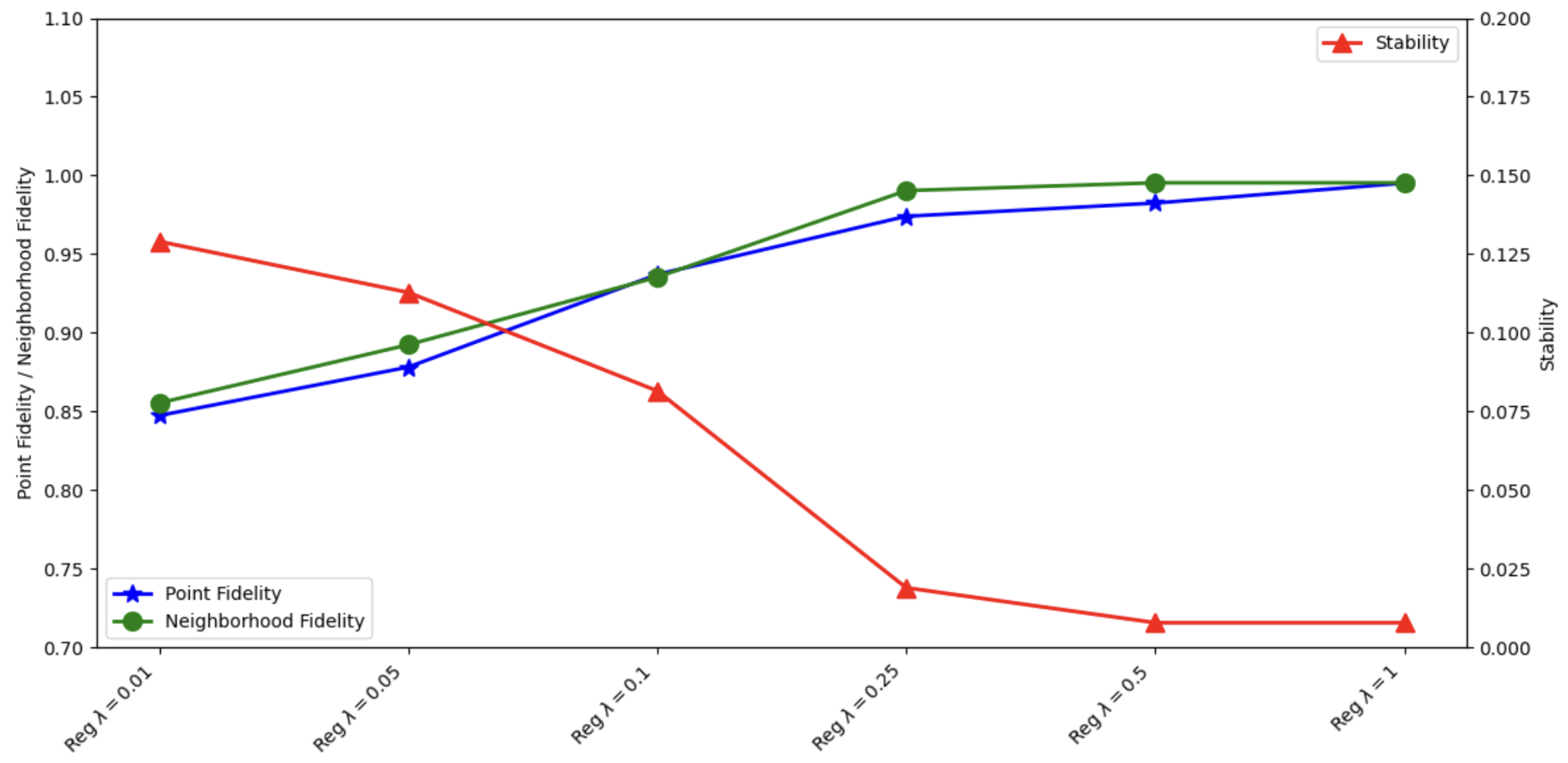
4.3. Effect of Regularization Parameter on Local Explainability Metrics
4.3.1. Effect of Neighborhood Size
4.3.2. Computational Efficiency
4.4. Qualitative Analysis of Explanations
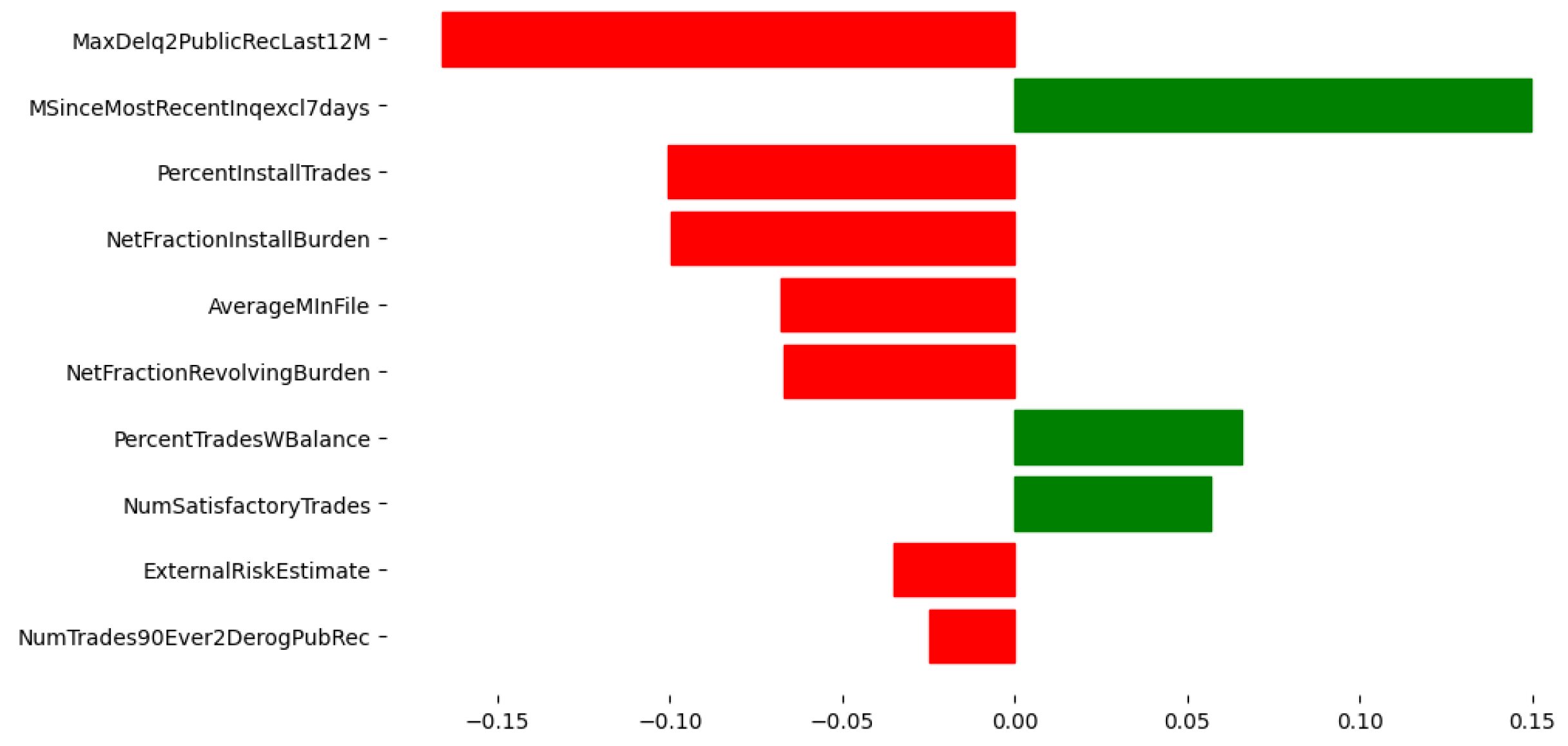
4.4.1. Global Explanations
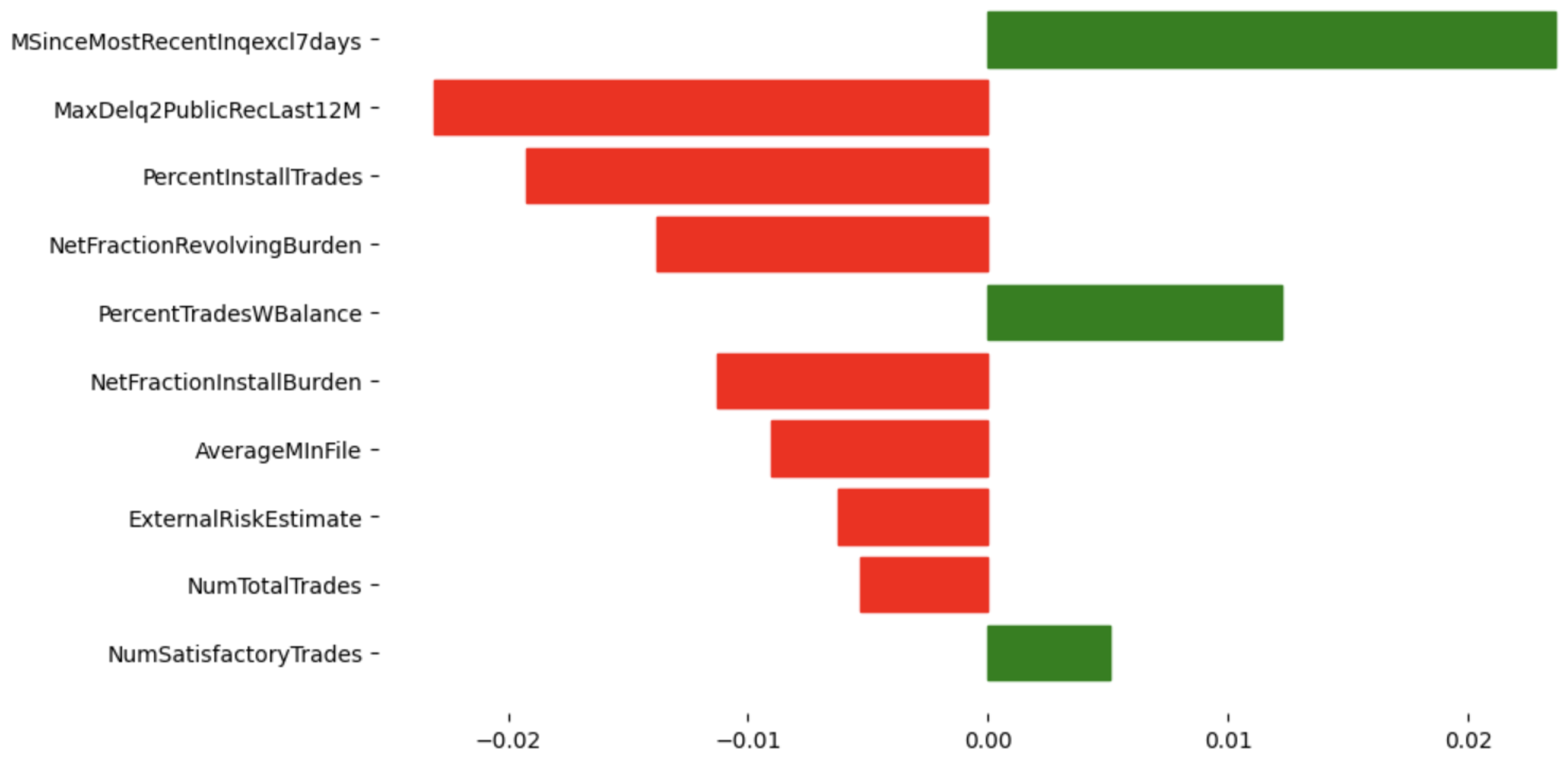
4.4.2. Local Explanations
5. Discussion
Limitations and Future Directions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AUC | Area Under the ROC Curve |
| BB | Black-Box |
| BCE | Binary Cross-Entropy |
| FM | Factorization Machine |
| HELOC | Home Equity Line of Credit |
| JS | Jensen–Shannon |
| KL | Kullback–Leibler |
| LIME | Local Interpretable Model-Agnostic Explanation |
| MAD | Mean Absolute Deviation |
| ROC | Receiver Operating Characteristic |
| SHAP | SHapley Additive exPlanation |
| TV | Total Variation |
| WB | White-Box |
| XAI | eXplainable Artificial Intelligence |
References
- Alvarez-Melis, D.; Jaakkola, T.S. On the Robustness of Interpretability Methods. arXiv 2018, arXiv:1806.08049. [Google Scholar] [CrossRef]
- Adebayo, J.; Gilmer, J.; Muelly, M.; Goodfellow, I.; Hardt, M.; Kim, B. Sanity Checks for Saliency Maps. arXiv 2020, arXiv:1810.03292. [Google Scholar] [CrossRef]
- Ghorbani, A.; Abid, A.; Zou, J. Interpretation of Neural Networks is Fragile. arXiv 2018, arXiv:1710.10547. [Google Scholar] [CrossRef]
- Adadi, A.; Berrada, M. Peeking Inside the Black-Box: A Survey on Explainable Artificial Intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- Doshi-Velez, F.; Kim, B. Towards a Rigorous Science of Interpretable Machine Learning. arXiv 2017, arXiv:1702.08608. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Why should I trust you?: Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Koh, P.W.; Liang, P. Understanding black-box predictions via influence functions. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1885–1894. [Google Scholar]
- Lapuschkin, S.; Wäldchen, S.; Binder, A.; Montavon, G.; Samek, W.; Müller, K.R. Unmasking Clever Hans predictors and assessing what machines really learn. Nat. Commun. 2019, 10, 1096. [Google Scholar] [CrossRef]
- Goodman, B.; Flaxman, S. European union regulations on algorithmic decision-making and a “right to explanation”. AI Mag. 2017, 38, 50–57. [Google Scholar] [CrossRef]
- Wachter, S.; Mittelstadt, B.; Floridi, L. Why a right to explanation of automated decision-making does not exist in the general data protection regulation. Int. Data Priv. Law 2017, 7, 76–99. [Google Scholar] [CrossRef]
- Dwork, C.; Hardt, M.; Pitassi, T.; Reingold, O.; Zemel, R. Fairness through awareness. In Proceedings of the 3rd Innovations in Theoretical Computer Science Conference, Cambridge, MA, USA, 8–10 January 2012; pp. 214–226. [Google Scholar]
- Selbst, A.D.; Barocas, S. The intuitive appeal of explainable machines. Fordham Law Rev. 2018, 87, 1085. [Google Scholar] [CrossRef]
- Bansal, G.; Wu, T.; Zhou, J.; Fok, R.; Nushi, B.; Kamar, E.; Ribeiro, M.T.; Weld, D. Updates in human-ai teams: Understanding and addressing the performance/compatibility tradeoff. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 2429–2437. [Google Scholar]
- Lage, I.; Chen, E.; He, J.; Narayanan, M.; Kim, B.; Gershman, S.; Doshi-Velez, F. An evaluation of the human-interpretability of explanation. arXiv 2019, arXiv:1902.00006. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Advances in Neural Information Processing Systems 30; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2017; pp. 4765–4774. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. Int. J. Comput. Vis. 2019, 128, 336–359. [Google Scholar] [CrossRef]
- Bordt, S.; Finck, M.; Raidl, E.; von Luxburg, U. Post hoc Explanations Fail to Achieve their Purpose in Adversarial Contexts. In Proceedings of the 2022 ACM Conference on Fairness, Accountability, and Transparency, Seoul, Republic of Korea, 21–24 June 2022. [Google Scholar] [CrossRef]
- Slack, D.; Hilgard, S.; Jia, E.; Singh, S.; Lakkaraju, H. Fooling LIME and SHAP: Adversarial Attacks on Post Hoc Explanation Methods. In Proceedings of the AAAI/ACM Conference on AI, Ethics, and Society, AIES’20, New York, NY, USA, 7–8 February 2020; pp. 180–186. [Google Scholar] [CrossRef]
- Alvarez-Melis, D.; Jaakkola, T.S. Towards Robust Interpretability with Self-Explaining Neural Networks. arXiv 2018, arXiv:1806.07538. [Google Scholar] [CrossRef]
- Ghorbani, A.; Wexler, J.; Zou, J.Y.; Kim, B. Towards Automatic Concept-based Explanations. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: New York, NY, USA, 2019; Volume 32. [Google Scholar]
- Rudin, C. Stop Explaining Black Box Machine Learning Models for High Stakes Decisions and Use Interpretable Models Instead. arXiv 2019, arXiv:1811.10154. [Google Scholar] [CrossRef]
- Acun, C.; Nasraoui, O. In-Training Explainability Frameworks: A Method to Make Black-Box Machine Learning Models More Explainable. In Proceedings of the 2023 IEEE/WIC International Conference on Web Intelligence and Intelligent Agent Technology (WI-IAT), Venice, Italy, 26–29 October 2023; pp. 230–237. [Google Scholar] [CrossRef]
- Acun, C.; Ashary, A.; Popa, D.O.; Nasraoui, O. Enhancing Robotic Grasp Failure Prediction Using A Pre hoc Explainability Framework. In Proceedings of the 2024 IEEE 20th International Conference on Automation Science and Engineering (CASE), Bari, Italy, 28 August–1 September 2024; pp. 1993–1998. [Google Scholar] [CrossRef]
- Laugel, T.; Lesot, M.J.; Marsala, C.; Renard, X.; Detyniecki, M. The Dangers of Post hoc Interpretability: Unjustified Counterfactual Explanations. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI-19, International Joint Conferences on Artificial Intelligence Organization, Macao, China, 10–16 August 2019; pp. 2801–2807. [Google Scholar] [CrossRef]
- Neter, J.; Kutner, M.H.; Nachtsheim, C.J.; Wasserman, W. Applied Linear Statistical Models; Irwin: Chicago, IL, USA, 1996. [Google Scholar]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; Wadsworth & Brooks/Cole Advanced Books & Software: Monterey, CA, USA, 1984. [Google Scholar]
- Abdollahi, B.; Nasraoui, O. Explainable matrix factorization for collaborative filtering. In Proceedings of the 25th International Conference Companion on World Wide Web, Montreal, QC, Canada, 11–15 May 2016; pp. 5–6. [Google Scholar]
- Ras, G.; Ambrogioni, L.; Haselager, P.; van Gerven, M.A.J.; Güçlü, U. Explainable 3D Convolutional Neural Networks by Learning Temporal Transformations. arXiv 2020, arXiv:2006.15983. [Google Scholar] [CrossRef]
- Fauvel, K.; Lin, T.; Masson, V.; Fromont, É.; Termier, A. XCM: An Explainable Convolutional Neural Network for Multivariate Time Series Classification. arXiv 2020, arXiv:2009.04796. [Google Scholar] [CrossRef]
- Miao, S.; Liu, M.; Li, P. Interpretable and Generalizable Graph Learning via Stochastic Attention Mechanism. arXiv 2022, arXiv:2201.12987. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Wu, M.; Hughes, M.C.; Parbhoo, S.; Zazzi, M.; Roth, V.; Doshi-Velez, F. Beyond Sparsity: Tree Regularization of Deep Models for Interpretability. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence and Thirtieth Innovative Applications of Artificial Intelligence Conference and Eighth AAAI Symposium on Educational Advances in Artificial Intelligence, AAAI’18/IAAI’18/EAAI’18, New Orleans, LA, USA, 2–7 February 2018; AAAI Press: Washington, DC, USA, 2018. [Google Scholar]
- Lipton, Z.C. The Mythos of Model Interpretability. arXiv 2017, arXiv:1606.03490. [Google Scholar] [CrossRef]
- Chen, J.; Song, L.; Wainwright, M.J.; Jordan, M.I. Learning to Explain: An Information-Theoretic Perspective on Model Interpretation. arXiv 2018, arXiv:1802.07814. [Google Scholar] [CrossRef]
- Ross, A.S.; Hughes, M.C.; Doshi-Velez, F. Right for the Right Reasons: Training Differentiable Models by Constraining their Explanations. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, IJCAI-17, Melbourne, Australia, 19–25 August 2017; pp. 2662–2670. [Google Scholar] [CrossRef]
- Lee, G.H.; Alvarez-Melis, D.; Jaakkola, T.S. Game-Theoretic Interpretability for Temporal Modeling. arXiv 2018, arXiv:1807.00130. [Google Scholar] [CrossRef]
- Lee, G.H.; Jin, W.; Alvarez-Melis, D.; Jaakkola, T. Functional Transparency for Structured Data: A Game-Theoretic Approach. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Plumb, G.; Al-Shedivat, M.; Cabrera, A.A.; Perer, A.; Xing, E.; Talwalkar, A. Regularizing Black-box Models for Improved Interpretability. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: New York, NY, USA, 2020; Volume 33, pp. 10526–10536. [Google Scholar]
- Sarkar, A.; Vijaykeerthy, D.; Sarkar, A.; Balasubramanian, V.N. A Framework for Learning Ante hoc Explainable Models via Concepts. arXiv 2021, arXiv:2108.11761. [Google Scholar] [CrossRef]
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Giannotti, F.; Pedreschi, D. A survey of methods for explaining black box models. ACM Comput. Surv. (CSUR) 2018, 51, 1–42. [Google Scholar] [CrossRef]
- Letham, B.; Rudin, C.; McCormick, T.H.; Madigan, D. Interpretable classifiers using rules and Bayesian analysis: Building a better stroke prediction model. Ann. Appl. Stat. 2015, 9, 1350–1371. [Google Scholar] [CrossRef]
- Sundararajan, M.; Najmi, A. Many shapley values. arXiv 2020, arXiv:2002.12296. [Google Scholar]
- Kim, B.; Wattenberg, M.; Gilmer, J.; Cai, C.; Wexler, J.; Viegas, F.; Sayres, R. Interpretability Beyond Feature Attribution: Quantitative Testing with Concept Activation Vectors (TCAV). In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 2668–2677. [Google Scholar]
- Bien, J.; Tibshirani, R. Prototype selection for interpretable classification. Ann. Appl. Stat. 2011, 5, 2403–2424. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Anchors: High-Precision Model-Agnostic Explanations. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Van Looveren, A.; Klaise, J. Global aggregations of local explanations for black box models. In Proceedings of the ECML PKDD 2019 Workshop on Automating Data Science, Würzburg, Germany, 16–20 September 2019. [Google Scholar]
- Caruana, R.; Lou, Y.; Gehrke, J.; Koch, P.; Sturm, M.; Elhadad, N. Intelligible models for healthcare: Predicting pneumonia risk and hospital 30-day readmission. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 1721–1730. [Google Scholar]
- Tonekaboni, S.; Joshi, S.; McCradden, M.D.; Goldenberg, A. What clinicians want: Contextualizing explainable machine learning for clinical end use. In Proceedings of the Machine Learning for Healthcare Conference, Ann Arbor, MI, USA, 8–10 August 2019; pp. 359–380. [Google Scholar]
- Bhatt, U.; Xiang, A.; Sharma, S.; Weller, A.; Taly, A.; Jia, Y.; Ghosh, J.; Puri, R.; Moura, J.M.; Eckersley, P. Explainable machine learning in deployment. In Proceedings of the 2020 Conference on Fairness, Accountability, and Transparency, Barcelona, Spain, 27–30 January 2020; pp. 648–657. [Google Scholar]
- Rendle, S. Factorization Machines. In Proceedings of the 2010 IEEE International Conference on Data Mining, ICDM ’10, Sydney, Australia, 13–17 December 2010; pp. 995–1000. [Google Scholar] [CrossRef]
- Lan, L.; Geng, Y. Accurate and Interpretable Factorization Machines. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 4139–4146. [Google Scholar] [CrossRef]
- Anelli, V.W.; Noia, T.D.; Sciascio, E.D.; Ragone, A.; Trotta, J. How to Make Latent Factors Interpretable by Feeding Factorization Machines with Knowledge Graphs. In Lecture Notes in Computer Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 38–56. [Google Scholar] [CrossRef]
- Xiao, J.; Ye, H.; He, X.; Zhang, H.; Wu, F.; Chua, T.S. Attentional Factorization Machines: Learning the Weight of Feature Interactions via Attention Networks. In Proceedings of the 26th International Joint Conference on Artificial Intelligence, IJCAI’17, Melbourne, Australia, 19–25 August 2017; AAAI Press: Washington, DC, USA, 2017; pp. 3119–3125. [Google Scholar]
- Nielsen, F.; Boltz, S. The Burbea-Rao and Bhattacharyya Centroids. IEEE Trans. Inf. Theory 2011, 57, 5455–5466. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Information theory and statistics. Elem. Inf. Theory 1991, 1, 279–335. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- FICO. The FICO HELOC Dataset. Available online: https://www.kaggle.com/datasets/averkiyoliabev/home-equity-line-of-creditheloc (accessed on 15 December 2023).
- GroupLens. MovieLens 100K Dataset. Available online: https://grouplens.org/datasets/movielens/100k/ (accessed on 15 December 2023).
- GroupLens. MovieLens 1M Dataset. Available online: https://grouplens.org/datasets/movielens/1M/ (accessed on 15 December 2023).
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. arXiv 2019, arXiv:1912.01703. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar] [CrossRef]

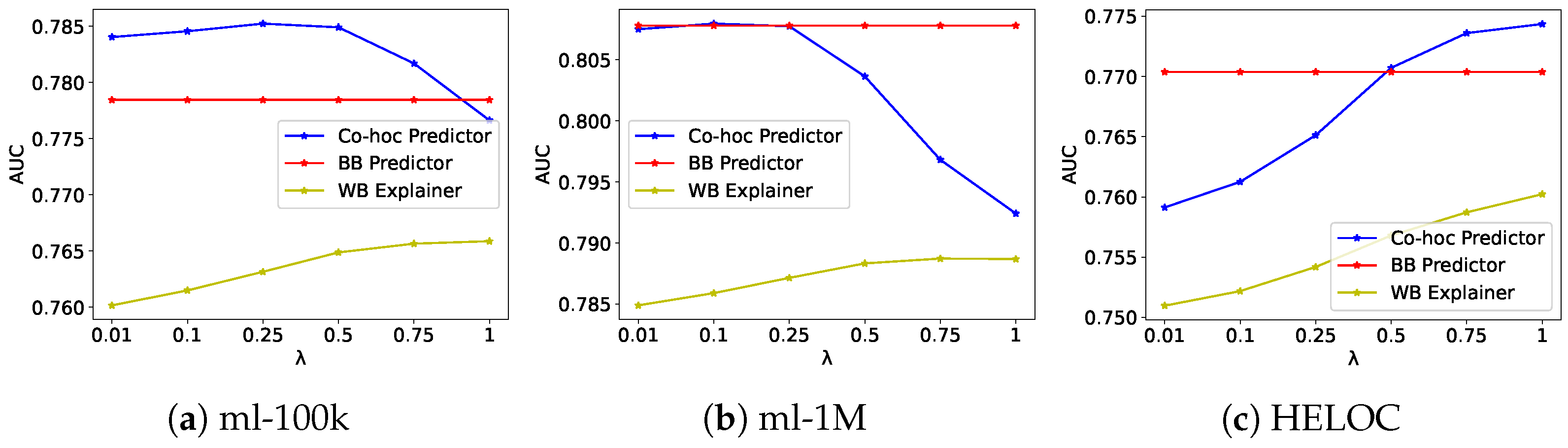
| Model | ML-100k | ML-1M | HELOC | |||
|---|---|---|---|---|---|---|
| AUC ↑ | Fidelity ↑ | AUC ↑ | Fidelity ↑ | AUC ↑ | Fidelity ↑ | |
| Explainer (WB) | 0.7655 ± 0.0042 | - | 0.7882 ± 0.0038 | - | 0.7616 ± 0.0051 | - |
| Original (BB) | 0.7784 ± 0.0039 | 0.8287 ± 0.0156 | 0.8078 ± 0.0041 | 0.8875 ± 0.0143 | 0.7703 ± 0.0048 | 0.7728 ± 0.0187 |
| Pre hoc (BB) | 0.7801 ± 0.0037 | 0.9094 ± 0.0098 | 0.8033 ± 0.0044 | 0.9404 ± 0.0076 | 0.7698 ± 0.0046 | 0.8454 ± 0.0134 |
| Co hoc (BB) | 0.7816 ± 0.0035 | 0.9194 ± 0.0087 | 0.8036 ± 0.0042 | 0.9484 ± 0.0065 | 0.7743 ± 0.0044 | 0.8572 ± 0.0121 |
| Explanation Method | Point Fidelity ↑ | Neighborhood Fidelity ↑ | Stability ↓ |
|---|---|---|---|
| LIME | 0.6083 ± 0.0050 | 0.6600 ± 0.1939 | 0.2152 ± 0.0175 |
| Pre hoc Framework | 0.8270 ± 0.0260 | 0.9587 ± 0.0766 | 0.0623 ± 0.0110 |
| Co hoc Framework | 0.8300 ± 0.0240 | 0.9647 ± 0.0575 | 0.0502 ± 0.0087 |
| Explanation Method | Point Fidelity ↑ | Neighborhood Fidelity ↑ | Stability ↓ |
|---|---|---|---|
| No-regularization | 0.8183 ± 0.3524 | 0.8050 ± 0.1268 | 0.3524 ± 0.0175 |
| Reg | 0.8473 ± 0.0351 | 0.8553 ± 0.1158 | 0.1290 ± 0.0010 |
| Reg | 0.8781 ± 0.0195 | 0.8923 ± 0.1043 | 0.1128 ± 0.0009 |
| Reg | 0.9370 ± 0.0230 | 0.9353 ± 0.0737 | 0.0815 ± 0.0019 |
| Reg | 0.9740 ± 0.0237 | 0.9903 ± 0.0329 | 0.0189 ± 0.0041 |
| Reg | 0.9824 ± 0.0234 | 0.9953 ± 0.0215 | 0.0078 ± 0.0010 |
| Reg | 0.9951 ± 0.0117 | 0.9953 ± 0.0215 | 0.0078 ± 0.0010 |
| Neighborhood Size | Neighborhood Fidelity ↑ | Stability ↓ | Computation Time (s) |
|---|---|---|---|
| 0.8833 ± 0.1939 | 0.2152 ± 0.0175 | 0.0121 ± 0.0014 | |
| 0.9350 ± 0.0381 | 0.0505 ± 0.0098 | 0.0127 ± 0.0009 | |
| 0.9670 ± 0.0013 | 0.0015 ± 0.00006 | 0.0144 ± 0.0061 |
| Method | Additional Training Time (s) | Avg Explanation Time (s) | Total Time for Single Instance (s) | Total Time for 100 Instances (s) |
|---|---|---|---|---|
| LIME | - | 0.3812 ± 0.0828 | 0.3812 ± 0.0828 | 62.580 |
| Pre hoc | 5.1020 ± 0.0315 | 0.0110 ± 0.0015 | 5.1130 ± 0.0330 | 6.202 |
| Co hoc | 5.3960 ± 0.0330 | 0.0135 ± 0.0030 | 5.4095 ± 0.0360 | 6.746 |
| Method | Additional Training Time (s) | Avg Explanation Time (s) | Total Time for Single Instance (s) | Total Time for 100 Instances (s) |
|---|---|---|---|---|
| LIME | - | 0.4523 ± 0.0912 | 0.4523 ± 0.0912 | 45.23 |
| Pre hoc | 8.989 ± 0.595 | 0.0186 ± 0.0013 | 9.0076 ± 0.5963 | 10.849 |
| Co hoc | 9.383 ± 0.623 | 0.0211 ± 0.0028 | 9.4041 ± 0.6258 | 11.493 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acun, C.; Nasraoui, O. Pre Hoc and Co Hoc Explainability: Frameworks for Integrating Interpretability into Machine Learning Training for Enhanced Transparency and Performance. Appl. Sci. 2025, 15, 7544. https://doi.org/10.3390/app15137544
Acun C, Nasraoui O. Pre Hoc and Co Hoc Explainability: Frameworks for Integrating Interpretability into Machine Learning Training for Enhanced Transparency and Performance. Applied Sciences. 2025; 15(13):7544. https://doi.org/10.3390/app15137544
Chicago/Turabian StyleAcun, Cagla, and Olfa Nasraoui. 2025. "Pre Hoc and Co Hoc Explainability: Frameworks for Integrating Interpretability into Machine Learning Training for Enhanced Transparency and Performance" Applied Sciences 15, no. 13: 7544. https://doi.org/10.3390/app15137544
APA StyleAcun, C., & Nasraoui, O. (2025). Pre Hoc and Co Hoc Explainability: Frameworks for Integrating Interpretability into Machine Learning Training for Enhanced Transparency and Performance. Applied Sciences, 15(13), 7544. https://doi.org/10.3390/app15137544







