The Simulation of Grouting Behavior in the Pea Gravel Filling Layer Behind a Double-Shield TBM Based on the Level Set Method
Abstract
1. Introduction
2. Numerical Model for Grout Permeability in Backfilling Layers
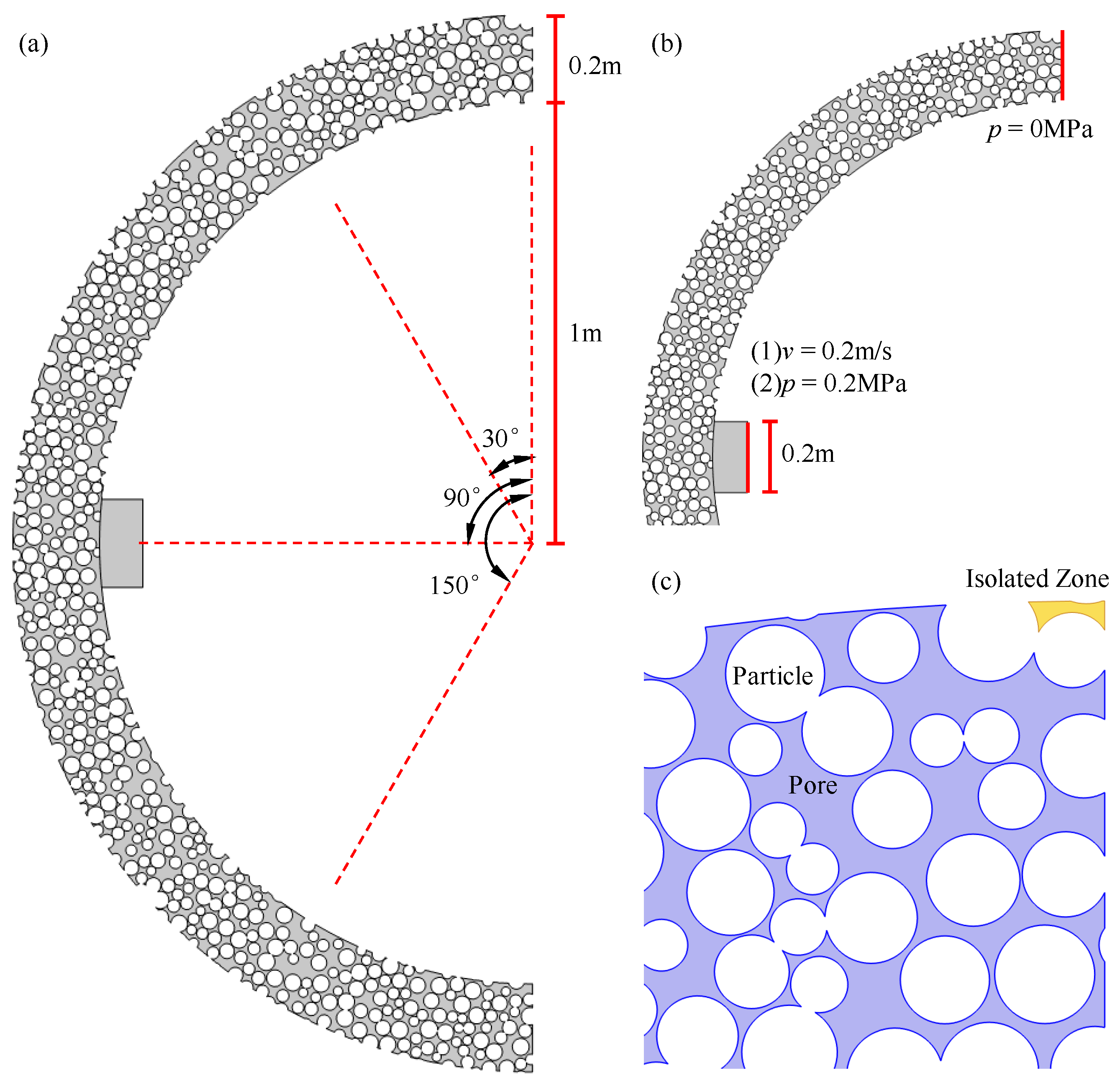
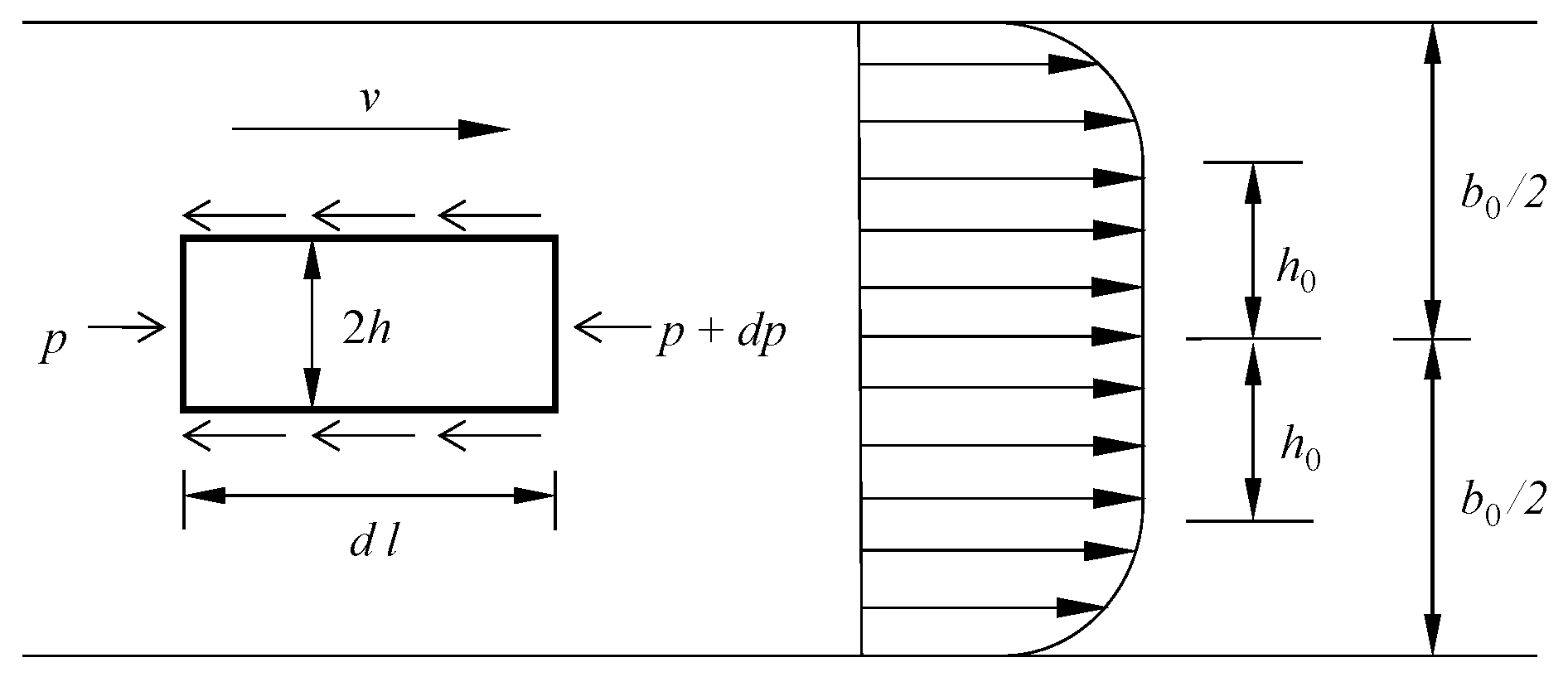
2.1. Modeling Strategy and Computational Methods
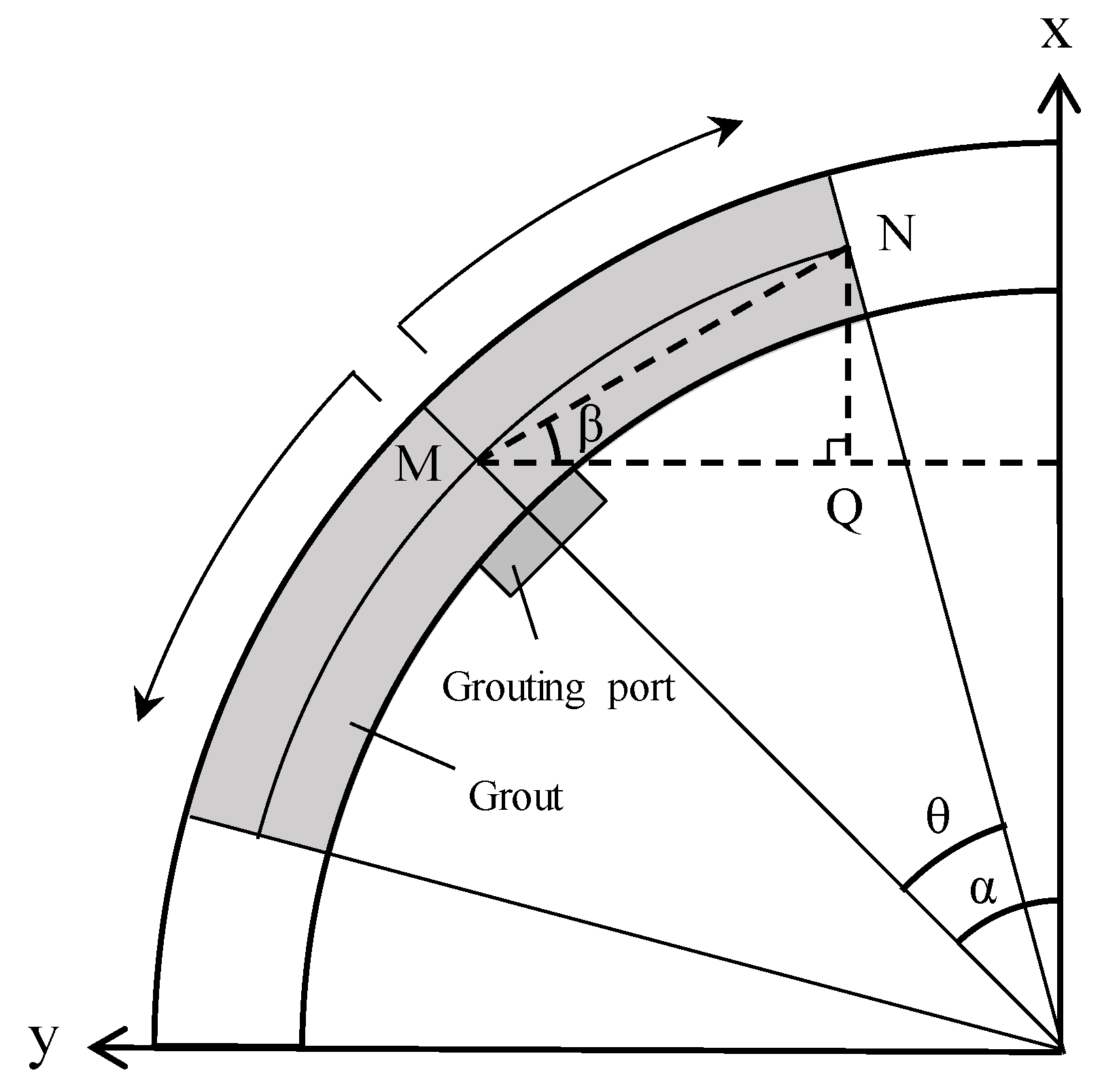
2.2. Construction of the Numerical Model
- Both segmental lining and surrounding rock can be treated as impermeable layers.
- The circumferential diffusion speed of the grout is generally much greater than the axial diffusion speed in engineering applications [24].
- The circumferential perimeter of the backfilling layer is significantly larger than its thickness and axial length, making circumferential diffusion the dominant mode of grout flow.
- Pressure Boundary Condition: A fixed pressure is applied at the inlet.
- Flow Velocity Boundary Condition: A constant flow velocity is applied at the inlet.
3. Analysis of Results
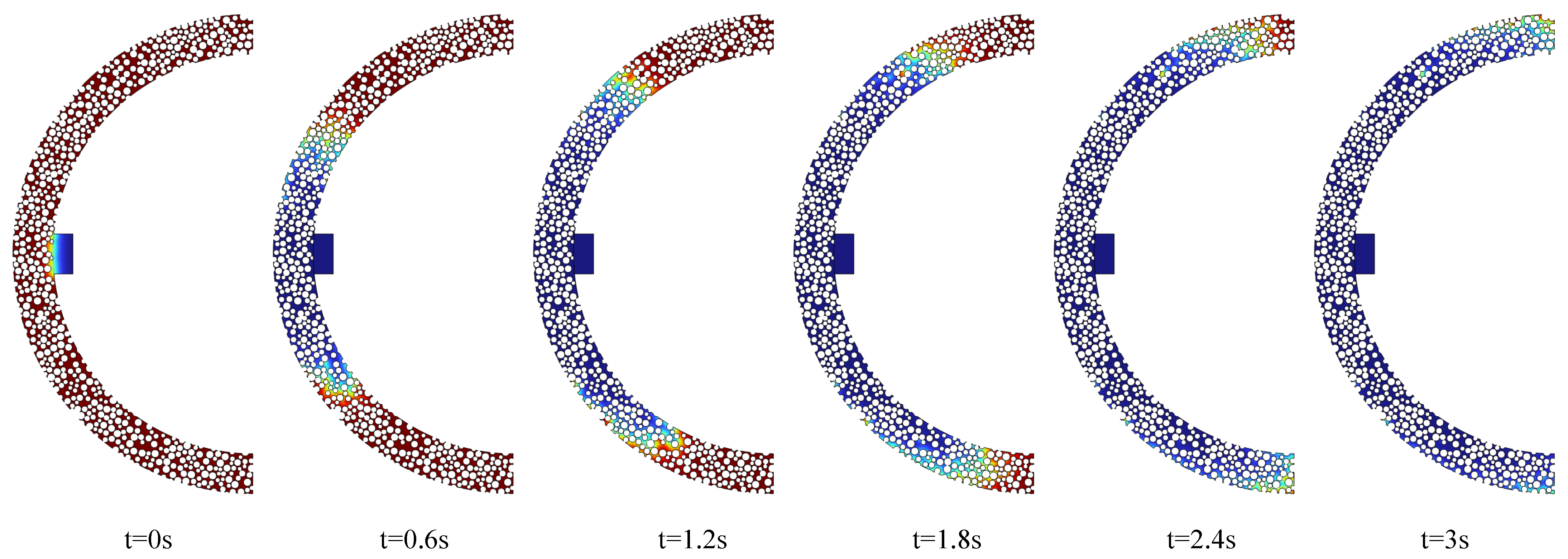
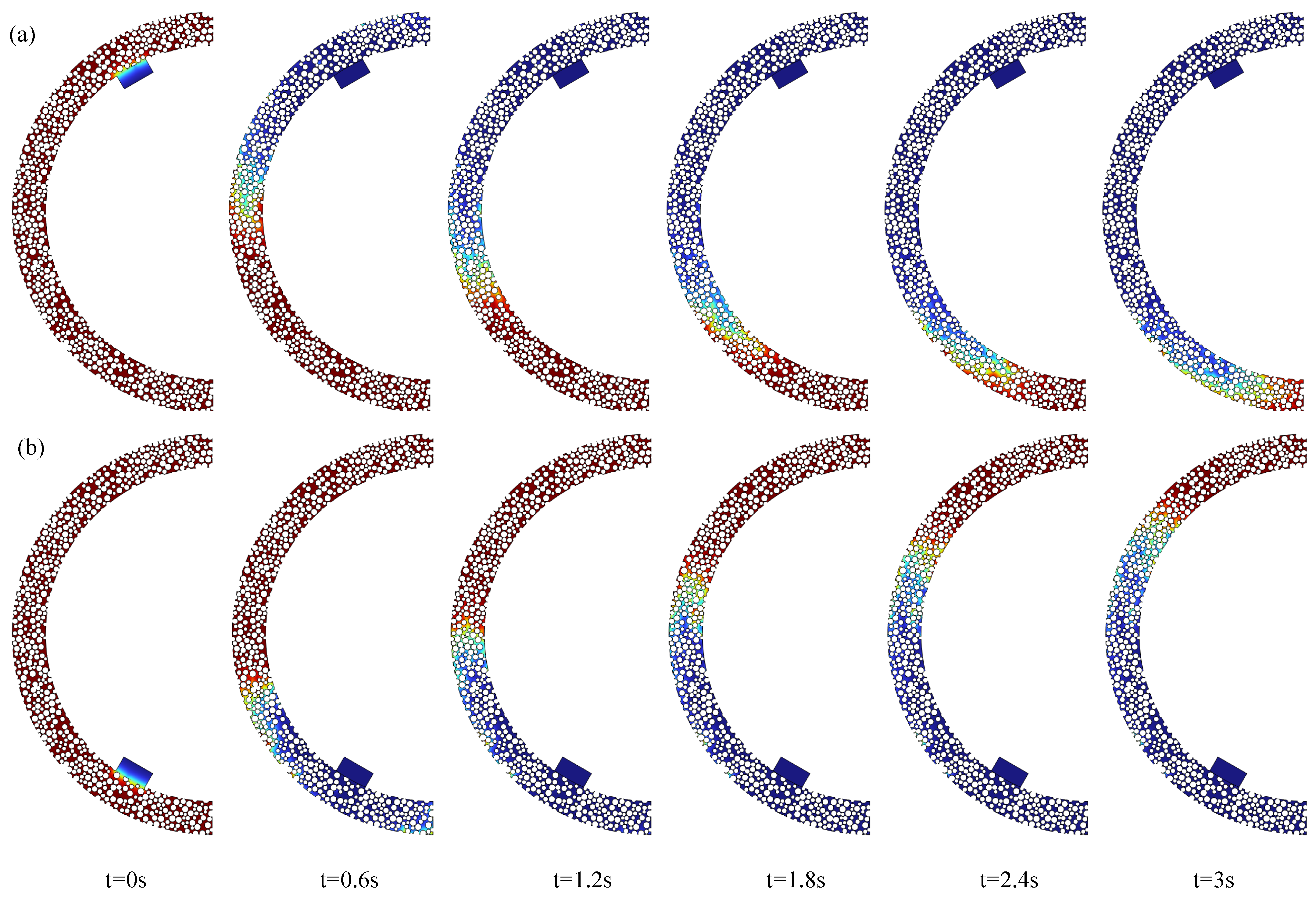
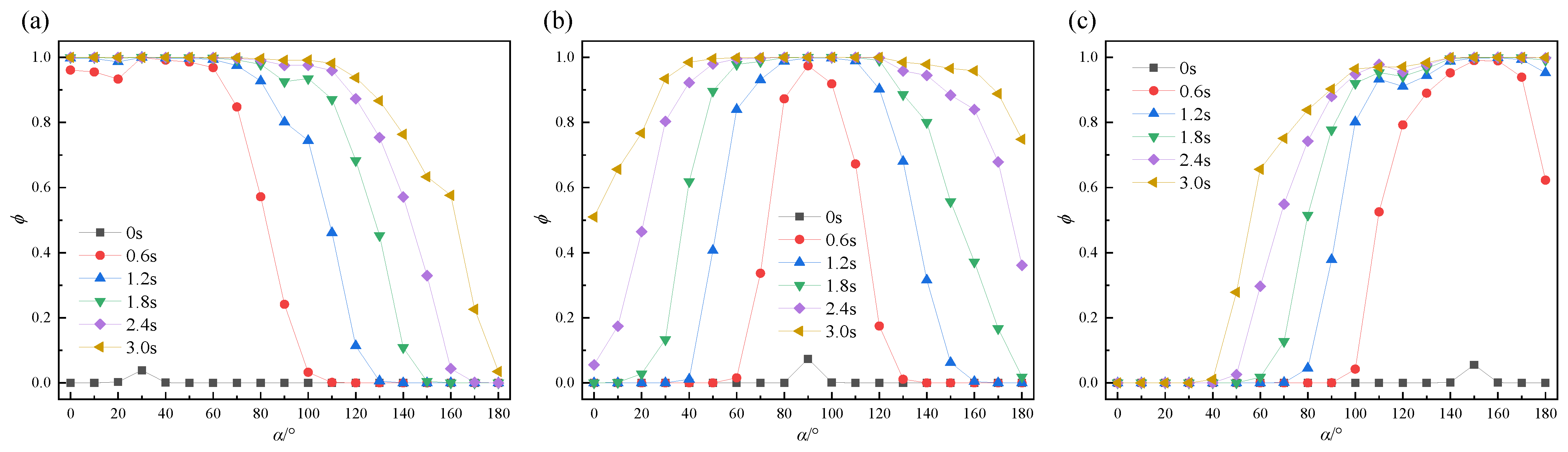
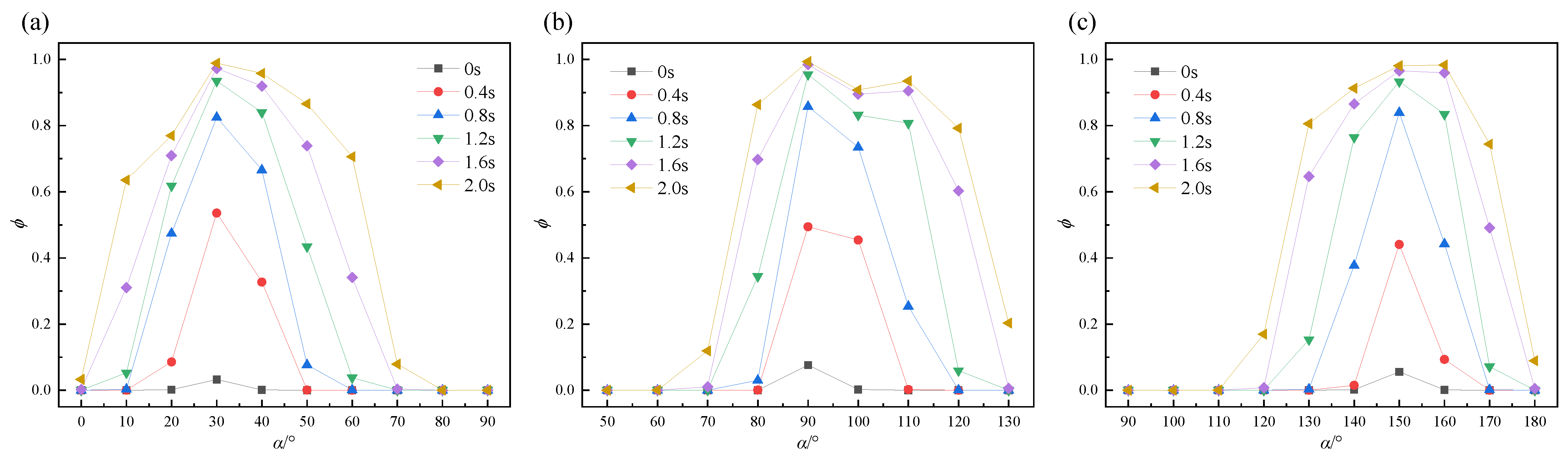
3.1. Diffusion Behavior
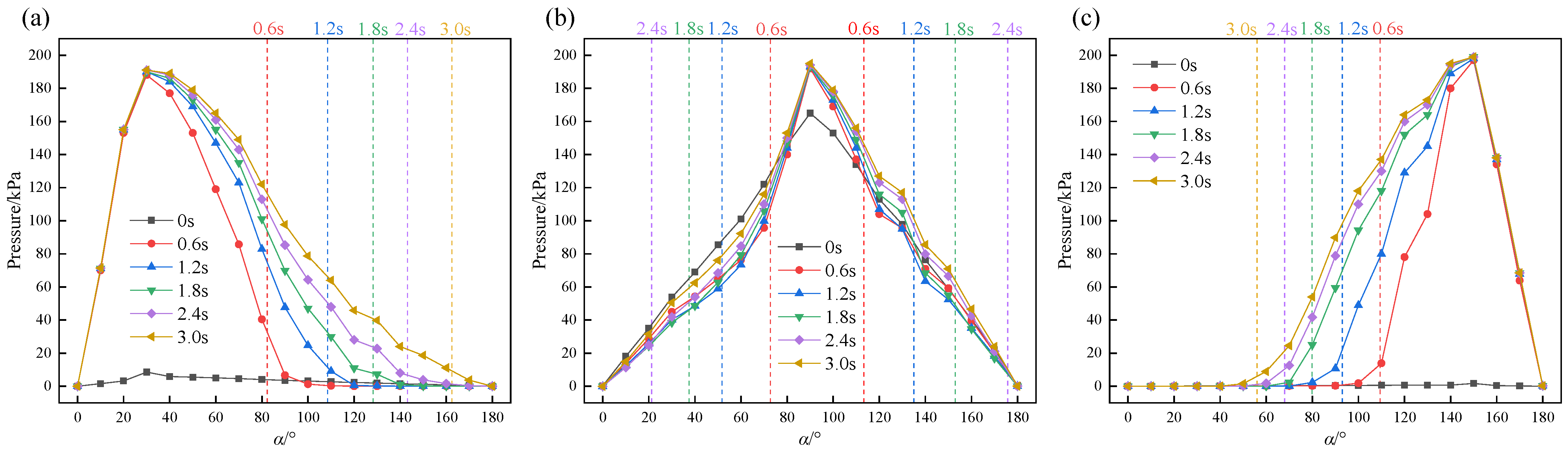
3.2. Pressure Boundary Conditions
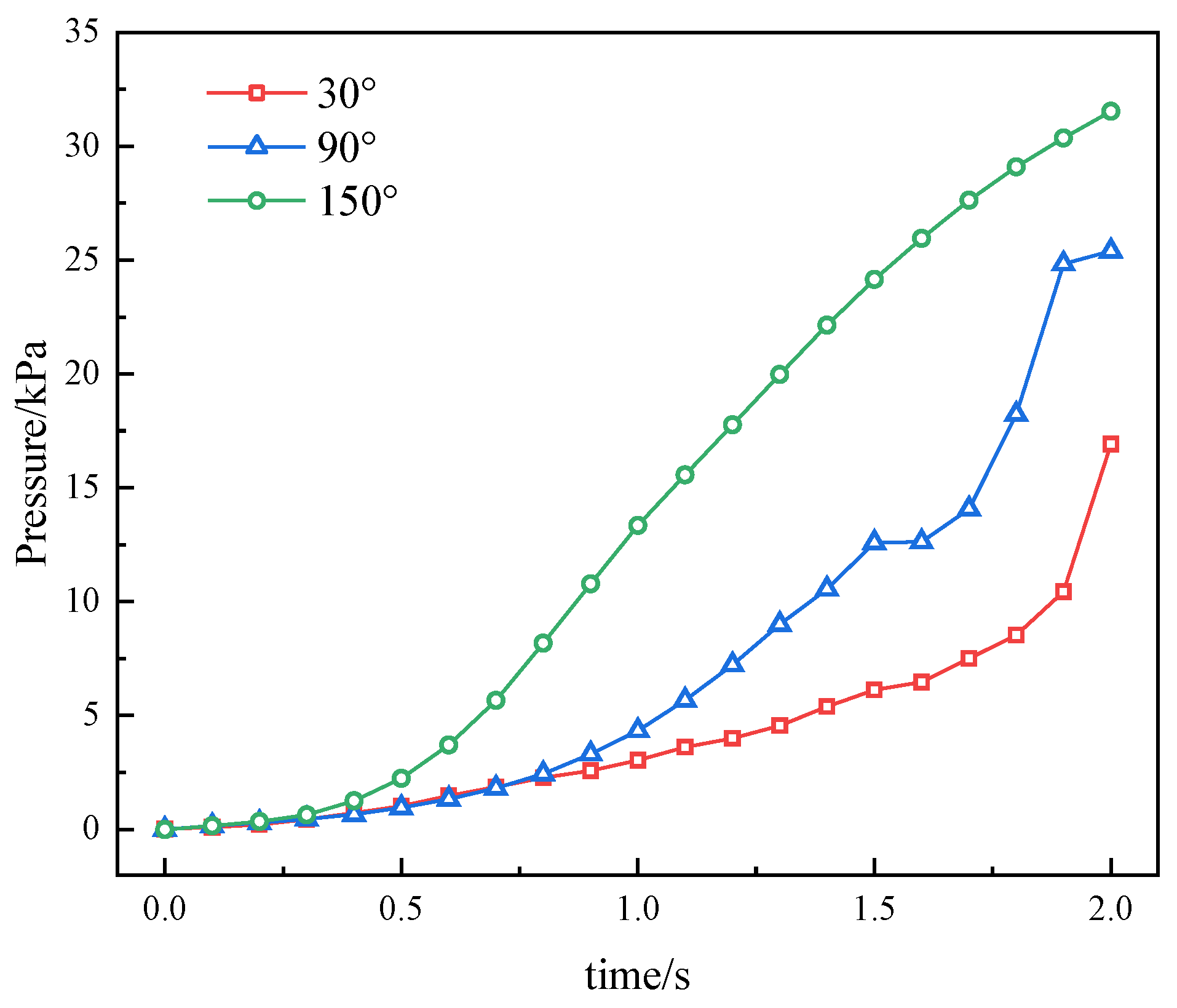
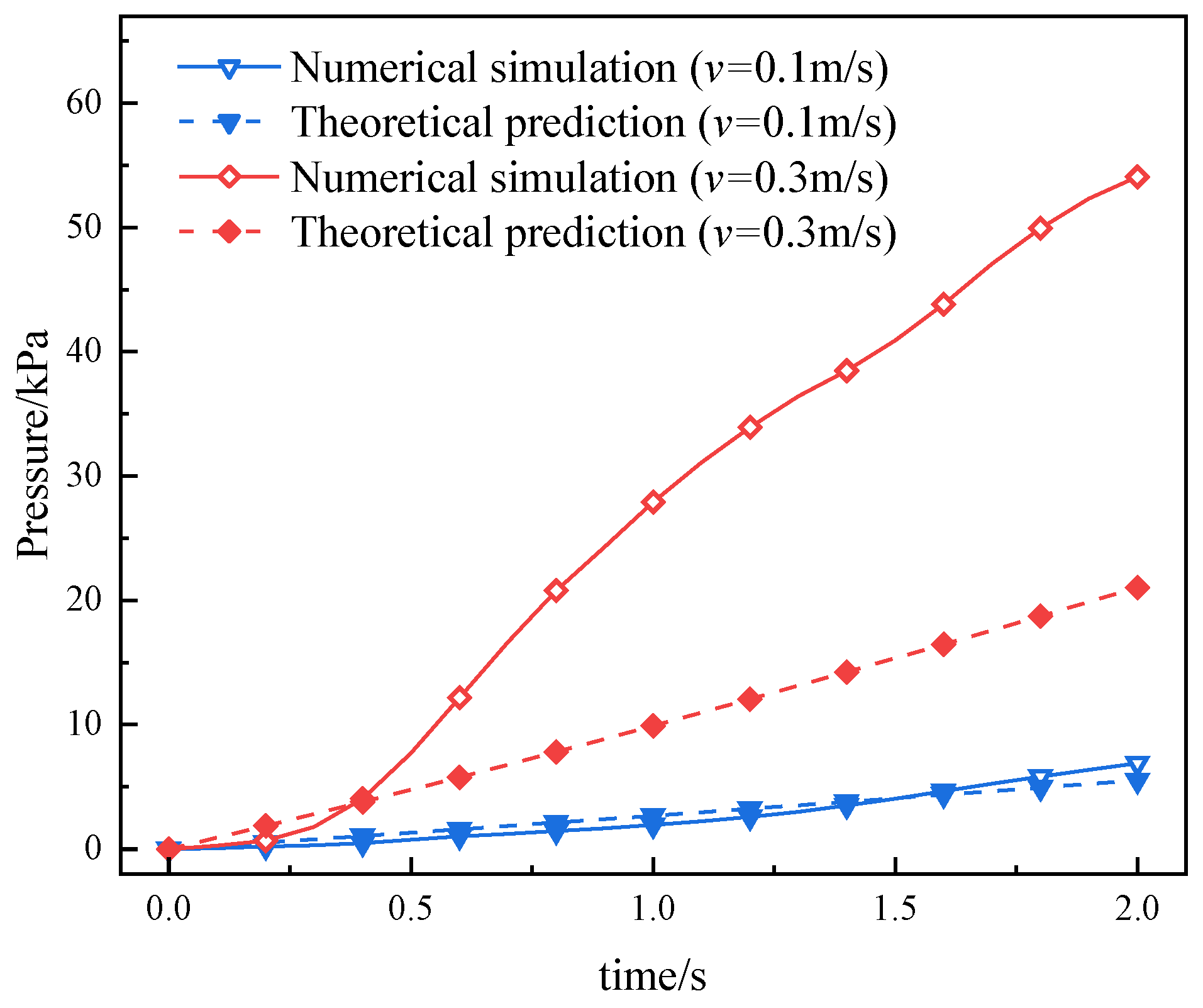
3.3. Velocity Boundary Conditions
4. Analytical Formula for Grouting Pressure
5. Conclusions
- (1)
- When grout diffuses downward, the diffusion speed is relatively fast, and the transition zone between the grout and air is longer. In contrast, when grout diffuses upward, the diffusion speed is slower, and the transition zone is shorter. Under the same time conditions, the grouting effect is better when the grouting port is at 90° compared to the cases at 30° and 150°.
- (2)
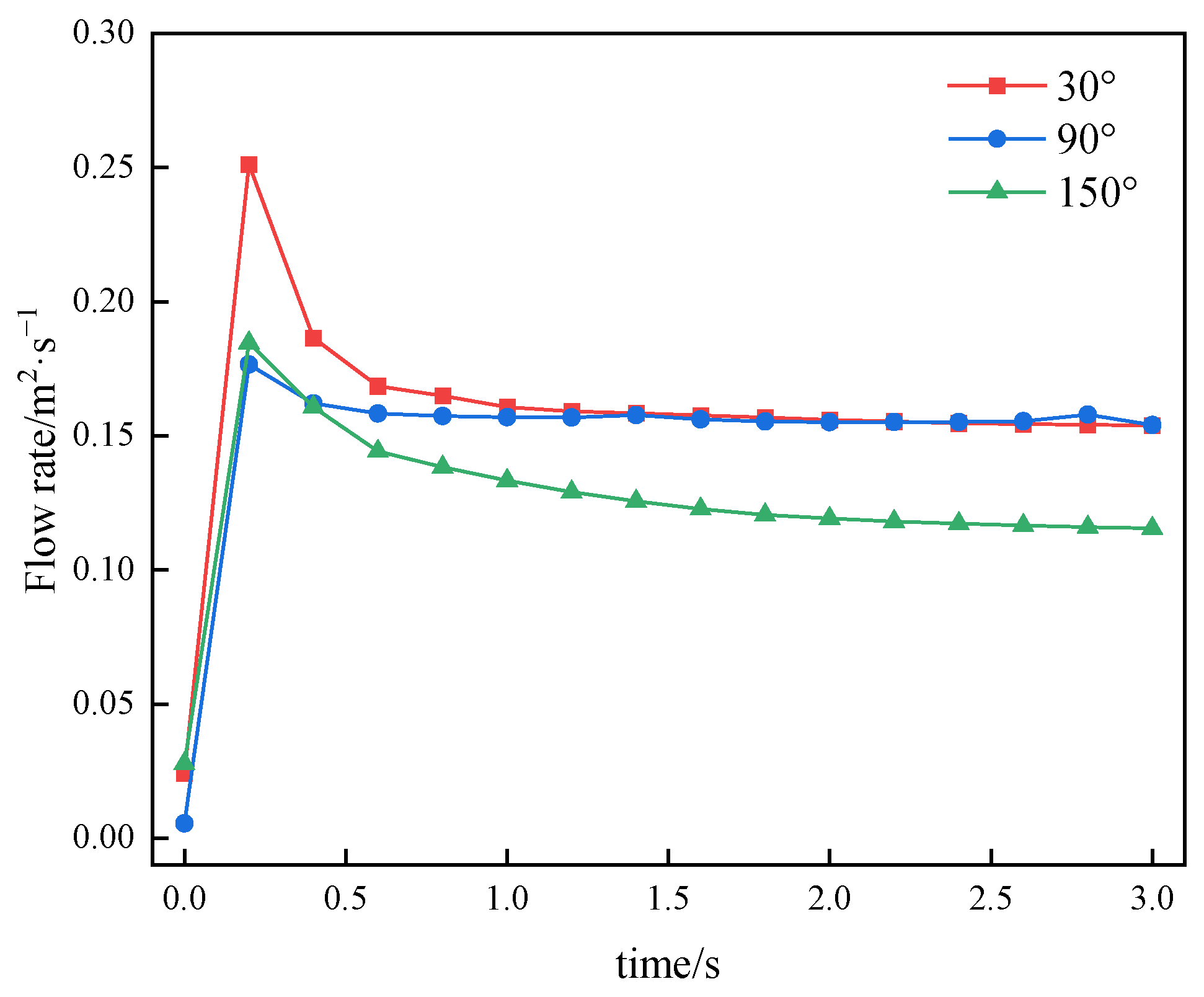
- Under the pressure boundar y condition, the grout flow rate increases rapidly during the initial stage and reaches its peak at approximately 0.2 s. The grouting position has a noticeable effect on the peak flow rate: when grouting is applied at the upper part of the segment, the peak flow rate is higher, reaching approximately 0.25 m2/s, whereas grouting at the middle and lower parts results in a lower peak, around 0.18 m2/s. Subsequently, the flow rate gradually decreases and stabilizes, entering a steady-state phase.
- (3)
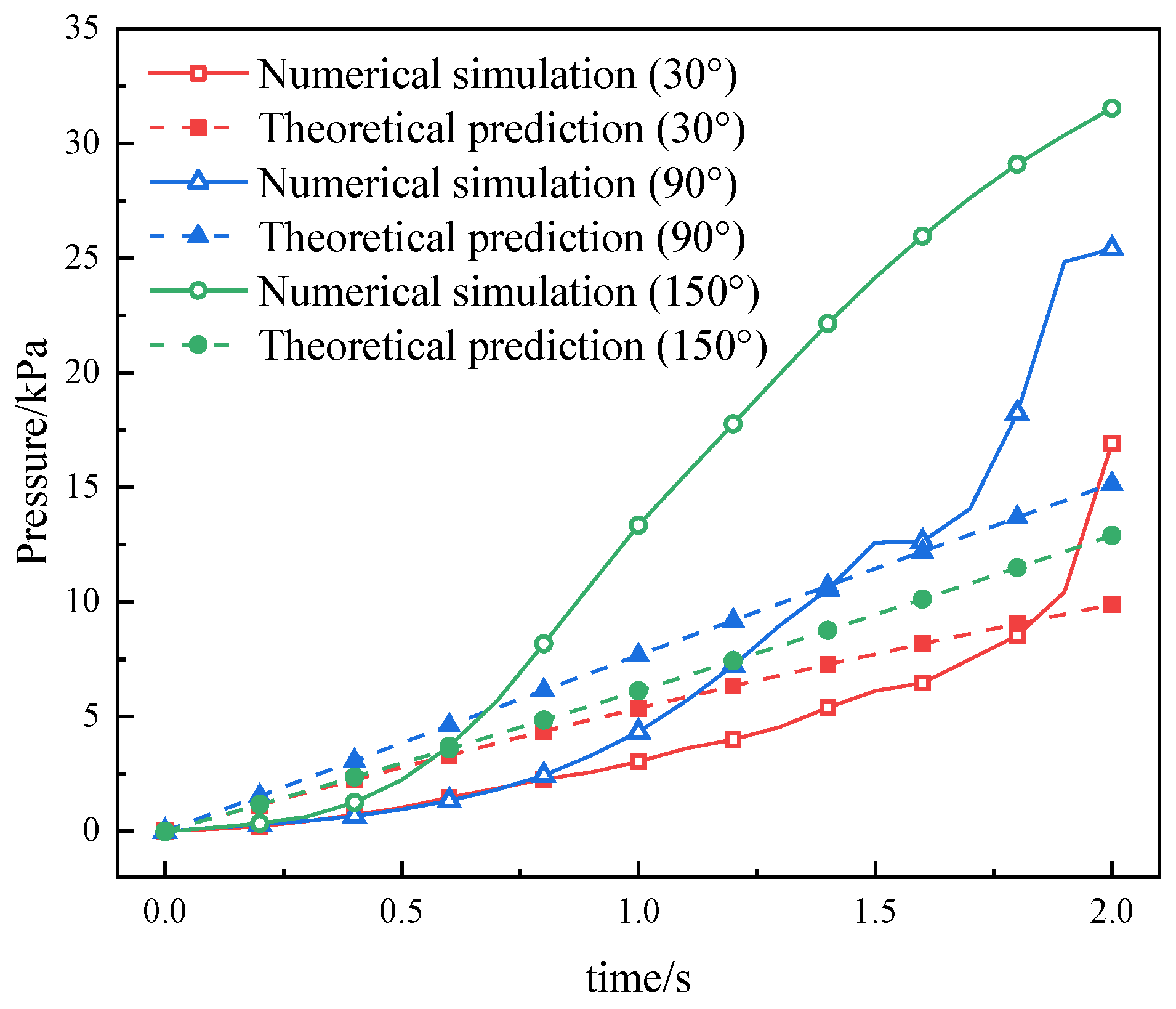
- Under velocity boundary conditions, the grouting pressure remains approximately stable during the initial stage of the process. As grouting progresses, the pressure gradually increases. The position of the grouting port has a significant influence on the pressure variation: the lower the port is positioned, the faster the pressure increases. At 2 s into the grouting process, the grouting pressures at the upper, middle, and lower ports are 16.92 kPa, 25.40 kPa, and 31.54 kPa, respectively. The abnormally high grouting pressure may be attributed to locally dense regions, which increase flow resistance and consequently result in elevated grouting pressure.
- (4)
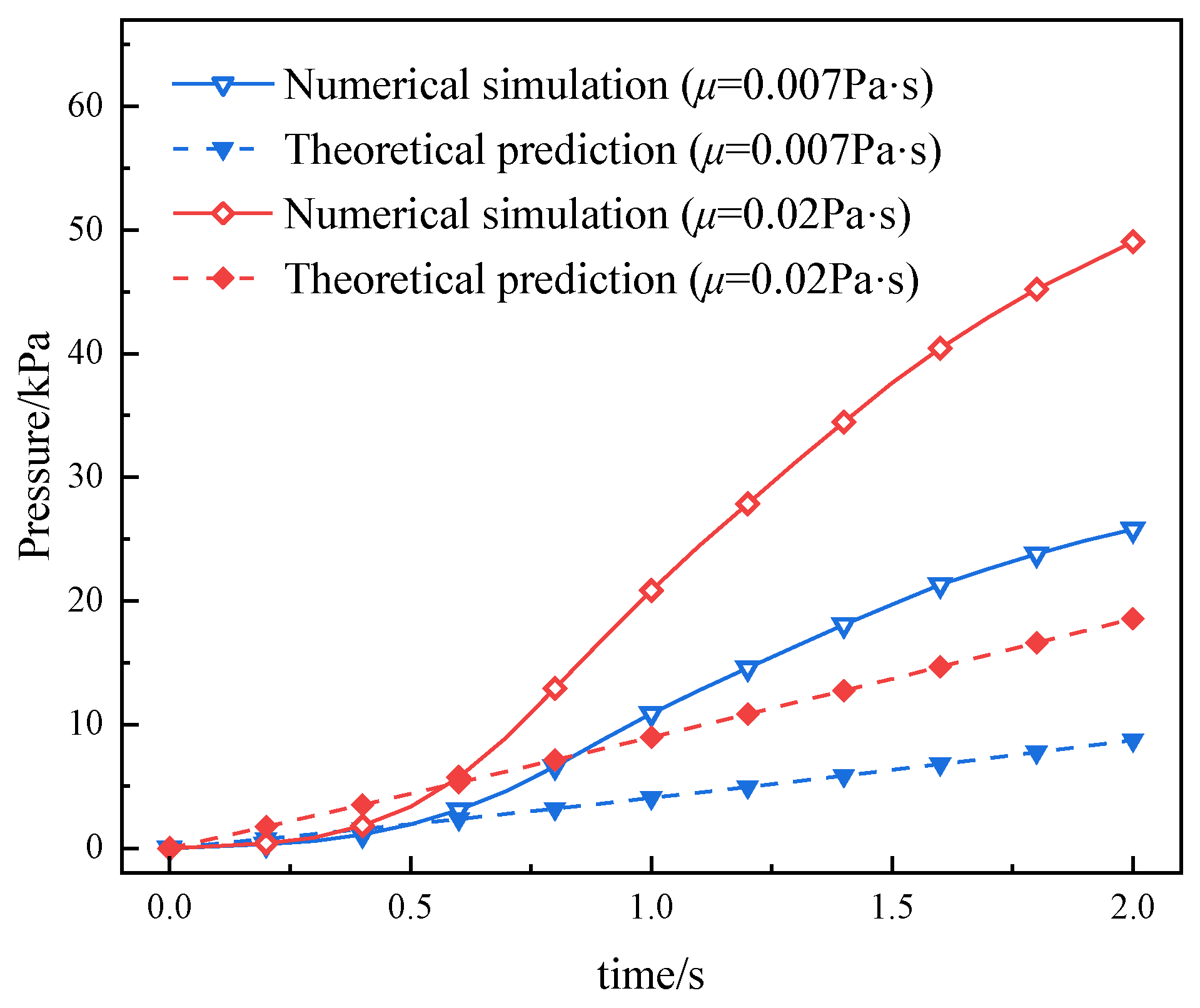
- The analytical formula developed in this study can predict the variation in grouting pressure to a certain extent. Compared to the predicted values, the simulated pressures are lower in the early stage of grouting and higher in the later stage. Porosity, grout viscosity, and injection velocity all have significant effects on grouting pressure. As porosity decreases or injection velocity increases, the discrepancy between the numerical simulation results and the theoretical predictions becomes more pronounced, indicating that the existing formula provides greater accuracy and applicability under low injection velocity conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Shi, C.; Lei, M.; Wang, Z.; Lin, Y. A study on damage mechanism modelling of shield tunnel under unloading based on damage–plasticity model of concrete. Eng. Fail. Anal. 2021, 123, 105261. [Google Scholar] [CrossRef]
- Cheng, Z.L.; Kannangara, K.K.P.M.; Su, L.J.; Zhou, W.H. Mathematical model for approximating shield tunneling-induced surface settlement via multi-gene genetic programming. Acta Geotech. 2023, 18, 4923–4940. [Google Scholar] [CrossRef]
- Wang, Z.; Jiang, Y.; Shao, X.; Liu, C. On-site measurement and environmental impact of vibration caused by construction of double-shield TBM tunnel in urban subway. Sci. Rep. 2023, 13, 17689. [Google Scholar] [CrossRef]
- Hou, S.; Liu, Y.; Zhuang, W.; Zhang, K.; Zhang, R.; Yang, Q. Prediction of shield jamming risk for double-shield TBM tunnels based on numerical samples and random forest classifier. Acta Geotech. 2023, 18, 495–517. [Google Scholar] [CrossRef]
- Xu, X.; Wu, Z.; Weng, L.; Chu, Z.; Liu, Q.; Zhou, Y. Numerical investigation of geostress influence on the grouting reinforcement effectiveness of tunnel surrounding rock mass in fault fracture zones. J. Rock Mech. Geotech. Eng. 2024, 16, 81–101. [Google Scholar] [CrossRef]
- Gan, X.; Yu, J.; Gong, X.; Hou, Y.; Zhu, M. Response of operating metro tunnels to compensation grouting of an underlying large-diameter shield tunnel: A case study in Hangzhou. Undergr. Space 2021, 7, 219–232. [Google Scholar] [CrossRef]
- Ma, F. Recent Advances in the GPR Detection of Grouting Defects behind Shield Tunnel Segments. Remote Sens. 2021, 13, 4596. [Google Scholar] [CrossRef]
- Sun, X.; Wang, Y.; Liu, H.; Yang, Z.; Ma, H. Development of multivariate-coupled grouting diffusion model for RCC. Constr. Build. Mater. 2024, 435, 136748. [Google Scholar] [CrossRef]
- Wang, H.; Yu, Y.; Zhang, P.; Yang, C.; Wen, H.; Zhang, F.; Du, S. Study on the Diffusion Mechanism of Infiltration Grouting in Fault Fracture Zone Considering the Time-Varying Characteristics of Slurry Viscosity Under Seawater Environment. Int. J. Concr. Struct. Mater. 2024, 18, 65. [Google Scholar] [CrossRef]
- Vorschulze, F.C. Variations in the rheology and penetrability of cement-based grouts—An experimental study. Cem. Concr. Res. 2004, 34, 1111–1119. [Google Scholar] [CrossRef]
- Jiang, D.; Cheng, X.; Luan, H.; Wang, T.; Zhang, M.; Hao, R. Experimental Investigation on the Law of Grout Diffusion in Fractured Porous Rock Mass and Its Application. Processes 2018, 6, 191. [Google Scholar] [CrossRef]
- Huayang, L.; Wangwei, Q.; Qianqian, L.; Caifeng, H. Study on the Impact of the Grouting Factors on Surface Subsidence in the Process of Shield Construction. Chin. J. Undergr. Space Eng. 2015, 11, 1303–1309. [Google Scholar]
- Yanbin, F.U.; Jun, Z.; Xiang, W.U.; Jingyu, Z. Back-fill Pressure Model Research of Simultaneous Grouting for Shield Tunnel. J. Disaster Prev. Mitig. Eng. 2016, 36, 107–113. [Google Scholar]
- Mittag, J.; Salvidis, S.A. The groutability of sands—Results from one-dimensional and spherical tests. In Grouting and Ground Treatment; ASCE Library: Lawrence, MA, USA, 2003. [Google Scholar] [CrossRef]
- Maghous, S.; Saada, Z.; Dormieux, L.; Canou, J.; Dupla, J.C. A model for in situ grouting with account for particle filtration. Comput. Geotech. 2007, 34, 164–174. [Google Scholar] [CrossRef]
- Eklund, D.; Stille, H. Penetrability due to filtration tendency of cement-based grouts. Tunn. Undergr. Space Technol. 2008, 23, 389–398. [Google Scholar] [CrossRef]
- Axelsson, M.; Gustafson, G.; Fransson, A. Stop mechanism for cementitious grouts at different water-to-cement ratios. Tunn. Undergr. Space Technol. 2009, 24, 390–397. [Google Scholar] [CrossRef]
- Lee, M.S.; Kim, J.S.; Lee, S.D.; Choi, Y.J.; Lee, I.M. Effect of Vibratory Injection on Grout Permeation Characteristics. Prog. Theor. Phys. 2010, 26, 73–84. [Google Scholar]
- Weng, L.; Wu, Z.; Zhang, S.; Liu, Q.; Chu, Z. Real-time characterization of the grouting diffusion process in fractured sandstone based on the low-field nuclear magnetic resonance technique. Int. J. Rock Mech. Min. Sci. 2022, 152, 105060. [Google Scholar] [CrossRef]
- Wang, C.; Diao, Y.; Guo, C.; Li, P.; Du, X.; Pan, Y. Two-stage column–hemispherical penetration diffusion model considering porosity tortuosity and time-dependent viscosity behavior. Acta Geotech. 2022, 18, 2661–2680. [Google Scholar] [CrossRef]
- Gou, C.F.; Ye, F.; Zhang, J.L.; Liu, Y.P. Ring distribution model of filling pressure for shield tunnels under synchronous grouting. Chin. J. Geotech. Eng. 2013, 35, 590–598. [Google Scholar]
- Ye, F.; Yang, T.; Mao, J.H.; Qin, X.Z.; Zhao, R.L. Half-spherical surface diffusion model of shield tunnel back-fill grouting based on infiltration effect. Tunn. Undergr. Space Technol. 2019, 83, 274–281. [Google Scholar] [CrossRef]
- Liu, J.; Li, P.; Shi, L.; Fan, J.; Huang, D. Spatial distribution model of the filling and diffusion pressure of synchronous grouting in a quasi-rectangular shield and its experimental verification. Undergr. Space 2021, 6, 650–664. [Google Scholar] [CrossRef]
- Ma, J.; Sun, A.; Jiang, A.; Guo, N.; Liu, X.; Song, J.; Liu, T. Pressure Model Study on Synchronous Grouting in Shield Tunnels Considering the Temporal Variation in Grout Viscosity. Appl. Sci. 2023, 13, 10437. [Google Scholar] [CrossRef]
- Rosquot, F.; Alexis, A.; Khelidj, A.; Phelipot, A. Experimental study of cement grout: Rheological behavior and sedimentation. Cem. Concr. Res. 2003, 33, 713–722. [Google Scholar] [CrossRef]
- Zhou, M.; Fan, F.; Zheng, Z.; Ma, C. Modeling of Grouting Penetration in Porous Medium with Influence of Grain Distribution and Grout–Water Interaction. Processes 2021, 10, 77. [Google Scholar] [CrossRef]
- Gustafson, G.; Claesson, J.; Fransson, S. Steering Parameters for Rock Grouting. J. Appl. Math. 2013, 1, 269594. [Google Scholar] [CrossRef]
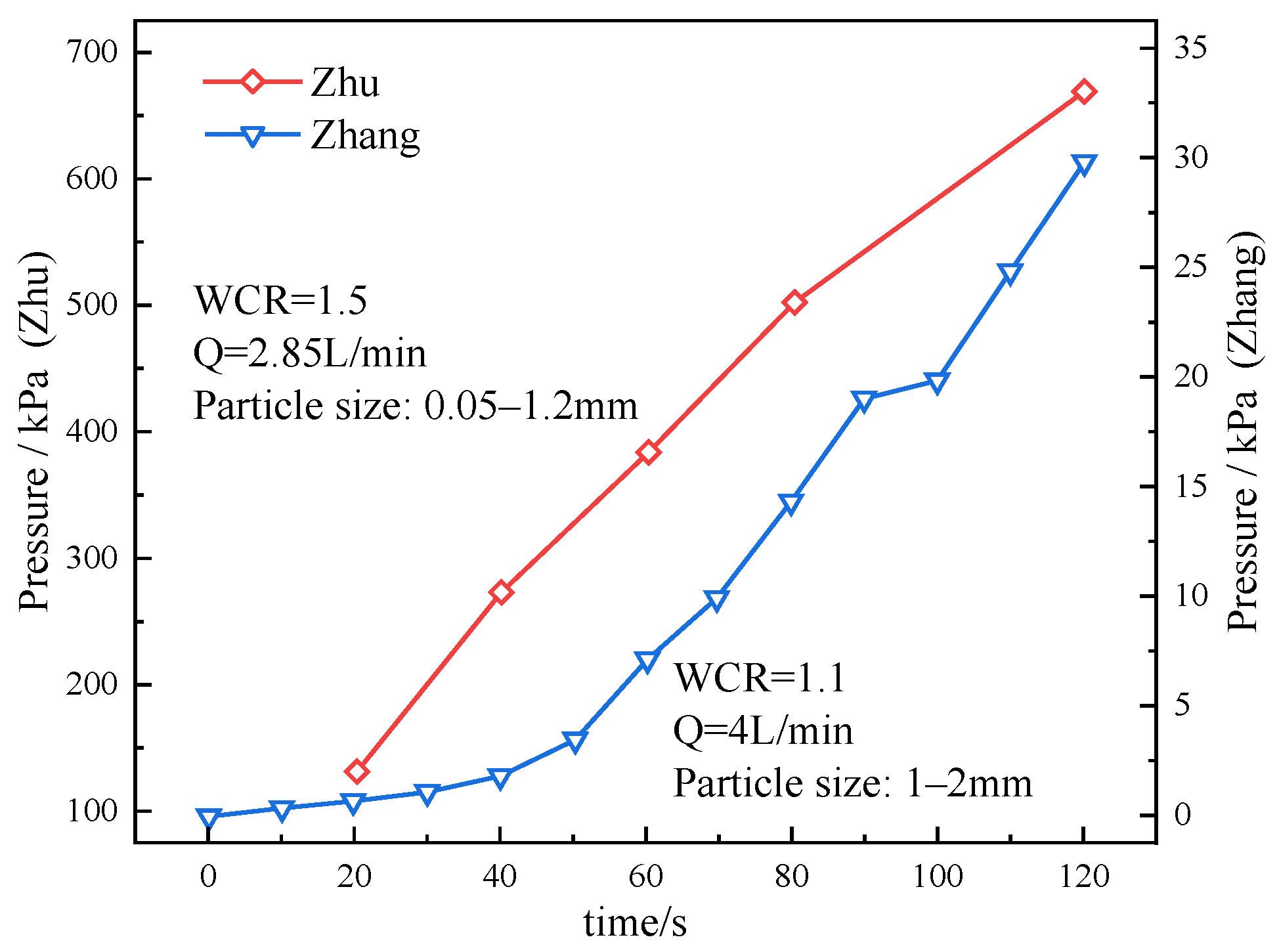
- Zhu, G.; Zhang, Q.; Liu, R.; Bai, J.; Li, W.; Feng, X. Experimental and numerical study on the permeation grouting diffusion mechanism considering filtration effects. Geofluids 2021, 1, 6613990. [Google Scholar] [CrossRef]
- Zhang, Q.S.; Wang, H.B.; Liu, R.T.; Li, S.C.; Zhang, L.W.; Zhu, G.X.; Zhang, L.Z. Infiltration grouting mechanism of porous media considering diffusion paths of grout. Chin. J. Geotech. Eng. 2018, 40, 918–924. [Google Scholar] [CrossRef]







| Density of Air | Viscosity of Air | Density of Grout | Viscosity of Grout |
|---|---|---|---|
| 1.204 kg/m3 | 1.81 × 10−5 Pa·s | 1500 kg/m3 | 0.01 Pa·s |
| Sum of Grain Perimeter | Length of Fluid Domain | Width of Fluid Domain | Equivalent Width |
|---|---|---|---|
| 55.414 m | 3.456 m | 0.2 m | 0.00185 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhang, Y.; Cao, D.; Liu, Y.; Chen, L. The Simulation of Grouting Behavior in the Pea Gravel Filling Layer Behind a Double-Shield TBM Based on the Level Set Method. Appl. Sci. 2025, 15, 7542. https://doi.org/10.3390/app15137542
Li X, Zhang Y, Cao D, Liu Y, Chen L. The Simulation of Grouting Behavior in the Pea Gravel Filling Layer Behind a Double-Shield TBM Based on the Level Set Method. Applied Sciences. 2025; 15(13):7542. https://doi.org/10.3390/app15137542
Chicago/Turabian StyleLi, Xinlong, Yulong Zhang, Dongjiao Cao, Yang Liu, and Lin Chen. 2025. "The Simulation of Grouting Behavior in the Pea Gravel Filling Layer Behind a Double-Shield TBM Based on the Level Set Method" Applied Sciences 15, no. 13: 7542. https://doi.org/10.3390/app15137542
APA StyleLi, X., Zhang, Y., Cao, D., Liu, Y., & Chen, L. (2025). The Simulation of Grouting Behavior in the Pea Gravel Filling Layer Behind a Double-Shield TBM Based on the Level Set Method. Applied Sciences, 15(13), 7542. https://doi.org/10.3390/app15137542







