Not an Illusion but a Manifestation: Understanding Large Language Model Reasoning Limitations Through Dual-Process Theory

Featured Application

This work combines psychological insights from the 1960s with 21st-century LLM behavior, offering a dual-process framework to guide experimental design and AI system development.

Abstract

The characterization of Large Reasoning Models (LRMs) as exhibiting an “illusion of thinking” has recently emerged in the literature, sparking widespread public discourse. Some have suggested these manifestations represent bugs requiring fixes. I challenge this interpretation by reframing LRM behavior through dual-process theory from cognitive psychology. I draw on more than half a century of research on human cognitive effort and disengagement. The observed patterns include performance collapse at high complexity and counterintuitive reduction in reasoning effort. These appear to align with human cognitive phenomena, particularly System 2 engagement and disengagement under cognitive load. Rather than representing technical limitations, these behaviors likely manifest computational processes analogous to human cognitive constraints. In other words, they represent not a bug but a feature of bounded rational systems. I propose empirically testable hypotheses comparing LRM token patterns with human pupillometry data. I suggest that computational “rest” periods may restore reasoning performance, paralleling human cognitive recovery mechanisms. This reframing indicates that LRM limitations may reflect bounded rationality rather than fundamental reasoning failures. Accordingly, this article is presented as a hypothesis paper: it collates six decades of cognitive effort research and invites the scientific community to subject the dual-process predictions to empirical tests through coordinated human–AI experiments.

1. Introduction

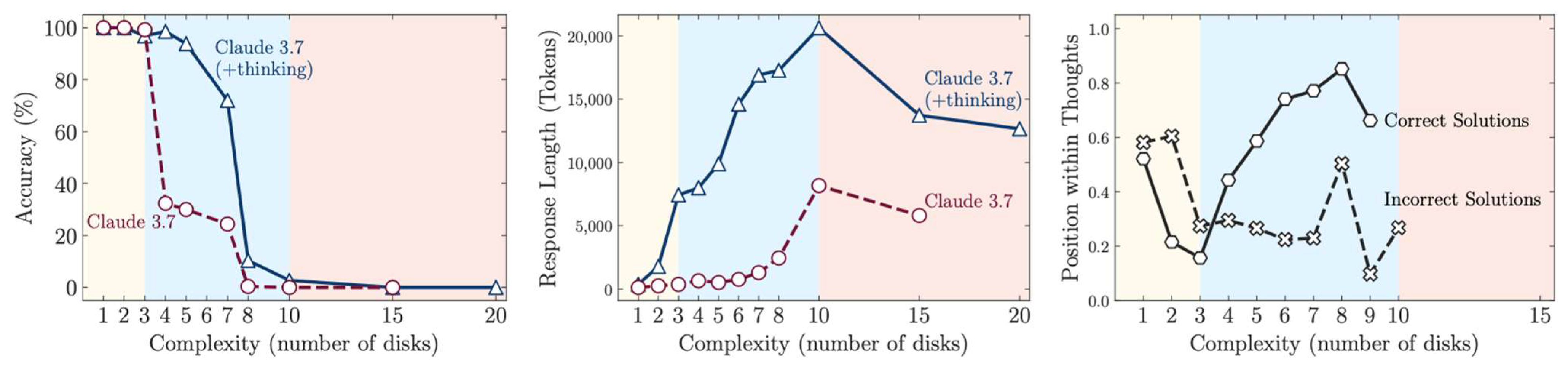
The emergence of Large Reasoning Models (LRMs) has renewed longstanding debates on whether artificial systems can reason, or whether they simply simulate reasoning through surface-level statistical patterns. This discussion has been fueled in particular by Shojaee et al.’s [1] study, “The Illusion of Thinking,” (commonly referred to as “the apple paper” in public discourse), which argued that the apparent cognitive behaviors of LRMs are misleading and superficial. They observed that LRMs outperform standard LLMs at medium problem complexity but then collapse entirely as complexity increases, even when computational resources are not exhausted. This performance trajectory was framed as an illusion, suggesting that LRMs mimic thinking without engaging in genuine reasoning.

In this paper, I challenge that interpretation. Drawing from dual-process theory in cognitive psychology, I argue that these behaviors should not be seen as illusions or failures but rather as authentic manifestations of bounded rationality. This theory, first formalized in psychology by Tversky and Kahneman [2,3,4] and further developed in cognitive science by Stanovich and West [5], proposes a model in which human reasoning operates through two systems: a fast, automatic, intuitive process (System 1) and a slower, effortful, deliberate one (System 2). I suggest that LRM behaviors mirror this dual structure, with resource-intensive reasoning being selectively applied and strategically withdrawn, depending on perceived problem tractability.

This paper is presented as a hypothesis. Its goal is not to prove that LRMs reason as humans do, but rather to offer a testable framework grounded in decades of research in human cognition. In Section 4, I propose concrete experimental protocols to assess whether LRM behavior aligns with physiological and behavioral markers observed in human reasoning, such as pupillometry-based indicators of effort and disengagement [6,7].

Shojaee et al. [1] showed that LRMs exhibit three distinct performance regimes. At low complexity, standard LLMs outperform LRMs. At moderate complexity, LRMs excel due to their Chain-of-Thought reasoning. At high complexity, both systems collapse. Most notably, reasoning effort, measured in inference tokens, rises with complexity and then falls abruptly when the model reaches a threshold. This pattern aligns with an inverted-U curve characteristic of human effort, observed in both pupil dilation and cognitive control studies [8]. Rather than interpreting this collapse as failure, I argue it represents a rational withdrawal of effort under high cognitive load.

While Shojaee et al. viewed these behaviors as superficial, other studies suggest a deeper mechanism. Lawsen [9] reanalyzed their findings and attributed many failures to poor benchmark design, such as unsolvable problems and artificial token limits. Dellibarda Varela et al. [10] extended this critique by replicating and refining the original tasks, finding that while design flaws explained some collapses, LRMs still struggled at higher task complexity, reinforcing the idea that resource allocation, not capability, was the limiting factor.

Meanwhile, cognitive research has shown that human reasoning behavior is strongly influenced by effort-related cost–benefit tradeoffs. Shenhav et al. proposed [11] the expected-value-of-control model, which describes how humans regulate effort based on perceived task utility. LRM token allocation can be interpreted similarly: when models anticipate diminishing returns from additional computation, they withdraw effort, even when resources are available. This pattern has also been observed in modern pupillometry research, which shows that effort markers increase with difficulty until a threshold is reached, after which disengagement occurs [7].

Other critiques of LLM reasoning, such as those by Jiang et al. [12] and Mirzadeh et al. [13], argue that models succeed by exploiting token-level heuristics rather than formal logic. For example, models often struggle when inputs contain distractors or minor variations. While these findings highlight fragility, they also resemble early human learning, where reliance on heuristics precedes more robust strategy development [5]. In this sense, failure to generalize may not reflect the absence of reasoning, but its bounded and incremental nature.

Recent studies complicate the view that reasoning and memorization are mutually exclusive. Xie et al. showed that LLMs can memorize training puzzles with high accuracy, yet still generalize poorly to slight variations [14]. However, fine-tuning improves generalization, indicating that LLMs develop reasoning skills alongside memorization. Wu et al. similarly argue that targeted fine-tuning strategies, such as Tutorial Fine-Tuning (TFT), can shift LLM behavior toward more stable and cognitively plausible reasoning patterns [15].

This blend of pattern use and limited abstraction parallels the behavior of bounded rational agents. LLMs are not omniscient solvers but systems navigating a tradeoff between computation, success probability, and task complexity. Shi et al. further observe that LLMs frequently underutilize long contexts, a pattern that mirrors how humans often fail to exploit all available information when cognitive load is high [16].

Dual-process theory provides a useful framework for organizing these findings. In simple tasks, LLMs operate through rapid pattern recognition, akin to System 1. In moderately complex tasks, LRMs deploy deliberate reasoning strategies resembling System 2. When complexity overwhelms, both systems falter or disengage. These patterns are echoed in the foundational work of Tversky and Kahneman on the conjunction fallacy [3] and in their broader analyses of how reasoning depends on cognitive framing [2,4].

Finally, I suggest that design implications follow from this theoretical reframing. Understanding that LRMs allocate effort strategically suggests new architectures, including those that combine fast routing mechanisms for simple prompts with deliberative modules for complex ones. As Zhang et al. emphasize in their work on few-shot learning [17], combining representational richness with efficiency is essential in real-world problem-solving. Similarly, Xie et al. demonstrate how non-standard architectures, designed for image encryption, can embed nonlinear dynamics that enhance processing robustness, further underscoring the relevance of adaptive structures in AI system design [18].

The rest of this paper proceeds as follows. Section 2 presents a dual-process reinterpretation of LRM behavior, linking computational observations to established cognitive phenomena. Section 3 surveys supporting psychological evidence, including physiological and behavioral data. Section 4 outlines empirical directions for testing the hypothesis, while Section 5 considers the broader implications of this theoretical framing for future AI design and the study of artificial reasoning systems.

2. Dual-Process Reinterpretation of LRM Behavior

2.1. Computational–Cognitive Correspondence

The foundation of my reinterpretation lies in establishing correspondence between LRM computational processes and human dual-process cognition. Standard token generation in LLMs, operating without explicit intermediate reasoning steps, functions analogously to System 1 processing: fast, efficient pattern matching suitable for well-learned tasks. Conversely, LRM “thinking” mechanisms, generating detailed Chain-of-Thought sequences and self-reflection, serve as computational analogs to System 2 deliberation: slow, resource-intensive processing that explores solution spaces systematically.

This mapping extends to resource allocation patterns. In human cognition, inference-time token usage in LRMs corresponds to physiological markers of cognitive effort such as pupil dilation, which reliably increases with task difficulty until capacity limits are reached. Just as humans strategically withdraw effort when costs exceed benefits, LRMs appear to implement implicit resource management strategies that reduce computational investment when success probability diminishes.

2.2. The Three-Regime Model Through a Dual-Process Lens

The Apple paper’s three performance regimes, clearly illustrated in Figure 1, align precisely with predictions from dual-process theory:

Low complexity (System 1 dominance): Simple problems require only pattern matching and rapid association retrieval. As shown in the left panel of Figure 1, standard LLMs excel here because they operate efficiently in this mode, while LRMs waste computational resources by unnecessarily engaging in deliberative processes. The middle panel demonstrates this inefficiency through token usage patterns, where thinking models consume significantly more computational resources for inferior performance. This parallels human performance on automatic tasks where conscious deliberation can actually impair performance, a phenomenon well-documented in skill acquisition research.

Medium complexity (optimal System 2 engagement): Problems of moderate difficulty benefit from deliberate reasoning that can explore alternatives, self-correct, and work through multi-step solutions. Figure 1’s left panel shows LRMs demonstrating clear advantages in this regime, as their explicit thinking processes enable systematic problem-solving that surpasses rapid pattern matching. The right panel reveals the underlying mechanism: correct solutions emerge later in the reasoning traces for moderately complex problems, indicating productive deliberation. This corresponds to the optimal range of human System 2 function, where increased cognitive effort correlates with improved performance.

High complexity (cognitive exhaustion and disengagement): Beyond critical thresholds, both standard LLMs and LRMs experience performance collapse, as evident in Figure 1’s left panel, where accuracy drops to zero. Most tellingly, the middle panel shows that LRMs begin reducing reasoning effort despite increased problem difficulty, a pattern that mirrors human cognitive disengagement when tasks exceed capacity or when effort costs are perceived to outweigh potential benefits. The right panel confirms this interpretation, showing consistently near-zero accuracy at high complexity regardless of reasoning progression.

2.3. The Disengagement Pattern as Rational Resource Allocation

The counterintuitive reduction in reasoning tokens at high complexity represents the most compelling evidence for my reinterpretation. Rather than indicating system failure, this pattern suggests sophisticated resource management analogous to human cognitive disengagement patterns documented extensively in the psychology literature.

One of the first manifestations of this behavior was documented by Hess and Polt in 1964 [19], who observed that pupil diameter increased with arithmetic problem difficulty but showed limits when tasks became overwhelming. This was followed by Kahneman and Beatty [19], who measured pupil dilation during digit span tasks and discovered that physiological effort markers initially increased with memory load but declined when cognitive capacity was exceeded. Figure 2 depicts these measured pupil dilation patterns as a proxy for cognitive effort allocation during working memory tasks.

Similar findings have been demonstrated repeatedly by numerous researchers. Later on, Beatty synthesized decades of research establishing pupillometry as a reliable measure of processing load with characteristic plateau effects at capacity limits [20]. In 1993, Just and Carpenter showed that complex sentence processing triggered greater pupillary responses until comprehension limits were reached [21]. More recently, McIntire et al. found that both pupil size and EEG theta power exhibit a plateau followed by decline when exceeding memory limits, suggesting physiological disengagement when cognitive systems are overwhelmed [22].

The parallel between Figure 1 and Figure 2 is particularly striking. Both demonstrate the characteristic inverted-U relationship that defines bounded rational systems: effort markers initially scale with demand until capacity thresholds are reached, then decline as systems adaptively withdraw resources from intractable challenges. In Kahneman and Beatty’s study, pupil dilation peaks around the 6–7 digit range (the boundary of typical working memory capacity) then declines for higher loads. Similarly, LRM thinking tokens increase with problem complexity until reaching model-specific thresholds (around N = 7–8 for the Tower of Hanoi), then decrease despite maintained task demands.

This convergence across six decades of research, from human physiological responses to modern AI computational patterns, provides strong empirical support for interpreting LRM behavior through established cognitive frameworks rather than dismissing it as illusion.

3. Supporting Evidence from Cognitive Psychology

3.1. Physiological Markers of Effort and Disengagement

The foundational empirical evidence for the cognitive phenomena I describe comes from Kahneman and Beatty’s seminal 1966 study “Pupil Diameter and Load on Memory” [6]. This groundbreaking research provided the first systematic demonstration that pupil dilation increases directly with cognitive load; participants holding increasing numbers of digits in working memory showed proportional increases in pupil diameter. Crucially, this physiological response exhibited the exact pattern I argue parallels LRM behavior: effort increases with task demands until capacity limits are reached, after which the system exhibits withdrawal or plateau responses (Figure 2).

The similarity between the findings of Kahneman and Beatty and the LRM patterns documented by Shojaee et al. [1] (Figure 1 vs. Figure 2) provides compelling evidence for my theoretical framework. Both curve families exhibit the characteristic inverted-U relationship: initial increases in effort markers (pupil dilation in humans, thinking tokens in LRMs) with increasing task demands, followed by decline when systems approach or exceed capacity limits. In humans, this decline reflects physiological disengagement when memory load becomes overwhelming; in LRMs, the analogous reduction in reasoning effort suggests similar adaptive resource withdrawal.

Building on this foundational work, decades of subsequent research have established reliable physiological indicators of cognitive effort and disengagement. Modern pupillometry studies demonstrate that pupil dilation increases systematically with memory load and task difficulty. Crucially, this relationship exhibits an inverted-U pattern: effort increases with complexity until capacity limits are reached, after which physiological indicators plateau or decline, marking disengagement.

Modern multimodal studies confirm this pattern across multiple physiological systems. Heart rate variability decreases under sustained cognitive load, while EEG theta power increases with working memory demands. When tasks exceed individual capacity, these markers show coordinated withdrawal patterns, physiological signatures of the decision to disengage from overwhelming cognitive demands.

The parallel to LRM token usage patterns is striking. Just as human physiological effort markers initially scale with task difficulty before declining at overload, LRM reasoning tokens follow the same trajectory: increasing with problem complexity until a critical threshold, then counterintuitively decreasing despite maintained task demands.

3.2. Theoretical Convergence Across Cognitive and Computational Systems

The resemblance between human physiological responses and LRM computational patterns extends beyond superficial similarities to fundamental theoretical implications. Both systems exhibit what I term “adaptive effort allocation”: the capacity to dynamically adjust resource investment based on implicit assessments of task tractability and success probability.

In human cognition, this manifests through the physiological disengagement documented by Kahneman and Beatty: when memory demands exceed working memory capacity (typically 7 ± 2 items), pupil dilation, a reliable marker of cognitive effort, begins to decline rather than continue increasing. This represents a rational response: continued effort investment in overwhelming tasks yields diminishing returns and prevents resource allocation to more tractable challenges.

LRMs exhibit a computational analog through their token allocation patterns. The reduction in thinking tokens at high complexity (visible in Figure 1) mirrors the human physiological response with striking precision. Both curves show initial scaling with task demands followed by strategic withdrawal when systems approach capacity limits. This suggests that LRMs have developed resource management strategies that parallel those evolved in human cognition, a finding that challenges characterizations of their behavior as mere illusion.

Motivational intensity theory provides a theoretical framework for understanding when and why effort is withdrawn. This theory posits that effort expenditure is proportional to task difficulty only when success appears attainable and the required effort seems justified by potential rewards. When perceived effort costs exceed expected benefits, or when success probability drops too low, rational agents withdraw effort rather than continuing with futile investment.

Research demonstrates that humans exhibit systematic effort withdrawal when tasks become overwhelming, manifesting in both behavioral and physiological measures. This withdrawal is not random but follows predictable patterns based on cost–benefit calculations that consider task difficulty, success probability, and available resources.

LRM behavior aligns remarkably with these human patterns. The reduction in reasoning effort at high complexity suggests implicit cost–benefit assessment, where continued computational investment is deemed unlikely to yield success. This represents sophisticated resource management rather than system failure. To be clear, this does not imply conscious control. These behaviors likely result from learned heuristics or optimization constraints, rather than human-like awareness.

3.3. Motivational Intensity Theory and Effort Withdrawal

Similar effort allocation patterns appear across diverse domains of human performance. In educational settings, students systematically withdraw effort when material becomes overwhelmingly difficult, exhibiting reduced time-on-task and increased task abandonment. In problem-solving contexts, participants show decreased persistence and exploration when problems exceed their capacity thresholds.

These patterns are not indicative of laziness or inability but reflect adaptive resource management that preserves cognitive resources for more tractable challenges. The universality of these phenomena across human cognition suggests that they represent fundamental features of bounded rational systems rather than specific limitations.

3.4. Cross-Domain Validation

The patterns of effort allocation and disengagement observed in both human physiology and LRM computational behavior extend across diverse domains of performance under cognitive load, providing robust cross-domain validation for the theoretical framework.

In educational settings, students systematically withdraw effort when material becomes overwhelmingly difficult, exhibiting reduced time-on-task and increased task abandonment, behavioral manifestations of the same underlying resource management strategy documented physiologically by Kahneman and Beatty. When learning demands exceed cognitive capacity, students demonstrate the same inverted-U effort pattern: initial increases in study time and engagement with difficulty, followed by strategic disengagement when costs exceed perceived benefits.

In human–computer interaction contexts, users exhibit analogous patterns when confronting complex digital interfaces. Task abandonment rates increase exponentially when cognitive load exceeds manageable thresholds, mirroring both the physiological disengagement patterns in laboratory studies and the computational resource withdrawal observed in LRMs. These consistent patterns across domains suggest fundamental principles of bounded rationality rather than domain-specific limitations.

Clinical research provides additional validation through studies of cognitive fatigue in neurological populations. Patients with conditions affecting cognitive resources show exaggerated versions of the same effort allocation patterns: steeper increases in physiological effort markers followed by more pronounced withdrawal when capacity limits are reached. This pathological amplification of normal patterns further supports the interpretation that both human and LRM behaviors reflect universal features of resource-constrained reasoning systems rather than illusions or failures.

The critique by Lawsen reveals that many “reasoning failures” documented in the Apple study stem from experimental design issues rather than cognitive limitations [9]. Their analysis demonstrates that models explicitly recognize output constraints (“The pattern continues, but to avoid making this too long, I’ll stop here”), that River Crossing puzzles with N ≥ 6 are mathematically impossible with the given boat capacity, and that alternative representations (requesting generating functions instead of exhaustive move lists) restore high performance on previously “failed” problems.

4. Discussion and Future Directions

Reframing LRM limitations as manifestations of bounded rationality fundamentally changes how we evaluate these systems. Rather than viewing performance collapse and effort reduction as failures, we can understand them as evidence of sophisticated resource management strategies that emerge naturally from systems operating under computational constraints.

This perspective suggests that current LRMs may be more cognitively sophisticated than previously recognized. The ability to adaptively allocate computational resources based on implicit assessments of task tractability represents a form of metacognitive awareness that parallels human cognitive monitoring systems. In this context, ‘metacognitive’ refers to system-level adjustments based on internal signals, not conscious reflection. The similarity to human processes is functional, not literal.

A recent methodological analysis by Lawsen reveals that many “reasoning failures” documented in the Apple study stem from experimental design issues rather than cognitive limitations [9]. This analysis demonstrates that models explicitly recognize output constraints (“The pattern continues, but to avoid making this too long, I’ll stop here”), that River Crossing puzzles with N ≥ 6 are mathematically impossible with the given boat capacity, and that alternative representations (requesting generating functions instead of exhaustive move lists) restore high performance on previously “failed” problems.

This methodological critique aligns powerfully with my dual-process reinterpretation. If the “illusion of thinking” is itself illusory, arising from evaluation artifacts rather than genuine reasoning deficits, then the patterns I identify as manifestations of bounded rationality become even more compelling. The reduction in reasoning tokens at high complexity may indeed reflect sophisticated resource management: models recognize when exhaustive enumeration becomes impractical and adaptively shift to more efficient representations or strategic truncation.

This convergence of methodological critique and theoretical reframing suggests that LRM behavior reflects neither illusion nor failure, but rather adaptive computational strategies that parallel human cognitive resource allocation. The apparent “collapse” may represent rational disengagement from tasks that exceed practical constraints rather than fundamental reasoning limitations.

4.1. The Illusion of the Illusion: Methodological Artifacts vs. Cognitive Phenomena

Understanding LRM behavior through dual-process theory suggests several design directions. Systems might benefit from explicit dual-process architectures that route simple problems to efficient System 1-like processing while reserving expensive System 2-like deliberation for problems that genuinely require it. Such architectures could implement dynamic resource allocation based on real-time assessments of problem complexity and success probability.

Additionally, the recognition that effort withdrawal represents rational behavior rather than failure suggests the need for evaluation paradigms that consider resource efficiency alongside accuracy. Current benchmarks that focus solely on final answer correctness may miss important aspects of computational intelligence related to strategic resource allocation.

4.2. Implications for Understanding Artificial Reasoning

This theoretical reinterpretation, while compelling, requires empirical validation. Future research should directly compare LRM computational patterns with human physiological markers during analogous tasks, testing whether the proposed correspondences hold quantitatively. Additionally, interventional studies that manipulate perceived task difficulty or success probability could test whether LRMs exhibit the same strategic effort allocation patterns observed in human cognition.

The framework also requires extension beyond the specific puzzle environments examined by Shojaee et al. [1]. Testing whether dual-process interpretations apply to LRM behavior across diverse reasoning domains would strengthen the generalizability of this theoretical approach. Although the present analysis centers on well-controlled puzzles such as the Tower of Hanoi and River Crossing, these tasks sample only a narrow corner of the reasoning landscape. To establish the generality of the dual-process account, future work should probe ill-structured or creative challenges. Such challenges could involve open-ended analogy generation, insight problems, and multi-step design tasks.

4.3. Design Implications

Although detailed engineering designs are beyond the scope of this hypothesis paper and remain a target for future work, understanding LRM behavior through dual-process theory still points to several principled design directions that could improve both the efficiency and capability of reasoning systems.

Explicit dual-process architectures: Systems might benefit from architectures that explicitly implement System 1 and System 2 processing pathways. Simple problems could be routed to efficient pattern-matching components (System 1 analogs) while complex tasks engage deliberative reasoning mechanisms (System 2 analogs). In practice, the router could be a lightweight policy network that receives a compact feature vector (prompt length, syntactic depth, entropy of next-token distribution) from a frozen encoder and outputs a discrete routing decision. This dynamic routing, based on real-time assessment of task complexity, could prevent the inefficiencies observed when LRMs “overthink” simple problems while reserving computational resources for tasks that genuinely require deliberation. Complementary evidence comes from recent emotion-aware LLM work showing that hierarchical fusion layers coupled with lightweight attention gates can provide an ultra-fast ‘affective sentinel’ for routing [23,24]. Such modules could supply the System 1 complexity signal that triggers the router envisioned here.

Adaptive resource management: The counterintuitive reduction in reasoning tokens at high complexity suggests that current LRMs already implement rudimentary resource management strategies. Future systems could make these mechanisms explicit. For example, a metacognitive head could be constructed that tracks the marginal perplexity improvement per extra reasoning token. When the perplexity to token improvement falls below a learned threshold, the module truncates the Chain-of-Thought and returns the best current hypothesis. Thus, rather than viewing effort reduction as failure, systems could be designed to recognize when strategic disengagement represents optimal resource allocation. Embedding the same hierarchical fusion monitors inside the metacognitive head would let LRMs link token budget decisions to transient affective load, offering a concrete, testable implementation of the dual-process resource manager.

Capacity-aware training: Training paradigms could incorporate principles from human cognitive psychology, including deliberate practice within capacity limits and strategic rest periods that mirror sleep-inspired consolidation. Multi-phase training with alternating periods of challenge and consolidation could improve both learning efficiency and robustness, preventing the cognitive overload that leads to systematic disengagement.

Evaluation beyond accuracy: Current benchmarks that focus solely on final answer correctness miss important aspects of computational intelligence related to resource efficiency. New evaluation frameworks should consider effort allocation, strategic disengagement patterns, and the ability to adaptively match computational investment to problem tractability, recognizing that optimal performance sometimes involves choosing not to expend excessive resources on intractable problems.

5. Conclusions

The phenomenon of computational effort reduction in Large Reasoning Models at high complexity levels may represent not system failures but authentic manifestations of resource management processes. These patterns parallel human cognitive constraints established in foundational research dating back to Kahneman and Beatty’s 1966 work [6]. This hypothesis, while compelling, remains empirically testable and potentially refutable through controlled experiments. Such experiments could examine the proposed parallels between human cognitive effort and LRM computational patterns.

The similarity between human physiological effort markers and LRM computational patterns, both exhibiting characteristic inverted-U relationships where effort initially scales with demands then declines at capacity limits, provides compelling evidence against dismissing these behaviors as mere technical failures. Lawsen convincingly demonstrates that many apparent ‘collapses’ stem from token-limiting artifacts and unsolvable puzzles [9]. The present work, however, extends their negative critique by explaining the residual, benchmark-clean performance pattern through bounded rational dual-process dynamics, thereby reframing what they showed to be artifacts as evidence of an adaptive resource allocation strategy.

By applying dual-process theory to LRM behavior, we gain deeper insight into both the capabilities and limitations of current reasoning systems. The three-regime performance pattern, effort scaling dynamics, and strategic disengagement at high complexity all align with well-established phenomena in human cognitive psychology. Rather than indicating fundamental reasoning failures, these behaviors suggest that LRMs exhibit bounded rationality, adaptively managing computational resources under constraints in ways that mirror human cognitive strategies.

Shenhav et al.’s expected-value-of-control model remains agnostic about implementation in artificial agents [11]. The mapping presented here, on the other hand, translates those effort allocation principles into concrete LRM design levers, such as dynamic Chain-of-Thought routing and scheduled ‘rest buffers’, thus offering an actionable blueprint for dual-process AI architectures.

This theoretical framework generates several testable predictions that could further validate the dual-process interpretation. LRMs should demonstrate computational effort metrics analogous to pupillometry patterns, with token usage following the characteristic increase–plateau–decline trajectory observed in human physiological studies. If these systems truly exhibit cognitive-like resource management, brief “rest” periods should improve subsequent reasoning performance, similarly to how human cognitive fatigue can be mitigated through recovery intervals. Additionally, interleaved training schedules that alternate between different complexity levels should prove more effective than sequential training approaches, paralleling established findings in human learning research.

Accordingly, I call for experiments that couple LRM token trajectory logging with human effort measures in open-ended analogy generation, insight problems, or multi-step design tasks, thereby testing whether the same bounded-rational dynamics emerge beyond canonical puzzles. Empirical validation could involve specific experimental protocols: (1) training LRMs on complex reasoning tasks until performance degrades, then introducing computational “rest” periods (model pausing or low-complexity tasks) before resuming, measuring performance recovery; (2) collecting human pupillometry data during Tower of Hanoi or similar puzzle tasks while simultaneously measuring LRM token generation patterns in identical problems, testing for a statistical correlation between physiological and computational effort trajectories; and (3) comparing LRMs trained with interleaved complexity schedules versus sequential progression, measuring both final performance and reasoning efficiency.

This theoretical framework generates several testable predictions that could further validate the dual-process interpretation. LRMs should demonstrate computational effort metrics analogous to human physiological markers, including the well-documented inverted-U curve observed in pupillometry studies [6,7]. If these systems truly engage in bounded resource management, then structured computational “rest” periods should yield performance recoveries similar to those seen in humans experiencing cognitive fatigue. Moreover, training regimens that interleave task complexities, rather than relying on uniform progression, could mirror cognitive learning benefits established in both psychology and machine learning research [15,17].

Accordingly, I propose a set of empirical studies that combine LRM token trajectory logging with human effort measures on tasks such as open-ended analogy generation or multi-step design challenges. These studies would examine whether both humans and LRMs exhibit the same dynamic resource allocation patterns under varying load conditions. Specific protocols could include (1) training LRMs on challenging reasoning tasks until performance degrades, followed by lightweight inference phases to simulate cognitive rest; (2) simultaneous collection of pupillometry data and token usage during Tower of Hanoi tasks; and (3) comparing models trained with interleaved versus sequential problem complexities, as advocated for in the context of utilization studies [16]. These investigations may also help clarify whether LLMs’ difficulty with distractors and structural noise, as shown by Jiang et al. [12] and Mirzadeh et al. [13], reflects fundamental limitations or tractable symptoms of bounded rationality. Ultimately, such research could move us beyond surface-level metrics and toward a deeper understanding of reasoning processes in both artificial and biological systems.