G-CTRNN: A Trainable Low-Power Continuous-Time Neural Network for Human Activity Recognition in Healthcare Applications
Abstract
Featured Application
Abstract
1. Introduction and Literature Review
1.1. Introduction
1.2. Related Work
2. Continuous-Time Recurrent Neural Network (CTRNN)
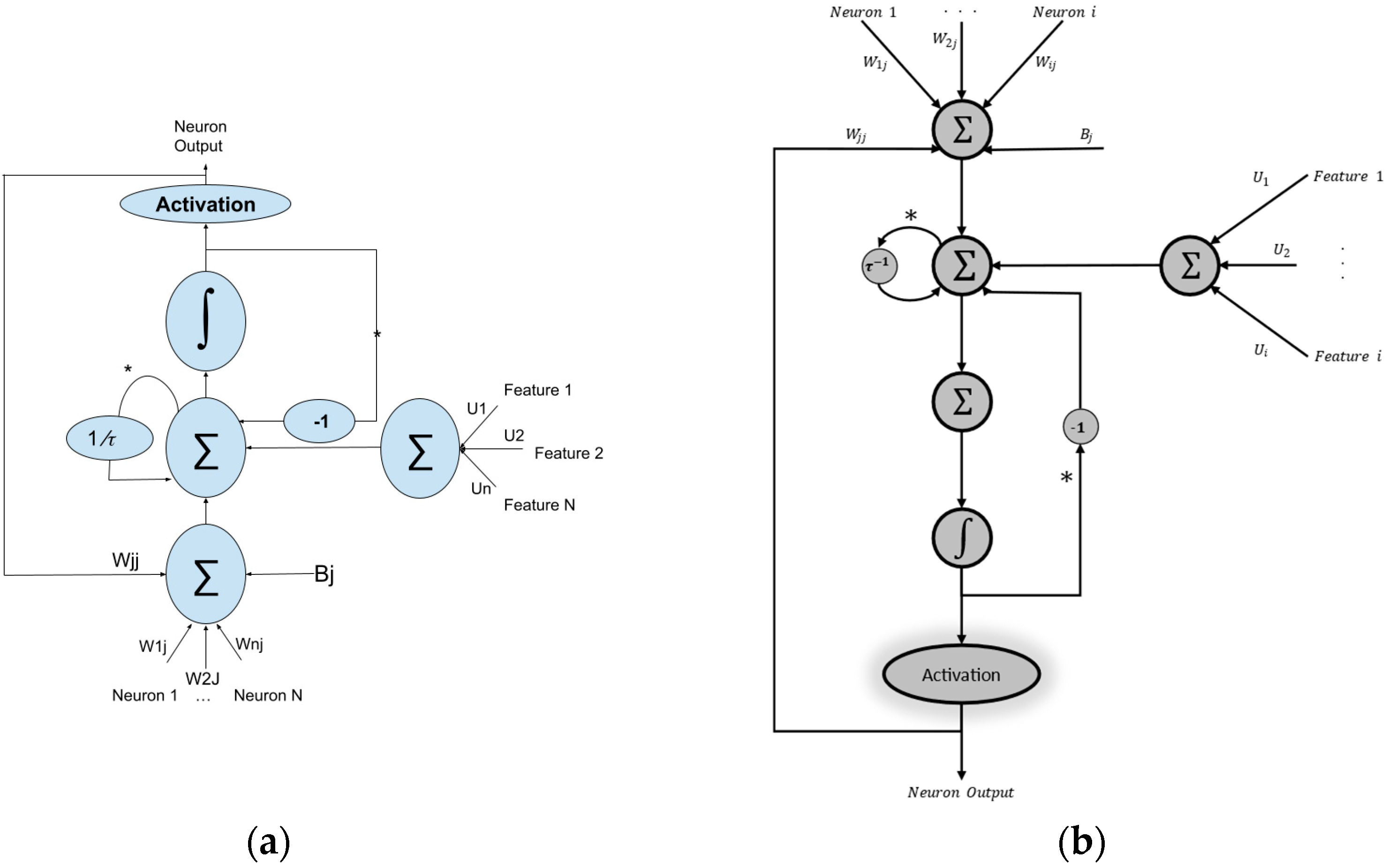
2.1. CTRNN Model
2.2. MEMS Analogy
2.3. Time Constant Effect
3. Model Development and Training
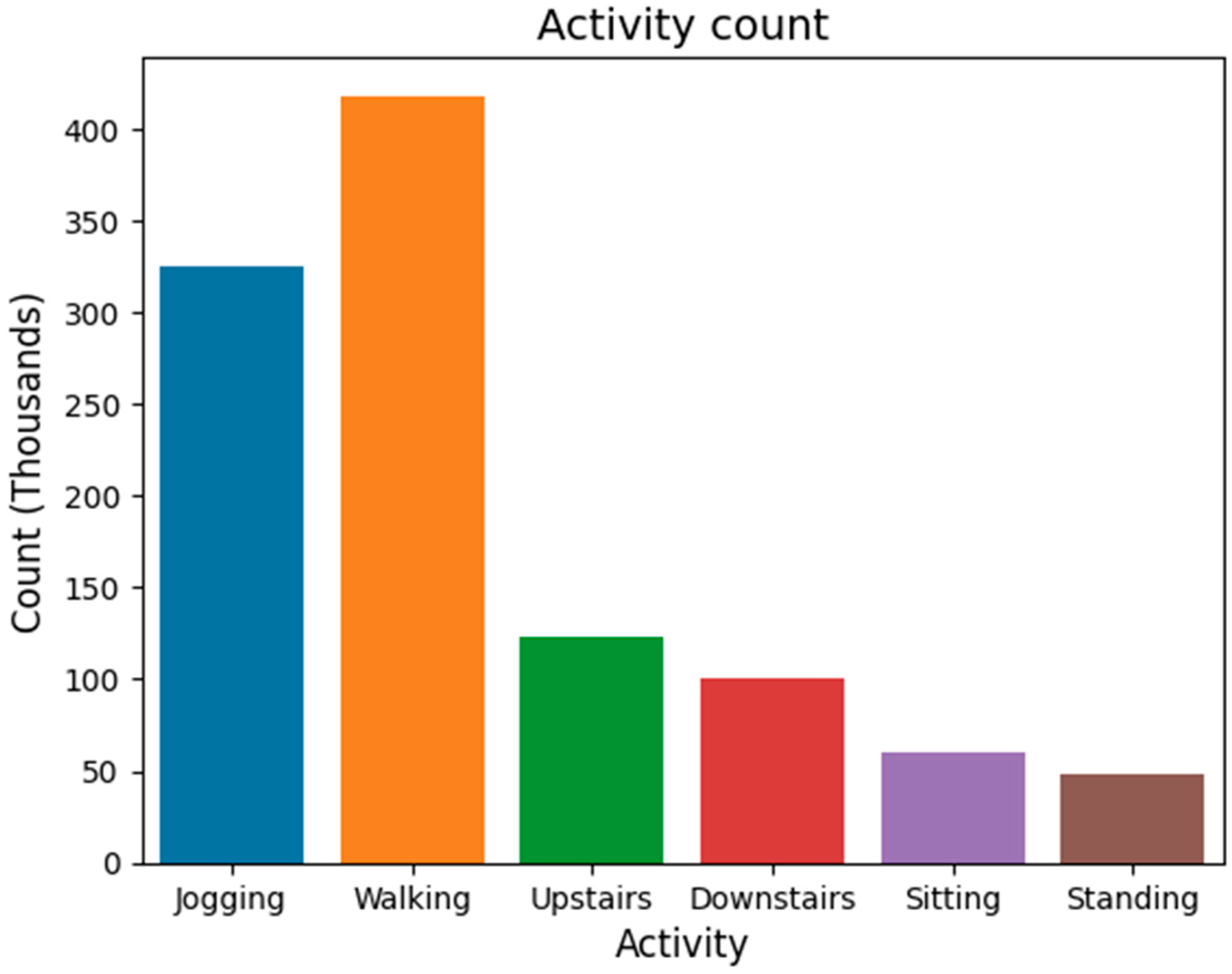
3.1. Human Activity Detection
3.2. Model Structure
3.3. Backpropagation and Backpropagation Through Time
3.4. G-CTRNN Time Constant Training
4. Result
4.1. Time-Constant Effects
4.2. A Parameter Size Comparison Between RNN and G-CTRNN
4.3. Computational Overhead
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Metric/Model | Activity Name | ||||||
|---|---|---|---|---|---|---|---|
| Metric | Model (Cells) | Downstairs | Jogging | Sitting | Standing | Upstairs | Walking |
| Sensitivity | G-CTRNN (16) | 0.44 | 0.96 | 0.93 | 0.96 | 0.64 | 0.88 |
| RNN (32) | 0.44 | 0.96 | 0.93 | 0.96 | 0.60 | 0.88 | |
| G-CTRNN (4) | 0.17 | 0.88 | 0.94 | 0.97 | 0.46 | 0.79 | |
| RNN (16) | 0.44 | 0.98 | 0.87 | 0.96 | 0.45 | 0.66 | |
| Specificity | G-CTRNN (16) | 0.96 | 0.97 | 0.99 | 0.99 | 0.91 | 0.94 |
| RNN (32) | 0.95 | 0.97 | 0.99 | 0.99 | 0.91 | 0.94 | |
| G-CTRNN (4) | 0.97 | 0.94 | 0.99 | 0.98 | 0.91 | 0.82 | |
| RNN (16) | 0.96 | 0.89 | 0.99 | 0.97 | 0.91 | 0.92 | |
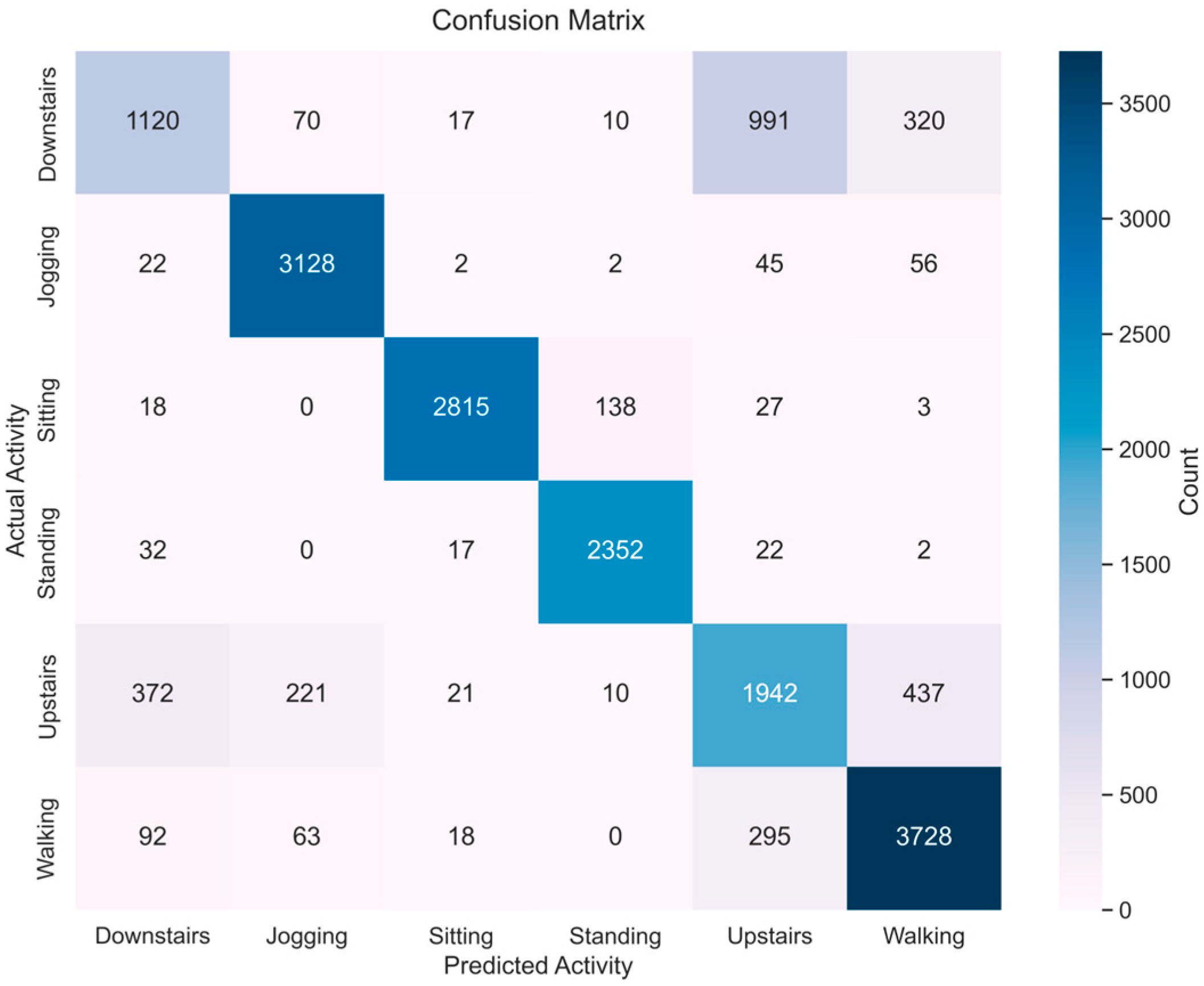
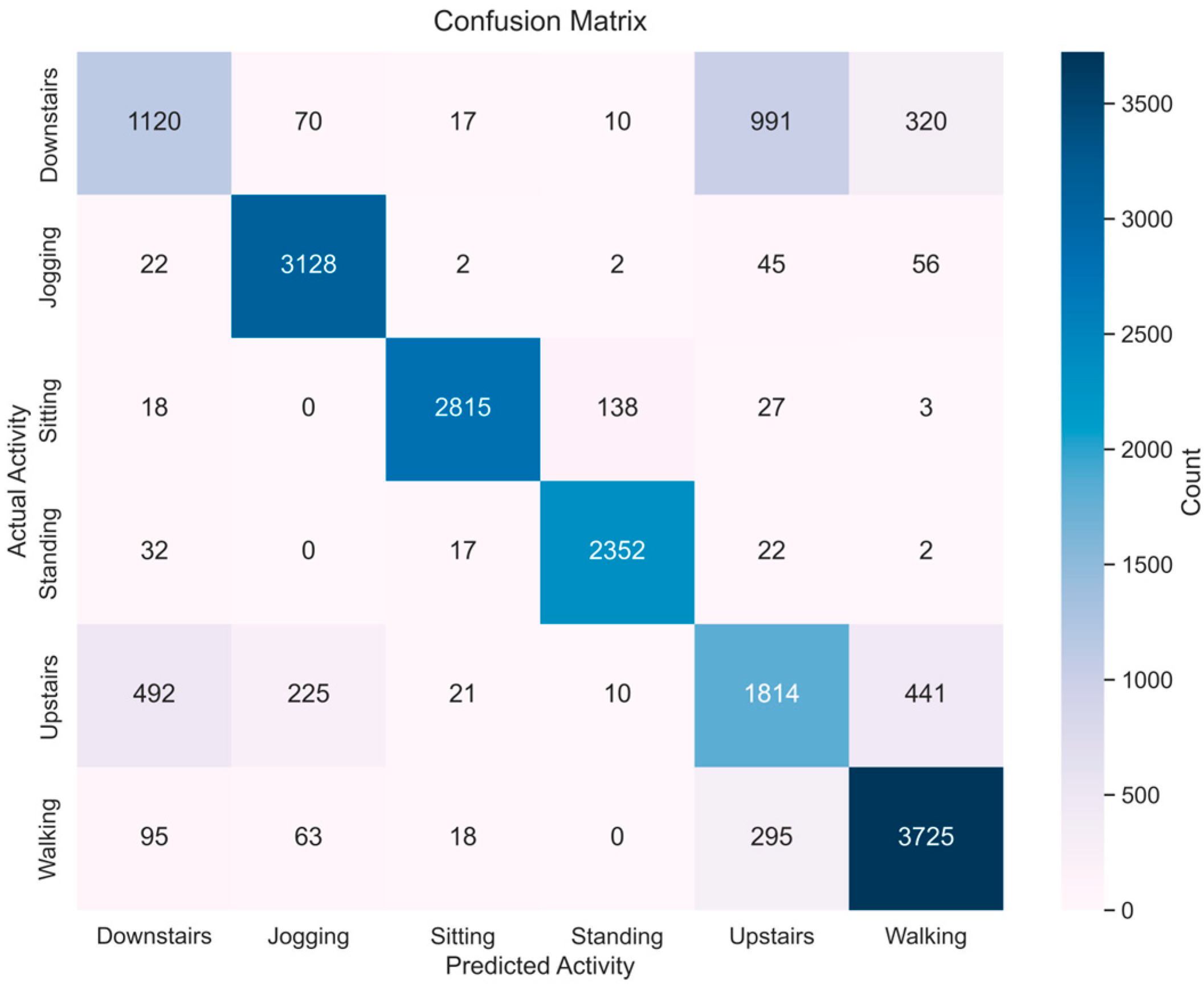


References
- Yu, Y.; Zhou, Z.; Xu, Y.; Chen, C.; Guo, W.; Sheng, X. Toward Hand Gesture Recognition Using a Channel-Wise Cumulative Spike Train Image-Driven Model. Cyborg Bionic Syst. 2025, 6, 0219. [Google Scholar] [CrossRef] [PubMed]
- Luo, M.; Yin, M.; Li, J.; Li, Y.; Kobsiriphat, W.; Yu, H.; Xu, T.; Wu, X.; Cao, W. Lateral Walking Gait Recognition and Hip Angle Prediction Using a Dual-Task Learning Framework. Cyborg Bionic Syst. 2025, 6, 0250. [Google Scholar] [CrossRef] [PubMed]
- Beer, R.D. On the dynamics of small continuous-time recurrent neural networks. Adapt. Behav. 1995, 3, 469–509. [Google Scholar] [CrossRef]
- Elman, J.L. Finding structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Cauwenberghs, G. An analog VLSI recurrent neural network learning a continuous-time trajectory. IEEE Trans. Neural Netw. 1996, 7, 346–361. [Google Scholar] [CrossRef] [PubMed]
- Alsaleem, F.M.; Hasan, M.H.H.; Tesfay, M.K. A MEMS Nonlinear Dynamic Approach for Neural Computing. J. Microelectromech. Syst. 2018, 27, 780–789. [Google Scholar] [CrossRef]
- Emad-Ud-Din, M.; Hasan, M.H.; Jafari, R.; Pourkamali, S.; Alsaleem, F. Simulation for a MEMS-Based CTRNN Ultra-Low Power Implementation of Human Activity Recognition. Front. Digit. Health 2021, 3, 731076. [Google Scholar] [CrossRef]
- Rafaie, M.; Hasan, M.H.; Alsaleem, F.M. Neuromorphic MEMS Sensor Network. Appl. Phys. Lett. 2019, 114, 163501. [Google Scholar] [CrossRef]
- Funahashi, K.; Nakamura, Y. Approximation of Dynamical Systems by Continuous Time Recurrent Neural Networks. Neural Netw. 1993, 6, 801–806. [Google Scholar] [CrossRef]
- De Falco, I.; Tarantino, E.; Della Cioppa, A.; Marcelli, A.; Salvatore, C. CTRNN Parameter Learning Using Differential Evolution. In ECAI 2008; IOS Press: Amsterdam, The Netherlands, 2008; pp. 783–784. [Google Scholar]
- Bown, O.; Lexer, S. Continuous-Time Recurrent Neural Networks for Generative and Interactive Musical Performance. In Applications of Evolutionary Computation; Springer: Berlin/Heidelberg, Germany, 2006; pp. 652–663. [Google Scholar]
- Chen, R.T.Q.; Rubanova, Y.; Bettencourt, J.; Duvenaud, D. Neural Ordinary Differential Equations. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 3–8 December 2018; Available online: https://arxiv.org/abs/1806.07366 (accessed on 28 May 2025).
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic Differentiation in Machine Learning: A Survey. J. Mach. Learn. Res. 2018, 18, 5595–5637. [Google Scholar]
- Ma, L.; Cheng, S.; Shi, Y. Enhancing Learning Efficiency of Brain Storm Optimization via Orthogonal Learning Design. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 6723–6742. [Google Scholar] [CrossRef]
- Li, N.; Xue, B.; Ma, L.; Zhang, M. Automatic Fuzzy Architecture Design for Defect Detection via Classifier-Assisted Multiobjective Optimization Approach. In Proceedings of the IEEE Transactions on Evolutionary Computation, Hangzhou, China, 8–12 June 2025. [Google Scholar]
- Wei, X.; Wang, Z. TCN-attention-HAR: Human activity recognition based on attention mechanism time convolutional network. Sci. Rep. 2024, 14, 7414. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Xiong, B.; Huang, Y.; Xu, C. Cross-modal federated human activity recognition. In IEEE Transactions on Pattern Analysis and Machine Intelligence; IEEE Computer Society: Washington, DC, USA, 2024; Volume 46. [Google Scholar]
- Hasan, M.H.; Alsaleem, F.; Rafaie, M. Sensitivity study for the PMV thermal comfort model and the use of wearable devices biometric data for metabolic rate estimation. Build. Environ. 2016, 110, 173–183. [Google Scholar] [CrossRef]
- Zhang, S.; Li, Y.; Zhang, S.; Shahabi, F.; Xia, S.; Deng, Y.; Alshurafa, N. Deep learning in human activity recognition with wearable sensors: A review on advances. Sensors 2022, 22, 1476. [Google Scholar] [CrossRef]
- Wu, J.; Jafari, R. Orientation independent activity/gesture recognition using wearable motion sensors. IEEE Internet Things J. 2018, 6, 1427–1437. [Google Scholar] [CrossRef]
- Patel, S.N.; Reynolds, M.S.; Abowd, G.D. Detecting human movement by differential air pressure sensing in HVAC system ductwork: An exploration in infrastructure mediated sensing. In Proceedings of the Pervasive Computing: 6th International Conference, Pervasive 2008, Sydney, Australia, May 19–22 May 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–18. [Google Scholar]
- Yin, J.; Yang, Q.; Pan, J.J. Sensor-based abnormal human-activity detection. IEEE Trans. Knowl. Data Eng. 2008, 20, 1082–1090. [Google Scholar] [CrossRef]
- Kwapisz, J.R.; Weiss, G.M.; Moore, S.A. Activity recognition using cell phone accelerometers. ACM SIGKDD Explor. Newsl. 2011, 12, 74–82. [Google Scholar]
- Perea, J.A.; Harer, J. Sliding windows and persistence: An application of topological methods to signal analysis. Found. Comput. Math. 2015, 15, 799–838. [Google Scholar] [CrossRef]
- Honda, H. Universal approximation property of a continuous neural network based on a nonlinear diffusion equation. Adv. Contin. Discrete Models 2023, 2023, 43. [Google Scholar] [CrossRef]
- Werbos, P.J. Backpropagation through time: What it does and how to do it. Proc. IEEE 2002, 78, 1550–1560. [Google Scholar] [CrossRef]
- Kingma, D.P. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A system for Large-Scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. Available online: https://www.usenix.org/conference/osdi16/technical-sessions/presentation/abadi (accessed on 28 May 2025).
- Geron, A. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow: Unsupervised Learning Techniques; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2019. [Google Scholar]
- Csáji, B.C. Approximation with artificial neural networks. Fac. Sci. Eötvös Loránd Univ. Hungary 2001, 24, 7. [Google Scholar]
- Krogh, A.; Hertz, J. A simple weight decay can improve generalization. Adv. Neural Inf. Process. Syst. 1991, 4, 951. [Google Scholar]
- Park, J.-T.; Shim, K.-S.; Lee, S.-H.; Kim, M.-S. Classification of application traffic using tensorflow machine learning. In Proceedings of the 2017 19th Asia-Pacific Network Operations and Management Symposium (APNOMS), Seoul, Republic of Korea, 27–29 September 2017; pp. 391–394. [Google Scholar]


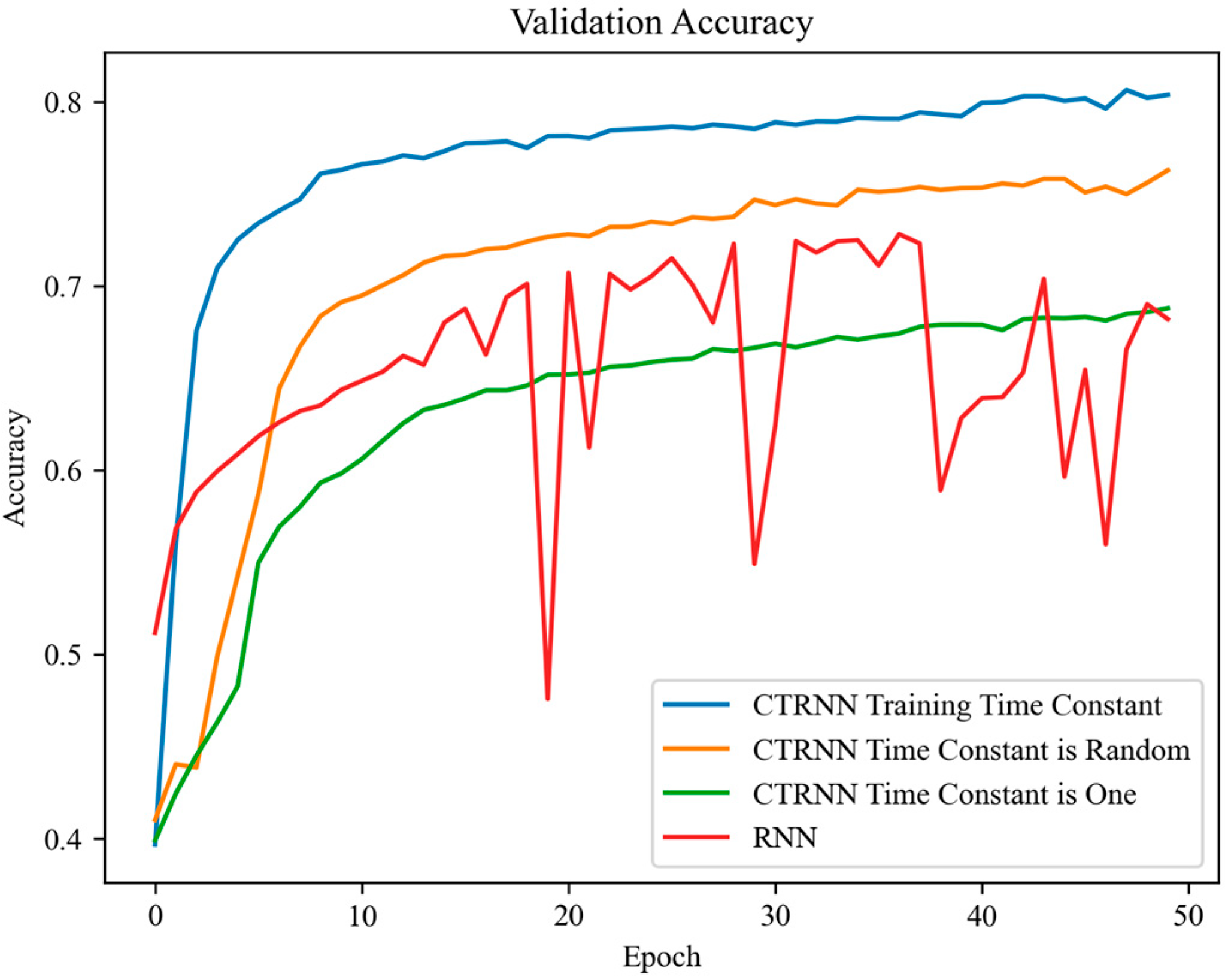
| G-CTRNN Model | Accuracy % |
|---|---|
| Static time constant equals one | 68.2 ± 0.6 |
| Random-initialization time constant | 76.1 ± 2.1 |
| Training the time constant | 81.9 ± 1.4 |
| G-CTRNN Model (Recurrent Cells) | Network Parameters Size | Accuracy % |
|---|---|---|
| G-CTRNN (16) | 572 | 81.9 ± 1.4 |
| RNN (32) | 1548 | 81.4 ± 1.2 |
| G-CTRNN (4) | 156 | 71.8 ± 1.1 |
| RNN (16) | 556 | 73.1 ± 0.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alzubi, A.; Lin, D.; Reimann, J.; Alsaleem, F. G-CTRNN: A Trainable Low-Power Continuous-Time Neural Network for Human Activity Recognition in Healthcare Applications. Appl. Sci. 2025, 15, 7508. https://doi.org/10.3390/app15137508
Alzubi A, Lin D, Reimann J, Alsaleem F. G-CTRNN: A Trainable Low-Power Continuous-Time Neural Network for Human Activity Recognition in Healthcare Applications. Applied Sciences. 2025; 15(13):7508. https://doi.org/10.3390/app15137508
Chicago/Turabian StyleAlzubi, Abdallah, David Lin, Johan Reimann, and Fadi Alsaleem. 2025. "G-CTRNN: A Trainable Low-Power Continuous-Time Neural Network for Human Activity Recognition in Healthcare Applications" Applied Sciences 15, no. 13: 7508. https://doi.org/10.3390/app15137508
APA StyleAlzubi, A., Lin, D., Reimann, J., & Alsaleem, F. (2025). G-CTRNN: A Trainable Low-Power Continuous-Time Neural Network for Human Activity Recognition in Healthcare Applications. Applied Sciences, 15(13), 7508. https://doi.org/10.3390/app15137508








