EPO Extension of Dispatching Rules to Minimize Effects of Time Uncertainty in Production Scheduling

Abstract

The increasingly widespread concept of Industry 4.0 and Digital Twins, as well as the competitive global markets, make it essential to produce goods in a timely and cost-effective manner. Therefore, one of the most important requirements for current production scheduling systems is to automate the control of production progress and to quickly correct schedules in response to feedback from production machines while minimizing the number of changes in the order of tasks to be performed. In this paper, we propose a new extension to the dispatching rules, which takes into account the uncertainty of job processing times and allows for the production of robust schedules. The important feature of the proposed extension is that it does not increase the computational time of the underlying techniques, i.e., it has no negative impact on their most important advantage over other production scheduling algorithms. The results obtained from the real data of a large international offset printing company with various machine and job heterogeneities confirm the effectiveness of the proposed EPO extension in producing schedules that are indeed robust to changes in production time.

1. Introduction

Fuller et al. [1] define the concept of digital twins as “dynamic virtual representations of physical objects or systems that rely on real-time and historical data to enable understanding, learning, and reasoning.” In the realm of modern manufacturing and production processes, the integration of digital twin technology is revolutionizing the way planning and scheduling are approached. Digital twin technology enables real-time monitoring, scenario analysis, and optimization of production processes by creating a virtual replica of physical resources, processes, or systems. DT plays an essential role in receiving real-time data for scheduling simulation and prediction, ultimately allowing adjustments to scheduling plans based on virtual feedback [2], enabling dynamic rescheduling in production systems, and improving overall efficiency and responsiveness to unexpected events [3]. Many research studies highlight the importance of integrating digital twin technology with planning and scheduling systems to effectively manage uncertain factors in production activities [4].

Competitive global markets make it essential to produce goods in a timely and cost-effective manner. However, this requires collaboration between supply chain participants to develop effective supply management strategies, planning, and scheduling of equipment and personnel. To maximize machine utilization, manufacturers must implement efficient operational schedules [5]. Recent literature reviews dedicated to production planning, scheduling, sequencing [6], as well as scheduling in Industry 4.0 [7] show that the problem of scheduling is still a pressing issue. This is also evidenced by a recent increase in the number of publications on this topic.

In this evolving industrial landscape, digital twins (DT) have emerged as a key enabler of real-time data acquisition and system transparency. However, the mere availability of real-time data does not inherently guarantee robust or effective planning. The inherent heterogeneity and dynamic nature of data generated within digital twin environments significantly exacerbate the complexity of scheduling tasks, which surpasses the capabilities of traditional algorithmic approaches to maintain robustness and responsiveness under uncertainty. Consequently, there is a growing demand for advanced algorithmic frameworks such as simheuristics, robust optimization, stochastic programming, and machine learning capable of dynamically interpreting real-time inputs and generating schedules that remain stable and efficient under a wide range of operational conditions [8].

Scheduling can be briefly defined as the process of allocation of scarce resources over time [9,10]. In the context of job scheduling, it deals with the allocation of resources to jobs over given time periods in order to optimize one or more objective functions. This decision-making process plays a very important role in the manufacturing and service industries [10]. The consequences of poor scheduling in manufacturing practice could be unnecessary tension on the shop floor, poor productivity, and problems with meeting due dates required by customers. According to APICS (American Production and Inventory Control Society), “detailed scheduling of jobs relies on assignment of resources starting and/or completion dates to operations or groups of operations to show when these must be done if the manufacturing order is to be completed on time” [11].

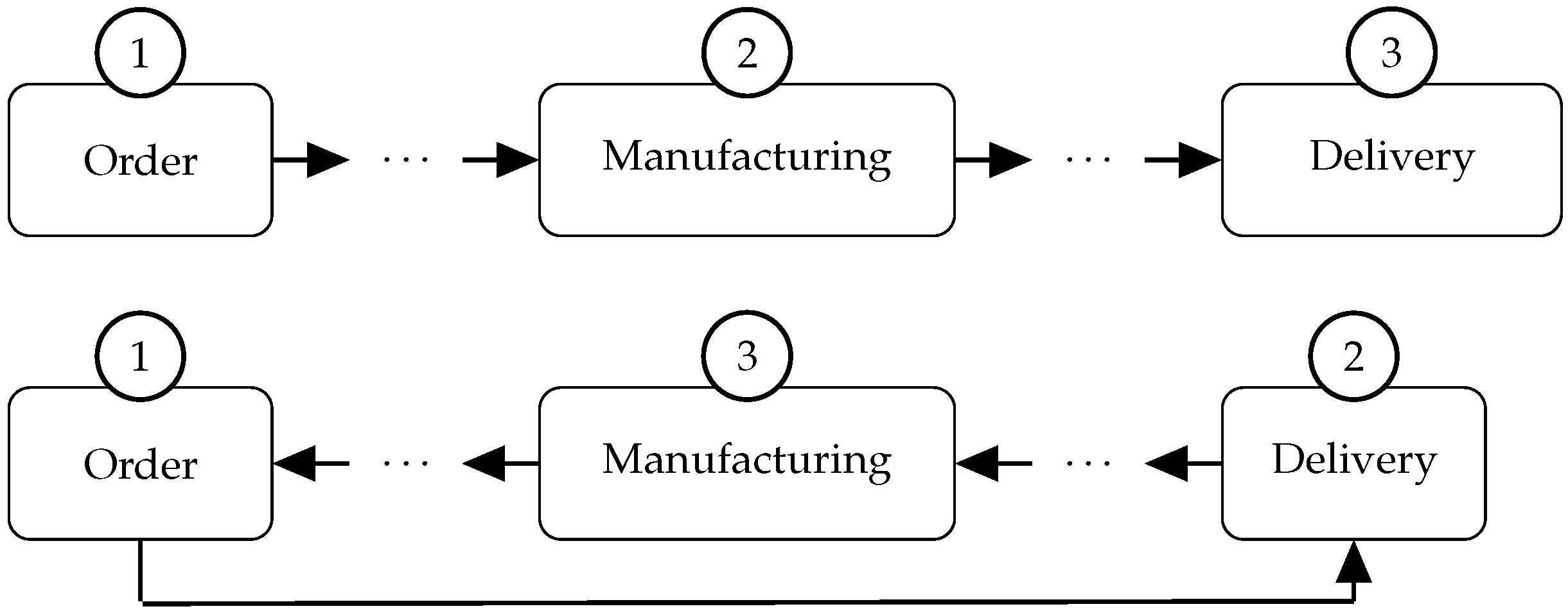
There are two most well-known approaches to production scheduling: forward and backward (see Figure 1). In forward scheduling, resources are assigned to jobs as early as possible, i.e., when both job and resource are available. This can be easily performed manually by a planner, and it typically ensures continuous machine utilization as long as there are jobs to be scheduled. Such an approach to scheduling may, however, result in larger inventories of finished products in the case of make-to-order production, capital being frozen in the produced but not yet delivered production, and the impossibility of planning new tasks that have appeared and have tight deadlines, without a significant reconstruction of the schedule. Backward scheduling works on a just-in-time basis; resources are assigned as late as possible to meet the due dates required by the customers.

The main advantage of this approach is the reduction in stocks of finished products and work in progress, which results in the reduction in storage costs. It also results in a more rational use of capacity—machines are used when necessary. Consequently, it is easier to react to unforeseen events such as the emergence of new orders. The main disadvantage of this approach is the lack of any time buffers, which, in the event of unexpected situations in the production process, such as machine failure or prolonged production, may result in the failure to meet the promised shipping dates.

The problem of forward or backward production scheduling can be solved in many different ways. The most frequently used methods in APS (Advanced Planning and Scheduling) systems are heuristics using static or dynamic dispatching rules. The reflection of changes in the state of production can be realized in two essential ways: through reactive or proactive scheduling. Reactive scheduling requires dynamic rescheduling of jobs each time production parameters change. It is necessary to develop algorithms that try to ensure the minimum number of changes in the schedule; but in cases of complex dependencies between jobs and continuous machine occupancy, this is not always possible. Proactive scheduling is about developing schedules that try to resist changes in parameters by modeling the applicable uncertainty. Ho [12] categorizes the uncertainty that affects the production process into two groups: environmental uncertainty (related to demand or supply) and system uncertainty (related to operation yield, production lead time, quality, or failure of production systems and changes to product structures). A more detailed classification of uncertainties in production systems can be found, for example, in [13]. Uncertainty in production scheduling can be taken into account in several ways—the most frequently used is the approach based on fuzzy numbers, stochastic optimization, or computer simulation.

The first applications of fuzzy logic in production planning and scheduling concerned its use in expert decision support systems in the field of aggregate production planning. Such systems were introduced, among others, by Rinks [14], Yao, and Türkşen [15]. Later, detailed scheduling systems with the use of fuzzy logic appeared. One of the first such systems, named OPAL, was proposed by Bensana et al. [16] and used 5 different selection criteria and 15 different static and dynamic dispatching rules. Grabot and Geneste [17] used fuzzy logic to create aggregated rules for job shop scheduling, achieving a compromise between several dispatching rules. A similar approach was also described by Türkşen and Zarandi [18]. Subsequently, fuzzy logic began to be applied not only to select priority rules but also to describe uncertain production parameters. McCahon and Lee [19] proposed a sequencing model with processing times described as trapezoidal fuzzy numbers. Hong et al. [20] presented a fuzzy Longest Processing Time (LTP) algorithm for scheduling, in which the processing time of each job was described by the discrete membership function. Execution times were similarly described in [21], but this time for the constraint satisfaction approach. Later, Dubois et al. [22] also pointed out that uncertainty may also apply to constraints to make them more flexible. In addition to theoretical works, examples of using fuzzy logic to describe uncertainty in real production systems are presented. Schultmann et al. [23] applied fuzzy numbers to plan and schedule under uncertain operation times in paints manufacturing, while Gholami-Zanjani et al. [24] applied fuzzy numbers to schedule the PCB (Printed Circuit Board) assembly facility.

However, using fuzzy numbers to handle uncertainty in the production process requires the definition of the membership function, which is not always possible or practical; moreover, this function may change depending on the current state of the production system. For the purposes of scheduling in Industry 4.0, alternatives are proposed [25], for example, by using tolerances, but this does not make the schedule robust for larger variations in production process parameters. Therefore, the stochastic approach is becoming more and more popular for the actual planning of production systems. In the review of different methods for the flow-shop scheduling problem under uncertainties [26], the stochastic approach was used in 60% of the articles (fuzzy logic in 21%). Basically, stochastic methods can be divided into a non-simulation approach and a simulation-optimization approach. Non-simulation methods are usually based on Markov chain processes and the use of, e.g., dynamic programming. This approach was already proposed in 1968 by Beebe et al. [27] and evolved over the following decades [28,29,30]. This approach can also be used successfully in the context of scheduling in Industry 4.0, but requires the definition of some superior objective function, such as inventory optimization [31] or revenue optimization [32], which is not always the case. The simulation-optimization approach is also increasingly used in production scheduling [33,34,35]. However, the use of such an approach requires a lot of computing power and may be ineffective if frequent rescheduling is required.

In this paper, we present a new approach to take into account the uncertainty of the job processing times. The proposed approach does not require the determination of the membership functions and guarantees that there is no need to recalculate the schedule as in the time-consuming simulation approach. The proposed approach is therefore a relatively simple but effective way to achieve the expected increase in the robustness of production schedules in the framework of Industry 4.0 and Digital Twins technology. Another advantage of this approach is that it does not increase the computational complexity of the scheduling algorithms.

The remainder of this paper is organized as follows. The concept of the proposed EPO extension for dispatching rules and the principle of its operation are described in Section 3. We show how it can be used in dispatching rules for both forward and backward scheduling. Section 4 presents an example of the use of the EPO extension in a real production system, a large offset printing house characterized by a diverse range of products. Section 5 summarizes the obtained results and provides final conclusions.

2. Dispatching Rules

Dispatching rules (DRs) are one of the most widely used scheduling methods in dynamic conditions. They are used to select the next job to be scheduled on a machine. An extensive review of the 26 dispatching rules that can be applied for scheduling in the environment of unrelated machines with release times and under dynamic conditions was discussed by Đurasević and Jakobović [36]. We considered the following ten scheduling objectives to evaluate the quality of the schedules produced using the tested DRs:

• Makespan ($C_{max}$)
• Average Completion Time (AC)
• Maximum flowtime ($F_{max}$)
• Maximum tardiness ($T_{max}$)
• Total weighted completion time (Cw)
• Total weighted tardiness (Twt)
• Total flowtime (Ft)
• Weighted number of tardy jobs (Nwt)
• Weighted earliness andweighted tardiness (Etwt)
• Machine utilization (Mut)

The selected dispatching rules are listed below:

• Minimum completion time (MCT) [37]
• Minimum execution time (MET) [37]
• Weighted shortest processing time (WSPT) [38]
• Sufferage [37]
• Sufferage2 [39]
• Just in time (JIT) [36]
• Longest processing time (LPT) [40]
• Work queue (WQ) [41]
• Relative cost (RC) [42]
• Max-min [37]
• Min-max, [41]
• Earliest realease date (ERD) [40]
• Minimum execution completion time (MECT) [43]
• k-percent best (KPB) [37]
• Ordered minimum completion time (OMCT) [44]
• Opportunistic load balancing (OLB) [45]

Dispatching rules are able to handle dynamic conditions; however, they do not guarantee the robustness of the whole schedule when actual job processing times can vary (in many cases, scheduling is performed on the basis of averaged production standards). The approach proposed (see Section 3) in this paper allows us to include the uncertainty of the job processing times, making the schedules much more robust to dynamic conditions.

3. EPO Extension

Production scheduling can be very time consuming if there is a large number of jobs. Therefore, a range of heuristic algorithms is used in practice. Dispatching rules are a common method to schedule jobs in practice due to their simplicity and efficiency, even for large datasets. However, they have a weakness that is important from a practical point of view, that is, they cannot take into account the uncertainty of processing times. The EPO extension proposed in this paper extends the functionality of the dispatching rules to include the uncertainty of the job processing times, which makes the generated schedules robust while keeping the time complexity of the method the same.

The EPO extension of decision rules describes the uncertain processing time of a job by using the following three values:

• E—expected processing time
• P—pessimistic processing time
• O—optimistic processing time

which satisfy the following inequalities:

$$O⩽E⩽P.$$

Using the values $E,P,O$ (EPO), we can take into account the uncertainty of processing time (PT) of jobs in production scheduling, and therefore we can minimize the makespan and downtime (stemming, for example, from the lack of components needed to continue the production process) of production lines and the need for frequent replanning.

To better illustrate the advantages of the EPO extension, we will use an example. Suppose that in the exemplary scenario, the expected, optimistic, and pessimistic job processing times are 10, 9, and 13 units, respectively. In this scenario, the EPO extension allows for scheduling with implicit time buffers. Specifically, if the job takes 9 time units, the next job can start earlier, as it should be ready to start by the 9th time unit. Conversely, if the job takes 13 time units, subsequent operations will not be delayed. Taking these dependencies into account enables us to achieve a robust schedule without the need to add extra time buffers explicitly.

3.1. Computing EPO Values

The $E,P,O$ values are computed from the respective processing time values per unit ($\mathit{PTU}$)-expected $\mathit{PTU}$ (${\mathit{PTU}}_E$), pessimistic $\mathit{PTU}$ (${\mathit{PTU}}_P$), and optimistic $\mathit{PTU}$ (${\mathit{PTU}}_O$). To compute the values ${\mathit{PTU}}_{*}$ for the given job $J_{\mathit{TD}}$ (job to do), we must collect historical data on the processing times of completed jobs that are similar to $J_{\mathit{TD}}$ or that are produced on a similar machine/class of machines. Each completed job $J_{\mathit{D}}$ (job done) is characterized by

$$PT{U}_{R,J_{\mathit{D}}}={\displaystyle \frac{{\mathit{PT}}_{R,J_{\mathit{D}}}}{U}},$$

(1)

where $P{T}_{R,J_{\mathit{D}}}$ is the actual (coming from historical data) processing time of the job $J_{\mathit{D}}$ and U is the number of units to be produced.

Now, we must select the jobs that are similar to $J_{\mathit{TD}}$. The similarity of two jobs $J_{\mathit{TD}}$ and $J_D$, which will be denoted as $J_{\mathit{TD}}\sim J_D$, must be well defined to ensure that the values of ${\mathit{PTU}}_{*}$ are reliable. Obviously, the similarity of jobs will strongly depend on the production specificity in a given production plant. In the trivial case, only jobs with identical production parameters will be considered as similar (such a defined similarity will be useful, for example, in enterprises with repetitive production). However, in many cases, the manufactured goods will differ from each other, sometimes to a large extent. In such a case, defining a good similarity measure might be a quite challenging classification task. One of the possible ways to handle this task is to use decision rules that are very helpful in solving classification/decision problems (cf. [46]). To become independent from the (enterprise-specific) definition of similarity of jobs, we introduce the following Similarity function:

$$\mathit{Similarity}\left(J_{\mathit{TD}},J_D\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}{J}_{\mathit{TD}}\sim J_D,\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(2)

where $J_{\mathit{TD}}$ is a job to be scheduled and $J_D$ is a job already completed. For example, if job similarity depends on changes to key production process parameters, a rule for determining the value of the similarity function could be defined as follows:

$${\mathrm{IF}\mathrm{parameter}}_A\left(J_D\right)\ne {\mathrm{parameter}}_A\left(J_{TD}\right)\mathrm{THEN}\mathrm{Similarity}=0$$

An alternative approach is to calculate the distance between the parameters of jobs using, for example, the Euclidean or Manhattan distance, and then use this to determine the value of the Similarity function.

Historical data necessary to calculate the expected processing time per unit should satisfy the time criterion; jobs completed more than 10 years earlier are not the best indicator for forecasting the processing time of current jobs. It seems reasonable that the time horizon (TH) should be as short as possible, but large enough to include at least a dozen similar jobs. To take into account the time horizon, the Similarity function should be extended to the following form:

$$\mathit{Similarity}(J_{\mathit{TD}},J_D,\mathit{TH})=\left\{\begin{array}{cc}1\hfill & \mathrm{if}{J}_{\mathit{TD}}\sim J_D\mathrm{and}{\mathit{PD}}_{J_D}\subseteq \mathit{TH},\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(3)

where ${\mathit{PD}}_{J_D}$ is the production start date of $J_D$.

Additionally, we define the set of ${\mathit{PTU}}_{R,J_D}$ of jobs that are similar to the job $J_{\mathit{TD}}$ and fit in the time window:

$${\mathit{SSJ}}_{J_{\mathit{TD}}}=\left\{{\mathit{PTU}}_{R,J_D}\mid \mathit{Similarity}(J_{\mathit{TD}},J_D,\mathit{TH})=1\right\}.$$

(4)

To compute ${\mathit{PTU}}_{E,J_{\mathit{TD}}}$ (expected $PTU$ for job $J_{TD}$), ${\mathit{PTU}}_{O,J_{\mathit{TD}}}$ (optimistic $PTU$ for job $J_{TD}$) and ${\mathit{PTU}}_{P,J_{\mathit{TD}}}$ (pessimistic $PTU$ for job $J_{TD}$), the values in ${\mathit{SSJ}}_{J_{\mathit{TD}}}$ are first sorted in non-increasing order, and then the following formulas are used (for PERT method, the ${\mathit{PTU}}_P$ and ${\mathit{PTU}}_O$ values must be computed from historical data):

1.

${\mathit{PTU}}_{E,J_{\mathit{TD}}}$

• mean,
• median,
• PERT = $(o+4m+p)/6$,
  where $m=$ mean, $p={\mathit{PTU}}_{P,J_{\mathit{TD}}}$, $o={\mathit{PTU}}_{O,J_{\mathit{TD}}}$.

2.

${\mathit{PTU}}_{P,J_{\mathit{TD}}}$

• 1 quartile,
• 1 decile,
• min,
• $p·{\mathit{PTU}}_{E,J_{\mathit{TD}}}$,
  where p is chosen value from the interval from 0.5 to 1.

3.

${\mathit{PTU}}_{O,J_{\mathit{TD}}}$

• 3 quartile,
• 9 decile,
• max,
• $o·{\mathit{PTU}}_{E,J_{\mathit{TD}}}$,
  where o is a value from the interval from 1 to 1.5.

The proposed formulas for ${\mathit{PTU}}_{P,J_{\mathit{TD}}}$ and ${\mathit{PTU}}_{O,J_{\mathit{TD}}}$ use quantiles to cut off extreme observations that often result from random events, such as a machine failure. Since extreme values may result from non-repetitive events, equipment failure, or human error, we decided to select values that are robust to such disturbances. It is also worth noting that the larger the scope of the analyzed data (e.g., from the first to the ninth decile), the greater the probability that

$${\mathit{PTU}}_{R,J_{\mathit{TD}}}\in \left[{\mathit{PTU}}_{O,J_{\mathit{TD}}},{\mathit{PTU}}_{P,J_{\mathit{TD}}}\right].$$

The processing time of the job $J_{\mathit{TD}}$ may increase due to the need to take into account also more pessimistic times of job completion. In the case of repetitive production with a very small time spread, it may be effective to select extreme values (min and max) as ${\mathit{PTU}}_{P,J_{\mathit{TD}}}$ and ${\mathit{PTU}}_{O,J_{\mathit{TD}}}$ values. So, the selection (or development) of ${\mathit{PTU}}_{*,J_{\mathit{TD}}}$ values is an individual matter of each enterprise and strongly depends on the predictability (or unpredictability) of the processing times.

Assuming the ${\mathit{PTU}}_{P,J_{\mathit{TD}}}$, ${\mathit{PTU}}_{E,J_{\mathit{TD}}}$ and ${\mathit{PTU}}_{O,J_{\mathit{TD}}}$ values are well defined, we can compute the key parameters of the EPO method according to the following formulas:

$$\begin{array}{cc}\hfill E& ={\mathit{PTU}}_{E,J_{\mathit{TD}}}·U+\mathit{AT},\hfill \\ \hfill P& ={\mathit{PTU}}_{P,J_{\mathit{TD}}}·U+\mathit{AT},\hfill \\ \hfill O& ={\mathit{PTU}}_{O,J_{\mathit{TD}}}·U+\mathit{AT},\hfill \end{array}$$

(5)

where $\mathit{AT}$ denotes the aggregated time that includes all preparatory and calibration activities necessary to start and carry out production.

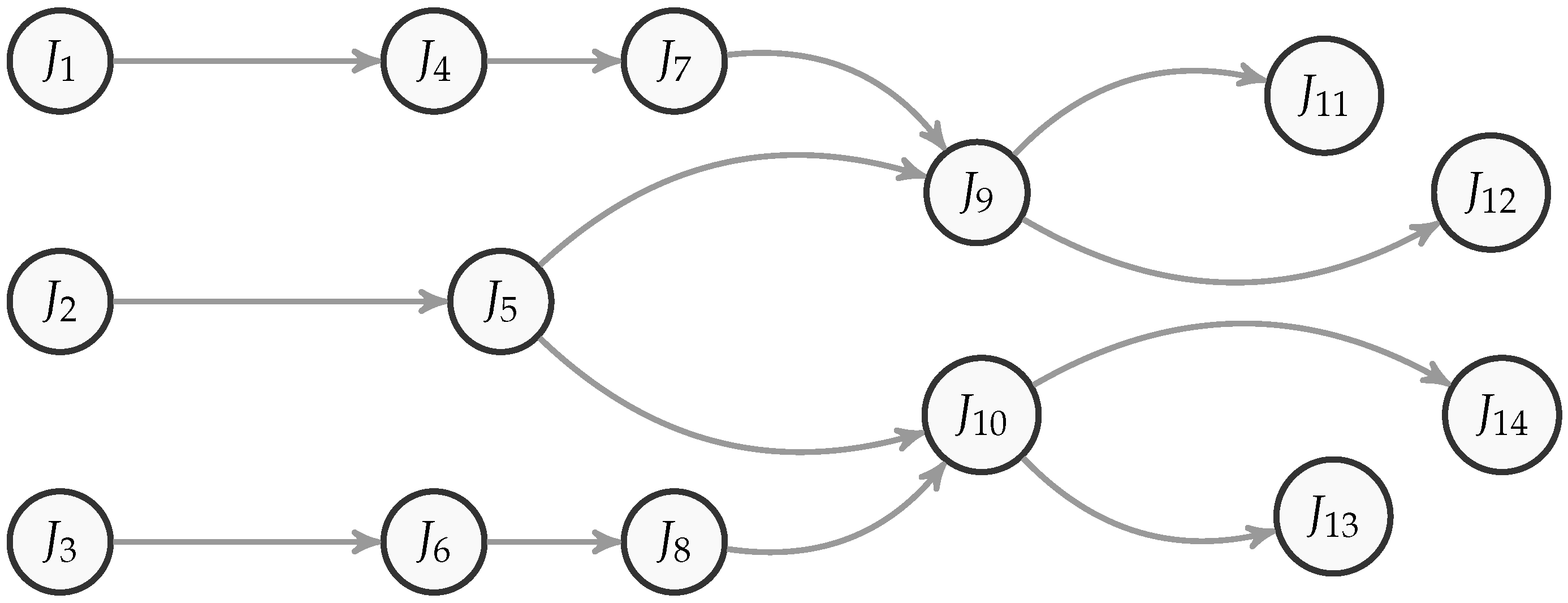
The EPO extension can be implemented for most scheduling methods since it uses values and concepts that are a basis of scheduling, including duration, possible start or completion time of a job, and production path (presented in Figure 2).

In what follows, we describe an implementation of the EPO extension on an example of forward and backward scheduling, and also schedule optimization.

3.2. EPO Extension in Forward Scheduling

In forward scheduling using dispatching rules with EPO extension, each job to be scheduled ($J_{\mathit{TD}}$) is characterized by its earliest start time (${\mathit{EST}}_{J_{\mathit{TD}}}$). ${\mathit{EST}}_{J_{\mathit{TD}}}$ of a job that starts the production path (${\mathit{Preds}}_{J_{\mathit{TD}}}=\varnothing$) is defined based on, e.g., the date of delivery of semi-finished products or raw materials that are necessary to start the job. ${\mathit{EST}}_{J_{\mathit{TD}}}$ of a job that has predecessors in a production path (${\mathit{Preds}}_{J_{\mathit{TD}}}\ne \varnothing$) must be computed based on the end times of all $J_{\mathit{PR}}\in {\mathit{Preds}}_{J_{\mathit{TD}}}$. To take into account the uncertainty of the processing time of predecessors, we compute the EPO end times for each $J_{\mathit{PR}}\in {\mathit{Preds}}_{J_{\mathit{TD}}}$ using the following formulas:

$$\begin{array}{cc}\hfill {\mathit{FT}}_{E,J_{\mathit{PR}}}& ={\mathit{ST}}_{J_{\mathit{PR}}}+E,\hfill \\ \hfill {\mathit{FT}}_{P,J_{\mathit{PR}}}& ={\mathit{ST}}_{J_{\mathit{PR}}}+P,\hfill \\ \hfill {\mathit{FT}}_{O,J_{\mathit{PR}}}& ={\mathit{ST}}_{J_{\mathit{PR}}}+O,\hfill \end{array}$$

(6)

where ${\mathit{ST}}_{J_{\mathit{PR}}}$ (${\mathit{ST}}_{J_{\mathit{PR}}}⩾{\mathit{EST}}_{J_{\mathit{PR}}}$) is the actual start time of $J_{\mathit{PR}}$. Based on the expected (${\mathit{FT}}_{E,J_{\mathit{PR}}}$), optimistic (${\mathit{FT}}_{O,J_{\mathit{PR}}}$) and pessimistic (${\mathit{FT}}_{P,J_{\mathit{PR}}}$) end times of all the predecessors of $J_{\mathit{TD}}$, we compute the earliest start time of $J_{\mathit{TD}}$ from the following formula:

$$\begin{array}{c}{\displaystyle {\mathit{EST}}_{J_{\mathit{TD}}}=\underset{J_{\mathit{PR}}\in {\mathit{Preds}}_{J_{\mathit{TD}}}}{max}\left\{\begin{array}{c}F{T}_{E,J_{\mathit{PR}}},\mathrm{if}{M}_{J_{\mathit{PR}}}=M_{J_{\mathit{TD}}}\mathrm{and}{\mathit{Lag}}_{J_{\mathit{PR}}}=0,\hfill \\ F{T}_{P,J_{\mathit{PR}}}+{\mathit{TT}}_{M_{J_{\mathit{PR}}},M_{J_{\mathit{TD}}}}+{\mathit{Lag}}_{J_{\mathit{PR}}},\mathrm{otherwise},\hfill \end{array}\right.}\hfill \end{array}$$

(7)

where $M_{J_{\mathit{PR}}}$ and $M_{J_{\mathit{TD}}}$ are machines used to produce, respectively, the jobs $J_{\mathit{PR}}$ and $J_{\mathit{TD}}$, $T{T}_{M_{J_{\mathit{PR}},M_{J_{\mathit{TD}}}}}⩾0$ is the transport time between the machines $M_{J_{\mathit{PR}}}$ and $M_{J_{\mathit{TD}}}$, and ${\mathit{Lag}}_{J_{\mathit{PR}}}⩾0$ is the lag time between the two subsequent stages of the production process imposed by a technology (for example, cooling down or drying of the semi-finished product before the next production stage). To minimize the probability of machine downtime (due, e.g., to the lack of production components), we use the pessimistic end time ($F{T}_{P,J_{\mathit{PR}}}$) if jobs $J_{\mathit{TD}}$ and $J_{\mathit{PR}}$ are produced on different machines. If $J_{\mathit{PR}}$ and $J_{\mathit{TD}}$ are produced on the same machine, there is no need to take into account a longer production time (constituting a kind of a safety buffer), because in such a case there is no risk of machine downtime (late termination of the predecessor will automatically delay the production of the successors). Let us note that if time windows are not taken into account, then the earliest start time is the same for all jobs and is equal to the scheduling start time.

The last important aspect of the EPO extension is an additional constraint on the start time of the job $J_{\mathit{TD}}$. For the purposes of the presentation, assume that the job $J_{\mathit{TD}}$ is to be scheduled on machine M. As already mentioned, ${\mathit{ST}}_{J_{\mathit{TD}}}$ must satisfy the inequality ${\mathit{ST}}_{J_{\mathit{TD}}}⩾{\mathit{EST}}_{J_{\mathit{TD}}}$, where ${\mathit{EST}}_{J_{\mathit{TD}}}$ must take into account the end times of all predecessors of $J_{\mathit{TD}}$ (cf. Formula (7)). However, ${\mathit{EST}}_{J_{\mathit{TD}}}$ should also take into account the end time of the job, which was last processed on the machine M. This additional condition can be written as follows:

$$ES{T}_{J_{\mathit{TD}}}⩽\left\{\begin{array}{cc}F{T}_{O,J_{\mathit{last}}}\hfill & \mathrm{if}\left|{\mathit{SVJ}}_{F{T}_{O,J_{\mathit{last}}}}\right|>0,\hfill \\ F{T}_{E,J_{\mathit{last}}}\hfill & \mathrm{if}\left|{\mathit{SVJ}}_{F{T}_{E,J_{\mathit{last}}}}\right|>0,\hfill \\ \infty \hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(8)

where $J_{\mathit{last}}$ is the last job completed on the respective machine, $F{T}_{O,J_{\mathit{last}}}$ and $F{T}_{E,\mathit{last}}$ are, respectively, optimistic and expected end times of the job $J_{\mathit{last}}$, and

$${\mathit{SVJ}}_t=\left\{J\mid {\mathit{EST}}_J⩽t\right\}$$

is the set of jobs that can be scheduled on the respective machine. Condition (8) is to ensure that there are either jobs available for production when the production of the last job ends earlier than expected (i.e., ends according to the optimistic end time), or there are jobs available at time $F{T}_{E,\mathit{last}}$; if there are no such jobs, the machine will be idle until the earliest start time of a job to be scheduled on that is reached. Moreover, we define the availability time (${\mathit{MAT}}_M$) of the machine M as follows:

$${\mathit{MAT}}_M=min\{{\mathit{EST}}_J\mid J\in {\mathit{JF}}_M\}.$$

(9)

3.3. EPO Extension in Backward Scheduling

In backward scheduling using dispatching rules with EPO extension, each job ($J_{\mathit{TD}}$) to be scheduled is characterized by its latest end time (${\mathit{LFT}}_{J_{\mathit{TD}}}$). ${\mathit{LFT}}_{J_{\mathit{TD}}}$ of a job that ends the production path (${\mathit{Succs}}_{J_{\mathit{TD}}}=\varnothing$) is usually defined based on the date of delivery to a customer. ${\mathit{LFT}}_{J_{\mathit{TD}}}$ of a job that has successors (${\mathit{Succs}}_{J_{\mathit{TD}}}\ne \varnothing$) must be calculated based on the start time of all its successors $J_{SC}\in {\mathit{Succs}}_{J_{\mathit{TD}}}$. To take into account uncertainty of the processing time of successors, we compute the EPO start times for each $J_{\mathit{SC}}\in {\mathit{Succs}}_{J_{\mathit{TD}}}$ using the following formulas:

$$\begin{array}{cc}\hfill {\mathit{ST}}_{E,J_{\mathit{SC}}}& ={\mathit{FT}}_{J_{\mathit{SC}}}-E,\hfill \\ \hfill {\mathit{ST}}_{P,J_{\mathit{SC}}}& ={\mathit{FT}}_{J_{\mathit{SC}}}-P,\hfill \\ \hfill {\mathit{ST}}_{O,J_{\mathit{SC}}}& ={\mathit{FT}}_{J_{\mathit{SC}}}-O,\hfill \end{array}$$

(10)

where ${\mathit{FT}}_{E,J_{\mathit{SC}}}$ is the actual end time of the job $J_{\mathit{SC}}$. Based on the expected (${\mathit{ST}}_{E,J_{\mathit{SC}}}$), pessimistic (${\mathit{ST}}_{P,J_{\mathit{SC}}}$), and optimistic (${\mathit{ST}}_{O,J_{\mathit{SC}}}$) start times of all the successors of $J_{\mathit{TD}}$, we compute the latest end time of the job $J_{\mathit{TD}}$ from the following formula:

$$\begin{array}{c}{\displaystyle {\mathit{LFT}}_{J_{\mathit{TD}}}=\underset{J_{\mathit{SC}}\in {\mathit{Succ}}_{J_{\mathit{TD}}}}{min}\left\{\begin{array}{c}S{T}_{E,J_{\mathit{SC}}},\mathrm{if}{M}_{J_{\mathit{SC}}}=M_{J_{\mathit{TD}}}\mathrm{and}{\mathit{Lag}}_{J_{\mathit{TD}}}=0,\hfill \\ S{T}_{P,J_{\mathit{SC}}}-{\mathit{TT}}_{M_{J_{\mathit{SC}}},M_{J_{\mathit{TD}}}}-{\mathit{Lag}}_{J_{\mathit{TD}}},\mathrm{otherwise},\hfill \end{array}\right.}\hfill \end{array}$$

(11)

where $M_{J_{\mathit{SC}}}$ and $M_{J_{\mathit{TD}}}$ are machines used to produce, respectively, the jobs $J_{\mathit{SC}}$ and $J_{\mathit{TD}}$, $T{T}_{M_{J_{\mathit{SC}},M_{J_{\mathit{TD}}}}}⩾0$ is the transport time between the machines $M_{J_{\mathit{SC}}}$ and $M_{J_{\mathit{TD}}}$, and ${\mathit{Lag}}_{J_{\mathit{SC}}}⩾0$ is the lag time between the two subsequent stages of the production process imposed by a technology. Similarly as in the case of EPO-forward scheduling, $LF{T}_{J_{\mathit{TD}}}$ should also take into account the following additional condition:

$$LF{T}_{J_{\mathit{TD}}}⩾\left\{\begin{array}{cc}S{T}_{O,J_{\mathit{first}}}\hfill & \mathrm{if}\left|{\mathit{SVJ}}_{S{T}_{O,J_{\mathit{first}}}}\right|>0,\hfill \\ S{T}_{E,J_{\mathit{first}}}\hfill & \mathrm{if}\left|{\mathit{SVJ}}_{S{T}_{E,J_{\mathit{first}}}}\right|>0,\hfill \\ -\infty \hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(12)

where $J_{\mathit{first}}$ is the first job completed on the machine M, $S{T}_{O,J_{\mathit{first}}}$ and $S{T}_{E,\mathit{first}}$ are, respectively, the optimistic and pessimistic start time of the last job, and

$${\mathit{SVJ}}_t=\left\{J\mid {\mathit{LFT}}_J⩾t\right\}$$

is the set of jobs that can be scheduled on the machine M at time t. In this case, the availability time of the machine M is defined as follows:

$${\mathit{MAT}}_M=max\{{\mathit{EST}}_J\mid J\in {\mathit{JF}}_M\}.$$

(13)

Schedules obtained from constructive algorithms can be far from optimal, but this is the trade-off between the computational cost and the quality of the solutions. However, even if the obtained solution (schedule) is not satisfactory, it can still be very useful. For example, it can be used as an initial solution for local search metaheuristics (LNS, VNS, ILS, etc.). The main advantage of the solutions obtained from constructive algorithms over the randomly generated solutions is the fact that the former solutions are certainly admissible, that is, they satisfy all constraints. The most basic constraint is the requirement that each successor job is performed after all its predecessors, and each predecessor job is performed prior to all its successors. Schedules built using dispatching rules with EPO extension can be optimized in the same way as the schedules created with the forward and backward methods. The conditions of admissibility of the given schedule should include the inequalities (8) or (12). This will ensure that the schedule will be robust, that is, it will take into account the uncertainty of processing times.

The proposed EPO extension ensures higher flexibility of production plans and also less frequent interventions (e.g., due to delays in production) by planners. The presented formulas allow one to easily determine all three times of the EPO extension. An example of using the EPO extension in a manufacturing company with complex production technology and a wide range of products is described in the next section.

4. Case Study

The EPO extension was tested on data coming from a company operating in the printing industry. The company is a leading communication services provider in Europe with deep expertise in print and print-related areas. It has several cooperating printing plants located in Poland, which are equipped with technologies enabling the production of printed materials of different sizes, volumes, and complexity. The range of company products comprises magazines, catalogs, brochures, retail leaflets, directories, manuals, and many more. Production planning in such a company is a very complex process due to the large variety of product types, variability in the page counts and production runs, as well as the variety of machinery (sheet-fed and web presses, folders, cutting and binding machines) and transport between plants.

4.1. Methodology

To verify the effectiveness of the EPO extension in the considered company, we first need to determine ${\mathit{PTU}}_{*,J_{\mathit{TD}}}$ for all the jobs to be planned. Eventually, based on the specificity of the company and the interviews with the employees, we have selected the following formulas:

(1)

${\mathit{PTU}}_{E,J_{\mathit{TD}}}$: mean,

(2)

${\mathit{PTU}}_{P,J_{\mathit{TD}}}$: 1 quartile,

(3)

${\mathit{PTU}}_{O,J_{\mathit{TD}}}$: 3 quartile.

The Similarity function, used to compute the ${\mathit{PTU}}_{*,J_{\mathit{TD}}}$ values was implemented using decision rules. The use of decision rules enabled us to consider different times horizons ($\mathit{TH}$). Based on analysis of historical data and interviews with employees, the maximum value of $\mathit{TH}$ was set to one year. The analyzes performed were based on the production data that covers jobs starting a year before the start date of the earliest scheduled task. The data was manually verified to detect and correct any potential errors or inconsistencies.

To analyze the performance of the proposed approach, we decided to use the forward method because it is the closest to the scheduling method currently used in the company considered. To evaluate the quality of the schedules, we use two objective functions: makespan ($C_{max}$) and average completion time ($\mathit{AC}$). Moreover, each operation carried out as part of the production process of a given order will be referred to as a single job. The next job ($J_{\mathit{next}}$) to be scheduled at the time t will be selected using the LPT dispatching rule, which is based on the longest processing time ($\mathit{LPT}$):

$$\begin{array}{c}\hfill {\mathit{LPT}}_M^t\leftarrow J_{\mathit{next}}:P{T}_{J_{\mathit{next}}}=\underset{J\in {\mathit{JF}}_M}{max}P{T}_J,\end{array}$$

(14)

where ${\mathit{JF}}_M$ is the set jobs that are feasible (admissible) on machine M, and $P{T}_J$ is the processing time of the job J (analogously, the set of jobs that are infeasible on machine M will be denoted as ${\mathit{JI}}_M$).

The LPT rule was chosen to illustrate the proposed approach because it is the best approximation of the actual rule used in the company, which is confidential and cannot be quoted. However, it should be emphasized that the EPO extension is universal and can be implemented with other dispatching rules, as well as the LPT rule. The analysis was performed on jobs with production start dates ranging between January 2022 and August 2022. We have selected nine random non-overlapping samples of jobs to be scheduled. To ensure greater representativeness of the results, the samples covered periods of different lengths: 5 days, 10 days, and 20 days. The analysis of the efficiency of the proposed EPO extension was performed in the following steps:

1.

Schedule jobs from a given sample using both the LPT dispatching rule and the EPO extension that integrates the LPT dispatching rule (14), called EPO.

2.

Compute the actual objective functions for the schedules obtained from LPT and EPO by replacing the theoretical processing times with the actual processing times.

3.

Compare the objective function values from the first step and the second step.

The pseudo-code of the EPO-forward algorithm is presented in Algorithm 1.

Algorithm 1 Pseudo-code of EPO-forward algorithm

{Initial phase – assignment of jobs} for $J\in$ Jobs do if $Pred{s}_J=\varnothing$ then Calculate ${\mathit{EST}}_J$ ${\mathit{JF}}_{M_J}^{{\mathit{EST}}_J}={\mathit{JF}}_{M_J}^{{\mathit{EST}}_J}\cup \left\{J\right\}$ else ${\mathit{JI}}_{M_J}={\mathit{JI}}_{M_J}\cup \left\{J\right\}$ end if end for {Scheduling phase} while There are jobs to be scheduled do Select $M^{\prime }$ with ${\mathit{MAT}}_{M^{\prime }}=min\{{\mathit{MAT}}_M\mid M:{\mathit{JF}}_M\ne \varnothing$} Select $J^{\prime }$ with $P{T}_{J^{\prime }}={max}_{J\in {\mathit{JF}}_{M^{\prime }}^t}P{T}_J$ Schedule $J^{\prime }$ on $M^{\prime }$ for all $J_s\in {\mathit{Succs}}_{J^{\prime }}$ do Update feasibility of $J_s\in {\mathit{Succs}}_{J^{\prime }}$ if $J_s$ is feasible then Calculate ${\mathit{EST}}_{J_s}$ end if end for for all $J\in {\mathit{JF}}_{M_{J^{\prime }}}^{{\mathit{FT}}_{E,J^{\prime }}}$ do Calculate ${\mathit{EST}}_J$ end for end while

The above-described three-step procedure was used to perform computations on real data coming from the considered company. The obtained results are presented and discussed in the next section.

4.2. Results

Table 1. Number of jobs in samples of 5-day, 10-day, and 20-day periods.

Days	Sample	Jobs
5	1	3804
	2	3542
	3	4056
10	1	5510
	2	5582
	3	5890
20	1	7635
	2	8083
	3	4889

shows the number of jobs in each of the nine samples used in the experiments. As can be seen, the length of the time window is not correlated with the number of jobs to be scheduled, which is due to the seasonal effect characteristic of the considered company. In the selected period, the smallest sample included approximately 3.5 thousand jobs to be scheduled (sample 2 of the 5-day period), and the largest sample included more than 8 thousand jobs (sample 2 of the 20-day period).

Table 2. Theoretical and actual makespan ($C_{max}$) obtained from LPT dispatching rule and LPT with EPO extension for samples of 5-day, 10-day, and 20-day periods.

Days	Sample	${\mathit{C}}_{max}$
		${\mathit{LPT}}_{\mathit{T}}$	${\mathit{EPO}}_{\mathit{T}}$	${\mathit{LPT}}_{\mathit{A}}$	${\mathit{EPO}}_{\mathit{A}}$
5	1	39.3	39.2	43.8	42.5
	2	43.3	44.3	46.0	45.7
	3	40.6	40.8	49.4	49.2
10	1	53.8	53.9	58.9	56.0
	2	65.2	65.4	68.2	68.2
	3	48.0	48.0	62.6	62.1
20	1	72.4	72.4	76.7	76.6
	2	74.4	74.4	79.1	78.0
	3	57.4	57.4	64.5	64.5

presents the makespan values obtained from the LPT dispatching rule ($LP{T}_T$) and the LPT with EPO extension ($EP{O}_T$), and also the actual makespan values, denoted as $LP{T}_A$ and $EP{O}_A$, respectively (the values were calculated using the three-step procedure described in the previous subsection). The results were scaled to anonymize sensitive data from the analyzed company. Each value presented in the table was divided by the same fixed factor (greater than 1); therefore, the proportions between the results have been preserved.

To better illustrate the effects of using the proposed EPO extension,

Table 3. Differences between theoretical and actual makespan obtained from LPT and LPT with EPO extension.

Days	Sample	${\mathit{LPT}}_{\mathit{T}}$-${\mathit{EPO}}_{\mathit{T}}$	${\mathit{LPT}}_{\mathit{A}}$-${\mathit{EPO}}_{\mathit{A}}$
5	1	0.1	1.3
	2	−1.0	0.3
	3	−0.2	0.2
10	1	−0.1	2.9
	2	−0.2	0
	3	0	0.5
20	1	0	0.1
	2	0	1.1
	3	0	0

presents the differences of the respective values from Table 2.

As can be seen from Table 3, the theoretical results of the EPO extension are no better (except for one sample) than the results of the LPT dispatching rule. This is not surprising, taking into account the construction of the EPO extension. However, the actual makespan values confirm the effectiveness of the EPO extension. Indeed, only in two cases did the EPO extension produce the same result as the forward heuristics. In 1/3 of the considered cases, the advantage of the EPO extension was very clear (exceeded 1 time unit). In the best case, the EPO extension allowed to save as much as 5% of the makespan compared to the forward method. Moreover, in each of the three groups of samples, there was a sample where the time savings exceeded 1 time unit. So, it seems that the length of the period does not affect the shortening of the actual makespan. Similarly, the difference between the theoretical makespan values obtained with the LPT and EPO extension also does not determine the actual time savings.

Table 4. Difference between theoretical and actual values for analyzed dispatching rules ($C_{max}$).

Days	Sample	${\mathit{LPT}}_{\mathit{A}}$-${\mathit{LPT}}_{\mathit{T}}$	${\mathit{EPO}}_{\mathit{A}}$-${\mathit{EPO}}_{\mathit{T}}$
5	1	4.5	3.3
	2	2.7	1.4
	3	8.8	8.4
10	1	5.1	2.1
	2	3.0	2.8
	3	14.6	14.1
20	1	4.3	4.2
	2	4.7	3.6
	3	7.1	7.1
Avg		6.1	5.2

shows the difference between the actual and theoretical makespan for each sample. This difference can be used to compare schedules in terms of how much theoretical value differs from the actual value. Of course, in an ideal situation, these two values should be equal (the difference between the values should be 0).

Based on the results in Table 4, it can be concluded that in one case only, the differences between the actual and theoretical times for LPT and the EPO extension are equal. In the remaining cases, the difference obtained with the EPO extension is smaller, which means that the theoretical makespan obtained with the EPO extension is closer to the actual makespan. A non-parametric Wilcoxon signed-rank test was used to analyse the statistical significance of the differences obtained. At a significance level of 0.1, the results were found to differ statistically from each other.

However, it is also important to compare the results in terms of machine availability. For this purpose, the AC (average completion time) objective function is used, which complements the makespan. The makespan value is crucial from the perspective of the total time required to complete production tasks, while the AC value provides information about the capacity to process new jobs on the given machines. The results obtained using the LPT rule and the LPT with EPO extension for the AC objective function are presented in

Table 5. Theoretical and actual average completion time (AC) obtained from LPT dispatching rule and LPT with EPO extension for samples of 5-day, 10-day, and 20-day periods. Best values are marked in bold.

Days	Numb.	AC
		${\mathit{LPT}}_{\mathit{T}}$	${\mathit{EPO}}_{\mathit{T}}$	${\mathit{LPT}}_{\mathit{A}}$	${\mathit{EPO}}_{\mathit{A}}$
5	1	23.9	23.8	26.9	26.7
	2	25.7	25.7	28	28.3
	3	27.7	27.6	34.6	33.6
10	1	35.3	35.1	40.2	40
	2	38.4	38.3	42.8	43
	3	35.4	35.5	41.4	41
20	1	51.5	51	58	56.2
	2	47.9	49.2	54.7	55
	3	33.1	32.9	39	37.2

,

Table 6. Differences between theoretical and actual average completion time obtained from LPT and LPT with EPO extension.

Days	Numb.	${\mathit{LPT}}_{\mathit{T}}$-${\mathit{EPO}}_{\mathit{T}}$	${\mathit{LPT}}_{\mathit{A}}$-${\mathit{EPO}}_{\mathit{A}}$
5	1	0.1	0.2
	2	0	−0.3
	3	0.1	1
10	1	0.2	0.2
	2	0.1	−0.2
	3	−0.1	0.4
20	1	0.5	1.8
	2	−1.3	−0.3
	3	0.2	1.8

,

Table 7. Difference between theoretical and actual values for analyzed dispatching rules ($AC$). Best values are marked in bold.

Days	Numb.	${\mathit{LPT}}_{\mathit{A}}$-${\mathit{LPT}}_{\mathit{T}}$	${\mathit{EPO}}_{\mathit{A}}$-${\mathit{EPO}}_{\mathit{T}}$
5	1	3	2.9
	2	2.3	2.6
	3	6.9	6
10	1	4.9	4.9
	2	4.4	4.7
	3	6	5.5
20	1	6.5	5.2
	2	6.8	5.8
	3	5.9	4.3
AVG		5.2	4.7

.

In two out of nine cases, based on theoretical data, the result of the LPT rule without the EPO extension proved to be more favorable, while in one case, the results were identical. It should be noted that for observation 2 of the 20-day sample, the LPT rule saved an average of 1.3 time units compared to the EPO extension. In fact, in seven out of nine cases, the differences between the theoretical values were between −0.1 and 0.2. These values confirm that, for theoretical data, the efficiency of the LPT rule and LPT with the EPO extension are at a comparable level. However, it may be surprising that in 2/3 of the cases, the EPO extension gave better results. Considering that the EPO extension includes time buffers to minimize potential delays, such a result is not trivial to predict.

For actual data, the differences between the results are significantly greater than for theoretical data. The LPT rule gave better results in three cases, with differences ranging from −0.2 to −0.3. In six of nine cases, LPT with EPO extension gave better results, and in three of these cases, the difference was substantial, exceeding the value of 1. Based on the results in Table 7, it is also worth emphasizing that the EPO extension allows obtaining lower prediction errors compared to when the extension is not applied. In 2/3 of the cases, the EPO extension led to a lower error and a significantly lower average prediction error.

The presented analysis of the results confirms the effectiveness of the EPO extension. Depending on the adopted evaluation factor, the results obtained for individual samples may differ in favor of one or the other rules (LPT and LPT with the EPO extension). However, for each of the analyzed objectives, the EPO extension allowed us to obtain more favorable results for the majority of samples. As in the previous case ($C_{max}$), the non-parametric Wilcoxon signed-rank test revealed statistically significant differences in the results.

5. Discussion and Conclusions

Automatic scheduling, tracking, and production control are an important aspects of modern production systems, including those implementing the concept of Industry 4.0. The concept of digital twins enables a more accurate monitoring of production and the collection of more reliable data about the production process, including the production time itself. Actual production times are essential for creating more reliable production schedules. One of the most popular and efficient approaches to automatic production scheduling is the dispatching rules. The main drawback of dispatching rules is that they do not take into account the uncertainty of the job processing times, which can cause machine downtime due to production delays.

The EPO extension proposed in this paper extends dispatching rules to include the uncertainty in the job processing times. The important feature of the proposed extension is that it does not increase the computational time of fast dispatching rules, i.e., it does not negatively affect their main advantage over other production scheduling algorithms. Furthermore, the EPO extension can be integrated with the digital twin of the production process, which is essential in an Industry 4.0 setting. This means that real-time data collected from machines (e.g., actual operation times) can be used to modify the EPO estimates for jobs within any chosen time window, enabling dynamic schedule adjustments and enhancing resilience to disruption. The proposed EPO extension eliminates the above-mentioned drawback of dispatching rules, and what follows enables us to obtain schedules that are robust to production delays, machine failures, and other factors that have an impact on the job processing times. The good operation of the EPO extension has been confirmed by experiments on real data coming from the company, which are characterized by a very complex production profile. The performed experiments have confirmed that the differences between the theoretical (computed based on job and machine parameters) and actual job processing times had a smaller impact (measured using makespan and AC) on the schedule obtained, with the EPO extension than with the LPT dispatching rule.

For both of the objective functions analyzed, the proposed EPO extension gives better results when dealing with data representing actual production times. In the case of makespan, in none of the samples analyzed did the LPT scheduling rule give better results than LPT with the EPO extension for actual data. For both makespan and AC, the difference between the results obtained by LPT and LPT with EPO extension was very significant in three out of nine samples.

The analysis of the proposed EPO extension clearly confirms its effectiveness in building schedules that are robust to the uncertainty of the processing time of jobs. Therefore, the proposed EPO extension can be used in enterprises where production orders are complex and highly volatile. It can also be used when both orders and machines are heterogeneous. In our future work, we plan to implement and test the proposed EPO extension in companies from various production industries.