Vibration Damage Analysis of Bottom Hole Assembly Under Axial Impact Based on Dynamic Analysis
Abstract
1. Introduction
2. Impact Simulation Model
2.1. Basic Assumptions
- The impact force is converted into an equivalent periodic excitation acting on the drill bit;
- The effect of drilling fluid on the drill string is neglected;
- Rock damage and fragmentation are taken into account. If rock failure occurs, an element is removed from the mesh;
- Initially, the borehole axis coincides with the drill string axis, and there exists an annular clearance between the borehole wall and the drill string. The borehole cross-section is assumed to be circular;
- The borehole wall is set as an undeformable rigid body, while the BHA is modeled as an elastic beam element.
2.2. Geometric Models, Boundary Conditions, and Material Properties
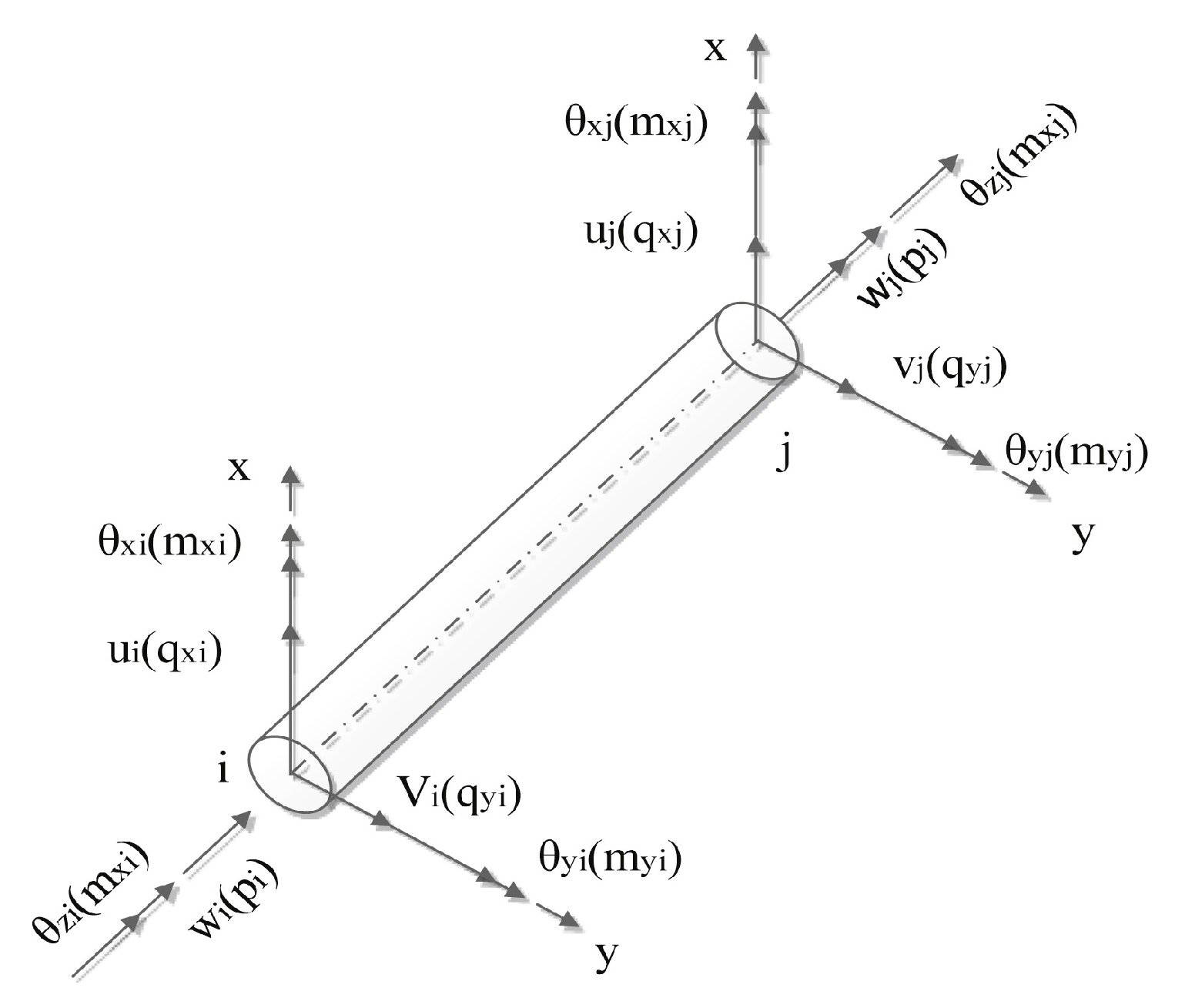
2.2.1. Model Construction
2.2.2. Materials and Boundary Conditions
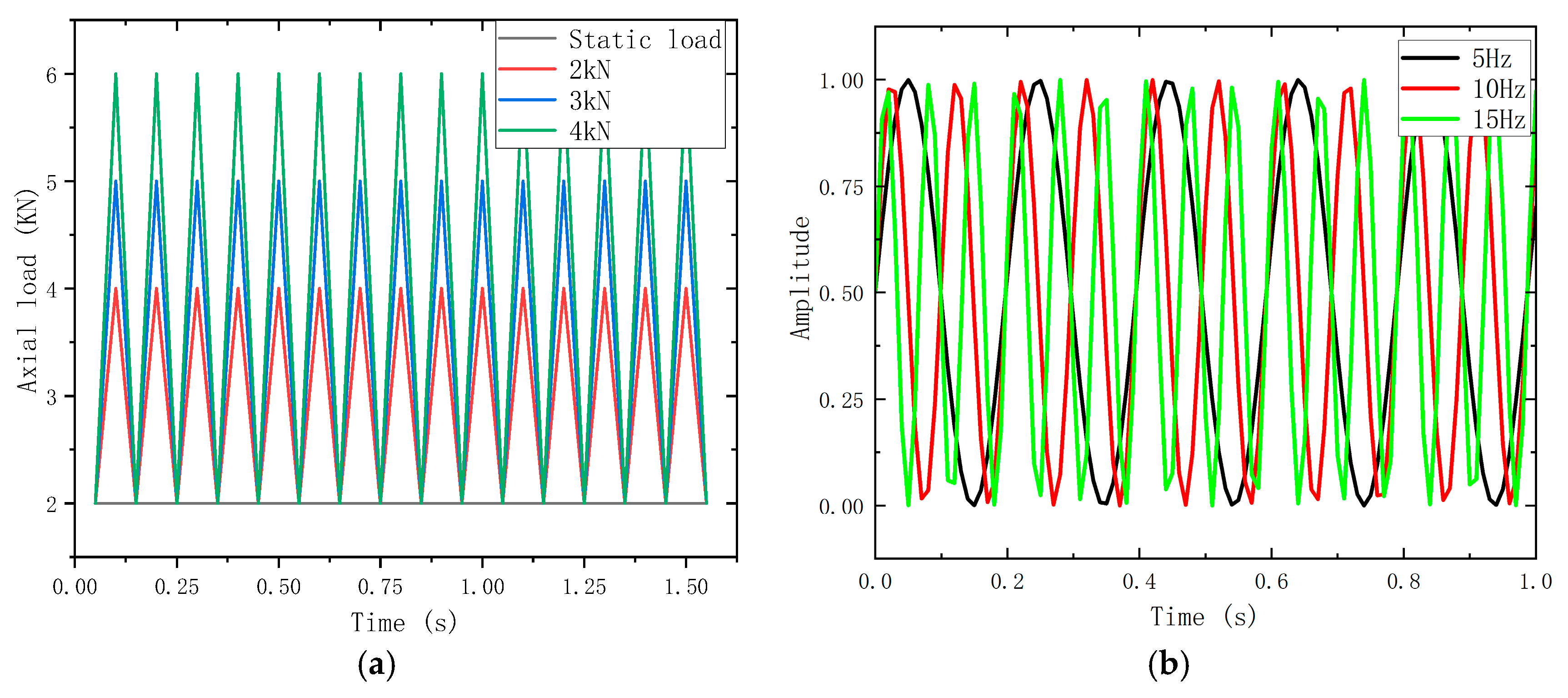
2.2.3. Application of Impact Load
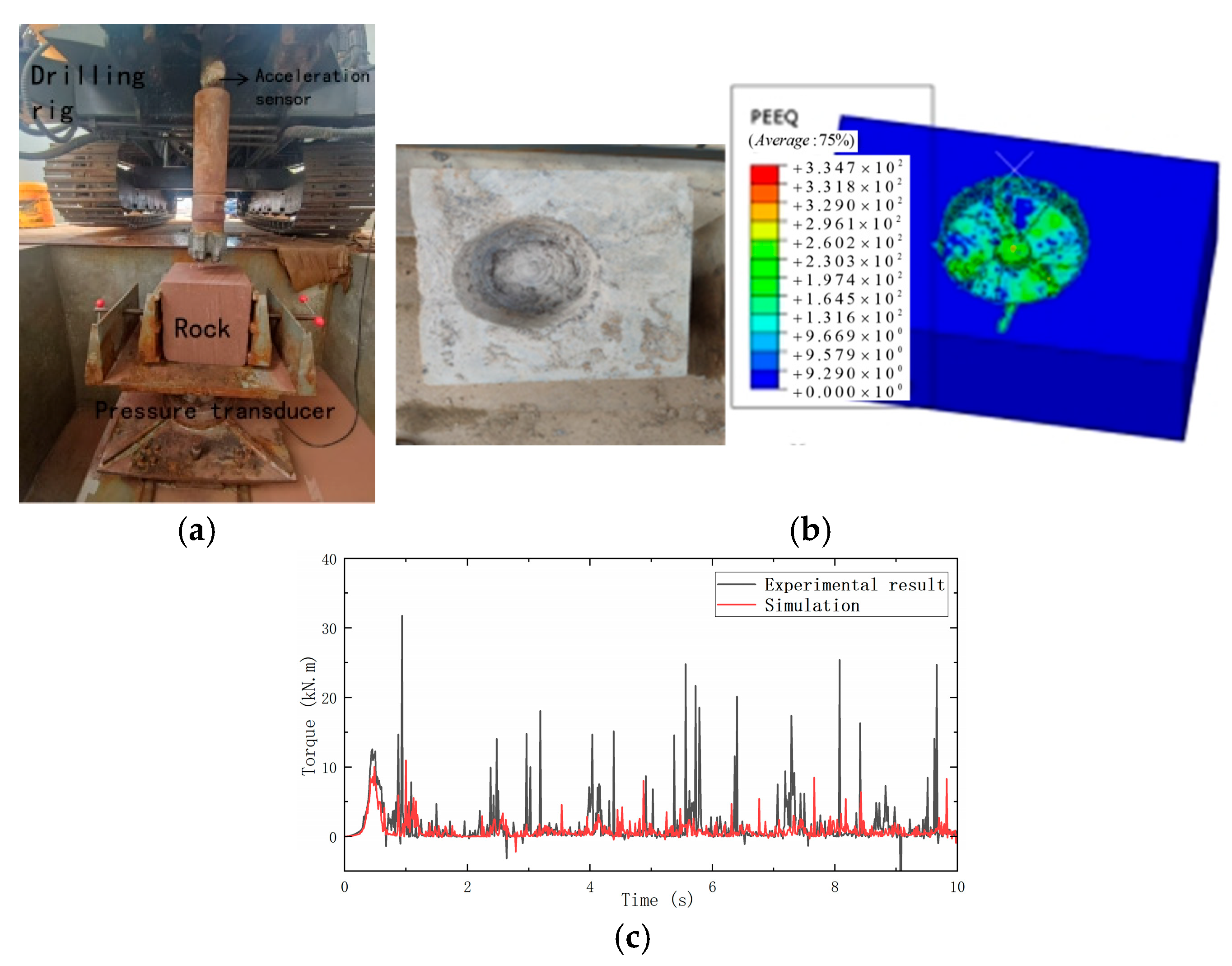
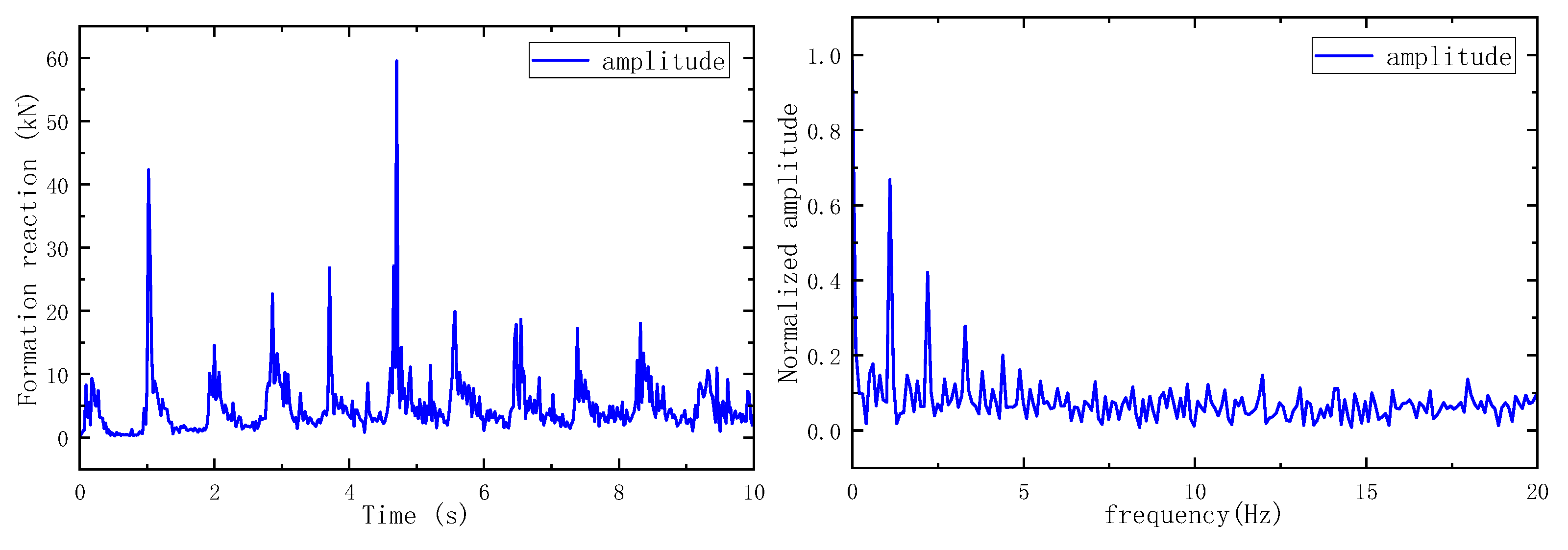
2.3. Model Validation
2.4. Drill String Vibration Model
2.5. Bit–Rock Interaction Analysis
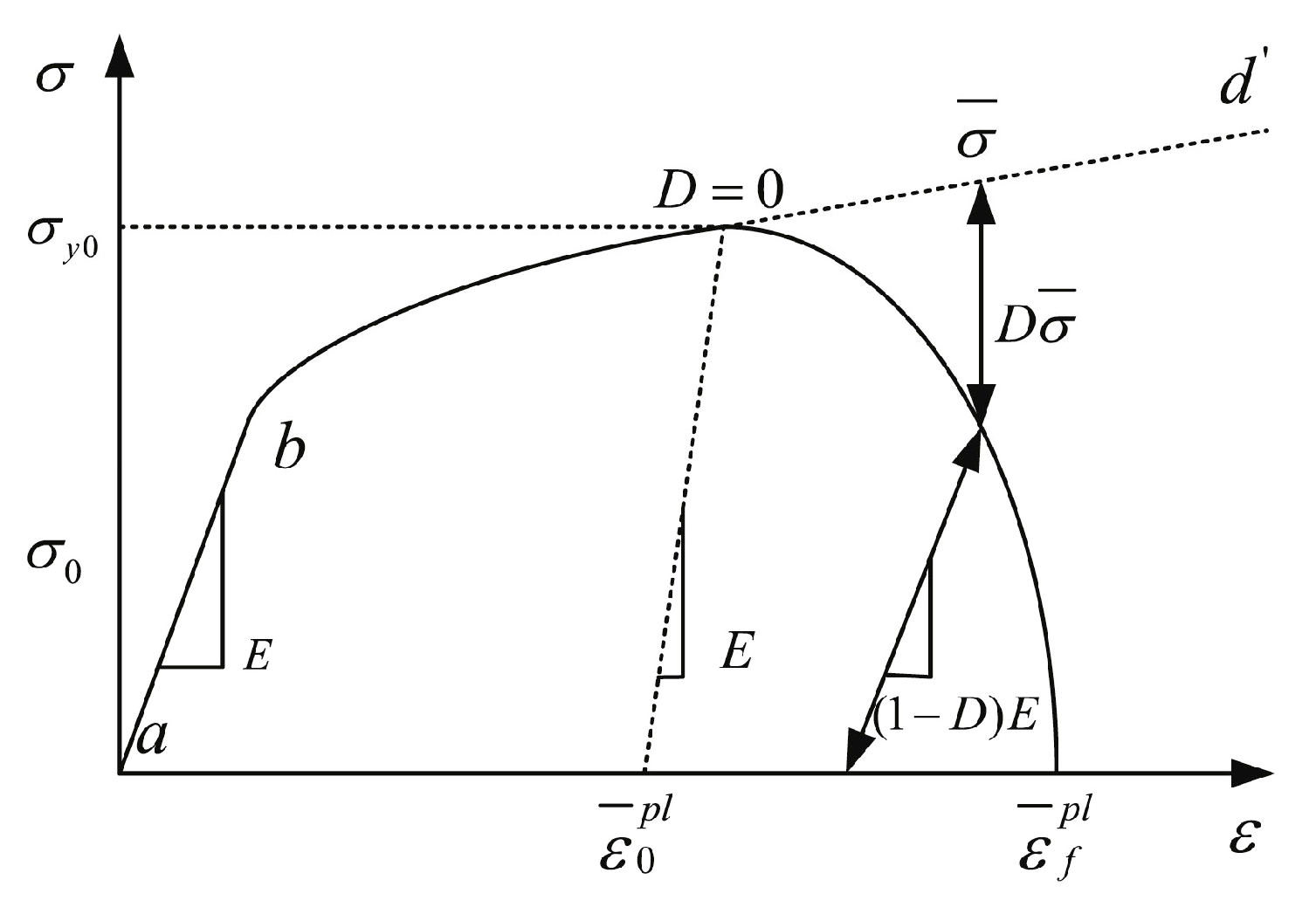
2.6. Rock Constitutive and Failure Criteria
2.7. Drill String Fatigue Solving Strategy
3. Results and Discussion
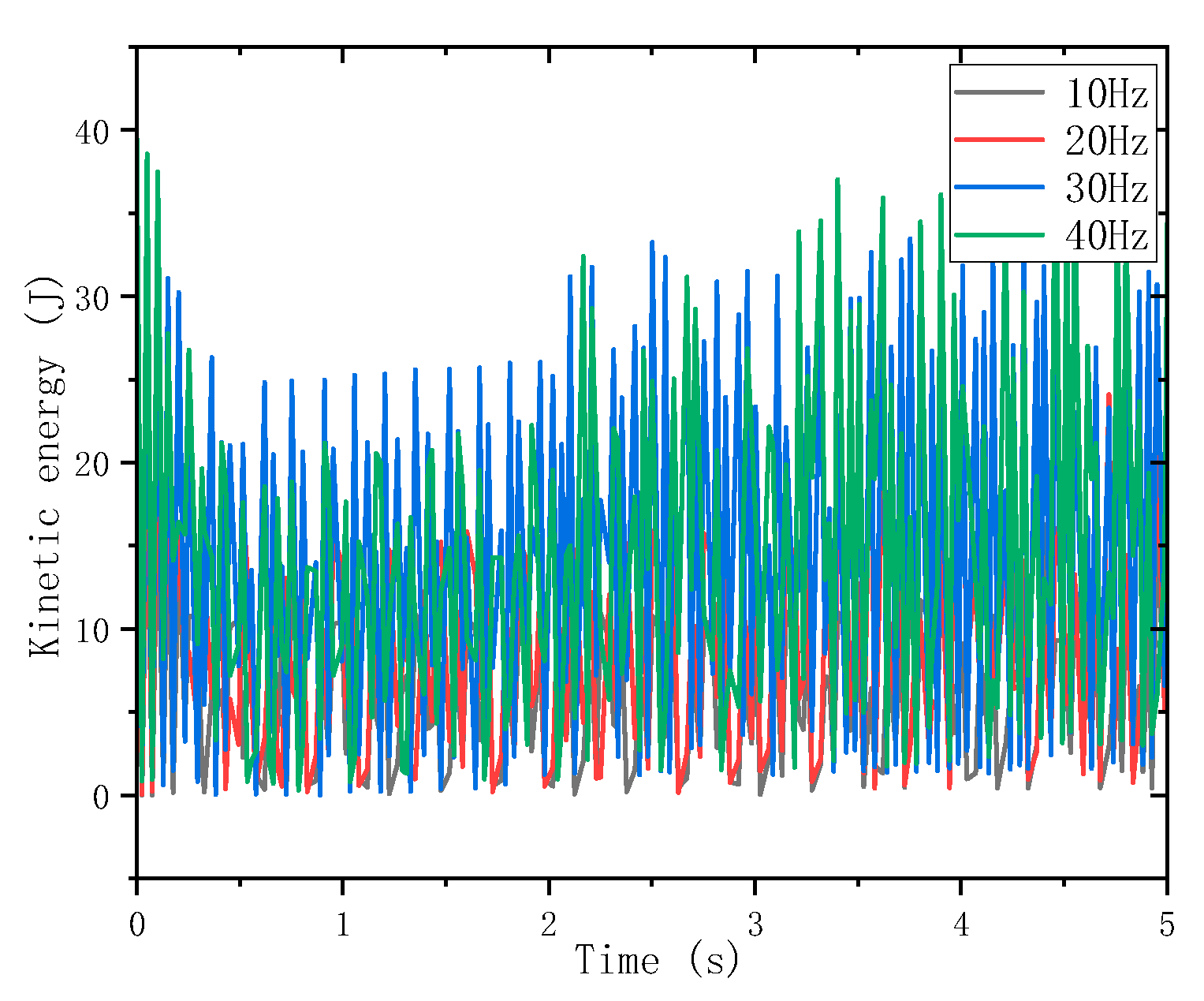
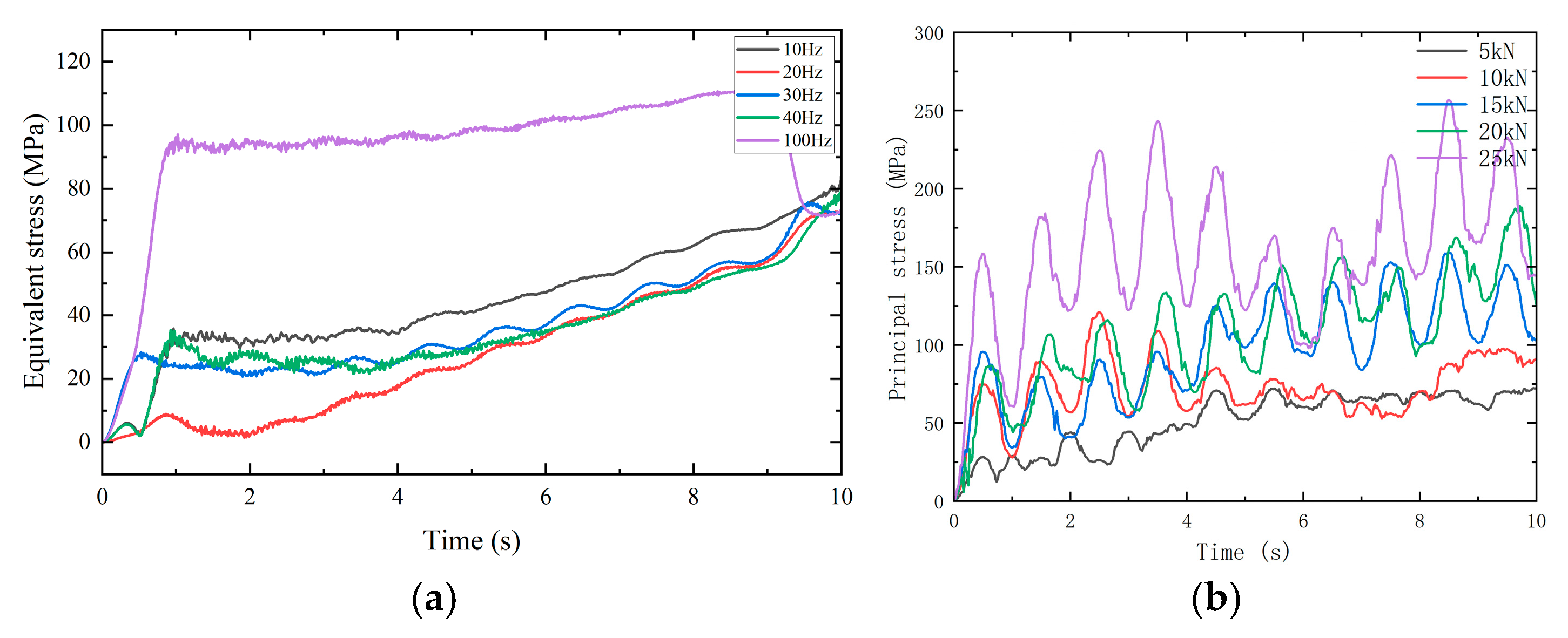
3.1. Effect of Different Impact Energies on BHA Vibration
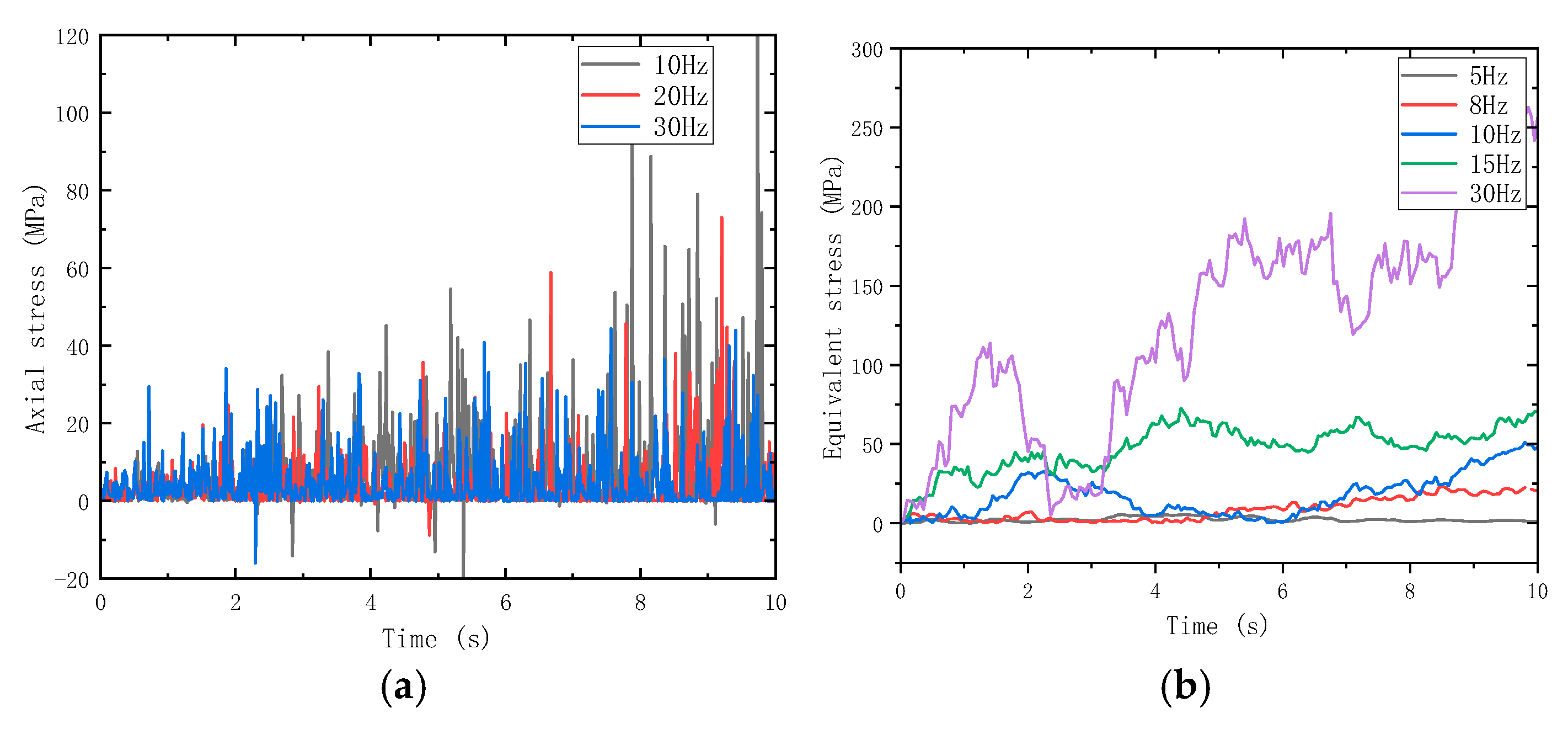
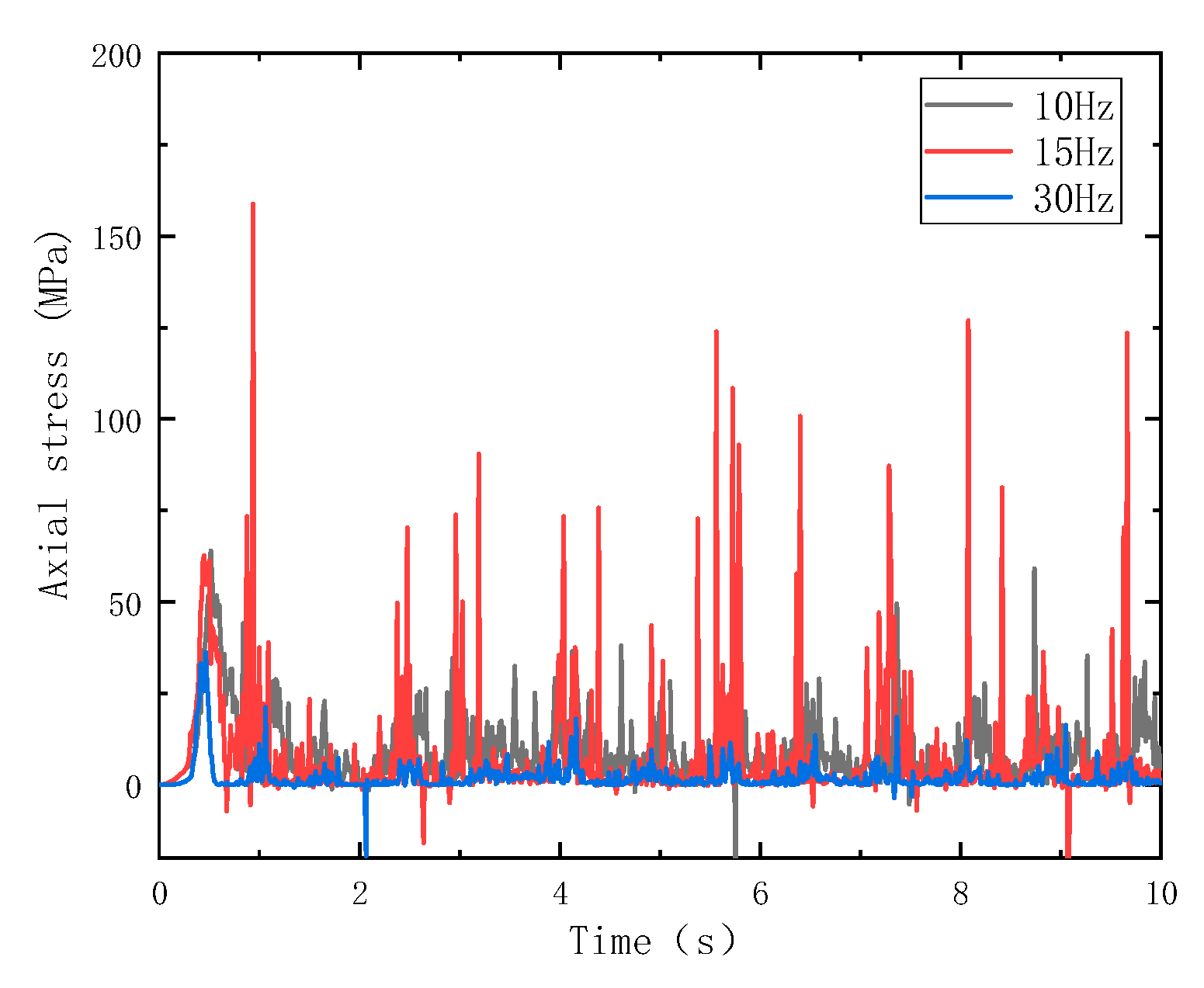
3.2. Effect of Different Impact Frequencies
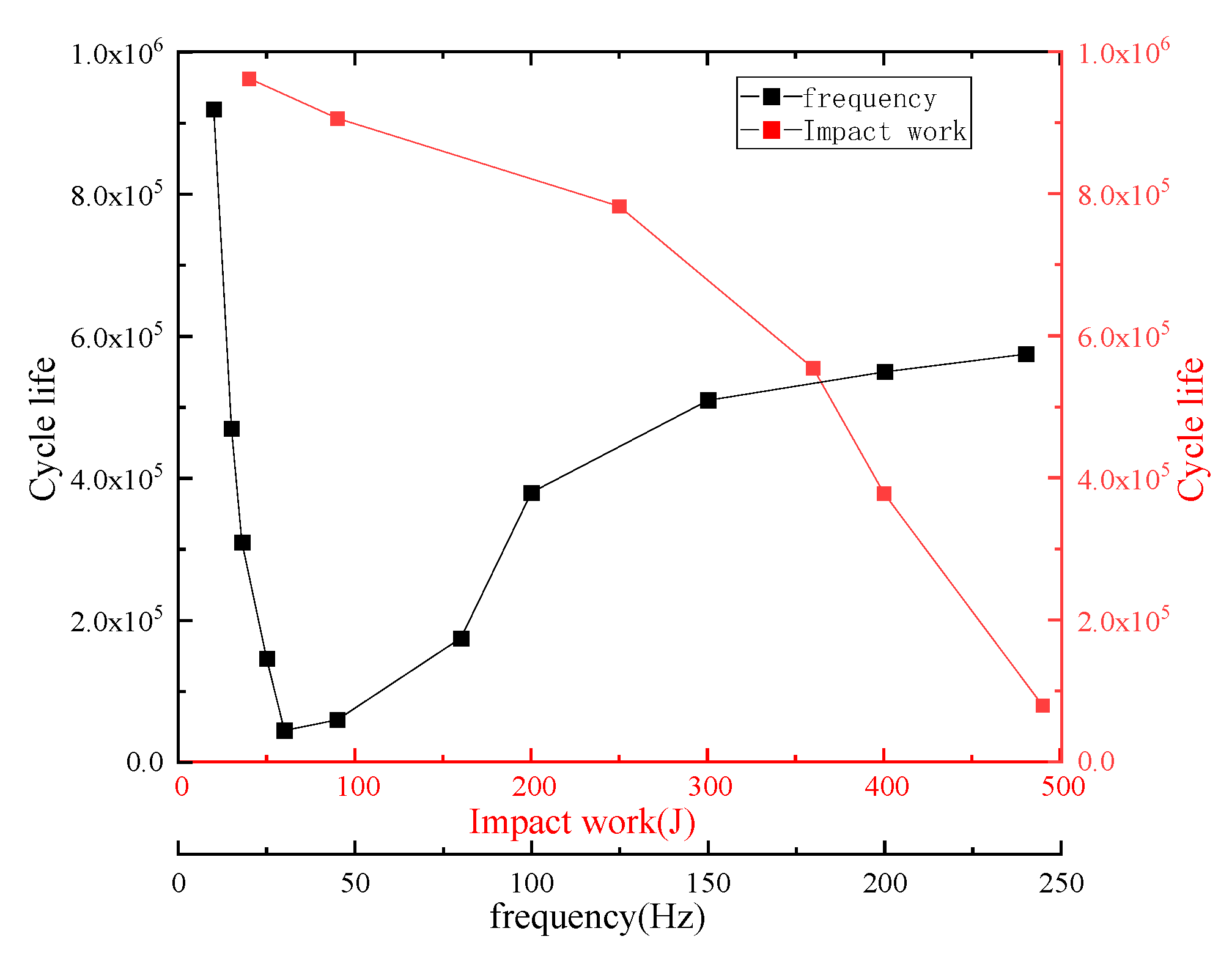
3.3. Fatigue Life Analysis of Drill Strings
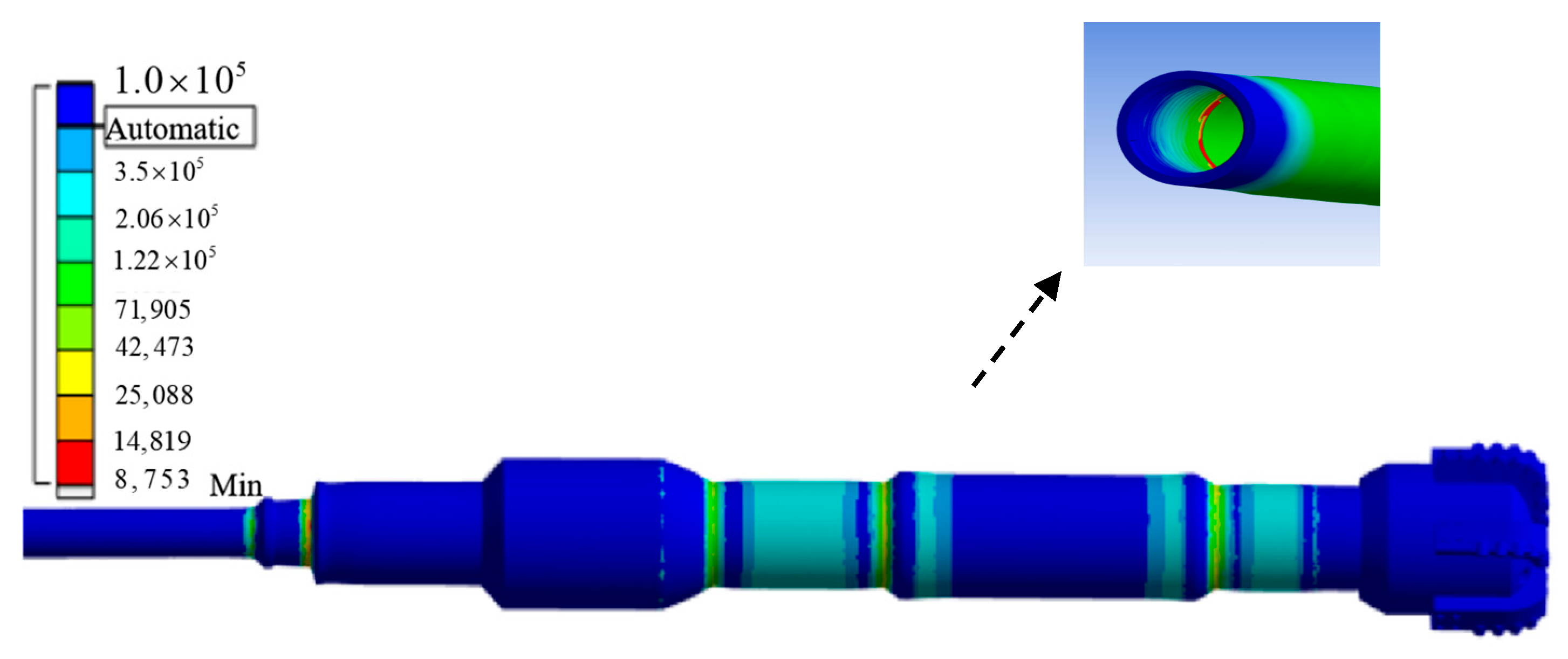
3.3.1. Equivalent Stress Analysis of Drill Strings
3.3.2. BHA Fatigue Life Analysis
4. Conclusions
- Under percussive drilling conditions, axial stress in the drill string fluctuates significantly during rock breaking and penetration. When the input impact force of the hydraulic impactor is increased, both the amplitude and frequency of drill string stress variations become more severe. With the increasing impact frequency, the influence of the impact load on drill string vibration first increases and then decreases, indicating that at high frequencies, the amplitude of alternating stress tends to stabilize and the vibration-induced damage to the drill string is reduced.
- The effects of impact energy and frequency on BHA behaviors—such as bit bounce, buckling, and fatigue—were analyzed. The results indicate that during impact drilling, slender sections like drill pipe connectors are prone to buckling. The usable fatigue life of these components can be up to four times shorter than that of the bit. Combined with fatigue life curve trends, it is demonstrated that under field conditions, a high-frequency range above 100 Hz coupled with appropriate impact energy effectively mitigates BHA vibration and extends the service life of the drill string system.
- Compared with conventional rotary drilling, the drill string motion in the borehole is more complex under percussive drilling. The rate of rock element damage and failure is higher, and both WOB and dynamic stress in the drill string are significantly greater. The findings from this simulation model help provide insight into the complex downhole behavior of the drill string during percussive drilling. This modeling approach offers a novel method for analyzing drill string fatigue life and holds practical significance for drilling optimization and system design.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jestin-Fleury, N. International energy agency. World energy outlook. Polit. Étrangère 1994, 59, 564–565. [Google Scholar]
- Ghasemloonia, A. Elastodynamic and Finite Element Analysis of Coupled Lateral-Axial Vibration of a Drillstring with a Downhole Vibration Generator and Shock Sub. Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2013. [Google Scholar]
- Smith, F.W.; Kopczynski, W. Oilfield percussion drilling. In Proceedings of the SPE Western Regional Meeting, Bakersfield, CA, USA, 2–3 November 1961; SPE: Richardson, TX, USA, 1961. [Google Scholar]
- Huang, J.; Zeng, B.; He, Y.; Wang, X.; Qian, L.; Xia, C.; Yi, X. Numerical study of rock-breaking mechanism in hard rock with full PDC bit model in compound impact drilling. Energy Rep. 2023, 9, 3896–3909. [Google Scholar] [CrossRef]
- Ju, P.; Tian, D. Improving breaking efficiency of hard rock: Research on the mechanism of impact-shear rock breaking technology. Energy Explor. Exploit. 2025, 43, 451–470. [Google Scholar] [CrossRef]
- Baryshnikov, A.; Calderoni, A.; Ligrone, A.; Ferrara, P. A new approach to the analysis of drillstring fatigue behavior. SPE Drill. Complet. 1997, 12, 77–84. [Google Scholar] [CrossRef]
- Dong, G.; Chen, P. A review of the evaluation, control, and application technologies for drill string vibrations and shocks in oil and gas well. Shock Vib. 2016, 2016, 7418635. [Google Scholar] [CrossRef]
- Guan, Z.-C.; Shao, D.-D.; Wen, X.; Shi, Y.-C. Experimental study on motion characteristics of rotary drill string in horizontal well. Mech. Eng. 2013, 30, 340–345. [Google Scholar]
- Dao, N.H.; Sellami, H. Stress intensity factors and fatigue growth of a surface crack in a drill pipe during rotary drilling operation. Eng. Fract. Mech. 2012, 96, 626–640. [Google Scholar] [CrossRef]
- Cui, F.; Cao, Y.; Ni, H.; Zhang, H. Impact frequency optimization of automatic vertical drilling and multi-dimensional vibration reduction combined acceleration system based on impact vibration fatigue analysis. China Sci. 2023, 18, 443. [Google Scholar]
- Zhi, Z.; Zhu, X. Multiaxial fatigue life of drill pipe joint. Acta Pet. Sin. 2019, 40, 839. [Google Scholar]
- Li, W.; Guan, Z.; Zhao, H. Fatigue life prediction of drill string based on reliability theory. Oil Drill. Prod. Technol. 2008, 30, 12–14. [Google Scholar]
- Lemma, T.A.; Nanji, P.; Gebremariam, M.A.; Ahsan, S. Remaining useful life prediction of drill string using fuzzy systems and cumulative damage theory. Key Eng. Mater. 2019, 796, 145–154. [Google Scholar] [CrossRef]
- Qiu, Z. Analysis of the influence of dynamic factors on BHA of rotary steerable system. West. Prospect. Proj. 2023, 35, 29–33. [Google Scholar]
- Li, S.; Yan, T.; Li, W.; Bi, F. Mechanism and test analysis of PDC bit torsional impact rock breaking. J. Yangtze Univ. 2015, 12, 48–51. [Google Scholar]
- Song, C.; Chung, J.; Cho, J.-S.; Nam, Y.-J. Optimal design parameters of a percussive drilling system for efficiency improvement. Adv. Mater. Sci. Eng. 2018, 2018, 2346598. [Google Scholar] [CrossRef]
- Depouhon, A.; Denoël, V.; Detournay, E. Numerical simulation of percussive drilling. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 889–912. [Google Scholar] [CrossRef]
- Yang, Y.; Liao, H.; Niu, J.; Wang, Z.; Chen, J. Three-dimensional simulation of rock breaking efficiency under various impact drilling loads. Arab. J. Geosci. 2020, 13, 444. [Google Scholar] [CrossRef]
- Liu, J.; Hei, C.; Luo, M.; Yang, D.; Sun, C.; Feng, A. A study on impact force detection method based on piezoelectric sensing. Sensors 2022, 22, 5167. [Google Scholar] [CrossRef]
- Pavlovskaia, E.; Hendry, D.C.; Wiercigroch, M. Modelling of high frequency vibro-impact drilling. Int. J. Mech. Sci. 2015, 91, 110–119. [Google Scholar] [CrossRef]
- Zhu, X.; Tang, L.; Tong, H. Effects of high-frequency torsional impacts on rock drilling. Rock Mech. Rock Eng. 2014, 47, 1345–1354. [Google Scholar] [CrossRef]
- Aydan, O.; Tokashiki, N.; Genis, M. Some considerations on yield (failure) criteria in rock mechanics. In Proceedings of the ARMA US Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 24–27 June 2012; p. ARMA–2012-2640. [Google Scholar]
- Yan, B.; Wang, P.; Ren, F.; Guo, Q.; Cai, M. A review of mechanical properties and constitutive theory of rock mass anisotropy. Arab. J. Geosci. 2020, 13, 487. [Google Scholar] [CrossRef]
- Vaisberg, O.; Vincke, O.; Perrin, G.; Sarda, J.; Fay, J. Fatigue of drillstring: State of the art. Oil Gas Sci. Technol. 2002, 57, 7–37. [Google Scholar] [CrossRef]
- Zheng, J. Fatigue Estimation of Drill-String and Drill-Pipe Threaded Connection Subjected to Random Loadings. Master’s Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2015. [Google Scholar]
- Ritto, T.; Soize, C.; Sampaio, R. Robust optimization of the rate of penetration of a drill-string using a stochastic nonlinear dynamical model. Comput. Mech. 2010, 45, 415–427. [Google Scholar] [CrossRef]
- Wada, R.; Kaneko, T.; Ozaki, M.; Inoue, T.; Senga, H. Longitudinal natural vibration of ultra-long drill string during offshore drilling. Ocean Eng. 2018, 156, 1–13. [Google Scholar] [CrossRef]


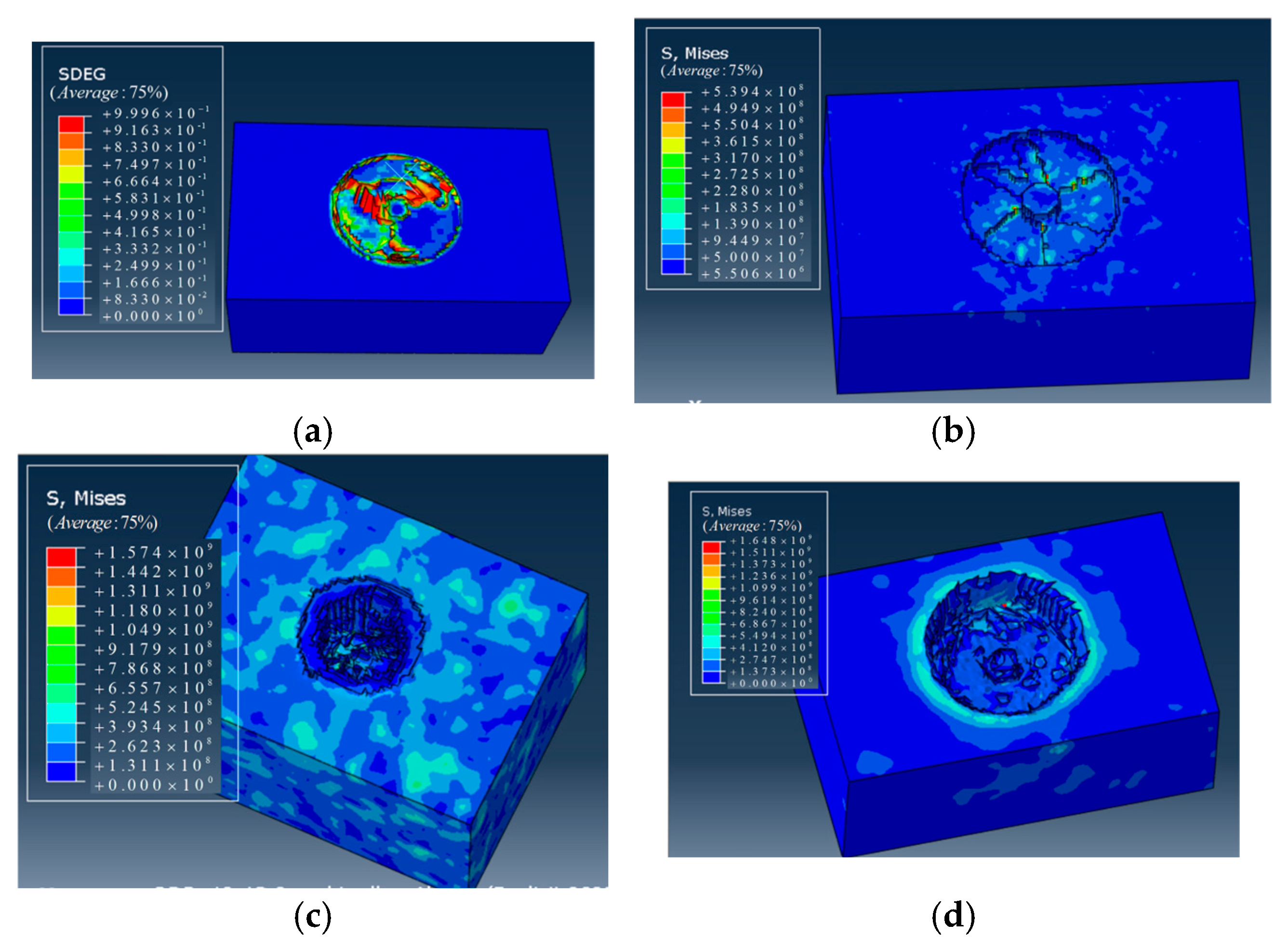
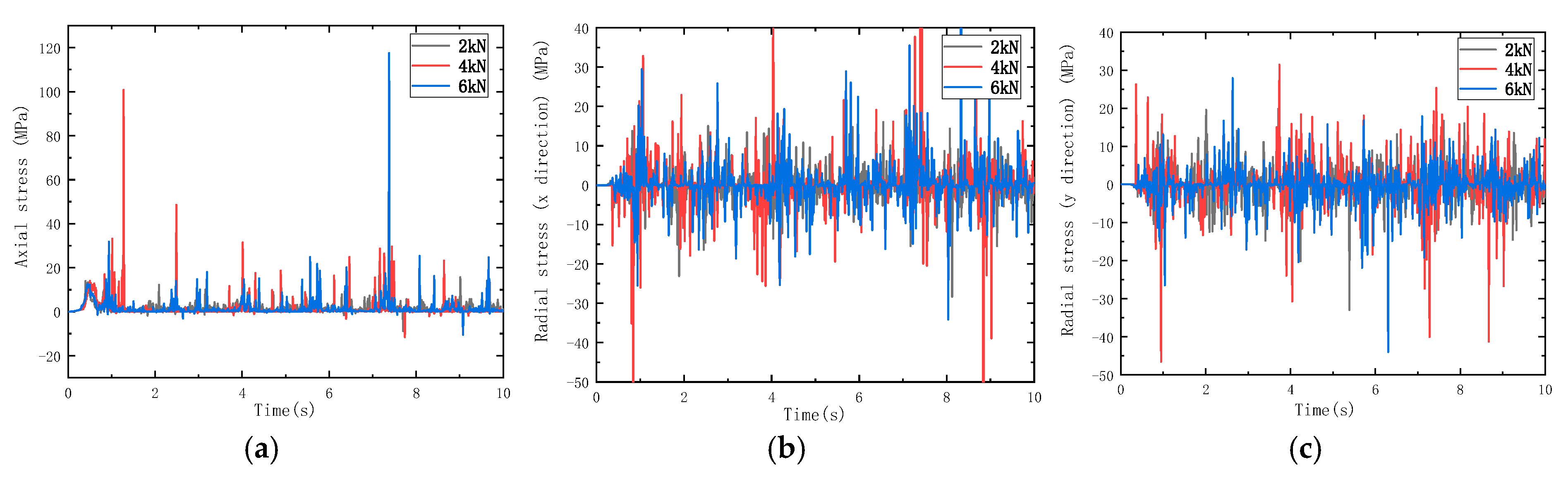
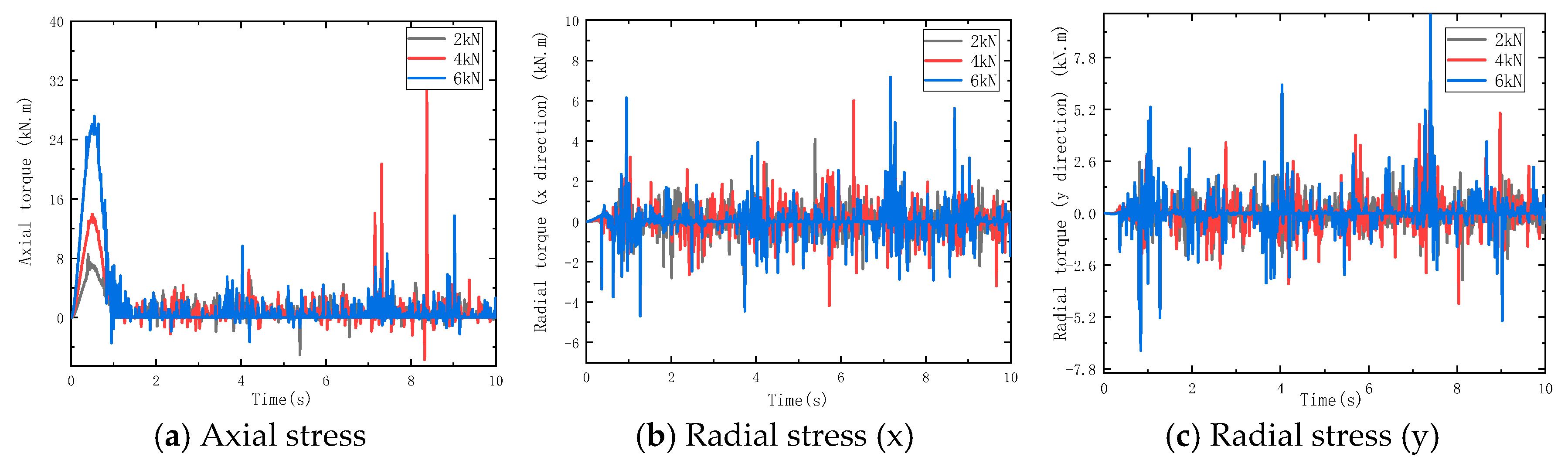
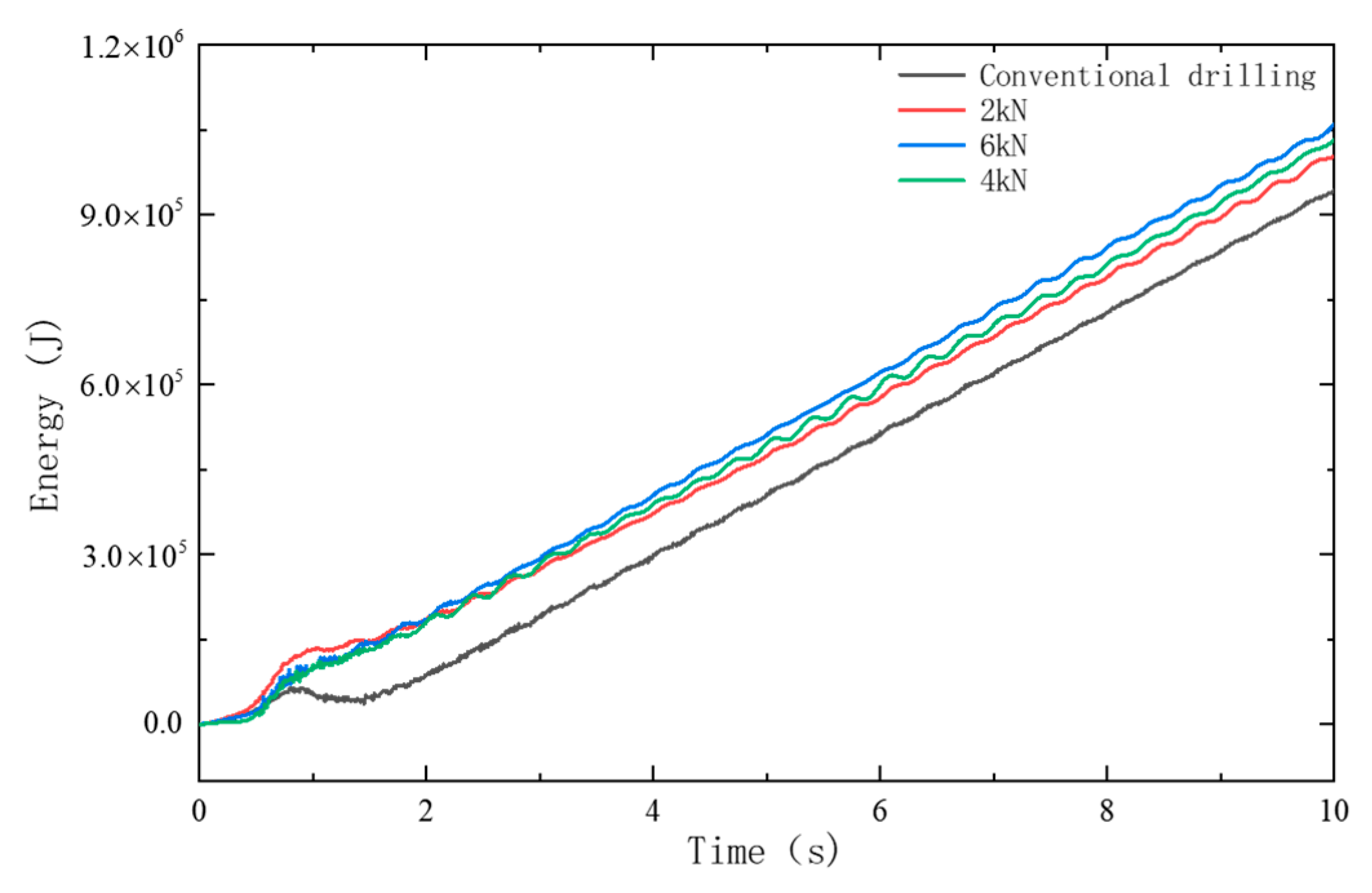


| Component | Elastic Modulus (GPa) | Density (kg/m3) | Poisson’s Ratio | Tensile Strength (MPa) |
|---|---|---|---|---|
| Impactors | 207 | 7850 | 0.30 | 1.08 × 103 |
| Drill Collar | 207 | 7850 | 0.30 | 1.05 × 103 |
| Stabilizer | 220 | 7850 | 0.30 | 1.03 × 103 |
| Drill Bit | 579 | 15,000 | 0.22 | 3.54 × 103 |
| Component | Density (kg/m3) | Young’s Modulus (GPa) | Poisson’s Ratio | Shear Strength (MPa) | Tensile Strength (MPa) |
|---|---|---|---|---|---|
| Drill String | 7864 | 215 | 0.32 | 100 | 1200 |
| Drill Bit | 7864 | Rigid Body | |||
| Borehole Wall | 2439 | Rigid Body | |||
| Ya an Granite | |
|---|---|
| Density (kg/m3) | 2750 |
| Young’s Modulus (GPa) | 36.5 |
| Poisson’s Ratio | 0.25 |
| Tensile Strength (MPa) | 8.91 |
| Uniaxial Compressive Strength (MPa) | 150 |
| Friction Angle (°) | 33.52 |
| Porosity (%) | 1.241 |
| Number | Main Surface | Slave Surface | Contact Property |
|---|---|---|---|
| CP-1 | Bit bottom surface | Rock mass part | IntOrop-1 |
| CP-2 | Drill bit top | BHA assembly | Bind |
| CP-3 | Drill string system | Wellbore wall | IntOrop-1 |
| CP-4 | Rock surface | Rock mass part | Self-contact |
| Rock-Confining Pressure (MPa) | Rotary Speed (rpm) | Impact Amplitude (kN) | Impact Frequency (Hz) | Weight on Bit (t) | Simulation Duration (s) |
|---|---|---|---|---|---|
| 20 | 30~210 | 4~12 | 10~400 | 1~3 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, Q.; Li, Y.; Jia, J.; Zhao, L. Vibration Damage Analysis of Bottom Hole Assembly Under Axial Impact Based on Dynamic Analysis. Appl. Sci. 2025, 15, 7388. https://doi.org/10.3390/app15137388
Xue Q, Li Y, Jia J, Zhao L. Vibration Damage Analysis of Bottom Hole Assembly Under Axial Impact Based on Dynamic Analysis. Applied Sciences. 2025; 15(13):7388. https://doi.org/10.3390/app15137388
Chicago/Turabian StyleXue, Qilong, Yafeng Li, Jianbo Jia, and Lun Zhao. 2025. "Vibration Damage Analysis of Bottom Hole Assembly Under Axial Impact Based on Dynamic Analysis" Applied Sciences 15, no. 13: 7388. https://doi.org/10.3390/app15137388
APA StyleXue, Q., Li, Y., Jia, J., & Zhao, L. (2025). Vibration Damage Analysis of Bottom Hole Assembly Under Axial Impact Based on Dynamic Analysis. Applied Sciences, 15(13), 7388. https://doi.org/10.3390/app15137388






