Abstract
Considering the complexity of laser cutting technology, and difficulties and limitations when applying traditional multi-criteria decision-making (MCDM) methods, this study proposes a fuzzy MCDM methodology for the analysis of the fibre laser cutting process, assessment of alternative cutting conditions and selection of favourable cutting conditions. The experiment in fibre laser cutting of mild steel was based on a Box–Behnken design by considering three input parameters (focus position, cutting speed and oxygen pressure) and four relevant criteria for the assessment of cutting conditions (kerf width on a straight and curved cut, surface roughness and surface productivity). The proposed fuzzy MCDM methodology makes use of expert knowledge and experimental data for criteria evaluation and decision matrix development, respectively, while three fuzzy MCDM methods (fuzzy TOPSIS, fuzzy WASPAS and fuzzy ARAS) were used to determine the complete ranking of alternatives. Kendall’s tau-b and Spearman’s rho correlation tests were applied to compare the obtained ranking lists, while the stability of the ranking was assessed with the application of the Monte Carlo simulation. Finally, to approximate the fuzzy decision-making rule, a second-order model was developed to reveal the significance of process parameters and identify favourable laser cutting conditions.
1. Introduction
Due to many advantages, laser cutting is one of the most widely used methods in modern industry for contour cutting of small- to medium-thickness metal sheets. The most common materials, such as mild steels, stainless steels, titanium and aluminium and their alloys, are usually processed with CO2, Nd:YAG or fibre lasers by fusion cutting and flame cutting methods [1]. Due to multiple advantages, fibre lasers have become omnipresent in the modern materials processing industry [2]. In addition, with the ability to achieve very high cutting speeds without compromising cut quality, fibre laser cutting technology outperforms turret punching technology, which is considered the cheapest technology [3].
Nevertheless, it is very difficult to attain excellent results from multiple techno-economical aspects due to the existence of numerous process parameters and complex physical phenomena. In the actual cutting process, multiple and interdependent physical phenomena take place during the interaction of the laser beam, workpiece material and assist gas [4]. At the same time, the existence of noise factors further affects cutting process variability and the resulting process performance [5], making it very difficult to select a particular combination of process parameters for each specific sheet material type and thickness. Moreover, as noted by Tercan et al. [6], in the laser cutting process, planning decisions include the consideration of the effect of multi-dimensional parameters on different preselected criteria and desirable process outputs. A comprehensive review related to the analysis of the effects of laser cutting parameters on different criteria in laser cutting of metals is available [7].
Nonetheless, the trial and error method is frequently seen as an acceptable approach for selecting laser cutting conditions during the manufacturing process [8]. However, although it may be sufficient for usual production requirements, it cannot efficiently handle multiple requirements, in terms of achieving particular process performance values, of different importance at the same time. Moreover, not only may the selection of laser cutting conditions be time-consuming and costly, but an inadequate selection of laser cutting conditions may also lead to different quality defects such as dross formation, wide heat affected zone, kerf taper, pittings, etc. [3]. In order to overcome these issues and select a particular combination of laser cutting parameters with respect to single or multiple criteria, different scientific/engineering approaches have been proposed, such as Taguchi’s robust design methodology [9,10,11], empirical modelling and optimization [12,13,14,15], artificial intelligence methods [16,17,18,19,20], fuzzy logic [21,22,23,24] and multi-criteria decision-making (MCDM) methodology [8,25,26,27,28,29,30].
Given the limited application of MCDM methodology for analysis and assessment of laser cutting conditions, along with certain limitations, such as difficulty in determining the exact quantitative values of criteria weights in situations where criteria weights, as determined by a panel of decision makers, may vary, as well as handling uncertain attribute values, the present study promotes the use of fuzzy MCDM methodology for the analysis of the fibre laser cutting process, assessment of alternative cutting conditions and selection of favourable cutting conditions. Within the proposed framework, an attempt has been made to compare applied fuzzy MCDM methods, such as fuzzy TOPSIS, fuzzy WASPAS and fuzzy ARAS methods, by using Kendall’s tau-b and Spearman’s rho tests to analyse the ranking consistency of alternatives. In addition, a mathematical model is proposed to approximate the fuzzy decision-making rule so as to gain insight into the significance of process parameters and to identify the process window with the most favourable laser cutting conditions. It is believed that the proposed methodology can provide a more objective and robust analysis. Experimental data for the development of the fuzzy MCDM model was acquired using a Box–Behnken design with different combinations of three laser cutting parameters (focus position, cutting speed and oxygen pressure). Kerf width on a straight cut, kerf width on a curved cut, surface roughness and surface productivity were considered the relevant criteria for the assessment of cutting conditions in fibre laser cutting of mild steel using oxygen as the assist gas.
2. Materials and Methods
2.1. Experimental Research
A plate with a thickness of 3 mm made of S235 steel was used for cutting specimens. S235 is low carbon structural steel known for its versatility in different engineering and construction applications. It is used for responsible welded structures without risk of brittle fracture. In addition to good weldability, it also has good cold-forming properties. Structural applications of S235 steel include boiler tanks, oil tanks, storage containers, condensers, rods, pins, levers, holders, etc. The chemical composition and mechanical properties of S235 steel are given in Table 1 and Table 2, respectively.

Table 1.
Chemical composition of S235 steel (% maximum).

Table 2.
Mechanical properties of S235 steel.
The experiment was conducted using a GWEIKE fibre laser-cutting machine with the maximal power of 2 kW. During the cutting process, laser power was set at 2 kW, while oxygen with a purity of 99.95% (3.5 grade) was supplied coaxially with a conical nozzle of 1.2 mm hole diameter. The distance between the sheet and the cutting head was set at 1 mm. The Box–Behnken experimental design was adopted to define 13 alternative laser cutting conditions by changing process parameters at three levels: focus position (f = 1, 1.5, 2 mm), cutting speed (v = 1.8, 2.7, 3.6 m/min) and oxygen pressure (p = 0.75, 0.85, 0.95 bar).
In previous research, in the context of the application of MCDM in laser cutting, other authors considered different criteria such as kerf width [25,28,30], material removal rate [25,30], surface roughness [26,28,30], heat-affected zone [26,30], machining time [26], kerf taper [28] and emission rate and carbonization [25]. In the present study, the multi-criteria analysis of the fibre laser cutting process considered the following criteria: kerf width on a straight cut, kerf width on a curved cut (radius of 30 mm), surface roughness and surface productivity. Kerf width is a very important kerf geometry characteristic for contour cutting technologies [5]. Also, given that kerf geometry depends on the cut profile [31], and that kerf width is closely related to the dimensional accuracy of cut features (positive or negative), i.e., adjustments of the offsets, kerf widths on a straight and on a curved cut were considered as criteria in the framework of the MCDM. On the other hand, surface roughness is one of the most important quality indicators for assessment of the cut surface, while surface productivity, as an indicator of material removal rate, is an important criterion to manufacturers. It should be noted that dross attachment, which is probably the most important quality criterion, was omitted from the MCDM matrix because no combination of parameters in the experiment resulted in dross formation. Likewise, due to the high negative correlation between linear specific energy, which is a useful indicator of cutting efficiency in terms of eco-friendly technology criteria [32], and surface productivity, this criterion was also omitted. Finally, economical aspects in fibre laser cutting using oxygen were not considered because of negligible influence of resulting assist gas flows, which are considerably lower than in the case of laser fusion cutting.
Surface roughness, in terms of average maximum height of the profile (Rz), was measured three times along the cut edge at the middle of the sheet thickness using a Marsurf XR 1 surface roughness tester.
The surface roughness parameter Rz is very important in defining cut quality categories according to the ISO 9013 standard [33]. Three measurements of kerf width on a straight cut and three measurements of kerf width on a curved cut were obtained optically using the optical coordinate measuring machine (CMM) DeMeet 443. Surface productivity is one of the productivity indicators in contour cutting, defined as the produced cut surface in unit time. It can be estimated as the product of the sheet thickness and the cutting speed. The investigated experimental space, along with the used measurement systems, are given in Figure 1.

Figure 1.
Experimental setup.
After measurements, it was observed that in the covered experimental space, the mean kerf width on a straight cut ranged from 0.33 to 0.506 mm, kerf width on a curved cut from 0.353 to 0.503 mm, surface roughness from 3.56 to 40.55 μm and surface productivity from 5.4 to 10.8 mm2/min. Although similar patterns for kerf width were observed, there was no experimental trial (alternative) with a particular combination of laser cutting parameter values which would result in minimal kerf width on both a straight and curved cut profile, minimal surface roughness and maximal surface productivity at the same time. As an example, alternative A3, conducted while focusing the laser beam at f = +1 mm with the combination of a cutting speed of v = 3.6 m/min and oxygen pressure of p = 0.85 bar, is characterized by minimal mean kerf width values (0.33 mm on a straight cut and 0.353 mm on a curved cut) and maximal surface productivity (10.8 mm2/min), but at the same time results in the highest surface roughness (40.55 μm). Therefore, a fuzzy MCDM methodology was proposed in order to consider expert opinions regarding relative criteria importance, handle uncertain attribute values related to the use of measurement systems for experimental data acquisition, rank alternative cutting conditions, determine the best possible trade-off solution and perform a more comprehensive analysis.
2.2. Fuzzy MCDM Methodology
In recent years, the application of different MCDM approaches has become increasingly significant when taking a number of aspects and different laser cutting performances into consideration [27]. To acknowledge a certain degree of uncertainty and vagueness in the decision-making process [34], this study proposes a fuzzy MCDM methodology (Figure 2).
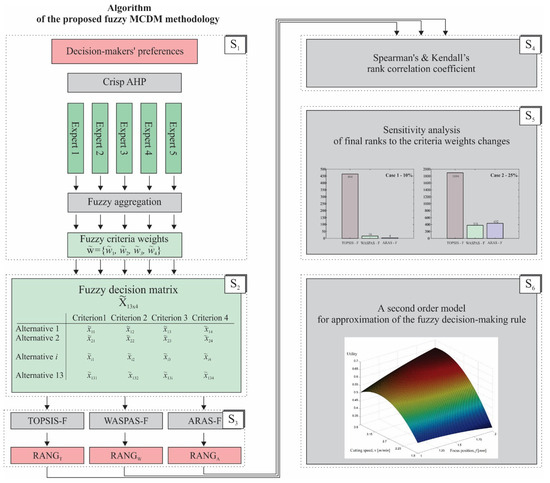
Figure 2.
A complete algorithm of the proposed fuzzy MCDM methodology.
The algorithm is implemented in six major steps:
Step 1. For the initial step, five experts (k = 1 ÷ 5) in the field of laser cutting evaluated four criteria using a regular analytic hierarchy process (AHP) and Saaty’s 1–9 scale [35]. The AHP can be implemented in a few simple steps, and in this case, it was used only for the determination of the criteria weights. The results are five criteria weights vectors wk = {wk1, wk2, wk3, wk4}. The aggregated fuzzy values of criteria weights for each criterion (j = 1 ÷ 4) are obtained using the minimal, arithmetic mean and maximal value of the corresponding crisp values wkj as shown by Equation (1).
The result is the fuzzy criteria weights vector .
Step 2. In the second step, a fuzzy decision matrix is obtained according to experimental data. In the case of the first three criteria (C1—kerf width on a straight cut [mm], C2—kerf width on a curved cut [mm], and C3—surface roughness [μm]), similarly to the approach described in Step 1, each alternative performance , according to the specific criterion, is obtained using Equation (2).
where i = 1 ÷ 13 is the index of the considered alternative and T is the number of experimental trials. In the case of the fourth criterion C4—surface productivity [mm2/min], values are equal. The result of this step is the fuzzy decision matrix .
Step 3. When solving a given decision-making problem, given the specificities of each MCDM method, it would be advisable to examine and compare results obtained by different methods [36]. Therefore, in this step, three fuzzy MCDM methods are used for determining the complete ranking of alternatives:
- Fuzzy Technique for the Order Preference by Similarity to Ideal Solution (TOPSIS-F), as an extension of the regular TOPSIS method proposed by Wang et al. [37].
- Fuzzy Weighted Aggregated Sum Product ASsessment (WASPAS-F) method proposed by Turskis et al. [38].
- Fuzzy Additive Ratio ASsessment (ARAS-F) method conceptualized and proposed by Turskis and Zavadskas [39].
Fuzzy TOPSIS ranks alternatives based on their distance from the ideal and the anti-ideal solutions, using fuzzy logic to express uncertainty in evaluations. In contrast, fuzzy WASPAS combines two methods—weighted sum and weighted product—providing greater flexibility in prioritization, especially when balancing between additive and multiplicative models. Fuzzy ARAS, on the other hand, evaluates alternatives relative to a predefined ideal solution and uses a direct comparison of total utility, which is simpler to interpret compared to fuzzy TOPSIS. While TOPSIS measures distances and WASPAS blends two distinct approaches, ARAS focuses on the overall utility in comparison to the best possible outcome. In comparison with traditional MCDM methods, all three applied fuzzy MCDM methods employ fuzzy numbers to better capture uncertainty and subjective assessments in decision-making. In addition, the fuzzy MCDM framework allows the use of linguistic assessments of attributes in the decision-making matrix. Considering that the performances of the alternatives in the decision matrix were obtained through experimental measurements on the samples tested, the fuzzy approach enabled the aggregation of results in the manner defined by Equation (2).
Step 4. In the fourth step, the results obtained using different fuzzy MCDM methods are compared using Kendall’s tau-b and Spearman’s rho correlation coefficient tests.
Step 5. The uncertainty in solving Decision-Making Problems (DMPs) with Multi-Criteria Decision-Making (MCDM) methods is often significantly influenced by the weighting of criteria. Thus, assessing how variations in criteria weights affect the ranking results produced by the chosen MCDM methods is crucial [40,41,42]. In this research, the Monte Carlo simulation was employed, generating 1000 different scenarios of criteria weights for two cases: Case 1 with 10% variations, and Case 2 with 25% variations of original weights. Each value wki in five criteria weights vectors wk = {wk1, wk2, wk3, wk4}, obtained by selected experts (k = 1 ÷ 5), has been randomly varied from interval [wkiu, wkil], where wkiu and wkil represent the upper and the lower boundary of each original weight wki (i = 1 ÷ 4, number of criteria) defined as ±10% (Case 1) or ±25% (Case 2) of original wki, as shown in Equation (3):
For each scenario, the aggregation procedure described in Step 1 of the proposed methodology incorporating Equation (1) is applied, so 1000 fuzzy criteria weights vectors are obtained (for both cases). In the next step for thus-defined fuzzy criteria weights vectors and for all selected fuzzy MCDM methods, complete rankings of the alternatives were calculated. The changes of alternative ranks relative to the first solution (obtained with original weights) are monitored and sums of all rank changes are calculated.
Step 6. In essence, the application of any MCDM method, i.e., generation of the decision-making rule, enables objective assessment and ranking within the set of previously known alternatives. However, if one can explicitly represent the decision rule in terms of alternative attribute values, one can obtain very insightful and useful information regarding the considered decision-making problem. Therefore, development and analysis of the mathematical model for approximation of the fuzzy MCDM decision-making rule is proposed as the final step in the presented methodology.
3. Results and Discussion
3.1. Ranking of Alternatives and Analysis of Results
The ranking results of alternative fibre laser cutting conditions after applying the above-discussed fuzzy MCDM methodology are given in Figure 3.
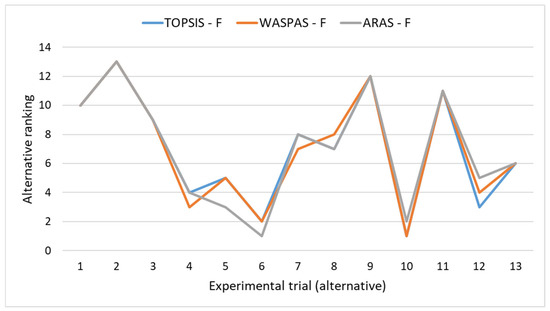
Figure 3.
Ranking of alternatives, i.e., different fibre laser cutting conditions.
The results from Figure 3 indicate that alternative A10 stands out as the most favourable combination of fibre laser cutting parameters (f = 1.5 mm, v = 3.6 m/min, and p = 0.75 bar). One needs to note that this cutting condition is favourable if one considers the spent energy to cut a unit length, i.e., linear specific energy, which is a useful indicator of laser cutting efficiency and eco-friendliness [32]. Moreover, attaining less interaction time means less heat input, heat affected zone (HAZ) and mechanical stress to the workpiece material being cut. It must be noted that the ARAS-F method identified alternative A6 as the best trade-off solution. On the other hand, alternative A2 represents the least preferable combination of fibre laser cutting parameters (f = 2 mm, v = 1.8 m/min, and p = 0.85 bar) by all three fuzzy MCDM methods. This lowest ranking can be explained given that shifting the focus position away from the upper sheet surface widens kerf width [43], and in addition, a decreasing cutting speed has a significant effect on the resulting material removal rate.
The results from Figure 3 also clearly indicate the complexity of the laser cutting process, variable effect of parameter inputs and existence of parameter interactions to a greater or lesser extent. Namely, alternative A1 (f = 1 mm, v = 1.8 m/min, and p = 0.85 bar) drops from 10 to 13 ranking position of alternative A2 (f = 2 mm, v = 1.8 m/min, and p = 0.85 bar) because of changing focusing position, which results in the following phenomena: kerf width on a straight cut increased by 31%, kerf width on a curved cut increased by 27% and surface roughness (Rz) increased from 15.84 μm to 22.49 μm, while the surface productivity remained unchanged. On the other hand, alternative A3 (f = 1 mm, v = 3.6 m/min, and p = 0.85 bar) rises from eight to four ranking position of alternative A4 (f = 2 mm, v = 3.6 m/min, and p = 0.85 bar) because of changing focusing position, which results in the following phenomena: kerf width on a straight cut increased by 42%, kerf width on a curved cut increased by 29% and surface roughness (Rz) significantly decreased from 40.55 μm to 5.51 μm, while the surface productivity remained unchanged. This observation indicates that the effect of focus position on cut quality characteristics should be considered through the interaction with the cutting speed, which can be explained by changing interaction time, laser energy absorption of the material, formation and behaviour of the melt front, melt flow and ejection, as well as cut kerf geometry characteristics at different combinations of cutting speed and focus position. Actually, the existence of a change in the effects of one parameter by the variation of another parameter has been previously observed in fibre laser cutting of aluminium [44], stainless steel [45], aluminium alloy [46] and carbon fibre reinforced polymer composites [47]. The previous observations clearly indicate that laser cutting parameters may have opposite effects on process performance characteristics due to the existence of interaction effects of laser cutting parameters to some extent, which is consequently reflected in the final ranking of alternatives.
The cut surface patterns obtained under the most preferable cutting condition and the least preferable cutting condition are given in Figure 4. As can be observed, there is a minimal difference between the upper (laser dominated) and the lower (melt-flow controlled) cut surface, indicating “striation free” fibre laser cutting of mild steel [48].

Figure 4.
Low magnification photographs of cut surface patterns of best cutting condition (A10) and least preferred cutting condition (A2).
As can be observed in Figure 4, relatively small changes in the assist gas pressure (0.1 bar) and focus position (0.5 mm), but significant considering cutting speed (1.8 m/min), result in a huge difference in the overall cutting performance. As discussed by Al-Mashikhi et al. [49], in laser reactive cutting, the change in the cutting speed has multiple effects affecting the melt temperature, viscosity and mass flow rates, as well as gas dynamics, cut front geometry and laser absorptivity. Stabilization of the melt film dynamics, decrease in striation wavelength and surface roughness with an increase in the cutting speed have also been previously reported [50].
A more detailed analysis of the obtained results indicated that all cutting conditions in which small cutting speed was used (A1, A2, A9, A11), as well as the combination of high cutting speed and low laser beam focusing (A3), are the least preferred laser cutting conditions that produce second quality group surface roughness (Rz) according to the ISO 9013 standard [33]. All other conditions result in the first quality group with Rz ≤ 11.8 μm.
3.2. Comparison of Ranking Lists Obtained by Different Fuzzy MCDM Methods
The fourth step in the proposed fuzzy MCDM methodology is the comparison of ranking lists obtained by different fuzzy MCDM methods (Table 3). Calculated Spearman’s correlation coefficients (rho) show a very strong correlation of obtained alternative rankings, i.e., consistent ranking of alternatives by applied fuzzy MCDM methods. Moreover, Kendall’s rank correlation coefficients (tau-b) confirm that there exist almost complete, highly positive associations between the obtained rankings.

Table 3.
Kendall’s (tau-b) and Spearman’s (rho) rank correlation coefficient.
3.3. Sensitivity Analysis of Ranking Lists
The results from Step 5, regarding the analysis of the sensitivity of final ranks to the criteria weights changes, are shown in Figure 5.
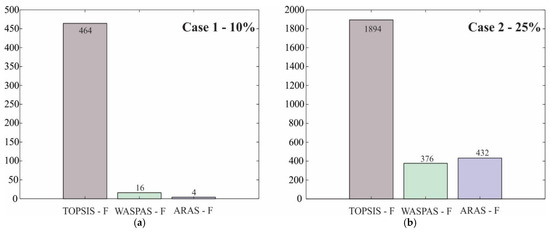
Figure 5.
The changes of alternative ranks relative to the solution obtained with original weights: (a) Case 1 (±10%), (b) Case 2 (±25%).
The results from Figure 5 clearly show that different scenarios of criteria weights do not significantly affect the ranking of alternatives in the case of the WASPAS-F and ARAS-F methods. On the other hand, the TOPSIS-F method showed 464 and 1894 changes in the ranks of alternatives (out of a possible 13 × 999 = 12,987 changes in 1000 scenarios). This can be explained by analysing the utility functions for all the considered MCDM ranking methods. The utility of an alternative represents the performance of that alternative considering all the criteria, and it is the parameter on the basis of which the ranking of alternatives is determined. In the case of TOPSIS-F, the utility values for all alternatives are between 0.119746 and 0.223525 (a relatively narrow range), while in the case of WASPAS-F and ARAS-F, this range is 0.39939–0.79856 and 0.360761–0.80879, respectively.
If only the best two alternatives, A10 and A6, are considered, in Case 1 (10% of value changes), no change in rank was observed. In Case 2 (25% of value changes), changes in the ranks of alternatives were observed only in the case of the TOPSIS-F method. Alternative A10 had 63 rank changes, while alternative A6 had 82 rank changes in 1000 scenarios. In the case of the other two methods, changes in the ranks of alternatives were insignificant (1–8 changes).
3.4. Modelling of the Aggregate Fuzzy Decision-Making Rule
The application of the proposed fuzzy MCDM methodology has so far enabled the assessment and ranking of existing solutions, i.e., laser cutting conditions that were tested in real manufacturing conditions, in the conducted experiment. In order to obtain insight into how laser cutting parameters (inputs) affect the ranking and provide useful information regarding the selection of favourable input values, with respect to the considered criteria, one needs to find a suitable approximation of the functional relationship between inputs (independent variables) and output (dependent variable), which in this study may refer to the average utility value assigned to each alternative. To this aim, given the type and resolution of the experimental matrix, in Step 6 of the proposed fuzzy MCDM methodology, a full quadratic model was developed (Table 4).

Table 4.
Model summary and analysis of variance (ANOVA).
As can be observed from Table 4, the linear and the quadratic effect of the cutting speed are statistically significant, i.e., one can argue that the cutting speed has dominant influence regarding the considered criteria with associated criteria weights and consequent ranking of a given cutting condition. In addition, the results indicate a statistically significant second-order model (p < 0.05), which is able to explain 96.6% of variation in the response (average utility value). Therefore, the developed model could serve to identify regions in the covered experimental hyper-space which have higher response values. Considering that it was determined that the assist gas pressure (p) has no statistically significant effect on the response, and as it is well known that cutting costs rise with an increase in assist gas pressure, a single contour diagram was developed (Figure 6).
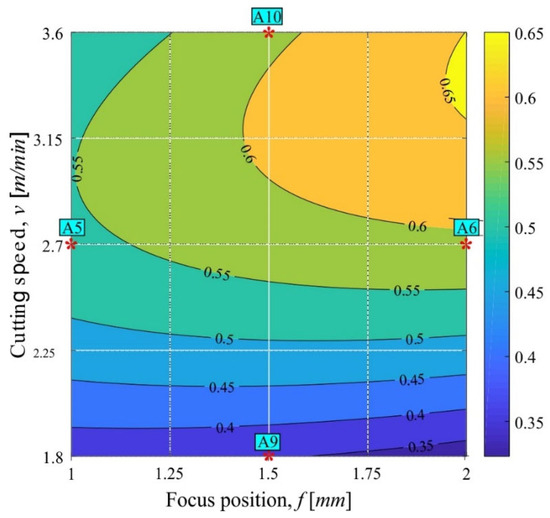
Figure 6.
Contour diagram showing the change in response for different values of cutting speed (v) and focus position (f) for constant assist gas pressure (p = 0.75 bar).
From Figure 6, one can observe that smaller cutting speeds, irrespective of focus position, result in lower response values, i.e., one obtains cuts which are less favourable. In contrast, the process window with the highest response values is enclosed within middle to high cutting speeds (v = 2.7–3.6 m/min) and higher focus positions (f = 1.5–2 mm). Moreover, the development of the second-order prediction model and its visualization via contour plot clearly indicate that there exist a number of input parameter combinations with which one can obtain better response values. For example, the best ranked alternatives in the experiment (A10, A6) had a response value of approximately 0.6 (Figure 6).
Through optimization, it can be shown that within the experimental space investigated, i.e., surface of a sphere, the minimal response value (average utility value) of 0.286 is obtained under the following combination of laser cutting parameters: focus position f = 1.81 mm, cutting speed v = 1.8 m/min and assist gas pressure p = 0.86 bar. On the other hand, the maximal response value of 0.625 is obtained under the following combination of laser cutting parameters: focus position f = 1.72 mm, cutting speed v = 3.12 m/min and assist gas pressure p = 0.75 bar. Among others, acceptable compromise solutions with higher response values than initial design points are, for example, the following: (1) f = 1.73 mm, v = 3.09 m/min, p = 0.75 bar with response value of 0.625, (2) f = 1.71 mm, v = 3.05 m/min, p = 0.75 bar with response value of 0.62 and (3) f = 1.66 mm, v = 2.95 m/min, p = 0.75 bar with response value of 0.61.
With the development of an average utility value prediction model, one can identify regions with higher response values within investigated experimental space and generate various compromise solutions, as well as direct further experimental investigation. However, the selection of a particular solution may be significantly influenced by the quality, dimensional accuracy and/or productivity requirements. In that regard, the applied approach, although simpler and more resource-efficient in comparison with the traditional multi-objective optimization based on the use of multiple models for each considered response, allows the prediction of the average utility value (as an aggregate function), but lacks prediction of individual responses (criteria), which can be considered as the main drawback.
3.5. Practicality and Feasibility of the Approach
The practicality of the proposed fuzzy MCDM methodology in industrial laser cutting settings is reflected in its ability to consider multiple issues, including the following:
- Merging qualitative (linguistic) and quantitative data from multiple decision makers (engineers and operators), i.e., cross-functional teams, with the possibility of handling imprecise judgments and decision makers’ opinions (e.g., “moderate dross”, or “acceptable kerf geometry”), as well as data variability and uncertainty (due to the actual cutting process or measurement system).
- Existence of multiple conflicting processing and cut quality characteristics that characterize the laser cutting technology (e.g., cutting costs, kerf width, kerf taper, productivity, dross existence, surface roughness, etc.), the absence of a single optimal cutting condition and the necessity to determine the ‘as good as possible’ trade-off solution(s) for a given case study (sheet thickness and material type, required cut specifications, type of laser cutting method, etc.).
- Screening the key input parameters that are of the greatest importance among numerous input parameters to adequately consider their adjustments and guide further experimental hyper-space exploration in order to achieve more favourable cutting results.
Although practical usage would require engineers’ and operators’ training or support from domain experts, at least in the beginning, it is believed that the approach discussed, with all its advantages and disadvantages, has a certain potential for practical application in industry. With the existence of available and accessible tools for fuzzy MCDM methods and applications, and their integration and adaptation with existing control and decision-support systems and Industry 4.0 technologies, it is believed to be a feasible solution that can be accepted by manufacturers using laser cutting technology.
4. Conclusions
Considering the complexity of laser cutting technology and difficulties and limitations of traditional MCDM methods, this study proposed a fuzzy MCDM methodology for the analysis of the fibre laser cutting process, assessment of alternative cutting conditions and identification of favourable cutting conditions. Based on the conducted analyses and obtained results, the following conclusions may be drawn:
- Laser cutting conditions in which a small cutting speed is used, or a combination of high cutting speed and low focus position, are less preferable with respect to meeting the considered criteria and associated significance levels.
- Generally consistent rankings of alternatives were obtained by the applied fuzzy MCDM methods, with highly positive associations.
- The conducted analysis, with respect to sensitivity of final ranks to the criteria weights changes, showed a high level of stability of individual solutions, even in cases of significant changes in the weighting coefficients.
- The development and statistical analysis of the mathematical model for the approximation of the fuzzy MCDM decision-making rule revealed statistically significant linear and quadratic effects of the cutting speed.
- The possibility to determine the resulting utility through the contour diagram for arbitrarily chosen input values is very important, considering that drastically different laser cutting conditions may achieve the same result. Moreover, through optimization, one can reveal the most preferable input parameter value combination.
- Unlike classical multi-objective optimization, based on the use of multiple models for each response, the applied approach lacks prediction of individual response values for a given combination of input parameter values, which makes it not very convenient for the selection of a particular solution in the presence of specific requirements and constraints.
The proposed fuzzy MCDM methodology may be additionally adapted when solving specific problems so as to include limitations and exact specifications that must be met with respect to the considered criteria.
Author Contributions
Conceptualization, M.M., G.P. and M.T.; methodology, G.P., M.M., M.T. and D.M.; software, G.P. and M.M.; validation, M.M. and P.J.; formal analysis, M.T., M.M., G.P., D.M. and P.J.; investigation, M.M., P.J. and M.T.; resources, M.T., M.M., G.P., D.M. and P.J.; data curation, M.T., M.M. and G.P.; writing—original draft preparation, M.T., M.M., G.P., D.M. and P.J.; writing—review and editing, M.T., M.M., G.P., D.M. and P.J.; visualization, M.T., M.M. and G.P.; supervision, M.M. and G.P.; project administration, M.M. and G.P.; funding acquisition, D.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Dataset available on request from the authors.
Acknowledgments
This research was financially supported by the Ministry of Science, Technological Development and Innovation of the Republic of Serbia (Contract No. 451-03-137/2025-03/200109).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AHP | Analytic Hierarchy Process |
| ARAS | Additive Ratio ASsessment |
| ARAS-F | Fuzzy Additive Ratio ASsessment |
| CMM | Coordinate Measuring Machine |
| DMP | Decision-Making Problem |
| HAZ | Heat Affected Zone |
| MCDM | Multi-Criteria Decision-Making |
| TOPSIS | Technique for the Order Preference by Similarity to Ideal Solution |
| TOPSIS-F | Fuzzy Technique for the Order Preference by Similarity to Ideal Solution |
| WASPAS | Weighted Aggregated Sum Product ASsessment |
| WASPAS-F | Fuzzy Weighted Aggregated Sum Product ASsessment |
References
- Zhang, Y.; Wang, C.; Xu, W.; Zhang, X.; Ren, K.; Wang, S.; Hua, Q. Laser Cutting of Titanium Alloy Plates: A Review of Processing, Microstructure, and Mechanical Properties. Metals 2024, 14, 1152. [Google Scholar] [CrossRef]
- Madić, M.; Jovanović, D.; Janković, P. Fiber Laser Cutting Technology: Pilot Case Study in Mild Steel Cutting. Spectr. Mech. Eng. Oper. Res. 2024, 1, 1–9. [Google Scholar] [CrossRef]
- Bohdal, Ł.; Schmidtke, D. Effect of fiber and CO2 lasers parameters on the cut surface quality of RVS 1.4301 stainless steel. J. Mech. Eng. Sci. 2022, 16, 8862–8872. [Google Scholar] [CrossRef]
- Riveiro, A.; Quintero, F.; Lusquiños, F.; Comesaña, R.; Pou, J. Study of melt flow dynamics and influence on quality for CO2 laser fusion cutting. J. Phys. D Appl. Phys. 2011, 44, 135501. [Google Scholar] [CrossRef]
- Madić, M.; Girdu, C.C.; Marinković, D.; Janković, P.; Trifunović, M. Analysis of Kerf Width and its Variation in CO2 Laser Cutting of Straight and Curved Cut Profiles. Teh. Vjesn. Tech. Gaz. 2024, 31, 1884–1891. [Google Scholar] [CrossRef]
- Tercan, H.; Al Khawli, T.; Eppelt, U.; Büscher, C.; Meisen, T.; Jeschke, S. Use of Classification Techniques to Design Laser Cutting Processes. Procedia CIRP 2016, 52, 292–297. [Google Scholar] [CrossRef][Green Version]
- Alsaadawy, M.; Dewidar, M.; Said, A.; Maher, I.; Shehabeldeen, T.A. A comprehensive review of studying the influence of laser cutting parameters on surface and kerf quality of metals. Int. J. Adv. Manuf. Technol. 2024, 130, 1039–1074. [Google Scholar] [CrossRef]
- Madić, M.; Antucheviciene, J.; Radovanović, M.; Petković, D. Determination of laser cutting process conditions using the preference selection index method. Opt. Laser Technol. 2017, 89, 214–220. [Google Scholar] [CrossRef]
- Nas, E.; Uzuner, S. Optimization of laser cutting parameters for improved surface quality in AISI 304 stainless steel. Gazi J. Eng. Sci. 2023, 9, 654–662. [Google Scholar] [CrossRef]
- Turkkan, Y.A.; Aslan, M.; Tarkan, A.; Aslan, Ö.; Yuce, C.; Yavuz, N. Multi-Objective Optimization of Fiber Laser Cutting of Stainless-Steel Plates Using Taguchi-Based Grey Relational Analysis. Metals 2023, 13, 132. [Google Scholar] [CrossRef]
- Prabhahar, M.; Praveen Athitya, M.; Thiru Chitrambalam, M.; Prabhu, L.; Prakash, S. Experimental investigation of MS material in laser cutting machine using Taguchi method. In Proceedings of the International Conference on Physics and Energy 2021, Kancheepuram, Tamilnadu, India, 21 April 2021. [Google Scholar] [CrossRef]
- Tamilarasan, A.; Renugambal, A.; Rajamani, D.; Shaik, M. Experiment-based process modelling and analysis in Nd:YAG laser cutting of Hastelloy C-276: RSM-CCD technique. OPSEARCH 2024, 62, 661–681. [Google Scholar] [CrossRef]
- Hasan, H.K. Analysis of the effecting parameters on laser cutting process by using response surface methodology (RSM) method. J. Achiev. Mater. Manuf. Eng. 2022, 110, 59–66. [Google Scholar] [CrossRef]
- Younis, M. Surface roughness study of laser cut surface. J. Egypt. Soc. Tribol. 2022, 19, 63–71. [Google Scholar] [CrossRef]
- Genna, S.; Menna, E.; Rubino, G.; Tagliaferri, V. Experimental Investigation of Industrial Laser Cutting: The Effect of the Material Selection and the Process Parameters on the Kerf Quality. Appl. Sci. 2020, 10, 4956. [Google Scholar] [CrossRef]
- Ürgün, S.; Yiğit, H.; Fidan, S.; Sınmazçelik, T. Optimization of Laser Cutting Parameters for PMMA Using Metaheuristic Algorithms. Arab. J. Sci. Eng. 2024, 49, 12333–12355. [Google Scholar] [CrossRef]
- Kechagias, J.D.; Fountas, N.A.; Ninikas, K.; Vaxevanidis, N.M. Kerf Geometry and Surface Roughness Optimization in CO2 Laser Processing of FFF Plates Utilizing Neural Networks and Genetic Algorithms Approaches. J. Manuf. Mater. Process. 2023, 7, 77. [Google Scholar] [CrossRef]
- Nikitjuk, Y.; Prokhorenko, V.; Semchenko, A.; Kovalenko, D. Multi-Criteria Optimization of Quartz Glass Laser Cleaving Parameters via Neural Network Simulation and Genetic Algorithm. In Proceedings of the 2023 7th International Conference on Information, Control, and Communication Technologies (ICCT), Astrakhan, Russia, 2–6 October 2023. [Google Scholar] [CrossRef]
- Vagheesan, S.; Govindarajulu, J. Comparative Regression and Neural Network Modeling of Roughness and Kerf Width in CO2 Laser Cutting of Aluminium. Teh. Vjesn. Tech. Gaz. 2021, 28, 1437–1441. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Deng, W.; Showaib, E.A. Improving laser cutting quality of polymethylmethacrylate sheet: Experimental investigation and optimization. J. Mater. Res. Technol. 2020, 9, 1325–1339. [Google Scholar] [CrossRef]
- Blaga, F.S.; Cristea, A.; Nastor, G.; Pop, A.; Buidos, T.; Lucaciu, I. Fuzzy set decision-making system for determining the technological parameters of the laser cutting process. In Proceedings of the International Conference Annual Session of Scientific Papers—IMT Oradea 2022, Oradea, Romania, 7–8 July 2022. [Google Scholar] [CrossRef]
- Lukic, D.; Cep, R.; Milosevic, M.; Antic, A.; Zivkovic, A.; Todic, V.; Rodic, D. A Grey Fuzzy Approach to the Selection of Cutting Process from the Aspect of Technological Parameters. Appl. Sci. 2022, 12, 12589. [Google Scholar] [CrossRef]
- Parthiban, A.; Sathish, S.; Ravikumar, R.; Prakash, P. Experimental investigation and fuzzy logic modelling of CO2 laser cutting parameter for AA6061-T6 sheet. Int. J. Rapid Manuf. 2020, 9, 48–57. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, V.; Sharma, G. Experimental Investigation of Multiple Quality Characteristics of Laser Beam Machined Surface using Integrated Taguchi and Fuzzy Logic Method. J. Manuf. Sci. Prod. 2016, 16, 189–199. [Google Scholar] [CrossRef]
- Khalaf, T.; Thangaraj, M.; Moiduddin, K. Performance Evaluation and MOORA Based Optimization of Pulse Width Control on Leather Specimens in Diode Laser Beam Cutting Process. Processes 2023, 11, 2901. [Google Scholar] [CrossRef]
- Srinivasan, D.; Ramakrishnan, H.; Balasundaram, R.; Ravichandran, M. Optimization of laser cutting process parameters on Ss347 using GRA and TOPSIS. Surf. Rev. Lett. 2023, 30, 2350039. [Google Scholar] [CrossRef]
- Madić, M.; Petrović, G.; Petković, D.; Antucheviciene, J.; Marinković, D. Application of a Robust Decision-Making Rule for Comprehensive Assessment of Laser Cutting Conditions and Performance. Machines 2022, 10, 153. [Google Scholar] [CrossRef]
- Das, P.P.; Chakraborty, S. Application of Superiority and Inferiority Multi-criteria Ranking Method for Parametric Optimization of Laser Cutting Processes. Process Integr. Optim. Sustain. 2020, 4, 409–427. [Google Scholar] [CrossRef]
- Madić, M.; Petrović, G.; Petković, D.; Janković, P. Traditional and Integrated MCDM Approaches for Assessment and Ranking of Laser Cutting Conditions. Spectr. Mech. Eng. Oper. Res. 2024, 1, 250–257. [Google Scholar] [CrossRef]
- Basar, G.; Der, O. Multi-objective optimization of process parameters for laser cutting polyethylene using fuzzy AHP-based MCDM methods. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2025. [Google Scholar] [CrossRef]
- Sharma, A.; Yadava, V.; Rao, R. Optimization of kerf quality characteristics during Nd:YAG laser cutting of nickel based super alloy sheet for straight and curved cut profiles. Opt. Lasers Eng. 2010, 48, 915–925. [Google Scholar] [CrossRef]
- Girdu, C.C.; Mihail, L.A.; Dragoi, M.V. Estimation of laser cutting process efficiency. In Proceedings of the 9th International Scientific Conference—Research and Development of Mechanical Elements and Systems (IRMES 2019), Kragujevac, Serbia, 5–7 September 2019. [Google Scholar] [CrossRef]
- ISO 9013:2017; Thermal cutting—Classification of thermal cuts—Geometrical product specification and quality tolerances. International Organization for Standardization: Geneva, Switzerland, 2017.
- Ulutaş, A.; Popovic, G.; Stanujkic, D.; Karabasevic, D.; Zavadskas, E.K.; Turskis, Z. A New Hybrid MCDM Model for Personnel Selection Based on a Novel Grey PIPRECIA and Grey OCRA Methods. Mathematics 2020, 8, 1698. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation; McGraw-Hill: New York, NY, USA, 1980; pp. 49–71. [Google Scholar]
- Biswas, S.; Božanić, D.; Pamučar, D.; Marinković, D. A spherical fuzzy based decision making framework with Einstein aggregation for comparing preparedness of SMEs in Quality 4.0. Facta Univ. Ser. Mech. Eng. 2023, 21, 453–478. [Google Scholar] [CrossRef]
- Wang, Y.J.; Lee, H.S.; Lin, K. Fuzzy TOPSIS for multi-criteria decision-making. Int. Math. J. 2003, 3, 367–379. [Google Scholar]
- Turskis, Z.; Zavadskas, E.K.; Antucheviciene, J.; Kosareva, N. A Hybrid Model Based on Fuzzy AHP and Fuzzy WASPAS for Construction Site Selection. Int. J. Comput. Commun. Control 2015, 10, 873–888. [Google Scholar] [CrossRef]
- Turskis, Z.; Zavadskas, E.K. A new fuzzy additive ratio assessment method (ARAS-F). Case study: The analysis of fuzzy multiple criteria in order to select the logistic centers location. Transport 2010, 25, 423–432. [Google Scholar] [CrossRef]
- Chakraborty, S.; Saha, A.K. Selection of forklift unit for transport handling using integrated MCDM under neutrosophic environment. Facta Univ. Ser. Mech. Eng. 2024, 22, 235–256. [Google Scholar] [CrossRef]
- Ristić, B.; Bogdanović, V.; Stević, Ž.; Marinković, D.; Papić, Z.; Gojković, P. Evaluation of Pedestrian Crossings Based on the Concept of Pedestrian Behavior Regarding Start-Up Time: Integrated Fuzzy MCDM Model. Teh. Vjesn. Tech. Gaz. 2024, 31, 1206–1214. [Google Scholar] [CrossRef]
- Pramanik, S. SVPNN-ARAS strategy for MCGDM under single-valued pentapartitioned neutrosophic number environment. Serbian J. Manag. 2023, 18, 405–420. [Google Scholar] [CrossRef]
- Lopez, A.B.; Assunção, E.; Quintino, L.; Blackburn, J.; Khan, A. High-power fiber laser cutting parameter optimization for nuclear Decommissioning. Nucl. Eng. Technol. 2017, 49, 865–872. [Google Scholar] [CrossRef]
- Adelmann, B.; Hellmann, R. Fast Laser Cutting Optimization Algorithm. Phys. Procedia 2011, 12, 591–598. [Google Scholar] [CrossRef]
- Duspara, M.; Matysiak, W.; Vidaković, I.; Sedmak, S. Optimization of Nitrogen Use Efficiency in Cutting of Austenitic Stainless Steel by a Fiber Laser. FME Trans. 2022, 50, 745–751. [Google Scholar] [CrossRef]
- Ullah, S.; Li, X.; Guo, G.; Rodríguez, A.R.; Li, D.; Du, J.; Cui, L.; Wei, L. Energy efficiency and cut-quality improvement during fiber laser cutting of aluminum alloy in the different hardened conditions. Mater. Today Commun. 2022, 33, 104236. [Google Scholar] [CrossRef]
- Rao, S.; Sethi, A.; Das, A.K.; Mandal, N.; Kiran, P.; Ghosh, R.; Dixit, A.R.; Mandal, A. Fiber laser cutting of CFRP composites and process optimization through response surface methodology. Mater. Manuf. Process. 2017, 32, 1612–1621. [Google Scholar] [CrossRef]
- Powell, J.; Al-Mashikhi, S.O.; Kaplan, A.F.H.; Voisey, K.T. Fibre laser cutting of thin section mild steel: An explanation of the ‘striation free’ effect. Opt. Lasers Eng. 2011, 49, 1069–1075. [Google Scholar] [CrossRef]
- Al-Mashikhi, S.O.; Powell, J.; Kaplan, A.F.H.; Voisey, K.T. An explanation of ‘striation free’ cutting of mild steel by fibre laser. In Proceedings of the Fifth International WLT-Conference Lasers in Manufacturing, LIM 2009, Munich, Germany, 15–18 June 2009. [Google Scholar]
- Halm, U.; Nießen, M.; Schulz, W. Simulation of melt film dynamics in laser fusion cutting using a boundary layer approximation. Int. J. Heat Mass Transf. 2021, 168, 120837. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).