Analysis of Cascading Failures and Recovery in Freeway Network Under the Impact of Incidents
Abstract
1. Introduction
- (1)
- Cascading Failure Model: An edge-based cascading failure model is developed to simulate failure propagation in transportation networks, explicitly incorporating realistic route choice behavior in freeway systems. We conduct simulations for a specific freeway network to observe the changes in network performance during the cascade process.
- (2)
- Identification and Ranking of Critical Edges: We propose a method to identify and rank important edges within the network. The proposed method aims to identify critical edge combinations and prioritize their recovery sequence to enhance overall network performance during restoration.
- (3)
- Recovery Strategy: Based on the identified critical edges, a targeted recovery strategy is developed. Simulations conducted on a real-world freeway network dataset show that the proposed strategy significantly outperforms existing benchmark methods in terms of recovery efficiency.
2. Literature Review
2.1. Cascading Failure
2.2. Recovery Strategy
2.3. Cascading Failure of Transportation Networks
3. Methodology
3.1. Network Representation
3.2. Modeling the Cascading Failures of the Freeway Network
3.2.1. Preliminaries
3.2.2. Load Redistribution
3.2.3. Cascading Failure Process
3.3. Recovery Strategies
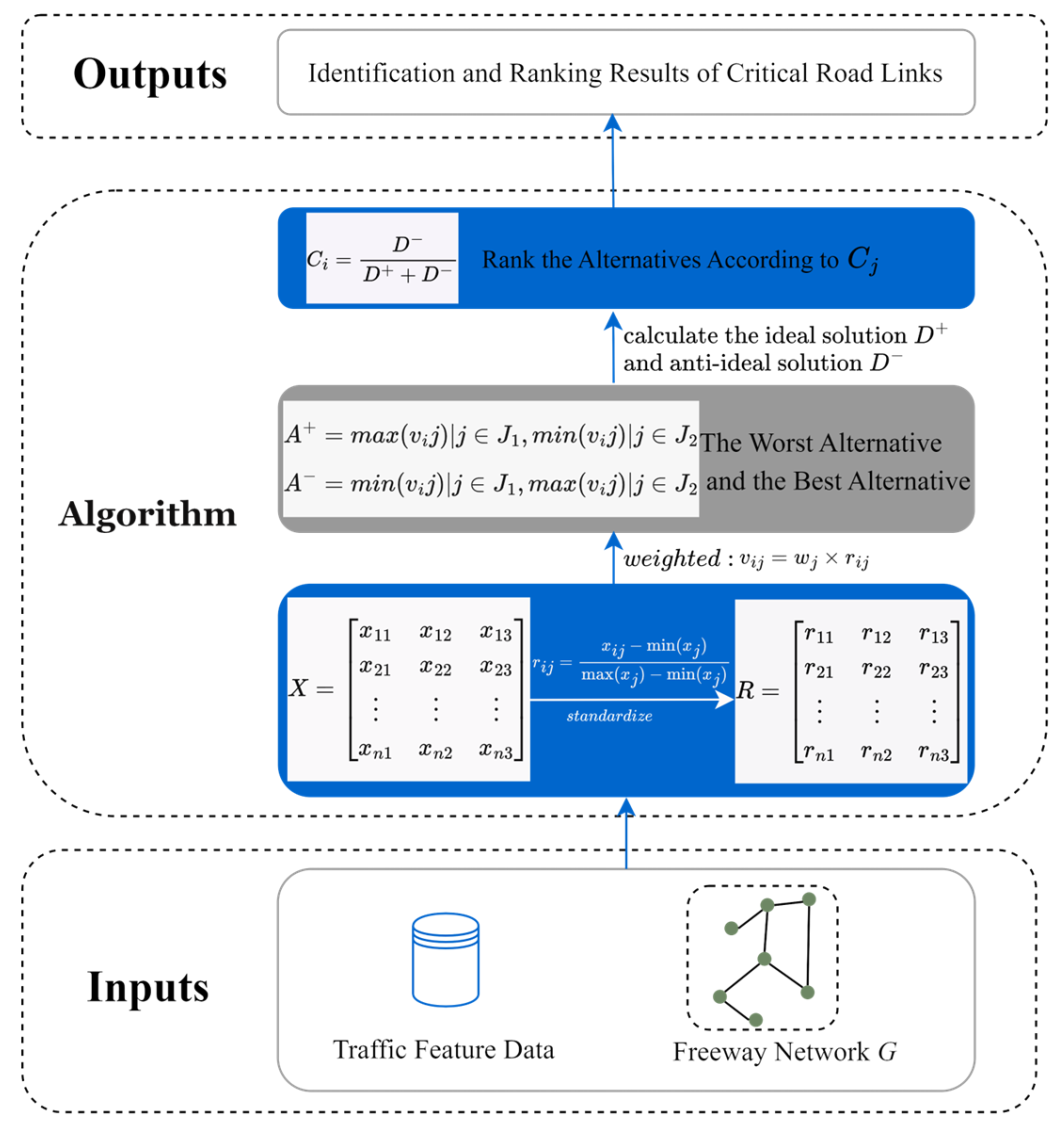
3.3.1. Identifying and Ranking Critical Road Segments
3.3.2. Recovery Process Based on Critical Links
3.4. Evaluation Metrics
4. Case Study
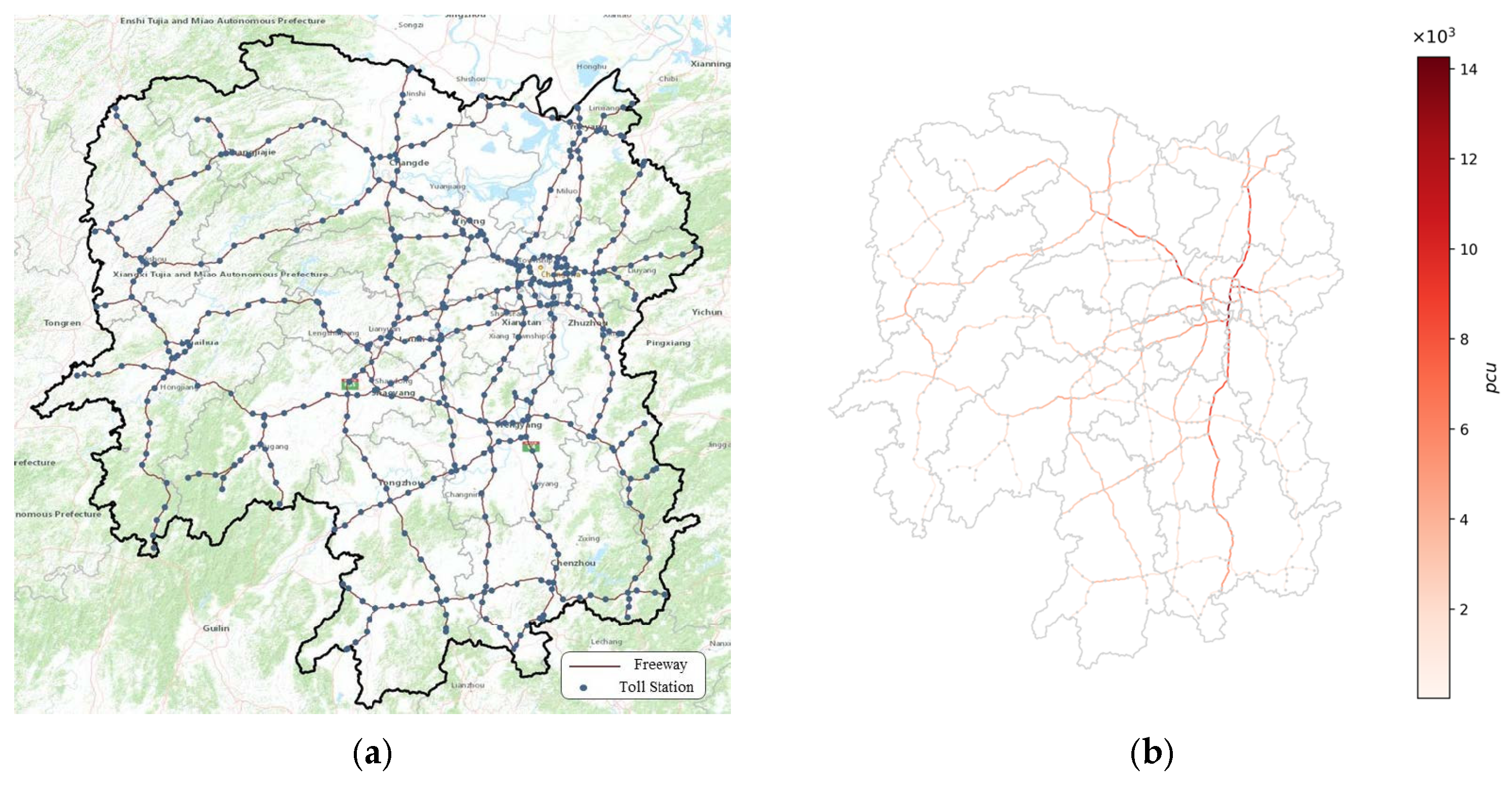
4.1. Data Preparation
4.2. Cascading Failure Simulation and Analysis
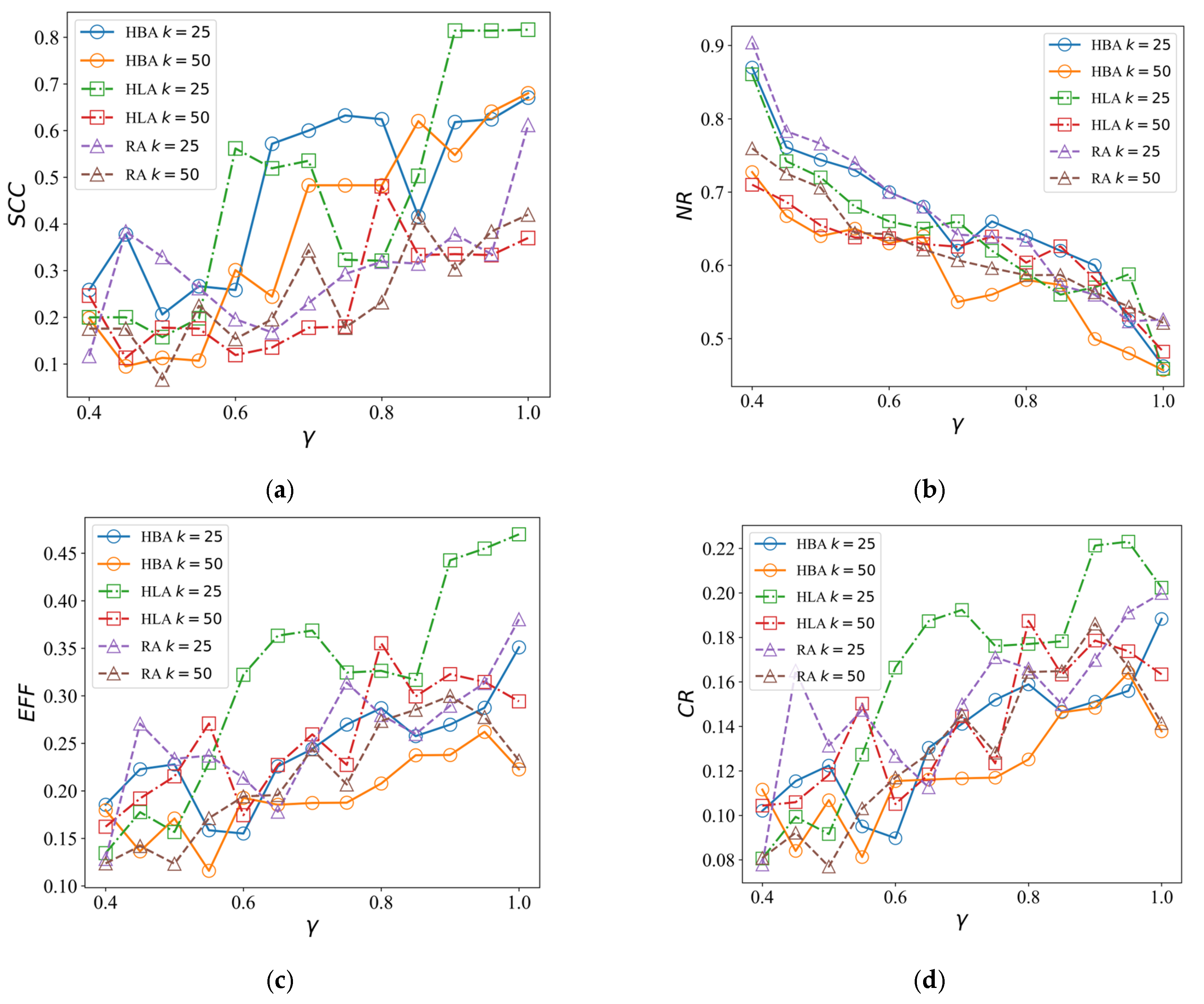
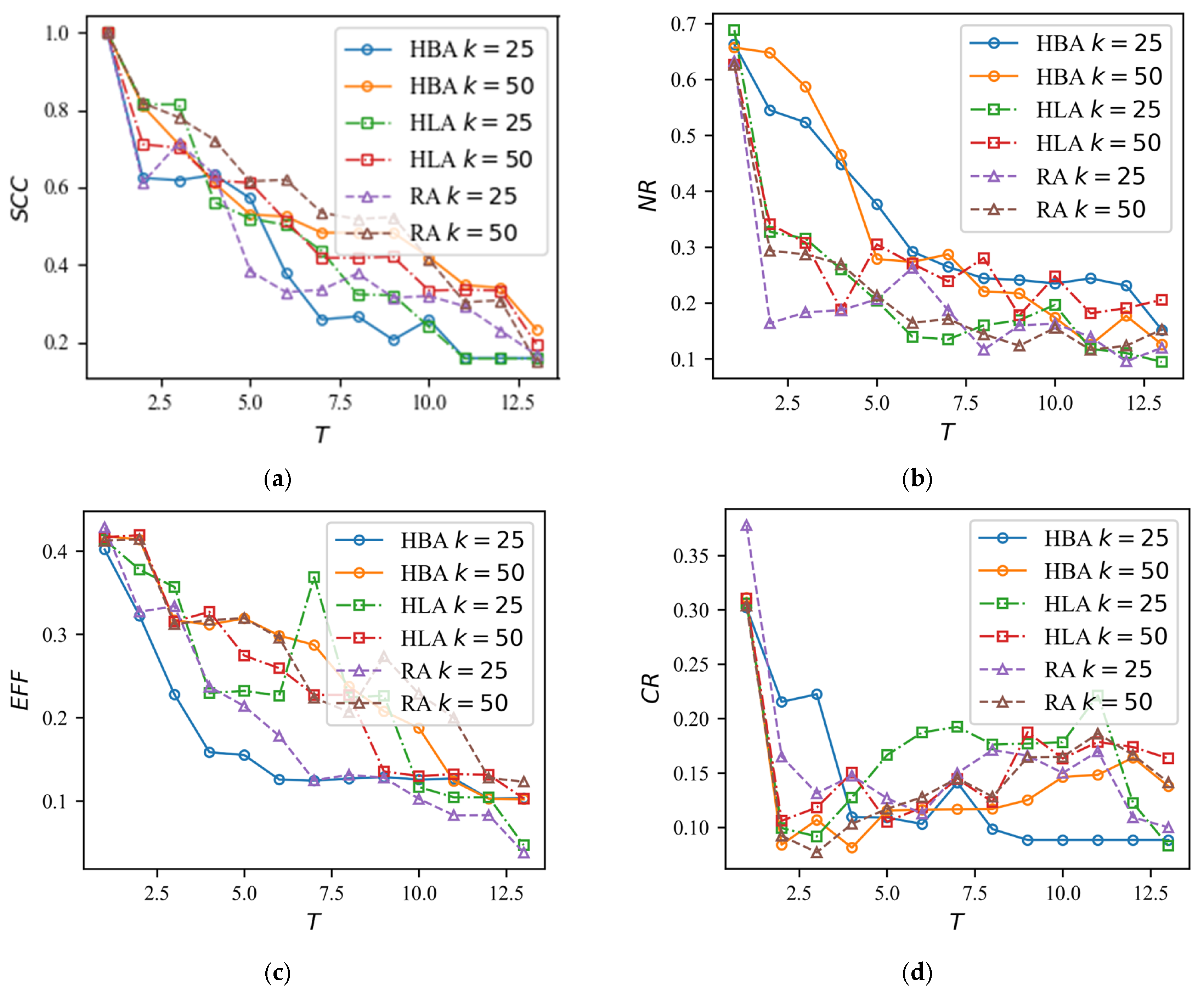
4.2.1. Different Initial Attack Strategies
4.2.2. Attack with Reduced Road Capacity
4.2.3. Evolution in the Failure Process
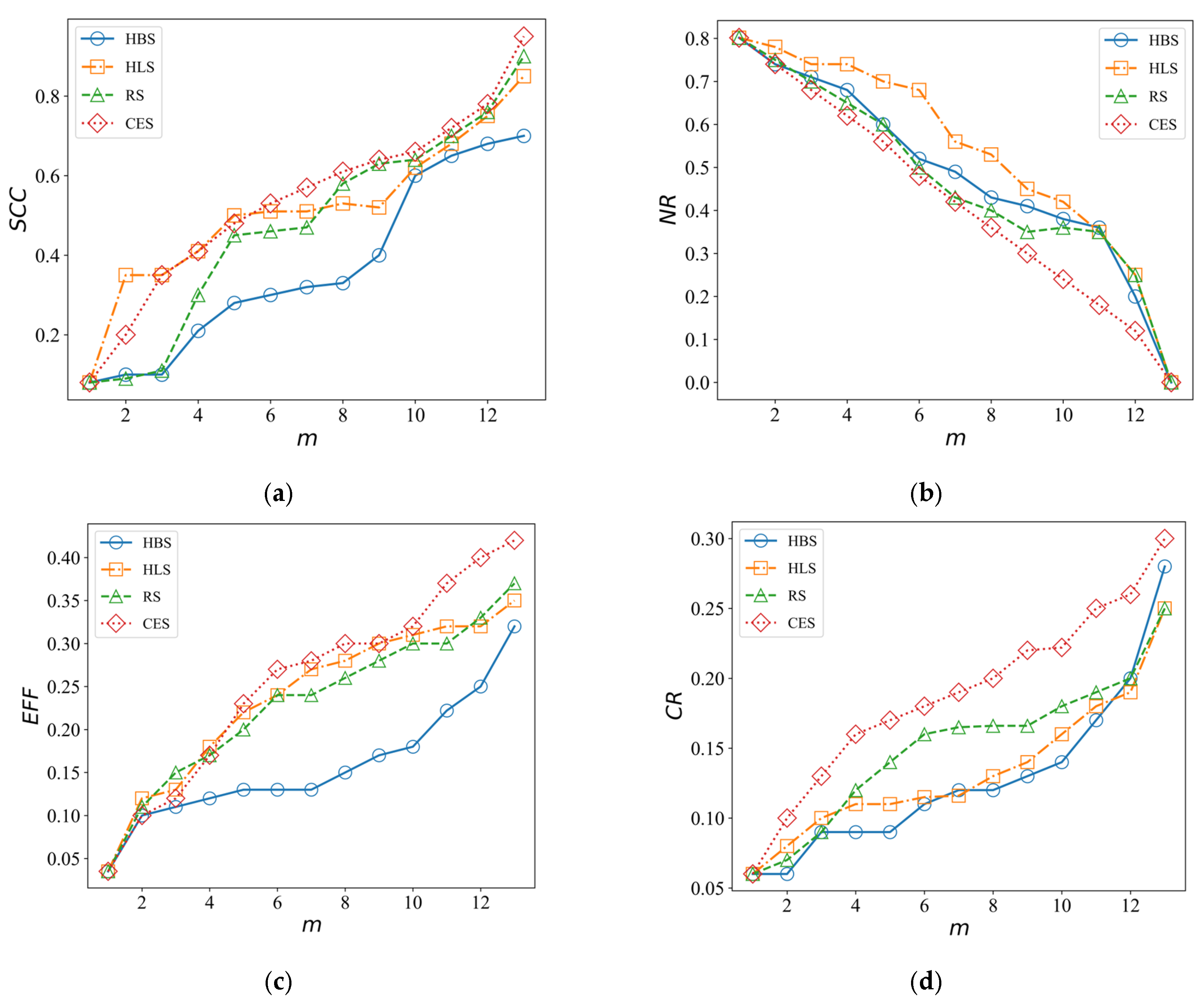
4.3. Recovery of Cascading Failure
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bai, L.; Han, X.; Zhang, Y.; Xie, X. Optimal project portfolio selection considering cascading failure among projects. IEEE Trans. Eng. Manag. 2023, 71, 4750–4760. [Google Scholar] [CrossRef]
- Gao, C.; Fan, Y.; Jiang, S.; Deng, Y.; Liu, J.; Li, X. Dynamic robustness analysis of a two-layer rail transit network model. IEEE Trans. Intell. Transp. Syst. 2022, 23, 6509–6524. [Google Scholar] [CrossRef]
- Shen, Y.; Ren, G.; Ran, B. Cascading failure analysis and robustness optimization of metro networks based on coupled map lattices: A case study of Nanjing, China. Transportation 2019, 48, 537–553. [Google Scholar] [CrossRef]
- Yin, R.; Yuan, H.; Wang, J.; Zhao, N.; Liu, L. Modeling and analyzing cascading dynamics of the urban road traffic network. Phys. A Stat. Mech. Its Appl. 2021, 566, 125600. [Google Scholar] [CrossRef]
- Zhang, Y.; Ng, S.T. Robustness of urban railway networks against the cascading failures induced by the fluctuation of passenger flow. Reliab. Eng. Syst. Saf. 2022, 219, 108227. [Google Scholar] [CrossRef]
- Lu, Q.; Zhang, L.; Xu, P.; Cui, X.; Li, J. Modeling network vulnerability of urban rail transit under cascading failures: A Coupled Map Lattices approach. Reliab. Eng. Syst. Saf. 2022, 221, 108320. [Google Scholar] [CrossRef]
- Sun, L.; Huang, Y.; Chen, Y.; Yao, L. Vulnerability assessment of urban rail transit based on multi-static weighted method in Beijing, China. Transp. Res. Part A Policy Pract. 2018, 108, 12–24. [Google Scholar] [CrossRef]
- Dobson, I. Estimating the Propagation and Extent of Cascading Line Outages From Utility Data With a Branching Process. IEEE Trans. Power Syst. 2012, 27, 2146–2155. [Google Scholar] [CrossRef]
- Zhou, D.; Elmokashfi, A. Network recovery based on system crash early warning in a cascading failure model. Sci. Rep. 2018, 8, 7443–7452. [Google Scholar] [CrossRef]
- Motter, A.E.; Lai, Y.-C. Cascade-based attacks on complex networks. Phys. Rev. E 2002, 66, 065102. [Google Scholar] [CrossRef]
- Duan, J.; Li, D.; Huang, H.-J. Reliability of the traffic network against cascading failures with individuals acting independently or collectively. Transp. Res. Part C Emerg. Technol. 2023, 147, 104017. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, N.; Xiang, L.; Wang, C. Abnormal cascading dynamics based on the perspective of road impedance. Phys. A Stat. Mech. Its Appl. 2023, 627, 129128. [Google Scholar] [CrossRef]
- Wu, J.; Chen, Z.; Zhang, Y.; Xia, Y.; Chen, X. Sequential Recovery of Complex Networks Suffering from Cascading Failure Blackouts. IEEE Trans. Netw. Sci. Eng. 2020, 7, 2997–3007. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, B. Network resilience and recovery mechanism: A review. J. Cyber Secur. 2021, 6, 44–59. [Google Scholar] [CrossRef]
- Hassan, M.; Al Nafees, A.; Sraban, S.S.; Paul, A.; Mahin, H.D. Application of machine learning in intelligent transport systems: A comprehensive review and bibliometric analysis. Discov. Civ. Eng. 2025, 2, 98. [Google Scholar] [CrossRef]
- Gheorghe, C.; Soica, A. Revolutionizing Urban Mobility: A Systematic Review of AI, IoT, and Predictive Analytics in Adaptive Traffic Control Systems for Road Networks. Electronics 2025, 14, 719. [Google Scholar] [CrossRef]
- Huang, J.; Wang, J. Travel behavior resilience: Theory, method, and empirical studies. J. Geogr. Sci. 2024, 34, 1657–1674. [Google Scholar] [CrossRef]
- Brummitt, C.D.; D’Souza, R.M.; Leicht, E.A. Suppressing cascades of load in interdependent networks. Proc. Natl. Acad. Sci. USA 2012, 109, E680–E689. [Google Scholar] [CrossRef]
- Kinney, R.; Crucitti, P.; Albert, R.; Latora, V. Modeling cascading failures in the North American power grid. Eur. Phys. J. B—Condens. Matter Complex Syst. 2005, 46, 101–107. [Google Scholar] [CrossRef]
- Schäfer, B.; Witthaut, D.; Timme, M.; Latora, V. Dynamically induced cascading failures in power grids. Nat. Commun. 2018, 9, 1975. [Google Scholar] [CrossRef]
- Doyle, J.C.; Alderson, D.L.; Li, L.; Low, S.; Roughan, M.; Shalunov, S.; Tanaka, R.; Willinger, W. The “robust yet fragile” nature of the Internet. Proc. Natl. Acad. Sci. USA 2005, 102, 14497–14502. Available online: https://www.pnas.org/doi/10.1073/pnas.0501426102 (accessed on 23 April 2025). [CrossRef]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality: An explanation of the 1/f noise. Phys. Rev. Lett. 1987, 59, 381–384. Available online: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.59.381 (accessed on 2 May 2025). [CrossRef] [PubMed]
- Dobson, I.; Carreras, B.A.; Lynch, V.E.; Newman, D.E. An initial model for complex dynamics in electric power system blackouts. In Proceedings of the 34th Annual Hawaii International Conference on System Sciences, Maui, HI, USA, 6 January 2001. [Google Scholar]
- Wang, J.-W.; Rong, L.-L. A model for cascading failures in scale-free networks with a breakdown probability. Phys. A Stat. Mech. Its Appl. 2009, 388, 1289–1298. [Google Scholar] [CrossRef]
- Wang, W.-X.; Chen, G. Universal robustness characteristic of weighted networks against cascading failure. Phys. Rev. E 2008, 77, 026101. [Google Scholar] [CrossRef]
- Crucitti, P.; Latora, V.; Marchiori, M. Model for cascading failures in complex networks. Phys. Rev. E 2004, 69, 045104. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Du, Q.; Li, Y.; Zhou, Y.; Wang, Y.; Huang, Y.; Martinez-Pastor, B. Cascading failure and recovery of metro–bus double-layer network considering recovery propagation. Transp. Res. Part D Transp. Environ. 2023, 122, 103861. [Google Scholar] [CrossRef]
- Cwilich, G.; Buldyrev, S.V. Cascading traffic jams in two-dimensional networks with Motter-Lai dynamics. Phys. Rev. E 2022, 106, 024303. [Google Scholar] [CrossRef] [PubMed]
- Perez, I.A.; Vaknin Ben Porath, D.; La Rocca, C.E. Cascading failures from localized overloads in isotropic and anisotropic spatial networks. arXiv 2021, arXiv:2112.11308. Available online: https://arxiv.org/abs/2112.11308 (accessed on 2 May 2025).
- Jiang, B.; Claramunt, C. Topological analysis of urban street networks. Environ. Plan. B Plan. Des. 2004, 31, 151–162. [Google Scholar] [CrossRef]
- Sienkiewicz, J.; Hołyst, J.A. Statistical analysis of 22 public transport networks in Poland. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2005, 72, 046127. [Google Scholar] [CrossRef]
- Liu, X.; Huang, S.; Chen, Q. Cause analysis of expressway traffic accidents based on accident statistics of Hunan provincial expressway in 2012–2018. Transp. Saf. Environ. 2024, 6, tdad010. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, J.; Haque, M.M.; Lee, J. Hazard-based duration modelling of merging time interval on freeway on-ramps. Transp. Saf. Environ. 2023, 5, tdac040. [Google Scholar] [CrossRef]
- Li, J.; Guo, F.; Zhou, Y.; Yang, W.; Ni, D. Predicting the severity of traffic accidents on mountain freeways with dynamic traffic and weather data. Transp. Saf. Environ. 2023, 5, tdad001. [Google Scholar] [CrossRef]
- Zhai, X.; Sze, N.N.; Lee, J.J.; Xu, P.; Huang, H. Multi-scale approaches to cope with scale effect issues in macroscopic crash analysis. Accid. Anal. Prev. 2025, 214, 107971. [Google Scholar] [CrossRef] [PubMed]
- Qian, Y.; Wang, B.; Xue, Y.; Zeng, J.; Wang, N. A simulation of the cascading failure of a complex network model by considering the characteristics of road traffic conditions. Nonlinear Dyn. 2015, 80, 413–420. [Google Scholar] [CrossRef]
- Ma, F.; Liu, F.; Yuen, K.F.; Lai, P.; Sun, Q.; Li, X. Cascading failures and vulnerability evolution in bus–metro complex bilayer networks under rainstorm weather conditions. Int. J. Environ. Res. Public Health 2019, 16, 329. [Google Scholar] [CrossRef]
- Wu, Q.; Han, Z.; Cui, C.; Liu, F.; Zhao, Y.; Xie, Z. Vulnerability identification and cascading failure spatiotemporal patterns on road network under the rainstorm disaster. ISPRS Int. J. Geo-Inf. 2022, 11, 564. [Google Scholar] [CrossRef]
- Jin, K.; Wang, W.; Li, X.; Chen, S.; Qin, S.; Hua, X. Cascading failure in urban rail transit network considering demand variation and time delay. Phys. A Stat. Mech. Its Appl. 2023, 630, 129290. [Google Scholar] [CrossRef]
- Wang, J. Mitigation strategies on scale-free networks against cascading failures. Phys. A Stat. Mech. Its Appl. 2013, 392, 2257–2264. [Google Scholar] [CrossRef]
- Smolyak, A.; Levy, O.; Vodenska, I.; Buldyrev, S.; Havlin, S. Mitigation of cascading failures in complex networks. Sci. Rep. 2020, 10, 16124. [Google Scholar] [CrossRef]
- Hu, F.; Yeung, C.H.; Yang, S.; Wang, W.; Zeng, A. Recovery of infrastructure networks after localised attacks. Sci. Rep. 2016, 6, 24522. [Google Scholar] [CrossRef] [PubMed]
- Lyu, R.; Zhang, M.; Wang, X.-J.; Wang, T.-J. Recovery strategy of multilayer network against cascading failure. Int. J. Mod. Phys. C 2022, 33, 2250039. [Google Scholar] [CrossRef]
- Hu, S.; Zhou, Q.; Li, J.; Wang, Y.; Roncoli, C.; Zhang, L.; Lehe, L. High Time-Resolution Queue Profile Estimation at Signalized Intersections Based on Extended Kalman Filtering. IEEE Trans. Intell. Transp. Syst. 2022, 23, 21274–21290. [Google Scholar] [CrossRef]
- Dai, H.; Yao, E.; Lu, N.; Bian, K.; Zhang, B. Freeway network connective reliability analysis based on a complex network approach. Procedia Eng. 2016, 137, 372–381. [Google Scholar] [CrossRef]
- Wang, P.; Liao, Y.; Li, S.; Ke, R.; Wang, T. Route guidance model of regional highway multi-layer transportation network for balancing individual and social benefits. J. Southwest Jiaotong Univ. 2024, 1–12, online first. [Google Scholar]


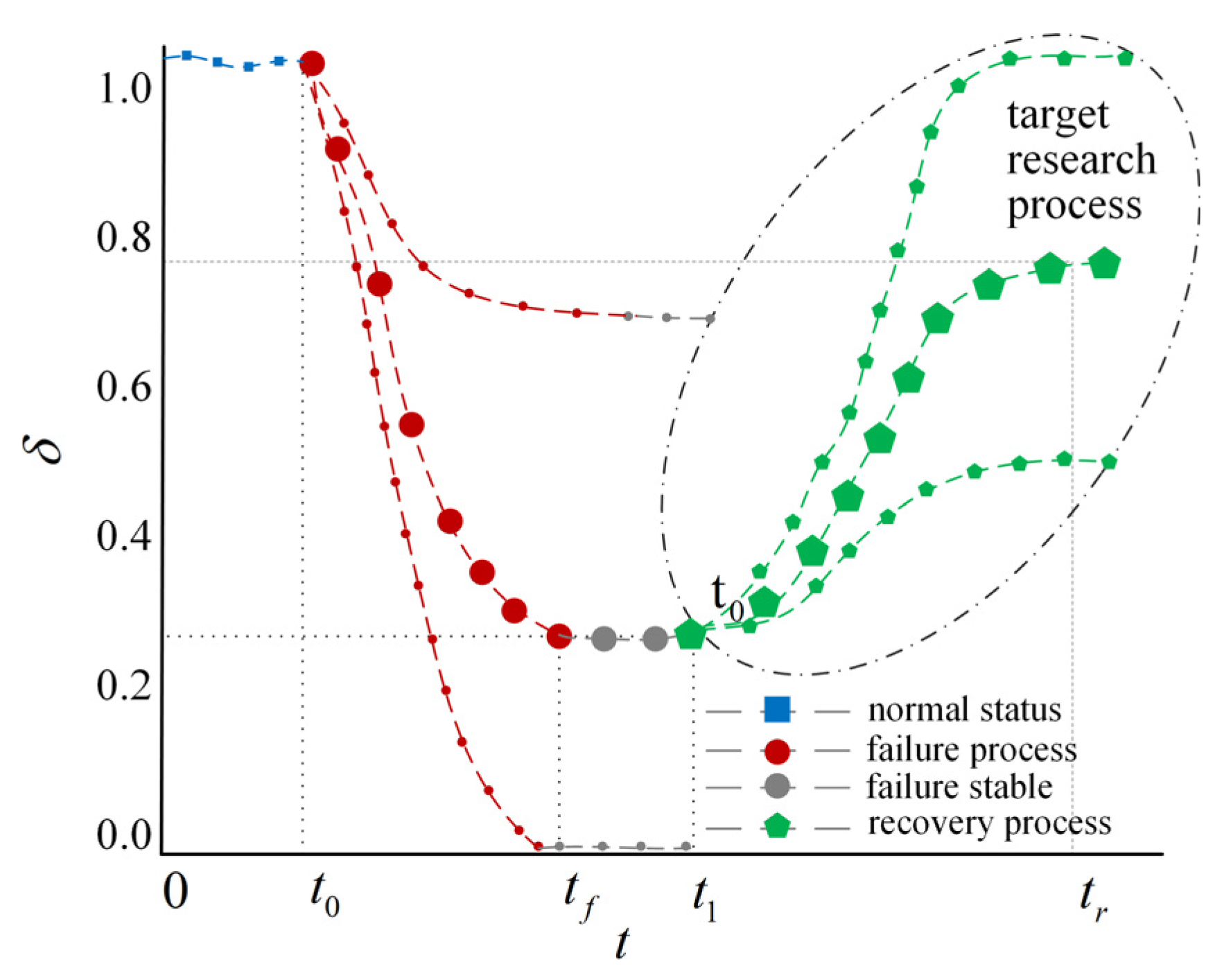

| Step | Initialization of network parameters 0.1 Initialize the cascade process by setting . 0.2 Generate the structural representation of the freeway network. 0.3 Import the origin–destination (OD) traffic demand and implement the Method of Successive Averages (MSA) to estimate baseline link loads. |
| 1 | Set the initial attack Remove the targeted links from the freeway network structure. |
| 2 | Move cascade. |
| 3 | Load the OD demand at cascade . |
| 4 | Update the link travel time function , if certain roads experience overload failures. |
| 5 | Solve for using an SUE model at each cascade step , applying the MSA algorithm for stochastic loading. 5.0 Initialize the traffic assignment variable , and set the iteration counter. 5.1 Update the travel time function for each network link. 5.2 Compute the auxiliary variable by solving an optimization problem. The result, denoted as , represents a feasible direction for descent in the solution space. 5.3 Update. Update the decision variable using the following relationship: . The coefficient decreases with each iteration, reducing the magnitude of adjustments and stabilizing the flow over time. 5.4 Convergence criterion. The iteration continues until the difference between successive values of falls below a defined gap threshold, ensuring that the flow stabilizes and fluctuations are minimized; otherwise, and go to step 5.1. |
| 6 | Overload conditions cause subsequent failures in previously unaffected links. |
| 7 | Quantify the additional failure occurrences and analyze the associated performance measures of the network. |
| 8 | Terminate the cascading failure process if no new failure links are generated; otherwise, return to step 2. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhang, S.; Luo, W.; Tang, J. Analysis of Cascading Failures and Recovery in Freeway Network Under the Impact of Incidents. Appl. Sci. 2025, 15, 7276. https://doi.org/10.3390/app15137276
Zhang X, Zhang S, Luo W, Tang J. Analysis of Cascading Failures and Recovery in Freeway Network Under the Impact of Incidents. Applied Sciences. 2025; 15(13):7276. https://doi.org/10.3390/app15137276
Chicago/Turabian StyleZhang, Xuan, Shuaijie Zhang, Wang Luo, and Jinjun Tang. 2025. "Analysis of Cascading Failures and Recovery in Freeway Network Under the Impact of Incidents" Applied Sciences 15, no. 13: 7276. https://doi.org/10.3390/app15137276
APA StyleZhang, X., Zhang, S., Luo, W., & Tang, J. (2025). Analysis of Cascading Failures and Recovery in Freeway Network Under the Impact of Incidents. Applied Sciences, 15(13), 7276. https://doi.org/10.3390/app15137276






