Multiple-Diffraction Subtractive Double Monochromator with High Resolution and Low Stray Light
Abstract
1. Introduction
2. Principle
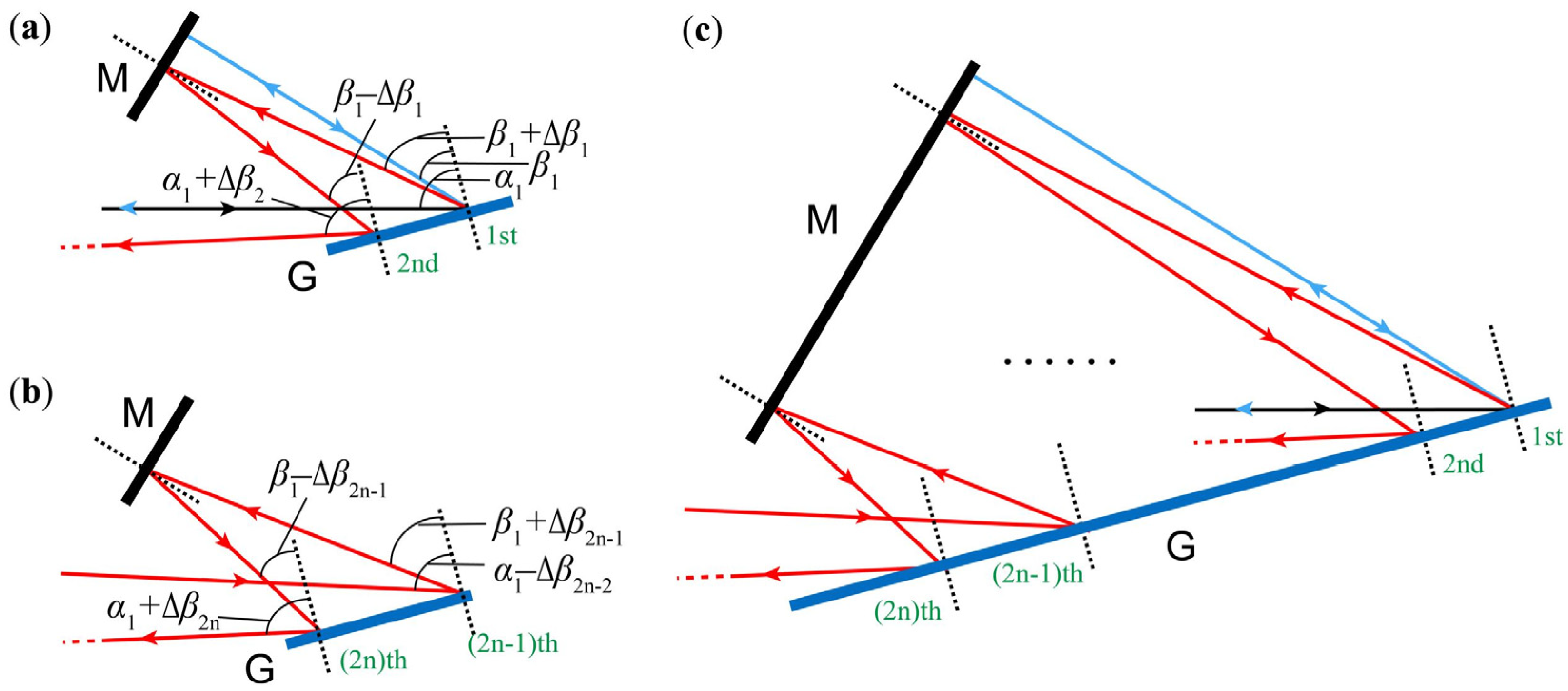
2.1. Multiple Diffractions
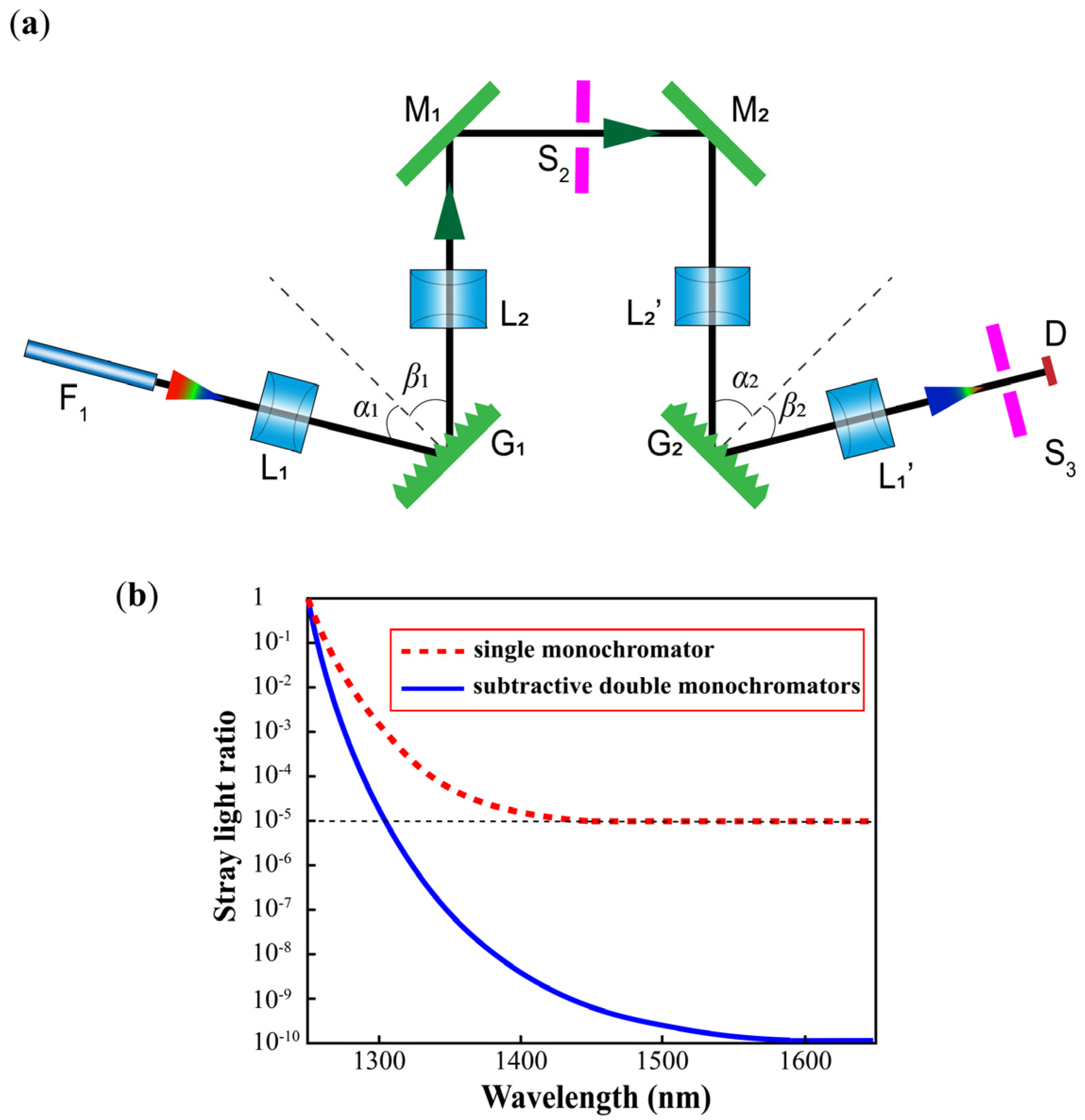
2.2. Subtractive Double Monochromator
3. Methods
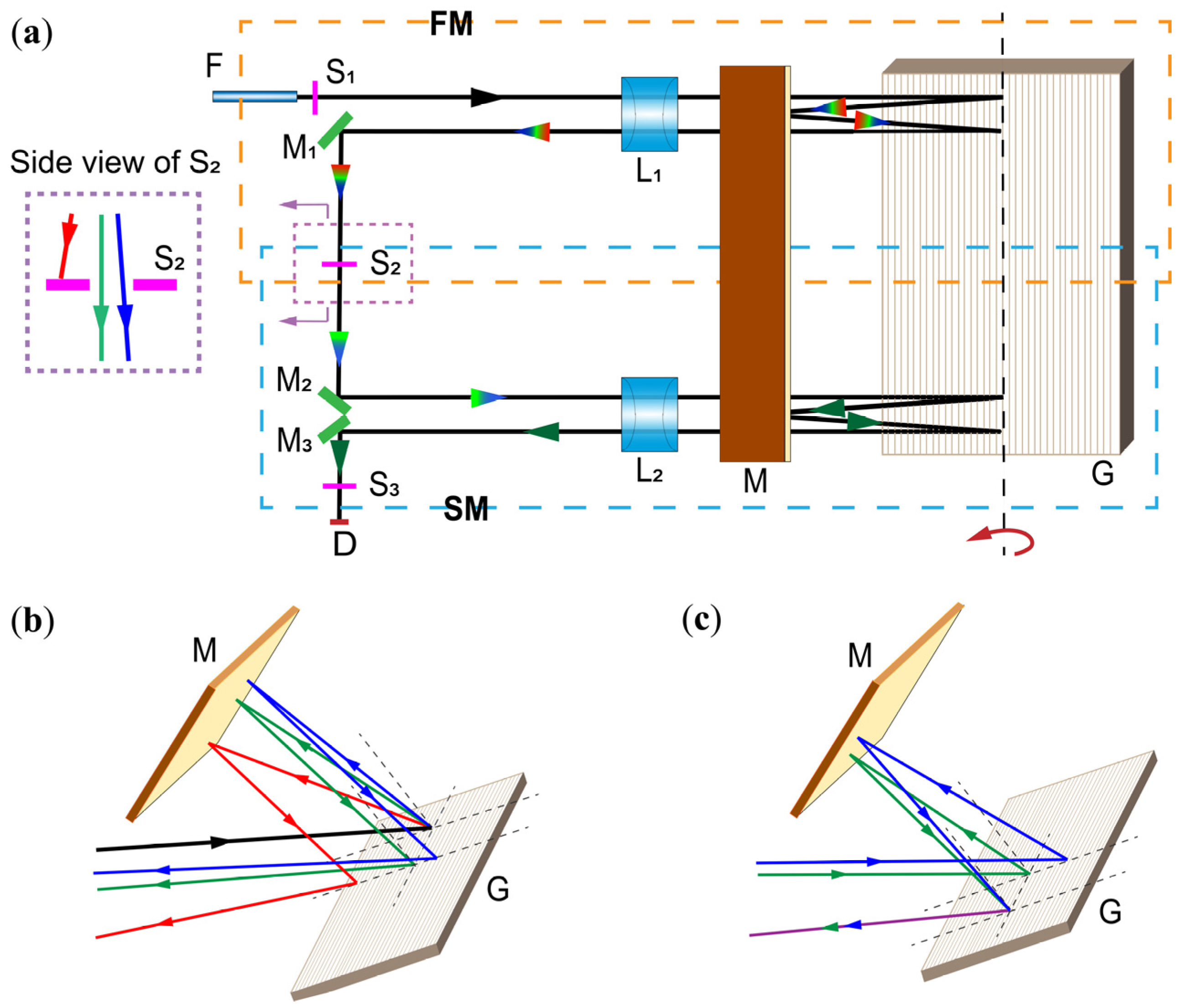
3.1. System Construction
3.2. Wavelength Scanning
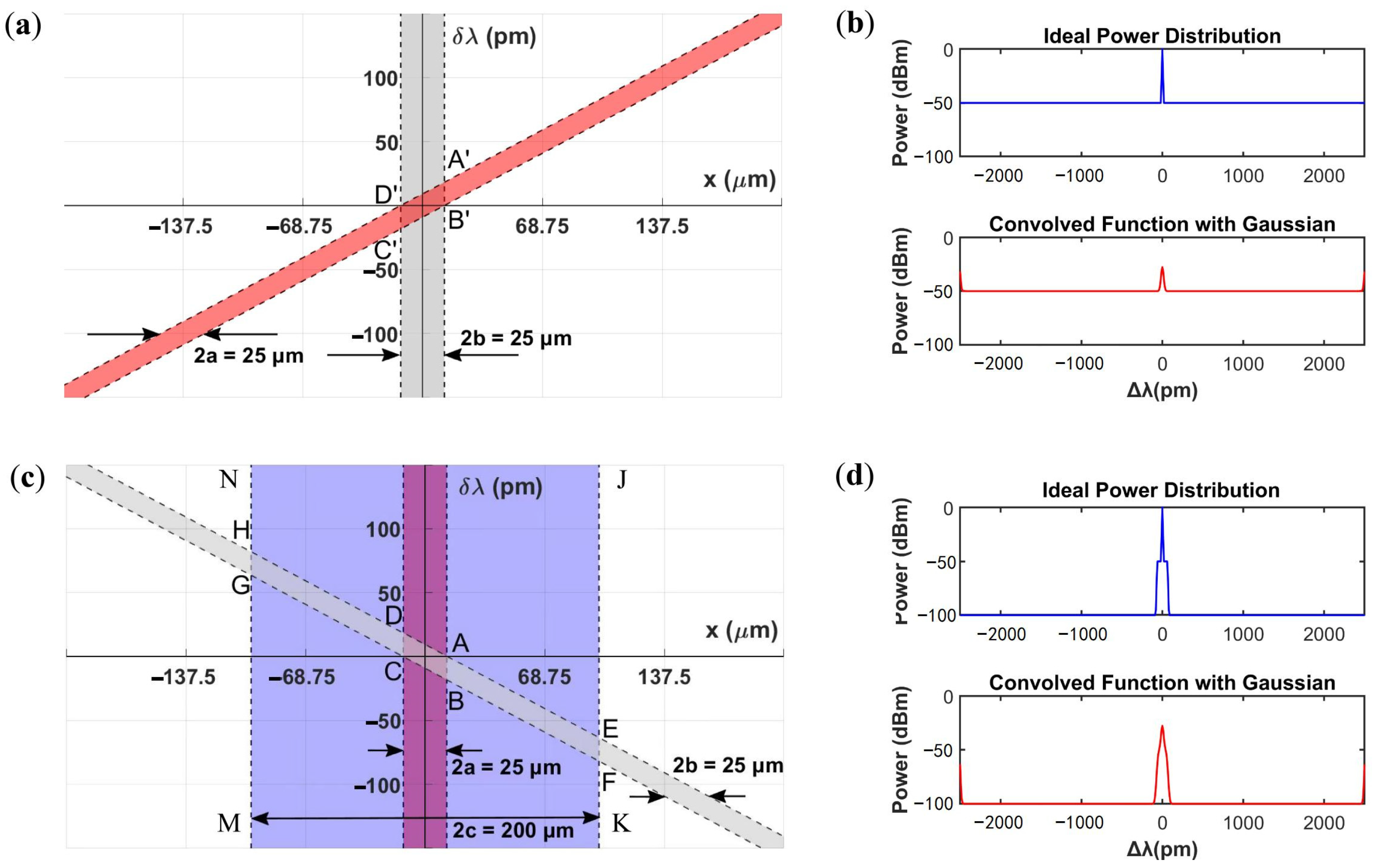
3.3. Stray-Light Analysis
4. Results
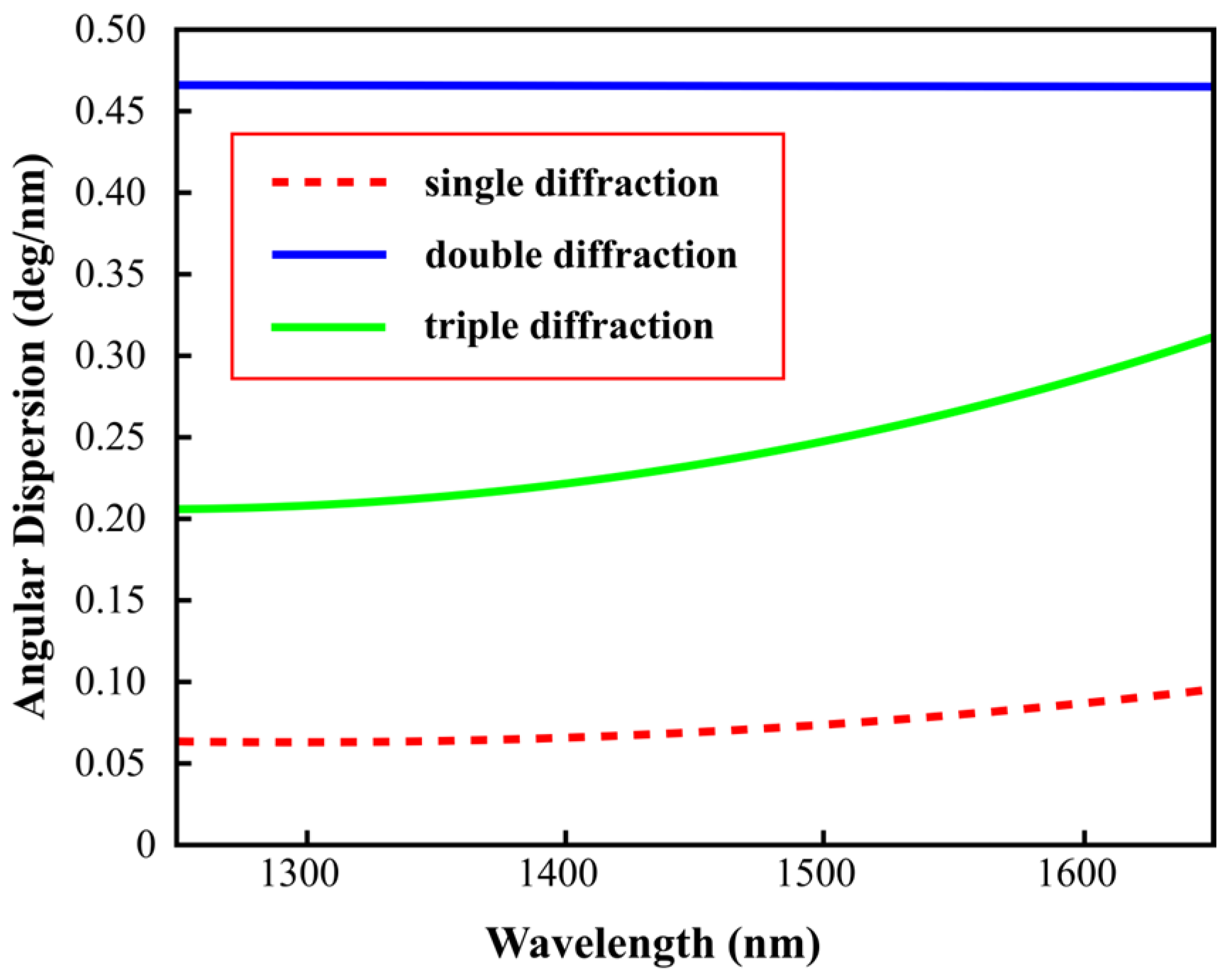
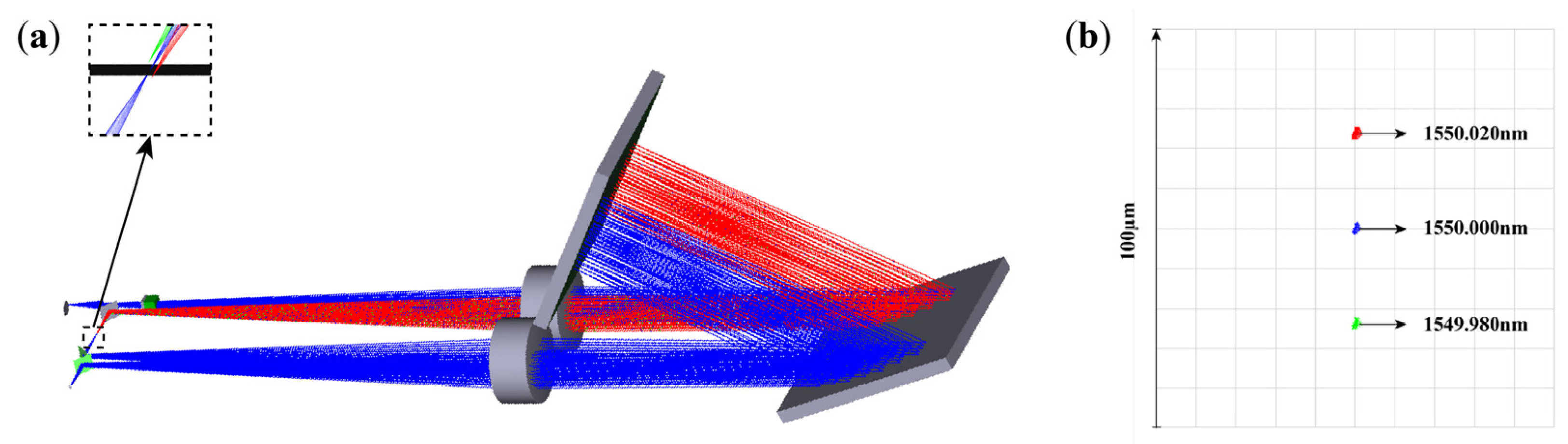
4.1. Simulations
4.2. Experiments
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VIPAs | Virtual imaging phased arrays |
| AWGs | Arrayed waveguide gratings |
| OSNR | Optical signal-to-noise ratio |
| FWHM | Full width at half maximum |
| MSDM | Multiple-diffraction subtractive double monochromator |
| FM | The first monochromator |
| SM | The second monochromator |
| DWDM | Dense wavelength division multiplexing |
References
- Yan, C.S.; Chen, Y.W.; Yang, H.M.; Ahokas, E. Optical Spectrum Analyzers and Typical Applications in Astronomy and Remote Sensing. Rev. Sci. Instrum. 2023, 94, 081501. [Google Scholar] [CrossRef] [PubMed]
- Das, R.S.; Agrawal, Y.K. Raman Spectroscopy: Recent Advancements, Techniques and Applications. Vib. Spectrosc. 2011, 57, 163–176. [Google Scholar] [CrossRef]
- Thuillier, G.; Zhu, P.; Snow, M.; Zhang, P.; Ye, X. Characteristics of Solar-Irradiance Spectra from Measurements, Modeling, and Theoretical Approach. Light Sci. Appl. 2022, 11, 79. [Google Scholar] [CrossRef] [PubMed]
- Zuev, S.M.; Varlamov, D.O.; Kuksa, V.V. Analysis of the Characteristics of a Laser Lighting Device. Instrum. Exp. Tech. 2021, 64, 834–839. [Google Scholar] [CrossRef]
- Stolyarevskaya, R.I. Review of the Features of Using Mini-Spectroradiometers with Ccd-Arrays in Applied Photometry. Light Eng. 2021, 29, 21–29. [Google Scholar] [CrossRef]
- Amirazar, A.; Azarbayjani, M.; Molavi, M.; Karami, M. A Low-Cost and Portable Device for Measuring Spectrum of Light Source as a Stimulus for the Human’s Circadian System. Energy Build. 2021, 252, 111386. [Google Scholar] [CrossRef]
- Yang, Z.; Albrow-Owen, T.; Cai, W.; Hasan, T. Miniaturization of Optical Spectrometers. Science 2021, 371, eabe0722. [Google Scholar] [CrossRef]
- Zhang, S.; Mi, X.; Zhang, Q.; Jirigalantu; Feng, S.; Yu, H.; Qi, X. Groove Shape Characteristics of Echelle Gratings with High Diffraction Efficiency. Opt. Commun. 2017, 387, 401–404. [Google Scholar] [CrossRef]
- Kukushkin, D.E.; Sazonenko, D.A.; Valyavin, G.G.; Bakholdin, A.V. High-Resolution Astronomical Spectrograph Design Method with a Single Echelle Grating. Appl. Opt. 2023, 62, 3004. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, W.; Duan, W.; Huang, Z.; Yang, H. Echelle Grating Spectroscopic Technology for High-Resolution and Broadband Spectral Measurement. Appl. Sci. 2022, 12, 11042. [Google Scholar] [CrossRef]
- Zhang, L.; Li, B.; Gu, G.; Wang, X.; Li, H. Miniaturized Hyperspectral Resolution Imaging Spectrometer of AOTF and Echelle Grating Combination. Acta Opt. Sin. 2023, 43, 1922001. [Google Scholar] [CrossRef]
- Chen, S.; Tang, Y.; Bayanheshig, X.; Qi, X.; Zhu, W. A New Type of Wide Spectral Coverage Echelle Spectrometer Design for ICP-AES. In Proceedings of the SPIE/COS Photonics Asia, Beijing, China, 5–7 November 2012. [Google Scholar]
- Muhammed Shameem, K.M.; Dhanada, V.S.; George, S.D.; Kartha, V.B.; Santhosh, C.; Unnikrishnan, V.K. Assessing the Feasibility of a Low-Throughput Gated Echelle Spectrograph for Laser-Induced Breakdown Spectroscopy (LIBS)-Raman Measurements at Standoff Distances. Opt. Laser Technol. 2022, 153, 108264. [Google Scholar] [CrossRef]
- Han, T.; Wu, Y.-H.; Chen, J.-K.; Kong, Y.-F.; Chen, Y.-R.; Sun, B.; Xu, C.-H.; Zhou, P.; Qiu, J.-H.; Zheng, Y.-X.; et al. Study of a High-Resolution Infrared Spectrometer by Using an Integrated Multigrating Structure. Rev. Sci. Instrum. 2005, 76, 083118. [Google Scholar] [CrossRef]
- Xia, G.; Wu, S.; Wang, G.; Hu, M.; Xing, J. Astigmatism-Free Czerny–Turner Compact Spectrometer with Cylindrical Mirrors. Appl. Opt. 2017, 56, 9069. [Google Scholar] [CrossRef]
- Yang, Q. First Order Design of Compact, Broadband, High Spectral Resolution Ultraviolet-Visible Imaging Spectrometer. Opt. Express 2020, 28, 5587. [Google Scholar] [CrossRef]
- Shi, J.; Sheng, B.; Huang, Y.-S.; Peng, L.-N.; Wang, L.-Y.; Ni, Z.-J.; Zhang, D.-W.; Zhao, Y.-F.; He, M. Multifacet Echelle Grating for Intensity Broadening on Spectral Plane Fabricated by Rotating Ion-Beam Etching. Appl. Opt. 2019, 58, 5040. [Google Scholar] [CrossRef]
- Lee, E.S. Spectral Resolution Enhancement without Increasing the Number of Grooves in Grating-Based Spectrometers. Opt. Lett. 2011, 36, 4803. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, W.; Fang, B.; Lv, B.; Cui, W.; Zhang, W.; Chen, W. A Broadband Picometer Resolution Visible CCD Spectrometer Based on Virtually Imaged Phased Array Technology. Analyst 2023, 148, 4421–4428. [Google Scholar] [CrossRef]
- Shirasaki, M. Large Angular Dispersion by a Virtually Imaged Phased Array and Its Application to a Wavelength Demultiplexer. Opt. Lett. 1996, 21, 366. [Google Scholar] [CrossRef]
- Kraus, M.; Förster, E.; Bagusat, V.; Hönle, T.; Uwurukundo, X.; Bohnert, P.; Brüning, R.; Hillmer, H.; Brunner, R. Compact, Astigmatism Corrected Cross-Grating Spectrometer. EPJ Web Conf. 2020, 238, 03005. [Google Scholar] [CrossRef]
- Yi, D.; Tsang, H.K. High-Resolution and Broadband Two-Stage Speckle Spectrometer. J. Lightware Technol. 2022, 40, 7969–7976. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Tsang, H.K. Tandem Configuration of Microrings and Arrayed Waveguide Gratings for a High-Resolution and Broadband Stationary Optical Spectrometer at 860 Nm. ACS Photonics 2021, 8, 1251–1257. [Google Scholar] [CrossRef]
- Pang, Y.; Zhang, Y.; Yang, H.; Liu, Z.; Huang, Z.; Jin, G. Compact High-Resolution Spectrometer Using Two Plane Gratings with Triple Dispersion. Opt. Express 2018, 26, 6382. [Google Scholar] [CrossRef]
- Pang, Y.; Zhang, Y.; Yang, H.; Huang, Z.; Jin, G. Compact Broadband High-Resolution Infrared Spectrometer with a Dihedral Reflector. Opt. Express 2017, 25, 14960. [Google Scholar] [CrossRef]
- Wang, J.; Liu, C.; Qin, S.; Zhu, G.; Shao, Y.; Fu, S.; Liu, D. Double-Grating with Multiple Diffractions Enabled Small Angle Measurement. Opt. Express 2019, 27, 5289. [Google Scholar] [CrossRef]
- Chen, J.; Li, X.; Chu, Q.; Galantu, J.; Sun, Y.; Zhang, B.; Yanheshig, B. An Ultrahigh-Resolution Spectrometer Using Parallel Double Gratings. Results Phys. 2023, 45, 106258. [Google Scholar] [CrossRef]
- Li, Y.; Yang, C.; Xue, C.; Li, X.; Ma, Z. Stray Light Analysis and Control of Grating Multistage Diffraction in HRS. Acta Opt. Sin. 2019, 39, 0630001. [Google Scholar] [CrossRef]
- Li, X.; Cen, Z. Stray Light Simulation and Control in Imaging Systems Including Diffraction Elements. In Proceedings of the Optical Design and Engineering VII, Frankfurt, Germany, 14–17 May 2018; Mazuray, L., Wartmann, R., Wood, A.P., Eds.; SPIE: Frankfurt, Germany, 2018; p. 5. [Google Scholar]
- Yang, J.; Zhang, R.; Yin, L.; Sun, C.; Li, T. Study on a Wideband, Variable Aperture, High Resolution Scatterometer for Planar Diffraction Grating Stray Light Measurement. Appl. Opt. 2017, 56, 247. [Google Scholar] [CrossRef]
- Shen, C.Y.; Cui, J.C.; Sun, C.; Wang, W.; Chen, J.J.; Li, X.T. A Detection System Design of Echelle Diffraction Efficiency and Stray Coefficient. Spectrosc. Spectr. Anal. 2017, 37, 2603–2609. [Google Scholar]
- Ciaffoni, L.; Matousek, P.; Parker, W.; McCormack, E.A.; Mortimer, H. Grating Spectrometry and Spatial Heterodyne Fourier Transform Spectrometry: Comparative Noise Analysis for Raman Measurements. Appl. Spectrosc. 2021, 75, 241–249. [Google Scholar] [CrossRef]
- Ji, K.; Xing, Y.; Niu, X.; He, C.; Dun, X.; Cheng, X. Stray Light Analysis and Suppression of Broad-Band Spectral Imaging System. Infrared Laser Eng. 2023, 52, 20220645. [Google Scholar] [CrossRef]
- Julien, C. A Triple Monochromator Used as a Spectrometer for Raman Scattering. J. Opt. 1980, 11, 257. [Google Scholar] [CrossRef]
- Mukhin, E.E.; Razdobarin, G.T.; Semenov, V.V.; Shilnikov, A.N.; Sukhanov, V.L.; Tolstjakov, S.Y.; Kochergin, M.M.; Mihailovskij, Y.K.; Bakh, L.I. Double-Grating Polychromator for Laser-Aided Plasma Diagnostics. Rev. Sci. Instrum. 2004, 75, 1261–1263. [Google Scholar] [CrossRef]
- Allemand, C. Monochromatic Imaging from UV to IR Using a Subtractive Double Monochromator. Appl. Opt. 1983, 22, 16. [Google Scholar] [CrossRef]
- Mukhin, E.E.; Semenov, V.V.; Razdobarin, A.G.; Tolstyakov, S.Y.; Kochergin, M.M.; Kurskiev, G.S.; Berezutsky, A.A.; Podushnikova, K.A.; Masyukevich, S.V.; Chernakov, P.V.; et al. The ITER Divertor Thomson Scattering System: Engineering and Advanced Hardware Solutions. J. Instrum. 2012, 7, C02063. [Google Scholar] [CrossRef]
- Okamoto, A.; Higuchi, S.; Sato, K.; Yamada, Y.; Koike, M.; Sugimoto, M.; Fujita, T. Laser Thomson Scattering System for Anisotropic Electron Temperature Measurement in NUMBER. J. Instrum. 2023, 18, C10013. [Google Scholar] [CrossRef]
- Gatto, A.; Pesch, A.; Kalies, A.; Diehl, T.; Erdmann, L.H.; Burkhardt, M.; Triebel, P.; Moeller, T. Space Applications: Monolithic Diffraction Grating Elements from EUV to NIR Spectral Range. In Proceedings of the International Conference on Space Optics—ICSO 2014, Tenerife, Canary Islands, Spain, 6–10 October 2014; Cugny, B., Sodnik, Z., Karafolas, N., Eds.; p. 93. [Google Scholar]
- Zarubin, I.A.; Labusov, V.A.; Babin, S.A. Characteristics of Compact Spectrometers with Diffraction Gratings of Different Types. Inorg. Mater. 2020, 56, 1436–1440. [Google Scholar] [CrossRef]



| Multiplexed Grating Spectrometer | Triple Dispersion Spectrometer | Multiple-Diffraction Subtractive Double Monochromator | |
|---|---|---|---|
| Times of diffraction | 2 | 3 | 2 × 2 |
| Spectral resolution | 57 pm | 36 pm | 18.8 pm |
| Wavelength range | 1250 to 1650 nm | 1250 to 1650 nm | 1250 to 1650 nm |
| OSNR | 55 dB | 30 dB | 69.17 dB |
| Commercial Instrument 1 | Commercial Instrument 2 | Multiple-Diffraction Subtractive Double Monochromator | |
|---|---|---|---|
| Spectral resolution | 20 pm | 60 pm | 18.8 pm |
| Wavelength range | 600 to 1700 nm | 600 to 1700 nm | 1250 to 1650 nm |
| OSNR | 73 dB | NaN | 69.17 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, Z.; Chen, K.; Cai, D.; Chen, T.; Yang, H. Multiple-Diffraction Subtractive Double Monochromator with High Resolution and Low Stray Light. Appl. Sci. 2025, 15, 7232. https://doi.org/10.3390/app15137232
Zhang Y, Wang Z, Chen K, Cai D, Chen T, Yang H. Multiple-Diffraction Subtractive Double Monochromator with High Resolution and Low Stray Light. Applied Sciences. 2025; 15(13):7232. https://doi.org/10.3390/app15137232
Chicago/Turabian StyleZhang, Yinxin, Zhenyu Wang, Kai Chen, Daochun Cai, Tao Chen, and Huaidong Yang. 2025. "Multiple-Diffraction Subtractive Double Monochromator with High Resolution and Low Stray Light" Applied Sciences 15, no. 13: 7232. https://doi.org/10.3390/app15137232
APA StyleZhang, Y., Wang, Z., Chen, K., Cai, D., Chen, T., & Yang, H. (2025). Multiple-Diffraction Subtractive Double Monochromator with High Resolution and Low Stray Light. Applied Sciences, 15(13), 7232. https://doi.org/10.3390/app15137232






