Importance of Using Modern Regression Analysis for Response Surface Models in Science and Technology

Abstract

Experimental design is important for researchers and those in other fields to find factors affecting an experimental response. The response surface methodology (RSM) is a special experimental design used to evaluate the significant factors influencing a process and confirm the optimum conditions for different factors. RSM models represent the relationship between the response and the influencing factors established with the regression analysis. Then these equations are used to produce the contour and response surface plots for observers to determine the optimization. The influence of regression techniques on model building has not been thoroughly studied. This study collected twenty-five datasets from the literature. The backward elimination procedure and t-test value of each variable were adopted to evaluate the significant effect on the response. Modern regression techniques were used. The results of this study present some problems of RSM studies in the previous literature, including using the complete equation without checking the statistical test, using the at-once variable deletion method to delete the variables whose p-values are higher than the preset value, the inconsistency between the proposed RSM equations and the contour and response surface plots, the misuse of the ANOVA table of the sequential model to keep all variables in the linear or square term without testing for each variable, the non-normal and non-constant variance conditions of datasets, and the finding of some influential data points. The suggestions for applying RSM for researchers are training in the modern regression technique, using the backward elimination technique for sequential variable selection, and increasing the sample numbers with three replicates for each run.

1. Introduction

The industry urgently needs technology to seek optimization to improve system efficiency, increase quality, save energy, and reduce carbon emissions. A system’s output or response is usually affected by several factors. Finding the optimum levels of these factors is called optimization. A simple method is to test the optimal levels of a factor and keep the other factors constant. This technique is impractical because of the interaction of other factors. To assess the effect of several factors on the response, the response surface methodology (RSM) is usually adopted to simultaneously assess the optimum conditions for several factors [1,2]. RSM has been a popular experimental design in the industry. RSM is a special experimental design used to improve the utilization of processing and develop processes for new products. Statistical techniques help evaluate the factors influencing the process and confirm the optimum conditions for different factors [1,3].

RSM’s special function is to test the experimental run for several factors with fewer samples. As the data are collected, the relationship between the system’s response and its influencing factors can be established by regression analysis. Then, the effect of factors on the response is graphed. Researchers can observe the relationship through the linear or curved distributions of these figures. This graphical function led to “response surface methodology” being widely used [1,2,3].

The relationship between the response (y) and the input factors (x₁, x₂, …, x_k) is expressed as

y = f(x₁, x₂, …, x_k) + ε

(1)

where y is the response, f is the unknown function in the response, x₁, x₂, …, and x_k are the independent variables, also called influencing factors, k is the number of factors, and ε is the model’s error.

The mathematical model also includes linear, quadratic, and interaction effects.

If the process system involves two factors, x₁ and x₂, the form of the RSM equation is

y = b_o + b₁x₁ + b₂x₂ + b₁₁x₁² + b₂₂x₂² + b₁₂x₁x₂ + ε

(2)

In the three-process-variable condition, x₁, x₂, and x₃, the mathematical equation of the RSM is

y = b_o + b₁x₁ + b₂x₂ + b₃x₃ + b₁₁x₁² + b₂₂x₂² + b₃₃x₃² + b₁₂x₁x₂ + b₁₃x₁x₃ + b₂₃x₂x₃ + ε

(3)

For the four-factor cases, x₁, x₂, x₃, and x₄, the RSM equation is

y = b_o + b₁x₁ + b₂x₂ + b₃x₃ + b₄x₄ + b₁₁x₁² + b₂₂x₂² + b₃₃x₃² + b₄₄x₄² + b₁₂x₁x₂ + b₁₃x₁x₃ + b₁₄x₁x₄ + b₂₃x₂x₃ + b₂₄x₂x₄ + b₃₄x₃x₄ + ε

(4)

If the RSM equation includes all variables as in Equations (2)–(4), it is called the complete RSM equation.

The more factors there are, the more complex the form of RSM becomes. In the introduction of Burns et al. [4], the RSM method’s development in the 1950s was described; the main advantage of this method is the reduced number of experiments. The unique feature of “response surface methodology” is deriving the optimum conditions with the graphical view provided by the fitting equation. The relationship between the independent variable and some dependent variables is established by regression analysis. This equation is an empirical model, not a theoretical one.

The experimental design is an experimental system with a combination of different levels of the influencing factor. These factors serve as the independent variables for the regression analysis. Experimental runs are a series of tests for the experiment. The response or output of experiments is the dependent variable.

Three experimental methodologies are used for response surface methodology in research: complete factorial design, Box–Behnken design, and central composite design [1,5,6,7,8,9,10].

The complete factor design (CCD) involves all related factors and levels. For example, if an experiment has three factors, each with three levels, and the experimental runs are 3³ = 27, the number of runs is high and the efficiency is lower than that of other methods [1,5,6,7,8,9,10].

The Box–Behnken design (BBD) adopts a specific subset of the factorial combination. The experiment ports are arranged at an equal hypersphere distance from the central point. This method is popular for evaluating factors’ interaction. However, it is inappropriate for factors with some extreme points and only suitable for factors with three levels [1,5,6,7,8,9,10].

The central composite design (CCD) method is good at constructing a second-order model. It has three types of points: factorial points, a central point, and an axial point. It can be used for three or more levels and to consider some extreme points [1,5,6,7,8,9,10].

The experimental matrices in the three methods for RSM design are easily found in a textbook [1]. The number of tests required for the three test methods with three factors and three levels is 27 for the FFD method, 22 for the BBD method, and 13 for the CCD method. The replicates of the center ports for CCD may influence the sample numbers.

The criteria to evaluate the fitting agreement and predictive ability of the selection of models are essential aspects of regression analysis. The key is to find the variables’ significant effect on the response. Many criteria have been used. For the fitting agreement, the criteria involve the F-value of ANOVA, coefficient of determination R², adjusted R² R²_adj, lack-of-fit test, etc. The criteria to evaluate predictive ability are PRESS, predicted R-squared R²_pred, and adequacy of precision. The VIF (variance inflation factor) is used to test the collinearity of these factors [1,5,11]. The “Materials and Methods” Section introduces the calculation equations and their meaning.

After evaluating the adequacy of the equation (RSM model), the final model is called an adequate regression equation. Two methods are used to determine the optimization. The first one uses the first partial derivatives of the response in terms of each factor. For example, if three factors are considered, three gradient equations of this equation are derived, and the three optimum conditions are solved with these derivative functions [1].

The second method is the graphic method, which provides the figures observed by researchers. The contour and 3D response surface plots are popular among researchers [1,3,12,13]. The investigated technique has been illustrated in detail [14].

Accuracy and validity are the keys to finding reliable results regarding the factors influencing the response. They involve the factors that affect the response and the degree to which these influencing factors influence. However, the adequacy of the regression equations is not of concern to researchers. Many researchers use commercial software directly. Reza et al. [15] mention the importance of the model’s validity and accuracy in their suggestions about the challenges associated with RSM application. The authors emphasized that the RSM model depends on the statistical technique and the importance of ensuring the accuracy and validity of the RSM model [15].

An excellent RSM textbook has been published [1]. Bas and Boyaci [2] provided an important concept of RSM. Asoo et al. [3] introduced the historical background of RSM. These papers involved science and technology, analytical methods, and process systems aplenty [16,17,18,19,20,21,22,23,24,25,26,27]. The topics of this literature included drying, extraction, fermentation, blending, mixing, and others [16,17,18,19,20,21,22,23,24,25,26,27].

The unique feature of response surface methodology is the graphical presentation of the relationship between the influential factors (variables) and the response. The contour plot represents the information in a two-dimensional form. The variation in the response under different conditions of influencing factors is indicated with the contour plot. The 3D response surface plot represents the information in three-dimensional form. The response is the z-coordinate, and the two influencing factors are the x- and y-coordinates. If a quadratic polynomial relationship does not exist, linear lines are plotted in this contour plot and a 3D response surface plot as the plateau. If the quadratic relationship is significant, two plots are presented with curves. The contour plot is usually used to observe visually the optimum levels of the influencing factors (the input variables) that can result in the maximum response [1,2,3].

The purpose of an RSM experiment in science and technology is to find the optimal conditions. If the RSM model is a linear equation, the contour plot and response surface plot indicate the response direction to the original design. Suppose that the RSM model is a quadratic equation. Both plots will indicate the maximum, minimum, or saddle conditions. Establishing an appropriate RSM equation is essential to ensure correct optimization conditions. The regression technique for RSM needs to be considered.

In the classical regression equation, the least squares method establishes the equation, and the estimated values of the parameter coefficients are directly used.

Modern regression techniques include considering the balance of the under- and overfitting of the model, testing the normality and the constant variance, using the criterion of predictive performance, and checking influential data points. These modern regression techniques are illustrated in Section 2, Materials and Methods.

To the best of the authors’ knowledge, modern regression techniques have not been fully adopted to evaluate the correction and validity of RSM equations in research. This study collected twenty-five datasets from the literature related to RSM studies in science and technology. These datasets were used to evaluate adequate RSM equations using modern regression techniques. The issues of the RSM studies in the literature were discussed. Some suggestions for researchers who have used RSM were proposed to enhance their research ability in RSM.

2. Materials and Methods

2.1. Data Sources for the Equations of the Response Surface Methodology

Table 1. Published data in the literature for evaluating the adequate equations of response surface methodology.

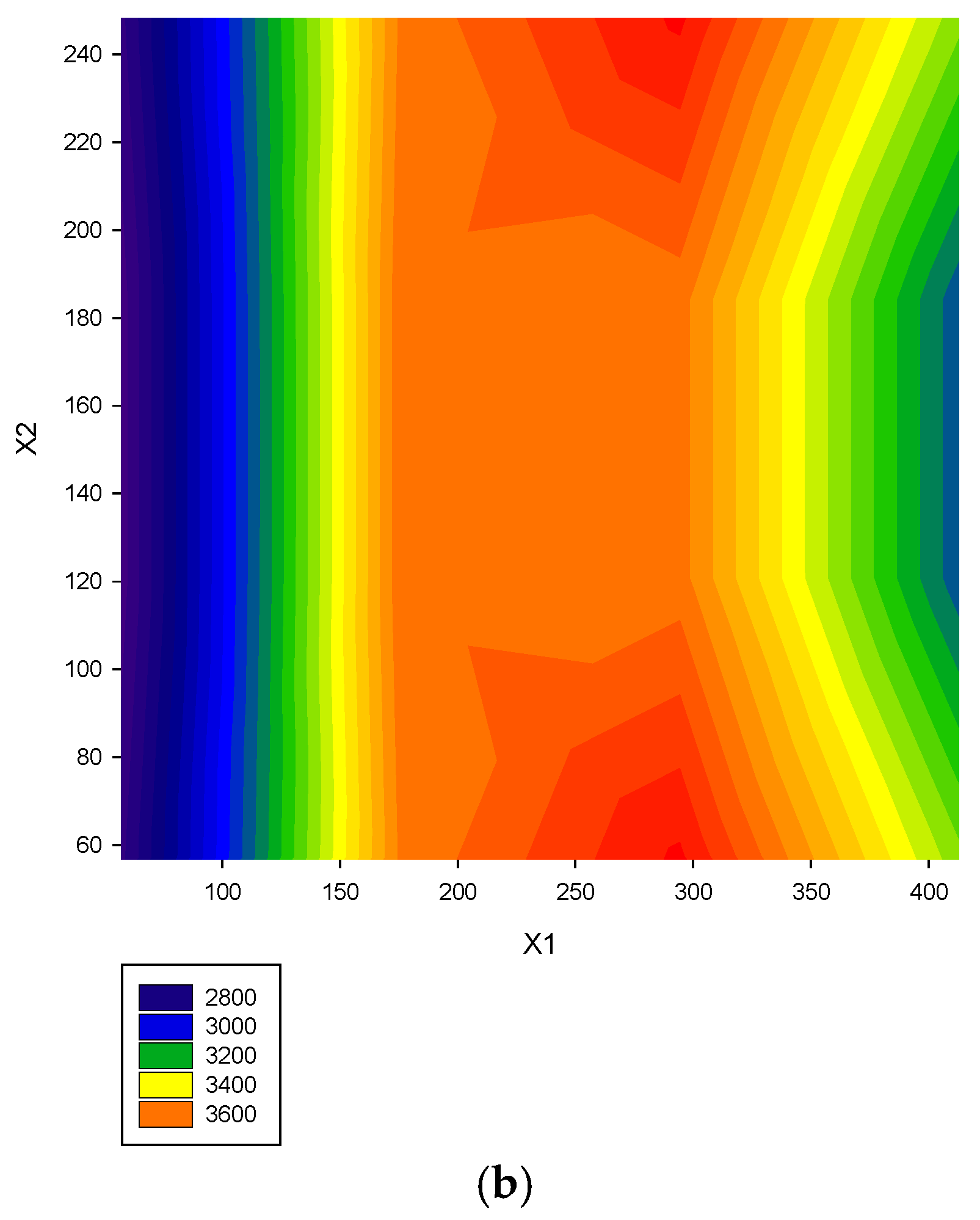
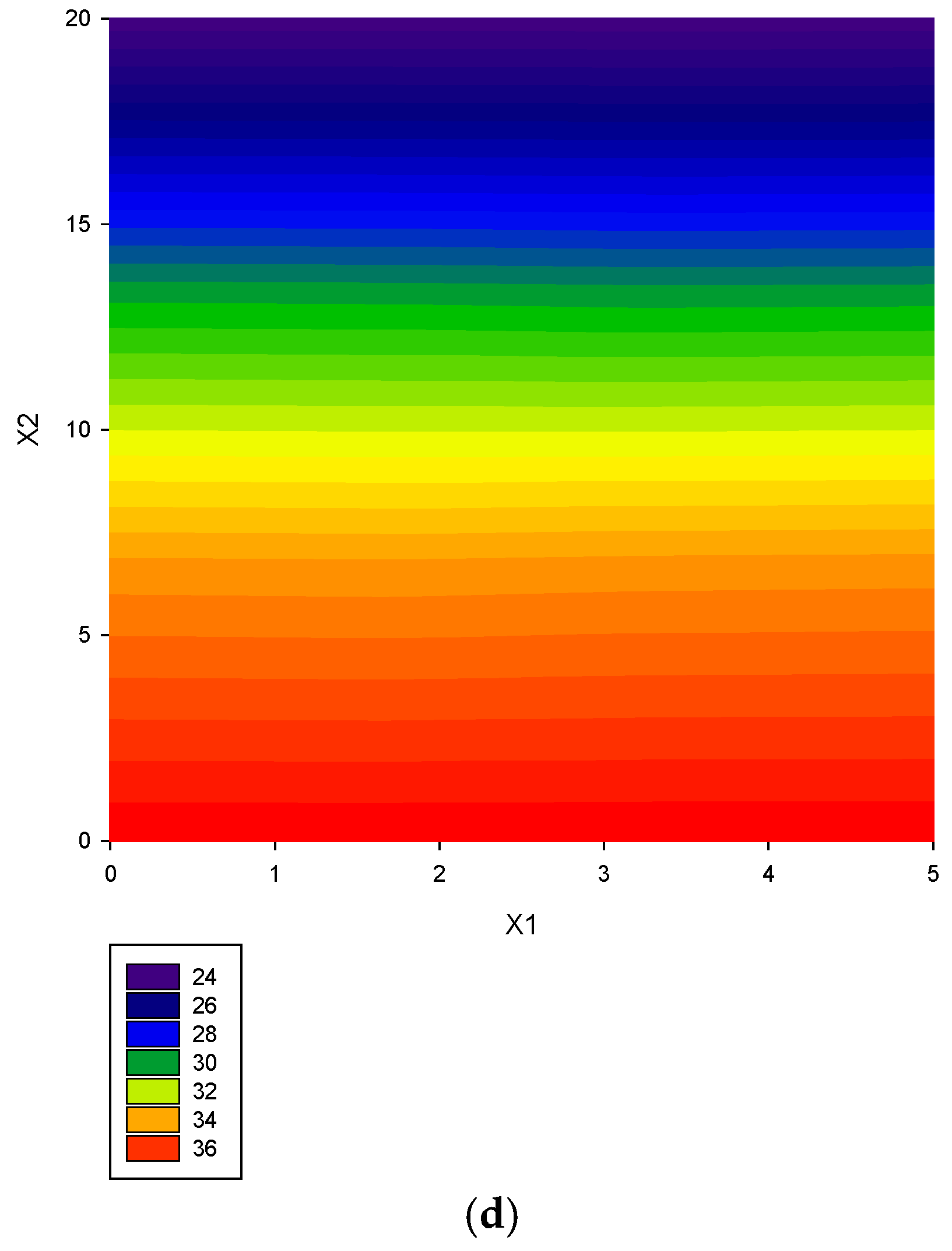
Study	Objects	No. of Data	Software	Model Evaluation	Criteria of Parameter Selection	Report Model	Plots
I. Two variables
1. Chen et al. [28]	Poly-cornstarch-blended composite	13	Minitab Ver. 14.2	R2, R2adj s	t-value, p-value	yWSI = f (x1, x2, x12) yWAI = f(x1, x2, x12) yML = f(x1, x2, x12, x1x2)	Contour plots, Response surface plot
2. Milan-carrillo et al. [29]	Amaranth flour	13	Design Expert Ver. 7.0	R2	p-value, Stepwise regression	Complete model	Contour plots, Response surface plot
3. Sinkhonde et al. [30]	Rubberized concrete with burnt clay brick powder	13	Not reported	Lack of fit	F-value, p-value	Complete model	Contour plots, Response surface plot
4. Diemer et al. [31]	Forced chicory roots	13	MOODE Ver. 12.0	R2, R2adj	t-value, p-value	y5-CQA = f (x1, x2, x12)	Contour plots
5. Adeyanju et al. [32]	Akara Ogbomoso Snacks	13	Design Expert Ver. 6.0.1	R2	p-value	yMC = Complete model yOC = f(x1, x2) yΔE = f(x1, x2) yBF = Complete model yS = f(x1, x2)	Contour plots, Response surface plot
II. Three variables
6. Nwabueze [33]	African breadfruit–corn–soy mixtures	15	Statistica	R2	p-value	YTIA= f(x3, x12) Yphytic acid = f(x12) Ytan = f(x32)	Response surface plot
7. Bimark et al. [34]	Bioactive flavonoid compounds	20	Minitab Ver.14	Lack of fit, R2, R2adj	p-value	Complete model	Response surface plot
8. Chen et al. [35]	Green asparagus juice	20	Design Expert, version not reported	R2, R2adj Lack of fit	p-value	Complete model	Contour plots, Response surface plot
9. Gong et al. [36]	Defatted marigold residue	20	Microsoft Excel	R2, R2adj Lack of fit	p-value, Stepwise regression	Complete model	Response surface plot
10. Chiu et al. [37]	Corn extruded with yam	15	Minitab 16	R2, R2adj Lack of fit	p-value	Not reported	Response surface plot
11. Idrus et al. [38]	Virgin coconut oil	17	Design Expert Ver. 8.0	R2, R2adj Lack of fit	p-value	Yyield = f (x1, x2, x12, x22, x32) YFFA = f(x1, x12) YAV = f (x2, x22) YPOV = f(x1, x2, x3, x1x3, x2x3, x12, x22, x32)	Contour plots, Response surface plot
12. Hong et al. [39]	Pumpkin floor blends with corn	15	Design Expert Ver. 7.0	R2, R2adj Lack of fit	p-value	Not reported, contour plot and response surface plots produced by complete model	Contour plots, Response surface plot
13. Wu et al. [40]	Biopolymer blend with Tapioca starch	15	Design Expert Ver.7.0	R2, R2adj, Lack of fit	p-value	Complete model	Contour plots, Response surface plot
14. Yu et al. [41]	Piper nigrum microcapsules	17	Design Expert, version not reported	R2, R2adj, Lack of fit	p-value	Complete model	Not reported
15. Tshizanga et al. [42]	Waste vegetable oil and eggshells	20	Design Expect Ver. 9.	R2, R2adj, PRESS	F-value	Complete model	Contour plots, Response surface plot
16. Wu et al. [43]	Sichuan paocai	17	SPSS Ver.22.0	Lack of fit	p-value, Confidence interval (CI)	Complete model	Response surface plot
17. Savik and Gajic [44]	Green walnut husks	17	Design Expert 13.0.1.0	R2, R2adj	F-value, p-value	Complete model	Contour plots, Response surface plot
III. Four variables
18. Ahn et al. [45]	Seed oil	31	MINITAB Release 14	R2	t-value, p-value	YEFF = f(x1, x2, x3, x12, x22)	Response surface plot
19. Lee et al. [46]	Peanut sprout	31	SAS Ver. 9.0	Not reported	t-value, p-value	Complete model	Contour plots, Response surface plot
20. Yu et al. [47]	Peanut sprout	29	Design Expert Ver. 8.05b	R2, Lack of fit	F-value, p-value	Complete model	Contour plots, Response surface plot
21. Javanbakht and Ghoreishi [48]	Lead removal from an aqueous solution	30	Design Expert Ver. 7.0.0	R2, R2adj, R2pred	F-value, p-value	Complete model	Contour plots, Response surface plot
22. Yemis et al. [49]	Haskap extract and tannic acid	28	Design Expert	R2, R2adj, PRESS, Lack of fit	F-value, p-value, Backward elimination	ySI = f(x1, x2, x3, x4, x1x2, x1x3, x12, x32, x42)	Contour plots, Response surface plot
23. Vega et al. [50]	Fruit by-product	60	Mathematica Ver.11.1.1.0	R2, R2adj	Not reported	Complete model	Contour plots, Response surface plot
24. Hiranpradith et al. [51]	Centella asiatica	30	Design Expert Ver. 13.0	R2, R2adj, R2pred	t-value	yTPC = f(x1, x2, x4, x22, x42), yTFC = f(x1, x2, x3, x4, x1x4, x12)	Contour plots, Response surface plot
IV. Five variables
25. Acikel et al. [52]	Rhizopus delemar	46	Design Expert Ver. 7.0	R2, R2adj	Not reported	Complete model	Contour plots, Response surface plot

shows 25 datasets from research used to evaluate adequate RSM equations. The datasets adopted in these published papers were used to evaluate adequate RSM equations with modern regression analysis. The parameters and criteria were estimated using Sigma Plot v.14.0 (SPSS Inc., Chicago, IL, USA).

2.2. Model Building of the Response Surface Methodology

The purpose of the regression analysis includes variable screening, parameter estimation, model specification, and prediction [53]. The first three categories are related to each other. Multiple regression data involves the dependent variable (response) and several independent variables. To establish the relationship between the independent and dependent variables, the significant effect of the variables on the response must be evaluated using statistical techniques for optimization in science and technology. When researchers propose dependent variables, model specifications, or model types, the estimated parameter values can be calculated using the regression technique.

A typical multiple regression model is expressed as follows:

$$y_i=b_0+b_1{x}_1+\cdots +{ b}_i{x}_i+b_j{x}_j+{\epsilon }_i$$

(5)

In the quadratic regression model, x_i² and the integration of x_ix_j are treated as the variables in a multiple regression model, such as in

$$y_i=b_0+b_1{x}_1+b_{11}{x_1}^2+b_{22}{x_1}^2+b_{12}{x}_1{x}_2+{\epsilon }_i$$

(6)

where ${\epsilon }_i$ is the model error.

2.2.1. The Assumptions Involved in Regression Analysis

The regression model assumes that ε_i is uncorrelated from one observation to another, ε_i has a mean of zero, ε_i has constant variance, and the x_i terms are not random. The data distribution must be normal.

Due to the basic assumption, the nonstandard conditions involved in regression analysis include [53]

• The overfitting or underfitting of the models;
• The non-normal condition of the datasets;
• Heterogeneous variance;
• Some outliers in the data;
• Multicollinearity.

These assumptions must be checked, and these five nonstandard conditions must be remedied, as they are the first concern of modern regression analysis. The second concern of modern regression is to classify the model’s performance into model fitting ability and predictive ability. Two kinds of criteria are used to introduce classic and modern concepts in regression modeling [53,54,55,56]. The predictive performance and the trade-off between bias and variance for selecting a limited number of important variables are illustrated.

2.2.2. Establishment of the Model

The key purpose of the response surface methodology is its prediction ability. When an adequate equation is established, the contour plot and 3D surface plot are plotted, and researchers make conclusions with these figures. If the selection of the regression equation is inappropriate, the conclusion and suggestion on the effect of the dependent variable (factors and levels) are meaningless.

Establishing the regression equation is called model building. This is an essential topic in regression analysis. Montgomery et al. [57] recommend these strategies:

• Fit the complete model, which includes all variables.
• Perform a thorough analysis of this model.
• Transform the response (y_i) or some variables (x_i) if necessary.
• Use the t-test or F-test on these individual variables.
• Check the adequacy of the RSM model.

2.3. The Three Methods of Sequential Variable Selection

Three methods for performing sequential variable selection are forward selection, stepwise regression, and backward elimination [53,57,58,59,60,61,62].

1.

Forward selection

In this procedure, all variables are selected as a single regressor with a constant term, and the variable that produces the largest R² is selected as the first variable. Then, the other variables are used as candidates for the second variable in terms of the constant and the first variable. The variable of the second term that produces the largest R² is selected as the second variable. A similar procedure is used to select the third variable, and then the procedure is continued. The selected variable’s partial F-value or p-value is compared with the preset value. If the t-values of this variable are less than the preselected value, the procedure ends.

2.

Stepwise regression

This method is a modification of forward selection. Two cutoff values of the partial F-value or p-value are preset. At each step, the previously selected variables in the equation are reevaluated with their partial F-value or p-value. If these values for a variable are larger than the cutoff p-value, the variable is excluded from the equation. In this method, one variable can be entered at each stage, and another can be eliminated.

3.

Backward elimination

• The procedures for backward elimination are as follows:

  a.

  Fit all variables for the regression equation. Determine the t-value and p-value for each variable in this model [58].

  b.

  Focus on the variable with the lowest observed t-values and its p-value.

  c.

  Compare the p-value with a preselected significance level, usually p < 0.05.

  d.

  Remove the variable if its p-value exceeds the preselected value [58].

  e.

  Recompute the regression equation for the remaining variables and find the variable with the lowest t-value and highest p-value.

  f.

  Repeat the backward elimination procedures of c, d, and e.

  g.

  If no variable is dropped, the procedure ends. The regression model’s selection consists of all remaining variables.

  h.

  Perform the influential data point test, and the normality and constant variance tests.

Theoretically, the final regression models of the above three procedures—forward selection, stepwise regression, and backward elimination—should be the same. However, the selected levels of significance and the collinearity among these variables influence the selection of model variables for forward and stepwise procedures.

The disadvantage of the forward procedure is that the critical t-values are not strictly appropriate in the early stages [53]. The backward elimination procedure is recommended because this technique selects all possible explanatory variables and eliminates those of little importance to explain the variation in response y step by step [57,61,62,63].

The special feature of the RSM model is its multicollinearity. These derived variables of square variables and the interaction of variables, such as x₁², x₂², x₃², x₁x₂, x₁x₃, and x₂x₃, are prone to multicollinearity problems [56,61,63]. Rowley [64] emphasized that backward elimination is particularly useful in the collinearity problem.

In this study, a t-test statistic is used to assess the statistical interpretation of a variable in the regression model. A detailed explanation of this procedure has been introduced [6,63].

2.4. The Criteria for the Evaluation of RSM Equations

• R-squared

The R² value is called the coefficient of determination. An R² value near 1.0 shows that the equation is very good at determining the relationship between the response and the independent variables.

2.

Adjustable R²

The adjusted R² considers the effect of the number of independent variables. Like R², an R²_adj value closer to 1.0 indicates a regression equation’s good descriptive ability.

3.

Standard error of the estimated value, s

The s value indicates the actual variability in the equation with the data distribution between the response and independent variables.

4.

t-value

The t-value of the variables is called the t-statistic. It is used to test the null hypothesis that the coefficients of independent variables are zero. A large t-value of the independent variable reveals that the coefficient is not zero and is valid. That is, the variable is effective.

5.

p-value

The p-value of a variable coefficient is calculated from its t-value. The p-value serves as the probability of being incorrect to determine whether the variable coefficient is not zero. A smaller p-value represents a greater probability of the validity of the variable.

6.

PRESS, the Predicted Residual Error Sum of Squares

This statistic is used to evaluate the predictive ability of the regression model. The calculation of PRESS is explained as follows:

To calculate the PRESS value of a regression model, for n samples, the first dataset (y₁) is removed, and the remaining n-1 datasets are used to calculate the regression equation. Then the first data point is substituted into this equation to find the predictive value ${\widehat{y}}_{1,-1}$. The predictive error is called the first PRESS residual. In other words, the predictive error for dataset 1 is e_−1,−1. The next step is to take out the second dataset, 2, and return the data x₁ to this dataset. The second regression equation is computed with datasets without the dataset y₂. The y₂ dataset is substituted in Equation (2) to calculate the predictive value, and the predictive error for dataset 2 is e_2,−2

The procedure is repeated n times for all data and produces a set of n PRESS residuals (e_1,−1, e_2,−2, …, e_{n, −n}). The PRESS statistic is calculated as the sum of the squares of the n PRESS residuals. A lower PRESS value of an RSM equation indicates that this equation has better predictive ability.

7.

Normality test

The normality test assesses whether the datasets are normally distributed. The regression analysis technique assumes that residuals are normally distributed about the regression line. In this study, the normality test technique used is the Kolmogorov–Smirnov method. The p-value calculated with this method is compared with the preset value (p = 0.05). Failure of the normality test reveals the inadequacy of the regression model.

8.

Constant variance test

This test evaluates the constant variance of the dependent variable (response) in its population source. This study uses the Spearman Rank correlation method, and the p-value calculated by this method assesses the assumption of constant variance. The cutoff value is p = 0.05.

If the constant variance test is failed, different models with weighted values must be proposed, or the response (y_i) must be transformed to stabilize the variance.

9.

Influential data point

Some statistics are used to observe influential data points. These suspicious data may be influencing data or outlier data.

• a.

  Externally studentized residuals, t_i

The t_i value is computed with the standard error of the residual of the estimated value, where the data is not involved in the model building. Values of ±2.0 are usually used to indicate the possibility of an outlier.

• b.

  DFFITSi

This statistic is a criterion to reflect the prediction effect for a data point. It compares the estimated standard errors when the observed value is removed.

Usually, the cutoffs of DFFITSi are ±2.0. The data point may be potentially influential if the criterion exceeds this threshold.

• c.

  Cook’s distance, $D_i$

This criterion evaluates the effect of each data point on the estimated values of the parameters in the regression model. The Di value will be more significant if a data point significantly affects the parameter values. The cutoff for the D_i value is 4 or an F-value equal to F (p, n − p, 50%), where p is the number of parameters and n is the number of data points.

2.5. The Meaning of the F-Test of the ANOVA Table

The dependent variables for a multiple regression equation are x₁, x₂, x₃, …x_k. Suppose that one variable, xi, significantly affects the response yi by the test of a partial F-value or p-value of the ANOVA table. In this case, a multiple regression equation including this xi variable will be recognized as having a significant effect on the response by the F-value of the ANOVA table.

For example, if x₁ has a significant effect on the y response, two equations are proposed:

$$y_1=b_0+b_1{x}_1+b_i{x}_i+b_k{x}_k$$

(7)

$${ y}_2=c_0+c_1{x}_1+c_i{x}_i+c_j{x}_j$$

(8)

With the ANOVA table, both equations will significantly affect the y response with statistical tests like the F-test. However, this does not mean that other variables, such as x_i, x_j, x_k, etc., will significantly affect the response. Maybe the x₁ variables are the only significant factors.

This is the first typical misunderstanding in the application of RSM equations.

The second misunderstanding in applying RSM equations is using the sequential-model sum of squares of the response. A typical ANOVA model with a sequential-model sum of squares of the response for an RSM equation includes x₁, x₂, and x_3, which are listed in

Table 2. Sequential-model sum of squares of response.

Source	df	SeqSS	MS	F-Value	p-Value
Regression (Mean)	dfm	SSm	SSm/dfm
Linear	dfl	SSl	SSi/dfl	Lf	Lp
Square	dfs	SSs	SSs/dfs	Sf	Sp
Interaction	dfi	SSi	SSi/dfi	If	IP
Residual Error	dfe	SSe	SSe/dfe
Total		SSt

Note: df: degree of freedom; SeqSS: sequential sum of squares; MS: mean square.

.

The partial F-value or p-value is used to help the researcher conclude whether a significant effect of the linear, square, and integration term significantly affects the y response.

The trick to misusing these methods is to test the linear, interaction, and square terms with the F-value or p-value. For example, the square terms of an equation involving three variables x₁², x₂², and x₃² has a significant effect on the y response by the F-value or p-value of the ANOVA table, and the form of this complete equation, y = b₀ + b₁x₁ + b₂x₂ + b₃x₃ + b₁₁x₁² + b₂₂x₂² + b₃₃x₃², may be used by researchers because the square terms have a significant effect on y.

However, besides this complete equation, other possible equations are

y = b₀ + b₁x₁ + b₂x₂ + b₃x₃ + b₁₁x₁² + b₂₂x₂²

(9)

y = b₀ + b₁x₁ + b₂x₂ + b₃x₃ + b₁₁x₁² + b₃₃x₃²

(10)

y = b₀ + b₁x₁ + b₂x₂ + b₃x₃ + b₂₂x₂² + b₃₃x₃²

(11)

y = b₀ + b₁x₁ + b₂x₂ + b₃x₃ + b₁₁x₁²

(12)

y = b₀ + b₁x₁ + b₂x₂ + b₃x₃ + b₂₂x₂²

(13)

y = b₀ + b₁x₁ + b₂x₂ + b₃x₃ + b₃₃x₃²

(14)

This RSM equation has seven possible combinations (complete equation and Equations (9)–(14)). That is, if the square term significantly affects response y, the form of b₁₁x₁² + b₂₂x₂² + b₃₃x₃² is not the only possible equation for this RSM equation. All square terms (x₁², x₂², and x₃²) must be evaluated individually.

2.6. The Effect of the Sampling Number

One advantage of response surface methodology is the small number of experimental runs for experiments. A smaller experimental sample can reduce the test cost and save time. However, the effect of the sampling number on the regression analysis was not mentioned by researchers who used this RSM technique.

Sample size is a criterion for ensuring the power of statistical techniques. Some complicated equations have been proposed to calculate the sample size for multiple regression [65,66,67]. Some easy-to-use sample size formulas have been proposed to evaluate the required sample size (n) for multiple regression equations.

• Snee [68]

n ≥ 2p + 20

(15)

2.

Green [69]

n ≥ 8p + 50

(16)

3.

Khamis and Kepler [70]

n ≥ 5p + 20

(17)

4.

Tabachnick and Fidell [71]

n ≥ p + 104

(18)

5.

Zaarour [72]

n ≥ 10p + 20

(19)

where p is the number of parameters.

3. Results

3.1. Two Variables

3.1.1. Extrusion Process for Producing High-Antioxidant Instant Amaranth Flour

In Study [29], the process variables are x₁, temperature, and x₂, screw speed, and the response variables are y_ORAC, antioxidant capacity (ORAC), and y_WSI, water solubility index (WSI)—used in a central composite design including 13 runs formed by five central points.

The proposed equations for the y response are complete models; that is, y_ORAC = b_o + b₁x₁ + b₂x₂ + b₁₁x₁² + b₂₂x₂² + b₁₂x₁x₂ and y_WSI = c_o + c₁x_{1 +} c₂x₂ + c₁₁x₁² + c₂₂x₂² + c₁₂x₁x₂.

Contour plots and response surface plots show the effect on y_ORAC and y_WSI of x₁ and x₂. The study presents all the curved relationships [29].

• The y_orac response

The experimental data are listed in the study [29]; the multiple regression results for y_orac are

y_orac = 1481.845 + 24.670x₁ − 0.490x₂ − 0.0262x₁² + 0.0217x₂² − 0.0725x₁x₂

(20)

(4.601) (−0.10) (−4.730) (2.065) (−2.396)

R² = 0.859, R²_adj = 0.758, s = 122.503, PRESS = 162,811,173

The numeric values in parentheses below the estimated values of parameters are the t-values of the estimated values of parameters.

The normality test is passed (p = 0.285), and the constant variance test is passed (p = 0.295).

The estimated values of each independent variable and its criteria are listed in

Table 3. The experimental values of each independent variable and its criteria for the y_orac response.

Coefficient	Estimated	Standard			Standard
	Value	Error	t-Value	p-Value	Coefficient	VIF
Constant	1481.845	571.865	2.591	0.036
x1	24.670	5.362	4.601	0.002	8.922	186.628
x2	−0.490	4.456	−0.110	0.916	−0.108	48.234
x12	−0.0262	0.00555	−4.730	0.002	−4.705	49.088
x22	0.0217	0.0105	2.065	0.078	1.498	26.095
x1x2	−0.0725	0.0302	−2.396	0.048	−4.320	161.328

.

Because the x₁², x₂², and x₁x₂ variables are derived from x₁ and x₂, the five variables’ variance inflation factor (VIF) is >10. This indicates the multicollinearity problems of these variables, and the backward elimination procedure is suitable for the RSM equations.

In a comparison of the t-values of x₁², x₂², and x₁x₂, the variable x₂² has the lowest t-value, and its p-value is 0.078 (>0.05). The term x₂² is deleted, and the regression equation is recalculated.

y_ORAC = 974.020 + 25.670x₁ + 6.138x₂ − 0.0285x₁² − 0.0725x₁x₂

(21)

 (4.039) (1.673) (−4.415) (−2.019)

In a comparison of the t-values of x₁² and x₁x₂, the x₁x₂ variable has a lower t-value, and its p-value is 0.078. The variable of x₁x₂ is deleted, and the regression equation is recalculated.

y_ORAC = 2079.174 + 14.550x₁ − 1.109x₂ − 0.0285x₁²

(22)

 (3.927) (−1.257) (−3.811)

The t-value of variable x₂ is −1.2557, and its p-value is 0.240 (> 0.05)

The variable x₂ is deleted, and the regression equation is recalculated.

y_ORAC = 1910.112 + 14.550x₁ − 0.0285x₁²

(23)

 (3.818) (−3.705)

R² = 0.597, R²_adj = 0.517, s = 173.208, PRESS = 133,405,010.

The normality test is passed (p = 0.228), and the constant variance test is passed (p = 0.723). The final equation is called the adequate equation.

The R² values for the complete and final adequate equations are 0.859 and 0.597, respectively. However, the R² value is affected by the number of variables in the equation. The more variables are used, the higher the R². So, it cannot be used as the sole criterion to evaluate the fitting ability of the equation [53,54,57,58,59,60].

The PRESS value of this adequate equation is 133,405,010. This numeric value is lower than the complete model (PRESS = 162,811,173), indicating that adequate equations have better predictive ability.

The results of regression diagnostics showed that some influential data points were found. With the t_i value, the fourth and fifth data points are influential. The Cook’s distance and DFFITS_i of data point 6 are 1475.4 and 68.411, respectively. Further experiments should be performed to check the validity of these data points.

Figure 1 shows the contour plots for the complete and adequate equations. The difference in the equations induces a difference in the distribution of curves between the two figures. The contour and response surface plots produced with the complete equation were presented in the study [29]. The inadequate RSM equation could induce incorrect results.

2.

The y_wsi response

The complete equation is

y_wsi = −3.679 + 0.333x₁ + 0.351x₂ − 0.00123x₁² − 0.00195x₂² + 0.00201x₁x₂

(24)

(2.632) (3.317) (−9.347) (−7.818) (2.801)

R² = 0.961, R²_adj = 0.932, s = 2.909, PRESS = 16,403.5

The normality test is passed (p = 0.236), and the constant variance test is passed (p = 0.723).

All the variables had a higher t-value. The variables x₁x₂ have the smallest t-value. However, the p-value is 0.026 (p < 0.05). So, the complete model is an adequate equation.

The results of regression diagnostics indicated some influential data points. For the tenth data point, t_i = 3.267, for the sixth data point, Di = 319.386, and DFFITSi = −42.548. The researchers showed that the runs of two data points should be performed with more replicates to find outliers or to recheck the validity of this model.

3.1.2. Compressive Strength of Rubberized Concrete

In Study [30], the experimental design was a CCD with 13 runs. The influencing factors included x₁ BCBP in %, and x₂ WTR in %. The two responses are y_7D (7-day compressive strength) and y_28D (28-day compressive strength).

The reported RSM equations for y₁ and y₂ are the complete equation; the independent variables involved are x₁, x₂, x₁², x₂², and x₁x₂ [30].

In the study, the contour and response surface plots of 7-day and 28-day compressive strength are curved distributions. The ANOVA table in the study for 7-day results showed that the p-values of x₁² and x₁x₂ were higher than p < 0.05. The ANOVA table for 28-day results indicated that the p-values of the x₁, x₁x₂, x₁², and x₂² variables were higher than the cutoff value (p < 0.05). Despite the higher p-value indicated in the ANOVA table presented in the study, the complete equations are still selected and used to produce contour and response surface plots [30].

The procedure to evaluate the adequate equation of the y₁ response (7-day compression) is listed as follows:

1. y_7D = 25.310 + 0.458x₁ + 0.130x₂ − 0.0183x₁² − 0.0272x₂² − 0.00401x₁x₂

(25)

 (1.267) (1.437) (−0.287) (−6.834) (−0.303)

R² = 0.979, R²_adj = 0.964, s = 0.664, PRESS = 12.070

The normality test is passed (p = 0.522), and the constant variance test is passed (p = 0.220).

The x₁² variable had the smallest t-value, and its p-value was higher than the cutoff value (p < 0.05). The variable was deleted.

The results of the recalculation are

2. y_7D = 25.352 + 0.549x₁ + 0.121x₂ − 0.0268x₁² − 0.00401x₁x₂

(26)

 (3.417) (1.512) (−7.730) (−0.322)

R² = 0.978, R²_adj = 0.968, s = 0.623, PRESS = 7.751

The x₁x₂ variable had the smallest t-value, and its p-value was larger than the cutoff value (p < 0.05). The variable was deleted.

The new equation is

3. y_7D = 25.452 + 0.509x₁ + 0.111x₂ − 0.0268x₁²

(27)

 (5.277) (1.586) (−8.147)

R² = 0.978, R²_adj = 0.971, s = 0.591, PRESS = 5.636

The normality test is passed (p = 0.652), and the constant variance test is passed (p = 0.236). No influential data point was found.

The adequate equation showed that x₁ has a curvilinear relationship with the response, and the quadratic equation x₂ variable has a linear relationship with response y_7D.

Compared with PRESS, the predictive ability of the adequate equation (PRESS = 5.636) is significantly improved over that of the complete equation (PRESS = 12.070).

Figure 2 shows the contour plots produced with complete or adequate equations. The distribution of each figure presents different results. When researchers use visual methods to conduct their experiments and observe the variables’ effect on the response, inadequate RSM equations will induce incorrect conclusions.

The procedure to evaluate the adequate equation of the y_28D response (28-day compression) is listed in Appendix A.1.

The adequate equation is

y_28D = 36.760 − 0.243x₂ − 0.0205x₂²

(28)

R² = 0.13, R²_adj = 0.895, s = 1.604, PRESS = 4.544

The normality test is passed (p = 0.406), and the constant variance test is passed (p = 0.378). No influential data point was found.

The adequate equation did not involve the x₁ variable. That is, the x₁ variable does not significantly affect y_28D. In Figure 2, the contour plots produced with different equations show different results. The comparison indicated the importance of producing response surface plots with adequate equations.

3.1.3. Poly-Cornstarch-Blended Biodegradable

The study used response surface methodology to evaluate the effect of x₁, amylase level, and x₂, glycerol level, on y_WSI, water solubility index (WSI), the y_WAI response, water absorption index (WAI), and the y_ML response, maximum load (ML), for a poly-cornstarch-blended biodegradable [28]. The experimental design is a CCD, and 13 runs were performed.

The forms of RSM equations reported in the study are

1. y_WSI = b_o + b₁x₁ − b₂₂x₂² ₋ b₁₂x₁²

(29)

2. y_WAI = c_o + c₁x₁ − c₂x₂ − c₁₁x₁²

(30)

3. y_ML = d_o + d₁x₁ + d₂x₂ + d₁₁x₁² + d₁₂x₁x₂

(31)

The variable selection method in the paper is the typical at-once variable deletion method. According to the reported results of the ANOVA tables, some variables whose p-value was higher than 0.05 were deleted simultaneously, and the coefficients of the remaining variables presented in the ANOVA table were used to construct these RSM models. No further calculations were performed. From the viewpoint of statistical concepts, this method is inappropriate.

The experimental data were listed in the study. In our study, the adequate regression models evaluated with the modern regression technique are

1. y_WSI = −3.679 + 0.627x₁ − 0.0792x₂ − 0.0446x₁²

(32)

The normality test was passed (p = 0.791). However, the constant variance test was failed (p < 0.001). There were two influential data points: the second data point, t_i = −2,145, and the seventh data point, DFFITS_i = 3.316. The y_WSI values need to be transformed to solve the constant variance problems. The runs of the influential data need to be checked by their means and standard deviations.

2. y_WAI = 5.206 − 0.228x₁ + 0.00434x₂ + 0.0148x₁²

(33)

The form of the y_WAL equation with modern regression is the same as in the literature. The normality and the constant variance tests are passed. In the equation, the x₂ variate only has a linear relationship with y_WAL. However, the contour and response surface plots revealed a curved relationship in the study. The authors presented the inconsistent results of their proposed RSM equations and their response surface plots [28].

3. y_ML = 45.480 − 0.761x₁ − 0.158x₂

(34)

The normality and constant variance tests were passed, and two influential data points were found: the fourth data point, t_i = −2.217, and sixth data point, t_i = −2.356.

In the research reported by the authors, the x₁ variable had a quadratic relationship with y_MD [28]. The contour and response surface plots in the study presented the curve distribution. However, the adequate equation indicated that both variables only have a linear relationship with the response y_ML. That is, an inappropriate equation will induce incorrect conclusions.

3.1.4. The Evaluation Results of the Other Literature with Two Variables

The evaluation results of the other literature with two variables are in

Table 4. The results of the evaluation of the adequate RSM equations for two variables.

Source	Purpose	Reported Equations	Contour and Response Surface Plots	Adequate Equations	Normality Test	Constant Variance Test	Influential Data
Diemer et al. [31]	Extraction of caffeoylquinic acid x1: temperature x2: ethanol (%)	y5-CQA = f (x1, x2, x22)	Curved surface	y5-CQA = f (x1, x2, x22)	Passed	Passed	1st
Adeyanju et al. [32]	Akara ogbonoso snacks	YMC (moisture) = f (x1, x2, x12, x22, x1x2)	Curved surface	YMC = f (x1, x2, x22)	Passed	Passed	No
	x1: temperature x2: time	YOC (oil content) = f (x1, x2)	Plane	YOC = f (x1, x2)	Passed	Passed	No
		yΔE = f (x1, x2)	Plane	yΔE = f (x2)	Passed	Passed	No
		yBF = f (x1, x2, x12, x22)	Curved surface	yBF = f (x2, x22)	Passed	Passed	No
		yS = f (x1, x2)	Plane	YS = f (x1, x2)	passed	passed	No

.

In the study of Diemer et al. [31], the complete datasets of the 5-CQA (chlorogenic acid) response and two variables were listed. When these datasets were obtained using modern regression, it was found that the adequate equation is in the same form as reported in the literature. One influential factor was found. In this adequate equation, the relationship between the variables x₁ and response was linear, and that between the variables x₂ and response was quadratic. However, the response surface plot presented in the study is a curve for both variables [31].

In the evaluation of the literature data of Adeyauju et al. [32], there are five responses. For the y_OC and y_ΔE responses, the literature report has the same results as the adequate equations calculated in this study. For the y_MC and y_BF responses, the authors recommended the use of the complete model and the curve distribution in their response surface plots. However, the results of the adequate equations calculated by modern regression are different. For the response y_ΔE, the authors reported that the x₁ and x₂ variables have a linear relationship. In this study, only x₂ variables significantly affect the y response. The authors’ selection of their equations in the literature was limited to the whole linear form (x₁, x₂) or whole quadratic form (x₁, x₂, x₁², x₂², and x₁x₂) with the sequential model of the response’s square. The effect of individual variables was not considered, so the results are different from modern regression. The selection of these variables in the study was carried out to use the results of the sequential model of the ANOVA table to justify the significant effects of the variables. When the linear or quadratic forms have a significant effect, all variables in the linear form (x₁ and x₂) or the whole quadratic form (x₁², x₂², x₁x₂) are accepted in these RSM models. The significant effect of each variable on response does not need to be tested individually. These problems have been illustrated in Section 2.5 of this study.

3.2. Three Variables

3.2.1. Extruded African Breadfruit–Corn–Soy

Nwabueze [33] reported the effect of three variables, x₁, feed composition, x₂, feed moisture, and x₃, screw speed, on three responses, y_TIA, trypsin inhibitor activity, TIA, y_{phytic acid}, phytic acid, and y_tan, tannin content, with a CCD experimental design. The replicates were performed at center points, and the total number of samples was twenty-five.

The p-value was used to justify the significant effect of the coefficients of the parameters for three responses. If the p-value was higher than 0.05, the parameter was removed. The RSM models of this response are recorded according to the estimated regression values of the remaining parameters [33].

Typical results of the ANOVA for y_TIA presented in the study are listed in

Table 5. Estimated regression coefficients for trypsin inhibitor activity (TIA) of extruded African breadfruit–corn–soy mixtures (data source: [33]).

	Estimated Values	Standard Error	p-Value
$b_0$	−2.980433	5.183862
$b_1$	0.107709	0.069684	0.1445
$b_2$	−0.174901	0.309534	0.5810
$b_3$	0.071086	0.037511	0.0789 *
$b_{11}$	−0.000427	0.000157	0.0168 **
$b_{12}$	−0.001111	0.002924	0.7098
$b_{13}$	−0.000500	0.000483	0.2347
$b_{22}$	0.004168	0.009179	0.6567
$b_{23}$	−0.00608	0.001728	0.7302
$b_{33}$	−0.000135	0.000115	0.5745

Note: * p < 0.1; ** p < 0.05.

. This table lists the p-values of x₁, x₂, x₃, x₁x₂, x₁x₃, x₂x₃, x₁², x₂², and x₃², and then compares them with the cutoff value, p <0.05.

In Table 5, only the coefficients of b₃ and b₁₁ significantly affected the response. The researchers then left these two variables alone and deleted all other variables at once. The estimated values of b₃ and b₁₁ in this table were used as the final estimated values.

By the elimination-at-once method, the authors reported that the RSM equations in the study are [33]

y_TIA = −2.980433 + 0.071086x₃ + 0.00427x₁²

(35)

With the same technique, the other equations are

y_{phytic acid} = 436.2951 + 0.022895x₁²

(36)

y_tan = 3.51248 − 0.0000186x₃²

(37)

The authors’ regression technique involved deleting all variables whose p-values were >0.05 at once, but the interaction effect of these variables was not considered.

Another question arises about the form of these equations [33]. The x₁² and x₃² variables are derived from the x₁ and x₃ variables for the polynomial equations. Suppose that the x_i², x_j², or x_ix_k variables are effective parameters. In this case, the x_i and x_j variables are validated parameters; the x_i and x_j variables should be included in this regression because the x_i², x_j², or x_ix_j variables are derived from the x_i and x_j variables.

The selection steps for y_TIA are listed in Appendix A.2. The adequate equations evaluated by modern regression analysis are

y_TIA =1.574 + 0.0622x₁ − 0.00307x₃ + 0.173x₁² + 0.168x₃²

(38)

y_{phytic acid} = 101.215 − 1.753x₁ − 0.984x₂ + 5.186x₁² − 8.441x₂²

(39)

y_tan = 103.957 − 0.984x₂ − 8.273x₂²

(40)

The normality and constant variance tests were passed. y_TIA, y_{phytic acid}, and y_tan have one, two, and two influential data points, respectively.

The study presented three 3D response surface plots. These plots are plotted with the complete models involving x₁², x₂², and x₃² [33]. However, the RSM equations proposed by the authors (Equations (35)–(37)) are not complete equations. The curves of these figures did not present appropriate results for the relationship among the three responses and variables. Adequate RSM equations are essential for providing helpful information for researchers.

3.2.2. Extraction of Bioactive Components from Defatted Marigold Residue

In Study [36], the influencing factors included x₁, ethanol concentration, x₂, temperature, and x₃, time. Four responses were measured. These were y_TPC, total phenolics (TPC), y_TFC, total flavonoids (TFC), y_ABTS, radical scavenging activity of ABTS, and y_DPPH, radical scavenging activity of DPPH.

The fitting models in the study were complete equations [36]. That is, all variables (x₁, x₂, x₃, x₁x₂, x₁x₃, x₂x₃, x₁², x₂², x₃²) were used in their models. The four responses’ contour and response surface plots were plotted with these quadratic and interaction terms. The four ANOVA tables of responses that showed the three variables’ effect on the responses were presented in the study [36]. The p-values indicated the insignificance of some variables. With the p-values, the quadratic terms of some variables had an insignificant effect on the responses. That is, the authors did not utilize the information of p-values of some variables to evaluate the adequacy of RSM equations.

The evaluation steps of the adequacy of RSM equations for the TPC and TFC responses are listed in Supplements S1 and S2.

The adequate RSM equations of the four responses are

1. y_TPC = −80.381 + 3.688x₁ + 0.219x₁²

(41)

Only the x₁ variable has a significant effect on the response y.

Two influential data points were found. For second data point, t_i = 4.407, with DFFITS_i = 5.075. For the 14th data point, t_i = −2.312.

The PRESS values of the complete and adequate equations are 3476.8 and 2083.706, respectively. The adequate equation has a better predictive ability than the complete equation.

2. y_TFC = −222.966 + 7.088x₁ + 2.165x₂ − 0.0354x₁^{2 −} 0.0272x₁x₂

(42)

Two influential data points were found. For the second data point, ti = 2.562, with DFFITSi = 2.151. For the 14th data point, ti = −2.198. The PRESS of the complete and adequate equations was 3073.183 and 1794.138, respectively.

3. y_ABTS = −2.902 + 0.114x₁ + 0.0102x₂ − 0.000735x₁²

(43)

One influential data point was found. For the second run, DFFITSi = 2.798. The PRESS of the complete and adequate equation was 3.266 and 1.919, respectively.

4. y_DPPH = −1.254 + 0.0664x₁ + 0.00561x₂ − 0.120x₃ − 0.00511x₁² + 0.00219x₁x₃

(44)

Two influential data points were present. For the 2nd and 14th runs, the DEFITS_i values are 2.266 and −2.123, respectively. The PRESS of the complete and adequate equations was 1.865 and 0.7861, respectively. The normality and constant variance tests were passed for four responses.

In the study, the authors’ reports of RSM equations for four variables were all complete models [36]. Modern regression analysis found different results. The predictive criterion, PRESS, of the four adequate equations was smaller than that of the complete equations. The adequate equation has a better predictive ability.

3.2.3. Corn Extrudate Fortified with Yam

Chiu et al. [37] studied the optimization of the extrusion characteristics of corn–yam extrudates. Their variables were x₁, yam flour contents, x₂, moisture content, and x₃, screw speed. The four responses included y_BD, bulk density, y_RER, radial expansion ratio, y_WAI, water absorption index, and y_HD, hardness. The authors reported that their RSM equations were quadratic polynomial models. Then, the quadratic polynomial equations were used to make the contour and response surface plots, and the effects of variables on these responses were observed in the two types of plots.

The authors used the coefficient of determination R² and lack of fit as criteria to evaluate significant effects for all quadratic equations. However, their ANOVA table in the study showed an insignificant effect of some variables at p < 0.01 and p < 0.05 [37]. That is, the authors misunderstood the meaning of a significant test.

The modern regression technique evaluates the adequate equation. The experimental data were listed in the study [37]. The results are listed as follows:

• y_BD, bulk density

The complete equation is

y_BD = 0.0449 − 0.00192x₁ + 0.00657x_{2 −} 0.000122x₃ + 0.0000221x₁² + 0.0000599 x₂²

 (−2.833) (3.258) (−0.559) (2.543) (1.104)

+ 0.000000483x₃² + 0.000113x₁x₂ + 0.000000501x₁x_{3 −} 0.0000201 x₂x₃,

(45)

(1.392) (5.395)  (0.200)   (−4.795)

$${\mathrm{R}}^2=0.996, {{\mathrm{R}}^2}_{\mathrm{adj}}=0.988, \mathrm{s}=0.002, \mathrm{PRESS}=1.031\times {10}^{-4}$$

The adequate equation is

y_BD = −0.0127 − 0.00171x₁ + 0.00825 x₂ + 0.000177 x₃ + 0.0000205x₁²

 (−3.741)  (6.206) (2.975)  (2.374)

+ 0.000113x₁x₂ − 0.0000201x₂x₃,

(46)

(5.586)  (−4.787)

$${\mathrm{R}}^2=0.993, {{\mathrm{R}}^2}_{\mathrm{adj}}=0.988, \mathrm{s}=0.002, \mathrm{PRESS}=7.71\times {10}^{-5}$$

The normality test was failed (p = 0.047), and the constant variance test was passed (p = 0.281). The influential data were the 8th data point (DFFITS_i =2.338) and the 13th (t_i = −3.737).

The adequate equation only involved the x₁² variable. In other words, x₁² was the only quadratic variable that influenced the y_BD response. x₂² and x₃² did not significantly affect the y₁ response. An inappropriate equation could induce an incorrect result when producing response surface plots. The datasets did not pass the normality test, and two influential data points were found. Further study needs to be performed.

2.

y_RER radial expansion ratio

The complete equation is

y_RER = 4.103 − 0.0494x₁ − 0.0487x_{2 −} 0.0136x₃ + 0.000658x₁² + 0.000547x₂²

  (−8.868) (−2.937) (7.534) (9.923)  (1.104)

−0.0000218x₃² + 0.000701x₁x₂ + 0.00000750x₁x_{3 −} 0.0000362 x₂x₃,

(47)

(−7.643)  (4.087)  (0.547)  (−1.058)

R² = 0.996, R²_adj = 0.989, s = 0.014, PRESS = 0.011

The adequate equation is

y_RER = 4.081 − 0.0469x₁ − 0.0442x₂ + 0.0134x₃ + 0.000651x₁²

 (−12.553) (−12.228) (7.861) (9.196)

−0.0000221x₃² + 0.000701x₂x₃,

(48)

(−7.796)  (4.106)

$${\mathrm{R}}^2=0.994, {{\mathrm{R}}^2}_{\mathrm{adj}}=0.990, \mathrm{s}=0.014, \mathrm{PRESS}=0.007$$

The normality test was passed (p = 0.442), and the constant variance test was passed (p = 0.620). Two influential data points were found, the fourth (t_i = 2.966, DFFITS_i = 4.494) and sixth (t_i = 2.657, DFFITS_i = 2.366).

The results of modern regression indicated that the x₁² and x₃² variables were valid, and only the x₂ variables had a linear relationship with the response y_RER.

3.

y_WAI, water adsorption index

The complete equation is

y_WAI = 6.754 + 0.0528x₁ + 0.329x_{2 −} 00232x₃ − 0.00148x₁² − 0.0178x₂²

(0.834)  (1.750) (−1.135) (−1.826) (−3.523)

+ 0.0000128x₃² + 0.000750x₁x₂ + 0.00000501x₁x_{3 −} 0.000801 x₂x₃,

(49)

(0.396) (0.385) (0.0321) (2.055)

R² = 0.937, R²_adj = 0.882, s = 0.156, PRESS = 1.278.

The adequate equation is

y_WAI = 2.730 + 0.570 x₂ − 0.00422 x₃ − 0.0173x₂²

(50)

(3.561) (−3.397) (−3.044)

R² = 0.906, R²_adj = 0.773, s = 0.176, PRESS = 0.696.

The normality test and constant variance tests were passed. One influential data point was found, the fifth (t_i = 2.539).

According to the modern regression, the x₁ variables did not significantly affect the y_WAI response. Only the x₂ variable had a quadratic relationship with the y_WAI response.

4.

y_HD, hardness

The complete equation is

y_HD = 1.958 − 0.196x₁ + 0.253x₂ + 0.00638x₃ + 0.00811x₁² − 0.00148 x₂²

(−1.968) (0.856) (0.198) (6.366) (−0.186)

−0.00000750x₃² + 0.00281x₁x_{2 −} 0.0000450x₁x_{3 −} 0.000338 x₂x₃

(51)

(−0.147)  (0.919) (−0.184) (−0.551)

R² = 0.988, R²_adj = 0.967, s = 0.245, PRESS = 4.543

The adequate equation is

y_HD = 3.812 − 0.171x₁ + 0.167 x₂ − 0.00375 x₃ + 0.00814x₁²

(52)

(−4.216) (9.764) (−2.743) (8.137)

R² = 0.986, R²_adj = 0.980, s = 0.193, PRESS = 0.938

The normality test and constant variance tests were passed. One influential data point was found (ninth, t_i = −3.102, DFFITS_i = −2.403).

For the y_HD response, x₂ and x₃ have a linear relationship, and only x₁ has a quadratic form (curves).

The authors used the complete models to produce the contour and response plots [37]. However, the ANOVA tables in their report indicated that some parameters did not significantly affect the response. In comparing the adequate equations with the complete equations proposed by the authors, the importance of using regression analysis correctly cannot be overstated.

3.2.4. The Adequate Equations of the RSM in the Other Literature

Table 6. The results of the evaluation of the adequate RSM equations for the three variables.

Source	Purpose	Reported Equations	Contour and Response Surface Plots	Adequate Equations	Normality Test	Constant Variance Test	Influential Data
Bimakv et al. [34]	CO2 extraction of bioactive flavonoid compounds x1: temperature x2: pressure x3: flow rate	yER extract ratio = complete equation	Curved surface	Complete equation	Passed	Passed	1st, 13th
Chen et al. [35]	Enzymatic clarification of asparagus juice	yclarity = f(x1, x2, x3, x2x3, x12, x22, x32)	Curved surface	yclarity = f(x1, x2, x3, x2x3, x12, x22, x32)	Passed	Passed	8th, 9th
	x1: temperature x2: pH x3: enzyme concentrations	yDPPH = f(x1, x3, x1x2, x1x3, x12, x22, x32)	Curved surface	yDPPH = f(x1, x2, x3, x1x2, x1x3, x12, x22, x32)	Failed (p = 0.001)	Passed	16th
Idrus et al. [38]	Extraction of virgin coconut oil	yyield = f(x1, x2, x12, x22, x32)	Curved surface	yyield = f(x1, x2, x3, x2x3, x12, x22, x32)	Passed	Passed	13th
	x1: coconut milk x2: fermentation time x3: refrigeration time	yFFA = f(x2, x12)	Curved surface	yFFA = f(x1, x2, x3, x12, x2x3)	Passed	Passed	1st, 5th, 6th
		yAV = f(x2, x12)	Curved surface	yAV = f(x1, x2, x3, x2x3, x12)	Passed	Passed	No
		yPOV = f(x1, x2, x3, x1x3, x2x3, x12, x22, x32)	Curved surface	yPOV = f(x1, x2, x3, x1x3, x2x3, x12, x22, x32)	Passed	Passed	3rd, 6th, 12th, 15th
Hong et al. [39]	Pumpkin flour with corn	Not reported	yRER: Curved surface	yRER = f(x1, x3, x1x2)	Passed	Passed	15th
	x1: pumpkin x2: moisture x3: screw speed	yRER (radial expansion ratio)	yBD: Curved surface	yBD = f(x1, x2, x3, x12)	Passed	Passed	no
		yBD (bulk density) yWAI (water adsorption index) yHD (hardness)	yWAI: Curved surface	yWAI = f(x1, x2, x3, x12, x22, x32)	Passed	Passed	3rd, 12th
			yHD: Curved surface	yHD = f(x1, x2, x3, x12)	Passed	Passed	8th
Wu et al. [40]	Maleic anhydride content in biopolymer blends	yTS (tensile strength) $=\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{t}\mathrm{e}$ $\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}$	yTS: Curved surface	yTS = f(x1, x2, x3, x1x2, x1x3, x2x3, x32)	Passed	Passed	1st
	x1: Tapioca starch content x2: maleic anhydride content x3: screen speed	yEL (Elongation) = complete equation	yEL: Curved surface	yEL = f(x1, x2, x3, x1x2, x2x3, x22, x32)	Passed	Passed	2nd, 3rd, 10th, 7th, 11th
		yWA (water ability) = complete equation	yWA: Curved surface	yWA = f(x1, x2, x3, x1x2, x12, x22)	Failed (p = 0.02)	Passed	2nd, 6th, 11th
Yu et al. [41]	Pipernigrum microcapsules x1: wall materials x2: wall concentration x3: air temperature	yEFF (efficiency) = complete equation	Not reported	yEFF = f(x1, x2, x3, x1x3, x2x3, x22, x32)	Passed	Failed (p = 0.044)	11th
Tshizanga et al. [42]	Biodiesel production x1: temperature x2: oil ratio x3: catalyst loading	yBY (biodiesel yield) = complete equation	Curved surface	yBY = f(x2, x22)	Passed	Passed	no
Wu et al. [43]	Cryoprotectants for direct vat set starters x1: skim milk powder x2: sucrose x3: L-proline or glycerol	ySICC = complete equation	Curved surface	ySICC = f(x1, x2, x3, x2x3, x12, x32)	Passed	Passed	2nd, 3rd, 6th, 7th, 10th, 11th
		y61 = complete equation	Curved surface	y61 = f(x1, x2, x3, x2x3, x12, x22, x32)	Passed	Passed	2nd, 3rd, 6th, 7th, 10th, 11th
Savik et al. [44]	Antioxidant cellulose from walnut husks x1: UAE time x2: temperature x3: MWP time	yTAC = complete equation	Curved surface	yTAC = f(x1, x2, x12)	Passed	Passed	No

lists the results of evaluating the adequate RSM equations for the three variables studied based on the literature.

The RSM model reported by Bimakr et al. [34] was a complete equation. The modern regression results are the same. Two influential data points were found, which required further study.

Two responses were studied for the enzymatic clarification of green asparagus juice [35]. With the ANOVA tables, the variables with a p-value > 0.05 were deleted at the same time in this study. Their RSM equations were proposed with the remaining variables and estimated values. After checking using modern regression, the y_clarity response had the same form as the RSM equations and the y_DPPH was different [35].

Idrus et al. [38] reported the aqueous extraction of virgin coconut oil. The affecting factors were screened with the p-values in their ANOVA tables, which were significant (p $\le$0.05). The RSM equations were then established with the remaining variables. In the study [38], only the proposed equations of the y_pov response have the same results as our study.

Hong et al. [39] investigated four physicochemical properties of a pumpkin flour blend with corn. The RSM equations were not reported in the study. The contour and response surface plots showed that all variables had a curvilinear effect on the response. However, the results of modern regression in Table 6 indicated that the variables of the adequate equations of the four responses were not complete models. The influence factors for y_RER (radial expansion ratio) were x₁, x₃, and x₁x₂; no quadratic relationship existed. The affecting factors for the y_HD response (hardness) were x_1, x_2, x_3, and x₁². Only the x₁ factor had a curvilinear relationship with y_HD. The coefficients of variables and a significant test with p-values were presented in a literature table. However, the authors did not use this information to select adequate models [39].

Wu et al. [40] used RSM to evaluate the effects of extrusion variables and maleic anhydride content on biopolymer blends. They used the complete models to describe the RSM equations and to present the curve distribution of the contour plot and response surface plots. Regression results of a significant effect of variables on response have been reported in the study [40]. However, these statistical results were not used to assess whether the variables had a significant effect. All variables were used as the affecting factors of the response. For the y_TS response, only x₃ has quadratic terms. The quadratic terms are x₂² and x₃² for y_EL, and x₁² and x₂² for y_WA. The complete model involved all factors in an appropriate equation. The influential data points were found for three responses. The normality test was failed for the y₃ response.

Yu et al. [41] studied the factors affecting piper nigrum microcapsules with spray drying. The results of ANOVA and the statistics of the model were presented in a table in the study [41]. The F-values and p-values showed that six variables did not significantly affect the response. However, the complete equation was reported in the study. The results of the modern regression showed that the x₁ term did not have a quadratic form with a response. The constant variance test was failed (p = 0.644). The transformation of y_EFF could be performed for the recalculation of the RSM models.

Tshizanga et al. [42] reported on optimizing biodiesel production from wastes. The authors proposed complete equations involving all variables and produced curve contour and response surface plots. The regression results of our study showed that only the x₂ variable affected the response. Two variables, x₁ and x₃, did not significantly influence the response.

In a study of cryoprotectants for direct vat set starters in Sichuan paocai, Wu et al. [43] used RSM to determine the optimization. The two responses were y_SICC (L. plantarum SICC) and y_Y61 (B. subtilis Y61). The ANOVA table and the p-values for each coefficient were listed in the study [43]. The p-values of some parameters indicated an insignificant effect on the response. However, the complete models were proposed and used to produce a curved relationship for contour and response surface plots. The results of modern regression analysis indicated that the influence factors for y_SICC were x₁, x₂, x₃, x₂x₃, x₁², and x₃². The variable x₂ only has a linear relationship with y_SICC$.$ Influence factors for y_Y61 were x₁, x₂, x₃, x₂x₃, x₁², x₂², and x₃². There was no interaction effect on y_Y61 for the x₁x₂ and x₁x₃ terms.

Savic and Gajic [44] reported the optimization of antioxidants and cellulose from walnut husks. The reported y_TAC equation was a complete model. The study’s results reported that the interaction between x₁ and x₃ was statistically insignificant (p > 0.05) and could be excluded from the equation. However, the term of x₁x₃ remained in their model [44]. Through the use of the experimental data in the study, the adequate model with modern regression included the variables of x₁, x₁², and x₂. The x₃ variable did not have a significant effect on the response.

3.3. Four Variables

3.3.1. Haskap Extract and Tannic Acid

Yemis et al. [49] investigated the effect of four variables, x₁, polyphenol-rich haskap extract, x₂, tannic acid, x₃, temperature, and x₄, time, on C. sakazakii inactivation (y_SI). The CCD included 28 runs. The statistics included PRESS and lack of fit. The response y_SI was transformed as a logarithmic reduction.

The significant effect of the variables on the logarithmic response was evaluated using the backward elimination method. The reported RSM model included the variables of x₁, x₂, x₃, x₄, x₁x₂, x₁x₃, x₁², x₃², and x₄². x₂² and other interaction terms were excluded. Contour and response surface plots were produced with this RSM equation.

The datasets listed in the study were obtained and evaluated using modern regression. The results indicated the validity of this reported RSM model. The original y_SI value could not pass the constant variance test, so the authors transformed these y_SI responses into a logarithmic form.

After the logarithmic response was used, the normality and constant variance tests were passed. One influential data point was found.

The RSM equation of Yemis et al. [49] is adequate. It proves that a correct regression analysis technique obtained an effective RSM model for further analysis.

3.3.2. Microencapsulation of Seed Oil

Ahn et al. [48] investigated microencapsulation efficiency with four variables: x₁, soy concentration, x₂, milk protein isolate ratio, x₃, soy lecithin concentration, and x₄, homogenizing pressure. The reported RSM equations involved the following variables: x₁, x₂, x₃, x₁², and x₂². The variable selection method used was to screen the variable with its p-value < 0.05 in the ANOVA table simultaneously. The x₃² variable was excluded. However, the response surface plots presented in the study showed a curved relationship between the x₃ variables and response y_EFF (efficiency) [48]. The reported equation and the response surface plots have inconsistent results.

The selection of effective variables for response in this study is outlined in Supplement S3. The final result with the modern regression included the following variables: x₁, x₂, x₃, x₁x₃, x₂x₃, x₁², and x₂². Compared with the reported variables, x₁x₃ and x₂x₃ were significant factors in the response. However, two variables were excluded from the study.

The normality test and constant variance test were passed. The t_i and DFFITSi criteria produced two influential data points.

3.3.3. Extraction of Total Phenolic and Flavonoid Content

Hiranpradith et al. [51] studied the factors affecting the maximization of y_TPC, total phenolic content, and y_TFC, total flavonoid content. The influencing variables included x₁, ethanol concentration, x₂, ultrasonic power, x₃, extraction time, and x₄, solvent volume. The authors reported that the influencing factors for y_TPC are x₁, x₂, x₄, x₂², and x₄², and those for y_TFC are x₁, x₂, x₃, x₄, x₁x₄, and x₁². The screening method of variables was to remove the variable terms with p-values > 0.05 at once. Some response surface plots in the study were inconsistent with the reported RSM equations.

The modern regression results differed from the reported RSM models in the study. Differences in statistical methods could explain the inconsistent results.

The adequate y_TpC was

y_TpC = −11.504 + 1.046x₁ + 1.238x₄ − 0.00829x₁²

(53)

The influencing factors included x₁, x₄, and x₁². Only the x₁ variable had a curvilinear effect on the response y_TpC.

The normality test was failed (p = 0.004), and the constant variance test was passed. Three influential points were found with the criteria of t_i and EFFITS.

The adequate y_TFC was

Y_TFC = −5.764 + 0.741x₁ + 0.564x₂

(54)

Only the variables of x₁ and x₂ significantly affected the response y_TFC$.$ No quadratic terms were found for x₁, x₂, x₃, and x₄. The normality test was passed, and the constant variance test was failed (p = 0.002). Two influential data points were found. Further regression analysis must be performed to remedy the violation of the assumption of constant variance.

3.3.4. The Regression Results of the Other Literature

The results of the RSM models of modern regression are listed in

Table 7. The results of the evaluation of the adequate RSM equations for the four variables.

Source	Purpose	Reported Equations	Contour and Response Surface Plots	Adequate Equations	Normality Test	Constant Variance Test	Influential Data
Lee et al. [46]	Microencapsulation of peanut sprout	Complete equation	curved surface	yyield = f(x1, x2, x4, x1x2)	Passed	Passed	4th 17th 30th
Yu et al. [47]	Yield of resveratrol content in peanut sprout	Complete equation	curved surface	yYRC = f(x1, x2, x3, x4, x1x3, x22, x32)	Passed	Passed	18th 19th
Javanbakht and Ghoreishi [48]	Lead removal from aqueous solution	Complete equation	curved surface	yLRC = f(x1, x2, x3, x4, x1x4, x22, x32)	Failed (p = 0.023)	Passed	7th 23rd
Vega et al. [50]	Natural food colorants from wild fruits	Complete equation	curved surface	yTAC = f(x1, x2, x3, x1x3)	Failed (p = 0.011)	Passed	30th 34th 46th

.

Lee et al. [46] reported the factors that influence the optimization of the microencapsulation of peanut sprouts. The influencing variables were x₁, water/oil ratio, x₂, first emulsifier, x₃, water/oil/water ratio, and x₄, second emulsifier. The response y was the yield of microencapsulation. The t-value and p-value of each variable were listed in the ANOVA table in the study [46]. The p-values of some variables were >0.05. However, the reported RSM equation was a complete model in the study. The results of modern regression revealed that only the variables x₁, x₂, x_4, and x₁x₂ were influence factors.

A study of optimizing germination conditions to improve the resveratrol content yield of peanut sprout was performed by Yu et al. [47]. The affecting variables were x₁, soaking temperature, x₂, soaking time, x₃, germinal temperature, and x₄, germinal time. In the study, the RSM model was a complete equation, and it was used to produce the contour and response surface plots. The F-value and t-value of each variable have been listed in the ANOVA table in the study. Some variables did not significantly affect the response with p-values > 0.05. However, the authors proposed a complete model [47]. The adequate equation evaluated by the modern regression only involves the variables x₁, x₂, x₃, x₄, x₁x₃, x₂², and x₃².

Javanbakht and Ghoreishi [48] studied the optimization of lead removal from aqueous solutions. The response, y_LRC, was the lead removal capacity. The influencing factors were x₁, pH, x₂, temperature, x₃, lead ion concentration, and x₄, adsorbent dose. The reported RSM equation was a complete equation. The curves of contour and response surface plots were presented. However, the ANOVA table in the study indicated that only six variables had a lower p-value (p < 0.05). The adequate regression evaluated with modern regression indicated that significant variables were x₁, x₂, x₃, x₄, x₁x₄, x₂², and x₃². The normality test was failed (p = 0.023), and the constant variance test was passed.

Vega et al. [50] studied optimization for wild Myrtus communis L. fruit by-products as a natural colorant source. The response was y_TAC (total anthocyanin content). The influencing factors were x₁, pH, x₂, ultrasound power, x₃, time, and x₄, solid/liquid ratio. The authors reported a complete equation and used this model to produce contour and response surface plots. In our study, the adequately evaluated model with modern regression only involved four variables (x₁, x₂, x₃, and x₁x₃). No quadratic terms exist in this adequate equation. The normality test was failed (p = 0.011), and the constant variance test was passed.

3.4. Five Variables

Acikel et al. [52] assessed the optimization of medium components for lipase production. Their research considered five variables: x₁, sucrose, x₂, molasses sucrose, x₃, yeast extract, x₄, sunflower oil, and x₅, Tuken−80. The authors proposed a complete equation, which included twenty variables for y_LA, lipase activity, and y_BC, biomass concentration. The contour and response surface plots were produced with two complete equations. The surface figures of the curve were presented for all variables [52].

The results of the modern regression technique are listed as follows:

y_LA = f(x₁, x₂, x₃, x₄, x₅, x₁x₂, x₁x₃, x₁x₄, x₁x₅, x₂x₄, x₃x₄, x₃x₄, x₃x₅, x₄x₅, x₁², x₂², x₄²)

(55)

The x₃² and x₅² variables did not significantly affect y₁. The normality and constant variance tests were passed, and there were no influential data points.

y_BC = f(x₁, x₂, x₃, x₄, x₅, x₁x₂, x₁x₃, x₁x₄, x₁x₅, x₂x₄, x₃x₄, x₃x₅, x₄x₅, x₁², x₂²)

(56)

The x₃², x₄², and x₅² variables did not significantly affect y_BC. The constant variance tests were passed. However, the normality test failed. Further studies are needed to treat the non-normality problem.

4. Discussion

This study collected twenty-five datasets related to research to check the adequacy of RSM models. Only some papers reported an adequate equation to express the relationship between the response and influencing factors [34,49]. All datasets are adopted from the literature. The original experimental data are listed in the studies. The common issues in the application of RSM in the literature are listed in

Table 8. The common issues in the application of RSM in the literature.

Issue	References
They adopted a complete model and then plotted contour and 3D response surface plots to present the optimization of these variables, without using the information of the coefficient value, t-value, and p-value for each variable in the ANOVA table.	[29,30,36,37,39,40,43,44,46,47,48,52]
2. The at-once variable deletion method was used to delete variables whose p-value was higher than the preselected value (usually p < 0.05).	[28,51]
3. Some variables were deleted with the at-once variable deletion method. However, the contour and response surface plots were produced with the complete equations.	[31,33,35,38,45].
4. The ANOVA table of the sequential model was misused to keep all variables in the linear or square term without significant testing for each variable.	[32,42]
5. Datasets did not pass the normality test.	[35,40,48,50,52]
6. Datasets failed the constant variance test.	[28,41,51]
7. Influential data points were found.	[28,29,31,33,34,35,36,37,38,39,40,41,43,44,45,46,47,48,49,50,51,52]
8. There were three replicates for each run in the experiment. However, only the mean of each run was used for the regression calculation.	[28,31,37,39,40,43,49].

.

Most papers adopted a complete model and then plotted contour plots and 3D response surface plots to present the optimization of these variables. In the literature, the ANOVA tables included the coefficient value, t-value, and p-value for each variable. However, researchers did not use this information to screen the adequate equation [29,30,36,37,39,40,43,44,46,47,48,52].

Some papers used the at-once variable deletion method. After the first regression calculation, the ANOVA table of regression results showed each parameter’s variables, coefficient values, standard error, t-value, and p-value. If the p-value of variables is higher than the preselected value (usually p < 0.05), these variables are deleted simultaneously. The equation is then proposed using the first regression calculation’s remaining variables and their coefficient values. This method is incorrect for model building [28,51].

Some studies proposed the reported RSM equations using the at-once variable deletion method. However, they still produced the contour and response surface plots with the complete equations [31,33,35,38,45].

Section 2.5 introduced the misuse of the ANOVA table of the sequential-model sum of squares of the response. As the linear or square term significantly affects the response, all variables in the linear or square terms were accepted as affecting factors. This incorrect result was found in two studies [32,42].

If the RSM models are inappropriate, the equations’ contour plots and 3D response surface plots are incorrect, and the conduct of the optimization conditions of these variables is meaningless for researchers.

For the twenty-five studies related to science and technology, some datasets did not pass the normality test [35,40,48,50,52], and some failed the constant variance test [28,41,51]. These datasets need to be transformed to correspond to the basic assumption of modern regression. The datasets of Yemis et al. [49] indicated the non-normal condition, and the authors used the logarithmic transformation to solve the problem. Yang et al. [73] emphasized that the homoscedasticity assumption plays a more critical role than normality in the validity of ANOVA in checking the linear regression models. Departures from the homogeneous assumption will induce serious incorrect results [73].

Influential data points are usually found in the datasets of these studies. They may be outliers or influencing data points in the literature. One research article states that a data point seriously influenced the coefficients’ values, and the Cook’s distance was very high [29]. In the study of Sinkhonde et al. [30], the authors reported the results of checking influential data points with some criteria.

The cause of the presence of influential data points could be experimental errors or the selection of the form of RSM models. Experimental errors may be due to sample preparation, instrument performance, or an operator’s mistake. Different forms of regression equations, such as some nonlinear equations, could be used to improve the RSM model’s fitting ability. Replicates of the experimental run at the same level could help the researcher to assess the significant difference between a data point and other data points under the same experimental conditions.

Most datasets of experiments did not have replicates for each run; only one data point was available at each level and factor. This makes it difficult to justify the correctness of these data points further. Some research reports three replicates for each case [28,31,37,39,40,43,49]. However, only the mean of each run is used to perform the regression analysis. Through the use of the mean value instead of all replicates, the results of the regression coefficient values are the same, but the statistics of the statistical test are different. For example, there are 17 runs with three replicates for each run in the study of Wu et al. [43]. As the mean of each run is used only, the sample size is 17. If all the original data are used, the sample number is increased to 51, and the degree of freedom for the residues is increased significantly. Then the statistical test of power could be improved significantly. The influencing points or outliers could be justified if some influential data points were found. Three replicates for each run could provide some evidence for assessing the datasets.

One advantage of RSM is the small number of experiments, which reduces the time and cost spent. However, a smaller number of samples becomes a disadvantage of the RSM method for evaluating an adequate equation. In comparing the required data numbers with some empirical equations (Equations (15)–(19)), the sample numbers of the RSM equation used in experiments were limited. In the experimental design, three replicates for each run could provide enough sample numbers to perform the regression analysis.

Fifteen papers, 60% of the total literature, used Design Expert software. However, only one study [49] obtained an appropriate equation. Bimark et al. [34] used Minitab Ver. 14 software and proposed an adequate RSM equation.

Based on the results of this study, some suggestions can be proposed for the utilization of RSM in experimental design:

1.

Training in the modern regression technique

Receiving regression analysis training could enhance researchers’ ability to propose adequate RSM equations

2.

The backward elimination technique has been proven helpful for sequential variable selection. This method could be incorporated into commercial software to help researchers establish an adequate RSM equation.

3.

Increasing the sample numbers to correspond to the minimum sample requirement is very important. This could enhance the power of the statistical test. Three replicates for one experiment run are recommended. All the data points with these replicates could be used to check the influential data point and decide whether it is an outlier or an influential point.

5. Conclusions

This study collected twenty-five research datasets from the literature to evaluate their adequate RSM equations with modern regression analysis. The results of this study indicated some common issues in establishing RSM models. Most papers used a complete model to express the relationship between the response and the influential variables, producing contour and response surface plots. When researchers observe these plots to optimize these variables, the conclusions of the experiments may be incorrect. The ANOVA tables included the coefficient value, t-value, and p-value for each variable in the literature. However, researchers did not use this information to screen the important influencing variables. Some researchers used the at-once variable deletion method. That is, as the p-value of these variables is higher than the preselected value, these variables are deleted simultaneously. Some RSM equations were proposed using the at-once variable deletion method, and contour and response surface plots were produced with the complete equations. Some papers misused the sequential model of the ANOVA to accept all variables in linear or square terms, as these terms significantly affect the response. Actually, all variables need to be tested individually. Some datasets did not pass the normality test. Some datasets failed the constant variance test. Influential data points are found in most of the literature in this study.

The suggestions for applying RSM for researchers are to enhance training in modern regression, use the back elimination method to evaluate the influencing variables in the RSM models, and increase the sample size with three replicates in each run. An adequate RSM model can optimize the influencing variables for response in science and technology.