Ontology Modeling Using Fractal and Fuzzy Concepts to Optimize Metadata Management

Abstract

To address the data management limitations of traditional ontology models in dynamic industrial settings, this study introduces the Fractal Fuzzy Ontology Modeling (FFOM) framework, a novel methodology for optimizing data management, integration, and decision making. FFOM’s value is rooted in two major contributions: firstly, the strategic use of fractal structures to achieve unparalleled scalability and modularity, which significantly reduces the effort required during data hierarchy updates by enabling self-similar, expandable data architectures. Secondly, FFOM features the synergistic use of fuzzy logic to meticulously manage ambiguity and uncertainty, including the representation of imprecise relationships and support for flexible, rule-based reasoning. The practical value of this integrated approach is demonstrated through a mold assembly case study, which validates FFOM’s effectiveness in structuring complex data hierarchies, managing uncertainty, and enabling automated reasoning. Implemented in the Web Ontology Language (OWL) for standardization and interoperability purposes, FFOM ultimately provides a clear pathway toward developing more intelligent, adaptive, and scalable data ecosystems in demanding manufacturing domains, where real-time data analysis is critical.

1. Introduction

The modern industrial environment is increasingly data driven, particularly in continuous process industries, where vast amounts of data are generated and analyzed in real time. These data play a critical role in process optimization, quality control, predictive maintenance, and energy efficiency [1]. However, the effective management and utilization of such data requires the systematic and consistent management of metadata. Metadata, by describing the properties, relationships, and context of data, supports data integration and interoperability, facilitating seamless data exchange across systems and platforms, while maximizing traceability and utility [2].

Traditional metadata management methodologies, often reliant on standard OWL/RDF implementations with binary logic and fixed hierarchies, face significant challenges in regard to scalability and adaptability when confronted with the volume of data, process interdependencies, and inherent uncertainties of modern industry [3]. Traditional ontology models are often developed based on fixed schemas and assumptions about domain stability. However, in real-world manufacturing settings, processes evolve, equipment changes, and new operational insights emerge. Without continuous adaptation, these static models become misaligned with current realities, undermining their usefulness over time. This necessitates an agile and dynamic ontology management approach capable of evolving with the data and context. This paper argues that a more transformative approach is needed. We propose Fractal Fuzzy Ontology Modeling (FFOM) not as a mere conceptual overlay or a set of standalone OWL adaptations, but as a novel, integrated framework that itself defines how OWL classes, properties, and values are structured and semantically enriched to model fractal patterns and fuzzy uncertainties. FFOM is presented as a substantive technical intervention that fundamentally extends OWL’s capabilities to transform how subject/predicate/object semantics represent and retrieve information in complex, dynamic systems.

To maximize data usability in such industries, an ontology model must effectively capture hierarchical data expansion and manage inherent uncertainties [4]. The FFOM framework is introduced to address these dual requirements by distinctively integrating fractal structures for scalable, self-similar hierarchies with fuzzy logic for nuanced uncertainty representation [5,6]. This combination is particularly suited for dynamic industrial contexts, where both structural complexity and data imprecision are prevalent. The foundational principles, analytical sophistication, and detailed mechanisms of this integration, demonstrating how FFOM enhances standard ontological approaches like OWL and RDF beyond superficial additions, are elaborated in Section 3. In doing so, FFOM not only enhances scalability and adaptability in continuous process industries, but also offers a flexible solution that can be generalized to other areas where complex, uncertain data environments require both structural flexibility and nuanced decision support.

This study, therefore, proposes the FFOM framework to address these challenges. Key objectives include effectively managing inherent data uncertainty through the integration of fuzzy logic [7] and ensuring interoperability by defining a systematic transformation process into the OWL, a critical step for standardization and data exchange [8]. The practical effectiveness of FFOM in handling hierarchical complexity and uncertainty is subsequently validated through a mold assembly case study.

This paper is organized as follows. Section 2 reviews the related literature on ontology modeling, fractal concepts, and fuzzy logic. Section 3 details the proposed FFOM methodology, including its formal components and the OWL transformation process. Section 4 presents a case study in the mold assembly domain, validates the framework’s practical application, and provides a discussion of its contributions and limitations. Finally, Section 5 provides a concise summary of the paper and its contributions and suggests areas for future research.

2. Literature Review

2.1. Ontology Modeling Methodologies

Ontology refers to a structural framework for systematically representing and managing knowledge within a specific domain [9,10]. Originally rooted in philosophy, ontology in informatics and industrial engineering has evolved as a critical methodology for defining data, its attributes, and relationships [11]. It has become essential for data integration, retrieval, and interoperability, facilitating seamless data exchange across systems and platforms. This capability is particularly significant in industrial settings, where vast and complex data structures must be efficiently managed to enhance traceability and utility [12].

Ontology consists of three primary components: concepts, attributes, and relationships [13]. Concepts provide the fundamental classification units within a domain. For example, in manufacturing, “Equipment,” “Process,” and “Product” represent primary data categories that are often hierarchically organized. Higher-level concepts encompass more specific, lower-level concepts, enabling clarity and flexibility in regard to data classification [14]. Attributes further describe the characteristics of data associated with a concept and are divided into data properties (i.e., quantitative information) and object properties (i.e., relationships between entities). For instance, “Equipment” might include a data property such as “Operational Status” and an object property linking it to a “Process.” Relationships define the interactions and dependencies among the concepts, such as how “Equipment” is part of or influences a “Process.” In addition to these core elements, ontology incorporates constraints and inference rules to maintain data integrity and derive new information, enabling automated decision making and real-time analysis [15,16].

As

Table 1. Exemplary ontology visualization methods.

	VOWL	Graffoo	OWLGrEd
Class
Individual	-
Instance of	-
Class hierarchies
Data type
Complex class	-	-
Object property
Object property assertation	-
Data property
Data property assertation	-
Property restriction	-	-
Disjoint

illustrates, while various approaches address aspects of manufacturing data management, FFOM’s distinct contribution lies in its integrated methodology. For instance, while specific manufacturing ontologies [1] provide rich domain semantics, and Digital Twin models [4,5] focus on asset-specific data integration, FFOM’s fractal foundation offers a more generalized mechanism for managing the structural evolution of complex, self-similar data hierarchies that are often found across different manufacturing scenarios. Similarly, while dedicated fuzzy ontology models [6] excel at uncertainty, FFOM combines this with fractal structuring for enhanced scalability and modularity in dynamic environments. This dual capability positions FFOM to handle large-scale, continuously changing data by leveraging a fractal-based hierarchy that can be expanded or updated with minimal disruption, while simultaneously managing inherent data imprecision through its fuzzy logic layer. FFOM stands out by being explicitly designed to address both of these critical aspects from the ground up, within an OWL-compatible framework.

As ontology models have grown more complex, visualization methodologies have emerged to enhance both their understandability and usability [17,18]. Ontology visualization techniques intuitively represent relationships, structures, and attributes, enhancing the user’s interaction with data [19,20], such as VOWL [21] (visual notation for OWL ontologies), Graffoo [22], and OWLGrEd [23,24]. VOWL uses a graphic-based approach to depict relationships between classes and properties, providing a simple and user-friendly interface [23]. Tools like ProtégéVOWL [21] and WebVOWL [23] have popularized VOWL, but its readability declines with large-scale ontologies, and it does not fully support all OWL 2 features. Graffoo employs a UML-style diagram to emphasize specific structural elements during ontology design. While effective for smaller models, it struggles with representing complex interactions or large datasets. OWLGrEd also uses a UML-style approach to visualize OWL 2 ontologies and supports mappings between UML and OWL. However, its accessibility is limited for users unfamiliar with UML, and the complexity of the graphs can hinder interpretation [24]. Table 1 provides a comparative overview of various ontology visualization techniques, illustrating their strengths and weaknesses in representing hierarchical structures and relationships. This comparison helps contextualize the necessity of FFOM’s approach for handling scalability and uncertainty in industrial applications.

Despite significant progress in regard to ontology modeling and visualization methodologies, most existing approaches still rely on rigid hierarchical structures that are difficult to adapt for large-scale or frequently updated data [25]. To overcome these issues, this study introduces the FFOM approach, which uniquely combines fractal structures with fuzzy logic. Although fractal principles have shown promise in large-scale system architectures, thanks to their self-similarity and repetitive patterns, they have rarely been integrated into ontology modeling. This gap presents an opportunity to harness fractal-based scalability in environments characterized by hierarchical complexity and frequent process modifications. Meanwhile, fuzzy logic has been widely adopted to address uncertain or imprecise data in various ontology frameworks. By leveraging fractal layers, FFOM allows new processes, modules, or data sources to be embedded, with minimal structural changes, thus preserving the overall consistency. Simultaneously, fuzzy logic enables ranges of membership instead of fixed binary relationships, offering more specific modeling of dynamic and uncertain variables. In doing so, FFOM not only streamlines scalability and flexibility beyond what traditional or purely fuzzy-based ontology models provide, but also lays a foundation for real-time adaptability in data-intensive industries.

Unlike existing approaches that solely apply fuzzy logic to ontology modeling, FFOM introduces a fractal-based hierarchical structure that enables seamless scalability and modular expansion without requiring modifications to the core model [26]. It allows FFOM to manage dynamic and complex manufacturing processes with greater efficiency than traditional fuzzy-based ontology models, which still rely on fixed hierarchical representations. FFOM stands out for its ability to handle large-scale, continuously changing data by leveraging a fractal-based hierarchy that can be expanded or updated with minimal disruption to existing structures.

Table 2. Comparison of ontology visualization methodologies.

Methodology	Pros	Cons
VOWL	- Provides an intuitive, graphical notation, making it relatively easy for users to grasp - Good tool support (e.g., WebVOWL, ProtégéVOWL) for quick ontology visualization	- Can become crowded or less clear for large-scale ontologies - Does not fully support all advanced OWL 2 features (e.g., complex property restrictions)
Graffoo	- Employs UML-style diagrams, familiar to those with a software engineering background - Useful for relatively small or mid-sized ontologies, offering a clean, structured view	- Lacks robust features for complex or large-scale ontologies - Does not inherently address uncertainty
OWLGrEd	- Offers a richer set of UML-like constructs than Graffoo, enabling more advanced modeling - Supports direct mappings between UML class diagrams and OWL	- Requires users to be comfortable with UML conventions - Complex ontologies visualization still becomes complex and there is no built-in capability to deal with uncertainty
FFOM	- Embraces fractal structures to ensure scalability and hierarchical consistency - Incorporates fuzzy logic to effectively manage uncertain or ambiguous data - Enables real-time adaptability, handles evolving data without major structural changes - Seamlessly transforms into OWL for standardization and interoperability purposes	- Relatively new approach, which may require additional learning by practitioners - Tool support may not be as widespread as established visualization techniques

highlights that while existing modeling methodologies clearly offer visual modeling and well-established tool support, they are limited in regard to scalability and flexibility when managing large or frequently updated data. Consequently, FFOM’s core strengths lie in its flexible scalability through a fractal structure, its ability to handle uncertainty and support real-time decision making via fuzzy logic, and its potential for OWL-based standardization, which is compatible with a wide range of ontology tools. Therefore, FFOM is the clear choice for dealing with massive dynamic data and when real-time decision making is required; it offers a far more robust and dependable alternative to traditional ontology modeling approaches.

2.2. Ontology in Metadata Management

Metadata, often described as “data about data,” provides information about the attributes, structure, relationships, and context of data. Metadata management is a critical component for efficient data utilization in modern industrial environments, particularly in continuous process industries, where large volumes of data are generated and need to be integrated from diverse sources [27]. Ontology plays a pivotal role in managing and utilizing metadata effectively, serving as a foundational tool that supports the organization, standardization, retrieval, and integration of data.

Ontology enhances the consistency and coherence of metadata by defining and structuring it explicitly [28]. This minimizes semantic discrepancies when integrating data from different systems. For instance, in continuous process industries, process and equipment data are often stored in disparate formats and structures. Ontology facilitates their unified representation and management through a shared conceptual model, ensuring seamless data integration and interoperability. This enables real-time data exchange and analysis across multiple systems, which is critical for industrial environments.

Furthermore, ontology supports automated retrieval and analysis of metadata [29]. By leveraging the relationships and rules defined within an ontology, users can infer new information that is not explicitly stored. For example, if equipment involved in a specific process is operating under an overload condition, an ontology-based reasoning engine is capable of analyzing the situation and generating a warning indicating the need for maintenance. Such automated capabilities significantly contribute to decision-making processes beyond traditional metadata management.

Ontology is also advantageous in regard to handling data uncertainty and ambiguity [30]. While traditional metadata management methods focus on structured data, ontology integrates flexible approaches like fuzzy logic to manage uncertain data effectively. For instance, in continuous process industries, variables such as “optimal temperature” may be defined as a range rather than a fixed value. Ontology represents this using fuzzy relationships, offering a more realistic and comprehensive data model.

The proposed FFOM framework further enhances these roles of ontology [31]. By employing a hierarchical fractal structure, FFOM improves the organization and management efficiency of large-scale data. Simultaneously, it integrates fuzzy logic to address uncertainties in metadata, enabling effective data integration and real-time decision making in continuous process industries. This approach not only redefines the possibilities of metadata management, but also significantly enhances data usability and reliability.

2.3. Fractal Concepts for Data Modeling and Management

Fractal concepts describe complex geometric shapes that exhibit self-similarity at various observation scales [32]. Unlike traditional Euclidean geometry, fractals often have non-integer dimensions, reflecting their complex and infinitely recursive nature. Common examples from nature, such as coastlines, snowflakes, and tree branches, intuitively demonstrate this repetitive pattern phenomenon. This property provides powerful metaphors and mechanisms for solving data modeling and management challenges, especially in large hierarchical systems [33]. The principle of self-similarity implies that small parts of a structure are similar to the whole, which allows for the recursive representation of nested hierarchies and repeating patterns.

Fractal-based approaches inherently support scalability and adaptability. The need for a structural redesign is minimized, as the same generative patterns can be reapplied to integrate new layers or components. This contrasts with rigid tree-based models that require restructuring for each additional detail. Furthermore, the idea that complex systems can be generated from simple recursive rules enhances the understandability and maintainability of the data models. The core concepts of recursive extensibility, pattern reuse, and structural consistency strongly support their use in frameworks such as FFOM.

2.4. Fuzzy Logic in Ontology and Data Management

Existing ontologies and data systems operate on the basis of clear Boolean logic, which assumes binary truths and precise data values. However, real-world data, especially in industrial settings, are often inaccurate, uncertain, or incomplete. Fuzzy logic provides a framework for reasoning under these conditions by allowing for class-based membership within sets rather than absolute inclusion [21,34]. In regard to ontology design, fuzzy logic introduces key features, such as linguistic variables and membership functions, which allow natural language expressions, such as ‘hot’ or ‘low efficiency,’ to be quantified [35]. Fuzzy logic also supports fuzzy IF–THEN rules and fuzzy inference systems, which enable the encoding of expert knowledge with soft boundaries and gradual transitions [36]. Fuzzy ontology is a research field that combines classical ontology and fuzzy logic. Fuzzy ontology often involves extending OWL to accommodate fuzzy relationships, data types, or integrating it with fuzzy reasoners [35,37]. This integration helps overcome the limitations of binary representations by enabling sophisticated modeling, the integration of data from uncertain sources, and reasoning when faced with ambiguity. These capabilities are key to FFOM’s goal of representing dynamic and uncertain industrial environments.

To conceptualize visually how fuzziness is generally incorporated into ontology models, Figure 1 presents an example of a fuzzy ontology structure used in the context of a recommender system [38]. The figure shows how the concept ‘BOOK’ is related to various types and specific options. For example, ‘BOOK’ is related to several types, such as type1 or type2, and each relationship is represented by a numerical value, such as 0.2 or 0.3. These values represent the strength of the association or the degree of uncertainty. In addition, individual books, Book1 and Book2, are represented with numerical values that reflect the uncertainty of the user ratings. This fuzzy ontology structure shows that relationships between concepts and entities in an ontology can be represented more flexibly through continuous values, such as the strength of membership or preference in a class, rather than simply true or false. This approach contributes to effectively introducing a certain level of fuzziness. However, the FFOM framework takes this approach a step further by structurally integrating fuzzy semantics, using triangular fuzzy numbers (TFNs). While existing fuzzy ontology models usually express the uncertainty of a relationship through a single scalar value, FFOM stores the entire TFN, consisting of a lower bound, a center, and an upper bound, in the ontology. Looking at the current research trends, it seems rare to find a case where the TFN itself is directly integrated into the ontology’s relationship definition in this way, which is one of the distinctive features of FFOM. Through this, FFOM can express not only the degree of uncertainty, but also its distribution range and central tendency, enabling more sophisticated inferences, and also supporting complex fuzzy operations, such as fuzzy multiplication. In addition, by utilizing a timestamp, it can effectively track changes in relationships among fractals over time. These functions are powerful means of dealing with uncertainty more richly and quantitatively in environments where data ambiguity and complexity coexist, such as in the manufacturing industry.

3. The FFOM Methodology

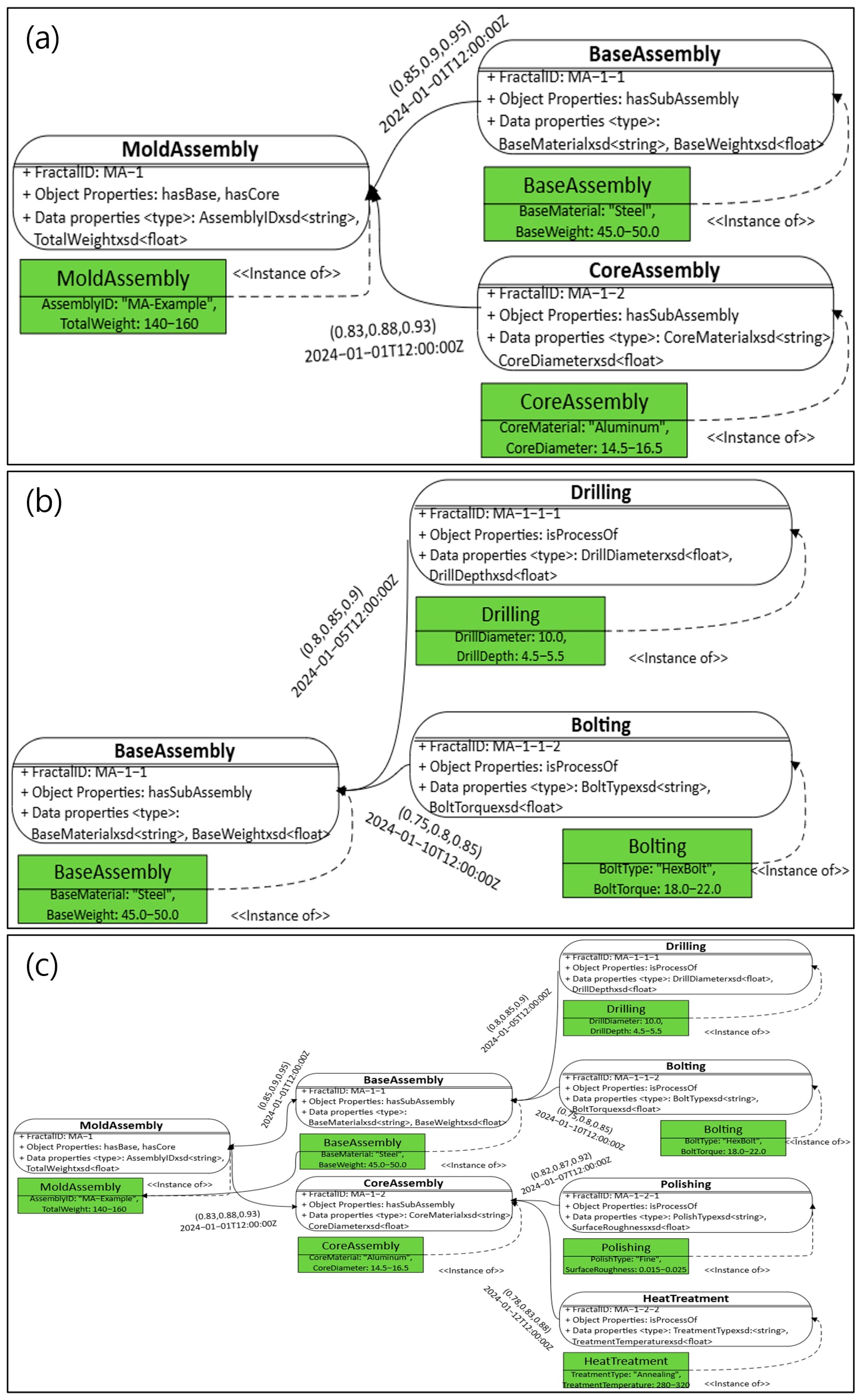
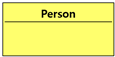
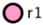3.1. Necessity of FFOM

FFOM is explicitly designed to enable agile and dynamic ontology evolution. By leveraging self-similar fractal patterns, it supports modular updates, without reengineering the overall structure. Fuzzy logic ensures that shifting process conditions and ambiguous real-world signals can be continuously reflected in the ontology. Thus, FFOM operationalizes adaptability in regard to both the structure and semantics.

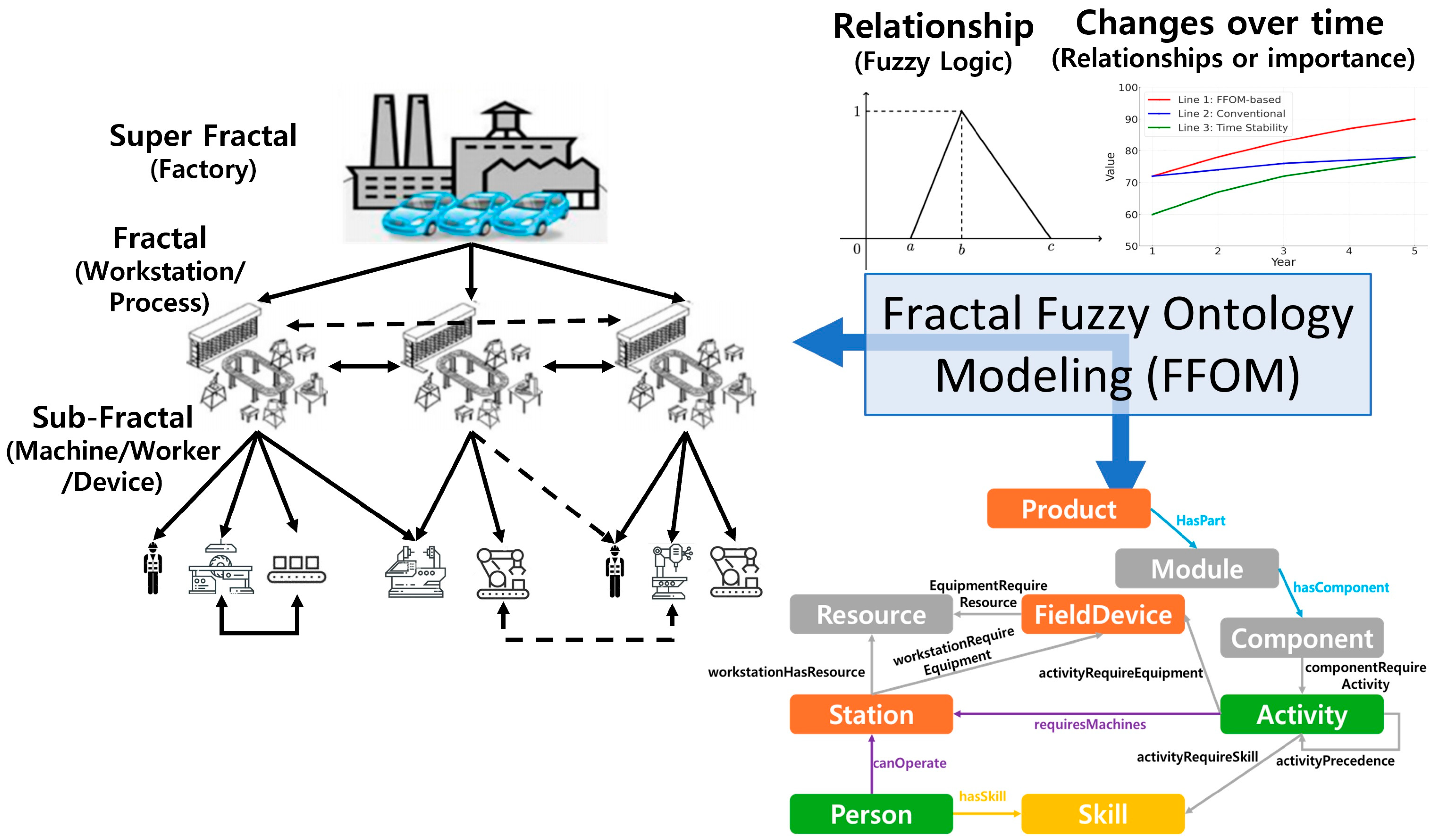
The fundamental concept of FFOM is inherently agile hierarchical data modeling, implemented through the application of fractal structures. Fractal structures, characterized by self-similarity, facilitate the construction of repetitive patterns commonly encountered in manufacturing environments, such as assembly and processing. They are not simply static representations. The fractal approach provides structural agility. New process steps, such as quality control, robotic handling, or entire sub-layers, can be seamlessly integrated as new instances of the defined fractal patterns, with minimal modifications to the overall ontology. This is in sharp contrast to traditional models that require significant restructuring, which is prone to errors due to this additional work. The fractal nature of FFOM, therefore, directly supports dynamic scalability and adaptability, allowing the ontology to evolve naturally with the manufacturing system it represents, ensuring its continued relevance and accuracy.

FFOM complements structural agility by incorporating fuzzy logic to provide semantic agility in regard to managing data uncertainty and ambiguity. In dynamic manufacturing environments, many critical variables, such as machine efficiency, material properties, and process tolerances, are inherently imprecise or change over time. Traditional binary logic struggles with this reality. FFOM leverages fuzzy membership functions and timestamped fuzzy values to model these variables and their relationships as ranges or distributions that can be updated in real time. That is, ontology can dynamically reflect the current state of uncertain parameters without changing the underlying classes or properties, enabling more realistic and context-sensitive reasoning and agile decision making, based on up-to-date but imprecise information. This semantic flexibility ensures that ontology continuously responds to real-world dynamics.

The necessity of FFOM arises from the increasing complexity and dynamic nature of modern manufacturing operations, where real-time data analysis and decision support are critical. Traditional static and rigid ontology models fail to meet these demands, due to limitations in terms of scalability and their inability to accommodate uncertainty. FFOM addresses these challenges by introducing a scalable and adaptable data management paradigm that aligns with the intricacy and variability of manufacturing processes. Figure 2 provides an expanded conceptual overview of FFOM, demonstrating how fractal structures achieve hierarchical scalability and how fuzzy logic handles uncertainties across various industrial scenarios. The diagram also emphasizes the role of OWL-based ontology for standardizing data representation and ensuring interoperability among diverse systems, enabling legacy platforms and new modules to communicate seamlessly. As a result, FFOM’s adaptive framework is unparalleled in its ability to support large-scale, dynamic processes, continuously evolving with data-driven insights. This paves the way for more intelligent and efficient industrial operations.

FFOM enhances automated reasoning and decision support by integrating fuzzy inference mechanisms, which provide intelligent recommendations based on uncertain data. It also incorporates temporal representation and historical data integration, enabling adaptive learning and trend analysis by tracking data changes over time. FFOM supports efficient querying and data retrieval through semantic reasoning, ensuring that industrial applications can extract meaningful insights for optimized decision making. FFOM is expected to be able to integrate these capabilities into a powerful and flexible ontology framework that can solve complex challenges in modern industrial environments.

This section details the FFOM methodology. It begins by providing a formal definition and outlining the foundational concepts of the framework. It then explains the principles of fractal-based structural design and concludes with details on the systematic process for transforming the conceptual FFOM model into a standard OWL implementation for practical use.

3.2. Foundational Concepts and Formal Definition

To address the increasing need for an adaptive and semantically enriched ontology framework capable of handling the complexities of dynamic industrial environments, FFOM is formally defined as a graphical and conceptual ontology modeling methodology. It is designed to represent rich and complex knowledge involving hierarchical structures, uncertain data, and evolving relationships by distinctively integrating key principles from fractal geometry, as explained in Section 2.3, and fuzzy set theory, as described in Section 2.4. FFOM provides a structured yet flexible approach for designing, managing, and evolving ontologies, specifically tailored for complex and dynamically changing domains.

The primary characteristic of FFOM is its synergistic combination of a fractal structural layer with a fuzzy semantic layer, supported by a graphical notation and an OWL transformation pathway. The fractal structural layer employs fractal pattern templates and principles of recursive instantiation to construct ontology structures that are inherently scalable, modular, and adaptable to change, with minimal redesign effort. This facilitates the systematic organization of complex, hierarchical information, often found in the manufacturing industry. Complementing this, the fuzzy semantic layer incorporates fuzzy logic to systematically manage vagueness, ambiguity, and imprecision. This is achieved through the explicit representation of fuzzy data, primarily using TFNs for attributes and relational strengths, alongside mechanisms for their defuzzification into crisp values, where needed, for practical application. FFOM also conceptually supports the use of linguistic variables for richer semantic expression and allows for the application of fuzzy operators and IF–THEN rules to enable nuanced reasoning under uncertainty, typically operationalized via external reasoning engines that constitute the FFOM–OWL model. The FFOM framework utilizes a set of graphical primitives, described in

Table 3. Definition of graphical primitives used in the FFOM ontology.

Primitive		Application
Fractal Representation		Depicted as a rounded rectangle. The top area contains the fractal name, while the bottom area lists its data properties (e.g., name, weight, etc.) Labels and cardinalities (e.g., “1…N”) are shown inside the rectangle or as separate notations next to it Denote quantitative or descriptive attributes within fractals or instances (e.g., temperature, capacity, etc.) Shown in the lower portion of the fractal or instance box and labeled with the data type (e.g., xsd:string)
Instance Representation		Each named individual is linked to its fractal with a dashed arrow labeled “Instance of”, typically shown below the relevant fractal The instance box may display both the instance Name (top) and its data properties (bottom)
Hierarchy and Inheritance		Fractal → subfractal relationships are indicated with a clear arrow labeled “SubFractalOf” or “Inheritance” Fractals appear above (or to the left) with subfractals below (or to the right) for clarity
Object Properties		Represented by solid arrows between fractals or instances (e.g., “hasPart,” “connectedTo”) Additional annotations (fuzzy_value, timestamp) can be included to handle dynamic or uncertain relationships
Joint/Disjoint		Indicates whether two fractals (or entities) can share overlapping instances (Joint) or must remain mutually exclusive (Disjoint) Represented by a solid line connecting the fractals, labeled either “Joint” or “Disjoint”
Label and Cardinalities		Labels such as ‘FractalID’, ‘Object Properties’, and ‘Data Properties’ are used within the fractal, and relationships are defined with cardinalities to represent structural characteristics

, for its visual construction, which are extended to accommodate fuzzy and temporal annotations. Finally, a defined OWL transformation pathway, detailed in Section 3.4, ensures that FFOM conceptual models can be formally represented in a standard, machine-interpretable, and interoperable format, leveraging existing semantic web tools and infrastructure. FFOM is thus proposed as an integrated and formalized approach to ontology engineering, offering enhanced capabilities for domains requiring both structural adaptability and robust uncertainty tolerance.

Complementing this fractal structural layer, the fuzzy semantic layer in FFOM introduces fuzzy logic to represent and reason about inherent vagueness, ambiguity, and uncertainty. For fuzzy value representation and defining the data type structure, FFOM primarily employs TFNs for representing a relational strength between fractals. A TFN is formally represented as an ordered triple (a, b, c), where a, b, c are real numbers in the interval [0, 1] satisfying a ≤ b ≤ c, denoting the lower bound, modal value, and upper bound, respectively. The encoding of these TFNs into the conceptual model is typically guided by domain expert knowledge or derived from empirical data. The decoding or defuzzification of the TFN into a single crisp value, which is essential for practical applications, such as deriving an assembly confidence score, is carried out using a centroid-based method that places greater weight on the modal value. For example, the result of a centroid calculation, i.e., (a + 2b + c)/4, can serve as its representative crisp output. This formulation reflects the central tendency more effectively by emphasizing the modal value, resulting in a more representative and context-sensitive crisp output. FFOM also conceptually supports linguistic fuzzy modifiers, such as ‘very’ or ‘slightly’, whose application typically involves transforming the membership function of the base fuzzy set they modify, for instance, by concentrating the membership degrees for ‘very’. Furthermore, to determine the strength of derived or composed relationships where intermediate links are expressed as TFNs, FFOM accommodates the use of fuzzy operators. A common method for such relational composition is fuzzy multiplication, often applying the product t-norm component wise to the TFNs. For example, if TFN_A→B = (a₁, b₁, c₁), which means that the TFN values from fractal A to B are a₁, b₁, and c₁, and TFN_B→C = (a₂, b₂, c₂), then the composed TFN_A→C can be approximated as (a₁·a₂, b₁·b₂, c₁·c₂). The execution of complex fuzzy IF–THEN rules, the operationalization of fuzzy modifiers, and the computation using fuzzy operators are generally managed by external fuzzy reasoning engines or specialized application logic, for which FFOM’s OWL representation provides the structured fuzzy data input. To ensure compatibility with existing semantic web technologies, FFOM also defines an OWL transformation pathway. This consists of a clear methodology and dedicated mapping strategies to translate both its fractal structural and fuzzy semantic layers into OWL 2, the Web Ontology Language standard. Through this transformation, detailed in Section 3.4, the full semantic richness and flexibility of FFOM can be formally represented in a machine-interpretable and interoperable format. Overall, FFOM is proposed as a structured and extensible modeling framework that supports the scalable evolution of ontology structures through fractal principles, and effectively manages semantic imprecision through these defined fuzzy logic mechanisms, offering a practical and formalized approach to ontology engineering for domains demanding both adaptability and uncertainty tolerance.

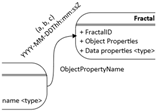
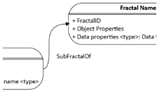
FFOM’s approach is supported by a graphical notation, designed to intuitively represent its core structural and semantic features. Table 3 summarizes these visual elements. A fundamental terminological clarification throughout FFOM’s conceptual model, and reflected in Table 3, is the use of the term “Fractal” to denote the primary structural components. Consequently, identifiers are referred to as “FractalID,” and hierarchical relationships between these components are termed “SubFractalOf.” This conceptual “Fractal” is then mapped to an owl:Class during the OWL transformation process. The primitives presented in Table 3, such as ‘Fractal Representation’ and ‘Instance Representation’, while building on standard ontological symbols, are employed by FFOM to explicitly visualize its novel fuzzy and fractal characteristics. A key aspect of FFOM’s notation, detailed in Table 3 under ‘Object Properties’, is the representation of fuzzy relational characteristics. Relationships between instances of fractals can be augmented with annotations to handle dynamic or uncertain aspects. Specifically, the strength of a relationship among fractals is represented as a TFN. For practical OWL implementation or certain reasoning tasks, these TFNs are typically defuzzified to scalar values. Furthermore, timestamps are associated with these fuzzy relationships to capture their temporal validity. As defined in Table 3, timestamps are represented in a date and time format YYYY-MM-DDThh:mm:ssZ (e.g., “2024-01-01T12:00:00Z”), where YYYY is the four-digit year, MM is the month, DD is the day, ‘T’ is the delimiter, hh is the hour (00–23), mm is the minute, and ss is the second, and Z indicates Universal Time Coordinated (UTC).

The fractal structure inherent in FFOM is visually conveyed not through a single, new “fractal” primitive, as presented in Table 3, but through the patterned application and recursive composition of the defined ‘Fractal’ primitives and their associated properties. FFOM diagrams emphasize the repetition of a defined ‘Fractal Pattern Template’, which is a specific arrangement of these base primitives across different scales or modules of the ontology. The elements defined in Table 3 thus serve as the foundational building blocks that are composed into these larger, self-similar fractal constructs. This approach ensures that the graphical representation focuses on FFOM’s novel contributions: the explicit visualization of fuzzy and temporal characteristics and the scalable, modular architectures that arise from applying fractal design principles.

3.3. Fractal-Based Structural Design

Figure 3 compares a traditional hierarchical approach, i.e., Figure 3a and FFOM’s fractal-based model, i.e., Figure 3b. In traditional models, each node such as “Line 1” or “Line 2” manages its own set of processes (e.g., Proc 1, Proc 2, Proc 3, Proc 4), independently. While this standard tree-like structure is straightforward to visualize, it becomes increasingly cumbersome to expand or modify, because each new process or layer often requires substantial restructuring. Over time, inconsistencies can arise between different lines or process branches, making it difficult to enforce uniform data rules or incorporate global updates, such as new quality metrics, across every part of the hierarchy. In contrast, FFOM’s fractal concept, detailed in Figure 3b, provides a single “Pattern Template” that can be repeated at different levels of the system. The idea is that every new line, process, or sub-process inherits the same underlying schema, thereby preserving consistency. If a new attribute (e.g., “EnergyConsumption”) or a fuzzy rule (e.g., “If temperature is High and pressure is Low, then reduce speed”) needs to be introduced, it can simply be added to the template. All existing and future lines or processes that use this pattern will automatically adopt the update, greatly simplifying maintenance and scalability.

In practice, this fractal architecture aligns well with fuzzy logic to handle uncertain or variable information. The fractal pattern template includes placeholders, such as “fuzzy_value”, or “timestamp”, to record and update these continuous or imprecise values. As each repeated pattern is instantiated for a specific sub-process, the fuzzy parameters can be adjusted to local conditions, without losing the overall structural uniformity. This blend of the fractal concept and fuzzy logic is especially valuable in dynamic manufacturing settings, where equipment states and process parameters are subject to frequent fluctuations. Overall, the FFOM approach offers a more adaptable and consistent framework compared to rigid hierarchical models. By defining a self-similar pattern, it becomes far easier to expand the data structure, integrate new processes, and manage ongoing changes, while accommodating uncertainty through fuzzy logic. This flexibility ensures that large-scale industrial environments can remain coherent and up to date with minimal reworking, supporting real-time decision making and streamlined metadata management.

3.4. OWL Transformation and Implementation

The programmatic generation of FFOM’s characteristic fractal structure, which emphasizes scalability and modularity through self-similarity, can be conceptualized as an iterative process. Figure 4 presents a high-level pseudocode, GenerateFFOM (rootFractalPattern, maxDepth), to outline this approach, focusing on the core iterative logic, while abstracting the implementation details.

The process commences by initializing an empty ontology. Crucially, a rootFractalPattern is used to establish the initial elements of the ontology via the CreateRootFromPattern function. The rootFractalPattern defines the fundamental, self-similar structural template comprising a specific arrangement of classes, properties, and their interrelations that serves as the basic building block for the fractal expansion. The initialization step returns a set of activeNodes, conceptualized as the initial points or interfaces within the instantiated root pattern from which further fractal growth will originate.

The core of the fractal generation unfolds in an iterative loop that proceeds for a specified maxDepth. In regard to each iteration, the ExpandFractalAtNodes function is invoked. This key abstracted function is responsible for taking the current set of activeNodes and the rootFractalPattern or potentially derived sub-patterns or variations suitable for the current depth or node type. For each node in activeNodes, it instantiates a new instance of the fractal pattern and connects this new instance appropriately to the expansionNode from which it originated, thereby maintaining the structural integrity and the desired relational semantics of the fractal design. This function then returns a new set of activeNodes derived from these newly created pattern instances, which will serve as the basis for the subsequent level of fractal expansion. The loop continues until the maximum depth is reached or if no further activeNodes are available for expansion.

Finally, once the complete fractal structure is generated through this iterative patterned expansion, a distinct step, ApplyFuzzySemantics, is performed. This conceptual function encapsulates the process of assigning relevant fuzzy parameters, such as fuzzy values for relationships or attributes and associated timestamps, throughout the now established ontological structure. The concise pseudocode presented in Figure 4, supported by this detailed explanation, aims to illustrate how FFOM systematically constructs complex and scalable ontologies through the controlled, iterative replication and interconnection of a foundational self-similar pattern, which is the essence of its fractal design philosophy, distinguishing it from simple hierarchical construction.

The transformation of FFOM into OWL translates its core structural and semantic characteristics into a standardized and machine-readable format. The hierarchical modularity that defines the fractal structural layer of FFOM is directly represented through OWL class hierarchies. For instance, a design pattern, such as a StandardMachineUnit, along with its specific subcomponents, is consistently instantiated across different use cases using clearly defined owl:Class declarations and corresponding owl:ObjectProperty or owl:DatatypeProperty assertions. To retain the conceptual identity and structural origin of each fractal pattern in FFOM, a unique identifier, known as a FractalID, can be embedded as an annotation or as a data type property assigned to the corresponding OWL class or related individuals. Fuzzy data parameters are also explicitly represented. For example, a fuzzy relationship strength modeled in FFOM as a TFN with values 0.7, 0.8, and 0.9 is captured in OWL through separate and queryable data type properties. These include a fuzzyLowerBound set to 0.7, a fuzzyModalValue set to 0.8, and a fuzzyUpperBound set to 0.9, each associated with the relevant individuals or reified relationship instances. In addition, defuzzified values and timestamps may be included to support further semantic processing. This comprehensive mapping ensures that critical structural information, conceptual fractal identities, and queryable uncertainty parameters are semantically integrated, providing a robust foundation, superior to superficial attribute additions.

However, certain conceptual or procedural elements inherent to FFOM represent translation nuances due to OWL’s declarative nature. The dynamic generation logic from fractal templates illustrates this; an FFOM directive to ‘generate a new production line instance using FractalTemplateAlpha’ is a procedural step whose resulting OWL structure is compliant, but the generative command itself is external. Similarly, the full operationalization of complex fuzzy inference rules, particularly those involving linguistic hedges like ‘very’ or specific aggregation methods for combining fuzzy inputs, requires capabilities beyond standard OWL reasoning. These aspects are practically managed through well-defined FFOM conventions, the use of external tools and APIs to execute procedural tasks, such as fractal instantiation or advanced fuzzy reasoning, and OWL annotations for FFOM-specific conceptual metadata like ‘isFractalPattern’. Despite these managed distinctions, the resulting FFOM-based OWL model offers a substantial analytical upgrade, facilitating the sophisticated querying of recursive structures and timestamped uncertain data, thereby significantly advancing its capabilities beyond traditional ontologies.

A critical aspect of ensuring the practical applicability and widespread adoption of the FFOM framework is its ability to interoperate with existing semantic web technologies and ontology-based systems. For this reason, a well-defined transformation into the OWL is essential, as OWL is the de facto standard for ontology representation, enabling data integration, knowledge sharing, and reuse across diverse platforms. The following discussion outlines the key concepts and procedures for translating FFOM into OWL, thereby safeguarding its core principles, while maximizing its interoperability and compatibility with established ontology tools and methodologies.

Moving FFOM to OWL involves specific translation strategies that achieve more than superficial attribute additions. These strategies ensure that the core fractal and fuzzy characteristics of FFOM are semantically preserved and fully machine-interpretable within standard ontology infrastructure. The concept of fractal layering is implemented by translating each recurring or self-similar structural element of FFOM into corresponding OWL classes and subclasses. Recursive relationships are expressed using OWL constructs, such as owl:equivalentClass or owl:Restriction, where recursion is modeled through class expressions like BaseModule and hasRecursivePart only RecursiveModule. This explicit encoding of recursive logic enables semantic reasoners to interpret and traverse hierarchical, self-similar patterns, providing a substantial improvement over approaches that merely tag elements with a ‘fractal’ attribute. In parallel, fuzzy parameters, including the TFNs introduced in Section 3.2, are represented in OWL through structured data properties. A TFN, such as (0.75, 0.85, 0.95), is stored as three distinct values, indicating the lower bound, modal value, and upper bound. These values are associated with specific individuals or relationship assertions, often by reifying the relationship into a separate OWL individual that contains these properties. In addition, a defuzzified crisp value, such as 0.85, derived from the centroid, and a timestamp, like 2024-01-01T12:00:00Z, are stored as supplementary data properties. This layered representation maintains the full fuzzy semantics for in-depth reasoning, while enabling efficient query access and summary-level inferences.

These fuzzy values and temporal annotations are modeled as instance-level data properties and can be updated dynamically, without requiring changes to the underlying ontology schema. This supports real-time adaptability in domains where uncertainty and context evolve continuously. Moreover, because the fuzzy parameters are explicitly modeled using semantically defined properties, they remain directly queryable via SPARQL, and interpretable by external fuzzy reasoners or custom logic engines. More complex inference tasks, such as applying fuzzy modifiers like ‘very’ or ‘slightly’, executing IF–THEN rules, or composing fuzzy relationships through t-norms, are typically carried out by external tools that consume the FFOM–OWL model. These components interpret the embedded TFN data to support nuanced, uncertainty-aware reasoning. In this way, FFOM bridges the gap between semantic ontology modeling and intelligent, real-time decision making that involves uncertainty. By relying on standard OWL 2 structures enhanced with well-defined data patterns, rather than opaque or ad hoc annotations, FFOM preserves its compatibility with existing semantic web technologies and tooling. This structured yet extensible approach enables robust and interoperable representation of both fractal and fuzzy semantics within a unified ontology framework.

Figure 5 provides an OWL snippet that demonstrates how FFOM principles, particularly the structured and recursive representation of fuzzy temporal relational data, are translated into a standard ontology format. The base class hierarchy includes core concepts such as MoldAssembly and its subclass BasePlate. To capture fuzzy relationships between instances, such as the confidence level between MainMoldAssy001 and BasePlate_XYZ7, a reification pattern is used. A dedicated object individual of the relationship class, HasComponentLink (e.g., #Link_Mold001_Plate7), holds fuzzy and temporal data as OWL data properties. The property, assemblyConfidence, stores a defuzzified scalar value of 0.92, derived from a TFN (0.89, 0.92, 0.95), using the centroid method. Using the centroid formula, the defuzzified value is calculated as (0.89 + 1.84 + 0.95)/4 = 0.92, which matches the stored confidence value. A lastChecked timestamp, such as “2024-02-15T09:30:00Z”, is also stored.

FFOM preserves the full fuzzy semantics by separately storing the TFN’s lower, modal, and upper values through data properties like fuzzyLowerBound, fuzzyModalValue, and fuzzyUpperBound. These values are directly queryable via SPARQL, enabling semantic reasoners and external systems to consume both crisp and fuzzy data. This modeling approach separates schema-level constructs from instance-level dynamics, supports real-time updates without requiring structural modifications, and remains interoperable with standard OWL tools. Moreover, the use of self-similar link structures aligns with FFOM’s fractal-inspired design, supporting recursive, scalable ontology development.

FFOM incorporates self-similarity and fuzzy logic into ontology design, enabling the representation of complex relationships and dynamic changes over time. Transforming FFOM into OWL ensures that its hierarchical structures and temporal dynamics are maintained. In this section, a unified process is introduced for converting FFOM into OWL, emphasizing how fractal principles simplify modeling and fuzzy relationships capture uncertainty and temporal evolutions. 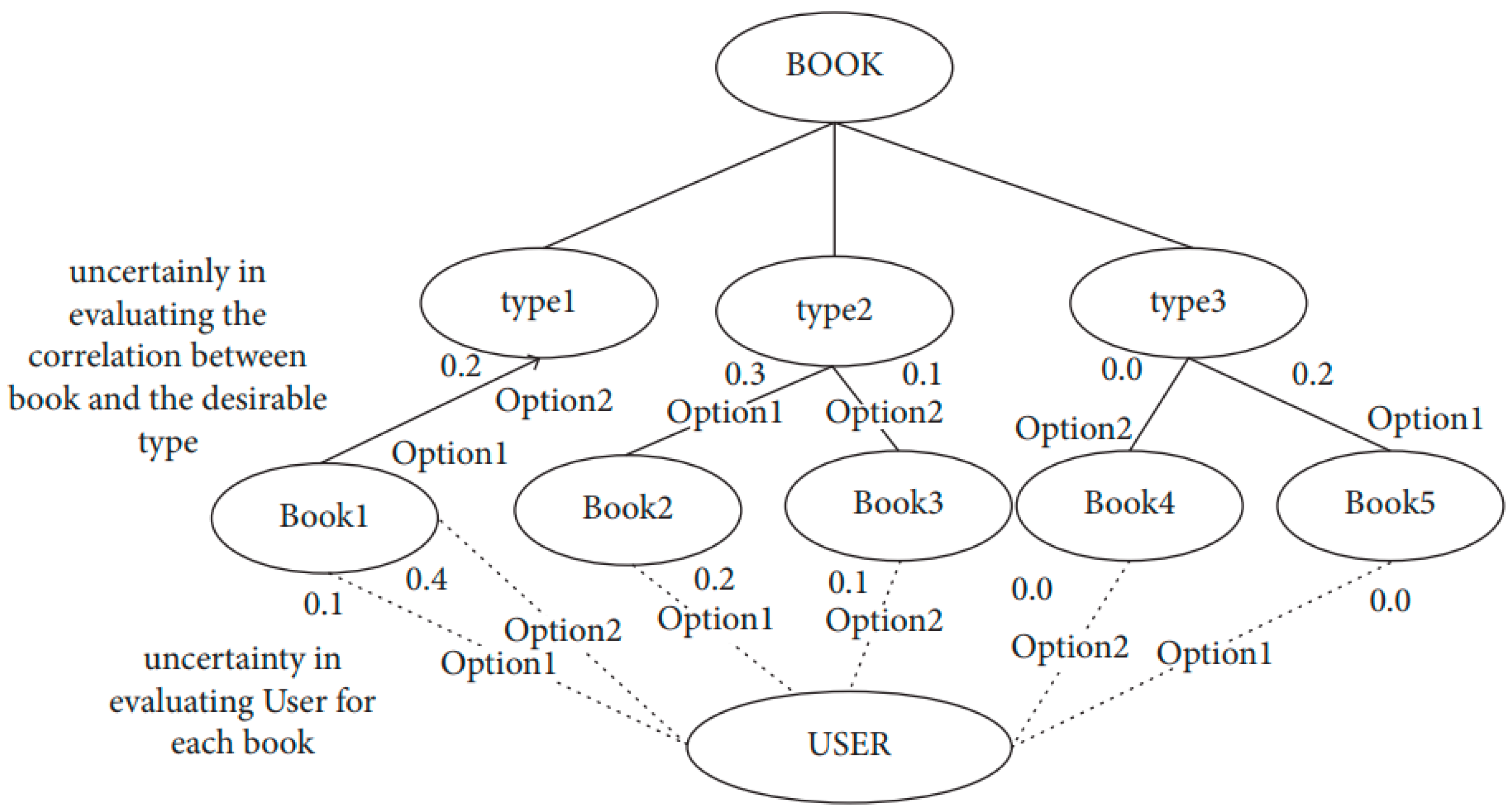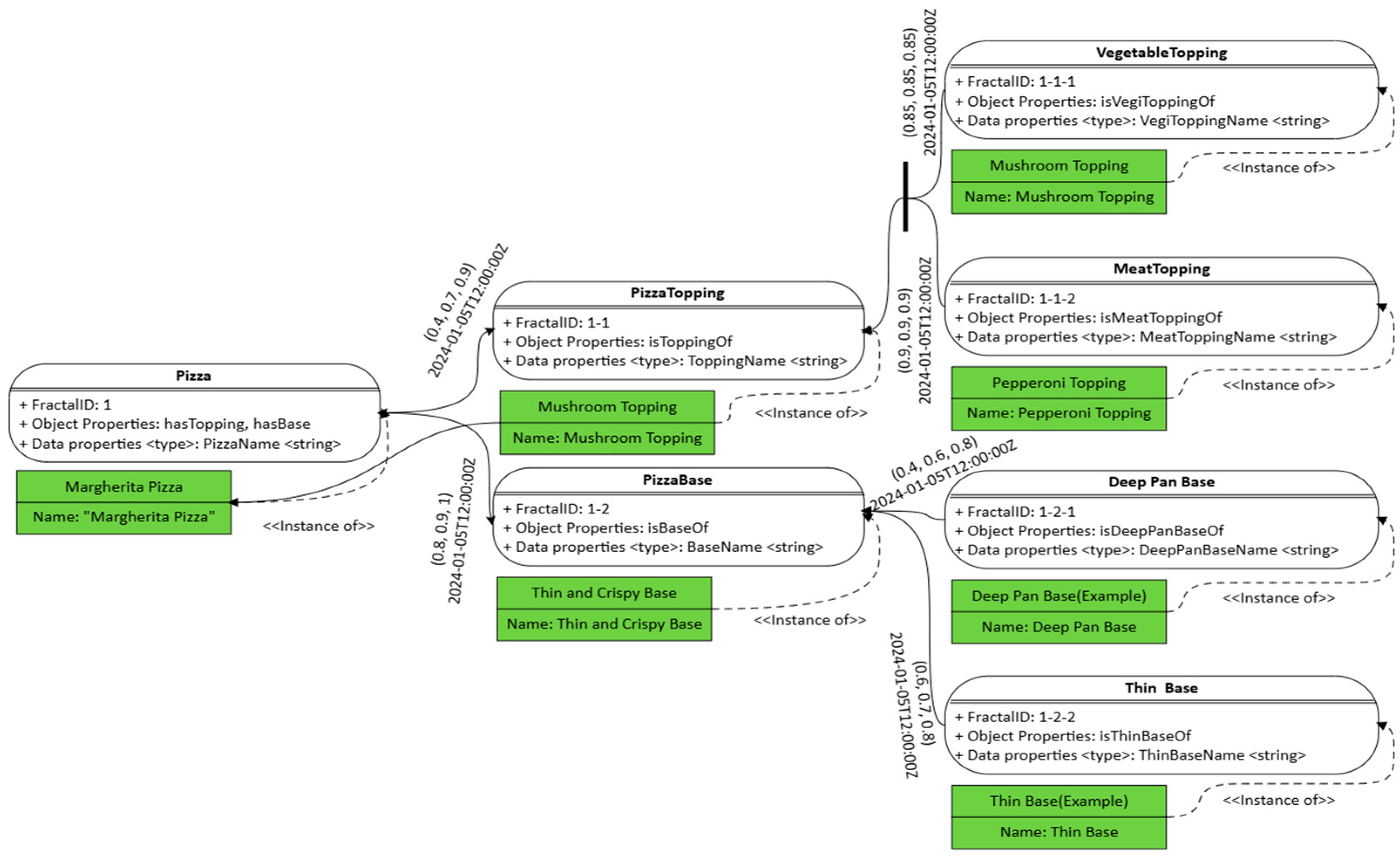Figure 6 presents an example of an ontology visualization for a pizza. The example illustrates how FFOM can hierarchically visualize complex data structures, while clearly defining object and data properties. Let us transform an FFOM model into OWL.

The transformation of FFOM into OWL begins with defining the classes and their hierarchical structure using <rdfs:subClassOf>. For instance, a parent fractal ‘Pizza’ may have fractals, such as ‘PizzaTopping’ and ‘PizzaBase,’ preserving the modular and scalable nature of FFOM’s fractal design. Relationships between individuals are modeled using a reification-like pattern, where an intermediate link individual (e.g., #Link_Margherita_Mushroom) represents a connection between instances and stores fuzzy and temporal data as properties such as fuzzy:strength and fuzzy:timestamp. This structure clearly separates schema definitions from instance-level uncertainty and dynamics.

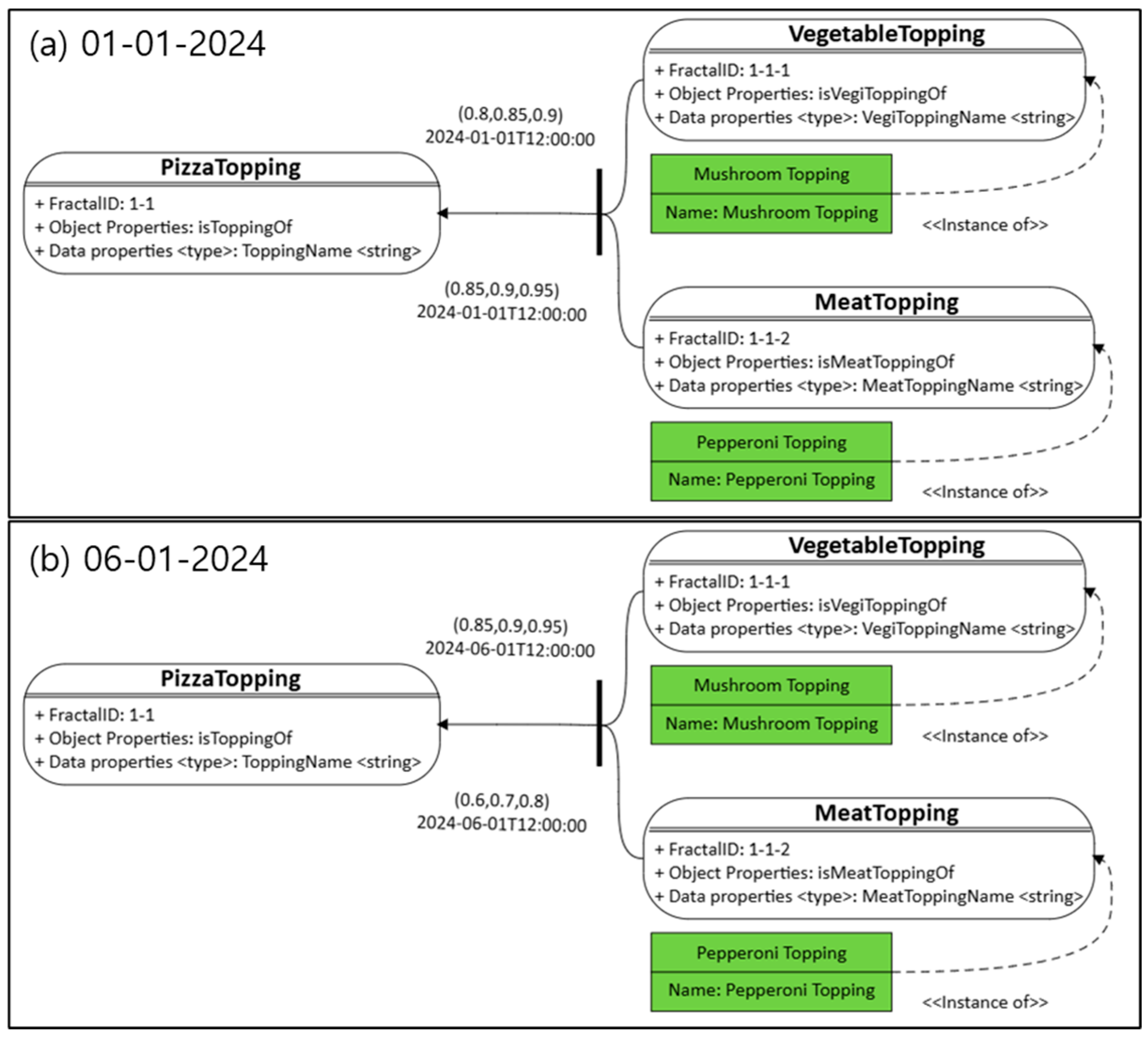
Fuzzy values in FFOM are typically expressed as TFNs and are stored as data properties, representing the lower, modal, and upper bounds. Defuzzified crisp values, such as centroids, are also included to support reasoning and real-time monitoring. As illustrated in Figure 7, these fuzzy values can evolve over time and are updated solely by modifying the associated data properties, without requiring any changes to the underlying class hierarchy. This approach is particularly important because, in real-world industrial environments, the relationships between concepts are not static, but naturally change over time. Traditional ontology models lack efficient mechanisms to capture and manage this temporal evolution. In contrast, FFOM enables the flexible representation of such dynamic relationships by allowing fuzzy relationship strengths and their corresponding timestamps to be updated independently. This eliminates the need to reconstruct the ontology structure, ensuring that evolving semantic contexts can be managed seamlessly within the existing model.

FFOM also supports fuzzy reasoning over composed relationships. As conceptually illustrated in Section 3.2, suppose the direct relationship from the fractal ‘MeatTopping’ to the fractal ‘PizzaTopping’ is defined by TFN_{MeatTopping→PizzaTopping} = (0.85, 0.90, 0.95), and the relationship of ‘PizzaTopping’ to the super fractal ‘Pizza’ is TFN_{PizzaTopping→Pizza} = (0.4, 0.7, 0.9). Using fuzzy multiplication (a product t-norm applied component wise), the composed relationship TFN_{MeatTopping→Pizza} is approximated as (0.85 × 0.4, 0.90 × 0.7, 0.95 × 0.9) = (0.34, 0.63, 0.855). This allows FFOM to propagate fuzzy relational information across chains of entities and infer indirect strengths, which is essential for reasoning in real-world, uncertain environments.

Crucially, FFOM’s fractal nature ensures that once a structural pattern is defined, each subcomponent recursively follows the same model. While each subfractal could be decomposed into its own model, their structure would mirror the top-level pattern. This supports consistent semantic modeling at multiple levels of abstraction. All fuzzy operations are typically handled by external reasoning engines or APIs consuming the TFN-enriched OWL model. Since all the values are stored at the data assertion level, the ontology remains fully SPARQL queryable and schema stable, aligning with FFOM’s goal of achieving dynamic adaptability within a formally structured framework.

FFOM’s approach allows for the representation of dynamic and uncertain information, including how fuzzy values associated with relationships might evolve. While fully modeling temporal fuzzy transition functions within OWL is complex, the foundational representation of timestamped fuzzy values for specific relationship instances is a key aspect. Figure 8 provides a concise OWL snippet from the ‘PizzaOntology’ example, illustrating how a specific, timestamped fuzzy preference strength between a pizza and a topping is correctly represented. A particular preference link, such as #Link_Margherita_Mushroom (an instance of #PizzaToppingLink), connects the specific pizza (#MargheritaSpecial) to the specific topping (#MushroomDelightTopping). This link individual then directly holds the preferenceStrength (e.g., “0.85”) and the preferenceDate (e.g., “2024-04-21T12:00:00Z”) as OWL Datatype Properties. This structure accurately captures a snapshot of a fuzzy, temporal relationship at the instance level. While this Figure 8 presents a static assignment, this OWL representation forms the basis upon which dynamic updates could be managed; new instances of such link individuals could be created over time with updated fuzzy values and timestamps, or external mechanisms could update these values, reflecting the evolving nature of, for instance, user preferences. This OWL structure thus provides a clear, standards-compliant way to represent the data needed for FFOM’s broader goal of supporting real-time updates and flexible ontology relationships.

The ontology is further populated with specific entities, known as named individuals, that instantiate the classes and link them to relevant object and data properties. To account for time-sensitive relationships, object properties are periodically updated with new fuzzy values and timestamps, enabling the ontology to adapt to dynamic conditions. Finally, the transformed OWL model is validated to ensure logical consistency, semantic accuracy, and structural integrity. This validation process involves using tools like Protégé to verify the ontology structure and SPARQL queries to test the data retrieval and reasoning capabilities. Through these comprehensive steps, FFOM is successfully transformed into an OWL model that preserves its hierarchical organization, fuzzy logic, and temporal dynamics, while ensuring its scalability and adaptability in complex data environments.

Table 4. FFOM to OWL transformation rule table.

Step	Description	OWL Element	Example Code
Initialization	Initialize the OWL model and define metadata, including ontology name and namespace declarations for standardization	<owl:Ontology>	<owl:Ontology rdf:about=“PizzaOntology”/>
Class Definition	Convert FFOM entities into OWL classes and subclasses, using <rdfs:subClassOf> to represent hierarchical relationships	<owl:Class>, <rdfs:subClassOf>	<owl:Class rdf:about=“Pizza”/> <owl:Class rdf:about=“PizzaTopping”> <rdfs:subClassOf rdf:resource =“Pizza”/> </owl:Class>
Object Property Definition	Define relationships between classes as OWL object properties. Add annotations such as <fuzzy:value> and <fuzzy:timestamp> to capture fuzzy relationships and temporal dynamics	<owl:ObjectProperty>	<owl:ObjectProperty rdf:about=“hasTopping”> <rdfs:domain rdf:resource =“Pizza”/> <rdfs:range rdf:resource=“PizzaTopping”/> <fuzzy:value>0.85</fuzzy:value> <fuzzy:timestamp>2024-04-21T12:00:00Z</fuzzy:timestamp> </owl:ObjectProperty>
Data Property Definition	Define attributes of classes using OWL data properties, specifying the domain “class” and range “data type”	<owl:DatatypeProperty>	<owl:DatatypeProperty rdf:about=“PizzaName”> <rdfs:domain rdf:resource =“Pizza”/> <rdfs:range rdf:resource =“xsd:string”/> </owl:DatatypeProperty>
Instance Creation	Populate the ontology with specific entities as OWL named individuals, linking them to classes, object properties, and data properties	<owl:NamedIndividual>	<owl:NamedIndividual rdf:about=“Margherita-Pizza”> <rdf:type rdf:resource=“Pizza”/> <PizzaName>Margherita</PizzaName> <hasTopping rdf:resource =“MushroomTopping”/> </owl:NamedIndividual>
Adding Temporal Relationships	Represent time-sensitive changes in relationships by updating <fuzzy:value> and <fuzzy:timestamp> annotations in object properties	<fuzzy:value>, <fuzzy:timestamp>	<owl:ObjectProperty rdf:about=“hasTopping”> <fuzzy:value>0.80</fuzzy:value> <fuzzy:timestamp>2024-05-01T12:00:00Z</fuzzy:timestamp> </owl:ObjectProperty>
Model Validation	Ensure logical consistency and structural integrity of the transformed OWL model using tools like Protégé and SPARQL queries	-	Validation tools: verify structure in Protégé, test data retrieval with SPARQL

outlines the transformation rules for converting FFOM into OWL, specifying how ontology components are structured to maintain hierarchical integrity and incorporate fuzzy logic. This structured representation ensures seamless integration and reasoning capabilities within OWL-based systems.

4. Case Study: Mold Assembly

4.1. FFOM Visualization and Analysis

To demonstrate the practical application and structural advantages of FFOM, particularly its fractal characteristics, the MoldAssembly domain is visualized as a multi-part illustration in Figure 9. This approach explicitly showcases the principle of self-similarity inherent in FFOM’s design.

Figure 9a depicts the top-level MoldAssembly Fractal (FractalID: MA-1), along with its immediate subfractals, namely BaseAssembly (MA-1-1) and CoreAssembly (MA-1-2), representing the mold’s primary structural components. These relationships are modeled using object properties, such as hasSubFractal, and are annotated with a TFN (e.g., (0.85, 0.9, 0.95)) and a timestamp (e.g., 2024-01-01T12:00:00Z) to capture the semantic strength and temporal context. Each fractal includes data properties, for instance, AssemblyID and TotalWeight for MoldAssembly, defining its core attributes.

Figure 9b focuses on one of these subfractals, BaseAssembly (MA-1-1), treating it as an independent fractal. It contains its own subfractals: Drilling (MA-1-1-1) and Bolting (MA-1-1-2), each connected using the same structural pattern and annotated with their own fuzzy values (e.g., (0.80, 0.85, 0.90)) and timestamps (e.g., 2024-01-05T12:00:00Z). The architectural structure in Figure 9b is intentionally identical to that of Figure 9a, thus visually reinforcing FFOM’s core principle of fractal self-similarity. Every fractal, whether it is a top-level assembly or a nested process, is instantiated based on a unified ‘Fractal Pattern Template’ that governs its internal and external relationships.

Figure 9c presents the fully expanded fractal view, integrating all subfractals and their nested subfractals into a single unified model. This complete structure shows how recursively applying the same pattern results in a scalable and semantically coherent ontology hierarchy. For example, CoreAssembly is decomposed into Polishing and HeatTreatment, with their respective data properties (e.g., PolishType, TreatmentTemperature) and fuzzy–temporal annotations.

The self-similar structure of FFOM is not only conceptually elegant, but also practically advantageous. Because each level reuses the same modeling schema, ontology extension becomes modular, predictable, and easier to maintain. Furthermore, this recursive pattern allows for scalable reasoning and querying: systems can infer or retrieve all instances of a recurring process (e.g., Drilling) across multiple fractal layers, without the explicit traversal of every path.

This modeling framework also captures nuanced uncertainty using fuzzy sets. For example, HeatTreatment temperatures are represented as fuzzy ranges (e.g., fuzzyRange (280 °C, 290 °C, 310 °C, 320 °C)), rather than fixed intervals, enabling the system to better reflect real-world variability. Scalar fuzzy values, such as alignment confidence or bolt torque, can also be used where appropriate. All such data remain updateable at the assertion level, without modifying the schema-level definitions.

Altogether, the progressive decomposition shown in Figure 9 illustrates how FFOM integrates fractal hierarchy, fuzzy logic, and temporal semantics within a standard OWL framework. This design enables dynamic, scalable, and uncertainty-aware modeling, ultimately enhancing semantic reasoning, SPARQL-based querying, and real-time decision support in regard to complex manufacturing systems.

4.2. FFOM OWL Implementation Method

The transformation of the FFOM model for MoldAssembly into OWL involves a systematic procedure that captures the hierarchical structure, object properties, and the representation of fuzzy relationships and temporal dynamics, as defined in the FFOM model. The OWL framework enables a standardized, machine-readable representation of the ontology, ensuring scalability, interoperability, and adaptability. This section outlines this transformation process, explaining how the MoldAssembly FFOM model is converted into OWL, while maintaining its core structural features and correctly representing its dynamic aspects.

The transformation begins with defining the ontology’s metadata, including the ontology name and appropriate namespace declarations, which are used to uniquely identify entities and ensure compliance with semantic web standards. Following initialization, FFOM classes are defined as OWL classes using <owl:Class> tags, with hierarchical relationships expressed via <rdfs:subClassOf>. For instance, BaseAssembly would be a subclass of MoldAssembly, reflecting FFOM’s hierarchical patterns. The next step involves defining the schema for object properties that indicate the potential for relationships, and then modeling specific, fuzzy-valued relationship instances. For example, to represent a MoldAssembly (like #MainMoldAssy001) having a BasePlate (like #BasePlate_XYZ7) as a sub-component with an associated fuzzy confidence and timestamp, a reification-like pattern is used, as shown in the Figure 10. An intermediate “link” class (e.g., #HasComponentLink) is defined. An object property (e.g., #hasLinkToComponent) connects the #MainMoldAssy001 individual to an instance of #HasComponentLink (e.g., #Link_Mold001_Plate7). This link individual, #Link_Mold001_Plate7, then uses another object property (e.g., #linkedComponent) to point to #BasePlate_XYZ7 and, crucially, holds the specific fuzzy:assemblyConfidence (e.g., “0.92”) and fuzzy:lastChecked timestamp (e.g., “2024-02-15T09:30:00Z”) as its own direct OWL Datatype Properties. This correctly associates fuzzy and temporal data with the specific relationship instance.

The data properties are then defined to capture the direct attributes of the classes or individuals, such as the #BaseMaterial of a BasePlate, using <owl:DatatypeProperty> tags with specified domains and ranges (e.g., xsd:string). Instances are created for each class (e.g., #MainMoldAssy001 of type #MoldAssembly) and linked via <rdf:type>. Direct attributes are asserted on these individuals. The fuzzy relationship between them is embodied by the specific link individual.

The OWL representation integrates temporal dynamics by allowing the fuzzy values and timestamps, now correctly attached as data type properties, to specific relationship link individuals, like #Link_Mold001_Plate7 in Figure 10, to be updated over time. For instance, if the assembly confidence for this link changes, the fuzzy:assemblyConfidence value on the #Link_Mold001_Plate7 individual is modified, along with its fuzzy:lastChecked timestamp, without altering the core schema.

Finally, the OWL model is validated using tools like Protégé for semantic and logical consistency. The resulting OWL model captures the MoldAssembly FFOM’s complexity, including its hierarchy and correctly represents instance-specific fuzzy relationships and temporal dynamics. While traditional models struggle with adaptability, FFOM, through its fractal-inspired structures and its method of incorporating fuzzy logic, enables the dynamic representation of uncertain relationships. Figure 10 thus demonstrates how FFOM’s OWL transformation supports a scalable, adaptable, and uncertainty-aware ontology, where dynamic relationships are represented in a formally sound manner.

4.3. Validation and Discussion

The case study of the mold assembly, modeled and implemented in the previous section, serves as a practical experiment to validate the core assertions of the FFOM methodology. This detailed application provides a basic validation of the effectiveness of the framework in key areas essential for dynamic industrial environments. First, the scalability and modularity of FFOM are validated through its unique fractal design. This integration is a local add-on, so there is no need to reconfigure the broader ontology or modify existing relationships between the MoldAssembly and CoreAssembly. This demonstrates that the fractal approach allows the ontology to be efficiently and predictably extended through non-disruptive updates, a significant advantage over rigid models that require complex maintenance. Second, the practical utility of the fuzzy semantic hierarchy is validated through the support of data-driven queries that demonstrate subtle differences. Engineers who need to identify the most reliable components for critical tasks can run a SPARQL query to retrieve all the BaseAssembly instances with an assembly confidence greater than 0.9. This ability to filter and reason based on confidence rather than simple binary states enables more intelligent and realistic decision support, such as prioritizing preventive maintenance or selecting premium quality assemblies for a given order. Finally, FFOM’s adaptability to real-time changes is verified by its ability to update relationship strengths at the instance level. If real-time sensor data indicates a gradual degradation in assembly alignment, the assemblyConfidence value of a particular linked entity and its lastChecked timestamp can be automatically updated. This is a simple data-level modification that keeps the core ontology schema intact. This demonstrates the framework’s ability to reflect changing operational realities, allowing the ontology to function as a living, dynamic model of the factory floor, rather than a static snapshot.

To further contextualize these validated contributions,

Table 5. Comparative analysis of FFOM with contemporary approaches.

Feature/ Capability	FFOM	Traditional OWL Ontologies (General)	Manufacturing Domain Ontologies	Fuzzy Ontologies
Primary Data Modeling Focus	- Hierarchical complexity with self-similarity and semantic uncertainty	- General semantic representation, often with crisp logic	- Domain-specific concepts and relationships for manufacturing processes/resources	- Semantic uncertainty - Imprecise data representation
Structural Scalability Mechanism	- Fractal patterns enabling recursive, modular expansion - Self-similarity reduces redundancy	- Standard OWL subclassing - Can be verbose for deep/repeating structures	- Typically, standard hierarchical modeling tailored to the domain	- Not a primary focus - Relies on the underlying ontology’s structural paradigm
Uncertainty Handling Approach	- Integrated fuzzy logic (linguistic variables, fuzzy sets, membership functions, fuzzy rules)	- Limited native support - Typically requires extensions or external logic	- May incorporate some uncertainty elements ad hoc, but not usually core	- Core feature using fuzzy set theory and fuzzy description logics
Modularity for Dynamic Updates	- High (modular) - Fractal patterns allow localized updates - Additions to self-similar modules	- Moderate to low - Changes can propagate extensively in fixed hierarchies	- Modularity based on domain decomposition (e.g., by process or resource type)	- Modularity related to fuzzy rule bases or concept definitions
Key Novelty Aspect Highlighted	- Synergistic integration of fractal concept for structural scalability - Formalized fuzzy logic for semantic uncertainty within a unified OWL framework	- Broad applicability and standardization	- Deep semantic capturing of specific manufacturing domains/processes	- Rigorous handling of vagueness and imprecision in knowledge representation

compares FFOM with other contemporary data management approaches. As the table illustrates, traditional OWL ontologies often lack native uncertainty handling, and domain-specific manufacturing ontologies do not prioritize structural scalability as a core feature. FFOM is unique in its synergistic integration of fractal structures for scalability and formalized fuzzy logic for uncertainty management. The ‘High (Modular)’ rating for FFOM’s modularity is specifically attributed to its fractal-based design; new components or entire process layers can be integrated by simply instantiating the established fractal pattern, a localized change that does not require the restructuring of the existing ontology. This dual capability, designed from the ground up, positions FFOM as a robust and novel solution for dynamic industrial environments, where both challenges are paramount.

5. Conclusions

The development of the FFOM framework represents a significant advancement in ontology-based data management by effectively overcoming the inherent limitations of traditional ontology models. Unlike conventional approaches that rely on static hierarchical structures and binary logic, FFOM enables sustained alignment between the ontology and evolving real-world operations. Its fractal modularity enables new data or processes to be integrated seamlessly, while fuzzy logic captures ambiguous, evolving conditions. This supports the dynamic lifecycle management of ontologies, essential for long-term reliability in changing industrial contexts.

The development of the FFOM framework has brought about significant progress in ontology-based data management by effectively overcoming the inherent limitations of existing ontology models. Unlike existing approaches that rely on static hierarchies and binary logic, FFOM enables continuous alignment between ontologies and changing real-world operations. Fractal modularity enables the seamless integration of new data or processes, while fuzzy logic captures ambiguous and changing conditions. This supports dynamic lifecycle management of ontologies, which is essential for maintaining long-term reliability in changing industrial environments. The hierarchical structure of the FFOM framework, based on the concept of fractals, creates self-similar and reusable patterns, minimizing the need for structural modifications when integrating new data. Incorporating fuzzy logic allows for more realistic modeling and adaptive decision making by expressing the ambiguity of real-world data through flexible fuzzy values. Implemented in the OWL framework for standardization and interoperability purposes, FFOM supports real-time data integration and analysis by systematically defining classes and properties using dynamic fuzzy annotations, such as timestamps. The practical application of FFOM to a mold assembly case study has proven the effectiveness of FFOM in managing hierarchical data and uncertainty, thereby reducing maintenance costs and improving scalability compared to existing models. As a result, the strength of FFOM is that it presents a new solution for data management and decision support in complex real-time industrial environments.

While this study demonstrates notable strengths of FFOM, several limitations warrant attention in future research. A limitation of this study is that the current validation is based on a single representative case study. Comprehensive and large-scale external validation across multiple domains has not yet been conducted. Furthermore, the framework is time consuming to implement for practitioners who are not familiar with fractal and fuzzy concepts. Existing ontology tools such as Protégé may have limited native support for advanced real-time fuzzy updates, which could potentially mean that custom plugins are required. Finally, the initial definition of fuzzy thresholds can be subjective and requires careful calibration by domain experts to ensure consistent results.

To further enhance FFOM’s versatility and real-world applicability, several key research directions should be pursued as follows:

• Cross-domain validation and expansion: Building upon FFOM’s demonstrated success in regard to mold assembly, future work should explore its application across a broader spectrum of industries, such as logistics, continuous processes, and other manufacturing sectors, in order to verify its adaptability under diverse operational conditions and in regard to large-scale data complexities.
• Advanced fuzzy logic integration: Incorporating more sophisticated fuzzy mechanisms, similar to those supported by SWRL (Semantic Web Rule Language), could significantly enhance FFOM’s inference capabilities. This integration would enable predictive analytics and decision making in highly dynamic environments, where both operational parameters and fuzzy thresholds may shift in real time.
• Automated tool development: The development of specialized automation tools to facilitate the creation and OWL transformation of FFOM ontologies has the potential to reduce the implementation barriers experienced by practitioners with limited ontology expertise. Such tools could include user-friendly interfaces or plugins for platforms like Protégé, facilitating rapid model generation and updates without the need for extensive manual configuration.
• Performance benchmarking and systematic evaluation: Implementing a rigorous benchmarking methodology, including real-world datasets and high-frequency data streams, will help quantify FFOM’s advantages in terms of scalability, efficiency, and uncertainty management. Key metrics could include structural modification overheads (when adding new processes), reasoning speed during incremental updates, fuzzy threshold detection accuracy, and SPARQL query performance.
• Standardization and ongoing enhancement: By continuing to refine FFOM’s core functionalities and aligning them with emerging industry standards, the framework can evolve into a pivotal data management tool that addresses the challenges of data complexity and interaction across diverse industrial contexts. As these refinements are developed, FFOM has the potential to revolutionize ontology-driven workflows, eventually becoming a vital solution for real-time, high-volume data environments.