Frictional Experiments on Granitic Faults: New Insights into Continental Earthquakes and Micromechanical Mechanisms
Abstract
1. Introduction
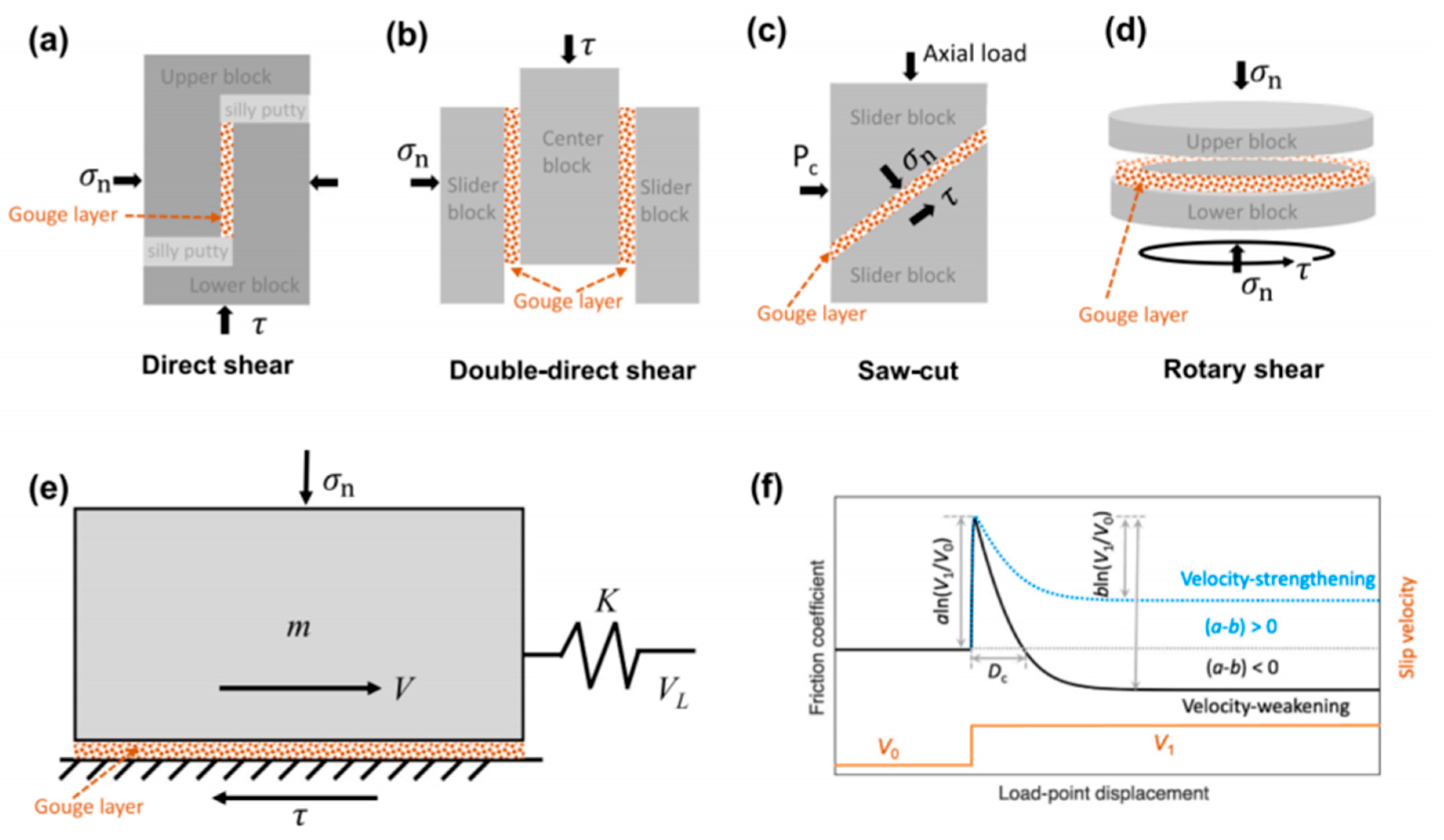
2. Friction Motions and Friction Law
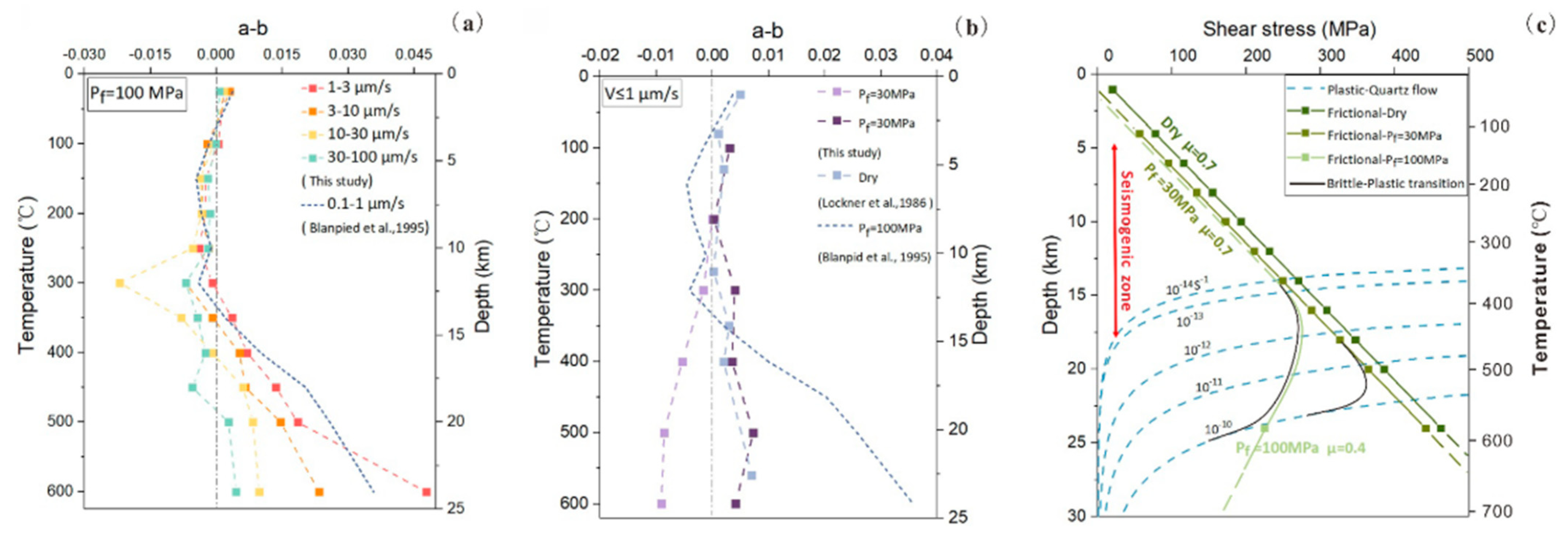
3. Friction Experiments of Granitoid Fault
| Gouge/Rock Sample | Temperature T (°C) | Effective Normal Stress (MPa) | Pore Fluid Pressure (MPa) | Slip Rate V (μm/s) | Shear Displacement S (mm) | Experiment Type | References |
|---|---|---|---|---|---|---|---|
| Westerly granite | ambient | 2–10 | dry | 0.1–10 | ~1 | [64] | |
| Westerly granite | ambient | 27–84 | dry | 0.01–10 | ~70 | Bare surface, CV/VS | [65] |
| Westerly granite | ambient-845 | CP: 250 | dry | 0.0476–0.476–4.76 | ~4 | VS | [36] |
| Westerly granite | ambient | 50 | dry | 0.001–3000 | ~376 | VS | [66] |
| Westerly granite gouge | 25–600 | 400 | dry, 100 | 0.01–0.1–1 | ~4 | VS | [37] |
| Westerly granite gouge | ambient | 25 | dry | 1–10 | ~400 | VS | [38] |
| Granitoid gouge | 100–600 | 200 | 30 | 0.04–0.2–1 | ~4 | VS | [67] |
| Granitoid gouge | 100–600 | 100, 200, 300 | 30 | 0.04–0.2–1 | ~4 | VS | [40] |
| Westerly granite, gouge | 25–600 | 5–40 | minor water | 0.1–30 | ~2.5 or ~112 | VS | [45] |
| Natural granite gouge | 25–600 | 200 | 30 | 0.04–0.2–1 | ~4 | VS | [68] |
| Westerly granite gouge | 25–250 | CP: 20 | 10 | 0.1 | ~5 | HSH | [69] |
| Natural granitoid gouge | 20–650 | 100 | 100 | 0.1–100 | ~15 | CV | [41] |
| Natural granite gouge | 25–600 | 100, 200 | 30,100 | 0.04–0.2–1 and 1–3-10–30-100 | ~25 | VS and CV | [9] |
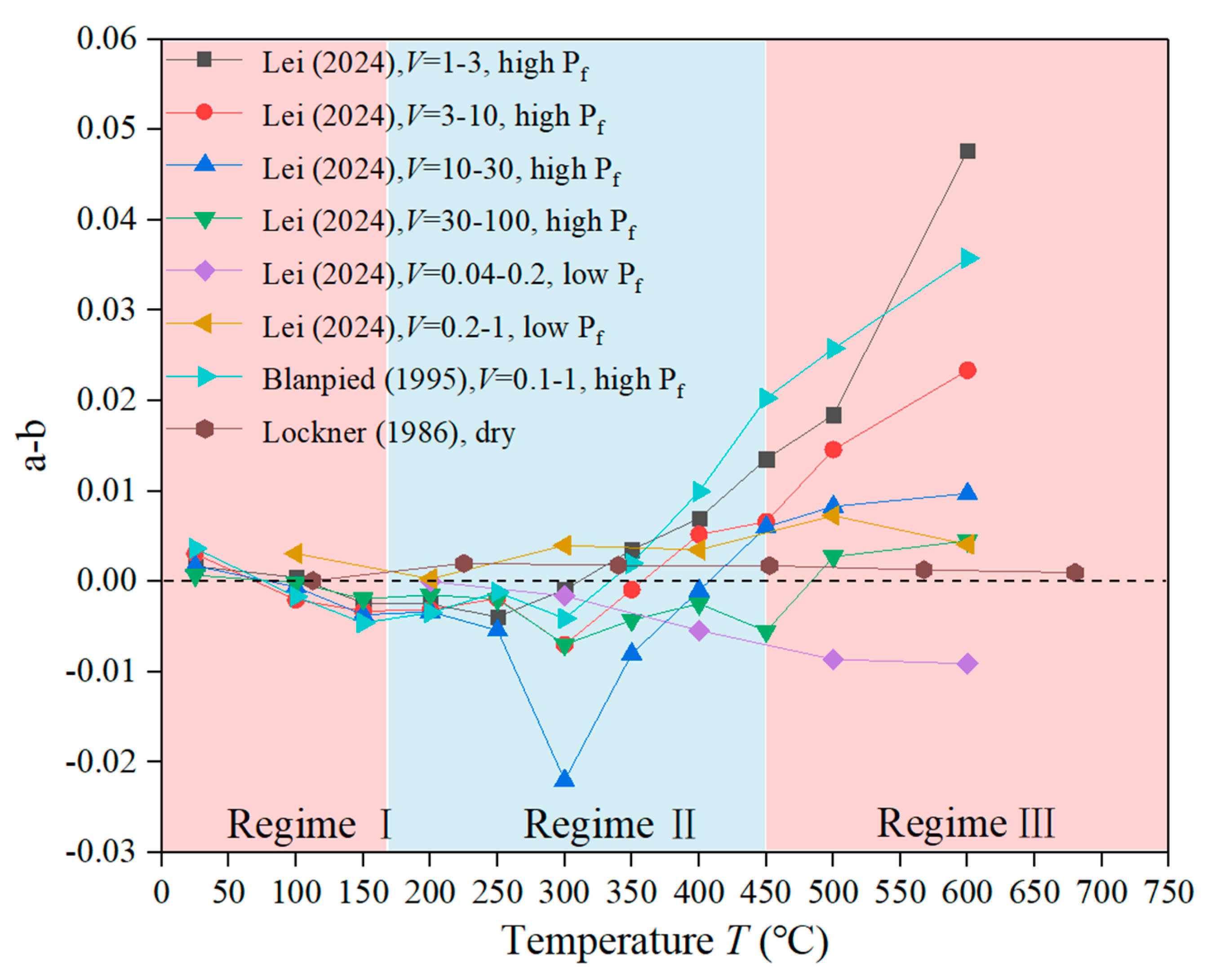
3.1. Velocity-Stepping Experiment
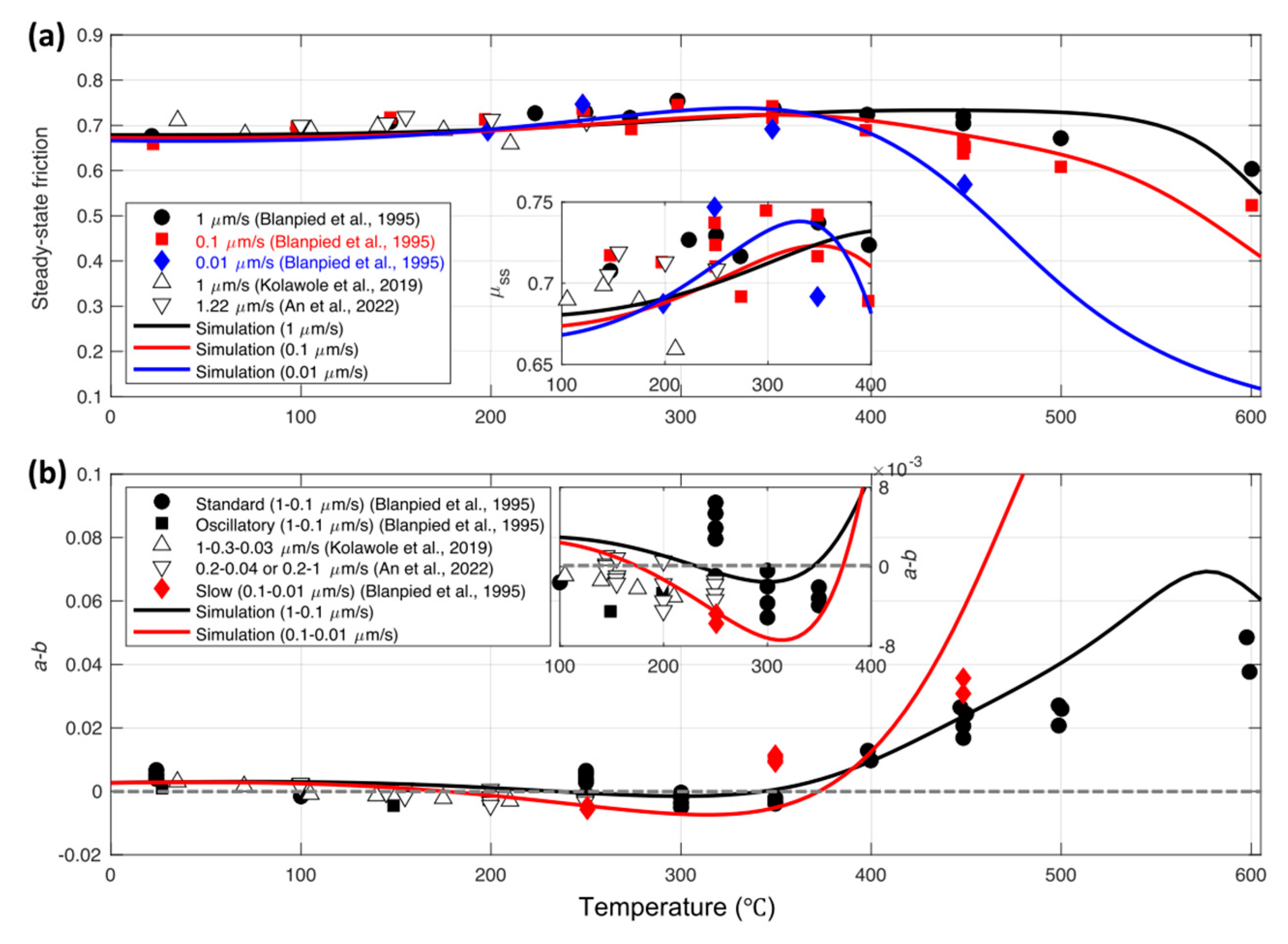
3.2. Constant-Velocity Experiment
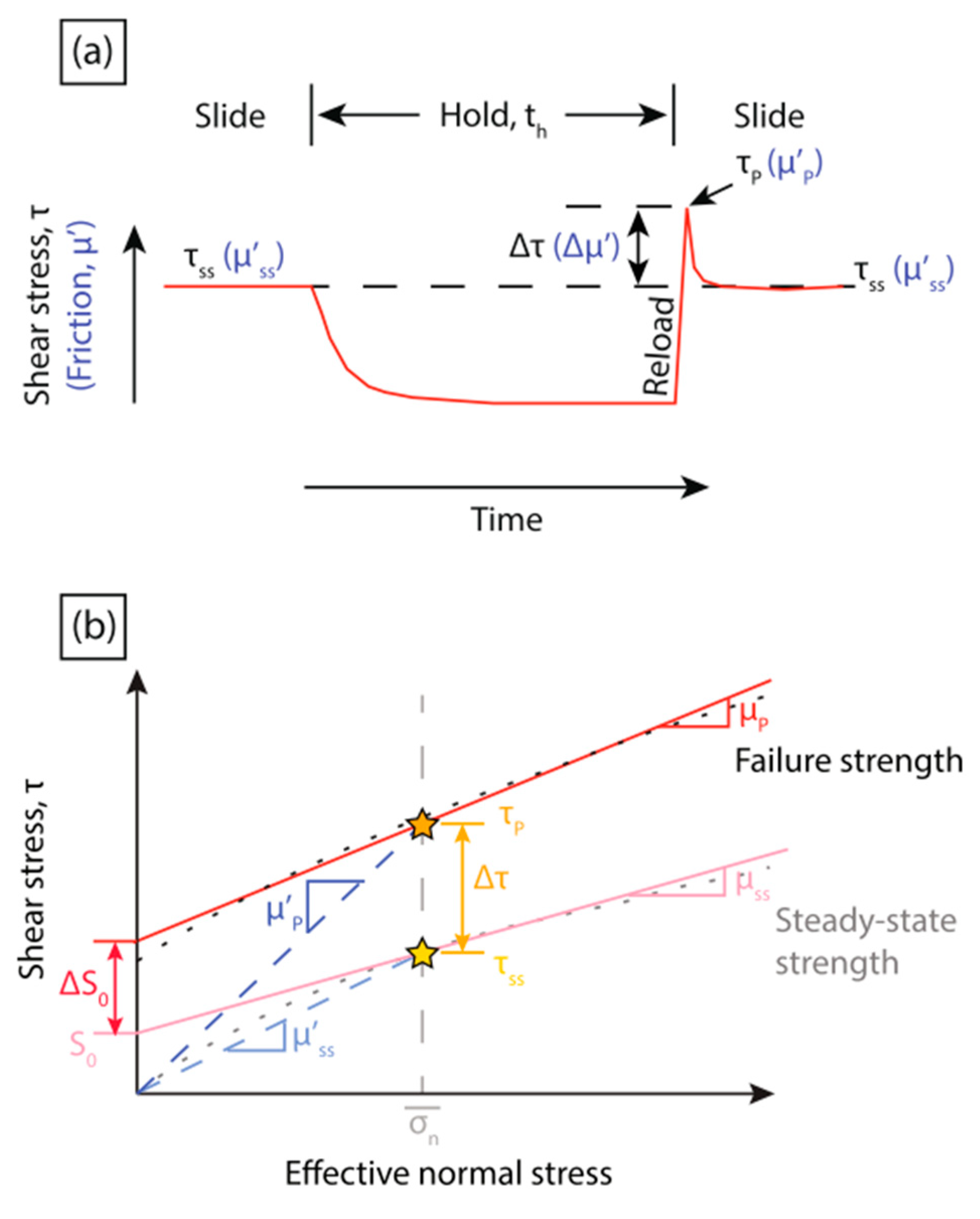
3.3. Slide-Hold-Slide Experiment
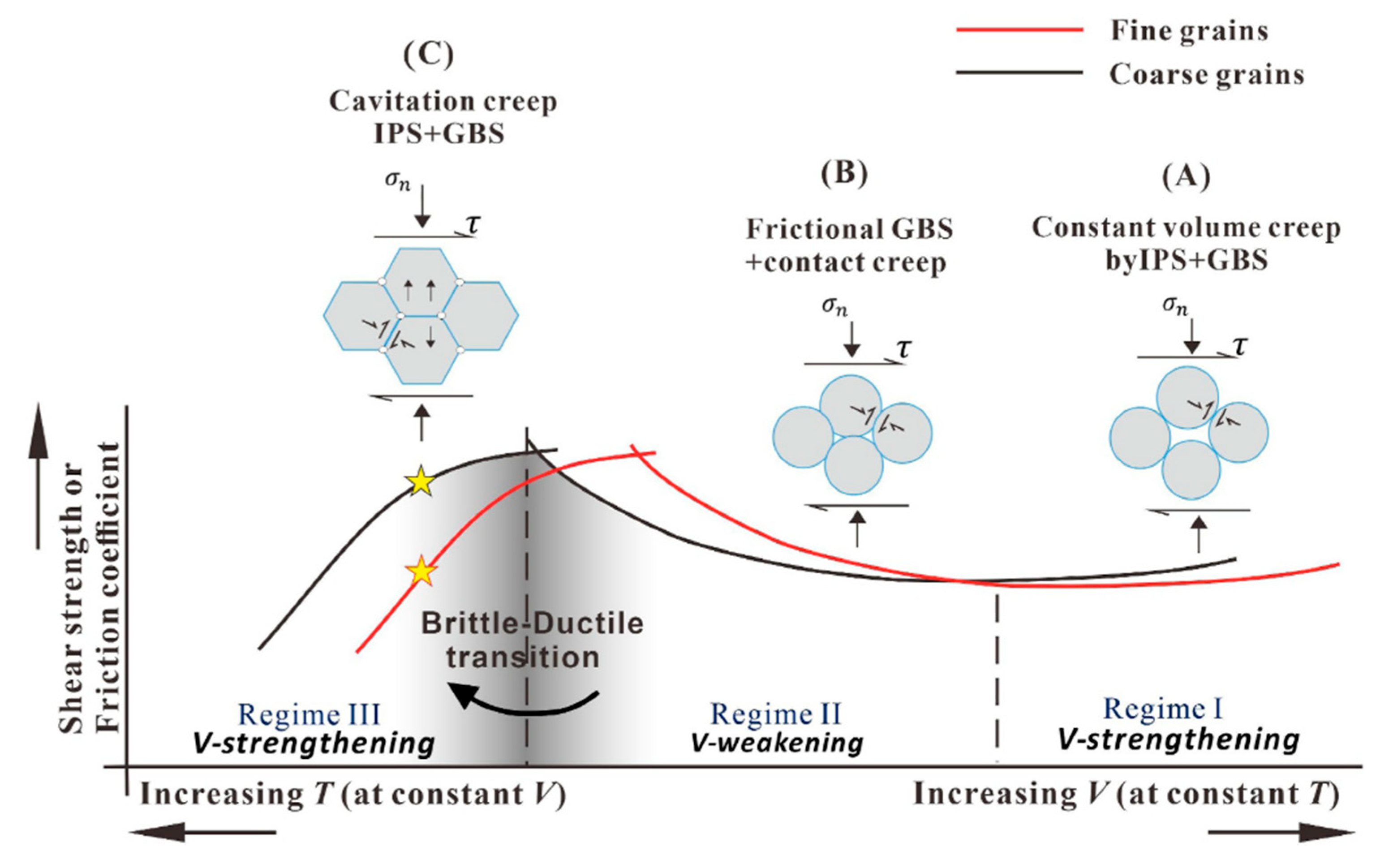
4. Velocity Dependence Behavior Explained Using Microphysical Model
5. Implications for Nucleation of Continental Earthquakes
6. Conclusions
- (1)
- Granitic faults in the crystalline upper-to-middle continental crust represent key structures controlling the seismogenic behavior and long-term deformation of the continental lithosphere. Their frictional properties are thus central to understanding earthquake initiation and rupture dynamics.
- (2)
- Laboratory friction experiments, including velocity-stepping (VS), constant-velocity (CV), and slide-hold-slide (SHS) protocols, consistently demonstrate that granitic gouges exhibit measurable and reproducible frictional behavior. Notably, the VS tests reveal frictional stability regimes (velocity-strengthening or -weakening), while SHS tests provide quantitative estimates of fault healing and restrengthening during interseismic periods.
- (3)
- Microstructural observations indicate that shear deformation induces localized shear, significant grain size reduction, pressure solution creep, and mineralogical alteration within the fault gouge. These microphysical processes are sensitive to temperature, normal stress, pore fluid pressure, and strain rate and play a pivotal role in modulating the rheology and frictional response of the fault zone.
- (4)
- In the continental crust, the interplay between microstructural evolution and frictional properties suggests that nucleation is favored in zones where brittle–frictional weakening mechanisms dominate but are bounded by ductile, velocity-strengthening regions that arrest rupture.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Scholz, C.H. Earthquakes and friction laws. Nature 1998, 391, 37–42. [Google Scholar] [CrossRef]
- Sibson, R.H. Fault zone models, heat flow, and the depth distribution of earthquakes in the continental crust of the United States. Bull. Seismol. Soc. Am. 1982, 72, 151–163. [Google Scholar]
- Scholz, C.H.; Molnar, P.; Johnson, T. Detailed studies of frictional sliding of granite and implications for the earthquake mechanism. J. Geophys. Res. 1972, 77, 6392–6406. [Google Scholar] [CrossRef]
- Blanpied, M.L.; Lockner, D.A.; Byerlee, J.D. Fault stability inferred from granite sliding experiments at hydrothermal conditions. Geophys. Res. Lett. 1991, 18, 609–612. [Google Scholar] [CrossRef]
- Blanpied, M.L.; Lockner, D.A.; Byerlee, J.D. An earthquake mechanism based on rapid sealing of faults. Nature 1992, 358, 574–576. [Google Scholar] [CrossRef]
- Sullivan, W.A.; Peterman, E.M. Pulverized granite at the brittle-ductile transition: An example from the Kellyland fault zone, eastern Maine, USA. J. Struct. Geol. 2017, 101, 109–123. [Google Scholar] [CrossRef]
- Niemeijer, A.R.; Boulton, C.; Toy, V.G.; Townend, J.; Sutherland, R. Large-displacement, hydrothermal frictional properties of DFDP-1 fault rocks, Alpine Fault, New Zealand: Implications for deep rupture propagation. J. Geophys. Res. Solid Earth 2016, 121, 624–647. [Google Scholar] [CrossRef]
- Guermani, A.; Pennacchioni, G. Brittle precursors of plastic deformation in a granite: An example from the Mont Blanc massif (Helvetic, western Alps). J. Struct. Geol. 1998, 20, 135–148. [Google Scholar] [CrossRef]
- Lei, H.; Niemeijer, A.R.; Zhou, Y.; Spiers, C.J. Frictional properties of natural granite fault gouge under hydrothermal conditions: A case study of strike-slip fault from Anninghe Fault zone, southeastern Tibetan Plateau. J. Geophys. Res. Solid Earth. 2024, 129, e2024JB028760. [Google Scholar] [CrossRef]
- Roger, F.; Calassou, S.; Lancelot, J.; Malavieille, J.; Mattauer, M.; Zhiqin, X.; Liwei, H. Miocene emplacement and deformation of the Konga Shan granite (Xianshui He fault zone, west Sichuan, China): Geodynamic implications. Earth Planet. Sci. Lett. 1995, 130, 201–216. [Google Scholar] [CrossRef]
- Marone, C.; Blanpied, M.L. Faulting, Friction and Earthquake Mechanics. Pure Appl. Geophys. 1994, 142. [Google Scholar]
- Savage, H.M.; Rowe, C.D. Localization and delocalization during seismic slip. Geophys. Res. Lett. 2024, 51, e2024GL110058. [Google Scholar] [CrossRef]
- Collettini, C.; Niemeijer, A.; Viti, C.; Smith, S.A.F.; Marone, C. Fault structure, frictional properties and mixed-mode fault slip behavior. Earth Planet. Sci. Lett. 2011, 311, 316–327. [Google Scholar] [CrossRef]
- Froment, B.; Campillo, M.; Chen, J.; Liu, Q. Deformation at depth associated with the 12 May 2008 mw 7.9 wenchuan earthquake from seismic ambient noise monitoring. Geophys. Res. Lett. 2013, 40, 78–82. [Google Scholar] [CrossRef]
- Schwartz, S.Y.; Rokosky, J.M. Slow slip events and seismic tremor at circum-Pacific subduction zones. Rev. Geophys. 2007, 45, RG3004. [Google Scholar] [CrossRef]
- Wallace, L.M. Slow slip events in New Zealand. Annu. Rev. Earth Planet. Sci. 2020, 48, 175–203. [Google Scholar] [CrossRef]
- Shelly, D.R.; Beroza, G.C.; Ide, S.; Nakamula, S. Low-frequency earthquakes in Shikoku, Japan, and their relationship to episodic tremor and slip. Nature 2006, 442, 188–191. [Google Scholar] [CrossRef] [PubMed]
- Shelly, D.R.; Beroza, G.C.; Ide, S. Non-volcanic tremor and low-frequency earthquake swarms. Nature 2007, 446, 305–307. [Google Scholar] [CrossRef]
- Ito, Y.; Obara, K.; Shiomi, K.; Sekine, S.; Hirose, H. Slow earthquakes coincident with episodic tremors and slow slip events. Science 2007, 315, 503–506. [Google Scholar] [CrossRef]
- Reinen, L.A.; Weeks, J.D.; Tullis, T.E. The frictional behavior of serpentinite: Implications for aseismic creep on shallow crustal faults. Geophys. Res. Lett. 1991, 18, 1921–1924. [Google Scholar] [CrossRef]
- Kaduri, M.; Gratier, J.P.; Renard, F.; Cakir, Z.; Lasserre, C. The implications of fault zone transformation on aseismic creep: Example of the North Anatolian Fault, Turkey. J. Geophys. Res. Solid Earth 2017, 122, 4208–4236. [Google Scholar] [CrossRef]
- Reid, H.F. The Mechanics of the Earthquake, The California Earthquake of April 18, 1906: Report of the State Investigation Commission, Volume 2. Carnegie Institution of Washington: Washington, DC, USA, 1910; pp. 16–28. [Google Scholar] [CrossRef]
- Lawson, A.C. The California Earthquake of April 18, 1906: Report of the State Earthquake Investigation Commission. Available online: https://oac.cdlib.org/view?docId=hb1h4n989f&brand=oac4&doc.view=entire_text (accessed on 5 May 2025).
- Bowden, F.P.; Tabor, D. The friction and lubrication of solids. Am. J. Phys. 1951, 19, 428–429. [Google Scholar] [CrossRef]
- Brace, W.F.; Byerlee, J.D. Stick-slip as a mechanism for earthquakes. Science 1966, 153, 990–992. [Google Scholar] [CrossRef]
- Dieterich, J.H. Modeling of rock friction: 1. Experimental results and constitutive equations. J. Geophys. Res. Solid Earth. 1979, 84, 2161–2168. [Google Scholar] [CrossRef]
- Marone, C. Laboratory-derived friction laws and their application to seismic faulting. Annu. Rev. Earth Planet. Sci. 1998, 26, 643–696. [Google Scholar] [CrossRef]
- Scuderi, M.M.; Niemeijer, A.R.; Collettini, C.; Marone, C. Frictional properties and slip stability of active faults within carbonate-evaporite sequences: The role of dolomite and anhydrite. Earth Planet. Sci. Lett. 2013, 369–370, 230–232. [Google Scholar] [CrossRef]
- Tsutsumi, A.; Shimamoto, T. High-velocity frictional properties of gabbro. Geophys. Res. Lett. 1997, 24, 699–702. [Google Scholar] [CrossRef]
- Di Toro, G.; Han, R.; Hirose, T.; De Paola, N.; Nielsen, S.; Mizoguchi, K.; Ferri, F.; Cocco, M.; Shimamoto, T. Fault lubrication during earthquakes. Nature 2011, 471, 494–498. [Google Scholar] [CrossRef]
- Sibson, R.H. Brecciation processes in fault zones: Inferences from earthquake rupturing. Pure Appl. Geophys. 1986, 124, 159–175. [Google Scholar] [CrossRef]
- Chen, K.H.; Burgmann, R.; Nadeau, R.M.; Chen, T.; Lapusta, N. Postseismic variations in seismic moment and recurrence interval of repeating earthquakes. Earth Planet. Sci. Lett. 2010, 299, 118–125. [Google Scholar] [CrossRef]
- Lui, S.K.; Lapusta, N. Repeating microearthquake sequences interact predominantly through postseismic slip. Nat. Commun. 2016, 7, 13020. [Google Scholar] [CrossRef] [PubMed]
- Dieterich, J.H. Constitutive properties of faults with simulated gouge. Mech. Behav. Crustal Rocks Handin Vol. 1981, 24, 103–120. [Google Scholar]
- Ruina, A. Slip instability and state variable friction laws. J. Geophys. Res. Solid Earth 1983, 88, 10359–10370. [Google Scholar] [CrossRef]
- Lockner, D.A.; Summers, R.; Byerlee, J.D. Effects of Temperature and Sliding Rate on Frictional Strength of Granite. In Friction and Faulting; Tullis, T.E., Ed.; Birkhäuser: Basel, Switzerland, 1986. [Google Scholar] [CrossRef]
- Blanpied, M.L.; Lockner, D.A.; Byerlee, J.D. Frictional slip of granite at hydrothermal conditions. J. Geophys. Res. 1995, 100, 13045–13064. [Google Scholar] [CrossRef]
- Beeler, N.M.; Tullis, T.E.; Weeks, J.D. Frictional behavior of large displacement experimental faults. J. Geophys. Res. 1996, 101, 8697–8715. [Google Scholar] [CrossRef]
- Bedford, J.D.; Faulkner, D.R. The role of grain size and effective normal stress on localization and the frictional stability of simulated quartz gouge. Geophys. Res. Lett. 2021, 48, e2020GL092023. [Google Scholar] [CrossRef]
- Zhang, L.; He, C.R. Frictional properties of phyllosilicate-rich mylonite and conditions for the brittle-ductile transition. J. Geophys. Res. Solid Earth 2016, 121, 3017–3047. [Google Scholar] [CrossRef]
- Zhan, W.; Niemeijer, A.R.; Berger, A.; Nevskaya, N.; Spiers, C.J.; Herwegh, M. The frictional-viscous transition in experimentally deformed granitoid fault gouge. J. Geophys. Res. Solid Earth 2024, 129, e2024JB028797. [Google Scholar] [CrossRef]
- Niemeijer, A.R.; Spiers, C.J.; Peach, C.J. Frictional behaviour of simulated quartz fault gouges under hydrothermal conditions: Results from ultra-high strain rotary shear experiments. Tectonophysics 2008, 460, 288–303. [Google Scholar] [CrossRef]
- Ma, S.; Shimamoto, T.; Yao, L.; Togo, T.; Kitajima, H. A rotary-shear low to high-velocity friction apparatus in Beijing to study rock friction at plate to seismic slip rates. Earthq. Sci. 2014, 27, 469–497. [Google Scholar] [CrossRef]
- He, C.; Ma, X.; Yao, S. Unstable sliding of plagioclase gouge and deformation mechanisms under hydrothermal conditions with effective normal stresses of 100-300 MPa. J. Geophys. Res. Solid Earth 2024, 129, e2024JB028883. [Google Scholar] [CrossRef]
- Mitchell, E.K.; Fialko, Y.; Brown, K.M. Velocity-weakening behavior of Westerly granite at temperature up to 600 °C. J. Geophys. Res. Solid Earth 2016, 121, 6932–6946. [Google Scholar] [CrossRef]
- Verberne, B.A.; He, C.; Spiers, C.J. Frictional properties of sedimentary rocks and natural fault gouge from the Longmen Shan fault zone, Sichuan, China. Bull. Seismol. Soc. Am. 2010, 100, 2767–2790. [Google Scholar] [CrossRef]
- Ma, X.; Zhou, Y.; Dang, J.; Zhang, L.; He, C. Mineralogical and frictional properties of fault rocks from the Laohushan creep segment of the Haiyuan fault, Northeastern Tibet. J. Struct. Geol. 2024, 178, 105017. [Google Scholar] [CrossRef]
- Chen, J.; Verberne, B.A.; Spiers, C.J. Interseismic re-strengthening and stabilization of carbonate faults by “non-Dieterich” healing under hydrothermal conditions. Earth Planet. Sci. Lett. 2015, 423, 1–12. [Google Scholar] [CrossRef]
- Nakatani, M.; Scholz, C.H. Frictional healing of quartz gouge under hydrothermal conditions: 1. Experimental evidence for solution transfer healing mechanisms. J. Geophys. Res. 2004, 109, B07201. [Google Scholar] [CrossRef]
- Hu, J.; Sun, Q. The effect of high temperature and pressure on rock friction coefficient: A review. Int. J. Earth Sci. 2020, 109, 409–419. [Google Scholar] [CrossRef]
- Mei, C.; Mercuri, M.; Rudnicki, J.W. Rock friction experiments and modeling under hydrothermal conditions. Earth-Sci. Rev. 2024, 254, 104824. [Google Scholar] [CrossRef]
- Rice, J.R. Spatio-temporal complexity of slip on a fault. J. Geophys. Res. Solid Earth 1993, 98, 9885–9907. [Google Scholar] [CrossRef]
- Segall, P. Earthquake and volcano deformation. In Earthquake and Volcano Deformation; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Rice, J.R. Heating and weakening of faults during earthquake slip. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef]
- Noda, H.; Dunham, E.M.; Rice, J.R. Earthquake ruptures with thermal weakening and the operation of major faults at low overall stress levels. J. Geophys. Res. Solid Earth 2009, 114. [Google Scholar] [CrossRef]
- Veedu, D.M.; Barbot, S. The Parkfield tremors reveal slow and fast ruptures on the same asperity. Nature 2016, 532, 361–365. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Barbot, S. Excitation of San Andreas tremors by thermal instabilities below the seismogenic zone. Sci. Adv. 2020, 6, eabb2057. [Google Scholar] [CrossRef]
- Im, K.; Saffer, D.; Marone, C.; Avouac, J.P. Slip-rate-dependent friction as a universal mechanism for slow slip events. Nat. Geosci. 2020, 13, 705–710. [Google Scholar] [CrossRef]
- He, C.; Tan, W.; Zhang, L. Comparing dry and wet friction of plagioclase: Implication to the mechanism of frictional evolution effect at hydrothermal conditions. J. Geophys. Res. Solid Earth 2016, 121, 6365–6383. [Google Scholar] [CrossRef]
- Leeman, J.R.; Saffer, D.M.; Scuderi, M.M.; Marone, C. Laboratory observations of slow earthquakes and the spectrum of tectonic fault slip modes. Nat. Commun. 2016, 7, 11104. [Google Scholar] [CrossRef] [PubMed]
- Leeman, J.R.; Marone, C.; Saffer, D.M. Frictional mechanics of slow earthquakes. J. Geophys. Res. Solid Earth 2018, 123, 7931–7949. [Google Scholar] [CrossRef]
- Tullis, J.; Yund, R.A. Experimental deformation of dry Westerly granite. J. Geophys. Res. 1977, 82, 5705–5718. [Google Scholar] [CrossRef]
- Zoback, M.; Hickman, S.; Ellsworth, W. Scientific drilling into the San Andreas fault zone. Eos Trans. Am. Geophys. Union 2010, 91, 197–199. [Google Scholar] [CrossRef]
- Dieterich, J.H. Time-dependent friction and the mechanics of stick-slip. Rock Frict. Earthq. Predict. 1978, 6, 445–469. [Google Scholar]
- Tullis, T.E.; Weeks, J.D. Constitutive behavior and stability of frictional sliding of granite. Pure Appl. Geophys. 1986, 124, 383–414. [Google Scholar]
- Blanpied, M.L.; Tullis, T.E.; Weeks, J.D. Frictional behavior of granite at low and high sliding velocities. Geophys. Res. Lett. 1987, 14, 554–557. [Google Scholar] [CrossRef]
- Ren, F.; He, C. An experimental study of frictional sliding of granitic mylonite under hydrothermal conditions. Chin. J. Geophys. 2014, 57, 877–883. [Google Scholar]
- Lei, H.; Zhou, Y.; Yao, W.; Ma, X.; He, C.; Dang, J.; Miao, S.; Dai, W. Earthquake nucleation conditions of Anninghe Fault: Constrains from frictional experiments on natural granite gouge. Chin. J. Geophys. 2022, 65, 978–991. (In Chinese) [Google Scholar] [CrossRef]
- Jeppson, T.N.; Lockner, D.A.; Beeler, N.M.; Moore, D.E. Time-dependent weakening of granite at hydrothermal conditions. Geophys. Res. Lett. 2023, 50, e2023GL105517. [Google Scholar] [CrossRef]
- Dong, L.; Luo, Q. Investigations and new insights on earthquake mechanics from fault slip experiments. Earth-Sci. Rev. 2022, 228, 104019. [Google Scholar] [CrossRef]
- den Hartog, S.A.; Spiers, C.J. Influence of subduction zone conditions and gouge composition on frictional slip stability of megathrust faults. Tectonophysics 2013, 600, 75–90. [Google Scholar] [CrossRef]
- Bos, B.; Spiers, C.J. Frictional-viscous flow of phyllosilicate-bearing fault rock: Microphysical model and implications for crustal strength profiles. J. Geophys. Res. Solid Earth 2002, 107, ECV-1. [Google Scholar] [CrossRef]
- den Hartog, S.A.; Spiers, C.J. A microphysical model for fault gouge friction applied to subduction megathrusts. J. Geophys. Res. Solid Earth 2014, 119, 1510–1529. [Google Scholar] [CrossRef]
- Chen, J.; Spiers, C.J. Rate and state frictional and healing behavior of carbonate fault gouge explained using microphysical model. J. Geophys. Res. Solid Earth 2016, 121, 8642–8665. [Google Scholar] [CrossRef]
- Chen, J.; Niemeijer, A.R.; Spiers, C.J. Seismic fault slip behavior predicted from internal microphysical processes. J. Geophys. Res. Solid Earth 2022, 127, e2022JB024530. [Google Scholar] [CrossRef]
- Rutter, E.H. The kinetics of rock deformation by pressure solution. Philos. Trans. R. Soc. Lond. A 1976, 283, 203–219. [Google Scholar]
- Gratier, J.P.; Dysthe, D.K.; Renard, F. The role of pressure solution creep in the ductility of the Earth’s upper crust. Adv. Geophys. 2013, 54, 47–179. [Google Scholar]
- De Boer, R.B.; Nagtegaal, P.J.C.; Duyvis, E.M. Pressure solution experiments on quartz sand. Geochim. Cosmochim. Acta 1977, 41, 257–264. [Google Scholar] [CrossRef]
- Spiers, C.J.; Schutjens, P.M.T.M.; Brzesowsky, R.H.; Peach, C.J.; Liezenberg, J.L.; Zwart, H.J. Experimental determination of constitutive parameters governing creep of rocksalt by pressure solution. Geol. Soc. Lond. 1990, 54, 215–227. [Google Scholar] [CrossRef]
- Stesky, R.M. The Mechanical Behavior of Faulted Rock at High Temperature and Pressure. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1975. [Google Scholar]
- Pec, M.; Stünitz, H.; Heilbronner, R.; Drury, M. Semi-brittle flow of granitoid fault rocks in experiments. J. Geophys. Res. Solid Earth 2016, 121, 1677–1705. [Google Scholar] [CrossRef]
- Logan, J.M.; Dengo, C.A.; Higgs, N.G.; Wang, Z.Z. Fabrics of experimental fault zones: Their development and relationship to mechanical behavior. In International Geophysics; Academic Press: Cambridge, MA, USA, 1992; Volume 51, pp. 33–67. [Google Scholar]
- Fusseis, F.; Regenauer-Lieb, K.; Liu, J.; Hough, R.M.; De Carlo, F. Creep cavitation can establish a dynamic granular fluid pump in ductile shear zones. Nature 2009, 459, 974–977. [Google Scholar] [CrossRef]
- Précigout, J.; Ledoux, E.; Arbaret, L.; Spriet, C. Porosity induced by dislocation dynamics in quartz-rich shear bands of granitic rocks. Sci. Rep. 2022, 12, 6141. [Google Scholar] [CrossRef]
- Duan, Q.; Fagereng, A.; Chen, J.; Blenkinsop, T. Fluid environment controls along-strike variation in slip style: Midcrustal geological signatures from the Red River fault, China. Geology 2024, 52, 405–410. [Google Scholar] [CrossRef]
- Berthoud, P.; Baumberger, T.; G’sell, C.; Hiver, J.M. Physical analysis of the state- and rate-dependent friction law: Static friction. Phys. Rev. B 1999, 59, 14313–14327. [Google Scholar] [CrossRef]
- Beeler, N.B.; Tullis, T.E.; Weeks, J.D. The roles of time and displacement in the evolution effect in rock friction. Geophys. Res. Lett. 1994, 21, 1987–1990. [Google Scholar] [CrossRef]
- Carpenter, B.; Ikari, M.; Marone, C. Laboratory observations of time-dependent frictional strengthening and stress relaxation in natural and synthetic fault gouges. J. Geophys. Res. Solid Earth 2016, 121, 1183–1201. [Google Scholar] [CrossRef]
- Dieterich, J.H. Time-dependent friction in rocks. J. Geophys. Res. 1972, 77, 3690–3697. [Google Scholar] [CrossRef]
- Dieterich, J.H.; Conrad, G. Effect of humidity on time- and velocity-dependent friction in rocks. J. Geophys. Res. 1984, 89, 4196–4202. [Google Scholar] [CrossRef]
- Jeppson, T.; Lockner, D.; Beeler, N.; Hickman, S. Strength recovery in quartzite is controlled by changes in friction in experiments at hydrothermal conditions up to 200 °C. J. Geophys. Res. Solid Earth 2023, 128, e2022JB025663. [Google Scholar] [CrossRef]
- Mei, C.; Rudnicki, J.W. Microphysical modeling of fault slip and stability transition in hydrothermal conditions. Geophys. Res. Lett. 2023, 50, e2023GL103730. [Google Scholar] [CrossRef]
- Kolawole, F.; Johnston, C.; Morgan, C.; Chang, J.; Marfurt, K.; Lockner, D.; Reches, Z.; Carpenter, B.M. The susceptibility of Oklahoma’s basement to seismic reactivation. Nat. Geosci. 2019, 12, 839–844. [Google Scholar] [CrossRef]
- An, M.; Zhang, F.; Min, K.-B.; Elsworth, D.; He, C.; Zhao, L. Frictional stability of metamorphic epidote in granitoid faults under hydro- thermal conditions and implications for injection-induced seismicity. J. Geophys. Res. Solid Earth 2022, 127, e2021JB023136. [Google Scholar] [CrossRef]
- Nur, A.; Mavko, G. Postseismic viscoelastic rebound. Science 1974, 183, 204–206. [Google Scholar] [CrossRef]
- Savage, J.C.; Prescott, W.H. Asthenosphere readjustment and the earthquake cycle. J. Geophys. Res. Solid Earth 1978, 83, 3369–3376. [Google Scholar] [CrossRef]
- Lachenbruch, A.H.; Sass, J.H. Heat flow from Cajon Pass, fault strength, and tectonic implications. J. Geophys. Res. Solid Earth 1992, 97, 4995–5015. [Google Scholar] [CrossRef]
- Hearn, E.H.; Thatcher, W.R. Reconciling viscoelastic models of postseismic and interseismic deformation: Effects of viscous shear zones and finite length ruptures. J. Geophys. Res. Solid Earth 2015, 120, 2794–2819. [Google Scholar] [CrossRef]
- Tse, S.T.; Rice, J.R. Crustal earthquake instability in relation to the depth variation of frictional slip properties. J. Geophys. Res. Solid Earth 1986, 91, 9452–9472. [Google Scholar] [CrossRef]
- Richter, B.; Stünitz, H.; Heilbronner, R. The brittle-to-viscous transition in polycrystalline quartz: An experimental study. J. Struct. Geol. 2018, 114, 1–21. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, H.; Liu, S.; Dai, W. Frictional Experiments on Granitic Faults: New Insights into Continental Earthquakes and Micromechanical Mechanisms. Appl. Sci. 2025, 15, 7207. https://doi.org/10.3390/app15137207
Lei H, Liu S, Dai W. Frictional Experiments on Granitic Faults: New Insights into Continental Earthquakes and Micromechanical Mechanisms. Applied Sciences. 2025; 15(13):7207. https://doi.org/10.3390/app15137207
Chicago/Turabian StyleLei, Huiru, Shimin Liu, and Wenhao Dai. 2025. "Frictional Experiments on Granitic Faults: New Insights into Continental Earthquakes and Micromechanical Mechanisms" Applied Sciences 15, no. 13: 7207. https://doi.org/10.3390/app15137207
APA StyleLei, H., Liu, S., & Dai, W. (2025). Frictional Experiments on Granitic Faults: New Insights into Continental Earthquakes and Micromechanical Mechanisms. Applied Sciences, 15(13), 7207. https://doi.org/10.3390/app15137207