A Simulation of the Densification Process of NdFeB Bulks by a Modified Drucker–Prager Cap Model
Abstract
1. Introduction
2. Materials and Methods
3. Results
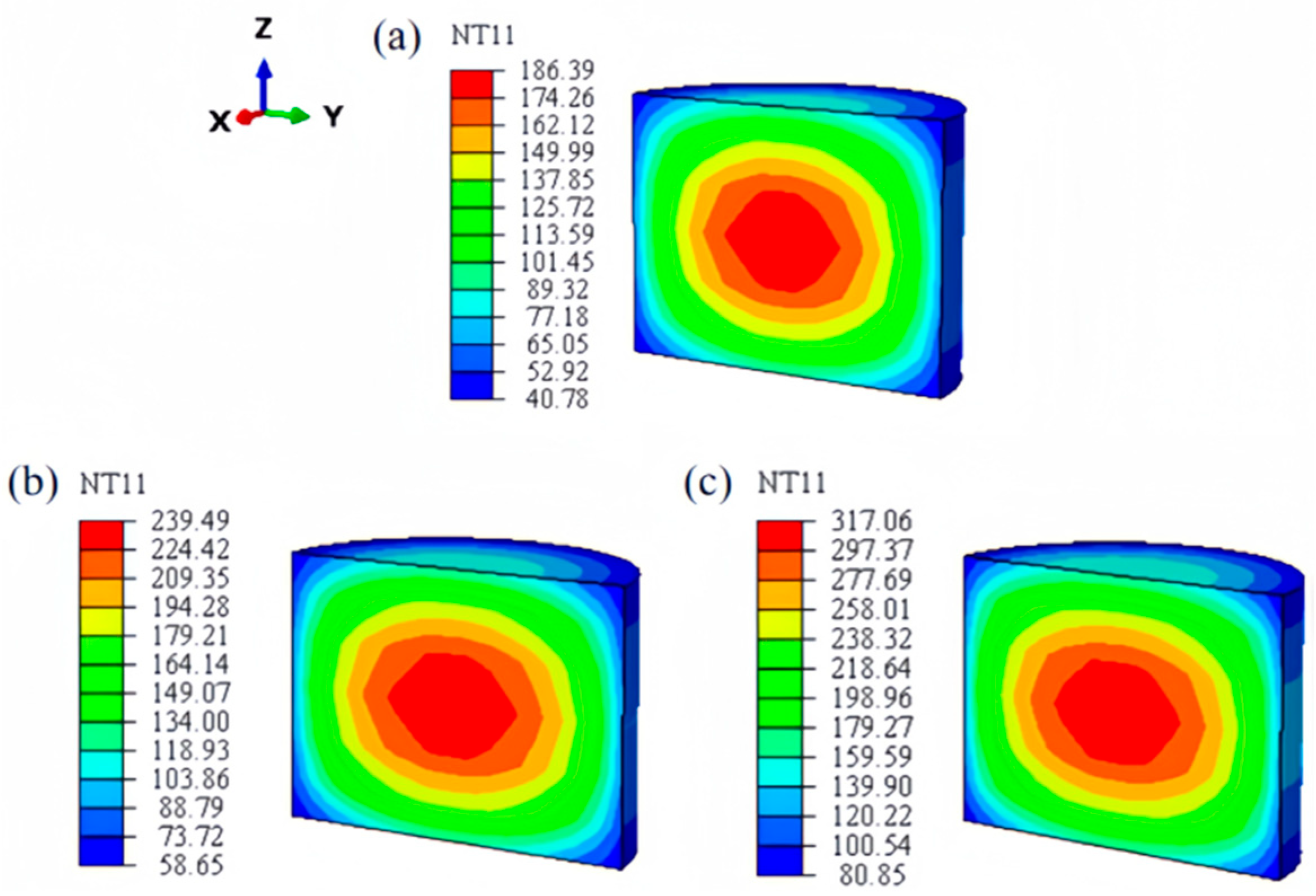
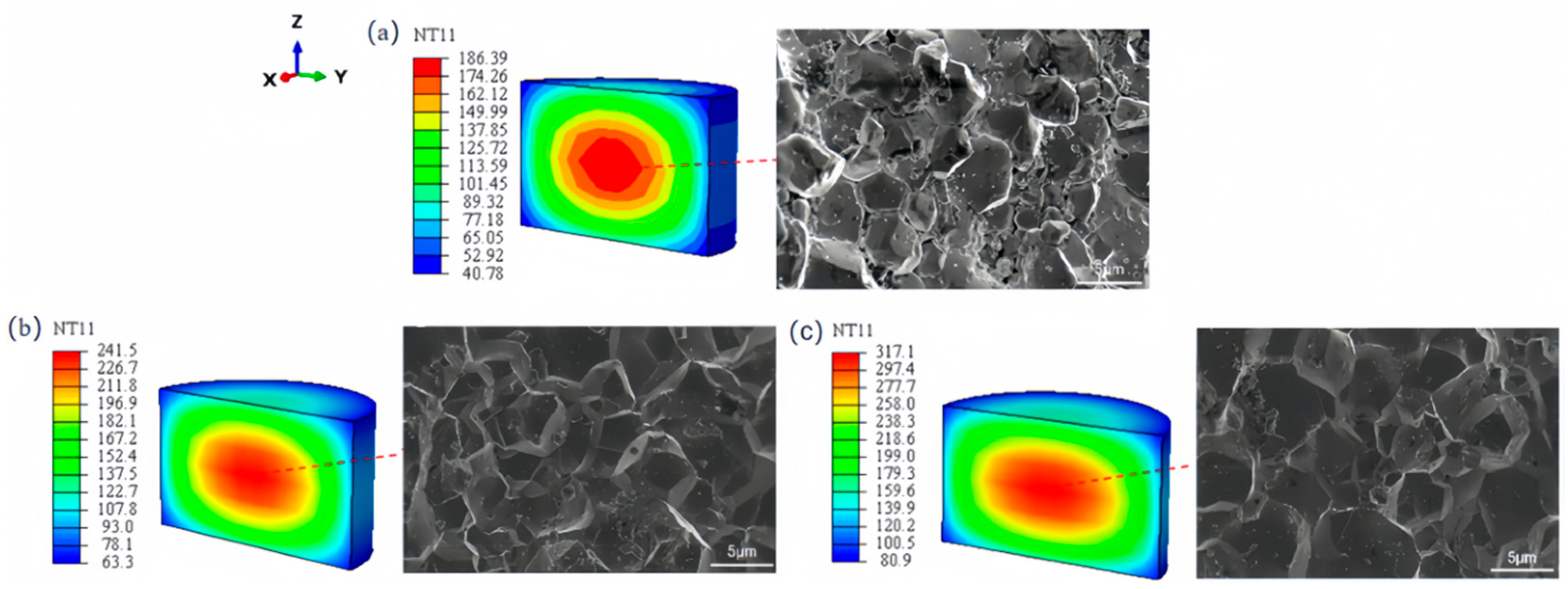
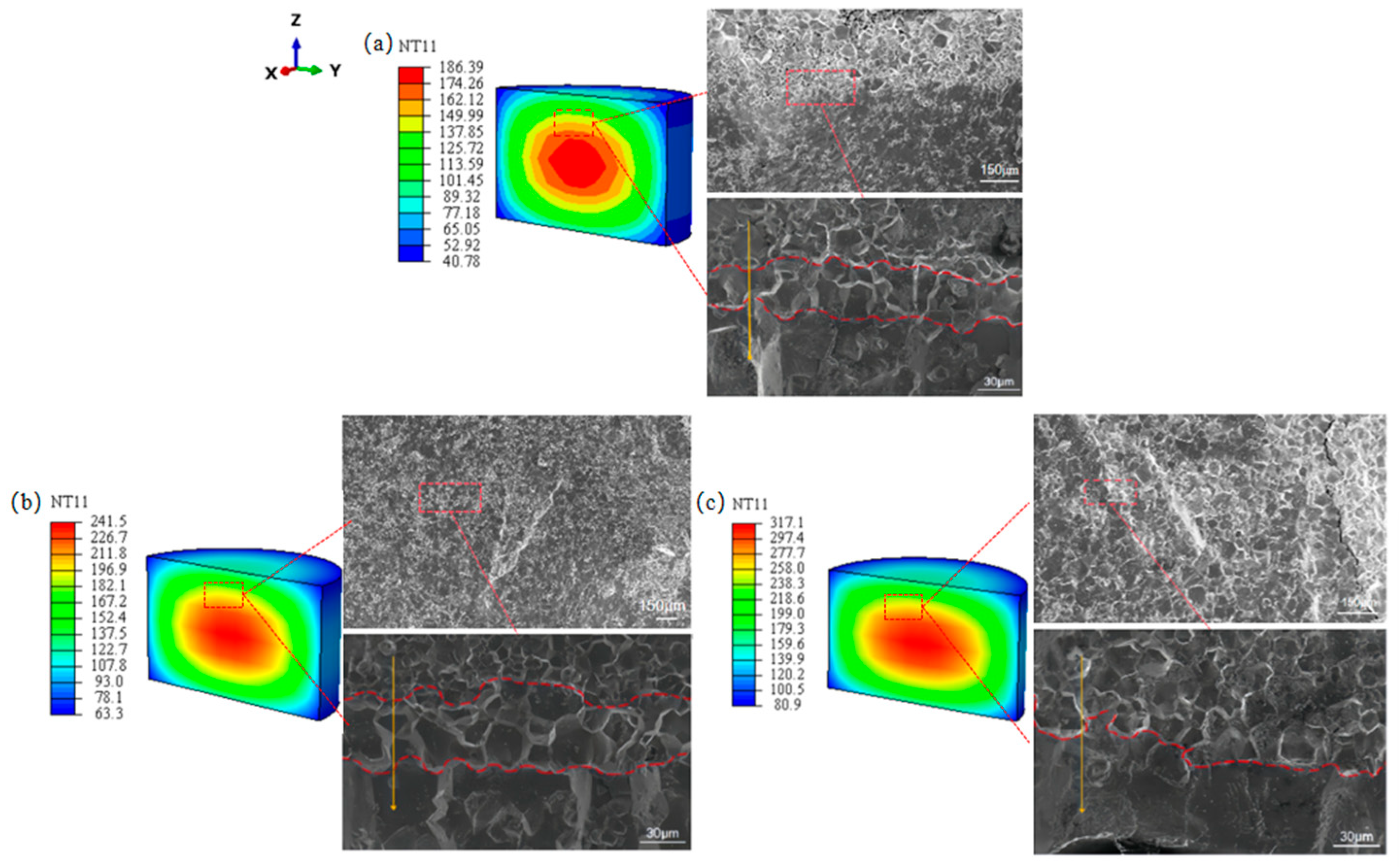
3.1. Analysis of Sintering Temperature Fields
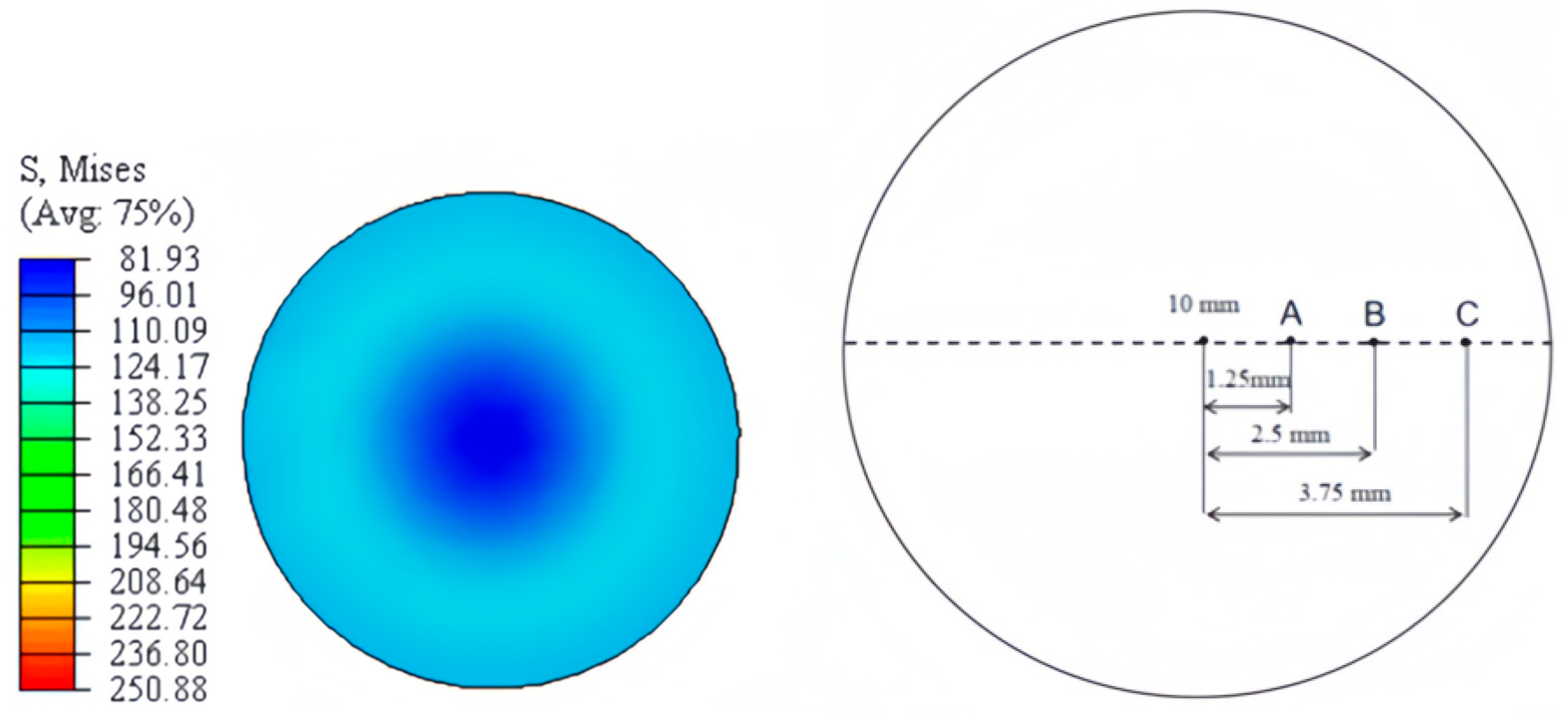
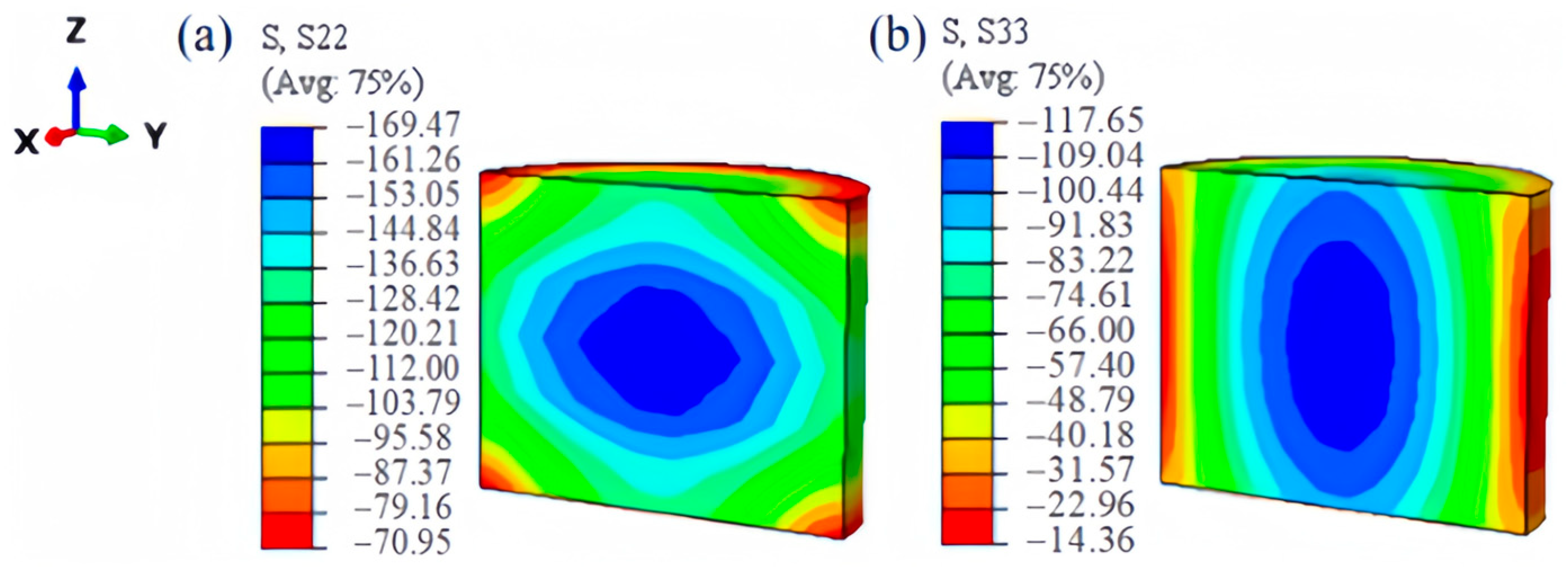
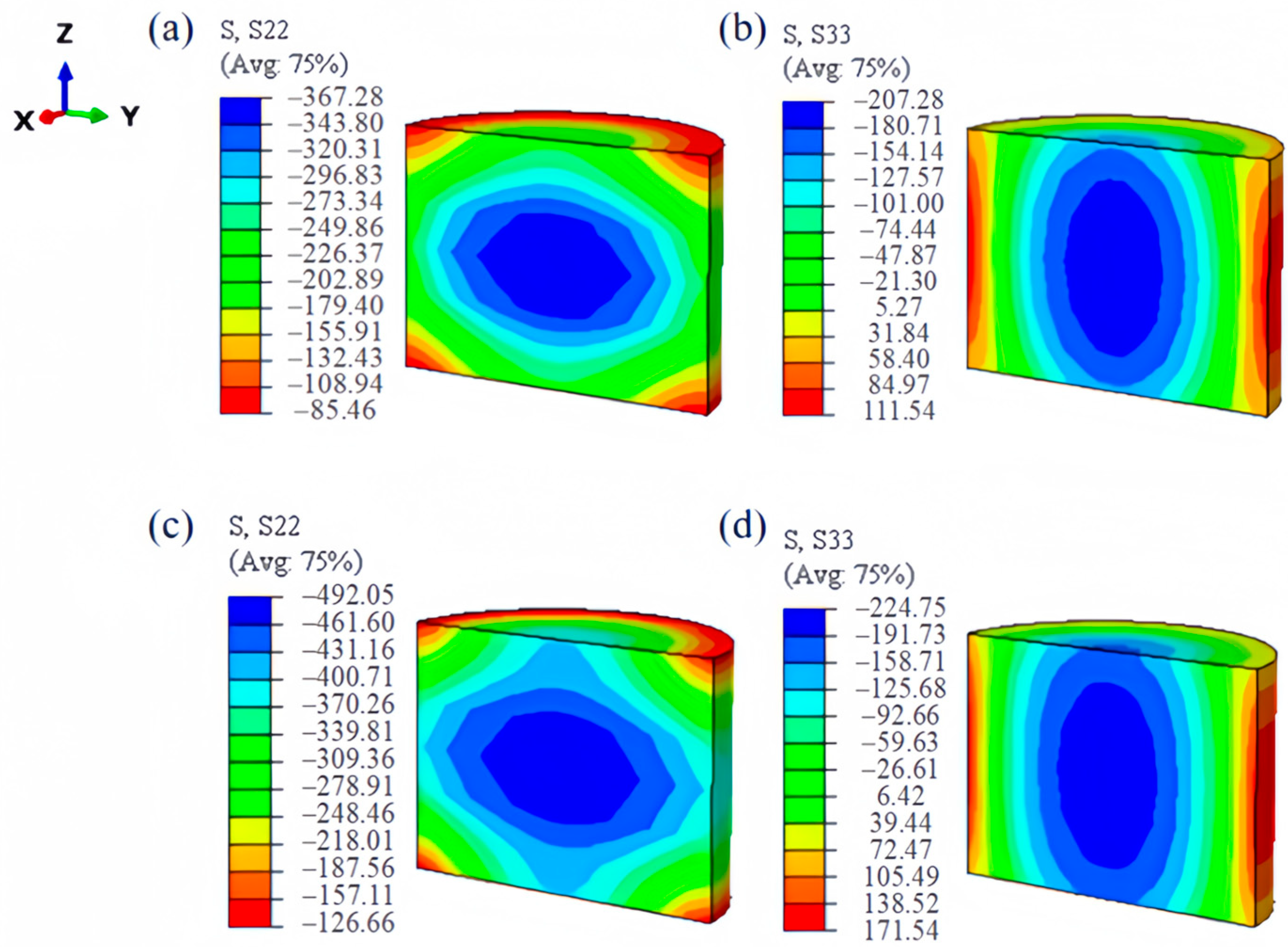
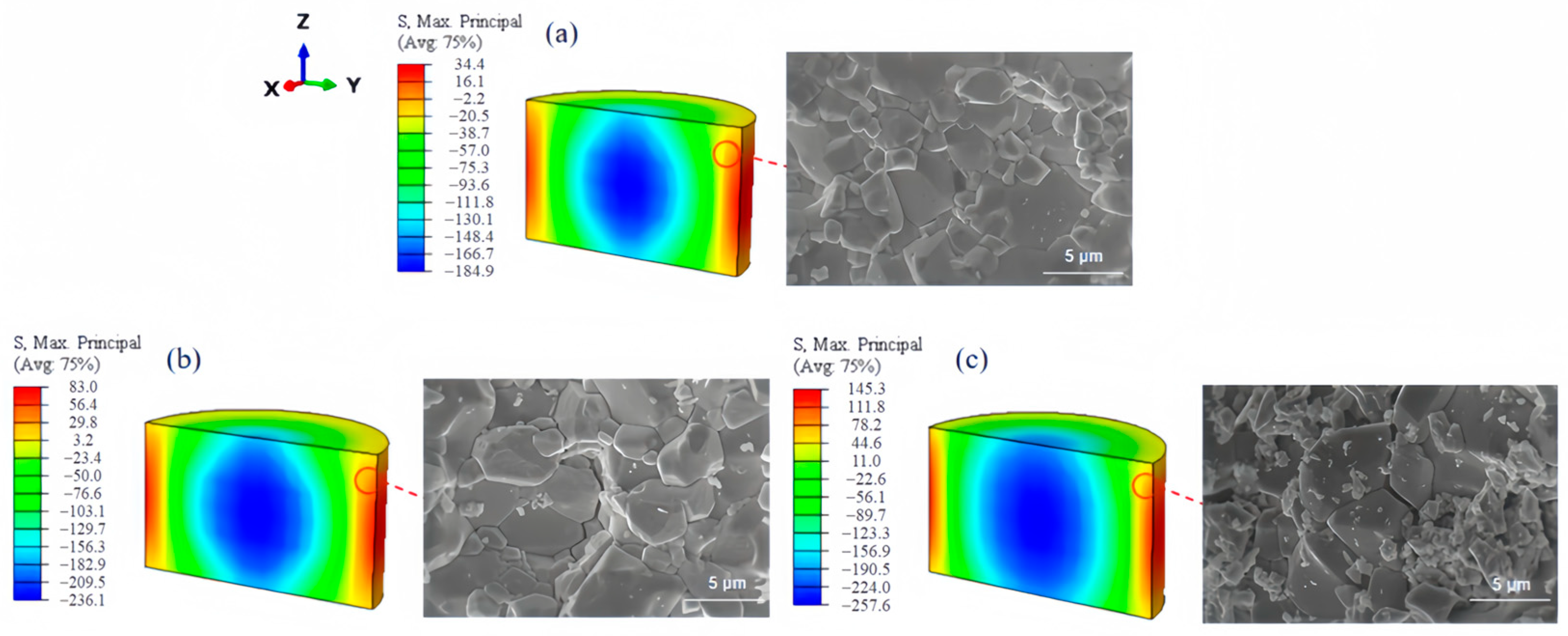
3.2. Analysis of Stress Field After Powder Sintering
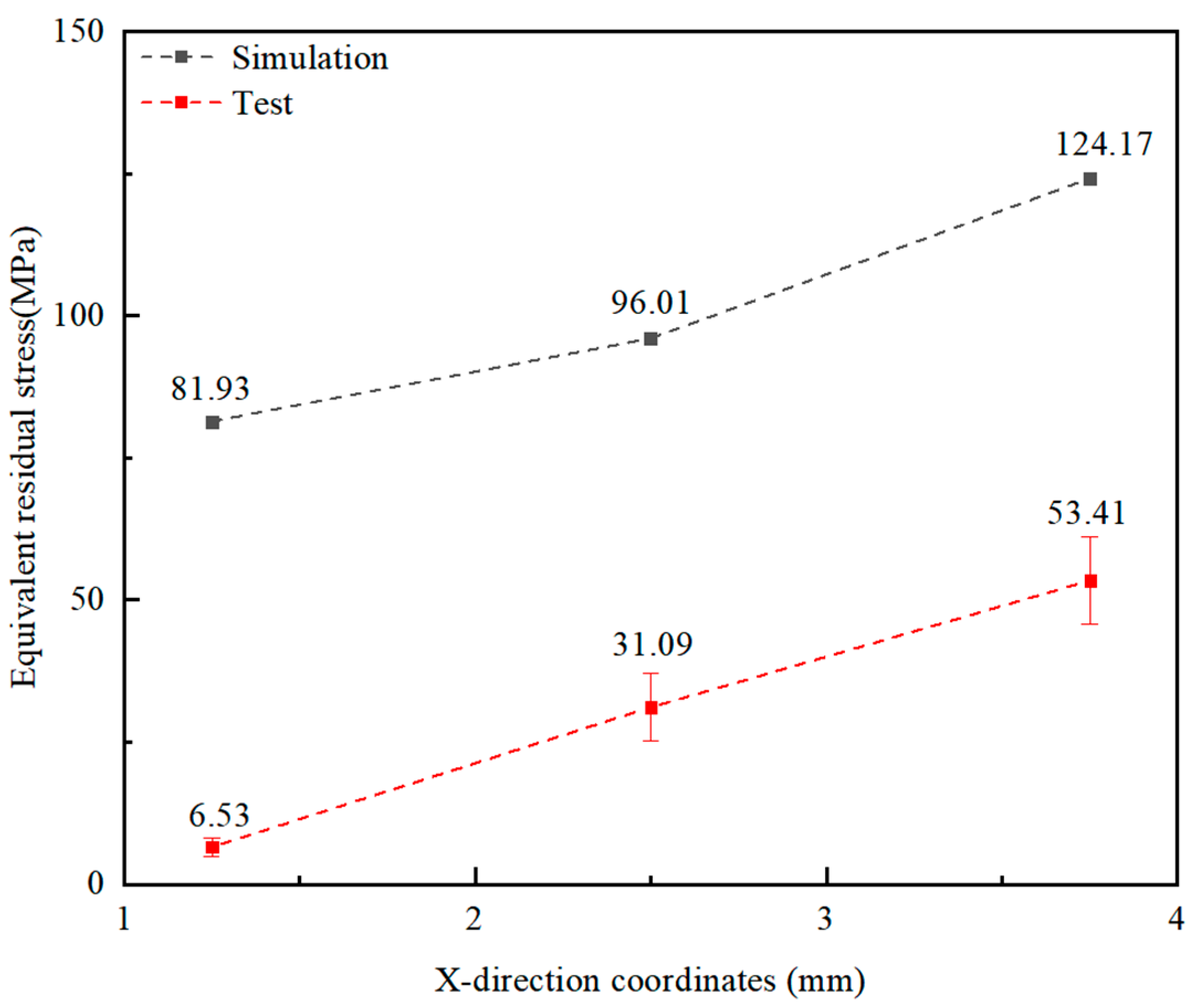
3.3. Simulation Analysis of Comparative Experiments
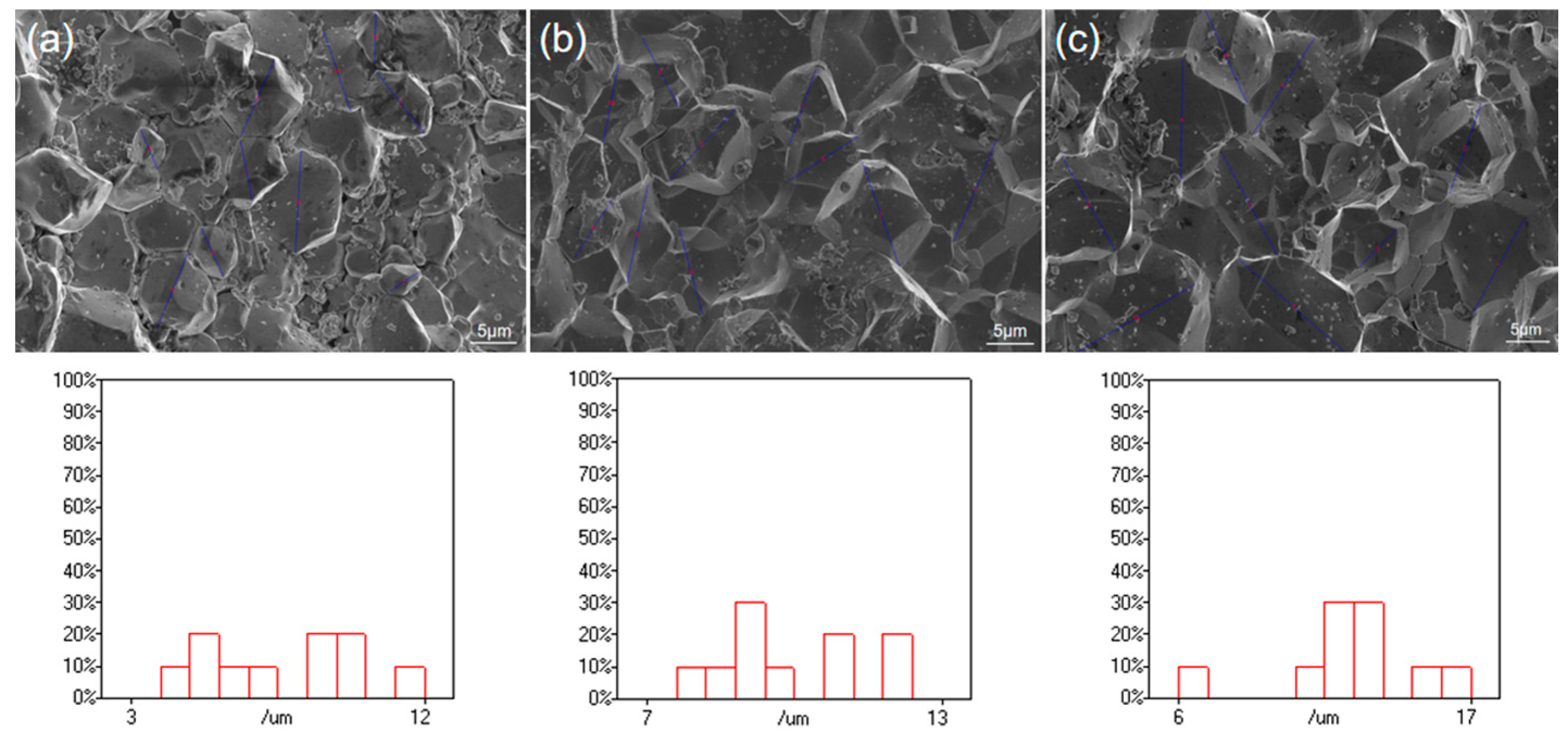
3.4. Scanning Electron Microscope Experiment Results
4. Discussion
- (1)
- As evidently demonstrated in the analysis of the sintering temperature field, at the preliminary stage of rising temperatures, the temperature of the outer layer of the powder’s compaction is much higher than that of the interior, while the densification rate of the outer powder’s compaction is much faster than the interior. Variations in sintering temperature exert a negligible influence on the trend in the temperature field.
- (2)
- The analysis of stress-field cloud charts at three sintering temperatures revealed that longitudinal compressive stress at the cross-sectional edge transitions to tensile stress. This transformation stems from grain growth and constrained internal contraction on account of the hard surface shell, ultimately giving rise to a stress-state transition from compression to tension at the surface.
- (3)
- The simulated results show good agreement with the experimental data, which not only validates the model’s accuracy but also addresses the challenge of non-visualizable temperature and stress fields. Aside from this, the model effectively forecasts crack-susceptible regions, providing a data-driven strategy to mitigate rupture in green bodies during processing.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Amato, A.; Becci, A.; Birloaga, I.; De Michelis, I.; Ferella, F.; Innocenzi, V.; Ippolito, N.; Gomez, C.P.J.; Vegliò, F.; Beolchini, F. Sustainability analysis of innovative technologies for the rare earth elements recovery. Renew. Sustain. Energy Rev. 2019, 106, 41–53. [Google Scholar] [CrossRef]
- Gutfleisch, O.; Kirchner, A.; Grünberger, W.; Hinz, D.; Schäfer, R.; Schultz, L.; Müller, K.H. Backward extruded NdFeB hddr ring magnets. J. Magn. Magn. Mater. 1998, 183, 359–364. [Google Scholar] [CrossRef]
- Sadullaho, A.G.; Altuncevahir, B.; Addemi, A.O. Effect of intergranular phase seg regation on magnetic properties of NdFeB magnet. Electron. Mater. Lett. 2014, 10, 153–157. [Google Scholar] [CrossRef]
- Henderson, R.; Chandler, H.; Akisanya, A.; Barber, H.; Moriarty, B. Finite element modelling of cold is ostatic pressing. J. Eur. Ceram. Soc. 2000, 20, 1121–1128. [Google Scholar] [CrossRef]
- Hamano, M. Overview and outlook of bonded magnets in Japan. J. Alloys Compd. 1995, 222, 8–12. [Google Scholar] [CrossRef]
- Ormerod, J.; Constantinides, S. Bonded permanent magnets: Current status and future opportunities (invited). J. Appl. Phys. 1997, 81, 4816–4820. [Google Scholar] [CrossRef]
- Herbst, J.F.; Croat, J.J. Neodymium-iron-boron permanent magnets. J. Magn. Magn. Mater. 1991, 100, 57–78. [Google Scholar] [CrossRef]
- Lee, R.W. Hot-pressed neodymium-iron-boron magnets. Appl. Phys. Lett. 1985, 46, 790–791. [Google Scholar] [CrossRef]
- Croat, J.J. Current status of rapidly solidified NdFeB permanent magnets. IEEE Trans. Magn. 1989, 25, 3550–3554. [Google Scholar] [CrossRef]
- Olevsky, E.A. Theory of sintering: From discrete to continuum. Mater. Sci. Eng. Rep. 1998, 23, 41–100. [Google Scholar] [CrossRef]
- Khoei, A.R.; Shamloo, A.; Azami, A.R. Extended finite element method in plasticity forming of powder compaction with contact friction. Int. J. Solids Struct. 2006, 43, 5421–5448. [Google Scholar] [CrossRef]
- Mardari, A.; Mazuru, S. Simulation of the pressing process with combined forces by using ABAQUS software. Appl. Mech. Mater. 2013, 371, 158–162. [Google Scholar] [CrossRef]
- Sun, Z.Z.; Peng, W.F.; Moliar, O.; Li, H. Simulation of Ti-30Cu powder rolling process based on Drucker Prager/Cap model. Mater. Mech. Eng. 2023, 47, 92–102. [Google Scholar]
- Staf, H.; Olsson, E.; Larsson, P.L. Mechanical characterization of powder materials: A general approach detailed for cemented carbides. Powder Technol. 2020, 364, 531–537. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, F.; Zhu, W. Calibration of a constitutive model for polycrystalline diamond sintering process. Diam. Relat. Mater. 2024, 148, 111422. [Google Scholar] [CrossRef]
- Li, X.Q.; Li, L.; Hu, K.; Chen, Z.C.; Qu, S.G.; Yang, C. Microstructure and magnetic properties of anisotropic Nd–Fe–B magnets prepared by spark plasma sintering and hot deformation. Trans. Nonferrous Met. Soc. China 2014, 24, 3142–3151. [Google Scholar] [CrossRef]
- Zhou, R.; Zhang, L.-H.; He, B.-Y.; Liu, Y.-H. Numerical simulation of residual stress field in green power metallurgy compacts by modified Drucker-Prager Cap model. Trans. Nonferrous Met. Soc. China 2013, 23, 2374–2382. [Google Scholar] [CrossRef]
- Shin, H.; Kim, J.B. Physical interpretations for cap parameters of the modified Drucker-Prager Cap model in relation to the deviator stress curve of a particulate compact in conventional triaxial testing. Powder Technol. 2015, 280, 94–102. [Google Scholar] [CrossRef]
- LaMarche, K.; Buckley, D.; Hartley, R.; Qian, F.; Badawy, S. Assessing materials’ tablet compaction properties using the Drucker-Prager Cap model. Powder Technol. 2014, 267, 208–220. [Google Scholar] [CrossRef]
- Manshoori Yeganeh, A.; Movahhedy, M.R.; Khodaygan, S. An efficient scanningalgorithm for improving accuracy based on minimising part warping in selected laser sintering process. Virtual Phys. Prototyp. 2018, 14, 59–78. [Google Scholar] [CrossRef]
- Panda, B.K.; Sahoo, S. Thermo-mechanical modeling and validation of stress field during laserpowder bed fusion ofAlSil0Mg built part. Results Phys. 2019, 12, 1372–1381. [Google Scholar] [CrossRef]
- Li, J.; Jin, Y.; Chang, Y.; Zuo, D. Finite element simulation and experimental study ofsingle-laser trackin laser polishing ofTi6Al4V. Int. J. Adv. Manuf. Technol. 2022, 121, 4571–4581. [Google Scholar]
- Yazici, B.A.; Kraft, T.; Riedel, H. Finite element modelling of pm surface densification process. Powder Metall. 2008, 51, 211–216. [Google Scholar] [CrossRef]
- Landi, E.; Tampieri, A.; Celotti, G.; Sprio, S. Densification behaviour and mechanisms of synthetic hydroxyapatites. J. Eur. Ceram. Soc. 2000, 20, 2377–2387. [Google Scholar] [CrossRef]
- Jiang, S.; Zhang, J.-C.; Yan, S.; Li, X.-L. A New Approach for Residual Stress Analysis of GH3535 Alloy by Using Two-Dimensional Synchrotron X-Ray Diffraction. Chin. Phys. Lett. 2020, 37, 070701. [Google Scholar] [CrossRef]
- Xie, L.; Jiang, C.; Lu, W. The influence of shot peening on the surface properties of (TiB+TiC)/Ti–6Al–4V. Appl. Surf. Sci. 2013, 280, 981–988. [Google Scholar] [CrossRef]
- Ren, X.; Zhang, T.; Zhang, Y.; Jiang, D.; Yongzhuo, H.; Guan, H.; Qian, X. Mechanical properties and residual stresses changing on 00Cr12 alloy by nanoseconds laser shock processing at high temperatures. Mater. Sci. Eng. A 2010, 528, 1949–1953. [Google Scholar] [CrossRef]
- Bhattacharya, S. Pressure-Assisted Densification of Non-Homogeneous Ceramic Compacts; University of Massachusetts Amherst: Amherst, MA, USA, 1997. [Google Scholar]
- Yin, W.; Chen, R.; Tang, X.; Ju, J.; Yan, A. Effect of pressless heat treatment on the magnetic performance and microstructure of hot-deformed Nd-Fe-B magnet. J. Magn. Magn. Mater. 2019, 482, 9–13. [Google Scholar] [CrossRef]
- Jing, Z.; Guo, Z.H.; Li, M.Y.; Hu, Y.H.; Song, K.K.; Fang, Y.K.; Zhu, M.G.; Li, W. Effects of Hot-Pressing Temperature on the Magnetic Properties of Hot-Pressed Nanocrystalline Nd–Fe–B Magnets. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]

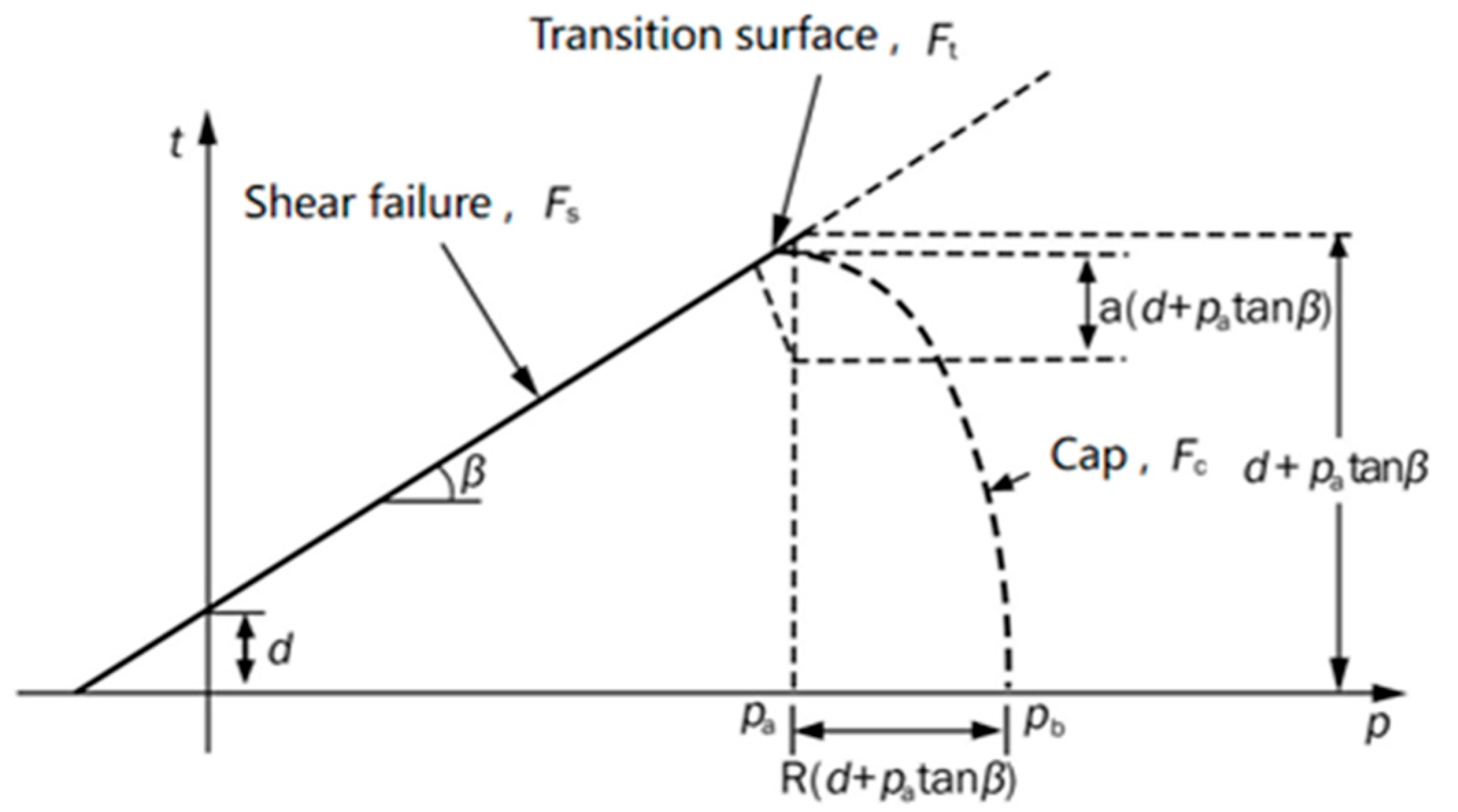

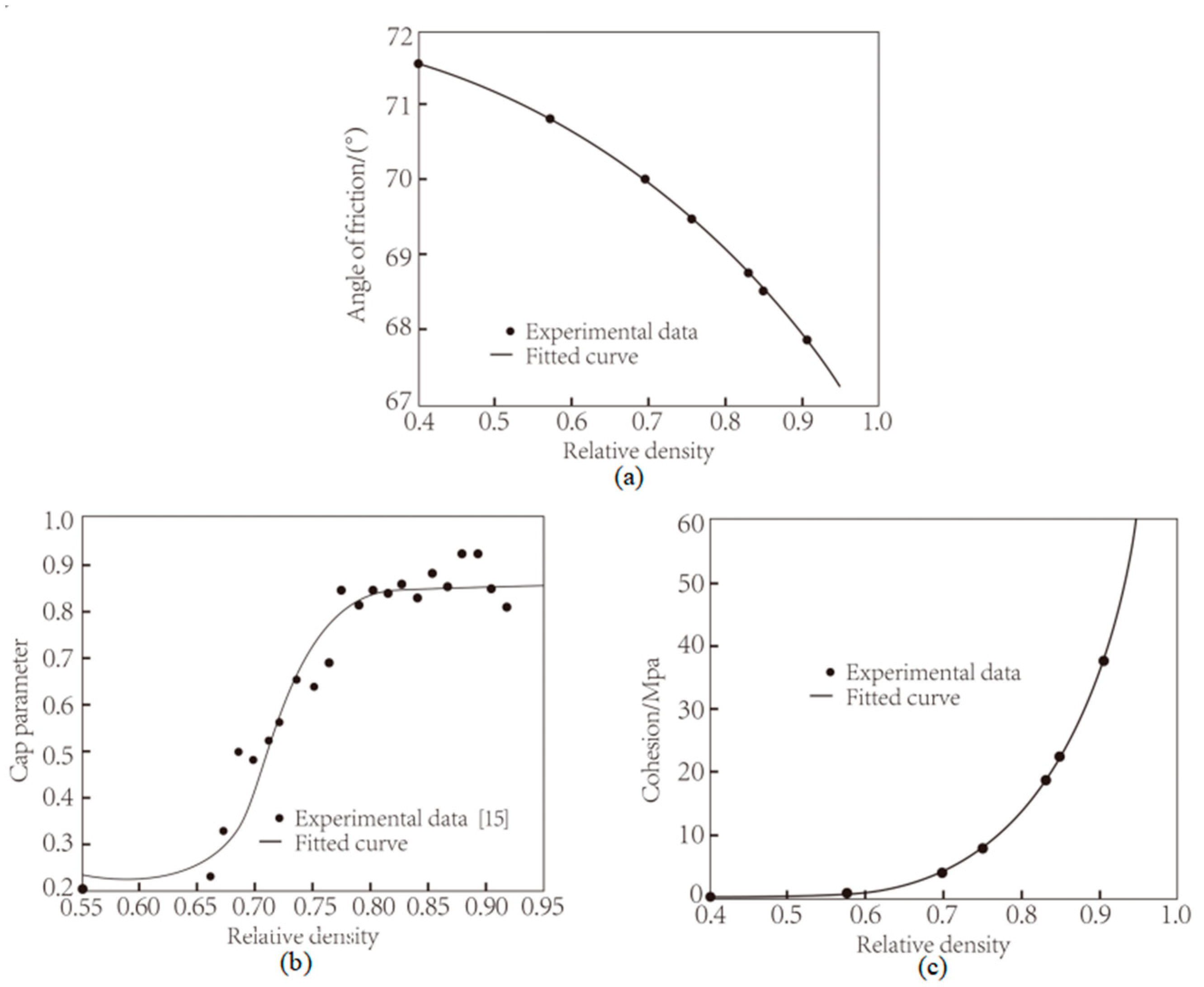

| Symbol | Properties | Quantity |
|---|---|---|
| ρ | Density (Kg/m3) | 7400 |
| v | Poisson’s Ratio | 0.24 |
| E | Young’s Modulus (MPa) | 158 × 103 |
| σbc | Compressive Strength (MPa) | 1100 |
| Rm | Tensile Strength (MPa) | 80 |
| αt | Coefficient of Thermal Expansion (1/k) | 5 × 10−6 |
| C | Specific Heat (J/kg/K) | 502 |
| d | Material Cohesion (MPa) | 204 |
| β | Angle of Friction | 10 |
| R | Cap Eccentricity | 0.4 |
| α | Flow Stress Ratio | 1 |
| Material | Coefficient of Static Friction | Coefficient of Rolling Friction |
|---|---|---|
| Powder–Powder | 0.545 | 0.010 |
| Powder–Tool | 0.300 | / |
| Temperature (°C) | X-Direction Coordinates (mm) | Sampling Points | Group 1 | Group 2 | Group 3 | Average |
|---|---|---|---|---|---|---|
| 740 | 1.25 | Point A | 4.99 | 8.32 | 6.28 | 6.53 |
| 2.5 | Point B | 24.25 | 34.85 | 34.19 | 31.09 | |
| 3.75 | Point C | 54.38 | 60.58 | 45.26 | 53.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, T.; Jin, W.; Cheng, F.; Sun, B.; Qiu, W.; Liu, N.; Ge, H.; Wang, R.; Mao, H. A Simulation of the Densification Process of NdFeB Bulks by a Modified Drucker–Prager Cap Model. Appl. Sci. 2025, 15, 7173. https://doi.org/10.3390/app15137173
Song T, Jin W, Cheng F, Sun B, Qiu W, Liu N, Ge H, Wang R, Mao H. A Simulation of the Densification Process of NdFeB Bulks by a Modified Drucker–Prager Cap Model. Applied Sciences. 2025; 15(13):7173. https://doi.org/10.3390/app15137173
Chicago/Turabian StyleSong, Tao, Wenbin Jin, Fang Cheng, Bo Sun, Wenbin Qiu, Nan Liu, Hongliang Ge, Rui Wang, and Huayun Mao. 2025. "A Simulation of the Densification Process of NdFeB Bulks by a Modified Drucker–Prager Cap Model" Applied Sciences 15, no. 13: 7173. https://doi.org/10.3390/app15137173
APA StyleSong, T., Jin, W., Cheng, F., Sun, B., Qiu, W., Liu, N., Ge, H., Wang, R., & Mao, H. (2025). A Simulation of the Densification Process of NdFeB Bulks by a Modified Drucker–Prager Cap Model. Applied Sciences, 15(13), 7173. https://doi.org/10.3390/app15137173








