Abstract
Coal and gas outburst remains a critical and persistent challenge in coal extraction, posing a profound threat for mine safety. The underlying mechanisms of such disaster, particularly the gas-driven coal fragmentation, continue to elude comprehensive understanding. To explore this problem, in this paper, gas seepage regularity in different structural bituminous coal and its influence on outburst-coal breaking were investigated through strength tests, isothermal adsorption tests, and gas seepage tests of stressed coal under various conditions. The results indicated that coal permeability decreased as axial stress, confining pressure, and gas kinetic diameter increased. That meant outburst-induced abrupt stress unloading and coal matrix destabilization changed gas seepage characteristics. As a result, a self-reinforcing cycle effect where outburst-coal breaking and gas seepage are mutually stimulated was formed in a short time period when outbursts initiated, which further promoted outburst-coal breaking and outburst initiation. The findings of this study enhance our understanding of the mechanism of gas participating in coal fragmentation during outbursts, which are significantly conducive to gas disaster prevention, sustainable coal production, and efficient CBM development, further ensuring global energy security.
1. Introduction
Under the consensus of coal and gas co-mining, coal mine safety and efficient production represent critical challenges in coal resource extraction [1,2], with coal and gas outburst prevention and coalbed methane (CBM) development being particularly vital [3], with both intrinsically associated with the migration behavior of methane within coal seams [4,5]. For CBM development, reservoir permeability serves as the governing parameter, that is, enhancing permeability to optimize methane migration through the coal’s pore-crack system constitutes the cornerstone technology for boosting its production [6,7]. While coal and gas outbursts, catastrophic and instantaneous dynamic disasters, manifest as a specific type of gas emission phenomena encountered during underground coal mining [8], where coal is fragmented and thereto ejected abruptly and violently with massive gas from the working face [9,10]. Although extensive domestic and international research spanning over a century has yielded significant insights, a definitive consensus on its triggering and developmental mechanism remains absent. However, some foundational insights have been gained, various theoretical hypotheses have been proposed, which commonly attribute the occurrence of coal and gas outburst to a comprehensive result of in situ stress, gas pressure, coal’s physico-mechanical properties, geological structure, etc. [11,12,13,14]. Notably, recent studies suggest gas release as a dominant energy contributor in both triggering outburst initiation and maintaining its further chain-type development, where gas migration plays a pivotal role [15,16].
Gas migration within coal structure involves gas desorption, diffusion, and seepage [4,16,17]. The well-developed porous network, comprising interconnected pores, joints, and cracks, serves as sites and pathways for gas migration [16,18,19]. Specifically, gas desorption is the physical process in which gas molecules obtain sufficient energy to overcome van der Waals force for escaping from coal matrix surface when adsorption equilibrium is disrupted, predominantly occurring on micropore surfaces (<0.01 μm) [20]. Gas diffusion is the process in which free gas migrates from micropores to fractures under concentration gradients, driven by the stochastic thermal motion of gas molecules, dominating in micropores and mesopores (<1 μm), generally subject to Fick’s law and its derivative laws [21]. While gas seepage is the directional gas flow through mesopores and macropores (>1 μm) under pressure gradient, governed by Darcy’s law for porous media [22]. Overall, the gas migration could alter the coal’s pore structure and redistribute effective stress within the matrix. Such stress state modifications could influence coal fragmentation and outbursts initiation [23,24,25,26]. Thus, elucidating the influence of gas migration, especially gas seepage, on coal’s physico-mechanical properties and coal breaking is of significance for clarifying outbursts mechanism.
Thus far, ongoing efforts intended to understand gas seepage regularity have acquired great progress. Shilova et al. [27] experimentally demonstrated that the permeability of Russian coking coals perpendicular to butt cleat direction decreases by 6.7 times under an 8-fold increase in confining pressure. Based on site characteristics of coal-gas co-mining in Pingdingshan, China, Xie et al. [28] introduced a mining-enhanced permeability parameter to quantify the permeability evolution of coal and other rocks. Their findings revealed a 0.14% increase in volumetric strain and 7.77% permeability enhancement under mining-induced stresses. Moreover, the impact of different factors on gas seepage regularity in coal was widely investigated. Liu et al. [29,30] explored true triaxial stress effects on intact and fractured coal, showing that macroscopic fractures elevated permeability by 1–3 orders of magnitude. Bai et al. [31] identified a sharp permeability rise in coal when deviatoric stress exceeded its compressive strength during triaxial loading/unloading cycles. Studies by Li and Zhu et al. [32,33] linked permeability evolution to adsorption-induced matrix swelling and pressure-driven pore deformation, highlighting synergistic effects of gas adsorption and mechanical deformation. Further, Tan et al. [34] and Yan et al. [35] emphasized the role of anisotropy, showing that permeability along the strike direction is higher than other orientations due to preferential fracture alignment. Wang and Li et al. [36,37] attributed nonmonotonic permeability changes to temperature effects, where gas-saturated coal exhibited matrix swelling, shrinkage, and microfracture generation under increased temperature. They pointed out that excessive thermal stresses are the essential causes of the coal damage and gas permeability enhancement. And permeability is further modulated by geological factors such as vitrinite reflectance and structural discontinuities (faults, folds) [38,39]. In addition, plentiful permeability theoretical models were established, including the empirical permeability models (EPM), volumetric strain permeability models (VSPM), plastic strain permeability models (PSPM) and damage variable permeability models (DVPM) [40].
Furthermore, significant advancements have been made in clarifying the effects of gas seepage on coal’s physico-mechanical properties and coal fragmentation. Under unloading conditions, Yin et al. [41] demonstrated that elevated gas pressure accelerated coal deformation and seepage velocity while reducing strength, establishing a power–law relationship between confining pressure and Poisson’s ratio during destabilization. Peng et al. [42] pioneered the triaxial seepage tests, revealing that gas seepage weakened coal strength, accelerated failure, and generated high-pressure gas zones capable of storing critical outburst energy. In addition, Vandamme [43] and Nikoosokhan et al. [44] attributed mechanical deterioration to adsorption-induced structural softening, where gas adsorption disrupted coal’s rigidity. Sampath et al. [24] believed that adsorbate-matrix interactions significantly reduced surface energy, leading to the deterioration of coal properties, consistent with the “Rehbinder effect” [45]. Liu and Cai et al. [46,47] validated gas-weakening effects through triaxial tests, revealing that increased gas pressure reduced compressive strength, elastic modulus, peak strain, and bearing capacity, while elevating Poisson’s ratio. Moreover, Ding and Zheng et al. [48] utilized shock tube experiments to demonstrate that gas-driven coal continuous failure exhibited multi-layered tensile cracking, predominantly governed by free gas seepage. Tan et al. [49] modeled gas-saturated coal failure under sudden pressure relief using a rupture wave framework, emphasizing transient stress wave propagation. The study of Lei et al. [50] indicated that free gas energy was primarily consumed during coal fragmentation, highlighting energy partitioning in outburst mechanisms. Finally, Guan [51] and Wang [52] simulated abrupt gas desorption in shock tubes, showing that rapid pressure drops triggered instantaneous coal fragmentation and ejection, with high ejection velocities in high-gas-pressure scenarios.
Despite significant advancements in characterizing gas permeability affected by multifactorial conditions, the gas seepage regularity in structural bituminous coals is still inadequately characterized. Current research predominantly focuses on permeability dependencies (e.g., stress state, gas type) and mechanical deformation effects, while investigations into gas seepage characteristics of heterogeneous bituminous coals and their role in promoting coal fragmentation and outburst initiation remain rarely reported. However, it is of significance to elucidate such seepage regularity and influence for understanding how gas participates in and gas seepage facilitates coal fragmentation and outburst initiation, encountering different geo-structural coal seams. Thus, in this paper, systematic gas seepage tests of stressed bituminous coal with different structures were conducted to probe the gas seepage regularity and further explore its influence on outburst-coal breaking. In addition, the mechanical and adsorptive properties were measured and analyzed to support the above investigations. The findings would provide crucial experimental evidence for advancing multi-field coupling theories of coal and gas outbursts, contributing to gas disaster prevention, sustainable coal production, and efficient CBM development, further ensuring global energy security.
2. Materials and Methods
2.1. Coal Sample Preparation
The coal samples were freshly obtained from a working face of Coal Seam No. 5 in the Panzhihua Coal Mine, located in western Guizhou Province, China. This bituminous seam, part of the Upper Permian Longtan Formation (P3l), was appraised as an outburst-prone stratum under the Chinese standard AQ 1024-2006 [53]. Intact coal blocks were vacuum-sealed onsite to preserve structural integrity and subsequently processed into powder and standard core samples. The powdered samples were sieved into 50–80 mesh (0.180–0.300 mm) for isothermal adsorption tests and <40 mesh (<0.5 mm) for remolding briquette coal samples. To probe the distinct behavior of gas seepage in hard and soft coal seams and its influence on outburst-coal breaking, both raw and briquette coal samples were utilized. For seepage tests and triaxial compression tests, drilled raw coal cores were processed using a Kemet rock-cutter and an M250 end-face grinder. Subsequently, the end faces were polished with a Kemet 15 fine end-face grinder, ensuring a surface flatness of ≤0.025 mm. Referred to the existing research on briquette coal permeability in which a 100 MPa was commonly selected as baseline [54], briquette coal samples were press-formed in a custom mold for 30 min using coal particles with 10% moisture content under forming pressures of 50, 70, 100, and 130 MPa, to analyze the differences in seepage regularity exhibited by weak coal seams under different geological forming pressures and their influences on outburst-coal breaking.
Proximate analysis of coal particles (<80 mesh) was conducted via a 5E-MACIII infrared analyzer in accordance with the Chinese standard GB/T 212-2008 [55], with results detailed in Table 1. To eliminate moisture interference, raw coal samples and particle samples were oven-dried at 353.15 K for 12 h, whereas briquette samples were dried at the same temperature for 96 h prior to testing.

Table 1.
Proximate analysis results for coal samples.
2.2. Experimental Procedure
2.2.1. Strength Tests of Coal Samples
Under natural geological conditions, deep-seated coal seams are subjected to a triaxial compressive stress state, commonly termed the in situ stress regime. The overburden pressure, originating from the weight of overlying strata, governs the internal stress distribution within coal seams. Variations in stress states induce significant alterations in the microstructural framework of coal mass, including structural planes, joints, pores, and fissures, thereby modulating fluid migration pathways. The migration dynamics of gas within stressed coal matrices are pivotal for elucidating the damage mechanisms and failure modes of outburst-coal. Thus, to investigate the seepage dynamics of different structural bituminous coal, uniaxial and triaxial compressive strength tests were performed on both raw and briquette coal samples using an MTS815 Rock Mechanics Testing System and with real-time acoustic emission monitoring to capture micro-fracturing events. The strength and failure characteristics of the samples were systematically analyzed to correlate mechanical behavior with gas seepage properties.
2.2.2. Isothermal Adsorption Tests
Coal exhibits significant adsorption capacity owing to its highly developed pore structure. To investigate the adsorption characteristics of collected coal samples and derive critical parameters for subsequent analyses, isothermal adsorption tests were conducted. The isothermal adsorption behavior of gases in porous coal mass is governed by the Langmuir theory [56], which postulates a dynamic equilibrium between adsorption and desorption processes. Specifically, gas molecules adhere to coal pore surfaces through adsorption, while simultaneously desorbing back into the gaseous phase, resulting in equal adsorption and desorption rates under constant temperature conditions. This equilibrium state is expressed as
where is the surface coverage of porous media (), defined as the ratio of monolayer adsorption amount (mmol/g) to the saturation adsorption capacity (mmol/g); and denote the adsorption and desorption rate constants, respectively; (MPa) is the adsorption equilibrium pressure under isothermal condition.
Through algebraic rearrangement, Equation (1) can be rewritten as the relationship between the adsorbed gas amount () and equilibrium pressure ():
where (MPa−1) represents the Langmuir equilibrium constant quantifying the adsorption energy, valued as the reciprocal of the pressure at half-saturation (), i.e., .
In engineering practice, the Langmuir adsorption constants and are widely adopted as key indicators of coal’s adsorption behavior. The parameter quantifies the theoretical maximum gas storage capacity, while proportionately indicates the adsorption affinity under specific thermodynamic conditions. Therefore, to evaluate the adsorbability of collected coal samples, Isothermal Adsorption Tests were conducted using an automated gravimetric analyzer (Hiden IGA-100, Cheshire, UK). This system employs a magnetic suspension microbalance to quantify adsorbed gas mass by tracking sample mass changes with a resolution of 0.1 µg. Coal particles (100 g, 50–80 mesh) were prepared for testing. In order to investigate the permeability difference in adsorbable gases in coal’s porous structure, the adsorption behaviors of samples exposed to three gases (N2, CO2, and CH4) were systematically compared.
2.2.3. Gas Seepage Tests of Stressed Coal Samples
It is well established that coal is a porous medium with a high adsorption capacity, and its intricate pore structure offers abundant adsorption sites and pathways for gas migration. Upon coal and gas outbursts, gas migration is promptly actuated by a significant and steep gas pressure gradient that emerges within the coal body. The migrating gas flow plays a crucial role in the outburst-induced coal fragmentation process, serving as an energetic medium that not only facilitates coal fragmentation but also conveys the resultant crushed coal particles. Specifically, gas migration occurs primarily through diffusion in mesopores and micropores with pore widths less than 1 μm, driven by the random thermal motion of gas molecules, or through seepage predominantly in macropores and fissures with pore widths greater than 1 μm, directed by a gas pressure gradient.
Generally, seepage gas is recognized to move as a laminar flow, obeying the Darcy’s law, a formula empirically derived by French engineer H.P.G. Darcy in 1856 [57], which describes the linear relationship between the discharge rate of a fluid through a porous medium and the hydraulic gradient driving the flow.
where is the seepage flow, is the cross-sectional area through fluid, represents the seepage head, and means the hydraulic gradient, is the seepage coefficient. When substituting the hydraulic gradient with the gas pressure gradient, the Darcy’s law describing gas seepage in the horizontal direction will be obtained as
where and denote the seepage velocity and dynamic viscosity of gas, respectively, indicates the gas pressure gradient, and is the permeability of the medium matrix.
Equation (4) is the general expression of Darcy’s law frequently used to solve the problem of gas seepage within coal seams. Based on the above equation, the permeability can be defined as the volume of unit-viscosity fluid traversing through a unit cross-sectional area of a medium in unit time under a unit of pressure gradient [57]. Notably, the permeability is an inherent constant solely determined by the structural characteristic of the seepage medium, and completely independent of the properties of the fluid. Therefore, we can obtain
from Equation (4), i.e.,:
where and represent the pressure at the inlet and outlet of the seepage medium, respectively.
In Equation (5), for steady-state seepage of liquid, the parameters of seepage velocity and pressure gradient both remain constant due to the incompressibility of liquid, thus ensuring the computed permeability is a constant as well. However, this issue becomes more intricate for gas seepage due to its significant compressibility. Unlike in liquid seepage, the gas velocity does not remain constant along the seepage direction but accelerates near the outlet as a result of gas expansion. In the same way, the gas pressure gradient also increases near the outlet, so that the computed permeability remains constant only when both the gas seepage velocity and gas pressure gradient simultaneously increase at an unchanged ratio . Hence, it is imperative to revise Equation (6) for its application in gas seepage for permeability calculations, given its inherent unreasonableness under such circumstances.
Supposing gas expands isothermally as an ideal gas, with the exception of extremely high flow velocities, the value of remains consistent throughout the expansion process. Therefore
where represents the algebraic mean value of gas pressure, i.e., . Then, substitute Equation (7) into Equation (5), and we obtain
According to the gas state equation, it is easy to obtain
Because of . The above Equation (9) suggests the commonly used method for computing the permeability in steady-state tests of coal containing gas. By introducing the algebraic mean gas pressure, the calculated value becomes more stable and tends to approach a constant under different experimental conditions (when the structural characteristics of the coal remain unchanged). Therefore, the calculation of permeability in this paper is all conducted using this equation.
Based on this, gas seepage tests of stressed coal samples were conducted via the self-designed Thermo–Hydro–Mechanical coupled triaxial experimental system, housed within the State key laboratory of coal mine disaster dynamics and control of Chongqing University. The experimental system is schematically shown in Figure 1, which comprises a power pump unit, compressed gas cylinder, test chamber, control unit, and flow measurement unit. Additionally, a measuring cylinder was used to confirm gas emission by observing bubbles. This experimental system accommodates a maximum axial load of 1000 kN, confining a pressure of 60 MPa and a gas pressure of 6 MPa, with a measurement accuracy of ±1% for all three parameters. Axial loading employs displacement closed-loop control. The apparatus enables comprehensive evaluation of seepage in porous media under static/dynamic loading-unloading cycles, replicating complex geo-environmental conditions including variable in situ stresses, gas pressure, and temperatures. Both prepared raw coal samples and briquette coal samples shaped under different forming pressures were utilized for gas seepage tests, with various test conditions including axial stress, confining pressure, gas pressure, and gas type being set. The detailed test protocol can be found in Table 2, and the specific test steps are outlined as follows:

Figure 1.
Thermo–Hydro–Mechanical coupled tri-axial experimental system.

Table 2.
Protocol of the seepage tests of gassy coal samples.
① Position a coal sample in the test chamber, ensuring its end surfaces are in smooth pre-contact with the axial indenters. To facilitate gas flow exclusively along the axial direction within the coal sample, it should be encased cylindrically with heat shrink tubing and securely fastened with steel hoops.
② Mount the extensometer to measure the coal sample’s circumferential deformation and then seal the test chamber.
③ Initiate operation of both the power pump unit and the control unit, filling the test chamber with hydraulic oil to provide confining pressure.
④ Input target axial stress and confining pressure into the program control system based on test conditions, then load to reach these specified conditions.
⑤ With the loading state unchanged and the outlet sealed, inject test gas into the chamber for the specimens to adsorb until equilibrium is reached.
⑥ Open the outlet, keep the inlet gas pressure unchanged, allowing gas outflow through the coal sample into the atmosphere, and simultaneously record the gas flow using a high-precision gas flowmeter.
⑦ Repeat steps 1 to 6 under different test conditions and then process and analyze the data.
3. Results and Discussion
3.1. Strength Characteristics of Coal Samples
The inherent anisotropy and porous microstructure of coal necessitate stringent experimental protocols to take its structural heterogeneity into account. In this study, uniaxial compression tests were conducted on five sets of briquette coal specimens prepared under varying forming pressures and four sets of raw coal specimens to determine statistically robust uniaxial compressive strength (UCS) values. This approach mitigates the influence of intrinsic material variability, ensuring reproducibility across heterogeneous coal matrices. The results were shown in Figure 2 and Figure 3.
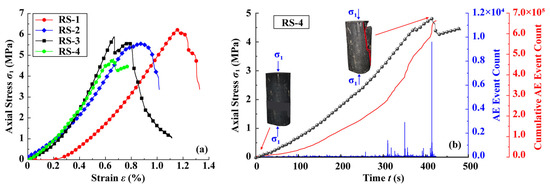
Figure 2.
UCS characteristics of raw coal samples. (a) UCS of raw coal samples; (b) real-time acoustic emission characteristics of raw coal samples under uniaxial compression.
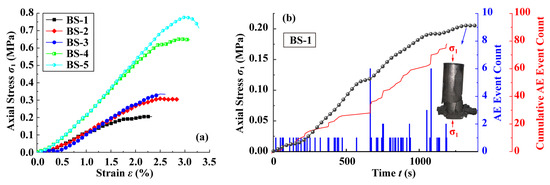
Figure 3.
UCS characteristics of briquette coal samples. (a) UCS of briquette coal samples with different sample forming pressure; (b) real-time acoustic emission characteristics of briquette coal samples under uniaxial compression.
As illustrated in Figure 2a, the UCS of raw coal samples displayed significant variability, a direct consequence of their well-developed pore-fracture networks and abundant structural discontinuities (e.g., weak planes). The experimental results, summarized in Table 3, reported average values of UCS (5.63 MPa), elastic modulus (1.014 GPa), and Poisson’s ratio (0.310) for the raw coal specimens. Acoustic emission (AE) monitoring could be employed to elucidate the instability, fracture propagation, and damage evolution mechanisms within coal-rock materials by tracking variations in AE event counts and energy release [58]. Figure 2b presents the AE characteristics of the RS-4 coal specimen under uniaxial compression. During the initial compaction and elastic deformation stages, the AE event count remained low, reflecting elastic energy accumulation within the coal matrix under low stress conditions. This phase was characterized by limited microcrack nucleation and localized propagation. As the specimen transitioned into the yield stage with increasing stress, the AE event count rose markedly, signaling crack propagation and internal damage—a precursor to structural instability. At macroscopic failure, both instantaneous and cumulative AE event counts surged abruptly, corresponding to the formation of an interconnected fracture network that established a continuous weak plane, along which the specimen ultimately failed. The sporadic occurrence of high-energy AE signals post-yield indicated that coal failure is not a continuous process but rather a progressive sequence involving microcrack nucleation, propagation, coalescence into macrocracks, and eventual structural collapse.

Table 3.
Results of the uniaxial compression tests for raw coal samples.
In contrast to raw coal, the briquette samples exhibited enhanced homogeneity due to the cementation of coal particles under forming pressure. Consequently, as shown in Figure 3, no distinct compaction stage was observed during uniaxial compression (Figure 3a). Acoustic emission (AE) monitoring revealed that the AE event count remained at a low level (Figure 3b), primarily originating from interparticle slippage and rearrangement within the briquette matrix. These signals were notably weaker than those generated by microfracture propagation in raw coal. The stable AE event count suggested uniform particle packing and consistent intergranular motion probabilities under axial loading. The cumulative AE event count exhibited a stepwise increase during compression, indicating significant static friction between coal particles. During static friction resistance phases, limited slippage occurred, suppressing detectable AE signals. Prior to macroscopic failure, AE activity intensified as axial stress approached peak strength, reflecting frequent interparticle shear motions, microcrack nucleation, and stable crack propagation. These processes culminated in the formation of interconnected macro-weak planes. Final failure occurred under combined axial and frictional forces, accompanied by a rapid surge in both instantaneous and cumulative AE event counts. Post-failure analysis identified the dominant failure mode as X-shaped conjugate inclined shear failure, characterized by intersecting shear bands. Furthermore, Specific UCS values are shown in Table 4. The experimental results demonstrated a direct linear proportionality between the UCS, elastic modulus, and forming pressure for briquette coal samples (Figure 3b). As forming pressure increases, interparticle cementation within the briquette matrix becomes denser, significantly enhancing resistance to intergranular slippage and shear-induced motion. This consolidation mechanism drives a progressive improvement in both the UCS and elastic modulus of the specimens.

Table 4.
Results of the uniaxial compression tests for briquette coal samples with different sample forming pressure.
Similarly, triaxial compression tests were conducted under varying confining pressures for five sets of raw coal samples and under a fixed confining pressure of 2 MPa for briquette coal samples prepared at different forming pressures, with results exhibited in Figure 4. The cohesion, and internal friction angle were systematically evaluated, as listed in Table 5 and Table 6. As shown in Figure 4a, the anisotropic nature of coal introduces variability in the conventional triaxial test results of raw coal samples, as evidenced by differing stress–strain curve slopes. The triaxial compressive strength of raw coal samples increased with higher confining pressures, accompanied by enhanced deformation capacity and elevated elastic limits. Based on experimental data, the calculated cohesion and internal friction angle of raw coal were 1.35 MPa and 49.43°, respectively (see Table 5). Figure 4b illustrates that the triaxial compressive strength and load-bearing capacity () of briquette coal samples increased with forming pressure. Furthermore, both cohesion and internal friction angle exhibited a linear dependence on forming pressure (see Table 6), which is consistent with the consolidation-driven enhancement of interparticle bonding.
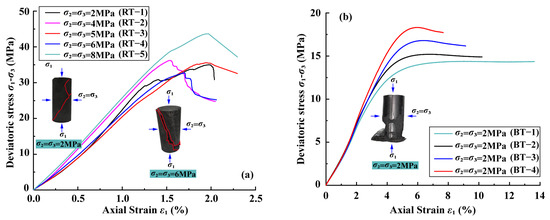
Figure 4.
Triaxial strength characteristics of raw coal and briquette coal samples. (a) Triaxial strength of raw coal samples under different confining pressures; (b) triaxial strength of briquette coal samples with different sample forming pressures under a fixed confining pressure of 2 MPa.

Table 5.
Results of cohesion force and internal friction angle of raw coal samples under different confining pressures.

Table 6.
Results of cohesion force and internal friction angle of briquette coal samples with different sample forming pressures under a fixed confining pressure of 2 MPa.
Coal, as a dual-porosity medium comprising pores and fractures, possesses a well-developed pore network that serves as critical pathways for gas migration. The gas transport capacity is governed by the abundance, complexity, connectivity, and spatial distribution of these pores. The overmentioned experimental results demonstrated that in raw coal, the initiation and propagation of microcracks, the formation of interconnected weak planes, and the coalescence of macrocracks significantly enhanced pore network connectivity, thereby improving gas migration efficiency. In contrast, briquette coal exhibited inherently higher porosity and lower compressive resistance. Under identical stress conditions, this structural heterogeneity facilitated the development of more extensive gas migration channels, resulting in superior gas permeability compared to raw coal.
3.2. Adsorption Characteristics of Coal Samples
Coal exhibits pronounced adsorption properties due to its intrinsic structural characteristics—abundant pore networks and well-developed microfractures. These features provide numerous binding sites for gas molecules. When gas molecules enter the coal matrix, they are attracted by the adsorptive potential generated through van der Waals forces between the molecules and coal surface, adhering to pore walls. Desorption occurs when molecules acquire sufficient kinetic energy to overcome this potential. The dynamic equilibrium between adsorption and desorption arises from the stochastic motion of molecules and real-time variations in adsorption conditions, predominantly occurring in micropores. This process is typically described by the Langmuir (monolayer adsorption) [59] and BET (multilayer adsorption) theories [60]. The Langmuir theory posits that gas molecules form a single adsorbed layer on specific surface sites, aligning with Type I isotherms classified by the IUPAC [61]. It is widely used to derive critical adsorption constants. In contrast, the BET theory accounts for multilayer adsorption by considering the attraction between adsorbed and free-phase molecules, primarily applied for specific surface area determination [62]. In this study, the Langmuir theory was applied to analyze experimental data. Figure 5 illustrates the adsorption characteristics of N2, CH4, and CO2 in coal. All three gases exhibited Type I isotherms, where adsorption volume increases with rising equilibrium pressure under constant temperature until reaching saturation. Adsorption capacity grows progressively as pressure escalates, with more molecules occupying available sites. At a critical pressure, adsorption equilibrium is established when adsorbed molecules dynamically balance with those escaping from sites. Notably, coal demonstrated distinct adsorption affinities for the three gases: CO2 adsorption capacity was the highest, followed by CH4, while N2 adsorption was the weakest. Using Equation (2), the Langmuir adsorption constants for the three gases were derived by fitting the experimental data (Table 7). The results indicated that the maximum adsorption capacity per unit mass of coal for CO2 was approximately twice that for CH4 and four times that for N2, highlighting CO2’s superior adsorption potential in coal matrices.
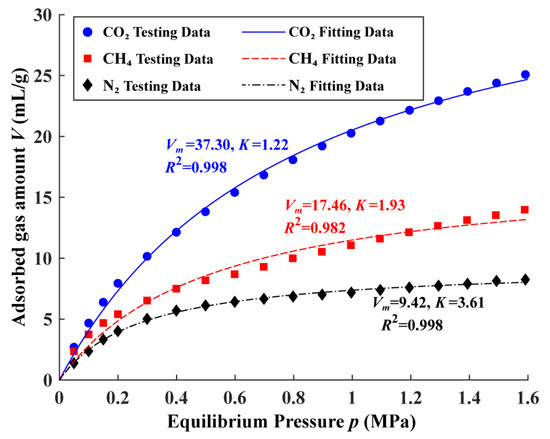
Figure 5.
Adsorption isotherms of tested coal samples.

Table 7.
Fitting parameters of Langmuir isothermal adsorption equation.
3.3. Gas Seepage Regularity in Different Structural Bituminous Coal Samples
The gas seepage behavior of raw coal samples under varying experimental conditions is illustrated in Figure 6. As shown, the permeability of raw coal exhibited a consistent trend across different gas types, axial pressures, and confining pressures: it initially decreased with increasing gas pressure, followed by a rapid rise and eventual stabilization. Notably, a critical inflection point marked the transition from permeability reduction to enhancement, occurring within a gas pressure range of . This phenomenon arises from the Klinkenberg effect [63,64], which distinguishes gas seepage from liquid flow. Due to the high compressibility of gases, gas density and viscosity vary significantly with pressure. At low pressures, gas density and viscosity were insufficient to form adsorption layers on pore walls with minimal gas adsorption occurring, resulting in negligible velocity gradients between pore centers and walls. This microscale behavior manifested macroscopically as the Klinkenberg effect, enhancing relative permeability. As gas pressure increased, gas density and viscosity rise, diminishing the Klinkenberg effect and reducing permeability. Beyond a critical pressure threshold, the Klinkenberg effect became negligible, and gas flow transitioned to Darcy-type behavior. Further pressure intensification elevated the gas pressure gradient, driving permeability growth at a decelerating rate.
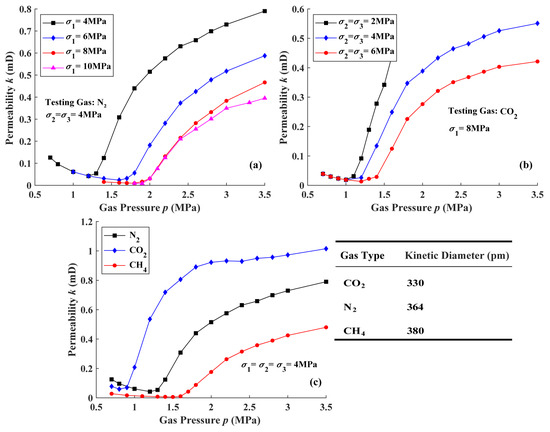
Figure 6.
Gas seepage characteristics of raw coal samples. (a) Gas seepage regularity of raw coal sample under different axial stress; (b) gas seepage regularity of raw coal sample under different confining pressures; (c) gas seepage regularity of raw coal sample with different gases.
Gas seepage regularity of raw coal samples under different axial stress and confining pressures were depicted in Figure 6a,b. The measured permeability range is consistent in order of magnitude with that in the existing studies [29,31], which can demonstrate the correctness of the measured data. Elevated axial stress and confining pressures compress the coal matrix, reducing pore connectivity and increasing flow resistance, thereby lowering permeability. The inflection point of the Klinkenberg effect shifted to higher gas pressures under increased axial stress and confining pressures. This shift reflected intensified compaction, which narrowed pore channels and heightened the gas pressure required to overcome the Klinkenberg effect and restore Darcy flow. Gas seepage regularity of raw coal sample with different gases are outlined in Figure 6c, highlighting gas-specific permeability trends, with CO2 exhibiting the highest permeability, followed by N2 and CH4. Thereby, the permeability of coal to different gases exhibits discernible variations, which correlate with differences in gas adsorption properties. However, the dominant factor governing these permeability disparities is the molecular kinetic diameter of the gas molecules (CO2: 330 pm, N2: 364 pm, CH4: 380 pm). Smaller CO2 molecules navigate pore channels more easily, requiring lower pressures to mitigate the Klinkenberg effect. Conversely, larger molecules (e.g., CH4) demand higher pressures to achieve Darcy flow, shifting the Klinkenberg inflection point to the right on the horizontal axis of coordinate. These findings underscore that the stress state of coal directly governs gas transport through its pore structure, primarily by modulating pore geometry and gas–matrix interactions.
In the same way, the gas seepage behavior of briquette coal samples under various experimental conditions is illustrated in Figure 7. Compared to raw coal, briquette samples exhibited permeability values two orders of magnitude higher, with no significant Klinkenberg effect observed across pressure conditions. This absence is attributed to the homogeneous and loosely compacted structure of briquette coal, characterized by larger pore sizes than raw coal. These enlarged pores, significantly exceeding the mean free path of gas molecules, result in Darcy-dominated flow even at low pressures. As is shown, permeability in all four experimental conditions increased rapidly with gas pressure before stabilizing.

Figure 7.
Gas seepage characteristics of raw coal samples. (a) Gas seepage regularity of briquette coal samples under different axial stress; (b) gas seepage regularity of briquette coal samples under different confining pressures; (c) gas seepage regularity of briquette coal samples with different gases; (d) gas seepage regularity of briquette coal samples with different sample forming pressure.
Gas seepage regularity of briquette coal samples under different axial stress and confining pressures were demonstrated in Figure 7a,b. Raised axial and confining pressures compress the briquette matrix, reducing pore connectivity and increasing flow resistance, thereby decreasing permeability. This trend aligned with observations in raw coal but occurred at a higher baseline due to briquette coal’s inherent structural homogeneity. From Figure 7c, briquette coal replicated the gas-specific permeability hierarchy of raw coal, also governed by molecular kinetic diameters and adsorption interactions. Additionally, from Figure 7d, higher forming pressures enhance particle cementation, reducing porosity and permeability. For instance, briquettes formed under a pressure of 130 MPa exhibited a permeability approximately one-tenth of those prepared at 50 MPa. It follows that the migration dynamics of gas within coal seams are fundamentally affected by the geological formation processes and in situ geo-mechanical conditions of the seam. Moreover, permeability increases nonlinearly with gas pressure due to the asynchronous growth of gas velocity and pressure gradients. This behavior persists across both raw and briquette coal, emphasizing the universal influence of gas dynamics on flow regimes.
According to the above test results, gas transport in coal is controlled by stress conditions, structural heterogeneity, gas type, and pressure gradients. Specifically, permeability scales with the ratio of gas molecular size to pore channel dimensions and the magnitude of pressure gradients. When the gas species remains constant, permeability increases proportionally with both the relative dimensions of the flow pathways and the magnitude of the gas pressure gradient. Under low-pressure conditions, the Klinkenberg effect amplifies permeability for small-pore systems (e.g., raw coal), while briquette coal’s larger pores miss out on this phenomenon. Thus, in outburst scenarios, where coal is highly fragmented, permeability increases dramatically due to enhanced pore connectivity. This accelerates gas flow velocity and volume, intensifying coal mass failure and its ejection—a critical feedback mechanism in outburst dynamics.
3.4. Influence of Gas Seepage on Outburst-Coal Breaking
The occurrence of coal and gas outbursts is intrinsically related to in situ stress, coal’s physico-mechanical properties, gas pressure, and geological structures. Structural instability and mechanical failure of coal constitute prerequisites for outburst initiation, primarily driven by stress redistribution due to mining disturbances, where stored gas within coal seams further contributes [3,4,11]. Post-failure, coal undergoes progressive fragmentation under residual energy until ejected from the working face, resulting in the characteristic ultrafine coal particles (size < 0.075 mm) observed in outburst events [2,9,65]. Current theories identify two dominant energy sources for outbursts: gas expansion energy (free and adsorbed gas release) and elastic strain energy stored in the coal matrix. Notably, it is verified that the elastic energy from the stress of overlying strata alone can hardly pulverize coal to sub-75 μm particles. This necessitates gas in driving coal fragmentation during outbursts [49,50,51,65].
Gas participates in the outburst-coal breaking through two primary means: gas adsorption and gas migration (encompassing desorption, diffusion, and seepage). It has been evidenced that gas adsorption, especially long-term adsorption, significantly degrades coal’s mechanical strength by altering its pore structure and surface energy. This degradation facilitates pore-crack system propagation and promotes coal fragmentation, which is conducive to outbursts initiation [4]. A positive feedback effect would be established in the gas desorption–diffusion process, where gas desorption–diffusion makes coal breaking into more tiny particles, increases the surface area, and further accelerates gas desorption and diffusion in turn. This feedback effect plays a positive role in outburst-coal breaking [16]. While gas seepage behaviors as the pressure-driven directional flow through the coal’s pore-crack network, in which a counterforce on pore surface, termed seepage force, arises from seepage resistance and gas–pore interactions, proportional to the gas pressure gradient as follows:
where represents the force induced by gas seepage, is the bulk density of gas, is the gas pressure gradient.
The experimental results demonstrated that briquette coal exhibited 1–2 orders of magnitude higher permeability than raw coal. Elevated axial and confining pressures compress the coal matrix, reducing pore connectivity and permeability, and higher forming pressures also diminish permeability due to enhanced particle cementation. Notably, the Klinkenberg effect at low pressures facilitates gas seepage by reducing flow resistance in micropores. That means, when coal and gas outbursts occur, mining-induced stress redistribution destabilizes the coal matrix, triggering abrupt unloading and structural failure. This abrupt unloading and failure accelerate gas seepage, which in turn promotes further coal fragmentation through energy transfer and pore pressure transients. These interactions establish a self-reinforcing cycle between gas seepage and coal fragmentation, as illustrated in Figure 8.

Figure 8.
The self-reinforcing cycle effect of gas seepage on outburst-coal breaking.
Specifically, when coal and gas outbursts are triggered by mining disturbances, abrupt stress unloading and coal matrix destabilization initiate coal fragmentation and accelerate gas seepage. The resulting propagation of pore-crack networks enhances gas seepage, meanwhile promoting gas desorption and diffusion. In this process, elevated coal permeability allows for more gas participating in seepage, inducing more stored gas to quickly and heavily desorb and diffuse. Since the expansion work performed by the gas desorbing and diffusing from coal is linear with the cumulative amount of diffused gas [16], the gas expansion energy therefore will be amplified. Thereafter, free gas in pore-crack networks will obtain more kinetic energy for moving, wherein a great gas pressure gradient will be generated. From Equation (10), the seepage force scales linearly with gas pressure gradient as defined, indicating that elevated means stronger seepage force applied to pore surface, which further intensifies coal fragmentation and pore-crack network propagation. Thus, a self-reinforcing cycle effect between gas seepage and coal fragmentation was established under these interactions when a coal and gas outburst occurred, where each process amplifies the others in cycle. This self-reinforcing cycle effect will play a significantly stimulative role in outburst initiation, and development and outburst could enhance this cycle’s effect in turn. Finally, enhanced outburst process will further exacerbate excavation disturbance and stress unloading in turn, thereby restarting another self-reinforcing cycle. This finding of self-reinforcing cycle effect was supported in the recent studies [29,31], in which permeability evolution during unloading was found to be non-monotonic and tied to microcrack coalescence, and it was also verified in the Multiphysics modeling studies [6]. As revealed by the experimental results in this study, different structural coal seams exhibited distinct levels of the cycle effect. Tectonic and soft coal seams exhibited stronger feedback gains compared to intact hard coal seams, driven by higher fracture density and smaller geo-forming stress.
From Figure 8, we can find that the self-reinforcing cycle comprised two semi-cycle feedback mechanisms and one sub-cycle feedback. In the first semi-cycle, coal fragmentation during destabilization propagated the pore-fracture network, increasing permeability and accelerating gas seepage. The second semi-cycle predicated that enhanced gas pressure gradient elevated the gas seepage force applied on pore surface, exacerbating coal fragmentation, further increasing permeability, and accelerating gas seepage. And in the sub-cycle, gas seepage promoted faster desorption and diffusion. The resulting greater gas expansion energy elevated the pressure gradient, which indirectly raised permeability, finally accelerating gas seepage in turn. Without doubt, these interdependent sub-cycle mechanisms would synergistically enhance the self-reinforcing cycle’s capacity to facilitate coal fragmentation and outburst escalation.
The self-reinforcing cycle effect is a significant finding for in-depth understanding of the initial and developed mechanisms of coal and gas outburst. It could apply a theoretical mechanism basis for further research on methods of outburst prevention and early warning. In practice, prior to a coal and gas outburst, many precursory changes in stress state, coal structures, mining circumstance, and some key parameters will appear. Such as stress concentration, coal fragmentation, sudden temperature drop on workface, sharp explosion sound, abnormal gas emission, and so on. Early warning of coal and gas outbursts can be achieved by real-time monitoring these precursor changes. The self-reinforcing cycle effect found in this study contains the key parameters of permeability, pore propagation extent, and gas emission amount. They can be quantitatively monitored in real-time through integration into an AI-driven big data monitoring system for proactive coal and gas outburst prevention and warning.
4. Conclusions
In this paper, gas seepage tests were carried out to study the gas seepage regularity of different structural bituminous coal and its influence on outburst-coal breaking. The main conclusions were obtained.
1. Coal’s structural difference and anisotropy yielded distinct mechanical properties. Tectonic and soft coal seams exhibit higher porosity and lower compressive resistance than intact hard ones, enhancing gas seepage, thereby increasing outburst propensity.
2. Both kinds of coal seams exhibited consistent seepage regularity that the raised axial stress, confining pressure and gas kinetic diameter would inhibit seepage. However, raw coal benefited from low-pressure Klinkenberg-enhanced seepage, while tectonic soft coal seams formed under higher geo-stress exhibited more limited gas seepage.
3. A self-reinforcing cycle mechanism was proposed to explain the cyclic enhancement in outburst initiation and development. In this cycle, mining-induced coal fragmentation accelerated gas seepage, which promoted gas diffusion and enlarged gas expansion energy, resulting in gas pressure gradient elevation, finally intensifying coal fragmentation in turn. At last, the self-reinforcing cycle promoted outburst-coal breaking and outburst initiation, which exhibits stronger in tectonic soft coal seams than intact hard ones.
The findings in this study will contribute to the in-depth understanding of outburst mechanisms, outburst prevention, and early-warning, further ensuring global energy security.
Author Contributions
Data curation, L.C.; Formal analysis, W.G.; Funding acquisition, J.Z. and G.H.; Investigation, J.Z. and L.C.; Methodology, J.Z., G.H. and J.W.; Resources, J.Z.; Validation, W.G.; Visualization, L.C. and W.G.; Writing—original draft, J.Z.; Writing—review and editing, J.Z. and L.C. All authors have read and agreed to the published version of the manuscript.
Funding
The authors gratefully acknowledge the financial support of the “Tianchi Talent” project funded by the Xinjiang Uygur Autonomous Region Introduction Plan, the National Natural Science Foundation of China (Grant Number 51674049), and Xinjiang Uygur Autonomous Region Special Program for Key R&D Tasks (2022B01034-1).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Jun Wang was employed by the company SINOPEC Geophysical Research Institute Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Wang, H.; Wang, E.Y.; Li, Z.H.; Shen, R.; Liu, X.F. Study and application of a new gas pressure inversion model in coal seam while drilling based on directional drilling technology. Fuel 2021, 306, 121679. [Google Scholar] [CrossRef]
- Beamish, B.B.; Crosdale, P.J. Instantaneous outbursts in underground coal mines: An overview and association with coal type. Int. J. Coal Geol. 1998, 35, 27–55. [Google Scholar] [CrossRef]
- Chen, K.P. A new mechanistic model for prediction of instantaneous coal outbursts–Dedicated to the memory of Prof. Daniel D. Joseph. Int. J. Coal Geol. 2011, 87, 72–79. [Google Scholar] [CrossRef]
- Zheng, J.; Huang, G.; Cheng, Q.; Zhen, L.B.; Cai, Y.; Wang, W.Z. Degradation of mechanical and microporous properties of coal subjected to long-term sorption. Fuel 2022, 315, 123245. [Google Scholar] [CrossRef]
- Wen, S.M.; Zhou, K.; Lu, Q. A discussion on CBM development strategies in China: A case study of PetroChina Coalbed Methane Co., Ltd. Nat. Gas Ind. B 2019, 6, 610–618. [Google Scholar] [CrossRef]
- Su, E.; Zhu, X.; Chen, X.; Zou, Q.L.; Yang, K.; Chen, H.D.; Wei, J.Q. Analysis of methane diffusion on permeability rebound and recovery in coal reservoirs: Implications for deep coalbed methane-enhanced extraction. Phys. Fluids 2024, 36, 076622. [Google Scholar] [CrossRef]
- An, H.; Wei, X.; Wang, G.; Massarotto, P.; Wang, F.Y.; Rudolph, V.; Golding, S.D. Modeling anisotropic permeability of coal and its effects on CO2 sequestration and enhanced coalbed methane recovery. Int. J. Coal Geol. 2015, 152, 15–24. [Google Scholar] [CrossRef]
- Black, D.J. Review of coal and gas outburst in Australian underground coal mines. Int. J. Min. Sci. Technol. 2019, 29, 815–824. [Google Scholar] [CrossRef]
- Xoдoт, B.; Song, S.; Wang, Y. Coal and Gas Outburst; China Industrial Press: Beijing, China, 1966. [Google Scholar]
- Fan, C.J.; Li, S.; Luo, M.K.; Du, W.Z.; Yang, Z.H. Coal and gas outburst dynamic system. Int. J. Rock Mech. Min. Sci. 2017, 27, 49–55. [Google Scholar] [CrossRef]
- Shepherd, J.; Rixon, L.K.; Griffiths, L. Outbursts and geological structures in coal mines: A review. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 267–283. [Google Scholar] [CrossRef]
- Zhou, B.; Xu, J.; Peng, S.J.; Yan, F.Z.; Yang, W.; Cheng, L.; Ni, G.H. Influence of Geo-stress on Dynamic Response Characteristics of Coal and Gas Outburst. Rock Mech. Rock Eng. 2020, 53, 4819–4837. [Google Scholar] [CrossRef]
- Zheng, J.; Huang, G.; Cheng, Q.; Jia, J.K.; Cai, Z.H. A Novel Experimental Apparatus for Evaluating Coal-and-Gas Outburst Risk. Nat. Resour. Res. 2022, 31, 535–550. [Google Scholar] [CrossRef]
- Skoczylas, N. Laboratory study of the phenomenon of methane and coal outburst. Int. J. Rock Mech. Min. Sci. 2012, 55, 102–107. [Google Scholar] [CrossRef]
- Sobczyk, J. A comparison of the influence of adsorbed gases on gas stresses leading to coal and gas outburst. Fuel 2014, 115, 288–294. [Google Scholar] [CrossRef]
- Zheng, J.; Liang, Q.M.; Zhang, X.; Huang, J.Y.; Yan, W.; Huang, G.; Liu, H.L. On Gas Desorption-Diffusion Regularity of Bituminous Coal with Different Particle Sizes and Its Influence on Outburst-Coal Breaking. Sustainability 2023, 15, 9894. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, T.; Jia, C.Z.; Li, X.F.; Wu, K.L.; He, M.X. Numerical simulation on natural gas migration and accumulation in sweet spots of tight reservoir. J. Nat. Gas Sci. Eng. 2020, 81, 103454. [Google Scholar] [CrossRef]
- Pan, Z.J.; Connell, L.D. A theoretical model for gas adsorption-induced coal swelling. Int. J. Coal Geol. 2007, 69, 243–252. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Liu, J.X.; Yu, S.; Sun, Z.H.; Wang, L.; Wu, S.W.; Ni, G.H.; Hao, C.M.; Zhang, R. Kinetic properties of coal gas desorption based on fractional order fractal diffusion equation in time. Energy 2025, 316, 134608. [Google Scholar] [CrossRef]
- An, F.H.; Cheng, Y.P.; Wu, D.M.; Wang, L. The effect of small micropores on methane adsorption of coals from Northern China. Adsorption 2013, 19, 83–90. [Google Scholar] [CrossRef]
- Wang, K.; Wang, Y.H.; Xu, C.; Li, X.P.; Guo, H.J.; Yi, K.Q. Influence of gas diffusion in coal matrix on gas extraction process: Modeling, definition, and quantitative analysis. Gas Sci. Eng. 2025, 134, 205545. [Google Scholar] [CrossRef]
- Butt, S.D. Development of an apparatus to study the gas permeability and acoustic emission characteristics of an outburst-prone sandstone as a function of stress. Int. J. Rock Mech. Min. Sci. 1999, 36, 1079–1085. [Google Scholar] [CrossRef]
- Wang, H.P.; Liu, Z.Z.; Yuan, L.; Wang, S.G.; Wei, S.M.; Zhang, D.M. Experimental test and particle mechanical analysis of gas adsorption-induced coal rock degradation. Powder Technol. 2020, 362, 75–83. [Google Scholar] [CrossRef]
- Sampath, K.H.S.M.; Perera, M.S.A.; Ranjith, P.G.; Matthai, S.K. CO2 interaction induced mechanical characteristics alterations in coal: A review. Int. J. Coal Geol. 2019, 204, 113–129. [Google Scholar] [CrossRef]
- Zhang, C.L.; Wang, E.Y.; Xu, J.; Peng, S.J. Experimental investigation on mechanics and seepage characteristics of tectonic and intact coal containing gas. Appl. Sci. 2020, 10, 7290. [Google Scholar] [CrossRef]
- Zhao, P.X.; Liu, H.; Li, S.G.; Lin, H.F.; Jia, Y.Y.; Yan, M.; Yuan, M.Q.; Lin, J. Experimental Investigation of the Adsorption Characteristics of Mixed Coal and Variations of Specific Surface Areas before and after CH4 Adsorption. Appl. Sci. 2019, 9, 524. [Google Scholar] [CrossRef]
- Shilova, T.; Serdyukov, S. Permeability of Coking Coals and Patterns of Its Change in Leninsky Area, Kuznetsk Coal Basin, Russia. Appl. Sci. 2021, 11, 3969. [Google Scholar] [CrossRef]
- Xie, H.P.; Xie, J.; Gao, M.Z.; Zhang, R.; Zhou, H.W.; Gao, F.; Zhang, Z.T. Theoretical and experimental validation of mining-enhanced permeability for simultaneous exploitation of coal and gas. Environ. Earth. Sci. 2015, 73, 5951–5962. [Google Scholar] [CrossRef]
- Liu, Y.B.; Zhao, D.; Li, Y.T.; Zhang, L. Permeability Evolution of Intact and Fractured Coal during Progressive Deformation Subjected to True Triaxial Stresses. Processes 2023, 11, 2826. [Google Scholar] [CrossRef]
- Liu, Y.B.; Yin, G.Z.; Zhang, D.M.; Li, M.H.; Deng, B.Z.; Liu, C.; Zhao, H.G.; Yin, S.Y. Directional permeability evolution in intact and fractured coal subjected to true-triaxial stresses under dry and water-saturated conditions. Int. J. Rock Mech. Min. 2019, 119, 22–34. [Google Scholar] [CrossRef]
- Bai, X.; Wang, Y.; He, G.C.; Zhou, Z.L.; Wang, D.K.; Zhang, D.M. Research on a permeability model of coal damaged under triaxial loading and unloading. Fuel 2023, 354, 129375. [Google Scholar] [CrossRef]
- Li, Z.B.; Fan, Z.C.; Wang, H.; Wang, S.R.; Li, C. The mechanism of pore pressure and adsorption swelling effect on permeability during geological storage of carbon dioxide in coal seams. Fuel 2025, 381, 133437. [Google Scholar] [CrossRef]
- Zhu, W.C.; Wei, C.H.; Liu, J.; Xu, T.; Elsworth, D. Impact of Gas Adsorption Induced Coal Matrix Damage on the Evolution of Coal Permeability. Rock Mech. Rock Eng. 2013, 46, 1353–1366. [Google Scholar] [CrossRef]
- Tan, Y.L.; Pan, Z.J.; Liu, J.S.; Zhou, F.B.; Connell, L.D.; Sun, W.J.; Haque, A. Experimental study of impact of anisotropy and heterogeneity on gas flow in coal. Part II: Permeability. Fuel 2018, 230, 397–409. [Google Scholar] [CrossRef]
- Yan, Z.M.; Wang, K.; Zang, J.; Wang, C.; Liu, A. Anisotropic coal permeability and its stress sensitivity. Int. J. Min. Sci. Technol. 2019, 29, 507–511. [Google Scholar] [CrossRef]
- Wang, D.K.; Zhang, P.; Wei, J.P.; Yu, C. The seepage properties and permeability enhancement mechanism in coal under temperature shocks during unloading confining pressures. J. Nat. Gas Sci. Eng. 2020, 77, 103242. [Google Scholar] [CrossRef]
- Li, X.C.; Yan, X.P.; Kang, Y.L. Effect of temperature on the permeability of gas adsorbed coal under triaxial stress conditions. J. Geophys. Eng. 2018, 15, 386–396. [Google Scholar] [CrossRef]
- Zou, G.G.; Zhang, Q.H.; Peng, S.P.; She, J.S.; Teng, D.L.; Jin, C.C.; Che, Y.Y. Influence of geological factors on coal permeability in the Sihe coal mine. Int. J. Coal Sci. Technol. 2022, 9, 6. [Google Scholar] [CrossRef]
- Wu, S.; Tang, D.Z.; Li, S.; Wu, H.Y.; Hu, X.; Zhu, X.G. Effects of geological pressure and temperature on permeability behaviors of middle-low volatile bituminous coals in eastern Ordos Basin. Chin. J. Pet. Sci. Eng. 2017, 153, 372–384. [Google Scholar] [CrossRef]
- Lu, S.Q.; Li, M.J.; Ma, Y.K.; Wang, S.C.; Zhao, W. Permeability changes in mining-damaged coal: A review of mathematical models. J. Nat. Gas Sci. Eng. 2022, 106, 104739. [Google Scholar] [CrossRef]
- Yin, G.Z.; Li, M.H.; Li, W.P.; Jiang, C.B.; Cao, J.; Zhang, Q.G. Influence of gas pressure on mechanical and seepage characteristics of coal under unloading condition. J. Chin. Coal Soc. 2012, 37, 1499–1504. [Google Scholar]
- Peng, S.J.; Xu, J.; Yang, H.W.; Liu, D. Experimental study on the influence mechanism of gas seepage on coal and gas outburst disaster. Saf. Sci. 2012, 50, 816–821. [Google Scholar] [CrossRef]
- Vandamme, M.; Brochard, L.; Lecampion, B.; Coussy, O. Adsorption and strain: The CO2-induced swelling of coal. J. Mech. Phys. Solids 2010, 58, 1489–1505. [Google Scholar] [CrossRef]
- Nikoosokhan, S.; Vandamme, M.; Dangla, P. A poromechanical model for coal seams saturated with binary mixtures of CH4 and CO2. J. Mech. Phys. Solids 2014, 71, 97–111. [Google Scholar] [CrossRef]
- Andrade, E.N.; Randall, R.F.; Makin, M.J. The Rehbinder Effect. In Proceedings of the Physical Society Section B; IOP Publishing: London, UK, 1950. [Google Scholar] [CrossRef]
- Liu, Y.J.; Xing, H.; Duan, Z.Y.; Yu, C.Y.; Tian, Z.C.; Teng, T. Study on Mechanical Characteristics of Deformation and the Failure of Gas-Containing Coal in the Wuhai Mining Area of China under Different Gas Pressure Conditions. Appl. Sci. 2022, 12, 10139. [Google Scholar] [CrossRef]
- Cai, F.; Yin, J.W.; Feng, J.Q. Effect of Methane Adsorption on Mechanical Performance of Coal. Appl. Sci. 2022, 12, 6597. [Google Scholar] [CrossRef]
- Ding, X.L.; Yu, S.B.; Ding, Y.S.; Kou, S.Q.; Tan, Q.M.; Zheng, Z.M. The mechanism of continuous failure of coal under the effect of gas seepage. Sci. Chin. 1989, 6, 600–607. [Google Scholar]
- Tan, Q.M.; Yu, S.B.; Zhu, H.Q.; Zheng, Z. Fracture of coal containing pressurized gas by sudden relieving. J. Chin. Coal Soc. 1997, 22, 514–518. [Google Scholar]
- Lei, Y.; Cheng, Y.P.; Ren, T.; Tu, Q.Y.; Shu, L.Y.; Li, Y.X. The Energy Principle of Coal and Gas Outbursts: Experimentally Evaluating the Role of Gas Desorption. Rock Mech. Rock Eng. 2021, 54, 11–30. [Google Scholar] [CrossRef]
- Guan, P.; Wang, H.Y.; Zhang, Y.X. Mechanism of instantaneous coal outbursts. Geology 2009, 37, 915–918. [Google Scholar] [CrossRef]
- Wang, S.G.; Elsworth, D.; Liu, J.S. Rapid decompression and desorption induced energetic failure in coal. J. Rock Mech. Geotech. 2015, 7, 345–350. [Google Scholar] [CrossRef]
- AQ 1024-2006; Specification for Identification of Coal and Gas Outburst Mine. Coal Industry Press: Beijing, China, 2006.
- Jiang, C.B.; Yin, G.Z.; Li, X.Q.; Cai, B. Experimental study of gas permeability of outburst coal briquettes in complete stress-strain process. Chin. J. Rock Mech. Eng. 2010, 29, 3482–3487. [Google Scholar]
- GB/T 212-2008; Proximate Analysis of Coal. Standards Press of China: Beijing, China, 2008.
- Kondo, S.; Ishikawa, T. Adsorption Science, 2nd ed.; Chemical Industry Press: Beijing, China, 2006. [Google Scholar]
- Kong, X.Y. Advanced Seepage Mechanics; University of Science and Technology of China Press: Hefei, China, 2010. [Google Scholar]
- Yin, S.; Wang, E.Y.; Li, Z.H.; Zang, Z.S.; Liu, X.F.; Zhang, C.L.; Ding, X.P.; Aihemaiti, A. Multifractal and b-value nonlinear time-varying characteristics of acoustic emission for coal with different impact tendency. Measurement 2025, 248, 116896. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, S.M. Experimental and theoretical characterization of methane and CO2 sorption hysteresis in coals based on Langmuir desorption. Int. J. Coal Geol. 2017, 171, 49–60. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of Gases in Multimolecular Layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Thommes, M.; Kaneko, K.; Neimark, A.V.; Olivier, J.P.; Rodriguez-Reinoso, F.; Rouquerol, J.; Sing, K.S.W. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef]
- Hill, T.L. Adsorption from a one-dimensional lattice gas and the Brunauer–Emmett–Teller equation. Proc. Natl. Acad. Sci. USA 1996, 93, 14328–14332. [Google Scholar] [CrossRef]
- Guria, C. Pressure- and temperature-dependent klinkenberg slippage effect in porous media to non-ideal gases. Geoenergy Sci. Eng. 2023, 224, 211629. [Google Scholar] [CrossRef]
- Moghadam, A.A.; Chalaturnyk, R. Expansion of the Klinkenberg’s slippage equation to low permeability porous media. Int. J. Coal Geol. 2014, 123, 2–9. [Google Scholar] [CrossRef]
- Luo, J.; Huang, G.; Zhang, L.; Huang, F.; Zheng, J. Micro shape of coal particle and crushing energy. Int. J. Min. Sci. Technol. 2018, 28, 1009–1014. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).