A Study on Sandstone Damage Model Based on the Correlation Between Energy Dissipation and Plastic Strain

Abstract

The process of rock damage and failure is accompanied by the dissipation of energy and an increase in plastic strain. This study attempts to determine the relationship between dissipated energy and plastic strain in sandstone during the damage and failure process. A conventional triaxial cyclic loading and unloading test was conducted on sandstone samples to analyze the energy evolution and plastic strain characteristics of rock during the mechanical performance degradation and deformation failure process. The analysis results indicate that the evolution law of rock energy dissipation and plastic growth during the whole stress–strain process is highly consistent. Before the peak stress, dissipated energy and plastic strain increased linearly with input energy and axial strain, respectively. In the residual stress stage, there is an approximate linear evolution relationship between dissipated energy and plastic strain. Based on the correlation characteristics of energy dissipation and plastic growth, a modified damage model was established by characterizing plastic deformation by damage. In addition, a numerical program was developed using the Finite Volume Method (FVM) based on the damage model. The rock damage model has been validated by experimental results and numerical test. The research findings may provide valuable insights into the correlation mechanism between energy dissipation and plastic growth.

1. Introduction

As is widely recognized, the process of rock damage and failure under external loading involves various energy-related phenomena, such as energy input, accumulation, conversion, dissipation, and release [1,2]. Prior to the occurrence of rock damage, a portion of the external work is stored within the rock as elastic energy, while the remaining portion is dissipated in the form of surface energy, thermal energy, sound energy, electromagnetic radiation energy, and other forms [3]. This part of the dissipated energy is collectively referred to as rock dissipated energy [4,5]. During this stage, the energy conversion and dissipation within the rock are balanced, whereby any excess energy resulting from the conversion of external work into elastic energy is dissipated as a consequence of rock damage. However, when the elastic energy accumulated within the rock reaches its limit, or when the rate of external work conversion into elastic energy surpasses the capacity for elastic energy conversion, the equilibrium between energy conversion and dissipation within the rock is disrupted, leading to rock failure. Throughout the rock failure process, the rock releases energy to its surroundings in various forms, including thermal energy, sound energy, electromagnetic radiation energy, and kinetic energy, among others.

In line with the principles of damage mechanics, the process of rock mechanical performance degradation and deformation failure involves the manifestation of dissipated energy and plastic strain as specific indicators of the influence exerted by damage variables on energy and deformation in rocks [6,7,8]. The evolution of dissipated energy and plastic strain reflects the physical processes of mechanical property degradation in rock materials [9,10]. Both dissipated energy and plastic strain are irreversible, meaning their evolution process is irrecoverable. This is consistent with the irreversible nature of the damage variable [11,12]. Therefore, dissipated energy and plastic strain can also be regarded as derived variables of rock damage [13,14]. Notably, dissipated energy and plastic strain are closely intertwined, with the occurrence of plastic strain in rocks being invariably accompanied by the dissipation of internal energy, and the dissipation of energy being accompanied by the irreversible deformation of rocks. As such, the investigation of the correlation characteristics between dissipated energy and plastic strain in the process of rock damage assumes paramount importance in comprehending the evolution of rock damage [15,16,17].

The study of energy conversion and dissipation mechanisms within rocks during the processes of damage and instability has garnered considerable attention for a long time [18,19]. Academician Xie Heping [20,21] conducted systematic research on the internal energy conversion and dissipation mechanisms in rocks and proposed the concept of characterizing rock damage states through energy release mechanisms. Arson [22] introduced internal constraints to the constitutive relationship, damage internal variables, and variables associated with rock damage, and derived the Clausius–Duhem inequality as well as the damage driving force inequality. This paved the way for the exploration of various aspects such as constitutive models, fissure damage, closure of frictional sliding in fissures, hydraulic coupling, and aging damage. Qin [23,24,25] explained the coal–rock damage and failure process based on thermodynamic theory, proposed an energy balance differential equation based on the first law of thermodynamics, and established a coal–rock constitutive model based on energy relationships under uniaxial compression. Zhang [26] established a constitutive model suitable for cyclic loading and unloading processes that considers energy dissipation and compaction effects, which can more accurately describe the nonlinear strength and deformation characteristics of coal materials. Gong [27] proposed a rock damage model based on the linear energy dissipation law, including the compression energy dissipation coefficient, and verified it by combining the experimental results of four typical brittle rocks under conventional uniaxial compression and single cycle loading unloading uniaxial compression.

Significant advancements have been made in the study of plastic behavior during the process of rock damage and failure [8,28]. Cui [29] incorporated the interaction between damage caused by the plastic deformation of rocks and the effects of void nucleation, growth, and agglomeration into the constitutive model, and conducted numerical studies to elucidate the influence of initial porosity and its evolution on macroscopic mechanical properties of rocks. Ma [30,31] employed a non-associated plastic flow rule to describe the plastic deformation of rocks and a damage–plasticity constitutive model was developed to account for the hardening and softening characteristics exhibited by rocks during the loading process. Hou [32] investigated the impact of confining pressure and plastic strain on the post-peak strength of brittle hard rocks, proposing an enhanced Hoek–Brown model that incorporates the determination of post-peak plastic strain. Ren [33] introduced a plastic–damage model for rocks based on the generalized plastic shear strain, providing a mathematical description of rock damage evolution during various loading and unloading processes.

Despite significant progress in studying the energy mechanisms and plastic behavior in rocks, previous research has primarily treated them as independent research topics, neglecting the comprehensive consideration of energy dissipation and plastic growth during rock damage [34,35]. The lack of research on the correlation between energy dissipation and plastic growth has resulted in an unclear relationship between rock dissipated energy and plastic strain evolution [36,37]. To address this issue, this study aims to explore the correlation between energy dissipation and plastic growth during rock damage. By analyzing the energy evolution characteristics and plastic strain evolution characteristics during rock damage separately, the evolution relationship between energy dissipation and plastic growth is established. Based on this, methods for calculating input energy, elastic energy, and dissipated energy during rock damage are proposed and verified using experimental results. A modified rock damage model is proposed for the development of numerical simulation programs based on the correlation between energy dissipation and plastic growth. The surrounding rock damage and vertical stress evolution process of the Yimaqianqiu Coal Mine were simulated, and the risk of inducing rockburst was analyzed.

2. Testing Process

The experimental setup utilized in this study involved an RLJW-2000 (Changchun City Chaoyang Test Instrument Co., Ltd., Changchun, China) electric hydraulic servo rock triaxial compression testing machine, as depicted in Figure 1. A total of 30 sandstone samples were employed, with three samples utilized per test. The experimental design comprised ten test sets, including five sets of uniaxial loading tests and five sets of cyclic loading and unloading tests. Confining pressures of 0 MPa, 5 MPa, 10 MPa, 20 MPa, and 30 MPa were selected. The rock samples were prepared in conformity with the specifications for rock samples outlined in the “Standard Test Methods for Engineering Rock Masses” (GB/T 50266-2013) [38], resulting in standardized cylindrical samples measuring 50 × 100 mm. The bottom surfaces of the samples were required to possess a roughness not exceeding 0.05 mm, to be perpendicular to the axis, with a maximum inclination angle not exceeding 0.25 degrees. There should be no visible defects on the surface of the samples. The processed sandstone samples are shown in Figure 2.

The samples underwent cyclic loading and unloading tests under varying confining pressures of 0 MPa, 5 MPa, 10 MPa, 20 MPa, and 30 MPa. The unloading points prior to reaching the peak were determined at different confining pressures, specifically at 20%, 30%, 40%, 50%, 60%, 70%, 80%, and 90% of the peak axial strain attained during uniaxial loading. During the testing procedure, a minimum of two cycles of loading and unloading were conducted during the stress softening stage, while another two cycles were performed in the residual stress stage. The primary objective of these tests was to acquire data related to strain, stress, elastic modulus, and other relevant parameters of the rock material during the cyclic loading and unloading process. These data serve as a foundation for the calculation of dissipated energy and plastic strain.

3. Results

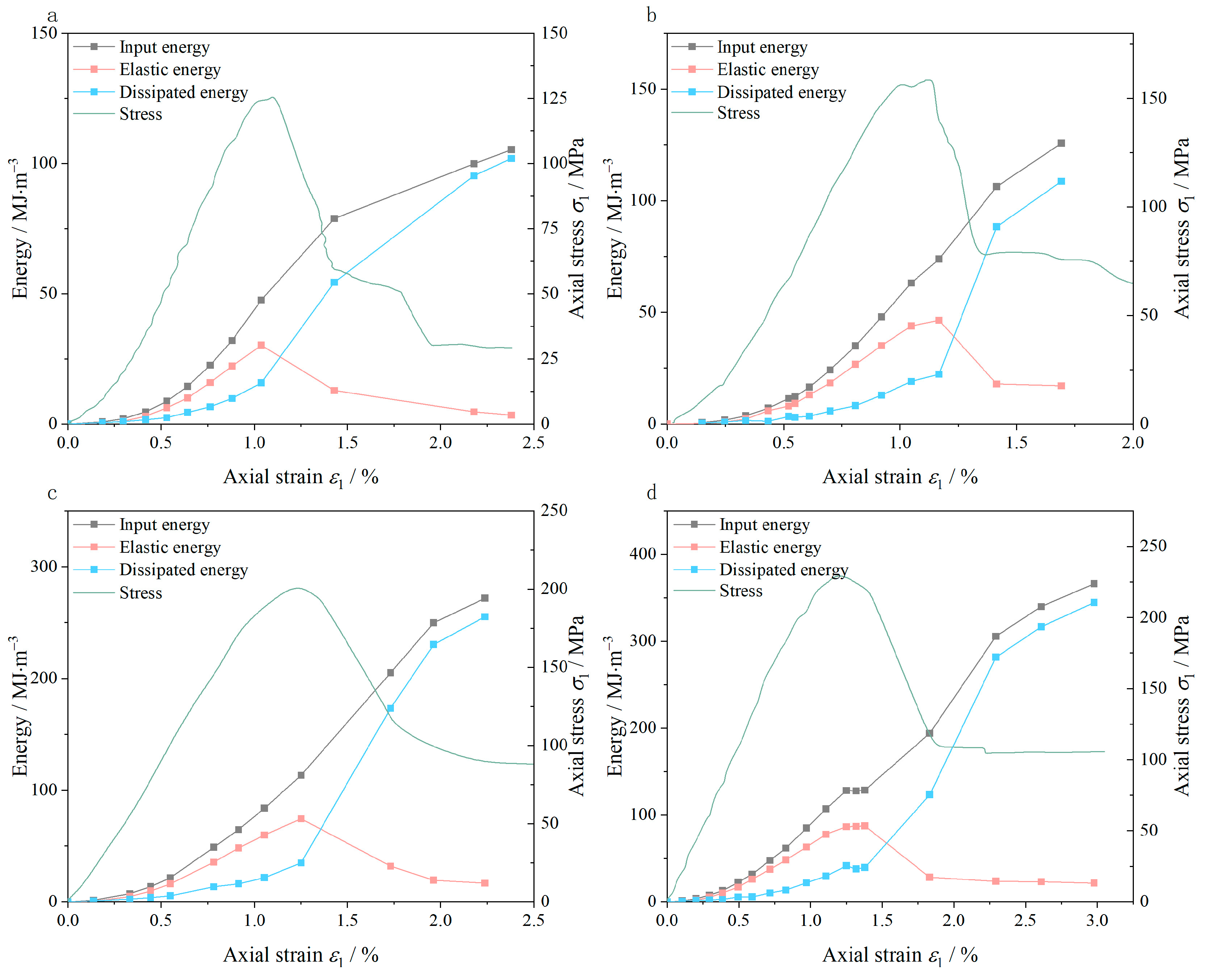
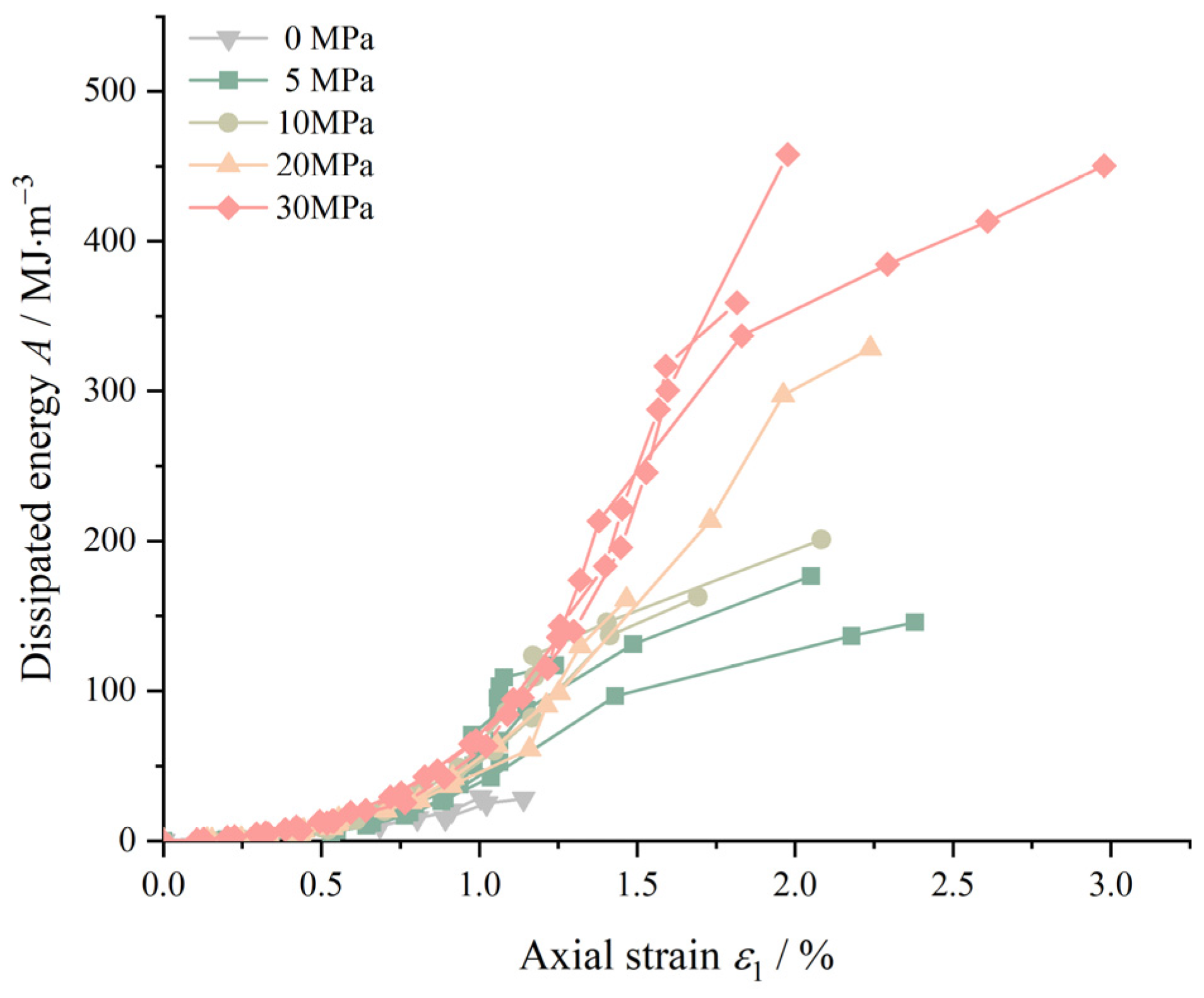
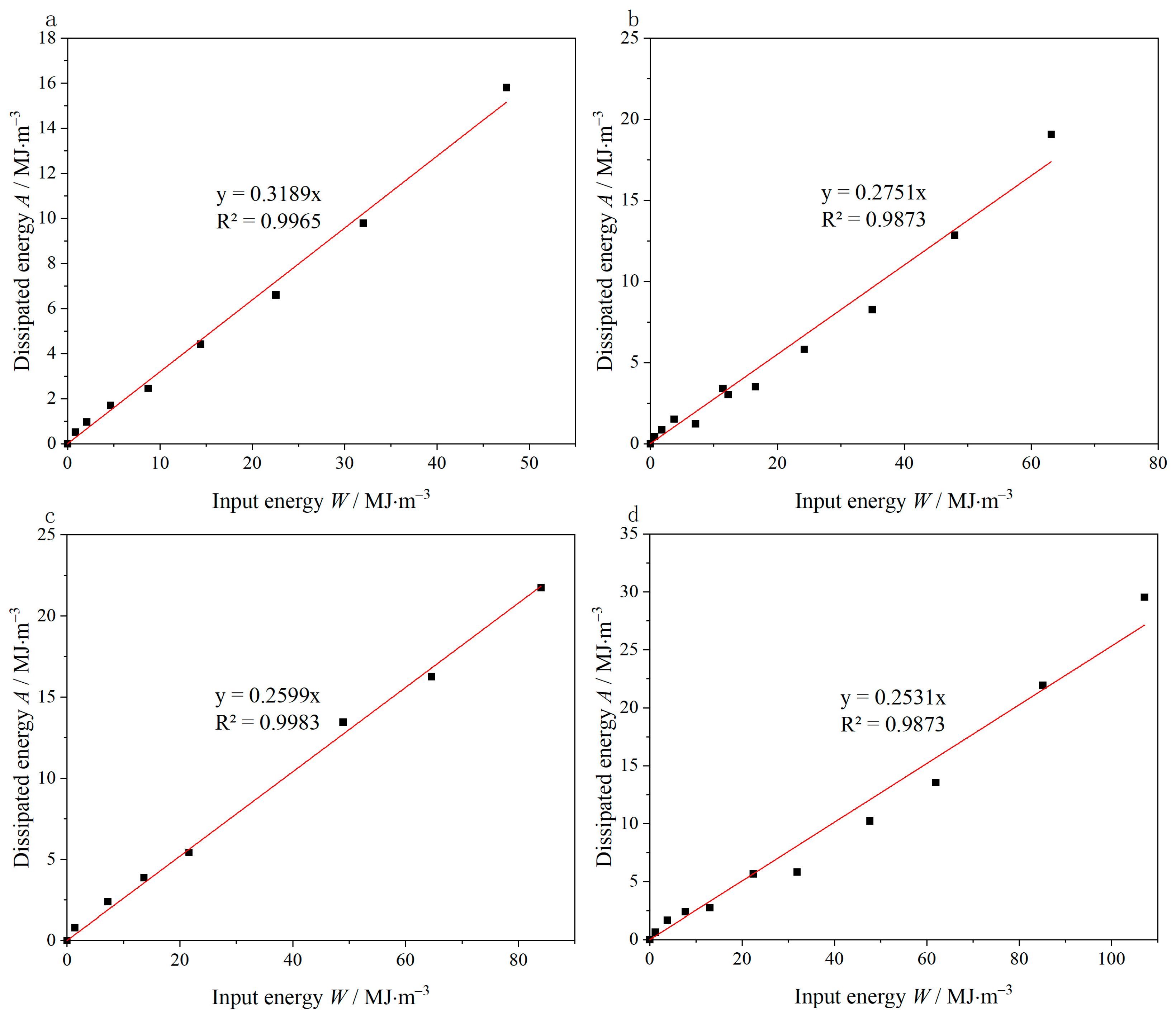
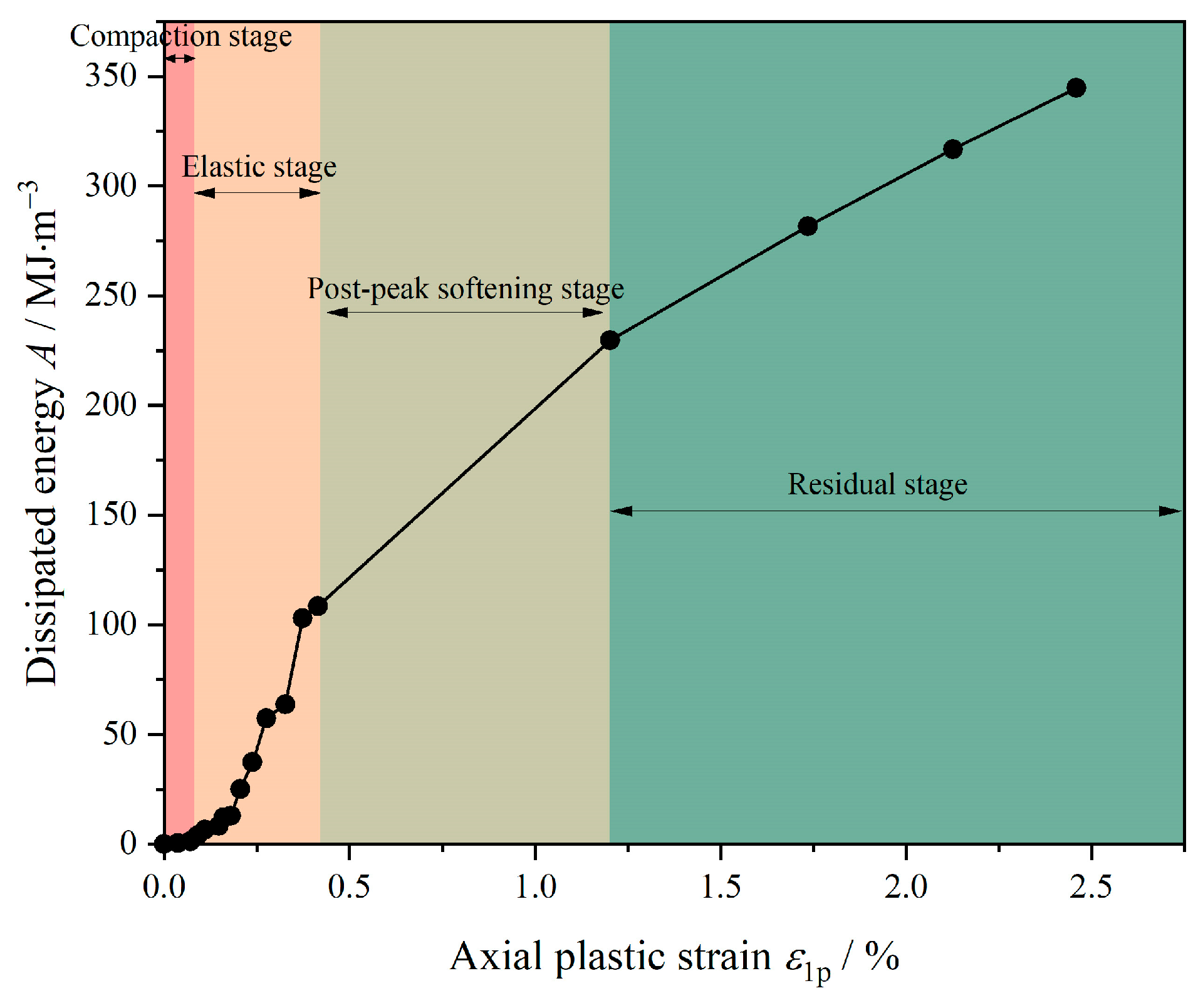
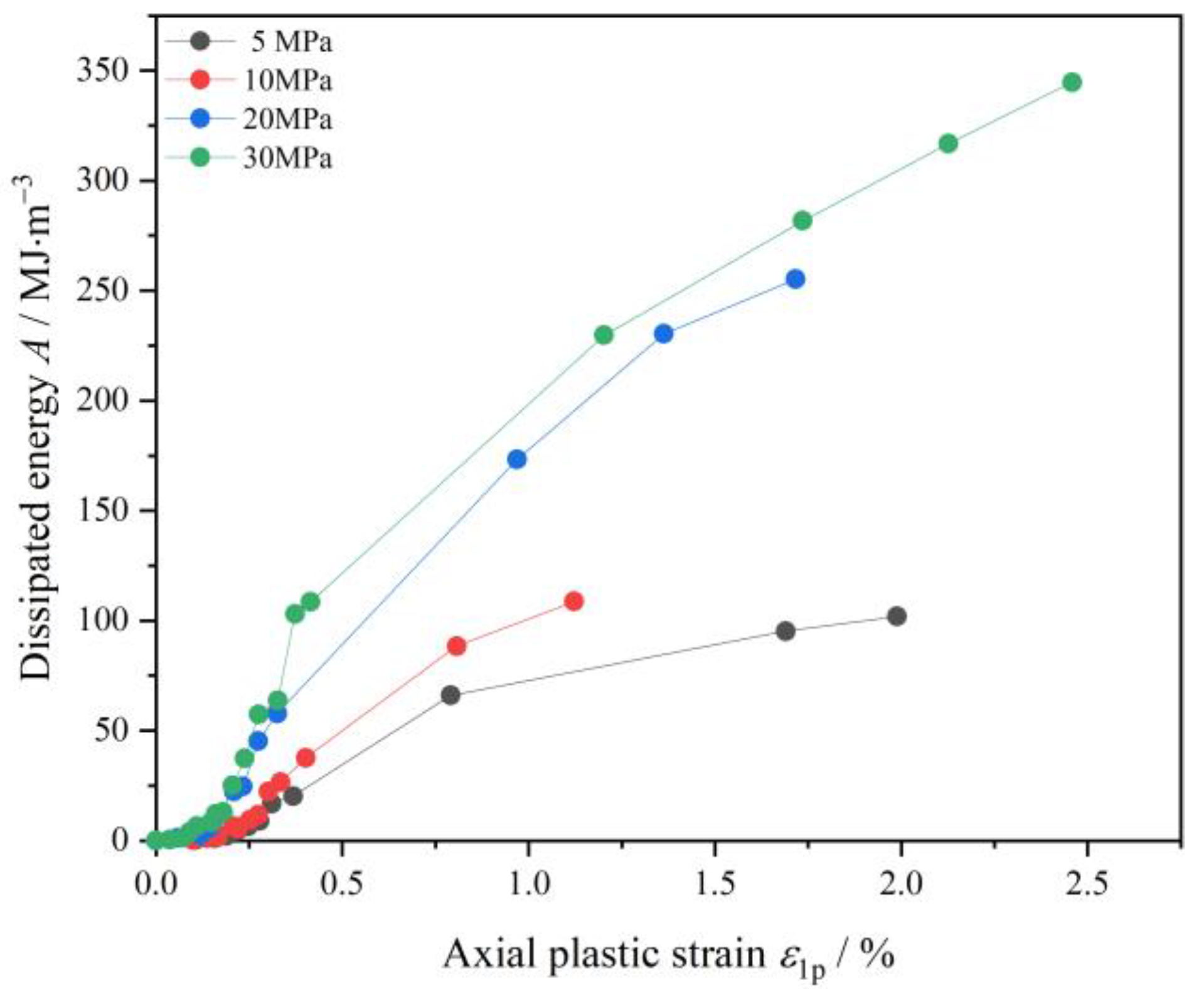
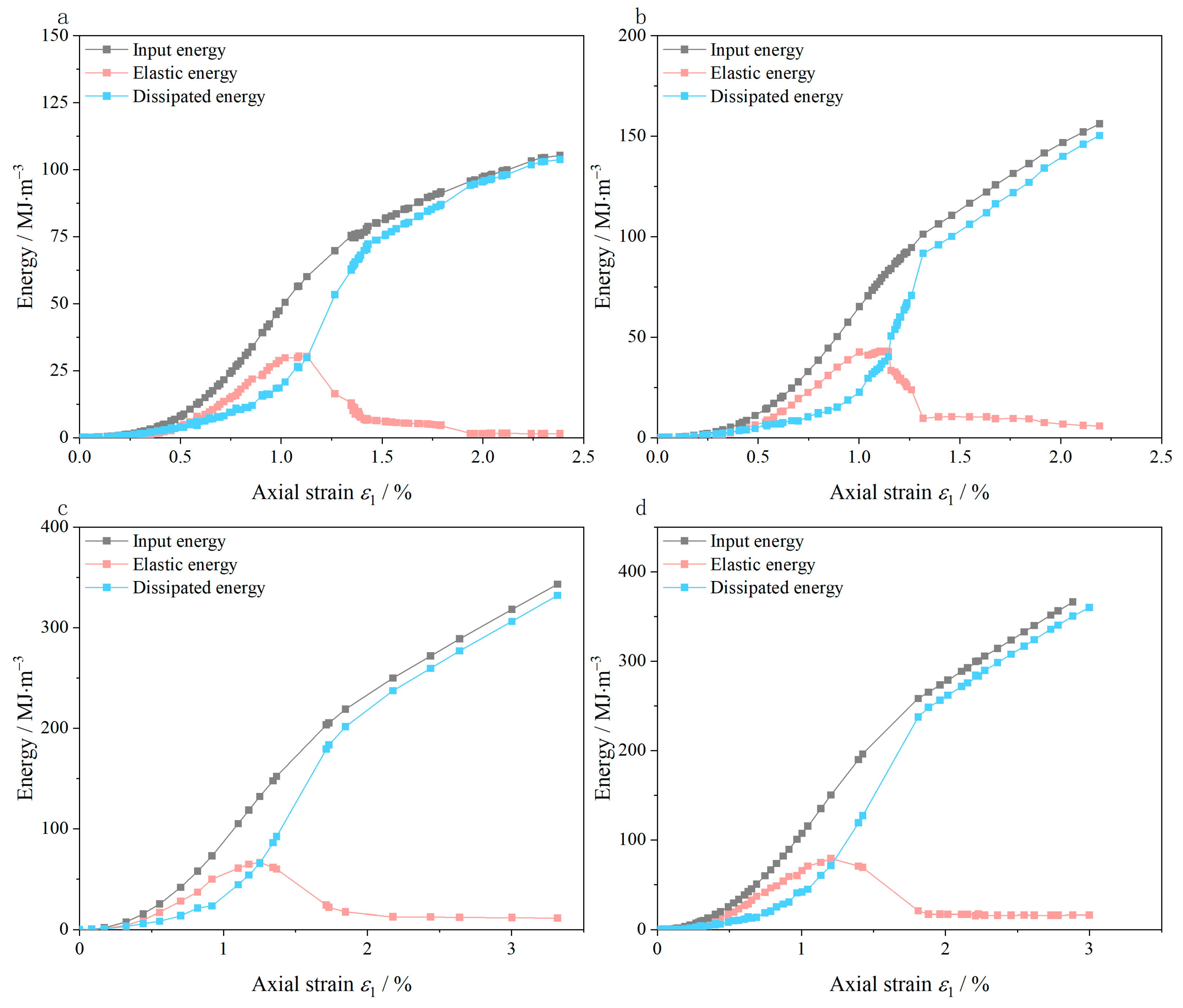
3.1. Energy Evolution

By integrating the stress–strain curve, it is possible to calculate the input energy resulting from external forces acting upon the rock, the elastic energy stored within the rock, and the dissipated energy generated by rock damage. As shown in Figure 3, the input energy is represented by the area beneath the loading curve, while the elastic energy is represented by the area beneath the unloading curve, and the dissipated energy is represented by the area between the loading and unloading curves.

By calculating the integral area of the stress–strain curve, the energy density of input energy, elastic energy, and dissipated energy for each loading and unloading cycle can be obtained. Under uniaxial conditions, the energy density only needs to be calculated based on the axial stress-strain curve. In the case of conventional triaxial loading, the dissipated energy can be obtained by subtracting the elastic energy in the axial and circumferential directions from the input energy, as expressed by Equation (1) below. It is assumed that positive external work is performed on the rock, while negative work is carried out by the rock on the external environment.

$$A=W_1+W_3-U_1-U_3$$

(1)

where A represents the dissipated energy; W₁ represents the input energy in the axial direction; W₃ represents the input energy in the circumferential direction; U₁ represents the elastic energy in the axial direction; and U₃ represents the elastic energy in the circumferential direction.

The energy curves within the rock under various confining pressures are presented in Figure 4. The axial strain is plotted on the horizontal axis, while the energy density is depicted on the left vertical axis, and the axial stress is illustrated on the right vertical axis. The different colored dotted lines correspond to the three distinct energy curves, while the smooth curve represents the axial stress–strain relationship.

From Figure 4, it can be observed that during the loading process under different confining pressures, the energy evolution within the rock exhibits distinct converging characteristics. In the initial compaction stage of the stress curve, the primary cracks and pores within the rock are compressed and closed, leading to a gradual increase in the input energy and corresponding elastic energy. Prior to the stress peak, the variation trend of rock elastic energy aligns roughly with the stress–strain trend of the rock, wherein the elastic energy undergoes an initial slow increase and then approximates a linear growth. In the elastic stage of the stress curve, the increased hardness of the rock enhances its energy storage capacity. The level of damage within the rock remains relatively low, resulting in minimal dissipated energy, with the external energy primarily being converted into elastic energy stored within the rock. Before yielding, when the rock is relatively intact, the energy from external forces is primarily transformed into elastic energy, which typically reaches its maximum value near the stress peak. After entering the post-peak softening stage of the rock loading process, cracks rapidly propagate and connect within the rock, leading to the rapid loss of overall integrity, with the rock mass being fragmented into multiple blocks. At this stage, interblock sliding occurs accompanied by distinct cracking sounds, and the elastic energy within the rock is rapidly released. Consequently, the stored elastic energy within the rock declines rapidly as the stress decreases, while the energy density of the dissipated energy gradually increases. In the residual stage of the stress curve, severe damage occurs within the rock due to the formation and propagation of primary cracks. The dissipated energy exhibits an approximately linear increase, while the elastic energy gradually decreases and tends to stabilize. The external work is primarily used to overcome the internal friction within the rock, resulting in approximately constant external work during the unit deformation process of the rock.

The cumulative damage dissipated energy curve under different confining pressures is presented in Figure 5, where curves of the same confining pressure are depicted in the same color. The figure reveals that the cumulative damage dissipated energy of the rock undergoes four distinct stages: low-speed increase, accelerated increase, rapid increase, and uniform increase. (1) Before the elastic stage, the internal damage and energy dissipation rate is small, resulting in a slow increase in the cumulative damage dissipated energy. (2) Upon entering the elastic and plastic stages, the rate of damage and energy dissipation increases, leading to an accelerated growth trend in the cumulative damage dissipated energy. The rock damage transitions into the stage of accelerated evolution. (3) After entering the post-peak softening stage, the elastic energy inside the rock is released, and all the external work is converted into the damage dissipated energy. (4) At the residual stress stage, as the internal damage evolution comes to a halt, the elastic energy within the rock remains relatively constant. At this point, all the external work is used for the friction work inside the rock, resulting in a linear increase in dissipated energy.

The cumulative damage dissipated energy curves under different confining pressures exhibit several noteworthy observations. (1) The variation patterns of the cumulative dissipated energy of rock are roughly the same under different confining pressures, experiencing slow increase, accelerated increase, rapid increase, and uniform increase stages. (2) During the initial slow increase stage of rock damage energy dissipation, the influence of confining pressure on the rate of increase in rock damage energy dissipation is relatively insignificant. (3) Under different confining pressures, at the same strain level, the cumulative damage dissipated energy of rock subjected to higher confining pressure surpasses that of rock under lower confining pressure, with the disparity becoming more prominent as strain increases. This suggests that as the confining pressure rises, the energy dissipation of rock gradually intensifies for a given strain level. (4) After the residual stress stage, the residual stress of rock escalates with increasing confining pressure, thereby amplifying the rate of increase in dissipated energy. (5) With the augmentation of confining pressure, the rapid increase stage of rock damage energy dissipation displays a higher energy dissipation rate, implying faster and more vigorous energy release.

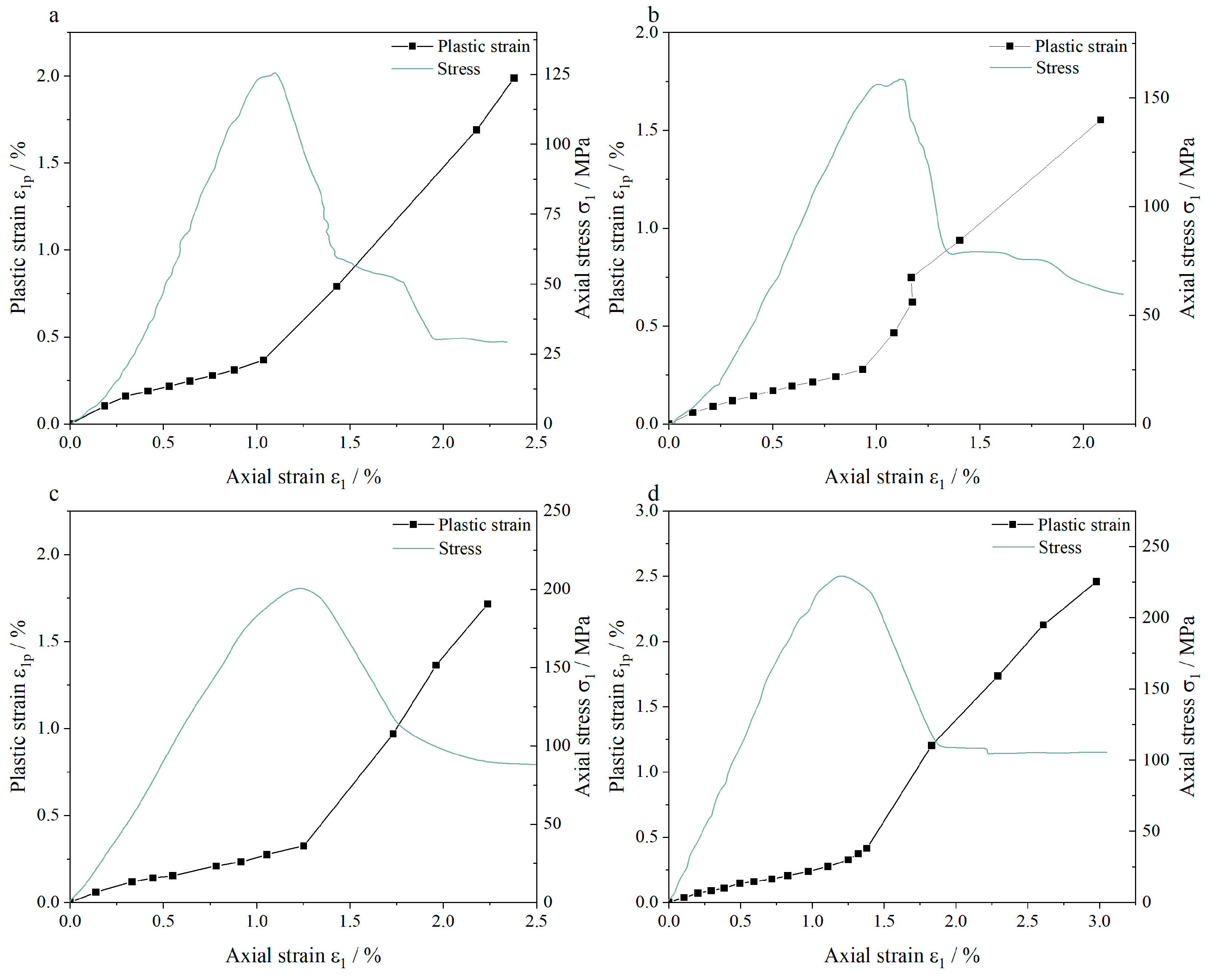
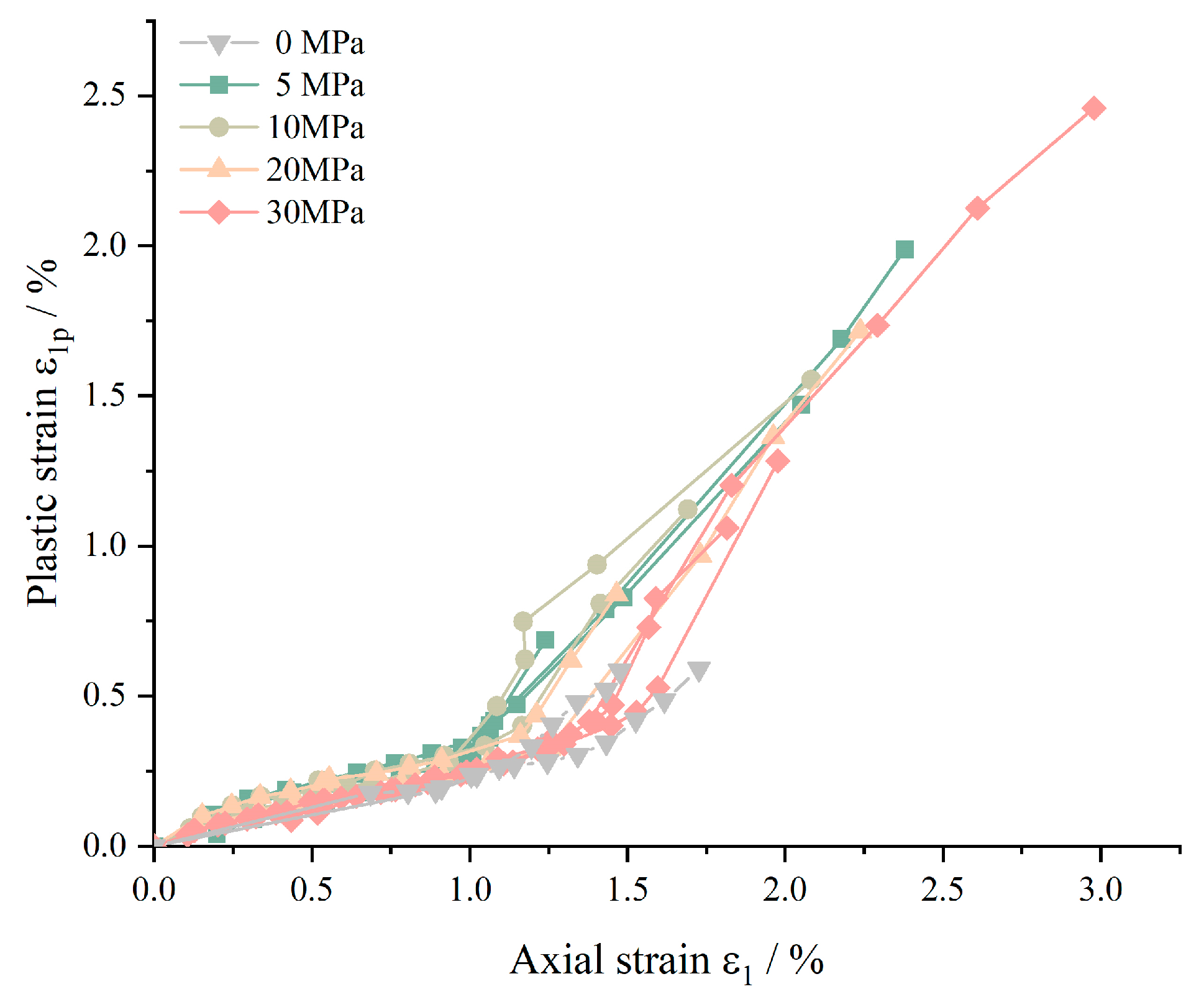
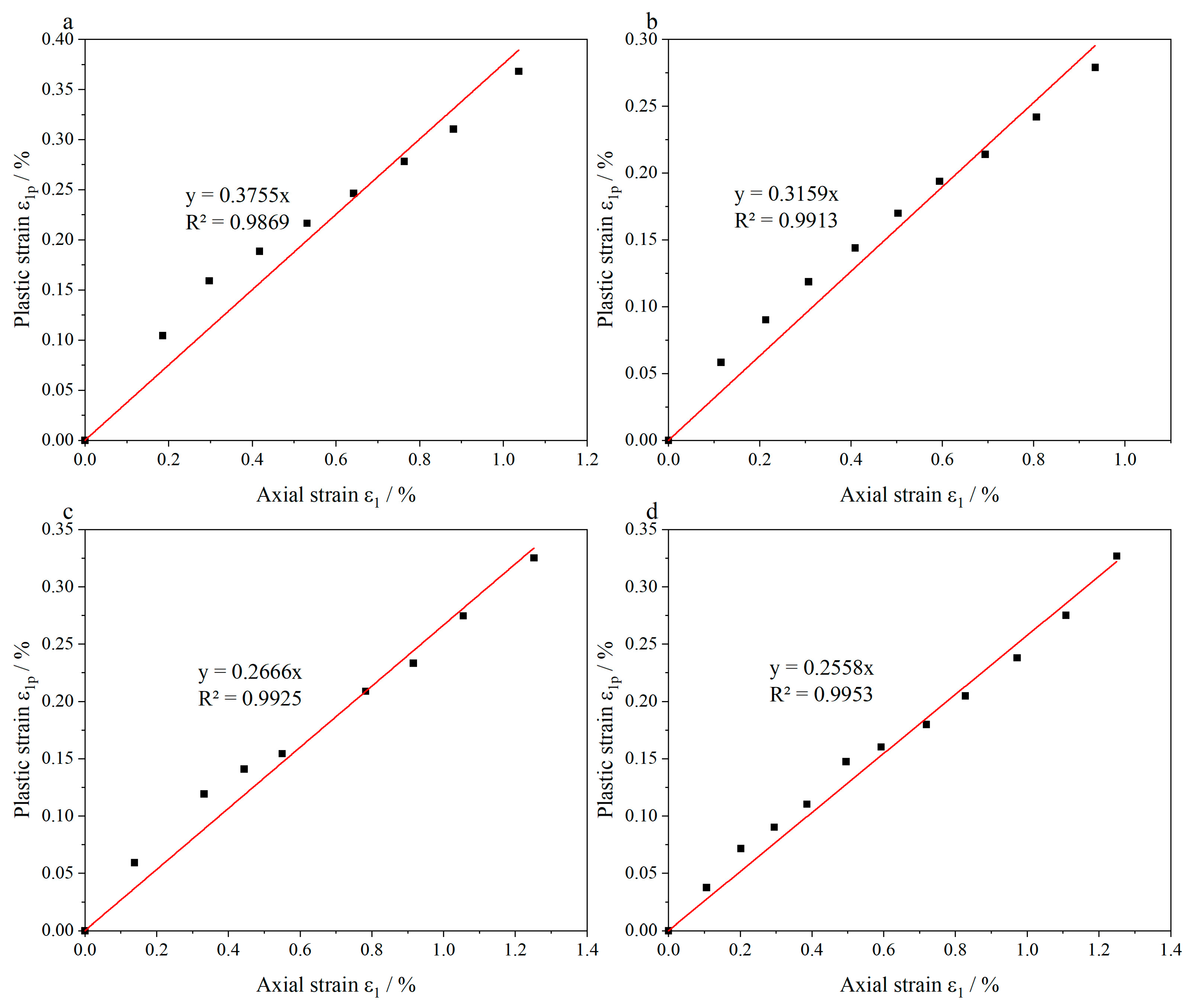
3.2. Plastic Deformation Evolution

The evolution of plastic strain accompanies the entire process of rock damage and failure. Contrary to previous empirical views, it is now recognized that rocks undergo irreversible deformation even in the compaction and elastic stages. Even at 20% unloading of the axial peak strain, rocks will undergo small irreversible plastic deformation. As the stress level increases, the plastic strain of rocks gradually increases irreversibly. Before reaching the stress peak, the plastic strain of rocks increases almost uniformly. In the plastic stage, the plastic strain begins to accelerate. After entering the softening stage, the plastic strain of rocks increases rapidly. In the residual stress stage, the residual elastic strain of rocks no longer changes significantly, and the increase in strain is almost entirely transformed into plastic strain. To further analyze the variation pattern of plastic strain during rock loading, the plastic strain corresponding to each unloading point is plotted, yielding the axial plastic strain curve depicted in Figure 6.

From Figure 6, the evolution curve of axial plastic strain in rocks can be divided into four distinct stages. (1) Compaction stage: corresponding to the initial compaction stage of the complete stress–strain curve, the curve of axial plastic strain in rocks exhibits a convex trend during the early loading phase. This indicates that the plastic strain of the rock increases relatively rapidly at the onset of loading. As the rock undergoes compaction, the rate of axial plastic strain gradually decreases. (2) Low-speed increase stage: prior to reaching the peak stress during rock loading, the axial plastic strain shows a linear increasing trend with the axial strain. However, it is evident from Figure 5 that the rate of plastic strain increase is notably slow. This suggests that before reaching the peak stress, the majority of axial deformation in the rock is transformed into elastic deformation, while the plastic strain demonstrates a gradual growth pattern. This is primarily due to the absence of interconnected cracks inside the rock before reaching the peak stress, where the strain is predominantly governed by the overall elastic deformation of the rock. (3) High-speed increase stage: upon entering the stress-softening stage, the rate of plastic strain increase abruptly escalates, and the curve of axial plastic strain in rocks displays an upward-opening blunt V-shape. In the post-peak softening stage, the cracks inside the rock rapidly propagate and form shear slip surfaces. Consequently, the axial deformation of the rock rapidly converts into plastic deformation through shear sliding, retaining only a small residual elastic strain. Hence, the rate of axial plastic strain increase reaches its maximum value during the post-peak stress-softening stage, which is referred to as the high-speed increase stage. (4) Residual stress stage: in the residual stress stage, the elastic strain within the rock remains nearly unchanged, and the axial strain is primarily transformed into shear sliding along the rock’s shear slip surface. As a result, the axial plastic strain of the rock exhibits a linear increase with the axial strain.

As previously mentioned, the evolution of axial plastic strain in rocks can be classified into four distinct stages: compaction, low-speed increase, high-speed increase, and residual stress. The overall axial plastic strain curve of rocks exhibits an upward-opening blunt V-shape. Furthermore, to investigate the impact of confining pressure on the variation of axial plastic strain in rocks, the axial plastic strain curves under different confining pressures were plotted in Figure 7. Each color in the figure represents the plastic strain curves of different rock samples subjected to the same confining pressure.

As depicted in Figure 7, the influence of confining pressure on the axial plastic strain curve of rocks can be summarized as follows: (1) Prior to reaching the peak stress, the axial plastic strain decreases slightly with increasing confining pressure, although the variation between different confining pressures is relatively small. (2) The inflection point between the low-speed increase stage and the high-speed linear increase stage of the plastic strain curve shifts to higher axial strains as the confining pressure increases. (3) Notably, a significant difference in plastic strain is observed among rocks subjected to different confining pressures within the axial strain range of 1% to 2%. Specifically, the axial plastic strain under low confining pressure is noticeably larger than that under high confining pressure. This disparity may arise from the fact that the axial plastic strain curve under low confining pressure enters the high-speed increase stage earlier than its counterpart under high confining pressure. (4) During the high-speed increase stage, the growth rate of the axial plastic strain curve under high confining pressure surpasses that under low confining pressure. This observation suggests that different confining pressure conditions can yield diverse growth paths for the plastic strain curve. However, with sufficient loading, the axial plastic strain curves of rocks under different confining pressures ultimately converge to a single point. (5) In the residual stress stage, the plastic strain of rocks under different confining pressures exhibits a comparable growth trend and rate. This similarity arises because, in this stage, the rock undergoes damage and plastic deformation primarily due to shear slip, which is minimally influenced by the confining pressure.

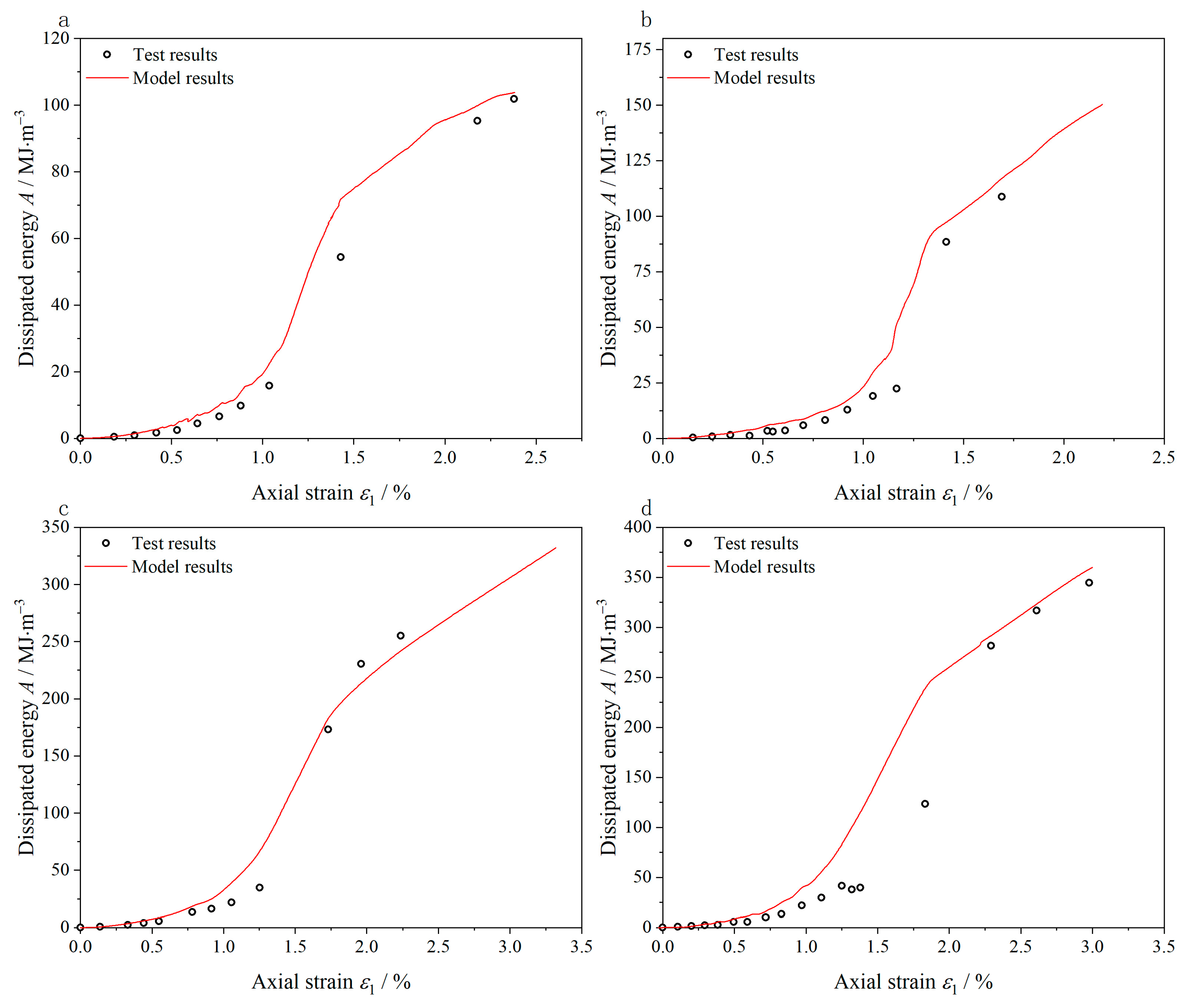
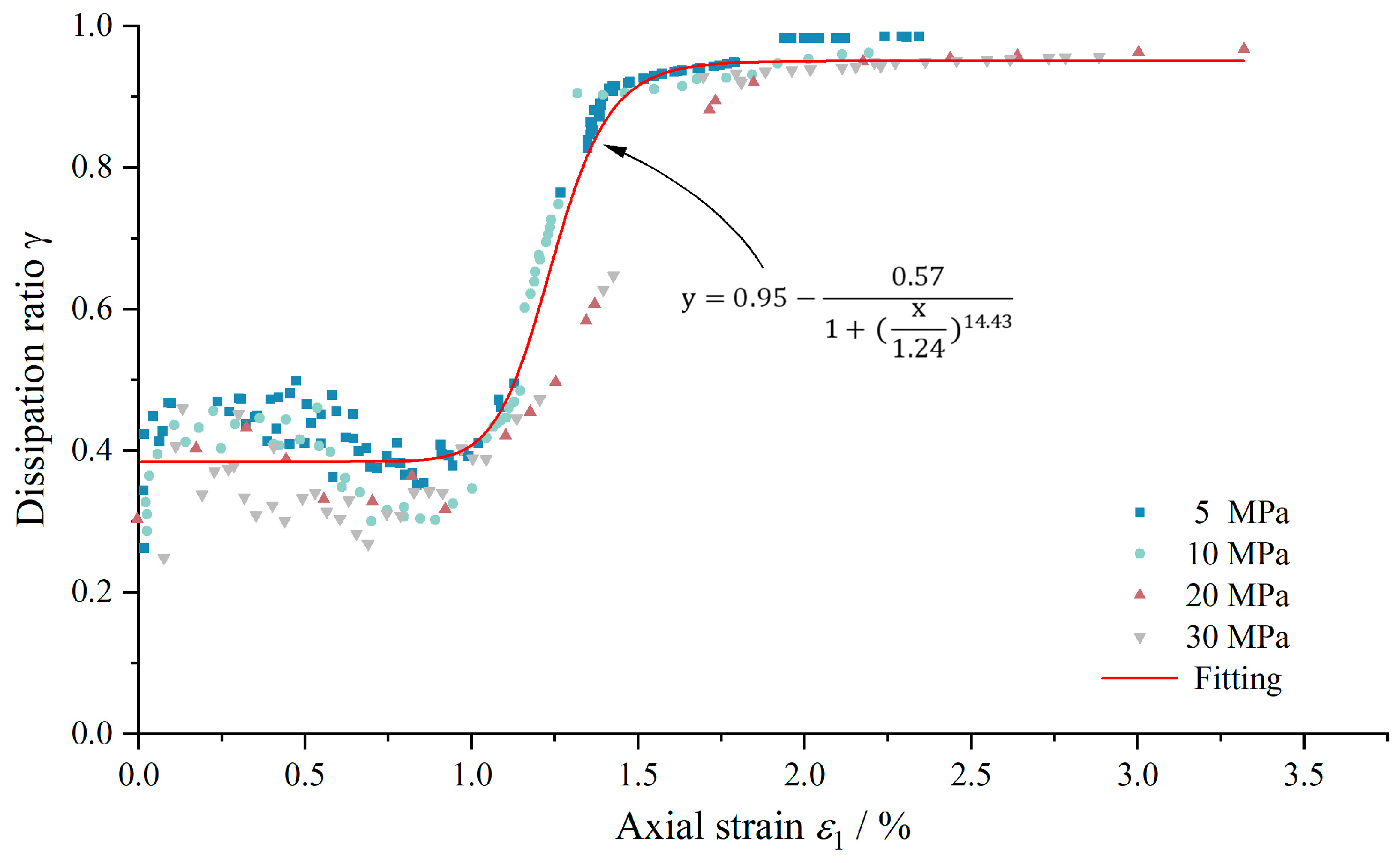
4. Analysis of Correlation Characteristics

By examining Figure 5 and Figure 7, it becomes evident that both dissipated energy and plastic strain exhibit consistent and incremental growth patterns as the axial strain progresses during the process of rock damage and failure. In order to further explore the correlation features between dissipated energy and plastic strain, the corresponding relationship between pre-peak dissipated energy and input energy under different confining pressures was plotted in Figure 8. The experimental results are represented by scatter points, while the red curve corresponds to the linear fitting curve. The figure illustrates that the dissipated energy of the rock follows a similar increasing trend to the input energy and a distinct linear relationship is observed. The linear fitting analysis reveals that, prior to the stress peak, the input energy is approximately transformed into dissipated energy at a fixed conversion ratio, which is approximately equal to the slope of the fitting curve. This conversion ratio serves as an indicator of the rock material’s capacity to convert dissipated energy, whereby a higher conversion ratio signifies a relatively weaker ability to store elastic energy within the rock material. Notably, as the confining pressure increases, the conversion ratio gradually diminishes, suggesting that the rock material exhibits an enhanced ability to store elastic energy under higher confining pressures.

In a similar vein, the relationship between axial plastic strain and axial strain prior to the stress peak under different confining pressures is depicted in Figure 9. The experimental results are represented by scatter points, while the red curve corresponds to the linear fitting curve. From the figure, it is evident that the axial plastic strain of the rock exhibits a distinct linear relationship with the axial strain. Based on the outcomes of the linear fitting analysis, prior to the stress peak, the axial strain undergoes an approximate conversion into plastic strain at a fixed transformation ratio, which aligns closely with the slope of the fitting curve. This transformation ratio serves as an indicator of the extent of plastic deformation in the rock, whereby a higher transformation ratio signifies a relatively weaker ability of the rock material to store elastic energy. Remarkably, as the confining pressure increases, the transformation ratio gradually diminishes, implying an augmented ability of the rock material to store elastic energy with rising confining pressures.

Combining Figure 8 and Figure 9, it can be observed that prior to the stress peak, dissipated energy and axial plastic strain have very similar evolution trends from both the energy and strain perspectives. Dissipated energy and axial plastic strain both increase linearly with input energy and axial strain, respectively. Prior to the stress peak, the proportion of input energy converted to dissipated energy is also relatively close to the proportion of axial strain converted to plastic strain. Under different confining pressures, the range of input energy converted to dissipated energy is approximately 0.24–0.32, while the proportion of axial strain converted to plastic strain is about 0.23–0.29. Furthermore, the evolution trends of the two quantities under the influence of confining pressure are also exactly the same.

According to the experimental data under a 30 MPa confining pressure, a curve is plotted with axial plastic strain as the horizontal axis and dissipated energy as the vertical axis, as shown in Figure 10. From Figure 10, the evolution process of dissipated energy and plastic strain can be divided into four stages. (1) During the compaction stage, plastic strain is generated due to the closure of primary pores and cracks in the rock, accompanied by a small amount of dissipated energy. The dissipated energy–plastic strain curve increases slowly, the slope gradually increases, and the curve is concave upward. (2) From the elastic stage to the stress peak, dissipated energy increases gradually with plastic strain, and the dissipated energy–plastic strain curve increases rapidly, the slope gradually increases, and the curve is concave upward. (3) In the post-peak softening stage, due to the difficulty in unloading the stress curve, there are fewer data points. The dissipated energy–plastic strain curve shows a generally increasing trend, with a reduced growth rate. (4) In the residual stage, the dissipated energy-plastic strain curve shows a generally linear increasing trend, and the slope of the curve can be regarded as a constant.

The dissipated energy–plastic strain curves are depicted in Figure 11. These curves exhibit a consistent evolution pattern and can be categorized into four stages: compaction, elastic, post-peak softening, and residual stress. From Figure 11, it is evident that, under identical plastic strain conditions, higher confining pressures result in greater dissipated energy. Conversely, under equivalent dissipated energy conditions, higher confining pressures lead to smaller plastic strains. All dissipated energy–plastic strain curves under different confining pressures undergo a progression characterized by a slow initial increase, rapid subsequent increase, a gradual decrease in the rate of increase, and eventual convergence toward a constant value. In the residual stress stage, the slopes of the dissipated energy–plastic strain curves display minimal variation, exhibiting no conspicuous relationship with the confining pressure.

The calculation of energy in different parts of a rock requires the collection of strain and stress data from cyclic loading–unloading tests. However, due to current experimental limitations, the number of loading–unloading cycles that can be performed in each test is limited. As a result, the obtained energy data for rocks suffer from problems such as a limited number of samples, high sample variability, and sample discontinuity, which hinder the study of rock damage evolution from an energy perspective. Therefore, it is urgent to calculate the rock energy at any time during the damage evolution process. Based on this, this paper explores the calculation of input energy, elastic energy, and dissipated energy in rock from a theoretical perspective. As expounded in the previous section, the rock damage process involves input energy, elastic energy, and dissipated energy. By leveraging the stress–strain curve of the rock obtained from experimentation, it becomes feasible to estimate the internal energy of the rock through the subsequent theoretical calculation process [39].

(1)

Input energy

In conventional triaxial compression tests, the input energy of the rock during the loading process includes two parts, namely, axial positive work and circumferential negative work, which can be calculated by integrating the stress–strain curve.

$$W=W_1+W_3={{\displaystyle \int }}_0^{{\epsilon }_1^t}{\sigma }_{1}d{\epsilon }_1+2{{\displaystyle \int }}_0^{{\epsilon }_3^t}{\sigma }_{3}d{\epsilon }_3$$

(2)

where ${\epsilon }_1^t$ represents the axial strain at time “t”; ${\epsilon }_3^t$ represents the circumferential strain at time “t”; ${\sigma }_i\left(i=1,2,3\right)$ represents the stress in different directions; and ${\epsilon }_i\left(i=1,2,3\right)$ represents the strain in different directions.

(2)

Elastic Energy

According to the theory of elasticity, the elastic energy can be expressed as:

$$U={\displaystyle \frac{1}{2}}\left({\sigma }_1{\epsilon }_1+{\sigma }_2{\epsilon }_2+{\sigma }_3{\epsilon }_3\right)$$

(3)

According to the generalized Hooke’s law:

$$\{\begin{array}{c}{\epsilon }_1={\displaystyle \frac{1}{E}}\left[{\sigma }_1-\nu \left({\sigma }_2+{\sigma }_3\right)\right]\\ {\epsilon }_2={\displaystyle \frac{1}{E}}\left[{\sigma }_2-\nu \left({\sigma }_1+{\sigma }_3\right)\right]\\ {\epsilon }_3={\displaystyle \frac{1}{E}}\left[{\sigma }_3-\nu \left({\sigma }_1+{\sigma }_2\right)\right]\end{array}$$

(4)

where E represents the elastic modulus, MPa; and $\nu$ represents the Poisson’s ratio.

In conventional triaxial compression tests, ${\sigma }_2={\sigma }_3$. By combining Equations (3) and (4), the elastic energy can be expressed as:

$$U={\displaystyle \frac{1}{2E}}\left[{{\sigma }_1}^2+2{{\sigma }_3}^2-2\nu \left(2{\sigma }_1{\sigma }_3+{\sigma }_3\right)\right]$$

(5)

However, Equation (5) is only applicable to the calculation of elastic energy for ideal elastic materials. To calculate the elastic energy of rock materials, a correction is needed. The elastic energy of rock can be expressed as:

$$\begin{gathered} U={\displaystyle \frac{k}{2E}}\left[{{\sigma }_1}^2+2{{\sigma }_3}^2-2\nu \left(2{\sigma }_1{\sigma }_3+{\sigma }_3\right)\right] \\ \mathrm{d}U={\displaystyle \frac{k}{2E}}\left[2{\sigma }_1\mathrm{d}{\sigma }_1-2\nu \left(2{\sigma }_3\mathrm{d}{\sigma }_1\right)\right] \end{gathered}$$

(6)

where k is the elastic energy correction parameter, which is dimensionless.

(3)

Dissipated energy

According to the energy conservation law, the dissipated energy during the process of rock damage is equal to the difference between the input energy generated by the external force doing work and the internal elastic energy of the rock. The dissipated energy can be calculated as:

$$A=W-U$$

(7)

To summarize, the energy of the rock at any given point can be determined by employing Equations (2), (6) and (7) based on the stress–strain curve. In this study, the proposed energy calculation method was applied to the collected stress–strain data obtained from experiments, with the elastic energy correction parameter set to 0.6. The calculated energy evolution curves of the rock under different confining pressures are presented in Figure 12. The horizontal axis represents the axial strain, while the vertical axis represents the energy density. Regarding the input energy derived from external forces using Equation (2), its calculation involves integrating the area under the stress–strain curve. The results of this calculation exhibit a high degree of agreement with experimental measurements and do not necessitate further comparison. The comparison between the calculated results of elastic energy and the corresponding experimental results is illustrated in Figure 13, where the scattered points represent the experimental data, and the curve represents the calculated results. Similarly, the comparison between the calculated results of dissipated energy and the corresponding experimental data is depicted in Figure 14, where the scattered points represent the experimental results, and the curve represents the calculated results.

Based on the findings presented in Figure 12, Figure 13 and Figure 14, the computed energy evolution curves of the rock provide valuable insights into the relationship between energy transformation and dissipation during the analyzed rock damage process. Specifically, the following observations can be made: (1) Comparison between Figure 4 and Figure 12 reveals that the proposed energy calculation method accurately captures the evolution relationship among input energy, elastic energy, and dissipated energy, demonstrating consistency with the experimental results. This indicates that the proposed energy estimation method can to some extent achieve a quantitative description of the internal energy distribution in the rock during the loading process. (2) Figure 13 demonstrates that the proposed energy calculation method effectively represents the evolution of internal elastic energy in the rock. Prior to reaching the peak stress, the computed elastic energy results align well with the experimental results. However, during the post-peak softening and residual stress stages, the computed elastic energy results exhibit some deviation from the experimental results, predominantly showing a lower overall trend. Moreover, the proposed energy estimation method exhibits inadequate accuracy in calculating the peak value of elastic energy stored in the rock. (3) Figure 14 illustrates that the proposed energy calculation method effectively portrays the evolution of dissipated energy in the rock. Prior to reaching the peak stress, the computed dissipated energy results closely match the experimental results. Nevertheless, during the post-peak softening and residual stress stages, the computed dissipated energy results show a certain degree of deviation from the experimental results, generally exhibiting a higher overall trend.

The calculation error of the proposed energy estimation method may be attributed to the inappropriate selection of the elastic energy correction parameter. In this study, the elastic energy correction parameter is treated as a constant and included in the energy calculation, while it may be influenced by confining pressure or mean stress. Additionally, in order to facilitate the calculation, the correction relationship for elastic energy in this study is assumed to be a simple linear relationship, whereas a nonlinear correction relationship for elastic energy may provide more accurate results.

The plastic strain of rock at each unloading point can be obtained from cyclic loading–unloading tests. However, due to limitations in current experimental conditions, the number of loading–unloading cycles that can be achieved in each test is limited. As a result, the amount of plastic strain data obtained for rock is insufficient, hindering the study of rock damage evolution from the perspective of plastic strain. Based on the study of the correlation between dissipated energy and plastic strain, this study proposes a method for calculating plastic strain based on dissipated energy, in order to estimate plastic strain at any given time during the rock damage evolution process.

Assuming the ratio of dissipated energy to input energy in rock is the dissipation ratio, the dissipation ratio can be expressed as:

$$\gamma ={\displaystyle \frac{A}{W}}$$

(8)

where $\gamma$ represents the dissipation ratio, which is dimensionless.

Assuming that the evolution law of dissipated energy is the same as that of plastic strain, the dissipation rate can be used to describe the relationship between plastic strain and total strain. The plastic strain tensor can be calculated as:

$${\mathit{\epsilon }}_{\mathit{p}}=\gamma \mathit{\epsilon }$$

(9)

where ${\mathit{\epsilon }}_{\mathit{p}}$ represents the plastic strain tensor, and $\mathit{\epsilon }$ represents the total strain tensor.

The calculated results of axial plastic strain in rocks under different confining pressures, obtained using the proposed plastic strain calculation method, are presented in Figure 15. The horizontal axis represents the axial strain, while the vertical axis represents the axial plastic strain. The scatter points correspond to the experimental results, whereas the curve represents the calculated results. From Figure 15, it is evident that the plastic strains calculated using the proposed method for different confining pressures align well with the experimental results. In the low-speed increase stage of rock plastic strain, the calculated results for various confining pressures closely match the experimental data. However, in the high-speed increase stage of rock plastic strain, there exist certain discrepancies between the calculated results and the experimental results for different confining pressures. Notably, the deviation of the calculated results tends to be more pronounced for lower confining pressures in the high-speed increase stage of rock plastic strain.

5. Damage Model and Numerical Test

5.1. Damage Model

Through analyzing experimental data, it was found that the dissipation rate under different confining pressures exhibits similar evolutionary trends. The dissipation rate under different confining pressures can be fitted by the same function, which can be expressed as:

$$\mathrm{y}=0.95-{\displaystyle \frac{0.57}{1+{\left(\frac{\mathrm{x}}{1.24}\right)}^{14.43}}}$$

(10)

The fitting results of the dissipation rate under different confining pressures are shown in Figure 16.

According to a previous work [31], the energy balance differential equation can be expressed as:

$$\mathsf{\delta }W=\mathrm{d}U+\mathsf{\delta }A$$

(11)

The input energy can be expressed as:

$$\mathsf{\delta }W=\mathit{\sigma }\mathrm{d}\mathit{\epsilon }$$

(12)

where $\mathit{\sigma }$ represents the stress tensor.

The elastic energy can be expressed as:

$$\mathrm{d}U=\mathit{\sigma }\mathrm{d}{\mathit{\epsilon }}_{\mathit{e}}-0.5{{\mathit{\epsilon }}_{\mathit{e}}}^{\mathsf{T}}{\mathit{M}}_{\mathbf{0}}{\mathit{\epsilon }}_{\mathit{e}}\mathrm{d}D$$

(13)

where ${\mathit{\epsilon }}_{\mathit{e}}$ represents the plastic strain tensor.

The dissipated energy can be expressed as:

$$\mathsf{\delta }A=Y\mathrm{d}D$$

(14)

where Y represents the damage energy dissipation rate, MPa.

Substitute Equations (12)–(14) into Equation (11), the rock damage can be calculated as follows:

$$\mathrm{d}D={\displaystyle \frac{\mathit{\sigma }\mathrm{d}{\mathit{\epsilon }}_{\mathit{p}}}{Y-0.5{\left(\mathit{\epsilon }-{\mathit{\epsilon }}_{\mathit{p}}\right)}^{\mathsf{T}}{M}_{\mathbf{0}}\left(\mathit{\epsilon }-{\mathit{\epsilon }}_{\mathit{p}}\right)}}$$

(15)

The plastic strain can be calculated by Equation (9), and the damage variable can be obtained by incremental calculation.

According to the stress–strain curves during the loading and unloading process, the damage can be solved as follows:

$$D_{\mathrm{i}}=1-{\displaystyle \frac{E_{\mathrm{i}}}{E_0}}$$

(16)

where $D_{\mathrm{i}}$ represents rock damage of the ith cycle; $E_{\mathrm{i}}$ represents the secant modulus of the unloading curve during the ith cycle, MPa; and $E_0$ represents the initial elastic modulus, MPa.

The comparison results of damage evolution curves under different confining pressures with experimental data are shown in Figure 17. It can be observed that the proposed model can reflect the rock damage evolution process, and the model error mainly exists in the instability process of rock near the peak stress.

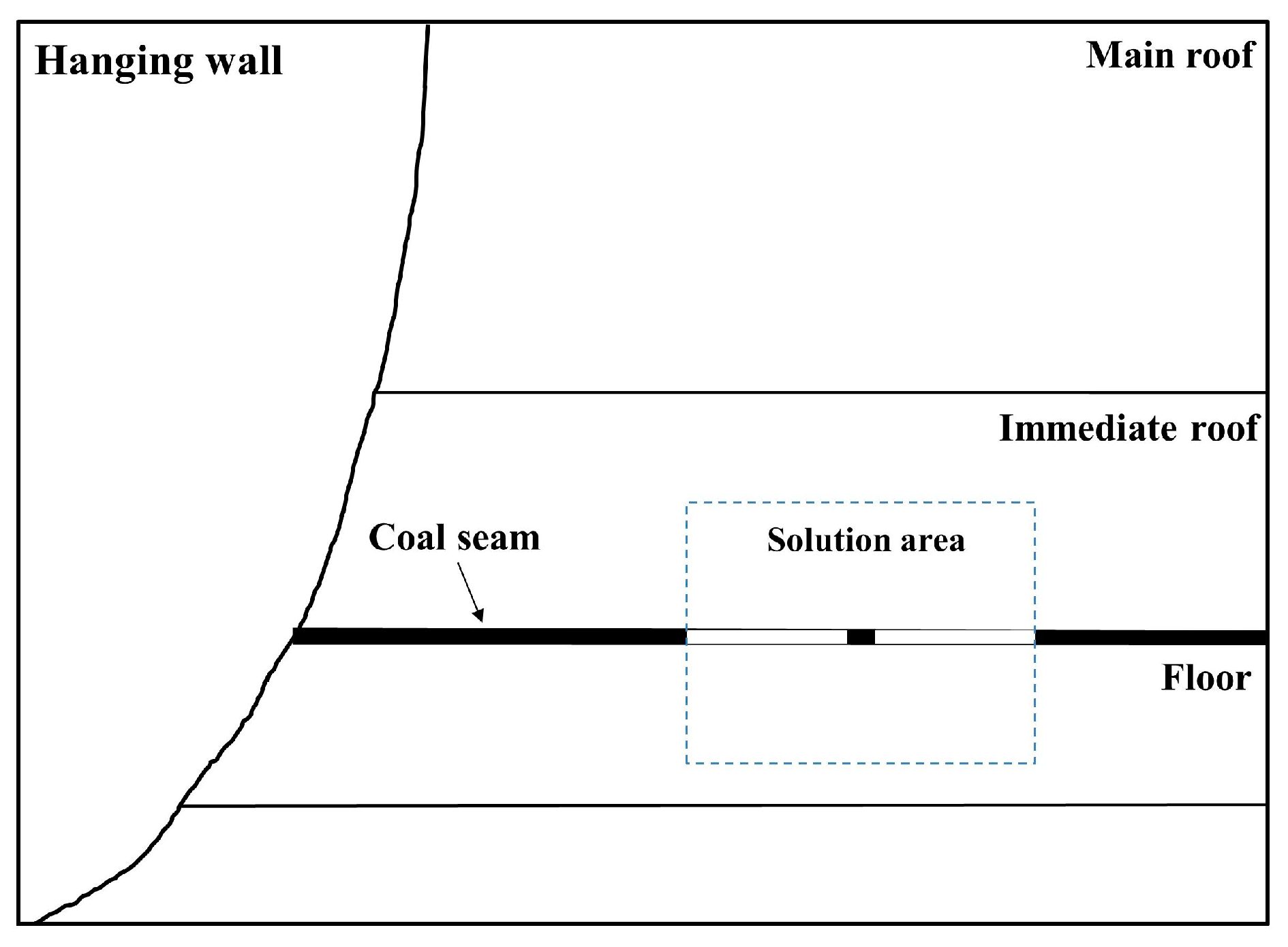
5.2. Numerical Test

Based on the proposed damage model, this work developed a numerical calculation program using the finite volume method (FVM), the numerical calculation program flow is shown in Figure 18.

(1)

Define constants, variables, and arrays. Input basic parameters and determine the solution area.

(2)

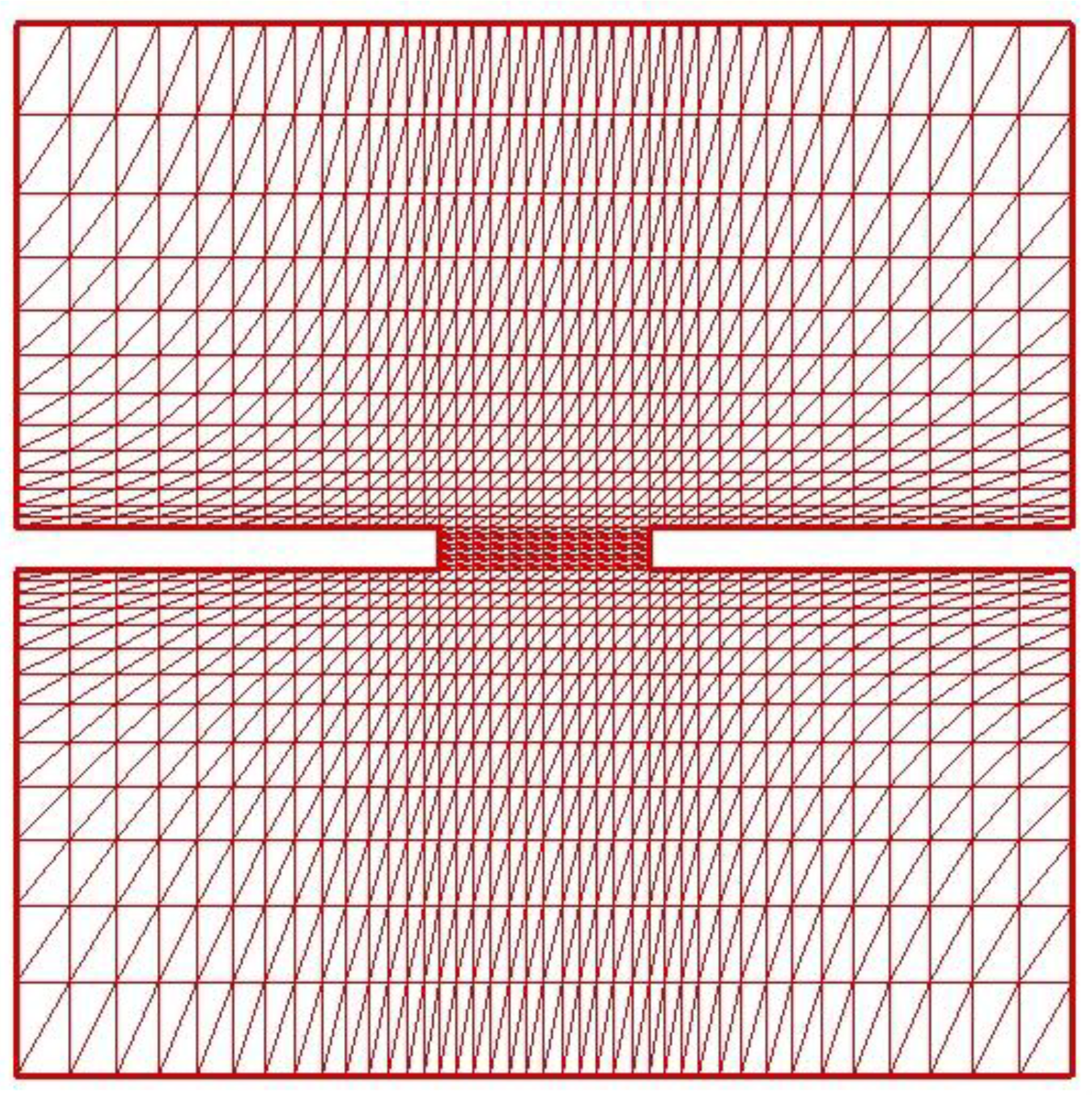
Grid division can be carried out according to certain rules within the solution area, radiating from the inner boundary to the outer boundary of the solution area. The grid gradually changes from dense to sparse from the tunnel wall to the surrounding rock in the distance. After dividing the grid cells, associate the cells with nodes.

(3)

Select an appropriate control volume, with node displacement as an unknown variable, and integrate and form a stiffness matrix using the finite volume method.

According to the geometric equations of elasticity mechanics, the element strain matrix can be expressed as:

$$\mathit{\epsilon }\left(x,y\right)=\mathit{B}\left(x,y\right)\mathit{d}$$

(17)

where $\mathit{\epsilon }\left(\mathrm{x},\mathrm{y}\right)$ represents the element strain matrix, $\mathrm{B}\left(\mathrm{x},\mathrm{y}\right)$ represents the element geometry matrix, and $\mathrm{d}$ represents the node displacement matrix.

The element stress matrix can be expressed as:

$$\mathit{\sigma }\left(x,y\right)=\left(1-D\right){\mathsf{M}}_{\mathbf{0}}\mathit{\epsilon }\left(x,y\right)$$

(18)

where $\mathit{\sigma }\left(x,y\right)$ represents the element stress matrix.

(4)

When solving, first set boundary conditions and constraints. Start the iterative calculation with a preset time step; the damage can be solved using Equation (15) so that the elastic modulus can be updated. Then, calculate the displacement, strain, and stress of each unit at the new time step.

(5)

When the running time is greater than the set time or the damage is greater than or equal to 1, the iterative calculation is ended and the result is output.

In order to explore the applicability of the theoretical models and numerical calculation programs in engineering practice, the Yimaqianqiu Coal Mine in Henan Province, China is taken as the engineering background. The area between the goaf of the 21,201 working face and the 21,181 working face is selected as the research object, and the numerical calculation program developed in this work is used for simulation.

The average thickness of the 2# coal seam in the mining area is set to 10.5 m, with an elastic modulus of 3.5 GPa and a Poisson’s ratio of 0.19. The direct top is composed of conglomerate and sandy mudstone, with an average thickness of about 310 m, an elastic modulus of 20.4 GPa, and a Poisson’s ratio of 0.23. The bottom plate is fine sandstone, with an average thickness of about 183 m, an elastic modulus of 18.5 GPa, and a Poisson’s ratio of 0.22. The on-site environment has been simplified, ignoring the influence of the north-south F16 fault. The spatial relationship of the solution area is shown in Figure 19.

The solution area is set to be 250 m long in the vertical direction and 250 m long in the horizontal direction. In coal seams, the grid is divided into equal lengths. In the rock layer, the grid is divided radially around the coal seam as the center. There are a total of 2376 units and 1295 nodes in the grid division. After conducting a time independence test and taking into account the impact of time step size on calculation accuracy and computational complexity, the time step size of the model can be determined to be 10 s. The lower boundary of the solution area is fixed with vertical displacement, and a geostress load is applied above the solution area, with a lateral coefficient of 1.2. A support force is applied in the goaf to simulate the support effect of gangue in the goaf. The grid division result is shown in Figure 20.

The initial state is taken as the moment when the 21,201 working face completes mining and reaches an equilibrium state. The numerical calculation results are shown in Figure 21, Figure 22 and Figure 23.

Through the simulation results, it was found that excavation construction resulted in the formation of isolated coal pillars between the goaf of the 21,201 working face and the 21,181 working face. The coal and rock mass around the isolated coal pillar is damaged greatly, and the two sides of the coal are the positions with the highest damage level. The damage evolves from both sides of the coal body towards the center and gradually spreads towards the adjacent rock mass, ultimately forming an arched damage area. However, the damage cannot continue to evolve towards the deep rock mass, and a large amount of elastic properties accumulate around the coal rock mass, which poses a risk of inducing rockburst. From the 5th day to the 30th day, the vertical stress above the coal body gradually increases and a stress concentration phenomenon occurs, with a stress concentration coefficient of about 2.4. Based on the above analysis, it can be concluded that the stress concentration phenomenon is obvious after the formation of the isolated coal body, and the elastic performance accumulates significantly in the arched damage area, which poses a risk of inducing rockburst. In addition, in the case of a rockburst accident at the Yimaqianqiu Coal Mine, the presence of the F16 reverse fault subjects the coal body to horizontal pressure from the hanging wall of the fault, which is also one of the potential triggering factors of an accident. In the above calculations, the influence of faults and protective coal pillars was not considered. However, by simulating the dynamic evolution of the damage field and stress field of isolated coal pillars, reference can be provided for the safety prevention and control of rockburst.

6. Conclusions

Based on the findings derived from cyclic loading and unloading tests conducted on sandstone samples, the relationship between rock dissipated energy and plastic strain was explored. The following conclusions were drawn:

(1)

Prior to reaching the stress peak, dissipated energy and plastic strain demonstrate a linear increase with input energy and axial strain. The conversion ratio of input energy to dissipated energy aligns closely with the transformation ratio of axial strain to plastic strain. In the residual stress stage, the growth trends of plastic strain under different confining pressures exhibit similarities, with comparable growth rates.

(2)

By introducing the elastic energy correction parameter, a method for estimating the input energy, elastic energy, and dissipated energy during the rock damage process was proposed, and it was validated using experimental results. A plastic strain estimation method based on the evolution mechanism of dissipated energy was also proposed, which enables the calculation of plastic deformation at any given time during the rock damage evolution process.

(3)

An improved rock damage model was proposed based on the correlation characteristics of energy dissipation and plastic growth in this work. The model can reflect the rock damage evolution process under different confining pressures, and the model error mainly exists in the instability process of rock near the peak stress.

(4)

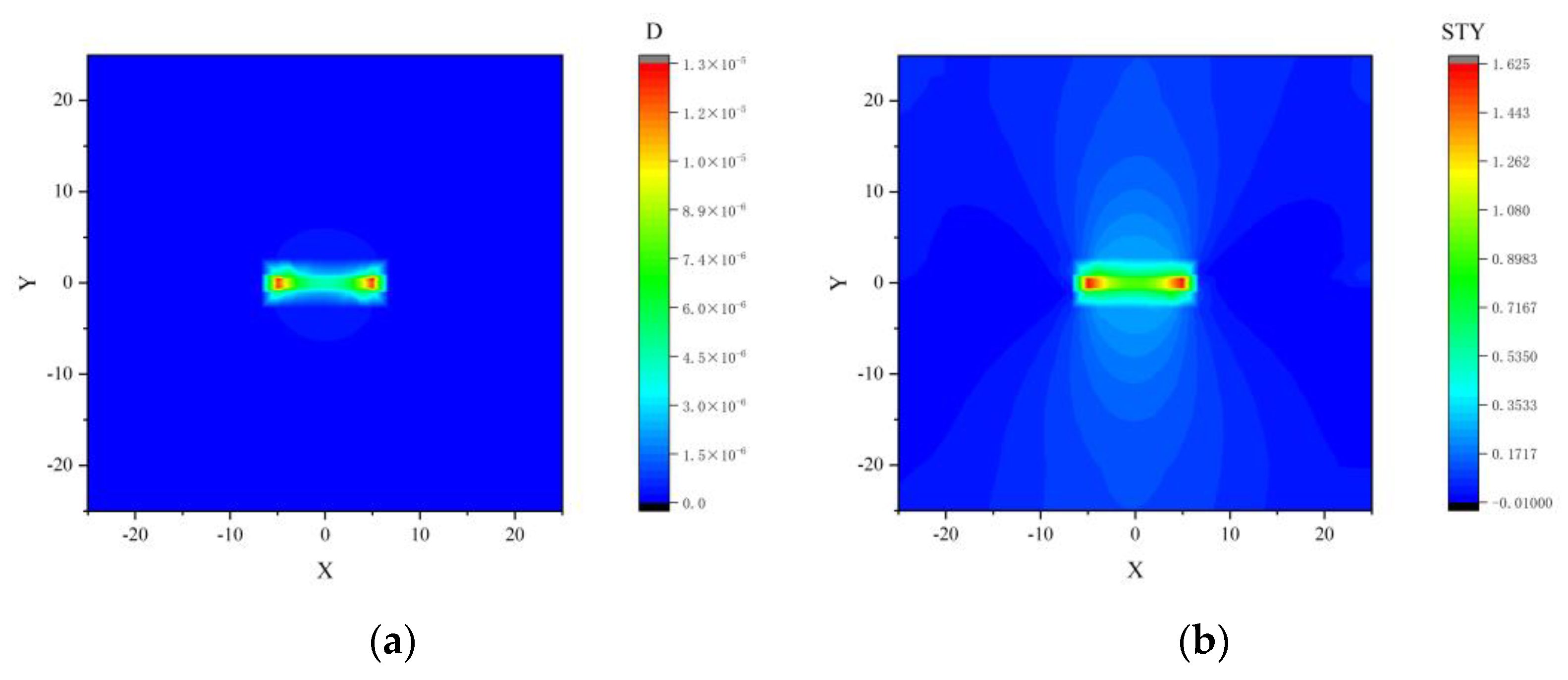
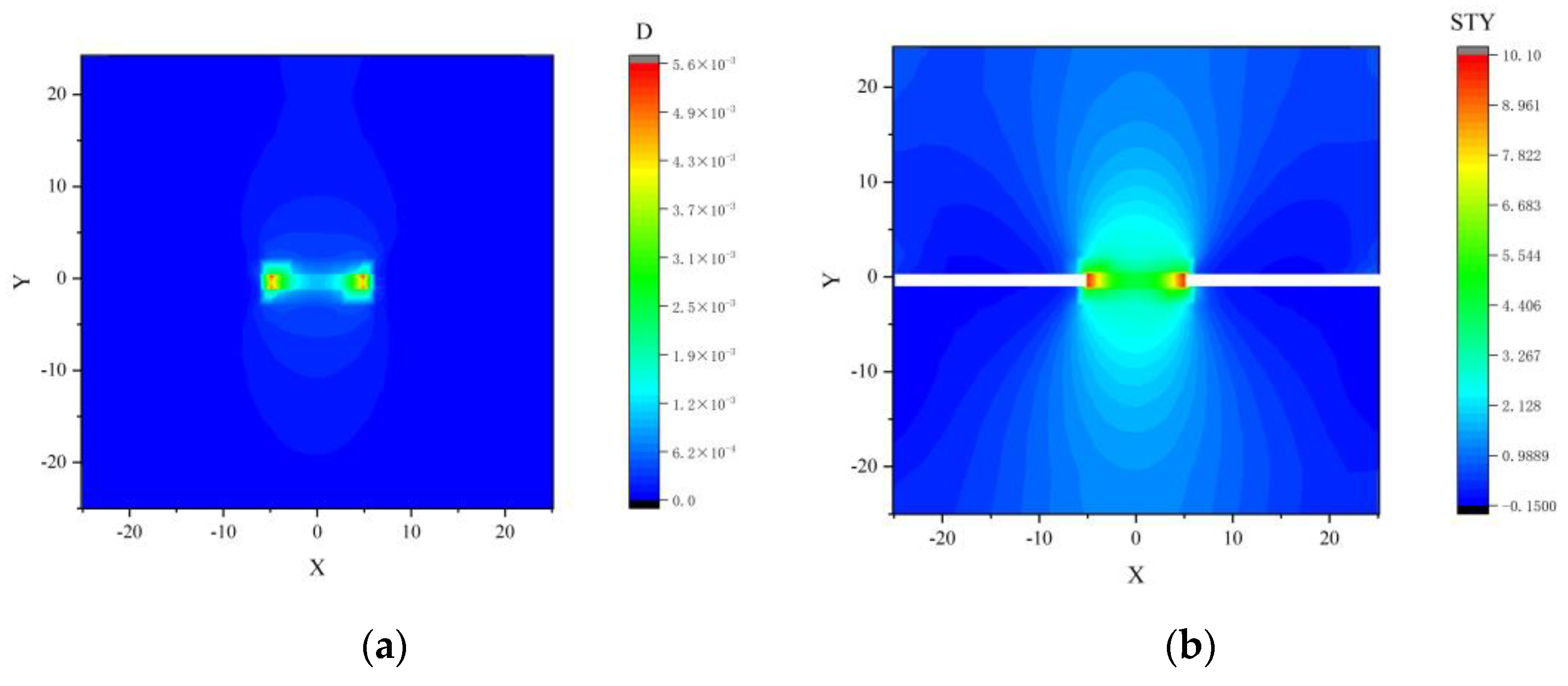
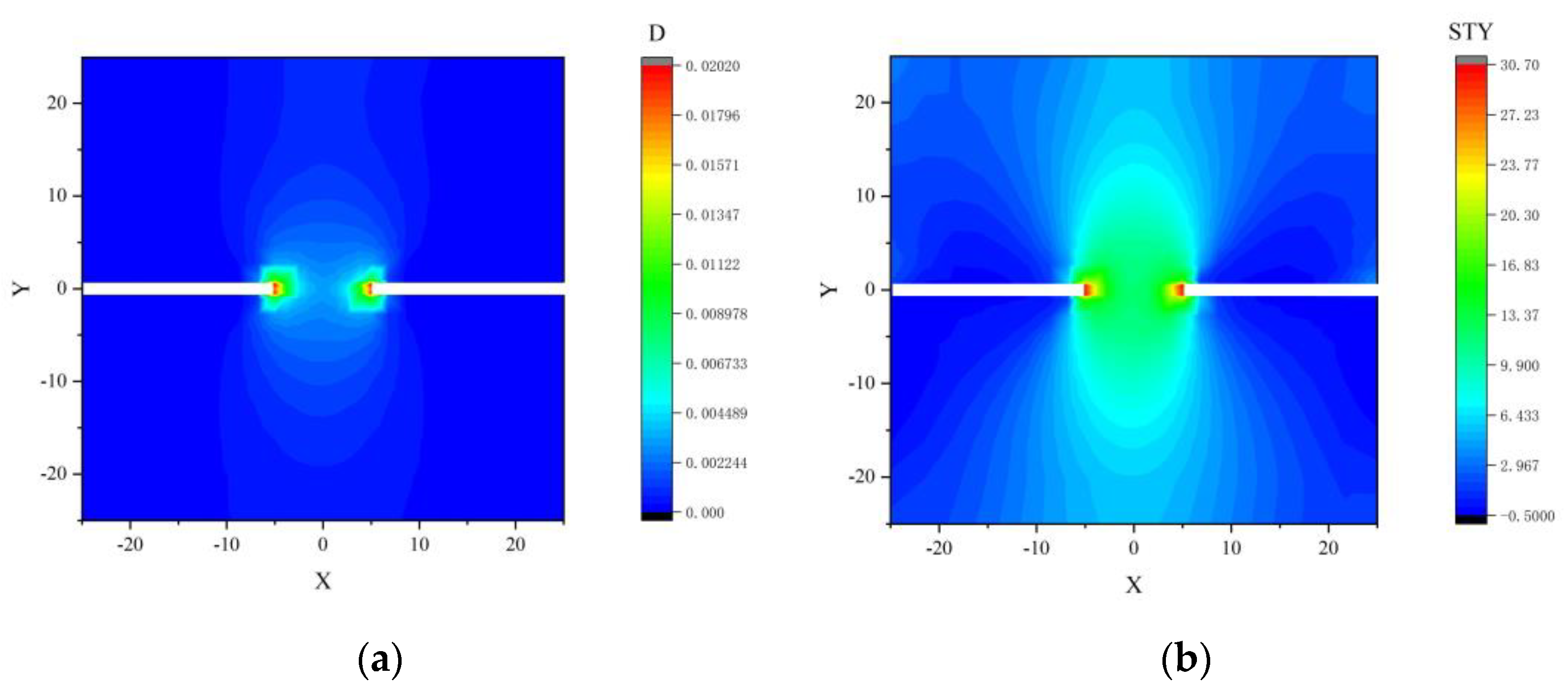
Based on the damage model, a numerical calculation program using the finite volume method (FVM) was developed. The surrounding rock damage and vertical stress evolution process in the Yimaqianqiu Coal Mine was simulated, and the results showed that the proposed program can provide a basis for risk analysis of rockburst.

(5)

In this work, due to only exploring the correlation between energy dissipation and plastic growth of sandstone specimens, the broader applicability of the proposed model has not been validated. Energy dissipation and plastic growth are common accompanying phenomena in the damage and failure process of rock materials. The difference between different rocks lies in the possible evolution relationship between energy dissipation and plastic growth, which is reflected in the selection of material parameters.