An Energy–Momentum Conserving Algorithm for Co-Rotational Quadrilateral Shell Elements in Nonlinear Multibody Dynamics
Abstract
1. Introduction
- (1)
- The formulation achieves symmetric tangent stiffness matrices in both global and local coordinate systems by introducing vectorial rotational variables, which ensures direct additivity and updates [13].
- (2)
- The nonlinear equation solving is significantly simplified by an incremental iterative algorithm, where nodal variable increments are directly superimposed onto the accumulated variables through algebraic summation operations. Therefore, complex iterative updates typically involved in conventional incremental approaches are avoided.
- (3)
- Extending Simo’s energy–momentum conservation algorithm, a midpoint interpolation strategy is rigorously implemented for all strain measures in the strain energy functional. Conservation of energy and momentum is achieved with symmetric element tangent stiffness matrices.
- (4)
- The algorithm incorporates two parameters—spectral radius and dissipation coefficient —to control energy dissipation in generalized midpoint variables and their time derivatives. It prevents high-frequency energy oscillations while maintaining numerical stability through energy dissipation controls.
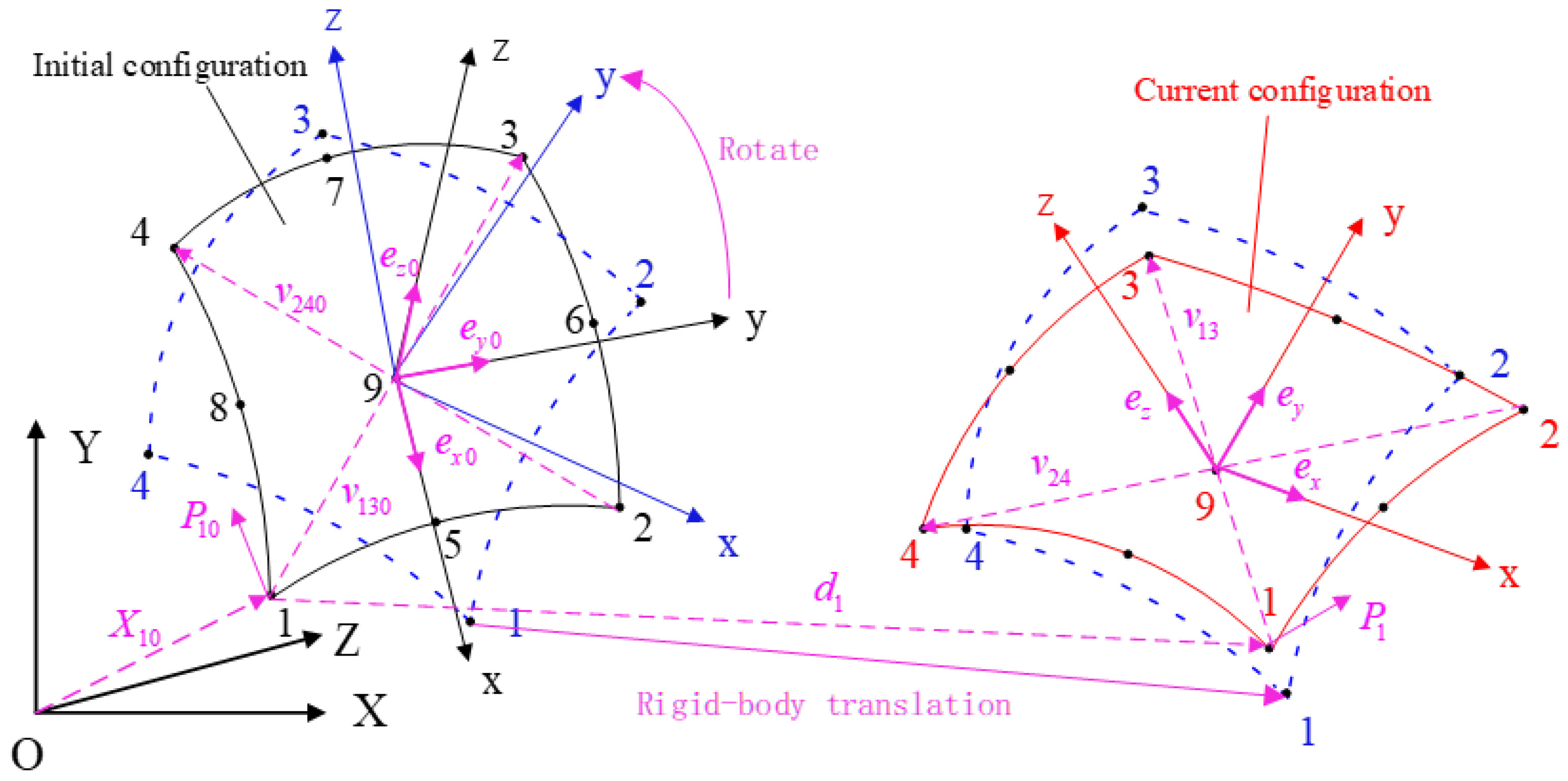
2. Formulation of Novel Co-Rotational Quadrilateral Elements
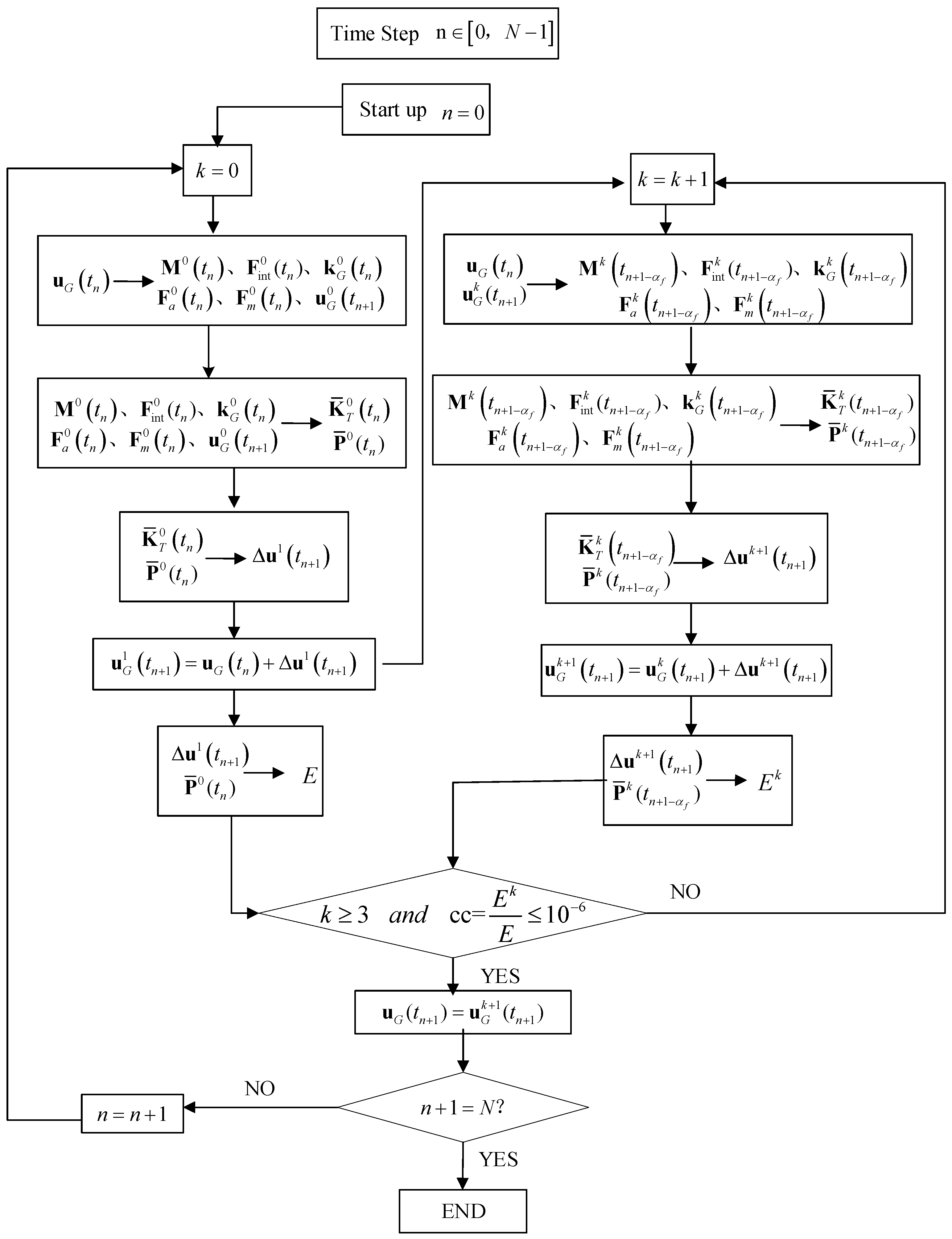
3. Solution Formulation Based on Energy–Momentum Conservation Algorithm
4. Examples
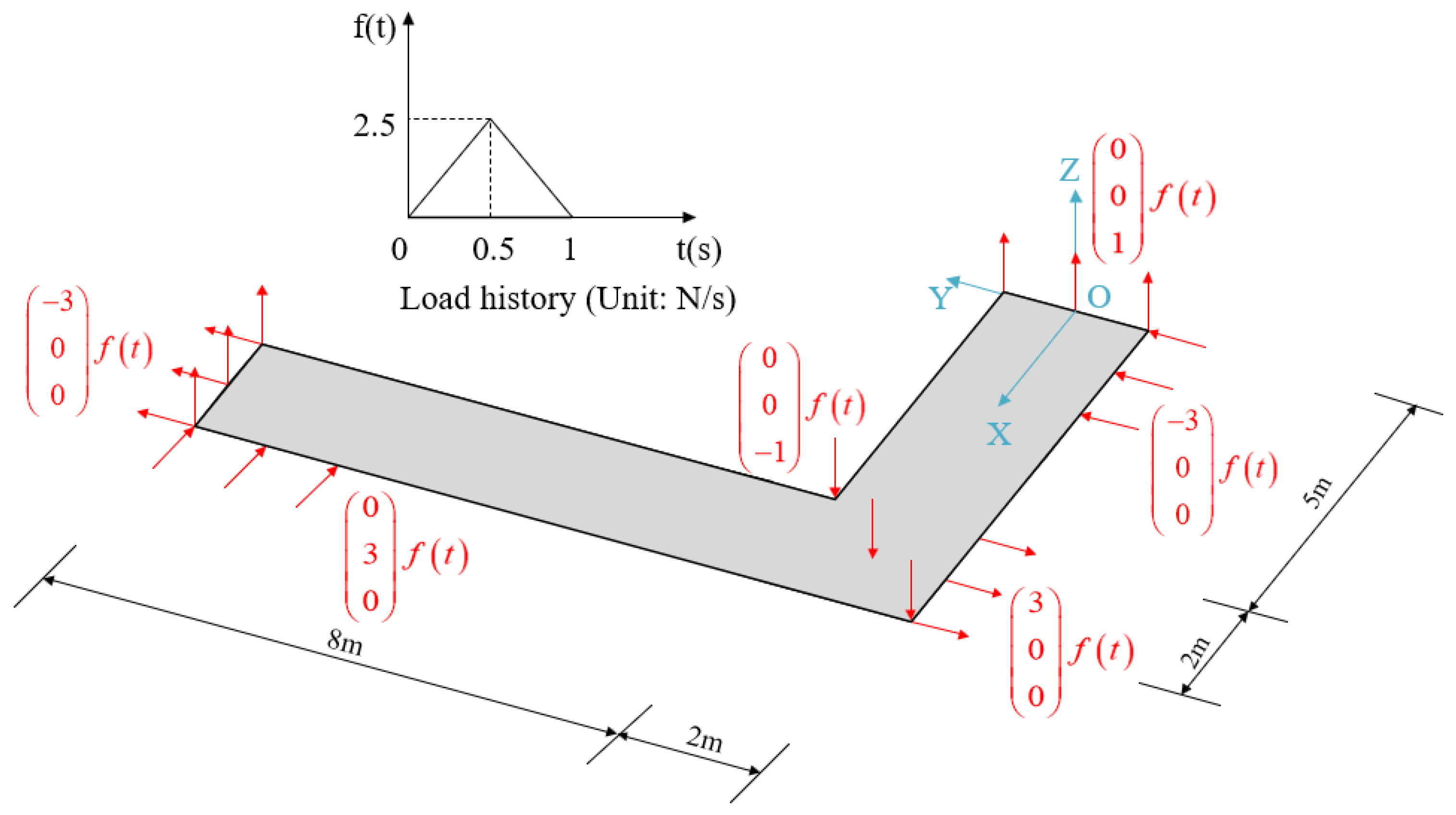
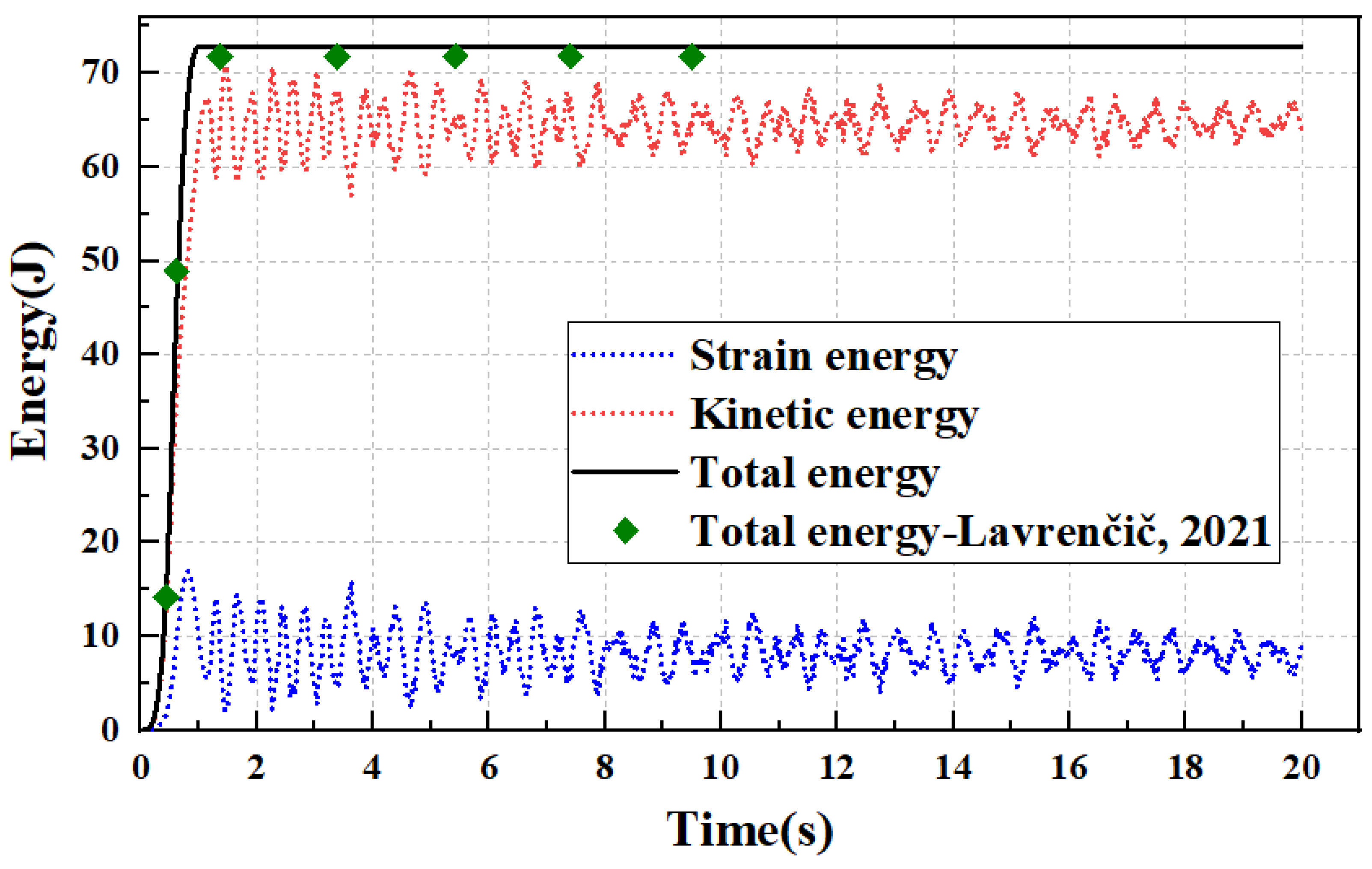
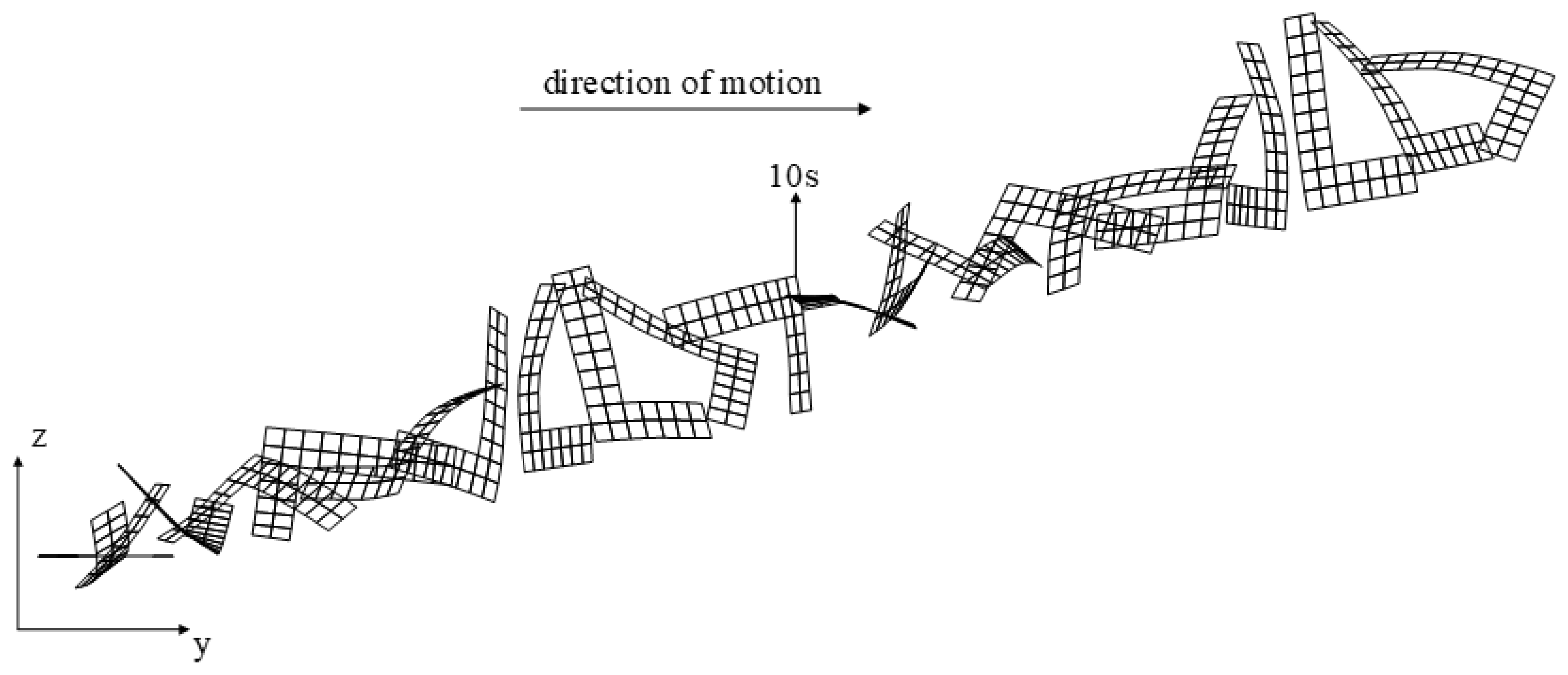
4.1. Flying L-Shaped Plate
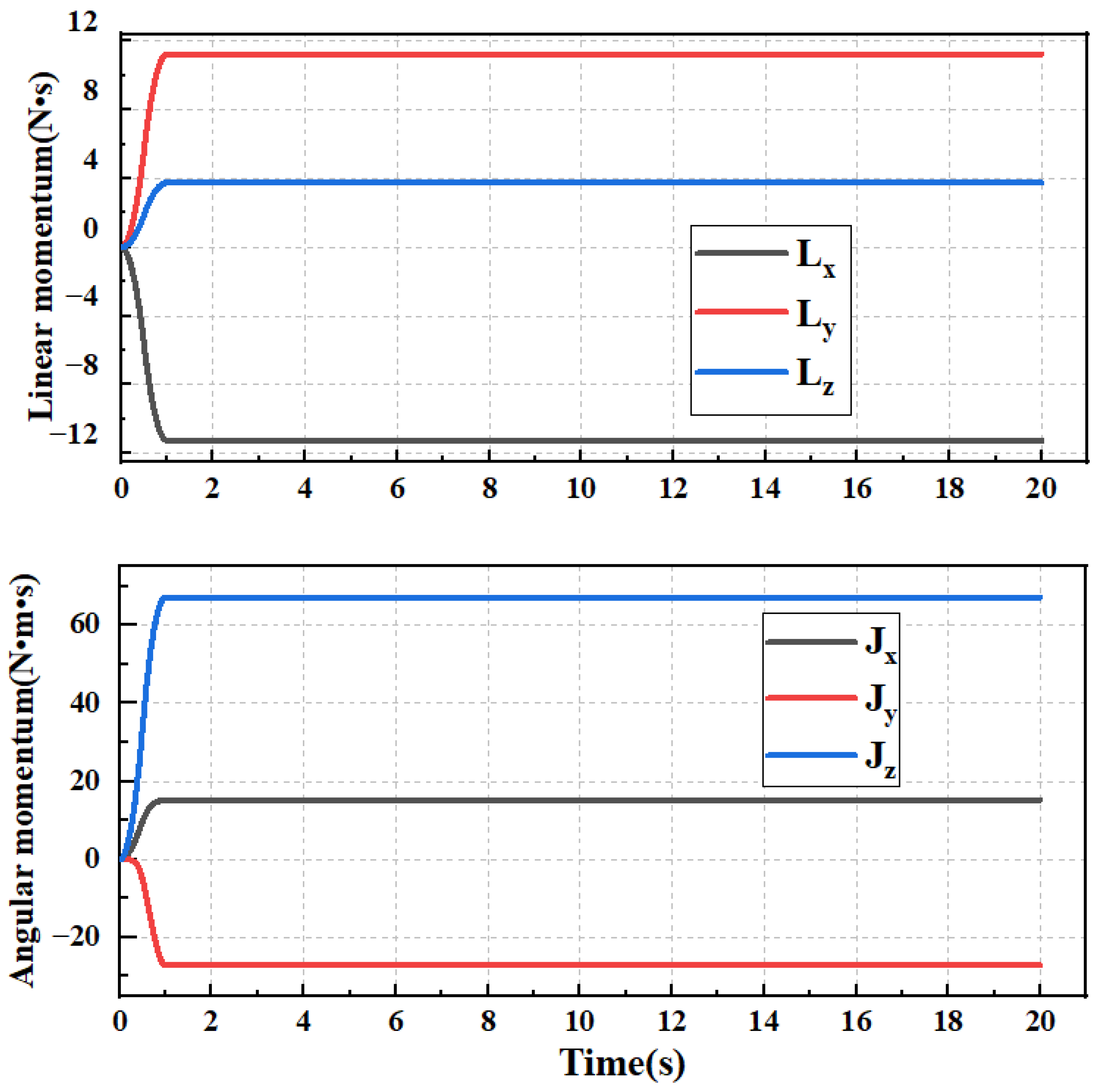
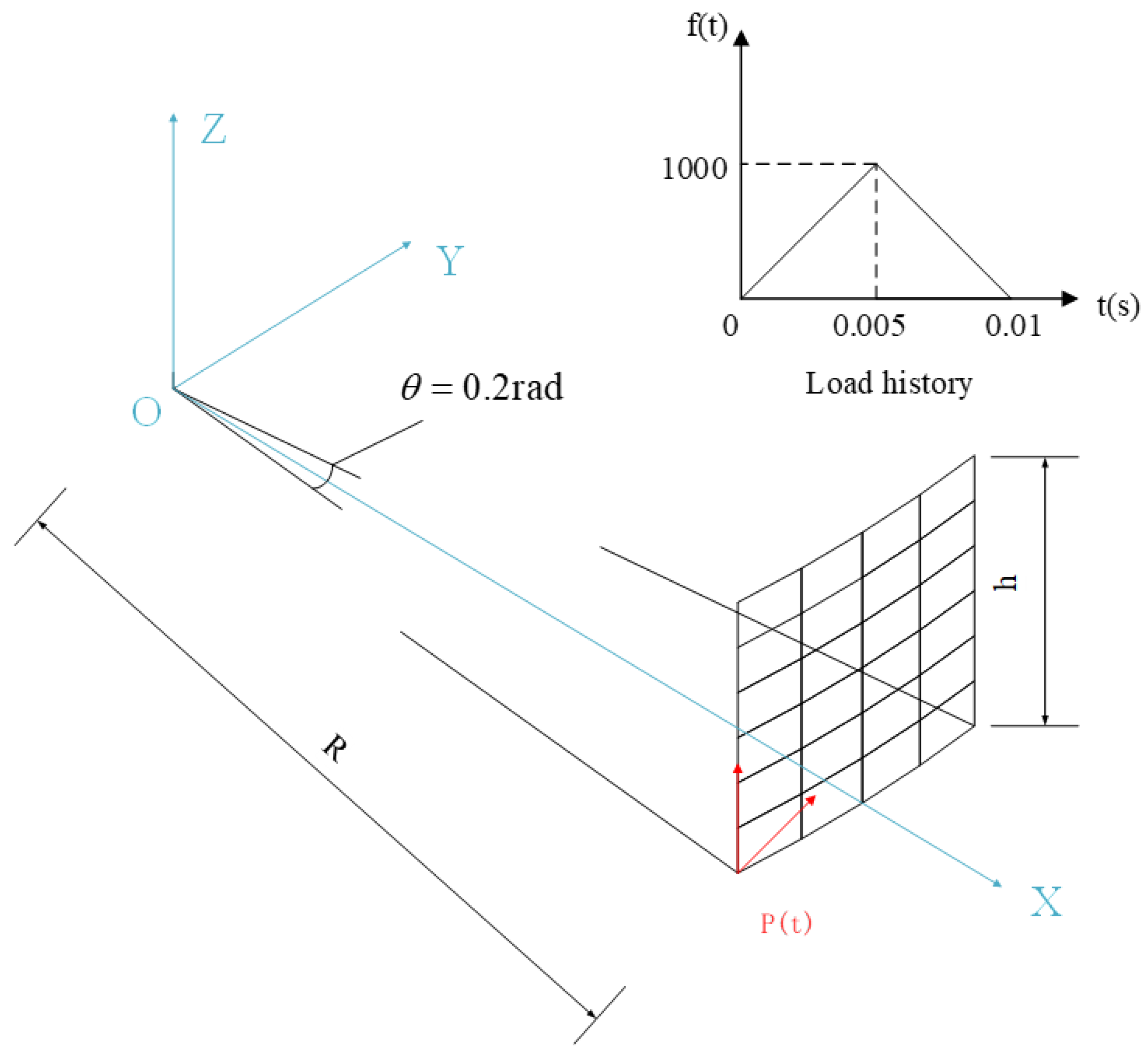
4.2. Free Large Overall Motion of a Cylindrical Panel
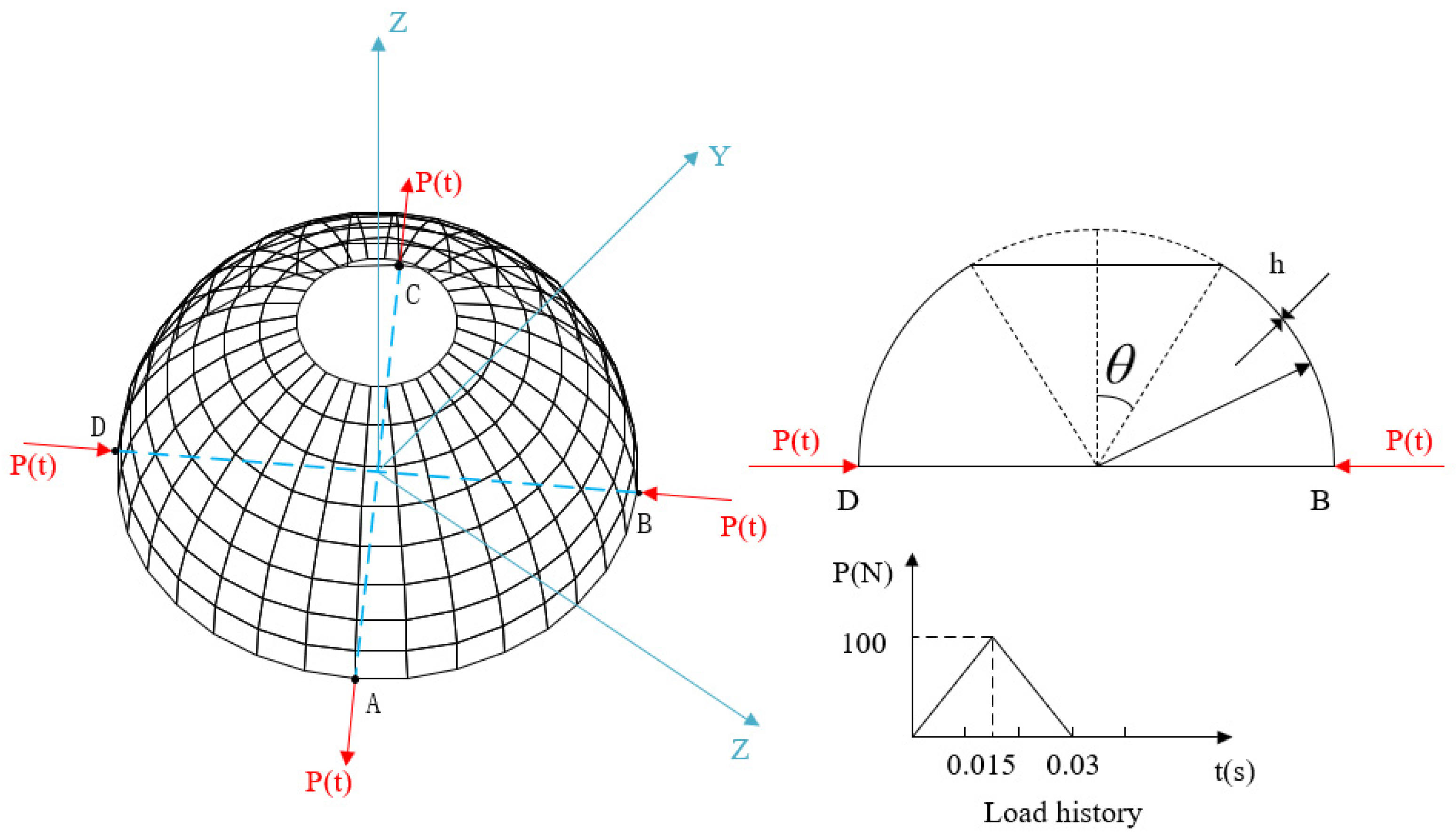
4.3. Pinched Hemispherical Shell
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Nomenclature | Description |
| The global coordinate system | |
| The local coordinate system | |
| The natural coordinate system | |
| Element nodal displacement variables in the global coordinate system | |
| Element nodal displacement variables in the local coordinate system | |
| Translational displacement of element node i in the global coordinate system | |
| Translational displacement of element node i in the local coordinate system | |
| Vectorial rotational variables of node i in the global coordinate system | |
| Vectorial rotational variables of node i in the local coordinate system | |
| Nodal normal vector of node i at the mid-surface | |
| Three components of the translational displacement of node i along the global coordinate system | |
| Three components of the translational displacement of node i along the local coordinate system | |
| The two minor components of the mid-surface normal vector along the three axes of the global coordinate system | |
| The components of the mid-surface normal vector along the x-axis and y-axis of the local coordinate system | |
| Local coordinates of node i in the deformed configuration | |
| The three components of the mid-surface normal vector of node i along the local coordinate axes in the initial configuration | |
| Unit vectors of the three coordinate axes of the local coordinate system in the initial configuration | |
| Vectors of diagonals 13 and 24 of the quadrilateral in the initial configuration | |
| Vector from the origin O of the global coordinate system to the corner node of the quadrilateral | |
| Unit direction vectors of the three coordinate axes of the local coordinate system in the deformed configuration | |
| Vectors of diagonals 13 and 24 of the quadrilateral in the deformed configuration | |
| the Lagrangian interpolation functions of node i | |
| Coordinate values of node i mapped to the natural coordinate system | |
| Mid-surface normal vector of node i in an element under the initial configuration | |
| Green–Lagrange strain, membrane strain, shear strain, bending strain | |
| Potential energy functional | |
| The elastic-moduli matrices | |
| The external forces | |
| , , | The first derivatives of strain vector , and with respect to the nodal variable |
| Tangent stiffness matrix in the local coordinate system | |
| Hamiltonian | |
| Kinetic energy, strain energy, and work done by external forces of the system | |
| The velocity of node i | |
| The superscript e denotes a certain variable of an element. | |
| The superscript denotes the first derivative of an arbitrary vector with respect to time. | |
| The superscript denotes the second derivative of an arbitrary vector with respect to time. | |
| Unit density | |
| Unit thickness (does not change with unit deformation) | |
| Second-order Jacobian matrix of the element | |
| Volume domain of the shell element | |
| Equivalent nodal load | |
| Equivalent mass matrix | |
| Element internal force, system external force | |
| A certain time step | |
| Total time steps for algorithm solution | |
| The step size of a certain time step | |
| Two generalized midpoints | |
| A certain dynamic variable at the starting end of a time step | |
| A certain dynamic variable at the generalized midpoint moment | |
| Spectral radius | |
| , , , | Integration parameters governed by the spectral radius |
| The equivalent force vector | |
| Tangent stiffness matrix in the global coordinate system | |
| Dissipative damping parameter | |
| Number of iterations within time step | |
| A certain dynamic variable in the k-th iteration within time step | |
| The equivalent stiffness matrix | |
| Equivalent load matrix | |
| Work done by the residual load generated in the first iteration within time step | |
| Work done by the residual load generated in the (k + 1)-th iteration within time step | |
| Ratio of work done by residual load | |
| Linear momentum values of the system along the coordinate axes X, Y, and Z | |
| Angular momentum values of the system along the coordinate axes X, Y, and Z |
References
- Shabana, A.A. Dynamics of Multibody Systems, 4th ed.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Wasfy, T.W.; Noor, A.K. Computational strategies for flexible multibody systems. Appl. Mech. 2003, 56, 553–613. [Google Scholar] [CrossRef]
- Rong, B.; Rui, X.; Tao, L.; Wang, G. Theoretical modeling and numerical solution methods for flexible multibody system dynamics. Nonlinear Dyn 2019, 98, 1519–1553. [Google Scholar] [CrossRef]
- Kadapa, C.; Dettmer, W.G.; Perić, D. On the advantages of using the first-order generalised-alpha scheme for structural dynamic problems. Comput. Struct. 2017, 193, 226–238. [Google Scholar] [CrossRef]
- Romero, I.; Armero, F. Numerical integration of the stiff dynamics of geometrically exact shells: An energy-dissipative momentum-conserving scheme. Int. J. Numer. Methods Eng. 2002, 54, 1043–1086. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Caughey, T.K.; Liu, W.K. Finite-Element Methods for Nonlinear Elastodynamics Which Conserve Energy. J. Appl. Mech. 1978, 45, 366–370. [Google Scholar] [CrossRef]
- Simo, J.C.; Wong, K.K. Unconditionally stable algorithms for rigid body dynamics that exactly preserve energy and momentum. Int. J. Numer. Methods Eng. 1991, 31, 19–52. [Google Scholar] [CrossRef]
- Zhang, H.M.; Xing, Y.F. A three-parameter single-step time integration method for structural dynamic analysis. Acta Me-Chanica Sin. 2019, 35, 112–128. [Google Scholar] [CrossRef]
- Zhang, R.; Stanciulescu, I.; Yao, X.H.; Zhong, H.Z. An energy–momentum conserving scheme for geometrically exact shells with drilling DOFs. Comput. Mech. 2021, 67, 341–364. [Google Scholar] [CrossRef]
- Gravouil, A.; Combescure, A.; Brun, M. Heterogeneous asynchronous time integrators for computational structural dynamics. Int. J. Numer. Methods Eng. 2015, 102, 202–232. [Google Scholar] [CrossRef]
- Ji, Y.; Wu, Y.; Xing, Y.F. An Accurate, Controllably Dissipative, Unconditionally Stable Three-Sub-Step Method for Nonlinear Dynamic Analysis of Structures. Int. J. Struct. Stab. Dyn. 2023, 23, 2350138. [Google Scholar] [CrossRef]
- Bridges, T.; Reich, S. Numerical methods for Hamiltonian PDEs. J. Phys. A-Math. Generical 2006, 39, 5287–5320. [Google Scholar] [CrossRef]
- Li, Z.X.; Li, T.Z.; Vu-Quoc, L.; Izzuddin, X.; Zhuo, X.; Fang, Q. A nine-node corotational curved quadrilateral shell element for smooth, folded, and multishell structures. Int. J. Numer. Methods Eng. 2018, 116, 570–600. [Google Scholar] [CrossRef]
- Kuhl, D.; Crisfield, M.A. Energy-conserving and decaying Algorithms in non-linear structural dynamics. Int. J. Numer. Methods Eng. 1999, 45, 569–599. [Google Scholar] [CrossRef]
- Ezquerro, J.A.; Hernández-Verón, M.A.; Magreñán, A.A. Starting points for Newton’s method under a center Lipschitz condition for the second derivative. J. Comput. Appl. Math. 2018, 330, 721–731. [Google Scholar] [CrossRef]
- Lavrenčič, M.; Brank, B. Energy-decaying and momentum-conserving schemes for transient simulations with mixed finite elements. Comput. Methods Appl. Mech. Eng. 2021, 375, 113625. [Google Scholar] [CrossRef]
- Sansour, C.; Wriggers, P.; Sansour, J. Nonlinear dynamics of shells: Theory, finite element formulation, and integration schemes. Nonlinear Dyn. 1997, 13, 279–305. [Google Scholar] [CrossRef]
- Sansour, C.; Wagner, W.; Wriggers, P.; Sansour, J. An energy–momentum integration scheme and enhanced strain finite elements for the non-linear dynamics of shells. Int. J. Non-Linear Mech. 2002, 37, 951–966. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, D.H.; Liu, Y.H. Degenerated shell element with composite implicit time integration scheme for geometric nonlinear analysis. Int. J. Numer. Methods Eng. 2016, 105, 481–560. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Qian, H. An Energy–Momentum Conserving Algorithm for Co-Rotational Quadrilateral Shell Elements in Nonlinear Multibody Dynamics. Appl. Sci. 2025, 15, 7153. https://doi.org/10.3390/app15137153
Li Z, Qian H. An Energy–Momentum Conserving Algorithm for Co-Rotational Quadrilateral Shell Elements in Nonlinear Multibody Dynamics. Applied Sciences. 2025; 15(13):7153. https://doi.org/10.3390/app15137153
Chicago/Turabian StyleLi, Zhongxue, and Hongtao Qian. 2025. "An Energy–Momentum Conserving Algorithm for Co-Rotational Quadrilateral Shell Elements in Nonlinear Multibody Dynamics" Applied Sciences 15, no. 13: 7153. https://doi.org/10.3390/app15137153
APA StyleLi, Z., & Qian, H. (2025). An Energy–Momentum Conserving Algorithm for Co-Rotational Quadrilateral Shell Elements in Nonlinear Multibody Dynamics. Applied Sciences, 15(13), 7153. https://doi.org/10.3390/app15137153





