Parametric Analysis of Static–Dynamic Characteristics of Adjacent Tunnels in Super-Large Twin Tunnels by DEM
Abstract
Featured Application
Abstract
1. Introduction
2. Modeling Procedure
2.1. Project Overview
2.2. Basic Model Information
3. Results and Discussion
3.1. Inner Walls
3.1.1. Sleeper
3.1.2. Liner
3.1.3. Surroundings
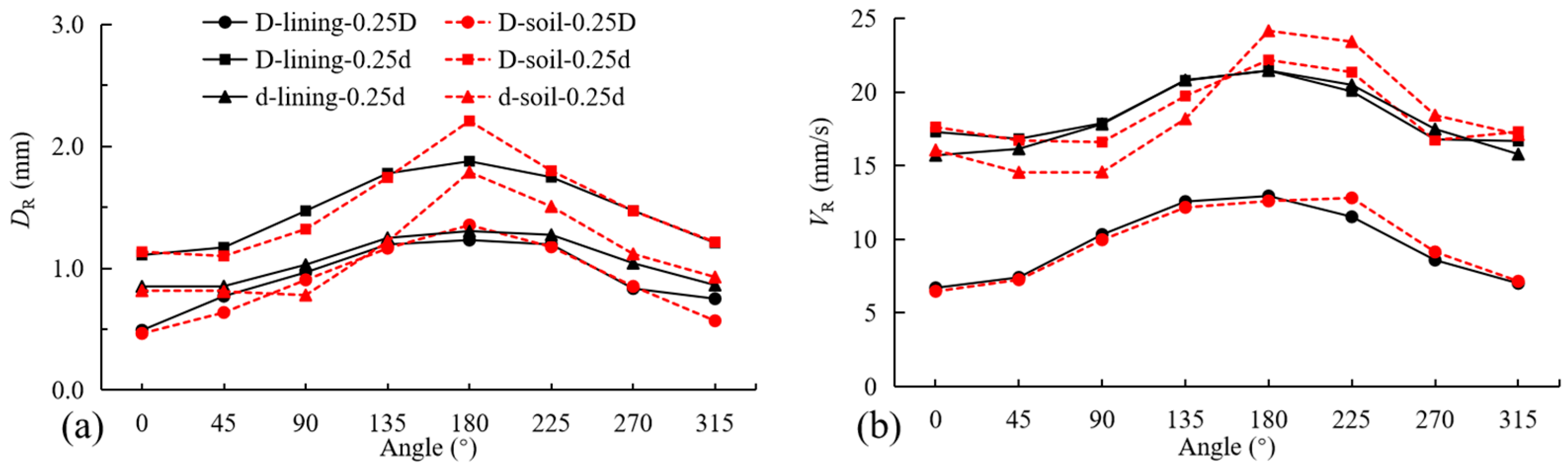
3.2. Absolute and Relative Spacing
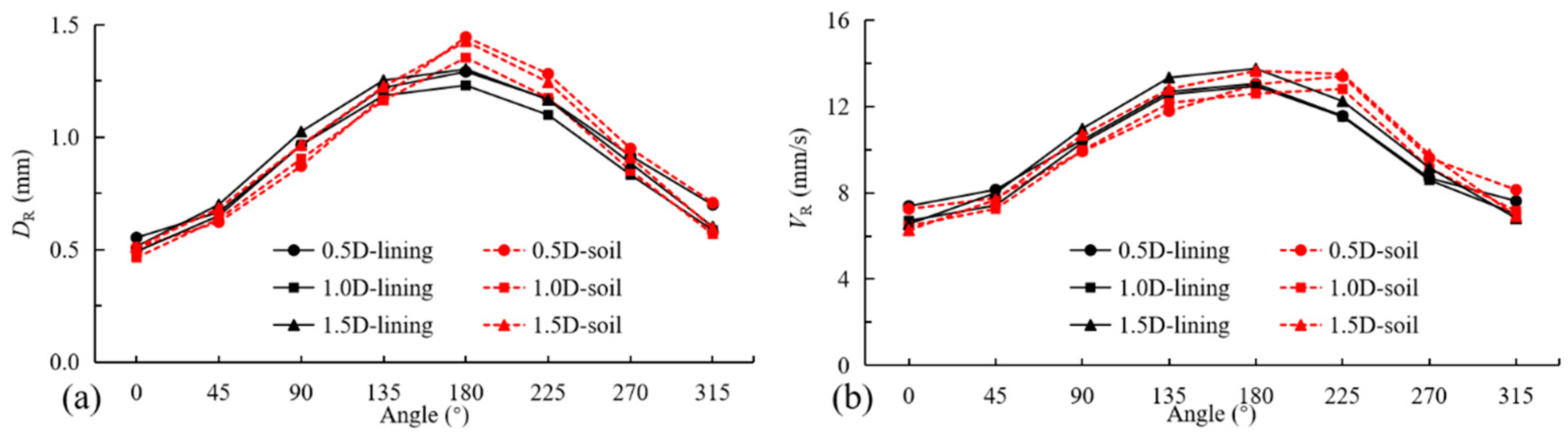
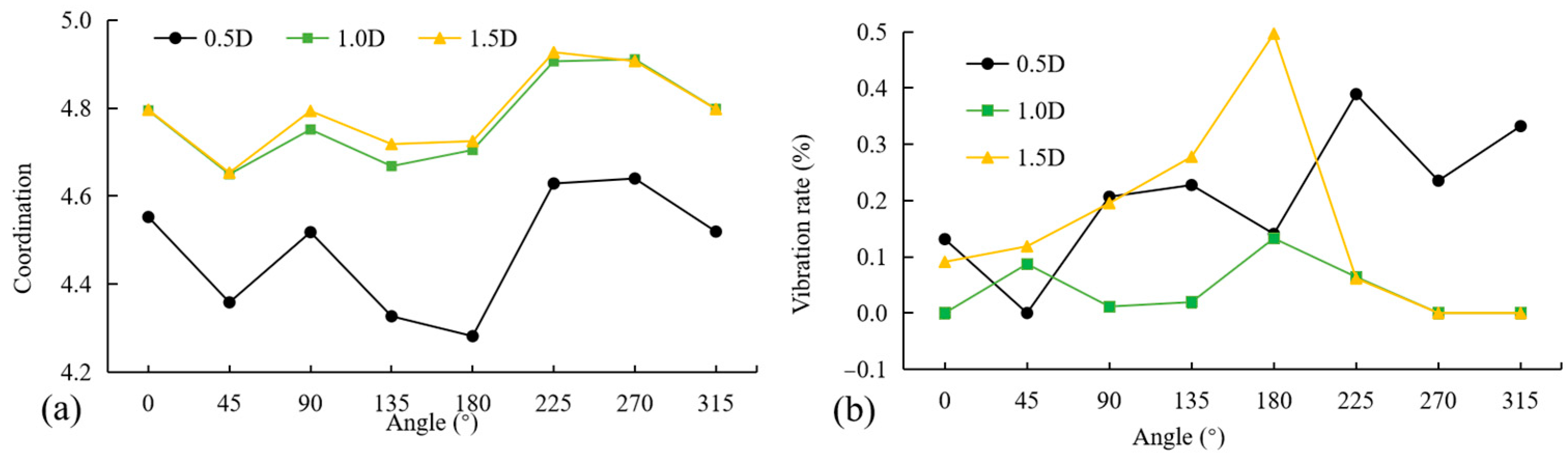
3.3. Water Pressure
4. Conclusions
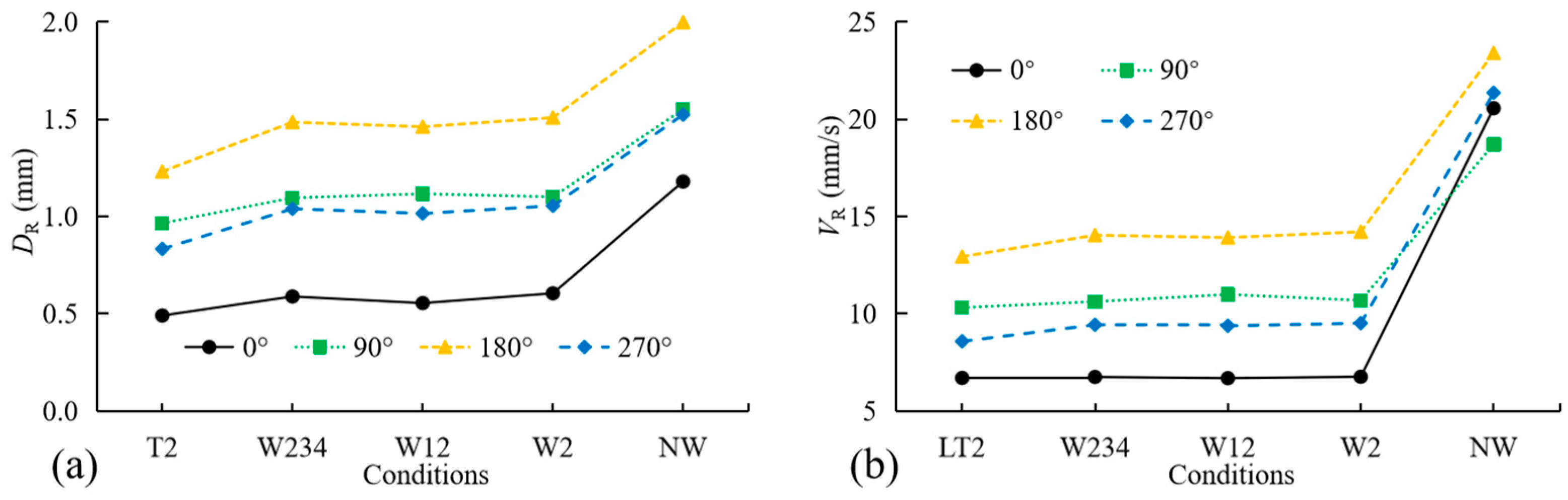
- The NW condition (no internal walls) of T2 exhibits significantly greater static–dynamic responses in both liners and surroundings compared to other conditions. Internal walls in super-large tunnels markedly reduce these responses, with their stabilizing effectiveness ranked as wall2 > wall1 > wall3 = wall4. Wall2 plays a particularly decisive role. DR and VR in liners and surroundings correlate strongly with the burial depth and distance to the vibration source.
- Under equivalent relative spacing, super-large twin tunnels show smaller static–dynamic responses in liners and surroundings than small twin tunnels. However, under equivalent absolute spacing, super-large twin tunnels exhibit significantly enhanced dynamic responses and larger discrepancies in liner and surroundings displacements and velocities. The static–dynamic characteristics of super-large twin tunnels fundamentally differ from those of small twin tunnels under any spacing.
- Optimal water pressure (P2 = 149 kPa) effectively suppresses displacements and velocities in liners and surroundings, while excessive pressure (P3 = 223 kPa) amplifies static–dynamic responses. Critical monitoring points requiring attention include the central tunnel region (180°), vault (90°), and 135°, where responses are most pronounced due to proximity to the vibration source and the surroundings easily sliding.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| D | Diameter of the large and super-large twin tunnels |
| d | Diameter of the small twin tunnels |
| t1 | First small tunnel |
| t2 | Second small tunnel |
| T1 | First super-large-diameter tunnel |
| T2/Tunnel 2 | Second super-large-diameter tunnel |
| DV | Vertical displacement |
| DR | Resultant displacement |
| VV | Vertical velocity |
| VR | Resultant velocity |
| wall1 | Smoke exhaust board |
| wall2 | Vehicular lane board |
| wall3 | Left partition wall |
| wall4 | Right partition wall |
| DEM | Discrete Element Method |
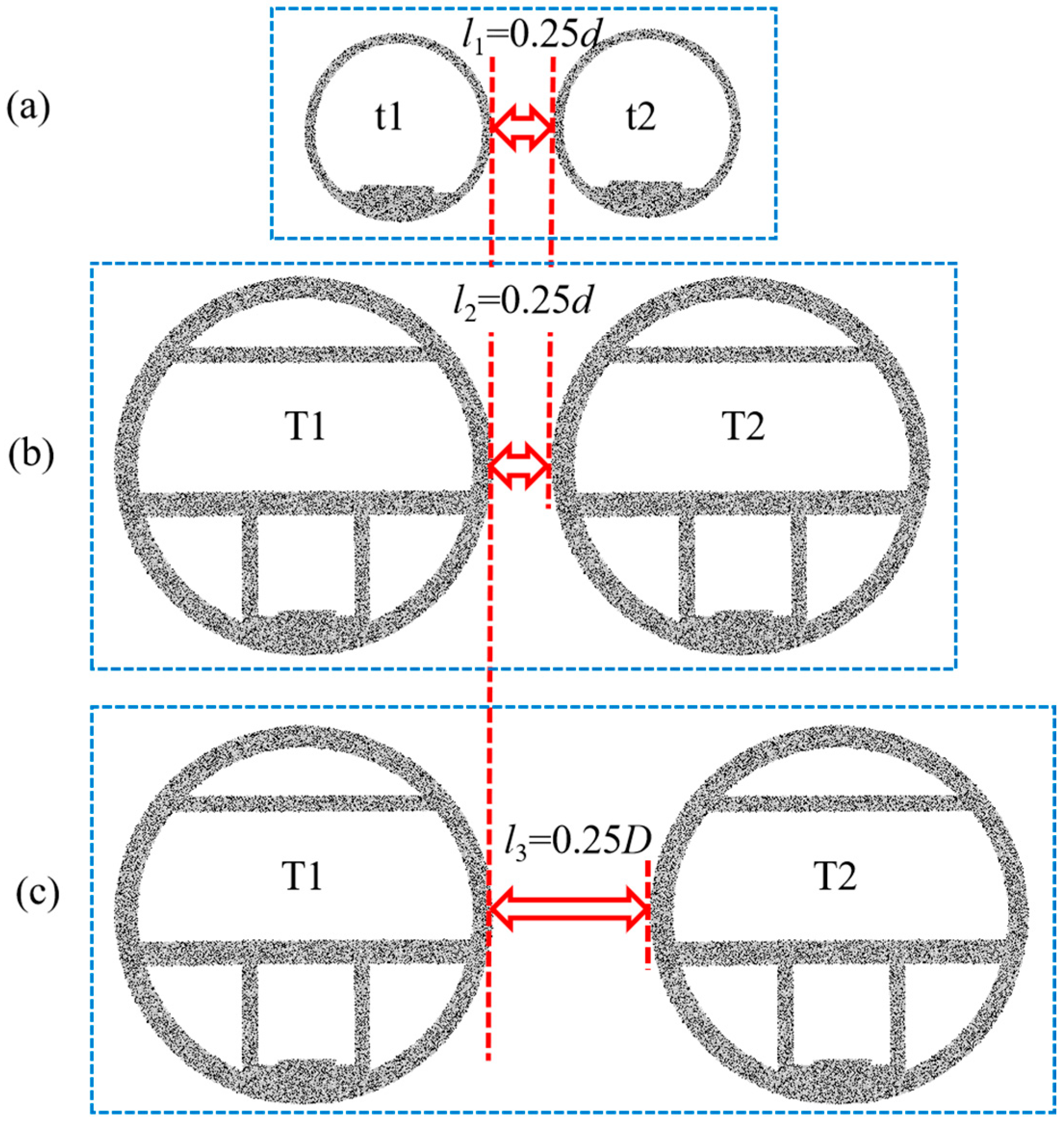
| l, l1, l2, l3 | Spacing between twin tunnels |
References
- Yang, W.; Yang, L.; Liang, Y.; Qian, Z.; Guo, W.; He, C.; Zhou, Y. Study on the Dynamic Response Characteristics of Road-metro Tunnels and Surrounding Soil under Train Vibration Loads. Chin. J. Rock Mech. Eng. 2022, 41, 1659–1670. [Google Scholar] [CrossRef]
- Yu, T.; Ying, K.; Wang, J.; Yao, Z.; Fang, Y. Stability Evaluation of the Sequential Excavation Method of Large-Section Double-Arch Tunnel in Fly Ash Accumulation Stratum Through Physical Model. Tunn. Undergr. Space Technol. 2025, 158, 106391. [Google Scholar] [CrossRef]
- Heidary, R.; Esmaeili, M.; Nik, M.G. Effects of Train Operational Parameters on Ground-Borne Vibrations Induced by Twin Metro Tunnels. Int. J. Rail Transp. 2020, 9, 144–156. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, W.; Yao, C.; Xu, Z. Centrifuge Modelling of the Dynamic Response of Twin Tunnels Under Train-Induced Vibration Load. Soil Dyn. Earthq. Eng. 2024, 185, 108908. [Google Scholar] [CrossRef]
- Li, L.; Yao, A. Investigation on Response of Site of Typical Soil–Rock Composite Strata in Changchun Induced by Shield Construction of Parallel Twin Tunnels. Appl. Sci. 2024, 14, 500. [Google Scholar] [CrossRef]
- Pang, Y.; Lin, H.; Cao, P.; Meng, G. The Influence of Overlying High-Speed Rail Dynamic Loads on the Stability of Shield Tunnel Faces During Excavation. Appl. Sci. 2025, 15, 2567. [Google Scholar] [CrossRef]
- Li, J.; Fang, X.; Yang, Y. Analysis of the Impact of the New Two-Lane Shield Tunnel Underpass on the Existing Tunnels. Appl. Sci. 2025, 15, 2642. [Google Scholar] [CrossRef]
- Wang, Y.-c.; Guo, Y.; Qiu, Y.; Jiang, W.; Li, Y.-h.; Cheng, C. Dynamic Behavior of Fault Tunnel Lining Under Seismic Loading Conditions. J. Cent. South Univ. 2023, 30, 584–598. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, R.; Fang, Q.; Li, Q.-q.; Jiang, A.-n.; Li, K.-c. Subgrade Settlements of Existing Railway Lines and Operational Parameters of Shield Machine Induced by Twin Shield Tunnel Excavations: A Case Study. J. Cent. South Univ. 2024, 31, 272–287. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, Z.; Shen, G.; E, J. Measurement of Earth Pressure of Shallow Buried Tunnel with Super Large Diameter and Applicability Evaluation of Calculation Method. Rock Soil Mech. 2019, 40, 91–98. [Google Scholar] [CrossRef]
- Amjadi, A.H.; Johari, A. Stochastic Nonlinear Ground Response Analysis Considering Existing Boreholes Locations by the Geostatistical Method. Bull. Earthq. Eng. 2022, 20, 2285–2327. [Google Scholar] [CrossRef]
- Johari, A.; Amjadi, A.H.; Heidari, A. Stochastic Nonlinear Ground Response Analysis via a Case Study Site in Shiraz City. Sci. Iran. 2021, 28, 2070–2086. [Google Scholar] [CrossRef]
- Li, C.; Zhang, W.; Wang, X.; Pan, B.; Zhu, H.-H.; Spencer, B.F. Modeling Dynamic Responses of a Cross-River Road Shield Tunnel Under Stochastic Vehicle Loads. Tunn. Undergr. Space Technol. 2020, 102, 103432. [Google Scholar] [CrossRef]
- Zhang, S.; Yuan, Y.; Li, C.; Yang, Y.; Yu, H.; Mang, H.A. Effects of Interior Structure as Double Deck Lanes on Seismic Performance of Segmental Linings. Tunn. Undergr. Space Technol. 2020, 103, 103441. [Google Scholar] [CrossRef]
- Shi, J.-K.; Zhang, J.-Z.; Zhao, S.; Guan, Z.-C.; Huang, H.-W. Probabilistic Analysis of Ground Surface Settlement Induced by Super Large Diameter Shield Tunneling Based on 3D Random Finite Element Method. Comput. Geotech. 2025, 181, 107111. [Google Scholar] [CrossRef]
- Kou, L.; Xiong, Z.; Cui, H.; Zhao, J. Study on Mechanical Characteristics of Segmental Joints of a Large-Diameter Shield Tunnel under Ultrahigh Water Pressure. Sensors 2021, 21, 8392. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Zhang, X.; Wang, W.; Meng, X.; Guo, H. Comparison of Dynamic Characteristics between Small and Super-Large Diameter Cross-River Twin Tunnels under Train Vibration. Appl. Sci. 2021, 11, 7577. [Google Scholar] [CrossRef]
- Wang, S.; He, X.; Peng, X.; Wang, Y.; Li, Z.; Song, Z. Influence of Secondary Lining Thickness on Mechanical Behaviours of Double-Layer Lining in Large-Diameter Shield Tunnels. Undergr. Space 2024, 18, 130–150. [Google Scholar] [CrossRef]
- Guo, W.; Yang, W.; Qian, Z.; Yang, L.; He, C.; Qu, S. The Effect of Internal Structure on Dynamic Response of Road-Metro Tunnels Under Train Vibration Loads: An Experimental Study. Tunn. Undergr. Space Technol. 2023, 138, 105182. [Google Scholar] [CrossRef]
- Li, Y.; Zou, Z. Numerical Investigation on the Influence of Super-Large-Diameter Shield Tunneling on Nearby Existing Metro Tunnels and the Protection Scheme. Appl. Sci. 2023, 13, 3179. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, M.; Javadi, A.A. Influence of a Super-Large Diameter Shield Tunnel Excavation on the Lining Structure of the Metro Lines in Operation. Iran. J. Sci. Technol. Trans. Civ. Eng. 2023, 47, 3851–3866. [Google Scholar] [CrossRef]
- Deng, L.; Lu, H.; Liu, S.; Hu, Q.; Yang, J.; Kang, Y.; Sun, P. Particle Anti-Accumulation Design at Impeller Suction of Deep-Sea Mining Pump and Evaluation by CFD-DEM Simulation. Ocean Eng. 2023, 279, 114598. [Google Scholar] [CrossRef]
- Yang, W.; Ge, F.; Chen, X.; Wang, L.; Ma, P.; Xu, Z. Optimization of Collection Efficiency for a Dual-Row Jet Mining Machine Based on CFD-DEM Coupling. Ocean Eng. 2024, 313, 119633. [Google Scholar] [CrossRef]
- Wang, X.; Gong, L.; Li, Y.; Yao, J. Developments and Applications of the CFD-DEM Method in Particle–Fluid Numerical Simulation in Petroleum Engineering: A Review. Appl. Therm. Eng. 2023, 222, 119865. [Google Scholar] [CrossRef]
- Lapshin, O.V.; Polyakov, I.S.; Boyangin, E.N. Macrokinetics of Mixing Binary Powder Compositions, Augmented by the DEM Method and Experimental Studies on the Chemically Reactive System 3Ni–Al. Powder Technol. 2025, 460, 121074. [Google Scholar] [CrossRef]
- Nadda, M.; Banaeizadeh, A.; Avilala, P.; Roy, S.; Yadav, A. Coupled Computational Fluid Dynamics-Discrete Element Method (CFD-DEM) Modeling of Moisture Removal in a Fluidized Bed Dryer for Heterogeneously Coated Solids. Chem. Eng. Sci. 2025, 316, 121811. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Lee, S.-D.; Baek, S.-M.; Baek, S.-Y.; Jeon, H.-H.; Lee, J.-H.; Abu Ayub Siddique, M.; Kim, Y.-J.; Kim, W.-S.; Sim, T.; et al. Development of DEM-MBD Coupling Model for Draft Force Prediction of Agricultural Tractor with Plowing Depth. Comput. Electron. Agric. 2022, 202, 107405. [Google Scholar] [CrossRef]
- Su, J.; Zhou, C.; Jiang, X.; Qiao, Z. Orderly Arrangement of Agricultural Biomass Particles in Designed Gas–Solid Fluidized Beds Using CFD-DEM and Image Experiment. Comput. Electron. Agric. 2023, 204, 107510. [Google Scholar] [CrossRef]
- Widartiningsih, P.M.; Mori, Y.; Takabatake, K.; Wu, C.-Y.; Yokoi, K.; Yamaguchi, A.; Sakai, M. Coarse graining DEM Simulations of a Powder Die-Filling System. Powder Technol. 2020, 371, 83–95. [Google Scholar] [CrossRef]
- Shi, H.; Zhao, C.; Du, B.; Shen, G.; Ren, H. Calibration of Discrete Element Parameters and FEM-DEM Coupling Analysis for Solid Granules Medium Deep Drawing Forming. Powder Technol. 2025, 463, 121129. [Google Scholar] [CrossRef]
- Chen, Z.; Ni, P.; Cheng, C.; Jia, P.; Hu, D.; Wu, M. Monitoring Interaction of Shallowly Buried, Large-Section, and Long-Distance Twin Box Jacking Tunnels with Small Spacing Under the Beijing-Hangzhou Grand Canal. Tunn. Undergr. Space Technol. 2024, 153, 105973. [Google Scholar] [CrossRef]
- Lei, H.; Liu, Y.; Zhang, Y.; Hu, Y. Ground Deformation Behaviour Induced by Overlapped Shield Tunnelling Considering Vibration Loads of Subway Train in Sand. Acta Geotech. 2022, 18, 519–533. [Google Scholar] [CrossRef]
- Wu, F.; He, C.; Kou, H.; Wang, B.; Meng, W.; Meng, H.; Guo, D. Discussion on Reasonable Clear Spacing of Twin-Tunnels in Weak Surrounding Rock: Analytical Solution and Numerical Analysis. KSCE J. Civ. Eng. 2022, 26, 2428–2442. [Google Scholar] [CrossRef]

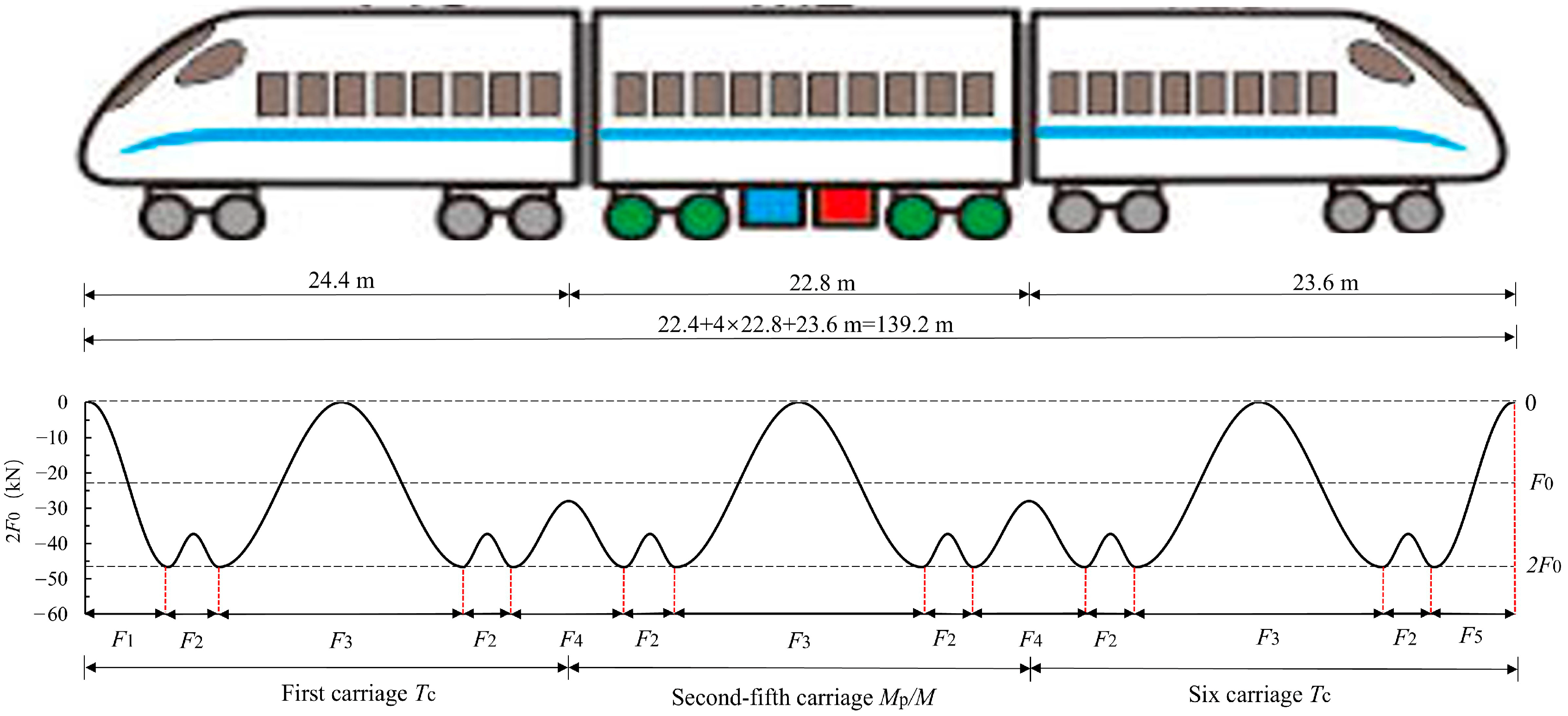






| Model Parameter | Diameter | Thickness of Liner | Thickness of Wall1 | Thickness of Wall2 | Thickness of Wall3 and Wall4 | Size of Sleeper (Length × Height) |
|---|---|---|---|---|---|---|
| Dimension (m) | 15.2 | 0.65 | 0.65 | 1.0 | 0.65 | 1.2 × 0.2 |
| Silty Sand | w/% | Es/MPa | c/kPa | φ/° | v | γ/kN/m3 |
|---|---|---|---|---|---|---|
| Physical and mechanical parameters | 20.4 | 21.9 | 7.0 | 31.9 | 0.49 | 20 |
| Parameters | Radius of Particles (m) | Density (kg/m3) | Normal Stiffness (N/m) | Tangential Stiffness (N/m) | Coefficient of Friction |
|---|---|---|---|---|---|
| Silty sand① | R1 = 0.12–0.2 | 2000 | 2.05 × 107 | 2.05 × 107 | 0.62 |
| Silty sand② | R2 = r1 = 0.06–0.1 | 2000 | 2.19 × 107 | 2.19 × 107 | 0.62 |
| Silty sand③ | r2 = 0.03–0.05 | 2000 | 2.27 × 107 | 2.27 × 107 | 0.63 |
| Parameters | C60① | C60② | Parameters | C60① | C60② |
|---|---|---|---|---|---|
| Radius of particles (m) | r3 = 0.009–0.012 | R3 = 0.02–0.03 | Normal strength of parallel bond (Pa) | 7.1 × 109 | 6.9 × 109 |
| Density (kg/m3) | 2500 | 2500 | Tangential strength of parallel bond (Pa) | 7.1 × 109 | 6.9 × 109 |
| Normal stiffness (N/m) | 9 × 108 | 9 × 108 | Normal stiffness of parallel bonding (N/m) | 9 × 108 | 8.6 × 108 |
| Tangential stiffness (N/m) | 9 × 108 | 9 × 108 | Parallel bonding tangential stiffness (N/m) | 9 × 108 | 8.6 × 108 |
| Coefficient of friction | 1.98 | 1.98 | Parallel bonding radius | 1.0 | 1.0 |
| No. | Objective | Condition | Explanation |
|---|---|---|---|
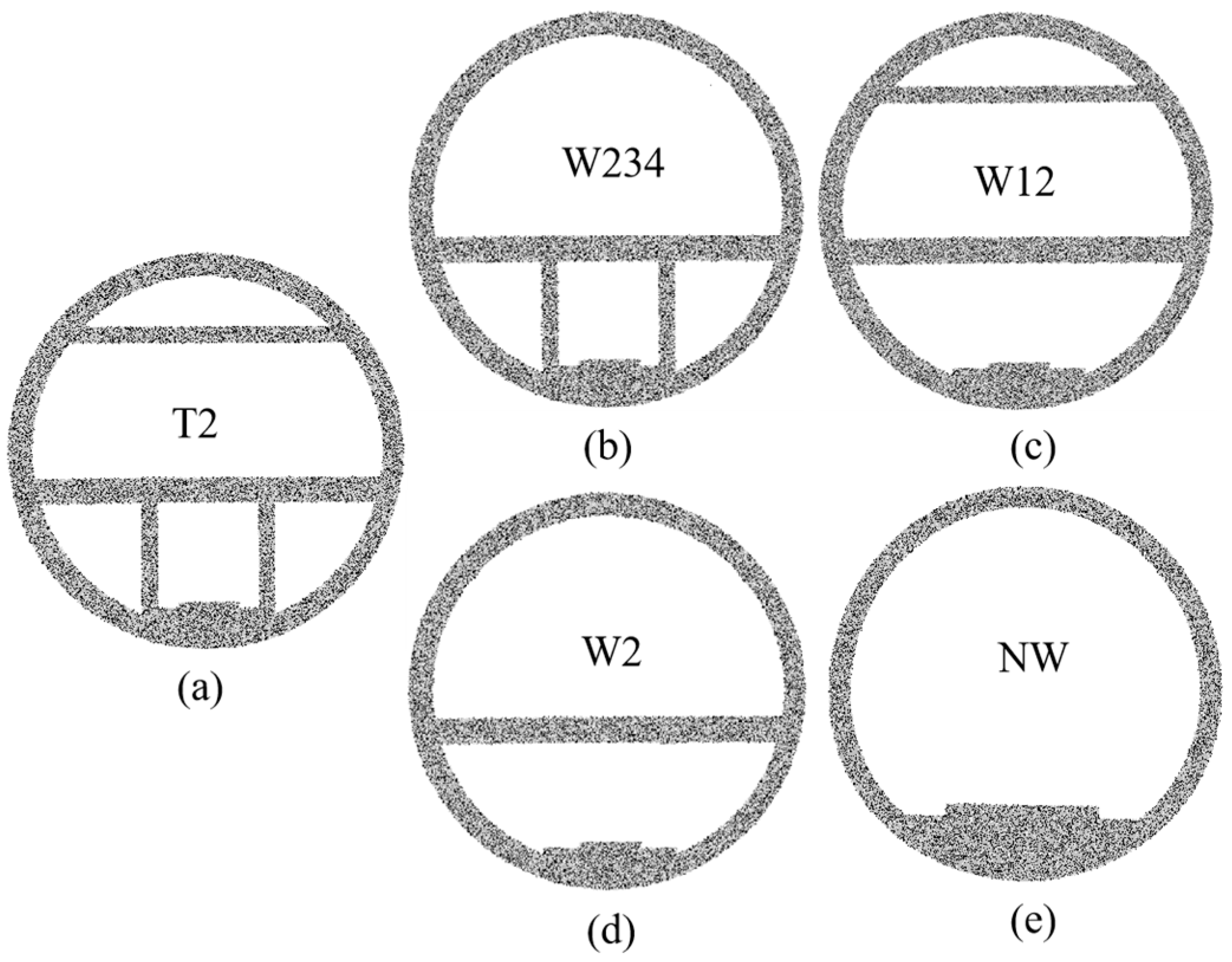
| 1 | Comparison of inner wall effects | A1 (T2) | Super-large-diameter twin tunnels |
| A2 (W234) | Super-large twin tunnels with wall2, wall3, and wall4 | ||
| A3 (W12) | Super-large twin tunnels with wall1 and wall2 | ||
| A4 (W2) | Super-large twin tunnels with wall2 | ||
| A5 (NW) | Super-large twin tunnels with no internal walls | ||
| 2 | Comparison of absolute and relative spacing | B1 | Small-diameter twin tunnels with 0.25 d spacing |
| B2 | Super-large twin tunnels with 0.25 d spacing | ||
| B3 | Super-large twin tunnels with 0.25 D spacing | ||
| 3 | Comparison of water pressure | C1 | 0.5 D water pressure |
| C2 | 1.0 D water pressure | ||
| C3 | 1.5 D water pressure |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Cao, Z.; Bian, X.; Wang, J.; Guo, H. Parametric Analysis of Static–Dynamic Characteristics of Adjacent Tunnels in Super-Large Twin Tunnels by DEM. Appl. Sci. 2025, 15, 7124. https://doi.org/10.3390/app15137124
Wu L, Cao Z, Bian X, Wang J, Guo H. Parametric Analysis of Static–Dynamic Characteristics of Adjacent Tunnels in Super-Large Twin Tunnels by DEM. Applied Sciences. 2025; 15(13):7124. https://doi.org/10.3390/app15137124
Chicago/Turabian StyleWu, Lin, Zhuoyuan Cao, Xiaoya Bian, Jiayan Wang, and Hong Guo. 2025. "Parametric Analysis of Static–Dynamic Characteristics of Adjacent Tunnels in Super-Large Twin Tunnels by DEM" Applied Sciences 15, no. 13: 7124. https://doi.org/10.3390/app15137124
APA StyleWu, L., Cao, Z., Bian, X., Wang, J., & Guo, H. (2025). Parametric Analysis of Static–Dynamic Characteristics of Adjacent Tunnels in Super-Large Twin Tunnels by DEM. Applied Sciences, 15(13), 7124. https://doi.org/10.3390/app15137124






