Precise Feature Removal Method Based on Semantic and Geometric Dual Masks in Dynamic SLAM

Abstract

In visual Simultaneous Localization and Mapping (SLAM) systems, dynamic elements in the environment pose significant challenges that complicate reliable feature matching and accurate pose estimation. To address the issue of unstable feature points within dynamic regions, this study proposes a robust dual-mask filtering strategy that synergistically integrates semantic segmentation information with geometric outlier detection techniques. The proposed method first identifies outlier feature points through rigorous geometric consistency checks, then employs morphological dilation to expand the initially detected dynamic regions. Subsequently, the expanded mask is intersected with instance-level semantic segmentation results to precisely delineate dynamic areas, effectively constraining the search space for feature matching and reducing interference caused by dynamic objects. A key innovation of this approach is the incorporation of a Perspective-n-Point (PnP)-based optimization module. This module dynamically updates the outlier set on a per-frame basis, enabling continuous monitoring and selective removal of dynamic features. Extensive experiments conducted on benchmark datasets demonstrate that the proposed method achieves average accuracy improvements of 3.43% and 11.42% on the KITTI dataset and 24% and 8.27% on the TUM dataset. Compared to traditional methods, this dual-mask collaborative filtering strategy improves the accuracy of dynamic feature removal and enhances the reliability of dynamic object detection, validating its robustness and applicability in complex dynamic environments.

1. Introduction

Simultaneous Localization and Mapping (SLAM) is a critical technology for autonomous robots, self-driving vehicles, unmanned aerial vehicles, and related fields. The aim of SLAM is to allow devices to construct maps of unknown environments while simultaneously performing autonomous localization and navigation [1,2,3]. With the rapid advancement of computer vision and deep learning in combination with continuous improvement of hardware computational capabilities, vision-based SLAM systems now demonstrate three core advantages over other sensors such as LiDAR, millimeter-wave radar, and satellite navigation systems. First, in terms of cost-effectiveness, SLAM can achieve centimeter-level positioning accuracy using only consumer grade cameras [4,5]. Second, in terms of environmental adaptability, independence from external signal sources ensures continuous localization capability in environments where global navigation satellite systems are unavailable (e.g., indoor spaces, tunnels). Most significantly, SLAM systems natively support synergistic processing with computer vision tasks, enabling direct environmental understanding through real-time semantic segmentation algorithms, a unique capability unattainable by other sensors. These competitive advantages establish visual SLAM as a predominant research direction in cost-sensitive applications requiring environmental intelligence, including autonomous mobile robots and augmented-reality navigation systems. Modern visual SLAM systems exhibit highly mature architectures typically comprising several core components, including a feature extraction frontend, a state estimation backend, and loop closure detection modules. Furthermore, advanced SLAM algorithms such as ORB-SLAM3 [6], DSO [7], VSO [8], and LSD-SLAM [9] have achieved highly satisfactory performance levels.

However, in practical application scenarios, vision-based SLAM systems typically assume a static environment in which the relative positions among scene points remain constant and all visual changes are attributed to camera motion [10]. This assumption often does not hold in real-world environments, especially in scenarios with dynamic objects, where the positional accuracy and map construction quality of traditional visual SLAM methods may be seriously compromised. Moreover, existing methods generally adopt a strategy of directly discarding all potential dynamic feature points. Although this approach can effectively avoid dynamic interference, it may also mistakenly eliminate some static feature points, thereby affecting the stability and map quality of the SLAM system [11].

In response to these issues, the objective of this study is to propose a dynamic feature point filtering method to enhance the feature point selection capability in dynamic environments. By combining semantic segmentation masks with geometric consistency constraints, we aim to more accurately identify and preserve static feature points, thereby improving the localization accuracy and map construction quality of SLAM systems. Concurrently, our method aims to reduce the interference of dynamic objects on the SLAM system, ensuring stable operation in complex and dynamic environments. Geometric consistency constraints are applied to the filtered feature points for validation (via reprojection error checks) and optimization (via bundle adjustment). Notably, the information of outlier feature points is preserved in order to assist in the ongoing judgment of dynamic regions under ever-changing environments [12,13,14]. The main contributions of this paper are as follows:

• A dual-mask dynamic feature point filtering method is proposed that combines semantic segmentation masks with outlier information to precisely filter dynamic feature points during the feature matching stage. Instead of simply eliminating the entire dynamic area, this method identifies the local motion areas of dynamic objects. This minimizes false eliminations while still preserving as many static feature points as possible. The low standard deviation achieved in our experimental evaluation serves as evidence demonstrating the effectiveness of dynamic masking in reducing false eliminations and preserving static feature points.
• A dynamic feature point update mechanism is designed. On the basis of dual-mask filtering, outliers are effectively identified and eliminated through PnP pose optimization to dynamically update the set of geometric outliers. This provides a reliable reference for subsequent frames, further improving the detection and elimination of dynamic areas.
• Empirical evaluations on public dynamic datasets, including KITTI and TUM, demonstrate that the proposed method significantly outperforms ORB-SLAM3 by reducing both the Absolute Trajectory Error (ATE) and Relative Pose Error (RPE) in dynamic environments, validating its superiority in terms of both accuracy and robustness. Specifically, the proposed method achieves average reductions in error of 3.43% (ATE) and 11.42% (RPE) on the KITTI dataset and 24% (ATE) and 8.27% (RPE) on the TUM dataset.

The remainder of this paper is structured as follows. Section 2 reviews the research progress in visual SLAM and focuses on discussing existing dynamic object handling techniques while analyzing the strengths and weaknesses of these methods and the challenges that they face. Section 3 introduces the design and implementation of the proposed system, including core ideas, system architecture, and key technologies. Section 4 evaluates the performance of the proposed method through experiments on the KITTI and TUM datasets and compares it with existing methods to demonstrate the system’s performance improvements. Finally, Section 5 concludes the main work of the paper, discusses the limitations of the research, and looks forward to potential future research directions and application prospects.

2. Related Work

2.1. Visual SLAM Literature

The core task of visual SLAM is to estimate camera poses and construct environmental maps through pixel matching in image sequences. Early MonoSLAM [15] utilized extended Kalman filtering as the backend, supporting single-threaded processing of a small number of sparse feature points. Subsequently, PTAM [16] introduced keyframes and a dual-thread architecture to achieve parallel processing of camera tracking and mapping, which significantly improved system performance. Building upon this foundation, ORB-SLAM2 [17] added loop closure detection and local bundle adjustment optimization, further enhancing robustness and accuracy. The latest ORB-SLAM3 [6] integrates visual–inertial information and introduces a multi-map system to improve adaptability in multi-sensor configurations. However, these methods generally assume a static environment; in dynamic scenes, the feature points on moving objects violate this assumption, easily introducing errors that reduce localization accuracy and map quality. Thus, optimizing SLAM for dynamic scenarios has become a current hot topic of research.

2.2. Geometry-Constrained Dynamic SLAM

Methods based on geometric constraints typically employ robust weighting functions or motion consistency constraints to eliminate dynamic targets, thereby improving localization accuracy. These methods usually rely on the motion trajectory or geometric relationships of feature points to detect dynamic objects [18,19,20]. Kim et al. [21] eliminated outliers by estimating a non-parametric background model of the depth scene, achieving camera motion estimation on the basis of this model. Li et al. [22] proposed an RGB-D SLAM system based on keyframes, incorporating static weights of foreground edge points into the Intensity-Assisted Iterative Closest Point method to improve pose estimation accuracy. Sun et al. [23] used optical flow to track dynamic targets, then constructed and updated foreground models based on RGB-D data to remove dynamic feature points. Additionally, StaticFusion [24] simultaneously estimates camera motion and probabilistic static segmentation for static background reconstruction. Overall, geometry-based approaches typically require the integration of additional geometric computation modules, which increases the system’s implementation complexity. In contrast, the method proposed in this paper fully leverages the existing PnP optimization residuals within ORB-SLAM3. By matching outlier points between consecutive frames and analyzing their geometric consistency, it can effectively identify dynamic features without introducing additional geometric models or structural assumptions, thereby achieving lower computational cost and greater practical efficiency.

2.3. Semantic Segmentation-Based Dynamic SLAM

Dynamic SLAM methods based on semantic segmentation utilize deep learning networks to semantically parse images, thereby eliminating potential dynamic targets to enhance localization accuracy and map quality [12,14,25,26,27]. DS-SLAM [28] combines ORB-SLAM2 with a segmentation network for instance segmentation and verifies the motion consistency of feature points using epipolar constraints; however, it is limited to predefined dynamic categories (e.g., pedestrians). DynaSLAM [29] employs Mask R-CNN for instance segmentation, which it uses along with geometric constraints to identify dynamic regions in RGB-D images. This approach significantly improves robustness in dynamic scenes, albeit with a high computational cost that limits real-time performance due to inference times exceeding 200 ms. VDO-SLAM [30] uses dense optical flows to track object motion and enhances mapping capabilities for multi-target dynamic scenes through joint optimization of camera and object poses. However, it is primarily suitable for offline processing. For greater efficiency and performance balance, methods such as Detect-SLAM [31] and RDS-SLAM [32] focus on semantic processing of keyframes. This approach performs instance segmentation on keyframes to reduce computation, but relies heavily on keyframe quality and lacks dynamic frame selection strategies, limiting system adaptability in complex scenes. Overall, while semantic-based dynamic SLAM has made progress in dynamic target perception, it still faces challenges such as computational complexity, erroneous elimination of static feature points, and over-reliance on keyframes, making it difficult to balance real-time performance with accuracy [33]. To address these issues, our paper proposes a dual-mask strategy that integrates instance segmentation with outlier residual information. The proposed approach first employs YOLOv11 to perform coarse segmentation of potential dynamic objects, then refines the detection by leveraging geometric residuals to further eliminate anomalous regions. This method effectively reduces the system’s dependence on keyframes and enables precise removal of dynamic features within local areas. By improving the system’s tolerance to erroneous rejection of static points, the proposed strategy enhances the overall robustness and stability of the system while maintaining real-time performance.

3. Methodology

This paper presents a visual SLAM system capable of handling dynamic environments. The proposed system is based on the monocular ORB-SLAM3 framework, with a focus on elimination of dynamic features to improve localization and mapping accuracy in dynamic scenes. As depicted in Figure 1, the overall framework of the system includes modules for image input, feature point extraction, semantic segmentation, dynamic feature point filtering, and pose optimization. The core contribution of this paper is centered on dynamic feature point filtering and dynamic region updating. Starting with image frame input, which serves as the carrier of the original visual information, the system utilizes the ORB-SLAM3 framework algorithm to extract feature points, providing a foundation for subsequent operations. Concurrently, the YOLOv11 neural network model is employed for semantic segmentation to generate segmentation masks that contain prior information about the location of dynamic content such as pedestrians and vehicles. Based on these segmentation masks derived from semantic segmentation along with feature points extracted using geometric constraints, a further in-depth analysis is conducted to precisely differentiate outliers into static and dynamic points. The overall process of the proposed system includes the following main steps:

• Image Input: Receives original video frames as the starting point for SLAM processing.
• Feature Point Extraction: Uses ORB-SLAM3 to extract feature points from each frame.
• Semantic Segmentation: Utilizes YOLOv11 to perform semantic segmentation, creating masks for potential dynamic objects.
• Mask Processing: Performs morphological dilation on the generated masks to enhance the capture precision of dynamic object boundaries.
• Dynamic Feature Point Filtering: Combines a dual-mask strategy with geometric information to effectively filter out dynamic feature points.
• Pose Optimization: Improves camera localization accuracy through PnP optimization calculations and dynamically updates the feature point set to support subsequent frame processing.

3.1. Detecting Dynamic Objects and Generating Masks with YOLOv11

To effectively detect dynamic objects and achieve high-precision pose estimation in dynamic environments, this paper employs the advanced YOLOv11 [34] deep learning model for semantic segmentation to identify potential dynamic objects. As a cutting-edge technology in the field of instance segmentation, YOLOv11 provides pixel-level instance segmentation and instance labeling of images. These capabilities are fundamental for enhancing our system’s ability to handle dynamic contexts.

Throughout the processing workflow, the semantic segmentation functionality of YOLOv11 is of primary importance within this system. It achieves pixel-level segmentation of each frame, allowing for accurate identification of different object regions. YOLOv11 interprets the input RGB raw images to recognize possible dynamic entities (e.g., people, bicycles, cars, motorcycles, buses) and items that might be moved (books, chairs, etc.). Dynamic objects such as these encompass the most common elements found in most environments. By combining all objects, a mask reflecting all dynamic regions in a single image is obtained, providing precise spatial localization for the subsequent feature point filtering.

To further enhance the semantic mask’s coverage accuracy over object boundaries, in this paper we apply a range of morphological dilation (e.g., 5 pixels) to the masks generated by YOLOv11. This effectively expands the boundaries of dynamic objects and compensates for local discontinuities and gaps caused by instance segmentation errors. This process strengthens the continuity and integrity of the mask around the target edge areas, addressing the common issue of "truncation" or "under-labeling" in instance segmentation at object edges. This treatment ensures that dynamic targets are not incorrectly classified as static regions due to incomplete boundaries during the geometric processing stage. The edge regions of dynamic objects often contain many inconsistent motion feature points or feature discrepancies caused by occlusion, especially in monocular SLAM systems. If these points are not fully captured, they may lead to mismatches and greatly impact the accuracy of pose estimation. Therefore, the morphological dilation step aids in improving the reliability of feature point matching as well as the overall robustness of the system in complex dynamic scenes.

3.2. Dual-Mask Method for Dynamic Feature Point Filtering

Under the assumption of a constant velocity model in monocular visual SLAM, the proposed system typically uses the pose from the previous frame as the initial value for the current frame’s initial pose, matching it with the 3D map points corresponding to feature points from the previous frame. To achieve feature matching, feature points associated with known map points from the previous frame are reprojected into the current frame and matches are sought based on their descriptor information. However, points determined as geometric outliers in the previous frame often have large reprojection errors, possibly due to inaccurate localization, descriptor anomalies, or being located on the surface of dynamic objects. Consequently, traditional ORB-SLAM systems usually adopt the strategy of excluding feature points marked as outliers from the previous frame, preventing them from participating in the current frame’s feature matching process. This avoids wasting computational resources and reduces potential mismatches.

To enhance the system’s ability to discriminate dynamic areas, this paper proposes a dual-mask dynamic feature filtering method that integrates semantic priors with geometric consistency verification. This approach re-utilizes feature points identified as outliers in the previous frame as clues for potential dynamic regions, combining them with instance masks provided by semantic segmentation to spatially constrain dynamic objects. When the number of outliers detected in the current frame falling within the semantic dynamic mask region exceeds a set threshold, these points are considered to be dynamic features. In this way, the system realizes dynamic detection driven by both semantic and geometric cues. This method not only combines information about dynamic physical objects from a semantic perspective, it also relies on geometric verification to identify unstable regions, effectively avoiding the influence of both pure semantic misjudgments (such as stationary pedestrians or parked vehicles) and pure geometric misjudgments (such as outlier points caused by sparse features).

For local dynamic targets, for instance a person moving only their head or hand, it would be inappropriate to label the entire body region as dynamic; to address this, the system initially identifies feature points that have been verified as outliers in the current frame and marks those that fall within the semantic dynamic mask as dynamic features. Subsequently, these outlier points undergo morphological dilation (approximately 60 pixels) to expand their influence area, creating a local dynamic point mask. Finally, this dilated mask is intersected with the semantic mask. This limits the dynamic region to only cover portions of potential dynamic objects, thereby obtaining a more precise final dynamic mask.

The processing flow is depicted in Figure 2. The input consists of two consecutive frames, from which the system first obtains semantic masks through semantic segmentation; then, combining geometric consistency checks, it identifies dynamic outliers to generate an outlier mask. Finally, the semantic mask and the outlier mask are combined to produce an accurate dynamic object mask, achieving more precise dynamic feature point removal.

The final mask generation process can be expressed by the following mathematical equation:

$$M_{\mathrm{final}}=M_{\mathrm{obj}}\cap \left(E_t\oplus \epsilon \right)$$

(1)

where $M_{\mathrm{obj}}$ represents the dynamic object mask generated by semantic segmentation, $E_t$ denotes the set of points identified as outliers through geometric verification and feature matching in the current frame, and $\oplus \epsilon$ represents the morphological dilation operation on the outlier set with a kernel size of $\epsilon$. The parameter $\epsilon$ is empirically set to 50 pixels, a value that was determined through extensive comparative experiments on the KITTI and TUM RGB-D datasets. This setting achieves a balance between dynamic and static regions. A larger value of $\epsilon$ tends to result in the direct removal of entire dynamic objects, while a smaller value leads to the elimination of only the dynamic points.

Furthermore, $E_{(t-1)}$ is the set of outliers from the previous frame, which can be utilized to assist in the prediction of dynamic areas in the next frame. Introducing temporal consistency further enhances the system’s dynamic perception stability in consecutive frames. This dual-mask strategy effectively removes dynamic interference features while preserving stable feature points in static regions, improving overall matching accuracy and the robustness of pose estimation.

3.3. Geometric Consistency Verification

During the pose estimation phase of ORB-SLAM3, the system minimizes the reprojection error of matched feature points through a PnP nonlinear optimization module to optimize the camera pose. To ensure the geometric validity of the matched points, ORB-SLAM3 incorporates a geometric consistency verification mechanism that verifies matched points through a reprojection model to identify and exclude mismatches. The core of geometric consistency verification lies in calculating the reprojection error. Let a map point in the world coordinate system be $P_w$ and the camera pose be $(R_{cw},t_{cw})$, which in the camera coordinate system is

$$P_c=R_{\mathrm{cw}}·P_w+t_{\mathrm{cw}}.$$

(2)

Projecting this onto the image plane using the intrinsic camera parameters yields the predicted pixel coordinates $\widehat{u}$, which when compared with the actual observed point u results in the reprojection error:

$$e=\widehat{u}-u.$$

(3)

ORB-SLAM3 minimizes the reprojection error of all matched points to solve for the camera pose during pose optimization, as follows:

$$\underset{R,t}{min}\sum _i\rho (\parallel {\widehat{u}}_i-u_i{\parallel }^2).$$

(4)

In the above equation, the matrix R represents the camera’s rotation matrix (belonging to the special orthogonal group $SO\left(3\right)$) with constraints $R^{\mathsf{T}}R=I$ and $det\left(R\right)=1$. These conditions ensure that the rotation matrix is orthogonal with a determinant of 1, conforming to the mathematical properties of rotational transformations in three-dimensional space, and are used to describe the rotational behavior of the camera’s pose in space. The translation vector $t\in {\mathbb{R}}^3$ can theoretically take any value in 3D Euclidean space without scene-specific constraints. Here, i represents the calculation of the i-th feature point, while $\rho$ is a robust kernel function (such as the Huber kernel) used to mitigate the influence of outliers on optimization. When the reprojection error $\parallel e\parallel$ of a feature point exceeds a set threshold, that point is determined to be a geometric outlier and is no longer involved in the pose optimization calculation for the current frame. The proposed approach utilizes the Levenberg–Marquardt nonlinear least-squares optimization algorithm to address the robust kernel-function formulated optimization problem. This represents a geometrically consistent validation process that operates synchronously during optimization iterations. As such, it forms a reliable outlier filtering mechanism within the system, particularly with innate recognition capabilities for feature points on dynamic objects.

During the feature matching process in the current frame, ORB-SLAM3 directly excludes those feature points that were marked as outliers in the previous frame, meaning that these outliers participate in neither feature matching nor pose estimation. To more effectively utilize this information, in this paper we propose an improved strategy. First, outliers are further classified in the feature matching stage, and those falling within the potential dynamic object mask are marked as dynamic points. During the pose estimation process, while outliers are excluded, both dynamic points and regular feature points participate in the computation, with the dynamic points being assigned a weight of zero. This approach aims to identify current-frame outliers. This approach provides support for the judgment of dynamic objects and areas in the next frame, thereby forming a closed-loop system process.

The strategy proposed in this paper is more efficient compared to methods that introduce additional binocular geometric constraints or lightweight PnP pose estimations for dynamic area filtering prior to the feature matching stage. We fully leverage the complete optimization process already inherent in ORB-SLAM3, allowing for dynamic point identification without additional computations. This reduces system overhead while also improving both the accuracy of dynamic object recognition and the overall robustness of the system.

4. Experimental Results and Analysis

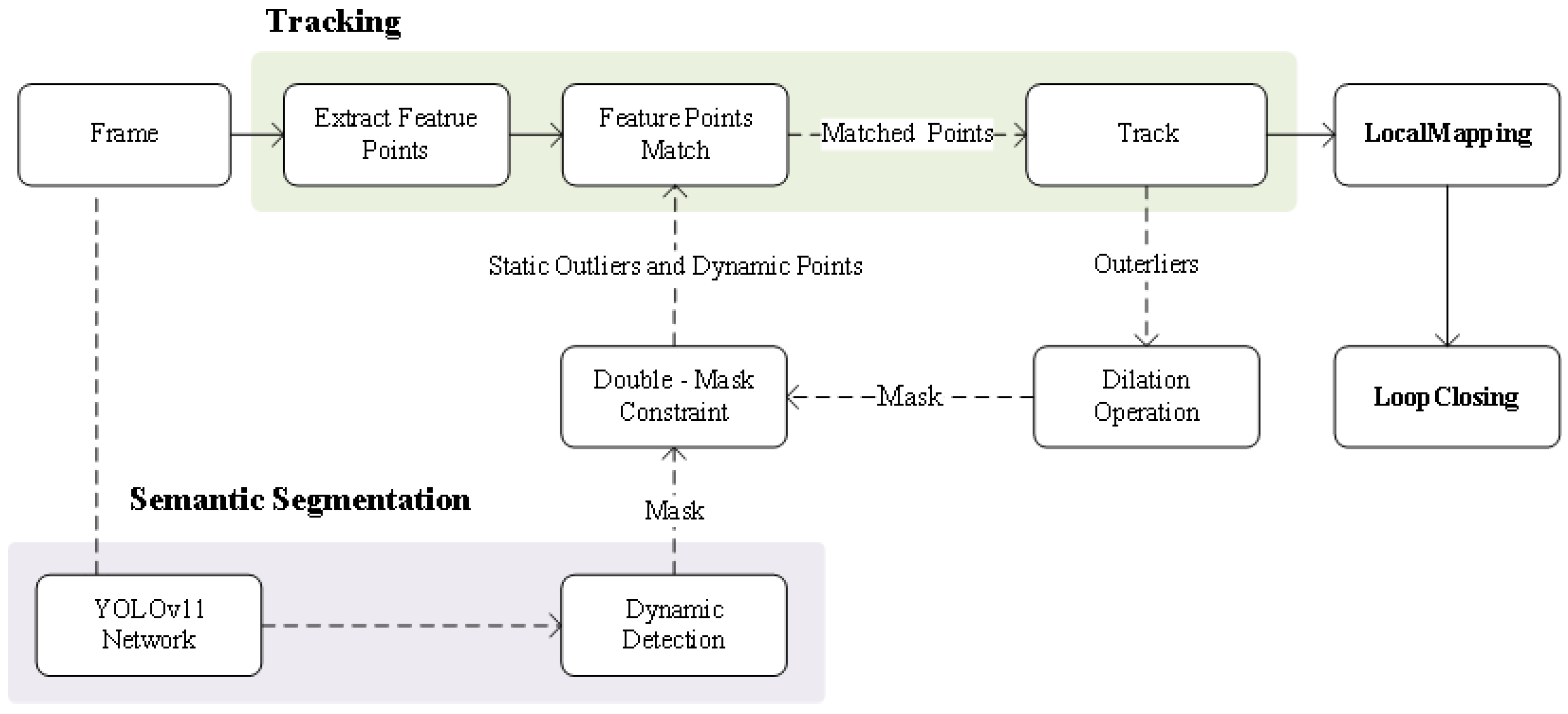
We conducted experimental validation of the proposed system using the public datasets KITTI and TUM. In our experiments, the proposed method was compared and evaluated against the mainstream ORB-SLAM3 system, with the Absolute Trajectory Error (ATE) and Relative Pose Error (RPE) selected as performance metrics. The ATE reflects the overall deviation between the system’s estimated trajectory and the actual trajectory, intuitively demonstrating the cumulative error caused by mismatches in dynamic features. The RPE measures the accuracy of relative pose estimation between adjacent frames but is more susceptible to instantaneous dynamic disturbances; as a result, it is primarily used to assess a system’s local stability. For error quantification, the ATE is assessed using the Root Mean Square Error (RMSE) to reflect the degree of overall trajectory deviation, while the RPE is measured using the mean in order to reflect the system’s stability performance in inter-frame pose estimation. The above evaluation methods enable a comprehensive verification of the system’s accuracy and robustness in different dynamic environments.

To reduce interference from external factors, each test sequence was subjected to ten repeated experiments, with the median taken as the final experimental outcome. All experiments were conducted on a desktop computer equipped with an Intel i5-14600KF processor, NVIDIA GeForce RTX 4070S graphics card, and 32GB of memory.

4.1. Evaluation on the KITTI Dataset

The KITTI dataset provides real vehicular scenes containing both dynamic and static objects, and is widely used to evaluate the effectiveness of visual SLAM systems in separating moving and stationary objects in dynamic environments. In this experiment, the performance of the SLAM system proposed in this paper was compared and analyzed against ORB-SLAM3 under a monocular setting across eleven image sequences, with a focus on the impact of the dynamic object elimination strategy on the system’s localization accuracy and robustness. The performance of different systems in each sequence is summarized in

Table 1. Comparative evaluation of Absolute Trajectory Error (ATE) for monocular SLAM systems.

Sequence	ORB-SLAM3			System(D)			System(D+O)
	RMSE	Mean	Std	RMSE	Mean	Std	RMSE	Mean	Std
KITTI 00	6.24	5.43	3.05	6.58	5.59	3.44	6.14	5.35	3.09
KITTI 01	295.24	264.75	129.86	232.57	205.63	108.08	269.23	241.76	118.03
KITTI 02	24.47	19.17	15.21	20.00	16.03	13.91	21.66	16.16	14.01
KITTI 03	0.79	0.55	0.56	1.14	0.93	0.65	0.86	0.69	0.52
KITTI 04	1.56	1.36	0.76	1.01	0.85	0.55	1.19	1.00	0.64
KITTI 05	6.32	5.88	2.31	6.46	5.97	2.46	5.64	5.19	2.22
KITTI 06	14.86	12.91	7.35	16.04	14.00	7.85	15.77	13.81	7.62
KITTI 07	2.94	2.16	1.77	2.47	2.25	0.99	2.44	1.90	1.41
KITTI 08	64.38	50.01	40.54	61.39	47.09	39.37	59.96	46.18	38.25
KITTI 09	9.03	8.09	4.00	8.87	7.93	3.96	8.86	7.90	4.00
KITTI 10	8.15	6.63	4.72	8.03	6.54	4.65	7.57	6.29	4.24

and

Table 2. Comparative evaluation of Relative Pose Error (RPE) for monocular SLAM systems.

Sequence	ORB-SLAM3			System(D)			System(D+O)
	RMSE	Mean	Std	RMSE	Mean	Std	RMSE	Mean	Std
KITTI 00	0.186	0.096	0.154	0.339	0.100	0.306	0.144	0.109	0.109
KITTI 01	2.026	1.902	0.948	2.079	1.751	1.302	1.962	1.723	0.869
KITTI 02	0.163	0.162	0.103	0.151	0.117	0.095	0.147	0.127	0.097
KITTI 03	0.024	0.019	0.014	0.030	0.023	0.020	0.025	0.020	0.016
KITTI 04	0.058	0.048	0.033	0.047	0.039	0.026	0.054	0.044	0.032
KITTI 05	0.321	0.224	0.230	0.376	0.243	0.286	0.346	0.242	0.247
KITTI 06	0.409	0.253	0.334	0.403	0.241	0.321	0.499	0.258	0.327
KITTI 07	1.858	0.264	1.814	0.345	0.199	0.279	0.989	0.245	1.439
KITTI 08	0.355	0.284	0.213	0.343	0.271	0.210	0.339	0.268	0.208
KITTI 09	0.248	0.248	0.199	0.252	0.150	0.203	0.242	0.144	0.195
KITTI 10	0.067	0.067	0.047	0.067	0.048	0.048	0.062	0.046	0.041

, where bold font indicates the best result for that metric.

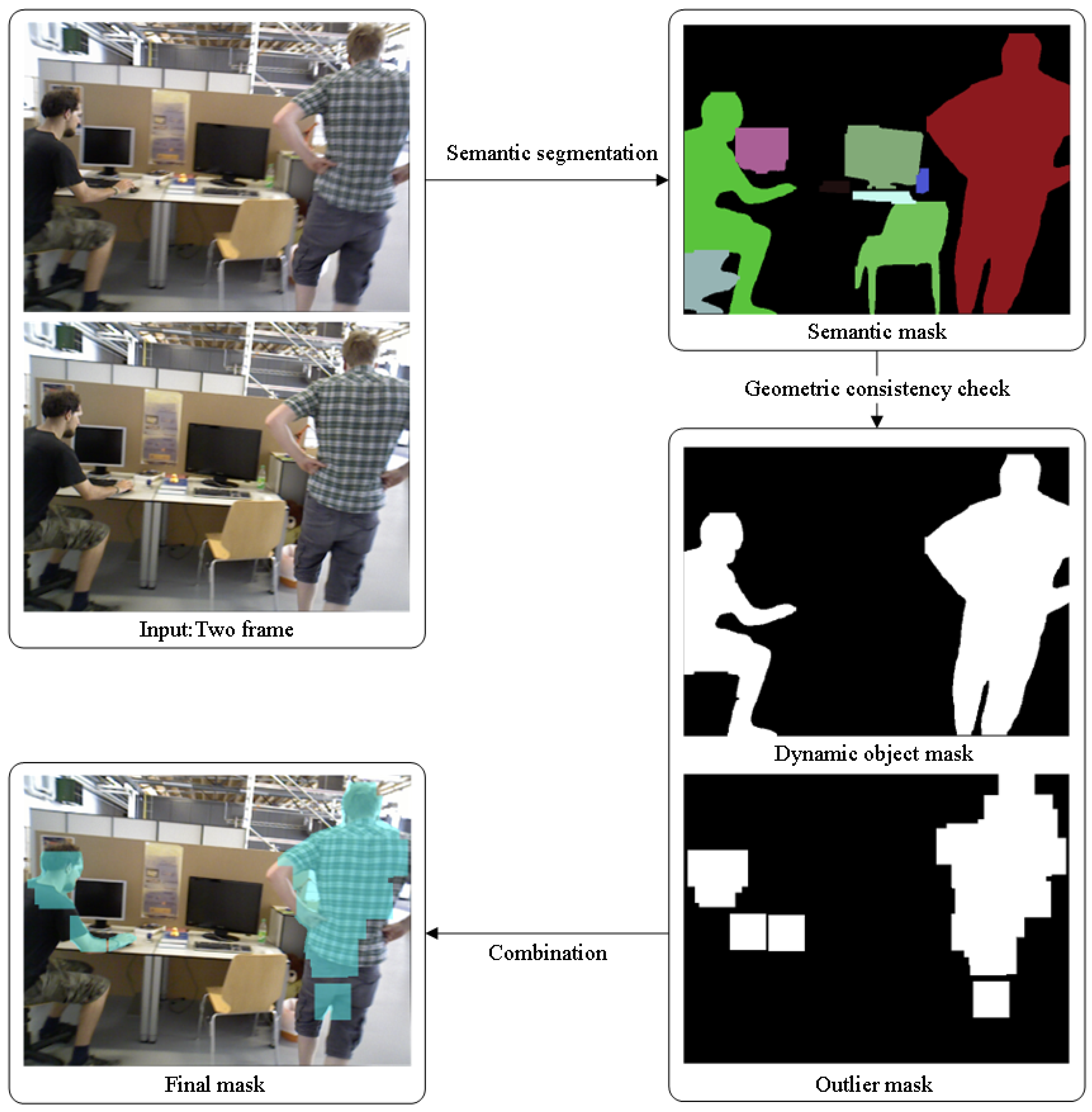
In Table 1 and Table 2, both System(D) and System(D+O) represent the dynamic SLAM systems proposed in this paper; System(D) refers to the system that uses a dynamic mask to directly eliminate the entire dynamic object, while System(D+O) refers to the system that uses a combination of dynamic mask and outlier mask in a dual-mask method to precisely exclude dynamic points. In the absolute trajectory evaluation on the KITTI dataset, System(D+O) is the most accurate in most sequences; in relative pose estimation, System(D) and System(D+O) are similar, with both performing better than the ORB-SLAM3 system.

Meanwhile, in the evaluation of ATE, the average standard deviations of ORB-SLAM3, System(D), and System(D+O) are 19.01, 16.90, and 17.64, respectively. Compared to ORB-SLAM3, System(D) achieves a reduction of approximately 11.1%, while System(D+O) achieves a reduction of about 7.2%. In the evaluation of RPE, the average standard deviations are 0.373, 0.282, and 0.325 for ORB-SLAM3, System(D), and System(D+O), respectively, with System(D) and System(D+O) reducing the standard deviation by 24.4% and 12.9%, respectively. These results indicate that System(D), which directly removes dynamic objects using a dynamic mask strategy, achieves the lowest average standard deviations in both ATE and RPE evaluations. This suggests significantly reduced error fluctuations compared to ORB-SLAM3 and verifies the effectiveness of the proposed strategy in suppressing error dispersion and enhancing the stability of the SLAM system, with particularly notable advantages in relative pose estimation.

To further investigate the specific impact of potential dynamic objects on SLAM system performance,

Table 3. Impact analysis of potential dynamic objects on SLAM system performance.

Sequence	Static Objects	Dynamic Objects	ATE (RMSE)	RPE (Mean)
KITTI 00	Many	Few	DO< 3 < D	3 < D < DO
KITTI 01	None	Many	D < DO < 3	DO < D < 3
KITTI 02	Many	Medium	D < DO < 3	D < DO < 3
KITTI 03	Few	Few	3 < DO < D	3 < DO < D
KITTI 04	None	Many	D < DO < 3	D < DO < 3
KITTI 05	Many	Medium	DO < D < 3	3 < D = DO
KITTI 06	Many	Few	3 < DO < D	D < 3 < DO
KITTI 07	Many	Many	DO < D < 3	D < DO < 3
KITTI 08	Many	Medium	DO < D < 3	DO < D < 3
KITTI 09	Many	Medium	DO < D < 3	DO < D < 3
KITTI 10	Medium	Few	DO < D < 3	DO < D < 3

lists the distribution of potential dynamic objects in each sequence along with an analysis of their impact on localization accuracy. For brevity, in this paper we denote System(D) as “D”, System(D+O) as “DO”, and ORB-SLAM3 as “3”.

The analysis shows that the distribution of dynamic and static objects significantly affects system performance. In the KITTI dataset sequences, ORB-SLAM3 only outperforms the dynamic SLAM system in sequences with fewer dynamic objects, such as sequences 03 and 06. This suggests that the dynamic SLAM system may erroneously eliminate static objects, resulting in reduced trajectory estimation accuracy.

Conversely, in scenarios with many dynamic objects, such as sequences 01, 04, and 07, the dynamic SLAM system significantly outperforms ORB-SLAM3 in terms of both ATE and RPE, further validating the effectiveness of the dynamic object elimination mechanism in complex dynamic environments. To quantify the degree of system performance improvement, this paper uses the following improvement rate (enhancement rate) calculation equation:

$$\eta ={\displaystyle \frac{o-r}{o}}\times 100\%$$

(5)

where o represents the error value of ORB-SLAM3, r represents the error value of the proposed method in this paper, and $\eta$ is the percentage of improvement.

As shown in

Table 4. Comparative performance improvement rates of ORB-SLAM3.

Sequence	System(D)		System(D+O)
	ATE (RMSE)	RPE (Mean)	ATE (RMSE)	RPE (Mean)
KITTI 00	1.63%	−13.54%	−5.47%	−4.30%
KITTI 01	8.81%	9.43%	21.23%	7.94%
KITTI 02	11.48%	21.35%	18.27%	28.04%
KITTI 03	−9.12%	−4.61%	−44.76%	−16.70%
KITTI 04	23.50%	7.63%	34.80%	17.44%
KITTI 05	10.74%	−8.08%	−2.16%	−8.37%
KITTI 06	−6.14%	−2.09%	−7.93%	4.55%
KITTI 07	16.86%	7.26%	15.84%	24.50%
KITTI 08	6.86%	5.58%	4.64%	4.67%
KITTI 09	1.92%	41.98%	1.82%	39.60%
KITTI 10	7.03%	30.67%	1.46%	28.28%

, based on this evaluation, System(D) achieves an average improvement of 6.69% in absolute trajectory accuracy and 8.69% in relative pose estimation accuracy compared to ORB-SLAM3, while System(D+O) achieves an average improvement of 3.43% and 11.42%, respectively. These results demonstrate the comprehensive advantage of the proposed systems in dynamic environments.

Further comparison between System(D) and System(D+O) reveals that because the KITTI dataset primarily consists of vehicular scenes, with potential dynamic objects mostly being vehicles, System(D) employs a strategy of globally removing dynamic objects, which requires high accuracy in dynamic object recognition. Any misclassification can lead to a significant performance degradation in the system. In scenes with a higher presence of static vehicles and pedestrians and with fewer dynamic vehicles (such as sequences 00, 08, 09, and 10), System(D+O) outperforms System(D) in both trajectory and relative pose accuracy. This indicates that its fine-grained dual-mask method effectively prevents performance fluctuations caused by the misremoval of static objects, demonstrating stronger stability.

In scenarios with a high density of dynamic objects but a lack of static ones (such as sequences 01 and 04), System(D) exhibits superior performance due to the absence of misjudged static object interference, as its coarse-grained elimination strategy is more advantageous in such contexts.

In summary, the experimental results demonstrate that the dual-mask dynamic object elimination method proposed in this paper can effectively reduce pose estimation errors in dynamic scenes. The proposed system achieves accuracy surpassing that of ORB-SLAM3 in most KITTI sequences, exhibiting robustness and versatility. Even in complex boundary scenarios with many static objects and fewer dynamic ones, the performance of our system remains stable, further validating the key role of the proposed dual-mask strategy in enhancing accuracy and stability in dynamic SLAM systems.

4.2. TUM RGB-D Dataset Evaluation

The TUM RGB-D dataset includes real indoor scenes with human activity and static objects, and is designed to assess system accuracy and stability in high-dynamic indoor environments. In this experiment, we conducted a comparative analysis of the impact of dynamic contexts on the performance of the proposed SLAM system versus ORB-SLAM3 in a monocular setting across six image sequences from the TUM RGB-D dataset. The performance of the different systems across the sequences is summarized in

Table 5. Comparative evaluation of Absolute Trajectory Error (ATE) for monocular SLAM systems.

Sequence	ORB-SLAM3			System(D)			System(D+O)
	RMSE	Mean	Std	RMSE	Mean	Std	RMSE	Mean	Std
s_halfsphere	0.026	0.023	0.011	0.025	0.023	0.010	0.027	0.026	0.008
s_static	0.323	0.323	0.006	0.312	0.312	0.003	0.285	0.285	0.003
s_xyz	0.031	0.026	0.017	0.027	0.021	0.017	0.024	0.019	0.015
w_halfsphere	0.044	0.038	0.023	0.032	0.027	0.017	0.030	0.026	0.014
w_rpy	0.455	0.454	0.033	0.137	0.128	0.048	0.138	0.138	0.011
w_static	0.730	0.730	0.003	0.368	0.368	0.003	0.640	0.640	0.003

,

Table 6. Comparative evaluation of Relative Pose Error (RPE) for monocular SLAM systems.

Sequence	ORB-SLAM3			System(D)			System(D+O)
	RMSE	Mean	Std	RMSE	Mean	Std	RMSE	Mean	Std
s_halfsphere	0.014	0.012	0.008	0.015	0.012	0.010	0.013	0.011	0.007
s_static	0.010	0.006	0.008	0.010	0.005	0.008	0.008	0.004	0.006
s_xyz	0.018	0.013	0.013	0.017	0.012	0.012	0.016	0.012	0.011
w_halfsphere	0.031	0.018	0.026	0.020	0.015	0.012	0.020	0.015	0.012
w_rpy	0.019	0.014	0.012	0.019	0.011	0.016	0.020	0.014	0.015
w_static	0.008	0.005	0.006	0.009	0.006	0.007	0.010	0.005	0.006

and

Table 7. Comparative performance improvement rates of ORB-SLAM3.

Sequence	System(D)		System(D+O)
	ATE (RMSE)	RPE (Mean)	ATE (RMSE)	RPE (Mean)
s_halfsphere	2.86%	−4.42%	−6.05%	0.56%
s_static	3.39%	2.05%	11.65%	21.65%
s_xyz	14.11%	6.47%	24.29%	6.35%
w_halfsphere	28.50%	14.60%	32.28%	14.60%
w_rpy	69.87%	20.73%	69.54%	2.88%
w_static	49.56%	−14.00%	12.27%	3.57%

, where bold font indicates the best results in each metric.

As presented in Table 7, compared to ORB-SLAM3, the proposed System(D) achieves an average reduction of 28% in ATE and 4.27% in RPE. The enhanced System(D+O) achieves an average reduction of 24% in ATE and 8.27% in RPE. These quantitative results verify that our methods effectively mitigate cumulative errors induced by dynamic feature mismatches. Furthermore, the experimental data in Table 5 and Table 6 reveal that both System(D) and System(D+O) exhibit lower standard deviation (Std) values, demonstrating the high adaptability and stability of our proposed approaches in dynamic environments. 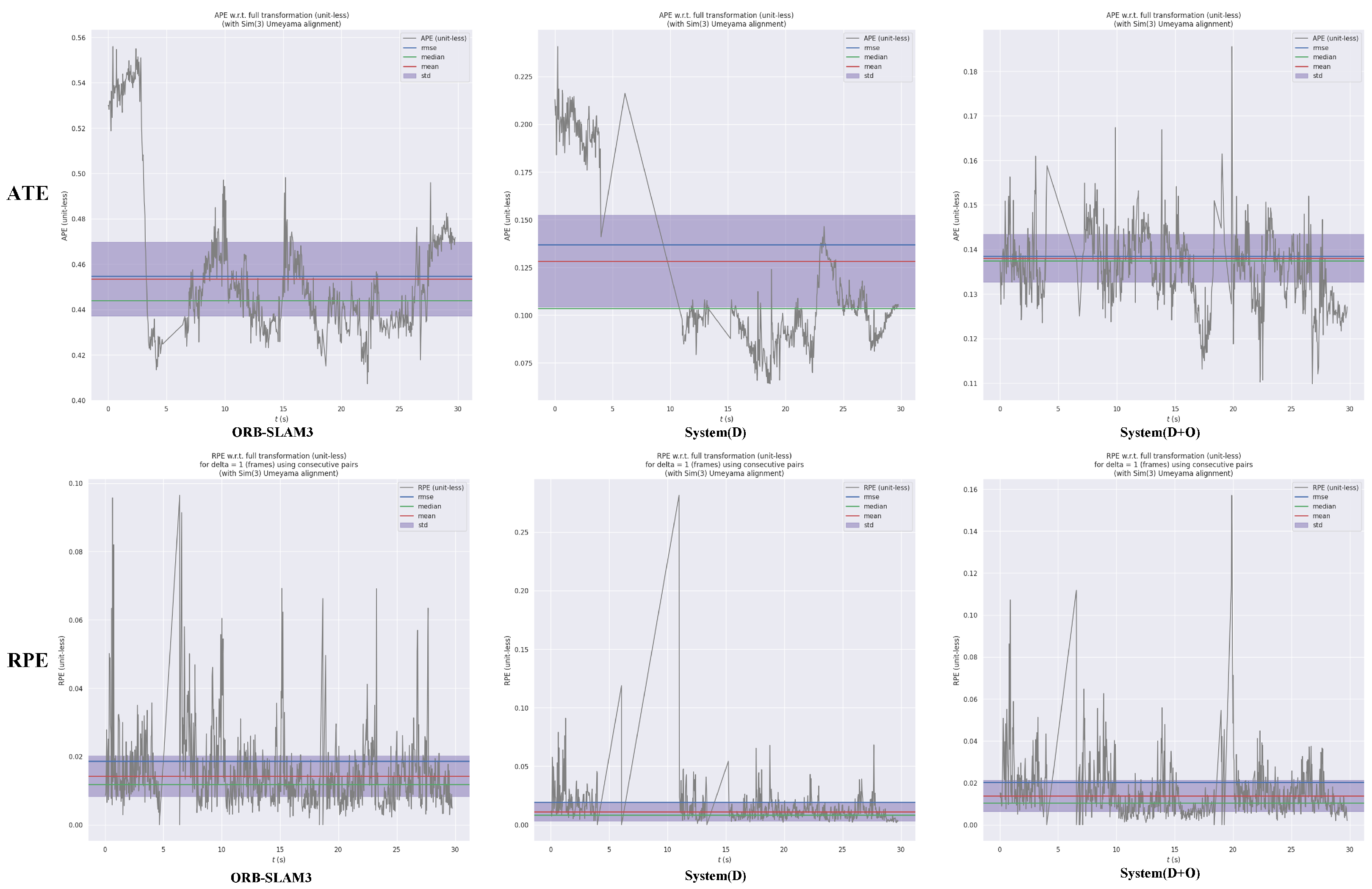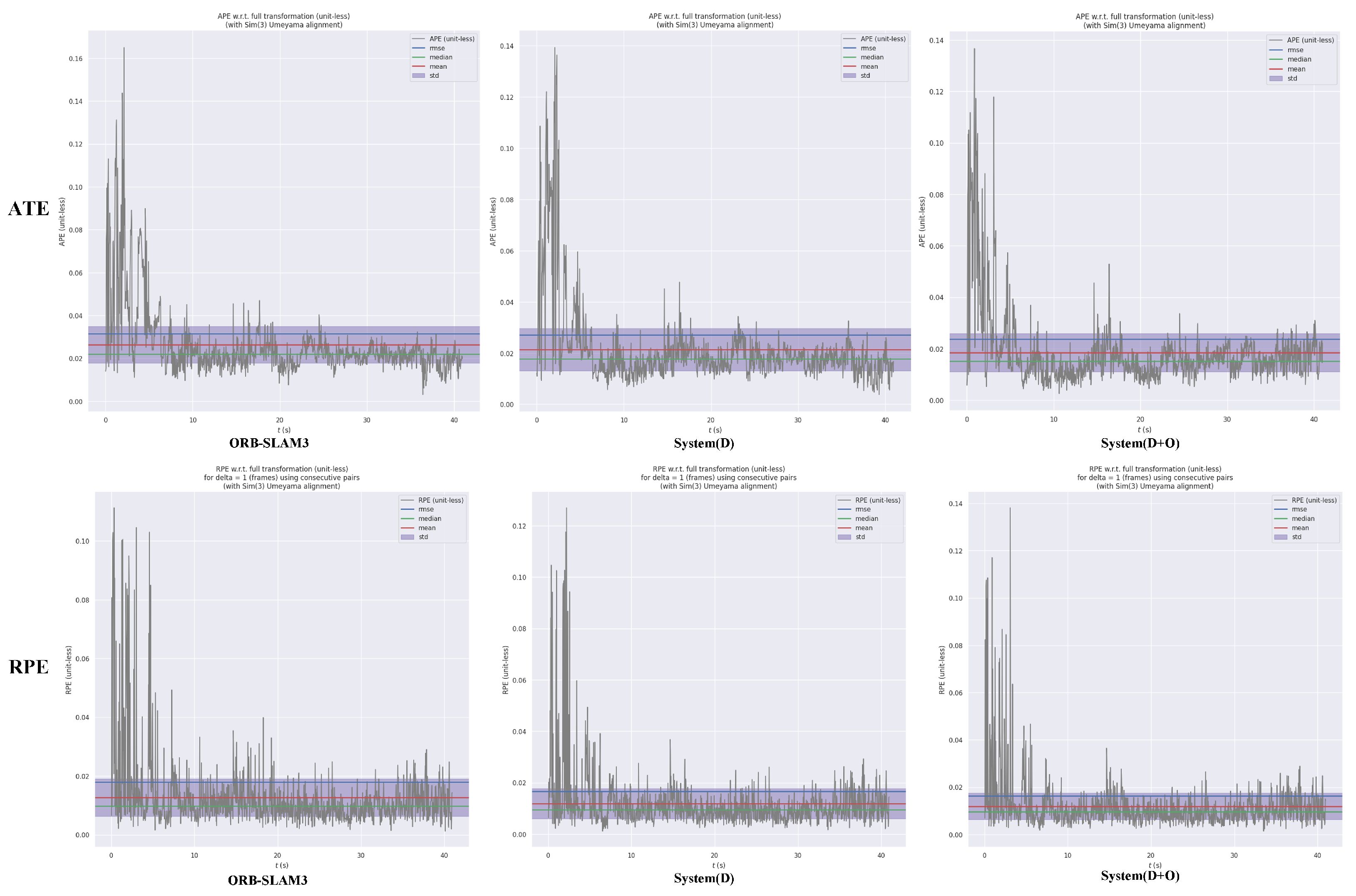Similarly, Figure 3 and Figure 5 visually demonstrate that both System(D) and System(D+O) exhibit narrower standard deviation ranges compared to ORB-SLAM3, indicating more stable performance.

From a specific scenario analysis, walking sequences such as w_halfsphere, w_rpy, and w_static contain significant overall motion by individuals, causing notable dynamic interference. Traditional methods are prone to feature matching failures and drift estimation due to the presence of dynamic points. In contrast, the proposed approaches exhibit greater accuracy improvements in these highly dynamic sequences, indicating that our dynamic point elimination mechanism has good suppression capabilities for widespread disturbances.

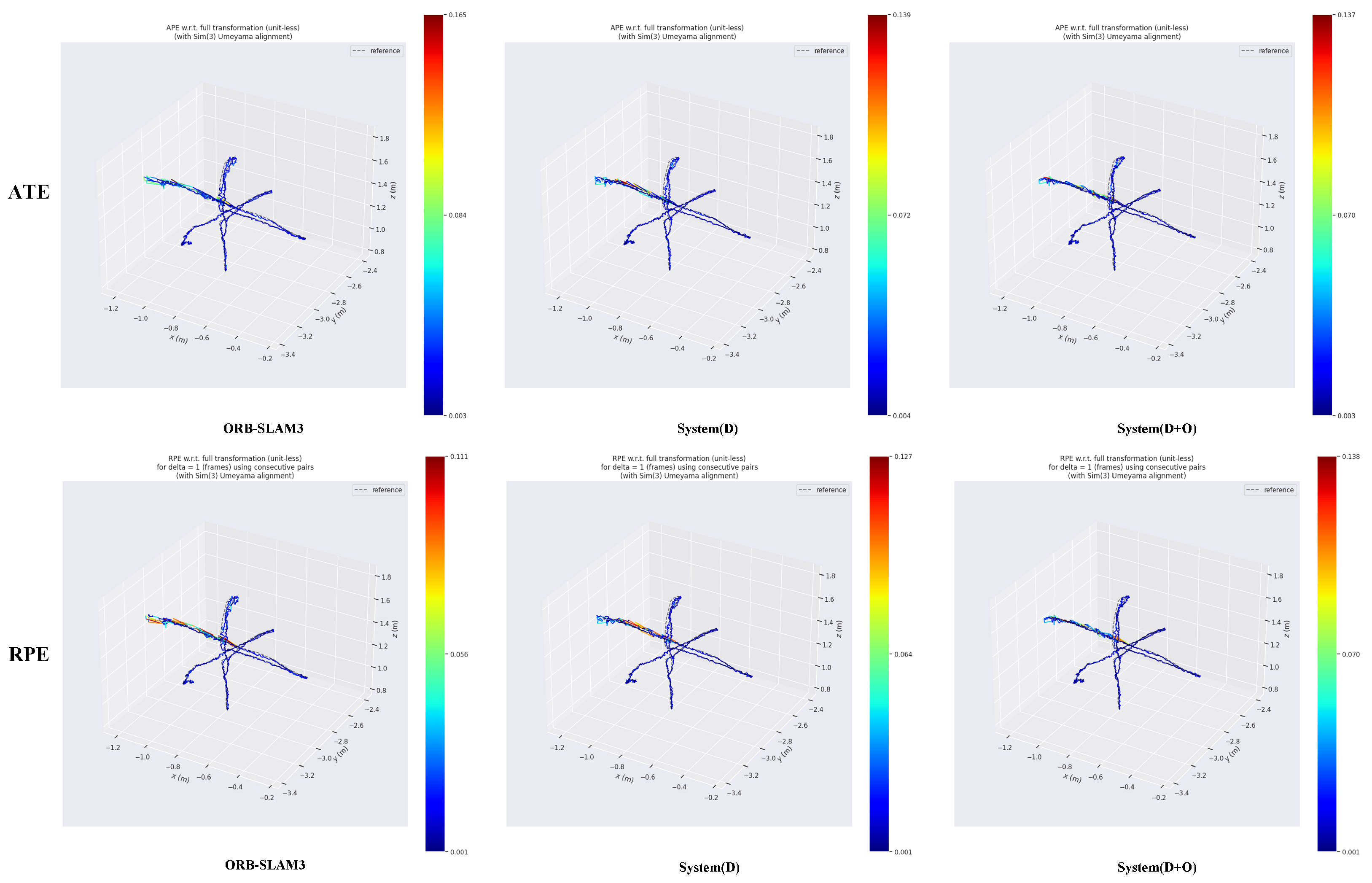
In the experimental results for the fre3_walking_rpy(w_rpy) sequence, Figure 3 shows that the trajectory error of ORB-SLAM is in the range of 0.019–0.035, the trajectory error of System(D) is in the error range is 0.018–0.03, and the trajectory error of System(D+O) is in the range of 0.017–0.043. The accuracy of System(D+O) is almost the same as that of System(D). Figure 4 presents the trajectory deviation map in comparison to ground truth, showing that ORB-SLAM3 experiences significant drift, while System(D) offers the most accurate trajectory estimation. In these results, System(D+O) exhibits marginally lower performance compared to System(D).

Conversely, sitting sequences such as s_halfsphere, s_rpy, and s_static are less dynamic, with only minor movements of the hands and head. In such scenarios, systems are more likely to misjudge local dynamics as global dynamics, leading to loss of static information. Therefore, the fine-grained dynamic discrimination strategy introduced in this paper is particularly crucial.

In the experimental results for the fre3_sitting_xyz(s_xyz) sequence, the constrained local movements in this sitting scenario are primarily limited to head and hand motions, resulting in negligible dynamic interference. Figure 5 shows that the trajectory error of ORB-SLAM is in the range of 0.019–0.035 and that the trajectory error is relatively small, while the trajectory error of System(D) is in the error range is 0.018–0.03 and the trajectory error of System(D+O) is in the range of 0.017–0.043. As evidenced in Figure 6, the trajectory deviation map demonstrates no visually discernible differences between the compared systems. Thus, both System(D) and System(D+O) continue to exhibit enhancements in the ATE and RPE metrics compared with the ORB-SLAM3 system.

When comparing the performance of System(D+O) and System(D), the former demonstrates superior ATE performance in the sitting sequences, indicating that its fine-grained dynamic point removal strategy can more effectively distinguish between local microdynamics and globally static regions, resulting in improved overall localization accuracy. System(D+O) also demonstrates measurable improvements over System(D), with enhancements of 3.18% in ATE and 8.15% in RPE. In contrast, the coarse-grained removal mechanism employed by System(D) is more prone to incorrectly eliminating static objects in such fine-grained scenarios, resulting in decreased accuracy. Conversely, in the highly dynamic walking sequences, the global removal strategy of System(D) exhibits greater advantages, as it can rapidly eliminate interfering features within large-scale moving regions. As a result, System(D) shows slightly better ATE performance in certain sequences compared to System(D+O).

In conclusion, the dual-mask dynamic point filtering method proposed in this paper demonstrates exceptional performance in complex indoor dynamic scenarios. In particular, it shows a distinct advantage in the ATE metric. System(D+O) is suitable for refined scenarios with a mix of dynamic areas and static backgrounds, while System(D) is more appropriate for handling environments with extensive highly dynamic disturbances. Regardless of the level of dynamism, the method presented in this paper significantly enhances the precision of pose estimation and the overall robustness of the system, demonstrating good versatility and potential for practical application.

5. Time Evaluation

In practical applications, real-time performance is a key metric for evaluating SLAM systems. We tested the average computation time of the main modules under different datasets. The experiments used the pretrained YOLOv11-seg.pt model for semantic segmentation. The results shown in

Table 8. Time evaluation.

Datasets	Semantic Segmentation		Geometric Consistency Check
	CPU	GPU
KITTI	360.78 ms	15.79 ms	0.78 ms
TUM	317.87 ms	13.36 ms	0.83 ms

indicate that the semantic segmentation processing speed with GPU hardware acceleration meets real-time requirements (KITTI: 15.79 ms/frame, TUM: 13.36 ms/frame). For the geometric consistency check phase, we utilized the existing PnP nonlinear optimization module in ORB-SLAM3, where the process involves matching outliers from the previous frame to the current frame to achieve geometric consistency detection. This is a simple modification, but proves to be both practical and cost-effective. Therefore, the additional time at this stage comes only from the calculation of the retained outliers, with an increase in processing time of less than 1 ms.

Next, we conducted a comparison with DS-SLAM. In the geometric consistency detection phase of DS-SLAM, optical flow is used to quickly match feature points, then the fundamental matrix is computed to complete the epipolar geometry constraint process for detecting feature point anomalies. The DS-SLAM experiments were conducted on a computer equipped with an Intel i7 CPU, P4000 GPU, and 32 GB of memory, with the process taking 29.51 ms. The semantic segmentation stage of DS-SLAM [28] uses a neural network called SegNet, which takes 37.57 ms. These data are taken from the DS-SLAM team’s experimental report.

Next, we conducted a comparison with DynaSLAM. The geometric consistency detection phase in DynaSLAM uses a multi-view geometry method to detect dynamic objects by analyzing the depth and angle between feature points in RGB-D images. DynaSLAM took 235.98 ms on the fre3_walking_rpy sequence from the TUM dataset. These data were taken from the DynaSLAM team’s experimental results [29]. The semantic segmentation stage of DynaSLAM uses a Mask R-CNN neural network. He et al. [35] reported that the running time of Mask R-CNN with an Nvidia Tesla M40 GPU was 195 ms per image.

Although both DS-SLAM and DynaSLAM were evaluated based on ORB-SLAM2 and the method proposed in this paper was implemented on ORB-SLAM3, the processing time of dynamic detection stages such as geometric consistency checks and semantic segmentation remains comparable across systems. Notably, the method proposed in this paper accomplishes these tasks with significantly lower computational cost and reduced processing time.

6. Conclusions

This paper introduces a monocular ORB-SLAM3 system optimized for dynamic environments. The proposed system is aimed at improving the localization accuracy and mapping robustness of visual SLAM in dynamic scenarios. By integrating semantic segmentation with YOLOv11, morphological dilation operations, and a geometric reprojection consistency discrimination mechanism, the proposed method achieves a dual-mask approach for precise identification and effective filtering of dynamic features, helping to mitigate the interference caused by dynamic objects on traditional SLAM systems.

Experimental results conducted on the KITTI and TUM RGB-D datasets demonstrate that the proposed method improves global trajectory accuracy across various dynamic scenes. Employing a dynamic object elimination mechanism reduces the influence of dynamic targets on trajectory estimation. In particular, this approach exhibits superiority over traditional methods in highly dynamic scenarios, where it helps to improve robustness. However, a notable limitation of this method is that the improvement in efficiency is relatively marginal, meaning that it may lead to a slight decrease in accuracy in scenarios with a large number of potentially dynamic objects but few truly dynamic ones. These issues primarily stem from misclassifications of dynamic objects, where some static feature points are incorrectly identified as dynamic during the geometric consistency verification phase. In contrast, the dual-mask approach proposed in this study demonstrates enhanced robustness; even when dynamic points are mistakenly detected, removal is confined to local regions rather than entire objects, helping to preserve the overall stability and robustness of the system. Overall, the proposed system shows improvements in both ATE and RPE, effectively overcoming the cumulative errors associated with mismatches in dynamic environments. This provides strong support for high-precision localization and mapping in practical applications such as autonomous driving and robotic navigation.

In terms of time and computational cost, classical dynamic SLAM methods typically introduce additional geometric constraints prior to the feature matching stage to determine whether candidate regions produced by instance segmentation truly correspond to dynamic objects. For example, DS-SLAM employs optical flow to implement a simplified geometric consistency check based on ORB-SLAM2, offering a lightweight mechanism to distinguish dynamic objects. On the other hand, DynaSLAM utilizes depth information to perform a more complex multi-view geometric analysis for dynamic object detection. In contrast, the method proposed in this paper leverages the existing optimization process within the SLAM pipeline to identify dynamic points, thereby avoiding additional computational overhead while maintaining reliable outlier detection capability. This leads to improved overall computational efficiency as well as better accuracy.

Future research should consider further optimizing the system’s real-time performance and local motion models to enhance its stability and accuracy in highly dynamic environments. The method proposed in this paper not only offers a superior solution for SLAM systems operating in dynamic environments but also provides important guidance and insights for future research and applications of SLAM systems.