Study on the Support Pressure of Tunnel Face for the Construction of Pipe-Jacking Across Thin Overburden River Channel Based on Mud-Water Balance

Abstract

Pipe-jacking construction technology is favored in urban construction due to its advantages of high safety and being a non-excavation technique. However, instability of the tunnel face often occurs due to unfavorable conditions, such as pipe jacking across the river channel, shallow soil cover, and improper control of the support pressure. In this study, we made a use of the limit balance method and mud–water balance theory. At this moment of passive damage and active destruction occurring at the pipe-jacking tunnel face, the general mathematical expressions of the tunnel-face support pressure (with lower limit value P_min and upper limit value P_max) are derived. In the non-river impact area and river impact area, the optimal value P_o of support pressure at the tunnel face is thus derived. Then, based on the Y25-Y26 pipe-jacking project across the Chu River channel in Hefei North District, a numerical simulation method is used to support further discussion. The results indicate that, when the river overburden is 3 m, the ultimate support pressure calculated by means of numerical simulation is 881.786 kN, and the optimal support ratio $\mathsf{\lambda }$ is taken in the interval of 1.0~1.5. Secondly, the upper limit value P_max, lower limit value P_min, and optimum value P_o calculated using the theoretical equations are 2669.977 kN, 309.910 kN, and 1044.870 kN, respectively. These results leads us to recommend setting the support pressure of the tunnel face in a reasonable range between the upper limit value P_max and the lower limit value P_min, to ensure that the tunnel-face support pressure and resistance during pipe jacking always remain in a balanced state. The relevant research results from this study provide an important technical guarantee for the successful implementation of the examined project and, at the same time, can serve as a reference example for similar projects.

1. Introduction

Keeping the tunnel-face support pressure, soil-layer groundwater pressure, and soil pressure in a balanced state is the key to ensuring the smooth construction of mud–water-balanced pipe jacking and reducing the impact of disturbance on the surrounding soil. In a pipe-jacking project, if the tunnel-face support pressure is not properly controlled, tunnel-face instability problems will be caused. When the tunnel-face support pressure is too low, the front soil is unloaded. And there is a large influx of soil into the mud and water silo, causing over-excavation, surface subsidence, and pipe-jacking obstruction. When the support pressure on the tunnel face is too high, the soil in front is compressed due to loading, causing uplift and damage in a certain area on the surface [1]. Therefore, in order to avoid problems such as surface subsidence with too much support pressure or uplift damage with too little support pressure, reasonable and accurate control of the support pressure on the tunnel face is key in mud–water-balanced pipe-jacking construction [2].

Research on the ultimate support pressure currently uses indoor physical model tests, the stability coefficient method, the limit analysis method, the limit equilibrium method, and numerical calculations [3,4]. However, physical model tests are costly and difficult to generalize to complex real-world projects [5,6,7]. The stability coefficient method was first proposed by Broms [8], who, in 1967, established a mathematical relationship between the support force and the surface load, soil gravity, overburden burial depth, and clay undrained strength and defined the ratio of each parameter as the stability coefficient N. Based on a large amount of surface settlement data, Peck [9] proposed that N values of 5 to 7 lead to destabilization of the excavation surface and induce surface collapse, and they explored the relationship between the stability coefficients and the overburden burial depth, the unsupported length, and variations in settlement. However, it was found in practice that the prediction error of the stability coefficient method was large, and it was very easy to misjudge an unstable condition as a stable condition. At the same time, the stabilization coefficient method can only be applied to clay formations (i.e., with cohesion ≠ 0) and cannot be applied to sandy soil formations. Although the stabilization factor method has received a series of improvements to diversify the form of expression, one point that has never been taken into account is that the effect of permeability on the excavated surface is suitable for calculations in groundwater-free construction conditions. In addition, the arc effect overestimates the destructive power. In contrast, the limit analysis [10,11,12,13] method is based on the kinematic permissive velocity field and the static permissive stress field. It establishes the equilibrium conditions and damage conditions in the critical state of the soil body and deduces the excavation surface support force based on the principle of virtual work [14,15].

The limit equilibrium method [16,17] assumes that damage to the soil body in front of the excavation produces a sliding body, and it analyzes the equilibrium of forces in the soil body at the moment of damage to find the solution to the problem. Then, the complex static indeterminate problem of soil damage is transformed into a simpler static deterministic solvable problem. The theory of the limit equilibrium method [18,19,20,21] is rigorous, the mechanical mechanism is clear, and the calculation formula is concise and refined. After decades of improvement and enhancement, it has been developed to a fairly perfect degree and is widely used in practical engineering [22,23]. Based on the two-dimensional limit equilibrium model and silo theory [24], Horn et al. [25] established a three-dimensional wedge-shaped model for the stability of a tunnel face; the model can determine the magnitude of the ultimate support pressure. R. P. Chen [26] considered the effects of the prism height and soil arching. Then, he proposed an improved three-dimensional wedge-shaped prism model and an analytical formula for the lateral stress ratio between the prism and adjacent soil, which reflects the arching effect of the soil. In a comparison of normalized support pressures S_lim by Vermeer [27], its tolerance was within ±0.3γD. P. Perazzell [28] introduced the supporting force of a single anchor in a wedge limit equilibrium model and proposed a limit equilibrium method for analyzing the stability of the tunnel faces of reinforced tunnels in purely cohesive soils without draining shear strength. Based on four typical pipe–slurry–soil contact modes, Weizheng Liu [29] proposed a calculation method for the jacking force of each pipe section, considering the jacking resistance at the excavation surface and the lateral friction resistance around the pipe. The reliability of the calculation method was verified by comparing the model test results with engineering example data.

Numerous scholars have carried out research on the stability of the pipe-jacking tunnel face. The results have been fruitful. However, some aspects are yet to be further deepened. Existing tunnel-face support pressure calculations are analyzed based on the plane strain [30], and the front earth pressure is simplified into a rectangular distribution calculation. This differs from the trapezoidal distribution of soil pressure in front of an actual tunnel face [31]. Moreover, the study above only focused on single pipe jacking, but double-row or even triple-row pipe jacking is widely used in engineering practice [32]. In addition, passive damage to the soil in front of the pipe jacking is more common in actual pipe-jacking projects. If the thickness of the overlying soil layer is not large and the construction involves pipe jacking crossing a river channel, active damage to the soil in front of the pipe jacking must be considered. Therefore, in this study, based on the mud–water balance and considering the conditions of pipe jacking through a river channel, the thin overburden of the river, and multi-line construction with small clearances, the support pressures of the tunnel face have been established. This research can provide a theoretical basis and practical guidance for the construction of pipe jacking under similar engineering conditions, which is of great practical significance. The organization of this paper is as follows: this study firstly investigates the mechanisms of different forms of damage occurring at the tunnel face of a pipe-jacking tunnel. And accordingly, the calculation and analysis model of the tunnel-face support pressure are constructed, respectively. Secondly, based on the principle of mud–water balance and combined with the limit equilibrium method, the upper limit (P_max), lower limit (P_min), and optimum values (P_o) of the support pressure are derived, respectively. Then, the mud–water-balanced pipe-jacking construction is numerically simulated by taking the dependent project as a prototype. Finally, the results of theoretical calculations and engineering measurements are discussed and the main conclusions of this paper are outlined.

2. Theoretical Analysis of Tunnel-Face Support Pressure

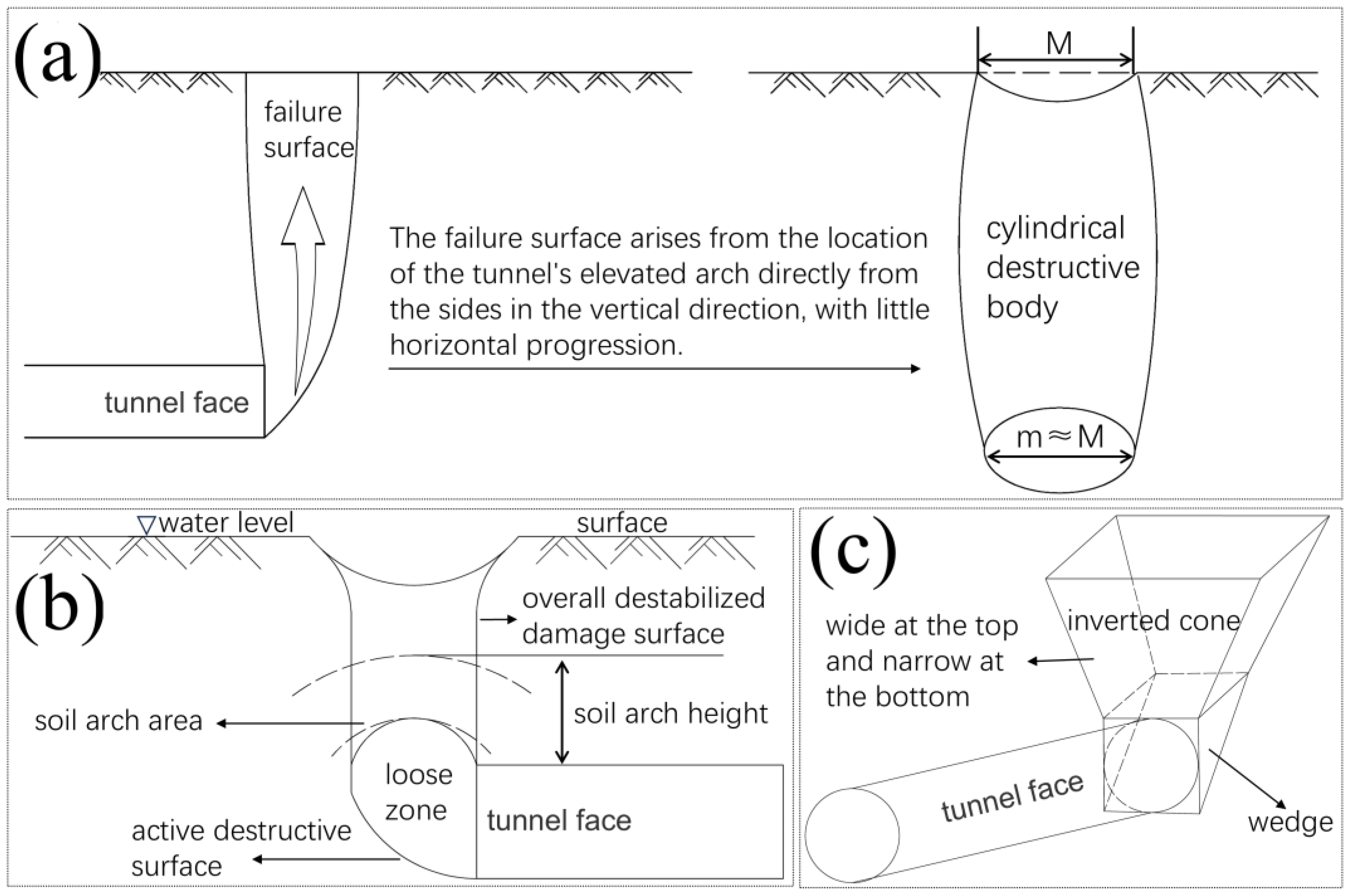
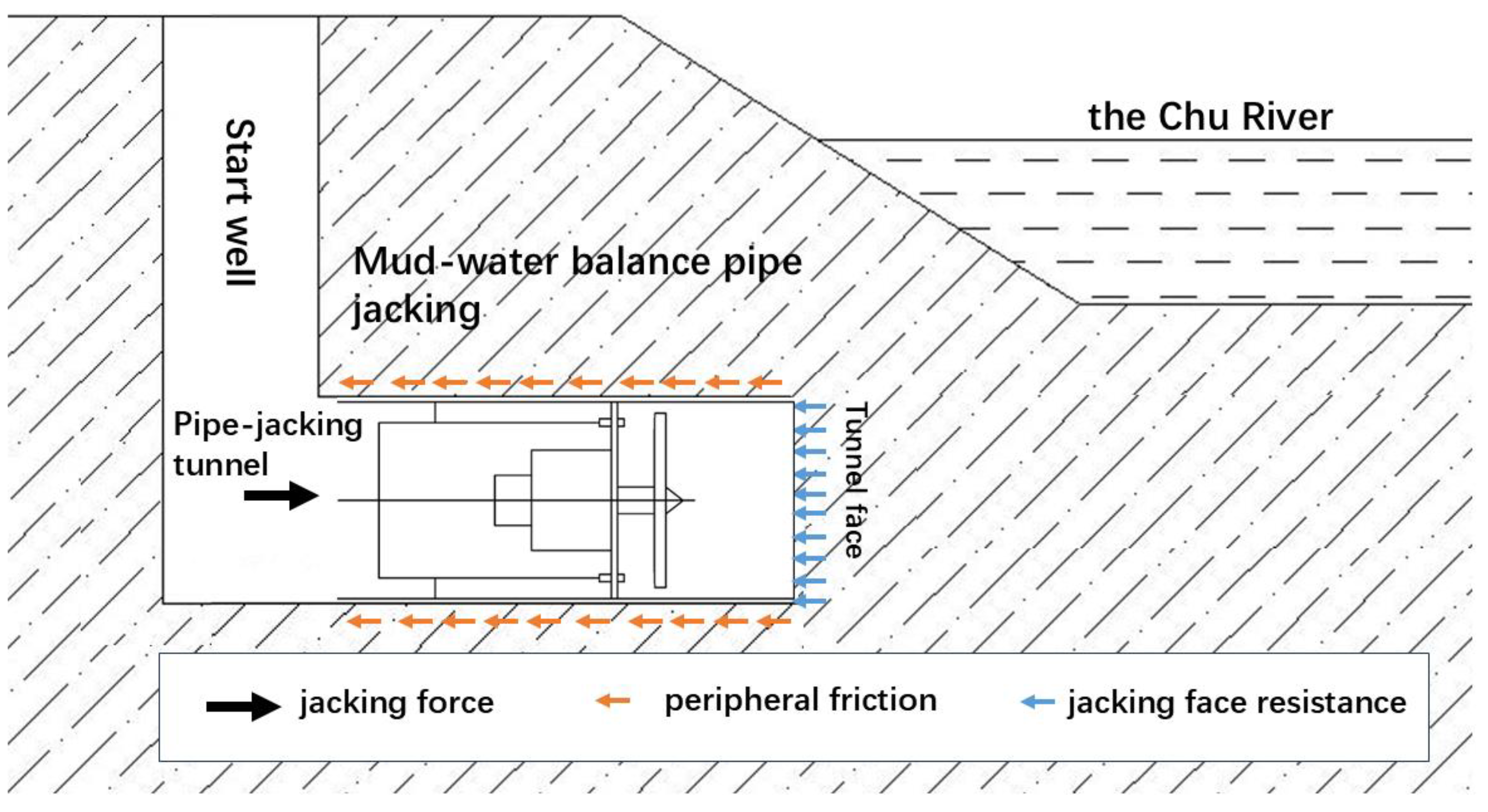
2.1. Mechanism of Support Pressure on Tunnel Face During Pipe Jacking

The mud–water balance theory is a pipe-jacking theory that balances the soil pressure and groundwater pressure in the soil layer where the tunneling machine is located. It does this using the pressure inside the mud compartment of the tunneling machine (i.e., the support pressure on the tunnel face). Theoretically, when the support pressure on the tunnel face is in balance with the soil and water pressure in front of it, the pipe jacking will not lead to deformation of the stratum in front of the tunnel face.

When the support pressure on the tunnel face is less than the soil and water pressure in front of it, the stratum in front of the tunnel face moves towards the tunnel. The interaction between the soils has a tendency to inhibit soil sliding, and the shear resistance increases. When the support force on the tunnel face decreases to a certain critical point, the displacement of the tunnel face suddenly increases sharply, and the tunnel face undergoes active damage. Established research results show that the damage pattern manifests as a chimney-like shear zone [33,34] when active damage occurs on the tunnel surface during shallow buried pipe jacking in sandy soil layers. The damage surface arises from the location of the tunnel’s elevated arch, directly from the sides in the vertical direction, with horizontal movement almost never occurring. The damage body is in the shape of a column with a small difference in width between its top and bottom (as shown in Figure 1a). When the water level is above the surface, the upper stratum in front of the tunnel face undergoes overall damage and slides downward to the surface [35], as depicted in Figure 1b.

When the tunnel-face support pressure is greater than the resistance, the soil body in front of the tunnel face shows an upward sliding displacement tendency. The interactions between soil grains inhibit the sliding tendency of the soil body, and the shear resistance increases. When the support pressure increases to a critical point, the displacement of the tunnel face suddenly increases sharply, and the pipe-jacking tunnel face undergoes passive damage. Existing research results show that when the tunnel surface in shallow buried pipe jacking in a sandy soil layer is passively damaged, the shape of the damaged area of the formation in front is similar to an inverted cone that is wide at the top and narrow at the bottom with a certain angle of inclination [36] (as shown in Figure 1c).

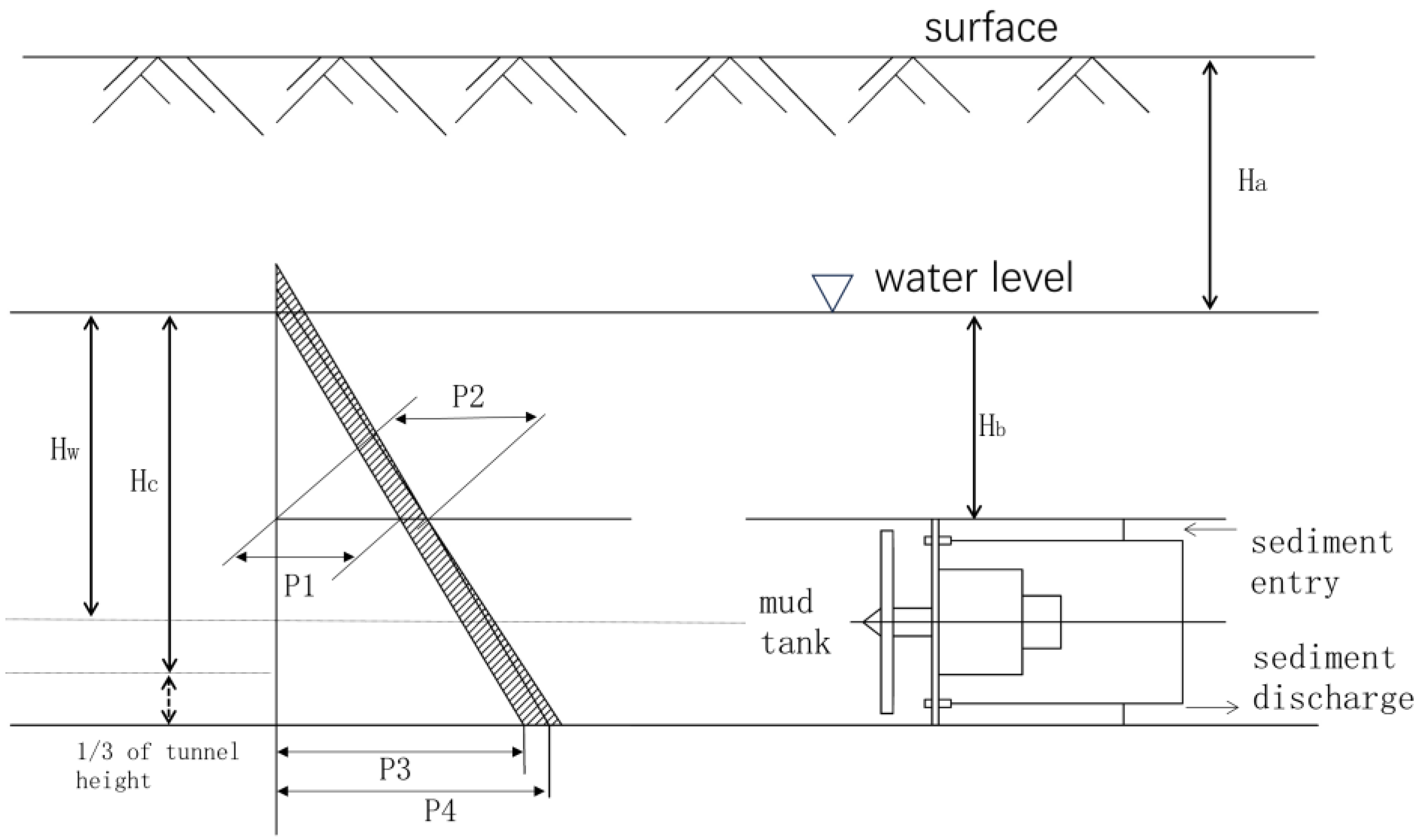
2.2. Theoretical Calculation Principle of Tunnel-Face Support Pressure

After simplifying and making assumptions about the background project, this study constructed a theoretical analysis model of different tunnel-face damage modes. For river-crossing pipe-jacking projects with significant features such as a small overburden thickness and a water level above the surface, the analytical model for calculating the support pressure at the tunnel face makes the following assumptions:

(1)

The project site strata are homogeneous, continuous, and isotropic. Tunnel-face damage is caused by sliding within the stratum soil body. The soil on the sliding surface obeys the Mohr–Coulomb failure criterion.

(2)

The support pressure on the tunnel face is uniformly distributed. Its vertical variation and the effect of seepage from the ground at the tunnel face are not considered.

(3)

The circular pipe-jacking tunnel face is simplified to a retaining wall of equal area and no thickness.

(4)

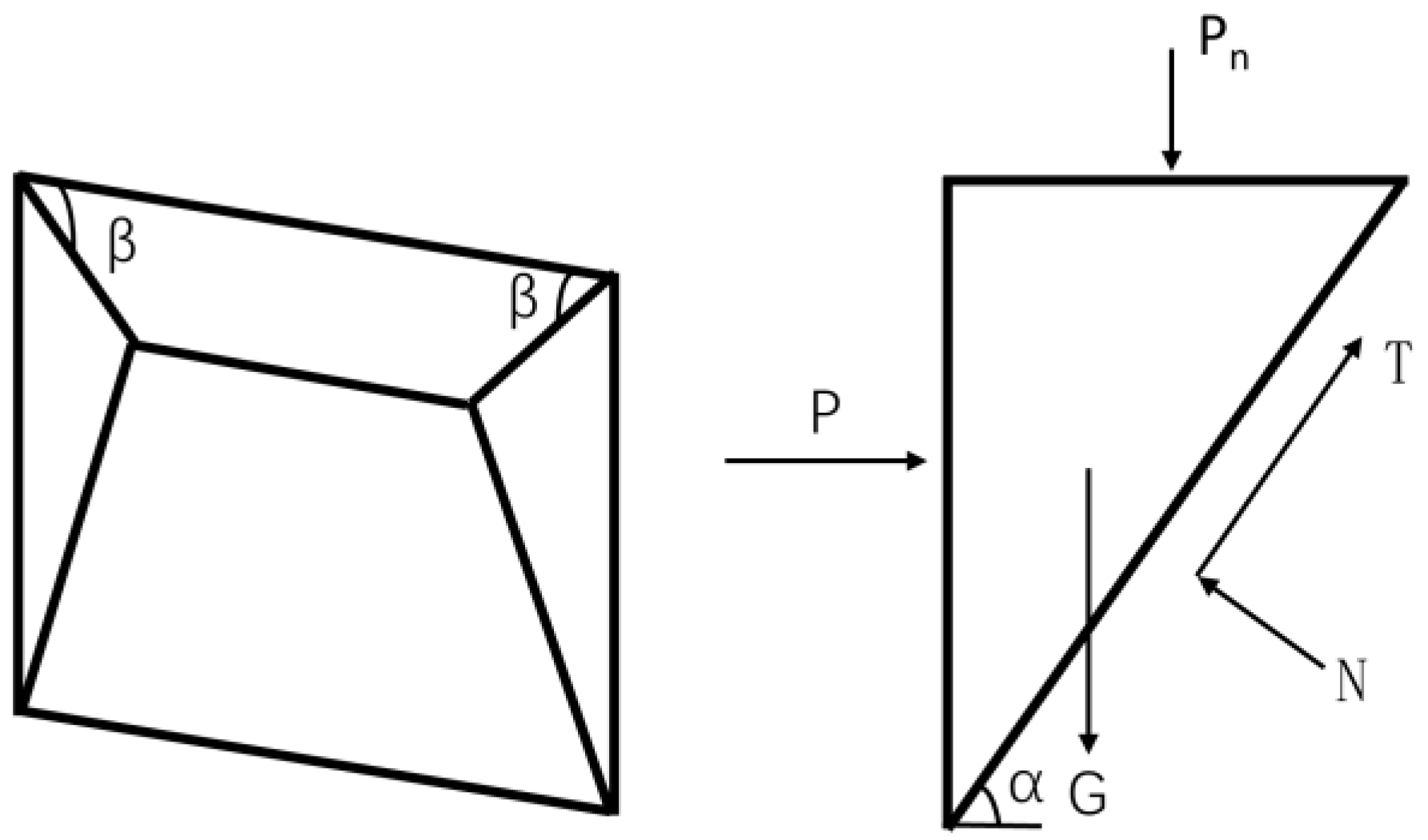
When the pipe-jacking tunnel face is damaged, there is a wedge-shaped block in front. The effect of friction on the contact surface of the wedge block is neglected, the wedge block does not undergo internal deformation, and the static equilibrium condition is satisfied.

The force on the wedge-shaped block in front of the pipe-jacking tunnel face is as shown in Figure 2a. The meaning of each parameter in the figure is as follows: P is the support pressure on the tunnel face; P_w is the hydrostatic pressure exerted on the tunnel face; P_n is the vertical force acting on the top of the wedge block; G is the self-weight of the wedge block; T and N are the frictional force (upward direction for active damage and downward direction for passive damage) and the normal stress on the diagonal section of the wedge block, respectively; and T′ and N′, respectively, represent the frictional resistance (upward direction for active failure, downward direction for passive failure) and normal force on the sliding surfaces on both sides of the wedge-shaped block.

The force characteristics of the wedge-shaped block were analyzed by taking the example of passive damage occurring on the pipe-jacking tunnel face. Equations (1) and (2) can be obtained from the conditions of an equilibrium of forces in the horizontal and vertical directions, respectively.

$$\mathrm{P}=\mathrm{T}\cos \mathsf{\alpha }+2{\mathrm{T}}^{\prime }\cot \alpha +\mathrm{N}\sin \mathsf{\alpha }+{\mathrm{P}}_{\mathrm{W}}$$

(1)

$${\mathrm{P}}_{\mathrm{n}}+\mathrm{G}=\mathrm{N}\cos \mathsf{\alpha }-\mathrm{T}\sin \mathsf{\alpha }+2{\mathrm{T}}^{\prime }\sin \mathsf{\alpha }$$

(2)

Equation (3) can be obtained from the relationship between the friction force T and the normal force N on the sliding surface of the block.

$$\mathrm{T}={\displaystyle \frac{\mathrm{c}{\mathrm{B}}^2}{\sin \mathsf{\alpha }}}+\mathrm{N}\tan \mathsf{\phi }$$

(3)

Here, c is the soil cohesion, kPa; $\mathsf{\alpha }$ is the angle of inclination of the sliding block, °, $\mathsf{\alpha }=45°+{\displaystyle \frac{\mathsf{\phi }}{2}}$; $\mathsf{\phi }$ is the angle of internal friction of the soil, °; $\mathrm{G}$ is the self-weight of the wedge block, $\mathrm{G}={\displaystyle \frac{{\mathrm{B}}^3{\mathsf{\gamma }}_{\mathrm{s}}}{2\mathrm{t}\mathrm{a}\mathrm{n}\mathsf{\alpha }}}$, kN; ${\mathsf{\gamma }}_{\mathrm{s}}$ is the volumetric weight of soil, kN/m³; and B is the wide of wedge block, m.

Equation (4) can be obtained by combining Equations (1)–(3) and simplifying.

$$\mathrm{P}={\displaystyle \frac{\sin \mathsf{\alpha }-\tan \mathsf{\phi }\cos \mathsf{\alpha }}{\cos \mathsf{\alpha }+\tan \mathsf{\phi }\sin \mathsf{\alpha }}}\left({\mathrm{P}}_{\mathrm{n}}+\mathrm{G}\right)-\left({\displaystyle \frac{\mathrm{c}{\mathrm{B}}^2}{\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\alpha }}}+2{\mathrm{T}}^{\prime }\right)\left({\displaystyle \frac{\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\alpha }-\mathrm{t}\mathrm{a}\mathrm{n}\mathsf{\phi }\mathrm{c}\mathrm{o}\mathrm{s}\mathsf{\alpha }}{\mathrm{c}\mathrm{o}\mathrm{s}\mathsf{\alpha }+\mathrm{t}\mathrm{a}\mathrm{n}\mathsf{\phi }\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\alpha }}}\sin \mathsf{\alpha }+\cos \mathsf{\alpha }\right)+{\mathrm{P}}_{\mathrm{W}}$$

(4)

Here, ${\mathrm{P}}_{\mathrm{w}}$ is the hydrostatic pressure, kN, ${\mathrm{P}}_{\mathrm{w}}={\mathrm{B}}^2({\mathrm{H}}_{\mathrm{u}}+0.5\mathrm{D}){\mathsf{\gamma }}_{\mathrm{w}}$; ${\mathsf{\gamma }}_{\mathrm{w}}$ is the volumetric weight of water, kN/m³; ${\mathrm{H}}_{\mathrm{u}}$ is the distance from the top of the pipe jacking to the underground water level, m; D is the outer diameter of the digging machine, m; ${\mathrm{T}}^{\prime }$ is the sliding friction force of the sliding surfaces on both sides of the wedge-shaped block, kN, ${\mathrm{T}}^{\prime }={\displaystyle \frac{\mathrm{c}{\mathrm{B}}^2}{2\mathrm{t}\mathrm{a}\mathrm{n}\mathsf{\alpha }}}+\mathrm{k}{\mathsf{\gamma }}_{\mathrm{s}}{(\mathrm{C}+\mathrm{D}/3)}^3\mathrm{t}\mathrm{a}\mathrm{n}\mathsf{\phi }$; $\mathrm{k}$ is the coefficient of lateral pressure of the soil, $\mathrm{k}=1-\sin \mathsf{\phi }$; and $\mathrm{C}$ is the length of the wedge block, m.

${\mathrm{P}}_{\mathrm{n}}$ is the vertical force on the top of the wedge block. Soil and water sub-calculations are used here. On the one hand, due to the small thickness of the pipe-jacking overburden, ${\mathrm{P}}_{\mathrm{n}}$ is taken as the self-weight of the overlying soil according to the soil column theory. That is to say, ${\mathrm{P}}_{\mathrm{n}}={\mathrm{B}}^2{\mathrm{H}}_{\mathrm{s}}{\mathsf{\gamma }}_{\mathrm{s}}\mathrm{c}\mathrm{o}\mathrm{t}\mathsf{\alpha }$. ${\mathrm{H}}_{\mathrm{s}}$ is the thickness of the overburden. On the other hand, ${\mathrm{P}}_{\mathrm{n}}={\mathrm{B}}^2{\mathrm{H}}_{\mathrm{w}}{\mathsf{\gamma }}_{\mathrm{w}}\mathrm{c}\mathrm{o}\mathrm{t}\mathsf{\alpha }$, ${\mathrm{H}}_{\mathrm{w}}$ is the distance from the point of soil pressure action to the underground water level.

Each of the above parameters was substituted into Equation (4) and simplified. The general mathematical equation for the tunnel-face support pressure $\mathrm{P}$ was then obtained as shown in Equation (5).

$$\begin{gathered} {\mathrm{P}}_{\mathrm{m}\mathrm{i}\mathrm{n}}=\mathsf{\epsilon }{\mathsf{\gamma }}_{\mathrm{s}}{\mathrm{B}}^2\left({\mathrm{H}}_{\mathrm{s}}\cos \mathsf{\alpha }+{\displaystyle \frac{\mathrm{B}}{2\tan \mathsf{\phi }}}\right)-\left[{\displaystyle \frac{\mathrm{c}{\mathrm{B}}^2\left(1-\cos \mathsf{\alpha }\right)}{\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\alpha }}}+2{\mathsf{\gamma }}_{\mathrm{s}}\tan \mathsf{\phi }\left(1-\sin \mathsf{\phi }\right){\left(\mathrm{C}+{\displaystyle \frac{\mathrm{D}}{3}}\right)}^3\right] \\ \left(\mathsf{\epsilon sin}\mathsf{\alpha }+\cos \mathsf{\alpha }\right)+{\mathrm{B}}^2\left({\mathrm{H}}_{\mathrm{u}}+0.5\mathrm{D}\right){\mathsf{\gamma }}_{\mathrm{w}} \end{gathered}$$

(5)

Here, $\epsilon ={\displaystyle \frac{\sin \alpha —\tan \phi \cos \alpha }{\cos \alpha +\tan \phi \sin \alpha }}$. The other symbols have the same meanings as defined above.

The slider inclination angle $\mathsf{\alpha }$ in Equation (5) was considered an unknown quantity. The lowest value of the support pressure on the tunnel face, $\mathrm{P}$, which is the lower limit of the support force ${\mathrm{P}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ on the pipe-jacking tunnel face, was obtained through an optimization search.

The horizontal unloading arch effect needs to be taken into account when active damage occurs (when the support pressure on the tunnel face is less than the soil and water pressure in front of it). A trapezoidal wedge was adopted in front of the tunnel face, and the angle between the balance arch and the tunnel face was assumed to be 50° [37]. The contact surface between the sliding soil and the horizontal unloading arch (the side of the original wedge model and the trapezoidal wedge) was assumed to be unstressed, as shown in Figure 3.

Based on the above assumptions, we have the following:

$$\mathrm{P}={\displaystyle \frac{\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\alpha }-\mathrm{t}\mathrm{a}\mathrm{n}\mathsf{\phi }\mathrm{c}\mathrm{o}\mathrm{s}\mathsf{\alpha }}{\mathrm{c}\mathrm{o}\mathrm{s}\mathsf{\alpha }+\mathrm{t}\mathrm{a}\mathrm{n}\mathsf{\phi }\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\alpha }}}\left({\mathrm{P}}_{\mathrm{n}}+\mathrm{G}\right)-{\displaystyle \frac{\mathrm{c}{\mathrm{B}}^2\left(\tan \mathsf{\beta }-1\right)}{\sin \mathsf{\alpha }\tan \mathsf{\beta }}}\left({\displaystyle \frac{\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\alpha }-\mathrm{t}\mathrm{a}\mathrm{n}\mathsf{\phi }\cos \mathsf{\alpha }\mathsf{\alpha }}{\cos \mathsf{\alpha }+\tan \mathsf{\phi }\sin \mathsf{\alpha }}}\sin \mathsf{\alpha }+\cos \mathsf{\alpha }\right)+{\mathrm{P}}_{\mathrm{W}}$$

(6)

According to the overall force balance of the trapezoidal wedge, the upper limit of the support pressure (maximum support pressure, ${\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$) on the tunnel face can be obtained as follows:

$${\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}=\mathsf{\epsilon }{\mathsf{\gamma }}_{\mathrm{s}}{\mathrm{B}}^2\left({\mathrm{H}}_{\mathrm{s}}\cot \mathsf{\alpha }+{\displaystyle \frac{\mathrm{B}}{2\tan \mathsf{\phi }}}\right)+{\mathrm{B}}^2\left({\mathrm{H}}_{\mathrm{u}}+0.5\mathrm{D}\right){\mathsf{\gamma }}_{\mathrm{w}}-{\displaystyle \frac{\mathrm{c}{\mathrm{B}}^2\left(\tan \mathsf{\beta }-1\right)}{\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\alpha }\tan \mathsf{\beta }}}\left(\mathsf{\epsilon sin}\mathsf{\alpha }+\cos \mathsf{\alpha }\right)$$

(7)

2.3. Pressure Calculation and Analysis of Optimal Support Pressure Value

The method utilized in this study is the limit equilibrium method, which requires high conditions for the prototype. Therefore, the conditions of the model are simplified to be relatively simple. Mud–water-balanced pipe jacking uses a balancing medium, such as mud and water, to obtain a certain pressure in the working silo and thereby balance out the pressure of the underground water and soil layer in front of the tunnel face. The sum of soil and water pressures in the soil above the front of the pipe-jacking machine was assumed to be ${\mathrm{P}}_1$. The corresponding tunnel-face support pressure was taken as ${\mathrm{P}}_2$, and the sum of soil and water pressures in the bottom soil at the front of the pipe-jacking machine was assumed to be ${\mathrm{P}}_3$. The corresponding tunnel-face support pressure was ${\mathrm{P}}_4$, as illustrated in Figure 4. Theoretically, ${\mathrm{P}}_1$ = ${\mathrm{P}}_2$ and ${\mathrm{P}}_3$ = ${\mathrm{P}}_4$ when the mud–water-balanced jacking tunnel face is in equilibrium.

In order to simplify the analysis and to highlight the main contradictions of the problem (in the actual construction process), the following assumptions were made: (1) the tunnel-face support pressure and resistance are trapezoidal in distribution, and the point of action is located at the center of gravity of the trapezoidal area; (2) the stratum in front of the pipe-jacking tunnel face is a semi-infinite body of homogeneous isotropy; and (3) the influence of the top pipe digging speed and friction between the cutter and the tunnel face are not considered.

Based on the above assumptions, the tunnel-face support pressure calculation model is constructed, as shown in Figure 2b. The static soil pressure at the point of action of the ground pressure at the tunnel face is used as a datum. Soil and water sub-calculations are adopted, and Equations (8) and (9) are obtained to calculate the optimal value of the tunnel-face support pressure.

$${\mathrm{P}}_{\mathrm{o}1}=\left[{\mathrm{K}}_0{\mathsf{\gamma }}_s\left({\mathrm{H}}_{\mathrm{a}}+{\mathrm{H}}_{\mathrm{w}}\right)+{\mathsf{\gamma }}_{\mathrm{w}}{\mathrm{H}}_{\mathrm{w}}\right]{\mathsf{\pi }\mathrm{D}}^2/4$$

(8)

$${\mathrm{P}}_{\mathrm{o}2}=\left[{\mathrm{K}}_0{\mathsf{\gamma }}_s\left({\mathrm{H}}_{\mathrm{b}}+{\mathrm{H}}_{\mathrm{c}}\right)+{\mathsf{\gamma }}_{\mathrm{w}}{\mathrm{H}}_{\mathrm{r}}\right]{\mathsf{\pi }\mathrm{D}}^2/4$$

(9)

Here, ${\mathrm{P}}_{\mathrm{o}1}$ is the optimal support pressure for the tunnel face in the area without river water influence, kPa; ${\mathrm{P}}_{\mathrm{o}2}$ is the optimal support pressure for the tunnel face in the area with river water influence, kPa; ${\mathrm{K}}_0$ is the static earth pressure coefficient; ${\mathsf{\gamma }}_{\mathrm{w}}$ is the volumetric weight of water, kN/m³; ${\mathrm{H}}_{\mathrm{a}}$ is the distance from the underground water level to the ground surface, m; ${\mathrm{H}}_{\mathrm{b}}$ is the pipe-jacking burial depth, m; ${\mathrm{H}}_{\mathrm{c}}$ is the distance from the point of ground-pressure action on the pipe-jacking tunnel face to the top axis of the digging machine (which took the value of 2/3D), m; ${\mathrm{H}}_{\mathrm{r}}$ is the river depth, m; and ${\mathrm{H}}_{\mathrm{w}}$ is the distance from the point of soil pressure action to the underground water level, m.

3. Numerical Simulation and Analysis of Support Pressure on Tunnel Face

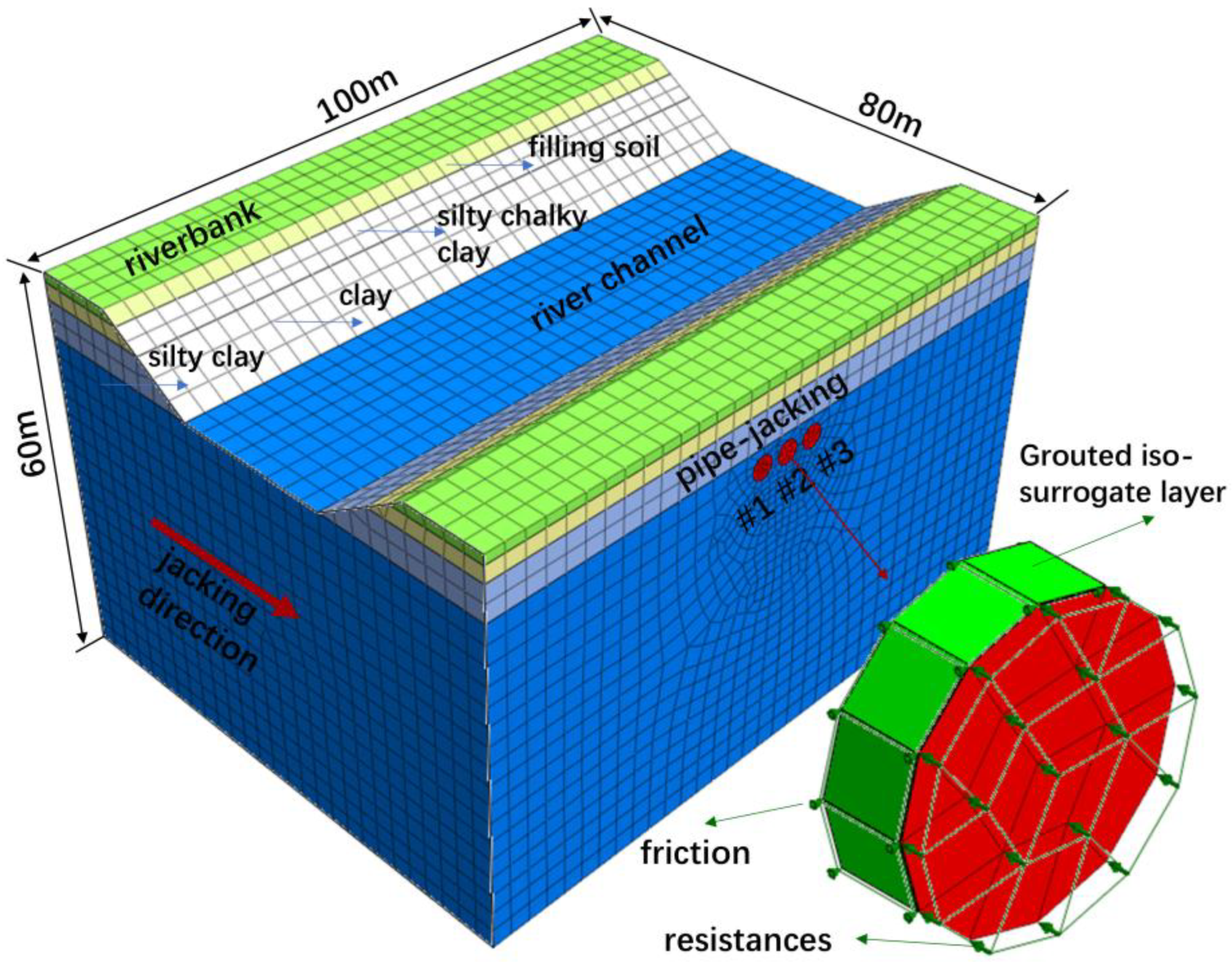
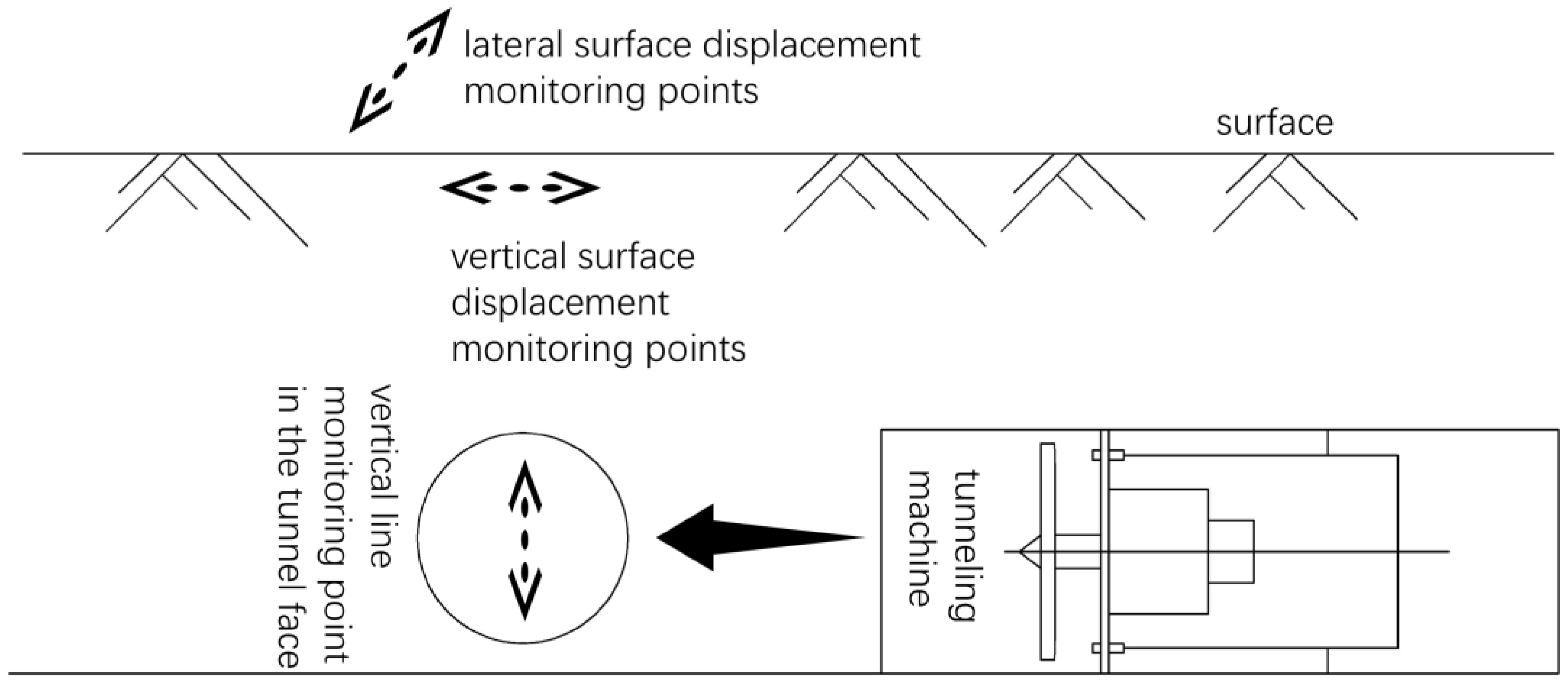
3.1. Simulation Model and Basic Assumptions

The numerical simulations were carried out in close connection with the actual situation of the Y25-Y26 pipe-jacking project. The derivation of mathematical expressions and numerical simulations of tunnel-face support pressures explored in this study were all in the context of the same project. The length, width, and height of the numerical simulation model were taken as 100 m × 80 m × 60 m, as shown in Figure 5. The bottom surface of the model was constrained with vertical and horizontal displacements, while the top surface was free. The pipe jacking was constructed using three circular reinforced concrete pipes with an internal diameter of 3.0 m and an external diameter of 3.6 m. The spacing between neighboring pipes was 2.8 m, and the length of the pipe-jacking excavation was 80 m. The reinforced concrete pipe sheet was considered an elastic material with a thickness of 0.3 m. The pipe-jacking machine casing was made of steel, which was also considered to be an elastic material. The values of the calculated parameters were taken as shown in

Table 1. Pipe-jacking sheet parameters.

Material Type	Elastic Modulus E (MPa)	Poisson’s Ratio $\mathit{\mu }$	Volumetric Weight γ (kN/m3)	Thickness (m)
Reinforced concrete	28,000	0.2	23	0.3
Digging machine housings	206,000	0.3	78.5	0.06

. The material properties of the strata and pipe joints were described using 3D cell entities. Partial components were meshed by means of geometric partitioning and then expanded with a 2D mesh. The pipe perimeter grid was 0.5 m. The model boundary calculation cell grid was set to 1.0 m in both the longitudinal and transverse directions. The pipe-jacking machine shield shell was modeled elastically, and its material properties were described using 2D plate cells, which were meshed by analyzing the outer surface of the iso-surrogate layer. The values of the stratigraphic parameters are taken as shown in

Table 2. Stratigraphic physical and mechanical parameters.

Parameter Type	Elastic Modulus E (MPa)	Poisson’s Ratio $\mathit{\mu }$	Cohesive Force c (kPa)	Angle of Internal Friction φ (°)	Volumetric Weight γ (kN/m3)	Thickness (m)
Filling soil	8.0	0.27	10	10.0	18.00	0.5~1.5
Silty chalky clay	3.2	0.27	6.2	5.8	17.52	1.2~2.7
Clay	12.0	0.25	70	16.9	19.22	5.9~7.5
Silty clay	11.3	0.25	40	15.5	19.22	4.8~6.0

, which comes from the survey report of the background project. In the geotechnical laboratory of the survey company, soil tests for the moisture content, liquid–plastic limit, straight shear, compression, and free swell and a uniaxial compression test of rock were completed. The coupling between the soil entities and the jacked tunnel entities was investigated using Boolean operations. The mesh size of the soil body was 5 m and the mesh size of the pipe jacking tunnel was 1 m. The numerical calculation process was divided into four stages, which were initial stress field equilibrium, pipe excavation, pipe jacking advancement, and pipe sheet application. At first, the initial boundary conditions and self-weight of the model were imposed. The initial displacement was zeroed out to start the analysis of the initial stress field. Secondly, a uniform digging force was applied to the tunnel face. The pipe jacking tunnel was passivated to simulate excavated soil. Then, the pipe jacking machine casing was activated and the friction force was activated at the same time. The casing of the pipe-jacking machine was blunted, the pipes were jacked, and the pipe sheets were applied. Finally, the soil of the next pipe section was excavated. The pipe-jacking machine casing was added and the excavation forces and friction forces exerted by the previous pipe section were blunted.

For pipe-jacking projects crossing a river, the grouting pressure, resistance, and friction between the pipe and soil should be considered. In order to highlight the main issues and reduce the amount of tedious work, we chose to simplify the conditions. Pipe jacking forms a boundary inside the formation and changes the original stress field of the formation, which leads to a series of complex physical and mechanical effects in the formation around the construction area. This is closely related not only to the physical properties of the formation but also to the construction method, construction process, and related construction parameters. When using numerical software for three-dimensional calculations of multi-line parallel pipe jacking, it is difficult to take all the factors of pipe jacking into account to completely and realistically reflect the construction process. Therefore, the mechanical behavior related to pipe jacking was appropriately simplified in our numerical simulations. This not only allowed the simulations to meet the requirements of the software for calculation but also led the numerical calculation results to better reflect the construction process and reveal the regularity of the construction’s impact. Based on the actual situation of the examined project, the numerical simulation included the following assumptions:

(1)

Each stratum was assumed to be ideally elasticoplasticity. The numerical simulation model only considered the soil settlement caused by self-weight and the pipe-jacking process and ignored the effects of underground water, as well as consolidation settlement of the soil.

(2)

The soil pressure was considered a circular distributed load acting on the tunnel face. It was assumed that the gap grouting units around the perimeter of the pipe were distributed in equal thicknesses along the radial direction of the pipe sheet (the modulus of elasticity was taken as 1/50 of the in situ stratigraphic unit, and the thickness of the grouted iso-surrogate layer was 2 cm). Friction between the pipe and soil was achieved by setting a coefficient of friction on the contact surface (the friction between the pipe and soil was a certain value and was uniformly distributed along the pipe-jacking direction). The model ignored the effect of grouting pressure on the construction process and the pipe joints. The jacking pressure was taken from the lateral static soil pressure at the center point of the pipe’s tunnel face, as 88.5 kPa. The friction between the pipe and soil was taken as 3.5 kPa.

The previous study [38] by our team used strength reduction and numerical simulation methods. This study analyzed in detail the stability of surrounding strata unloaded by pipe jacking under different water depths, overburden thicknesses, and clearances. The surrounding strata were divided into the mutual-influence non-self-stability zone, the mutual-influence self-stability zone, and the no-mutual-influence self-stability zone. The assumptions for the numerical simulation and the specific simulated construction conditions in this study are consistent with those in [38], so they are not described here in detail.

3.2. Simulation Conditions and Implementation Steps

Numerical simulations were directed at analyzing the river-bottom cross-section. In order to investigate the effect of the overburden thickness on the support pressure, the river-bottom section conditions were categorized into three conditions: an overburden thickness of 3 m was considered in Case Ⅰ, an overburden thickness of 2 m was considered in Case Ⅱ, and an overburden thickness of 1 m was considered in Case Ⅲ. The theoretical values of the tunnel-face support pressures were applied, as shown in

Table 3. Calculation cases.

Case	Ⅰ	Ⅱ	Ⅲ
Thickness of overburden (m)	3.00	2.00	1.00
Theoretical value of support pressure (kPa)	88.5	74.3	60.0

.

To explore the variation characteristics of the support pressure in the tunnel face, the support pressure ratio coefficient $\mathsf{\lambda }$ of the tunnel face was adopted, as demonstrated in Equation (10).

$$\mathsf{\lambda }={\displaystyle \frac{{\mathsf{\sigma }}_{\mathrm{s}}}{{\mathsf{\sigma }}_0}}$$

(10)

Here, $\mathsf{\lambda }$ is the support pressure ratio at the pipe-jacking tunnel face; ${\mathsf{\sigma }}_{\mathrm{s}}$ is the support pressure at the center point of the pipe-jacking tunnel face, kPa; and ${\mathsf{\sigma }}_0$ is the soil and water pressure at the center point of the pipe-jacking tunnel face, kPa.

Displacement monitoring points were arranged on the center vertical line of the tunnel face and on the ground surface along lateral and vertical lines, as depicted in Figure 6.

Mud–water-balancing pipe construction is a step-by-step process. To simulate dynamic construction that matches reality, step-by-step excavation was used. The effect of the jacking force on the disturbance of the soil in front of the tunnel face was considered. The numerical simulation calculation process was as follows:

(1)

The basic numerical model was established. Material properties were assigned, and corresponding displacement boundary conditions were imposed. Ground stress equilibrium calculations were performed under initial stress conditions that were designed to simulate the initial ground stress state.

(2)

Support pressure equal to the resistance applied in front of the tunnel face was set. The next step was to simulate the disturbance caused by the jacking to the strata ahead until a steady state was reached.

(3)

In actual construction, pipe jacking excavates to the bottom of the river channel. The soil is removed, and the pipe support structure is activated. At the same time, an excavation process can be completed by setting up a support pressure applied to the tunnel face.

(4)

The overall deformation of the tunnel face and the displacement changes at the corresponding monitoring points were observed and recorded.

(5)

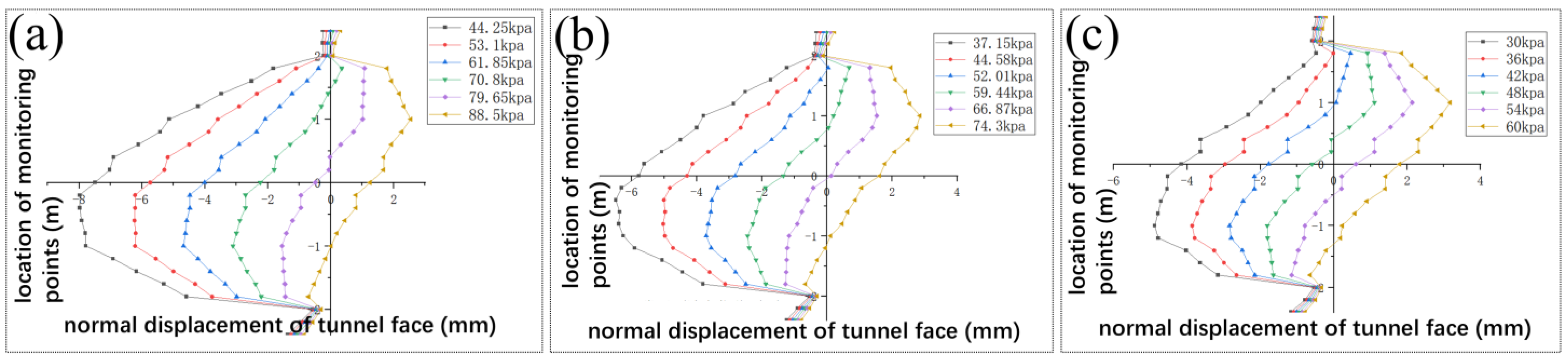
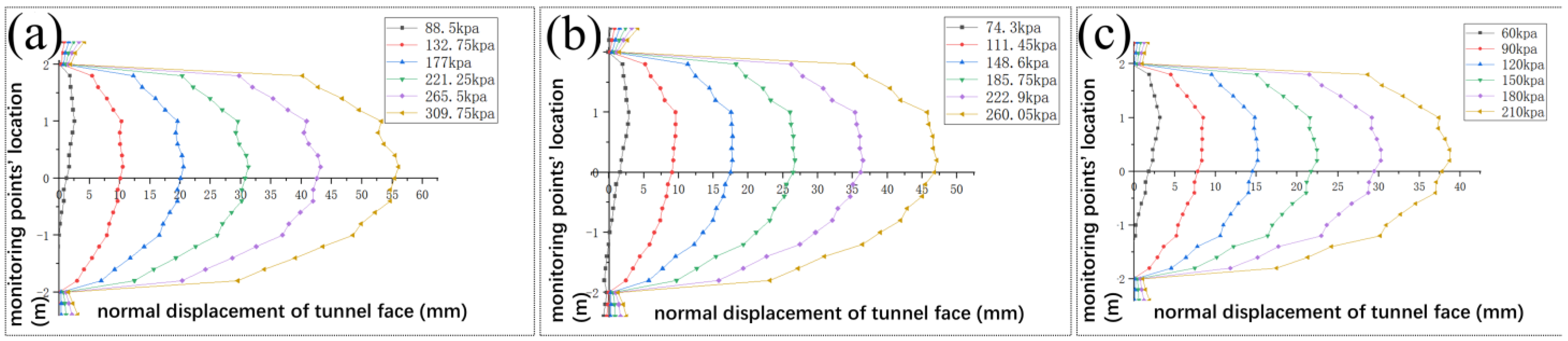
According to the support pressure ratio $\mathsf{\lambda }$, the magnitude of the mud–water pressure applied at the center point of the tunnel face was altered. Re-excavation calculations were carried out, and the overall deformation of the tunnel face, as well as the displacement changes at the corresponding monitoring points, were observed and recorded.

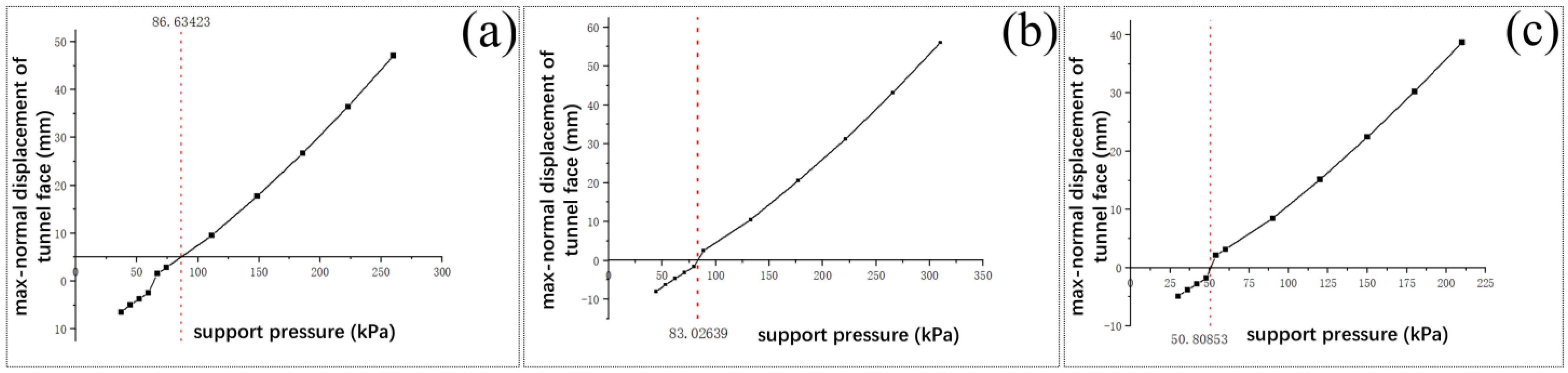
3.3. Analysis of Calculation Results

To investigate the effect of overburden thickness on the tunnel-face support pressure under a river, the support ratio $\mathsf{\lambda }$ was taken as 0.5, 0.6, 0.7 0.8, 0.9, 1.0, 1.5, 2.0, 2.5, 3.0, and 3.5. The 11 working conditions are shown in

Table 4. Support pressure values for different support ratios.

Support Ratio λ		0.5	0.6	0.7	0.8	0.9	1.0	1.5	2.0	2.5	3.0	3.5
Support pressure/kPa	${\mathrm{H}}_s=3 \mathrm{m}$	44.25	53.10	61.85	70.80	79.65	88.50	132.75	177.00	221.25	265.50	309.75
	${\mathrm{H}}_s=2 \mathrm{m}$	37.15	44.58	52.01	59.44	66.87	74.30	111.45	148.6	185.75	222.9	260.05
	${\mathrm{H}}_s=1 \mathrm{m}$	30	36	42	48	54	60	90	120	150	180	210

.

As shown in Figure 7, when the river overburden is 3 m, the applied pressure obtained from the calculation of the theoretical tunnel-face support pressure decreases, and the normal displacement of the tunnel face gradually increases. When $\mathsf{\lambda }$ = 1.0~0.9, the tunnel face is slightly concave towards the soil. The displacement change is not significant and could be considered to satisfy the equilibrium stabilization requirements. As the support pressure continues to decrease to the active soil pressure (as $\mathsf{\lambda }$ changes from 0.9 to 0.6), the tunnel face displacement shows an approximately linear increasing trend with decreasing support pressure. The tunnel face gradually bulges towards the digging machine, and the surrounding soil slips and fails. When the river channel overburden is 2 m or 1 m, the trend is the same as when the river channel overburden is 3 m. However, as the thickness of the overburden decreases, the displacement of the soil monitoring points caused by the active support pressure continues to increase. When ${\mathrm{H}}_s$ = 3 m, the maximum normal displacement of the tunnel face is -8 mm; when ${\mathrm{H}}_s$ = 2 m, it is −6.5 mm; and when ${\mathrm{H}}_s$ = 1 m, it is −5 mm.

As shown in Figure 8, when the river overburden is 3 m, the support pressure exerted on the tunnel face increases from static soil pressure to passive soil pressure. The trend is the same when the river channel overburden is 2 m or 1 m. The displacement of the tunnel face increases along the soil direction. However, as the thickness of the overburden decreases, the displacement of the soil monitoring points caused by the passive support pressure continues to decrease. When ${\mathrm{H}}_s$ = 3 m, the maximum normal displacement of the tunnel face is 56 mm; when ${\mathrm{H}}_s$ = 2 m, it is 47 mm; and when ${\mathrm{H}}_s$ = 1 m, it is 38 mm.

As illustrated in Figure 9, according to the calculation results, the ultimate support force is 86.63 kPa when the river channel overburden is 3 m (86.63 kPa multiplied by the area of the tunnel surface πD²/4 is 881.786 kN), 83.03 kPa when the river channel overburden is 2 m (83.03 kPa multiplied by the area of the tunnel surface πD²/4 is 845.142 kN), and 50.81 kPa when the river channel overburden is 1 m (50.81 kPa multiplied by the area of the tunnel surface πD²/4 is 517.183 kN). This support force can control the position of the tunnel face to keep it in the best condition. Junfeng Tang [39] concluded that one factor controlling the settlement deformation of shallow buried jacked pipes was the ground loss rate. The ground loss rate has a significant effect on the variation in maximum deformation values. The effect of the ground loss rate becomes smaller as the depth of the jacking pipe increases. This study focuses on the effect of support pressure on the deformation and stability of the pipes. Based on the above results, it can be seen that as the thickness of the channel overburden decreases, the support force of the excavation surface required to reach the optimal stabilization state also decreases. From Figure 9, it can be seen that the optimal support force is in the interval of $\mathsf{\lambda }$ = 1.0~1.5 when ${\mathrm{H}}_s$ = 3 m, in the interval of $\mathsf{\lambda }$ = 0.9~1.0 when ${\mathrm{H}}_s$ = 2 m, and in the interval of $\mathsf{\lambda }$ = 0.8~0.9 when ${\mathrm{H}}_s$ = 1 m. This indicates that when the overburden thickness is small, the support pressure needs to be set at a reduced support ratio; conversely, the support ratio needs to be increased when the overburden thickness is large.

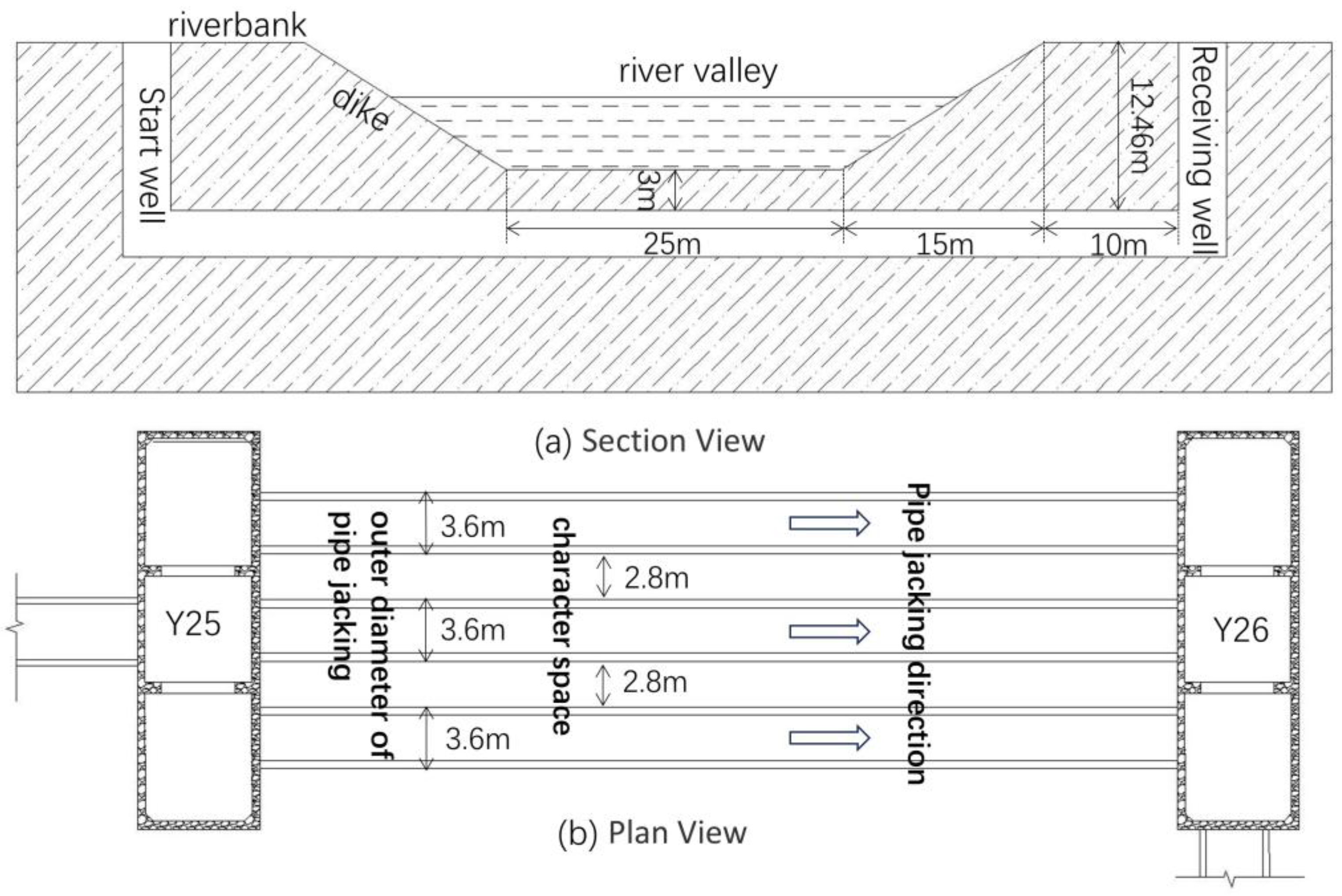
4. Engineering Case Study

4.1. Engineering Background

The Y25-Y26 pipe-jacking project across the Chu River channel is located in Shuangdun Town, Changfeng County, Hefei City, Anhui Province. The project site belongs to the Jianghuai undulating plain landform, with a micro-landform of hills and valleys. The geotectonic location of the region belongs to the southern edge of the North China Plateau, and the secondary tectonic unit belongs to the Hefei Basin. The stratigraphic distribution from top to bottom is as follows: filling soil, 0.5 to 1.5 m thick; silty chalky clay, 1.2 to 2.7 m thick; clay, 5.9 to 7.5 m thick; silty clay, 4.8 to 6.0 m thick; strongly weathered mudstone, 1.7 to 2.6 m thick. The physical and mechanical parameters of each stratigraphic layer are shown in Table 2.

The Y25-Y26 project crossing the Chu River channel adopted mud–water-balanced mechanical pipe jacking. The pipe jacking crossed the stratum of silty clay, and the thickness of the pipe-jacking cover layer was 3.0 m. The width of the river valley in the section where the pipeline crosses is 55 m, the width of the river bed is 25 m, the height of the river bank is 9.46 m, and the average depth of the river water in the dry season is about 3.0 m. The pipe jacking was composed of three circular reinforced concrete pipes with an internal diameter of 3.0 m and an external diameter of 3.6 m. The sandwich width of adjacent pipes was 2.8 m. The project had remarkable features such as high environmental requirements, a small overburden thickness, and a large pipe diameter. Controlling the stability of the pipe-jacking tunnel surface was the priority of engineering control. Section and plan views of the place where the pipe jacking crosses the river are shown in Figure 10.

4.2. Comparative Analysis and Discussion of Engineering Effects

Considering the Y25-Y26 pipe-jacking project crossing the Chu River channel in Hefei North City, and according to the theoretical formulas (5) and (7)–(9), the upper limit value P_max, lower limit value P_min, and optimal value P_o of the tunnel-face support pressure at different jacking distances were calculated, as shown in

Table 5. Calculation of upper limit, lower limit, and optimal values.

Jacking Distances (m)	Upper Limit Value Pmax (kN)	Lower Limit Value Pmin (kN)	Optimal Value Po (kN)
1–10	4868.249	2230.598	3098.977
11	4777.464	2158.328	3012.564
12	4686.679	2086.059	2926.288
13	4596.038	2013.904	2839.876
14	4505.253	1941.634	2753.463
15	4394.509	1849.406	2672.566
16	4222.220	1695.603	2608.338
17	4049.658	1541.555	2544.110
18	3877.368	1387.752	2479.984
19	3704.806	1233.705	2415.755
20	3532.243	1079.658	2351.527
21	3359.954	925.855	1133.573
22	3187.391	771.807	1111.388
23	3014.829	617.760	1089.204
24	2842.540	463.957	1067.055
25–50	2669.977	309.910	1044.870

.

Table 6. Background project measurements.

Jacking Distances (m)	Jacking Force (kN)	Measured Value P′ (kN)	Jacking Distances (m)	Jacking Force (kN)	Measured Value P′ (kN)
2	3000	2639	41	6000	1926
4	4000	3278	43	6000	1819
6	4000	2917	45	7000	2712
8	4000	2556	47	7000	2605
10	4000	2195	49	7000	2498
12	4000	1834	51	7000	2391
14	5000	2509	53	7000	2284
16	5000	2242	55	7000	2137
18	5000	2036	57	8000	2930
20	5000	1889	59	8000	2264
22	5000	1782	61	8000	2338
24	6000	2675	63	9000	2977
26	6000	2568	65	9000	2616
28	6000	2461	67	9000	2255
30	6000	2354	69	10,000	2894
32	6000	2247	71	11,000	3533
35	6000	2140	73	11,000	3172
38	6000	2033	75	10,000	2811

presents measured values of the tunnel-face support pressure, obtained by means of testing during the project’s jacking process. Since the upper limit, lower limit, and optimal values of support pressure on the tunnel face during pipe jacking for jacking distances from 50 m to 75 m were the same as those for jacking distances from 25 m to 1 m; they are not shown in detail in Table 5. For a more direct and graphic depiction of the variation in the different support pressure values at different jacking distances, we created a simple model of the project to produce diagrams corresponding to Table 5 and Table 6, as shown in Figure 11.

In Figure 11, according to the principle of optimal value calculation, the jacking area was divided into a non-river impact area (0–20.24 m and 54.76–75 m) and a river impact area (20.24–54.76 m). The underground water level was −3 m from the surface of the riverbank. The construction stratum was located in a silty clay layer, and ${\mathrm{K}}_0$ was the static soil pressure coefficient, taken as 0.7. The heights described by H_a, H_b, H_c, H_r, H_s, H_u, and H_w in the above equation are also given in the upper part of Figure 11. The dimension of the simple model of the project in the upper half of Figure 11 was kept the same as the jacking length in the bottom half of the figure. The bottom half of Figure 11 describes the upper limit value P_max, the lower limit value P_min, the optimal value P_o, and the measured value P′ of the support pressure on the tunnel face for different jacking distances. A partial enlargement of the optimum value for jacking distances from 20.24 m to 25 m is also given.

The change rules for the upper limit value P_max, lower limit value P_min, and optimal value P_o of the tunnel-face support pressure were basically the same: At jacking distances from 0 m to 10 m (non-river impact area), the support pressure values were constant at 4868.249 kN, 2230.598 kN, and 3098.977 kN, respectively. The support pressure decreased for jacking distances from 10 m to 25 m. At jacking distances from 25 m to 50 m (river impact area), the support pressure values were also constant, at 2669.977 kN, 309.910 kN, and 1044.870 kN, respectively. However, there were some differences between the three: when the jacking distance exceeded the intersection of the underground water level line and the dike line, the decrease rates for the upper limit value P_max and lower limit value P_min increased, while the optimal value P_o did not change significantly. When the jacking distance was greater than 20.24 m (moving from the non-river impact area to the river impact area), the optimal value of the tunnel-face support pressure, P_o, changed abruptly, decreasing from 2351.527 kN to 1133.573 kN, but there was no significant change in the upper limit value P_max or the lower limit value P_min. In the process of pipe jacking at distances from 20.24 m to 25 m, the rate of decrease in the optimal value P_o showed a linearly decreasing law. Each decrement was approximately 22.5 kN, which is reflected in the partial enlargement in the upper left corner of the bottom half of the graph in Figure 11. The overburden thickness was 3 m at jacking distances from 25 m to 50 m. In Section 3.3, the numerical simulation allowed us to calculate the ultimate support pressure as 881.786 kN, while the optimal value of support pressure at the tunnel face was 1044.87 kN. These results are relatively similar. It can be seen in Figure 11 that the measured value of the tunnel-face support pressure, P′, fluctuated between 1700 kN and 3600 kN. The measured value P′ basically lay between the upper limit value P_max and the lower limit value P_min, and it was most similar to the optimal value P_o in the non-river impact area and to the upper limit value P_max in the river impact area.

In an actual pipe-jacking process, the parameters that need to be considered include the jacking force, peripheral friction, and jacking face resistance, as shown in Figure 12. Firstly, the jacking force exerted by the jacking machine should not be varied frequently over short distances and needs to be kept constant. It is difficult to achieve a continuous change in the applied jacking force over a short period of time. Secondly, if the jacking force is kept constant, the peripheral friction becomes larger and the jacking face resistance becomes smaller as the pipe is jacked (a pair of interacting forces, the jacking face resistance and the support force, which is equal in magnitude and opposite in direction to the jacking face resistance). Finally, as the jacking distance increases, the peripheral friction increases and the jacking speed decreases. When the pipe is jacked a certain distance, the jacking force needs to be increased to restore the jacking speed. In this background project, when the jacking distance is from 4 to 12 m, the jacking force is kept constant at 4000 kN. In this process, the peripheral friction gradually becomes larger, and the jacking face resistance becomes smaller (the support force becomes smaller), its value decreases from 3278 kN to 1834 kN. When the jacking distance is from 24 m to 43 m, the jacking force remains unchanged at 6000 kN, but the peripheral friction becomes larger and the jacking face resistance decreases from 2675 kN to 1819 kN. As a result, the measured value P′ fluctuates up and down.

The focus of this paper is on the study of support pressure in the tunnel face. There is not a lot of research work carried out on the construction of three lines of pipe jacking. Clearance $D$ is a very important parameter in pipe-jacking construction projects. With an increase in clear distance $D$, the potential failure pattern of the surrounding strata for three-line parallel pipe-jacking construction unloading transited from double pipe-jacking overall collapse to gradual separation collapse, and the final collapse pattern was consistent with that of single pipe jacking [38]. Wang Yazheng [40] superimposed the settlement deformation caused by additional horizontal thrust, friction of the pipe-jacking machine, friction of the pipe jacking, grouting pressure, and soil loss to obtain the total surface vertical displacement mathematical expression. However, this study derived the corresponding support pressure values from the perspective of different damage modes to ensure that the deformation of the soil would not be serious for pipe-jacking construction. The measured value of the support pressure, P′, on the tunnel face was between the upper limit value P_max and the lower limit value P_min, which ensured that the pipe jacking did not involve active or passive damage. The process would be more economical and reasonable if the measured value of the tunnel-face support pressure P′ was close to the optimum value P_o. During mud–water-balanced pipe jacking, the jacking machine adopts a mud–water balancing device to ensure the balance of water and soil pressure on the tunnel face. Theoretically, if the tunnel-face support pressure and the resistance are kept in equilibrium during the jacking process, the pipe jacking’s frontal propulsion will not cause deformation of the stratum. However, in the actual jacking process, due to the complexity of geological conditions, the limitations of mechanical equipment, and other factors, it is difficult to always maintain a balanced state between the support pressure and resistance of the tunnel face. Therefore, the support pressure at the tunnel face can be set within a reasonable range between the upper limit value P_max and the lower limit value P_min.

5. Conclusions

The support pressure at the tunnel face during mud–water-balanced pipe jacking is an important construction control parameter. If the support pressure is not set properly, it can cause stratum displacement or tunnel-face collapse, which causes high safety hazards in the pipe-jacking process. In this study, the support pressure on the tunnel face during pipe jacking under the conditions of a thin overburden, mud–water balance, and construction crossing a river channel was examined in depth, and the performed analyses allowed the formulation of general conclusions:

(1)

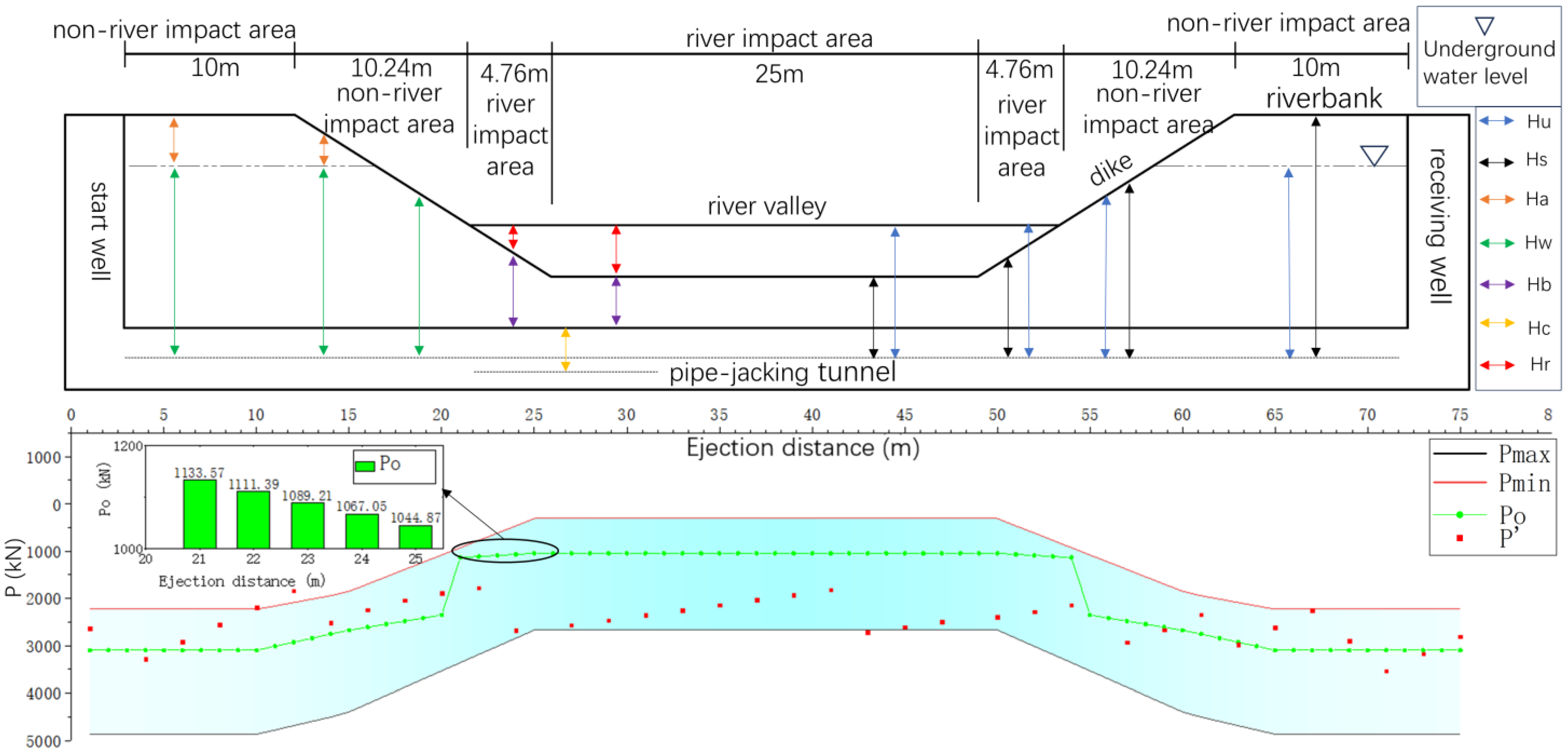
The damage mechanism of the tunnel face during pipe jacking under conditions of a thin overburden, mud–water equilibrium, and construction crossing a river was examined. Mathematical expressions for the lower and upper limit values of the tunnel-face support pressure, P_min and P_max, were derived from analyses of the passive and active damage occurring at the tunnel face of the pipe tunnel, in conjunction with the limit equilibrium method. The jacking area was divided into a non-river impact area and a river impact area. Mathematical expressions for the optimal support pressure values, P_o1 and P_o2, for the two areas were also given separately.

(2)

By studying the Y25-Y26 pipe-jacking project crossing the Chu River in Hefei North City, and through numerical simulation, the displacement and ultimate support pressure of the tunnel face under different river overburdens and different support ratios were discussed. As the thickness of the overburden decreased, the soil monitoring point displacement caused by the active support pressure continued to increase, while the displacement caused by the passive support pressure continued to decrease. When large-diameter pipe jacking crosses a river channel, if the overburden thickness is small, the setting of the support pressure requires a reduced support ratio, while the support ratio needs to be increased if the overburden thickness is large. The optimal support force is in the interval of $\mathsf{\lambda }$ = 1.0~1.5 when ${\mathrm{H}}_s$ = 3 m, in the interval of $\mathsf{\lambda }$ = 0.9~1.0 when ${\mathrm{H}}_s$ = 2 m, and in the interval of $\mathsf{\lambda }$ = 0.8~0.9 when ${\mathrm{H}}_s$ = 1 m.

(3)

For pipe jacking crossing a thin-cover river channel, the theoretically calculated upper limit value P_max, lower limit value P_min, and optimal value P_o and the numerically simulated limit value of the support pressure were 2669.977 kN, 309.910 kN, 1044.870 kN, and 881.786 kN, respectively. The values measured during pipe jacking fluctuated between the upper limit value P_max and the lower limit value P_min. They were more similar to the optimal value P_o in the non-river impact area and more similar to the upper limit value P_max in the river impact area. To overcome the complexity of geological conditions, the limitations of mechanical equipment, and other factors to ensure the stability of the tunnel face without damage, it is necessary to set the tunnel-face support pressure within a reasonable range between the upper limit value P_max and the lower limit value P_min; we suggest adopting the optimal value P_o. The analysis will make it possible in the future to develop longitudinally in pipe-jacking construction. The evolution characteristics of support pressure and damage alarm of a tunnel face under complex conditions should be more greatly explored and tested in practice in combination with artificial intelligence and algorithms.