A Joint Decoherence-Based AOA and TDOA Positioning Approach for Interference Monitoring in Global Navigation Satellite System
Abstract
1. Introduction
- A decoherence-based AOA-solving algorithm is proposed, which effectively addresses the problem that coherent signals cannot be directionally measured and is applicable to narrowband interference.
- A TDOA solving algorithm based on the least squares method is proposed, and the simulation results show that this solving method is better than the maximum likelihood estimation algorithm.
- A joint AOA and TDOA localization algorithm is proposed, and the simulation results show that the joint localization algorithm is better than the single localization algorithm with higher accuracy and better robustness.
2. The Joint Positioning Approach
2.1. Decoherence-Based AOA Positioning Scheme
2.2. Joint TDOA Positioning Program
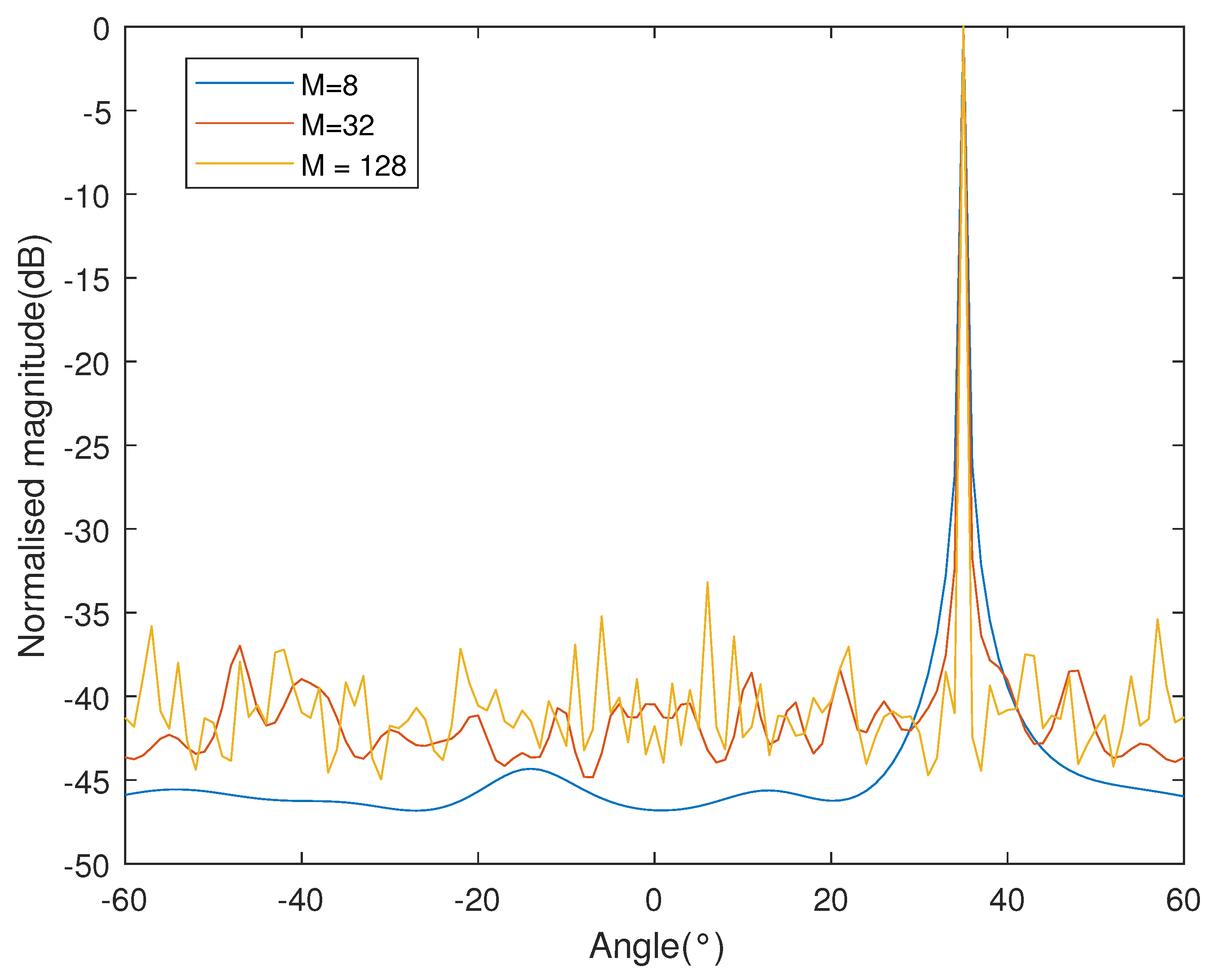
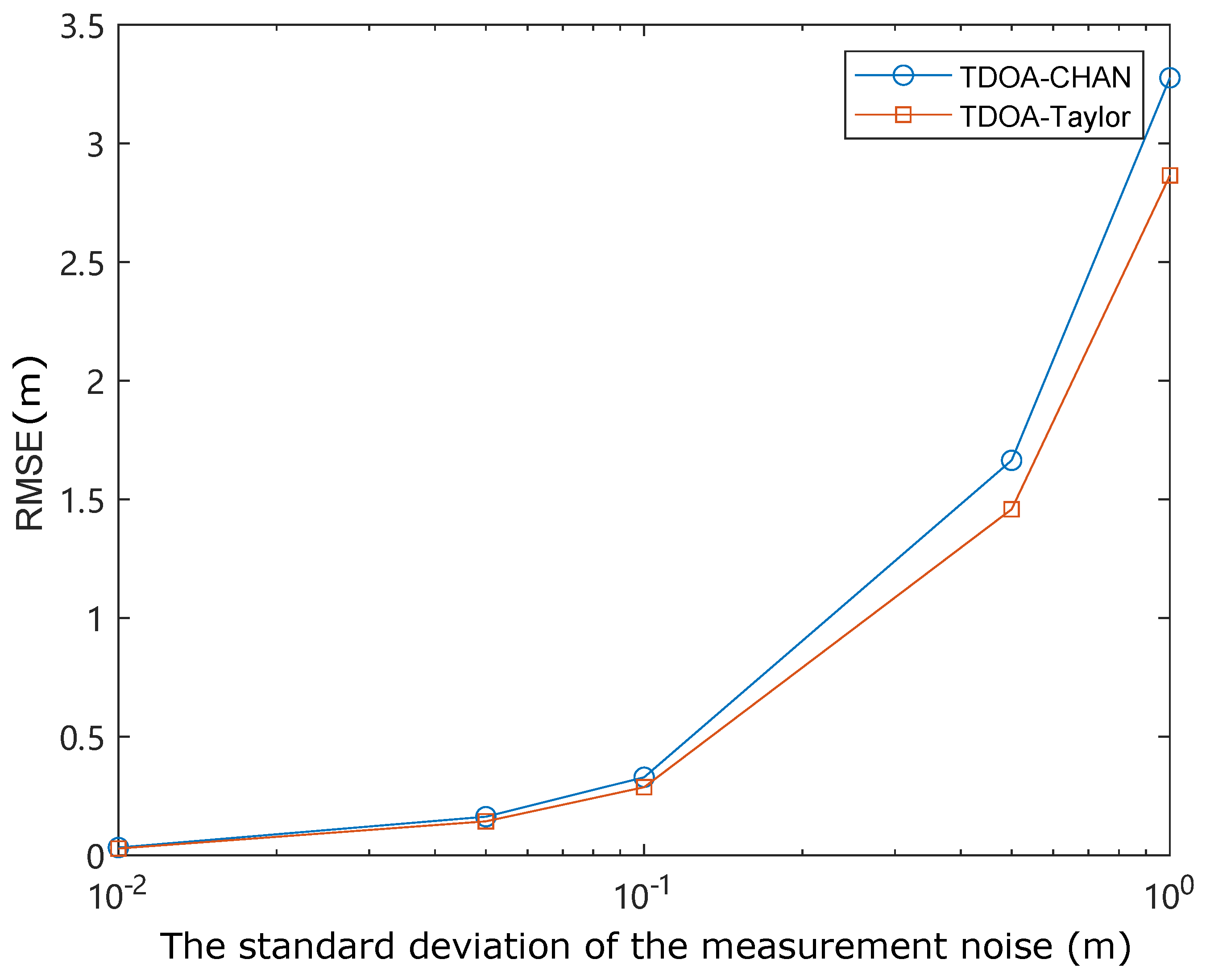
3. Numerical Simulation
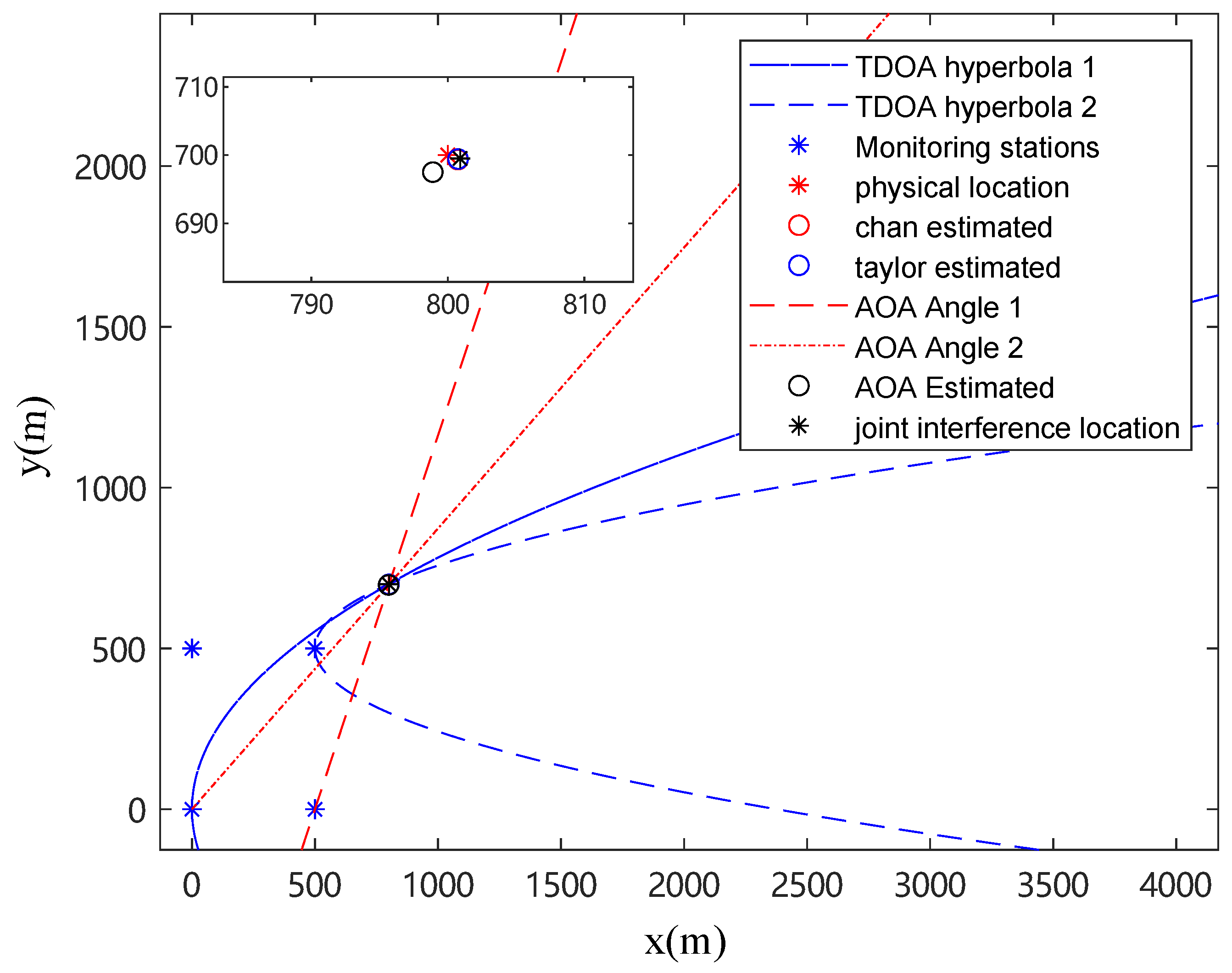
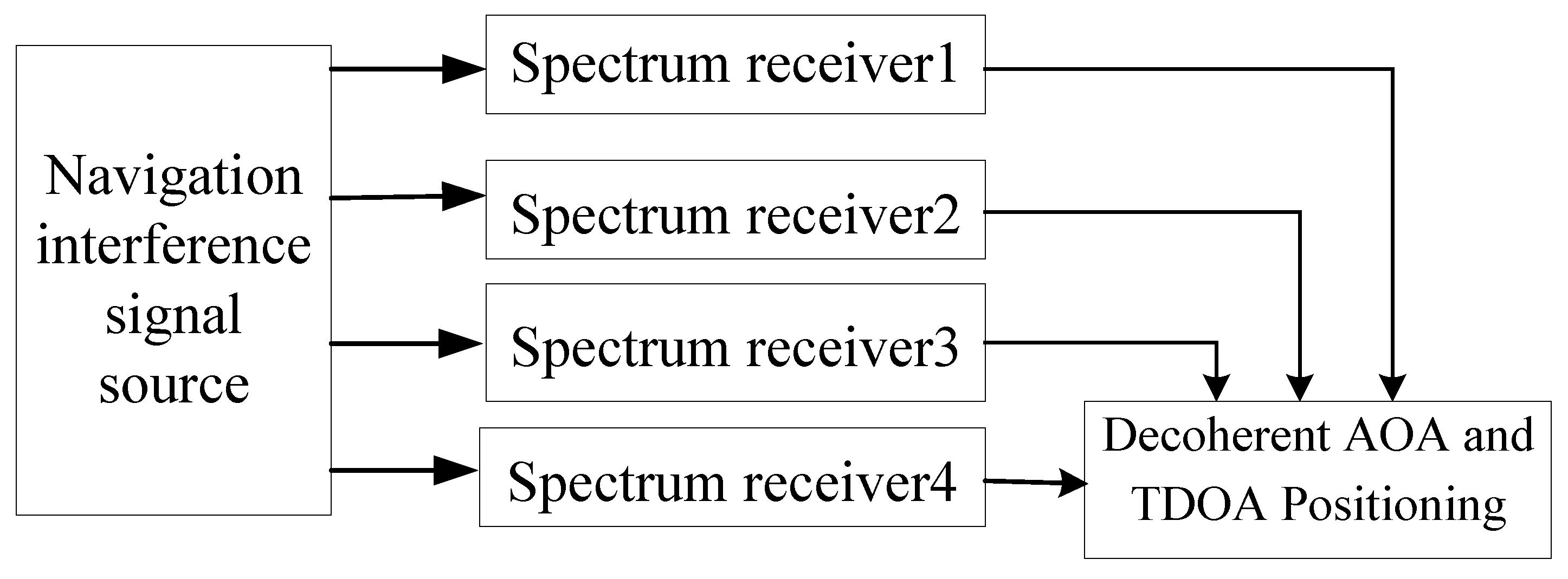
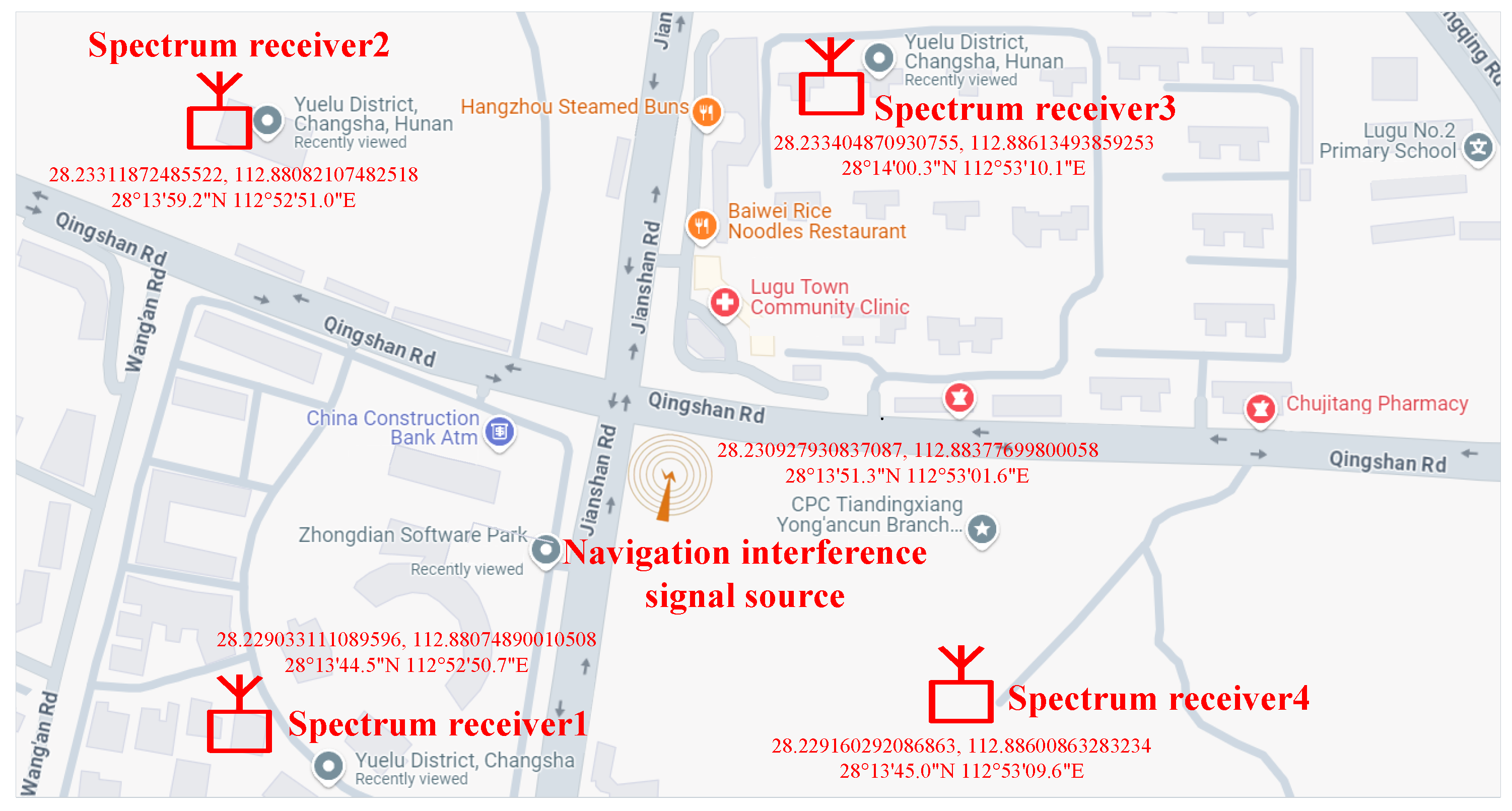
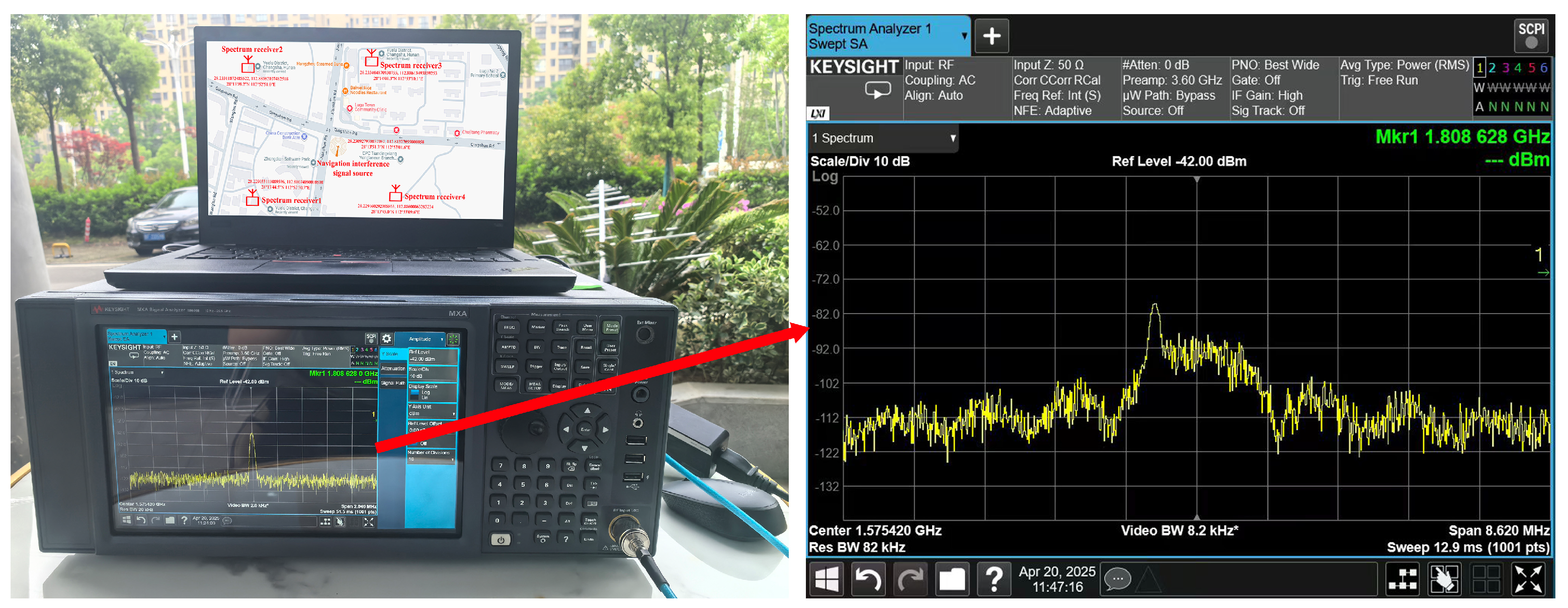
4. Experiment Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kolomijeca, A.; López-Salcedo, J.A.; Lohan, E.-S.; Seco-Granados, G. GNSS applications: Personal safety concerns. In Proceedings of the 2016 International Conference on Localization and GNSS (ICL-GNSS), Barcelona, Spain, 28–30 June 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Fokin, G. Interference Suppression Using Location Aware Beamforming in 5G Ultra-Dense Networks. In Proceedings of the 2020 IEEE Microwave Theory and Techniques in Wireless Communications (MTTW), Riga, Latvia, 1–2 October 2020; pp. 13–17. [Google Scholar] [CrossRef]
- Wendel, J.; Kurzhals, C.; Houdek, M.; Samson, J. An interference monitoring system for GNSS reference stations. In Proceedings of the 2012 15 International Symposium on Antenna Technology and Applied Electromagnetics, Toulouse, France, 25–28 June 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Gamba, M.T.; Falletti, E. Performance Comparison of FLL Adaptive Notch Filters to Counter GNSS Jamming. In Proceedings of the 2019 International Conference on Localization and GNSS (ICL-GNSS), Nuremberg, Germany, 4–6 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Bethi, P.; Pathipati, S.; P, A. GNSS Intentional Interference Mitigation via Average KF Innovation and Pseudo Track Updation. In Proceedings of the 2020 IEEE 17th India Council International Conference (INDICON), New Delhi, India, 10–13 December 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Yu, X.; Tu, L.; Yang, Q.; Yu, M.; Xiao, Z.; Zhu, Y. Hybrid Beamforming in mmWave Massive MIMO for IoV with Dual-Functional Radar Communication. IEEE Trans. Veh. Technol. 2023, 72, 9017–9030. [Google Scholar] [CrossRef]
- Yu, X.; Yang, Q.; Xiao, Z.; Chen, H.; Havyarimana, V.; Han, Z. A Precoding Approach for Dual-Functional Radar-Communication System with One-Bit DACs. IEEE J. Sel. Areas Commun. 2022, 40, 1965–1977. [Google Scholar] [CrossRef]
- Liu, R.; Yang, Z.; Chen, Q.; Liao, G.; Zhen, W. GNSS Multi-Interference Source Centroid Location Based on Clustering Centroid Convergence. IEEE Access 2021, 9, 108452–108465. [Google Scholar] [CrossRef]
- Chang, Y.T. Simulation and Implementation of an Inte-grated TDOA/AOA Monitoring System for Preventing Broadcast Interference. J. Appl. Res. Technol. 2014, 12, 1051–1062. [Google Scholar] [CrossRef]
- An, D.J.; Moon, C.-M.; Lee, J.-H. Derivation of an explicit expression of an approximate location estimate in AOA-based localization. In Proceedings of the 2017 7th IEEE International Symposium on Microwave, Antenna, Propagation, and EMC Technologies (MAPE), Xi’an, China, 24–27 October 2017; pp. 552–555. [Google Scholar] [CrossRef]
- Ding, R.; Qian, Z.-h.; Wang, X. UWB Positioning System Based on Joint TOA and DOA Estimation. J. Electron. Inf. Technol. 2010, 32, 313–317. (In Chinese) [Google Scholar] [CrossRef]
- Shao, S.; Liang, Q.; Deng, K.; Tang, Y. Optimal location of the base station based on measured interference power. In Proceedings of the 2015 IEEE International Wireless Symposium (IWS 2015), Shenzhen, China, 30 March–1 April 2015; pp. 1–3. [Google Scholar] [CrossRef]
- Wang, Y.; Ho, K.C. Unified Near-Field and Far-Field Localization for AOA and Hybrid AOA-TDOA Positionings. IEEE Trans. Wirel. Commun. 2018, 17, 1242–1254. [Google Scholar] [CrossRef]
- Li, Y.-Y.; Qi, G.-Q.; Sheng, A.-D. Performance Metric on the Best Achievable Accuracy for Hybrid TOA/AOA Target Localization. IEEE Commun. Lett. 2018, 22, 1474–1477. [Google Scholar] [CrossRef]
- Qi, H.; Wu, X.; Jia, L. Semidefinite Programming for Unified TDOA-Based Localization Under Unknown Propagation Speed. IEEE Commun. Lett. 2020, 24, 1971–1975. [Google Scholar] [CrossRef]
- Yin, Z.; Zhen, W.; Jin, R.; Lin, Z.; Wang, R.; Che, L. Satellite navigation multi-interference source direction finding and positioning technology and application. Glob. Position. Syst. 2023, 48, 111–116. [Google Scholar]
- Liu, Z.; Wu, J.; Yang, S.; Lu, W. DOA Estimation Method Based on EMD and MUSIC for Mutual Interference in FMCW Automotive Radars. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3504005. [Google Scholar] [CrossRef]
- Dabak, O.C.; Orduyilmaz, A.; Serin, M.; Yildirim, A. Direction finding with music algirithm for ES systems under interference. In Proceedings of the 2018 26th Signal Processing and Communications Applications Conference (SIU), Izmir, Turkey, 2–5 May 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Liu, C.; Yun, J.; Su, J. Direct solution for fixed source location using well-posed TDOA and FDOA measurements. J. Syst. Eng. Electron. 2020, 31, 666–673. [Google Scholar] [CrossRef]
- Ghany, A.A.; Uguen, B.; Lemur, D. A Pre-processing Algorithm Utilizing a Paired CRLB for TDoA Based IoT Positioning. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Shi, W.; Huang, B.; Sun, K. A CRLB Analysis of AoA Estimation Using Bluetooth 5. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; pp. 5158–5162. [Google Scholar] [CrossRef]
- Giacometti, R.; Baussard, A.; Cornu, C.; Khenchaf, A.; Jahan, D.; Quellec, J.-M. Accuracy studies for TDOA-AOA localization of emitters with a single sensor. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Song, P.; Pang, F.; Lu, J. Combined AOA and TDOA Target Localization Method Under Distance-Dependent Noise Model. IEEE Sens. J. 2023, 23, 19444–19456. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Wen, Y.; Liu, Y. A Joint Decoherence-Based AOA and TDOA Positioning Approach for Interference Monitoring in Global Navigation Satellite System. Appl. Sci. 2025, 15, 7050. https://doi.org/10.3390/app15137050
Wang W, Wen Y, Liu Y. A Joint Decoherence-Based AOA and TDOA Positioning Approach for Interference Monitoring in Global Navigation Satellite System. Applied Sciences. 2025; 15(13):7050. https://doi.org/10.3390/app15137050
Chicago/Turabian StyleWang, Wenjian, Yinghong Wen, and Yongxia Liu. 2025. "A Joint Decoherence-Based AOA and TDOA Positioning Approach for Interference Monitoring in Global Navigation Satellite System" Applied Sciences 15, no. 13: 7050. https://doi.org/10.3390/app15137050
APA StyleWang, W., Wen, Y., & Liu, Y. (2025). A Joint Decoherence-Based AOA and TDOA Positioning Approach for Interference Monitoring in Global Navigation Satellite System. Applied Sciences, 15(13), 7050. https://doi.org/10.3390/app15137050





