Mitigating Multicollinearity in Induction Motors Fault Diagnosis Through Hierarchical Clustering-Based Feature Selection
Abstract
1. Introduction
1.1. Vibration-Based Fault Diagnosis
1.2. Current Signature-Based Fault Diagnosis
- Unlike many prior studies that rely on vibration or acoustic signals (as in [1,2,4,9]), the proposed work in this study leverages voltage and current phasor measurements to diagnose faults in IMs. This nonintrusive method eliminates the need for expensive or difficult-to-install sensors while ensuring minimal disruption to ongoing industrial processes.
- Most conventional fault diagnosis methods rely on statistical [28,30,34] or deep feature extraction techniques [7,9,27] applied to vibration or acoustic data for bearing fault detection. In contrast, the proposed approach leverages harmonic-based features extracted from voltage and current phasors. This methodology captures subtle variations that indicate bearing-related faults.
- While hierarchical or clustering-based methods have been used in other domains (e.g., [31,32] use k-means clustering for feature selection, and [33] applies hierarchical clustering in cancer diagnosis), this work is distinct because it directly targets the multicollinearity challenge in IM fault diagnosis, a crucial factor that many existing methods do not explicitly address.
- The practical viability of the developed method is demonstrated via validation on the NI CRIO-9056 platform, confirming its applicability in real-world scenarios. Furthermore, this study provides a rigorous comparative analysis against established feature selection techniques (such as random forest feature selection) and evaluates performance using three high-performance estimators (RFC, ANN, and SVC). This comprehensive evaluation underscores that the AHC-based approach not only improves classification performance but also mitigates the overfitting risk associated with multicollinearity, which is a gap in the current literature.
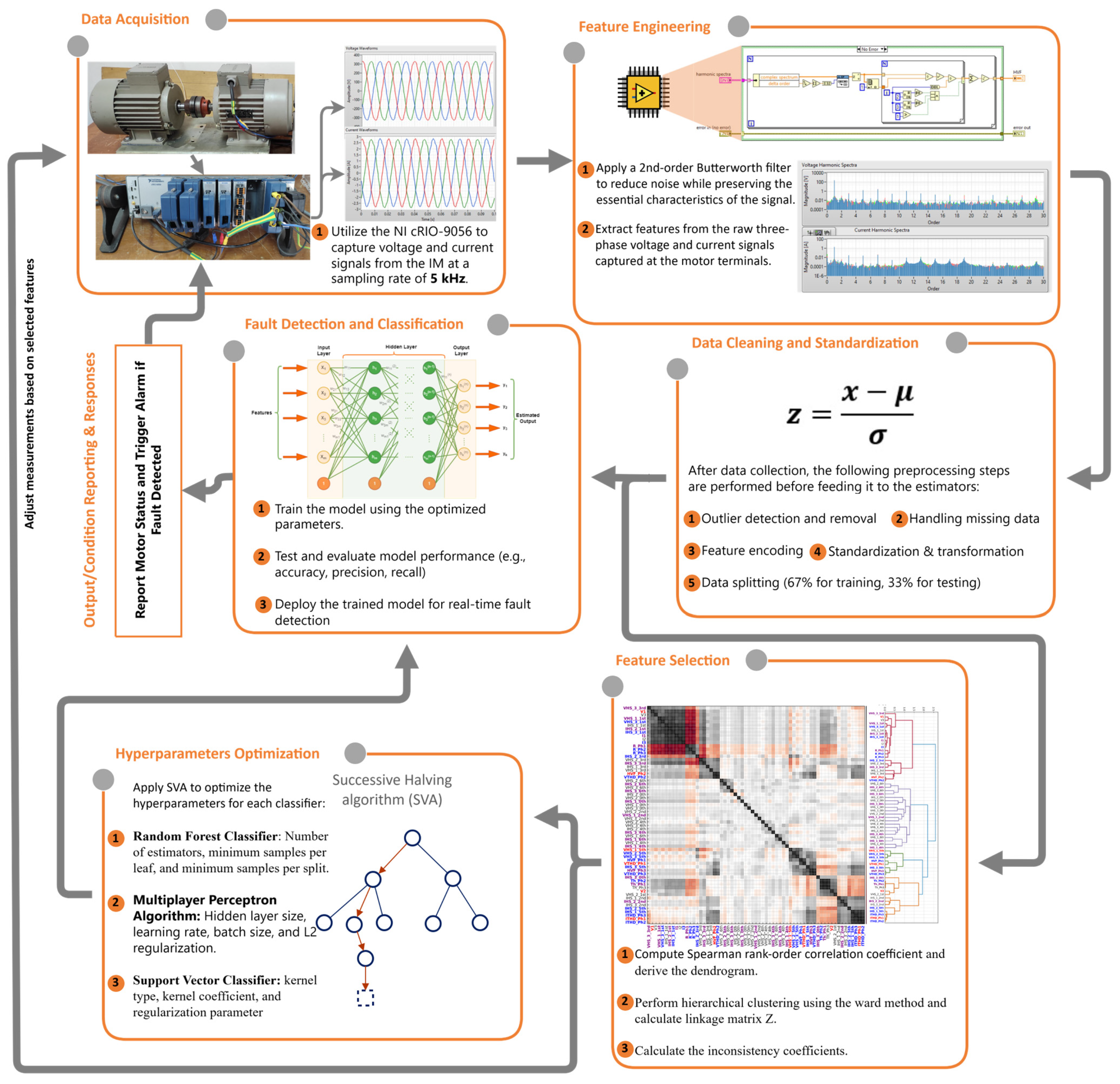
2. Feature Engineering
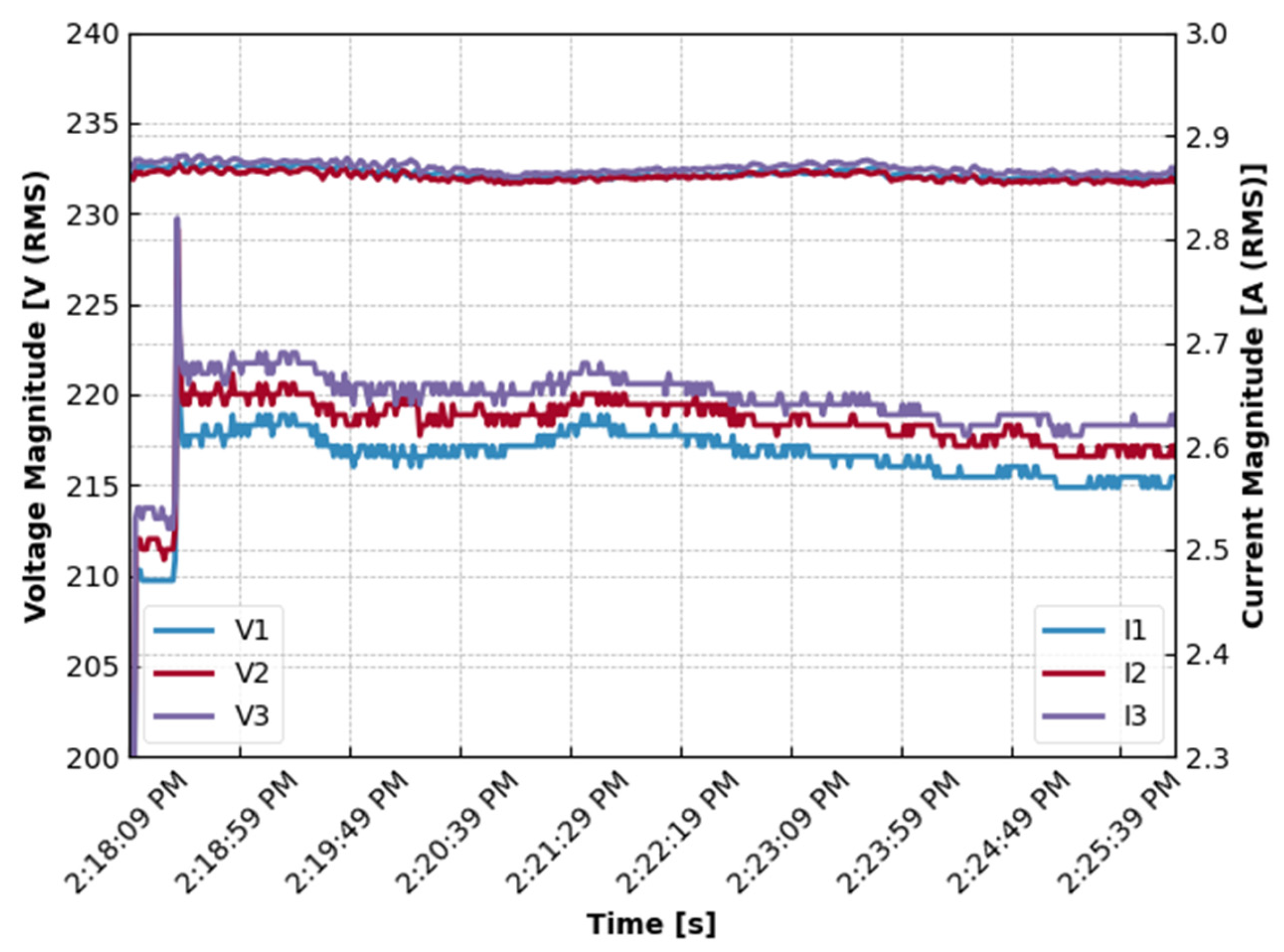
2.1. FFT Analysis of Voltage and Current Signals
2.2. Total Harmonic Distortion
2.3. Harmonic Voltage Factor
3. Feature Selection Using Agglomerative Hierarchical Clustering
4. Machine Learning Algorithms
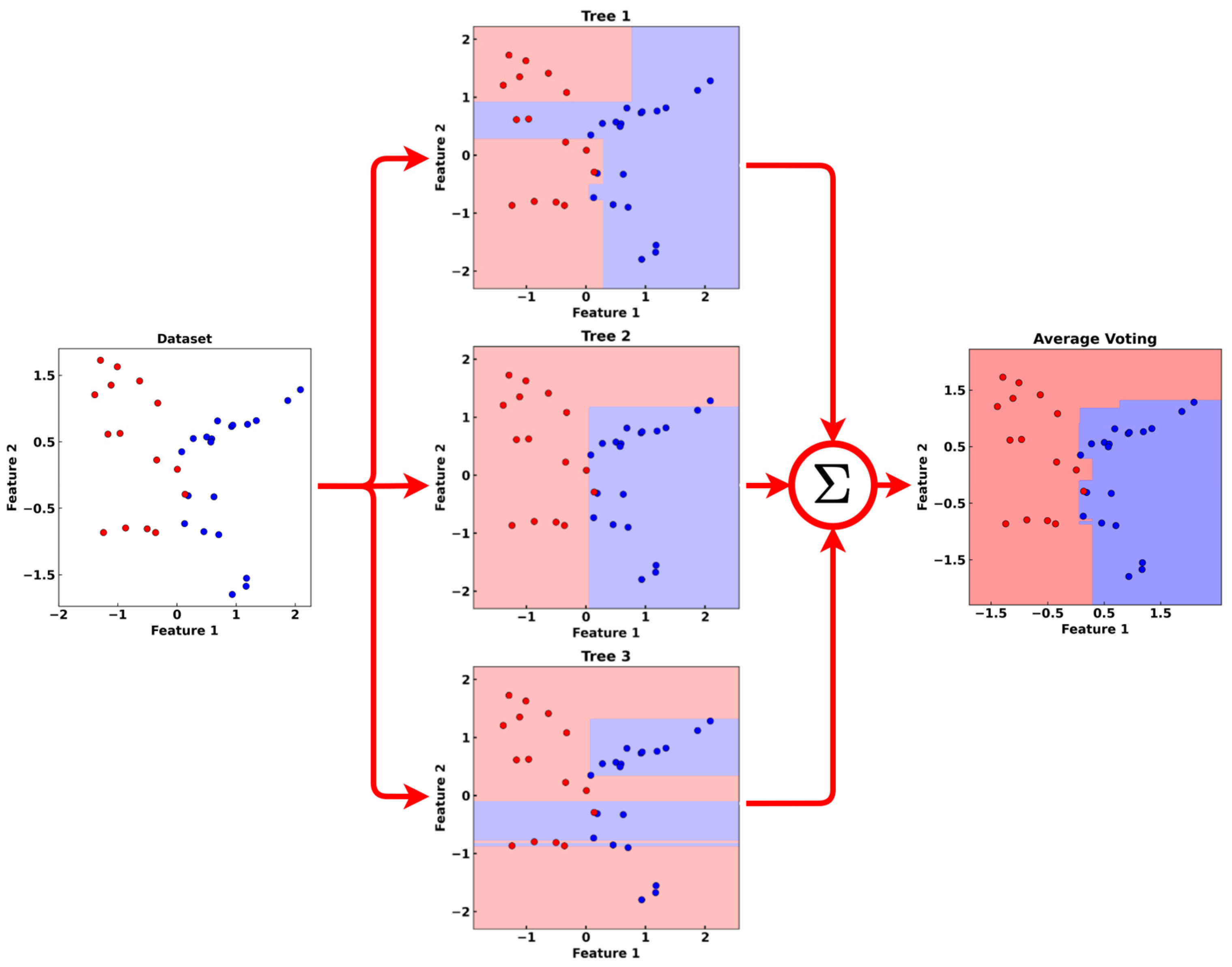
4.1. Random Forest Classifier
4.2. Multiplayer Perceptron Algorithm (MLP)
4.3. Support Vector Classifier (SVC)

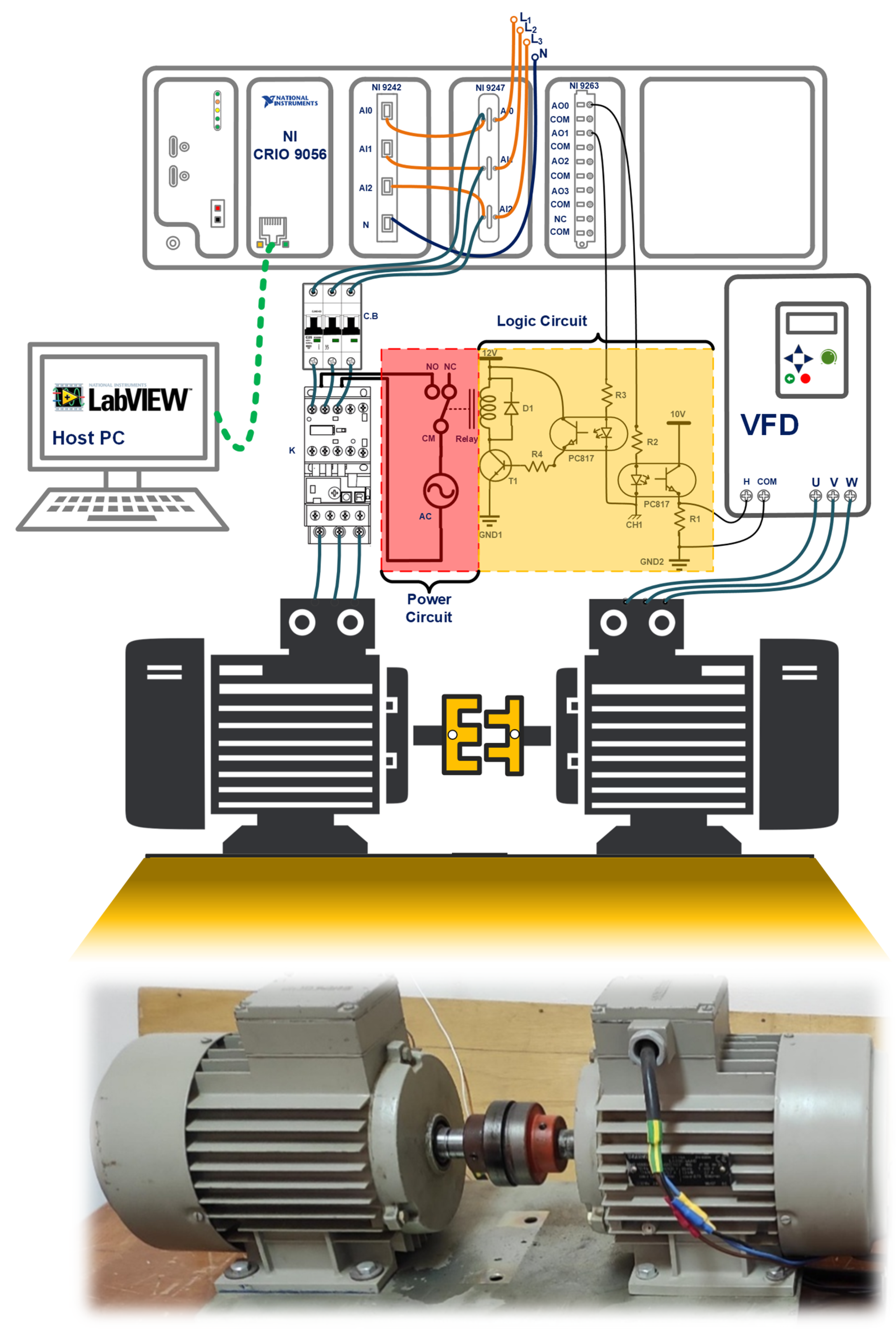
5. Research Methodology
Experimental Setup
6. Exploration of Findings
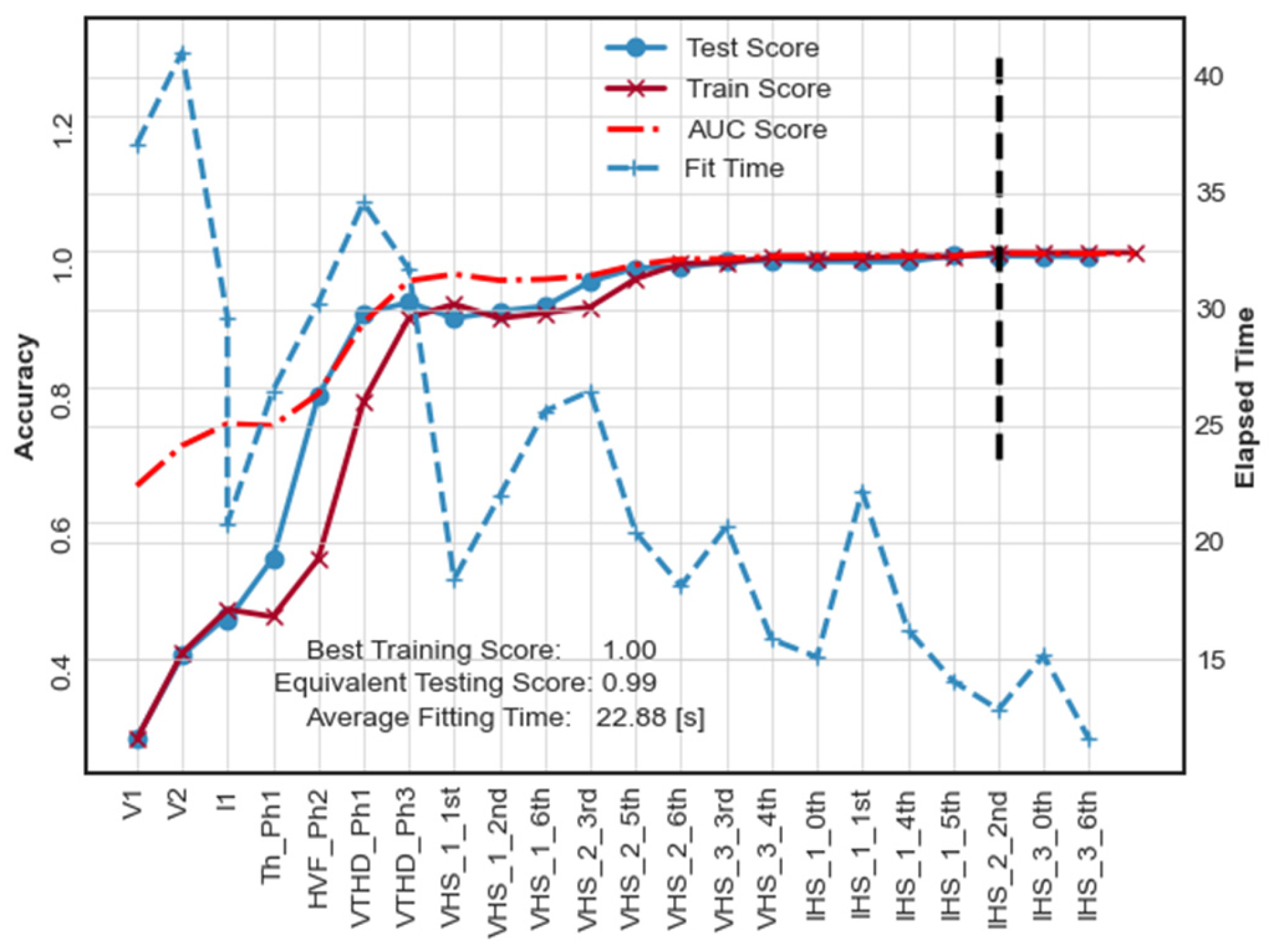
6.1. Case No. 1: RF-Based Feature Selection
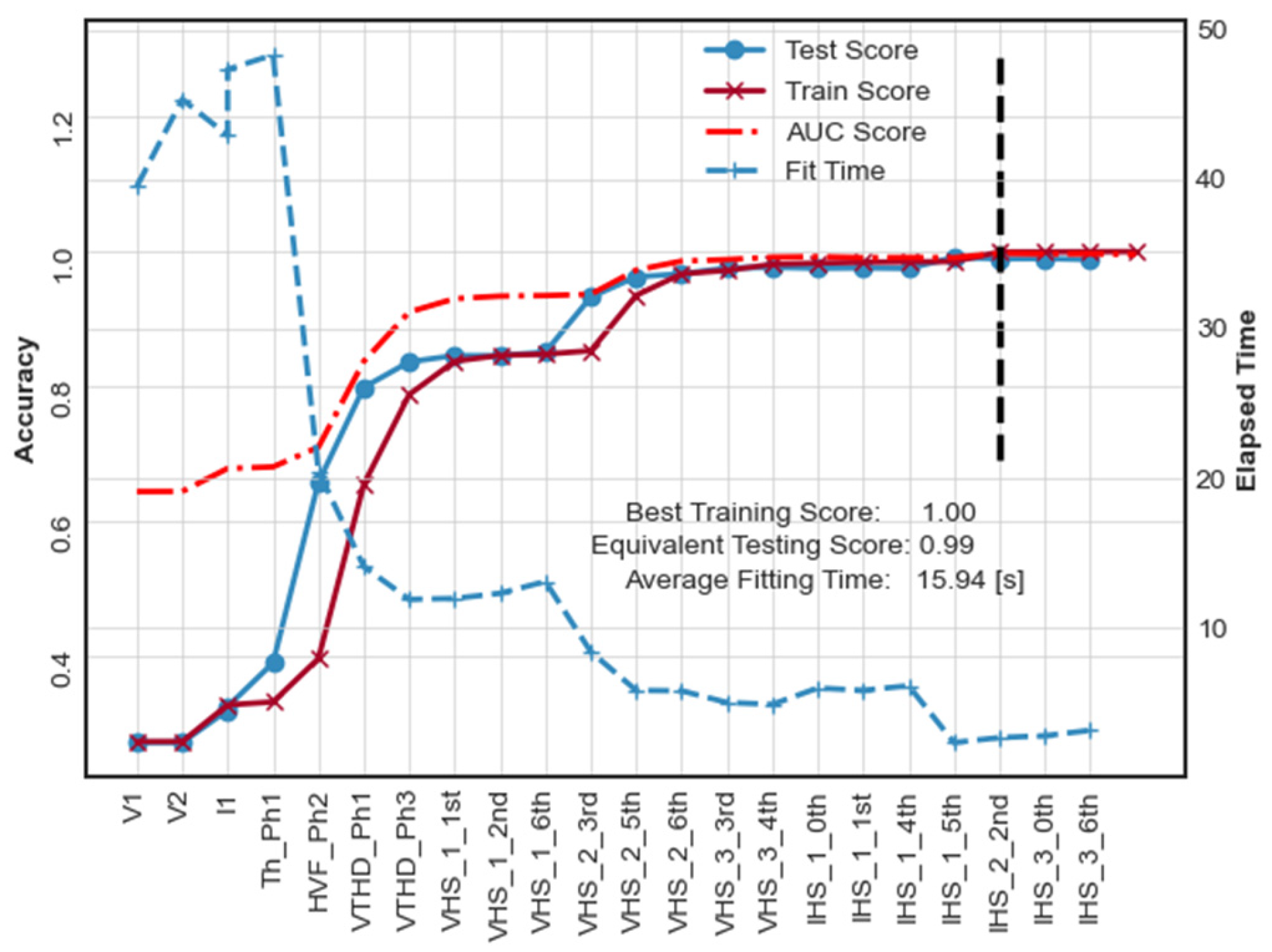
6.2. Case No. 2: AHC-Based Feature Selection
6.3. Case No. 3: Comparative Analysis of Classifiers’ Performance Considering Feature Selection Algorithms
6.3.1. Random Forest Classifier (RFC)
6.3.2. Artificial Neural Networks (ANNs)
6.3.3. Support Vector Machines (SVC)
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AHC | Agglomerative hierarchical clustering |
| ANN | Artificial Neural Network |
| BGWO | Binary grey wolf optimization |
| BPNN | Backpropagation Neural Network |
| AUC | Area Under the ROC Curve |
| CLSTM | Convolutional Long Short-Term Memory |
| CSA | Current Signature Analysis |
| CWRU MFPT | Case of Western Reserve University Machinery Failure Prevention Technology Dataset |
| DWT | Discrete wavelet transform |
| EDMFE | Ensemble Deep Models Features Extraction |
| EFS | Ensemble feature selection |
| EHD | Empirical mode decomposition |
| EPO | Emperor penguin optimizer |
| EPRI | Electric Power Research Institute |
| FCM | Fuzzy C-Means |
| FFT | Fast Fourier transform |
| FSDD | Feature selection based on distance discriminant |
| HANFIS | Hierarchical Adaptive Neuro-Fuzzy Inference System |
| HGBCSO | Hybrid genetic binary chicken swarm optimization |
| HVF | Harmonic voltage factor |
| IEC | International Electrotechnical Commission |
| IoT | Internet of Things |
| LMD | Local mean decomposition |
| LR | Logistic Regression |
| LightGBM | Light Gradient Boosting Machine |
| MIV | Mean impact value |
| MLP | Multi-layer perceptron |
| MRA | Multi-resolution analysis |
| NI cRIO | National Instruments Compact Reconfigurable Input/Output |
| PCA | Principal component analysis |
| PNN | Probabilistic neural network |
| PSO | Particle swarm optimization |
| RBFNN | Radial basis function neural network |
| Recall | True positive rate in classification |
| RFC | Random forest classifier |
| RFE | Recursive Feature Elimination |
| ROC | Receiver operating characteristic |
| SVC | Support Vector Classifier |
| SU | Symmetrical uncertainty |
| t−SNE | t-distribution stochastic neighbor embedding |
| VFD | Variable Frequency Drive |
| WPD | Wavelet packet decomposition |
Nomenclature
| αi | Lagrange multiplier |
| Bias vector for layer n | |
| C | Slack penalty parameter in SVC optimization |
| Distance between clusters K and L in AHC | |
| F1-score | Harmonic mean of precision and recall |
| Distance at which clusters are merged at level i in the AHC tree (linkage matrix Z) | |
| Input vector to hidden layer n | |
| I1−I3 | Line current for phases 1 to 3 |
| ITHD_Ph1−Ph3 | Total harmonic distortion of current for phases 1 to 3 |
| K, L | Indices of two clusters in AHC |
| M | Number of neurons in each neural network layer |
| R_Ph1−Ph3 | Impedance real part of phases 1 to 3 |
| Standard deviation of distances for the last n merges at level i | |
| Gradient of the loss function with respect to the bias vector in layer n | |
| Gradient of the loss function with respect to the weight matrix in layer n | |
| THD | Total harmonic distortion |
| Th_Ph1−Ph3 | Impedance phase angle for phases 1 to 3 |
| V1−V3 | Line voltage for phases 1 to 3 |
| VHS_i_nth | ith phase voltage harmonic at nth order |
| VTHD_Ph1−Ph3 | Total harmonic distortion of voltage for phases 1 to 3 |
| Weight matrix for layer n | |
| Captured time-domain signal (voltage or current) | |
| Transformed frequency-domain signal | |
| Estimated output of a classifier or regression model | |
| Mean of distances for the last n merges at level i | |
| Slack variable in SVC to accommodate margin violations |
References
- Saberi, A.N.; Belahcen, A.; Sobra, J.; Vaimann, T. LightGBM-Based Fault Diagnosis of Rotating Machinery under Changing Working Conditions Using Modified Recursive Feature Elimination. IEEE Access 2022, 10, 81910–81925. [Google Scholar] [CrossRef]
- Hou, J.; Wu, Y.; Ahmad, A.S.; Gong, H.; Liu, L. A Novel Rolling Bearing Fault Diagnosis Method Based on Adaptive Feature Selection and Clustering. IEEE Access 2021, 9, 99756–99767. [Google Scholar] [CrossRef]
- Saucedo-Dorantes, J.J.; Jaen-Cuellar, A.Y.; Delgado-Prieto, M.; Romero-Troncoso, R.D.J.; Osornio-Rios, R.A. Condition Monitoring Strategy Based on an Optimized Selection of High-Dimensional Set of Hybrid Features to Diagnose and Detect Multiple and Combined Faults in an Induction Motor. Measurement 2021, 178, 109404. [Google Scholar] [CrossRef]
- Xue, S.; Hou, Y.; Mi, J.; Zhou, C.; Xiang, T.; He, W.; Wu, D.; Huang, W. Induction Motor Failure Identification Based on Multiscale Acoustic Entropy Feature Selection and Hierarchical Adaptive Neuro-Fuzzy Inference System With Localized Recurrent Input. IEEE Sens. J. 2023, 23, 30821–30834. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Le, T.-A.; Chien, W.-L.; Hsu, S.-C. Application of Symmetric Uncertainty and Emperor Penguin—Grey Wolf Optimisation for Feature Selection in Motor Fault Classification. IET Electr. Power Appl. 2024, 18, 1107–1121. [Google Scholar] [CrossRef]
- Islam, R.; Khan, S.A.; Kim, J.-M. Discriminant Feature Distribution Analysis-Based Hybrid Feature Selection for Online Bearing Fault Diagnosis in Induction Motors. J. Sens. 2016, 2016, 7145715. [Google Scholar] [CrossRef]
- Gangsar, P.; Bajpei, A.R.; Porwal, R. A Review on Deep Learning Based Condition Monitoring and Fault Diagnosis of Rotating Machinery. Noise Vib. Worldw. 2022, 53, 550–578. [Google Scholar] [CrossRef]
- Hsu, S.; Lee, C.; Fang Wu, W.; Lee, C.; Jiang, J. Machine Learning-Based Online Multi-Fault Diagnosis for IMs Using Optimization Techniques with Stator Electrical and Vibration Data. IEEE Trans. Energy Convers. 2024, 39, 2412–2424. [Google Scholar] [CrossRef]
- Jigyasu, R.; Shrivastava, V.; Singh, S. Deep Optimal Feature Extraction and Selection-Based Motor Fault Diagnosis Using Vibration. Electr. Eng. 2024, 106, 6339–6358. [Google Scholar] [CrossRef]
- Jigyasu, R.; Shrivastava, V.; Singh, S. Hybrid Multi-Model Feature Fusion-Based Vibration Monitoring for Rotating Machine Fault Diagnosis. J. Vib. Eng. Technol. 2024, 12, 2791–2810. [Google Scholar] [CrossRef]
- Buchaiah, S.; Shakya, P. Bearing Fault Diagnosis and Prognosis Using Data Fusion Based Feature Extraction and Feature Selection. Measurement 2022, 188, 110506. [Google Scholar] [CrossRef]
- Yadav, S.; Patel, R.K.; Singh, V.P. Multiclass Fault Classification of an Induction Motor Bearing Vibration Data Using Wavelet Packet Transform Features and Artificial Intelligence. J. Vib. Eng. Technol. 2023, 11, 3093–3108. [Google Scholar] [CrossRef]
- Eddine Cherif, B.D.; Seninete, S.; Defdaf, M. A Novel, Machine Learning-Based Eature Extraction Nethod for Detecting and Localizing Bearing Component Defects. Metrol. Meas. Syst. 2022, 29, 333–346. [Google Scholar] [CrossRef]
- Jalayer, M.; Orsenigo, C.; Vercellis, C. Fault Detection and Diagnosis for Rotating Machinery: A Model Based on Convolutional LSTM, Fast Fourier and Continuous Wavelet Transforms. Comput. Ind. 2021, 125, 103378. [Google Scholar] [CrossRef]
- Panigrahy, P.S.; Chattopadhyay, P. Tri-Axial Vibration Based Collective Feature Analysis for Decent Fault Classification of VFD Fed Induction Motor. Measurement 2021, 168, 108460. [Google Scholar] [CrossRef]
- Panigrahy, P.S.; Santra, D.; Chattopadhyay, P. Decent Fault Classification of VFD Fed Induction Motor Using Random Forest Algorithm. Artif. Intell. Eng. Des. Anal. Manuf. 2020, 34, 492–504. [Google Scholar] [CrossRef]
- Mari, S.; Bucci, G.; Ciancetta, F.; Fiorucci, E.; Fioravanti, A. Impact of Measurement Uncertainty on Fault Diagnosis Systems: A Case Study on Electrical Faults in Induction Motors. Sensors 2024, 24, 5263. [Google Scholar] [CrossRef]
- Singh, M.; Shaik, A.G. Faulty Bearing Detection, Classification and Location in a Three-Phase Induction Motor Based on Stockwell Transform and Support Vector Machine. Measurement 2019, 131, 524–533. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Hung, C.-H.; Le, T.-A. Intelligent Fault Diagnosis for BLDC With Incorporating Accuracy and False Negative Rate in Feature Selection Optimization. IEEE Access 2022, 10, 69939–69949. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Ou, H.-Y. Induction Motor Multiclass Fault Diagnosis Based on Mean Impact Value and PSO-BPNN. Symmetry 2021, 13, 104. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Zhuo, G.-L. Effective Rotor Fault Diagnosis Model Using Multilayer Signal Analysis and Hybrid Genetic Binary Chicken Swarm Optimization. Symmetry 2021, 13, 487. [Google Scholar] [CrossRef]
- de las Morenas, J.; Moya-Fernández, F.; López-Gómez, J.A. The Edge Application of Machine Learning Techniques for Fault Diagnosis in Electrical Machines. Sensors 2023, 23, 2649. [Google Scholar] [CrossRef] [PubMed]
- Zhukovskiy, Y.; Buldysko, A.; Revin, I. Induction Motor Bearing Fault Diagnosis Based on Singular Value Decomposition of the Stator Current. Energies 2023, 16, 3303. [Google Scholar] [CrossRef]
- Khan, M.A.; Asad, B.; Kudelina, K.; Vaimann, T.; Kallaste, A. The Bearing Faults Detection Methods for Electrical Machines—The State of the Art. Energies 2023, 16, 296. [Google Scholar] [CrossRef]
- Kudelina, K.; Asad, B.; Vaimann, T.; Rassõlkin, A.; Kallaste, A.; Van Khang, H. Methods of Condition Monitoring and Fault Detection for Electrical Machines. Energies 2021, 14, 7459. [Google Scholar] [CrossRef]
- Kumar, R.R.; Andriollo, M.; Cirrincione, G.; Cirrincione, M.; Tortella, A. A Comprehensive Review of Conventional and Intelligence-Based Approaches for the Fault Diagnosis and Condition Monitoring of Induction Motors. Energies 2022, 15, 8938. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.; Wang, B.; Habetler, T.G. Deep Learning Algorithms for Bearing Fault Diagnosticsx—A Comprehensive Review. IEEE Access 2020, 8, 29857–29881. [Google Scholar] [CrossRef]
- Marmouch, S.; Aroui, T.; Koubaa, Y. Statistical Neural Networks for Induction Machine Fault Diagnosis and Features Processing Based on Principal Component Analysis. IEEJ Trans. Electr. Electron. Eng. 2021, 16, 307–314. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Lin, W.-C. Induction Motor Fault Classification Based on ROC Curve and T-SNE. IEEE Access 2021, 9, 56330–56343. [Google Scholar] [CrossRef]
- Nayana, B.R.; Geethanjali, P. Analysis of Statistical Time-Domain Features Effectiveness in Identification of Bearing Faults from Vibration Signal. IEEE Sens. J. 2017, 17, 5618–5625. [Google Scholar] [CrossRef]
- Ismi, D.P.; Panchoo, S.; Murinto, M. K-Means Clustering Based Filter Feature Selection on High Dimensional Data. Int. J. Adv. Intell. Inform. 2016, 2, 38–45. [Google Scholar] [CrossRef]
- Källberg, D.; Vidman, L.; Rydén, P. Comparison of Methods for Feature Selection in Clustering of High-Dimensional RNA-Sequencing Data to Identify Cancer Subtypes. Front. Genet. 2021, 12, 632620. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Chen, D. A Breast Cancer Diagnosis Method Based on VIM Feature Selection and Hierarchical Clustering Random Forest Algorithm. IEEE Access 2022, 10, 3284–3293. [Google Scholar] [CrossRef]
- Boukra, T.; Lebaroud, A.; Clerc, G. Statistical and Neural-Network Approaches for the Classification of Induction Machine Faults Using the Ambiguity Plane Representation. IEEE Trans. Ind. Electron. 2013, 60, 4034–4042. [Google Scholar] [CrossRef]
- IEEE Std 519-2022; IEEE Standard for Harmonic Control in Electric Power Systems. IEEE: Piscataway, NJ, USA, 2022; (Revision of IEEE Std 519-2014).
- Barros, J.; De Apráiz, M.; Diego, R.I. On-Line Monitoring of Electrical Power Quality for Assessment of Induction Motor Performance. In Proceedings of the 2009 IEEE International Electric Machines and Drives Conference, IEMDC’ 09, Miami, FL, USA, 3–6 May 2009. [Google Scholar]
- IEC 60034-1 2010; Rotating Electrical Machines—Part 1: Rating and Performance Machines. International Electrotechnical Commission (IEC): Geneva, Switzerland, 2014.
- Oppenheim, A.V.; Schafer, R.W. Discrete Time Signal Processing, 2nd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1998. [Google Scholar]
- Hemad, B.A.; Ibrahim, N.M.A.; Fayad, S.A.; Talaat, H.E.A. Hierarchical Clustering-Based Framework for Interconnected Power System Contingency Analysis. Energies 2022, 15, 5631. [Google Scholar] [CrossRef]
- Dodge, Y. Spearman Rank Correlation Coefficient. In The Concise Encyclopedia of Statistics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Hollander, M.; Wolfe, D.A.; Chicken, E. Nonparametric Statistical Methods; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Ward, J.H. Hierarchical Grouping to Optimize an Objective Function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Müllner, D. Modern Hierarchical, Agglomerative Clustering Algorithms. arXiv 2011, arXiv:1109.2378. [Google Scholar]
- MathWorks. Inconsistent Function. MATLAB Documentation. Available online: https://www.mathworks.com/help/stats/inconsistent.html (accessed on 20 March 2024).
- Gangsar, P.; Tiwari, R. A Support Vector Machine Based Fault Diagnostics of Induction Motors for Practical Situation of Multi-Sensor Limited Data Case. Measurement 2019, 135, 694–711. [Google Scholar] [CrossRef]
- Hassan, O.E.; Amer, M.; Abdelsalam, A.K.; Williams, B.W. Induction Motor Broken Rotor Bar Fault Detection Techniques Based on Fault Signature Analysis—A Review. IET Electr. Power Appl. 2018, 12, 895–907. [Google Scholar] [CrossRef]
- Lang, W.; Hu, Y.; Gong, C.; Zhang, X.; Xu, H.; Deng, J. Artificial Intelligence-Based Technique for Fault Detection and Diagnosis of EV Motors: A Review. IEEE Trans. Transp. Electrif. 2022, 8, 384–406. [Google Scholar] [CrossRef]
- Ali, M.Z.; Shabbir, M.N.S.K.; Zaman, S.M.K.; Liang, X. Single- and Multi-Fault Diagnosis Using Machine Learning for Variable Frequency Drive-Fed Induction Motors. IEEE Trans. Ind. Appl. 2020, 56, 2324–2337. [Google Scholar] [CrossRef]
- Ali, M.Z.; Shabbir, M.N.S.K.; Liang, X.; Zhang, Y.; Hu, T. Machine Learning-Based Fault Diagnosis for Single- and Multi-Faults in Induction Motors Using Measured Stator Currents and Vibration Signals. IEEE Trans. Ind. Appl. 2019, 55, 2378–2391. [Google Scholar] [CrossRef]
- Kim, M.; Jung, J.H.; Ko, J.U.; Kong, H.B.; Lee, J.; Youn, B.D. Direct Connection-Based Convolutional Neural Network (DC-CNN) for Fault Diagnosis of Rotor Systems. IEEE Access 2020, 8, 172043–172056. [Google Scholar] [CrossRef]
- Devi, N.R.; Siva Sarma, D.V.S.S.; Rao, P.V.R. Diagnosis and Classification of Stator Winding Insulation Faults on a Three-Phase Induction Motor Using Wavelet and MNN. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 2543–2555. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Quinlan, J.R. Bagging, Boosting, and C4.5. In Proceedings of the National Conference on Artificial Intelligence, Menlo Park, CA, USA, 4–8 August 1996; Volume 1, pp. 725–730. [Google Scholar]
- Breiman, L. Bagging Predictors. In Machine Learning; Springer: Berlin/Heidelberg, Germany, 1996; Volume 45. [Google Scholar]
- Saberi, A.N.; Sandirasegaram, S.; Belahcen, A.; Vaimann, T.; Sobra, J. Multi-Sensor Fault Diagnosis of Induction Motors Using Random Forests and Support Vector Machine. In Proceedings of the 2020 International Conference on Electrical Machines, ICEM 2020, Gothenburg, Sweden, 23–26 August 2020; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2020; pp. 1404–1410. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Dhandhia, A.; Pandya, V.; Bhatt, P. Multi-Class Support Vector Machines for Static Security Assessment of Power System. Ain Shams Eng. J. 2020, 11, 57–65. [Google Scholar] [CrossRef]
- Gangsar, P.; Tiwari, R. Comparative Investigation of Vibration and Current Monitoring for Prediction of Mechanical and Electrical Faults in Induction Motor Based on Multiclass-Support Vector Machine Algorithms. Mech. Syst. Signal Process 2017, 94, 464–481. [Google Scholar] [CrossRef]
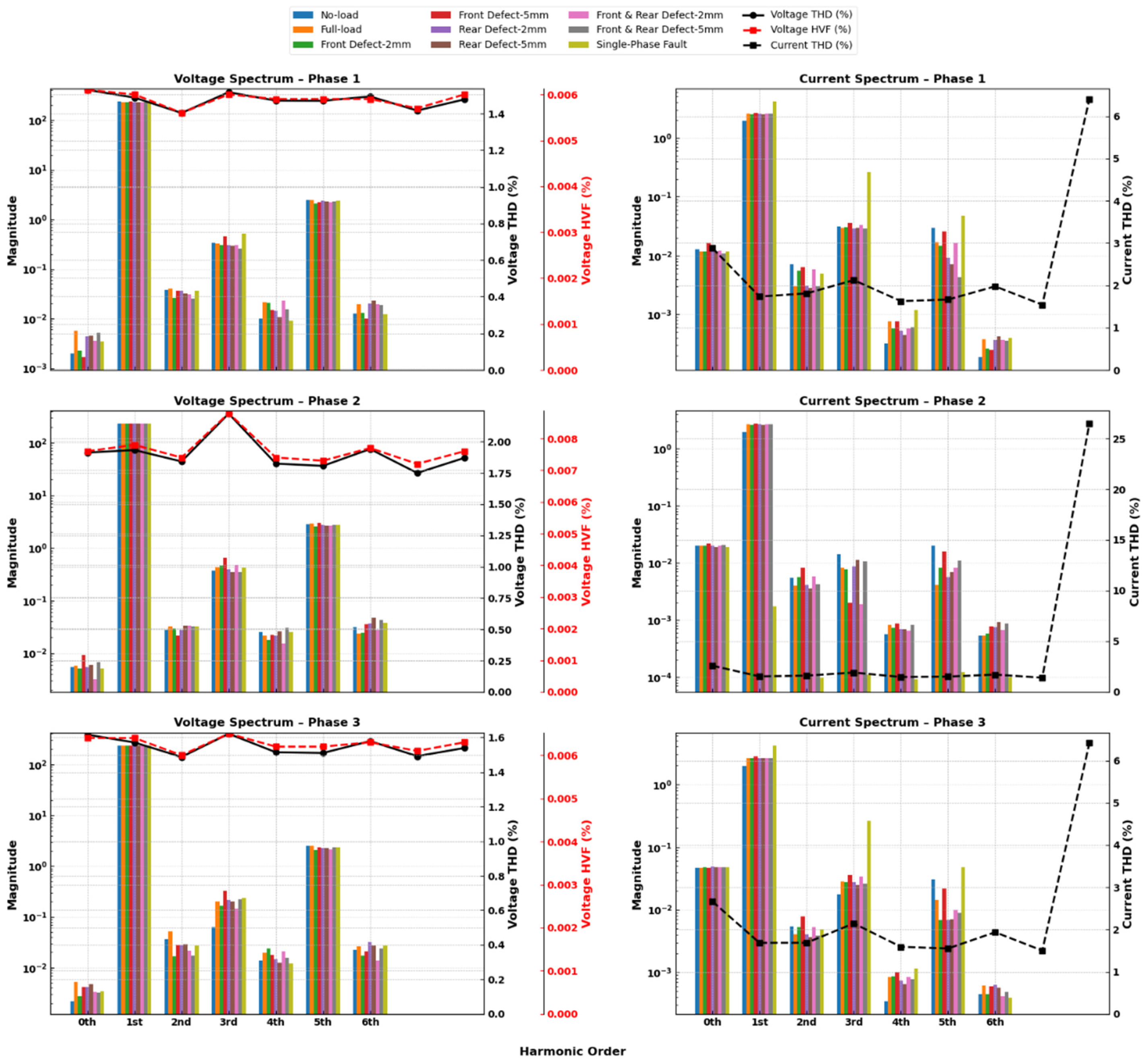
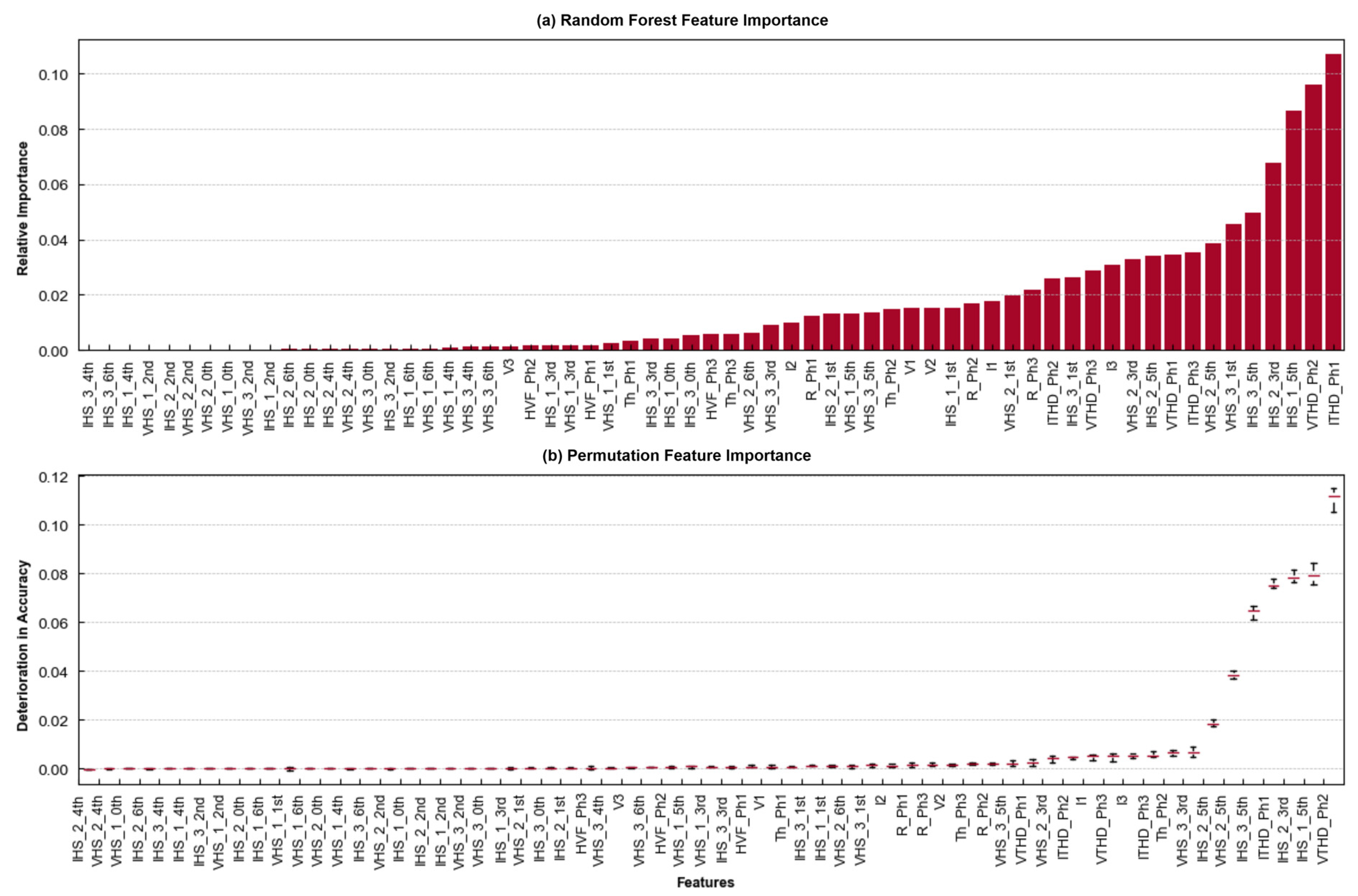
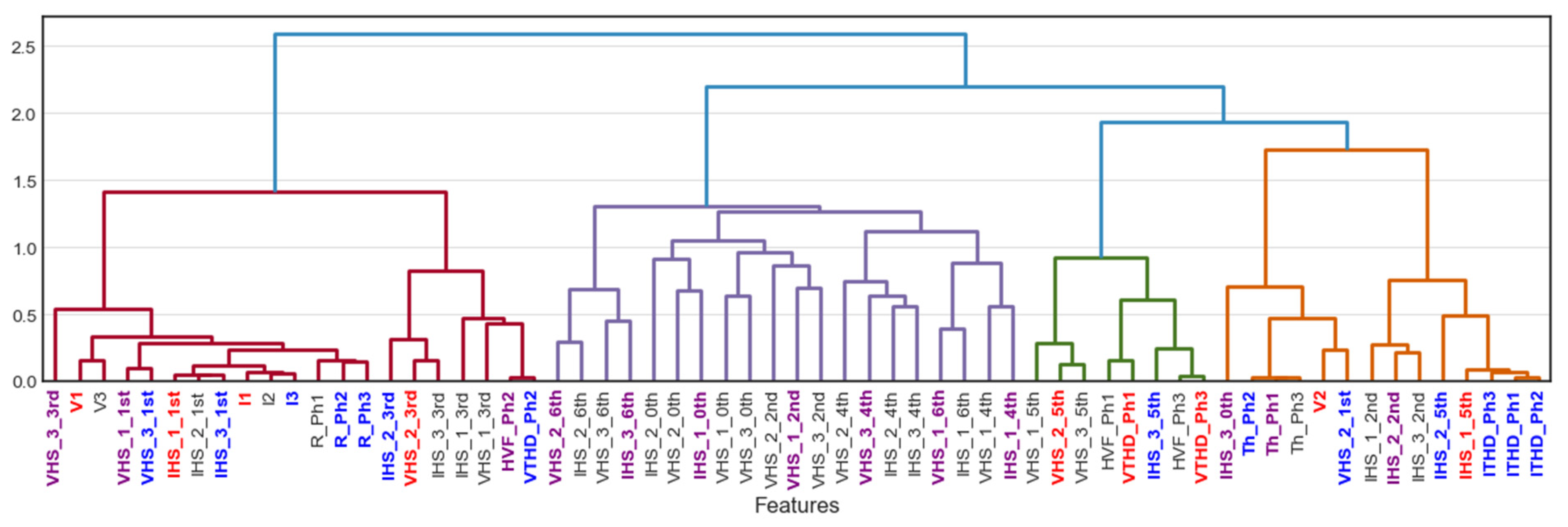

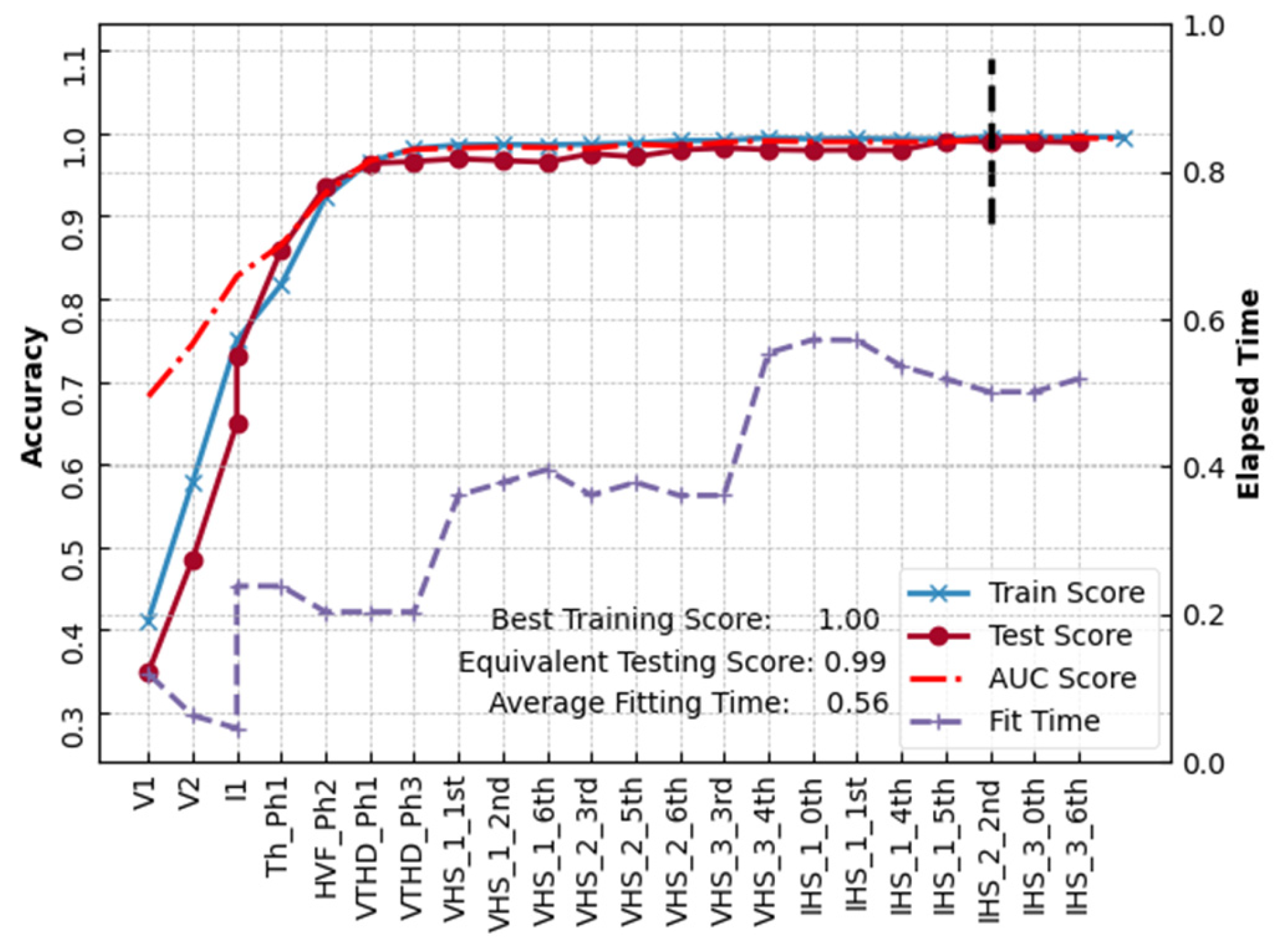



| Operating Scenario | Description | Scenario Duration | Operating Scenario | Description | Scenario Duration |
|---|---|---|---|---|---|
| No-load | Motor running under no-load condition. | 10 min | Rear Defect (5 mm) | Motor at full load with a 5 mm defect in the outer race of the rear bearing. | 10 min |
| Full-load | Motor running at full load, drawing a current of 2.73 A. | Front and Rear Defect (2 mm) | Motor at full load with a 2 mm defect in the outer races of both the front and rear bearings. | ||
| Front Defect (2 mm) | Motor at full load with a 2 mm defect in the outer race of the front bearing. | Front and Rear Defect (5 mm) | Motor at full load with a 5 mm defect in the outer races of both the front and rear bearings. | ||
| Front Defect (5 mm) | Motor at full load with a 5 mm defect in the outer race of the front bearing. | Phase loss fault | Motor operating with a single-phase open fault, where one phase is disconnected during operation. | 3 min | |
| Rear Defect (2 mm) | Motor at full load with a 2 mm defect in the outer race of the rear bearing. |
| Metrics | Precision | Recall | F1-Score | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Classifier | RFC | ANN | SVC | RFC | ANN | SVC | RFC | ANN | SVC |
| No-load | 1.000 | 1.000 | 0.868 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.929 |
| Full-load | 0.997 | 0.965 | 1.000 | 0.995 | 0.768 | 0.000 | 0.996 | 0.855 | 0.000 |
| Front Defect (2 mm) | 1.000 | 0.996 | 1.000 | 0.999 | 0.955 | 0.000 | 0.999 | 0.975 | 0.000 |
| Front Defect (5 mm) | 1.000 | 0.995 | 1.000 | 0.997 | 0.997 | 0.000 | 0.999 | 0.996 | 0.000 |
| Rear Defect (2 mm) | 0.994 | 0.680 | 1.000 | 0.986 | 0.165 | 0.000 | 0.990 | 0.266 | 0.000 |
| Rear Defect (5 mm) | 1.000 | 0.813 | 1.000 | 0.982 | 0.644 | 0.000 | 0.991 | 0.718 | 0.000 |
| Front and Rear Defect (2 mm) | 1.000 | 0.992 | 1.000 | 0.996 | 0.978 | 0.000 | 0.998 | 0.985 | 0.000 |
| Front and Rear Defect (5 mm) | 0.999 | 0.870 | 1.000 | 0.983 | 0.781 | 0.000 | 0.991 | 0.823 | 0.000 |
| Single-Phase Fault | 0.970 | 0.987 | 0.957 | 0.985 | 0.900 | 0.605 | 0.977 | 0.941 | 0.741 |
| micro avg | 0.997 | 0.946 | 0.885 | 0.992 | 0.797 | 0.154 | 0.995 | 0.865 | 0.263 |
| macro avg | 0.996 | 0.922 | 0.981 | 0.991 | 0.799 | 0.178 | 0.993 | 0.840 | 0.186 |
| weighted avg | 0.997 | 0.920 | 0.982 | 0.992 | 0.797 | 0.154 | 0.995 | 0.838 | 0.153 |
| Metrics | Precision | Recall | F1-Score | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Classifier | RFC | ANN | SVC | RFC | ANN | SVC | RFC | ANN | SVC |
| No-load | 1.000 | 0.997 | 0.999 | 1.000 | 1.000 | 1.000 | 1.000 | 0.999 | 0.999 |
| Full-load | 0.992 | 0.980 | 0.974 | 0.995 | 0.995 | 0.995 | 0.994 | 0.987 | 0.984 |
| Front Defect (2 mm) | 1.000 | 0.997 | 0.996 | 0.996 | 1.000 | 0.993 | 0.998 | 0.999 | 0.994 |
| Front Defect (5 mm) | 1.000 | 1.000 | 0.997 | 0.997 | 0.997 | 0.997 | 0.999 | 0.999 | 0.997 |
| Rear Defect (2 mm) | 0.997 | 0.996 | 0.940 | 0.987 | 0.991 | 0.920 | 0.992 | 0.994 | 0.930 |
| Rear Defect (5 mm) | 0.997 | 0.959 | 0.947 | 0.992 | 0.996 | 0.968 | 0.994 | 0.977 | 0.957 |
| Front and Rear Defect (2 mm) | 1.000 | 0.997 | 0.996 | 0.996 | 0.999 | 1.000 | 0.998 | 0.998 | 0.998 |
| Front and Rear Defect (5 mm) | 0.999 | 0.997 | 0.996 | 0.983 | 0.947 | 0.964 | 0.991 | 0.971 | 0.979 |
| Single-Phase Fault | 0.976 | 0.990 | 0.963 | 0.976 | 0.945 | 0.936 | 0.976 | 0.967 | 0.949 |
| micro avg | 0.997 | 0.990 | 0.980 | 0.992 | 0.988 | 0.978 | 0.995 | 0.989 | 0.979 |
| macro avg | 0.996 | 0.990 | 0.978 | 0.991 | 0.986 | 0.975 | 0.993 | 0.988 | 0.977 |
| weighted avg | 0.997 | 0.990 | 0.980 | 0.992 | 0.988 | 0.978 | 0.995 | 0.989 | 0.979 |
| Metrics | Precision | Recall | F1-Score | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Classifier | RFC | ANN | SVC | RFC | ANN | SVC | RFC | ANN | SVC |
| No-load | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Full-load | 0.996 | 0.992 | 0.997 | 0.994 | 0.991 | 0.992 | 0.995 | 0.992 | 0.995 |
| Front Defect (2 mm) | 1.000 | 0.997 | 0.997 | 0.999 | 0.999 | 0.993 | 0.999 | 0.998 | 0.995 |
| Front Defect (5 mm) | 1.000 | 0.999 | 1.000 | 0.997 | 0.997 | 0.996 | 0.999 | 0.998 | 0.998 |
| Rear Defect (2 mm) | 0.996 | 0.997 | 0.994 | 0.990 | 0.991 | 0.989 | 0.993 | 0.994 | 0.991 |
| Rear Defect (5 mm) | 0.994 | 0.989 | 0.985 | 0.968 | 0.989 | 0.981 | 0.981 | 0.989 | 0.983 |
| Front and Rear Defect (2 mm) | 1.000 | 1.000 | 0.999 | 0.992 | 0.997 | 0.993 | 0.996 | 0.999 | 0.996 |
| Front and Rear Defect (5 mm) | 0.989 | 0.992 | 0.989 | 0.981 | 0.986 | 0.985 | 0.985 | 0.989 | 0.987 |
| Single-Phase Fault | 0.972 | 0.973 | 0.964 | 0.964 | 0.991 | 0.985 | 0.968 | 0.982 | 0.974 |
| micro avg | 0.996 | 0.995 | 0.994 | 0.989 | 0.994 | 0.991 | 0.992 | 0.994 | 0.992 |
| macro avg | 0.994 | 0.993 | 0.992 | 0.987 | 0.993 | 0.990 | 0.991 | 0.993 | 0.991 |
| weighted avg | 0.996 | 0.995 | 0.994 | 0.989 | 0.994 | 0.991 | 0.992 | 0.994 | 0.992 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hemade, B.A.; Ataya, S.; El-Fergany, A.A.; Ibrahim, N.M.A. Mitigating Multicollinearity in Induction Motors Fault Diagnosis Through Hierarchical Clustering-Based Feature Selection. Appl. Sci. 2025, 15, 7012. https://doi.org/10.3390/app15137012
Hemade BA, Ataya S, El-Fergany AA, Ibrahim NMA. Mitigating Multicollinearity in Induction Motors Fault Diagnosis Through Hierarchical Clustering-Based Feature Selection. Applied Sciences. 2025; 15(13):7012. https://doi.org/10.3390/app15137012
Chicago/Turabian StyleHemade, Bassam A., Sabbah Ataya, Attia A. El-Fergany, and Nader M. A. Ibrahim. 2025. "Mitigating Multicollinearity in Induction Motors Fault Diagnosis Through Hierarchical Clustering-Based Feature Selection" Applied Sciences 15, no. 13: 7012. https://doi.org/10.3390/app15137012
APA StyleHemade, B. A., Ataya, S., El-Fergany, A. A., & Ibrahim, N. M. A. (2025). Mitigating Multicollinearity in Induction Motors Fault Diagnosis Through Hierarchical Clustering-Based Feature Selection. Applied Sciences, 15(13), 7012. https://doi.org/10.3390/app15137012








