Featured Application
This work could be used by scientists to gain knowledge about fuzzy neural networks and their potential for practical implementation in real-world systems.
Abstract
This publication focuses on the use of fuzzy neural networks for data prediction. The author reviews papers in which fuzzy neural networks were used. The papers were selected mainly from 2020 to 2025 and were selected if fuzzy neural network were used for practical applications. Also, some chosen networks are described: FALCON, ANFIS, and a fuzzy network with Ordered Fuzzy Numbers. The networks with the implementation code presented in other publications were tested and compared to K Neighbors Classifier, Decision Tree Classifier, and Random Forest Classifier. The methodology and configuration of the networks are provided. Finally, the conclusions discuss limitations, future research prospects, and guidelines for future work.
1. Introduction
Practical and Methodological Aims of the Study; Motivation for Conducting Research; The contributions of the study; Organization of the Paper.
In the era of data explosion and the growing need for instance controlling, as well as parameter optimization, the choice of appropriate machine learning methods plays a key role. One of the algorithm’s tasks is, i.a., to solve a variety of classification problems. Classic algorithms such as k-Nearest Neighbors (KNN), decision trees (Decision Tree Classifier), and Random Forest are the foundation of data analysis systems. They are characterized by their simplicity and efficiency. However, in recent years, fuzzy networks have been attracting growing attention, combining the advantages of fuzzy logic and machine learning methods. Fuzzy networks such as Adaptive Neuro-Fuzzy Inference System (ANFIS), Falcon, or approaches using Ordered Fuzzy Numbers offer the unique capability of modeling uncertainty and imprecision in the data. This allows them to be used in situations where data is subject to measurement errors or is imprecise in its nature.
The aim of this publication is to review and compare selected fuzzy networks with classical classification algorithms in the context of their effectiveness in the task of classifying the Iris set. The analyzed models include ANFIS networks, two implementations using Ordered Fuzzy Numbers, as well as KNN, Decision Tree Classifier, and Random Forest implemented in the TensorFlow library. The comparison will be carried out in terms of the use of fuzzy networks and the results they produce for the aforementioned algorithms. This research aims to evaluate the potential of fuzzy networks as an alternative or complement to traditional algorithms in modern analytical systems.
The motivation of this review was to check where fuzzy neural networks are used, and which of them could be easy to use according to their configuration and implementation-code accessibility.
The structure of the paper is as follows:
Section 2 presents the fuzzy neural network description with the review criteria and summary of the reviewed papers.
Section 3 provides more information on selected networks: FALCON, ANFIS, and fuzzy neural networks with Ordered Fuzzy Numbers.
Section 4 provides the methodology.
Section 5 provides the results achieved during a test.
Section 6 includes the discussion.
Finally, Section 7 presents the conclusions.
2. Fuzzy Neural Network Description
2.1. The Aim and Critieria of Review
The application of fuzzy logic is convenient wherever it is difficult to create a mathematical model, but it is possible to describe a situation using fuzzy rules, qualitatively. For instance, one can imagine the fuzzy controller rule that imprecisely describes the event, e.g., if it is falling over, push it. For Fuzzy Logic, many industry applications have been found, mainly concerning process control. For medical applications, imprecise language can be translated into fuzzy rules. One of the applications is the use of the architecture of fuzzy neural networks. The topic of fuzzy neural networks is widely covered in publications.
The aim of this review is to:
- Analyze information about the purpose of using fuzzy neural networks;
- Examine which types of networks are used for specific purposes;
- Investigate whether fuzzy neural networks can be used similarly to traditional deep neural networks provided by popular frameworks such as PyTorch (version 2.6.0+cu124 ) and TensorFlow (version 2.18.0);
- Examine the implementation code presented to the fuzzy network with a widely used dataset.
The criteria for selecting the papers were:
- Year of publication—primarily a six-year span—from 2020 to 2025;
- Use of fuzzy neural networks in practical applications—either well-known problems or the author’s own proposed solutions.
A search process was conducted using the phrase ‘fuzzy network,’ and then the abstracts were checked to determine if the papers presented any practical implementations.
These practical applications were particularly important because data science specialists typically use well-established frameworks to build neural networks that solve real-world problems. The year of publication was also a key factor, as data science has seen rapid progress in recent years, making it essential to consider current trends.
2.2. Papers Review on Defined Criteria
Some propose the use of the McCuloch–Pitts neuron when extended to a fuzzy model with activation calculation in the fuzzy logic domain [1]. Some authors propose the use of fuzzy number representation in the triangular form [2]. Such network solutions allow both fuzzy and real vectors as input. However, in both cases, the network outputs are fuzzy outputs. The relation between the inputs and outputs is defined as a Zadeh extension. Many publications use fuzzy signals and weights [3]. Paul Vitor presented a new logic of the fuzzy neuron in his publication [4]. In the applied structure, the neuron can perform fuzzy calculations involving logical AND and OR operations, which, according to the author of the publication, allow better interpretation and understanding of the problem. The proposed three-layer model uses a fuzzy approach with weight assignment allowing knowledge extraction in an iterative manner. One of the broad applications of fuzzy networks is the construction of fuzzy controllers, which, in principle, are supposed to perform better than traditional solutions [2,5]. Fuzzy logic algorithms are also used, for example, for labeling large sets of images [6]. One can also find proposals for unsupervised multilayer neural network solutions for image clustering using fuzzy system and convolutional networks [7]. Fuzzy networks have also already been used to recognize medical images. These images often have blurred object boundaries; in such a case, traditional methods have difficulties in recognizing the objects. Fuzzy logic comes in here as assistance, where due to a fuzzy processing block, the image is converted by assigning individual pixels the value of a fuzzy set membership function. After image processing in the convolutional layer of the neural network [8], the fuzzy rules are used. A combination of fuzzy logic and neural networks has also been used to predict bankruptcy [9]. Some authors propose the use of adaptive neural networks to solve the state estimation problem using the fuzzy Takagi–Sugeno model and the control of nonlinear systems through an adaptive neural network in which the system parameters comply with Markov switching rules [10]. One of the advantages of using fuzzy logic in neural networks is that it accelerates the learning process of the network [11]. Fuzzy neural networks have also been used to synchronize the feedback controller [12,13], where the authors proposed several innovative criteria. Fuzzy logic has also been used for the signal filtering process, using an adaptive fuzzy, progressive Gaussian filter supported by neural networks in navigation and positioning systems [14]. Deep fuzzy neural networks have also been used to control the integrity of the reactor core, reactor cooling system, or containment [15]. The application of fuzzy logic in reinforcement learning allowed a gain in accuracy 43.6% higher in comparison with the accuracy achieved by some classic models described in the literature [16]. An increase in the network accuracy following the implementation of fuzzy logic has also been reported in self-organizing networks [17]. One can also find proposals of fuzzy recurrence neural networks, e.g., consisting of two fuzzy neural networks with Takagi–Sugeno–Kang rules. One is used to generate a fuzzy result and the other to determine the state of the system while maintaining the coupling between these networks [18]. Proposing new fuzzy networks generates the problem of developing learning algorithms, often hybrid algorithms developed from existing ones [19]. Learning algorithms have already been proposed that are not sensitive to the initial values of the weights and do not require high computing power, which is very important for the application of solutions in, for example, the Internet of Things [20]. In fuzzy networks, it is necessary to develop activation functions (e.g., sigmoidal) [21,22].
There are solutions in which authors have combined convolutional networks with a fuzzy extraction mechanism using fuzzy analysis, naming the combination a fuzzy convolutional network [9].
Fuzzy networks have been applied within an embedding model for recommendation systems [11]. This approach combines a hierarchical fusion of neural fuzzy and deep network-based embedding architectures. As a result, it enables effective learning of user and item representations while minimizing feature ambiguity and noise.
Another approach involves a logical fuzzy neuron based on the concept of null-uninorm [4], known as a null-unineuron, which forms the core of an evolving neuro-fuzzy model. This method allows the neuron to derive complex fuzzy rules that incorporate AND and OR connections of antecedents, improving the interpretability and understanding of the problem being analyzed. However, implementing this solution requires specialized knowledge in fuzzy logic.
Fuzzy neural networks have also been utilized multiple times in image processing.
In [8], the authors introduced a novel fuzzy metric for quantifying pixel uncertainty. They developed a method where the membership function is used to represent an input image in such a way that the uncertainty of pixels is described by fuzzy rules. The fuzzy layers are then integrated with the convolution results in the neural network.
In [23], the authors proposed a solution using a fuzzy neural network in a vehicle braking system that employs an electromechanical actuator.
In [24], the authors employed the Takagi–Sugeno–Kang wavelet fuzzy neural network to develop a comprehensive framework dedicated to modeling nonlinear systems by learning from data. Additionally, they utilized Lyapunov stability theory for system optimization.
A semi-supervised soft computing approach was proposed in [25] to improve NH3-N prediction accuracy. The authors utilized a fuzzy neural network with a self-constructed architecture and proposed an appropriate learning algorithm, incorporating IF–THEN rules as part of the model.
In [26], the authors present the results of a comparison between two solutions: a well-known neural network and a fuzzy network. The conducted tests demonstrate that incorporating a fuzzy layer into the neural network can lead to higher accuracy.
In [27] authors used an ANFIS network for the analysis of thermo-acoustic systems. The authors highlighted the advantages of ANFIS:
- ANFIS is highly effective at modeling complex, nonlinear relationships between inputs and outputs, making it suitable for systems with intricate patterns. It also adapts well to changing environments by dynamically updating its parameters during training to improve performance.
They also noted the disadvantages of ANFIS:
- The effectiveness of ANFIS depends heavily on the quality and amount of training data; insufficient or biased data can result in inaccurate models. Additionally, training ANFIS can be computationally intensive, especially with large datasets or complex rule sets, which leads to longer training times and higher resource consumption.
In [28], the ANFIS network was used to develop a solution for electricity load forecasting. In [29] such a network was used for data analysis to examine and compare the links between the labor market, demographic factors, and economic performance of developed and less developed European countries. In [30] the same solution was used for clustering American countries affected by the COVID-19 pandemic.
In [31], the authors presented a novel version of Support Vector Machines that incorporates an auto-encoder deep neural network consisting of three layers: input, hidden, and output. The encoder functions within the fuzzy domain and employs fuzzy weights, which enhance its robustness against outliers.
In [32], a new method was introduced to improve pooling operations in convolutional neural networks by using type-2 fuzzy-based pooling. This technique applies type-2 fuzzy membership functions to better handle local uncertainties in feature maps. The approach delivers better performance for the proposed solutions compared to traditional convolutional neural networks.
In [33], the authors developed a thermal control strategy to stabilize hydrogen production by improving temperature control precision during the electrolysis process. This was achieved by adding a fuzzy controller as an additional layer to a Long Short-Term Memory (LSTM) network.
In [34], an ARIMA (autoregressive integrated moving average) model combined with a neural network for membership function utilization was proposed for predicting business cycles.
In [35], the authors proposed a fuzzy BAM neural network that was a discrete-time, fractional-order, complex-valued system. Achieving quasi-projective synchronization of the proposed system required developing a quantitative control strategy.
In [36], the authors developed a fuzzy neural network for breast cancer prediction. This fuzzy network achieved accuracy, sensitivity, and specificity all above 99%. However, it required the definition of fuzzy rules and membership functions. The testing was conducted in a Matlab environment.
In [37], the authors introduced a fuzzy neural network for controlling the position of an unmanned aerial vehicle. Flight data captured from a real vehicle was used during testing. For the position control loop, an adaptive tuning method based on a fuzzy neural network-compensated proportional-integral-derivative (PID) controller was employed, allowing online adjustments. This approach leveraged the strengths of both fuzzy systems and neural networks while reducing the computational complexity typically associated with cascade neural network control.
In [38], a fuzzy neural network PID controller was used to reduce the vibration levels of helicopters, achieving up to a 60% reduction in vibration.
In [39], the authors proposed a fuzzy neural network PID control strategy optimized by Particle Swarm Optimization (PSO) for managing pH levels in water and fertilizer integration systems. Their approach combined a fuzzy preprocessing controller with a neural network PID controller. The experiments were carried out using MATLAB/SIMULINK software.
In [40], a fuzzy neural network PID controller was utilized as an automatic speed regulator for a motor system. A fuzzy single-neuron neural network was applied for this purpose and the proposed fuzzy controller achieved better results compared to traditional methods.
Such fuzzy neural network PID solutions have also been used for active suspension control in vehicles [41].
In [42], the authors proposed a solution for a servo drive system. They used a recurrent fuzzy neural network combined with backstepping control. This approach enabled the motor to adapt to nonlinear changes in behavior during operation.
In [43], a fuzzy neural network was utilized to assess the signal quality indices of photoplethysmography pulses obtained via impedance cardiography.
In [44], a fuzzy neural network was applied to predict k-barriers for intrusion detection in wireless sensor networks. This network effectively addressed data stream regression problems while maintaining a high level of interpretability.
In [45], a fuzzy neural network was applied in a mobile robot as a control mechanism for trajectory tracking. This network utilized a self-organizing algorithm that included rule growth. A similar problem was addressed in [46], where a fuzzy neural network was used for the same purpose. This solution incorporated Kalman filters.
In [47], a fuzzy neural network was used as a motion compensator for gantry robots to correct synchronous errors between dual servo motors, improving precision in movement.
In [48], a fuzzy neural network was utilized for rotor fault diagnosis, achieving an average recognition accuracy exceeding 99%, outperforming other solutions. However, the definition of membership functions was necessary.
In [49], a type-2 fuzzy neural network was used for nonlinear system control. The operation of the network required the definition of fuzzy rules.
In [50], such a network, combined with a swarm optimization algorithm, was used for control systems and data prediction.
In [51], the authors developed a Taguchi-based multiscale convolutional compensatory fuzzy neural network model for automatic sleep stage detection and classification. In this solution, the data comes from electroencephalogram signals. The proposed approach used a fuzzy neural network for data classification and achieved a better learning convergence rate with a lower number of model parameters.
In [52], a type-2 fuzzy neural network with a Gaussian regression model was used for high-resolution image classification.
In [53], a fuzzy neural network was utilized for traffic flow prediction, which also required defining fuzzy rules and membership functions.
In [54], a fuzzy neural network was applied for photovoltaic failure analysis. The type-2 fuzzy neural network achieved results comparable to those of conventional artificial neural networks.
In [55], the authors used a fuzzy neural network to predict heart problems based on sound data. This paper proposed a new method for data fuzzification, and the fuzzy network was self-organizing.
In [56], the authors introduced a fuzzy neural network for multi-feedback feature selection. The entire solution was applied in power filter systems, enhancing signal filtering capabilities. By integrating carefully designed feedback loops and hidden layers, this approach improves signal evaluation, filtering, and feedback performance.
In [57], a vector convolutional neural network was used for fault diagnosis. This solution analyzed the condition of a machine tool and diagnosed faults from signals. Feature extraction utilized convolutional and pooling layers, while classification was conducted using a fuzzy neural network.
In [58], the authors utilized a Takagi–Sugeno (T-S) fuzzy neural network for applications in rural logistics. The network consisted of four layers: an input layer, a fuzzification layer, a fuzzy rule computation layer, and an output layer.
In [59], the authors developed a probabilistic type-2 fuzzy neural network that is a self-evolving, non-singleton solution. This solution was used for system synchronization and control.
In [60], a type-2 fuzzy network was used to control an active power filter.
In [61], the authors proposed a wavelet energy fuzzy neural network-based technique for fault protection in microgrids operating in grid-connected mode. This solution required defining fuzzy rules and membership functions.
In [62], a fuzzy neural network was utilized for the safe charging of electric vehicles.
In [63], the authors used a T-S fuzzy neural network to evaluate water quality. The T-S fuzzy theoretical system is defined using “if-then” rules and typically includes four layers: input layer, fuzzification layer, fuzzy rule calculation layer, and output layer.
In [64], the authors proposed a recurrent wavelet fuzzy neural network to enhance the performance of a shunt active power filter for harmonic compensation. This filter mitigates reactive power and harmonic current in a power grid. The proposed solution employed a well-known fuzzy network structure with five layers: Layer 1 (input layer), Layer 2 (membership layer), Layer 3 (wavelet layer), Layer 4 (rule layer), and Layer 5 (output layer).
In [65], the authors proposed a hybrid approach that integrates deep learning architectures for feature extraction. They used a machine learning classifier combined with a fuzzy min–max neural network. This enabled them to develop a solution for Pap-smear image classification, which is used for cancer detection. The proposed fuzzy classifier consists of three layers: the first for input feature vectors, the second for fuzzy hyperbox sets, and the last for classification nodes. It uses fuzzy membership functions to evaluate how input patterns correspond to different hyperboxes, enabling class label assignment based on membership values.
In [66], the authors proposed the adaptive optimization of fuzzy membership functions and fuzzy rules for controllers used in hybrid electric vehicles.
In [67], a self-organizing interval type-2 fuzzy neural network was employed to a motion control system. The use of a fuzzy network allowed for the suppression of disturbances in the data, including those caused by base vibrations.
In [68], the authors developed a deep neural network incorporating fuzzy wavelets to forecast energy consumption patterns in urban buildings.
In [69], gated recurrent fuzzy neural networks were employed in micro gyroscopes characterized by high data uncertainties. The proposed solution enabled the elimination of disturbances and provided data without delays.
In [70], a fuzzy neural network was also used in gyroscopes. However, in this solution, a network architecture with feedback connections was employed. This approach addressed scenarios where lumped parameter uncertainties were unmeasurable, and system parameters were unknown.
In [71], the authors introduced a hesitant fuzzy graph neural network model. This model was used for text classification tasks because it enabled the analysis of relationships between samples.
In [72], a fuzzy neural network architecture was utilized to design a reliable voltage controller for buck DC/DC converters. This model approximated unknown nonlinear dynamics caused by variations in input voltage and load conditions. The network weights were updated in real time using an adaptive law, enhancing system robustness and its ability to handle uncertainties.
In [73] a neuro-fuzzy model was adjusted using the Artificial Bee Colony algorithm for predicting results of consulting services in construction.
2.3. Papers Summary
The aims of using fuzzy neural networks are summarized in Table 1. As observed, fuzzy neural networks are primarily utilized for image recognition, data prediction, and control systems. Table 2 presents the correlations between the types of networks used and their respective aims. It is evident that the self-organizing networks are the more flexible solutions. However, these solutions require the definition of rules and membership functions.

Table 1.
The aim of using fuzzy neural network.

Table 2.
Type of fuzzy neural network used.
As can be noticed, the fuzzy network solutions are widely used for systems control, data prediction, and image recognition/clustering. The author is still working on their own solutions.
FALCON and ANFIS networks are widely known. One fuzzy network solution is the application of Ordered Fuzzy Numbers to represent the weights of neurons.
This review aims to compare fuzzy network solutions:
- (a) Widely described in the literature in terms of potential usage;
- (b) With available code implemented in the network or its description.
The comparison of fuzzy networks in this publication aims to:
- (a) Demonstrate the feasibility of using these networks in terms of their simplicity compared to available neural network solutions in well-known frameworks;
- (b) Evaluate the results obtained by these networks using a well-known dataset in comparison to established solutions.
The next chapter presents selected fuzzy networks.
3. The Selected Fuzzy Networks
3.1. Fuzzy Network FALCON
Lin and Lee proposed the FALCON fuzzy network [76]. In this network architecture, two sets of parameters are important: the assignment function and the rule parameters (or weights). Learning the network involves modifying just these two sets of parameters. In the learning process, the rule parameters (or weights) are modified first, while the parameters of the membership function remain constant. Then the parameters of just the assignment function are updated with a gradient of decline, while the rule parameters remain at the values set in the earlier step. Unfortunately, this two-step learning process may not give satisfactory results for a specific group of problems, because the learning algorithm assumes that the two mentioned parameter sets are almost independent. However, it turns out that usually, the two sets are strongly dependent on each other [76,77,78]. The network architecture is shown in Figure 1. The input layer accepts input data that is processed by the system; it is responsible for data fuzzing. The task of the second layer is to calculate the IF degree of the fuzzy inference, while in layer four, the THEN part is processed. The third layer corresponds to the inference rules. Layer five is responsible for sharpening the result.
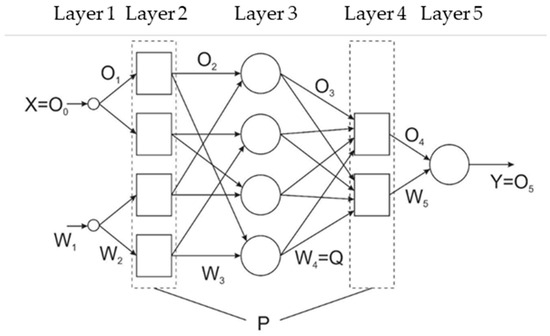
Figure 1.
FALCON network architecture.
In this network architecture, the rules are represented through the matrix of combinations of the relevant weights, which are called rule parameters and denoted by Q: the assignment function defined by Gaussian distribution and its parameters (standard deviation and average value) and appropriate to the defined function of the values of the inputs and outputs stored in the matrix P. The task of the network is to calculate the mapping F of the input vector X into the output vector Y, using P and Q:
Y = F (X, P, Q).
Suppose ui(j) represents the input of i to layer j, and oi(j) represents the output of i from layer j, then layer one transmits the inputs to the appropriate place in the network in order to obtain a single entry point. Thus
In the second layer, the assignment function is calculated for each input using the parameters for the type of assignment function. When using a Gaussian function, the level of assignment is determined by the following parameters: the mean value mi and the variance σi2
It is not necessary to choose a distribution in the form of a Gaussian function, as other functions can also be used; however, it is necessary to use a finite number of parameters.
Taking Oi and Wi as the output vector and weighting connection matrix w for layer i, respectively, the output value can be calculated as follows:
wherein
Further, assuming:
a single output from layer three can be determined by:
where is a nonlinear function defining the fuzzing of the input space. According to the adopted assumptions, W4 is responsible for the rule parameters defined by the matrix Q; then, we get:
Based on the specified formulas, the outputs can be calculated as follows:
where
where and are defined matrices on including standard deviations and average assignments and represents the column and matrix and .
In the learning process, the parameters of the matrix Q are optimized. The optimization is typically performed using gradient descent or another numerical method. No prepared FALCON network code was found in online resources.
3.2. ANFIS Fuzzy Network
ANFIS [79] Adaptive Neuro-Fuzzy Interface System is a fuzzy neural inference system. It uses the following assumptions in its operation:
- the vector xp is mapped to the scalar yp according to the following formula:
- The entrance space is divided into K subspaces;
- Sugeno’s fuzzy inference rule is used;
- To calculate the weights, the product rule is used;
- A weighted average of the individual rules is used to calculate the output value;
- A hybrid method is used for learning.
The input space is partitioned to determine the individual zones for which fuzzy inference rules are defined.
The Sugeno inference model mentioned above works according to the following rule:
Which, in vector notation, can be written as follows
where is a non-fuzzy function. It means that the input variable x must satisfy specific conditions defined by the fuzzy set A and once these conditions are met, the output is calculated using function , linking the inputs to the output through a deterministic relationship.
In the classical approach, the most common form of the function f(x) is a first-order polynomial:
in which the coefficients , are numerical weights that are selected during the learning process.
In this case, the assumption is made that the function f(x) is a zero-order polynomial:
The wk weights are calculated based on the product rule, which corresponds to the division of the input space:
According to assumptions, the output of the system is determined by a weighted average formula of the individual rules. After assigning the appropriate weighting wk for each rule, an output signal is then obtained according to the following formula:
Parameters for ANFIS are calculated using a hybrid learning approach. It operates in such a way that the parameters of the conclusion are calculated ‘forward’ using the least squares method, while the parameters of the premise (assignment function) are calculated ‘backward’ using the backward error propagation method. Figure 2 shows a scheme of ANFIS for an equal division of the two-dimensional entrance space.
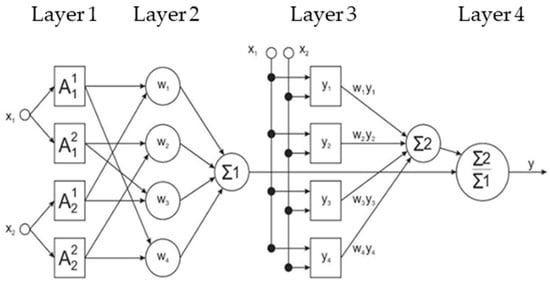
Figure 2.
The scheme of fuzzy ANFIS with rectangular division of the two-dimensional input space [79].
Several implementations of ANFIS networks can be found online, including a solution with ready-to-use code for recognizing the Iris dataset. ANFIS network code is available in both R and Python (version 3.11.13). On GitHub, there is a solution [80] that implements Iris dataset recognition. The use of ANFIS networks differs from deep networks in only one aspect of the code: the definition of membership functions. In the code, this appears as follows: make_gauss_mfs(1, [−5, 0.08, 1.67]), setting a Gaussian-type function with parameters that may vary depending on the analyzed example. This requires some expert knowledge from the network researcher. Figure 3 presents an example distribution of membership functions observed during the conducted studies. The plot shows the membership functions for an input variable in an Adaptive Neuro-Fuzzy Inference System (ANFIS) applied to classify flowers based on the Iris dataset. The horizontal axis represents the values of the input variable (e.g., sepal length, sepal width, petal length, or petal width), while the vertical axis represents the membership levels, indicating the degree of activation of fuzzy rules for a given input value. The membership functions (mf0, mf1, mf2) correspond to Gaussian-shaped distributions, each representing a different class of flowers in the Iris dataset: Setosa, Versicolor, and Virginica. The Gaussian shapes provide smooth transitions between the classes, a characteristic feature of fuzzy logic systems. For smaller input values, mf0 dominates, while mf1 and mf2 take over as the input values increase. This structure reflects how the network maps the input features to specific classes. The overlap between the membership functions in the middle range (e.g., around 5.5) illustrates the fuzzy nature of the classification, where more than one rule can be activated simultaneously. The final classification result is determined by a weighted combination of these activated rules. The parameters of the Gaussian functions (mean and standard deviation) are adjusted during the training process to optimize the system’s performance and improve classification accuracy. In the presented example of the Iris dataset, these membership functions demonstrate ANFIS’s ability to distinguish between different classes of flowers based on the input features. The smooth transitions between the functions allow the model to handle uncertainties and borderline cases effectively, ensuring accurate classification of the samples into the correct flower classes.
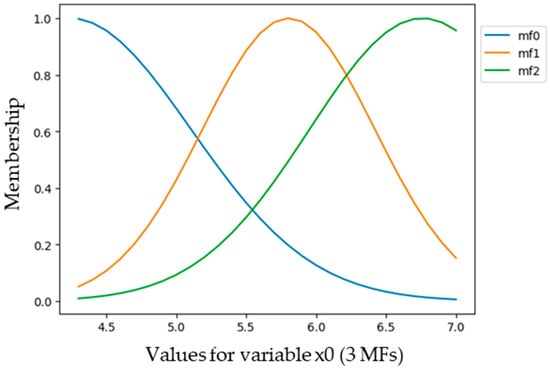
Figure 3.
Membership function during tests.
3.3. Fuzzy Network with the Application of Ordered Fuzzy Numbers
The first implementation of a fuzzy network with the application of fuzzy neural networks worked by using fuzzy data as input and returned a result in the form of a fuzzy number [74]. This implementation is fraught with the problem of entering data only as singletons. As all calculations took place in the fuzzy number domain, according to directed fuzzy number arithmetic, a very high speed and quality of network performance was achieved; however, according to OFN arithmetic, no merging of fuzzy number components took place. Therefore, in the study carried out using a known dataset representing Iris flower types [81], the dataset had to be limited to two classes. Only then was it possible to compare the network with the deep network. For the test, the collection was limited to two classes: Setosa and Veriscolour. The disadvantage of this network is that the network cannot be freely scaled, and the application is limited to only two-element data classification. The network code was not presented in publication [74]; it is the property of the project funder. However, it was prepared in R, and as mentioned, scaling the solution is problematic, but the gradient back propagation algorithm was used in the learning process.
3.4. Scaled Deep Fuzzy Network with the Application of Ordered Fuzzy Numbes
To construct a deep fuzzy neural network, a modification of the McCulloch–Pitts neuron model has been proposed. However, instead of using traditional numerical values, the inputs, weights, and outputs are represented using Ordered Fuzzy Number (OFN) notation [75]. These neurons are then assembled into a network composed of deep, fully connected layers. The OFN notation allows for expressing uncertainty and imprecision in numerical data. Arithmetic operations with OFNs are carried out through two main steps:
Step 1: The process begins by multiplying each input value X by its associated weight W, followed by summing all the resulting products to calculate a final value S.
Step 2: Then the output Y using OFN arithmetic is calculated:
The elements within sets S, W, X, and Y are expressed as values using OFN notation. Equations (18) and (19) correspond to those in the McCulloch–Pitts neuron model, but here the variables are represented with OFN notation. Initially, the inputs are multiplied by their respective weights, followed by the calculation of an activation function.
This approach requires implementing multiple layers:
- The first layer performs fuzzification to convert the input data into OFN notation,
- The final layer carries out defuzzification to process the network’s output data,
- Intermediate (deep) layers adapt the network’s learning and training algorithms to effectively work with OFN arithmetic within the network.
The operational structure of the proposed deep network is shown in Figure 4.
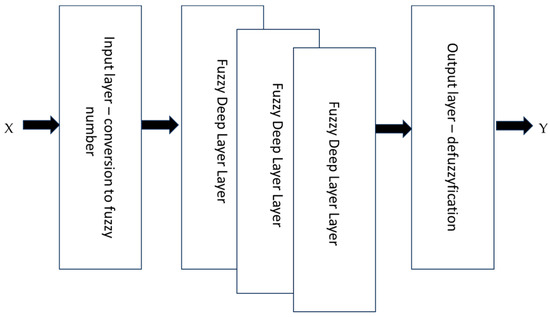
Figure 4.
Proposed scaled fuzzy neural network with Ordered Fuzzy Numbers.
A network based on these principles, incorporating a fuzzy learning algorithm, was created and tested. The implementation was performed using the Python programming language.
This approach enables flexible scaling of the network and does not limit the format of input or output data, allowing the network to be tested on the complete Iris dataset. The example code for defining the network does not differ from the definition of deep networks in frameworks familiar to researchers:
networkCSVs = OFNNeuralNetwork()
networkCSVs.add_layer(Dense(4,2))
networkCSVs.add_layer(Tanh())
networkCSVs.add_layer(Dense(2,1))
networkCSVs.add_layer(Tanh())
The definition of the network requires specifying the layers along with the number of neurons, while the prepared network training function takes parameters in the form of the number of epochs and learning_rate.
4. Methodology
In the study, it was decided to verify the following fuzzy networks for which the author had access to their code:
- ANFIS network according to the implementation available on github [36];
- FNN—Fuzzy network with application Ordered Fuzzy Numbers [33];
- SFNN—scalable deep fuzzy neural network using OFN notation [35].
To compare solutions, the Iris set was also classified using the following algorithms:
- KNeighborsClassifier;
- Decision Tree Classifier;
- Random Forest Classifier.
The Iris dataset is a well-known and widely used collection in machine learning and pattern recognition. It consists of 150 instances (samples) of iris flowers, evenly divided among three species: Iris setosa, Iris versicolor, and Iris virginica, each with 50 samples. Each sample in the dataset includes four numerical features (measured in centimeters): the length and width of the sepal and petal.
The dataset is commonly used for:
- Classification algorithms (e.g., Decision Trees, SVM, Neural Networks).
- Supervised learning experiments,
- Feature selection and dimensionality reduction.
Prior to training, the data were scaled individually for each feature to the range [0, 1] using min–max scaling. The dataset was then split into a training set (80%) and a test set (20%), maintaining proportional class distribution through stratified sampling.
The learning of the network and algorithms was then performed. Finally, the entire dataset was tested. For the fuzzification process, the data were transformed into singleton representations of Ordered Fuzzy Number.
5. Results
The study achieved the following results (presented in Table 3):

Table 3.
Test results for Iris dataset classification.
- The ANFIS network—As a result of learning for 240 epochs, this network was able to recognize 125 out of 150 samples correctly, giving 83.33% correct solutions for full dataset and 100% when dataset the was limited to two classes: Setosa and Veriscolour;
- Fuzzy network with the application of Ordered Fuzzy Numbers (FNN) [74]—For this network, it was necessary to limit the set to two classes: Setosa, Veriscolour. The network had an input layer of four neurons, a deep layer of one neuron, and an output layer of two neurons. After 550 learning epochs it was able to recognize 99.97% of the flowers;
- Scalable deep fuzzy neural network using OFN (SFNN) [75]—The network had an input layer of four neurons, a deep layer of two neurons, and an output layer of one neuron, and after 5000 learning epochs, with learning rate 0.002, the network was able to recognize 83.33% of the flowers for the full dataset and 100% when the dataset was limited to two classes: Setosa and Veriscolour,
- KNeighborsClassifier (KNN) was implemented in TensorFlow library for the following parameters: n_neighbors = 100, weights = ‘distance’. The network was able to recognize 93.33% of flowers for full dataset and 100% when the dataset was limited to two classes: Setosa and Veriscolour,
- Decision Tree Classifier (DTC) was implemented in TensorFlow library for the following parameters: criterion = ‘entropy’, max_depth = 30, min_samples_split = 2. The network was able to recognize 96.67% of flowers correctly for the full dataset and 100% when the dataset was limited to two classes: Setosa and Veriscolour,
- Random Forest Classifier (RFC) was implemented in the TensorFlow library. The network was able to recognize 96.67% of the flowers correctly for the full dataset and 100% when the dataset was limited to two classes: Setosa and Veriscolour.
Table 4 presents a comparison of the networks based on the number of neurons and epochs used during training. It is evident that networks utilizing OFNs are smaller and require less computing power during operation. However, their learning process requires more epochs.

Table 4.
Neuron and epoch numbers for the used networks.
Table 5 presents the results of the ANFIS network and SFNN for the full Iris dataset recognition. Figure 5 and Figure 6 present the ROC curve for this network. The confusion matrix summarizes the performance of a classification model by showing the number of correct and incorrect predictions for each class. It includes values like true positives (correctly predicted positive samples), true negatives (correctly predicted negative samples), false positives (negative samples incorrectly classified as positive), and false negatives (positive samples incorrectly classified as negative). From this, various performance metrics can be derived. Accuracy measures the overall correctness of the model by calculating the proportion of correctly classified samples out of all predictions. Precision focuses on the quality of positive predictions, indicating the proportion of correctly identified positive samples among all samples predicted as positive. Recall, also known as sensitivity, measures how well the model identifies actual positive samples, representing the proportion of true positives out of all actual positive cases. The F1-score is a balanced measure that combines precision and recall into a single metric, offering a harmonic mean that is particularly useful for imbalanced datasets, where the distribution of classes is unequal.

Table 5.
ANFIS and SFNN results of full Iris dataset recognition.
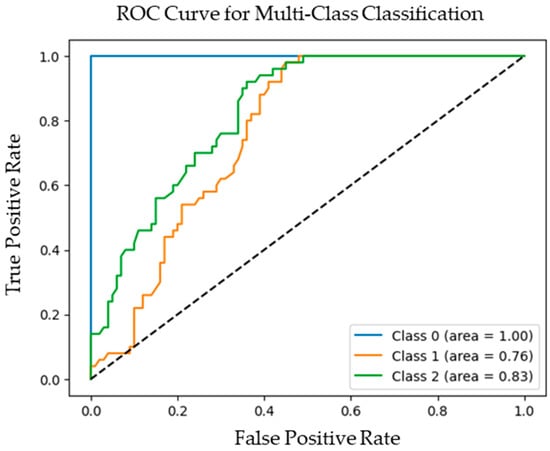
Figure 5.
ROC curve for ANFIS network during the test.
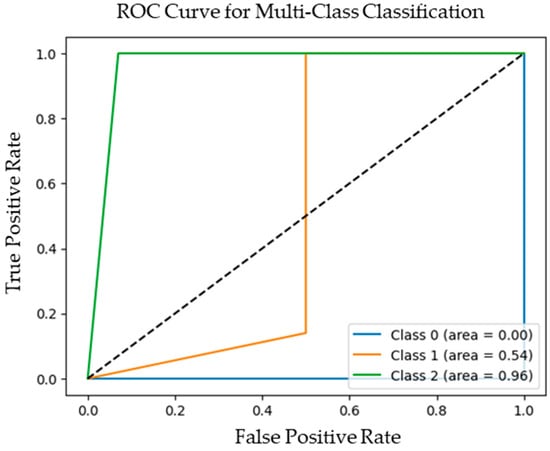
Figure 6.
ROC curve for SFNN network during the test.
6. Discussion
The author of the publication has reviewed fuzzy network solutions, considering those solutions whose code is obtainable. In addition, the solutions were compared with publicly available algorithms. The biggest challenge is to get the ANFIS network up and running correctly, and selecting its parameters—the membership function. This process is not an easy one compared to the use of deep networks, and the selection of parameters requires expert knowledge. It is worth noting that in the first network using OFNs, it was not possible to recognize the entire Iris set. Only the implementation of a fully scaled network, with the sharpening of the result, allowed, according to OFN arithmetic, the use of any input dataset. An interesting result is that for both the ANFIS network and the scaled fuzzy deep network with OFN, the level of correctly recognized flowers was 83.33%. The author of the publication did not carry out any additional optimization. The ANFIS network algorithm was the same as the one that can be downloaded from the github portal. Further optimization of the network parameters is possible. However, comparing the solution with the KNN, Decision Tree Classifier, and Random Foert Classifier algorithms, it seems that this work is pointless. These algorithms achieved significantly better results without any special parametrization.
Table 6 presents information on the ease-of-use of fuzzy neural networks. Unfortunately, using the ANFIS network without knowledge of fuzzy logic concepts appears to be difficult. It requires defining membership functions, which complicates its application. The FNN network cannot be used for classifying datasets with more than two elements, making it impractical for real-world applications. In contrast, the SFNN network does not require expert knowledge of fuzzy logic, and its definition and training process do not differ significantly from those of deep networks.

Table 6.
Fuzzy neural network usability.
7. Conclusions
As can be noticed, the fuzzy network solutions are widely used for systems control, data prediction, and image recognition/clustering. The author is still working on their own solutions, as this topic is very interesting, because new methods are continuously developed that could be used for different purposes.
The implementations of fuzzy networks are different; e.g., the ANFIS network in the practical application requires selecting the membership function, which is a difficult task, while another solution, the fuzzy network with Ordered Fuzzy Numbers, does not vary from the use of deep networks. In this case there is no necessity for the selection of an assignment function, which makes the usage much easier.
The fuzzy networks could be used in many situations and for many purposes. As can be noticed, there should be no restriction if we choose the appropriate solutions. Some implementation could be limited, e.g., for only two-way classification, but others not. The other limitation is the learning process. The SFNN required 5000 epochs, while ANFIS only required 240. This means that the learning process for the ANFIS network was much faster than SFNN in this experiment.
The fuzzy neural networks could be an interesting choice for many purposes. The author reviewed over 80 papers from 2020 to 2025 describing real applications, and noticed that only few solutions are presented with their whole code for future use. So, the future directions for research should ensure that the authors should provide more information for future implementation of proposed solutions or better open-source code as an appendix.
The future direction on fuzzy networks should be a connection between them and other methods and algorithms. As can be noticed, some authors connect ANFIS with the Swarm Intelligence. There are some works on SFNN optimization for GPU usage, also a graph neural network or meta-learning should be met in the near future. The author is aware that the presented fuzzy networks require further research, including studies on issues related to the analysis of topics such as time series, fuzzy identification of nonlinear dynamic systems, and controller tuning. Currently, research is being conducted on a system for anomaly prediction in time series and a fuzzy controller for heating control. Preliminary results are very promising.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available in a publicly accessible repository.
Conflicts of Interest
The author declare no conflict of interest.
References
- Lee, S.C.; Lee, E.T. Fuzzy Neural Networks. Math. Biosci. 1975, 23, 151–177. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Kwon, K.; Tanaka, H. A learning algorithm of fuzzy neural networks with triangular fuzzy weights. Fuzzy Sets Syst. 1995, 71, 277–293. [Google Scholar] [CrossRef]
- Buckley, J.J.; Hayashi, Y. Fuzzy neural networks: A survey. Fuzzy Sets Syst. 1994, 66, 1–13. [Google Scholar] [CrossRef]
- de Campos Souza, P.V.; Lughofer, E. EFNN-NullUni: An evolving fuzzy neural network based on null-uninorm. Fuzzy Sets Syst. 2022, 449, 1–31. [Google Scholar] [CrossRef]
- Yadav, P.K.; Bhasker, R.; Upadhyay, S.K. Comparative study of ANFIS fuzzy logic and neural network scheduling based load frequency control for two-area hydro thermal system. Mater. Today Proc. 2022, 56, 3042–3050. [Google Scholar] [CrossRef]
- Khan, S.; Asim, M.; Khan, S.; Musyafa, A.; Wu, Q. Unsupervised domain adaptation using fuzzy rules and stochastic hierarchical convolutional neural networks. Comput. Electr. Eng. 2023, 105, 108547. [Google Scholar] [CrossRef]
- Wang, Y.; Ishibuchi, H.; Er, M.J.; Zhu, J. Unsupervised multilayer fuzzy neural networks for image clustering. Inf. Sci. 2023, 622, 682–709. [Google Scholar] [CrossRef]
- Wang, C.; Lv, X.; Shao, M.; Qian, Y.; Zhang, Y. A novel fuzzy hierarchical fusion attention convolution neural network for medical image super-resolution reconstruction. Inf. Sci. 2023, 622, 424–436. [Google Scholar] [CrossRef]
- Jabeur, S.B.; Serret, V. Bankruptcy prediction using fuzzy convolutional neural networks. Res. Int. Bus. Financ. 2023, 64, 101844. [Google Scholar] [CrossRef]
- Wu, Z.; Jiang, B.; Gao, Q. State estimation and fuzzy sliding mode control of nonlinear Markovian jump systems via adaptive neural network. J. Frankl. Inst. 2022, 359, 8974–8990. [Google Scholar] [CrossRef]
- Pham, P.; Nguyen, L.T.T.; Nguyen, N.T.; Kozma, R.; Vo, B. A hierarchical fused fuzzy deep neural network with heterogeneous network embedding for recommendation. Inf. Sci. 2023, 620, 105–124. [Google Scholar] [CrossRef]
- Liu, J.; Shu, L.; Chen, Q.; Zhong, S. Fixed-time synchronization criteria of fuzzy inertial neural networks via Lyapunov functions with indefinite derivatives and its application to image encryption. Fuzzy Sets Syst. 2022, 459, 22–42. [Google Scholar] [CrossRef]
- Gong, S.; Guo, Z.; Wen, S. Finite-time synchronization of T-S fuzzy memristive neural networks with time delay. Fuzzy Sets Syst. 2022, 459, 67–81. [Google Scholar] [CrossRef]
- Lai, X.; Tong, S.; Zhu, G. Adaptive fuzzy neural network-aided progressive Gaussian approximate filter for GPS/INS integration navigation. Measurement 2022, 200, 111641. [Google Scholar] [CrossRef]
- Koo, Y.D.; Jo, H.S.; Na, M.G.; Yoo, K.H.; Kim, C.-H. Prediction of the internal states of a nuclear power plant containment in LOCAs using rule-dropout deep fuzzy neural networks. Ann. Nucl. Energy 2021, 156, 108180. [Google Scholar] [CrossRef]
- Huang, W.; Oh, S.-K.; Pedrycz, W. Fuzzy reinforced polynomial neural networks constructed with the aid of PNN architecture and fuzzy hybrid predictor based on nonlinear function. Neurocomputing 2021, 458, 454–467. [Google Scholar] [CrossRef]
- de Campos Souza, P.V.; Lughofer, E.; Guimaraes, A.J. An interpretable evolving fuzzy neural network based on self-organized direction-aware data partitioning and fuzzy logic neurons. Appl. Soft Comput. 2021, 112, 107829. [Google Scholar] [CrossRef]
- Nasiri, H.; Ebadzadeh, M.M. MFRFNN: Multi-Functional Recurrent Fuzzy Neural Network for Chaotic Time Series Prediction. Neurocomputing 2022, 507, 292–310. [Google Scholar] [CrossRef]
- Dong, L.; Jiang, F.; Wang, M.; Li, X. Fuzzy deep wavelet neural network with hybrid learning algorithm: Application to electrical resistivity imaging inversion. Knowl.-Based Syst. 2022, 242, 108164. [Google Scholar] [CrossRef]
- Kuo, R.J.; Zulvia, F.E. The application of gradient evolution algorithm to an intuitionistic fuzzy neural network for forecasting medical cost of acute hepatitis treatment in Taiwan. Appl. Soft Comput. 2021, 111, 107711. [Google Scholar] [CrossRef]
- Kadak, U. Multivariate fuzzy neural network interpolation operators and applications to image processing. Expert Syst. Appl. 2022, 206, 117771. [Google Scholar] [CrossRef]
- Kong, Y.; Chen, S.; Jiang, Y.; Wang, H.; Chen, H. Zeroing neural network with fuzzy parameter for cooperative manner of multiple redundant manipulators. Expert Syst. Appl. 2023, 212, 118735. [Google Scholar] [CrossRef]
- Li, J.; Ma, C.; Jiang, Y. Fuzzy Neural Network PID-Based Constant Deceleration Control for Automated Mine Electric Vehicles Using EMB System. Sensors 2024, 24, 2129. [Google Scholar] [CrossRef] [PubMed]
- Pham, D.H.; Vu, M.T. Takagi–Sugeno–Kang Fuzzy Neural Network for Nonlinear Chaotic Systems and Its Utilization in Secure Medical Image Encryption. Mathematics 2025, 13, 923. [Google Scholar] [CrossRef]
- Zhou, H.; Huang, Y.; Yang, D.; Chen, L.; Wang, L. Semi-Supervised Soft Computing for Ammonia Nitrogen Using a Self-Constructing Fuzzy Neural Network with an Active Learning Mechanism. Water 2024, 16, 3001. [Google Scholar] [CrossRef]
- Kontogiannis, S.; Koundouras, S.; Pikridas, C. Proposed Fuzzy-Stranded-Neural Network Model That Utilizes IoT Plant-Level Sensory Monitoring and Distributed Services for the Early Detection of Downy Mildew in Viticulture. Computers 2024, 13, 63. [Google Scholar] [CrossRef]
- Ngcukayitobi, M.; Tartibu, L.K.; Bannwart, F. Enhancing Thermo-Acoustic Waste Heat Recovery through Machine Learning: A Comparative Analysis of Artificial Neural Network–Particle Swarm Optimization, Adaptive Neuro Fuzzy Inference System, and Artificial Neural Network Models. AI 2024, 5, 237–258. [Google Scholar] [CrossRef]
- Al-Qaysi, A.M.M.; Bozkurt, A.; Ates, Y. Load Forecasting Based on Genetic Algorithm–Artificial Neural Network-Adaptive Neuro-Fuzzy Inference Systems: A Case Study in Iraq. Energies 2023, 16, 2919. [Google Scholar] [CrossRef]
- Bosna, J. Examining regional economic differences in Europe: The power of ANFIS analysis. J. Decis. Anal. Intell. Comput. 2025, 5, 1–13. [Google Scholar] [CrossRef]
- Yazdi, A.K.; Komasi, H. Best Practice Performance of COVID-19 in America continent with Artificial Intelligence. Spectr. Oper. Res. 2024, 1, 1–12. [Google Scholar] [CrossRef]
- El Moutaouakil, K.; Roudani, M.; Ouhmid, A.; Zhilenkov, A.; Mobayen, S. Decomposition and Symmetric Kernel Deep Neural Network Fuzzy Support Vector Machine. Symmetry 2024, 16, 1585. [Google Scholar] [CrossRef]
- Lin, C.-J.; Chen, B.-H.; Lin, C.-H.; Jhang, J.-Y. Design of a Convolutional Neural Network with Type-2 Fuzzy-Based Pooling for Vehicle Recognition. Mathematics 2024, 12, 3885. [Google Scholar] [CrossRef]
- Yu, H.-C.; Wang, Q.-A.; Li, S.-J. Fuzzy Logic Control with Long Short-Term Memory Neural Network for Hydrogen Production Thermal Control System. Appl. Sci. 2024, 14, 8899. [Google Scholar] [CrossRef]
- Chai, S.H.; Lim, J.S.; Yoon, H.; Wang, B. A Novel Methodology for Forecasting Business Cycles Using ARIMA and Neural Network with Weighted Fuzzy Membership Functions. Axioms 2024, 13, 56. [Google Scholar] [CrossRef]
- Xu, Y.; Li, H.; Yang, J.; Zhang, L. Quasi-Projective Synchronization of Discrete-Time Fractional-Order Complex-Valued BAM Fuzzy Neural Networks via Quantized Control. Fractal Fract. 2024, 8, 263. [Google Scholar] [CrossRef]
- Algehyne, E.A.; Jibril, M.L.; Algehainy, N.A.; Alamri, O.A.; Alzahrani, A.K. Fuzzy Neural Network Expert System with an Improved Gini Index Random Forest-Based Feature Importance Measure Algorithm for Early Diagnosis of Breast Cancer in Saudi Arabia. Big Data Cogn. Comput. 2022, 6, 13. [Google Scholar] [CrossRef]
- Rao, J.; Li, B.; Zhang, Z.; Chen, D.; Giernacki, W. Position Control of Quadrotor UAV Based on Cascade Fuzzy Neural Network. Energies 2022, 15, 1763. [Google Scholar] [CrossRef]
- Yang, R.; Gao, Y.; Wang, H.; Ni, X. Fuzzy Neural Network PID Control Used in Individual Blade Control. Aerospace 2023, 10, 623. [Google Scholar] [CrossRef]
- Zhou, R.; Zhang, L.; Fu, C.; Wang, H.; Meng, Z.; Du, C.; Shan, Y.; Bu, H. Fuzzy Neural Network PID Strategy Based on PSO Optimization for pH Control of Water and Fertilizer Integration. Appl. Sci. 2022, 12, 7383. [Google Scholar] [CrossRef]
- Yin, H.; Yi, W.; Wu, J.; Wang, K.; Guan, J. Adaptive Fuzzy Neural Network PID Algorithm for BLDCM Speed Control System. Mathematics 2022, 10, 118. [Google Scholar] [CrossRef]
- Li, M.; Li, J.; Li, G.; Xu, J. Analysis of Active Suspension Control Based on Improved Fuzzy Neural Network PID. World Electr. Veh. J. 2022, 13, 226. [Google Scholar] [CrossRef]
- Lin, F.-J.; Huang, M.-S.; Chien, Y.-C.; Chen, S.-G. Intelligent Backstepping Control of Permanent Magnet-Assisted Synchronous Reluctance Motor Position Servo Drive with Recurrent Wavelet Fuzzy Neural Network. Energies 2023, 16, 5389. [Google Scholar] [CrossRef]
- Liu, S.-H.; Wang, J.-J.; Chen, W.; Pan, K.-L.; Su, C.-H. Classification of Photoplethysmographic Signal Quality with Fuzzy Neural Network for Improvement of Stroke Volume Measurement. Appl. Sci. 2020, 10, 1476. [Google Scholar] [CrossRef]
- de Campos Souza, P.V.; Lughofer, E.; Rodrigues Batista, H. An Explainable Evolving Fuzzy Neural Network to Predict the k Barriers for Intrusion Detection Using a Wireless Sensor Network. Sensors 2022, 22, 5446. [Google Scholar] [CrossRef]
- Zhao, T.; Qin, P.; Zhong, Y. Trajectory Tracking Control Method for Omnidirectional Mobile Robot Based on Self-Organizing Fuzzy Neural Network and Preview Strategy. Entropy 2023, 25, 248. [Google Scholar] [CrossRef]
- Qin, P.; Zhao, T.; Liu, N.; Mei, Z.; Yan, W. Predefined-Time Fuzzy Neural Network Control for Omnidirectional Mobile Robot. Processes 2023, 11, 23. [Google Scholar] [CrossRef]
- Chen, C.-S.; Hu, N.-T. Model Reference Adaptive Control and Fuzzy Neural Network Synchronous Motion Compensator for Gantry Robots. Energies 2022, 15, 123. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, X.; Wang, H.; Cao, L.; Xing, Z.; Yang, Z. Rotor Fault Diagnosis Method Based on VMD Symmetrical Polar Image and Fuzzy Neural Network. Appl. Sci. 2023, 13, 1134. [Google Scholar] [CrossRef]
- Liu, L.; Fei, J.; Yang, X. Adaptive Interval Type-2 Fuzzy Neural Network Sliding Mode Control of Nonlinear Systems Using Improved Extended State Observer. Mathematics 2023, 11, 605. [Google Scholar] [CrossRef]
- Lin, C.-J.; Jeng, S.-Y.; Lin, H.-Y.; Yu, C.-Y. Design and Verification of an Interval Type-2 Fuzzy Neural Network Based on Improved Particle Swarm Optimization. Appl. Sci. 2020, 10, 3041. [Google Scholar] [CrossRef]
- Lin, C.-J.; Lin, C.-J.; Lin, X.-Q. Automatic Sleep Stage Classification Using a Taguchi-Based Multiscale Convolutional Compensatory Fuzzy Neural Network. Appl. Sci. 2023, 13, 10442. [Google Scholar] [CrossRef]
- Wang, C.; Wang, X.; Wu, D.; Kuang, M.; Li, Z. Meticulous Land Cover Classification of High-Resolution Images Based on Interval Type-2 Fuzzy Neural Network with Gaussian Regression Model. Remote Sens. 2022, 14, 3704. [Google Scholar] [CrossRef]
- An, J.; Zhao, J.; Liu, Q.; Qian, X.; Chen, J. Self-Constructed Deep Fuzzy Neural Network for Traffic Flow Prediction. Electronics 2023, 12, 1885. [Google Scholar] [CrossRef]
- Janarthanan, R.; Maheshwari, R.U.; Shukla, P.K.; Shukla, P.K.; Mirjalili, S.; Kumar, M. Intelligent Detection of the PV Faults Based on Artificial Neural Network and Type 2 Fuzzy Systems. Energies 2021, 14, 6584. [Google Scholar] [CrossRef]
- de Campos Souza, P.V.; Lughofer, E. Identification of Heart Sounds with an Interpretable Evolving Fuzzy Neural Network. Sensors 2020, 20, 6477. [Google Scholar] [CrossRef]
- Pan, Q.; Zhou, Y.; Fei, J. Feature Selection Fuzzy Neural Network Super-Twisting Harmonic Control. Mathematics 2023, 11, 1495. [Google Scholar] [CrossRef]
- Lin, C.-J.; Lin, C.-H.; Lin, F. Bearing Fault Diagnosis Using a Vector-Based Convolutional Fuzzy Neural Network. Appl. Sci. 2023, 13, 3337. [Google Scholar] [CrossRef]
- Lu, H.; Bao, J. Spatial Differentiation Effect of Rural Logistics in Urban Agglomerations in China Based on the Fuzzy Neural Network. Sustainability 2022, 14, 9268. [Google Scholar] [CrossRef]
- Shao, K.-Y.; Feng, A.; Wang, T.-T. Fixed-Time Sliding Mode Synchronization of Uncertain Fractional-Order Hyperchaotic Systems by Using a Novel Non-Singleton-Interval Type-2 Probabilistic Fuzzy Neural Network. Fractal Fract. 2023, 7, 247. [Google Scholar] [CrossRef]
- Wang, J.; Fang, Y.; Fei, J. Adaptive Super-Twisting Sliding Mode Control of Active Power Filter Using Interval Type-2-Fuzzy Neural Networks. Mathematics 2023, 11, 2785. [Google Scholar] [CrossRef]
- Chen, C.-I.; Lan, C.-K.; Chen, Y.-C.; Chen, C.-H.; Chang, Y.-R. Wavelet Energy Fuzzy Neural Network-Based Fault Protection System for Microgrid. Energies 2020, 13, 1007. [Google Scholar] [CrossRef]
- Gao, H.; Zang, B.; Sun, L.; Chen, L. Evaluation of Electric Vehicle Integrated Charging Safety State Based on Fuzzy Neural Network. Appl. Sci. 2022, 12, 461. [Google Scholar] [CrossRef]
- Ye, W.; Song, W.; Cui, C.-F.; Wen, J.-H. Water Quality Evaluation Method Based on a T-S Fuzzy Neural Network—Application in Water Environment Trend Analysis of Taihu Lake Basin. Water 2021, 13, 3127. [Google Scholar] [CrossRef]
- Chen, C.-I.; Chen, Y.-C.; Chen, C.-H. Recurrent Wavelet Fuzzy Neural Network-Based Reference Compensation Current Control Strategy for Shunt Active Power Filter. Energies 2022, 15, 8687. [Google Scholar] [CrossRef]
- Kalbhor, M.; Shinde, S.; Popescu, D.E.; Hemanth, D.J. Hybridization of Deep Learning Pre-Trained Models with Machine Learning Classifiers and Fuzzy Min–Max Neural Network for Cervical Cancer Diagnosis. Diagnostics 2023, 13, 1363. [Google Scholar] [CrossRef]
- Zhang, Q.; Fu, X. A Neural Network Fuzzy Energy Management Strategy for Hybrid Electric Vehicles Based on Driving Cycle Recognition. Appl. Sci. 2020, 10, 696. [Google Scholar] [CrossRef]
- Sun, Y.; Zhao, T.; Liu, N. Self-Organizing Interval Type-2 Fuzzy Neural Network Compensation Control Based on Real-Time Data Information Entropy and Its Application in n-DOF Manipulator. Entropy 2023, 25, 789. [Google Scholar] [CrossRef]
- Ahmadi, M.; Soofiabadi, M.; Nikpour, M.; Naderi, H.; Abdullah, L.; Arandian, B. Developing a Deep Neural Network with Fuzzy Wavelets and Integrating an Inline PSO to Predict Energy Consumption Patterns in Urban Buildings. Mathematics 2022, 10, 1270. [Google Scholar] [CrossRef]
- Xie, J.; Fei, J.; An, C. Gated Recurrent Fuzzy Neural Network Sliding Mode Control of a Micro Gyroscope. Mathematics 2023, 11, 509. [Google Scholar] [CrossRef]
- Fang, Y.; Chen, F.; Fei, J. Multiple Loop Fuzzy Neural Network Fractional Order Sliding Mode Control of Micro Gyroscope. Mathematics 2021, 9, 2124. [Google Scholar] [CrossRef]
- Guo, X.; Tian, B.; Tian, X. HFGNN-Proto: Hesitant Fuzzy Graph Neural Network-Based Prototypical Network for Few-Shot Text Classification. Electronics 2022, 11, 2423. [Google Scholar] [CrossRef]
- Babes, B.; Hamouda, N.; Albalawi, F.; Aissa, O.; Ghoneim, S.S.M.; Abdelwahab, S.A.M. Experimental Investigation of an Adaptive Fuzzy-Neural Fast Terminal Synergetic Controller for Buck DC/DC Converters. Sustainability 2022, 14, 7967. [Google Scholar] [CrossRef]
- Pamučar, D.; Bozanic, D.; Puška, A.; Marinković, D. Application of neuro-fuzzy system for predicting the success of a company in public procurement. Decis. Mak. Appl. Manag. Eng. 2022, 5, 135–153. [Google Scholar] [CrossRef]
- Apiecionek, Ł.; Moś, R.; Ewald, D. Fuzzy Neural Network with Ordered Fuzzy Numbers for Life Quality Technologies. Appl. Sci. 2023, 13, 3487. [Google Scholar] [CrossRef]
- Apiecionek, Ł. Fully Scalable Fuzzy Neural Network for Data Processing. Sensors 2024, 24, 5169. [Google Scholar] [CrossRef]
- Lin, C.T.; Lee, C.G. Neural-network-based fuzzy logic control and decision system. IEEE Trans. Comput. 1991, 40, 1320–1336. [Google Scholar] [CrossRef]
- Chow, M.Y. Methodologies of Using Artificial Neural Network and Fuzzy Logic Technologies for Motor Incipient Fault Detection; World Scientific: Singapore, 1997. [Google Scholar]
- Goode, P.; Chow, M.Y. Using a neural/fuzzy system to extract knowledge of incipient fault in induction motors part I—Methodology. IEEE Trans. Ind. Electron. 1995, 42, 131–138. [Google Scholar] [CrossRef]
- Jang, J.-S.; Sun, C.-T.; Mizutani, E. Neuro-Fuzzy and Soft Computing. A Computational Approach to Learning and Machine Intelligence; Prentice Hall Intern. Inc.: Upper Saddle River, NY, USA, 1997. [Google Scholar]
- Available online: https://github.com/jfpower/anfis-pytorch/blob/master/iris_example.py (accessed on 8 February 2025).
- Available online: http://archive.ics.uci.edu/ml/datasets/Iris (accessed on 4 November 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).